Тема: Энергия электрического поля

Ляпин Али Ибрагимович, доцент БРУ

1.

Энергия уединенного заряженного проводника

Wпр =

1

Cϕ

2

=

Q2

=

1

Q ϕ

2

2

C

2

1

n

и системы заряженных проводников

W =

∑Qi

ϕi

2

i=1

2.

Энергия заряженного конденсатора

Wк =

1

CU

2

=

Q2

=

1

Q U

2

2

C

2

3.

Энергия электростатического поля. Объемная

W

= w =

ε

0

ε E2

плотность энергии.

V

2

4.

Пондеромоторные силы. Применение закона

сохранения энергии к расчету пондеромоторных

сил.

2Ляпин Али Ибрагимович, доцент БРУ

1.Энергия уединенного заряженного проводника и системы проводников

При сообщении проводнику некоторого заряда вокруг него возникает электрическое поле. Чтобы сообщить проводнику следующую порцию заряда необходимо совершить работу против сил этого поля. Так как электростатическое поле потенциально, то совершаемая работа идет на увеличение потенциальной энергии проводника.

Рассмотрим уединенный проводник с емкостью С и потенциалом ϕ. При перенесении заряда dQ из бесконечности на поверхность проводника необходимо совершить работу dA против сил поля

dA = ϕ dQ . (1)

Обе величины в правой части формулы (1) являются переменными. Используя связь между величинами С, ϕ и Q приведем праву часть к одной переменной. Для этого выразим dQ через ϕ и подставим в формулу (1)

Q = C ϕ dQ = C dϕ dA = C ϕ dϕ . (2)

Чтобы найти работу по зарядке проводника от нулевого потенциала до некоторого потенциала ϕ проинтегрируем выражение (2)

	ϕ	1
	A = ∫C ϕ dϕ =		Cϕ2	.(3)
		2
	0

По определению эта работа равна изменению потенциальной энергии. Поэтому энергия уединенного проводника, заряженного до потенциала ϕ определяется формулой

Wпр = 12 Cϕ2 . (4)

Используя связь между величинами С, ϕ и Q формула (4) может быть представлена в нескольких видах

Wпр =	1	Cϕ	2	=	Q2	=	1	Q ϕ . (5)
	2				2 C		2

Применяя принцип суперпозиции электрических полей можно получить следующую формулу для энергии системы из n неподвижных заряженных проводников

W= 1 ∑n Qi ϕi , (6) 2 i=1

где ϕi – потенциал суммарного поля в той точке, где находится проводник с зарядом Qi.

2. Энергия заряженного конденсатора

Процесс зарядки конденсатора можно представить как последовательное перемещение малых порций dQ заряда с одной пластины (обкладки) на другую. Если первоначально пластины нейтральны, то перенос, например, положительного заряда с первой пластины на вторую приведет к возникновению отрицательного заряда на первой пластине. Следовательно, в результате таких переносов первая пластина будет заряжаться отрицательно, а вторая – положительно. Между пластинами возникнет постепенно

возрастающая разность потенциалов ϕ1–ϕ2=U. Вывод формулы для энергии заряженного

3	Ляпин Али Ибрагимович, доцент БРУ

конденсатора аналогичен приведенному выше выводу формулы (4). Отличие состоит в замене потенциала ϕ на разность потенциалов U

	A = U∫C U dU =	1	CU 2	. (7)
		2
	0

Таким образом, формула для энергии заряженного конденсатора имеет следующий

вид

Wк =	1	CU	2	=	Q2	=	1	Q U . (8)
	2				2 C		2

3. Энергия электростатического поля. Объемная плотность энергии.

При изучении поля неподвижных зарядов мы не можем рассматривать отдельно электрический заряд и созданное им электрическое поле. Поэтому, оставаясь в рамках электростатики, нельзя однозначно указать, является ли носителем электрической энергии электрический заряд либо электрическое поле. Изучение переменных электромагнитных полей показало, что они могут существовать отдельно от породивших их электрических зарядов и распространяться в пространстве в виде электромагнитных волн. Факт существования электромагнитных волн и переноса ими энергии позволяет утверждать, что энергия заряженных проводников сосредоточена в электрическом поле. Учитывая это, преобразуем формулу (7) для энергии заряженного конденсатора таким образом, чтобы в него входила характеристика поля – его напряженность. Для этого в (7) вместо емкости С

подставим выражение для емкости плоского конденсатора	C =	ε0 ε S	, а напряжение U
		d

заменим выражением U = E d . Тогда для энергии заряженного конденсатора получим

W =	ε	0	ε E2	S d . (9)
			2

Произведение S d в формуле (9) равно объему V, занимаемому электрическим полем. Поделив левую и правую части формулы (9) на объем V получим формулу для объемной

плотности энергии w (энергии, приходящейся на единицу объема)

	w =	ε0 ε E 2		или	w =	1	E D . (10)
			2			2
Учитывая связь	электрического		смещения		D с		поляризованностью Р диэлектрика
D = ε0 E + P ,	можно получить		другую формулу для объемной плотности энергии
электрического поля

w = 12 ε0 E 2 + 12 E P . (11)

Вформуле (11) первое слагаемое выражает плотность энергии электрического поля в вакууме, а второе слагаемое выражает энергию, затрачиваемую на поляризацию единицы объема диэлектрика.

Вобщем случае неоднородного электрического поля его энергию в некотором объеме V можно вычислить по формуле

		4	Ляпин Али Ибрагимович, доцент БРУ
W =	ε0	V∫ε E2 dV . (12)
	2	0

4. Пондеромоторные силы. Применение закона сохранения энергии к расчету пондеромоторных сил.

На всякое заряженное тело, помещенное в электрическое поле, действуют механическая сила. Пондеромоторными называются силы, действующие со стороны электрического поля на макроскопические заряженные тела.

Определим силу взаимного притяжения между разноименно заряженными пластинами плоского конденсатора (пондеромоторную силу) двумя способами.

С одной стороны эту силу можно определить как силу F2 , действующую на вторую пластину со стороны первой

F2 = Q2 E1 , (14)

где Q2 – величина заряда на второй пластине, E1– напряженность поля первой пластины. Величина заряда Q2 второй пластины определяется формулой

Q2 =σ2 S , (15)

где σ2 – поверхностная плотность заряда на второй пластине, а напряженность Е1 поля, создаваемого первой пластиной вычисляется формулой

E1 = σ1 , (16)

2 ε ε

0

где σ1 – поверхностная плотность заряда на первой пластине. Подставим формулы (16) и (15) в формулу (14)

	F2 =	σ1 σ2	S или F2 =	σ 2	S (17) т.к. σ1= σ2.
		2 ε0 ε		2 ε0 ε

Учитывая, что σ = D = ε0 ε E , получим формулу для силы, действующей на одну пластину со стороны другой

F =	ε		ε	E 2
		0		S .
2			2

Для силы, действующей на единицу площади пластины, формула будет иметь следующий вид

F = ε0 ε E2 . (18)

S 2

Теперь получим формулу для пондеромоторной силы, используя закон сохранения энергии. Если тело перемещается в электрическом поле, то пондеромоторными силами

5	Ляпин Али Ибрагимович, доцент БРУ

поля будет совершаться работа А. По закону сохранения энергии эта работа будет совершаться за счет энергии поля, то есть

A + W = 0 или A = W . (19)

Работа по изменению расстояния между пластинами заряженного конденсатора на величину dx определяется формулой

A = F dx , (20)

где F – сила взаимодействия между обкладками (пондеромоторная сила).

Энергия заряженного конденсатора определяется формулой (9). При смещении одной из обкладок на расстояние dx энергии конденсатора изменится на величину W

W =	ε	0	ε E2	S dx (21).
			2

Приравняв формулы (20) и (21), получим формулу для силы, действующей на единицу площади пластины

F	=	ε	0	ε E2	(22).
S				2

Как видим, формулы (18) и (22) одинаковые. Вместе с тем использование закона сохранения энергии для расчета пондеромоторных сил намного упрощает расчеты.

Вопросы для самопроверки:

1.Вывести формулу для энергии уединенного заряженного проводника и системы проводников.

2.Что является носителем электрической энергии? Что понимают под объемной

плотностью энергии?	Вывести формулу	для	объемной плотности энергии
электрического поля.
3. Что понимают под	пондеромоторными	силами? Как можно рассчитать силу

взаимодействия обкладок заряженного конденсатора?

5.Энергия электрического поля

Если обкладки заряженного конденсатора замкнуть металлической про­волокой, то в ней возникает электрический ток, а конденсатор разрядится. Электрический ток разряда конденсатора выделяет в проволоке определённое количество тепла, а это значит, что заряженный конденсатор обладает энергией.

Вычислим энергию заряженного конденсатора С. Для этого обозначим через U мгновенное значение напряжения на обкладках конденсатора в процессе разряда. Если малое количество заряда dq проходит в процессе разряда с одной обкладки на другую, то работа электрических сил dА будЕТ dА =U dq.

Выражая в этой формуле заряд обкладок q через напряжение Q = CU, получим dA = CU dU.

Полную работу, совершаемую электрическими силами за все время разряда, равную энергии кон­денсатора W, мы получим, интегрируя это выражение между значениями напряжения U (начало разряда) и 0 (конец разряда). Это дает:

A= — W = C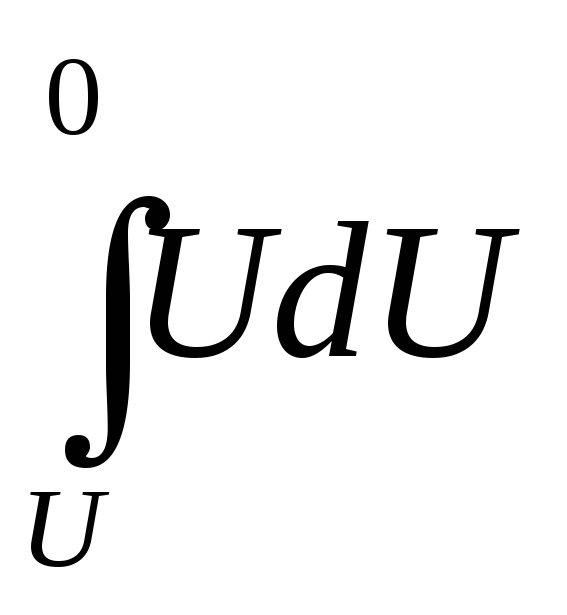= — CU²/2. (1)

Можно (1) переписать:

W = CU²/2 = q²/2C = qU/2. (2)

А где именно, т.е. в каком месте в конденсаторе локализована эта энергия? — На об­кладках конденсатора, т.е. на электрических зарядах, или в его электрическом поле, т.е. в пространстве между обкладками. В дальнейшем мы сможем ответить на этот вопрос, что энергия сосредоточена в электрическом поле. Дальнейшее развитие теории и эксперимента показало, что переменные во времени электрические и магнитные поля могут существовать обособленно, независимо от возбудивших их зарядов, и распространяются в пространстве в виде электромагнитных волн, способных переносить энергию.

Учитывая это, мы можем преобразовать (2) т.о., чтобы в него входила характеристи­ка поля — его напряженность.

Рассмотрим вначале однородное поле и применим формулу (1) к плоскому конденсатору. Мы получим

W = ee₀SU²/2d = ee₀(U/d)²Sd/2, но

U/d=E, a Sd — объём, занимаемый полем.

Мы видим, что энергия однородного электрического поля пропорциональна объёму, занимаемому полем. Поэтому целесообразно говорить об энергии каждой единицы объёма, или об объёмной плотности энергии электрического поля. Она равна

W₁ = ee₀E²/2 = ED/2, т.к. V = Sd = 1.

Последнее выражение справедливо только для изотропного диэлектрика.

Если электрическое поле неоднородно, то его можно разбить на элементарные объемы dV и считать, что в пределах бесконечно малого объема это поле однородно. Поэтому энергия, заключенная в объеме поля dV, будет W₁dV, а полная энергия любого электрического поля может быть представлена в виде

W = (e₀/2)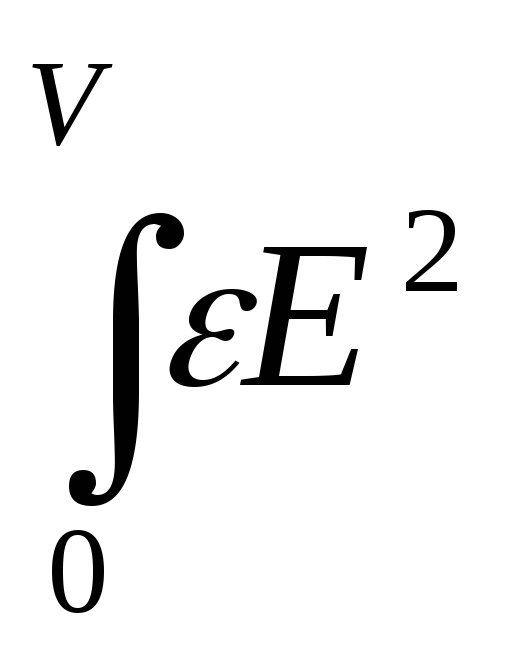dV,

Причем интегрирование проводится по всему объему V, где имеется электрическое поле.

6.Постоянный электрический ток

Электрическим током называется направленное движение электрических зарядов. Ток, воз­никающий в проводнике вследствие того, что в нем создастся электрическое поле, называется током проводимости. При движении зарядов нарушается их равновесное распределение: поверхность проводника уже не является эквипотенциальной и электрические силовые линии не на­правлены ^ ей, т.к. для движения зарядов необходимо, чтобы на поверхности провод­ника тангенциальная составляющая напряженности электрического поля не равнялась нулю (E_t¹ 0). Но тогда и внутри проводника должно существовать электрическое поле, ибо, как известно из электростатики, внутри проводника нет поля лишь в случае равновесного распределения зарядов по поверхности этого проводника. Перемещение зарядов — электрический ток — продолжается до тех пор, пока все точки проводника не станут эквипотенциаль­ными.

Т.о., для появления и существования электрического тока проводимости необходимы два условия.

Первое- наличие в данной среде носителей заряда, т.е. заряженных частиц, которые могли бы в ней перемещаться. Такими частицами, как мы убедимся далее, в металлах являются электроны проводимости, в жидких проводниках (электролитах) — положи­тельные и отрицательные ионы; в газах — положительные ионы и электроны, а также иногда и отрицательные ионы.

Второе — наличие в данной среде электрического поля, энергия которого затрачивалась бы на пе­ремещение электрических зарядов. Для того чтобы ток был длительным, энергия поля должна все время пополняться, иными словами, нужен источник электрической энергии -устройство, в котором осуществляется преобразование какого-либо вида энергии в энергию электрического поля. В зависимости от свойств этих источников в электротехнике различают источники напряжения и источники тока. Поэтому во избежание неточностей мы будем в дальнейшем пользоваться только термином «источник электрической энергии».

Упорядоченное движение зарядов можно осуществить и другим способом — перемещением в пространстве заряженного тела (проводника или диэлектрика). Такой электрический ток называется конвекционным током. Например, движение по орбите Земли, обладающей избыточным отрицательным зарядом, можно рассматривать как конвекционный ток.

За направление тока условно принимают направление движения положительных заря­дов.

Для характеристики электрического тока через какую либо поверхность (например, в случае тока проводимости — через поперечное сечение проводника) вводится понятие силы тока.

Силой тока называется физическая величина I, равная отношению заряда dq, переносимого через рассматриваемую поверхность S за малый промежуток времени dt, к величине этого промежутка:

I=dq/dt (1)

Если сила тока и его направление не изменяются с течением времени, то ток называется по­стоянным. Сила постоянного тока

I=q/t, (2)

где q — заряд, переносимый через поверхность S за конечный промежуток t.

Для того чтобы ток проводимости был постоянным, заряды не должны накапливаться или убывать ни в одной части проводника. Поэтому цепь постоянного тока должна быть замкнутой, а суммарный электрический заряд, который поступает за 1 секунду. сквозь по­верхность S₁ в объем проводника, заключенный между двумя произвольно выбранными поперечными сечениями S₁ и S₂ (рис.1), должен быть равным суммарному заряду, выхо­дящему из этого объема за то же время сквозь поверхность S₂ Т.о., сила постоянного тока I во всех сечениях проводника одинакова.

Рис.1

Единица силы тока в СИ — ампер (А) — определяется на основании электромагнитного взаимодействия двух параллельных прямолинейных проводников, по которым протекает постоянный ток. Из (2) следует, что 1А — равен силе постоянного электрического тока, при котором через поперечное сечение проводника в 1секунду переносится заряд, равный 1К:

1А=1К/с.

Для характеристики направления электрического тока в различных точках рассматриваемой по­верхности вводится вектор плотности электрического тока, который совпадает по направлению с движением положительно заряженных частиц — носителей заряда и численно равен от­ношению силы тока dI сквозь малый элемент поверхности, нормальный к направлению движения заряженных частиц, к площади dS_^ этого элемента:

`J = dI/ dS_^, (3)

В СИ плотность тока измеряется в (А/м²).

Очевидно, что dI = Jсоsa dS = J_n dS , или dI = J 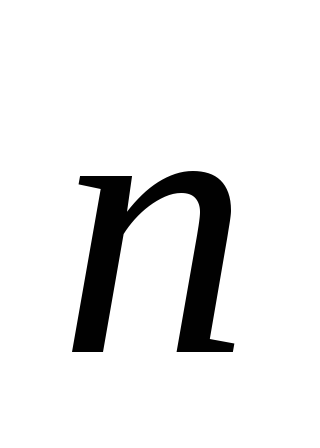dS,

где `n — единичный вектор, перпендикулярный площадке dS, J<sub>n</sub> – проекции J на направление нормали `n.

Сила тока через произвольную поверхность S равна

I = òJ_n dS = ò J dS,

где интегрирование проводится по всей площади этой поверхности. В дальнейшем S- это поперечное сечение проводника. Для постоянного тока

I = JS (4)

В цепи постоянного тока, состоящей из проводников с переменной площадью поперечного сечения, рис. 1, плотности тока в различных сечениях S₁ и S₂ обратно пропорциональны площадям этих сечений: J₁: J₂ = S₂ : S₁.

ЗАКОН ОМА

Рассмотрим отрезок однородного цилиндрического проводника длиной l

Рис.2.

Для того чтобы в этом проводнике шел постоянный электрический ток I, необходимо внутри провод­ника поддерживать постоянное электрическое поле Е. Т.к. E=dU/dI=- (U₂— U₁)/I=(U₁-U₂)/I= U/I, где U = U₁— U₂ — падение потенциала на участке 1-2, наз. напряжением, приложенным к проводнику.

При изменении U меняется и ток I. В 1826 г. Ом установил

I = GU = U/R, (5)

где G — электрическая проводимость, а R = 1/G — электрическое сопротивление проводника. Формула (5) выражает закон Ома в интегральной форме: ток, идущий в проводнике, численно равен отношению приложенного напряжения к сопротивлению проводника. Если U = 1В, I = 1А, то R = 1 Oм — сопротивление такого проводника, в котором при напряжении 1В идет электрический ток в 1А.

Сопротивление проводника зависит от геометрических размеров и формы, а также материала, из которого сделан.Где р – удельное сопротивление в-ва.

R = r1/S, (6)

Подставляя (6) в (5), преобразуем закон Ома

I = U/R = US/rl к виду I/S = U/l)/r.

Величина, обратная удельному сопротивлению, 1/r = g — называется удельной проводимостью или электропроводимостью данного вещества. Тогда j = g`E -закон Ома в дифференциальной форме.

Опыт показывает, что в первом приближении сопротивление металлических провод­ников линейно возрастает с температурой по закону R = R₀(1+at), где a» 4× 10^-3 град-¹— температурный коэффициент. При Т®0 и R®0.

Для некоторых металлов и сплавов вблизи абсолютного нуля температуры наблю­дается (при некоторой характерной для каждого из них температуре) скачкообразное падение сопротивления практически до нуля. Проводник при этом переходит в так называемое сверхпроводящее состояние. Если в замкнутом контуре из сверхпроводника создать электрический ток, то этот ток будет неделями течь в сверхпроводнике, практически не уменьшаясь по величине. Температуры перехода в сверхпроводящее состояние для различных металлов раз­личны и лежат в интервале примерно от 2К до 10К. Несколько лет назад открыта сверхпроводимость при более высоких температурах (азотные температуры).

Зависимость R = R(Т) широко используется в технике для создания термометров со­противлений.

Вернемся опять к электрическому току. Очевидно, что для поддержания постоянного тока в цепи на сво­бодные заряды должны действовать помимо кулоновских сил еще какие — то иные, не­ электростатические силы. Эти силы носят название сторонних сил. Если кулоновские силы вызывают соединение разноименных зарядов, что ведет к выравниванию потен­циалов и исчезновению электрического поля в проводнике, то сторонние силы вызывают разделение разноименных зарядов и поддерживают разность зарядов на концах проводника. Доба­вочное поле сторонних сил в цепи создается источниками электрической энергии (гальваническими элементами, аккумуляторами, электрическими генераторами). За счет поля сторонних сил электрические заряды движутся внутри источника электрической энергии против сил электростатического поля. В следствие это го на концах внешней цепи поддерживается разность потенциалов и в цепи идет постоянный ток. Перемещая заряды, сторонние силы совершают работу за счет энергии, затрачиваемой в источнике электрической энергии. Так, например, в электромагнитном ге­нераторе работа сторонних сил производится за счет механической энергии, расходуе­мой на вращение ротора генератора, а в гальванических элементах — за счет энергии, ко­торая выделяется при хим. процессах растворения электродов в электролите.

Для любой точки внутри проводника напряженность Е результирующего поля равна

`Е = `Е_стор. + `Е_кул., (8)

эксперименты и формулы :: SYL.ru

Когда рассматривается энергия электрического поля, следует изучать ее накопление и расходование. Накопителями энергии являются электроконденсаторы. При небольших габаритах такое устройство способно сосредотачивать в себе большое количество энергии.

При изучении конденсаторов становится легче понимать электростатические законы и возможности современных приборов. Таковыми являются, например, известные цифровые мультимеры, с помощью которых проводят измерения в пикофарадах. Сначала параметры следует оценивать, используя электростатические методы, а после этого — с применением мультимера.

Электрическая емкость удлиненного проводника

Изучение этого устройства дает лучшее понимание в вопросе, что такое энергия электрического поля. Проводники способны накапливать и сохранять заряды. Это свойство называется электрической емкостью.

Для понимания зависимости потенциала удлиненного проводника от заряда необходимо измерить потенциалы заряженного тела. Удобно это сделать относительно земли.

Электрометр с полым проводящим шаром и заземленным корпусом используют в виде электростатического вольтметра и измеряют потенциал тела относительно земли.

Шариком-пробником касаются электрического источника, перенося таким образом внутрь него заряд. При этом вольтметр покажет наличие определенного потенциала.

Повторяя опыт можно прийти к выводу, что отношение заряда к потенциалу постоянно.

Поменяв полый шар на другой и проделав те же опыты, если вольтметр покажет большие значения по сравнению с предыдущими, можно сделпть вывод о меньшей емкости второго шарика.

В международной системе СИ единица измерения электрической емкости — фарад.

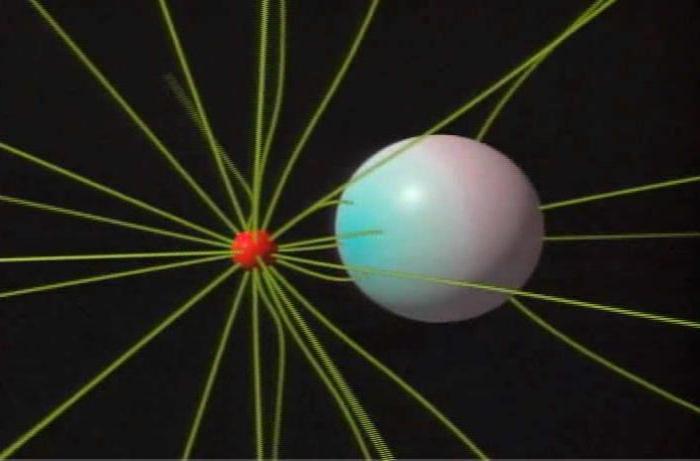
Опыт со сферическим проводником

Если в среде с диэлектрической проницаемостью взять сферический проводник, где потенциал в бесконечности равен нулю, то потенциал в сфере с зарядом будет равен Q/4ПƐ˳ƐR, а электрическая емкость C=4ПƐ˳ƐR,

Получается, что электрическая емкость удлиненного шара пропорциональна его радиусу.

Из опытов следует, что тела считаются удлиненными в случае, если окружающие тела не вызывают существенного перераспределения заряда в них.

Конденсатор

Из двух одинаковых параллельных пластин делают конденсатор и подсоединяют к нему электрометр, который будет работать в виде вольтметра. К его стержню подводят проводящую сферу. Пластину заряжают, перенося заряд с эбонитовой палочки. Тогда вольтметр покажет наличие напряжения, возникшего между пластинами.

Перенеся равные заряды внутрь полой сферы, увеличим показания прибора. Поэтому емкость у пластин будет следующей: C=q/U, способной работать в роли конденсатора, накапливающего заряд электричества (где q – это заряд одной из пластин).

Емкость плоского конденсатора

Емкость плоского конденсатор C=ε̥ε/d, где d – расстояние между пластинами.

Формула может быть подтверждена экспериментом. Собирается плоский конденсатор, заряжается и соединяются пластины с вольтметром. Не изменяя заряд, меняют другие показатели, наблюдая в это время за прибором. Показания будут обратно пропорциональны емкости: U=q/C–1/C.

Делая расстояние между пластинами больше, будем наблюдать увеличение напряжения. Смещая пластины параллельно и увеличивая площадь, получим сокращение напряжения, а емкость при этом увеличится. Если в промежуток между пластинами поместить диэлектрик, то показания вольтметра сократятся.

Так как в ходе эксперимента значение заряда не меняли, получается, что емкость конденсатора прямо пропорциональна перекрытию пластин и обратно пропорциональна d.

Параллельное и последовательное соединение конденсаторов

При параллельном соединении емкости приборов и их напряжения имеют одинаковые значения, а заряды — разное. Общий заряд равен их сумме по отдельности.

При последовательном соединении подключают вольтметр, имеющий полую сферу. Для одной обкладки первого конденсатора дается положительный заряд, тогда другая обкладка приобретет отрицательный, а при соединении с проводником второго прибора — положительный. Тогда оба конденсатора получат идентичные заряды, а напряжения у них будут иметь разные значения.

В результате емкость здесь будет определена по формуле: 1/C=1/C1+1/C2

Энергия плоского и произвольного конденсатора

На пластину подают заряд, имеющий значение, при котором разность потенциалов между пластинами стала равной U. Тогда напряженность будет равна E=U/d, где d – расстояние между объектами.

Одна из пластин находится в электрическом поле другой, где напряженность E/2. Тогда сила притяжения к другой пластине будет f=qE/2. Потенциальная энергия электрического поля заряда равна работе этого поля при сближении пластин.

Подставив ряд значений, получим, что энергия поля W=qU/2=q²/2C=CU²/2.

Такая формула подходит для любого конденсатора. Полная работа поля равна A=1/2qU.

То же самое получится, если применить удлиненный проводник вместо конденсатора.

Определение энергии экспериментальным путем

Замер энергии прибора производится по тепловому действию. В пробирку помещают спираль из металла, закрывают пробкой с трубкой, в которой имеется капелька воды. Получится газовый термометр. К спирали подключают конденсатор, а параллельно — электрометр с шаром, полым внутри.

Конденсатор заряжают при помощи шариков, а затем разряжают посредством спирали. Можно будет заметить перемещение капли в трубке.

После охлаждения воздуха и перемещения капли в начальное положение напряжение увеличивают. Капля переместится на несколько значений выше. Конденсатор меняют на большую емкость в два раза. Зарядив его до начального уровня, можно наблюдать перемещение, увеличенное вдвое.

Плотность энергии электрического поля

Задают энергию такую, чтобы конденсатор не имел значений, а принимались во внимание только величины, характеризующие поле. При этом должна быть вычислена энергия электрического поля на единицу объема.

В результате подстановок плотность энергии получается: ω=W/V=ε̥εΕ²/2, то есть она пропорциональна квадрату напряженности.

Энергия взаимодействия зарядов или энергия в электрическом поле

Итак, для зарядки конденсатора необходима работа, чтобы преодолеть силы электростатического притяжения между разными зарядами при их разделении. За счет этого возникнет запас потенциальной энергии.

Для зарядки любого тела также необходима работа, в данном случае для преодоления электростатического отталкивания между одноименными зарядами.

Взяв уединенный проводник, подаем заряд q. Потенциал поля на бесконечности будет равен нулю, а потенциал проводника — φ(q). Для перенесения малого заряда ∆q требуется работа:

∆A=φ(q)∆q.

Работа по зарядке уединенного проводника определяется по формуле:

A=W=1/2 φ(Q)Q=1/2C(φ(Q))²

На вопрос, где запасается энергия, отвечают двумя вариантами. По одному из них, это энергия взаимодействия зарядов на проводнике, а по другому, энергия — электрического поля получается, так как распределена в окружающем пространстве.

Какому ответу из этих двух отдать предпочтение — личное решение каждого ученика. Но, следует учесть, что при изучении переменных полей возможным становится только второй вариант, где энергия связывается с электрическим полем.

11. Энергия электрического поля. Объемная плотность энергии

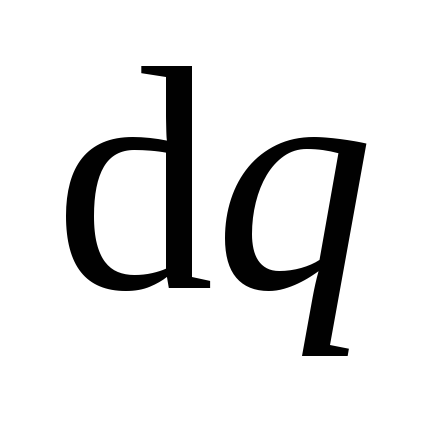Рассмотрим процесс зарядки уединенного проводника. Чтобы его заряд достиг величины Q, будем сообщать проводнику заряд порциями dq, перенося их из бесконечно удаленной точки 1 на поверхность проводника в точку 2 (рис. 3.14). Для передачи проводнику новой порции заряда внешние силы должны совершить работу против сил электрическогополя : 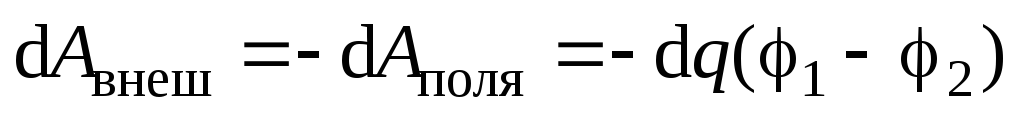. Поскольку проводник уединенный (точка1 бесконечно далека от проводника), то 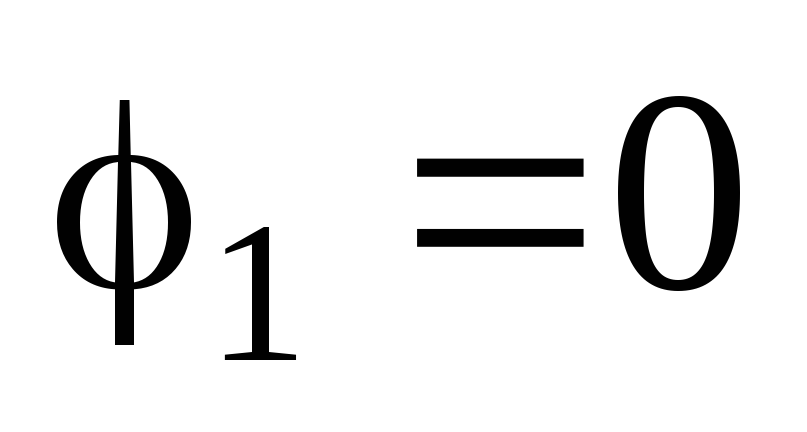. 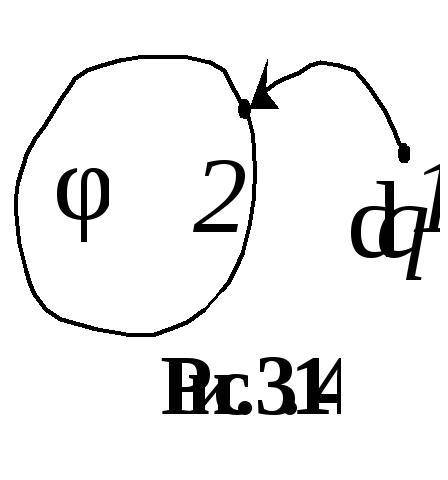Потенциал точки2 равен потенциалу проводника . Поэтому 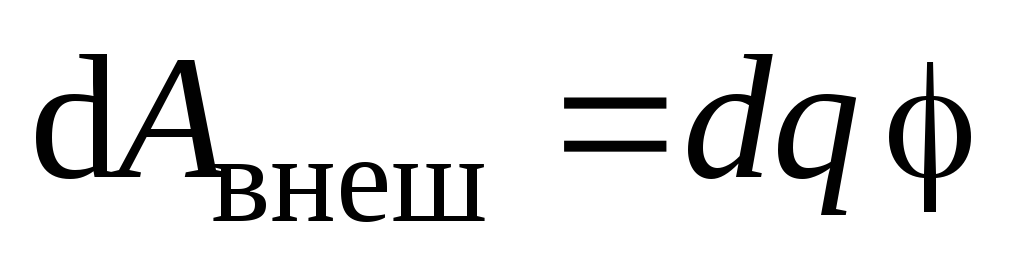. Если проводнику передан зарядq, то его потенциал . Полная работа внешних сил по зарядке проводника до значения зарядаQ будет равна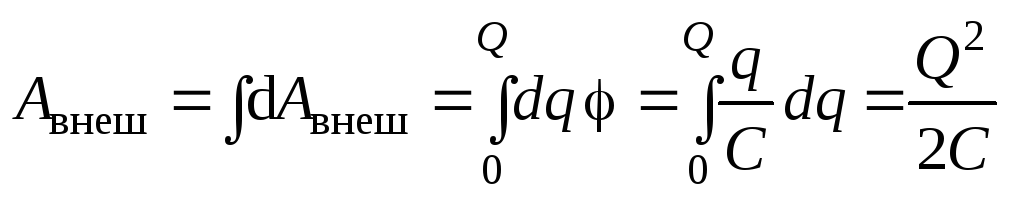

.

Согласно закону сохранения энергии, работа внешних сил по зарядке проводника увеличивает энергию создаваемого электростатического поля, т.е. проводник запасает определенную энергию:

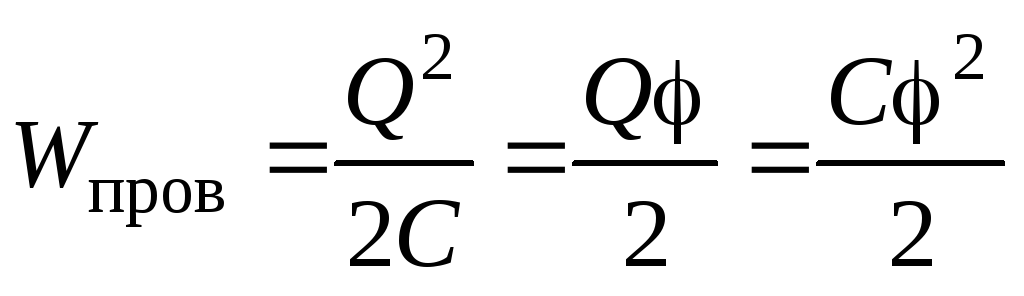. (3.13)

Рассмотрим процесс зарядки конденсатора от источника ЭДС. Источник в процессе зарядки переносит заряды с одной пластины на другую, причем сторонние силы источника совершают работу по увеличению энергии конденсатора:

,

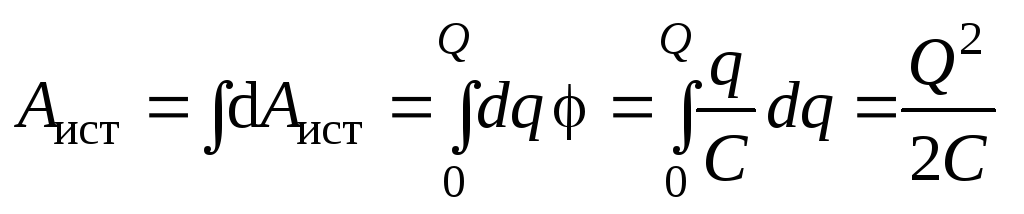где Q – заряд конденсатора после зарядки. Тогда энергия электрического поля, созданного конденсатором, определится как

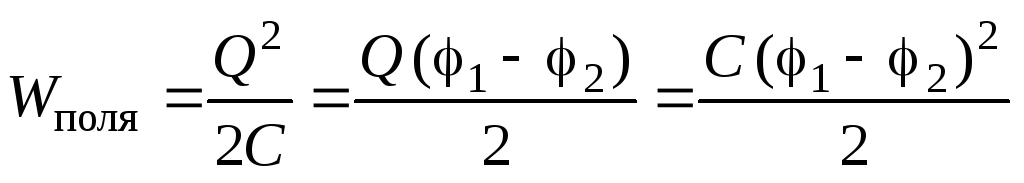. (3.14)

Выражение (3.14) позволяет записать величину энергии электростатического поля двумя способам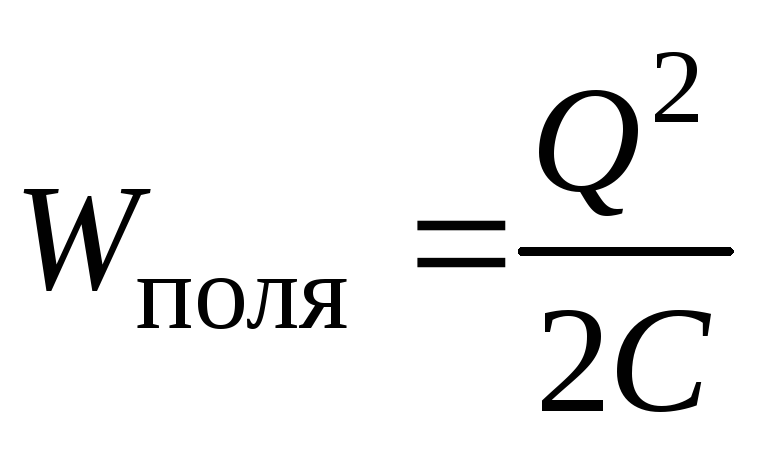и:

и .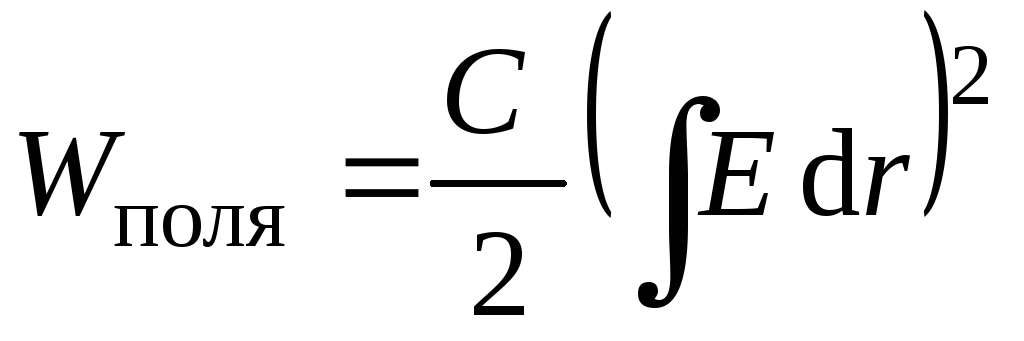

Сопоставление двух соотношений позволяет задать вопрос: что является носителем электрической энергии? Заряды (первая формула) или поле (вторая формула)? Оба записанных равенства прекрасно согласуются с результатами экспериментов, т.е. расчет энергии поля можно одинаково правильно вести по обеим формулам. Однако такое наблюдается только в электростатике, т.е. когда осуществляется расчет энергии поля неподвижных зарядов. При рассмотрении теории электромагнитного поля в дальнейшем (гл. 8) мы увидим, что электрическое поле может создаваться не только неподвижными зарядами. Электростатическое поле – это частный случай электромагнитного поля, существующего в пространстве в виде электромагнитной волны. Его энергия распределена в пространстве с определенной плотностью. Введем понятие объемной плотности энергии поля следующим образом.

Преобразуем последнее равенство (3.14) для случая плоского конденсатора, воспользовавшись связью разности потенциалов и напряженности однородного поля:

,

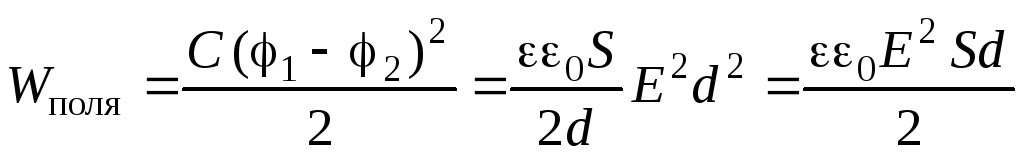где 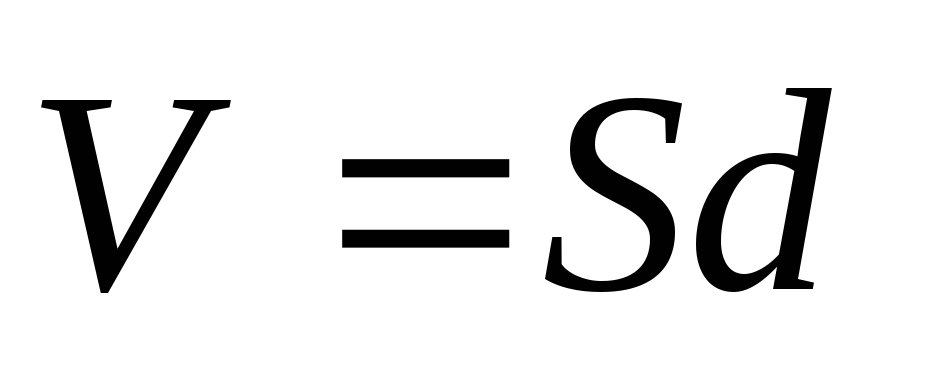– объем конденсатора, т.е. объем части пространства, в котором создано электрическое поле.

Объемной плотностью энергии поля называется отношение энергии поля, заключенного в малом объеме пространства к этому объему:

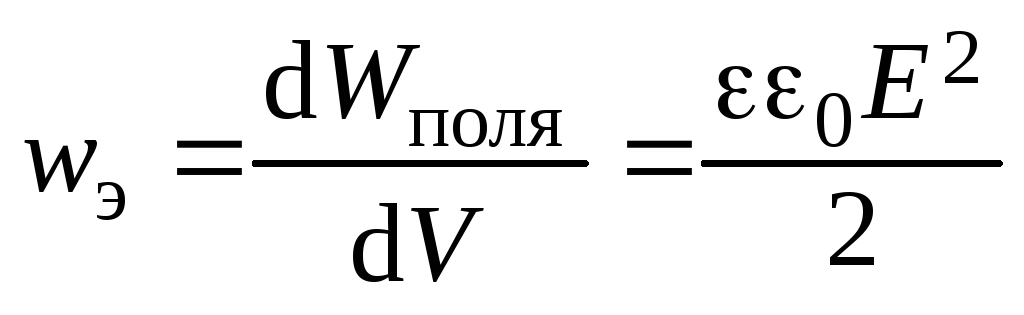. (3.15)

Следовательно, энергию однородного электрического поля можно рассчитать так: .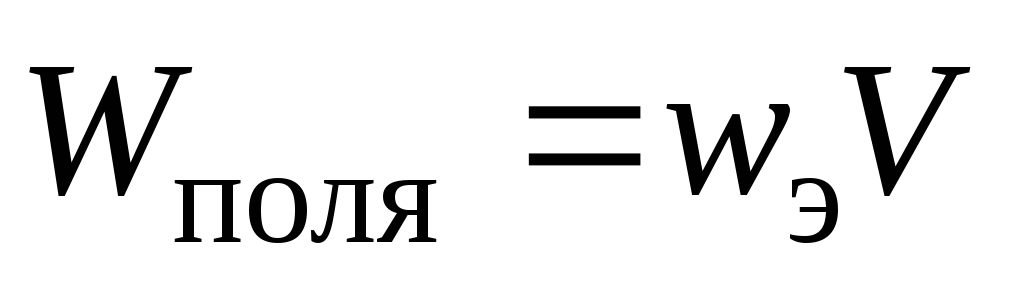

Сделанный вывод можно распространить на случай неоднородного поля таким образом:

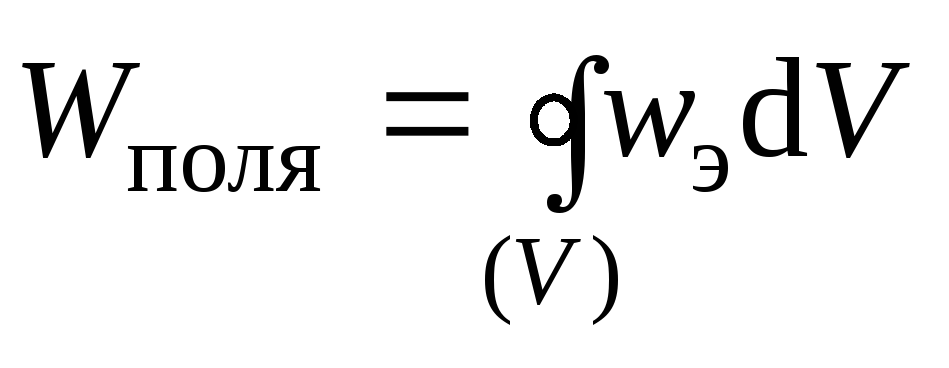, (3.16)

где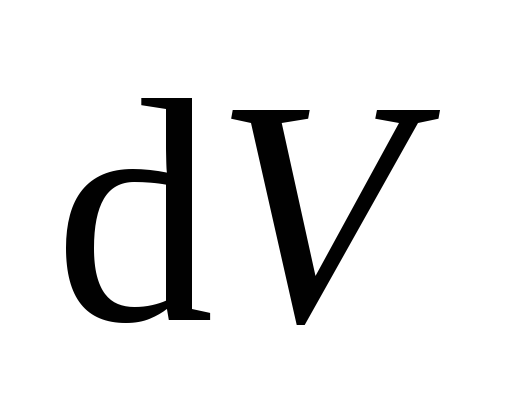– такой элементарный объем пространства, в пределах которого поле можно считать однородным.

Для примера рассчитаем энергию электрического поля, созданного уединенным металлическим шаром радиусом R, заряженным зарядом Q, и находящимся в среде с относительной диэлектрической проницаемостью . Повторив рассуждения примера из п.2.5, получим модуль напряженности поля в виде функции :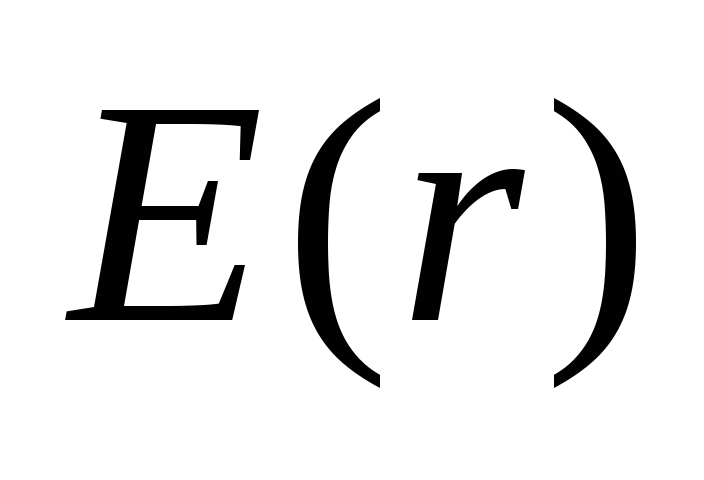

Тогда выражение для объемной плотности энергии поля примет вид:

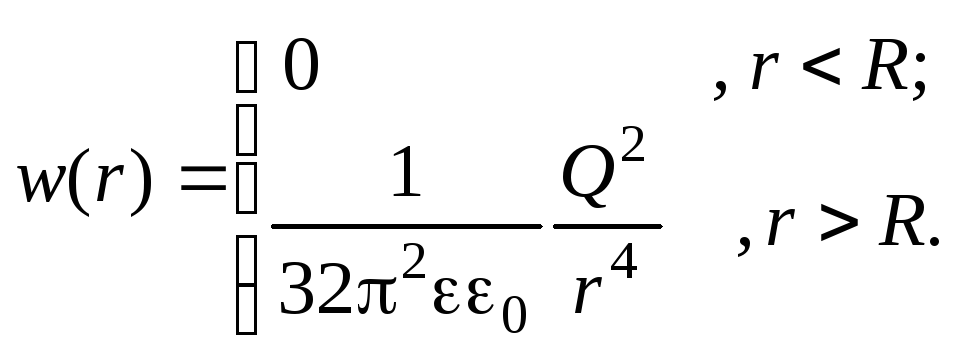
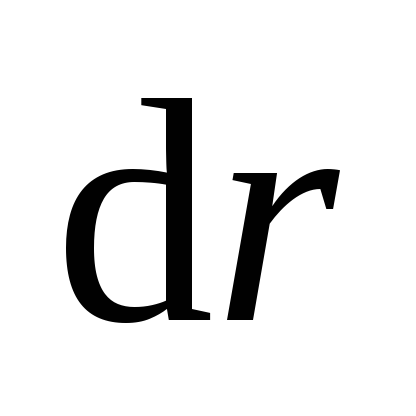Поскольку напряженность поля зависит только от радиальной координаты, то она будет практически постоянна в пределах тонкого сферического слоя с внутренним радиусом r и толщиной (рис. 3.15). Объем этого слоя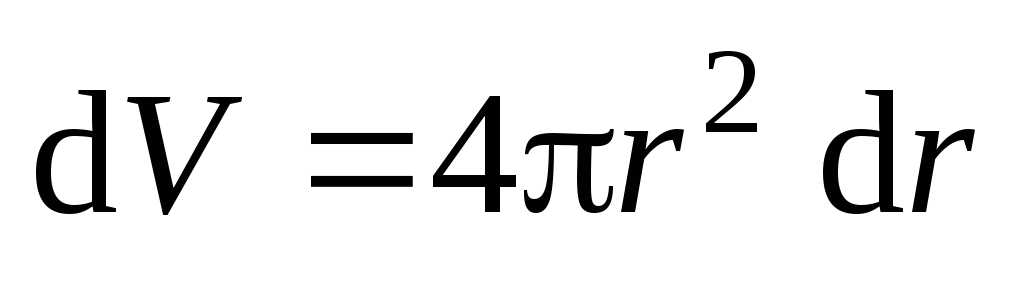. Тогда энергия поля определится так: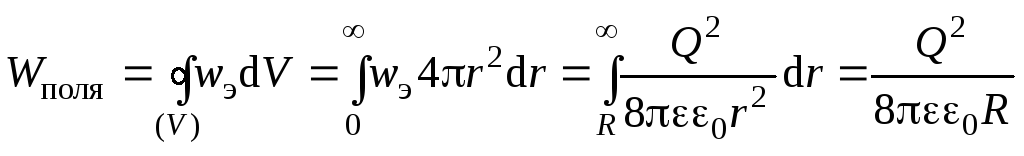

.

Аналогичный результат мы бы получили, если бы вычисляли энергию заряженного шара по формуле (3.13), воспользовавшись (3.6):

.

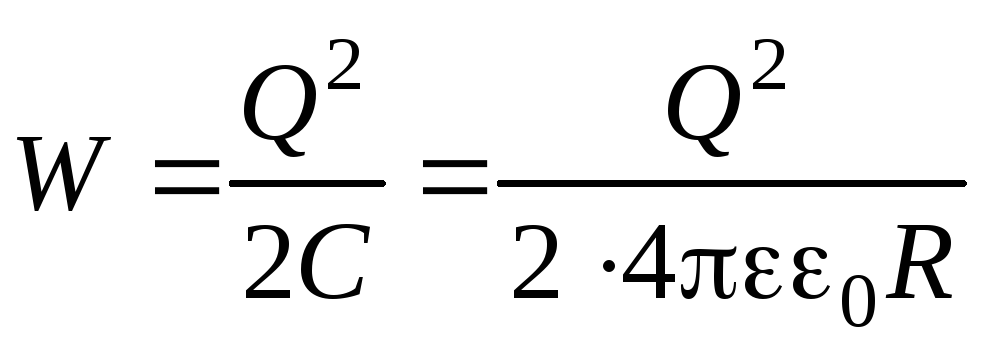Однако следует помнить, что такой способ неприменим, если необходимо найти энергию электрического поля, заключенную не во всем объеме поля, а лишь в его части. Также метод расчета по формуле (3.13) нельзя использовать при определении энергии поля системы, для которой неприменимо понятие “емкость”.

Энергия электрического поля | Все Формулы

   

Энергия электрического поля — Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор

   

Энергия электрического поля

В формуле мы использовали :

   

— Энергия электрического поля

   

— Диэлектрическая проницаемость среды

   

— Диэлектрическая постоянная

   

— Объем занимаемый электрическим полем

   

— Напряжение

   

— Площадь обкладок

   

— Расстояние между обкладками конденсатора

Энергия электрического поля

Опыт показывает, что заряженный конденсатор содержит запас энергии.

Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.

Процесс зарядки конденсатора можно представить как последовательный перенос достаточно малых порций заряда Δq > 0 с одной обкладки на другую (рис. 1.7.1). При этом одна обкладка постепенно заряжается положительным зарядом, а другая – отрицательным. Поскольку каждая порция переносится в условиях, когда на обкладках уже имеется некоторый заряд q, а между ними существует некоторая разность потенциалов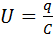
  при переносе каждой порции Δq внешние силы должны совершить работу

Энергия W_е конденсатора емкости C, заряженного зарядом Q, может быть найдена путем интегрирования этого выражения в пределах от 0 до Q:

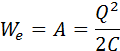
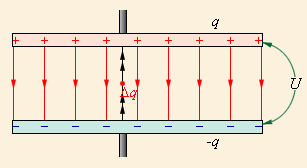Рисунок 1.7.1. Процесс зарядки конденсатора

Формулу, выражающую энергию заряженного конденсатора, можно переписать в другой эквивалентной форме, если воспользоваться соотношением Q = CU.

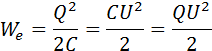
Электрическую энергию W_е следует рассматривать как потенциальную энергию, запасенную в заряженном конденсаторе. Формулы для W_е аналогичны формулам для потенциальной энергии E_р деформированной пружины (см. ч. I, § 2.4)

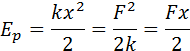
где k – жесткость пружины, x – деформация, F = kx – внешняя сила.

По современным представлениям, электрическая энергия конденсатора локализована в пространстве между обкладками конденсатора, то есть в электрическом поле. Поэтому ее называют энергией электрического поля. Это легко проиллюстрировать на примере заряженного плоского конденсатора.

Напряженность однородного поля в плоском конденсаторе равна

E = U/d, а его емкость 

Поэтому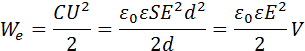

где V = Sd – объем пространства между обкладками, занятый электрическим полем. Из этого соотношения следует, что физическая величина

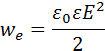
является электрической (потенциальной) энергией единицы объема пространства, в котором создано электрическое поле. Ее называют объемной плотностью электрической энергии.

Энергия поля, созданного любым распределением электрических зарядов в пространстве, может быть найдена путем интегрирования объемной плотности w_е по всему объему, в котором создано электрическое поле.

Энергия электрического поля | Все формулы

Сообщение от администратора:

Ребята! Кто давно хотел выучить английский?
Переходите по моей ссылке и получите два бесплатных урока в школе английского языка SkyEng! 
Занимаюсь там сам — очень круто. Прогресс налицо.

В приложении можно учить слова, тренировать аудирование и произношение.

Попробуйте. Два урока бесплатно по моей ссылке!
Жмите СЮДА

Энергия электрического поля — Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор

В формуле мы использовали :

— Энергия электрического поля

— Диэлектрическая проницаемость среды

— Диэлектрическая постоянная

— Объем занимаемый электрическим полем

— Напряжение

— Площадь обкладок

— Расстояние между обкладками конденсатора