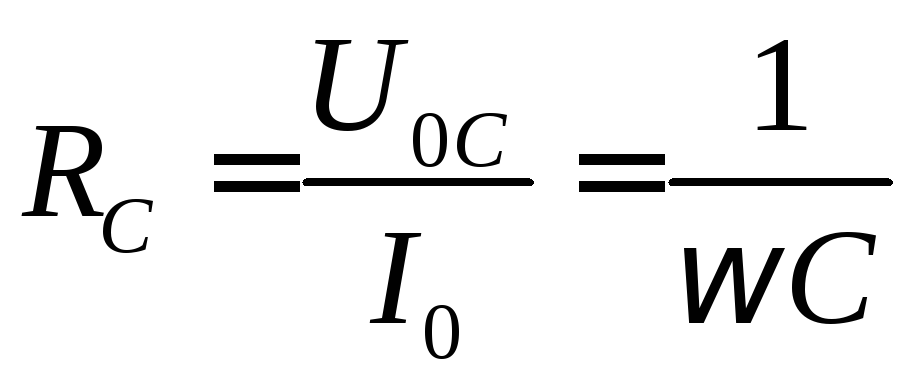Цепь переменного тока с емкостным сопротивлением.
Цепь с емкостью
Вели конденсатор емкостью С подключить к источнику с постоянным напряжением U (рис. 11.5а), то ток зарядки конденсатора проходит в цепи очень короткое время, пока напряжение на конденсаторе Uс не станет равным напряжению источника U.
Ток в рассматриваемой цепи (рис. 11.5а) практически отсутствует (амперметр А покажет I= 0).
Вели же конденсатор подключить к источнику с синусоидальном напряжением (рис. 11.56), то ток в цепи конденсатора существует все время, пока цепь замкнута, и амперметр А покажет этот ток. Ток в цепи конденсатора, подключенного к источнику с синусоидальным напряжением, имеет место потому, что напряжение на конденсаторе Uc

Таким образом, если к конденсатору емкостью С приложено синусоидальное напряжение
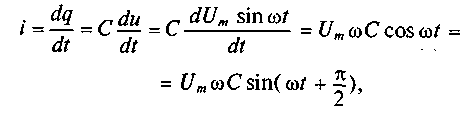
где q= Си согласно (6.3).
О чевидно,
ток в цепи конденсатора достигает
амплитудного
значения
тогда, когда
чевидно,
ток в цепи конденсатора достигает
амплитудного
значения
тогда, когда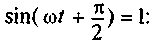

Тогда
Следовательно, напряжение отстает по фазе от тока на 90° = π/2 (рис.11.66)
Е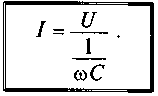 сли
уравнение (11.17) разделить на √2 =1,41, то
получится равенство
I=
UώC
или
сли
уравнение (11.17) разделить на √2 =1,41, то
получится равенство
I=
UώC
или
Э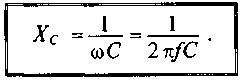
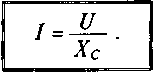
Тогда закон Ома для цепи с конденсатором можно записать:
Емкостное сопротивление — это противодействие, которое оказывает напряжение заряженного конденсатора напряжению, приложенному к нему (рис. 11.5а).
Неразветвленная RL-цепь.
Неразветвленная RC-цепь.
Неразветвленная RLC-цепь.
Построение векторно-топографической диаграммы и нахождение по ней напряжений отдельных участков.
Резонанс напряжений.
Расчет цепи, состоящей из параллельно включенных активного индуктивного и емкостного сопротивлений.
Неразветвленная цепь с активным сопротивлением, индуктивностью и емкостью
Если в неразветвленной цепи с R, L и С (рис. 12.4а) протекает синусоидальный ток i=Imsinώt, то он создает падение напряжения на всех участках цепи: uа= Umasinώt, uL= UmLsin (ώt +π/2) и
uс= Um
Мгновенное значение напряжения цепи определяется по формуле
Т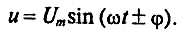 ак
как в рассматриваемой цепи включены
два реактивных сопротивления XL и Хс, то
возможны три режима работы цепи: l)XL>Xc;2)XL<Xc;3)XL = Xc.
ак
как в рассматриваемой цепи включены
два реактивных сопротивления XL и Хс, то
возможны три режима работы цепи: l)XL>Xc;2)XL<Xc;3)XL = Xc.
Векторная диаграмма цепи для режима XL>Хс
Знак
перед углом сдвига фаз φ зависит от
режима работы цепи. Если
в рассматриваемой цепи преобладает
индуктивное напряжение
(сопротивление), т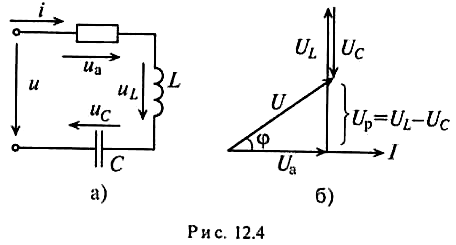 .е. UL> Uc, то
цепь имеет индуктивный характер
и напряжение U опережает
по фазе ток I(+φ).
.е. UL> Uc, то
цепь имеет индуктивный характер
и напряжение U опережает
по фазе ток I(+φ).
Если
в цепи преобладает емкостное напряжение
(сопротивление),
т.е. UL< Uc, то
цепь имеет емкостной характер и
напряжение U отстает
по фазе от тока I(—φ) 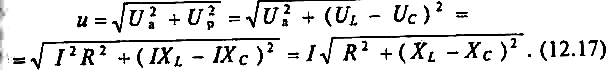
Сопротивление R может включать в себя сопротивление самостоятельного резистора или активное сопротивление реальной катушки и конденсатора.
М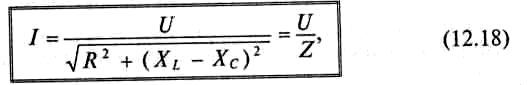 атематическое
выражение закона Ома для неразветвленной
цепи с активным сопротивлением,
индуктивностью и емкость:
атематическое
выражение закона Ома для неразветвленной
цепи с активным сопротивлением,
индуктивностью и емкость:
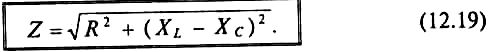

На рис. 12.5 изображены треугольники напряжений, сопротивлений и мощностей для рассматриваемой цепи.
Знак и значение угла φ можно определить из треугольника сопротивлений (рис. 12.56):
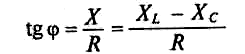
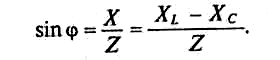
Из выражений (12.20) и (12.21) видно, что если XL
Из
треугольника мощностей (рис. 12.5в) видно,
что в цепи с R, L и
С кроме активной мощности P=Scosφ имеется
реактивная мощность Q=S sinφ. Кроме
того, в цепи происходит колебание
мощности
(меньшей из двух реактивных, в нашем
случае Uc) между
электрическим полем конденсатора С и
магнитным полем катушки
индуктивности L, так
как мощности QL и Q
И з
треугольника мощностей (рис. 12.5в) видно,
что реактивная мощность,
которая загружает источник и провода, Q= QL — Qc. Эта
реактивная мощность (энергия) колеблется
между источником
и магнитным полем катушки индуктивности,
так как Ql>Qc
з
треугольника мощностей (рис. 12.5в) видно,
что реактивная мощность,
которая загружает источник и провода, Q= QL — Qc. Эта
реактивная мощность (энергия) колеблется
между источником
и магнитным полем катушки индуктивности,
так как Ql>Qc
Полная мощность цепи определяется по формуле
Расчет разветвленной цепи методом проводимостей.
Резонанс токов.
Значение коэффициента мощности в электроэнергетике.
2.4. Цепь переменного тока с ёмкостным сопротивлением.
Как известно из физики, два проводника, разделённых слоем диэлектрика, образуют электрический конденсатор, обладающий определённой электрической емкостью.
Рассмотрим цепь переменного тока, в которую включен конденсатор емкостью С (рис. 2.8).

Рис. 2.8 Цепь переменного тока с ёмкостной нагрузкой.
К зажимам цепи
подведено синусоидальное напряжение,
мгновенное значение которого равно 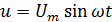 (2.14)
(2.14)
Под действием этого напряжения в замкнутой цепи возникает ток, мгновенное значение которого равно:
 (2.15)
(2.15)
где q – количество электрических зарядов, измеряемое в кулонах.
Этот ток вызывает падение напряжения между пластинами конденсатора uc. В любой момент времени напряжение между пластинами конденсатора уравновешивает напряжение, приложенное к зажимам цепи, т.е.
 (2.16)
(2.16)
Количество электрических зарядов на пластинах конденсатора в любой момент времени определяется по формуле
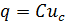 (2.17)
(2.17)
Подставляя (2.17) и (2.16) в (2.15), получим
 (2.18)
(2.18)
Подставляя (2.14) в (2.18), получаем
 (2.19)
(2.19)
где 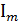 — амплитудное значения тока
— амплитудное значения тока
 (2.20)
(2.20)
Разделив обе части
уравнения (2.20) на 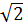 получим, закон Ома для цепи переменного
тока с конденсатором.
получим, закон Ома для цепи переменного
тока с конденсатором.
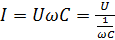 (2.21)
(2.21)
Рассмотрим размерность знаменателя выражения (2.21)

Обозначим  и назовем емкостным сопротивлением
конденсатора. Емкостное сопротивление
зависит от емкости конденсатора и
частоты тока.
и назовем емкостным сопротивлением
конденсатора. Емкостное сопротивление
зависит от емкости конденсатора и
частоты тока.
Сравнивая между собой выражения (2.14) и (2.19) делаем вывод: в цепи переменного тока с конденсатором напряжение отстаёт от тока по фазе на 90°.
Мгновенная мощность цепи с конденсатором равна
 (2.22)
(2.22)
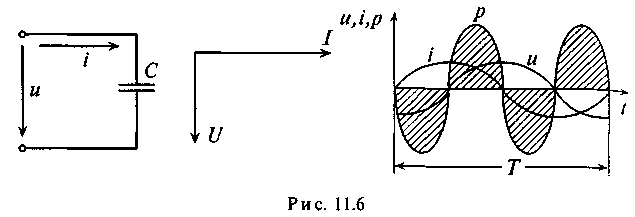
Построим векторную и волновую диаграммы цепи с емкостным сопротивлением (рис. 2.9).

Рис. 2.9 Волновая и векторная диаграммы цепи переменного тока с емкостным сопротивлением.
Из выражения (2.22)
и векторной диаграммы видно, что
мгновенная мощность в цепи с конденсатором
изменяется во времени с удвоенной
частотой, по отношению к частоте тока.
В течении 1 и 3 четвертей периода при
изменении напряжения от нуля до
амплитудного значения мощность
положительна. Это означает, что энергия
посылаемая во внешнюю цепь источником
запасается в конденсаторе в виде энергии
электрического поля 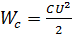 .
В течение второй и четвёртой четвертей
периода, при изменении напряжения от
амплитудного значения до нуля мощность
отрицательна. Это означает, что конденсатор
возвращает запасенную энергию обратно
источнику.
.
В течение второй и четвёртой четвертей
периода, при изменении напряжения от
амплитудного значения до нуля мощность
отрицательна. Это означает, что конденсатор
возвращает запасенную энергию обратно
источнику.
Таким образом в цепи переменного тока с конденсатором происходит периодический обмен энергией между внешним источником и электрическим полем конденсатора. Средняя мощность, потребляемая конденсатором за период, равна нулю, т.е. в такой цепи источник не расходует энергию и, следовательно, в конденсаторе не происходит необратимого преобразования электрической энергии в другие виды энергий.
Мощность цепи с конденсатором оценивается по величине емкостной мощности, измеряемой, как и индуктивная мощность, в вольт-ампер реактивных и характеризующей интенсивность обмена энергией между генератором и электрическим полем конденсатора
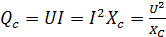 [ВАр]
[ВАр]
Индуктивная и емкостная мощности называются реактивными мощностями. Емкостная мощность конденсатора не может быть использована в практических целях.
Цепь переменного тока с ёмкостью
Поскольку после того, как конденсатор зарядился полностью, он не пропускает через себя электрический ток, и поэтому идеальный конденсатор (ёмкость), установленный в цепи постоянного тока, обладает бесконечно большим сопротивлением.
Цепь переменного тока с ёмкостью
Если же произвести подключение конденсатора к источнику переменного тока, то процесс его заряда и разряда будет осуществляться непрерывно. Это означает, что через ёмкость будет проходить переменный электрический ток.
Ток i при условии включения в цепь переменного тока некоторой ёмкости будет определяется количеством электричества q, протекающего по этой цепи в единицу времени. Из этого следует, что:
где Δq – это изменение заряда q (то есть количества электричества) в течение времени Δt.
Что касается заряда q, который накоплен при изменениях напряжения u в конденсаторе, то он также подвержен непрерывному изменению, которое выражается формулой:
где Δu – это изменение напряжения u в течение промежутка времени Δt.
Та скорость, с которой изменяется напряжение (она выражается отношением Δu/Δt) будет иметь свои наибольшие значения тогда, когда угол ωt равняется 360°, 180° и 0°. Из этого следует, что значение тока i принимает свои наибольшие величины именно в эти моменты времени. Если же угол ωt равняется 270° и 90°, то i = 0, поскольку скорость изменения напряжения Δu/Δt = 0.
Ток и напряжение в цепи переменного тока с ёмкостью
Ток заряда, который принято считать положительным, в цепи течет тогда, когда происходит заряд конденсатора, то есть на протяжение первой четверти периода. По мере того, как разница потенциалов на электродах ёмкости растет вследствие накопления ею электрического заряда, значение тока i падает. Когда ωt = 90°, наступает полный заряд емкости, значение i = 0, а разность потенциалов между электродами конденсатора обретает то же самое значение, что и напряжение источника тока.
Значение тока i становится отрицательным тогда, когда он меняет свое направление. Это происходит тогда, когда ёмкость начинает разряжаться, то есть во второй четверти периода. Тогда, когда u = 0 а ωt = 180°, значение тока i становится максимальным. В этот же самый момент ток i начинает течь в обратном направлении (его принято считать отрицательным), начинается процесс перезарядки емкости, а полярность напряжения u источника также меняется на противоположную. Когда ωt = 270° значение тока i становится равным нулю, и поэтому процесс заряда прекращается. После чего начинается разряд при первоначальном (то есть положительном) направлении тока.
Получается, что ёмкость и заряжается, и разряжается два раза на протяжении одного периода изменения напряжения. Из этого следует, что переменный ток i протекает в цепи непрерывно. Когда ёмкость включается в цепь переменного тока, то ток i опережает напряжение u по фазе на угол, равный 90°. Можно также сказать, что напряжение u отстает по фазе от тока i на угол, равный 90°.
Емкостное сопротивление
Сопротивление, которое проявляет ёмкость к переменному току, носит название емкостного.
Единицей измерения этой величины является Ом, а обозначается оно Хс. Физическая природа емкостного сопротивления заключается в том, что оно обусловлено возникающей в конденсаторе ЭДС ес. Направление этой электродвижущей силы противоположно приложенному напряжению u, поскольку заряженная ёмкость рассматривается в качестве источника, у которого между пластинами действует некоторая ЭДС ес. Именно она препятствует тому, чтобы под действием напряжения u происходило изменение тока, то есть оказывает определенное сопротивление его прохождению.
2. Индуктивность, емкость и активное сопротивление в цепи переменного тока
Р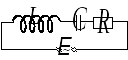 ассмотрим
контур, который включает в себя
индуктивность
ассмотрим
контур, который включает в себя
индуктивность 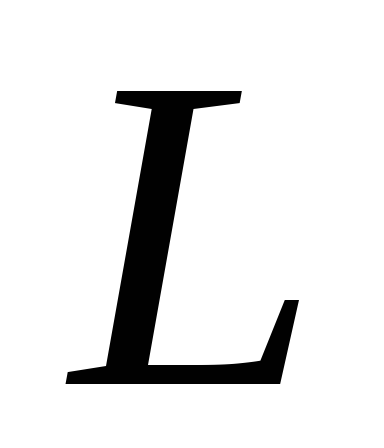 ,
емкость
,
емкость  и активное сопротивление
и активное сопротивление  .
Пусть в этот контур включен источник
ЭДС, который изменяется по гармоничному
закону (синуса или косинуса) с амплитудой
.
Пусть в этот контур включен источник
ЭДС, который изменяется по гармоничному
закону (синуса или косинуса) с амплитудой 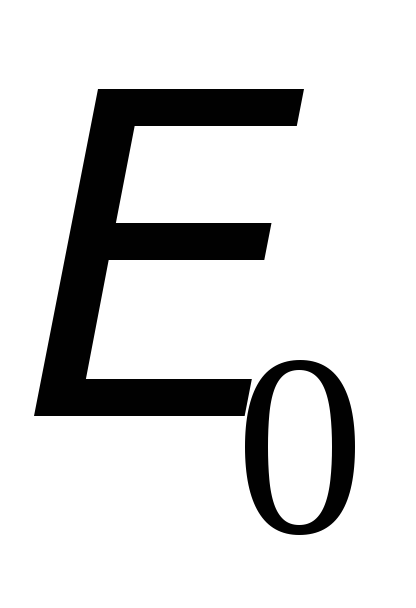 и циклической частотой
и циклической частотой 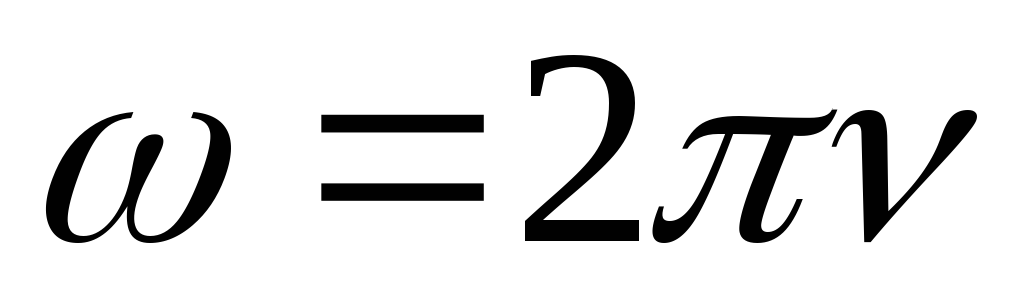 ,
где
,
где 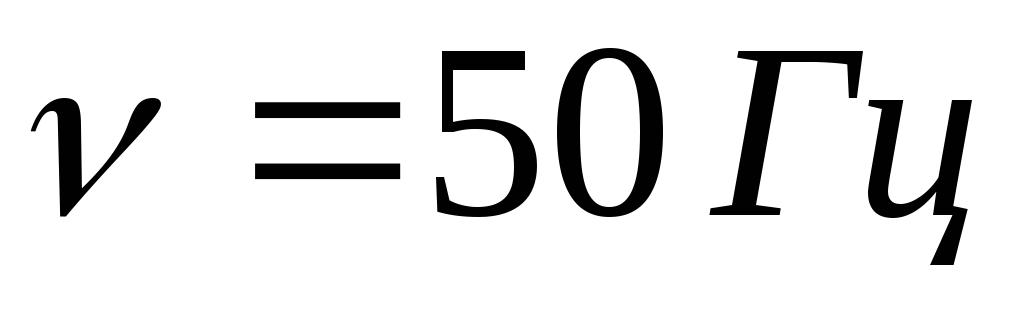 – линейная частота. Выясним, как влияют
– линейная частота. Выясним, как влияют 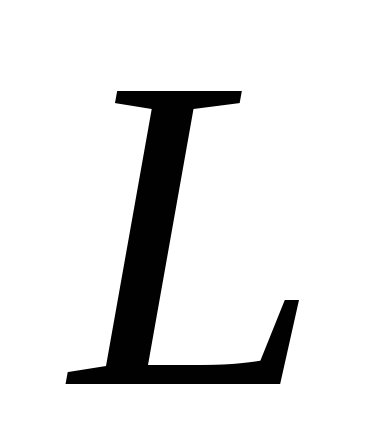 ,
,  и
и  отдельно и вместе на ток в этом цепи и
какие падения напряжения будут на этих элементах. Ток на всех
элементах цепи будет одинаковым (ток
неразрывный). Пусть он меняется по закону
синуса
отдельно и вместе на ток в этом цепи и
какие падения напряжения будут на этих элементах. Ток на всех
элементах цепи будет одинаковым (ток
неразрывный). Пусть он меняется по закону
синуса
| (1) |
где 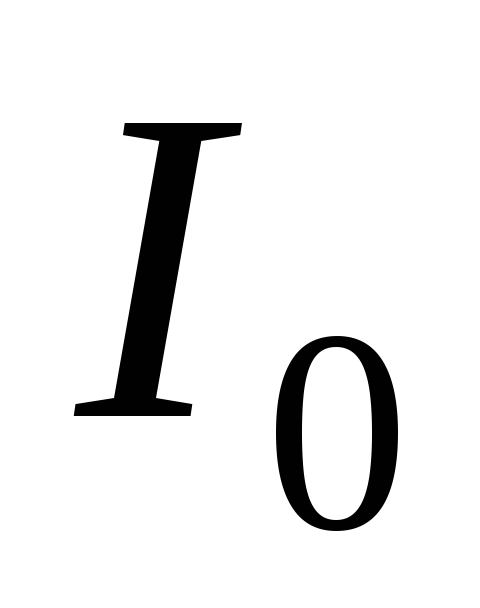 – амплитудное значение силы тока (пока
еще неизвестное).
– амплитудное значение силы тока (пока
еще неизвестное).
2 .1.Активное
сопротивление в цепи переменного тока
.1.Активное
сопротивление в цепи переменного тока
Рассмотрим электрическую цепь, которая состоит только из источника переменного тока и активного сопротивления R. Падение напряжения на активном сопротивлении определяется из закона Ома и выражения (1)

 .
(2)
.
(2)
Величина 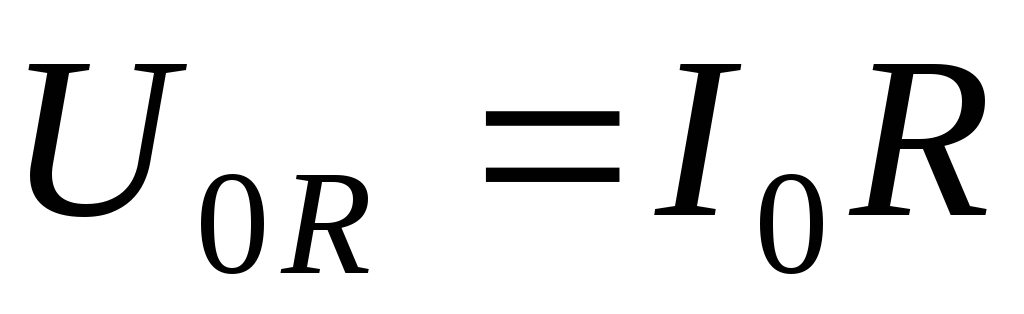 будет представлять собой амплитудное
значение напряжения на активном
сопротивлении. Сравнивая выражения (1)
и (2) видим, что колебания напряжения и
тока на активном сопротивлении происходит
с одинаковой фазой (по закону синуса,
рис.1). Заметим, что в цепи с активным
сопротивлением происходит необратимый
процесс преобразования электрической
энергии в тепловую.
будет представлять собой амплитудное
значение напряжения на активном
сопротивлении. Сравнивая выражения (1)
и (2) видим, что колебания напряжения и
тока на активном сопротивлении происходит
с одинаковой фазой (по закону синуса,
рис.1). Заметим, что в цепи с активным
сопротивлением происходит необратимый
процесс преобразования электрической
энергии в тепловую.
2.2.Индуктивность в цепи переменного тока
 Если
катушка индуктивности
Если
катушка индуктивности 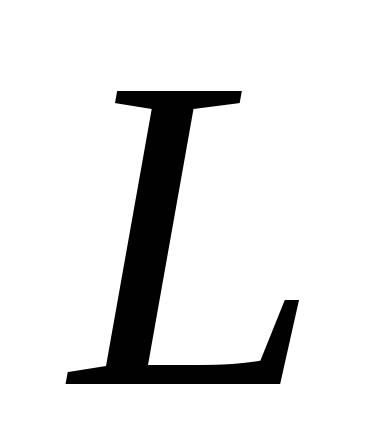 находится в контуре с переменным током,
то в ней все время будет возникать ЭДС
самоиндукции, которая противодействует
внешний переменной ЭДС. Вследствие
этого катушка будет создавать сопротивление
(дополнительное к активному) переменному
току, который называют индуктивным
сопротивлением. Найдем это сопротивление.
находится в контуре с переменным током,
то в ней все время будет возникать ЭДС
самоиндукции, которая противодействует
внешний переменной ЭДС. Вследствие
этого катушка будет создавать сопротивление
(дополнительное к активному) переменному
току, который называют индуктивным
сопротивлением. Найдем это сопротивление.
Пусть
активное сопротивление катушки очень
мало ( ).
Тогда на индуктивности создается падение
напряжения
).
Тогда на индуктивности создается падение
напряжения 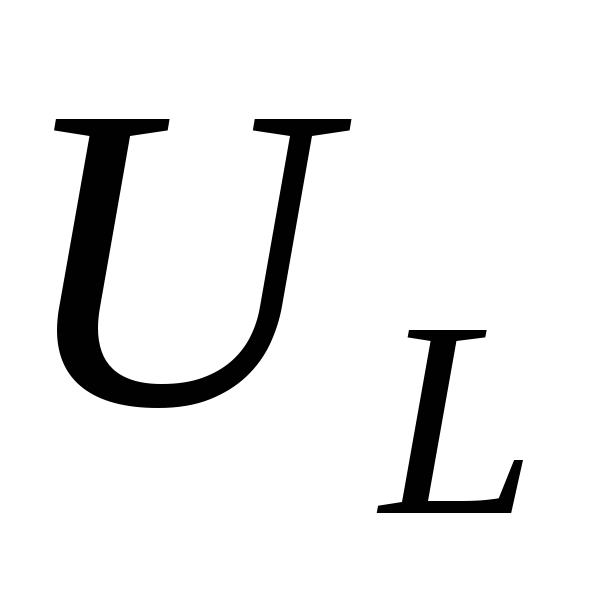 ,
которое равняется минус ЭДС самоиндукции
(ЭДС самоиндукции противодействует
внешнему напряжению),
,
которое равняется минус ЭДС самоиндукции
(ЭДС самоиндукции противодействует
внешнему напряжению), 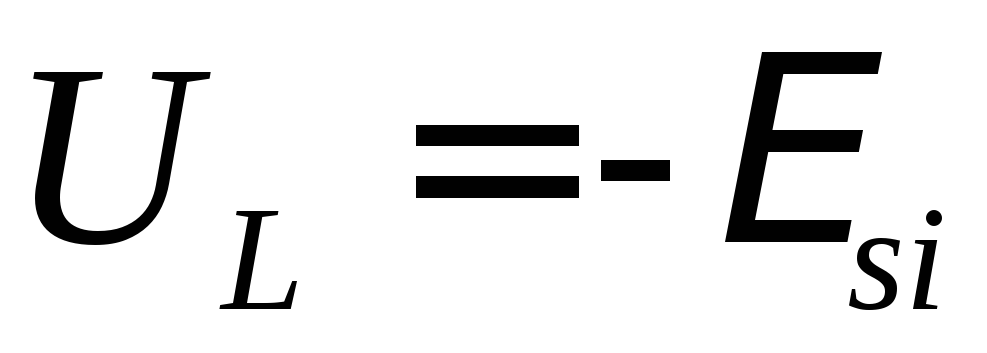 .
Подставив выражение для силы тока (1) в
выражение для ЭДС самоиндукции (11*),
получим значение напряжения на
индуктивности
.
Подставив выражение для силы тока (1) в
выражение для ЭДС самоиндукции (11*),
получим значение напряжения на
индуктивности  ,
или учитывая, что
,
или учитывая, что 
| (3) |
Величина  является амплитудным значением напряжения
на индуктивности, а отношение
является амплитудным значением напряжения
на индуктивности, а отношение
| (4) |
называют индуктивным
сопротивлением. Анализируя это выражение, можно сделать
вывод, что катушка
индуктивности хорошо пропускает
постоянный ток (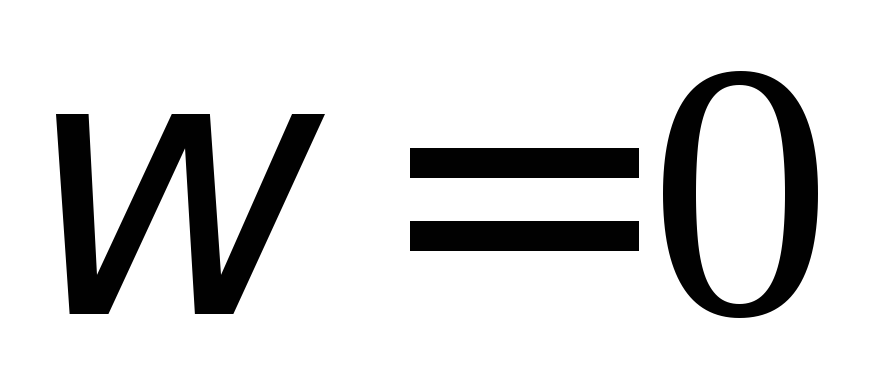 )
и хуже пропускает переменный ток (
)
и хуже пропускает переменный ток (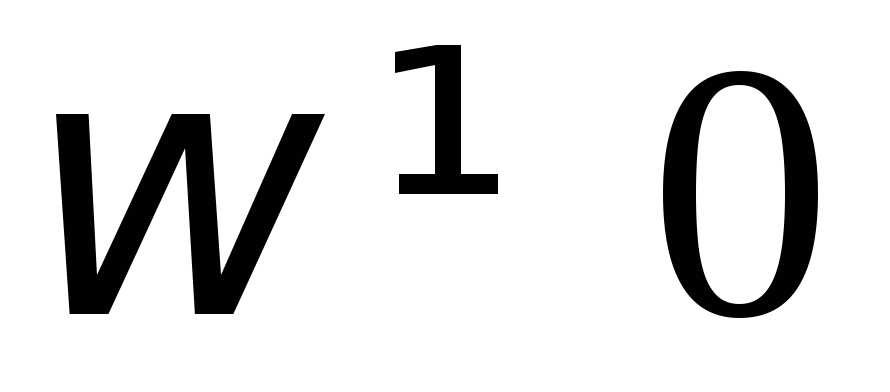 ).
В отличие от активного сопротивления,
индуктивное сопротивление не вызывает
выделение джоулева тепла.
).
В отличие от активного сопротивления,
индуктивное сопротивление не вызывает
выделение джоулева тепла.
И з
сравнения выражений для тока (1) и
напряжения (3) на индуктивности вытекает,
что колебания напряжения на катушке
опережают колебания тока на
з
сравнения выражений для тока (1) и
напряжения (3) на индуктивности вытекает,
что колебания напряжения на катушке
опережают колебания тока на  (рис. 2). Это означает, что на катушке
сначала возникает напряжение – ЭДС
самоиндукции, а уже потом начинает
возрастать ток (мгновенному росту тока
мешает ЭДС самоиндукции, которая
противодействует
первичной переменной ЭДС).
Когда ток достигает максимального
значения – напряжение на катушке
минимально (производная в максимуме
равна нулю), И наоборот, когда напряжение
максимально – ток равняется нулю.
(рис. 2). Это означает, что на катушке
сначала возникает напряжение – ЭДС
самоиндукции, а уже потом начинает
возрастать ток (мгновенному росту тока
мешает ЭДС самоиндукции, которая
противодействует
первичной переменной ЭДС).
Когда ток достигает максимального
значения – напряжение на катушке
минимально (производная в максимуме
равна нулю), И наоборот, когда напряжение
максимально – ток равняется нулю.
2.3.Емкость в цепи переменного тока
Р ассмотрим
электрическую цепь, которая состоит
только из источника переменного тока
и конденсатора
ассмотрим
электрическую цепь, которая состоит
только из источника переменного тока
и конденсатора  .
Как
известно, конденсатор (две металлические
пластины, между которыми – диэлектрик)
вообще не пропускает постоянный ток
(ток будет протекать только до тех пор,
пока конденсатор заряжается, а потом
исчезает). Но если на конденсатор подавать
переменное напряжение, он все время
будет перезаряжаться, то есть через
конденсатор может идти переменный ток
.
Как
известно, конденсатор (две металлические
пластины, между которыми – диэлектрик)
вообще не пропускает постоянный ток
(ток будет протекать только до тех пор,
пока конденсатор заряжается, а потом
исчезает). Но если на конденсатор подавать
переменное напряжение, он все время
будет перезаряжаться, то есть через
конденсатор может идти переменный ток 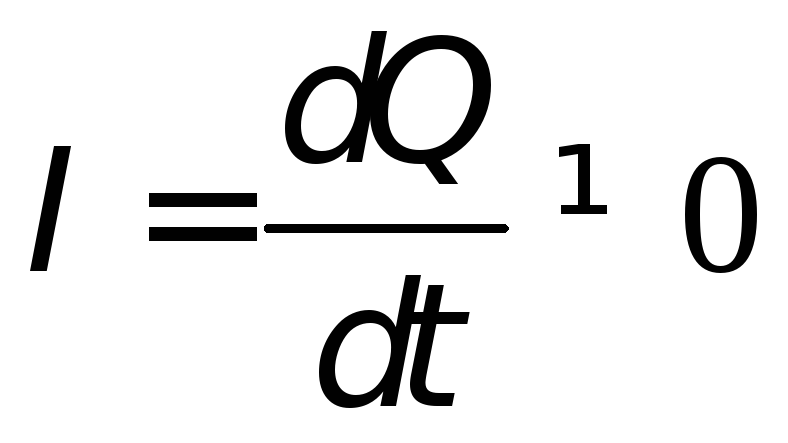 .
Чем больше частота переменного тока и
емкость конденсатора, тем лучше он
пропускает ток, тем меньшим будет его емкостное
сопротивление.
Найдем это сопротивление, то есть
сопротивление, которое создает конденсатор
переменному току.
.
Чем больше частота переменного тока и
емкость конденсатора, тем лучше он
пропускает ток, тем меньшим будет его емкостное
сопротивление.
Найдем это сопротивление, то есть
сопротивление, которое создает конденсатор
переменному току.
Пусть
через конденсатор течет ток, который
меняется по закону (1) 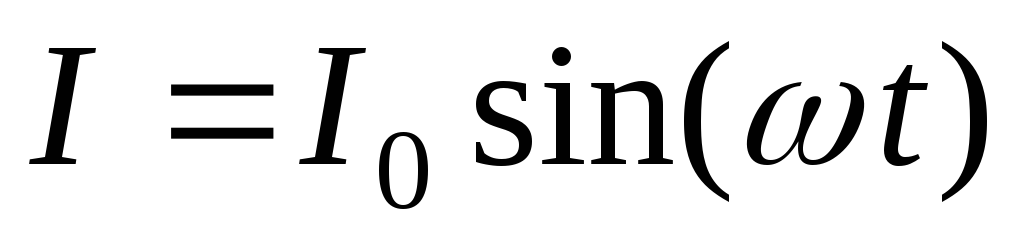 .
Из определения силы тока (1*)
.
Из определения силы тока (1*)  ,
можно найти заряд
,
можно найти заряд  на обкладках конденсатора:
на обкладках конденсатора: 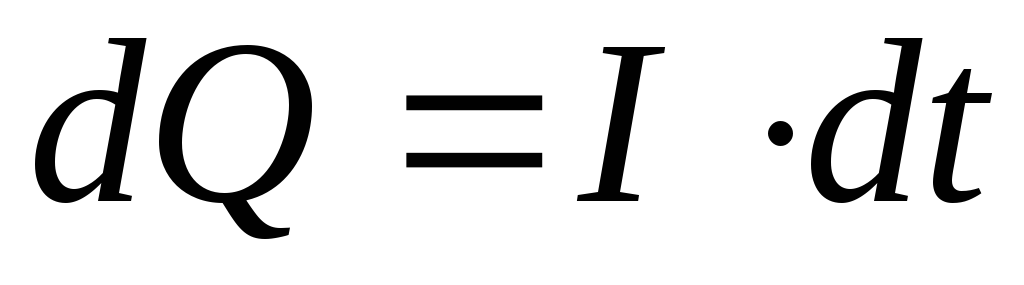 ,
, 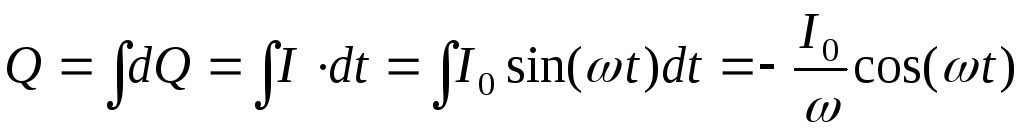 .
Учитывая,
что
.
Учитывая,
что 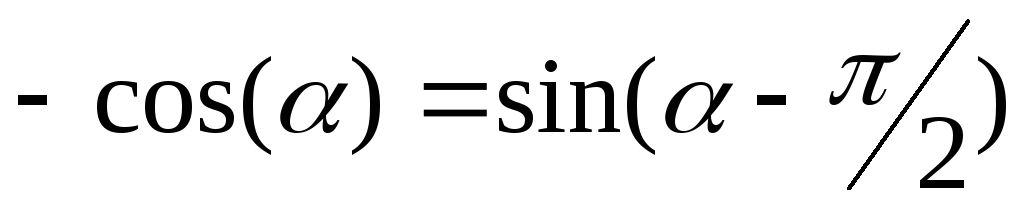 ,
получаем
,
получаем  .
Из определения электроемкости конденсатора
(7)
.
Из определения электроемкости конденсатора
(7) 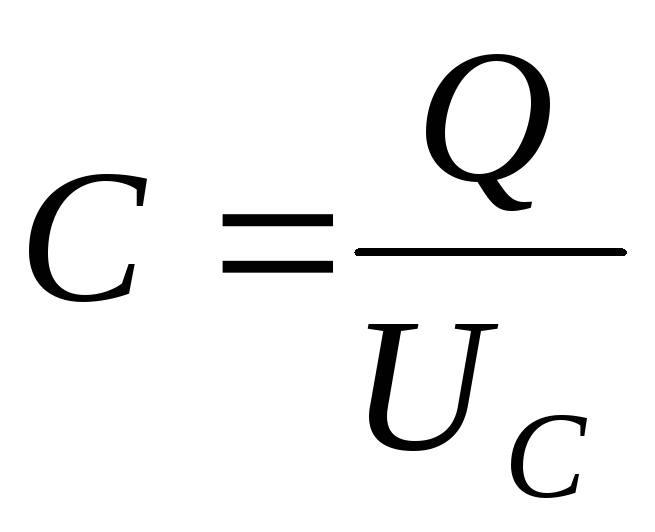 ,
вытекает, что напряжение на его обкладках
будет
,
вытекает, что напряжение на его обкладках
будет
| (5) |
Величина 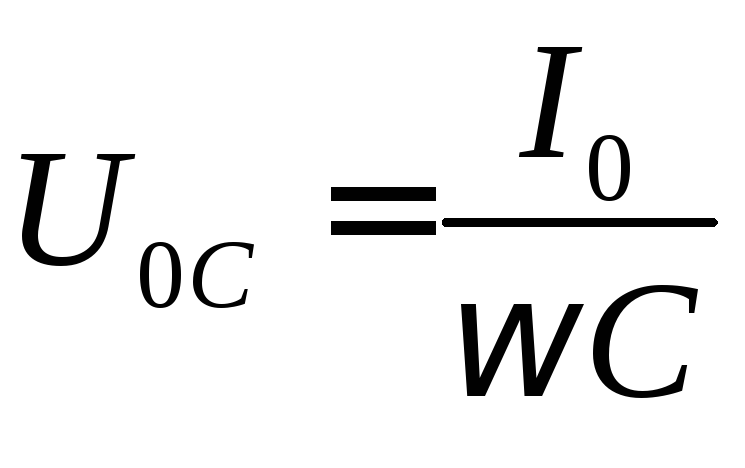 является амплитудным значением напряжения
на емкости, а отношение
является амплитудным значением напряжения
на емкости, а отношение
| (6) |
называют емкостным сопротивлением. На емкостном сопротивлении, как и на индуктивном, джоулево тепло не выделяется. Анализируя это выражение, можно сделать вывод, что конденсатор хорошо пропускает переменный ток высокой частоты и хуже пропускает ток малой частоты.
И з
сравнения выражений для тока (1) и
напряжения (5) на конденсаторе вытекает,
что колебания напряжения на конденсаторе
отстают от колебаний тока на
з
сравнения выражений для тока (1) и
напряжения (5) на конденсаторе вытекает,
что колебания напряжения на конденсаторе
отстают от колебаний тока на 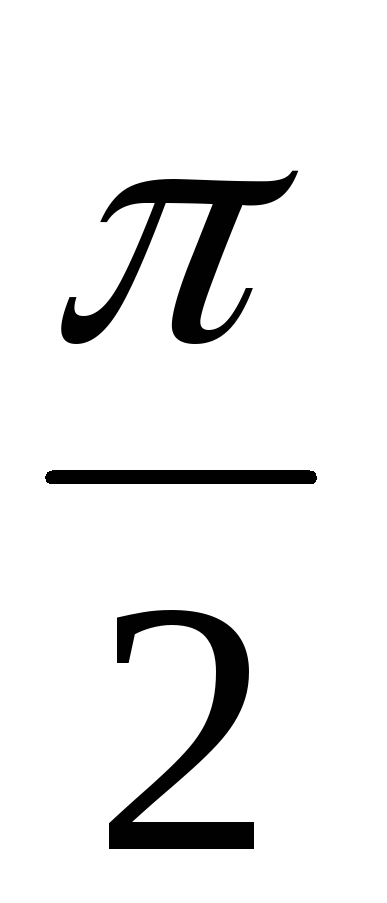 (рис. 3). То есть сначала через конденсатор
протекает ток (конденсатор заряжается),
а уже потом на нем возникает напряжение.
Когда ток достигает максимального
значения – напряжение на конденсаторе
равняется нулю, и наоборот, когда
напряжение максимальное – ток равняется
нулю.
(рис. 3). То есть сначала через конденсатор
протекает ток (конденсатор заряжается),
а уже потом на нем возникает напряжение.
Когда ток достигает максимального
значения – напряжение на конденсаторе
равняется нулю, и наоборот, когда
напряжение максимальное – ток равняется
нулю.




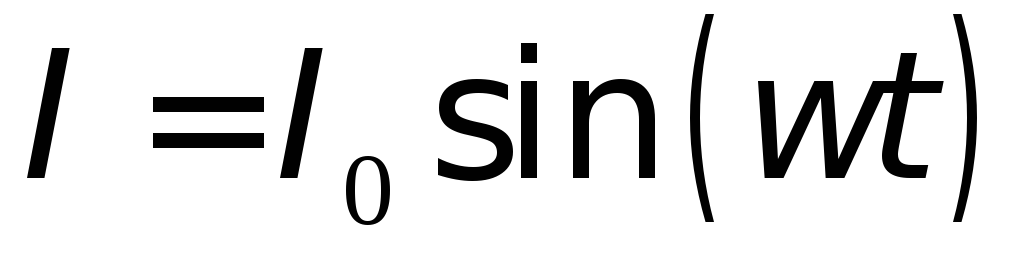 ,.
,.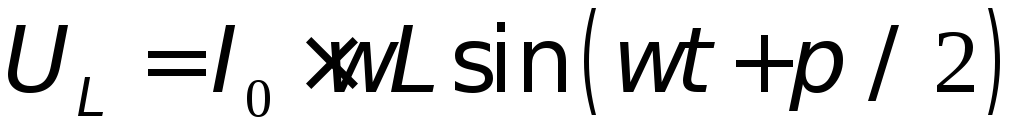 .
.
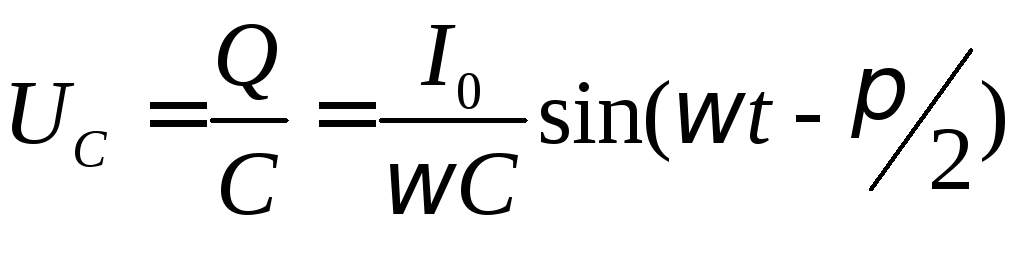 .
.