Электромагнитные волны — Мегаэнциклопедия Кирилла и Мефодия — статья
Существование электромагнитных волн было предсказано М. Фарадеем еще в 1832 году. Дж. Максвелл в 1865 году в результате анализа предложенной им системы уравнений (см. Максвелла уравнения), описывающей электромагнитное поле, теоретически показал, что электромагнитное поле в вакууме может существовать и в отсутствие источников — зарядов и токов. Поле без источников имеет вид волн, распространяющихся с конечной скоростью, которая в вакууме равна скорости света: с = 299792458±1, 2 м/с. Совпадение скорости распространения электромагнитных волн в вакууме с измеренной ранее скоростью света позволило Максвеллу сделать вывод о том, что свет представляет собой электромагнитные волны. Подобное заключение в дальнейшем легло в основу электромагнитной теории света.В 1888 году теория электромагнитных волн получила экспериментальное подтверждение в опытах Г. Герца. Используя источник высокого напряжения и вибраторы (см. Герца вибратор), Герцу удалось выполнить тонкие эксперименты по определению скорости распространения электромагнитной волны и ее длины. Экспериментально подтвердилось, что скорость распространения электромагнитной волны равна скорости света, что доказывало электромагнитную природу света.В электродинамике электромагнитное поле описывается четырьмя уравнениями Максвелла, благодаря которым существует возможность единым образом подойти к описанию радиоволн, света, рентгеновских лучей и гамма-излучения. Оказалось, что они представляют собой не излучения различной природы, а электромагнитные волны с различной длиной волны.так как e= 1 и m= 1.
В веществе скорость распространения электромагнитных волн всегда меньше, чем в вакууме.
Колебания электрического и магнитного полей в свободной электромагнитной волне происходят во взаимно перпендикулярных плоскостях в направлениях, перпендикулярных направлению распространения волны. Из уравнений Максвелла следует, что векторы напряженностей
DЕ = d2Е/v2dt2
DН = d2Н/v2dt2
Всякая функция, удовлетворяющая этим уравнениям, описывает некоторую волну. Следовательно, электромагнитные поля могут существовать в виде электромагнитных волн.
В отличие от статического электрического и магнитного полей, которые не существуют в отрыве от источника, электромагнитная волна существует без источника в том смысле, что после ее излучения электромагнитное поле не связано с источником.
Если среда неоднородна или содержит поверхности, на которых изменяются ее электрические или магнитные свойства, или если в пространстве имеются проводники, то тип возбуждаемых и распространяющихся электромагнитных волн может существенно отличаться от плоской линейно-поляризованной волны. Электромагнитные волны могут распространяться вдоль направляющих поверхностей (поверхностные волны), в передающих линиях и в полостях, образованных хорошо проводящими стенками.
В бегущей монохроматической электромагнитной волне плотности энергии электрического и магнитного полей, совершая гармоническое колебание с частотой 2ω, равны друг другу в каждой точке в любой момент времени.
Колебания электрического и магнитного полей происходят во времени в одинаковой фазе, то есть электрическое и магнитное поля одновременно достигают минимумов и максимумов. Напряженности электрического и магнитного полей в свободной электромагнитной волне взаимосвязаны:
v(eeо).Е = v(mmо).Н,
причем эти соотношения связывают как мгновенные, так и амплитудные значения полей.
Электромагнитные волны различных частотных диапазонов характеризуются различными способами возбуждения. Источником электромагнитных волн может быть любой электрический колебательный контур или проводник, по которому течет переменный электрический ток, так как для возбуждения электромагнитных волн необходимо создать в пространстве переменное электрическое поле или соответственно переменное магнитное поле. На расстоянии от источника много большем λ образуется волновая зона (зона излучения), где распространяются сферические электромагнитные волны. Они поперечные и линейно поляризованы. Монохроматическую и когерентную волну излучает гармонический осциллятор. Ее рассматривают как монохроматическую волну, у которой постоянна частота колебаний. Свет представляет собой электромагнитные волны определенной длины волны. Опыты, в которых была открыта поляризация света, указывают на то, что эти волны поперечные.Характер изменения во времени Е и Н электромагнитной волны определяется законом изменения тока I и зарядов e, ее возбуждающих. Однако ее форма повторяет форму тока только в случае, если электромагнитные волны распространяются в линейной среде, электрические и магнитные свойства которой не зависят от Е и Н.
Частота колебаний электрического и магнитного полей в электромагнитной волне связана с длиной волны соотношением:
Электромагнитная волна обладает энергией, импульсом, массой, а если она является эллиптически- и циркулярнополяризованной, то обладает еще и моментом импульса.
Электромагнитная волна переносит энергию. Средняя величина энергии плоской поляризованной волны
W> = eeoA2/2Дж/см3.
Энергия волны Ев, протекающая через поверхность S, перпендикулярную распространению волны, за время t, равна Ев = W>cSt.
Величину I =W>cназывают интенсивностью.
Если электромагнитные волны поглощаются или отражаются телами, то из теории Максвелла следует, что электромагнитные волны должны оказывать на тела давление. Когда волна поглощается, ее импульс передается тому объекту, который ее поглощает, следовательно, при поглощении электромагнитная волна оказывает давление на преграду. Давление электромагнитных волн объясняется том, что под действием электрического поля волны заряженные частицы вещества начинают упорядоченно двигаться и подвергаются со стороны магнитного поля действию сил Лоренца. Однако величина этого давления ничтожно мала. Существование давления электромагнитных волн приводит к выводу о том, что электромагнитному полю присущ механический импульс, модуль которого равен энергии, деленной на скорость света. Впервые давление электромагнитных волн экспериментально было обнаружено П. Н. Лебедевым в 1900 году.Появление квантовых генераторов, в частности лазеров, позволило получить значения напряженности электрического поля в электромагнитных волнах, сравнимых с внутриатомными полями. Это привело к развитию нелинейной теории электромагнитных волн. При распространении электромагнитной волны в нелинейной среде ее форма изменяется.В зависимости от длины электромагнитных волн существуют различные способы их излучения и регистрации, такие волны по-разному взаимодействуют с веществом и т. п. В вакууме электромагнитные волны распространяются со скоростью света независимо от частоты колебаний. Радиоволны, рентгеновские лучи и гамма-излучение находят свое место в единой шкале электромагнитных волн, причем между соседними диапазонами шкалы нет резкой границы. Процессы излучения и поглощения электромагнитных волн от самых длинных волн до инфракрасного излучения достаточно полно описываются соотношениями электродинамики.Электромагнитные колебания — Википедия
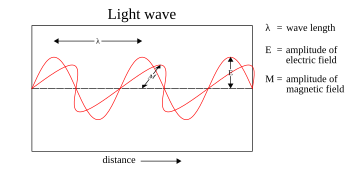 Электромагнитные колебания можно изобразить в виде самораспространяющихся поперечных колебаний электрического и магнитного полей. На рисунке — плоскополяризованная волна, распространяющаяся слева направо. Колебания электрического поля изображены в вертикальной плоскости, а колебания магнитного поля — в горизонтальной.[1]
Электромагнитные колебания можно изобразить в виде самораспространяющихся поперечных колебаний электрического и магнитного полей. На рисунке — плоскополяризованная волна, распространяющаяся слева направо. Колебания электрического поля изображены в вертикальной плоскости, а колебания магнитного поля — в горизонтальной.[1] 
Электромагнитные колебания — периодические изменения напряжённости E{\displaystyle E} и индукции B{\displaystyle B}.
Электромагнитными колебаниями являются радиоволны, микроволны, инфракрасное излучение, видимый свет, ультрафиолетовое излучение, рентгеновские лучи, гамма-лучи.[1]
Существует близкий термин — электрические колебания. Периодические ограниченные изменения величин заряда, тока или напряжения называют электрическими колебаниями[2]. Переменный электрический ток является одним из видов электрических колебаний.
Электромагнитные волны как универсальное явление были предсказаны классическими законами электричества и магнетизма, известными как уравнения Максвелла. Если вы внимательно посмотрите на уравнения Максвелла в отсутствие источников (зарядов или токов), то обнаружите, что помимо тривиального решения, когда напряжённости электрического и магнитного поля равны нулю в каждой точке пространства и ничего не меняется, существуют нетривиальные решения, представляющие собой изменения обеих напряжённостей в пространстве и времени. Начнём с уравнений Максвелла для вакуума:[1]
- ∇⋅E=0,(1){\displaystyle \nabla \cdot \mathbf {E} =0,\qquad (1)}
- ∇×E=−∂∂tB,(2){\displaystyle \nabla \times \mathbf {E} =-{\frac {\partial }{\partial t}}\mathbf {B} ,\qquad (2)}
- ∇⋅B=0,(3){\displaystyle \nabla \cdot \mathbf {B} =0,\qquad (3)}
- ∇×B=μ0ϵ0∂∂tE,(4){\displaystyle \nabla \times \mathbf {B} =\mu _{0}\epsilon _{0}{\frac {\partial }{\partial t}}\mathbf {E} ,\qquad (4)}
где
- ∇{\displaystyle \nabla } — векторный дифференциальный оператор набла.
Система уравнений (1)—(4) имеет тривиальное решение
- E=B=0.{\displaystyle \mathbf {E} =\mathbf {B} =\mathbf {0} .}
Чтобы найти нетривиальное решение, мы воспользуемся векторным тождеством, которое справедливо для любого вектора, в виде:[1]
- ∇×(∇×A)=∇(∇⋅A)−∇2A.{\displaystyle \nabla \times \left(\nabla \times \mathbf {A} \right)=\nabla \left(\nabla \cdot \mathbf {A} \right)-\nabla ^{2}\mathbf {A} .}
Чтобы посмотреть как мы можем использовать его, возьмём операцию вихря от выражения (2):
- ∇×(∇×E)=∇×(−∂B∂t).(5){\displaystyle \nabla \times \left(\nabla \times \mathbf {E} \right)=\nabla \times \left(-{\frac {\partial \mathbf {B} }{\partial t}}\right).\quad (5)}
Левая часть (5) эквивалентна:
- ∇×(∇×E)=∇(∇⋅E)−∇2E=−∇2E,(6){\displaystyle \nabla \times \left(\nabla \times \mathbf {E} \right)=\nabla \left(\nabla \cdot \mathbf {E} \right)-\nabla ^{2}\mathbf {E} =-\nabla ^{2}\mathbf {E} ,\qquad (6)}
где мы упрощаем, используя уравнение (1).
Правая часть эквивалентна:
- ∇×(−∂B∂t)=−∂∂t(∇×B)=−μ0ϵ0∂2∂t2E.(7){\displaystyle \nabla \times \left(-{\frac {\partial \mathbf {B} }{\partial t}}\right)=-{\frac {\partial }{\partial t}}\left(\nabla \times \mathbf {B} \right)=-\mu _{0}\epsilon _{0}{\frac {\partial ^{2}}{\partial t^{2}}}\mathbf {E} .\qquad (7)}
Уравнения (6) и (7) равны, таким образом эти результаты в дифференциальном уравнении для электрического поля, а именно
∇2E=μ0ϵ0∂2∂t2E,{\displaystyle \nabla ^{2}\mathbf {E} =\mu _{0}\epsilon _{0}{\frac {\partial ^{2}}{\partial t^{2}}}\mathbf {E} ,}
[1]Применяя аналогичные исходные результаты в аналогичном дифференциальном уравнении для магнитного поля:
∇2B=μ0ϵ0∂2∂t2B.{\displaystyle \nabla ^{2}\mathbf {B} =\mu _{0}\epsilon _{0}{\frac {\partial ^{2}}{\partial t^{2}}}\mathbf {B} .}
Эти дифференциальные уравнения эквивалентны волновому уравнению:
- ∇2f=1c02∂2f∂t2,{\displaystyle \nabla ^{2}f={\frac {1}{{c_{0}}^{2}}}{\frac {\partial ^{2}f}{\partial t^{2}}},}[1]
где c0{\displaystyle c_{0}} — скорость волны в вакууме, f{\displaystyle f} — описывает смещение.
Или
- ◻f=0,{\displaystyle \Box f=0,}
где ◻{\displaystyle \Box } — оператор Д’Аламбера:
- ◻=∇2−1c02∂2∂t2=∂2∂x2+∂2∂y2+∂2∂z2−1c02∂2∂t2.{\displaystyle \Box =\nabla ^{2}-{\frac {1}{{c_{0}}^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}={\frac {\partial ^{2}}{\partial x^{2}}}+{\frac {\partial ^{2}}{\partial y^{2}}}+{\frac {\partial ^{2}}{\partial z^{2}}}-{\frac {1}{{c_{0}}^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}.}
Заметьте, что в случае электрического и магнитного полей скорость[3].:
- c0=1μ0ϵ0,{\displaystyle c_{0}={\frac {1}{\sqrt {\mu _{0}\epsilon _{0}}}},}
которая есть скорость света в вакууме. Уравнения Максвелла объединили диэлектрическую проницаемость вакуума ε0{\displaystyle \varepsilon _{0}}, магнитную проницаемость вакуума μ0{\displaystyle \mu _{0}} и непосредственно скорость света c0{\displaystyle c_{0}}. До этого вывода не было известно, что была такая строгая связь между светом, электричеством и магнетизмом.
Но имеются только два уравнения, а мы начали с четырёх, поэтому имеется ещё больше информации относительно волн, спрятанных в уравнениях Максвелла. Давайте рассмотрим типичную векторную волну для электрического поля.
- E=E0f(k^⋅x−c0|k|t).{\displaystyle \mathbf {E} =\mathbf {E} _{0}f\left({\hat {\mathbf {k} }}\cdot \mathbf {x} -c_{0}|\mathbf {k} |t\right).}
Здесь E0{\displaystyle \mathbf {E} _{0}} — постоянная амплитуда колебаний, f{\displaystyle f} — любая мгновенная дифференцируемая функция, k^{\displaystyle {\hat {\mathbf {k} }}} — единичный вектор в направлении распространения, а x{\displaystyle {\mathbf {x} }} — радиус-вектор. Мы замечаем, что f(k^⋅x−c0|k|t){\displaystyle f\left({\hat {\mathbf {k} }}\cdot \mathbf {x} -c_{0}|\mathbf {k} |t\right)} — общее решение волнового уравнения. Другими словами
- ∇2f(k^⋅x−c0|k|t)=1c02∂2∂2tf(k^⋅x−c0|k|t),{\displaystyle \nabla ^{2}f\left({\hat {\mathbf {k} }}\cdot \mathbf {x} -c_{0}|\mathbf {k} |t\right)={\frac {1}{{c_{0}}^{2}}}{\frac {\partial ^{2}}{\partial ^{2}t}}f\left({\hat {\mathbf {k} }}\cdot \mathbf {x} -c_{0}|\mathbf {k} |t\right),}
для типичной волны, распространяющейся в k^{\displaystyle {\hat {\mathbf {k} }}} направлении.
Эта форма будет удовлетворять волновому уравнению, но будет ли она удовлетворять всем уравнениям Максвелла, и с чем соответствуется магнитное поле?
- ∇⋅E=k^⋅E0f′(k^⋅x−c0|k|t)=0,{\displaystyle \nabla \cdot \mathbf {E} ={\hat {\mathbf {k} }}\cdot \mathbf {E} _{0}f’\left({\hat {\mathbf {k} }}\cdot \mathbf {x} -c_{0}|\mathbf {k} |t\right)=0,}
- E⋅k^=0.{\displaystyle \mathbf {E} \cdot {\hat {\mathbf {k} }}=0.}
Первое уравнение Максвелла подразумевает, что электрическое поле ортогонально (перпендикулярно) направлению распространению волны.
- ∇×E=k^×E0f′(k^⋅x−c0|k|t)=−∂∂tB,{\displaystyle \nabla \times \mathbf {E} ={\hat {\mathbf {k} }}\times \mathbf {E} _{0}f’\left({\hat {\mathbf {k} }}\cdot \mathbf {x} -c_{0}|\mathbf {k} |t\right)=-{\frac {\partial }{\partial t}}\mathbf {B} ,}
- B=1c0k^×E.{\displaystyle \mathbf {B} ={\frac {1}{c_{0}}}{\hat {\mathbf {k} }}\times \mathbf {E} .}
Второе уравнение Максвелла порождает магнитное поле. Оставшиеся уравнения будут удовлетворяться выбором E,B{\displaystyle \mathbf {E} ,\mathbf {B} }.
Мало того, что волны электрического и магнитного полей распространяются со скоростью света, но они имеют ограниченную ориентацию и пропорциональную величину, E0=c0B0{\displaystyle E_{0}=c_{0}B_{0}}, которую можно сразу же заметить из вектора Пойнтинга. Электрическое поле, магнитное поле и направление распространения волны все являются ортогональными, и распространение волны в том же направлении как вектор E×B{\displaystyle \mathbf {E} \times \mathbf {B} }.
С точки зрения электромагнитной волны, перемещающейся прямолинейно, электрическое поле может колебаться вверх и вниз, в то время как магнитное поле может колебаться вправо и влево, но эта картина может чередоваться с электрическим полем, колеблющемся вправо и влево, и магнитным полем, колеблющимся вверх и вниз. Эта произвольность в ориентации с предпочтением к направлению распространения известна как поляризация.[1]
Шкала электромагнитных волн — это… Что такое Шкала электромагнитных волн?
Электромагни́тное излуче́ние (электромагнитные волны) — распространяющееся в пространстве возмущение электрических и магнитных полей.
Характеристики электромагнитного излучения
Основными характеристиками электромагнитного излучения принято считать частоту, длину волны и поляризацию. Длина волны зависит от скорости распространения излучения. Групповая скорость распространения электромагнитного излучения в вакууме равна скорости света, в других средах эта скорость меньше. Фазовая скорость электромагнитного излучения в вакууме также равна скорости света, в различных средах она может быть как меньше, так и больше скорости света (принцип максимальности скорости света не нарушается, так как скорость переноса энергии и информации в любом случае не превышает световой скорости).
Описанием свойств и параметров электромагнитного излучения занимается электродинамика.
Существуют различные теории, позволяющие смоделировать и исследовать свойства и проявления электромагнитного излучения. Наиболее фундаментальной из них является квантовая электродинамика, из которой путём тех или иных упрощений можно в принципе получить все перечисленные ниже теории, имеющие широкое применение в своих областях. Для описания относительно низкочастотного электромагнитного излучения в макроскопической области используют, как правило, классическую электродинамику, основанную на уравнениях Максвелла, причём существуют упрощения в прикладных применениях. Для оптического излучения (вплоть до рентгеновского диапазона) применяют оптику (в частности, волновую оптику, когда размеры некоторых частей оптической системы близки к длинам волн; квантовую оптику, когда существенны процессы поглощения, излучения и рассеяния фотонов; геометрическую оптику — предельный случай волновой оптики, когда длиной волны излучения можно пренебречь). Гамма-излучение чаще всего является предметом ядерной физики, с других позиций изучается воздействие электромагнитного излучения в радиологии.
Некоторые особенности электромагнитных волн c точки зрения теории колебаний и понятий электродинамики:
- наличие трёх взаимно перпендикулярных (в вакууме) векторов: волнового вектора, вектора напряжённости электрического поля E и вектора напряжённости магнитного поля H.
- Электромагнитные волны — это поперечные волны, в которых вектора напряжённостей электрического и магнитного полей колеблются перпендикулярно направлению распространения волны, но они существенно отличаются от волн на воде и от звука тем, что их можно передать от источника к приёмнику в том числе и через вакуум.
Диапазоны электромагнитного излучения
Электромагнитное излучение принято делить по частотным диапазонам (см. таблицу). Между диапазонами нет резких переходов, они иногда перекрываются, а границы между ними условны. Поскольку скорость распространения излучения постоянна, то частота его колебаний жёстко связана с длиной волны в вакууме.
Радиоволны. Ультракороткие радиоволны принято разделять на метровые, дециметровые, сантиметровые, миллиметровые и субмиллиметровые (микрометровые). Волны с длиной λ < 1 м (ν > 300 МГц) принято также называть микроволнами или волнами сверхвысоких частот (СВЧ). Деление радиоволн на диапазоны см. в статьях Радиоизлучение и Диапазоны частот.
Ионизирующее электромагнитное излучение. К этой группе традиционно относят рентгеновское и гамма-излучение, хотя, строго говоря, ионизировать атомы может и ультрафиолетовое излучение, и даже видимый свет. Границы областей рентгеновского и гамма-излучения могут быть определены лишь весьма условно. Для общей ориентировки можно принять, что энергия рентгеновских квантов лежит в пределах 20 эВ — 0,1 МэВ, а энергия гамма-квантов — больше 0,1 МэВ. В узком смысле гамма-излучение испускается ядром, а рентгеновское — атомной электронной оболочкой при выбивании электрона с низколежащих орбит, хотя эта классификация неприменима к жёсткому излучению, генерируемому без участия атомов и ядер (например, синхротронному или тормозному излучению).
Радиоволны
Из-за больших значений λ распространение радиоволн можно рассматривать без учёта атомистического строения среды. Исключение составляют только самые короткие радиоволны, примыкающие к инфракрасному участку спектра. В радиодиапазоне слабо сказываются и квантовые свойства излучения, хотя их всё же приходится учитывать, в частности, при описании квантовых генераторов и усилителей сантиметрового и миллиметрового диапазонов, а также молекулярных стандартов частоты и времени, при охлаждении аппаратуры до температур в несколько кельвинов.
Радиоволны возникают при протекании по проводникам переменного тока соответствующей частоты. И наоборот, проходящая в пространстве электромагнитная волна возбуждает в проводнике соответствующий ей переменный ток. Это свойство используется в радиотехнике при конструировании антенн.
Естественным источником волн этого диапазона являются грозы. Считается, что они же являются источником стоячих электромагнитных волн Шумана.
Микроволновое излучение
Инфракрасное излучение (Тепловое)
Видимое излучение (Оптическое)
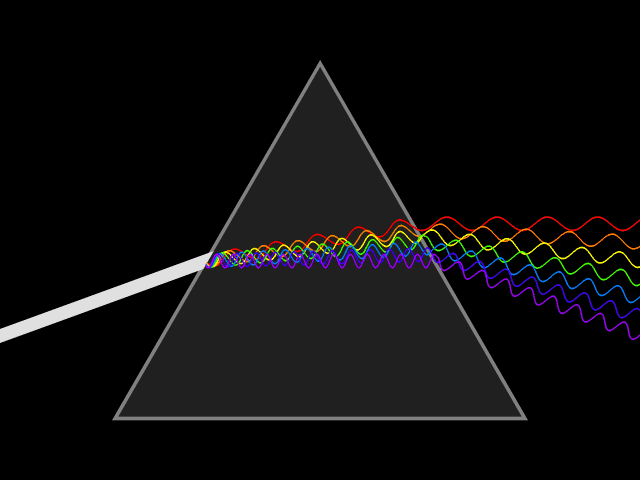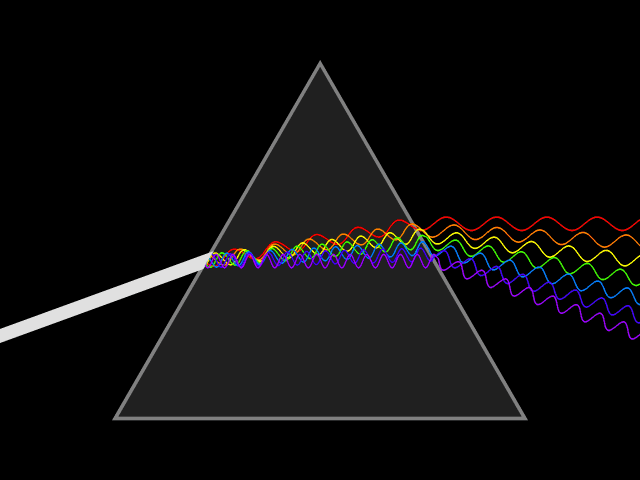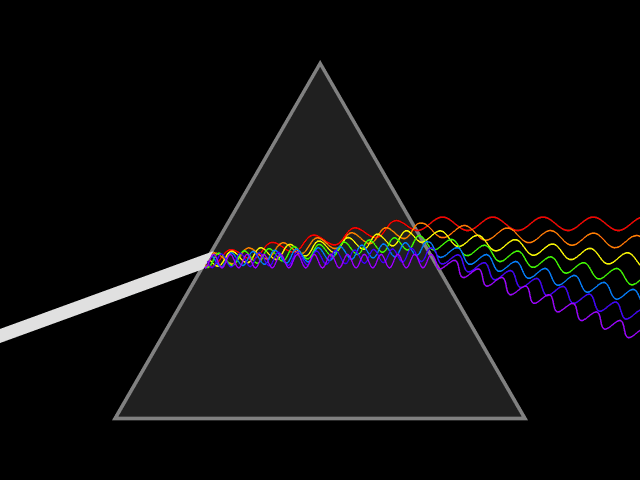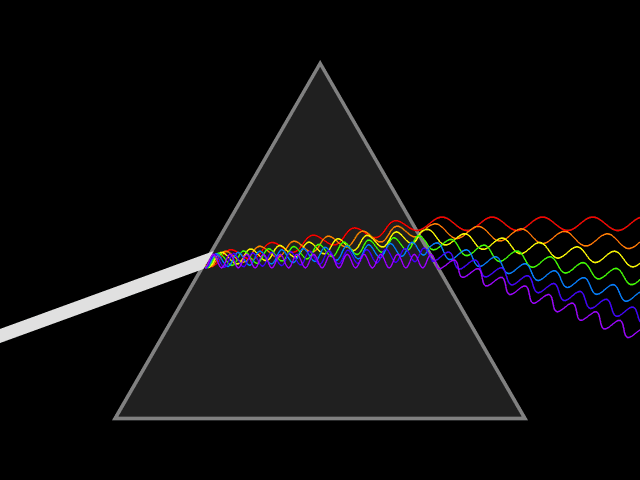 Прозрачная призма разлагает луч белого цвета на составляющие его лучи.
Прозрачная призма разлагает луч белого цвета на составляющие его лучи.Видимое, инфракрасное и ультрафиолетовое излучение составляет так называемую оптическую область спектра в широком смысле этого слова. Выделение такой области обусловлено не только близостью соответствующих участков спектра, но и сходством приборов, применяющихся для её исследования и разработанных исторически главным образом при изучении видимого света (линзы и зеркала для фокусирования излучения, призмы, дифракционные решётки, интерференционные приборы для исследования спектрального состава излучения и пр.).
Частоты волн оптической области спектра уже сравнимы с собственными частотами атомов и молекул, а их длины — с молекулярными размерами и межмолекулярными расстояниями. Благодаря этому в этой области становятся существенными явления, обусловленные атомистическим строением вещества. По этой же причине, наряду с волновыми, проявляются и квантовые свойства света.
Самым известным источником оптического излучения является Солнце. Его поверхность (фотосфера) нагрета до температуры 6000 градусов и светит ярко-белым светом (максимум непрерывного спектра солнечного излучения расположен в «зелёной» области 550 нм, где находится и максимум чувствительности глаза). Именно потому, что мы родились возле такой звезды, этот участок спектра электромагнитного излучения непосредственно воспринимается нашими органами чувств.
Излучение оптического диапазона возникает, в частности, при нагревании тел (инфракрасное излучение называют также тепловым) из-за теплового движения атомов и молекул. Чем сильнее нагрето тело, тем выше частота, на которой находится максимум спектра его излучения (см. Закон смещения Вина). При определённом нагревании тело начинает светиться в видимом диапазоне (каление), сначала красным цветом, потом жёлтым и так далее. И наоборот, излучение оптического спектра оказывает на тела тепловое воздействие (см. Болометрия).
Оптическое излучение может создаваться и регистрироваться в химических и биологических реакциях. Одна из известнейших химических реакций, являющихся приёмником оптического излучения, используется в фотографии. Источником энергии для большинства живых существ на Земле является фотосинтез — биологическая реакция, протекающая в растениях под действием оптического излучения Солнца.
Ультрафиолетовое излучение
Жёсткое излучение
В области рентгеновского и гамма-излучения на первый план выступают квантовые свойства излучения. Рентгеновское излучение возникает при торможении быстрых заряженных частиц (электронов, протонов и пр.), а также в результате процессов, происходящих внутри электронных оболочек атомов. Гамма-излучение появляется в результате процессов, происходящих внутри атомных ядер, а также в результате превращения элементарных частиц. Оно появляется и при торможении быстрых заряженных частиц.
Особенности электромагнитного излучения разных диапазонов
Распространение электромагнитных волн, временны́е зависимости электрического 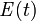 и магнитного
и магнитного 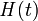 полей, определяющий тип волн (плоские, сферические и др.), вид поляризации и прочие особенности зависят от источника излучения и свойств среды.
полей, определяющий тип волн (плоские, сферические и др.), вид поляризации и прочие особенности зависят от источника излучения и свойств среды.
Электромагнитные излучения различных частот взаимодействуют с веществом также по-разному. Процессы излучения и поглощения радиоволн обычно можно описать с помощью соотношений классической электродинамики; а вот для волн оптического диапазона и, тем более, жестких лучей необходимо учитывать уже их квантовую природу.
История исследований
В 1800 году английский учёный У. Гершель открыл инфракрасное излучение.
Существование электромагнитного излучения теоретически предсказал английский физик Фарадей в 1832 году.
В 1865 году английский физик Дж. Максвелл рассчитал теоретически скорость электромагнитных волн в вакууме.
В 1888 году немецкий физик Герц подтвердил теорию Максвелла опытным путём. Интересно, что Герц не верил в существование этих волн и проводил свой опыт с целью опровергнуть выводы Максвелла.
Электромагнитная безопасность
Излучения электромагнитного диапазона при определённых уровнях могут оказывать отрицательное воздействие на организм человека, животных и других живых существ, а также неблагоприятно влиять на работу электрических приборов. Различные виды неионизирующих излучений (электромагнитных полей, ЭМП) оказывают разное физиологическое воздействие. На практике выделяют диапазоны магнитного поля (постоянного и квазипостоянного, импульсного), ВЧ- и СВЧ-излучений, лазерного излучения, электрического и магнитного поля промышленной частоты от высоковольтного оборудования, СВЧ-излучения и др..
Влияние на живые существа
Существуют национальные и международные гигиенические нормативы уровней ЭМП, в зависимости от диапазона, для селитебной зоны и на рабочих местах.
Оптический диапазон
Существуют гигиенические нормы освещённости; также разработаны нормативы безопасности при работе с лазерным излучением.
Радиоволны
Допустимые уровни электромагнитного излучения (плотность потока электромагнитной энергии) отражаются в нормативах, которые устанавливают государственные компетентные органы, в зависимости от диапазона ЭМП. Эти нормы могут быть существенно различны в разных странах.
Нахождение в зоне с повышенными уровнями ЭМП в течение определённого времени приводит к ряду неблагоприятных последствий: наблюдается усталость, тошнота, головная боль. При значительных превышениях нормативов возможны повреждение сердца, мозга, центральной нервной системы. Излучение может влиять на психику человека, появляется раздражительность, человеку трудно себя контролировать. Возможно развитие трудно поддающихся лечению заболеваний, вплоть до раковых. В частности, корреляционный анализ показал прямую средней силы корреляцию заболеваемости злокачественными заболеваниями головного мозга с максимальной нагрузкой от ЭМИ даже от использования такого маломощного источника, как мобильные радиотелефоны.[1] Эти данные не должны быть причиной для радиофобии, однако очевидна необходимость в существенном углублении сведений о действии ЭМИ на живые организмы.
В России действует СанПиН 2.2.4.1191—03 Электромагнитные поля в производственных условиях, на рабочих местах. Санитарно-эпидемиологические правила и нормативы, а также гигиенические нормативы ГДР (ПДУ) 5803-91 (ДНАОП 0.03-3.22-91) Предельно допустимые уровни (ПДУ) воздействия электромагнитных полей (ЭМП) диапазона частот 10—60 кГц Промышленное электроснабжение 50 Гц [2][3]
- Допустимые уровни излучения базовых станций мобильной связи (900 и 1800 МГц, суммарный уровень от всех источников) в санитарно-селитебной зоне в некоторых странах заметно различаются:
- Украина: 2,5 мкВт/кв.см. (самая жёсткая санитарная норма в Европе)
- Россия, Венгрия: 10 мкВт/кв.см.
- США, Скандинавские страны: 100 мкВт/кв.см.
Параллельное развитие гигиенической науки в СССР и западных странах привело к формированию разных подходов к оценке действия ЭМИ. Для части стран постсоветского пространства сохраняется преимущественно нормирование в единицах плотности потока энергии (ППЭ), а для США и стран ЕС типичным является оценка удельной мощности поглощения (мобильных радиотелефонов (МРТ) не позволяют прогнозировать все неблагоприятные последствия, многие аспекты проблемы не освещены в современной литературе и требуют дополнительных исследований. В связи с этим, согласно рекомендациям ВОЗ, целесообразно придерживаться предупредительной политики, т. е. максимально уменьшить время использования сотовой связи.»
Проникающая неионизирующая радиация
Допустимые нормативы регулируются нормами радиационной безопасности — НРБ-99.
Влияние на радиотехнические устройства
Существует административные и контролирующие органы — инспекция по радиосвязи (на Украине, например, Укрчастотнадзор), которая регулирует распределение частотных диапазонов для различных пользователей, соблюдение выделенных диапазонов, отслеживает незаконное пользование радиоэфиром.
См. также
Ссылки
Литература
- Физика. Большой энциклопедический словарь/Гл. ред. А. М. Прохоров. — 4-е изд. — М.: Большая Российская энциклопедия, 1999. — С. 874—876. ISBN 5-85270-306-0 (БРЭ)
- Кудряшов Ю. Б., Перов Ю. Ф. Рубин А. Б. Радиационная биофизика: радиочастотные и микроволновые электромагнитные излучения. Учебник для ВУЗов. — М.: ФИЗМАТЛИТ, 2008. — 184 с — ISBN 978-5-9221-0848-5
Примечания
- ↑ В. Н. Дунаев «Электромагнитные излучения и риск популяционному здоровью при использовании средств сотовой связи» //Гигиена и санитария, № 6, 2007, с. 56—57
- ↑ ПДУ магнитных полей частот 50 Гц. Харьков, 1986, СН-3206-85.2
- ↑ Методические указания но гигиенической оценке основных параметров полей частотой 50Гц. Харьков, 1986. СН 3207-85
Wikimedia Foundation. 2010.
Поляризация волн — Википедия
У этого термина существуют и другие значения, см. Поляризация. Демонстрация поляризации волн: шнур от ротора перед щелью колеблется по кругу, а за щелью до точки закрепления — линейно
Демонстрация поляризации волн: шнур от ротора перед щелью колеблется по кругу, а за щелью до точки закрепления — линейноПоляриза́ция волн — характеристика поперечных волн, описывающая поведение вектора колеблющейся величины в плоскости, перпендикулярной направлению распространения волны.
В продольной волне поляризация возникнуть не может, так как направление колебаний в волнах этого типа всегда совпадает с направлением распространения[1].
 Отличие волн с круговой и плоской поляризацией
Отличие волн с круговой и плоской поляризациейПоперечная волна характеризуется двумя направлениями: волновым вектором и вектором амплитуды, всегда перпендикулярным к волновому вектору с точностью до движения пространства. Волновой вектор показывает направление распространения волны, а вектор амплитуды показывает, в какую сторону происходят колебания. В трёхмерном пространстве имеется ещё одна степень свободы — возможность вращения вектора амплитуды вокруг волнового вектора. Тройка векторов, сопоставленная каждой точке бирегулярной кривой образует репер Френе.
Причиной возникновения поляризации волн может быть:
- несимметричная генерация волн в источнике возмущения;
- анизотропность среды распространения волн;
- преломление и отражение на границе двух сред.
Поляризация описывается фигурами Лиссажу, и соответствует сложению поперечных колебаний равной частоты (с различным сдвигом фаз). При равенстве частоты колебаний фигуры Лиссажу представляют собой эллипс, двумя крайними формами которого являются круг и отрезок прямой.
В общем случае для гармонических волн конец вектора колеблющейся величины описывает в плоскости, поперечной направлению распространения волны, эллипс: это эллиптическая поляризация. Важными частными случаями являются линейная поляризация, при которой колебания возмущения происходят в какой-то одной плоскости, в таком случае говорят о «плоско-поляризованной волне», и круговая или циркулярная поляризация, при которой конец вектора амплитуды описывает окружность в плоскости колебаний; круговая поляризация (как и эллиптическая) в зависимости от направления вращения вектора может быть положительной или правой и отрицательной или левой.
 Зависимость мгновенных потенциалов при круговой поляризации
Зависимость мгновенных потенциалов при круговой поляризации-

круговая
поляризация -

эллиптическая
поляризация -

линейная
поляризация
Для электромагнитных волн поляризация — явление направленного колебания векторов напряжённости электрического поля E или напряжённости магнитного поля H.
Теория явления[править | править код]
Электромагнитная волна может быть разложена (как теоретически, так и практически) на две поляризованные составляющие, например, поляризованные вертикально и горизонтально. Возможны другие разложения, например, по иной паре взаимно перпендикулярных направлений, или же на две составляющие, имеющие левую и правую круговую поляризацию. При попытке разложить линейно поляризованную волну по круговым поляризациям (или наоборот) возникнут две составляющие половинной интенсивности.
Как с квантовой, так и с классической точки зрения, поляризация может быть описана двумерным комплексным вектором (вектором Джонса). Поляризация фотона является одной из реализаций q-бита.
Свет солнца, являющийся тепловым излучением, не имеет поляризации, однако рассеянный свет неба приобретает частичную линейную поляризацию. Поляризация света меняется также при отражении. На этих фактах основаны применения поляризующих фильтров в фотографии и т. д.
Линейную поляризацию имеет обычно излучение антенн.
По изменению поляризации света при отражении от поверхности можно судить о структуре поверхности, оптических постоянных, толщине образца.
 Ограничить прохождение поляризованного света можно простым поворачиванием поляризационного фильтра.
Ограничить прохождение поляризованного света можно простым поворачиванием поляризационного фильтра.Если рассеянный свет поляризовать, то, используя поляризационный фильтр с иной поляризацией, можно ограничивать прохождение света. Интенсивность света, прошедшего через поляризаторы, подчиняется закону Малюса. На этом принципе работают жидкокристаллические экраны.
Некоторые живые существа, например пчёлы, способны различать линейную поляризацию света, что даёт им дополнительные возможности для ориентации в пространстве. Обнаружено, что некоторые животные, например рак-богомол[2], способны различать циркулярно-поляризованный свет, то есть свет с круговой поляризацией. Некоторые люди также обладают способностью различать поляризацию света[источник не указан 291 день], в частности, эти люди могут наблюдать невооружённым глазом эффекты, связанные с частичной поляризацией света дневного неба. Так описывает этот[источник не указан 291 день] эффект Лев Николаевич Толстой в своей повести «Юность»: «и, вглядываясь в растворенную дверь балкона … , и в чистое небо, на котором, как смотришь пристально, вдруг показывается как будто пыльное желтоватое пятнышко и снова исчезает;»
История открытия поляризации электромагнитных волн[править | править код]
Открытию поляризованных световых волн предшествовали работы многих учёных. В 1669 г. датский учёный Расмус Бартолин сообщил о своих опытах с кристаллами известкового шпата (CaCO3), чаще всего имеющими форму правильного ромбоэдра, которые привозили возвращающиеся из Исландии моряки. Он с удивлением обнаружил, что луч света при прохождении сквозь кристалл расщепляется на два луча (называемых теперь обыкновенным и необыкновенным). Бартолин провёл тщательные исследования обнаруженного им явления двойного лучепреломления, однако объяснения ему дать не смог.
Через двадцать лет после опытов Э. Бартолина его открытие привлекло внимание нидерландского учёного Христиана Гюйгенса. Он сам начал исследовать свойства кристаллов исландского шпата и дал объяснение явлению двойного лучепреломления на основе своей волновой теории света. При этом он ввёл важное понятие оптической оси кристалла, при вращении вокруг которой отсутствует анизотропия свойств кристалла, то есть их зависимость от направления (конечно, такой осью обладают далеко не все кристаллы).
В своих опытах Гюйгенс пошёл дальше Бартолина, пропуская оба луча, вышедшие из кристалла исландского шпата, сквозь второй такой же кристалл. Оказалось, что если оптические оси обоих кристаллов параллельны, то дальнейшего разложения этих лучей уже не происходит. Если же второй ромбоэдр повернуть на 180 градусов вокруг направления распространения обыкновенного луча, то при прохождении через второй кристалл необыкновенный луч претерпевает сдвиг в направлении, противоположном сдвигу в первом кристалле, и из такой системы оба луча выйдут соединёнными в один пучок. Выяснилось также, что в зависимости от величины угла между оптическими осями кристаллов изменяется интенсивность обыкновенного и необыкновенного лучей.
 Волна с круговой поляризацией.
Волна с круговой поляризацией.Эти исследования вплотную подвели Гюйгенса к открытию явления поляризации света, однако решающего шага он сделать не смог, поскольку световые волны в его теории предполагались продольными. Для объяснения опытов Х. Гюйгенса И. Ньютон, придерживавшийся корпускулярной теории света, выдвинул идею об отсутствии осевой симметрии светового луча и этим сделал важный шаг к пониманию поляризации света.
В 1808 г. французский физик Этьен Луи Малюс, глядя сквозь кусок исландского шпата на блестевшие в лучах заходящего солнца окна Люксембургского дворца в Париже, к своему удивлению заметил, что при определённом положении кристалла было видно только одно изображение. На основании этого и других опытов и опираясь на корпускулярную теорию света Ньютона, он предположил, что корпускулы в солнечном свете ориентированы беспорядочно, но после отражения от какой-либо поверхности или прохождения сквозь анизотропный кристалл они приобретают определённую ориентацию. Такой «упорядоченный» свет он назвал поляризованным.
В 1810 году Малюс открыл закон, выражающий зависимость интенсивности линейно-поляризованного света после его прохождения через поляризатор от угла между плоскостями поляризации падающего света и поляризатора. В том же году он создал количественную корпускулярную теорию поляризации света, объяснившую все известные к тому времени поляризационные явления: двойное лучепреломление света в кристаллах, закон Малюса, поляризацию при отражении и преломлении. Несколькими годами позже Био открыл вращение плоскости поляризации, которое сам же и объяснил на основе теории Малюса.
Явление поляризации считалось доказательством корпускулярной теории света и опровержением волновой теории. Но в 1815 году Ампер сказал Френелю, что поляризацию можно объяснить, предположив, что эфир совершает поперечные колебания. В 1817 году ту же гипотезу выдвинул Юнг. В 1821 году Френель создал волновую теорию поляризации света.
В случае плоской монохроматической волны компоненты вектора E→{\displaystyle {\vec {E}}} напряжённости электрического поля (также как и компоненты вектора H→{\displaystyle {\vec {H}}} напряжённости магнитного поля) меняются совместно по гармоническому закону:
- {Ex=E1cos(τ+δ1)Ey=E2cos(τ+δ2)Ez=0{\displaystyle {\begin{cases}E_{x}=E_{1}\cos \left(\tau +\delta _{1}\right)\\E_{y}=E_{2}\cos \left(\tau +\delta _{2}\right)\\E_{z}=0\end{cases}}}
Здесь набег фазы τ=kz−ωt{\displaystyle \tau =kz-\omega t}.
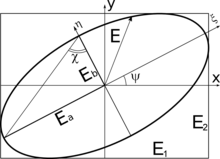 Поляризационный эллипс
Поляризационный эллипсПреобразовав и сложив первые два уравнения, можно получить уравнение движения вектора E→{\displaystyle {\vec {E}}}:
- (ExE1)2+(EyE2)2−2ExE1EyE2cos(δ)=sin2δ{\displaystyle \left({\frac {E_{x}}{E_{1}}}\right)^{2}+\left({\frac {E_{y}}{E_{2}}}\right)^{2}-2{\frac {E_{x}}{E_{1}}}{\frac {E_{y}}{E_{2}}}\cos(\delta )=\sin ^{2}{\delta }}, где разность фаз δ=δ1−δ2{\displaystyle \delta =\delta _{1}-\delta _{2}}.
Эта квадратичная форма описывает эллипс. То есть конец вектора напряжённости плоской монохроматической волны описывает эллипс. Для того, чтобы привести её к каноническому виду, нужно повернуть эллипс на угол ψ{\displaystyle \psi }:
- {Eξ=Excosψ+EysinψEη=−Exsinψ+Eycosψ{\displaystyle {\begin{cases}E_{\xi }=E_{x}\cos {\psi }+E_{y}\sin {\psi }\\E_{\eta }=-E_{x}\sin {\psi }+E_{y}\cos {\psi }\end{cases}}}
Любой эллипс можно задать в параметрической форме:
- {Eξ=Eacos(τ+δ)Eη=Ebsin(τ+δ){\displaystyle {\begin{cases}E_{\xi }=E_{a}\cos \left(\tau +\delta \right)\\E_{\eta }=E_{b}\sin \left(\tau +\delta \right)\end{cases}}}
Здесь Ea{\displaystyle E_{a}} и Eb{\displaystyle E_{b}} — амплитудные значения компонент вектора E→{\displaystyle {\vec {E}}}, соответствующие большой и малой полуосям эллипса. Из последних двух систем уравнений можно сделать следующий вывод:
- S0∼Ea2+Eb2=E12+E22{\displaystyle S_{0}\sim E_{a}^{2}+E_{b}^{2}=E_{1}^{2}+E_{2}^{2}},
где S0{\displaystyle S_{0}} — вектор Пойнтинга. Таким образом, в плоской монохроматической волне величина вектора Пойнтинга равна сумме потоков в двух произвольных ортогональных направлениях. Вводя обозначения tgα=E1/E2{\displaystyle \mathrm {tg} \,{\alpha }=E_{1}/E_{2}} и tgχ=Eb/Ea{\displaystyle \mathrm {tg} \,{\chi }=E_{b}/E_{a}}, из тех же двух систем уравнений можно вывести соотношения:
- tg2ψ=−tg2αcosδ{\displaystyle \mathrm {tg} \,{2\psi }=-\mathrm {tg} \,{2\alpha }\cos {\delta }}
и
- ±tg2χ=sin2ψtgδ{\displaystyle \pm \mathrm {tg} \,{2\chi }=\sin {2\psi }\,\mathrm {tg} \,{\delta }}.[3]
С помощью последних трёх уравнений можно вычислить все параметры эллиптически поляризованной волны. А именно, зная величины E1{\displaystyle E_{1}} и E2{\displaystyle E_{2}} в произвольной системе координат, можно вычислить величину вектора Пойнтинга. С помощью разности фаз δ{\displaystyle \delta } можно определить угол поворота большой оси эллипса ψ{\displaystyle \psi } относительно нашей системы координат, а также величины большой и малой полуосей эллипса Ea{\displaystyle E_{a}} и Eb{\displaystyle E_{b}}.
Направление вращения вектора E→{\displaystyle {\vec {E}}} определяется разностью фаз δ{\displaystyle \delta }. Если sinδ>0{\displaystyle \sin \delta >0}, тогда поляризация называется правой, а если, напротив, sinδ<0{\displaystyle \sin \delta <0}, поляризация называется левой. В оптике (где важна плоскость изображения) если наблюдатель смотрит навстречу световому лучу, то правой поляризации соответствует движение конца вектора по часовой стрелке, а левой поляризации — против часовой стрелки. В радиофизике принято наоборот: если смотреть навстречу излучению, то вращение E→{\displaystyle {\vec {E}}} против часовой — правая поляризация, по часовой — левая. Если разность фаз равна mπ{\displaystyle m\pi }, где m{\displaystyle m} — целое число, то эллипс вырождается в отрезок. Такая поляризация называется линейной. Другой важный случай возникает, когда E1=E2=E{\displaystyle E_{1}=E_{2}=E} и δ=π2(1+2m){\displaystyle \delta ={\frac {\pi }{2}}\left(1+2m\right)}. В этом случае эллипс превращается в окружность, параметрическое уравнение которой имеет вид:
- {Ex=EcosτEy=±Ecos(τ−π2){\displaystyle {\begin{cases}E_{x}=E\cos \tau \\E_{y}=\pm E\cos {\left(\tau -{\frac {\pi }{2}}\right)}\end{cases}}}
Нетрудно убедиться, что произвольная эллиптическая поляризация может быть разложена на сумму правой и левой круговых поляризаций.
Параметры Стокса[править | править код]
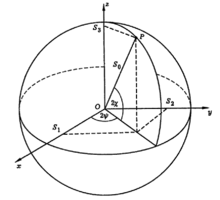 Изображение поляризации языком параметров Стокса на сфере Пуанкаре
Изображение поляризации языком параметров Стокса на сфере ПуанкареДля описания поляризации плоской монохроматической волны достаточно трёх параметров, например:
амплитуд колебаний по осям X и Y (полудлин сторон прямоугольника, в который вписан эллипс поляризации) E1{\displaystyle E_{1}}, E2{\displaystyle E_{2}} и разностью фаз δ{\displaystyle \delta }(между колебаниями по X и по Y), либо
полуосей эллипса Ea{\displaystyle E_{a}}, Eb{\displaystyle E_{b}} и угла ψ{\displaystyle \psi } между осью x{\displaystyle x} и большой осью эллипса (азимутального угла эллипса или азимута, иначе называемого углом наклона эллипса). Стоксом было предложено альтернативное описание поляризации с помощью четырёх параметров, получивших его имя.
- S0=E12+E22{\displaystyle S_{0}=E_{1}^{2}+E_{2}^{2}},
- S1=E12−E22{\displaystyle S_{1}=E_{1}^{2}-E_{2}^{2}},
- S2=2E1E2cosδ{\displaystyle S_{2}=2E_{1}E_{2}\cos {\delta }},
- S3=2E1E2sinδ{\displaystyle S_{3}=2E_{1}E_{2}\sin {\delta }}.
Независимыми являются только три из них, ибо справедливо тождество:
- S02=S12+S22+S32{\displaystyle S_{0}^{2}=S_{1}^{2}+S_{2}^{2}+S_{3}^{2}}.
И в этом представлении для описания поляризации плоской монохроматической волны достаточно знать три параметра за исключением того, что не будет известен знак вычисляемого S1{\displaystyle S_{1}}, S2{\displaystyle S_{2}} или S3{\displaystyle S_{3}}.
Примечание: случай частичной поляризации с S02>S12+S22+S32{\displaystyle S_{0}^{2}>S_{1}^{2}+S_{2}^{2}+S_{3}^{2}} здесь не рассматривается.
Если использовать вспомогательные углы
угол эллиптичности эллипса поляризации χ{\displaystyle \chi }, определяемый выражением tg(χ)=±Eb/Ea{\displaystyle \mathrm {tg} \,(\chi )=\pm E_{b}/E_{a}} (в радиофизике знак +{\displaystyle +} соответствует левой, а −{\displaystyle -} — правой поляризации[4], в оптике — наоборот) , и
азимут эллипса поляризации ψ{\displaystyle \psi }, то можно получить следующие выражения для параметров Стокса:
- S1=S0cos(2χ)cos(2ψ){\displaystyle S_{1}=S_{0}\cos(2\chi )\cos(2\psi )},
- S2=S0cos(2χ)sin(2ψ){\displaystyle S_{2}=S_{0}\cos(2\chi )\sin(2\psi )},
- S3=S0sin(2χ){\displaystyle S_{3}=S_{0}\sin(2\chi )}.
На основе этих формул можно характеризовать поляризацию световой волны наглядным геометрическим способом. При этом параметры Стокса S1{\displaystyle S_{1}}, S2{\displaystyle S_{2}}, S3{\displaystyle S_{3}} интерпретируются, как декартовы координаты точки, лежащей на поверхности сферы радиуса S0{\displaystyle S_{0}}. Углы 2χ{\displaystyle 2\chi } и 2ψ{\displaystyle 2\psi } имеют смысл сферических угловых координат этой точки. Такое геометрическое представление предложил Пуанкаре [уточнить], поэтому эта сфера называется сферой Пуанкаре. В математике этой модели соответствует сфера Римана, в других разделах физики — сфера Блоха.
Наряду с S1{\displaystyle S_{1}}, S2{\displaystyle S_{2}}, S3{\displaystyle S_{3}} используют также нормированные параметры Стокса s1=S1/S0{\displaystyle s_{1}=S_{1}/S_{0}}, s2=S2/S0{\displaystyle s_{2}=S_{2}/S_{0}}, s3=S3/S0{\displaystyle s_{3}=S_{3}/S_{0}}. Для поляризованного света s12+s22+s32=1{\displaystyle s_{1}^{2}+s_{2}^{2}+s_{3}^{2}=1}.
s— и p-поляризации волн[править | править код]
Подробнее смотрите Формулы Френеля.
В оптике и электродинамике s-поляризованная волна (сравните нем. senkrecht — перпендикулярный) имеет вектор электрического поля E, перпендикулярный плоскости падения. s-поляризованную волну также называют σ-поляризованной, сагиттально поляризованной, волной E-типа[5], TE-волной (Transverse Electric)[6]. p-поляризованная волна (сравните лат. parallel — параллельный) имеет вектор электрического поля E, параллельный плоскости падения. p-поляризованную волну также называют π-поляризованной, поляризованной в плоскости падения, волной H-типа[5], TM-волной (Transverse Magnetic)[6].
Термины TM-волна и TE-волна в работах ряда авторов[7][8] меняются местами. Дело в том, что классически плоская граница предполагает однородность структуры в двух направлениях. В этом случае определяют плоскость падения и перпендикулярность напряжённостей по отношению к ней. Разделение электромагнитного поля на два несвязанных решения возможно в более общем случае структуры, однородной в одном направлении. В этом случае удобно определять перпендикулярность напряжённостей по отношению к направлению однородности[7]. Распространение последнего определения на частный классический случай приводит к тому, что напряжённость, перпендикулярная к направлению однородности, оказывается в плоскости падения. Отмечается, что в случае металлической поверхности существенны только волны с электрической напряжённостью, перпендикулярной к границе металла[7]. Такие волны также удобнее называть TE-волнами. Термины TM и TE связаны также с обозначением поперечных мод в лазерном резонаторе или волноводе.
В сейсмологии p-волна (от англ. primary — первичный) — продольная волна, приходящая от эпицентра землетрясения первой. s-волна (от англ. secondary — вторичный) — поперечная волна (shear wave), имеющая меньшую скорость распространения, чем продольная, и поэтому приходящая от эпицентра позднее.
 Левое изображение снято без фильтра, правое — через поляризационный фильтр
Левое изображение снято без фильтра, правое — через поляризационный фильтрСкорость распространения волны может зависеть от её поляризации.
Две волны, линейно поляризованные под прямым углом друг к другу, не интерферируют.
Чаще всего это явление используется для создания различных оптических эффектов, а также в 3D-кинематографе (технология IMAX), где поляризация используется для разделения изображений, предназначенных правому и левому глазу.
Круговая поляризация применяется в антеннах космических линий связи, так как для приёма сигнала не важно положение плоскости поляризации передающей и приёмной антенн. То есть вращение космического аппарата не повлияет на возможность связи с ним. Направление вращения круговой поляризации космической приемопередающей антенны должно совпадать с направлением вращения наземной приёмопередающей антенны, работающей с космической. То же самое с антеннами линейной поляризации. В космической связи используется поляризационная развязка, то есть на одной частоте работают антенны противоположных направлений вращения поляризации или ортогональные с линейной поляризацией.
Антенну круговой поляризации выполнить сложнее, чем антенну линейной поляризации, для этого нужен поляризатор. Антенну с поляризацией правого направления вращения легко переделать в левого направления вращения. Для этого нужно повернуть на 90 градусов относительно оси вращения её поляризатор. Вообще, круговая поляризация — вещь теоретическая. На практике говорят об антеннах эллиптической поляризации — с левым или правым направлением вращения.
Круговая поляризация света используется также в технологиях стереокинематографа RealD и MasterImage. Эти технологии подобны IMAX с той разницей, что круговая поляризация вместо линейной позволяет сохранять стереоэффект и избегать двоения изображения при небольших боковых наклонах головы.
Поляризация волн находит применение в поляризационной голографии[9].
Аналогичный эффект наблюдается при квантовомеханическом рассмотрении пучка частиц, обладающих спином. Состояние отдельной частицы в этом случае, вообще говоря, не является чистым и должно описываться соответствующей матрицей плотности. Для частицы со спином ½ (скажем, электрона) это эрмитова матрица 2×2 ρba{\displaystyle \rho _{b}^{a}} со следом 1:
- ρab=ρab†=ρ¯ba
Микроволновое излучение — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 3 марта 2017; проверки требуют 15 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 3 марта 2017; проверки требуют 15 правок.Микрово́лновое излучение, сверхвысокочасто́тное излуче́ние (СВЧ-излучение) — электромагнитное излучение, включающее в себя дециметровый, сантиметровый и миллиметровый диапазоны радиоволн, частоты микроволнового излучения изменяются от 300 МГц до 300 ГГц (длина волны от 1 м до 1 мм). Данное определение относит к микроволнам как УВЧ диапазон (дециметровые волны), так и КВЧ диапазон (миллиметровые волны), тогда как в радиолокации микроволновым диапазоном принято обозначать волны с частотами от 1 до 100 ГГц (с длинами волн от 300 до 3 мм). В обоих определениях микроволновое излучение включает в себя СВЧ диапазон.
Микроволновое излучение большой интенсивности используется для бесконтактного нагрева тел (в бытовых микроволновых печах — для разогрева продуктов, в промышленных — для термообработки металлов, в хирургии — при радиочастотной абляции вен[1]; основным элементом здесь служит магнетрон), а также для радиолокации.
Микроволновое излучение малой интенсивности используется в средствах связи, преимущественно портативных — рациях, сотовых телефонах (кроме первых поколений), устройствах Bluetooth, Wi-Fi и WiMAX.
Поддиапазоны СВЧ в различных системах обозначений различаются; используемые в спутниковой связи приведены в таблице.
| Диапазоны частот | ||
| Название | Частотный диапазон, ГГц | |
|---|---|---|
| Название диапазона | Диапазон частот РЛС | Диапазон частот в спутниковой связи |
| L | 1,0—2,0 | |
| S | 2,0—4,0 | |
| C | 4,0—8,0 | 3,4—8,0 |
| X | 8,0—12,0 | 7,0—10,7 |
| Ku | 12,0—18,0 | 10,7—18,0 |
| K | 18,0—26,5 | 18,3—20,2; 27,5—31,5 |
| Ka | 26,5—40,0 | |
Геликон (физика) — Википедия
Геликон (др.-греч. ἕλιξ, род. падеж. ἕλικος — кольцо, спираль) — низкочастотная электромагнитная волна, которая возникает в некомпенсированной плазме, находящейся во внешнем постоянном магнитном поле.
Существование электромагнитных возбуждений геликонного типа в плазме твердых тел было предсказано в 1960 году: в металлах — О. В. Константиновым и В. И. Перелем[1], в полупроводниках — П. Эгреном[2]. Термин «геликон» был введен Эгреном и отражал круговой характер поляризации этой волны. Через год геликоны были экспериментально обнаружены в натрии[3]. В том же году было установлено, что так называемые «свистящие атмосферики» (вистлеры) представляют собой геликонные волны, распространяющиеся в газовой плазме ионосферы Земли.
Возможность распространения электромагнитных волн в хорошо проводящих средах в присутствии сильного магнитного поля можно пояснить следующим образом. В отсутствие магнитного поля в среде имеет место скин-эффект: под действием излучения с частотой, меньшей плазменной, возникают токи, которые экранируют электромагнитное возмущение и препятствуют его проникновению вглубь вещества. Магнитное поле ослабляет это экранирование, заставляя носители заряда под действием силы Лоренца двигаться более упорядоченно и мешая им эффективно реагировать на поле электромагнитной волны. Это дает возможность распространения в среде низкочастотных геликонов.
В зависимости от соотношения длины свободного пробега носителей заряда и длины волны электромагнитного возбуждения выделяют «локальный» и «нелокальный» режимы распространения геликонов. Для рассмотрения каждого из этих случаев приходится применять различные теоретические и экспериментальные подходы.
Локальный режим[править | править код]
Условие локальности может быть записано в виде ql<<1{\displaystyle ql<<1}, где q{\displaystyle q} — волновое число геликона, l{\displaystyle l} — длина свободного пробега носителей заряда (электронов). Основные особенности геликонных волн могут быть получены в модели свободных электронов. Рассматривая падение на проводящую среду электромагнитной волны частоты ω{\displaystyle \omega } в условиях мгновенного равновесия, можно получить дисперсионное соотношение для геликона:
q±2=ωμ0/ρ(±u+i)cosϕ{\displaystyle q_{\pm }^{2}=\omega \mu _{0}/\rho (\pm u+i)\cos \phi },
где μ0{\displaystyle \mu _{0}} — магнитная проницаемость вакуума, ρ=m/ne2τ{\displaystyle \rho =m/ne^{2}\tau } — сопротивление, u=RB0/ρ=ωcτ{\displaystyle u=RB_{0}/\rho =\omega _{c}\tau } — тангенс угла Холла между током и напряженностью электрического поля, B0{\displaystyle B_{0}} — постоянное магнитное поле, ϕ{\displaystyle \phi } — угол между q{\displaystyle q} и B0{\displaystyle B_{0}}. Здесь m{\displaystyle m} — масса электрона, e{\displaystyle e} — его заряд, n{\displaystyle n} — плотность электронов, τ{\displaystyle \tau } — характерное время, за которое носители теряют импульс при столкновениях с решеткой; R=1/ne{\displaystyle R=1/ne} — константа Холла, ωc=eB0/m{\displaystyle \omega _{c}=eB_{0}/m} — циклотронная частота носителей. Условием распространяющихся волн является неравенство |Req|>>|Imq|{\displaystyle |{\rm {Re}}q|>>|{\rm {Im}}q|}. В полубесконечном металле геликон, распространяющийся вдоль постоянного магнитного поля, является поперечной циркулярно поляризованной волной, электрическое и магнитное поля которой вращаются вокруг направления распространения в том же направлении, что и электроны.
В общем случае необходимо учитывать тензорный характер параметров среды, в частности сопротивления ρ{\displaystyle \rho }, а также граничные условия в ситуации пространственно ограниченных структур.
Нелокальный режим[править | править код]
Условием нелокальности является соотношение ql>>1{\displaystyle ql>>1}, то есть на длине свободного пробега укладывается много длин волн геликона. Поэтому в данном случае нельзя пренебрегать микроскопическим (циклотронным) движением носителей заряда. С математической точки зрения это приводит к необходимости вычисления нелокального тензора проводимости. Физическую картину в нелокальном случае определяют эффекты бесстолновительного поглощения волны носителями, крайними случаями которого являются доплер-сдвинутый циклотронный резонанс (условие поглощения qVF/ωc>1{\displaystyle qV_{F}/\omega _{c}>1}, где VF{\displaystyle V_{F}} — скорость свободных электронов, равная скорости Ферми) и магнитное затухание Ландау (qVF/ωc<<1{\displaystyle qV_{F}/\omega _{c}<<1}). Эти процессы существенно ограничивают диапазон существования распространяющихся геликонных волн.
Методы исследования[править | править код]
К основным методам наблюдения и изучения геликонов относятся:
Результаты исследований[править | править код]
Экспериментальные наблюдения геликонов в локальном режиме позволяют измерить константу Холла, магнетосопротивление, поверхностное поглощение волн при различных геометриях образцов.
Эксперименты в нелокальном режиме в условиях циклотронного поглощения и затухания Ландау позволяют определять поверхностный импеданс образцов, форму поверхности Ферми, оценить роль столкновений в процессах затухания. Отдельным направлением исследований является изучение взаимодействия геликонов с другими типами возбуждения в веществе: со звуком (геликон-фононное взаимодействие, позволяющее осуществлять электромагнитное возбуждение акустических волн), с магнитными моментами ядер (ЯМР-поглощение геликона), со спиновыми волнами в ферромагнетиках (геликон-магнонное взаимодействие).
Обычно геликоны в лабораторных экспериментах получают в плазме твёрдых тел или разрядных трубках с газовой плазмой. В 2015 году американские исследователи сообщили о получении геликонов в неограниченной плазме, вдали от каких-либо поверхностей. Это достижение позволяет изучить в лаборатории возникновение таких волн в ситуации, близкой к условиям, имеющимся в космическом пространстве.[4]
- ↑ О.В. Константинов, В.И. Перель. О возможности прохождения электромагнитных волн через металл в сильном магнитном поле. // ЖЭТФ. — 1960. — Т. 38. — С. 161.
- ↑ P. Aigrain. Les «Helicons» dans les semiconducteurs. // Рrос. Int. Conf. on Semiconduction Phys., Prague, 1960. — С. 224.
- ↑ R. Bowers, C. Legendy, and F. Rose. Oscillatory Galvanomagnetic Effect in Metallic Sodium. // Phys. Rev. Lett. — 1961. — Т. 7, № 9. — С. 339-341.
- ↑ Stenzel R. L., Urrutia J. M. Helicons in Unbounded Plasmas // Physical Review Letters. — 2015. — Vol. 114. — DOI:10.1103/PhysRevLett.114.205005.
Шкала электромагнитных волн — это… Что такое Шкала электромагнитных волн?
Электромагни́тное излуче́ние (электромагнитные волны) — распространяющееся в пространстве возмущение электрических и магнитных полей.
Характеристики электромагнитного излучения
Основными характеристиками электромагнитного излучения принято считать частоту, длину волны и поляризацию. Длина волны зависит от скорости распространения излучения. Групповая скорость распространения электромагнитного излучения в вакууме равна скорости света, в других средах эта скорость меньше. Фазовая скорость электромагнитного излучения в вакууме также равна скорости света, в различных средах она может быть как меньше, так и больше скорости света (принцип максимальности скорости света не нарушается, так как скорость переноса энергии и информации в любом случае не превышает световой скорости).
Описанием свойств и параметров электромагнитного излучения занимается электродинамика.
Существуют различные теории, позволяющие смоделировать и исследовать свойства и проявления электромагнитного излучения. Наиболее фундаментальной из них является квантовая электродинамика, из которой путём тех или иных упрощений можно в принципе получить все перечисленные ниже теории, имеющие широкое применение в своих областях. Для описания относительно низкочастотного электромагнитного излучения в макроскопической области используют, как правило, классическую электродинамику, основанную на уравнениях Максвелла, причём существуют упрощения в прикладных применениях. Для оптического излучения (вплоть до рентгеновского диапазона) применяют оптику (в частности, волновую оптику, когда размеры некоторых частей оптической системы близки к длинам волн; квантовую оптику, когда существенны процессы поглощения, излучения и рассеяния фотонов; геометрическую оптику — предельный случай волновой оптики, когда длиной волны излучения можно пренебречь). Гамма-излучение чаще всего является предметом ядерной физики, с других позиций изучается воздействие электромагнитного излучения в радиологии.
Некоторые особенности электромагнитных волн c точки зрения теории колебаний и понятий электродинамики:
- наличие трёх взаимно перпендикулярных (в вакууме) векторов: волнового вектора, вектора напряжённости электрического поля E и вектора напряжённости магнитного поля H.
- Электромагнитные волны — это поперечные волны, в которых вектора напряжённостей электрического и магнитного полей колеблются перпендикулярно направлению распространения волны, но они существенно отличаются от волн на воде и от звука тем, что их можно передать от источника к приёмнику в том числе и через вакуум.
Диапазоны электромагнитного излучения
Электромагнитное излучение принято делить по частотным диапазонам (см. таблицу). Между диапазонами нет резких переходов, они иногда перекрываются, а границы между ними условны. Поскольку скорость распространения излучения постоянна, то частота его колебаний жёстко связана с длиной волны в вакууме.
Радиоволны. Ультракороткие радиоволны принято разделять на метровые, дециметровые, сантиметровые, миллиметровые и субмиллиметровые (микрометровые). Волны с длиной λ < 1 м (ν > 300 МГц) принято также называть микроволнами или волнами сверхвысоких частот (СВЧ). Деление радиоволн на диапазоны см. в статьях Радиоизлучение и Диапазоны частот.
Ионизирующее электромагнитное излучение. К этой группе традиционно относят рентгеновское и гамма-излучение, хотя, строго говоря, ионизировать атомы может и ультрафиолетовое излучение, и даже видимый свет. Границы областей рентгеновского и гамма-излучения могут быть определены лишь весьма условно. Для общей ориентировки можно принять, что энергия рентгеновских квантов лежит в пределах 20 эВ — 0,1 МэВ, а энергия гамма-квантов — больше 0,1 МэВ. В узком смысле гамма-излучение испускается ядром, а рентгеновское — атомной электронной оболочкой при выбивании электрона с низколежащих орбит, хотя эта классификация неприменима к жёсткому излучению, генерируемому без участия атомов и ядер (например, синхротронному или тормозному излучению).
Радиоволны
Из-за больших значений λ распространение радиоволн можно рассматривать без учёта атомистического строения среды. Исключение составляют только самые короткие радиоволны, примыкающие к инфракрасному участку спектра. В радиодиапазоне слабо сказываются и квантовые свойства излучения, хотя их всё же приходится учитывать, в частности, при описании квантовых генераторов и усилителей сантиметрового и миллиметрового диапазонов, а также молекулярных стандартов частоты и времени, при охлаждении аппаратуры до температур в несколько кельвинов.
Радиоволны возникают при протекании по проводникам переменного тока соответствующей частоты. И наоборот, проходящая в пространстве электромагнитная волна возбуждает в проводнике соответствующий ей переменный ток. Это свойство используется в радиотехнике при конструировании антенн.
Естественным источником волн этого диапазона являются грозы. Считается, что они же являются источником стоячих электромагнитных волн Шумана.
Микроволновое излучение
Инфракрасное излучение (Тепловое)
Видимое излучение (Оптическое)
 Прозрачная призма разлагает луч белого цвета на составляющие его лучи.
Прозрачная призма разлагает луч белого цвета на составляющие его лучи.Видимое, инфракрасное и ультрафиолетовое излучение составляет так называемую оптическую область спектра в широком смысле этого слова. Выделение такой области обусловлено не только близостью соответствующих участков спектра, но и сходством приборов, применяющихся для её исследования и разработанных исторически главным образом при изучении видимого света (линзы и зеркала для фокусирования излучения, призмы, дифракционные решётки, интерференционные приборы для исследования спектрального состава излучения и пр.).
Частоты волн оптической области спектра уже сравнимы с собственными частотами атомов и молекул, а их длины — с молекулярными размерами и межмолекулярными расстояниями. Благодаря этому в этой области становятся существенными явления, обусловленные атомистическим строением вещества. По этой же причине, наряду с волновыми, проявляются и квантовые свойства света.
Самым известным источником оптического излучения является Солнце. Его поверхность (фотосфера) нагрета до температуры 6000 градусов и светит ярко-белым светом (максимум непрерывного спектра солнечного излучения расположен в «зелёной» области 550 нм, где находится и максимум чувствительности глаза). Именно потому, что мы родились возле такой звезды, этот участок спектра электромагнитного излучения непосредственно воспринимается нашими органами чувств.
Излучение оптического диапазона возникает, в частности, при нагревании тел (инфракрасное излучение называют также тепловым) из-за теплового движения атомов и молекул. Чем сильнее нагрето тело, тем выше частота, на которой находится максимум спектра его излучения (см. Закон смещения Вина). При определённом нагревании тело начинает светиться в видимом диапазоне (каление), сначала красным цветом, потом жёлтым и так далее. И наоборот, излучение оптического спектра оказывает на тела тепловое воздействие (см. Болометрия).
Оптическое излучение может создаваться и регистрироваться в химических и биологических реакциях. Одна из известнейших химических реакций, являющихся приёмником оптического излучения, используется в фотографии. Источником энергии для большинства живых существ на Земле является фотосинтез — биологическая реакция, протекающая в растениях под действием оптического излучения Солнца.
Ультрафиолетовое излучение
Жёсткое излучение
В области рентгеновского и гамма-излучения на первый план выступают квантовые свойства излучения. Рентгеновское излучение возникает при торможении быстрых заряженных частиц (электронов, протонов и пр.), а также в результате процессов, происходящих внутри электронных оболочек атомов. Гамма-излучение появляется в результате процессов, происходящих внутри атомных ядер, а также в результате превращения элементарных частиц. Оно появляется и при торможении быстрых заряженных частиц.
Особенности электромагнитного излучения разных диапазонов
Распространение электромагнитных волн, временны́е зависимости электрического 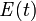 и магнитного
и магнитного 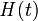 полей, определяющий тип волн (плоские, сферические и др.), вид поляризации и прочие особенности зависят от источника излучения и свойств среды.
полей, определяющий тип волн (плоские, сферические и др.), вид поляризации и прочие особенности зависят от источника излучения и свойств среды.
Электромагнитные излучения различных частот взаимодействуют с веществом также по-разному. Процессы излучения и поглощения радиоволн обычно можно описать с помощью соотношений классической электродинамики; а вот для волн оптического диапазона и, тем более, жестких лучей необходимо учитывать уже их квантовую природу.
История исследований
В 1800 году английский учёный У. Гершель открыл инфракрасное излучение.
Существование электромагнитного излучения теоретически предсказал английский физик Фарадей в 1832 году.
В 1865 году английский физик Дж. Максвелл рассчитал теоретически скорость электромагнитных волн в вакууме.
В 1888 году немецкий физик Герц подтвердил теорию Максвелла опытным путём. Интересно, что Герц не верил в существование этих волн и проводил свой опыт с целью опровергнуть выводы Максвелла.
Электромагнитная безопасность
Излучения электромагнитного диапазона при определённых уровнях могут оказывать отрицательное воздействие на организм человека, животных и других живых существ, а также неблагоприятно влиять на работу электрических приборов. Различные виды неионизирующих излучений (электромагнитных полей, ЭМП) оказывают разное физиологическое воздействие. На практике выделяют диапазоны магнитного поля (постоянного и квазипостоянного, импульсного), ВЧ- и СВЧ-излучений, лазерного излучения, электрического и магнитного поля промышленной частоты от высоковольтного оборудования, СВЧ-излучения и др..
Влияние на живые существа
Существуют национальные и международные гигиенические нормативы уровней ЭМП, в зависимости от диапазона, для селитебной зоны и на рабочих местах.
Оптический диапазон
Существуют гигиенические нормы освещённости; также разработаны нормативы безопасности при работе с лазерным излучением.
Радиоволны
Допустимые уровни электромагнитного излучения (плотность потока электромагнитной энергии) отражаются в нормативах, которые устанавливают государственные компетентные органы, в зависимости от диапазона ЭМП. Эти нормы могут быть существенно различны в разных странах.
Нахождение в зоне с повышенными уровнями ЭМП в течение определённого времени приводит к ряду неблагоприятных последствий: наблюдается усталость, тошнота, головная боль. При значительных превышениях нормативов возможны повреждение сердца, мозга, центральной нервной системы. Излучение может влиять на психику человека, появляется раздражительность, человеку трудно себя контролировать. Возможно развитие трудно поддающихся лечению заболеваний, вплоть до раковых. В частности, корреляционный анализ показал прямую средней силы корреляцию заболеваемости злокачественными заболеваниями головного мозга с максимальной нагрузкой от ЭМИ даже от использования такого маломощного источника, как мобильные радиотелефоны.[1] Эти данные не должны быть причиной для радиофобии, однако очевидна необходимость в существенном углублении сведений о действии ЭМИ на живые организмы.
В России действует СанПиН 2.2.4.1191—03 Электромагнитные поля в производственных условиях, на рабочих местах. Санитарно-эпидемиологические правила и нормативы, а также гигиенические нормативы ГДР (ПДУ) 5803-91 (ДНАОП 0.03-3.22-91) Предельно допустимые уровни (ПДУ) воздействия электромагнитных полей (ЭМП) диапазона частот 10—60 кГц Промышленное электроснабжение 50 Гц [2][3]
- Допустимые уровни излучения базовых станций мобильной связи (900 и 1800 МГц, суммарный уровень от всех источников) в санитарно-селитебной зоне в некоторых странах заметно различаются:
- Украина: 2,5 мкВт/кв.см. (самая жёсткая санитарная норма в Европе)
- Россия, Венгрия: 10 мкВт/кв.см.
- США, Скандинавские страны: 100 мкВт/кв.см.
Параллельное развитие гигиенической науки в СССР и западных странах привело к формированию разных подходов к оценке действия ЭМИ. Для части стран постсоветского пространства сохраняется преимущественно нормирование в единицах плотности потока энергии (ППЭ), а для США и стран ЕС типичным является оценка удельной мощности поглощения (мобильных радиотелефонов (МРТ) не позволяют прогнозировать все неблагоприятные последствия, многие аспекты проблемы не освещены в современной литературе и требуют дополнительных исследований. В связи с этим, согласно рекомендациям ВОЗ, целесообразно придерживаться предупредительной политики, т. е. максимально уменьшить время использования сотовой связи.»
Проникающая неионизирующая радиация
Допустимые нормативы регулируются нормами радиационной безопасности — НРБ-99.
Влияние на радиотехнические устройства
Существует административные и контролирующие органы — инспекция по радиосвязи (на Украине, например, Укрчастотнадзор), которая регулирует распределение частотных диапазонов для различных пользователей, соблюдение выделенных диапазонов, отслеживает незаконное пользование радиоэфиром.
См. также
Ссылки
Литература
- Физика. Большой энциклопедический словарь/Гл. ред. А. М. Прохоров. — 4-е изд. — М.: Большая Российская энциклопедия, 1999. — С. 874—876. ISBN 5-85270-306-0 (БРЭ)
- Кудряшов Ю. Б., Перов Ю. Ф. Рубин А. Б. Радиационная биофизика: радиочастотные и микроволновые электромагнитные излучения. Учебник для ВУЗов. — М.: ФИЗМАТЛИТ, 2008. — 184 с — ISBN 978-5-9221-0848-5
Примечания
- ↑ В. Н. Дунаев «Электромагнитные излучения и риск популяционному здоровью при использовании средств сотовой связи» //Гигиена и санитария, № 6, 2007, с. 56—57
- ↑ ПДУ магнитных полей частот 50 Гц. Харьков, 1986, СН-3206-85.2
- ↑ Методические указания но гигиенической оценке основных параметров полей частотой 50Гц. Харьков, 1986. СН 3207-85
Wikimedia Foundation. 2010.






