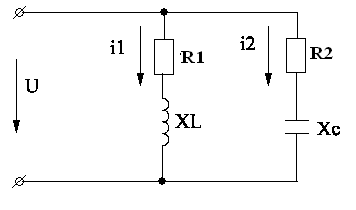
Однофазные электрические цепи переменного тока

Основные понятия и определения

Широкое применение в электрических цепях находят периодические ЭДС, напряжения и токи.

Периодические величины изменяются во времени по значению и направлению, причем эти изменения повторяются через некоторые промежутки времени Т, называемые периодом.

На практике подавляющее большинство промышленных источников переменного тока (генераторы электростанций) создают ЭДС, изменяющуюся по синусоидальному закону.

Преимущества такого закона:

а) простота получения;

б) напряжение легко трансформируется;

в) синусоидальная функция является единственной, которая в процессе интегрирования и дифференцирования не меняет своей формы и в процессе передачи и преобразования (в процессе трансформации) напряжения временная зависимость остается неизменной, т.е. синусоидальной.

Любая периодическая величина, изменяющаяся по синусоидальному закону, имеет ряд характерных параметров:

1. период — Т [c];

2) частота — f [Гц] .

Величина обратная периоду называется частотой:

.

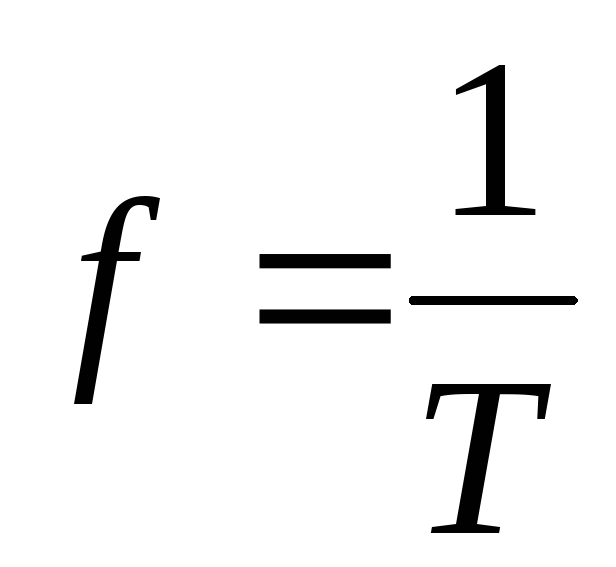Частота для всех электроустановок строго нормируется:

— для наземных систем — 50 (60)Гц;

— в авиации — 400Гц;

— космические летательные аппараты — 1000Гц.

Увеличение частоты позволяет уменьшить габариты электроустановок.

3) Циклическая частота — ω=2πf.

Для частоты 50Гц циклическая частота ω=2*3,14*50=314рад/с или 1/с.

4) Мгновенное значение — значение периодически изменяющейся величины в рассматриваемый момент времени.

Мгновенные значения обозначают — e, i, u.

5) Амплитудное значение

Максимальное значение или амплитуду ЭДС, напряжения и тока обозначают — E_m, U_m, I_m.

6) Действующее значение

Действующее значение ЭДС, напряжения и тока обозначают — E, U, I.

Для количественной оценки синусоидального тока, который в течение времени непрерывно, периодически изменяется, используют значение постоянного тока, эквивалентное значению переменного тока по совершаемой работе. Такое значение будет действующим для синусоидального тока.

Действующим (или эффективным)значением

синусоидального тока называют такое значение постоянного тока, при протекании которого в одном и том же резисторе с сопротивлением R за время одного периода Т выделятся столько же тепла, сколько при прохождении синусоидальнего тока.

При синусоидальном токе:

i=I_msinωt

количество теплоты, выделяемое в резисторе R за время Т равно:

,

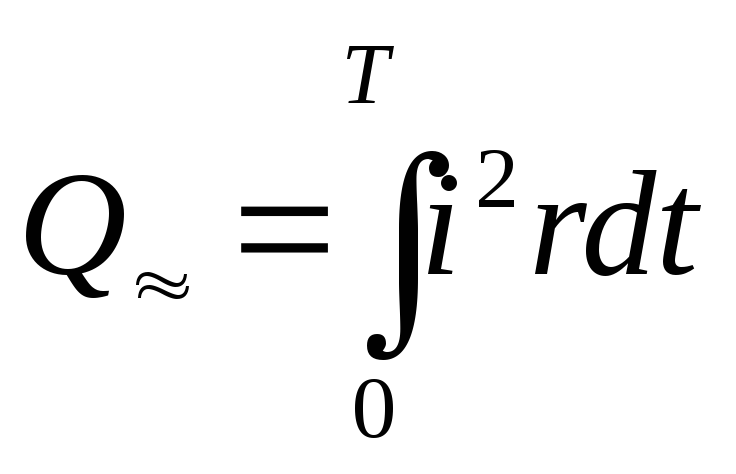а при постоянном токе

.

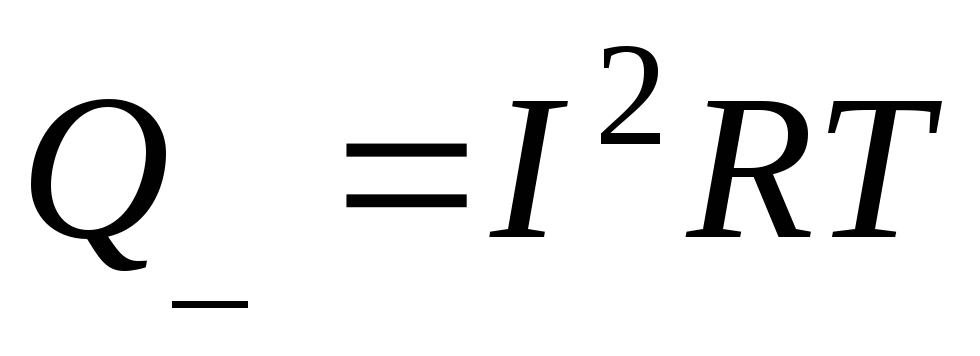
Согласно определению Q_≈=Q_— , тогда

, .

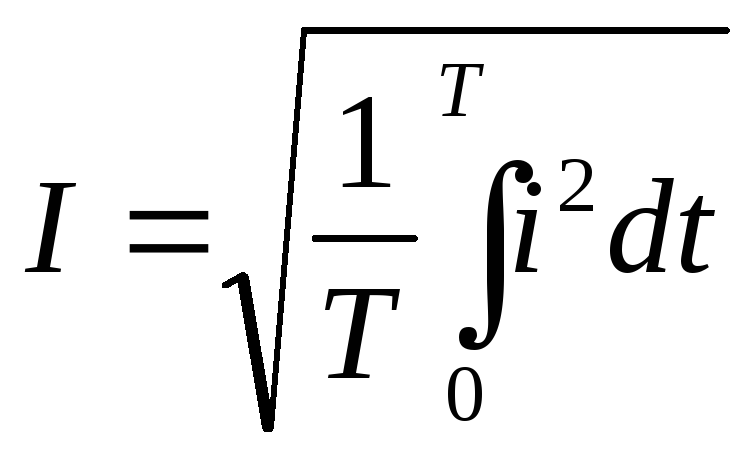Таким образом действующее значение синусоидального тока I является его среднеквадратичным значением за период Т

Действующее значение переменного тока обозначается как постоянный ток и в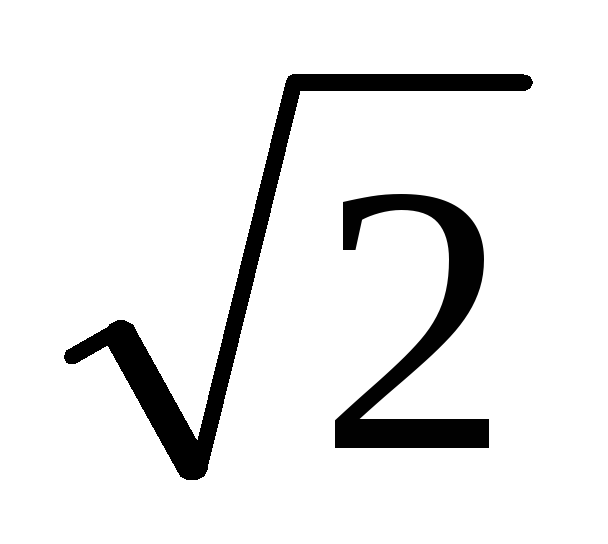

раз меньше чем его амплитуда.

Аналогично

.

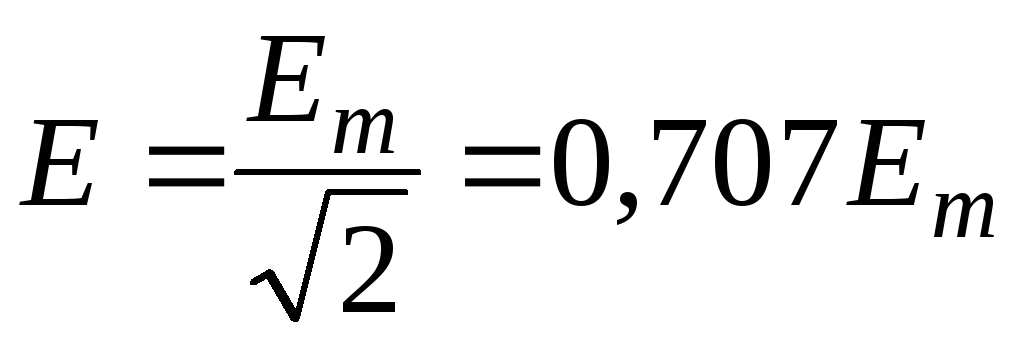
Большинство электроизмерительных приборов работают на тепловом или электродинамическом эффекте, поэтому они всегда показывают действующее значение. Основные расчеты электроцепей синусоидального тока проводятся по действующим значениям. Для несинусоидальных величин эти соотношения будут другими.

7)

Среднее значение

Среднее значение синусоидальной величины это ее среднеарифметическое значение. Однако, если определять среднее значение синусоидальной величины за период Т, то оно будет равно нулю, так как положительная и отрицательная полуволны синусоидальной кривой совпадают по форме. Поэтому среднее значение определяют за полпериода.

За среднее значение синусоидального тока принимают такое значение постоянного тока, при котором за полпериода переносится такой же электрический заряд, что и при синусоидальном токе:

,

,

/

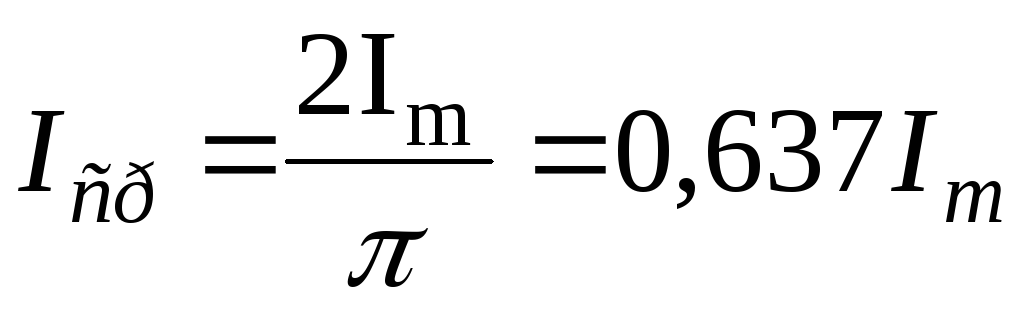
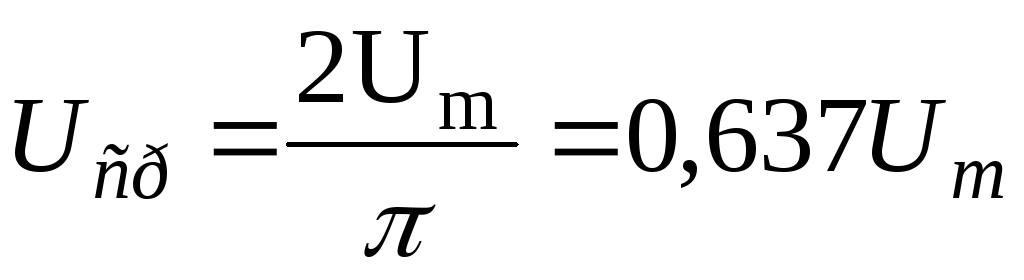Таким образом, среднее значение меньше действующего.

Изображение синусоидальных величин в прямоугольных координатах

В общем случае синусоидальные величины (рис.1), могут быть записаны:

e=E_msin(ωt+ψ_e)

u=U_msin(ωt+

ψ_u),

i=I_msin(ωt+ψ_i),

где e,u,i — мгновенные значения ЭДС, напряжения и тока;

E_m,U_m,I_m — амплитуды ЭДС, напряжения и тока.

(ωt+ψ_e) — фазовый угол;

ψ_e, ψ_u, ψ_i — начальные фазы ЭДС, тока и напряжения.

На практике чаще имеют место случаи, когда электрические величины не совпадают по фазе.

Из рис. 1 видно, что напряжение опережает ток на угол ψ_u-ψ_i . Разность фазовых углов называется разностью или сдвигом фаз.

φ=ψ_u-ψ_i — разность фаз между напряжением и током.

При этом пользуются правилом: начальные фазы расположенные по левую сторону от начала координат имеют положительные значения, а по правую отрицательные.

Если угол φ >0, то ток отстает от напряжения по фазе. Если φ<0, то ток опережает напряжение по фазе.

При сложении двух синусоидальных величин (одинаковой частоты), изображенных в прямоугольных координатах, необходимо сложить ординаты для ряда значений угла

ωt и по точкам построить суммарную синусоиду. Получается новая амплитуда, новый фазовый сдвиг, причем:

I_m ≠ I_m1 + I_m2;

φ_i≠ φ_i1+ φ_i2.

Такой расчет является трудоемким и имеет недостаточную точность.

В

екторное изображение синусоидальных величин

Рис.2

Наиболее просто складывать синусоидальные величины, представив их вращающимися векторами (рис.3).

Рис.3

В плоскости с осями ОX и ОY рассмотрим вращающийся с постоянной скоростью, равной угловой частоте ω, вектор ОА, длина которого равна амплитуде синусоидальной ЭДС, т.е.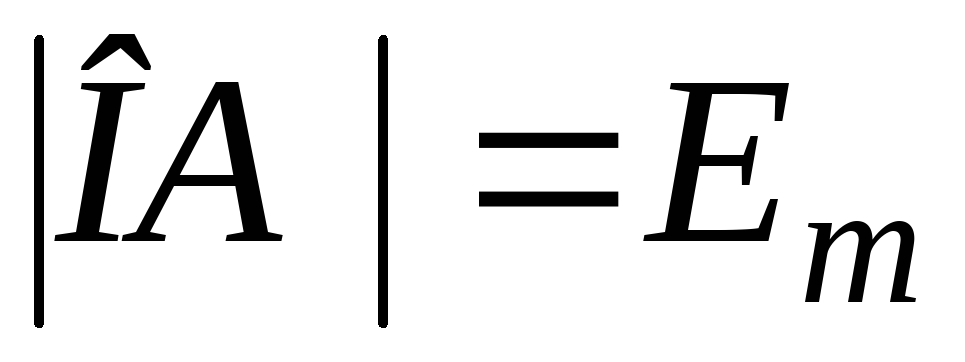

.

Мгновенное значение ЭДС описывается известным соотношением:

e=E_msin(ωt+ψ_e).

За положительное направление вращения принимают направление против часовой стрелки, а угол поворота отсчитывают от оси ОX. В начальном положении (при t=0) вектор ОА повернут по отношению к оси OX на угол ψ_e

Построим проекцию вектора ОА на ось OY, которые изменяются по мере поворота вектора на угол ωt по отношению к начальному положению. В начальном положении (при t=0) проекция ОА₀= E_msinψ_e=e₀, т.е. равна мгновенному значению ЭДС при t=0.

Через некоторое время (t=t₁) вектор ОА будет повернут на угол ωt₁ и составлять с осью ОX угол (ωt₁+ψ_e). Проекция его на ось OY :

ОА₁= E_msin(ωt₁+ψ_e)=e₁, т.е. равна мгновенному значению ЭДС при t=t₁.

При t=t₂ вектор ОА совпадает с осью OY и его проекция ОА₂= E_m= e₂. При дальнейшем вращении вектора АО его проекции на ось YO начнут уменьшаться, затем станут отрицательными и т.д.

Таким образом, проекции на ось OY вектора, вращающегося с постоянной скоростью ω и имеющего длину, равную амплитуде ЭДС, изменяются по синусоидальному закону, т.е. представляют собой мгновенные значения синусоидальной ЭДС. Следовательно, справедливо и обратное: если имеем синусоидальную величину. то ее можно представить вращающимся вектором.

Правила построения векторных диаграмм

1. Любую синусоидально изменяющуюся во времени величину (ЭДС, напряжение, ток) можно представить в виде вращающегося вектора, длина которого равна амплитуде, а угловая скорость угловой частоте этой синусоидальной величины.

2. Начальное положение вращающегося вектора определяется углом, равным начальной фазе синусоидальной величины и откладываем от положительного направления оси O в сторону, противоположную вращению часовой стрелки.

3. В одних и тех же осях можно представить векторы всех ЭДС, действующих в данной цепи, напряжений на всех участках данной цепи и токов во всех ее ветвях (в заданных масштабах).

4. Так как синусоидальные величины имеют одинаковую частоту, то изображающие их векторы вращаются с одинаковой скоростью. Их взаимное положение на плоскости, относительно друг друга, остается неизменным. Поэтому на практике векторы не вращают, а строят их, соблюдая углы между векторами (углы сдвига фаз).

5. Отказавшись от вращения вектора можно строить векторы не только максимальных, но и действующих значений.

6. Вектора можно складывать, по правилу параллелограмма, получив при этом суммарный вектор (рис. 4).

Рис.4

7. В связи с отсутствием необходимости вращения нас интересует только взаимное расположение векторов, один из которых можно строить по направления оси OX, остальные вектора направляются относительно этого вектора (рис.5).

Например, если к элементам электрической цепи подается переменное напряжение u=U_msin(ωt+ψ_u), то возникнет переменный ток i=I_msin(ωt-ψ_i). В этом случае ток отстает от напряжения по фазе на угол φ=ψ_u-ψ_i. Начальные фазы ψ_u и ψ_i на векторной диаграмме не изображают, так как взаимное положение векторов определяется полностью разностью фаз — φ. Принимаем начальную фазу тока равную нолю (ψ_i=0), тогда начальная фаза напряжения ψ_u равна сдвигу фаз — φ.

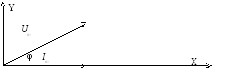
Рис.5

Графический метод расчета является грубым неточным. На практике переходят к точным математическим методам расчета на основе теории комплексных чисел.

Понятия о комплексных числах

Комплексная плоскость — прямоугольная системе координат, на которой по одной оси откладываются вещественные числа +1, на другой (перпедикулярной) — мнимые числа +j.

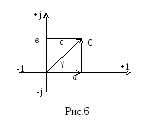
Здесь j=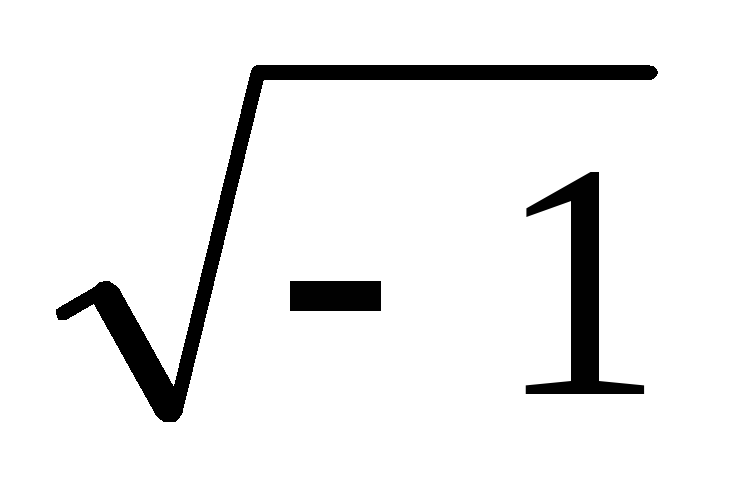 — мнимая единица.

Действия с мнимой единицей:

1) j²=-1; 2)

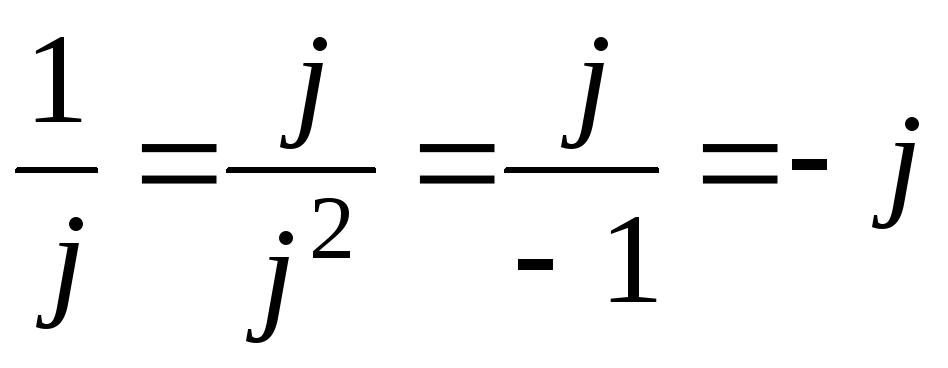
Любую точку на комплексной плоскости можно охарактеризовать комплексным числом. Известно, что комплексное число С имеет вещественную Re и мнимую Im составляющие.

Алгебраическая форма записи комплексного числа:

С=а+jв,

где а= Аcosα – реальная часть комплексного числа,

в= Аsinα – мнимая часть, γ=arctg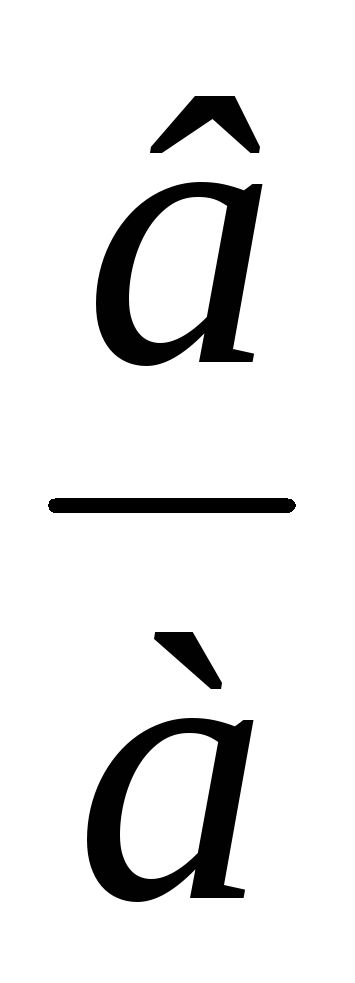 — фаза,

с=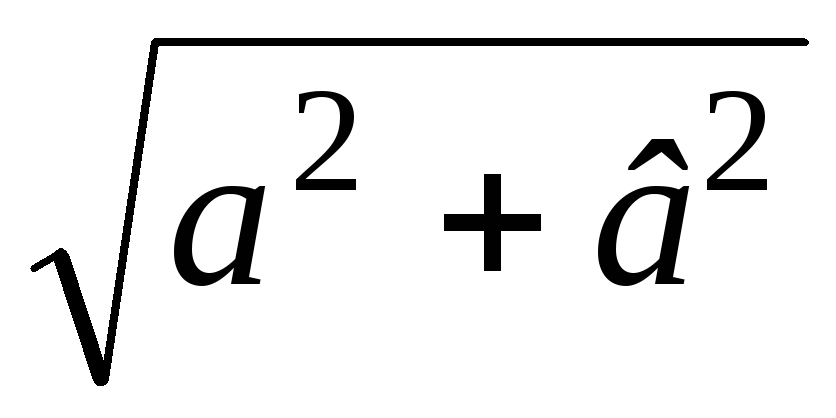 — модуль комплексного числа.

Тригонометрическая форма записи комплексного числа:

С=с(cosγ+jsinγ).

Показательная форма записи комплексного числа:

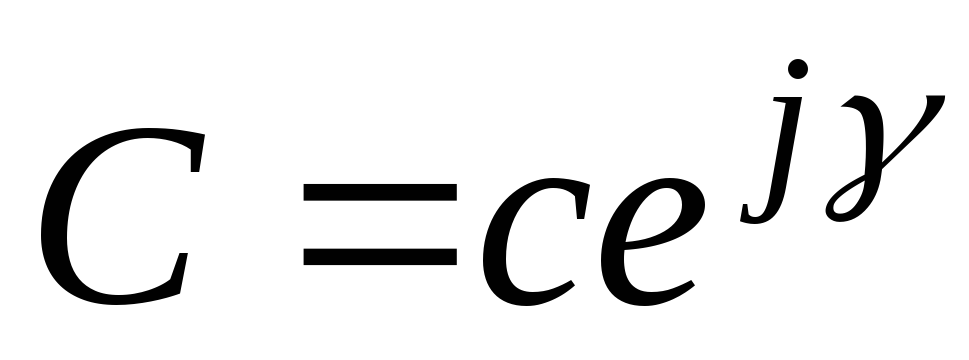, где — оператор поворота (поворотный множитель).

cosγ + jsinγ = 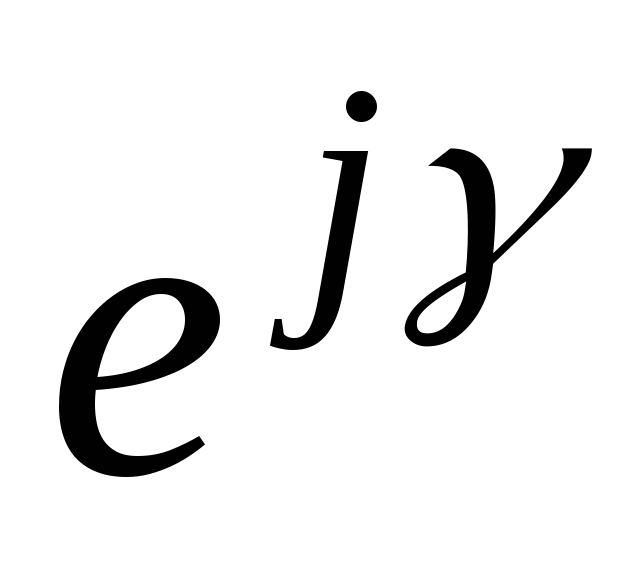— формула Эйлера.

Частные случаи:

Для γ= π/2 ;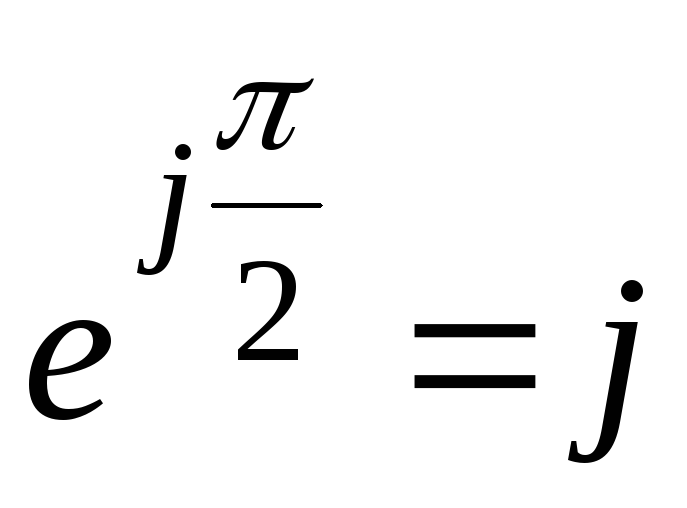

γ= -π/2 ;

γ= π .

Тригонометрическая форма записи служит для перехода из алгебраической формы в показательную и наоборот.

Электрические цепи переменного тока

Электрическая энергия почти во всех случаях производится, распределяется и потребляется в виде энергии переменного тока.

Широкое применение переменного тока в различных областях техники объясняется легкостью его получения и преобразования, а также простотой устройства генераторов и двигателей переменного тока, надежностью их работы и удобством эксплуатации.

Переменный ток, меняет свое значение и направление, определенное число раз в секунду. При переменном токе электроны движутся вдоль провода сначала в одном направлении, затем на мгновение останавливаются, далее движутся в обратную сторону, опять останавливаются и снова повторяют движение вперед и назад. То есть электроны совершают в проводе колебательное движение. Вследствие своей малой скорости движения (V_эл= 10^-4м/с = 0,1 мм/с) электроныпри таких колебаниях успевают сделать лишь небольшие перемещения вдоль провода.

Наиболее часто встречается, так называемый синусоидальный переменный ток. Изменение электрических величин (силы тока, напряжения, ЭДС) со временем показывает плавная кривая линия, называемая синусоидой).

Электрические цепи, в которых значения и направления ЭДС, напряжения и тока периодически изменяются со временем по синусоидальному закону, называются цепями синусоидального тока. Иногда их называют просто цепями переменного тока.

Для переменного тока была выбрана синусоидальная форма, так как она обеспечивает более экономичные производство, передачу, распределение и использование электрической энергии.

Кроме того, именно синусоидальная форма электрических величин остается неизменной во всех участках сколь угодно сложной электрической цепи, то есть индуктивные и емкостные элементы, входящие в состав электрических цепей не изменяют синусоидальной формы тока и напряжения.

Электрические цепи переменного тока по сравнению с цепями постоянного тока имеют ряд особенностей. Эти особенности определяются:

• во-первых, тем, что в состав цепей переменного тока входят новые элементы: трансформаторы, конденсаторы, катушки индуктивности;

• во-вторых, тем, что переменные токи и напряжения в этих элементах порождают переменные электрические и магнитные поля, которые в свою очередь приводят к возникновению явления самоиндукции, взаимной индукции и токов смещения.

Все это оказывает существенное влияние на протекающие электрической цепи процессы. Анализ процессов в цепях усложняется.

Для цепи переменного синусоидального тока большое значение имеет частота f. От частоты зависит влияние емкостей и индуктивностей на процессы в цепи.

Особенности цепей синусоидального тока обуславливают ряд новых, специфических для этих цепей явлений: сдвиг фаз, явление резонанса, появление реактивных мощностей.

Коэффициент мощности.

На современных промышленных предприятиях большинство потребителей электрической энергии переменного тока представляют собой активно-индуктивную нагрузку в виде асинхронных электродвигателей, силовых трансформаторов, сварочных трансформаторов, преобразователей и так далее. В такой нагрузке в результате протекания переменного тока индуктируются ЭДСсамоиндукции, обуславливающие сдвиг по фазе между током и напряжением. Этот сдвиг по фазе обычно увеличивается, аcos уменьшается при малой нагрузке. Например, еслиcos двигателей переменного тока при полной нагрузке составляет 0,75 — 0,8, то при малой нагрузке он уменьшается до 0,2 — 0,4.

Если мощность, потребляемая всеми приемниками в данных цепях, является вполне определенной, то при неизменном напряжении на зажимах приемника их ток: I = P / (Ucos )

С уменьшением cos ток нагрузки электростанций и подстанций будет увеличиваться при одной и той же отдаваемой мощности.

Вместе с тем электрические генераторы, трансформаторы и линии электропередачи рассчитываются на определенное напряжение и ток. Увеличение тока потребителя при снижении cosне должно превышать определенных пределов, так как питающие их генераторы рассчитываются на определенную номинальную мощностьS_ном = U_ном I_ном, вследствие чего они не должны оказаться перегруженными. Для того чтобы ток генератора не превышал номинального значения при сниженииcos потребителя, необходимо снижать его активную мощность. Таким образом, понижениеcos потребителей вызывает неполное использование мощности синхронных генераторов, трансформаторов и линий электропередачи. Они бесполезно загружаются за счет индуктивного реактивного тока.

cos, характеризующий использование установленной мощности, часто называют коэффициентом мощности.

Коэффициентом мощности определяют как отношение активной мощности к полной:

cos  = P/S.

(2.71)

2.25 Коэффициент мощности (Адрес Блок 4) Коэффициентом мощности определяют как отношение активной мощности к полной:cos  = P/S. Коэффициент мощности показывает, какая часть электрической энергии необратимо преобразуется в другие виды энергии и, в частности, используется на выполнение полезной работы.

Коэффициент мощности (2.25)показывает, какая часть электрической энергии необратимо преобразуется в другие виды энергии и, в частности, используется на выполнение полезной работы. Нормальным считаетсяcos 0,85 — 0,9. При низком коэффициенте мощности на предприятия, потребляющие электроэнергию, накладывается штраф, при высоком — предприятия премируются.

Для улучшения коэффициента мощности проводится ряд мероприятий:

2.заменяются двигатели переменного тока, нагруженные относительно мало, двигателями меньшей мощности;

2.включаются параллельно приемникам конденсаторы.

Урок 8. переменный электрический ток — Физика — 11 класс

Физика, 11 класс

Урок 8. Переменный электрический ток

Перечень вопросов, рассматриваемых на уроке:

1) Свойства переменного тока;

2) Понятия активного сопротивления, индуктивного и ёмкостного сопротивления;

3) Особенности переменного электрического тока на участке цепи с резистором;

4) Определение понятий: переменный электрический ток, активное сопротивление, индуктивное сопротивление, ёмкостное сопротивление.

Глоссарий по теме

Переменный электрический ток — это ток, периодически изменяющийся со временем.

Сопротивление элемента электрической цепи (резистора), в котором происходит превращение электрической энергии во внутреннюю называют активным сопротивлением.

Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты, что и при переменном токе за то же время.

Величину Х_C, обратную произведению ωC циклической частоты на электрическую ёмкость конденсатора, называют ёмкостным сопротивлением.

Величину Х_L, равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением.

Основная и дополнительная литература по теме урока:

Мякишев Г.Я., Буховцев Б.Б., Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2014. – С. 86 – 95.

Рымкевич А.П. Сборник задач по физике. 10-11 класс. — М.: Дрофа, 2014. – С. 128 – 132.

Степанова. Г.Н. Сборник задач по физике. 10-11 класс. М., Просвещение 1999 г.

Е.А. Марон, А.Е. Марон. Контрольные работы по физике. М., Просвещение, 2004

Основное содержание урока

Сейчас невозможно представить себе нашу цивилизацию без электричества. Телевизоры, холодильники, компьютеры – вся бытовая техника работает на нем. Основным источником энергии является переменный ток.

Электрический ток, питающий розетки в наших домах, является переменным А что это такое? Каковы его характеристики? Чем же переменный ток отличается от постоянного? Об этом мы поговорим на данном уроке.

В известном опыте Фарадея при движении полосового магнита относительно катушки появлялся ток, что фиксировалось стрелкой гальванометра, соединенного с катушкой. Если магнит привести колебательное движение относительно катушки, то стрелка гальванометра будет отклоняться то в одну сторону, то в другую – в зависимости от направления движения магнита. Это означает, что возникающий в катушке ток меняет свое направление. Такой ток называют переменным.

Электрический ток, периодически меняющийся со временем по модулю и направлению, называется переменным током.

Переменный электрический ток представляет собой электромагнитные вынужденные колебания. Переменный ток в отличие от постоянного имеет период, амплитуду и частоту.

Сила тока и напряжение меняются со временем по гармоническому закону, такой ток называется синусоидальным. В основном используется синусоидальный ток. Колебания тока можно наблюдать с помощью осциллографа.

Если напряжение на концах цепи будет меняться по гармоническому закону, то и напряженность внутри проводника будет так же меняться гармонически. Эти гармонические изменения напряженности поля, в свою очередь вызывают гармонические колебания упорядоченного движения свободных частиц и, следовательно, гармонические колебания силы тока. При изменении напряжения на концах цепи, в ней с очень большой скоростью распространяется электрическое поле. Сила переменного тока практически во всех сечениях проводника одинакова потому, что время распространения электромагнитного поля превышает период колебаний.

Рассмотрим процессы, происходящие в проводнике, включенном в цепь переменного тока. Сопротивление проводника, в котором происходит превращение электрической энергии во внутреннюю энергию, называют активным. При изменении напряжения на концах цепи по гармоническому закону, точно так же меняется напряженность электрического поля и в цепи появляется переменный ток.

При наличии такого сопротивления колебания силы тока и напряжения совпадают по фазе в любой момент времени.

𝒾 — мгновенное значение силы тока;

ℐ_m— амплитудное значение силы тока.

– колебания напряжения на концах цепи.

Колебания ЭДС индукции определяются формулами:

При совпадении фазы колебаний силы тока и напряжения мгновенная мощность равна произведению мгновенных значений силы тока и напряжения. Среднее значение мощности равно половине произведения квадрата амплитуды силы тока и активного сопротивления.

Часто к параметрам и характеристикам переменного тока относят действующие значения. Напряжение, ток или ЭДС, которая действует в цепи в каждый момент времени — мгновенное значение (помечают строчными буквами — і, u, e). Однако оценивать переменный ток, совершенную им работу, создаваемое тепло сложно рассчитывать по мгновенному значению, так как оно постоянно меняется. Поэтому применяют действующее, которое характеризует силу постоянного тока, выделяющего за время прохождения по проводнику столько же тепла, сколько это делает переменный.

Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты, что и при переменном токе за то же время.

U_m — амплитудное значение напряжения.

Действующие значения силы тока и напряжения:

Электрическая аппаратура в цепях переменного тока показывает именно действующие значения измеряемых величин.

Конденсатор включенный в электрическую цепь оказывает сопротивление прохождению тока. Это сопротивление называют ёмкостным.

Величину Х_C, обратную произведению циклической частоты на электрическую ёмкость конденсатора, называют ёмкостным сопротивлением.

Ёмкостное сопротивление не является постоянной величиной. Мы видим, что конденсатор оказывает бесконечно большое сопротивление постоянному току.

Если включить в электрическую цепь катушку индуктивности, то она будет влиять на прохождение тока в цепи, т.е. оказывать сопротивление току. Это можно объяснить явлением самоиндукции.

Величину Х_L, равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением.

X_L= ωL

Если частота равна нулю, то индуктивное сопротивление тоже равно нулю.

При увеличении напряжения в цепи переменного тока сила тока будет увеличиваться так же, как и при постоянном токе. В цепи переменного тока содержащем активное сопротивление, конденсатор и катушка индуктивности будет оказываться сопротивление току. Сопротивление оказывает и катушка индуктивности, и конденсатор, и резистор. При расчёте общего сопротивления всё это надо учитывать. Основываясь на этом закон Ома для переменного тока формулируется следующим образом: значение тока в цепи переменного тока прямо пропорционально напряжению в цепи и обратно пропорционально полному сопротивлению цепи.

Если цепь содержит активное сопротивление, катушку и конденсатор соединенные последовательно, то полное сопротивление равно

Закон Ома для электрической цепи переменного тока записывается имеет вид:

Преимущество применения переменного тока заключается в том, что он передаётся потребителю с меньшими потерями.

В электрической цепи постоянного тока зная напряжение на зажимах потребителя и протекающий ток можем легко определить потребляемую мощность, умножив величину тока на напряжение.   В цепи переменного тока мощность равна произведению напряжения на силу тока и на коэффициент мощности.

Мощность цепи переменного тока

P=IU cosφ

Величина cosφ – называется коэффициентом мощности

Коэффициент мощности показывает какая часть энергии преобразуется в другие виды. Коэффициент мощности находят с помощью фазометров. Уменьшение коэффициента мощности приводит к увеличению тепловых потерь. Для повышения коэффициента мощности электродвигателей параллельно им подключают конденсаторы. Конденсатор и катушка индуктивности в цепи переменного тока создают противоположные сдвиги фаз. При одновременном включении конденсатора и катушки индуктивности происходит взаимная компенсация сдвига фаз и повышение коэффициента мощности. Повышение коэффициента мощности является важной народнохозяйственной задачей.

Разбор типовых тренировочных заданий

1. Рамка вращается в однородном магнитном поле. ЭДС индукции, возникающая в рамке, изменяется по закону e=80 sin 25πt. Определите время одного оборота рамки.

Дано: e=80 sin 25πt.

Найти: T.

Решение:

Колебания ЭДС индукции в цепи переменного тока происходят по гармоническому закону

Согласно данным нашей задачи:

Время одного оборота, т.е. период связан с циклической частотой формулой:

Подставляем числовые данные:

Ответ: T = 0,08 c.

2. Чему равна амплитуда силы тока в цепи переменного тока частотой 50 Гц, содержащей последовательно соединенные активное сопротивление 1 кОм и конденсатор емкости С = 1 мкФ, если действующее значение напряжения сети, к которой подключен участок цепи, равно 220 В?

Дано:

ν=50 Гц,

R=1 кОм=1000 Ом,

C=1 мкФ=10^-6 Ф,

U=220 В.

Найти: I_m

Решение:

Напишем закон Ома для переменного тока:

I=U/Z

Для амплитудных значений силы тока и напряжения, мы можем записать I_m=U_m/Z?

Полное сопротивление цепи равно:

Подставляя числовые данные находим полное сопротивление Z≈3300 Ом. Так как действующее значение напряжения равно:

то после вычислений получаем I_m ≈0,09 Ом.

Ответ: I_m ≈0,09 Ом.

2. Установите соответствие между физической величиной и прибором для измерения.

Физические величины	Физические приборы
Сила тока	Омметр
Напряжение	Вольтметр
Сопротивление	Амперметр
Мощность	Ваттметр

Правильный ответ:

Физические величины	Физические приборы
Сила тока	Амперметр
Напряжение	Вольтметр
Сопротивление	Омметр
Мощность	Ваттметр

Основные понятия об электрических цепях переменного тока

ЭЛЕКТРИЧЕСКИЕ цепи переменного тока

Урок 5

Тема урока: Получение переменного тока. Основные понятия и определения, изображение переменного тока

Цель урока: формирование знаний по теме, воспитывать познавательный интерес; расширять кругозор учащихся; развивать мышление и память.

Теоретическая часть

Переменный ток, в отличие от тока постоянного, непрерывно изменяется как по величине, так и по направлению, причем изменения эти происходят периодически, т. е. точно повторяются через равные промежутки времени.

Чтобы вызвать в цепи такой ток, используются источники переменного тока, создающие переменную ЭДС, периодически изменяющуюся по величине и направлению. Такие источники называются генераторами переменного тока.

На рисунке показана схема устройства (модель) простейшего генератора переменного тока.

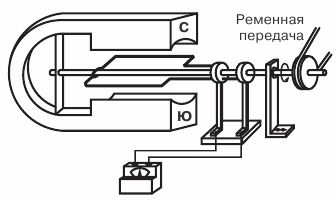
Прямоугольная рамка, изготовленная из медной проволоки, укреплена на оси и при помощи ременной передачи вращается в поле магнита. Концы рамки припаяны к медным контактным кольцам, которые, вращаясь вместе с рамкой, скользят по контактным пластинам (щеткам).

Магнит создает между своими полюсами равномерное магнитное поле, в котором плотность магнитных силовых линий в любой части поля одинаковая. Вращаясь, рамка пересекает силовые линии магнитного поля, и в каждой из ее сторон а и б индуктируются ЭДС.

Стороны в и г рамки — нерабочие, так как при вращении рамки они не пересекают силовых линий магнитного поля и, следовательно, не участвуют в создании ЭДС.

В любой момент времени ЭДС, возникающая в стороне а, противоположна по направлению ЭДС, возникающей в стороне б, но в рамке обе ЭДС действуют согласно и в сумме составляют обшую ЭДС, т. е. индуктируемую всей рамкой. В этом можно убедиться, если использовать для определения направления ЭДС известное как правило правой руки.

Для этого надо ладонь правой руки расположить так, чтобы она была обращена в сторону северного полюса магнита, а большой отогнутый палец совпадал с направлением движения той стороны рамки, в которой мы хотим определить направление ЭДС. Тогда направление ЭДС в ней укажут вытянутые пальцы руки.

Для какого бы положения рамки мы ни определяли направление ЭДС в сторонах а и б, они всегда складываются и образуют общую ЭДС в рамке. При этом с каждым оборотом рамки направление общей ЭДС изменяется в ней на обратное, так как каждая из рабочих сторон рамки за один оборот проходит под разными полюсами магнита.

Величина ЭДС также изменяется, так как изменяется скорость, с которой стороны рамки пересекают силовые линии магнитного поля. Действительно, в то время, когда рамка подходит к своему вертикальному положению и проходит его, скорость пересечения силовых линий сторонами рамки бывает наибольшей, и в рамке индуктируется наибольшая ЭДС. В те моменты времени, когда рамка проходит свое горизонтальное положение, ее стороны как бы скользят вдоль магнитных силовых линий, не пересекая их, и ЭДС не индуктируется.

Таким образом, при равномерном вращении рамки в ней будет индуктироваться ЭДС, периодически изменяющаяся как по величине, так и по направлению. ЭДС, возникающую в рамке, можно измерить прибором и использовать для создания тока во внешней цепи. Используя явление электромагнитной индукции, можно получить переменную ЭДС и, следовательно, переменный ток.

Переменный ток для промышленных целей и для освещения вырабатывается мощными генераторами, приводимыми во вращение паровыми или водяными турбинами и двигателями внутреннего сгорания.

Графическое изображение переменного тока

Построение графиков переменных величин, меняющихся с течением времени, начинают с построения двух взаимно перпендикулярных линий, называемых осями графика. Затем на горизонтальной оси в определенном масштабе откладывают отрезки времени (или угол поворота рамки), а на вертикальной, также в некотором масштабе, — значения той величины, график которой собираются построить (ЭДС, напряжения или тока).

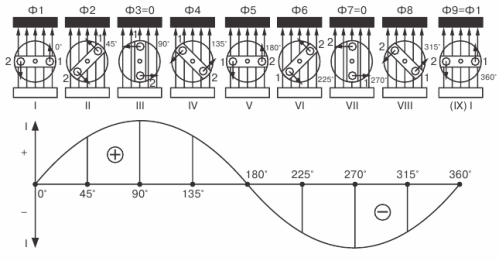
Полученная волнообразная кривая называется синусоидой, а ток, ЭДС или напряжение, изменяющиеся по такому закону, называются синусоидальными.

Синусоидальный характер изменения тока — самый распространенный в электротехнике, поэтому, говоря о переменном токе, в большинстве случаев имеют в виду синусоидальный ток.

Для сравнения различных переменных токов (ЭДС и напряжений) существуют величины, характеризующие тот или иной ток. Они называются параметрами переменного тока.

Переменный ток характеризуется периодом, амплитудой и частотой.

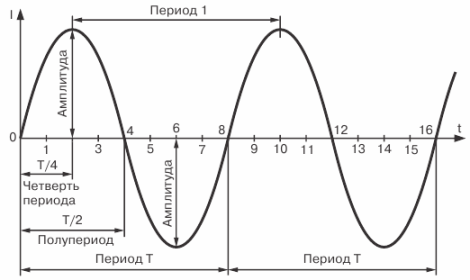
Промежуток времени, на протяжении которого совершается полный цикл изменения тока, называется периодом. Период обозначается буквой Т и измеряется в секундах.

Максимальное значение переменного тока (ЭДС или напряжения) называется его амплитудой или амплитудным значением тока. Общепринятые обозначения амплитуд тока, ЭДС и напряжения — Im, Em и Um.

Значение переменного тока (ЭДС, напряжения), соответствующее любому выбранному моменту времени, называется его мгновенным значением (i, u, е соответственно).

Мгновенное значение тока, как и амплитудное его значение, легко определить с помощью графика. Для этого из любой точки на горизонтальной оси, соответствующей интересующему нас моменту времени, проведем вертикальную линию до точки пересечения с кривой тока; полученный отрезок вертикальной прямой определит значение тока в данный момент, т. е. мгновенное его значение.

Число полных периодов, совершаемых током в 1 секунду, называется частотой переменного тока и обозначается латинской буквой f. Чтобы определить частоту переменного тока, т. е. узнать, сколько периодов своего изменения ток совершил в течение 1 секунды, необходимо 1 секунду разделить на время одного периода f = 1/T. Частота переменного тока измеряется единицей, называемой герцем.

При определении сопротивления различных цепей переменному току использовать еще одна вспомогательную величину, характеризующую переменный ток, так называемую угловую или круговую частоту.

Круговая частота обозначается буквой ω, измеряется в радианах и связана с частотой соотношением

ω = 2πf

В общем виде в момент времени t=0 мгновенное значение переменных величин можно записать в виде:

i = I_m sin ωt ,

u = U_m sin ωt,

е = Е_msin ωt.

При этом начальный период времени t=0 совпадает с нулевыми значениями функций. Но в общем случае на оси времени можно выбрать любой момент отсчета, тогда формулы мгновенных значений будут иметь вид:

i = I_m sin(ωt + φ_i),

u = U_m sin(ωt +φ_u),

е = Е_m sin(ωt +φ_е),

где φ_i,_{φu,φе – начальный фазовый угол или начальная фаза.}

Временно́й сдвиг между максимальными значениями в разных витках определяется разностью фаз:

Если для синусоидальных величин разность фаз равна ±π, то они противоположны по фазе, если начальные фазы одинаковые и их разность равна 0, то это означает. Что они совпадают по фазе.

При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений из-за емких расчетов. Для этих целей ввели понятие действующих значений тока, напряжения.

Действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии.

Электрические приборы показывают действующие значения переменных величин, которые обозначаются прописными буквами без индексов (I, U, Е).

; ;

Вопросы для самопроверки:

— Объясните понятие «переменный ток».

— Что такое амплитуда переменного тока?

— Что такое частота тока? Единицы измерения частоты?

— Что такое угловая частота? Единицы измерения угловой частоты?

— Что такое разность фаз?

— В чем разница между действующими и амплитудными значениями синусоидальных величин?

— Запишите и расшифруйте математическое выражение мгновенного синусоидального тока.

— Запишите и расшифруйте математическое выражение мгновенного синусоидального напряжения.

Практическая часть:

Пример 1. Определите угловую частоту, если частота сети равна 50Гц? 60Гц? 1кГц?

Пример 2. Амперметр показывает значение 10А. Определите амплитудное (максимальное) значение тока и запишите мгновенное значение тока (фазовый угол равен нулю).

Пример 3. Мгновенное значение напряжение равно u=282sin(ωt-47). Определить действующее значение и начальную фазу напряжения.

Урок 6

Тема урока: Элементы электрической цепи синусоидального тока.

Цель урока: расширение и обобщение знаний по теме, применение теоретических знаний на практике; развитие памяти и логики.

Теоретическая часть

На любом участке цепи переменного тока одновременно осуществляются необратимые процессы преобразования электрической энергии в другие виды и проявляется действие переменного электромагнитного поля.

При решении большинства электротехнических задач вводят допущения, которые позволяют раздельно учитывать каждое из явлений и упрощают задачу расчета электрических цепей переменного тока.

1. Цепь с идеальным резистивным элементом.

Рассмотрим, например, процессы, происходящие в обыкновенной лампе накаливания, включенной в сеть переменного тока. Между отдельными витками нити накаливания существует электрическая емкость, и нить обладает определенной индуктивностью, но они незначительны. Поэтому считают, что С=0 и L=0. В этом случае при анализе электрической цепи лампу называют идеальным резистивным элементом цепи с сопротивлением R.

Величина сопротивления переменному току больше, чем сопротивлению постоянному току, за счет неравномерного распределения тока в проводе (поверхностный эффект). Поэтому в отличие от сопротивления постоянному току сопротивление в цепи переменного тока называют активным сопротивлением. Активное сопротивление измеряется в омах.

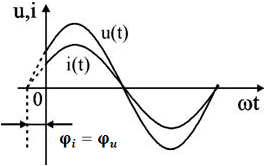
Если напряжение u = U_msinωt),подключить к сопротивлению R, то через него протекает ток

Это показывает, что напряжение на сопротивлении и ток, протекающий через него, совпадают по фазе: .

Напряжение, совпадающее по фазе с током, называют активным напряжением и обозначают U_a.

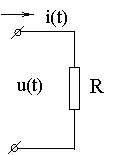
2. Цепь с идеальным индуктивным элементом.

Примером идеального индуктивного элемента может служить индуктивная катушка. Электрическая энергия, выделяемая в катушке за счет нагрева провода обмотки, как правило, невелика, как и межвитковая емкость, и во многих практических случаях ими можно пренебречь (R=0, C=0). При принятых допущениях индуктивную катушку называют идеальным индуктивным элементом цепи или L-элементом.

Параметром идеального индуктивного элемента является индуктивность L, а энергетические процессы в нем определяются только явлениями, происходящими в магнитном поле.

Индуктивность — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность, краем которой является этот контур. На электрических схемах используют условные графические обозначения катушек индуктивностей, примеры которых приведены на рисунке.

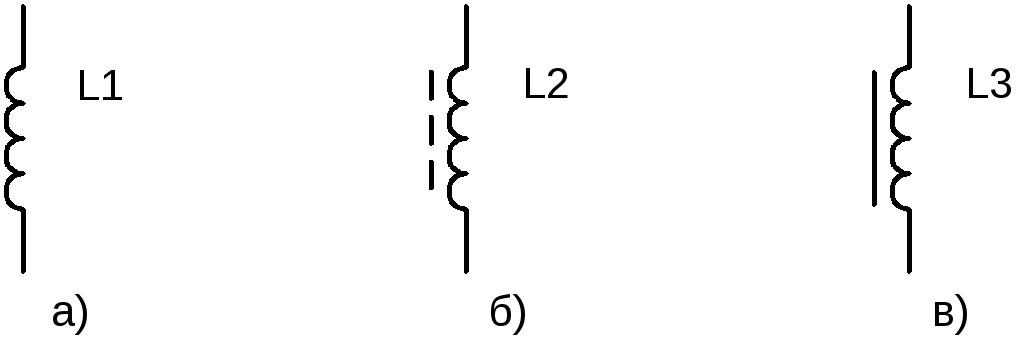
Условные графические обозначения индуктивностей:

а – обозначение катушки индуктивности; б – с магнитодиэлектрическим сердечником;

в – с ферромагнитным сердечником

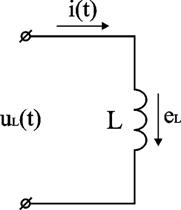
При прохождении электрического тока по катушке, ток создаст переменный магнитный поток Ф. Силовые линии этого потока, пересекая витки катушки, будут индуктировать в ней э.д.с. самоиндукции. По закону электромагнитной индукции

e_L=

Так как в цепи, куда включена индуктивность L, отсутствует активное сопротивление (рассматривается идеальная катушка индуктивности), то по второму закону Кирхгофа u+e_L=0, т. е. u = -e_L Следовательно, напряжение источника всегда равно по величине и противо-положно по направлению э. д. с. самоиндукции.

Если в формулу подставить значение тока и продифференцировать, то получим:

Обозначим величину ωL· равной амплитуде напряжения U_m. Тогда по закону Ома

Величину называют индуктивным сопротивлением, измеряют в Омах и обозначают

Так как , то начальную фазу напряжения можно представить как φ _u= φ _i+ 90 и, следовательно,

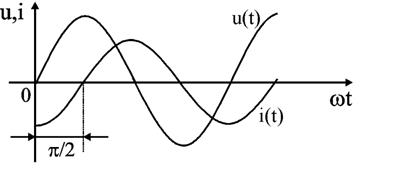
Выведенное соотношение показывает, что если в катушке протекает синусоидальный ток, то напряжение также имеет синусоидальный характер, но при этом оно опережает ток на четверть периода (90).

3. Цепь с идеальным емкостным элементом

Конденсатор – элемент электрической цепи, предназначенный для использования его ёмкости. В конденсаторе накапливается энергия электрического поля. Свойство элемента запасать электрический заряд характеризует ёмкость (С). Этот параметр является коэффициентом пропорциональности между зарядом q (Кл) и прикладываемым напряжением u (В).

q = C·u,

При изменении напряжения на конденсаторе изменяется заряд и возникает электрический ток

Идеализированный конденсатор обладает только ёмкостью С (R=0, L=0).

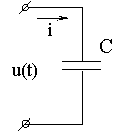
Рассмотрим электрические процессы в цепи с идеальным ёмкостным элементом. Пусть напряжение источника изменяется по закону u = Um·sinωt, (φ_u = 0).

В цепи возникает ток

 Из полученного выражения видно, что начальная фаза тока φ_i = . Угол сдвига фаз между напряжением и током составляет

Следовательно, синусоида напряжения на емкости отстаёт от синусоиды тока на угол 90. На практике, если в электрической цепи напряжение отстаёт по фазе от тока, говорят об ёмкостном характере нагрузки.

Амплитуда тока будет равна Im = ω·C·Um=.

Величину называют ёмкостным сопротивлением конденсатора и измеряют в Омах 

Xc=1/ ω•C =1/2πfC.

Итак, в цепях переменного тока выделяют следующие виды сопротивлений:

— активное (активным называют сопротивление резистора). Единицей измерения сопротивления является Ом. Сопротивление резистора не зависит от частоты сети.

— реактивное (индуктивное X_L и емкостное Х_С). Единицей измерения индуктивного и емкостного сопротивления также является Ом. Величина индуктивного сопротивления линейно зависит от частоты. А величина ёмкостного сопротивления обратнопропорциональна частоте сети. В цепях со смешанным соединением нагрузки (активной, индуктивной, ёмкостной) реактивным сопротивлением цепи называют величину

X = X_L — X_C.

Для того, чтобы найти общее сопротивление электрической цепи со смешанным соединением нагрузки используют понятие полного сопротивления цепи, которое определяется как

Вопросы для самопроверки:

— Объясните физический смысл активного сопротивления проводника переменному току по сравнению с сопротивлением проводника постоянному току?

— Что такое индуктивность катушки? От чего она зависит?

— Что понимается под действующим значением переменного синусоидального тока? Как его рассчитать через амплитудное значение тока?

— Опишите физические явления, наблюдаемые в резисторе в цепи переменного синусоидального тока?

— Запишите математическую связь между мгновенным напряжением, мгновенным током и активным сопротивлением?

— Запишите математические выражения мгновенного напряжения и тока на активном сопротивлении, приняв начальную фазу напряжения φ=45.

— Что понимается под углом сдвига фаз? Чему он равен на участке цепи с резистором? индуктивностью? ёмкостью?

— Как рассчитать индуктивное сопротивление идеальной катушки?

— Запишите математическое выражение мгновенного напряжения на индуктивном сопротивлении, приняв начальную фазу тока φ=45.

— Объясните физический смысл ёмкостного сопротивления. Как рассчитать ёмкостное сопротивление идеального конденсатора?

— Чему равен угол сдвига фаз в ёмкости?

— Что понимается под термином реактивное сопротивление? Как его определить?

— Как в сети переменного тока определяется полное сопротивление?

Практическая часть:

Пример 1. В цепи переменного тока к резистору подведено напряжение u=141sin(t-30)В. Сопротивление идеального резистора равно 100 Ом. Определить амплитуду и начальную фазу тока; записать мгновенное и действующее значение тока.

Пример 2. К идеальной катушке подведено напряжение u=141sin(t+73)В. Частота тока в сети равна 50Гц. Индуктивность катушки равна 12,7 мГн. Определить индуктивное сопротивление катушки, амплитуду и начальную фазу тока; записать мгновенное и действующее значение тока.

Пример 3. К идеальному конденсатору подведено напряжение u=282sin(t+30)В. Частота тока в сети равна 50Гц. Ёмкость конденсатора равна 159мкФ. Определить ёмкостное сопротивление конденсатора, амплитуду и начальную фазу тока; записать мгновенное и действующее значение тока.

Урок 7

Тема урока: Неразветвленные цепи переменного тока. Мощность цепи синусоидального тока. Коэффициент мощности.

Цель урока: получение практического навыка расчета элементов цепи переменного тока; расширение знаний о физических явлениях в реальной катушке и реальном конденсаторе.

Теоретическая часть

Рассмотрим более сложные варианты цепи, где последовательно с активным сопротивлением в цепь включено индуктивное и ёмкостное сопротивление.

1. Цепь с активно-индуктивным сопротивлением.

Фаза напряжения на индуктивном сопротивлении опережает фазу тока на 90°, а фаза напряжения на активном сопротивлении совпадает с фазой тока.

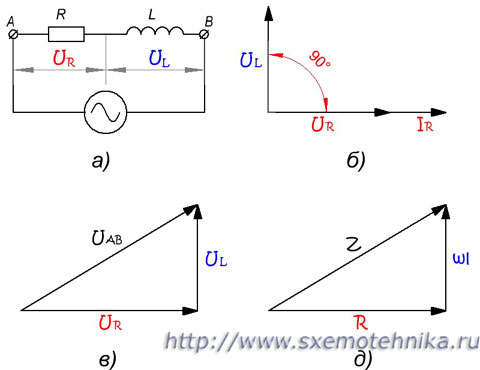
Полное сопротивление цепи с активным сопротивлением и индуктивностью

а) — схема цепи; б) — сдвиг фаз тока и напряжения; в) — треугольник напряжений; д) — треугольник сопротивлений

Произведем геометрическое сложение радиусов-векторов U_L и U_R. Результирующий вектор U_AB будет являеться гипотенузой прямоугольного треугольника. Из геометрии известно, что квадрат гипотенузы равен сумме квадратов катетов.

По закону Ома напряжение должно равняться силе тока, умноженной на сопротивление. Разделим обе части уравнение на

Извлекая квадратный корень из обеих частей этого равенства, получим,

Полное сопротивление можно находить не только путем вычисления, но и путем построения треугольника сопротивлений

2. Цепь с активно-ёмкостным сопротивлением.

Полное сопротивление такой цепи можно определить при помощи треугольника сопротивлений.

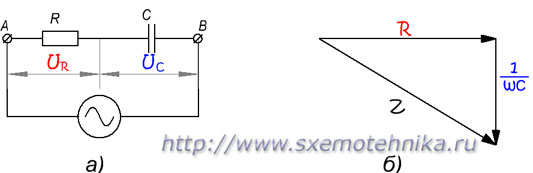
Полное сопротивление цепи с активным сопротивлением и емкостью

а) — схема цепи; б) — треугольник сопротивлений.

Разница между обоими случаями состоит лишь в том, что треугольник сопротивлений для активно-емкостной цепи будет повернут в другую сторону вследствие того, что ток в емкостной цепи не отстает от напряжения, а опережает его

В общем случае, когда цепь содержит все три вида сопротивлений, сначала определяется реактивное сопротивление этой цепи, а затем уже полное сопротивление цепи.

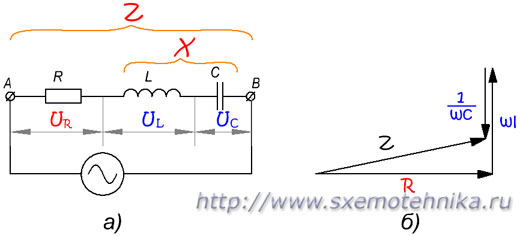
Полное сопротивление цепи содержащей R, L и C

а) — схема цепи; б) — треугольник сопротивлений.

Реактивное сопротивление этой цепи состоит из индуктивного и емкостного сопротивлений. Так как эти два вида реактивного сопротивления противоположны друг другу по своему характеру, то общее реактивное сопротивление цепи будет равно их разности

Общее реактивное сопротивление цепи может иметь индуктивный или емкостный характер, в зависимости от того, какое из этих двух сопротивлений преобладает.

Полное сопротивление цепи при параллельном соединении активного и реактивного сопротивления.

3. Параллельное соединение активного и реактивного элемента

Для того чтобы вычислить полное сопротивление цепи, составленной из активного и индуктивного сопротивлений, соединенных между собой параллельно, нужно сначала вычислить проводимость каждой из параллельных ветвей.

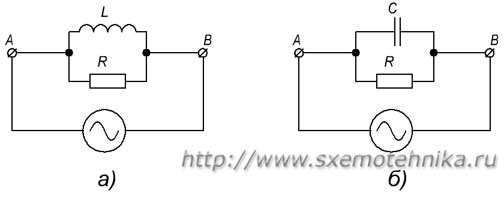
Полное сопротивление цепи при параллельном соединении активного и реактивных элементов

а) — параллельное соединение R и L; б) — параллельное соединение R и C.

Проводимость активной ветви, как известно, равна 1/R, аналогично проводимость индуктивной ветви равна 1/ωL , а полная проводимость равна 1/Z

Полная проводимость равна корню квадратному из суммы квадратов активной и реактивной проводимости, т. е.

откуда:

Нахождение полного сопротивления для этого случая может быть произведено и геометрическим путем. Для этого нужно построить в соответствующем масштабе треугольник сопротивлений, и затем произведение длин катетов разделить на длину гипотенузы. Полученный результат и будет соответствовать полному сопротивлению.

Аналогично случаю, рассмотренному выше, полное сопротивление при параллельном соединении R и С :

Мощность цепи синусоидального тока

Мгновенной мощностью называют произведение мгновенного напряжения на входе цепи на мгновенный ток.

Пусть мгновенные напряжение и ток определяются по формулам:

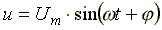
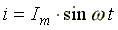
Тогда

Среднее арифметическое значение мощности за период называют активной мощностью и обозначают буквой P.

Эта мощность измеряется в ваттах и характеризует необратимое преобразование электрической энергии в другой вид энергии, например, в тепловую, световую и механическую энергию.

Возьмем реактивный элемент (индуктивность или емкость). Активная мощность в этом элементе 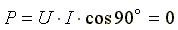, так как напряжение и ток в индуктивности или емкости различаются по фазе на 90. В реактивных элементах не происходит нагрева элементов. Происходит обратимый процесс в виде обмена электрической энергией между источником и приемником. Для качественной оценки интенсивности обмена энергией вводится понятие реактивной мощности Q.

Реактивная мощность, измеряемая в вольтамперах реактивных (Вар), расходуется на создание магнитного поля в индуктивности или электрического поля в емкости. Энергия, накопленная в емкости или в индуктивности, периодически возвращается источнику питания.

Полная мощность, измеряемая в вольтамперах, равна произведению действующих значений напряжения и тока:

, ВА

В соответствии с формулой , реактивная мощность может быть как положительной величиной (если нагрузка имеет активно-индуктивный характер), так и отрицательной (если нагрузка имеет активно-ёмкостный характер). Данное обстоятельство подчёркивает тот факт, что реактивная мощность не участвует в работе электрического тока. Когда устройство имеет положительную реактивную мощность, то принято говорить, что оно её потребляет, а когда отрицательную — то производит, но это чистая условность, связанная с тем, что большинство электропотребляющих устройств (например, асинхронные двигатели), а также чисто активная нагрузка, подключаемая через трансформатор, являются активно-индуктивными.

Синхронные генераторы, установленные на электрических станциях, могут как производить, так и потреблять реактивную мощность в зависимости от величины тока возбуждения, протекающего в обмотке ротора генератора. За счёт этой особенности синхронных электрических машин осуществляется регулирование заданного уровня напряжения сети. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности.

Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения.

Измерительные преобразователи реактивной мощности, использующие формулу , более просты и значительно дешевле измерительных преобразователей на микропроцессорной технике.

Коэффициент мощности и его экономическое значение

Коэффициент мощности — безразмерная физическая величина, характеризующая потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей. Коэффициент мощности показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.

Численно коэффициент мощности равен косинусу этого фазового сдвига.

Значения коэффициента мощности электрических установок переменного тока различны. Электрические лампы обладают, главным образом, активным сопротивлением, поэтому при их включении сдвиг фаз между током и напряжением практически отсутствует. Следовательно, для осветительной нагрузки коэффициент мощности можно считать равным единице. Коэффициент мощности для двигателей переменного тока зависит от нагрузки. При номинальной расчетной нагрузке двигателя cosφ = 0,8-0,9, а у крупных двигателей даже выше. При недогрузке двигателей коэффициент мощности их резко снижается (при холостом ходе cosφ = 0,25-0,3).

Коэффициент мощности учитывают при проектировании электросетей. Низкий коэффициент мощности ведёт к увеличению доли потерь электроэнергии в электрической сети в общих потерях. Коэффициент мощности повышают различными способами. Основной из них — включение параллельно приемникам электрической энергии специальных устройств, называемых компенсаторами. В качестве последних чаще всего используют батареи конденсаторов.

Практическая часть

Задача. Катушка с активным сопротивлением R1=200 Ом и индуктивностью L=0,24 Гн соединена параллельно с конденсатором, активным сопротивлением R2=70 Ом и емкостью С=8*10^-6Ф и подключена к источнику переменного тока с частотой f=200 Гц и амплитудным значением напряжения Um=300 В. Определить действующее значение токов в каждой ветке и общее значение тока в цепи, полное сопротивление цепи, полную, активную и реактивную мощности. Построить векторную диаграмму тока и напряжения.