Электростатика напряженность: Электростатика — Физика — Теория, тесты, формулы и задачи — groupnk.ru — Группа НК — комплексные поставки электрооборудования в Москве и регионах

Содержание

Электростатика — Физика — Теория, тесты, формулы и задачи

Основные теоретические сведения

Электрический заряд и его свойства

К оглавлению…

Электрический заряд – это физическая величина, характеризующая способность частиц или тел вступать в электромагнитные взаимодействия. Электрический заряд обычно обозначается буквами q или Q. В системе СИ электрический заряд измеряется в Кулонах (Кл). Свободный заряд в 1 Кл – это гигантская величина заряда, практически не встречающаяся в природе. Как правило, Вам придется иметь дело с микрокулонами (1 мкКл = 10^–6 Кл), нанокулонами (1 нКл = 10^–9 Кл) и пикокулонами (1 пКл = 10^–12 Кл). Электрический заряд обладает следующими свойствами:

1. Электрический заряд является видом материи.

2. Электрический заряд не зависит от движения частицы и от ее скорости.

Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.

4. Существует два рода электрических зарядов, условно названных положительными и отрицательными.

5. Все заряды взаимодействуют друг с другом. При этом одноименные заряды отталкиваются, разноименные – притягиваются. Силы взаимодействия зарядов являются центральными, то есть лежат на прямой, соединяющей центры зарядов.

6. Существует минимально возможный (по модулю) электрический заряд, называемый

элементарным зарядом. Его значение:

e = 1,602177·10^–19 Кл ≈ 1,6·10^–19 Кл.

Электрический заряд любого тела всегда кратен элементарному заряду:

где: N – целое число. Обратите внимание, невозможно существование заряда, равного 0,5е; 1,7е; 22,7е и так далее. Физические величины, которые могут принимать только дискретный (не непрерывный) ряд значений, называются квантованными. Элементарный заряд e является квантом (наименьшей порцией) электрического заряда.

7. Закон сохранения электрического заряда.

В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной:

Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака. Из закона сохранения заряда так же следует, если два тела одного размера и формы, обладающие зарядами q₁ и q₂ (совершенно не важно какого знака заряды), привести в соприкосновение, а затем обратно развести, то заряд каждого из тел станет равным:

С современной точки зрения, носителями зарядов являются элементарные частицы.

Все обычные тела состоят из атомов, в состав которых входят положительно заряженные протоны, отрицательно заряженные электроны и нейтральные частицы – нейтроны. Протоны и нейтроны входят в состав атомных ядер, электроны образуют электронную оболочку атомов. Электрические заряды протона и электрона по модулю в точности одинаковы и равны элементарному (то есть минимально возможному) заряду e.

В нейтральном атоме число протонов в ядре равно числу электронов в оболочке. Это число называется атомным номером. Атом данного вещества может потерять один или несколько электронов, или приобрести лишний электрон. В этих случаях нейтральный атом превращается в положительно или отрицательно заряженный ион. Обратите внимание, что положительные протоны входят в состав ядра атома, поэтому их число может изменяться только при ядерных реакциях. Очевидно, что при электризации тел ядерных реакций не происходит. Поэтому в любых электрических явлениях число протонов не меняется, изменяется только число электронов.

Так, сообщение телу отрицательного заряда означает передачу ему лишних электронов. А сообщение положительного заряда, вопреки частой ошибке, означает не добавление протонов, а отнимание электронов. Заряд может передаваться от одного тела к другому только порциями, содержащими целое число электронов.

Иногда в задачах электрический заряд распределен по некоторому телу. Для описания этого распределения вводятся следующие величины:

1. Линейная плотность заряда. Используется для описания распределения заряда по нити:

где: L – длина нити. Измеряется в Кл/м.

2. Поверхностная плотность заряда. Используется для описания распределения заряда по поверхности тела:

где: S – площадь поверхности тела. Измеряется в Кл/м².

3. Объемная плотность заряда. Используется для описания распределения заряда по объему тела:

где: V – объем тела. Измеряется в Кл/м³.

Обратите внимание на то, что масса электрона равна:

m_e = 9,11∙10^–31 кг.

Закон Кулона

К оглавлению…

Точечным зарядом называют заряженное тело, размерами которого в условиях данной задачи можно пренебречь. На основании многочисленных опытов Кулон установил следующий закон:

Силы взаимодействия неподвижных точечных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними:

где: ε – диэлектрическая проницаемость среды – безразмерная физическая величина, показывающая, во сколько раз сила электростатического взаимодействия в данной среде будет меньше, чем в вакууме (то есть во сколько раз среда ослабляет взаимодействие). Здесь k – коэффициент в законе Кулона, величина, определяющая численное значение силы взаимодействия зарядов. В системе СИ его значение принимается равным:

k = 9∙10⁹ м/Ф.

Силы взаимодействия точечных неподвижных зарядов подчиняются третьему закону Ньютона, и являются силами отталкивания друг от друга при одинаковых знаках зарядов и силами притяжения друг к другу при разных знаках. Взаимодействие неподвижных электрических зарядов называют

электростатическим или кулоновским взаимодействием. Раздел электродинамики, изучающий кулоновское взаимодействие, называют электростатикой.

Закон Кулона справедлив для точечных заряженных тел, равномерно заряженных сфер и шаров. В этом случае за расстояния r берут расстояние между центрами сфер или шаров. На практике закон Кулона хорошо выполняется, если размеры заряженных тел много меньше расстояния между ними. Коэффициент k в системе СИ иногда записывают в виде:

где: ε₀ = 8,85∙10^–12 Ф/м – электрическая постоянная.

Опыт показывает, что силы кулоновского взаимодействия подчиняются принципу суперпозиции: если заряженное тело взаимодействует одновременно с несколькими заряженными телами, то результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других заряженных тел.

Запомните также два важных определения:

Проводники – вещества, содержащие свободные носители электрического заряда. Внутри проводника возможно свободное движение электронов – носителей заряда (по проводникам может протекать электрический ток). К проводникам относятся металлы, растворы и расплавы электролитов, ионизированные газы, плазма.

Диэлектрики (изоляторы) – вещества, в которых нет свободных носителей заряда. Свободное движение электронов внутри диэлектриков невозможно (по ним не может протекать электрический ток). Именно диэлектрики обладают некоторой не равной единице диэлектрической проницаемостью ε.

Для диэлектрической проницаемости вещества верно следующее (о том, что такое электрическое поле чуть ниже):

Электрическое поле и его напряженность

К оглавлению…

По современным представлениям, электрические заряды не действуют друг на друга непосредственно.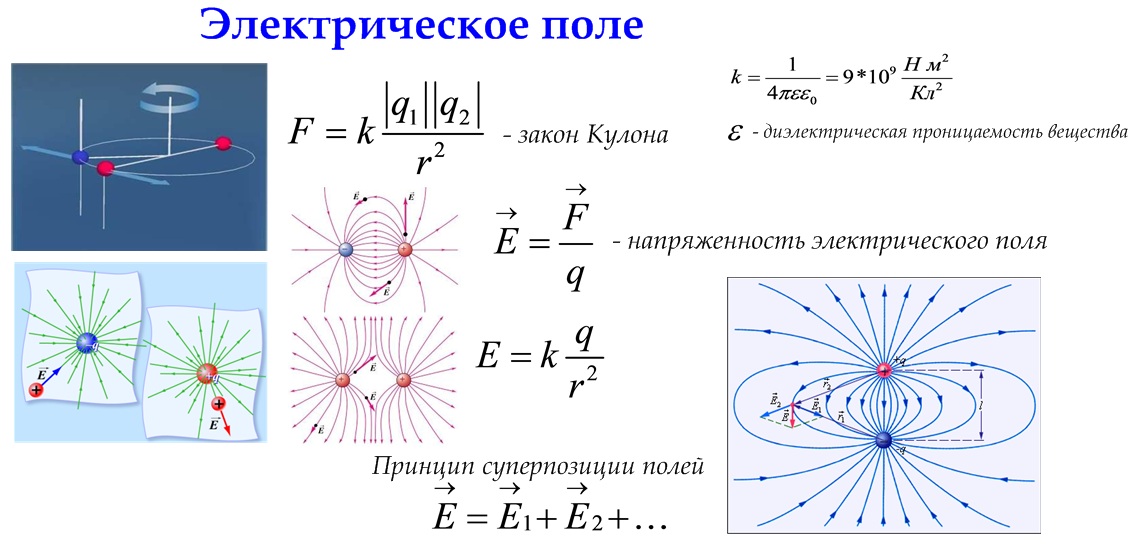

Каждое заряженное тело создает в окружающем пространстве электрическое поле. Это поле оказывает силовое действие на другие заряженные тела. Главное свойство электрического поля – действие на электрические заряды с некоторой силой. Таким образом, взаимодействие заряженных тел осуществляется не непосредственным их воздействием друг на друга, а через электрические поля, окружающие заряженные тела.

Электрическое поле, окружающее заряженное тело, можно исследовать с помощью так называемого пробного заряда – небольшого по величине точечного заряда, который не вносит заметного перераспределения исследуемых зарядов. Для количественного определения электрического поля вводится силовая характеристика —

напряженность электрического поля E.

Напряженностью электрического поля называют физическую величину, равную отношению силы, с которой поле действует на пробный заряд, помещенный в данную точку поля, к величине этого заряда:

Напряженность электрического поля – векторная физическая величина. Направление вектора напряженности совпадает в каждой точке пространства с направлением силы, действующей на положительный пробный заряд. Электрическое поле неподвижных и не меняющихся со временем зарядов называется электростатическим.

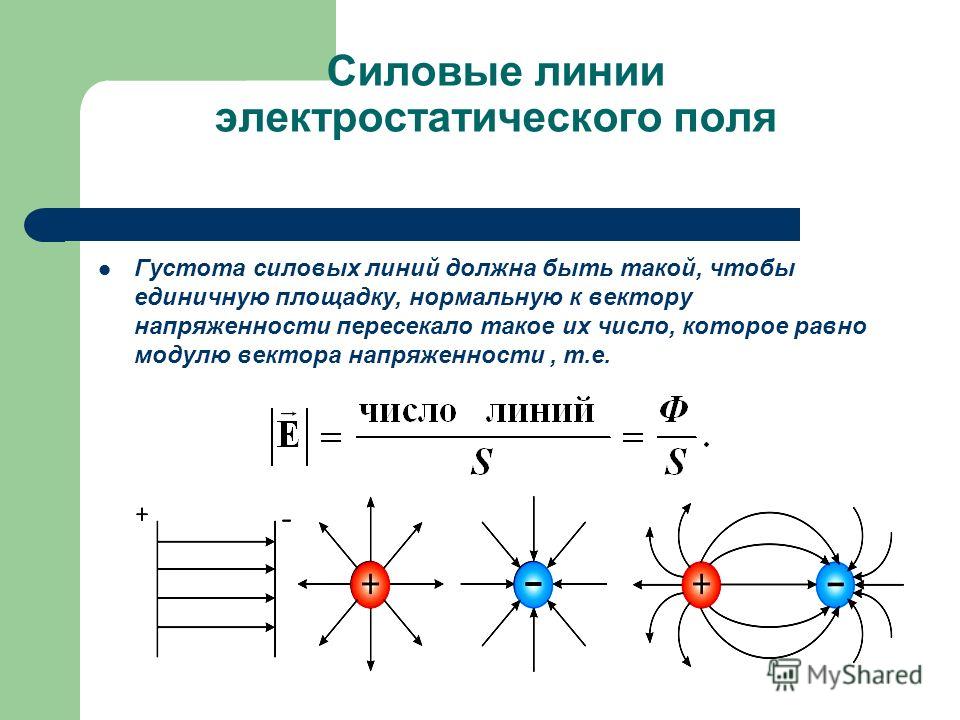
Для наглядного представления электрического поля используют силовые линии. Эти линии проводятся так, чтобы направление вектора напряженности в каждой точке совпадало с направлением касательной к силовой линии. Силовые линии обладают следующими свойствами.

Силовые линии электростатического поля никогда не пересекаются.
Силовые линии электростатического поля всегда направлены от положительных зарядов к отрицательным.
При изображении электрического поля с помощью силовых линий их густота должна быть пропорциональна модулю вектора напряженности поля.
Силовые линии начинаются на положительном заряде или бесконечности, а заканчиваются на отрицательном или бесконечности. Густота линий тем больше, чем больше напряжённость.
В данной точке пространства может проходить только одна силовая линия, т.к. напряжённость электрического поля в данной точке пространства задаётся однозначно.

Электрическое поле называют однородным, если вектор напряжённости одинаков во всех точках поля. Например, однородное поле создаёт плоский конденсатор – две пластины, заряженные равным по величине и противоположным по знаку зарядом, разделённые слоем диэлектрика, причём расстояние между пластинами много меньше размеров пластин.

Во всех точках однородного поля на заряд q, внесённый в однородное поле с напряжённостью E, действует одинаковая по величине и направлению сила, равная F = Eq. Причём, если заряд q положительный, то направление силы совпадает с направлением вектора напряжённости, а если заряд отрицательный, то вектора силы и напряжённости противоположно направлены.

Силовые линии кулоновских полей положительных и отрицательных точечных зарядов изображены на рисунке:

Принцип суперпозиции

К оглавлению. ..

Если с помощью пробного заряда исследуется электрическое поле, создаваемое несколькими заряженными телами, то результирующая сила оказывается равной геометрической сумме сил, действующих на пробный заряд со стороны каждого заряженного тела в отдельности. Следовательно, напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряжённостей электрических полей, создаваемых в той же точке зарядами в отдельности:

Это свойство электрического поля означает, что поле подчиняется принципу суперпозиции. В соответствии с законом Кулона, напряженность электростатического поля, создаваемого точечным зарядом Q на расстоянии r от него, равна по модулю:

Это поле называется кулоновским. В кулоновском поле направление вектора напряженности зависит от знака заряда Q: если Q > 0, то вектор напряженности направлен от заряда, если Q < 0, то вектор напряженности направлен к заряду. Величина напряжённости зависит от величины заряда, среды, в которой находится заряд, и уменьшается с увеличением расстояния.

Напряженность электрического поля, которую создает заряженная плоскость вблизи своей поверхности:

Итак, если в задаче требуется определить напряженность поля системы зарядов, то надо действовать по следующему алгоритму:

Нарисовать рисунок.
Изобразить напряженность поля каждого заряда по отдельности в нужной точке. Помните, что напряженность направлена к отрицательному заряду и от положительного заряда.
Вычислить каждую из напряжённостей по соответствующей формуле.
Сложить вектора напряжённостей геометрически (т.е. векторно).

Потенциальная энергия взаимодействия зарядов

К оглавлению…

Электрические заряды взаимодействуют друг с другом и с электрическим полем. Любое взаимодействие описывается потенциальной энергией. Потенциальная энергия взаимодействия двух точечных электрических зарядов рассчитывается по формуле:

Обратите внимание на отсутствие модулей у зарядов. Для разноименных зарядов энергия взаимодействия имеет отрицательное значение. Такая же формула справедлива и для энергии взаимодействия равномерно заряженных сфер и шаров. Как обычно, в этом случае расстояние r измеряется между центрами шаров или сфер. Если же зарядов не два, а больше, то энергию их взаимодействия следует считать так: разбить систему зарядов на все возможные пары, рассчитать энергию взаимодействия каждой пары и просуммировать все энергии для всех пар.

Задачи по данной теме решаются, как и задачи на закон сохранения механической энергии: сначала находится начальная энергия взаимодействия, потом конечная. Если в задаче просят найти работу по перемещению зарядов, то она будет равна разнице между начальной и конечной суммарной энергией взаимодействия зарядов. Энергия взаимодействия так же может переходить в кинетическую энергию или в другие виды энергии. Если тела находятся на очень большом расстоянии, то энергия их взаимодействия полагается равной 0.

Обратите внимание: если в задаче требуется найти минимальное или максимальное расстояние между телами (частицами) при движении, то это условие выполнится в тот момент времени, когда частицы движутся в одну сторону с одинаковой скоростью. Поэтому решение надо начинать с записи закона сохранения импульса, из которого и находится эта одинаковая скорость. А далее следует писать закон сохранения энергии с учетом кинетической энергии частиц во втором случае.

Потенциал. Разность потенциалов. Напряжение

К оглавлению…

Электростатическое поле обладает важным свойством: работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.

Следствием независимости работы от формы траектории является следующее утверждение: работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.

Свойство потенциальности (независимости работы от формы траектории) электростатического поля позволяет ввести понятие потенциальной энергии заряда в электрическом поле. А физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:

Потенциал φ является энергетической характеристикой электростатического поля. В Международной системе единиц (СИ) единицей потенциала (а значит и разности потенциалов, т.е. напряжения) является вольт [В]. Потенциал — скалярная величина.

Во многих задачах электростатики при вычислении потенциалов за опорную точку, где значения потенциальной энергии и потенциала обращаются в ноль, удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом: потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

Вспомнив формулу для потенциальной энергии взаимодействия двух точечных зарядов и разделив ее на величину одного из зарядов в соответствии с определением потенциала получим, что потенциал φ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:

Потенциал рассчитанный по этой формуле может быть положительным и отрицательным в зависимости от знака заряда создавшего его. Эта же формула выражает потенциал поля однородно заряженного шара (или сферы) при r ≥ R (снаружи от шара или сферы), где R – радиус шара, а расстояние r отсчитывается от центра шара.

Для наглядного представления электрического поля наряду с силовыми линиями используют эквипотенциальные поверхности. Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала. Силовые линии электрического поля всегда перпендикулярны эквипотенциальным поверхностям. Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы.

Электрическое напряжение это просто разность потенциалов, т.е. определение электрического напряжения может быть задано формулой:

В однородном электрическом поле существует связь между напряженностью поля и напряжением:

Работа электрического поля может быть вычислена как разность начальной и конечной потенциальной энергии системы зарядов:

Работа электрического поля в общем случае может быть вычислена также и по одной из формул:

В однородном поле при перемещении заряда вдоль его силовых линий работа поля может быть также рассчитана по следующей формуле:

В этих формулах:

φ – потенциал электрического поля.
∆φ – разность потенциалов.
W – потенциальная энергия заряда во внешнем электрическом поле.
A – работа электрического поля по перемещению заряда (зарядов).
q – заряд, который перемещают во внешнем электрическом поле.
U – напряжение.
E – напряженность электрического поля.
d или ∆l – расстояние на которое перемещают заряд вдоль силовых линий.

Во всех предыдущих формулах речь шла именно о работе электростатического поля, но если в задаче говорится, что «работу надо совершить», или идет речь о «работе внешних сил», то эту работу следует считать так же, как и работу поля, но с противоположным знаком.

Принцип суперпозиции потенциала

Из принципа суперпозиции напряженностей полей, создаваемых электрическими зарядами, следует принцип суперпозиции для потенциалов (при этом знак потенциала поля зависит от знака заряда, создавшего поле):

Обратите внимание, насколько легче применять принцип суперпозиции потенциала, чем напряженности. Потенциал – скалярная величина, не имеющая направления. Складывать потенциалы – это просто суммировать численные значения.

Электрическая емкость. Плоский конденсатор

К оглавлению…

При сообщении проводнику заряда всегда существует некоторый предел, более которого зарядить тело не удастся. Для характеристики способности тела накапливать электрический заряд вводят понятие электрической емкости. Емкостью уединенного проводника называют отношение его заряда к потенциалу:

В системе СИ емкость измеряется в Фарадах [Ф]. 1 Фарад – чрезвычайно большая емкость. Для сравнения, емкость всего земного шара значительно меньше одного фарада. Емкость проводника не зависит ни от его заряда, ни от потенциала тела. Аналогично, плотность не зависит ни от массы, ни от объема тела. Емкость зависит лишь от формы тела, его размеров и свойств окружающей его среды.

Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:

Величина электроемкости проводников зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники. Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, называются обкладками.

Простейший конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика. Такой конденсатор называется плоским. Электрическое поле плоского конденсатора в основном локализовано между пластинами.

Каждая из заряженных пластин плоского конденсатора создает вблизи своей поверхности электрическое поле, модуль напряженности которого выражается соотношением уже приводившимся выше. Тогда модуль напряженности итогового поля внутри конденсатора, создаваемого двумя пластинами, равен:

За пределами конденсатора, электрические поля двух пластин направлены в разные стороны, и поэтому результирующее электростатическое поле E = 0. Электроёмкость плоского конденсатора может быть рассчитана по формуле:

Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз. Обратите внимание, что S в этой формуле есть площадь только одной обкладки конденсатора. Когда в задаче говорят о «площади обкладок», то имеют в виду именно эту величину. На 2 умножать или делить её не надо никогда.

Еще раз приведем формулу для заряда конденсатора. Под зарядом конденсатора понимают только заряд его положительной обкладки:

Сила притяжения пластин конденсатора. Сила, действующая на каждую обкладку, определяется не полным полем конденсатора, а полем, созданным противоположной обкладкой (сама на себя обкладка не действует). Напряженность этого поля равна половине напряженности полного поля, и сила взаимодействия пластин:

Энергия конденсатора. Ее же называют энергией электрического поля внутри конденсатора. Опыт показывает, что заряженный конденсатор содержит запас энергии. Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор. Существует три эквивалентные формы записи формулы для энергии конденсатора (они следуют одна из другой если воспользоваться соотношением q = CU):

Особое внимание обращайте на фразу: «Конденсатор подключён к источнику». Это означает, что напряжение на конденсаторе не изменяется. А фраза «Конденсатор зарядили и отключили от источника» означает, что заряд конденсатора не изменится.

Энергия электрического поля

Электрическую энергию следует рассматривать как потенциальную энергию, запасенную в заряженном конденсаторе. По современным представлениям, электрическая энергия конденсатора локализована в пространстве между обкладками конденсатора, то есть в электрическом поле. Поэтому ее называют энергией электрического поля. Энергия заряженных тел сосредоточена в пространстве, в котором есть электрическое поле, т.е. можно говорить об энергии электрического поля. Например, у конденсатора энергия сосредоточена в пространстве между его обкладками. Таким образом, имеет смысл ввести новую физическую характеристику – объёмную плотность энергии электрического поля. На примере плоского конденсатора, можно получить такую формулу для объёмной плотности энергии (или энергии единицы объёма электрического поля):

Соединения конденсаторов

К оглавлению…

Параллельное соединение конденсаторов – для увеличения ёмкости. Конденсаторы соединены одноименно заряженными обкладками, как бы увеличивая площадь одинаково заряженных пластин. Напряжение на всех конденсаторах одинаковое, общий заряд равен сумме зарядов каждого из конденсаторов, и общая ёмкость также равна сумме емкостей всех конденсаторов соединенных параллельно. Выпишем формулы для параллельного соединения конденсаторов:

При последовательном соединении конденсаторов общая ёмкость батареи конденсаторов всегда меньше, чем ёмкость наименьшего конденсатора, входящего в батарею. Применяется последовательное соединение для увеличения напряжения пробоя конденсаторов. Выпишем формулы для последовательного соединения конденсаторов. Общая емкость последовательно соединенных конденсаторов находится из соотношения:

Из закона сохранения заряда следует, что заряды на соседних обкладках равны:

Напряжение равно сумме напряжений на отдельных конденсаторах.

Для двух последовательно соединённых конденсаторов формула выше даст нам следующее выражение для общей емкости:

Для N одинаковых последовательно соединённых конденсаторов:

Проводящая сфера

К оглавлению…

Напряженность поля внутри заряженного проводника равна нулю. В противном случае на свободные заряды внутри проводника действовала бы электрическая сила, которая вынуждала бы эти заряды двигаться внутри проводника. Это движение, в свою очередь, приводило бы к разогреванию заряженного проводника, чего на самом деле не происходит.

Факт того, что внутри проводника нет электрического поля можно понять и по-другому: если бы оно было то заряженные частицы опять таки двигались бы, причем они бы двигались именно так, чтобы свести это поле к нолю своим собственным полем, т.к. вообще-то двигаться им не хотелось бы, ведь всякая система стремится к равновесию. Рано или поздно все двигавшиеся заряды остановились бы именно в том месте, чтобы поле внутри проводника стало равно нолю.

На поверхности проводника напряжённость электрического поля максимальна. Величина напряжённости электрического поля заряженного шара за его пределами убывает по мере удаления от проводника и рассчитывается по формуле, аналогичной формулам для напряженности поля точечного заряда, в которой расстояния отсчитываются от центра шара.

Так как напряженность поля внутри заряженного проводника равна нулю, то потенциал во всех точках внутри и на поверхности проводника одинаков (только в этом случае разность потенциалов, а значит и напряжённость равна нулю). Потенциал внутри заряженного шара равен потенциалу на поверхности. Потенциал за пределами шара вычисляется по формуле, аналогичной формулам для потенциала точечного заряда, в которой расстояния отсчитываются от центра шара.

Электрическая емкость шара радиуса R:

Если шар окружен диэлектриком, то:

Свойства проводника в электрическом поле

К оглавлению…

Внутри проводника напряженность поля всегда равна нулю.
Потенциал внутри проводника во всех точках одинаков и равен потенциалу поверхности проводника. Когда в задаче говорят, что «проводник заряжен до потенциала … В», то имеют в виду именно потенциал поверхности.
Снаружи от проводника вблизи от его поверхности напряженность поля всегда перпендикулярна поверхности.
Если проводнику сообщить заряд, то он весь распределится по очень тонкому слою вблизи поверхности проводника (обычно говорят, что весь заряд проводника распределяется на его поверхности). Это легко объясняется: дело в том, что сообщая заряд телу, мы передаем ему носители заряда одного знака, т.е. одноименные заряды, которые отталкиваются. А значит они будут стремиться разбежаться друг от друга на максимальное расстояние из всех возможных, т.е. скопятся у самых краев проводника. Как следствие, если из проводника удалить сердцевину, то его электростатические свойства никак не изменятся.
Снаружи проводника напряженность поля тем больше, чем кривее поверхность проводника. Максимальное значение напряженности достигается вблизи остриев и резких изломов поверхности проводника.

Замечания к решению сложных задач

К оглавлению…

1. Заземление чего-либо означает соединение проводником данного объекта с Землей. При этом потенциалы Земли и имеющегося объекта выравниваются, а необходимые для этого заряды перебегают по проводнику с Земли на объект либо наоборот. При этом нужно учитывать несколько факторов, которые следуют из того, что Земля несоизмеримо больше любого объекта находящегося не ней:

Общий заряд Земли условно равен нолю, поэтому ее потенциал также равен нолю, и он останется равным нолю после соединения объекта с Землей. Одним словом, заземлить – означает обнулить потенциал объекта.
Для обнуления потенциала (а значит и собственного заряда объекта, который мог быть до этого как положительным так и отрицательным), объекту придется либо принять либо отдать Земле некоторый (возможно даже очень большой) заряд, и Земля всегда сможет обеспечить такую возможность.

2. Еще раз повторимся: расстояние между отталкивающимися телами минимально в тот момент, когда их скорости становятся равны по величине и направлены в одну сторону (относительная скорость зарядов равна нулю). В этот момент потенциальная энергия взаимодействия зарядов максимальна. Расстояние между притягивающимися телами максимально, также в момент равенства скоростей, направленных в одну сторону.

3. Если в задаче имеется система, состоящая из большого количества зарядов, то необходимо рассматривать и расписывать силы, действующие на заряд, который не находится в центре симметрии.

Электростатика. Основные понятия. Электрический заряд. Закон сохранения электрического заряда. Закон Кулона. Принцип суперпозиции. Теория близкодействия. Потенциал электрического поля. Конденсатор.

Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Физический справочник / / Физика для самых маленьких. Шпаргалки. Школа. / / Электростатика. Основные понятия. Электрический заряд. Закон сохранения электрического заряда. Закон Кулона. Принцип суперпозиции. Теория близкодействия. Потенциал электрического поля. Конденсатор.

Электростатика. Основные понятия. Электрический заряд. Закон сохранения электрического

заряда. Закон Кулона. Принцип суперпозиции. Теория близкодействия. Потенциал электрического
поля. Конденсатор.

Основные понятия электростатики: электрический заряд, элементарный заряд, электрическое поле, проводник, диэлектрик:
Электрический заряд Q [Кл]: это физическая величина, характеризующая свойство тел вступать в электрическое взаимодействие. Одноименные заряды отталкиваются, а разноименные заряды притягиваются Элементарный заряд: e=1,610^-19 Кл это минимальная порция заряда, котрая может передаваться от одного тела к другому (заряд протона или электрона) Электрическое поле:* это создаваемый любым электрическим зарядом материальный объект, непрерываный в пространстве, проявляющийся в том, что действет на другие заряды. Проводник: это материал, по которому заряд может свободно перемещаться от одного тела к другому. Диэлектрик: это материал, по которому электрический заряд при обычных условиях перемещаться не может.
Закон сохранения электрического заряда:
Закон сохранения электрического заряда: в замкнутой системе алгебраическая (с учетом знаков +/-) сумма зарядов остается постоянной
Закон Кулона, кулоновская сила:
Закон Кулона: сила взаимодействия двух точечных зарядов (=кулоновская сила) направлена вдоль прямой, соединяющей заряды, прямо пропорциональна модулю зарядов и обратно пропорциональна квадрату расстояния между ними:
Принцип суперпозиции для электрических зарядов:
Принцип суперпозиции для электрических зарядов: результирующая сила, действующая на данный заряд q₁ со стороны нескольких зарядов q₂…..q_n, равна геометрической сумме (= векторной сумме) сил F₁₂+….F_1n, действующих на данный заряд со стороны каждого из зарядов:
Теория близкодействия электрических зарядов:
Взаимодействие между заряженными частицами осуществляется посредством электрического поля и осуществляется с конечной скоростью
Напряженность электрического поля, напряженность поля точечного заряда:
Напряженность электрического поля [В/м]: E (векторная величина) это отношение силы F (векторной величины) с которой поле действует на точечный заряд q (скалярной величины), к этому заряду (с учетом знака заряда): Напряженность электрического поля единичного точечного заряда Q: на расстоянии r от него (напрямую следует из закона Кулона):
Принцип суперпозиции электрических полей:
Принцип суперпозиции электрических полей: если в данной точке пространства различные заряженные частицы создают электрические поля, напряженности которых E₁,E₂,….E_n, то результирующая напряженность электрического поля в этой точке равна векторной сумме отдельных напряжённостей:
Потенциал электрического поля, потенциальная энергия заряда, разность потенциалов = напряжение, связь разности потенциалов и напряженности в однородном поле:
Потенциальная энергия: заряда q в однородном электростатическом поле напряженности E: , где d — расстояние до плоскости, где потенциальная энергия принимается равной нулю Потенциал электростатического поля в точке [В]: это отношение потенциальной энергии заряда в поле, к этому заряду (с учетом знака заряда): Вариант 2: это работа по перемещению единичного положительного заряда из данной точки в бесконечность Напряжение = Разность потенциалов между точками: это отношение работы поля при перемещении заряда из начальной точки в конечную к этому заряду ( с учетом знака заряда): Численно (но не по размерности) это работа поля по перемещению единичного положительного заряда из одной точки в другую Связь разности потенциалов и напряженности: в однородном поле: где U это разность потенциалов между точками, которые cвязаны вектором перемещения Δd, совпадающим по направлению с вектором E
Конденсатор, электроемкость, напряженность, энергия:
Электроемкость двух проводников: это отношение заряда Q одного из проводников к разности потенциалов U между этим проводником и соседним: Конденсатор: это система двух проводников (обкладок конденсатора), разделенных слоем диэлектрика, толщина которого мала по отношению к размерам обкладок Напряженность поля плоского конденсатора: Электроемкость плоского конденсатора: Энергия заряженного конденсатора:

Поиск в инженерном справочнике DPVA. Введите свой запрос:

Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.

Коды баннеров проекта DPVA.ru
Начинка: KJR Publisiers

Консультации и техническая
поддержка сайта: Zavarka Team

Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator

Урок Электростатика — Физика 10 класс

Электростатика

Взаимодействие электрических зарядов. Два вида заряда. Закон сохранения электрического заряда.

Электрический заряд , наряду с массой , является важнейшей характеристикой частицы.
Электрическим зарядом называется величина, определяющая интенсивность электромагнитного взаимодействия заряженных частиц. [q] =Кулон (Кл)
Электрические заряды могут быть положительными и отрицательными, причем, одноименные заряды отталкиваются, разноименные – притягиваются. Обычно носителем элементарного отрицательного заряда является электрон, а положительного – протон. По модулю значение элементарного заряда равно: Кл.
Любые заряды в целое число раз больше элементарного:

Из опыта следует закон сохранения заряда: в электрически замкнутой системе полный заряд сохраняется.
Экспериментально также установлен закон инвариантности электрического заряда: величина заряда не зависит от скорости, с которой он движется (т.е. инвариантна относительно инерциальных систем отсчета).
Электростатика изучает законы взаимодействия электрических неподвижных зарядов.
Точечный заряд – это заряженное тело, размерами которого можно пренебречь в условиях данной задачи.

Закон Кулона.

Сила взаимодействия двух неподвижных точечных зарядов определяется законом Кулона:

, r – расстояние между зарядами,
e — диэлектрическая проницаемость среды (табличное данное), — модули зарядов.
, Можно записать закон Кулона: .

Электрическое поле. Напряженность. Принцип суперпозиции.

Силовой характеристикой электростатического поля является напряженность :

F – сила, действующая на неподвижный точечный заряд q.
Модуль напряженности электростатического поля, созданного точечным зарядом q на расстоянии r от заряда вычислим по формуле:

. Если поле создано не одним, а несколькими точечными зарядами, то напряженность поля в каждой точке равна векторной сумме напряженностей полей, создаваемых каждым зарядом в отдельности (принцип суперпозиции полей):

. Если a — угол между векторами , то напряженность поля, созданного двумя зарядами, вычисляют по формуле:.

Графическое изображение поля
Для графического изображения электрического поля используют линии напряженности (силовые линии). Линии напряженности начинаются на положительных зарядах, заканчиваются на отрицательных или уходят в бесконечность.
Вектор напряженности направлен по касательной к линии напряженности в каждой точке.

Густота линий пропорциональна модулю напряженности поля.

Примеры изображений электрических полей

Потенциал и разность потенциалов. Работа по перемещению заряда.

Энергетической характеристикой поля является потенциал.

W – потенциальная энергия точечного заряда q, помещенного в данную точку поля.
Потенциал – величина алгебраическая. Потенциал поля, создаваемого точечным зарядом q на расстоянии r от заряда, вычисляется по формуле:
, q > 0, j > 0, q Связь разности потенциалов с напряженностью
(j1 — j2) – разность потенциалов
Электрическое поле, в котором напряженность одинакова по модулю и направлению в любой точке пространства, называется однородным.
В однородном поле , d – расстояние между точками с потенциалами j1 и j2.
Работа электростатического поля при перемещении заряда
Работа, совершаемая силами поля по перемещению заряда из точки 1 вточку 2 вычисляется по формуле: .

Поверхность, во всех точках которой потенциал электрического поля имеет одинаковое значение, называется эквипотенциальной поверхностью. Эквипотенциальными поверхностями точечного заряда являются сферы, в центре которых расположен заряд.

Электрическая емкость. Конденсатор. Энергия электрического поля.

Для накопления значительных разноименных электрических зарядов применяются конденсаторы.
Конденсатор – это две проводящих поверхности, обычно плоской, цилиндрической или сферической формы, расположенные на небольшом расстоянии друг от друга. Проводники — обкладки конденсатора — заряжают разноименными зарядами, равными по абсолютной величине — — разность потенциалов между обкладками.

Электроемкость конденсатора: , [C]=Фарада (Ф)

Электроемкость плоского конденсатора:
S – площадь обкладок,
d – расстояние между обкладками,
e — диэлектрическая проницаемость вещества, заполняющего пространство между обкладками,
e_o — электрическая постоянная (eо=8,85 10-12 Ф/м).

Энергия заряженного конденсатора
Энергия заряженного конденсатора любой формы вычисляется по формуле:

С – емкость конденсатора, — разность потенциалов между обкладками конденсатора,

q – заряд пластины конденсатора.

Энергия электрического поля плоского конденсатора:

— объем конденсатора.

ТЕСТОВЫЕ ЗАДАНИЯ

Два одинаковых металлических шарика заряжены одноименно так, что величина зарядов на одном шарике в n раз больше, чем на другом. Шарики привели в соприкосновение и раздвинули на прежнее расстояние, много больше размеров шарика. Во сколько раз изменилась сила взаимодействия между шариками?
Два шарика радиусом R1 и R2 заряжены до потенциалов j1 и j2 соответственно, находятся на большом расстоянии друг от друга. Шарики соединяют длинным тонким проводником. Какой общий потенциал устанавливается на шариках?
При перемещении заряда в электрическом поле по любой замкнутой траектории работа сил электрического поля оказалась равной нулю. Какое это было поле?
Две параллельные металлические пластины находятся на расстоянии 5 см одна от другой. Между пластинами приложено напряжение 20 В. Какова напряженность электрического поля между пластинами?
Как изменится электроемкость конденсатора при уменьшении расстояния между пластинами в 4 раза?
Укажите направление и рассчитайте напряженность электрического поля в точке, лежащей посередине между зарядами q1=2 10-7 Кл и q2=-4 10-7 Кл . Расстояние между зарядами равно 10 см.
Пластины плоского конденсаторы имеют электрические заряды +q и –q, площадь одной пластины S. Расстояние между пластинами d. Какую работу нужно совершить для того, чтобы раздвинуть пластины на небольшое расстояние Dd?
Напряжение на обкладках конденсатора было 100 В. При полной разрядке конденсатора через резистор в цепи прошел электрический заряд 0,1 Кл. Какова электроемкость конденсатора и какое количество энергии выделилось на резисторе?
К положительному заряду q1 с большого расстояния приближается на расстояние R отрицательный заряд q2. Как изменятся напряженность и потенциал электрического поля в точке на середине расстояния между зарядами q1 и q2 ?
На нейлоновой нити подвешен электрически нейтральный алюминиевый стержень. Имеется стеклянный стержень, обладающий отрицательным электрическим зарядом. Как сообщить алюминиевому стержню положительный заряд?

Ответы и решения

Так как расстояние между шариками значительно больше их размеров, то силу взаимодействия заряженных шариков вычислим по закону Кулона. До соприкосновения: После соприкосновения заряды шариков станут одинаковыми. По закону сохранения заряда:, , ,
Заряд шариков до соединения проводником: q1=j1×c1, q2=j2×c2. Электроемкость уединенного проводника, шара радиусом R вычисляем по формуле: с=4pee_oR. Тогда:. Если шарики соединить, то будет происходить перераспределение зарядов между шариками до тех пор, пока потенциалы шариков j не станут равными. Заряд первого шара второго шара и .
Работа перемещения заряда в электростатическом поле
Если контур замкнут, то , значит
.
, т.к. d уменьшается в 4 раза, то С увеличивается в 4 раза.
В/м В/м . Определим направление , выполним рисунок. Так как направлены в одну и ту же сторону, то: В/м.
Работа равна изменению энергии заряженного конденсатора: .
По определению: .
Энергия заряженного конденсатора выделится на резисторе при полном разряде?
Напряженность увеличится на величину . Потенциал– величина алгебраическая: — потенциал в точке в 1-ом случае. При приближении отрицательного заряда потенциал , значит потенциал уменьшится.
Нужно поднести стеклянный стержень к одному концу алюминиевого стержня без соприкосновения и в это же время коснуться рукой противоположного конца алюминиевого стержня.{2}}

Линии напряженности электростатического поля

Непрерывные линии, касательные к которым в каждой точке совпадают по направлению с вектором напряженности, называются линиями напряженности электростатического поля.
Линии напряженности никогда не пересекаются друг с другом. Они начинаются на положительных зарядах, заканчиваются на отрицательных, а затем уходят на бесконечность.
Картины линий напряженности точечных зарядов:

Поле, напряженность которого одинакова во всех точках, называется однородным.
Линии напряженности однородного поля параллельны друг другу.

Например, поле, близкое к однородному, создают разноименные заряженные пластины. Искажения поля наблюдаются только по краям.
электростатика
на главную

Официальный сайт АНО ДО Центра «Логос», г.Глазов
http://logos-glz.ucoz.net/

ГОТОВИМСЯ К УРОКУ
Кинематика
Динамика
МКТ
Термодинамика
Электростатика
Электрический ток
Электрический ток в средах
Магнитное поле Электромагнитная индукция
Оптика
Методы познания
электростатика                                                       немного о физике:
Электродинамика – раздел физики, изучающий законы взаимодействия электрических зарядов и действия на них электромагнитных полей.
Электростатика — раздел электродинамики, изучающий взаимодействие покоящихся электрических зарядов и действия на них электромагнитных полей.

В процессе познания природы человек обнаружил, что не все явления можно объяснить с помощью законов механики и молекулярно-кинетической теории.
Было замечено, что некоторые тела (янтарь, стекло, смола и др.), испытавшие трение, начинают притягивать к себе более мелкие тела. Изучение этого явления показало, что оно вызвано появлением на телах электрического заряда.
Тело, обладающее свойством притягивать к себе легкие тела, благодаря наличию на нем электрического заряда, называют наэлектризованным. Явление возникновения зарядов на телах называют электризацией.
Опыты по взаимодействию наэлектризованных тел показали, что в природе проявляются только два вида взаимодействия: притяжение и отталкивание.
Поэтому можно сделать вывод, что в природе существует только два рода зарядов, которые условно названы положительный и отрицательный. Принято, что стеклянная палочка, потертая о шелк, приобретает положительный заряд, а эбонитовая палочка, потертая о шерсть – отрицательный заряд.

Получить заряды на телах можно следующими способами:
1.
В состав всех тел входят атомы, которые состоят из ядра и вращающихся вокруг него электронов. Электроны в атомах одних веществ удерживаются сильнее, в атомах других — слабее. При соприкосновении тел электроны, удерживаемые слабо, переходят на поверхность другого тела, перенося с собой свой отрицательный заряд – 1,6 ×10^-19Кл. Поэтому тело с избытком электронов стает отрицательно заряженным, а тело с недостатком электронов – положительно заряженным.
Натирание тел позволяет увеличить площадь соприкосновения, что способствует переходу большего количества электронов, а, следовательно, получению больших по модулю зарядов тел.
2.
При соприкосновении незаряженного тела с заряженным происходит перераспределение заряда. При этом оба тела будут иметь одинаковые по знаку заряды.
Так, при соприкосновении нейтрального тела с отрицательно заряженным телом происходит переход определенной доли избыточных электронов с отрицательно заряженного тела на первоначально нейтральное тело. Поэтому при таком соприкосновении оба тела будут иметь отрицательные заряды.
Если происходит соприкосновение нейтрального тела с положительно заряженным телом, то электроны с нейтрального тела переходят на положительно заряженное тело, частично компенсируя его заряд. При этом на первоначально нейтральном теле появляется недостаток электронов, что определяет получение им положительного заряда.

3.
Под воздействием световых лучей электроны могут покидать атомы, унося с собой отрицательный заряд. Следовательно, в составе тел появляется не скомпенсированный положительный заряд, и тела стают положительно заряжены.

Что называют электрическим зарядом?
Электрический заряд – физическая величина, определяющая интенсивность электромагнитных взаимодействий.
Принято электрический заряд обозначать Q или q.
Модуль заряда тела определяется по формуле:
Q= n ∙ e
где е = 1,6 × 10^-19Кл — элементарный заряд, n-количество избыточных (недостающих) электронов.

Закон сохранения электрического заряда.

Т.к. электризация обусловлена только переходом электронов, а, следовательно, переходом соответствующего отрицательного заряда с одного тела на другое, то можно утверждать:
внутри изолированной системы при любых взаимодействиях алгебраическая сумма электрических зарядов остается постоянной.
q₁ + q₂^{+ q₃ + q}_n = const

Систему называют изолированной или замкнутой, если в нее не вводятся или из нее не выводятся электрические заряды.

Как взаимодействуют заряженные тела?

Мы можем наблюдать, что заряженные тела взаимодействуют (притягиваются или отталкиваются), находясь на некотором расстоянии друг от друга.
Взаимодействие неподвижных зарядов, находящихся на некотором расстоянии друг от друга, осуществляется посредством электрического поля, порожденного зарядами. Это взаимодействие происходит не мгновенно, а распространяется в вакууме со скоростью с

Закон Кулона:
Сила взаимодействия двух точечных неподвижных зарядов в вакууме прямо пропорциональна произведению модулей этих зарядов и обратно пропорциональна квадрату расстояния между зарядами.

где ε₀ = 8,854 ∙ 10^-12 Кл²/(Н м²) — электрическая постоянная, k = 9 ∙ 10⁹ Нм²/ Кл² .

Электростатическое поле и его характеристики.

Электрический заряд, помещенный в некоторую точку пространства, изменяет свойства данного пространства. То есть заряд порождает вокруг себя электрическое поле.
Электростатическое поле — вид материи, существующий вокруг неподвижный заряженных тел.
Электростатическое поле не изменяется во времени.
Оно действует на заряд, помещенный в какую-либо его точку.

Силовой характеристикой электрического поля является напряженность.
Напряженностью электрического поля в данной точке называется векторная физическая величина, численно равная силе, действующей на единичный положительный заряд, помещенный в данную точку поля.
где — напряженность электрического поля,
— сила, действующая со стороны электрического поля на пробный заряд .

За единицу измерения напряженности электрического поля в системе СИ принимают
Если на пробный заряд, действуют силы со стороны нескольких зарядов, то эти силы по принципу суперпозиции сил независимы, и результирующая этих сил равна векторной сумме сил. Поэтому можно сформулировать принцип суперпозиции (наложения) электрических полей.

Напряженность электрического поля системы зарядов в данной точке пространства равна векторной сумме напряженностей электрических полей, создаваемых в данной точке пространства, каждым зарядом системы в отдельности:
.

Электрическое поле удобно представлять графически с помощью силовых линий.
Силовыми линиями (линиями напряженности электрического поля) называют такие линии, касательные к которым в каждой точке поля совпадают с направлением вектора напряженности в данной точке.
Силовые линии начинаются на положительном заряде и заканчиваются на отрицательном.
Густота линий напряженности характеризует напряженность поля (чем плотнее располагаются линии, тем поле сильнее).
Силовые линии электростатических полей точечных зарядов.
Электростатическое поле точечного заряда неоднородно ( ближе к заряду поле сильнее).

Силовые линии электростатических полей бесконечных равномерно заряженных плоскостей.
Электростатическое поле бесконечных равномерно заряженных плоскостей однородно .
Электрическое поле, напряженность во всех точках которого одинакова, называется однородным.

Силовые линии электростатических полей двух точечных зарядов.

Число силовых линий, пронизывающих некоторую площадку, площадью S, и перпендикулярных ей, определяет поток вектора напряженности электрического поля.
Поток вектора напряженности сквозь площадку площадью S равен:
где Е_n— проекция вектора напряженности на нормаль к площадке.
Теорема Остроградского-Гаусса: поток вектора напряженности электрического поля в вакууме сквозь любую замкнутую поверхность равен отношению алгебраической суммы зарядов, заключенных внутри этой поверхности, к значению электрической постоянной

Потенциал — энергетическая характеристика электрического поля.
Потенциал — скалярная физическая величина, равная отношению потенциальной энергии, которой облает электрический заряд в данной точке электрического поля, к величине этого заряда.
Потенциал показывает какой потенциальной энергией будет обладать единичный положительный заряд, помещенный в данную точку электрического поля.
где — потенциал в данной точке поля, — потенциальная энергия заряда в данной точке поля.
За единицу измерения потенциала в системе СИ принимают
(1В = 1Дж/Кл )
За единицу потенциала принимают потенциал в такой точке, для перемещения в которую из бесконечности электрического заряда 1 Кл, требуется совершить работу, равную 1 Дж.

Рассматривая электрическое поле, созданное системой зарядов, следует для определения потенциала поля использовать принцип суперпозиции:
Потенциал электрического поля системы зарядов в данной точке пространства равен алгебраической сумме потенциалов электрических полей, создаваемых в данной точке пространства, каждым зарядом системы в отдельности:
Воображаемая поверхность, во всех точках которой потенциал принимает одинаковые значения, называется эквипотенциальной поверхностью. При перемещении электрического заряда от точки к точке вдоль эквипотенциальной поверхности энергия его не меняется.
Эквипотенциальных поверхностей для заданного электростатического поля может быть построено бесконечное множество.
Вектор напряженности в каждой точке поля всегда перпендикулярен к эквипотенциальной поверхности, проведенной через данную точку поля.
Вектор напряженности в данной точке поля всегда направлен в область уменьшения потенциала.

Примеры электрических полей.
1. Электрическое поле точечного заряда.
Напряженность и потенциал поля точечного заряда в данной точке электрического поля равны:

где q — значение заряда, ε — диэлектричеcкая постоянная, r — расстояние от заряда до точки поля, в которой определяются напряженность и потенциал.
Эквипотенциальные поверхности и силовые линии электростатических полей точечных зарядов.

2. Электрическое поле бесконечной равномерно заряженной плоскости.
Напряженность электрического поля равна:

где σ — поверхностная плотность заряда
q — значение заряда, s — площадь поверхности плоскости, ε — диэлектрическая постоянная.

Эквипотенциальные поверхности и силовые линии электростатических полей бесконечных равномерно заряженных плоскостей.

3. Электрическое поле бесконечно длинной заряженной нити.
Напряженность электрического поля равна:
где τ — линейная плотность заряда,
q — значение заряда, l -длина нити, ε — диэлектрическая постоянная, r — расстояние от нити до точки , в которой определяется напряженность

Оглавление
Глава 3

Электричество и магнетизм
3.1 Электростатика
3.1.1 Пример – поле и потенциал сферы
Найти напряженность поля и потенциал во всем пространстве тонкой сферы радиуса R, равномерно заряженной до заряда q.
Решение
Применим теорему Гаусса. Выберем в качестве замкнутой поверхности концентрическую сферу радиуса r > R (рис.). Очевидно, что напряженность на поверхности этой сферы будет одинакова по величине и направлена по радиусу. Тогда поток напряженности через нее будет E ⋅ 4πr². Согласно теореме Гаусса
откуда
Выбрав в качестве поверхности сферу радиуса r < R, получим E = 0. Таким образом, однородно заряженная сфера во внешней области пространства создает такое же поле, как и заряд, помещенный в ее центре. Внутри сферы поля нет.
Найдем потенциал сферы во всем пространстве. Так как вне сферы напряженность поля совпадает с напряженностью заряда, находящегося в центре, то и потенциал при r > R выразится в виде
Пронесем единичный положительный заряд из бесконечности до расстояния r от центра, меньшего радиуса сферы. Тогда работа, которую необходимо совершить по переносу до поверхности сферы будет равна kq∕R. Внутри сферы поле равно нулю и работа не совершается. Таким образом

На рис. 3.1 изображены графики зависимости напряженности и потенциала поля от расстояния до центра однородно заряженной сферы.
3.1.2 Пример – поле и потенциал шара
Однородно заряженный шар. Пусть радиус шара R, полный заряд Q. Повторяя рассуждения, приведенные в предыдущей задаче, получим, что вне шара напряженность и потенциал поля совпадают с полем заряда Q, помещенного в центр шара:
Чтобы найти напряженность электрического поля внутри шара, выберем в качестве замкнутой поверхности сферу радиуса r < R с центром в центре шара. Из симметрии ясно, что напряженность поля направлена по радиусу и одинакова по величине на всей поверхности сферы. Из теоремы Гаусса следует
где q(r) – заряд внутри выбранной поверхности. Введем плотность заряда шара ρ. Тогда
Плотность заряда равна полному заряду, деленному на объем шара:
Для напряженности поля внутри шара получим
Найдем потенциал внутри шара.
Первый интеграл имеет смысл работы по переносу единичного положительного заряда из бесконечности до поверхности шара и равен kQ∕R. Второй член
Значение потенциала внутри шара определится выражением

Окончательно имеем
Заметим, что непрерывен не только потенциал (что и должно быть), но и напряженность электрического поля. Последнее связано с тем, что в системе нет заряженных тонких поверхностей. Поэтому нет и скачка напряженности. На рис. 3.2 приведены графики зависимости напряженности и потенциала от расстояния до центра однородно заряженного по объему шара.
3.1.3 Пример – заземленная сфера

Пусть есть две проводящие концентрические сферы радиусов a и b. На внутреннюю сферу помещен заряд q, а внешняя заземлена (рис. 3.3). Требуется определить напряженность и потенциал электрического поля во всем пространстве.
Решение
Так как внешняя сфера заземлена, на ней появляется некоторый заряд Q. Если бы он был известен, напряженность поля легко определилась бы из принципа суперпозиции (напомним, что во внешнем пространстве сфера создает поле, такое же, как точечный заряд, расположенный в ее центре, а внутри поля нет)
Для потенциала при r > b имеем φ = k(q + Q)∕r. На поверхности внешней сферы φ(b) = k(q + Q)∕b.
Так как эта сфера заземлена, φ(b) = 0. Отсюда
Тогда напряженность поля при r > b равна нулю. Вне заземленной сферы поля нет. Этот результат не зависит от формы заземленного проводника. Говорят, что заземленная оболочка экранирует находящиеся внутри заряды: никакие изменения их величины или положения не сказываются снаружи.

Понятно, что при r > b потенциал равен нулю. Для нахождения потенциала между сферами пронесем единичный положительный заряд из бесконечности в данную точку, используя принцип суперпозиции. В поле заряда Q работа совершается лишь до поверхности внешней сферы: φ₁= kQ∕b—kq∕b. А в поле внутренней сферы φ₂= kq∕r. Полный потенциал
Внутри малой сферы E = 0, потенциал не меняется и равен потенциалу на поверхности
На рис. 3.4 приведены графики зависимостей E(r) и φ(r).
3.1.4 Пример – разлетающиеся частицы
Четыре одинаковых частицы массы m и заряда q первоначально удерживаются в углах квадрата со стороной a. Заряды отпускают. Найти скорости зарядов по прошествии большого промежутка времени.
Решение
Из симметрии ясно, что в любой момент времени частицы будут находиться в углах некоторого квадрата и обладать одинаковыми по величине скоростями, направленными по диагоналям этого квадрата. В результате вся начальная потенциальная энергия U перейдет в кинетическую энергию частиц
где v – искомая скорость.

Дело, таким образом, сводится к вычислению начальной потенциальной энергии системы U. Перенумеруем заряды (рис. 3.5) и начнем собирать систему. Принесем из бесконечности первый заряд. Для этого не понадобиться совершать работу (внешних сил нет): A₁= 0.
Принесем второй заряд. Работа в поле первого заряда будет
Третий заряд уже придется двигать в поле, как первого, так и второго заряда: Наконец, для последнего Полная потенциальная энергия системы Тогда откуда получаем ответ
3.1.5 Пример – столкновение зарядов
С большого расстояния навстречу друг другу со скоростями, соответственно, v₁и v₂движутся две одинаковых частицы массы m и заряда q. Определите минимальное расстояние, на которое они сблизятся.
Решение
При минимальном расстоянии скорости частиц u будут одинаковы. Из закона сохранения импульса
Начальная потенциальная энергия электрического взаимодействия равна нулю.
Запишем закон сохранения энергии:
где r – минимальное расстояние. Из первого уравнения u = ∕2. И, подставляя во второе, получаем ответ:
3.1.6 Пример – система конденсаторов
Определите емкость системы конденсаторов, изображенных на рисунке (рис. 3.6).
Решение
Пронумеруем конденсаторы и обозначим на схеме заряды (рис. 3.7). Из симметрии схемы ясно, что заряды на конденсаторах 1, 2 и 3, 4, соответственно, одинаковы. Так как батарея электронейтральна q₁= q₂.
Тогда ясно, что средний (5-й) конденсатор не заряжен и его можно убрать. Эквивалентная схема будет выглядеть так: (рис 3.8).
Так как емкость последовательно соединенных конденсаторов определяется по формуле
Отсюда C′ = C. И имеем новую эквивалентную схему (рис. 3.9). По правилу определения емкости параллельно соединенных конденсаторов полная емкость цепи:
Можно было поступить иначе. Так как средний конденсатор не заряжен, точки, к которым он подсоединен, имеют одинаковый потенциал. Тогда их можно соединить проводником: это не приведет к перераспределению зарядов на остальных конденсаторах. Соответствующая эквивалентная схема (рис. 3.10. Или, учитывая, что имеется две пары параллельно соединенных конденсаторов, получаем еще одну эквивалентную схему (рис. 3.11). Отсюда
В итоге получаем тот же ответ:
3.2 Постоянный ток
3.2.1 Пример – соединение сопротивлений
Каким должно быть сопротивление r, чтобы входное сопротивление между клеммами было равно тоже r (рис. 3.12)?
Решение
Последние два сопротивления, соединенные последовательно, имеют сопротивление
Тогда имеем эквивалентную схему: (рис. 3.13)). Параллельное соединение сопротивлений R и R′ приводит к схеме (рис. 3.14)). Где По условию: R + R′′ = r.
То есть:
Откуда получаем ответ
3.2.2 Пример – ЭДС и внутреннее сопротивление батареи
Батарея, замкнутая на сопротивление R₁= 10 Ом, дает ток I₁= 3 А; замкнутая на сопротивление R₂= 20 Ом, она дает ток I₂= 1,6 А. Найдите ЭДС и внутреннее сопротивление r батареи.
Решение
Из условия
Приравнивая правые части, получим Откуда
Подставляя r в первое уравнение, получим
3.2.3 Пример – внутреннее сопротивление аккумулятора
Аккумулятор подключен один раз к внешней цепи с сопротивлением R₁, другой раз – с R₂. При этом количество теплоты, выделяющейся во внешней цепи в единицу времени, одинаково. Определите внутреннее сопротивление аккумулятора.
Решение
Обозначим ЭДС аккумулятора через , а внутреннее сопротивление – через r.
Условие равенства количества теплоты дает: Или Разрешая это уравнение относительно r, получим ответ:
3.2.4 Пример – цепь с конденсаторами

Конденсаторы емкости C₁и C₂и резисторы, сопротивления которых равны R₁,R₂,R₃, включены в электрическую цепь, как показано на рисунке 3.15). Найти установившиеся заряды на конденсаторах. Напряжение U известно.
Решение
В установившемся режиме через резисторы течет постоянный ток, определяющийся из уравнения
Рассмотрим контур, содержащий C₁,R₁,R₂. Для него:
Откуда (подставляя I):
Аналогично, рассматривая контур, содержащий C₂,R₂,R₃, получим
3.3 Магнитное поле
3.3.1 Пример – движение заряда в магнитном поле
На заряд q = 1 Кл, движущийся со скоростью v = 1 м/с, в магнитном поле действует сила F = 10 Н. Заряд движется под углом α = 30^∘к направлению индукции магнитного поля. Чему равна индукция этого поля?
Решение
На заряд действует сила Лоренца:
Откуда B = F∕(qv sin α). Подставляя числа, получим ответ: B = 20 Тл.
3.3.2 Пример – проводник с током в магнитном поле

В вертикальном однородном магнитном поле на двух тонких нитях подвешен горизонтально проводник массы m = 0,16 кг и длины l = 0,8 м. Концы проводника при помощи гибких проводов, находящихся вне поля, подсоединены к источнику тока. Найдите угол, на который отклоняются от вертикали нити подвеса, если по проводнику течет ток I = 2 А, а индукция магнитного поля B = 1 Тл.
Решение
На проводник действуют две силы: тяжести mg, направленная вертикально, и Ампера IBl, направленная горизонтально (см. рис. 3.16). Тогда в равновесии
Принимая g = 10 м∕с²и подставляя числа, получим tgα = 1. Откуда α = 45^∘.
3.3.3 Пример – радиусы траекторий
Как относятся радиусы траекторий двух электронов с кинетической энергией K₁и K₂, если однородное магнитное поле перпендикулярно их скорости?
Решение
Скорости электронов определяются из формул:
Радиусы определятся из закона Ньютона Тогда отношение радиусов
3.4 ЭДС индукции
3.4.1 Пример – падение в магнитном поле
В однородном магнитном поле индукции B находятся две вертикальные рейки, расположенные в плоскости, перпендикулярной линиям поля (рис. 3.17). По рейкам, расстояние между которыми равно L, может скользить без трения проводник массой m. Определите установившуюся скорость этого проводника, если верхние концы реек замкнуты на сопротивление R. В какие виды энергии переходит работа силы тяжести?


Решение
На скользящий проводник действуют две силы: тяжести mg и Ампера IBL. При установившемся движении
ЭДС индукции Выражая ток из второго уравнения и подставляя в первое, получим ответ: Можно получить ответ другим способом. Мощность силы тяжести в установившемся режиме переходит в тепло, выделяющееся на сопротивлении:
3.4.2 Пример – стержень в магнитном поле
Металлический стержень AB, сопротивление единицы длины которого ρ, движется с постоянной скоростью v, перпендикулярной AB, замыкая два идеальных проводника OC и OD, образующих друг с другом угол α. Длина OC равна l, и AB перпендикулярен OC (рис. 3.18). Вся система находится в однородном постоянном магнитном поле индукции B, перпендикулярном плоскости системы. Найдите полное количество теплоты, которое выделится в цепи за время движения стержня от точки O до точки C.
Решение
Площадь треугольника в зависимости от времени S = xy∕2, где x = vt,y = x ⋅ tgα = vt ⋅ tgα.
Тогда
Сопротивление R = ρx = ρvt. Мощность, выделяющаяся в цепи Полное время движения t₀= l∕v.
Тогда ответ
3.4.3 Пример – вихревое электрическое поле
Индукция однородного магнитного поля внутри цилиндра радиуса r = 0,1 м линейно возрастает со временем: B = αt (коэффициент α = 10^-3Тл/с). Магнитное поле направлено вдоль оси цилиндра. Чему равна напряженность вихревого электрического поля на расстоянии l = 0,2 м от оси цилиндра?
Решение
Циркуляция электрического поля равна скорости изменения магнитного потока через сечение цилиндра:
Отсюда Подставляя числа: E = 2,5 ⋅ 10^-5В/м.
ЭЛЕКТРОСТАТИКА И ПОСТОЯННЫЙ ТОК
%PDF-1.6 % 1 0 obj > endobj 6 0 obj /CreationDate (D:20110602100030+03’00’) /Creator (Acrobat PDFMaker 9.0 for Word) /ModDate (D:20110602104751+03’00’) /Producer (Acrobat Distiller 9.0.0 $Windows$) /Title >> endobj 2 0 obj > stream 2011-06-02T10:47:51+03:002011-06-02T10:00:30+03:002011-06-02T10:47:51+03:00Acrobat PDFMaker 9.0 for Wordapplication/pdf
ЭЛЕКТРОСТАТИКА И ПОСТОЯННЫЙ ТОК
кафедра физики_2
кафедра физики_2
ЭЛЕКТРОСТАТИКА И ПОСТОЯННЫЙ ТОК
Бобрович
СОДЕРЖАНИЕ
Олег
Тема 2
user
СПИСОК ИСПОЛЬЗОВАННОЙ И РЕКОМЕНДОВАННОЙ ЛИТЕРАТУРЫ
Оксана
Учебное издание

Законы Ньютона и электрическая сила

Притягивающее или отталкивающее взаимодействие между любыми двумя заряженными объектами — это электрическая сила . Как и любая сила, ее действие на объекты описывается законами движения Ньютона. Электрическая сила — F _elect — присоединяется к длинному списку других сил, которые могут действовать на объекты. Законы Ньютона применяются для анализа движения (или отсутствия движения) объектов под действием такой силы или комбинации сил.Анализ обычно начинается с построения диаграммы свободного тела, на которой тип и направление отдельных сил представлены векторными стрелками и помечены в соответствии с типом. Затем величины сил складываются в виде векторов, чтобы определить результирующую сумму, также известную как чистая сила. Затем чистую силу можно использовать для определения ускорения объекта.

В некоторых случаях целью анализа не является определение ускорения объекта.Вместо этого диаграмма свободного тела используется для определения пространственного разделения или заряда двух объектов, находящихся в статическом равновесии. В этом случае диаграмма свободного тела сочетается с пониманием векторных принципов, чтобы определить некоторую неизвестную величину посреди головоломки, включающей геометрию, тригонометрию и закон Кулона. В этом последнем разделе Урока 3 мы исследуем оба типа приложений законов Ньютона к явлению статического электричества.

Электрическая сила и ускорение

Предположим, что резиновый шар и пластиковая трубка для гольфа заряжаются отрицательно, натирая их шерстью животных.Предположим, что воздушный шар подбрасывается в воздух, а трубка для гольфа удерживается под ним, чтобы поднять воздушный шар в воздухе. Эта цель будет достигнута, если пространственное разделение между заряженными объектами отрегулировано таким образом, чтобы уравновешивать направленную вниз силу тяжести (F _grav) и направленную вверх электрическую силу (F _elect). Это представляет собой сложную задачу манипулирования, поскольку воздушный шар будет постоянно перемещаться из стороны в сторону, вверх и вниз под воздействием как силы тяжести, так и силы электрического тока.Когда трубка для гольфа находится слишком глубоко под воздушным шаром, воздушный шар упадет и ускорится вниз. Это, в свою очередь, уменьшит разделительное расстояние и приведет к увеличению электрической силы. По мере увеличения F _elect, он, вероятно, превысит F _grav, и воздушный шар внезапно ускорится вверх. И, наконец, если точка заряда на трубке для гольфа не находится непосредственно под точкой заряда воздушного шара (вероятный сценарий), электрическая сила будет приложена под углом к вертикали, и воздушный шар будет иметь боковое ускорение.Вероятным результатом такой попытки поднять воздушный шар будет множество мгновенных ускорений в разных направлениях.

Предположим, что в какой-то момент в процессе попытки поднять воздушный шар, существовали следующие условия:

Баллон массой 0,90 грамма с зарядом -75 нКл расположен на расстоянии 12 см над пластиковой трубкой для гольфа с зарядом -83 нКл.

Как можно применить законы Ньютона, чтобы определить ускорение воздушного шара в этот момент?

Как и любая проблема, связанная с силой и ускорением, задача начинается с построения диаграммы свободного тела.На воздушный шар действуют две силы. Сила тяжести на воздушном шаре направлена вниз. Электрическая сила, действующая на воздушный шар, направлена вверх, поскольку баллон и трубка для гольфа имеют одинаковый заряд, а трубка для гольфа удерживается под воздушным шаром. Эти две силы показаны на диаграмме свободного тела справа. Второй шаг включает определение величины этих двух сил. Сила тяжести определяется умножением массы (в килограммах) на ускорение свободного падения.

F _grav = m • g = (0.00090 кг) • (9,8 м / с / с)
F _грав = 8,82 x 10 ^-3 N, вниз
Электрическая сила определяется по закону Кулона. Как показано ниже, соответствующей единицей измерения заряда является кулон (C), а соответствующей единицей измерения расстояния — метры (м). Использование этих единиц приведет к единице силы Ньютон. Спрос на эти единицы возникает из единиц постоянной Кулона.
F _elect = k • Q ₁ • Q ₂ / d ²
F _elect = (9 x 10 ⁹ Н • м ² / C ²) • (-75 x 10 ^-9 C) • (-83 x 10 ^-9 C) / (0.12) ²
F _elect = 3,89 x 10 ^-3 N, вверх
Чистая сила — это векторная сумма этих двух сил. Восходящие и нисходящие силы складываются как векторы.
F _net = · F = F _grav (вниз) + F _elect (вверх)
F _net = 8,82 x 10 ^-3 N, вниз + 3,89 x 10 ^-3 N, вверх
F _сетка = 4,93 x 10 ^-3 N, вниз
Последний шаг этой проблемы включает использование второго закона Ньютона для определения ускорения объекта.Ускорение — это чистая сила, деленная на массу (в килограммах).
a = F _{, нетто} / м = (4,93 x 10 ^-3 Н, вниз) / (0,00090 кг)
a = 5,5 м / с / с, вниз
Приведенный выше анализ показывает, как можно применить закон Ньютона и закон Кулона для определения мгновенного ускорения. Следующий анализ включает случай, когда два объекта находятся в состоянии статического равновесия.
Электрическая сила и статическое равновесие
Предположим, что два резиновых шара подвешены к потолку на двух длинных веревках так, что они свисают вертикально.Затем предположим, что каждому воздушному шарику дано 10 растираний средней силы шерстью животных. Воздушные шары, притягивающие электроны сильнее, чем мех животных, приобретут отрицательный заряд. Воздушные шары будут иметь одинаковый заряд, и впоследствии они будут отталкиваться друг от друга. В результате их отталкивания струны и подвешенные шары теперь образуют угол с вертикалью. Угол веревки с вертикалью будет математически связан с количеством заряда на воздушных шарах.По мере того, как шары приобретают большее количество заряда, сила отталкивания между ними будет увеличиваться, и угол, который образует струна с вертикалью, также увеличится. Как и любую ситуацию, связанную с электростатической силой, эту ситуацию можно проанализировать с помощью векторных принципов и законов Ньютона.
Предположим, что существуют следующие условия.
Два шара весом 1,1 грамма подвешены на веревках длиной 2,0 метра и подвешены к потолку. Затем их десять раз натирают мехом животных, чтобы передать одинаковый заряд Q каждому шарику.Воздушные шары отталкиваются друг от друга, и видно, что каждая струна составляет угол 15 градусов с вертикалью. Определите электрическую силу отталкивания, заряд на каждом воздушном шаре (предполагается, что он одинаковый) и количество электронов, перенесенных на каждый воздушный шар в результате 10 касаний шерстью животных.
Из-за сложности физической ситуации было бы разумно представить ее в виде диаграммы. Диаграмма будет служить средством определения известной информации для этой ситуации.На схеме ниже изображены два воздушных шара с веревкой длиной L и углом «тета». Масса ( м ) аэростатов известна; здесь он выражается в килограммах (стандартная единица массы). Расстояние между воздушными шарами (переменная в законе Кулона) отмечено на диаграмме и представлено переменной d . Проведена вертикальная линия, идущая от точки поворота на потолке; эта вертикальная линия является одной стороной прямоугольного треугольника, образованного горизонтальной линией, соединяющей воздушные шары, и веревкой, идущей от воздушного шара до потолка.Этот прямоугольный треугольник будет полезен при анализе ситуации с использованием векторных принципов. Обратите внимание, что вертикальная линия делит пополам отрезок линии, соединяющий воздушные шары; таким образом, одна сторона прямоугольного треугольника имеет расстояние d / 2 .

Применение законов Ньютона к этой ситуации начинается с построения диаграммы свободного тела для одного из воздушных шаров. На воздушные шары действуют три силы: сила натяжения, сила тяжести и электростатическая сила отталкивания.Эти три силы представлены для воздушного шара справа. (См. Диаграмму ниже.) Обратите внимание, что сила натяжения направлена под углом к вертикали. В физике такие ситуации обрабатываются путем разделения вектора силы на горизонтальную и вертикальную составляющие. Это показано ниже; компоненты обозначены как F _x и F _y . Эти компоненты связаны с углом, который струна образует с вертикалью, с помощью тригонометрических функций. Поскольку воздушный шар находится в равновесии, силы, действующие на воздушный шар, должны уравновешивать друг друга.Это означало бы, что вертикальная составляющая силы натяжения ( F _y ) должна уравновешивать направленную вниз силу тяжести ( F _grav ). Горизонтальная составляющая силы натяжения ( F _x ) должна уравновешивать направленную вправо электростатическую силу ( F _elect ).

Поскольку масса воздушного шара известна, сила тяжести, действующая на него, может быть определена.
F _grav = m • g = (0.0011 кг) • (9,8 м / с / с)
F _грав = 0,01078 N
Сила тяжести равна вертикальной составляющей силы натяжения ( F _y = 0,0108 N ). Компонент F _y связан с компонентом F _x и углом theta функцией касательной. Это соотношение можно использовать для определения горизонтальной составляющей силы натяжения.Работа представлена ниже.
Касательная (тета) = противоположная сторона / смежная сторона
Касательная (тета) = F _x / F _y
Касательная (15 градусов) = F _x / (0,01078 Н)
F _x = (0,01078 Н) • Касательная (15 градусов)
F _x = 0,00289 N
Горизонтальная составляющая силы натяжения равна электростатической силе.Таким образом,
F _{избранный} = 0,00289 N
Теперь, когда электростатическая сила была определена с использованием законов Ньютона и векторных принципов, закон Кулона теперь может быть применен для определения заряда на воздушном шаре.
Предполагается, что воздушные шары имеют одинаковое количество заряда, поскольку они заряжаются одинаковым образом с помощью 10 трений средней силы. Поскольку Q ₁ равно Q ₂, уравнение можно переписать как
Это уравнение можно алгебраически преобразовать, чтобы найти Q.Шаги показаны ниже.
F • d ² = k • Q ²
Q ² = F • d ² / k
Q = SQRT (F • d ² / k)
Для завершения решения необходимо знать значение d . Это требует анализа прямоугольного треугольника, чтобы определить длину стороны, противоположной 15-градусному углу. Эта длина составляет половину расстояния d. Поскольку длина гипотенузы известна, используется синусоидальная функция.
Синус (Тета) = противоположная сторона / сторона гипотенузы
Синус (15 градусов) = противоположная сторона / (2,0 м)
Противоположная сторона = (2,0 м) • Синус (15 градусов)
противоположная сторона = d /2 = 0,518 м
Удвоение этого расстояния дает значение d 1,035 м. Теперь можно произвести замены, чтобы определить стоимость Q.
Q = SQRT (F • d ² / k)
Q = КОРЕНЬ [(0.00289 Н) • (1,035 м) ² / (9 x 10 ⁹ Н • м ² / C ²)]
Q = 5,87 x 10 ^-7 C (отрицательный)
Заряд объекта связан с количеством избыточных (или дефицитных) электронов в объекте. Используя заряд одного электрона (-1,6 x 10 ^-19 Кл), можно определить количество электронов на этом объекте:
# избыток электронов = (-5,87 x 10-7 C) / (-1.6 x 10 ^-19 C / электрон)
# избыточных электронов = 3,67 x 10 ¹² электронов
В процессе зарядки более трех триллионов электронов переместились из шерсти животного в каждый из воздушных шаров. Вау!
Конфигурации из трех или более зарядов
В каждом из приведенных выше примеров мы исследовали взаимодействие двух заряженных объектов.Для анализа ситуаций были объединены законы Ньютона и закон Кулона. Но что, если есть три или более зарядов? Закон Кулона может рассматривать только взаимодействие между Q ₁ и Q ₂. Нужно ли переписывать закон для электрической силы, чтобы учесть Q ₃? Нет!
Электрические силы возникают в результате взаимодействия двух зарядов. В ситуациях, включающих три или более зарядов, электрическая сила, действующая на один заряд, является просто результатом комбинированных эффектов взаимодействия каждого отдельного заряда этого заряда со всеми другими зарядами.Если конкретный заряд сталкивается с двумя или более взаимодействиями, то чистая электрическая сила представляет собой векторную сумму этих отдельных сил. В качестве примера этого подхода предположим, что присутствуют четыре заряда (A, B, C и D), которые пространственно расположены в форме квадрата. Заряды A и D заряжены отрицательно и занимают противоположные углы квадрата, а заряды B и C заряжены положительно и занимают оставшиеся два угла, как показано. Если вас интересует чистая электрическая сила, действующая на заряд A, то необходимо вычислить электрические силы между A и каждым из трех других зарядов.То есть F _BA, F _CA и F _DA должны сначала определяться применением закона Кулона к каждой из этих пар зарядов. Обозначение F _BA используется для обозначения силы B на A .
F _BA = k • Q _A • Q _B / d _BA ²
F _CA = k • Q _A • Q _C / d _CA ²
F _DA = k • Q _A • Q _D / d _DA ²
Направление каждой из этих трех сил можно определить, применяя основные правила взаимодействия зарядов: противоположно заряженные объекты притягиваются, а одноименно заряженные объекты отталкиваются.Применительно к этому сценарию можно предположить, что силы F _BA, F _CA и F _DA направлены, как показано на диаграмме ниже. Заряд B притягивает A, а заряд C притягивает A, поскольку это пары противоположно заряженных объектов. Но Заряд D отталкивает А, поскольку они представляют собой пару одинаково заряженных объектов.

Итак, величины отдельных сил определяются расчетами по закону Кулона. Направление отдельных сил определяется применением правил взаимодействия зарядов.И как только известны величина и направление трех векторов силы, эти три вектора можно сложить, используя правила сложения векторов, чтобы определить чистую электрическую силу. Это показано на диаграмме выше.
Проверьте свое понимание
Используйте свое понимание заряда, чтобы ответить на следующие вопросы.По завершении нажмите кнопку, чтобы просмотреть ответы.
1. Положительно заряженный объект с зарядом +85 нКл используется для уравновешивания направленной вниз силы тяжести на 1,8-граммовом воздушном шаре с зарядом -63 нКл. На какой высоте над воздушным шаром должен удерживаться объект, чтобы сбалансировать воздушный шар? (ПРИМЕЧАНИЕ: 1 нКл = 1 x 10 ^-9 ° С)

2. Воздушный шар A и шарик B заряжаются аналогичным образом, протираясь шерстью животных.Каждый получает более 25 триллионов электронов. Если масса воздушных шаров составляет 1 грамм, то как далеко ниже воздушного шара B должен удерживаться воздушный шар A, чтобы воздушный шар B левитировал? Предположим, что воздушные шары действуют как точечные заряды.
3. Два шара весом 1,2 грамма подвешены на легких веревках, прикрепленных к потолку в одной и той же точке. Чистый заряд воздушных шаров -540 нКл. В состоянии равновесия воздушные шары разнесены на 68,2 см друг от друга. Определите длину строки.

4. ZINGER : по оси X размещены три заряда. Заряд A — это заряд +18 нКл, помещенный в начало отсчета. Заряд B представляет собой заряд -27 нКл, размещенный на расстоянии 60 см. Где по оси (в какой координате x?) Должен быть помещен положительно заряженный C, чтобы он находился в состоянии равновесия?

Напряжение в изогнутом заряженном проводе (электростатическая сила) — имеет ли значение толщина провода?
Дж.М. Хьюре рассмотрел части проблемы в статье «Решения акси-симметричного уравнения Пуассона на основе эллиптических интегралов» (2005), давая форму электрического поля в окрестности петлевого заряда. Я опубликую здесь его опубликованный результат с его обозначениями.
Эти уравнения относятся к массе, распределенной в петле с линейной массой $ \ lambda $, радиусом $ a $ и расположенной на высоте $ z $ (насколько мне известно, $ z = 0 $). Затем используются координаты $ R $ для расстояния до вертикальной оси и $ Z $ для вертикального положения.2} $$
И да, это то, что у меня было. Я раскрыл потенциал в своем вопросе, потому что это было самое простое выражение, которое могло передать математику для геометрии цикла. Хьюре также отметил статью Дюрана 1964 года относительно этих уравнений: Electrostatique. I. Распределения Les , которые могут иметь первую опубликованную форму для геометрии петель. Хьюре также обсуждает самогравитацию петлевой геометрии и вводит концепцию петлевой сингулярности . Я думаю, он имеет в виду сказать, что сингулярность петли подразумевает бесконечную самогравитацию, но я думаю, что его формулировка явно не говорит об этом.Тем не менее, он избегает проблемы, написав интеграл для самогравитации с использованием плотности массы $ \ rho $, а не линейной плотности массы $ \ lambda $ (аналогично моему $ F_ {effective} $ ниже), указывая, что проблема бесконечной самогравитации. Затем в статье Хюре предлагаются эмпирические методы самогравитации, а также некоторые другие проблемы.
Прежде чем перейти к собственному решению, я должен отметить одно отличие гравитационной задачи. Этот вопрос касается силы электрического провода, и в этом случае заряд является поверхностным. 2 l} E \ left (2 \ frac {\ sqrt {R \ rho}} {l} \ right) $$
Начиная с этого момента, я перейду непосредственно к заданному мной вопросу.Вспомните уравнение для поля вокруг бесконечного линейного заряда, приведенное выше. Потенциал затем следует форме $ ln (r) $, но имейте в виду, что потенциал является относительной мерой, но также, поскольку потенциал вокруг кольцевого заряда, указанный выше, был найден путем интегрирования дифференциальных потенциалов $ 1 / r $, он будет такое же смещение.
$$ E (r) = — 2 \ lambda k ln (r) = 2 k \ lambda ln \ left (\ frac {C} {r} \ right) $$
Объективно, мы найдем упрощенную аппроксимацию ранее данного $ E (\ rho, z) $, когда $ r $ стремится к нулю, и его часть будет идентифицирована как эквивалентная $ E (r) $ выше, вдоль с другим, пока неизвестным, компонентом.Я так и сделал, и это была нелегкая задача. Вот что я получил. Две части обозначены и написаны отдельно, чтобы сделать результат кристально ясным.
$$ E (\ rho, z) \ приблизительно 2 k \ lambda \ left (ln (\ frac {8 R} {r}) + \ frac {\ rho-R} {R} \ left (1-ln ( \ frac {8 R} {r}) \ right) \ right) $$ $$ E_ {line} (\ rho, z) = 2 k \ lambda \ left (ln (\ frac {8 R} {r}) \ right) $$ $$ E_ {loop} (\ rho, z) = 2 k \ lambda \ left (\ frac {\ rho-R} {R} \ left (1-ln (\ frac {8 R} {r}) \ right ) \ вправо) $$
Опять же, это приближение предыдущего уравнения для $ E (\ rho, z) $, когда $ r $ стремится к нулю.Я обнаружил, что это хорошее приближение для $ r / R <0,1 $ или около того, и приближение становится более правильным по мере дальнейшего уменьшения $ r $. Это почти точно для проволоки с радиусом $ cm $ или $ mm $ с радиусом петли $ m $. Затем для решения проблемы используется электрическое поле, обусловленное геометрией глобального контура, $ E_ {loop} $. Градиент этой величины дает поле $ \ vec {F} _ {loop} $, которое затем можно использовать для получения силы. Проблема в том, что это поле действует очень неравномерно при некотором $ r $. Обратите внимание, что $ E_ {line} $ действует равномерно, и потенциал и поле для приближения бесконечной линии будут преобладать по величине по сравнению с эффектами глобальной петли, но не приводит к действию результирующей силы на провод, в то время как $ E_ {loop} $ делает, это означает, что равномерное распределение заряда на поверхности является допустимым приближением.2 k (ln (\ frac {8 R} {r}) - \ frac {3} {2}) = 1,7 GN $$
Теперь другая часть вопроса заключалась в том, что происходит, когда толщина проволоки становится равной нулю. В этом случае (постоянный заряд) сила стремится к бесконечности. Что ж, все это знали (иначе зачем мне задавать этот вопрос). Но как насчет случая постоянного напряжения и постоянной плотности поверхностного заряда? Предыдущее написано с использованием $ V $ для напряжения на проводе и $ \ sigma $ для поверхностной плотности заряда. Обратите внимание, что напряжение провода радиуса $ r $ может быть действительно найдено с помощью приближения бесконечного линейного заряда в соответствии с моими предыдущими аргументами.2 к (ln (\ frac {8 R} {r}) — \ frac {3} {2}) $$
Теперь ограничения могут быть рассмотрены. Вот что происходит с силой в проводе, когда радиус стремится к бесконечности при постоянных величинах. Для полноты картины я обращаюсь к тем же вопросам с точки зрения растягивающего напряжения.
Постоянный заряд -> бесконечность, бесконечность
Постоянное напряжение -> ноль, бесконечность
Постоянная плотность заряда поверхности -> ноль, бесконечность
Это интересный результат.Я должен отметить, что из-за растягивающего напряжения это означает, что никакая изогнутая проволока с чрезвычайно малым радиусом, изгибом и зарядом не может существовать без разрыва. Я приветствую разногласия по этому поводу.
Электростатическое притяжение и силы поверхностного натяжения для точной самосборки микродеталей
Реферат
Самосборка не широко используется в промышленном микропроизводстве, хотя потенциально может включать значительно менее сложные процессы сборки.В последнее время были введены и исследованы различные процедуры самовыравнивания деталей. В этих процедурах в основном используются капиллярные, гравитационные или электростатические силы в микромасштабе. В этой статье исследуются две разные концепции точной самостоятельной сборки деталей. Один хорошо описан в литературе третьими сторонами и включает выравнивание деталей с использованием поверхностного натяжения микромасштабных клеевых пленок, которые выборочно наносятся на гидрофобные выравнивающие структуры.В настоящей публикации обсуждается влияние размеров таких структурированных центров выравнивания на ход процесса. Вторая концепция — это новый подход к самовыравниванию микроструктур с помощью электростатического притяжения. Несколько дополнительных и электропроводящих микроструктурированных паттернов служат в качестве сайтов связывания для выравнивания частей в этом подходе. Чтобы получить знания о том, как работают эти два подхода, они были смоделированы и смоделированы. Кроме того, для анализа выполнимости этих процедур и проверки результатов моделирования были проведены эксперименты на микроструктурированных частях и подложках.В частности, расположение выравнивающих структур и размер деталей были идентичны для обеих концепций, описанных в экспериментальной работе; поэтому сравнивались эти два метода. При процедуре самосборки, использующей электростатическое притяжение, наблюдались высокая точность центровки и силы, влияющие на деталь на больших расстояниях. Наконец, части с микроструктурированными сайтами связывания, которые были всего лишь 10 × 10 мкм ², могли точно самовыравниваться за счет электростатического притяжения.
Ключевые слова
Самосборка
Капиллярные силы
Поверхностное натяжение
Электростатические силы
Рекомендуемые статьиЦитирующие статьи (0)
Полный текст
Copyright © 2009 Elsevier B.V. Все права защищены.
Рекомендуемые статьи
Цитирование статей
Произошла ошибка при настройке вашего пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки вашего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, используйте кнопку «Назад» и примите файлы cookie.
Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файлах cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
18.8 Применение электростатики — Физика в колледже для курсов AP®
Ускорение заряженной капли бензина
Если не предпринять никаких шагов для заземления бензонасоса, статическое электричество может быть передано бензину при заправке бензобака.Предположим, крошечная капля бензина имеет массу 4,00 × 10–15 кг, 4,00 × 10–15 кг и имеет положительный заряд 3,20 × 10–19C 3,20 × 10–19 ° C. а) Найдите вес капли. (b) Вычислите электрическую силу, действующую на каплю, если имеется направленное вверх электрическое поле с напряженностью 3,00 × 105 Н / К3,00 × 105 Н / К из-за другого статического электричества поблизости. (c) Рассчитайте ускорение капли.
Стратегия
Чтобы решить проблему комплексной концепции, мы должны сначала определить задействованные физические принципы и определить главы, в которых они встречаются.В части (а) этого примера запрашивается вес. Это тема динамики, которая определяется в книге «Динамика: сила и законы движения Ньютона». В части (b) рассматривается электрическая сила, действующая на заряд, тема «Электрический заряд и электрическое поле». Часть (c) запрашивает ускорение, зная силы и массу. Это часть законов Ньютона, которые также можно найти в «Динамике: сила и законы движения Ньютона».
Следующие решения для каждой части примера показывают, как применяются конкретные стратегии решения проблем.Это включает выявление известных и неизвестных, проверку правильности ответа и т. Д.
Решение для (a)
Вес — это масса, умноженная на ускорение свободного падения, как сначала выражено в
w = mg.w = mg. размер 12 {w = ital «mg»} {}
18.20
Ввод заданной массы и среднего ускорения свободного падения дает
w = (4,00 × 10-15 кг) (9,80 м / с2) = 3,92 × 10-14 Н .w = (4,00 × 10–15 кг) (9,80 м / с2) = 3,92 × 10–14 Н. размер 12 {w = \ («44» «.» «00» умножить на «10» rSup {size 8 {- «15»}} «» кг «\) \ (9″.»» 80 «м / с» rSup {size 8 {2}} \) = 3 «.» «92» умножить на «10» rSup {размер 8 {- «14»}} N} {}
18,21
Обсуждение (a)
Это небольшой вес, соответствующий небольшой массе капли.
Решение для (b)
Сила, которую электрическое поле оказывает на заряд, определяется преобразованием следующего уравнения:
F = qE.F = qE. размер 12 {F = ital «qE»} {}
18,22
Здесь даны заряд (3,20 × 10–19C 3,20 × 10–19C — это удвоенная основная единица заряда) и напряженность электрического поля, и поэтому электрическая сила составляет
F = (3.20 · 10−19C) (3,00 · 105N / C) = 9,60 · 10−14N.F = (3,20 · 10−19C) (3,00 · 105N / C) = 9,60 · 10−14N. размер 12 {F = \ (3 «.» «20» умножить на «10» rSup {размер 8 {- «19»}} C \) \ (3 «.» «» 00 «умножить на» 10 «rSup {размер 8 { 5}} «N / C» \) = 9 «.» «60» умножить на «10» rSup {размер 8 {- «14»}} N} {}
18,23
Обсуждение (b)
Хотя это малая сила, она больше веса капли.
Решение для (c)
Ускорение можно найти, используя второй закон Ньютона, при условии, что мы можем определить все внешние силы, действующие на каплю.Мы предполагаем, что значительными являются только вес капли и электрическая сила. Поскольку капля имеет положительный заряд и электрическое поле направлено вверх, электрическая сила направлена вверх. Таким образом, у нас есть одномерная задача (в вертикальном направлении), и мы можем сформулировать второй закон Ньютона как
a = Fnetm.a = Fnetm. размер 12 {a = {{ital «net» `F} over {m}}`} {}
18,24
, где Fnet = F − wFnet = F − w размер 12 {F = F — w} {}. Ввод этого и известных значений в выражение для второго закона Ньютона дает
a = F − wm = 9.60 × 10−14N − 3,92 × 10−14N 4,00 × 10−15 кг = 14,2 м / с 2. a = F − wm = 9,60 × 10−14N − 3,92 × 10−14N 4,00 × 10−15 кг = 14,2 м / с s2.alignl {stack { размер 12 {a = {{F — w} больше {m}}} {} # размер 12 {{} = {{9 «.» «60» умножить на «10» rSup {размер 8 {- «14»}} N — 3 «.» «92» `умножить на» 10 «rSup {размер 8 {-» 14 «}} N} больше {4″. » «00» умножить на «10» rSup {size 8 {- «15»}} ital «kg»}}} {} # = «14» «.» 2 м / с rSup {размер 8 {2}} {} }} {}
18,25
Обсуждение для (c)
Это восходящее ускорение, достаточно большое, чтобы перенести падение в места, где вы, возможно, не захотите получать бензин.
Этот рабочий пример показывает, как применять стратегии решения проблем к ситуациям, которые включают темы в разных главах. Первый шаг — определить физические принципы, связанные с проблемой. Второй шаг — решить неизвестное, используя знакомые стратегии решения проблем. Они встречаются по всему тексту, и многие рабочие примеры показывают, как использовать их для отдельных тем. В этом примере интегрированных концепций вы можете увидеть, как применить их в нескольких темах. Вы найдете эти методы полезными в приложениях физики за пределами курса физики, например, в вашей профессии, в других научных дисциплинах и в повседневной жизни.Следующие ниже задачи помогут вам развить навыки широкого применения физических принципов.
% PDF-1.4 % 81 0 объект > эндобдж xref 81 99 0000000016 00000 н. 0000002328 00000 н. 0000002478 00000 н. 0000002540 00000 н. 0000002569 00000 н. 0000003527 00000 н. 0000003807 00000 н. 0000003988 00000 н. 0000004169 00000 п. 0000004351 00000 п. 0000004442 00000 н. 0000004533 00000 н. 0000004625 00000 н. 0000004716 00000 н. 0000004807 00000 н. 0000004897 00000 н. 0000004989 00000 н. 0000005079 00000 п. 0000005170 00000 н. 0000005262 00000 н. 0000005354 00000 п. 0000005449 00000 п. 0000005543 00000 н. 0000005637 00000 н. 0000005730 00000 н. 0000005824 00000 н. 0000005918 00000 н. 0000006011 00000 н. 0000006105 00000 н. 0000006199 00000 н. 0000006292 00000 н. 0000006387 00000 н. 0000006481 00000 н. 0000006575 00000 н. 0000006668 00000 н. 0000006763 00000 н. 0000006857 00000 н. 0000006951 00000 п. 0000007044 00000 н. 0000007139 00000 н. 0000007233 00000 н. 0000007327 00000 н. 0000007420 00000 н. 0000007513 00000 н. 0000007607 00000 н. 0000007700 00000 н. 0000007795 00000 н. 0000007889 00000 н. 0000007982 00000 н. 0000008075 00000 н. 0000008167 00000 н. 0000008260 00000 н. 0000008352 00000 н. 0000008445 00000 н. 0000008537 00000 н. 0000008630 00000 н. 0000008809 00000 н. 0000009692 00000 п. 0000009843 00000 н. 0000010241 00000 п. 0000010686 00000 п. 0000011009 00000 п. 0000011743 00000 п. 0000012352 00000 п. 0000012552 00000 п. 0000012890 00000 н. 0000013114 00000 п. 0000013783 00000 п. 0000014454 00000 п. 0000014832 00000 п. 0000015260 00000 п. 0000015845 00000 п. 0000016110 00000 п. 0000016204 00000 п. 0000016226 00000 п. 0000017065 00000 п. 0000017087 00000 п. 0000017809 00000 п. 0000017831 00000 п. 0000018677 00000 п. 0000018699 00000 п. 0000019513 00000 п. 0000019535 00000 п. 0000020341 00000 п. 0000020363 00000 п. 0000021212 00000 п. 0000021573 00000 п. 0000021898 00000 п. 0000021920 00000 п. 0000022750 00000 п. 0000022772 00000 п. 0000023437 00000 п. 0000023608 00000 п. 0000025568 00000 п. 0000029092 00000 н. 0000034715 00000 п. 0000042634 00000 п. 0000002627 00000 н. 0000003505 00000 н. трейлер ] >> startxref 0 %% EOF 82 0 объект > эндобдж 83 0 объект > эндобдж 84 0 объект [ 85 0 руб. ] эндобдж 85 0 объект > >> эндобдж 178 0 объект > ручей Hb«f`rf`g`g` @
Универсальная сольватационная модель, основанная на плотности растворенных электронов и континуальной модели растворителя, определяемой объемной диэлектрической проницаемостью и поверхностным натяжением атомов
Мы представляем новую модель сольватации континуума, основанную на квантовомеханической плотности заряда молекулы растворенного вещества, взаимодействующей с континуальным описанием растворителя.Модель называется SMD, где «D» означает «плотность», чтобы обозначить, что используется полная плотность растворенных электронов без определения частичных зарядов атомов. «Континуум» означает, что растворитель не представлен явно, а скорее как диэлектрическая среда с поверхностным натяжением на границе растворенное вещество-растворитель. SMD — это универсальная модель сольватации, где «универсальный» означает его применимость к любому заряженному или незаряженному растворенному веществу в любом растворителе или жидкой среде, для которых известны несколько ключевых дескрипторов (в частности, диэлектрическая проницаемость, показатель преломления, объемное поверхностное натяжение и кислотность. и параметры основности).Модель разделяет наблюдаемую свободную энергию сольватации на два основных компонента. Первый компонент — это объемный электростатический вклад, возникающий в результате обработки поля самосогласованной реакции, которое включает решение неоднородного уравнения Пуассона для электростатики в терминах модели поляризуемого континуума формализма интегральных уравнений (IEF-PCM). Полости для объемного электростатического расчета определяются суперпозициями ядерно-центрированных сфер. Второй компонент называется термином «полость-дисперсия-структура растворителя» и представляет собой вклад, возникающий в результате короткодействующих взаимодействий между молекулами растворенного вещества и растворителя в первой сольватной оболочке.Этот вклад представляет собой сумму членов, которые пропорциональны (с зависящими от геометрии константами пропорциональности, называемыми атомными поверхностными натяжениями) доступным для растворителя площадям поверхности отдельных атомов растворенного вещества. Модель SMD параметризована обучающим набором из 2821 данных о сольватации, включая 112 значений свободной энергии водной ионной сольватации, 220 значений свободной энергии сольватации для 166 ионов в ацетонитриле, метаноле и диметилсульфоксиде, 2346 значений свободной энергии сольватации для 318 нейтральных растворенных веществ в 91 растворителе ( 90 неводных органических растворителей и вода), и 143 переносят свободную энергию для 93 нейтральных растворенных веществ между водой и 15 органическими растворителями.В растворенных веществах присутствуют следующие элементы: H, C, N, O, F, Si, P, S, Cl и Br. Модель SMD использует единый набор параметров (собственные атомные кулоновские радиусы и коэффициенты поверхностного натяжения атомов), оптимизированный для шести методов электронной структуры: M05-2X / MIDI! 6D, M05-2X / 6-31G, M05-2X / 6-31 + G, M05-2X / cc-pVTZ, B3LYP / 6-31G и HF / 6-31G. Хотя модель SMD была параметризована с использованием протокола IEF-PCM для объемной электростатики, ее также можно использовать с другими алгоритмами для решения неоднородного уравнения Пуассона для расчетов сольватации континуума, в которых растворенное вещество представлено его электронной плотностью в реальном пространстве.Это включает, например, алгоритм экранирования типа проводника. С базисным набором 6-31G модель SMD достигает средних беззнаковых ошибок 0,6-1,0 ккал / моль в свободных энергиях сольватации тестируемых нейтралов и средних ошибок без знака 4 ккал / моль в среднем для ионов с Gaussian03 или GAMESS.

Электростатика напряженность: Электростатика — Физика — Теория, тесты, формулы и задачи

Электростатика — Физика — Теория, тесты, формулы и задачи

Оглавление:

Основные теоретические сведения

Электрический заряд и его свойства

Закон Кулона

Электрическое поле и его напряженность

Принцип суперпозиции

Потенциальная энергия взаимодействия зарядов

Потенциал. Разность потенциалов. Напряжение

Принцип суперпозиции потенциала

Электрическая емкость. Плоский конденсатор

Энергия электрического поля

Соединения конденсаторов

Проводящая сфера

Свойства проводника в электрическом поле

Замечания к решению сложных задач

Электростатика. Основные понятия. Электрический заряд. Закон сохранения электрического

Основные понятия электростатики: электрический заряд, элементарный заряд, электрическое поле, проводник, диэлектрик:

Закон сохранения электрического заряда:

Закон Кулона, кулоновская сила:

Принцип суперпозиции для электрических зарядов:

Теория близкодействия электрических зарядов:

Напряженность электрического поля, напряженность поля точечного заряда:

Принцип суперпозиции электрических полей:

Потенциал электрического поля, потенциальная энергия заряда, разность потенциалов = напряжение, связь разности потенциалов и напряженности в однородном поле:

Конденсатор, электроемкость, напряженность, энергия:

Урок Электростатика — Физика 10 класс

Линии напряженности электростатического поля

электростатика

Оглавление

Глава 3

3.1 Электростатика

3.1.1 Пример – поле и потенциал сферы

3.1.2 Пример – поле и потенциал шара

3.1.3 Пример – заземленная сфера

3.1.4 Пример – разлетающиеся частицы

3.1.5 Пример – столкновение зарядов

3.1.6 Пример – система конденсаторов

3.2 Постоянный ток

3.2.1 Пример – соединение сопротивлений

3.2.2 Пример – ЭДС и внутреннее сопротивление батареи

3.2.3 Пример – внутреннее сопротивление аккумулятора

3.2.4 Пример – цепь с конденсаторами

3.3 Магнитное поле

3.3.1 Пример – движение заряда в магнитном поле

3.3.2 Пример – проводник с током в магнитном поле

3.3.3 Пример – радиусы траекторий

3.4 ЭДС индукции

3.4.1 Пример – падение в магнитном поле

3.4.2 Пример – стержень в магнитном поле

3.4.3 Пример – вихревое электрическое поле

ЭЛЕКТРОСТАТИКА И ПОСТОЯННЫЙ ТОК

Законы Ньютона и электрическая сила

Напряжение в изогнутом заряженном проводе (электростатическая сила) — имеет ли значение толщина провода?

Электростатическое притяжение и силы поверхностного натяжения для точной самосборки микродеталей

Реферат

Ключевые слова

Рекомендуемые статьи

Цитирование статей

Произошла ошибка при настройке вашего пользовательского файла cookie

Настройка вашего браузера для приема файлов cookie

Почему этому сайту требуются файлы cookie?

Что сохраняется в файле cookie?

18.8 Применение электростатики — Физика в колледже для курсов AP®

Ускорение заряженной капли бензина

Стратегия

Решение для (a)

Обсуждение (a)

Решение для (b)

Обсуждение (b)

Решение для (c)

Обсуждение для (c)

Добавить комментарий Отменить ответ