Дырка — Википедия
Ды́рка — квазичастица, носитель положительного заряда, равного элементарному заряду, в полупроводниках.
Определение термина «дырка» по ГОСТ 22622-77: «Незаполненная валентная связь, которая проявляет себя как положительный заряд, численно равный заряду электрона»[1].
Понятие дырки вводится в зонной теории твёрдого тела для описания электронных явлений в не полностью заполненной электронами валентной зоне.
В электронном спектре валентной зоны часто возникает несколько зон, различающихся величиной эффективной массы и энергетическим положением (энергетические зоны легких и тяжёлых дырок, зона спин-орбитально отщепленных дырок).
В физике твёрдого тела дырка — это отсутствие электрона в почти полностью заполненной валентной зоне. В некотором смысле, поведение дырки в полупроводнике похоже на поведение пузырька в полной бутылке с водой[2].
Для создания заметной концентрации дырок в полупроводниках используется легирование полупроводника акцепторными примесями.
Кроме того, дырки могут возникать в собственном (нелегированном) полупроводнике из-за возбуждения электронов и переходом их из валентной зоны в зону проводимости в результате внешних воздействий: нагрева, освещения светом с достаточной энергией фотонов для перевода электронов из валентной зоны в зону проводимости, или облучения полупроводника ионизирующим излучением.
В случае кулоновского взаимодействия дырка с электроном из зоны проводимости могут образовать связанное состояние, квазичастицу, называемую экситоном.
Тяжёлые дырки — название одной из ветвей энергетического спектра в валентной зоны кристалла.
Упрощённая аналогия дырки[править | править код]

Дырочную проводимость можно объяснить при помощи следующей аналогии: имеется ряд кресел с сидящими людьми в аудитории, причём все кресла в ряду заполнены. Если кто-нибудь где-то из середины ряда хочет уйти, он перелезает через спинку кресла в соседний ряд свободных кресел и уходит. Здесь пустой ряд — аналог зоны проводимости, а ушедшего человека можно сравнить со свободным электроном. Представим, что ещё кто-то пришёл и хочет сесть. Из пустого ряда плохо видно сцену, поэтому там он не садится. Но и занять освободившееся кресло в заполненном ряду он не может, так как оно расположено далеко внутри ряда. Для того чтобы усадить нового зрителя человек, сидящий возле свободного стула, пересаживается на него, на освободившееся место пересаживается другой человек из соседнего с пустым кресла и это повторяют все соседи с пустым местом. Таким образом, пустое место как бы сдвигается к краю ряда. Когда это пустое место окажется рядом с новым зрителем, он сможет сесть.
В этом процессе каждый сидящий передвинулся. Если бы зрители обладали отрицательным зарядом, такое движение можно было бы уподобить электрической проводимости. Если вдобавок в этой модели предположить, что стулья заряжены положительно, а люди отрицательно, и их заряды равны по модулю, то ненулевым суммарным зарядом будет обладать только свободное место. Это грубая модель объяснения дырочной проводимости.
Однако на самом деле, из-за волновой природы электрона и свойств кристаллической решётки, дырка не локализована в определённом месте, как описано выше, а «размазана» по части кристалла размером во много сотен размеров элементарной ячейки кристалла.
Более подробное описание[править | править код]
Приведённая модель дырки в виде перемещения людей в аудитории сильно упрощена и не в состоянии объяснить, почему дырки ведут себя в твёрдом теле подобно положительно заряженным частицам с некоторой массой, что на макроскопическом уровне проявляется в эффекте Холла и эффекте Зеебека. Более точное и подробное с квантовомеханической точки зрения объяснение приведено ниже
- Квантовомеханическое рассмотрение электронов в твёрдом теле
В квантовой механике электроны можно рассматривать как волны де Бройля, а энергию электрона — как частоту этих волн.
Локализованный электрон представляет собой волновой пакет, и движение электрона как отдельной частицы определяется через формулу для групповой скорости волнового пакета.
Приложенное электрическое поле воздействует на электрон, смещая все волновые векторы в волновом пакете, и электрон ускоряется, когда изменяется групповая скорость его волны. Дисперсионное соотношение определяет, как электроны реагируют на силы (с привлечением понятия эффективной массы). Дисперсионное соотношение — это выражение для связи между волновым вектором (или
- E=ℏ2k22m,{\displaystyle E={\frac {\hbar ^{2}k^{2}}{2m}},}
- где m{\displaystyle m} — масса покоящегося электрона в вакууме;
- ℏ{\displaystyle \hbar } — редуцированная постоянная Планка.
Вблизи дна зоны проводимости полупроводника в дисперсионное соотношение E=ℏ2k22m∗{\displaystyle E={\frac {\hbar ^{2}k^{2}}{2m^{*}}}} входит эффективная масса электрона m∗{\displaystyle m^{*}}, поэтому электрон с энергией вблизи дна зоны проводимости реагирует на внешнюю приложенную силу как обычная частица с положительной эффективной массой — при увеличении волнового числа энергия увеличивается, что выражается на графике в изгибе дна зоны проводимости вверх.
Электроны с энергиями вблизи верха валентной зоны при приложении силы ведут себя так, как будто они имеют отрицательную массу, так как при увеличении волнового числа энергия уменьшается.
Таким образом, электроны сверху валентной зоны движутся противоположно направлению силы, причём это движение не зависит от того, заполнена зона или нет, а только от зависимости энергии от волнового числа — при увеличении волнового числа энергия уменьшается, что выражается на графике в изгибе верха валентной зоны вниз.
Если бы была физическая возможность убрать все электроны из валентной зоны и поместить туда только один электрон с энергией вблизи максимума валентной зоны, то этот электрон двигался бы противоположно направлению внешней силы.
- Проводимость в валентной зоне
Полностью заполненная электронами валентная зона не участвует в электропроводности полупроводника
Один из вариантов объяснения этого явления состоит в том, что электронные состояния вблизи верха валентной зоны имеют отрицательную эффективную массу, в то время как электронные состояния в глубине валентной зоны имеют положительную эффективную массу. При приложении внешней силы, вызванной, например, электрическим полем на электроны валентной зоны, возникают два равных и противоположно направленных тока которые взаимно компенсируют друг друга и суммарная плотность тока в результате равна нулю, то есть материал ведёт себя как изолятор.
Если из валентной зоны, полностью заполненной электронными состояниями удалить один электрон, то баланс токов нарушится. При наложении поля движение электронов с отрицательной эффективной массой движущемся в обратном направлении (относительно электронов с положительной эффективной массой) эквивалентно движению положительного заряда с положительной эффективной массой в том же направлении.
Дырка в верхней части валентной зоны будет двигаться в том же направлении что и электрон вблизи верха валентной зоны и поэтому аналогия с аудиторий тут не подходит, так как пустующее кресло в той модели движется противоположно направлению пересаживания людей и имеет «нулевую массу», в случае же электронов в валентной зоне происходит движение электронов в пространстве волновых векторов и приложенная сила перемещает все электроны валентной зоны в пространстве волновых векторов, а не в реальном пространстве, тут ближе аналогия с пузырьком воздуха в потоке воды, который перемещается вместе с потоком, а не против потока.
Так как F=ma{\displaystyle F=ma}, где F{\displaystyle F} — сила, m{\displaystyle m} — ускорение, электрон с отрицательной эффективной массой сверху валентной зоны будет двигаться в противоположном направлении, также как электрон с положительной эффективной массой снизу зоны проводимости при воздействии электрических и магнитных сил.
Исходя из вышесказанного, можно положить, что дырка — это квазичастица с положительным зарядом и положительной массой и реагирует на электрическое и магнитное поля как реальная частица с положительными зарядом и массой, это связано с тем, что частица с отрицательными зарядом и массой ведёт себя в полях так же, как частица с положительными зарядом и массой. Поэтому в рассмотренном случае дырки можно рассматривать как обычные положительно заряженные квазичастицы, что и наблюдается, например, при экспериментальном определении знака заряда носителей заряда в эффекте Холла.
Термин «дырка» также используется в вычислительной химии, где основное состояние молекулы интерпретируется как вакуумное состояние — условно принимается, что в этом состоянии нет электронов. В такой модели отсутствие электрона в разрешенном состоянии называется «дыркой» и рассматривается как некоторая частица. А присутствие электрона в обычно пустом пространстве просто называют «электроном». Такая терминология практически идентична используемой в физике твердого тела.
Электроны и «дырки»
Добавлено 6 февраля 2016 в 17:10
Сохранить или поделиться
Чистые полупроводники являются относительно хорошими диэлектриками по сравнению с металлами, хотя и не настолько хорошими, как настоящий диэлектрик, например, стекло. Чтобы быть полезным в полупроводниковых применениях, собственный полупроводник (чистый нелегированный полупроводник) должен иметь не более одного атома примеси на 10 миллиардов атомов полупроводника. Это аналогично крупинке соли в железнодорожном вагоне сахара. Нечистые, или грязные полупроводники являются значительно более проводящими, хотя и такими хорошими, как металлы. Почему так происходит? Чтобы ответить на этот вопрос, мы должны рассмотреть электронную структуру этих материалов на рисунке ниже.
Рисунок ниже (a) показывает 4 электрона в валентной оболочке полупроводника, образующих ковалентные связи с четырьмя другими атомами. Это плоская, более простая для рисования, версия рисунка, приведенного ранее. Все электроны атома связаны в четырех ковалентных связях, в парах общих электронов. Электроны не могут свободно перемещаться по кристаллической решетке. Таким образом, собственные, чистые, полупроводники являются относительно хорошими диэлектриками по сравнению с металлами.
 (a) Собственный полупроводник является диэлектриком, имеющим полную электронную оболочку.
(a) Собственный полупроводник является диэлектриком, имеющим полную электронную оболочку.(b) Тем не менее, тепловая энергия может создать несколько пар электрон-дырка, что в результате даст слабую проводимость.
Тепловая энергия иногда может освобождать электрон из кристаллической решетки, как показано на рисунке выше (b). Этому электрону становится доступно передвижение по кристаллической решетке. Когда электрон освобождается, он оставляет в кристаллической решетке пустое место с положительным зарядом, известное как дырка. Эта дырка не прикреплена к решетке и может свободно по ней перемещаться. Свободные электрон и дырка вносят свой вклад в движение электронов по кристаллической решетке. То есть, электрон свободен, пока он не попадает в дырку. Это явление называется рекомбинацией. При воздействии на полупроводник внешним электрическим полем электроны и дырки разводятся в противоположных направлениях. Увеличение температуры увеличит и количество электронов и дырок, что в свою очередь уменьшит сопротивление. Это противоположно поведению металлов, у которых сопротивление увеличивается с ростом температуры за счет увеличения столкновений электронов с кристаллической решеткой. Количество электронов и дырок в собственном полупроводнике одинаково. Тем не менее, оба носителя при воздействии внешнего поля необязательно будут двигаться с одинаковой скоростью. Другими словами, подвижность у электронов и дырок неодинакова.
Чистые полупроводники, сами по себе, не особенно полезны. Хотя полупроводники и должны быть в большой степени очищены от примесей для создания отправной точки перед добавлением определенных примесей.
В материал полупроводника, с долей содержания примесей 1 к 10 миллиардам, для увеличения количества носителей могут добавляться определенные примеси в соотношении примерно 1 часть на 10 миллионов. Добавление в полупроводник необходимой примеси известно, как легирование. Легирование увеличивает проводимость полупроводника, и, таким образом, он становится более сопоставим с металлом, а не с диэлектриком.
Можно увеличить количество отрицательно заряженных носителей в кристаллической решетке полупроводника путем легирования таким электронным донором, как фосфор. Электронные доноры, также известные, как примеси N-типа, включают в себя элементы группы VA (группы 15 по IUPAC) периодической таблицы: азот, фосфор, мышьяк и сурьма. Азот и фосфор являются примесью N-типа для алмаза. Фосфор, мышьяк и сурьма используются совместно с кремнием.
Кристаллическая решетка на рисунке ниже (b) содержит атомы, содержащие четыре электрона во внешней оболочке, формирующих ковалентные связи с соседними атомами. Эта кристаллическая решетка ожидаема. Добавление атома фосфора с пятью электронами во внешней оболочке вводит в решетку дополнительный электрон по сравнению с атомом кремния. Пятивалентная примесь образует четыре ковалентные связи с четырьмя атомами кремния с помощью четырех из пяти электронов, встраиваясь в решетку с одним электроном в запасе. Обратите внимание, что этот лишний электрон не сильно привязан к решетке, как электроны обычных атомов Si. Будучи не привязанным к узлу фосфора в кристаллической решетке, он свободен для перемещения по ней. Так как мы легировали одну часть фосфора на 10 миллионов атомов кремния, то по сравнению с многочисленными атомами кремния было создано лишь несколько свободных электронов. Тем не менее, по сравнению с немногочисленными парами электрон-дырка в собственном полупроводнике, в этом случае было создано достаточно много электронов.
 (a) Конфигурация электронов внешней оболочки донора N-типа фосфора, кремния (для сравнения) и акцептора P-типа бора.
(a) Конфигурация электронов внешней оболочки донора N-типа фосфора, кремния (для сравнения) и акцептора P-типа бора.(b) Примесь донора N-типа создает свободный электрон.
(c) Примесь акцептора P-типа создает дырку, положительно заряженный носитель.
Кроме того, можно вводить примеси, у которых, по сравнению с кремнием, не хватает электрона, то есть, которые имеют три электрона в валентной оболочке, по сравнению с кремнием с четырьмя валентными электронами. На рисунке выше (c) они оставляют пустое место, известное как дырка, положительно заряженный носитель. Атом бора пытается связаться с четырьмя атомами кремния, но в валентной зоне имеет только три электрона. В попытке сформировать четыре ковалентные связи три его электрона двигаются вокруг, пытаясь образовать четыре связи. Это заставляет двигаться появляющуюся дырку. Кроме того, трехвалентный атом может занимать электрон от соседнего (или более отдаленного) атома кремния, чтобы сформировать четыре ковалентные связи. Однако это оставляет атом кремния с нехваткой одного электрона. Другими словами, дырка перемещается к соседнему (или более отдаленному) атому кремния. Дырки располагаются в валентной зоне, уровнем ниже зоны проводимости. Легирование электронным акцептором, атомом, который может принять электрон, создает дефицит электронов и избыток дырок. Так как дырки являются носителями положительного заряда, примесь электронного акцептора также известна, как примесь P-типа. Легирующая примесь P-типа оставляет полупроводник с избытком дырок, носителей положительного заряда. Элементы P-типа из группы IIIA (группы 13 по IUPAC) периодической таблицы включают в себя: бор, алюминий, галлий и индий. Бор используется в качестве легирующей примеси P-типа для полупроводников кремний и алмаз, в то время как индий используется с германием.
Подобно «шарику в трубе» передвижение электронов (рисунок ниже) зависит от движения дырок и движения электронов. Шарик представляет собой электроны в проводнике, в трубе. Движение электронов слева направо в проводнике или полупроводнике N-типа объясняется входом электрона в трубу слева, заставляя выйти электрон справа. Передвижение электронов в полупроводнике N-типа происходит в зоне проводимости. Сравните это с движением дырок в валентной зоне.
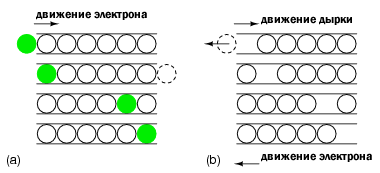 Аналогия с шариком в трубе:
Аналогия с шариком в трубе:(a) Электроны двигаются вправо в зоне проводимости.
(b) Дырки двигаются вправо в валентной зоне, в то время как электроны двигаются влево.
Чтобы дырка вошла в левой части рисунка выше (b), электрон должен быть удален. При перемещении дырки слева направо электрон должен двигаться справа налево. Первый электрон выбрасывается из левого конца трубы, чтобы дырка могла двигаться вправо в трубу. Электрон двигается в направлении, противоположном движению положительных дырок. Чтобы дырка двигалась дальше вправо, электроны должны перемещаться влево, заполняя дырку. Дырка – это отсутствие электрона в валентной зоне за счет легирования P-типа. Она имеет локальный положительный заряд. Чтобы переместить дырку в заданном направлении, валентные электроны двигаются в противоположном направлении.
Поток электронов в полупроводнике N-типа аналогичен движению электронов в металлическом проводе. Атомы примеси N-типа дадут электроны, доступные для передвижения. Эти электроны из-за легирующей примеси известны, как основные носители, так как они находятся в большинстве, по сравнению с немногочисленными тепловыми дырками. Если к пластине полупроводника N-типа приложить электрическое поле (рисунок ниже (a)), электроны перейдут в отрицательный (левый) конец пластины, пройдут кристаллическую решетку и выйдут справа к клемме (+) батареи.
 (a) Полупроводник N-типа с электронами, перемещающимися через кристаллическую решетку слева направо.
(a) Полупроводник N-типа с электронами, перемещающимися через кристаллическую решетку слева направо.(b) Полупроводник P-типа с дырками, перемещающимися слева направо, что соответствует движению электронов в противоположном направлении.
Объяснить протекание тока в полупроводнике P-типа немного сложнее. Примесь P-типа, акцептор электронов, придает локальным областям положительный заряд, известный как дырки. Эти дырки и являются основными носителями в полупроводнике P-типа. Хотя дырки и образуются в местах трехвалентных атомов примеси, они могут перемещаться по пластине полупроводника. Обратите внимание, что включение батареи на рисунке выше (b) противоположно включению на рисунке (a). Положительный вывод батареи подключен к левому концу пластины P-типа. Поток электронов выходит из отрицательного вывода батареи и через пластину P-типа возвращается к положительному выводу батареи. Электрон покидает положительный (левый) конец пластины полупроводника, чтобы положительный вывод батареи оставил дырку в полупроводнике, которая может двигаться вправо. Дырки проходят через кристаллическую решетку слева направо. В отрицательном конце пластины электрон из батареи соединяется с дыркой, нейтрализуя её. Это дает возможность другой дырке в положительном конце пластины двигаться вправо. Имейте в виду, что когда дырки перемещаются слева направо, это на самом деле электроны двигаются в противоположном направлении, что и делает видимым движение дырок.
Элементы, используемые для производства полупроводников, приведены на рисунке ниже. Полупроводниковый материал германий из группы IVA (14 по IUPAC) сейчас используется довольно ограничено. Полупроводники на основе кремния составляют около 90% всего промышленного производства полупроводников. Полупроводники на основе алмаза сейчас широко исследуются и обладают значительным потенциалом. Составные полупроводники включают в себя кремний-германий (тонкие слои на пластинах Si), карбид кремния и соединения групп III-V, например, арсенид галлия. Полупроводниковые соединения групп III-VI включают в себя AlN, GaN, InN, AlP, AlAs, AlSb, GaP, GaAs, GaSb, InP, InAs, InSb, AlxGa1-xAs и InxGa1-xAs. Столбцы II и VI периодической таблицы, не показанные на рисунке, также формируют составные полупроводники.
 Группа IIIA – примеси P-типа, группа IV – основные полупроводниковые материалы, и группа VA – примеси N-типа.
Группа IIIA – примеси P-типа, группа IV – основные полупроводниковые материалы, и группа VA – примеси N-типа.Основной причиной включения групп IIIA и VA на рисунок выше является возможность показать примеси, используемые с группой полупроводников IVA. Элементы группы IIIA являются акцепторами, примесями P-типа, которые принимают электроны, оставляя дырки (положительные носители) в кристаллической решетке. Бор является примесью P-типа для алмаза и самой распространенной примесью для кремниевых полупроводников. Индий является примесью P-типа для германия.
Элементы группы VA являются донорами, примесями N-типа, дающими свободный электрон. Азот и фосфор подходят в качестве примеси N-типа для алмаза. Фосфор и мышьяк являются наиболее используемыми примесями N-типа для кремния, хотя может использоваться и сурьма.
Итоги
Собственные полупроводники, максимальная доля примеси в которых составляет 1 на 10 миллиардов, являются плохими проводниками.
Полупроводник N-типа легируется пятивалентной примесью, чтобы создать свободные электроны. Такой материал является проводящим. Электрон в нем является основным носителем.
Полупроводник P-типа, легированный трехвалентной примесью, имеет множество свободных дырок. Это носители положительного заряда. Материал P-типа является проводящим. Дырки в нем являются основными носителями.
Большинство полупроводников основаны на элементах из группы IVA периодической таблицы. Причем кремний является наиболее распространенным, германий устарел, а углерод (алмаз) в настоящее время исследуется.
Широко используются и составные полупроводники, такие как карбид кремния (группа IVA) и арсенид галлия (группа III-V).
Оригинал статьи:
Теги
УчебникЭлектронЭлектроникаСохранить или поделиться
§ 1. Электроны и дырки в полупроводниках
Г л а в a 12 ПОЛУПРОВОДНИКИ
§ 2. Примесные полупроводники
§ 3. Эффект Холла
§ 4. Переходы между полупроводниками
§ 5. Выпрямление на полупроводниковом переходе
§ 6. Транзистор
§ 1. Электроны и дырки в полупроводниках
Одним из самых замечательных и волнующих открытий последних лет явилось применение физики твердого тела к технической разработке ряда электрических устройств, таких, как транзисторы. Изучение полупроводников привело к открытию их полезных свойств и ко множеству практических применений. В этой области все меняется так быстро, что рассказанное вам сегодня может через год оказаться уже неверным или, во всяком случае, неполным. И совершенно ясно, что, подробнее изучив такие вещества, мы со временем сумеем осуществить куда более удивительные вещи. Материал этой главы вам не понадобится для понимания следующих глав, но вам, вероятно, будет интересно убедиться, что по крайней мере кое-что из того, что вы изучили, как-то все же связано с практическим делом.
Полупроводников известно немало, но мы ограничимся теми, которые больше всего применяются сегодня в технике. К тому же они и изучены лучше других, так что разобравшись в них, мы до какой-то степени поймем и многие другие. Наиболее широко применяемые в настоящее время полупроводниковые вещества это кремний и германий. Эти элементы кристаллизуются в решетке алмазного типа — в такой кубической структуре, в которой атомы обладают четверной (тетраэдральной) связью со своими ближайшими соседями. При очень низких температурах (вблизи абсолютного нуля) они являются изоляторами, хотя при комнатной температуре они немного проводят электричество. Это не металлы; их называют полупроводниками.
Если каким-то образом в кристалл кремния или германия при низкой температуре мы введем добавочный электрон, то возникнет то, что описано в предыдущей главе. Такой электрон начнет блуждать по кристаллу, перепрыгивая с места, где стоит один атом, на место, где стоит другой. Мы рассмотрели только поведение атома в прямоугольной решетке, а для реальной решетки кремния или германия уравнения были бы другими. Но все существенное может стать ясным уже из результатов для прямоугольной решетки.
Как мы видели в гл. И, у этих электронов энергии могут находиться только в определенной полосе значений, называемой зоной проводимости. В этой зоне энергия связана с волновым числом k амплитуды вероятности С [см. (11.24)1 формулой

Разные A — это амплитуды прыжков в направлениях х, у и z, а а, b, с — это постоянные решетки (интервалы между узлами) в этих направлениях.
Для энергий возле дна зоны формулу (12.1) можно приблизительно записать так:

(см. гл. 11, § 4).
Если нас интересует движение электрона в некотором определенном направлении, так что отношение компонент k все время одно и то же, то энергия есть квадратичная функция волнового числа и, значит, импульса электрона. Можно написать

где — некоторая постоянная, и начертить график зависимости Е от k (фиг. 12.1).

Фиг. 12.1. Энергетическая диаграмма для электрона в кристалле изолятора.
Такой график мы будем называть «энергетической диаграммой». Электрон в определенном состоянии энергии и импульса можно на таком графике изобразить точкой (S на рисунке).
Мы уже упоминали в гл. 11, что такое же положение вещей возникнет, если мы уберем электрон из нейтрального изолятора. Тогда на это место сможет перепрыгнуть электрон от соседнего атома. Он заполнит «дырку», а сам оставит на том месте, где стоял, новую «дырку». Такое поведение мы можем описать, задав амплитуду того, что дырка окажется возле данного определенного атома, и говоря, что дырка может прыгать от атома к атому. (Причем ясно, что амплитуда А того, что дырка перепрыгивает от атома а к атому b, в точности равна амплитуде того, что электрон от атома b прыгает в дырку от атома а.)
Математика для дырки такая же, как для добавочного электрона, и мы опять обнаруживаем, что энергия дырки связана с ее волновым числом уравнением, в точности совпадающим с (12.1) и (12.2), но, конечно, с другими численными значениями амплитуд Ах, Ay и Аz. У дырки тоже есть энергия, связанная с волновым числом ее амплитуд вероятности. Энергия ее лежит в некоторой ограниченной зоне и близ дна зоны квадратично меняется с ростом волнового числа (или импульса) так же, как на фиг. 12.1. Повторяя наши рассуждения гл. 11, § 3, мы обнаружим, что дырка тоже ведет себя как классическая частица с какой-то определенной эффективной массой, с той только разницей, что в некубических кристаллах масса зависит от направления движения. Итак, дырка напоминает частицу с положительным зарядом, движущуюся сквозь кристалл. Заряд частицы-дырки положителен, потому что она сосредоточена в том месте, где нет электрона; и когда она движется в какую-то сторону, то на самом деле это в обратную сторону движутся электроны.
Если в нейтральный кристалл поместить несколько электронов, то их движение будет очень похоже на движение атомов в газе, находящемся под низким давлением. Если их не слишком много, их взаимодействием можно будет пренебречь. Если затем приложить к кристаллу электрическое поле, то электроны начнут двигаться и потечет электрический ток. В принципе они должны очутиться на краю кристалла и, если там имеется металлический электрод, перейти на него, оставив кристалл нейтральным.
Точно так же в кристалл можно было бы ввести множество дырок. Они бы начали повсюду бродить как попало. Если приложить электрическое поле, то они потекут к отрицательному электроду и затем их можно было бы «снять» с него, что и происходит, когда их нейтрализуют электроны с металлического электрода.
Электроны и дырки могут оказаться в кристалле одновременно. Если их опять не очень много, то странствовать они будут независимо. В электрическом поле все они будут давать свой вклад в общий ток. По очевидной причине электроны называют отрицательными носителями, а дырки — положительными носителями.
До сих пор мы считали, что электроны внесены в кристалл извне или (для образования дырки) удалены из него. Но можно также «создать» пару электрон—дырка, удалив из нейтрального атома связанный электрон и поместив его в том же кристалле на некотором расстоянии. Тогда у нас получатся свободный электрон и свободная дырка, и движение их будет таким, как мы описали.
Энергия, необходимая для того, чтобы поместить электрон в состояние S (мы говорим: чтобы «создать» состояние S),— это энергия Е—, показанная на фиг. 12.2.

Фиг. 12.2, Энергия Е, требуемая для «рождения» свободного
электрона.
Это некоторая энергия,
превышающая Е—мин. Энергия, необходимая для того, чтобы «создать» дырку в каком-то состоянии S‘,— это энергия Е+ (фиг. 12.3), которая на какую-то долю выше, чем Е (=Е+мин).

Фиг. 12.3. Энергия Е+ , требуемая для «рождения» дырки в состоянии S’.
А чтобы создать пару в состояниях S и S’, потребуется просто энергия Е—+Е+.
Образование пар — это, как мы увидим позже, очень частый процесс, и многие люди предпочитают помещать фиг. 12.2 и 12.3 на один чертеж, причем энергию дырок откладывают вниз, хотя, конечно, эта энергия положительна. На фиг. 12.4 мы объединили эти два графика.

Фиг. 12.4. Энергетические диаграммы для электрона и дырки.
Преимущества такого графика в том, что энергия Eпары=Е—+Е+ , требуемая для образования пары (электрона в S и дырки в S’ ), дается попросту расстоянием по вертикали между S и S’, как показано на фиг. 12.4. Наименьшая энергия, требуемая для образования пары, называется энергетической шириной, или шириной щели, и равняется
е—мин+e+мин.
Иногда вам может встретиться и диаграмма попроще. Ее рисуют те, кому не интересна переменная k, называя ее диаграммой энергетических уровней. Эта диаграмма (она показана на фиг. 12.5) просто указывает допустимые энергии у электронов и дырок.

Фиг. 12.5. Диаграмма энергетических уровней для электронов и дырок.
Как создается пара электрон—дырка? Есть несколько способов. Например, световые фотоны (или рентгеновские лучи)
могут поглотиться и образовать пару, если только энергия фотона больше энергетической ширины. Быстрота образования пар пропорциональна интенсивности света. Если прижать к торцам кристалла два электрода и приложить «смещающее» напряжение, то электроны и дырки притянутся к электродам. Ток в цепи будет пропорционален силе света. Этот механизм ответствен за явление фотопроводимости и за работу фотоэлементов. Пары электрон — дырка могут образоваться также частицами высоких энергий. Когда быстро движущаяся заряженная частица (например, протон или пион с энергией в десятки и сотни Мэв) пролетает сквозь кристалл, ее электрическое поле может вырвать электроны из их связанных состояний, образуя пары электрон — дырка. Подобные явления сотнями и тысячами происходят на каждом миллиметре следа. После того как частица пройдет, можно собрать носители и тем самым вызвать электрический импульс. Перед вами механизм того, что разыгрывается в полупроводниковых счетчиках, в последнее время используемых в опытах по ядерной физике. Для таких счетчиков полупроводники не нужны, их можно изготовлять и из кристаллических изоляторов. Так и было на самом деле: первый из таких счетчиков был изготовлен из алмаза, который при комнатных температурах является изолятором. Но нужны очень чистые кристаллы, если мы хотим, чтобы электроны и дырки
I могли добираться до электродов, не боясь захвата. Потому и используются кремний и германий, что образцы этих полупроводников разумных размеров (порядка сантиметра) можно получать большой чистоты.
До сих пор мы касались только свойств полупроводниковых кристаллов при температурах около абсолютного нуля. При любой ненулевой температуре имеется еще другой механизм создания пар электрон — дырка. Энергией пару может снабдить тепловая энергия кристалла. Тепловые колебания кристалла могут передавать паре свою энергию, вызывая «самопроизвольное» рождение пар.
Вероятность (в единицу времени) того, что энергия, достигающая величины энергетической щели Eщели, сосредоточится в месте расположения одного из атомов, пропорциональна ехр(-Ещеяи/kТ), где Т—температура, а k— постоянная Больцмана [см. гл. 40 (вып. 4)]. Вблизи абсолютного нуля вероятность эта мало заметна, но по мере роста температуры вероятность образования таких пар возрастает. Образование пар при любой конечной температуре должно продолжаться без конца, давая все время с постоянной скоростью все новые и новые положительные и отрицательные носители. Конечно, на самом деле этого не будет, потому что через мгновение электроны случайно снова повстречаются с дырками, электрон скатится в дырку, а освобожденная энергия перейдет к решетке. Мы скажем, что электрон с дыркой «аннигилировали». Имеется определенная вероятность того, что дырка встретится с электроном и оба они друг друга уничтожат.
Если количество электронов в единице объема есть Nn (n означает негативных, или отрицательных, носителей), а плотность положительных (позитивных) носителей Np, то вероятность того, что за единицу времени электрон с дыркой встретятся и проаннигилируют, пропорциональна произведению NnNp. При равновесии эта скорость должна равняться скорости, с какой образуются пары. Стало быть, при равновесии произведение NnNp должно равняться произведению некоторой постоянной на больцмановский множитель

Говоря о постоянной, мы имеем в виду ее примерное постоянство. Более полная теория, учитывающая различные детали того, как электроны с дырками «находят» друг друга, свидетельствует, что «постоянная» слегка зависит и от температуры; но главная зависимость от температуры лежит все же в экспоненте.
Возьмем,
например, чистое вещество, первоначально
бывшее нейтральным. При конечной
температуре можно ожидать, что число
положительных и отрицательных носителей
будет одно и то же, Nn = Nр. Значит,
каждое из этих чисел должно с температурой
меняться как .
Изменение многих свойств полупроводника
(например, его проводимости) определяется
главным образом экспоненциальным
множителем,
потому
что все другие факторы намного слабее
зависят от температуры. Ширина щели
для германия примерно равна 0,72 эв, а
для кремния 1,1 эв.
.
Изменение многих свойств полупроводника
(например, его проводимости) определяется
главным образом экспоненциальным
множителем,
потому
что все другие факторы намного слабее
зависят от температуры. Ширина щели
для германия примерно равна 0,72 эв, а
для кремния 1,1 эв.
При комнатной температуре kТ составляет около 1/40 эв. При таких температурах уже есть достаточно дырок и электронов чтобы обеспечить заметную проводимость, тогда как, скажем, при 30°К (одной десятой комнатной температуры) проводимость незаметна. Ширина щели у алмаза равна 6—7 эв, поэтому при комнатной температуре алмаз — хороший изолятор.
2.10. Электроны и дырки
Из
(2.77) следует, что эффективная масса
блоховских электронов в энергетической
зоне определяется кривизной поверхности  в
в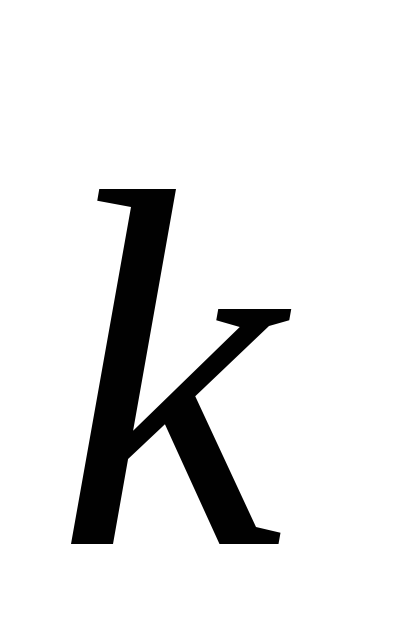 -пространстве:
чем больше эта кривизна, тем меньше
эффективная масса.
-пространстве:
чем больше эта кривизна, тем меньше
эффективная масса.
Анализ дисперсионной зависимости (2.65) в модели сильной связи показывает, что для электронов, располагающихся у дна энергетической зоны
 ,
(2.79)
,
(2.79)
т.е. эффективная масса m* положительна. Вблизи максимумов, т.е. у потолка зоны
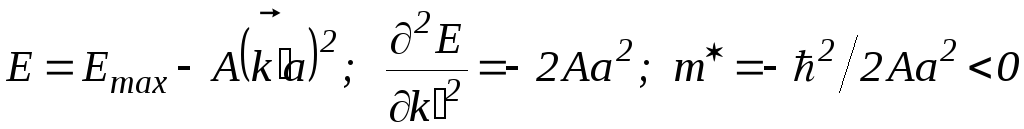 ,
(2.80)
,
(2.80)
где
вектор 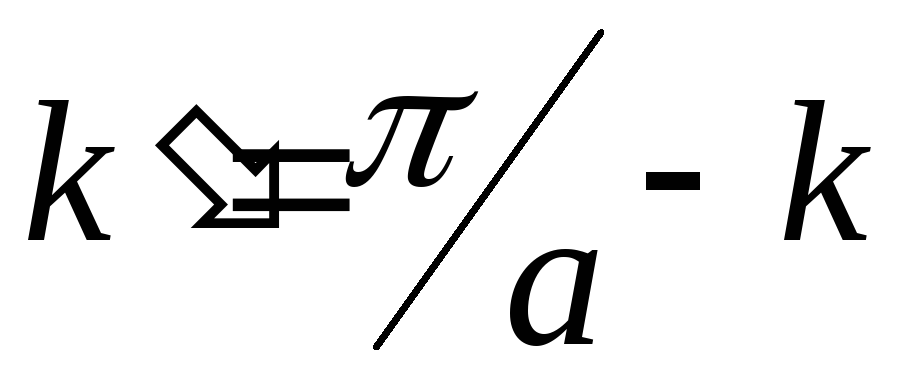 ,
эффективная масса m*
оказывается отрицательной. Поскольку
масса не может быть отрицательной, то
для состояний у верхнего края энергетической
зоны вводится понятие дырки,
рассматривая ее как квазичастицу с
положительной эффективной массой, но
и с положительным зарядом +е.
Такая частица будет перемещаться по
кристаллу по направлению действия
внешней силы.
,
эффективная масса m*
оказывается отрицательной. Поскольку
масса не может быть отрицательной, то
для состояний у верхнего края энергетической
зоны вводится понятие дырки,
рассматривая ее как квазичастицу с
положительной эффективной массой, но
и с положительным зарядом +е.
Такая частица будет перемещаться по
кристаллу по направлению действия
внешней силы.
Главной особенностью дырки является то, что ее скорость совпадает со скоростью недостающего энергетического состояния в зоне; волновой пакет будет двигаться с той же скоростью, что и его соседи со всех сторон от дырки.
Поэтому, если считать, что ток переносится не электронами, а дырками, то электроны лучше всего рассматривать как отсутствие дырок; уровни, занятые дырками, есть уровни, не занятые дырками. Состояния, свободные от электронов, находятся в самой верхней части зоны, т.е. дырки располагаются у потолка зоны, где их энергия минимальна. Следовательно, энергия дырок отсчитывается в направлении, противоположном отсчету энергии для электрона.
Дырки простым способом описывают движение большого числа электронов в кристалле при почти заполненной зоне. Действительно, если из почти заполненной энергетической зоны удален один электрон, плотность тока в электрическом поле составит
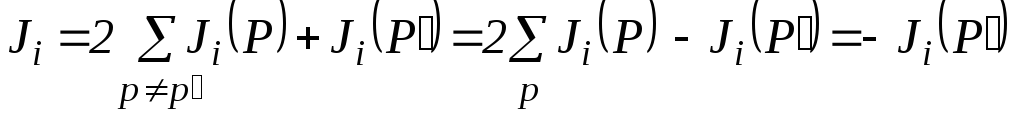 ,
(2.81)
,
(2.81)
где  — плотность тока в полностью заполненной
зоне, поскольку каждому электрону с
квазиимпульсом
— плотность тока в полностью заполненной
зоне, поскольку каждому электрону с
квазиимпульсом в ней можно сопоставить электрон с
квазиимпульсом
в ней можно сопоставить электрон с
квазиимпульсом и с то же энергией.
и с то же энергией.
Следовательно, плотность тока, создаваемая электронами зоны с одним незаполненным состоянием, равна по величине и противоположна по направлению плотности тока, создаваемой недостающим электроном.
Плотность тока, связанная с одним электроном (n = 1), равна
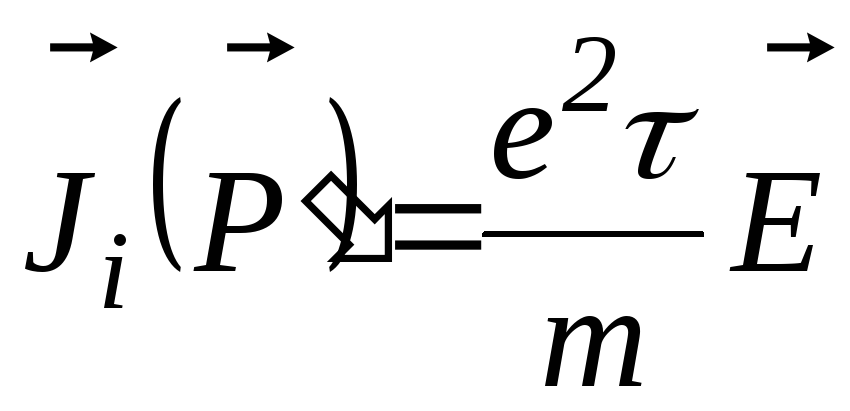 .
(2.82)
.
(2.82)
Так
как  ,
имеем
,
имеем
 .
(2.83)
.
(2.83)
Это
та плотность тока, которая создавалась
бы частицей с массой  и зарядомe.
Фактически движутся, естественно,
электроны. Однако электрон у потолка
зоны движется против действия силы. По
это причине удаление такого электрона
приводит к увеличению плотности тока,
такому, как если бы появилась частица
с положительной массой и положительным
зарядом.
и зарядомe.
Фактически движутся, естественно,
электроны. Однако электрон у потолка
зоны движется против действия силы. По
это причине удаление такого электрона
приводит к увеличению плотности тока,
такому, как если бы появилась частица
с положительной массой и положительным
зарядом.
Отметим еще раз: эффективная масса m* отражает способность электрона у дна зоны или дырки у ее потолка реагировать на внешнее поле, действующее совместно с межатомным периодическим потенциалом
2.11. Металлы, диэлектрики, полупроводники
в зонной теории
Рассмотрим теперь, как зонная теория твердого тела объясняет физические свойства реальных веществ и прежде всего различие этих свойств для металлов, полупроводников и диэлектриков.
Определим валентную зону как наивысшую энергетическую зону в твердом теле, которая целиком заполнена электронами в основном состоянии (при Т=0), зону проводимости — как самую нижнюю энергетическую зону в твердом теле, которая содержит свободные уровни в основном состоянии (незаполненную или содержащую некоторое число носителей при Т=0).
Рассмотрим случай, когда зона проводимости отделена от валентной зоны энергетической щелью Eg (рис.2.12). Пусть при Т=0 все состояния в зоне проводимости свободны, а в валентной зоне полностью заполнены электронами. В таком кристалле требуется конечная энергия возбуждения, больше ширины запрещенной зоны Eg, для перевода электронов вверх через энергетическую щель в зону проводимости. Если ширина запрещенной зоны Eg велика, так что ни температура, ни постоянное электрическое поле (и другие воздействия, которые не разрушают твердое тело) не могут сообщить электронам достаточную энергию для перехода в зону проводимости, то такое твердое тело не проводит электрический ток и я
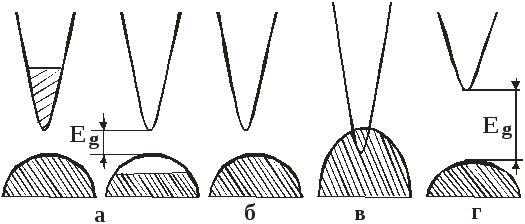
Рис. 2.12. Схема энергетических зон металла (а), полупроводника (б), полуметалла (в) и диэлектрика (г)
вляетсядиэлектриком.Аналогичный вывод мы получим, если рассмотрим полностью свободную от носителей заряда разрешенную зону, так как при приложении электрического поля к такой зоне она не даст никакого вклада в электропроводность. Такой кристалл также будет диэлектриком.
Если
ширина запрещенной щели невелика, то
при конечной температуре T в результате тепловых флуктуаций
некоторое число электронов, определяемое
характерным больцмановским множителем ,
перейдет из валентной зоны в зону
проводимости. Как электроны в зоне
проводимости, так и дырки (свободные,
незаполненные состояния), образовавшиеся
в результате ухода электронов из
валентной зоны, будут являться носителями
тока и будут давать свой вклад в величину
проводимости. Вещества с таким
энергетическим спектром обладают
конечной электропроводностью, быстро
возрастающей с ростом температуры,
называютсяполупроводниками.
,
перейдет из валентной зоны в зону
проводимости. Как электроны в зоне
проводимости, так и дырки (свободные,
незаполненные состояния), образовавшиеся
в результате ухода электронов из
валентной зоны, будут являться носителями
тока и будут давать свой вклад в величину
проводимости. Вещества с таким
энергетическим спектром обладают
конечной электропроводностью, быстро
возрастающей с ростом температуры,
называютсяполупроводниками.
Следовательно,
в основном состоянии полупроводники
не проводят тока, так как в основной
разрешенной зоне все состояния
заняты, и проводимость возникает только
при сообщении
электрону дополнительной энергии для
перехода в незаполненную
разрешенную зону. Значит, полупроводники
и диэлектрики
относятся к одному типу веществ — между
ними нет принципиальной разницы. Различие
носит количественный характер — по
величине запрещенной зоны. Если 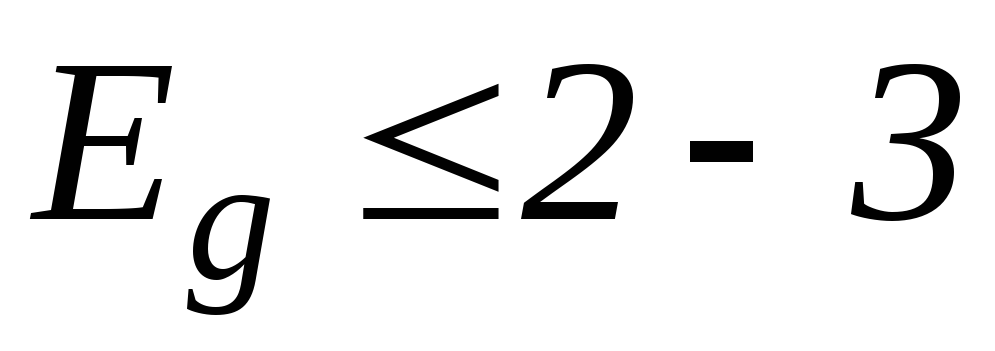 эВ,
то такие непроводники называют полупроводниками.
эВ,
то такие непроводники называют полупроводниками.
Удельное
электросопротивление полупроводников
при комнатной температуре лежит в
интервале от 10-6 до 108 .
По величине сопротивления они находятся
между хорошими проводниками (~ 10-8 – 10-6
.
По величине сопротивления они находятся
между хорошими проводниками (~ 10-8 – 10-6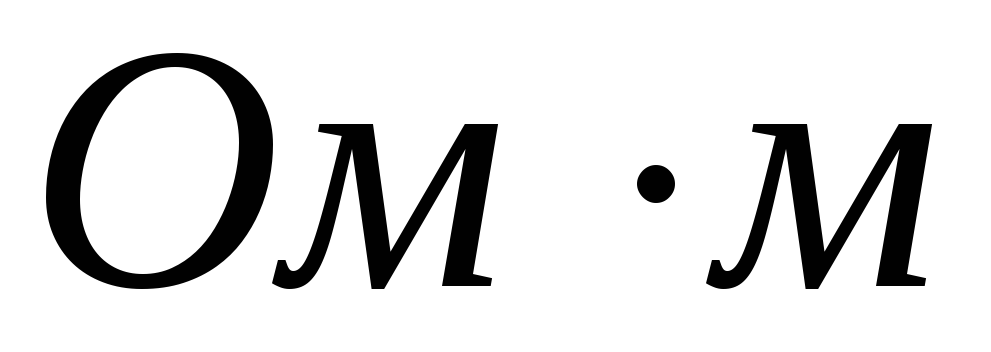 )
и изоляторами (>108
)
и изоляторами (>108 ).
).
Если зона проводимости заполнена не полностью и электронов достаточно много, то концентрация носителей тока не будет зависеть от температуры. Такие вещества являются металлами. Металлическая проводимость образуется и при перекрытии заполненной энергетической зоны с незаполненной зоной.
Зная, что число состояний в зоне Бриллюэна определяется как 2N, т. е. по два состояния на элементарную ячейку в зоне, можно, подсчитывая число электронов, приходящихся на элементарную ячейку, классифицировать вещество на металлы, полупроводники и диэлектрики.
Вещества, в которых на элементарную ячейку приходится один свободный электрон, являются металлами, так как электроны заполняют половину зоны. К ним относятся одновалентные щелочные металлы Li, Na, K, Rb, Cs и благородные металлы Cu, Ag, Au.
Вещества, в которых на элементарную ячейку приходится нечетное число электронов, также будут металлами, как и в предыдущем случае. К ним относятся металлы Al, Ga, In, Tl, в которых на один атом приходится три электрона. При этом валентная энергетическая зона заполнена полностью, а зона проводимости — наполовину.
Вещества, в которых на элементарную ячейку приходится четное число электронов, не обязательно будет изоляторами, так как энергетические зоны, как мы уже видели, могут перекрываться.
Элементы As, Sb, Bi, в которых на элементарную ячейку приходится по два атома, а каждый атом имеет пять электронов, представляют собой полуметаллы. Зонную структуру их можно рассматривать, как для полупроводников, однако минимум зоны проводимости лежит немного ниже максимума валентной зоны, т. е. разрешенные энергетические зоны перекрываются, и понятие запрещенной зоны теряет, как и для металла, смысл. С этим обстоятельством и связано название полуметалла.
Все двухвалентные вещества — металлы с хорошей проводимостью, за исключением Sr и Br, которые являются плохими проводниками из-за слабого перекрытия зон. Четырехвалентный углерод существует или в виде алмаза, со столь широкой запрещенной зоной, что его практически можно считать изолятором или в виде графита, являющегося полуметаллом. Кремний и германий — типичные полупроводники. Олово в одной фазе представляет собой металл, а в другой — полупроводник. Свинец — типичный металл.
Электроны и дырки. Статьи о светодиодах.
Полупроводники занимают промежуточное положение между проводниками и диэлектриками. Полупроводниковые материалы имеют кристаллическую структуру. При низкой температуре большинство внешних электронов в полупроводнике находятся в атомах на своих местах и полупроводник плохо проводит ток. Но связаны электроны с атомами слабее, чем в диэлектрике. При росте температуры, сопротивление полупроводников падает, то есть проводимость полупроводника в отличии от металлов при нагревании увеличивается. Иначе говоря, при нагревании в полупроводнике увеличивается количество свободных электронов, тем самым увеличивая способность проводить электрический ток. Этот эффект называют электронной проводимостью полупроводника.
С другой стороны, поскольку атомы полупроводника закреплены в кристаллической решетке, атомы лишившиеся электрона приобретают положительный заряд, получается «дырка». Электроны соседних атомов перескакивают к атому с положительным зарядом, таким образом возникает видимость движения положительного заряда — «дырочная» проводимость. Закономерности «дырочной» проводимости таковы, что этим «дыркам» физики условно приписывают и заряд (положительный, равный заряду электрона), и «эффективную массу».
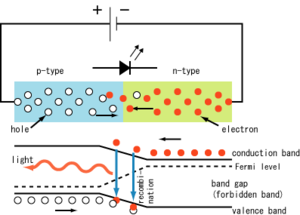
В чистом полупроводнике, проводимость которого обусловлена тепловым возбуждением, при приложении потенциала, одинаковое число электронов и дырок движется в разных направлениях. При добавлении в полупроводник атомов легко отдающих электроны, в полупроводнике превалирует электронная проводимость и сопротивление электрическому току резко падает. Такой полупроводник называют полупроводником n-типа.
Аналогично, при легировании материалами, способными захватывать лишние электроны, получают полупроводник p-типа.
Если в полупроводнике одна часть обладает проводимостью p-типа, а другая — n-типа, между этими областями возникает граница, обладающая односторонней проводимостью. На этом принципе работает большинство полупроводниковых диодов и транзисторов. Кроме того, на границе возникает энергетический барьер, для преодоления которого необходимо приложить дополнительный потенциал. В результате этого, полупроводниковый диод имеет падение напряжения при прямом токе. При положительной полярности внешнего напряжения, плюс — к p-зоне, минус — к n-зоне, происходит перескакивание электронов и дырок (рекомбинирование), в результате чего выделяется энергия. В случае выпрямительных диодов и транзисторов, стараются максимально уменьшить энергетический барьер, так как рекомбинация происходит с выделением тепла, равным энергии барьера, или энергии рекомбинации. Если же увеличить энергию рекомбинации, то при достижении уровня энергии фотонов видимого света, частично процесс рекомбинации происходит с излучением света. Соотношение тепловой и излучательной рекомбинации называют квантовым выходом, или эффективностью светодиода.
Поскольку энергия рекомбинации равна величине энергетического барьера, излучение происходит в узкой области спектра. Поэтому все светодиоды излучают монохроматическое излучение. Белые (полихромные) светодиоды в своей основе имеют также монохроматические светодиодные чипы.
Сначала полупроводниковые приборы делали «гомопереходными», в них p-n- переход возникал в полупроводнике одного базового вещества. Но вскоре появилась устройства, в которых такой переход создавался на границе двух различных полупроводников. В результате, появилась возможность создать полупроводниковые приборы меньшего размера и с большей эффективностью. Так, первые «гомопереходные» полупроводниковые светодиоды могли работать только при температуре жидкого азота, а «гетеропереходные» работают и при комнатной температуре.
При выборе материалов для изготовления светодиодов, существенными становятся оптические свойства полупроводников. Материал одного из компонентов должен быть прозрачным или чрезвычайно тонким, а граница или второй материал должен хорошо отражать свет в области излучаемого спектра. Наряду с квантовым выходом, это наиболее важные условия увеличения эффективности светодиодов.
Далее о светодиодах >>>
1.2. Структура полупроводников
1.2. Структура полупроводников.
Понятие дырки
Структура полупроводников
Наиболее распространенными полупроводниками
являются атомарные полупроводники
кремний Si, германий Ge,
и полупроводниковые соединения типа 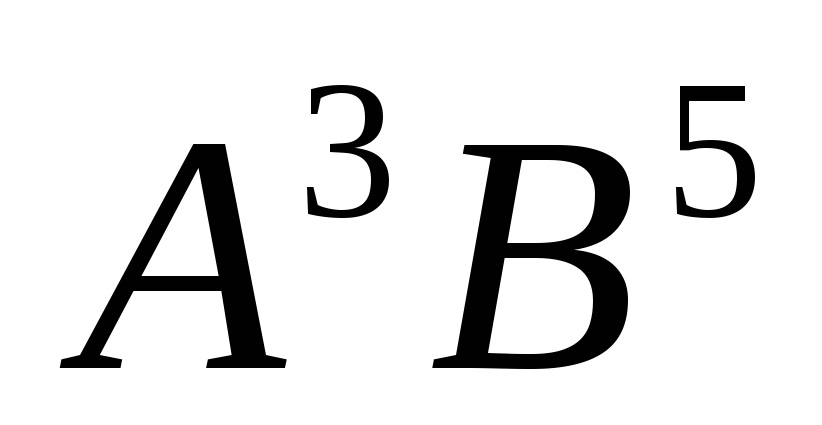 (арсенид
галлия GaAs, фосфид индия
InP). Используются также
полупроводники типа
(арсенид
галлия GaAs, фосфид индия
InP). Используются также
полупроводники типа 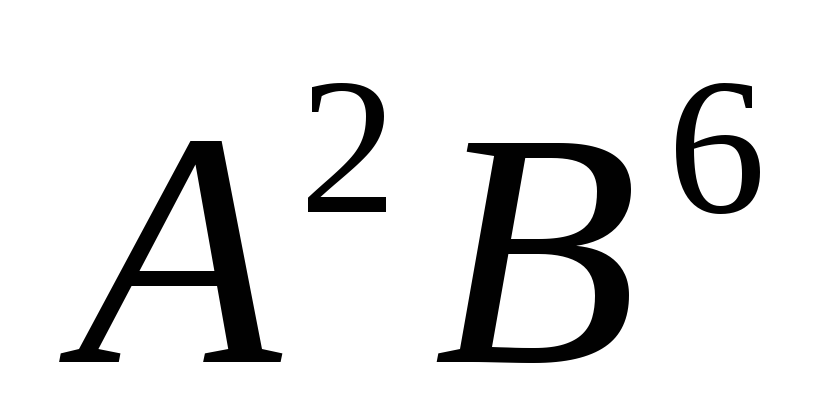 и
и 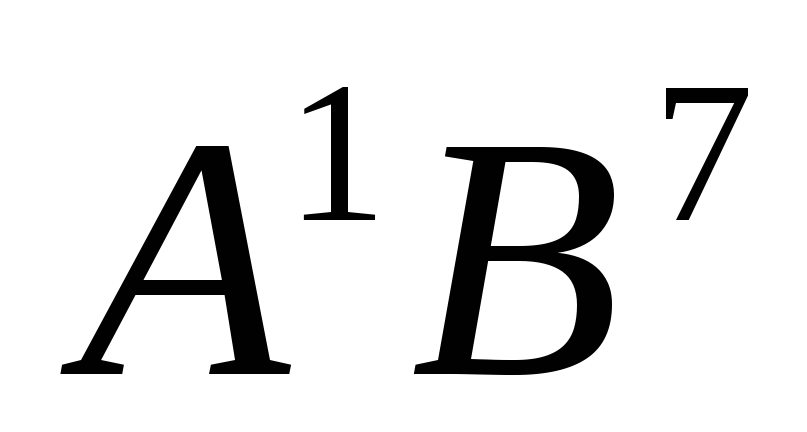 ,
где
,
где  и
и  -элементы
соответствующих групп таблицы Менделеева.
-элементы
соответствующих групп таблицы Менделеева.
Полупроводниковые кристаллы имеют
структуру типа алмаза. В этой кристаллической
структуре каждый атом кристалла окружен
4-мя соседями, находящимися на одинаковом
расстоянии от атома. Связь между атомами
в кристалле парно электронная или
ко валентная.
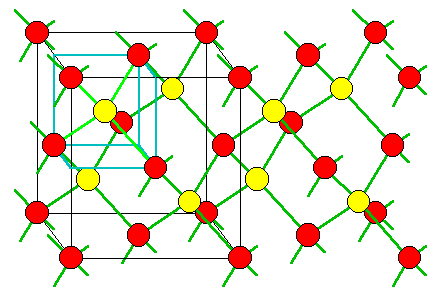
На рисунках ХХХ приведены
объемный трехмерный и двухмерный
варианты решетки кремния. Тетраэдрическая
структура представляет собой вдвинутые
друг в друга две гранецентрированных
кубических решетки. Смещение решеток
относительно друг друга проводится
вдоль главной диагонали куба на
расстояние, равное одной четверти длины
главной диагонали (см. рис.)
валентная.
На рисунках ХХХ приведены
объемный трехмерный и двухмерный
варианты решетки кремния. Тетраэдрическая
структура представляет собой вдвинутые
друг в друга две гранецентрированных
кубических решетки. Смещение решеток
относительно друг друга проводится
вдоль главной диагонали куба на
расстояние, равное одной четверти длины
главной диагонали (см. рис.)
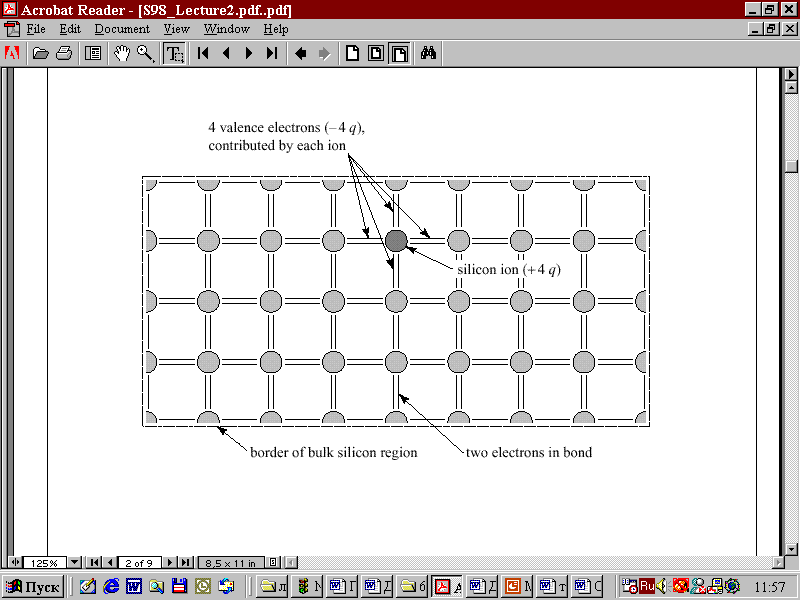
Сложные полупроводниковые соединения, такие как GaAs, InP, PbS и другие двойные или тройные соединения также имеют решетку типа алмаза. Но в этих соединениях один атом одного элемента окружен четырьмя атомами другого. Связь между атомами – ковалентная.
Понятие дырки
При переходе электрона в зону проводимости из заполненной (валентной) зоны в валентной зоне остается незаполненное место, которое легко может занять какой-либо электрон из той же зоны. В результате образовавшаяся вакансия приобретает возможность перемещаться в пределах валентной зоны. Ее поведение во многом напоминает поведение частицы с положительным зарядом.
Как отмечалось, полупроводники отличаются от металлов и диэлектриков тем, что их зона проводимости при температуре отличной от абсолютного нуля “почти пуста”, а валентная зона “почти заполнена”. Но это означает, что при рассмотрении проводимости в полупроводниках необходимо учитывать движение носителей тока и в зоне проводимости, и в валентной зоне.
Чтобы упростить рассмотрение переноса носителей в “почти заполненной” валентной зоне вводится понятие “дырки”. Однако нужно всегда помнить, что существует только один тип носителей тока в полупроводниках – это электроны. Дырки – это квазичастицы, введение которых позволяет только упростить представление движения электронов в валентной зоне. Дырка – это отсутствие электрона. Свойства дырок аналогичны свойствам электронов, поскольку они занимают одно и тоже энергетическое состояние. Но дырка несет положительный заряд.
На рисунке приведена энергетическая
диаграмма полупроводника, помещенного
во внешнее электрическое поле с
напряженностью  .
Градиент энергетических уровней зонной
диаграммы полупроводника в однородном
электрическом поле будет постоянным,
и он определяется величиной электрического
поля (позже мы подробнее рассмотрим
энергетические диаграммы полупроводников
в условиях действия электрических
полей).
.
Градиент энергетических уровней зонной
диаграммы полупроводника в однородном
электрическом поле будет постоянным,
и он определяется величиной электрического
поля (позже мы подробнее рассмотрим
энергетические диаграммы полупроводников
в условиях действия электрических
полей).
 Электроны
зоны проводимости движутся противоположно
направлению внешнего электрического
поля, т.е. в сторону спада уровня
Электроны
зоны проводимости движутся противоположно
направлению внешнего электрического
поля, т.е. в сторону спада уровня 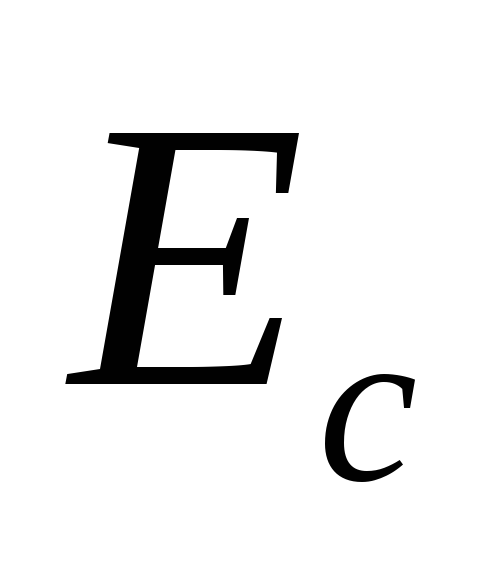 .
Электроны валентной зоны движутся в
том же направлении. Общую плотность
тока электронов валентной зоны можно
записать в виде
.
Электроны валентной зоны движутся в
том же направлении. Общую плотность
тока электронов валентной зоны можно
записать в виде
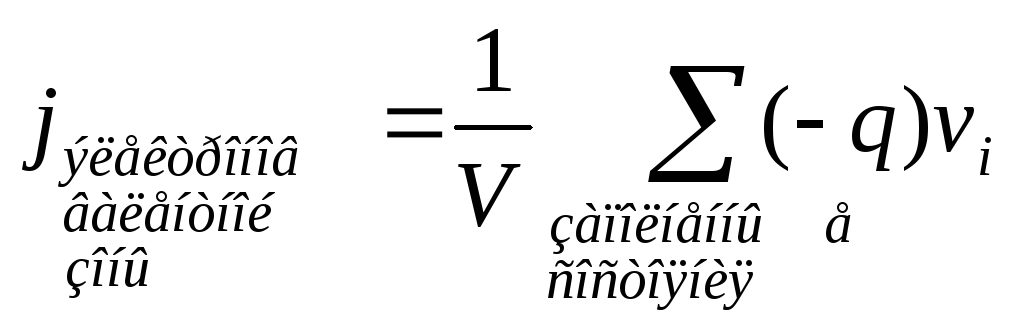
где  —
объем полупроводника,
—
объем полупроводника,  —
заряд электрона,
—
заряд электрона,  -скорость i— того электрона
валентной зоны. Суммирование проводится
по всем электронам валентной зоны. Это
выражение можно записать иначе, выразив
его через количество состояний валентной
зоны, не занятых электронами.
-скорость i— того электрона
валентной зоны. Суммирование проводится
по всем электронам валентной зоны. Это
выражение можно записать иначе, выразив
его через количество состояний валентной
зоны, не занятых электронами.
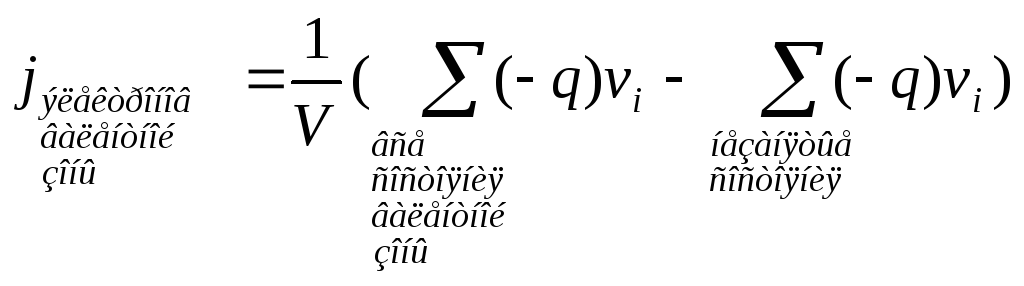
Но плотность тока, создаваемая всеми электронами заполненной валентной зоны, равна нулю. Поэтому в последней формуле остается только одно последнее слагаемое, которое можно записать как

Это соотношение можно трактовать следующим образом. Ток создается положительными носителями, связанными с незаполненными состояниями валентной зоны. Эти носители и называют дырками. Напоминаем, что нет реальных носителей – дырок. Это просто модель, удобная для представления тока, создаваемого электронами валентной зоны. Причиной ввода понятия дырка является то, что это позволяет упростить описание ансамбля из очень большого числа электронов в почти заполненной валентной зоне. Часто оказывается более удобным следить за имеющимися вакансиями, рассматривая их как некоторые гипотетические частицы — дырки (простым гидромеханическим аналогом дырки может служить пузырек в стакане с газированным напитком). Не являющиеся реальными объектами природы дырки часто обладают весьма экзотическими свойствами. Так их эффективная масса не обязательно должна выражаться положительным числом, а зачастую оказывается тензорной величиной. Наряду с фононами дырки представляют собой квазичастицы, вводимые в теорию на основе аналогий с формулами, описывающими поведение реальных объектов. Подобно положительным частицам дырки ускоряются электрическим полем и вносят свой вклад в проводимость полупроводниковых кристаллов.
Попутно отметим, что электроны проводимости, строго говоря, так же являются квазичастицами. С точки зрения квантовой механики все электроны кристалла являются принципиально неразличимыми, что делает бессмысленными попытки ответа на вопрос, какой именно электрон перешел в зону проводимости. Электрический ток в кристалле обусловлен весьма сложным поведением всех без исключения имеющихся в нем электронов. Однако описывающие это поведение уравнения обнаруживают близкое сходство с уравнениями движения лишь очень небольшого числа заряженных частиц — электронов и дырок.
воскресенье, 1 сентября 2002 г.
Шуренков В.В.
Электроны и дырки в полупроводниках
Цель работы — ознакомление с физическими процессами в ЭДП, изучение вольтамперных характеристик диодов из германия и кремния и их зависимости от ширины запрещенной зоны полупроводника и температуры, определение ширины запрещенной зоны германия, изучение p-n-перехода как приемника света (фотодиода).
ЭЛЕКТРОНЫ И ДЫРКИ В ПОЛУПРОВОДНИКАХ
В твердом теле атомы находятся
друг от друга на расстоянии порядка
атомного размера, поэтому в нем
валентные электроны могут
Разорванная связь становится блуждающей по кристаллу дыркой, поскольку электрон соседней связи быстро занимает место ушедшего. Недостаток электрона у одной из связей означает наличие у пары атомов единичного положительного заряда, который переносится вместе с дыркой. Электроны и дырки — свободные носители заряда в полупроводниках. В идеальных кристаллах, не имеющих ни примесей, ни дефектов, возбуждение одного из связанных электронов и превращение его в электрон проводимости неизбежно вызывает появление дырки, так что концентрация обоих типов носителей равны между собой.
Для образования электронно-
Помимо процесса образования электронов и дырок идет обратный процесс — их исчезновение, или рекомбинация. Электрон проводимости, оказавшись рядом с дыркой, восстанавливает разорванную связь. При этом исчезают один электрон проводимости и одна дырка. При отсутствии внешних воздействий, например света, устанавливается динамическое равновесие процессов, протекающих в обоих направлениях. Равновесные концентрации электронов и дырок определяются абсолютной температурой Т, шириной запрещенной зоны Ед, концентрацией примесей и другими факторами. Однако произведение концентраций электронов и дырок (n и p соответственно) не зависит от количества примесей и определяется для данного полупроводника температурой и величиной Eд:
где k – постоянная Больцмана; А – коэффициент пропорциональности.
Рассмотрим два следствия из формулы. В собственном (беспримесном) полупроводнике одинаковые концентрации электронов и дырок будут равны
В примесных полупроводниках при достаточно большом количестве примеси концентрация основных носителей примерно равна концентрации примеси. Например, в полупроводнике n-типа концентрация электронов равна концентрации донорных атомов; тогда концентрация дырок (неосновных носителей) равна:
ЭЛЕКТРОННО-ДЫРОЧНОЙ ПЕРЕХОД В РАВНОВЕСНОМ СОСТОЯНИИ
В монокристалле можно создать резкий переход от полупроводника n-типа к полупроводнику p-типа. На рисунке левая от линии ММ часть кристалла, p-типа, содержит основные -носители — дырки, примерно такое же количество отрицательных акцепторных ионов и незначительное количество электронов. Правая часть, n-типа, содержит соответственно электроны проводимости (основные носители), положительные донорные ионы и небольшое количество дырок.
ВОЛЬТ-АМПЕРНАЯ ХАРАКТЕРИСТИКА ИДЕАЛЬНОГО ЭДП
Зависимость I(U) называют вольт-амперной характеристикой ЭДП (диода).
В зависимости от значения питающего напряжении и полярности источника изменяется высота барьера в ЭДП при неизменной полярности двойного слоя зарядов. Поскольку неосновные носители «скатываются» с барьера, ток неосновных носителей остается постоянным при изменениях высоты барьера. Ток основных носителей, которые «взбираются» на барьер, очень чувствителен к его высоте: при повышении барьера он быстро уменьшается до нуля, а при понижении барьера может возрасти на несколько порядков. Чтобы получить зависимость тока от напряжения, необходимо знать энергетический спектр частиц. В целом эта зависимость довольно сложная, но для описания процессов в ЭДП необходимо знать только самую «энергетическую» честь спектра, «хвост» распределения, поскольку в практических случаях только самые быстрые частицы способны преодолеть барьер. Спектр таких быстрых электронов экспоненциальный.
При прямом смешении ток
протекает в положительном
Теоретическая вольт-амперная характеристика р — п -перехода, рассчитанная по формуле при комнатной температуре Т= 295 К, представлена на рисунке и в таблице (напряжение U в вольтах). Зависимость I(U) обладает резко выраженной нелинейностью, т.е. проводимость (или сопротивление) р — п -перехода сильно зависит от U. При обратном смещении через переход течет ток Is неосновных носителей, называемые током насыщения, который обычно мал и почти не зависит от напряжения.
Как видно из формулы, ток насыщения задает масштаб по оси I вольт-амперной характеристики. Значение Is пропорционально площади перехода, концентрации неосновных носителей и их скорости хаотического движения. Учитывая формулу, получаем следующую зависимость тока насыщения от ширины запрещенной зоны и температуры:
где С — коэффициент
Экспоненциальный множитель
Из опыта, в котором измерен ток насыщения при различной температуре, можно найти значение Ед. Полученную зависимость следует сравнить с формулой, которую логарифмированием преобразуем к виду
Если точки ложатся на прямую, то опыт подтверждает экспоненциальную зависимость тока от обратной температуры.
ЭДП В КАЧЕСТВЕ ПРИЕМНИКА СВЕТА (Фотодиод)
Свет может разорвать
электронную связь в
При освещении p-n-перехода образуются дополнительные электронно-дырочные пары. При достаточном освещении они могут существенно увеличить концентрацию неосновных носителей, которых было мало, практически не изменяя в процентном отношении количество основных носителей. При этой к существовавшему в темноте току неосновных носителей — Is добавляется фототок — I, протекающий в том же направлении.
Фототок равен разности тока и тока называемого в данной случае темновым током. При достаточно большой освещенности темновой ток может составлять пренебрежимо малую долю полного тока. Электронно-дырочный переход, специально изготовленный для детектирования света и работающий при обратном смещении, называется фотодиодом. Это простой и удобный приемник света, фототок которого пропорционален освещенности Е.
ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ
Упрощенная схема, в которой не показаны переключатели, дана на рис. Диод Д (кремниевый или германиевый) через резистор R подключен к источнику постоянного напряжения (ИП), изменяемого от 0 до 15 В. Переменный резистор R1 также используется для изменения напряжения на диоде. Цифровым вольтметром с большим сопротивлением измеряют напряжения U на диоде и Ur на известном сопротивлении R для вычисления тока I=Ur/R. Для измерения малых токов устанавливают большое сопротивление.
Два диода, нагреватель и один спай термопары плотно закреплены на металлической пластине, расположенной в камере с крышкой. Для опытов со светом защитная оболочка кремниевого диода удалена, и при открытой крышке р-п -переход можно осветить лампой. Для измерения температуры диодов служит термопара. Она состоит из двух металлических проводников — медного и константанового (специальный сплав), спай которых находится в тепловом контакте с диодами при измеряемой температуре Т. Другие концы проводов соединены с вольтметром, они имеют комнатную температуру T1 — 295 К. Когда температуры Т и Т1 различны, в цепи возникает термоЭДС UT, пропорциональная разности температур и измеряемая вольтметром. Температуру диодов в Кельвинах можно вычислить по формуле
T=295+24.4 UT,
где напряжение UT следует взять в милливольтах.



