Уравнения Максвелла — Википедия

Уравне́ния Ма́ксвелла — система уравнений в дифференциальной или интегральной форме, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах. Вместе с выражением для силы Лоренца, задающим меру воздействия электромагнитного поля на заряженные частицы, эти уравнения образуют полную систему уравнений классической электродинамики, называемую иногда уравнениями Максвелла — Лоренца. Уравнения, сформулированные Джеймсом Клерком Максвеллом на основе накопленных к середине XIX века экспериментальных результатов, сыграли ключевую роль в развитии представлений теоретической физики и оказали сильное, зачастую решающее влияние не только на все области физики, непосредственно связанные с электромагнетизмом, но и на многие возникшие впоследствии фундаментальные теории, предмет которых не сводился к электромагнетизму (одним из ярчайших примеров здесь может служить специальная теория относительности).

Джеймс Клерк Максвелл

Уравнения, сформулированные Джеймсом Клерком Максвеллом, возникли на основе ряда важных экспериментальных открытий, которые были сделаны в начале XIX века. В 1820 году Ганс Христиан Эрстед обнаружил^[1], что пропускаемый через провод гальванический ток заставляет отклоняться магнитную стрелку компаса. Это открытие привлекло широкое внимание учёных того времени. В том же 1820 году Био и Савар экспериментально нашли выражение^[2] для порождаемой током магнитной индукции (закон Био — Савара), а Андре Мари Ампер обнаружил также, что взаимодействие на расстоянии возникает между двумя проводниками, по которым пропускается ток. Ампер ввёл термин «электродинамический» и выдвинул гипотезу, что природный магнетизм связан с существованием в магните круговых токов

[3].

Влияние тока на магнит, обнаруженное Эрстедом, привело Майкла Фарадея к идее о том, что должно существовать обратное влияние магнита на токи. После длительных экспериментов, в 1831 году, Фарадей открыл, что перемещающийся возле проводника магнит порождает в проводнике электрический ток. Это явление было названо электромагнитной индукцией. Фарадей ввёл понятие «поля сил» — некоторой среды, находящейся между зарядами и токами. Его рассуждения носили качественный характер, однако они оказали огромное влияние на исследования Максвелла.

После открытий Фарадея стало ясно, что старые модели электромагнетизма (Ампер, Пуассон и др.) неполны. Вскоре появилась теория Вебера, основанная на дальнодействии. Однако к этому моменту вся физика, кроме теории тяготения, имела дело только с близкодействием (оптика, термодинамика, механика сплошных сред и др.). Гаусс, Риман и ряд других учёных высказывали догадки, что свет имеет электромагнитную природу, так что теория электромагнитных явлений тоже должна быть близкодейственной. Этот принцип стал существенной особенностью теории Максвелла.

В своём знаменитом «Трактате об электричестве и магнетизме» (1873) Максвелл писал^[4]:

Приступая к изучению труда Фарадея, я установил, что его метод понимания явлений был так же математическим, хотя и не представленным в форме обычных математических символов. Я также нашёл, что этот метод можно выразить в обычной математической форме и таким образом сравнить с методами профессиональных математиков.

Заменяя фарадеевский термин «поле сил» на понятие «напряжённость поля», Максвелл сделал его ключевым объектом своей теории^[5]:

Если мы примем эту среду в качестве гипотезы, я считаю, что она должна занимать выдающееся место в наших исследованиях, и что нам следовало бы попытаться сконструировать рациональное представление о всех деталях её действия, что и было моей постоянной целью в этом трактате.

Подобная электродинамическая среда явилась абсолютно новым понятием для ньютоновской физики. Последняя изучала взаимодействие между собой материальных тел. Максвелл же записал уравнения, которым должна подчиняться среда, определяющая взаимодействие зарядов и токов и существующая даже в их отсутствие.

Электрический ток создаёт магнитную индукцию (закон Ампера)

Анализируя известные эксперименты, Максвелл получил систему уравнений для электрического и магнитного полей. В 1855 году в своей самой первой статье «О фарадеевых силовых линиях»

[6] («On Faraday’s Lines of Force»^[7]) он впервые записал в дифференциальной форме систему уравнений электродинамики, но не вводя ещё ток смещения. Такая система уравнений описывала все известные к тому времени экспериментальные данные, но не позволяла связать между собой заряды и токи и предсказать электромагнитные волны^[8]. Впервые ток смещения был введён Максвеллом в работе «О физических силовых линиях»^[9] («On Physical Lines of Force»^[10]), состоящей из четырёх частей и опубликованной в 1861—1862 годах. Обобщая закон Ампера, Максвелл вводит ток смещения, вероятно, чтобы связать токи и заряды уравнением непрерывности, которое уже было известно для других физических величин

[8]. Следовательно, в этой статье фактически была завершена формулировка полной системы уравнений электродинамики. В статье 1864 года «Динамическая теория электромагнитного поля»^[11] («A dynamical theory of the electromagnetic field»^[12]) рассмотрена сформулированная ранее система уравнений из 20 скалярных уравнений для 20 скалярных неизвестных. В этой статье Максвелл впервые сформулировал понятие электромагнитного поля как физической реальности, имеющей собственную энергию и конечное время распространения, определяющее запаздывающий характер электромагнитного взаимодействия^[8].

Переменный поток магнитного поля создаёт электрическое поле (закон Фарадея)

Оказалось, что не только ток, но и изменяющееся со временем электрическое поле (ток смещения) порождает магнитное поле. В свою очередь, в силу закона Фарадея, изменяющееся магнитное поле снова порождает электрическое. В результате, в пустом пространстве может распространяться электромагнитная волна. Из уравнений Максвелла следовало, что её скорость равна скорости света, поэтому Максвелл сделал вывод об электромагнитной природе света.

Часть физиков выступила против теории Максвелла (особенно много возражений вызвала концепция тока смещения). Гельмгольц предложил свою теорию, компромиссную по отношению к моделям Вебера и Максвелла, и поручил своему ученику Генриху Герцу провести её экспериментальную проверку. Однако опыты Герца однозначно подтвердили правоту Максвелла.

Максвелл не использовал векторных обозначений и записывал свои уравнения в достаточно громоздком компонентном виде. В своём трактате^[13] он, кроме того, частично использовал кватернионную формулировку. Современная форма уравнений Максвелла появилась около 1884 года после работ Хевисайда, Герца и Гиббса. Они не только переписали систему Максвелла в векторном виде, но и симметризовали её, переформулировав в терминах поля, избавившись от электрического и магнитного потенциалов, игравших в теории Максвелла существенную роль, поскольку полагали, что эти функции являются лишь ненужными вспомогательными математическими абстракциями

[14]. Интересно, что современная физика поддерживает Максвелла, но не разделяет негативное отношение его ранних последователей к потенциалам. Электромагнитный потенциал играет важную роль в квантовой физике и проявляется как физически измеряемая величина в некоторых экспериментах, например, в эффекте Ааронова — Бома^[15].

Система уравнений в формулировке Герца и Хевисайда некоторое время называлась уравнениями Герца — Хевисайда^[16]. Эйнштейн в классической статье «К электродинамике движущихся тел»^[17] назвал их уравнениями Максвелла — Герца. Иногда в литературе встречается также название уравнения Максвелла — Хевисайда

[18].

Уравнения Максвелла сыграли важную роль при возникновении специальной теории относительности (СТО). Джозеф Лармор (1900 год)^[19] и независимо от него Хенрик Лоренц (1904 год)^[20] нашли преобразования координат, времени и электромагнитных полей, которые оставляют уравнения Максвелла инвариантными при переходе от одной инерциальной системы отсчёта к другой. Эти преобразования отличались от преобразований Галилея классической механики и, с подачи Анри Пуанкаре^[21], стали называться преобразованиями Лоренца. Они стали математическим фундаментом специальной теории относительности.

Распространение электромагнитных волн со скоростью света первоначально интерпретировалось как возмущения некоторой среды, так называемого эфира^[22]. Были предприняты многочисленные попытки (см.исторический обзор) обнаружить движение Земли относительно эфира, однако они неизменно давали отрицательный результат.^[23] Поэтому Анри Пуанкаре высказал гипотезу о принципиальной невозможности обнаружить подобное движение (принцип относительности). Ему же принадлежит постулат о независимости скорости света от скорости его источника и вывод (вместе с Лоренцем), исходя из сформулированного так принципа относительности, точного вида преобразований Лоренца (при этом были показаны и групповые свойства этих преобразований). Эти две гипотезы (постулата) легли и в основу статьи Альберта Эйнштейна (1905 год)

[17]. С их помощью он также вывел преобразования Лоренца и утвердил их общефизический смысл, особо подчеркнув возможность их применения для перехода из любой инерциальной системы отсчёта в любую другую инерциальную. Эта работа фактически ознаменовала собой построение специальной теории относительности. В СТО преобразования Лоренца отражают общие свойства пространства и времени, а модель эфира оказывается ненужной. Электромагнитные поля являются самостоятельными объектами, существующими наравне с материальными частицами.

Классическая электродинамика, основанная на уравнениях Максвелла, лежит в основе многочисленных приложений электро- и радиотехники, СВЧ и оптики. До настоящего времени не было обнаружено ни одного эффекта, который потребовал бы видоизменения уравнений. Они оказываются применимы и в квантовой механике, когда рассматривается движение, например, заряженных частиц во внешних электромагнитных полях. Поэтому уравнения Максвелла являются основой микроскопического описания электромагнитных свойств вещества.

Уравнения Максвелла востребованы также в астрофизике и космологии, поскольку многие планеты и звезды обладают магнитным полем. Магнитное поле определяет, в частности, свойства таких объектов, как пульсары и квазары.

На современном уровне понимания все фундаментальные частицы являются квантовыми возбуждениями («квантами») различных полей. Например, фотон — это квант электромагнитного поля, а электрон — квант спинорного поля^[24]. Поэтому полевой подход, предложенный Фарадеем и существенно развитый Максвеллом, является основой современной физики фундаментальных частиц, в том числе её стандартной модели.

Исторически несколько раньше он сыграл важную роль в появлении квантовой механики в формулировке Шрёдингера и вообще открытии квантовых уравнений, описывающих движение частиц, в том числе и релятивистских (уравнение Клейна — Гордона, уравнение Дирака), хотя первоначально аналогия с уравнениями Максвелла здесь виделась скорее лишь в общей идее, тогда как впоследствии оказалось, что она может быть понята как более конкретная и детальная (как это описано выше).

Также полевой подход, в целом восходящий к Фарадею и Максвеллу, стал центральным в теории гравитации (включая ОТО).

Запись уравнений Максвелла и системы единиц[править | править код]

Запись большинства уравнений в физике не зависит от выбора системы единиц. Однако в электродинамике это не так. В зависимости от выбора системы единиц в уравнениях Максвелла возникают различные коэффициенты (константы). Международная система единиц (СИ) является стандартом в технике и преподавании, однако споры среди физиков о её достоинствах и недостатках по сравнению с конкурирующей системой единиц СГС не утихают^[25]; здесь и всюду далее под СГС подразумевается исключительно симметричная гауссова система СГС. Преимущество системы СГС в электродинамике состоит в том, что все поля в ней имеют одну размерность, а уравнения, по мнению многих учёных, записываются проще и естественней^[26]. Поэтому СГС продолжает применяться в научных публикациях по электродинамике и в преподавании теоретической физики, например, в курсе теоретической физики Ландау и Лифшица. Однако для практических применений вводимые в СГС единицы измерений, многие из которых неименованы и неоднозначны, часто неудобны. Система СИ стандартизована и лучше самосогласованна, на этой системе построена вся современная метрология^[27]. Кроме того, система СИ обычно используется в курсах общей физики. В связи с этим все соотношения, если они по-разному записываются в системах СИ и СГС, далее приводятся в двух вариантах.

Иногда (например, в «Фейнмановских лекциях по физике», а также в современной квантовой теории поля) применяется система единиц, в которой скорость света, электрическая и магнитная постоянные принимаются за единицу (c=ε0=μ0=1{\displaystyle c=\varepsilon _{0}=\mu _{0}=1}). В такой системе уравнения Максвелла записываются вообще без коэффициентов, все поля имеют единую размерность, а все потенциалы — свою единую. Такая система особенно удобна в ковариантной четырёхмерной формулировке законов электродинамики через 4-потенциал и 4-тензор электромагнитного поля.

Уравнения Максвелла в дифференциальной форме[править | править код]

Уравнения Максвелла представляют собой в векторной записи систему из четырёх уравнений, сводящуюся в компонентном представлении к восьми (два векторных уравнения содержат по три компоненты каждое плюс два скалярных^[28]) линейным дифференциальным уравнениям в частных производных первого порядка для 12 компонент четырёх векторных функций (D,E,H,B{\displaystyle \mathbf {D} ,\;\mathbf {E} ,\;\mathbf {H} ,\;\mathbf {B} }):

Жирным шрифтом в дальнейшем обозначаются векторные величины, курсивом — скалярные.

Введённые обозначения:

Приведённые выше уравнения Максвелла не составляют ещё полной системы уравнений электромагнитного поля, поскольку они не содержат свойств среды, в которой возбуждено электромагнитное поле. Соотношения, связывающие величины E{\displaystyle \mathbf {E} }, B{\displaystyle \mathbf {B} }, D{\displaystyle \mathbf {D} }, H{\displaystyle \mathbf {H} } и j{\displaystyle \mathbf {j} } и учитывающие индивидуальные свойства среды, называются материальными уравнениями.

Уравнения Максвелла в интегральной форме[править | править код]

При помощи формулы Остроградского — Гаусса и теоремы Стокса дифференциальным уравнениям Максвелла можно придать форму интегральных уравнений:

Поток электрического поля через замкнутую поверхность

Введённые обозначения:

• s {\displaystyle s\ } — двумерная замкнутая в случае теоремы Гаусса поверхность, ограничивающая объём v {\displaystyle v\ }, и открытая поверхность в случае законов Фарадея и Ампера — Максвелла (её границей является замкнутый контур l {\displaystyle l\ }).
• Q=∫vρdv {\displaystyle Q=\int \lim

Электромагнитное поле | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

Тема:

Электромагнетизм

Электромагнитное поле связано с источниками (заряда­ми) и обладает определенной структурой. Его структура и связь с источниками описываются уравнениями поля (уравнениями Максвелла).

На частицу с зарядом q и скоростью v в пустоте в присутствии внешнего (создаваемого другими частицами) электромагнитного поля действует сила

F̅ = qE̅ + qv̅ × B̅. [1]

Вектор E̅ называется напряженностью электрического поля в точке нахождения частицы, вектор B̅ — индукцией магнитного поля в той же точке. Эти векторы в разных точ­ках пространства, вообще говоря, различны и могут менять­ся во времени. Таким образом, мы имеем дело с двумя век­торными функциями координат и времени:

E̅ = E̅ (r̅, t), B̅ = B̅ (r̅, t).

Задание этих функций полностью определяет электромаг­нитное поле.

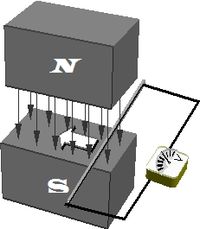
На фотографии видны силовые линии мощного электрического поля около металлического шарика, под которым установлен ионизатор

Из формулы [1] следует, что напряженность электрическо­го поля определяет силу, действующую на заряженную ча­стицу, не зависящую от состояния движения частицы. Си­ла, действующая на частицу со стороны магнитного поля, определяется векторным произведением скорости и ин­дукции поля, направлена перпендикулярно плоскости, в ко­торой лежат векторы скорости и индукции, и зависит от ве­личины скорости. Неподвижный заряд не «чувствует» магнитного поля. Материал с сайта http://worldofschool.ru

Силовые линии поля

Электромагнитное поле обнаруживается (и измеряется) по силе, действующей на заряженную частицу. Оно полно­стью описывается двумя векторными функциями — напря­женностью электрического поля и индукцией магнитного. Векторные поля, представляющие электромагнитное поле, должны обладать специальной структурой. Математически эта структура определяется уравнениями, которым долж­ны удовлетворять векторные поля, обладающие свойства­ми реального электромагнитного поля. Эти уравнения на­зываются уравнениями поля.

Наглядно поле изображается с помощью силовых линий, представляющих собой множество кривых, проведенных та­ким образом, что в каждой точке кривой вектор E̅ в этой точ­ке касателен к кривой. Это силовые линии электрического по­ля. Аналогично проводятся силовые линии магнитного поля.

На этой странице материал по темам:

• Конспект «электромагнитное поле»

• Электромагнитное поле доклад по физике

• Доклад по физике электромагнитное поле

• Все физические формулы по теме электромагнитное поле

• Электромагнитное поле кратко с формулами

Электромагнитное взаимодействие — Википедия

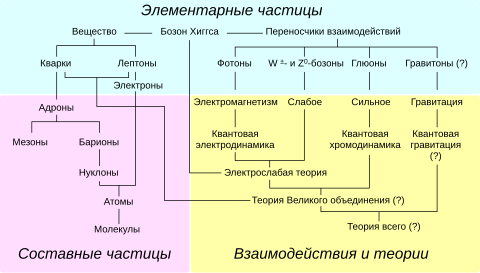
Электромагни́тное взаимоде́йствие — одно из четырёх фундаментальных взаимодействий. Электромагнитное взаимодействие существует между частицами, обладающими электрическим зарядом^[1]. С современной точки зрения электромагнитное взаимодействие между заряженными частицами осуществляется не прямо, а только посредством электромагнитного поля.

С точки зрения квантовой теории поля^[2] электромагнитное взаимодействие переносится безмассовым бозоном — фотоном (частицей, которую можно представить как квантовое возбуждение электромагнитного поля). Сам фотон электрическим зарядом не обладает, но может взаимодействовать с другими фотонами путём обмена виртуальными электрон-позитронными парами.

Из фундаментальных частиц в электромагнитном взаимодействии участвуют также имеющие электрический заряд частицы: кварки, электрон, мюон и тау-лептон (из фермионов), а также заряженные калибровочные W^±-бозоны. Остальные фундаментальные частицы Стандартной Модели (все типы нейтрино, бозон Хиггса и переносчики взаимодействий: калибровочный Z⁰-бозон, фотон, глюоны) электрически нейтральны.

Электромагнитное взаимодействие отличается от слабого^[3] и сильного^[4] взаимодействия своим дальнодействующим характером — сила взаимодействия между двумя зарядами спадает только как вторая степень расстояния (см.: закон Кулона). По такому же закону спадает с расстоянием гравитационное взаимодействие. Электромагнитное взаимодействие заряженных частиц намного сильнее гравитационного, и единственная причина, по которой электромагнитное взаимодействие не проявляется с большой силой в космических масштабах — электрическая нейтральность материи, то есть наличие в каждой области Вселенной с высокой степенью точности равных количеств положительных и отрицательных зарядов. В то же время, некоторые космологические модели, такие как плазменная космология Альфвена, предполагают, что на больших масштабах электромагнитное взаимодействие является определяющим в космических процессах.

В классических (неквантовых) рамках электромагнитное взаимодействие описывается классической электродинамикой.

В электромагнитном взаимодействии могут принимать участие только объекты, обладающие электрическим зарядом (в том числе и нейтральные в целом, но состоящие из заряженных частиц). Таковыми являются большинство известных фундаментальных элементарных частиц, в частности, все кварки, все заряженные лептоны (электрон, мюон и тау-лептон), а также заряженные калибровочные бозоны W^±. По современным представлениям электромагнитное взаимодействие осуществляется через электромагнитное поле, кванты которого — фотоны — являются переносчиками электромагнитного взаимодействия^[5].

В отличие от слабого и сильного взаимодействий, электромагнитное взаимодействие так же, как и гравитационное, является дальнодействующим. В частности, сила притяжения неподвижных противоположно заряженных тел спадает на больших расстояниях степенным образом — по закону обратного квадрата (см. закон Кулона). Дальнодействие электромагнитных сил обусловлено отсутствием массы у фотонов как переносчиков этого взаимодействия^[5].

В микромире интенсивность (эффективное сечение) электромагнитного взаимодействия характеризуется величиной постоянной тонкой структуры (в СГСЭ):

α=e2ℏc≈1137{\displaystyle \alpha ={\frac {e^{2}}{\hbar c}}\approx {\frac {1}{137}}},

где e{\displaystyle e} — элементарный электрический заряд, ℏ{\displaystyle \hbar } — постоянная Планка, c{\displaystyle c} — скорость света в вакууме. На уровне ядерных реакций по «силе» электромагнетизм занимает промежуточное положение между сильным и слабым взаимодействиями. Характерные времена распадов, вызванных электромагнитным взаимодействием, — около 10⁻¹² — 10⁻²⁰ с, в то время, как для сильного взаимодействия — порядка 10⁻²³ с, а для слабого — 10³ — 10⁻¹³ с. В качестве примера можно привести сравнение сечения рассеяния на протоне фотона с энергией 1 ГэВ и пиона с соответствующей полной энергией в системе центра масс. Для пиона, взаимодействие которого с протоном обусловлено сильным взаимодействием, сечение в 10 000 раз больше^[5].

Электромагнитное взаимодействие сохраняет пространственную чётность (так называемую Р-чётность), зарядовую чётность (так называемую C-чётность), а также такие квантовые числа, как странность, очарование, красота. Это отличает электромагнетизм от слабого взаимодействия. Одновременно, в отличие от сильного взаимодействия, электромагнитное взаимодействие в процессах с адронами не сохраняет изотопический спин (сопровождаясь испусканием фотона, он может меняться на ±1 или 0) и нарушает G-чётность^[5].

Наличие законов сохранения с учётом свойств фотонов накладывает определённые правила отбора на процессы с участием электромагнитного взаимодействия. Например, поскольку спин фотона равен 1, запрещены излучательные переходы между состояниями с нулевым моментом импульса. Необходимость сохранять зарядовую чётность приводит к тому, что системы с положительной зарядовой чётностью распадаются с испусканием только чётного количества фотонов, а с отрицательной зарядовой чётностью — только нечётного. В частности, парапозитроний распадается на два фотона, а ортопозитроний — на три (см. позитроний)^[5].

За счёт дальнодействия электромагнитное взаимодействие заметно проявляется как на макроскопическом, так и на микроскопическом уровнях. Фактически, подавляющее большинство физических сил в классической механике — силы упругости, силы трения, силы поверхностного натяжения и т. д. — имеют электромагнитную природу^[5].

Электромагнитное взаимодействие определяет большинство физических свойств макроскопических тел и, в частности, изменение этих свойств при переходе из одного агрегатного состояния в другое. Электромагнитное взаимодействие лежит в основе химических превращений. Электрические, магнитные и оптические явления также сводятся к электромагнитному взаимодействию^[5].

На микроскопическом уровне электромагнитное взаимодействие (с учётом квантовых эффектов) определяет структуру электронных оболочек атомов, структуру молекул, а также более крупных молекулярных комплексов и кластеров. В частности, величина элементарного электрического заряда определяет размеры атомов и длину связей в молекулах. Например, радиус Бора равен 4πε0ℏ2mee2{\displaystyle {{4\pi \varepsilon _{0}\hbar ^{2}} \over {m_{e}e^{2}}}}, где ε0{\displaystyle \varepsilon _{0}} — электрическая постоянная, ℏ{\displaystyle \hbar } — постоянная Планка, me{\displaystyle m_{e}} — масса электрона, e{\displaystyle e} — элементарный электрический заряд^[5].

Классическая электродинамика[править | править код]

В большинстве случаев макроскопические электромагнитные процессы с необходимой степенью точности могут быть описаны в рамках классической электродинамики. В этом случае взаимодействующие объекты рассматриваются как совокупность материальных точек, характеризуемых помимо массы также и электрическим зарядом. При этом полагается, что взаимодействие осуществляется посредством электромагнитного поля — отдельным видом материи, пронизывающим всё пространство.

Электростатика[править | править код]

Электростатика рассматривает взаимодействие неподвижных заряженных тел. Основным законом электростатики является закон Кулона, устанавливающий связь между силой притяжения/отталкивания двух заряженных материальных точек, величиной их заряда и расстоянием между ними. В математической форме закон Кулона имеет вид^[6]:

F→12=kq1q2r123r→12,{\displaystyle {\vec {F}}_{12}=k{\frac {q_{1}q_{2}}{r_{12}^{3}}}{\vec {r}}_{12},}

где F→12{\displaystyle {\vec {F}}_{12}} — сила, с которой частица 1 действует на частицу 2, q1,2{\displaystyle q_{1,2}} — величины зарядов частиц 1 и 2 соответственно, r→12{\displaystyle {\vec {r}}_{12}} — радиус-вектор, проведённый из точки расположения частицы 1 в точку расположения частицы 2 (r12{\displaystyle r_{12}} — модуль этого вектора), k{\displaystyle k} — размерный коэффициент, значение которого зависит от используемой системы единиц, в СГС он равен 1, в СИ:

k=14πε0,{\displaystyle k={\frac {1}{4\pi \varepsilon _{0}}},}

где ε0{\displaystyle \varepsilon _{0}} — электрическая постоянная.

В рамках электростатики величина электрического поля, создаваемого точечным зарядом, определяется выражением^[6]:

E→=kqr3r→,{\displaystyle {\vec {E}}=k{\frac {q}{r^{3}}}{\vec {r}},}

где E→{\displaystyle {\vec {E}}} — напряжённость электрического поля в данной точке, q{\displaystyle q} — величина заряда частицы, создающей это поле, r→{\displaystyle {\vec {r}}} — радиус-вектор, проведённый из точки расположения частицы в точку, где определяется поле (r{\displaystyle r} — модуль этого вектора).

Сила, действующая на заряженную частицу, помещённую в электрическое поле, определяется выражением:

F→=qE→,{\displaystyle {\vec {F}}=q{\vec {E}},}

где q{\displaystyle q} — величина электрического заряда частицы, E→{\displaystyle {\vec {E}}} — векторная сумма напряжённостей электрических полей, созданных всеми частицами (за исключением рассматриваемой) в точке, где находится частица^[6].

В случае, если заряд распределён в некотором объёме с плотностью ρ(r→){\displaystyle \rho ({\vec {r}})}, то электростатическое поле, создаваемое им, может быть найдено из электростатической теоремы Гаусса, имеющей в дифференциальной форме в системе СГС следующий вид^[7]:

divE→=4πρ.{\displaystyle \mathrm {div} {\vec {E}}=4\pi \rho .}

В присутствии поляризуемой диэлектрической среды величина электрического поля, создаваемого свободными зарядами, изменяется из-за влияния связанных зарядов, входящих в состав среды. Это изменение во многих случаях может быть охарактеризовано посредством введения вектора поляризации среды P→{\displaystyle {\vec {P}}} и вектора электрической индукции D→.{\displaystyle {\vec {D}}.} При этом выполняется следующее соотношение^[8]:

D→=E→+4πP→.{\displaystyle {\vec {D}}={\vec {E}}+4\pi {\vec {P}}.}

Теорема Гаусса в этом случае записывается в виде^[8]:

divD→=4πρ,{\displaystyle \mathrm {div} {\vec {D}}=4\pi \rho ,}

где под ρ{\displaystyle \rho } понимается плотность только свободных зарядов.

В большинстве случаев рассматриваемые поля значительно слабее внутриатомных полей, поэтому справедлива линейная связь между вектором поляризации и напряжённостью электрического поля в данной точке. Для изотропных сред математически этот факт выражается следующим равенством^[9]:

P→=αE→,{\displaystyle {\vec {P}}=\alpha {\vec {E}},}

где α{\displaystyle \alpha } — коэффициент, характеризующий поляризуемость данного диэлектрика при данных температуре и давлении. Аналогично, справедлива линейная связь между напряжённостью и индукцией^[9]:

D→=εE→,{\displaystyle {\vec {D}}=\varepsilon {\vec {E}},}

где коэффициент ε=1+4πα{\displaystyle \varepsilon =1+4\pi \alpha } носит название диэлектрической проницаемости^[9].

С учётом поляризуемой среды приведённые выше формулы для силы электростатического взаимодействия и напряжённости электростатического поля принимают вид^[10]:

F→12=kq1q2εr123r→12,{\displaystyle {\vec {F}}_{12}=k{\frac {q_{1}q_{2}}{\varepsilon r_{12}^{3}}}{\vec {r}}_{12},}

E→=kqεr3r→.{\displaystyle {\vec {E}}=k{\frac {q}{\varepsilon r^{3}}}{\vec {r}}.}

Магнитостатика[править | править код]

Магнитостатика изучает взаимодействие постоянных по величине и неподвижных в пространстве электрических токов, представляющих по своей сути поток заряженных частиц. В основе магнитостатики лежат закон Био — Савара — Лапласа и закон Ампера. Закон Био — Савара — Лапласа позволяет находить величину магнитного поля, создаваемого малым элементом тока. Если имеется линейный элемент тока длиною dl,{\displaystyle \mathrm {d} l,} сила тока в котором равна I,{\displaystyle {\mathcal {I}},} то он создаёт в окружающем пространстве магнитное поле, индукция которого определяется выражением^[11]:

dB→=k′I[dl→×r→]r3,{\displaystyle {\vec {\mathrm {d} B}}=k^{\prime }{\mathcal {I}}{\frac {\left[{\vec {\mathrm {d} l}}\times {\vec {r}}\right]}{r^{3}}},}

где r→{\displaystyle {\vec {r}}} — радиус-вектор, проведённый от точки расположения элемента тока до точки пространства, в которой определяется магнитное поле (r{\displaystyle r} — модуль этого радиус-вектора), dl→{\displaystyle {\vec {\mathrm {d} l}}} — вектор, длина которого равна dl,{\displaystyle \mathrm {d} l,} а направление совпадает с направлением тока I{\displaystyle {\mathcal {I}}} (считая, что направление тока определяется движением положительно заряженных частиц), k′{\displaystyle k^{\prime }} — константа, зависящая от выбора системы единиц: в системе СИ k′=μ0/4π{\displaystyle k^{\prime }=\mu _{0}/4\pi } (μ0{\displaystyle \mu _{0}} — магнитная постоянная), в системе СГС k′=1/c{\displaystyle k^{\prime }=1/c} (c{\displaystyle c} — скорость света в вакууме). Знаком × в квадратных скобках здесь и ниже обозначается векторное произведение.

Закон Ампера определяет величину силы, с которой магнитное поле в данной точке действует на элемент тока^[12]:

dF→=k′′I[dl→×B→],{\displaystyle {\vec {\mathrm {d} F}}=k^{\prime \prime }{\mathcal {I}}\left[{\vec {\mathrm {d} l}}\times {\vec {B}}\right],}

где B→{\displaystyle {\vec {B}}} — величина магнитного поля в данной точке, равная векторной сумме магнитных полей, создаваемых всеми другими токами, k′′{\displaystyle k^{\prime \prime }} — коэффициент, зависящий от выбранной системы единиц: в системе СИ он равен единице, в системе СГС — k′′=1/c{\displaystyle k^{\prime \prime }=1/c} (c{\displaystyle c} — скорость света в вакууме).

Закон Ампера является прямым следствием выражения для магнитной составляющей силы Лоренца — силы, с которой электромагнитное поле действует на заряженную частицу^[13]:

F→=k′′q[v→×B→],{\displaystyle {\vec {F}}=k^{\prime \prime }q\left[{\vec {v}}\times {\vec {B}}\right],}

где q{\displaystyle q} — заряд частицы, v→{\displaystyle {\vec {v}}} — её скорость.

Закон Био — Савара — Лапласа может быть переписан в виде для плотности тока j→{\displaystyle {\vec {j}}}^[14]:

dB→=k′[j→×r→]r3dV,{\displaystyle {\vec {\mathrm {d} B}}=k^{\prime }{\frac {\left[{\vec {j}}\times {\vec {r}}\right]}{r^{3}}}\mathrm {d} V,}

где dV{\displaystyle \mathrm {d} V} — объём элемента объёмного тока, создающего поле. Из этой формы закона Био — Савара — Лапласа можно вывести теорему о циркуляции магнитной индукции, которая в дифференциальной форме принимает вид^[15]:

rotB→=4πk′j→.{\displaystyle \mathrm {rot} {\vec {B}}=4\pi k^{\prime }{\vec {j}}.}

В присутствии магнитной среды (то есть среды, способной к намагничиванию) её влияние характеризуется векторами намагниченности среды I→{\displaystyle {\vec {I}}} и напряжённости магнитного поля H→.{\displaystyle {\vec {H}}.} При этом справедлива связь:

H→=B→μ0−I→{\displaystyle {\vec {H}}={\frac {\vec {B}}{\mu _{0}}}-{\vec {I}}} — в системе СИ^[16],

H→=B→−4πI→{\displaystyle {\vec {H}}={\vec {B}}-4\pi {\vec {I}}} — в системе СГС^[17].

В линейных изотропных средах справедлива простая связь между величиной намагниченности и приложенным магнитным полем (физически более правильным было бы связывать намагниченность с величиной магнитной индукции, однако по историческим причинам её выражают обычно через напряжённость магнитного поля — ввиду линейной связи между величинами B→,{\displaystyle {\vec {B}},} H→{\displaystyle {\vec {H}}} и I→{\displaystyle {\vec {I}}} принципиального значения это не имеет)^[18][19]:

I→=κH→,{\displaystyle {\vec {I}}=\kappa {\vec {H}},}

где коэффициент κ{\displaystyle \kappa } называется магнитной восприимчивостью среды. Часто оперируют также величиной магнитной проницаемости μ,{\displaystyle \mu ,} определяемой как:

μ=1+κ{\displaystyle \mu =1+\kappa } — в системе СИ^[19],

μ=1+4πκ{\displaystyle \mu =1+4\pi \kappa } — в системе СГС^[18].

В этом случае справедливы соотношения:

B→=μμ0H→{\displaystyle {\vec {B}}=\mu \mu _{0}{\vec {H}}} — в системе СИ^[19],

B→=μH→{\displaystyle {\vec {B}}=\mu {\vec {H}}} — в системе СГС^[18].

Следует отметить, что ферромагнетики являются принципиально нелинейными средами, в частности, они подвержены явлению гистерезиса, и поэтому простые соотношения, указанные выше, для них несправедливы.

Теорема о циркуляции в магнитных средах принимает следующий вид^[17]:

rot

Обсуждение:Электромагнитное поле — Википедия

Материал из Википедии — свободной энциклопедии

«При переходе от одной инерциальной системы отсчета к другой электрическое и магнитное поле в новой системе отсчета — каждое зависит от обоих — электрического и магнитного — в старой, и это еще одна из причин, заставляющая рассматривать электрическое и магнитное поле как проявления единого электромагнитного поля.» — Предложение составлено неправильно. «Электрическое и магнитное поле», по-видимому , подлежащее; а где же сказуемое? Что делает поле-то? Непонятно. 83.172.125.144 15:33, 11 марта 2009 (UTC)

• Зависит. Конкретнее:

E′=f1(E,B){\displaystyle \mathbf {E} ‘=f_{1}(\mathbf {E} ,\mathbf {B} )}

B′=f2(E,B){\displaystyle \mathbf {B} ‘=f_{2}(\mathbf {E} ,\mathbf {B} )}

Если сформулируете это менее коряво — ничего не имею против. Смысл в том, что электрическое поле в новой системе отсчета выражается не только через электрическое в старой, но через оба — электрическое и магнитное, какими они являются в старой. Так же — магнитное. В этом одно из проявлений их единства (они смешиваются при переходе к новой системе отсчета). Другое проявление единства электромагнитного поля — взаимосвязь E{\displaystyle \mathbf {E} } и B{\displaystyle \mathbf {B} } в уравнениях Максвелла. Сергей Сашов 19:48, 11 марта 2009 (UTC)

Это предложение не является корявым. Оно является неграмотным, т.е. не имеет права на существование. Это как бы Вы написали =kF∫S∂B→∂tdS→={\displaystyle =k_{F}\int \limits _{S}\!{\partial {\vec {B}} \over \partial t}\,d{\vec {S}}=}, а потом объясняли бы смысл этого. Набор букв, не подчиняющийся правилам данного языка, не является утверждением и не несет смысла. 213.135.34.101 09:03, 10 марта 2010 (UTC)

Можно было бы сделать одноимённую категорию, включить туда его компонтенты (категория «Составляющие электромагнитного поля»): Магнитное поле, Электрическое поле. Fractaler 15:29, 16 октября 2010 (UTC)