Методическая разработка урока » Электрический заряд.Закон кулона «
ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ ГОРОДА МОСКВЫ
Государственное бюджетное профессиональное образовательное учреждение города Москвы
«МОСКОВСКИЙ ТЕХНОЛОГИЧЕСКИЙ КОЛЛЕДЖ»
(ГБПОУ МТК)
Методическая разработка урока
по теме «ЭЛЕКТРИЗАЦИЯ ТЕЛ. ЗАКОН КУЛОНА»
Специальность15.02.06 «Монтаж и техническая эксплуатация холодильно-компрессорных машин и установок»
Автор: Мокрова Ирина
Иннокентьевна
Москва
2016
Тема урока : Электрический заряд. Закон Кулона
Цель урока: познакомить учащихся со значением, структурой и особенностями электродинамики как раздела физической науки, повторить основные понятия электростатики, углубляя и развивая изучаемые ранее; рассмотреть роль статического электричества в производстве и быту; формировать умение объяснять электрические явления на основе знаний об электрическом заряде и законе сохранения заряда, познакомить с историей открытия закона Кулона, сформулировать основной закон электростатики, формировать умение применять закон при решении качественных, вычислительных задач.
Ход урока
I.Актуализация знаний
Беседа по вопросам:
Из каких частиц состоит атом?
Чему равен заряд нейтрального атома?
Какой заряд приобретет атом, лишенный одного или нескольких электронов?
Как называется атом, лишенный нескольких электронов?
Какой заряд приобретет атом, если будет иметь избыточное количество электронов?
Как называется атом, имеющий недостаток электронов?
Как взаимодействуют два одноименно, разноименно заряженных тела?
Назовите единицы измерения заряда
I I. Изучение нового материала.
1. Знакомство с логической структурой раздела «Электродинамика»

2.Формирование основных понятий электростатики.
Электростатика — раздел теории электричества, изучающий взаимодействие неподвижных электрических зарядов.
Электрический заряд — физическая величина, определяющая
силу электромагнитного взаимодействия, которая в 1039 раз превышает силу гравитационного притяжения.
Виды зарядов. Существуют два вида электрических зарядов -положительный и отрицательный. Элементарный заряд
минимальным отрицательным зарядом — электрон (- е)
Взаимодействие зарядов. Заряды одинаковых знаков отталкиваются, а с противоположными знаками — притягиваются друг к другу.
Точечный заряд — заряд, размерами которого можно пренебречь по сравнению с расстоянием его взаимодействия на другие тела.
Дискретность заряда. Суммарный заряд равен сумме зарядов, входящих в состав атома, Q = N*e.
Способы электризации: трение, соприкосновение, световое облучение.
Закон сохранения зарядов. Алгебраическая сумма зарядов в электрически замкнутой системе состояния постоянной.
q1+q2+q3+…= const
Экспериментальное обоснование закона сохранения заряда:
Фронтальный эксперимент:
положите на полоску бумаги полоску из полиэтилена. Погладьте их тыльной стороной ладони. Попробуйте развести их в разные стороны, а затем медленно сближайте. Что вы наблюдаете?
подвесьте небольшую алюминиевую гильзу на шелковой нити к штативу и прикоснитесь наэлектризованной палочкой из плексигласа, потерев ее о бумагу. Как объяснить дальнейшее поведение гильзы?
у каждого на парте есть небольшое количество мелко нарезанной бумаги . Потрите пластмассовую авторучку газетным листом бумаги и поднесите к мелким полоскам бумаги Что вы наблюдаете?
потрите газетой надутый воздухом детский воздушный шар , поднесите его в стене класса и отпустите. Шар останется у стены и будет находится в таком положении долгое время.
Студенты ( по одному от каждой парты) с разноцветными шарами проходят по кабинету и украшают его стены, прикрепляя шары вышеизложенным способом.
3. Исторические сведения об обнаружении электрических свойств тел.(Заслушиваются
сообщения учащихся)
Способность тел после натирания притягивать к себе мелкие предметы была известна в VI веке до нашей эры. Греческий философ Фалес Милецкий ( из г. Милета) обнаружил, что янтарь, потертый о мех , приобретает свойство притягиват пушинки, соломинки,. Легенда гласит, что дочь Фалеса пряла шерсть янтарным веретеном. Уронив его однажды в воду, она стала обтирать веретено шерстяным хитоном и заметила , что к веретену пристало несколько шерстинок , и , чем сильнее она вытирала веретено, тем больше прилипало шерстинок. Девушка рассказала об этом явлении отцу, и он не замедлил провести эксперимент с различными изделиями янтаря и обнаружил, что все они после натирания вели себя одинаково.
Первые научные представления об электричестве были изложены придворным врачом английской королевы Елизаветы Уильямом Гильбертом(1544 -1603), который доказал, что способностью янтаря обладают стекло, сургуч, сера и притягивают не только соломинки, но и металлы, дерево, листья , камешки, комочки земли и воду. Именно Гильберту принадлежит введение в науку термина « электричество» , что значит «янтарь» от греческого слова «электрон».
Губернатор немецкого города Магдебурга Отто Герике проводил любопытные опыты по электризации тел . Он изготовил из серы большой шар. Для этого он наполнил расплавленной серой стеклянный полый шар и разбил стеклянную оболочку шара после затвердевания серы. Натирая рукой шар из серы, он наблюдал притяжение к нему легких предметов, а также заметил, что пушинки *: кусочки бумаги, коснувшись шара, отскакивали от него. Ему также удалось заставить пушинку, коснувшуюся шара, плавать над наэлектризованным телом.
Американский физик и политический деятель Бенжамин Франклин в 1778 г изменил понятие «стеклянное» электричество на положительное , а «смоляное» назвал отрицательным. Так появились положительно и отрицательно заряженные тела.
Воспроизведение опытов Гильберта с помощью простых приспособлений.
Эксперимент 1.Положим на круглую опору ( можно использовать небольшую полиэтиленовую бутылку, наполненную водой или электрическую лампу накаливания на опоре) деревянную линейку. Потрем кусочком меха эбонитовую палочку и поднесем ее к деревянной линейке. Наблюдаем, что линейка пришла в движение, притягиваясь к эбонитовой палочке.
Эксперимент 3. Установим на опоре пластмассовую линейку и повторим предыдущий опыт. Наблюдаем процесс притяжения линейки к эбонитовой палочке .
Эксперимент 4.Возьмем полиэтиленовую бутылку из — под лимонада, сделаем в ней небольшое отверстие и нальем слегка подкрашенную жидкость . Наэлектризуем
пластмассовую линейку и откроем отверстие, сделанное в нижней части бутылки и предварительно закрытое кусочком пластилина. Поднесем линейку к струйке воды. Объясните , почему струя воды притягивается к линейке?
Практическое значение электризации тел (Сообщение учащихся в форме доклада или презентации).
На самых различных производствах с успехом применяют статическое электричество. Например, при электроокраске деталей движущиеся на контейнере окрашиваемые детали , например, корпус автомобиля, заряжают положительно, а частицам краски придают отрицательный заряд , и они устремляются к положительно заряженной детали. Слой краски получается тонкий, равномерный и плотный. Расход краски снижается.
Искусственный мех, бархат, плюш, замша изготавливаются методом электроворсирования.
Эксперимент по демонстрации изготовления ворса
Установим на штативе пластины плоского конденсатора в горизонтальном положении. Обкладки конденсатора соединим с полюсами электрофорной машины, а на нижнюю пластину конденсатора насыпаем мелко нарезанные листочки станиоля ( можно использовать новогоднюю мишуру). Заряжаем конденсатор с помощью электрофорной машины и одновременно протягиваем между его пластинами полоску бумаги, смазанную клеем. Листочки станиоля при своем движении к верхней пластине встречают бумагу и прилипают к ней.
Для очистки воздуха используются электрофильтры. При изготовлении тканей в текстильной промышленности волокна заряжаются и отталкиваются друг от друга, прилипают к металлическим частям машины, путаются, вследствие этого учащаются обрывы.
В типографиях при работе ротационных машин бумага электризуется, что приводит к ее свертыванию и браку при печатании. При перевозке горючих жидкостей в автоцистернах жидкости взбалтываются и электризуются, чтобы избежать возникновения искр и пожара, к корпусу автомашины прикрепляют металлическую цепь , которая при движении волочится по земле и отводит заряды в землю.
6.Способы борьбы со статическим электричеством
В домашних условиях устранит заряды статического электричества довольно легко , повышая относительную влажность воздуха квартиры до 60 -70%. Электризация устраняется, если к воде добавить гидрофильные вещества, напримв{ хлорид кальции, а также если протирать электризующиеся поверхности глицерином. Химическая промышленность сейчас выпускает препарат «Антистатик», который снимает электрический заряд с синтетической одежды.
На производстве, в местах скопления электрических зарядов устанавливаются специальные металлические щетки , которые заземляются. Заряды, возникающие н; деталях и узлах машин и станков , через эти щетки отводятся в землю.
Можно бороться с электрическим зарядами с помощью специальных приборов -ионизаторов.
II. Изучение нового материала.
1. Знакомство с устройством и принципом действия крутильных весов.
2. Формулировка закона Кулона. Следует обратить внимание на точечность зарядов, для которых справедлив закон Кулона, на аналогию с законом всемирного тяготения.
3. Основные особенности кулоновских сил:
а) направлены вдоль прямой , соединяющей заряженные тела;
б) равны по модулю, противоположны по направлению, приложены к разным телам.
4. Формулирование понятия о единице заряда (1 кулон), которая устанавливается с помощью единицы силы тока (1 ампер).
1Кл = 1А*с
III. Углубление знаний, умений.
Решение задач
1. С какой силой взаимодействуют два заряда по 10 нКл, находящихся на расстоянии 3 см друг от друга?

2. На каком расстоянии друг от друга заряды 1мкКл и 10 нКл взаимодействуют с силой 9мн?

3. Два точечных одинаковых заряда взаимодействуют друг с другом с силой 0,4 мн, находясь на расстоянии 5 см друг от друга. Чему равен каждый заряд?

4. Два одинаковых шарика, расположенных на расстоянии 10 см друг от друга, имеют одинаковые отрицательные заряды и взаимодействуют с силой 0,23мн. Найти число избыточных электронов на каждом шарике.

5. Два одинаковых металлических шарика, заряженные одинаковыми зарядами q и 4q, находятся на расстоянии г друг от друга. Шарики привели в соприкосновение. На какое расстояние надо их развести, чтобы сила взаимодействия осталась прежней?

6.Самостоятельная работа
ЗАПОЛНИТЕ ПРОПУСКИ В ТЕКСТЕ
Атом состоит из положительно заряженного …….. вокруг которого движутся..
Ядро состоит из …….. и …………
Протоны имеют ……… заряд, а электроны …………
У электрически нейтрального атома заряд ядра …… ..заряду электронов.
Атом, потерявший один или несколько электронов, называется …….. ионом.
Атом, присоединивший один или несколько электронов, называется .. ..ионом
п
 ри электризации происходит переход,,,,,,,,,,,, с одного вещества на другое.
ри электризации происходит переход,,,,,,,,,,,, с одного вещества на другое.Минимальным положительным зарядом обладает…………., минимальным положительным зарядом обладает,,,,,,,,,,,,,.
РЕШИТЕ ЗАДАЧИ
1 вариант
1.С какой силой взаимодействуют два заряда по 12 нКл каждый , находящиеся на расстоянии 3 см друг от друга.
2.На каком расстоянии друг от друга заряды 1 мк КЛ и 6 нКл взаимодействуют с силой 12 мН.
Вариант
1.С какой силой взаимодействуют два заряда по 10 нКл , находящиеся на
расстоянии 2 см друг от друга.
2.Два шарика, расположенные на расстоянии 10 см друг от друга , имеют одинаковые положительные заряды и взаимодействуют с силой 3 мН. Определите заряды шариков.
Литература
1.Физика для профессий и специальностей технического профиля. Дмитриева В.Ф. М.Образовательно-издательский центр «Академия», 2012. 448 с.
Физика: Учебник для студ. образоват. учреждений сред. проф. образования – 14-е изд., стер. Дмитриева В.Ф М.: Издательский центр «Академия», 2012. 464 с.
Буров В.А., Иванов А.И., Свиридов В.И. Фронтальные экспериментальные задания по физике. 9-й класс. – М.: Просвещение, 1986.
Горев Л.А. Занимательные опыты по физике. – М.: Просвещение, 1985.
Электрический заряд. Закон сохранения электрического заряда, Закон Кулона.
Электрический заряд. Закон сохранения электрического заряда, Закон Кулона.
Электрический заряд это количественная мера свойства тел притягиваться или отталкиваться друг от друга с электрической силой. Свойства электрических зарядов:
1. В природе существуют только два типа электрических зарядов: положительные и отрицательные.
2. Любой электрический заряд квантован, то есть кратен целому числу минимальных порций заряда. Носителем такой минимальной порции отрицательного заряда является электрон, положительного — протон. Численно эти минимальные заряды одинаковы и составляют е = 1.6∙10–19 Кл. Равенство элементарных зарядов разного знака объясняет электронейтральность атомов и молекул.
3. Закон сохранения электрических зарядов: полный электрических заряд изолированной системы не меняется.
4. Опыт показывает, что электрический заряд релятивистски инвариантен, то есть его величина не зависит от того, движется он или находится в покое.
Важнейшим свойством электрических зарядов является их силовое взаимодействие друг с другом. Это взаимодействие точечных зарядов экспериментально было исследовано Ш. Кулоном.
Закон Кулона
Два точечных неподвижных электрических заряда взаимодействуют с силой, прямо пропорциональной произведению величины этих зарядов и обратно пропорциональной квадрату расстояния между ними. Силы электрического взаимодействия направлены по линии, соединяющей заряды. Одноимённые заряды отталкиваются , разноимённые — притягиваются.
Коэффициент пропорциональности к0 в этой системе равен к0 = 9 ∙ 109
В рационализованной системе СИ коэффициент пропорциональности к0 представляют в виде:
Теорема Гаусса для электрического поля в вакууме.
Потоком вектора напряжённости электрического поля через выделенную поверхность называется скалярное произведение этих двух векторов:
Таким образом, поток вектора напряжённости через поверхность dS численно равен числу силовых линий, пронизывающих эту поверхность (!).
Этот вывод справедлив и для потока электрического поля через замкнутую поверхность: этот поток будет равен алгебраической сумме силовых линий втекающих (–) и вытекающих (+) из замкнутой поверхности.
Силовая линия — в общем случае кривая, касательная к которой в любой точке совпадает по направлению с направлением вектора напряжённости в этой точке.
Эта теорема представляет собой только следствие закона Кулона и принципа суперпозиции электрических полей. Вот её формулировка:
Поток вектора напряжённости электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме электрических зарядов, заключённых внутри этой поверхности, делённой на электрическую постоянную e0.
Работа сил электрического поля по переносу заряда. Разность потенциалов. Теорема о циркуляции электростатического поля. Электрический потенциал. Связь между напряжённостью электростатического поля и потенциалом.
Существуют две характеристики электрического поля. В любой точке пространства поле можно задать либо вектором напряжённости — это «силовая» характеристика поля, либо потенциалом — это его энергетическая характеристика.
Потенциал — энергетическая характеристика поля, связанная и с энергией заряда в электростатическом поле и с работой, совершаемой электрической силой при перемещении заряда.
Вспомним, что силы, работа которых не зависит от вида траектории и определяется только положением её начальной и конечной точек, называются консервативными.
Мы пришли к выводу, что кулоновская сила консервативна. Впрочем, ничего неожиданного в этом выводе нет: ведь сила взаимодействия двух точечных зарядов может быть отнесена к классу центральных сил, а все центральные силы, как было установлено в механике, консервативны.
Итак, вычислим работу кулоновской силы при перемещении заряда q из точки 1 в положение 2 (по любой траектории):
Энергия единичного (q = 1) точечного заряда уже не будет связана с величиной этого пробного заряда q и может быть принята в качестве энергетической характеристики данной точки электростатического поля:
.
Эта энергетическая характеристика поля получила название потенциал — j.
Потенциал произвольной точки электростатического поля равен энергии единичного положительного заряда, помещённого в эту точку.
Потенциал некоторой точки электростатического поля равен работе, совершаемой электрической силой при эвакуации единичного положительного заряда из этой точки в бесконечность:
.
Потенциал поля, созданного системой точечных зарядов, равен алгебраической сумме потенциалов, создаваемых в рассматриваемой точке каждым из зарядов в отдельности: . — «принцип суперпозиции для потенциала»
Разность потенциалов двух точек поля равна работе, совершаемой электрической силой при перемещении единичного заряда из первой точки во вторую:
Потенциал и напряжённость — две локальные характеристики электростатического поля. То есть, это две характеристики — энергетическая и силовая — одной и той же точки поля.
Разумно предположить, что между ними должна существовать однозначная связь.
напряжённость электростатического поля равна градиенту потенциала с обратным знаком. . Здесь векторный оператор «градиент»
grad = .
Так как это сферически симметричное поле, его потенциал будет меняться только как функция r. Поэтому связь напряжённости и потенциала можно упростить и записать так: .
Теорема о циркуляции электростатического поля. Интеграл по замкнутому контуру = называется циркуляцией вектора напряжённости электростатического поля по контуру L. По своей сути циркуляция вектора напряжённости — это работа электростатического поля, совершаемая при перемещении по замкнутому контуру единичного положительного заряда.
Так как речь идёт о работе консервативной силы, то на замкнутой траектории она равна нулю: .
Теорема о циркуляции в электростатике: циркуляция вектора напряжённости электростатического поля по любому замкнутому контуру равна нулю.
Правила Кирхгофа.
Рассмотренные нами законы постоянного тока позволяют рассчитать токи в сложных разветвлённых электрических цепях. Эти расчёты упрощаются, если пользоваться правилами Кирхгофа.
Правил Кирхгофа два: правило токов и правило напряжений.
Правило токов относится к узлам цепи, то есть, к таким точкам схемы, где сходятся не менее трёх проводников (рис. 7.4.). Правило токов гласит: алгебраическая сумма токов в узле равняется нулю:
.
При составлении соответствующего уравнения, токи, втекающие в узел, берутся со знаком плюс, а покидающие его — со знаком минус. Это первое правило Кирхгофа является следствием уравнения непрерывности (см. (6.7)) или закона сохранения электрического заряда.
Правило напряжений относится к любому замкнутому контуру разветвлённой цепи.
Правило напряжений формулируется так: в любом замкнутом контуре алгебраическая сумма падений напряжения равна алгебраической сумме э.д.с., встречающихся в этом контуре:
.
При составлении уравнения второго правила Кирхгофа задаются направлением обхода.
Токи, совпадающие с направлением обхода, берутся со знаком плюс, токи противоположного направления — со знаком минус Э.д.с. источника берётся со знаком плюс, если он создаёт ток, совпадающий с направлением обхода. В противном случае э.д.с. отрицательна.
Правило Ленца
Индукционный ток всегда имеет такое направление, что его собственное магнитное поле препятствует тому изменению исходного магнитного потока, которое стало причиной возникновения индукционного тока.
Так мы установили искомую связь э.д.с. индукции и магнитного поля:
.
Электродвижущая сила индукции равна скорости изменения магнитного потока, пронизывающего замкнутый контур (закон Фарадея). Или при любом изменении магнитного потока, пронизывающего замкнутый контур, в последнем возникает э.д.с. индукции, численно равная скорости изменения магнитного потока (закон Фарадея).
Квазистационарные процессы в электрических цепях. Экспериментальное изучение процессов разрядки конденсатора в RC-цепи. Определение времени релаксации и оценка ёмкости конденсатора(по материалам лабораторной работы номер 1 стр. 3 всё по лабе)
Квазистационарные процессы в электрических цепях
В цепях постоянного тока распределение электрических зарядов на проводниках и токов на участках цепи стационарно, то есть неизменно во времени. Электромагнитное поле в таких цепях состоит из электростатического поля неподвижных зарядов и магнитного поля постоянных токов. Эти поля существуют независимо друг от друга. Если на каком-то участке цепи происходят изменения силы тока или напряжения, то другие участки цепи могут «почувствовать» эти изменения только через некоторое время, которое по порядку величины равно времени τ распространения электромагнитного возмущения от одной точки цепи к другой. Так как электромагнитные возмущения распространяются с конечной скоростью, равной скорости света c , то где l – расстояние между наиболее удаленными точками цепи. Если это время τ много меньше длительности процессов, происходящих в цепи, то можно считать, что в каждый момент времени сила тока одинакова во всех последовательно соединенных участках цепи. Процессы такого рода в электрических цепях называются квазистационарными. Квазистационарные процессы можно исследовать с помощью законов постоянного тока, если применять эти законы к мгновенным значениям сил токов и напряжений на участках цепи. Из-за огромного значения скорости света время установления электрического равновесия в цепи оказывается весьма малым.
Поэтому к квазистационарным можно отнести многие достаточно быстрые в обычном смысле процессы. Например, быстрые колебания в радиотехнических цепях с частотами порядка миллиона колебаний в секунду и даже выше очень часто еще можно рассматривать как квазистационарные. Простыми примерами квазистационарных процессов могут служить процессы, происходящие в RC- и RL-цепях при подключении и отключении источника постоянного тока.
Емкость конденсатора
Электрическая емкость конденсатора — физическая величина, измеряемая отношением:
— заряда одной из обкладок конденсатора; к
— напряжению между обкладками.
Единицей электрической емкости конденсатора является фарад.
Теоретически, в любой идеальный конденсатор можно закачать заряд бесконечного размера. Просто наш шарик сильней растянется и стенки создадут большее давление, бесконечно большое давление.
А что же тогда насчет Фарад, что пишут на боку конденсатора в качестве показателя емкости? А это всего лишь зависимость напряжения от заряда (q = CU). У конденсатора малой емкости рост напряжения от заряда будет выше.
Представь два стакана с бесконечно высокими стенками. Один узкий, как пробирка, другой широкий, как тазик. Уровень воды в них — это напряжение. Площадь дна — емкость. И в тот и в другой можно набузолить один и тот же литр воды — равный заряд. Но в пробирке уровень подскочит на несколько метров, А в тазике будет плескаться у самого дна. Также и в конденсаторах с малой и большой емкостью. Залить то можно сколько угодно, но напряжение будет разным.
Плюс в реале у конденсаторов есть пробивное напряжение, после которого он перестает быть конденсатором, а превращается в годный проводник 🙂
Время релаксации — время, за которое первоначальное отклонение того или иного термодинамического параметра от равновесного значения уменьшается в е (2.718) раз.
RC -цепь — это цепь состоящая из сопротивления R и конденсатора С. Постоянная времени этой цепи определяется как t = RC.
Электрический колебательный контур. Экспериментальное изучение собственных затухающих колебаний в колебательном контуре. измерение логарифмического декремента затухания и добротности контура(лаба 4 стр. 17 чисто всё по лабе)
Логарифмический декремент затухания — безразмерная характеристика затухающих колебаний, измеряемая натуральным логарифмом отношения двух последовательных максимальных отклонений колеблющейся величины в одну и ту же сторону.
Вопрос 29
Теорема Гаусса для магнитной индукции
Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:
Это эквивалентно тому, что в природе не существует «магнитных зарядов» (монополей), которые создавали бы магнитное поле, как электрические заряды создают электрическое поле. Иными словами, теорема Гаусса для магнитной индукции показывает, что магнитное поле является вихревым.
Применение теоремы Гаусса
Для вычисления электромагнитных полей используются следующие величины:
Объёмная плотность заряда (см. выше).
Поверхностная плотность заряда
где dS — бесконечно малый участок поверхности.
Линейная плотность заряда
где dl — длина бесконечно малого отрезка.
Теорема о циркуляции магнитного поля — одна из фундаментальных теорем классической электродинамики, сформулированная Андре Мари Ампером в 1826 году. В 1861 году Джеймс Максвелл снова вывел эту теорему, опираясь на аналогии с гидродинамикой. В математической форме входит в число уравнений Максвелла. Теорема гласит:
Циркуляция магнитного поля постоянных токов по всякому замкнутому контуру пропорциональна сумме сил токов, пронизывающих контур циркуляции.
Математическая формулировка
В математической формулировке теорема имеет следующий вид:
Здесь B — вектор магнитной индукции, j — плотность тока; интегрирование слева производится по произвольному замкнутому контуру, справа — по произвольной поверхности, натянутой на этот контур. Данная форма носит название интегральной, поскольку в явном виде содержит интегрирование. Теорема может быть также представлена в дифференциальной форме:
Эквивалентность интегральной и дифференциальной форм следует из теоремы Стокса.
Приведённая выше форма справедлива для вакуума. В веществе часто удобно из полного тока выделить ток намагничения, выразив его через величину намагниченности I и введя вектор напряжённости магнитного поля
Тогда теорема о циркуляции запишется в форме
Практическое значение
Теорема о циркуляции играет в магнитостатике приблизительно ту же роль, что и теорема Гаусса в электростатике. В частности, при наличии определённой симметрии задачи, она позволяет просто находить величину магнитного поля во всём пространстве по заданным токам. Например, для вычисления магнитного поля от бесконечного прямолинейного проводника с током по закону Био — Савара — Лапласа потребуется вычислить неочевидный интеграл, в то время как теорема о циркуляции (с учётом осевой симметрии задачи) позволяет дать мгновенный ответ:
Применение теоремы о циркуляции к тороидальной катушке.
Предполагается, что катушка плотно, то есть виток к витку, намотана на немагнитный тороидальный сердечник. В такой катушке линии магнитной индукции замыкаются внутри катушки и представляют собой концентрические окружности. Они направлены так, что глядя вдоль них, мы увидели бы ток в витках, циркулирующим по часовой стрелке. Одна из линий индукции некоторого радиуса r1 ≤ r < r2 изображена на рис. 4.17.3. Применим теорему о циркуляции к контуру L в виде окружности, совпадающей с изображенной на рис. 4.17.3 линией индукции магнитного поля. Из соображений симметрии ясно, что модуль вектора одинаков вдоль всей этой линии. По теореме о циркуляции можно записать:B ∙ 2πr = μ0IN,
где N – полное число витков, а I – ток, текущий по виткам катушки. Следовательно,
Таким образом, модуль вектора магнитной индукции в тороидальной катушке зависит от радиуса r. Если сердечник катушки тонкий, то есть r2 – r1 << r, то магнитное поле внутри катушки практически однородно. Величина n = N / 2πr представляет собой число витков на единицу длины катушки. В этом случае B = μ0In.
В это выражение не входит радиус тора, поэтому оно справедливо и в предельном случае r → ∞. Но в пределе каждую часть тороидальной катушки можно рассматривать как длинную прямолинейную катушку. Такие катушки называют соленоидами. Вдали от торцов соленоида модуль магнитной индукции выражается тем же соотношением, что и в случае тороидальной катушки. На рис. 4.17.4 изображено магнитное поле катушки конечной длины. Следует обратить внимание на то, что в центральной части катушки магнитное поле практически однородно и значительно сильнее, чем вне катушки. На это указывает густота линий магнитной индукции. В предельном случае бесконечно длинного соленоида однородное магнитное поле целиком сосредоточено внутри соленоида.
Применение теоремы о циркуляции к расчету магнитного поля бесконечно длинного соленоида.
Вектор магнитной индукции имеет отличную от нуля проекцию на направление обхода контура abcd только на стороне ab. Следовательно, циркуляция вектора по контуру равна Bl, где l – длина стороны ab. Число витков соленоида, пронизывающих контур abcd, равно n · l, где n – число витков на единицу длины соленоида, а полный ток, пронизывающий контур, равен Inl. Согласно теореме о циркуляции,Bl = μ0Inl,
откуда B = μ0In.
Это выражение совпадает с полученной ранее формулой для магнитного поля тонкой тороидальной катушки
Вопрос 30
Силовые линии электрического поля.
Силовые линии электрического поля — воображаемые линии, касательные к которым в каждой точке совпадают с направлением вектора напряженности электрического поля в этой точке.
Силовые линии электрического поля начинаются на положительных и заканчиваются на отрицательных зарядах.
Силовые линии электрического поля не пересекаются.
Теорема Гаусса для напряжённости электрического поля в вакууме (электростатическая теорема Гаусса)
Общая формулировка: Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.
где
— поток вектора напряжённости электрического поля через замкнутую поверхность S.
Q — полный заряд, содержащийся в объёме, который ограничивает поверхность S.
— электрическая постоянная.
Данное выражение представляет собой теорему Гаусса в интегральной форме.
В дифференциальной форме теорема Гаусса выражается следующим образом:
Здесь ρ — объёмная плотность заряда (в случае присутствия среды — суммарная плотность свободных и связанных зарядов), а — оператор набла.
Для теоремы Гаусса справедлив принцип суперпозиции, то есть поток вектора напряжённости через поверхность не зависит от распределения заряда внутри поверхности.
Физической основой теоремы Гаусса является закон Кулона или, иначе, теорема Гаусса является интегральной формулировкой закона Кулона.
Теорема Гаусса для электрической индукции (электрическое смещение)
Для поля в веществе электростатическая теорема Гаусса может быть записана иначе — через поток вектора электрического смещения (электрической индукции). При этом формулировка теоремы выглядит следующим образом: поток вектора электрического смещения через замкнутую поверхность пропорционален заключённому внутри этой поверхности свободному электрическому заряду:
Если же рассматривать теорему для напряжённости поля в веществе, то в качестве заряда необходимо брать сумму свободного заряда, находящегося внутри поверхности и поляризационного (индуцированного, связанного) заряда диэлектрика:
QΣ = Q + Qb,
где
— вектор поляризации диэлектрика.
1. Напряженность электростатического поля, создаваемого равномерно заряженной сферической поверхностью.
Пусть сферическая поверхность радиуса R (рис. 13.7) несет на себе равномерно распределенный заряд q, т.е. поверхностная плотность заряда в любой точке сферы будет одинакова.
Заключим нашу сферическую поверхность в симметричную поверхность S с радиусом r>R. Поток вектора напряженности через поверхность S будет равен
По теореме Гаусса
Следовательно
Сравнивая это соотношение с формулой для напряженности поля точечного заряда, можно прийти к выводу, что напряженность поля вне заряженной сферы такова, как если бы весь заряд сферы был сосредоточен в ее центре.
Для точек, находящихся на поверхности заряженной сферы радиуса R, по аналогии с вышеприведенным уравнением, можно написать
Проведем через точку В, находящуюся внутри заряженной сферической поверхности, сферу S радиусом г<R. Внутри сферы S зарядов нет, т.к. все они расположены на внешней сферической поверхности, т.е. Следовательно, по теореме Гаусса, и напряженность электростатического поля внутри полой равномерно заряженной сферы будет равна нулю. Зависимость напряженности поля заряженной сферы от расстояния r приведена на рис
2. Электростатическое поле шара.
Пусть имеем шар радиуса R, равномерно заряженный с объемной плотностью .
В любой точке А, лежащей вне шара на расстоянии r от его центра (r>R), его поле аналогично полю точечного заряда , расположенного в центре шара. Тогда вне шара (13.10)
а на его поверхности (r=R) (13.11)
В точке В, лежащей внутри шара на расстояний r от его центра (r>R), поле определяется лишь зарядом , заключенным внутри сферы радиусом r. Поток вектора напряженности через эту сферу равен
с другой стороны, в соответствии с теоремой Гаусса
Из сопоставления последних выражений следует (13.12)
где — диэлектрическая проницаемость внутри шара. Зависимость напряженности поля, создаваемого заряженной сферой, от расстояния до центра шара приведена на (рис.13.10)
Вопрос 31.
Электрическое поле в диэлектриках
Тело, обладающее электрическим зарядом, создает в окружающем пространстве электрическое поле, которое может быть обнаружено по его воздействию на другие заряженные тела.
Электрическое поле является формой материи. Сила, действующая в электрическом поле на заряженное тело, пропорциональна величине его заряда и зависит от интенсивности самого поля.
Отношение этой силы к величине заряда называется напряженностью поля (Е). В практической системе единиц напряженность поля точечного заряда
где εа — коэффициент, характеризующий среду, в которой происходит взаимодействие.
Коэффициент εа называют абсолютной диэлектрической проницаемостью; для вакуума в СИ εа = 8,86-10-12 ф/м; эту величину обозначают через ε0 и называют электрической постоянной. Отношение εа, данного вещества к ε0 называется относительной диэлектрической проницаемостью ε’.
Напряженность электрического поля в диэлектрике, при которой происходит пробой, называют электрической прочностью диэлектрика (Епр).
Поляризация диэлектрика — смещение положительных и отрицательных связанных зарядов в макрообъеме диэлектрика в противоположные стороны, что приводит к появлению поверхностных связанных зарядов.
Диэлектрик, помещенный во внешнее электрическое поле, поляризуется под действием этого поля. Поляризацией диэлектрика называется процесс приобретения им отличного от нуля макроскопического дипольного момента.
Степень поляризации диэлектрика характеризуется векторной величиной, которая называется поляризованостью или вектором поляризации (P). Поляризованность определяется как электрический момент единицы объема диэлектрика
где N — число молекул в объеме . Поляризованность P часто называют поляризацией, понимая под этим количественную меру этого процесса.
В диэлектриках различают следующие типы поляризации: электронную, ориентационную и решеточную (для ионных кристаллов).
Вектор электрического смещения
Если электрическое поле имеет место в диэлектрике, то наблюдается поляризация вещества и появляются связанные электрические заряды.
Учитывают поляризацию с помощью вектора поляризации , который для анизотропных и однородных сред выражается через напряженность поля следующим образом: , где c – диэлектрическая восприимчивость вещества (диэлектрика). Вектор поляризации равен также поверхностной плотности связанных зарядов, возникающих в диэлектрике под воздействием внешнего электрического поля (Р = sсвяз ).
Кроме этого, при анализе электростатических полей используют вектор электрического смещения:
Единицей электрического смещения является кулон на метр квадратный (Кл/м2).
Величина e = e0 + c является основной характеристикой диэлектрика и называется абсолютной диэлектрической проницаемостью. Отношение er = e/e0 называют относительной диэлектрической проницаемостью.
Электрическая поляризуемость определяется как коэффициент пропорциональности между напряжённостью приложенного электрического поля и получающимся наведённым электрическим дипольным моментом частицы в формуле для системы физических единиц СИ:
где — электрическая постоянная.
Если моделировать начальную конфигурацию распределения зарядов в виде нейтральной хорошо проводящей тонкостенной пустотелой сферы, либо в виде нейтрального в целом шара, то можно показать, что равно кубу радиуса этой сферы (шара). Отсюда следует, что размерность есть м3, совпадая с размерностью объёма.
Диэлектрическая проницаемость, величина, характеризующая диэлектрические свойства среды — её реакцию на электрическое поле. В соотношении D = eЕ, где Е — напряжённость электрического поля, D — электрическая индукция в среде, Д. п. — коэффициент пропорциональности e. В большинстве диэлектриков при не очень сильных полях Д. п. не зависит от поля Е. В сильных электрических полях (сравнимых с внутриатомными полями), а в некоторых диэлектриках (например, сегнетоэлектриках) в обычных полях зависимость D от Е — нелинейная.
Величина Д. п. существенно зависит от типа вещества и от внешних условий (температуры, давления и т.п.). В переменных электрических полях Д. п. зависит от частоты поля Е . О методах измерения Д. п. см. Диэлектрические измерения.
Электрический заряд. Закон сохранения электрического заряда, Закон Кулона.
Электрический заряд это количественная мера свойства тел притягиваться или отталкиваться друг от друга с электрической силой. Свойства электрических зарядов:
1. В природе существуют только два типа электрических зарядов: положительные и отрицательные.
2. Любой электрический заряд квантован, то есть кратен целому числу минимальных порций заряда. Носителем такой минимальной порции отрицательного заряда является электрон, положительного — протон. Численно эти минимальные заряды одинаковы и составляют е = 1.6∙10–19 Кл. Равенство элементарных зарядов разного знака объясняет электронейтральность атомов и молекул.
3. Закон сохранения электрических зарядов: полный электрических заряд изолированной системы не меняется.
4. Опыт показывает, что электрический заряд релятивистски инвариантен, то есть его величина не зависит от того, движется он или находится в покое.
Важнейшим свойством электрических зарядов является их силовое взаимодействие друг с другом. Это взаимодействие точечных зарядов экспериментально было исследовано Ш. Кулоном.
Закон Кулона
Два точечных неподвижных электрических заряда взаимодействуют с силой, прямо пропорциональной произведению величины этих зарядов и обратно пропорциональной квадрату расстояния между ними. Силы электрического взаимодействия направлены по линии, соединяющей заряды. Одноимённые заряды отталкиваются , разноимённые — притягиваются.
Коэффициент пропорциональности к0 в этой системе равен к0 = 9 ∙ 109
В рационализованной системе СИ коэффициент пропорциональности к0 представляют в виде:
Закон Кулона. Единица электрического заряда
Электростатика — это ветвь электродинамики, которая изучает взаимодействие покоящихся зарядов.
Проводя свои опыты, Шарль Кулон пришел к выводу, что сила взаимодействия между двумя покоящимися зарядами прямо пропорциональна величине зарядов и обратно пропорциональна квадрату расстояния между ними.
Обратите внимание, насколько похожа эта формулировка на формулировку закона всемирного тяготения. Да и сам эксперимент, проведенный Шарлем Кулоном, очень напоминает эксперимент Генри Кавендиша. Кулон тоже использовал крутильные весы, находящиеся в цилиндре, в котором был откачан весь воздух. Стеклянная палочка, на которой укреплены два одинаковых металлических шарика, подвешена на тонкой упругой проволочке.

Один из металлических шариков является заряженным, а другой служит противовесом. К заряженному шарику подводится третий шарик, с одноименным зарядом той же величины. В результате шарики начинают отталкиваться, что приводит к закручиванию проволочки. По этому закручиванию можно определить силу взаимодействия, а расстояние между шариками можно узнать с помощью несложных измерений. Основная сложность заключалась в изменении величины заряда, поскольку в то время даже не было единиц измерения электрического заряда. Однако Кулон предположил (и это предположение верно), что одинаковые шарики одинаково заряжаются при соприкосновении. Иными словами, если прикоснуться незаряженным шариком к заряженному шарику тех же размеров и массы, то заряд разделится пополам. Таким образом, Шарль Кулон нашел способ уменьшать заряд в 2, 4, 8 и более раз. Итак, закон Кулона гласит следующее: сила взаимодействия двух точечных зарядов в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними:

Данную силу взаимодействия часто называют силой Кулона или кулоновской силой. Напомним, что точечными зарядами обладают тела, размерами которых можно пренебречь по сравнению с расстоянием между ними.
Закон Кулона также применим, если оба тела имеют правильную форму, то есть форму шара. В этом случае, за расстояние между телами принимается расстояние между центрами этих тел. В формуле, описывающей закон Кулона, k — это коэффициент пропорциональности, о котором мы поговорим чуть позже. Для вычисления силы Кулона мы используем модули зарядов, а, следовательно, можем определить только модуль силы. Как вы понимаете, если мы подвесим заряженные шарики на нитях, то они будут либо притягиваться, либо отталкиваться. Таким образом, силы взаимодействия между двумя неподвижными точечными зарядами направлены вдоль прямой, проходящей через эти заряды. Исходя из третьего закона Ньютона, шарики действуют друг на друга с силами равными по модулю и противоположными по направлению.
Как вы знаете из курса физики восьмого класса, величина электрического заряда измеряется в кулонах, именно в честь Шарля Кулона, который открыл только что изученный нами закон. 1 Кл — это заряд, проходящий через поперечное сечение проводника за 1 с при силе тока 1 А.
Теперь мы можем вернуться к коэффициенту пропорциональности в законе кулона и определиться с его единицами измерения:

Надо сказать, что 1 Кл — это очень большой заряд. Даже находясь на расстоянии 200 м друг от друга, два точечных разноименных заряда будут притягиваться примерно с той же силой, с которой Земля притягивает укомплектованный истребитель.
Напомним теперь, что заряд электрона является наименьшим зарядом в природе:

Необходимо отметить, что заряд любого тела всегда кратен минимальному заряду, поскольку к телу может присоединиться только целое число электронов:

Однако, если речь идет о заряде многократно превышающим минимальный заряд, то проверять кратность не имеет смысла. Тем не менее, в ядерной физике данное правило очень важно.
Хотелось бы еще раз отметить, насколько закон Кулона похож на закон всемирного тяготения. В обоих случаях силы взаимодействия обратно пропорциональны квадрату расстояния. Также, кулоновская сила прямо пропорциональна произведению модулей зарядов, а сила тяготения прямо пропорциональна массам. Это тоже является очевидным сходством (если считать заряды за количество электричества, а массу за количество вещества). Даже области применения и того, и другого закона совпадают. Оба закона применимы к материальным точкам или к телам сферической формы.
Примеры решения задач.
Задача 1. Два равных по модулю разноимённых точечных заряда взаимодействуют с силой, равной 10 Н. Определите величину этих зарядов, если они находятся на расстоянии 5 м друг от друга.

Задача 2. Два одинаковых шарика висят на нитях так, как показано на рисунке. После того, как шарикам сообщили заряды, равные 0,3 мкКл, они разошлись на расстояние, равное 36 см. Если натяжение на каждой нити равно 45 мН, то чему равен угол альфа, указанный на рисунке?

24. Взаимодействие заряженных тел. Закон Кулона. Закон сохранения электрического заряда.
Взаимодействие тел, имеющих заряды одинакового или разного знака, можно продемонстрировать на следующих опытах. Наэлектризуем эбонитовую палочку трением о мех и прикоснёмся ею к металлической гильзе, подвешенной на шёлковой нити. На гильзе и эбонитовой палочке распределяются заряды одного знака (отрицательные заряды). Приближая заряженную отрицательно эбонитовую палочку к заряженной гильзе, можно увидеть, что гильза будет отталкиваться от палочки
 Взаимодействие тел с зарядами одного
знака.
Взаимодействие тел с зарядами одного
знака.
Если теперь поднести к заряженной гильзе стеклянную палочку, потёртую о шёлк (положительно заряженную), то гильза будет к ней притягиваться
 Взаимодействие
тел с зарядами разных знаков.
Взаимодействие
тел с зарядами разных знаков.
Отсюда следует, что тела, имеющие заряды одинакового знака (одноимённо заряженные тела), взаимно отталкиваются, а тела, имеющие заряды разного знака (разноименно заряженные тела), взаимно притягиваются. Аналогичные вводы получаются, если приближать два султана, одноименно заряженные и разноименно заряженные
Закон Куллона: Был открыт Шарлем Кулоном в 1785 г. Проведя большое количество опытов с металлическими шариками, Шарль Кулон дал такую формулировку закона:
Модуль силы взаимодействия двух точечных зарядов в вакууме прямо пропорционален произведению модулей этих зарядов и обратно пропорционален квадрату расстояния между ними.
для того, чтобы закон был верен, необходимы:
Точечность зарядов, то есть расстояние между заряженными телами должно быть много больше их размеров. Впрочем, можно доказать, что сила взаимодействия двух объёмно распределённых зарядов со сферически симметричными непересекающимися пространственными распределениями равна силе взаимодействия двух эквивалентных точечных зарядов, размещённых в центрах сферической симметрии;
Их неподвижность. Иначе вступают в силу дополнительные эффекты: магнитное поле движущегося заряда и соответствующая ему дополнительная сила Лоренца, действующая на другой движущийся заряд;
Расположение зарядов в вакууме.
В векторном виде в формулировке Ш. Кулона закон записывается следующим образом:


где 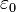 ≈
8,854187817·10−12Ф/м — электрическая
постоянная.
≈
8,854187817·10−12Ф/м — электрическая
постоянная.
Формулировка закона сохранения заряда
В телах, которые находятся в покое и электрически нейтральны, заряды противоположных знаков равны по величине и взаимно компенсируют друг друга. Когда происходит электризация одних тел другими, заряды переходят с одного тела на другое, однако их общий суммарный заряд остается прежним.
В изолированной системе тел общий суммарный заряд всегда равен некоторой постоянной величине: q_1+q_2+⋯+q_n=const, где q_1, q_2, …, q_n заряды тел или частиц, входящих в систему.
25. Электростатическое поле и его характеристики
Электростатическое поле— поле, созданное неподвижными в пространстве и неизменными во времени электрическими зарядами (при отсутствии электрических токов). Электрическое поле представляет собой особый вид материи, связанный с электрическими зарядами и передающий действия зарядов друг на друга.
Основные характеристики электростатического поля:
Напряженность(— векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы
 действующей
на неподвижный пробный заряд,
помещенный в данную точку поля, к
величине этого заряда
действующей
на неподвижный пробный заряд,
помещенный в данную точку поля, к
величине этого заряда :
:
 .)
.)
Потенциал(скалярная энергетическая характеристика электростатического, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля. Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда:

Урок 26. электрический заряд. закон кулона — Физика — 10 класс
Физика, 10 класс
Урок 26. Электрический заряд. Закон Кулона
Перечень вопросов, рассматриваемых на уроке:
1) электродинамика;
2) электризация;
3) два рода зарядов;
4) закон Кулона;
5) применение электризации;
6) вредные действия электризации.
Глоссарий по теме:
Электродинамика – это наука о свойствах и закономерностях поведения особого вид материи – электромагнитного поля, осуществляющего взаимодействие между электрически заряженными телами или частицами.
Электрический заряд – физическая величина, характеризующая электрические свойства частиц.
Элементарный заряд — заряд электрона (или протона).
Электрон — частица с наименьшим отрицательным зарядом.
Электризация — явление приобретения телом заряда.
Кулоновская сила — сила взаимодействия зарядов
Основная и дополнительная литература по теме урока:
1. Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. С. 277 – 282.
2. Тульчинский М.Е. Сборник качественных задач по физике. – М.: Просвещение, 1965. С.81.
3. Алексеева М. Н. Физика юным. – М.: Просвещение, 1980. С. 68-78.
Теоретический материал для самостоятельного изучения
Элементарные частицы – это мельчайшие частицы, которые не делятся на более простые, из которых состоят все тела.
Если частицы взаимодействуют друг с другом с силами, которые убывают с увеличением расстояния так же, как и силы всемирного тяготения, но превышают силы тяготения во много раз, то говорят, что эти частицы имеют электрический заряд, а частицы называются заряженными.
Взаимодействие заряженных частиц называется электромагнитным.
Заряды одного знака отталкиваются друг от друга, а разного знака – притягиваются.
При электризации трением оба тела приобретают заряды, противоположные по знаку, но одинаковые по модулю.
При электризации тел выполняется закон сохранения электрического заряда:
В изолированной системе алгебраическая сумма зарядов всех тел сохраняется.
Заряженные тела, размерами и формой которых можно пренебречь при их взаимодействии, называются точечными зарядами.
Силу взаимодействия зарядов называют кулоновской силой.
Сила, с которой взаимодействуют заряды, прямо пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между ними.
Закон Кулона:

где  — это электрическая постоянная.
— это электрическая постоянная.
 — заряд электрона
— заряд электрона
 — заряд протона
— заряд протона
Единица измерения электрического заряда – Кулон.
Заряд в 1 Кл очень велик. Сила взаимодействия двух точечных зарядов по1 Кулон каждый, расположенных на расстоянии 1 км друг от друга, чуть меньше силы, с которой Земля притягивает груз массой 1т.
Примеры и разбор решения заданий:
1. Два заряда q1 и q2 взаимодействуют в вакууме с силой F. Если заряд каждой частицы увеличить в два раза и расстояние между ними уменьшить в два раза, то как изменится сила их взаимодействия?
Решение:
Используя закон Кулона  можем рассчитать, что сила взаимодействия между зарядами увеличится в 16 раз.
можем рассчитать, что сила взаимодействия между зарядами увеличится в 16 раз.
2. Два шарика, расположенные на расстоянии 10 см друг от друга, имеют одинаковые отрицательные заряды и взаимодействуют с силой 0,23 мН. Найти число избыточных электронов на каждом шарике.
Решение:
Число избыточных электронов:

Сила взаимодействия между двумя заряженными шариками:

Отсюда выражаем заряд шарика:

Заряд электрона равен e =|-1,6·10-31| Kл

Вычисления:

Ответ:  .
.




 ри электризации происходит переход,,,,,,,,,,,, с одного вещества на другое.
ри электризации происходит переход,,,,,,,,,,,, с одного вещества на другое.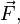 действующей
на неподвижный пробный заряд,
помещенный в данную точку поля, к
величине этого заряда
действующей
на неподвижный пробный заряд,
помещенный в данную точку поля, к
величине этого заряда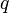 :
: