Электрический ток в металлах

Определение 1

Электрическим током в металлах называют упорядоченное движение электронов под действием электрического поля.

Исходя из опытов, видно, что металлический проводник вещество не переносит, то есть ионы металла не участвуют в передвижении электрического заряда.

Носители тока в металлах

При исследованиях были получены доказательства электронной природы тока в металлах. Еще в 1913 году Л.И. Мандельштам и Н.Д. Папалекси выдали первые качественные результаты. А в 1916 году Р. Толмен и Б. Стюарт модернизировали имеющуюся методику и выполнили количественные измерения, которые доказывали, что движение электронов происходит под действием тока в металлических проводниках.

Рисунок 1.12.1 показывает схему Толмена и Стюарта. Катушка, состоящая из большого количества витков тонкой проволоки, приводилась в действие при помощи вращения вокруг своей оси.

Ее концы были прикреплены к баллистическому гальванометру Г. Производилось резкое торможение катушки, что было следствием возникновения кратковременного тока, обусловленного инерцией носителя заряда. Измерение полного заряда производилось при помощи движения стрелок гальванометра.

Рисунок 1.12.1. Схема опыта Толмена и Стюарта.

Во время торможения вращающейся катушки сила F=-mdυdt, называемая тормозящей, действовала на каждый носитель заряда е. F играла роль сторонней силы, иначе говоря, неэлектрического происхождения. Именно эта сила, характеризующаяся единицей заряда, является напряженностью поля сторонних сил Eст  :

Eст=-medυdt.

То есть при торможении катушки происходит возникновение электродвижущей силы δ, равной δ=Eстl=medυdtl, где l – длина проволоки катушки. Определенный промежуток времени процесса торможения катушки обусловлен протеканием по цепи заряда q:

q=∫Idt=1R∫δdt=melυ0R.

Данная формула объясняет, что l – это мгновенное значение силы тока в катушке, R – полное сопротивление цепи, υ0 – начальная линейная скорость проволоки. Видно, что определение удельного заряда em в металлах производится, исходя из формулы:

em=lυ0Rq.

Величины, находящиеся с правой стороны, можно измерить. Основываясь на результатах опытов Толмена и Стюарта, установили, что носители свободного заряда имеют отрицательный знак, а отношение носителя в его массе близко по значению удельного заряда электрона, получаемого в других опытах. Было выявлено, что электроны – это носители свободных зарядов.

Современные данные показывают, что модуль заряда электрона, то есть элементарный заряд, равняется e=1,60218·10-19 Кл, а обозначение его удельного заряда – em=1,75882·1011 Кл/кг.

При наличии отличной концентрации свободных электронов есть смысл говорить о хорошей электропроводимости металлов. Это выявили еще перед опытами Толмена и Стюарта. В 1900 году П. Друде, основываясь на гипотезе о существовании свободных электронов в металлах, создал электронную теорию проводимости металлов. Ее развил и расширил Х. Лоренц, после чего она получила название классическая электронная теория.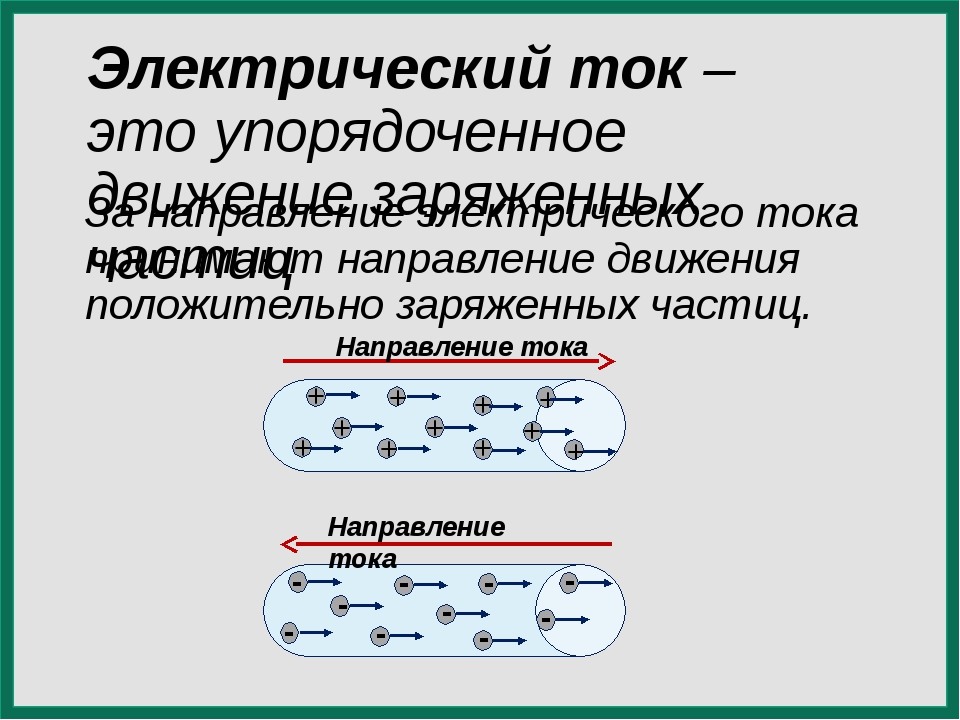

На ее основании поняли, что электроны ведут себя как электронный газ, похожий на идеальный по своему состоянию. Рисунок 1.12.2 показывает, каким образом он может заполнить пространство между ионами, которые уже образовали кристаллическую решетку металла.

Рисунок 1.12.2. Газ свободных электронов в кристаллической решетке металла. Показана траектория одного из электронов.

Потенциальный барьер. Движение электронов в кристаллической решетке

Определение 2

После взаимодействия электронов с ионами первые покидают металл, преодолевая только потенциальный барьер.

Высота такого барьера получила название работы выхода.

Наличие комнатной температуры не позволяет электронам проходить этот барьер. Потенциальная энергия выхода электрона после взаимодействия с кристаллической решеткой намного меньше, чем при удалении электрона из проводника.

Определение 3

Расположение е в проводнике характеризуется наличием потенциальной ямы, глубина которой получила название потенциального барьера.

Ионы, образующие решетку, и электроны принимают участие в тепловом движении. Благодаря тепловым колебаниям ионов вблизи положений равновесий и хаотичному движению свободных электронов, при столкновении первых со вторыми происходит усиление термодинамического равновесия между электронами и решеткой.

Теорема 1

По теории Друде-Лоренца имеем, что электроны имеют такую же среднюю энергию теплового движения, как и молекулы одноатомного идеального газа. Это делает возможным оценивание средней скорости υт¯ теплового движения электронов, используя молекулярно-кинетическую теорию.

Комнатная температура дает значение, равное 105 м/с.

Если наложить внешнее электрическое поле в металлический проводник, тогда произойдет тепловое упорядоченное движения электронов (электрический ток), то есть дрейф. Определение средней его скорости υд¯ выполняется по интервалу имеющегося времени ∆t через поперечное сечение S проводника электронов, которые находятся в объеме Sυд∆t.

Количество таких е равняется nSυд∆t, где n принимает значение средней концентрации свободных электронов, равняющейся числу атомов в единице объема металлического проводника. За имеющееся количество времени ∆t через сечение проводника проходит заряд ∆q=enSυд∆t.

Тогда I=∆q∆t=enSυд или υд=IenS.

Концентрация n атомов в металлах находится в пределах 1028-1029м-3.

Формула дает возможность оценить среднюю скорость υд¯ упорядоченного движения электронов со значением в промежутке 0,6-6 мм/с для проводника с сечением 1 мм2 и проходящим током в 10 А.

Определение 4

Средняя скорость υд¯ упорядоченного движения электронов в металлических проводниках на много порядков меньше скорости υт их теплового движения υд≪υт.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Рисунок 1.12.3 демонстрирует характер движения свободного е, находящегося в кристаллической решетке.

Рисунок 1.12.3. Движение свободного электрона в кристаллической решетке: а – хаотическое движение электрона в кристаллической решетке металла; b – хаотическое движение с дрейфом, обусловленным электрическим полем.

Масштабы дрейфа υд¯∆t сильно преувеличены.

Наличие малой скорости дрейфа не соответствует опыту, когда ток всей цепи постоянного тока устанавливается мгновенно. Замыкание производится при помощи воздействия электрического поля со скоростью c=3·108 м/с. По прошествии времени lc (l — длина цепи) вдоль цепи устанавливается стационарное распределение электрического поля. В ней происходит упорядоченное движение электронов.

Классическая электронная теория металлов предполагает, что их движение подчинено законам механики Ньютона. Данная теория характеризуется тем, что происходит пренебрежение взаимодействием электронов между собой, а взаимодействие с положительными ионами расценивается как соударения, при каждом из которых e сообщает накопленную энергию решетке. Поэтому принято считать, что после соударения движение электрона характеризуется нулевой дрейфовой скоростью.

Абсолютно все выше предложенные допущения приближенные. Это дает возможность объяснения законов электрического тока в металлических проводниках, основываясь на электронной классической теории.

Закон Ома

Определение 5

В промежутке между соударениями на электрон действует сила, равняющаяся по модулю eE, в результате чего получает ускорение emE.

Конец свободного пробега характеризуется дрейфовой скоростью электрона, которую определяют по формуле

υд=υдmax=eEmτ.

Время свободного пробега обозначается τ. Оно способствует упрощению расчетов для нахождения значения всех электронов. Средняя скорость дрейфа υд равняется половине максимального значения:

υд=12υдmax=12eEmτ.

Если имеется проводник с длиной l, сечением S с концентрацией электронов n, тогда запись нахождения тока в проводнике имеет вид:

I=enSυд=12e2τnSmE=e2τnS2mlU.

U=El – это напряжение на концах проводника. Формула выражает закон Ома для металлического проводника. Тогда электрическое сопротивление необходимо находить:

R=2me2nτlS.

Удельное сопротивление ρ и удельная проводимость ν выражаются как:

ρ=2me2nτ; ν=1ρ=e2nτ2m.

Закон Джоуля-Ленца

Конец пробега электронов под действием поля характеризуется кинетической энергией

12m(υд)max2=12e2τ2mE2.

Определение 6

Исходя из предположений, энергия при соударениях передается решетке, а в последствии переходит в тепло.

Время ∆t каждого электрона испытывается ∆tτ соударений. Проводник с сечение S и длиной l имеет nSl электронов. Тогда выделившееся тепло в проводнике за ∆t равняется

∆Q=nSl∆tτe2τ22mE2=ne2τ2mSlU2∆t=U2R∆t.

Данное соотношение выражает

закон Джоуля-Ленца.

Благодаря классической теории, имеет место трактовка существования электрического сопротивления металлов, то есть законы Ома и Джоуля-Ленца. Классическая электронная теория не в состоянии ответить на все вопросы.

Она не способна объяснить разницу в значении молярной теплоемкости металлов и диэлектрических кристаллов, равняющейся 3R, где R записывается как универсальная газовая постоянная. Теплоемкость металла не зависит от количества свободных электронов.

Классическая электронная теория не объясняет температурную зависимость удельного сопротивления металлов. По теории ρ~T, а исходя из экспериментов – ρ~T. Примером расхождения теории с практикой служит сверхпроводимость.

Сопротивление металлического проводника

Исходя из классической теории, удельное сопротивление металлов должно постепенно уменьшаться при понижении температуры, причем остается конечным при любой T. Данная зависимость характерна для проведения опытов при высоких температурах. Если T достаточно низкая, тогда удельное сопротивление металлов теряет зависимость от температуры и достигает предельного значения.

Особый интерес представило явление сверхпроводимости. В 1911 году его открыл Х. Каммерлинг-Оннес.

Теорема 2

Если имеется определенная температура Tкр, различная для разных веществ, тогда удельное сопротивление уменьшается до нуля с помощью скачка, как изображено на рисунке 1.12.4.

Пример 1

Критической температурой для ртути считается значение 4,1 К, для алюминия – 1,2 К, для олова – 3,7 К. Наличие сверхпроводимости может быть не только у элементов, но и у химических соединений и сплавов. Ниобий с оловом Ni3Snимеют критическую точку температуры в 18 К. Существуют вещества, которые при низкой температуре переходят в сверхпроводящее состояние, тогда как в обычных условиях ими не являются. Серебро и медь являются проводниками, но при понижении температуры сверхпроводниками не становятся.

Рисунок 1.12.4. Зависимость удельного сопротивления ρ от абсолютной температуры T при низких температурах: a – нормальный металл; b – сверхпроводник.

Сверхпроводящее состояние говорит об исключительных свойствах вещества. Одним из важнейших является способность на протяжении длительного времени поддерживать электрический ток, возбужденный в сверхпроводящей цепи, без затухания.

Классическая электронная теория не может объяснить сверхпроводимость. Это стало возможным спустя 60 лет после его открытия, основываясь на квантово-механических представлениях.

Рост интереса к данному явлению увеличивался по мере появления новых материалов, способных обладать высокими критическими температурами. В 1986 было обнаружено сложное соединение с температурой Tкр=35 К. На следующий год сумели создать керамику с критической Т в 98 К, которая превышала Т жидкого азота (77 К).

Определение 7

Явление перехода веществ в сверхпроводящее состояние при Т, превышающих температуру кипения жидкого азота, называют высокотемпературной сверхпроводимостью.

Позже в 1988 году создали Tl-Ca-Ba-Cu-O соединение с критической Т, достигающей 125 К. На данный момент ученые заинтересованы в поиске новых веществ с наиболее высокими значениями Tкр. Они рассчитывают на получение сверхпроводящего вещества при комнатной температуре. Если это будет сделано, произойдет революция в науке и технике. До настоящего времени все свойства и механизмы состава сверхпроводимых керамических материалов до конца не исследованы.

Ток в металлах

   Носителями свободных зарядов в металлах являются электроны. -4 м/с.

Экспериментальное доказательство существования свободных электронов в металлах.

   Наиболее убедительное доказательство электронной природы тока в металлах было получено в опытах с инерцией электронов (опыт Толмена и Стьюарта): 

На катушку наматывают проволоку, концы которой припаивают к двум металлическим дискам, изолированным друг от друга. К концам дисков при помощи скользящих контактов подключают гальванометр.

   Катушку приводят в быстрое вращение, а затем резко останавливают. После резкой остановки катушки свободные заряженные частицы некоторое время движутся относительно проводника по инерции и, следовательно, в катушке возникает электрический ток. Ток существует незначительное время, так как из-за сопротивления проводника заряженные частица тормозятся и упорядоченное движение частиц, образующее ток, прекращается.

. 

  

 

   Направление тока в этом опыте говорит о том, что он создается движением отрицательно заряженных частиц. 11 Кл/кг. Эта величина совпадала с отношением заряда электрона к его массе e/m, найденным ранее из других опытов.

Движение электронов в металле.

  Электроны под влиянием силы, действующей на них со стороны электрического поля, приобретают определенную скорость упорядоченного движения. Эта скорость не увеличивается в дальнейшем со временем, так как, сталкиваясь с ионами кристаллической решетки, электроны теряют направленное движение, а затем опять под действием электрического поля начинают двигаться направлено. В результате средняя скорость упорядоченного движения электронов оказывается пропорциональной напряженности электрического поля в проводнике и, следовательно, разности потенциалов на концах проводника, так как Е = U/l, где l — длина проводника.

   Сила тока в проводнике пропорциональна скорости упорядоченного движения частиц. Поэтому можем сказать, что сила тока пропорциональна разности потенциалов на концах проводника. В этом состоит качественное объяснение закона Ома на основе электронной теории проводимости металлов. 6 К.Такая температура существует внутри звезд. Движение электронов в металле подчиняется законом квантовой механики.

Вывод.

Экспериментально доказано, что носителями свободных зарядов в металлах являются электроны. Под действием электрического поля электроны движутся с постоянной средней скоростью, испытывая тормозящее влияние со стороны кристаллической решетки. Скорость упорядоченного движения электронов прямо пропорциональна напряженности поля в проводнике. 

  

Электрически ток в металлах. Сверхпроводимость.

     Электрический ток в металлах – это упорядоченное движение электронов под действием электрического поля. Опыты показывают, что при протекании тока по металлическому проводнику переноса вещества не происходит, следовательно, ионы металла не принимают участия в переносе электрического заряда.

     Наиболее убедительное доказательство электронной природы тока в металлах было получено в опытах с инерцией электронов. Идея таких опытов и первые качественные результаты (1913 г.) принадлежат русским физикам Л. И. Мандельштаму и Н. Д. Папалекси. В 1916 году американский физик Р. Толмен и шотландский физик Б. Стюартусовершенствовали методику этих опытов и выполнили количественные измерения, неопровержимо доказавшие, что ток в металлических проводниках обусловлен движением электронов.

     Схема опыта Толмена и Стюарта показана на рис. 1.12.1. Катушка с большим числом витков тонкой проволоки приводилась в быстрое вращение вокруг своей оси. Концы катушки с помощью гибких проводов были присоединены к чувствительному баллистическому гальванометру Г. Раскрученная катушка резко тормозилась, и в цепи возникал кратковременных ток, обусловленный инерцией носителей заряда. Полный заряд, протекающий по цепи, измерялся по отбросу стрелки гальванометра.

     Сверхпроводимость. В 1911 г. нидерландский ученый Гейке Камерлинг-0ннес (1853— 1926) обнаружил, что при понижении температуры ртути до 4,1 К ее удельное сопротивление скачком уменьшается до нуля (рис. 153). Явление уменьшения удельного сопротивления до нуля при температуре, отличной от абсолютного нуля, называется сверхпроводимостью. Материалы, обнаруживающие способность переходить при некоторых температурах, отличных от абсолютного нуля, в сверхпроводящее состояние, называются сверхпроводниками.Прохождение тока в сверхпроводнике происходит без потерь энергии, поэтому однажды возбужденный в сверхпроводящем кольце электрический ток может существовать неограниченно долго без изменения.
     Сверхпроводящие материалы уже используются в электромагнитах. Ведутся исследования, направленные на создание сверхпроводящих линий электропередачи. Применение явления сверхпроводимости в широкой практике может стать реальностью в ближайшие годы благодаря открытию в 1986 г. сверхпроводимости керамик — соединений лантана, бария, меди и кислорода. Сверхпроводимость таких керамик сохраняется до температур около 100 К.

???Вопросы

1. Что называют электрическим током?
2. В чем заключается опыт Рике?
3. В чем заключается опыт Мандельштама и Папалекси?
4. Какими зарядами создается электрический ток в металлах?
5. Как зависит сопротивление металлов от  температуры? Формула?

Электрический ток в металлах

 

 Электрический ток в металлах

Электрический ток в металлах –  это упорядоченное движение электронов под действием электрического поля. Опыты показывают, что при протекании тока по металлическому проводнику переноса вещества не происходит, следовательно, ионы металла не принимают участия  в переносе электрического заряда.

Наиболее убедительное доказательство электронной природы тока в металлах было получено в опытах с инерцией электронов. Идея таких опытов и  первые качественные результаты (1913 г. ) принадлежат русским физикам Л. И. Мандельштаму и Н. Д. Папалекси. В 1916 году американский физик Р. Толмен и шотландский физик Б. Стюартусовершенствовали методику этих опытов и выполнили количественные измерения, неопровержимо доказавшие, что ток в металлических проводниках обусловлен движением электронов.

Схема опыта Толмена и Стюарта показана на рис. 1.12.1. Катушка с большим числом витков тонкой проволоки приводилась в быстрое вращение вокруг своей оси. Концы катушки с помощью гибких проводов были присоединены к чувствительному баллистическому гальванометру Г. Раскрученная катушка резко тормозилась, и в цепи возникал кратковременных ток, обусловленный инерцией носителей заряда. Полный заряд, протекающий по цепи, измерялся по отбросу стрелки гальванометра.

Рисунок 1.12.1. Схема опыта Толмена и Стюарта

При торможении вращающейся катушки  на каждый носитель заряда e действует тормозящая сила   которая играет роль сторонней силы, то есть силы неэлектрического происхождения. Сторонняя сила, отнесенная к единице заряда, по определению является напряженностью E_ст поля сторонних сил: 

Следовательно, в цепи при торможении катушки возникает электродвижущая  сила  , равная 

где l – длина проволоки катушки. За время торможения катушки по цепи протечет заряд q, равный 

Здесь I – мгновенное значение силы тока в катушке, R – полное сопротивление цепи, υ₀ – начальная линейная скорость проволоки.

Отсюда удельный заряд e / m свободных носителей тока в металлах равен: 

Все величины, входящие в правую часть  этого соотношения, можно измерить. На основании результатов опытов Толмена и Стюарта было установлено, что носители свободного заряда в металлах имеют отрицательный знак, а отношение заряда носителя к его массе близко к удельному заряду электрона, полученному из других опытов. Так было установлено, что носителями свободных зарядов в металлах являются электроны.

По современным данным модуль заряда электрона (элементарный заряд) равен 

а его удельный заряд есть 

Хорошая электропроводность металлов объясняется высокой 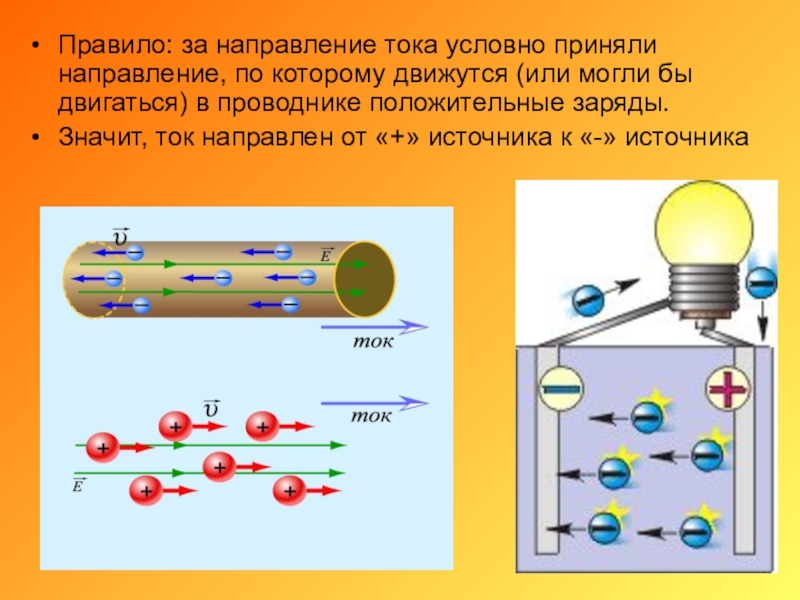концентрацией  свободных электронов, равной по порядку  величины числу атомов в единице  объема.

Предположение о том, что за электрический  ток в металлах ответственны электроны, возникло значительно раньше опытов Толмена и Стюарта. Еще в 1900 году немецкий ученый П. Друде на основании гипотезы о существовании свободных электронов в металлах создал электронную теорию проводимости металлов. Эта теория получила развитие в работах голландского физика Х. Лоренца и носит название классической электронной теории. Согласно этой теории, электроны в металлах ведут себя как электронный газ, во многом похожий на идеальный газ. Электронный газ заполняет пространство между ионами, образующими кристаллическую решетку металла (рис. 1.12.2).

Рисунок 1.12.2. Газ свободных электронов в кристаллической решетке металла. Показана траектория одного из электронов

Из-за взаимодействия с ионами электроны  могут покинуть металл, лишь преодолев  так называемый потенциальный барьер. Высота этого барьера называется работой выхода. При обычных (комнатных) температурах у электронов не хватает энергии для преодоления потенциального барьера.

Из-за взаимодействия с кристаллической  решеткой потенциальная энергия  выхода электрона внутри проводника оказывается меньше, чем при удалении электрона из проводника. Электроны  в проводнике находятся в своеобразной «потенциальной яме», глубина которой  и называется потенциальным барьером.

Как ионы, образующие решетку, так  и электроны участвуют в тепловом движении. Ионы совершают тепловые колебания вблизи положений равновесия – узлов кристаллической решетки. Свободные электроны движутся хаотично и при своем движении сталкиваются с ионами решетки. В результате таких  столкновений устанавливается термодинамическое  равновесие между электронным газом и решеткой. Согласно теории Друде–Лоренца, электроны обладают такой же средней энергией теплового движения, как и молекулы одноатомного идеального газа. Это позволяет оценить среднюю скорость   теплового движения электронов по формулам молекулярно-кинетической теории. При комнатной температуре она оказывается примерно равной 10⁵ м/с.

При наложении внешнего электрического поля в металлическом проводнике кроме теплового движения электронов возникает их упорядоченное движение (дрейф), то есть электрический ток. Среднюю скорость   дрейфа можно оценить из следующих соображений. За интервал времени Δt через поперечное сечение S проводника пройдут все электроны, находившиеся в объеме 

Число таких электронов равно   где n – средняя концентрация свободных электронов, примерно равная числу атомов в единице объема металлического проводника. Через сечение проводника за время Δt пройдет заряд   Отсюда следует: 

или 

Концентрация n атомов в металлах находится в пределах 10²⁸–10²⁹ м^–3.

Оценка по этой формуле для металлического проводника сечением 1 мм², по которому течет ток 10 А, дает для средней скорости   упорядоченного движения электронов значение в пределах 0,6–6 мм/c.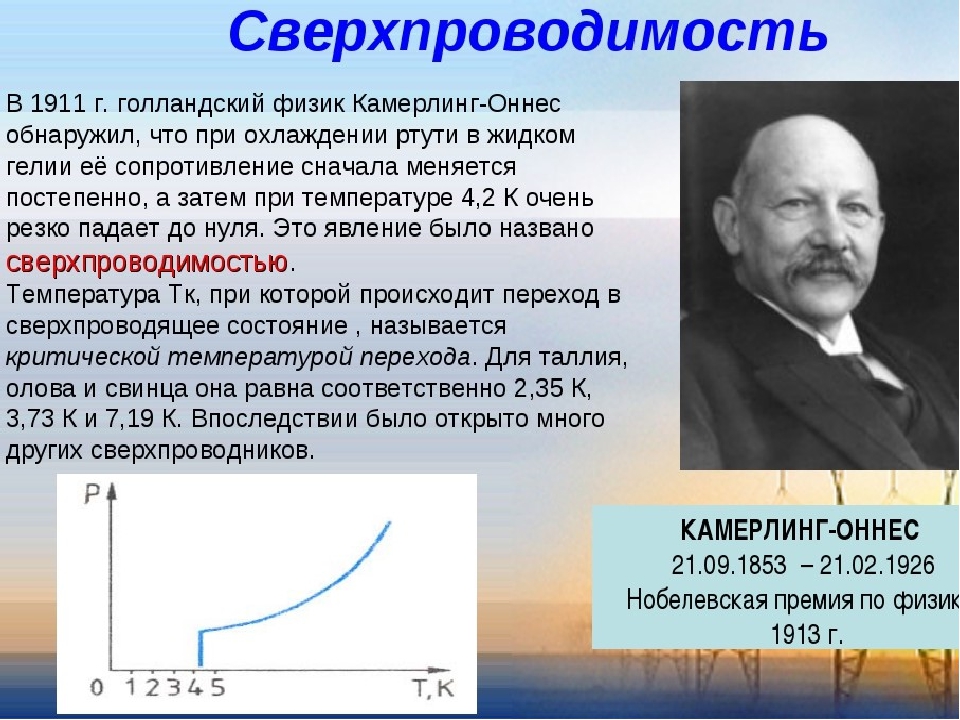 Таким образом, средняя скорость   упорядоченного движения электронов в металлических проводниках на много порядков меньше средней скорости   их теплового движения   Рис. 1.12.3 дает представление о характере движения свободного электрона в кристаллической решетке.

Рисунок 1.12.3. Движение свободного электрона  в кристаллической решетке: а – хаотическое движение электрона в кристаллической решетке металла; b – хаотическое движение с дрейфом, обусловленным электрическим полем. Масштабы дрейфа   сильно преувеличены

Малая скорость дрейфа на противоречит опытному факту, что ток во всей цепи постоянного тока устанавливается практически мгновенно. Замыкание цепи вызывает распространение электрического поля со скоростью c = 3·10⁸ м/с. Через время порядка l / c (l – длина цепи) вдоль цепи устанавливается стационарное распределение электрического поля и в ней начинается упорядоченное движение электронов.

В классической электронной теории металлов предполагается, что движение электронов подчиняется законам  механики Ньютона. В этой теории пренебрегают взаимодействием электронов между собой, а их взаимодействие с положительными ионами сводят только к соударениям. Предполагается также, что при каждом соударении электрон передает решетке всю накопленную в электрическом поле энергию и поэтому после соударения он начинает движение с нулевой дрейфовой скоростью.

Несмотря на то, что все эти  допущения являются весьма приближенными, классическая электронная теория качественно объясняет законы электрического тока в металлических проводниках.

Закон Ома. В промежутке между соударениями на электрон действует сила, равная по модулю eE, в результате чего он приобретает ускорение   Поэтому к концу свободного пробега дрейфовая скорость электрона равна 

где τ – время свободного пробега, которое для упрощения расчетов предполагается одинаковым для всех электронов. Среднее значение скорости дрейфа   равно половине максимального значения: 

Рассмотрим проводник длины l и сечением S с концентрацией электронов n. Ток в проводнике может быть записан в виде: 

где U = El – напряжение на концах проводника. Полученная формула выражает закон Ома для металлического проводника. Электрическое сопротивление проводника равно: 

а удельное сопротивление ρ и  удельная проводимость ν выражаются соотношениями: 

Какие частицами создается ток в металле. Применение электрического тока в металлах

Электрический ток в металлах – это упорядоченное движение электронов под действием электрического поля. Опыты показывают, что при протекании тока по металлическому проводнику не происходит переноса вещества, следовательно, ионы металла не принимают участия в переносе электрического заряда.

Наиболее убедительное доказательство электронной природы тока в металлах было получено в опытах с инерцией электронов.

Идея таких опытов и первые качественные результаты принадлежат русским физикам Л. И. Мандельштаму и Н. Д. Папалекси (1913 г.). В 1916 году американский физик Р. Толмен и шотландский физик Б. Стюарт усовершенствовали методику и выполнили количественные измерения, доказав, что ток в металлических проводниках обусловлен движением электронов.

Хорошая электропроводность металлов объясняется высокой концентрацией свободных электронов.

В 1900 году немецкий ученый П. Друде на основе гипотезы о существовании свободных электронов в металлах создал электронную теорию проводимости металлов. Эта теория получила развитие в работах голландского физика Х. Лоренца и носит название классической электронной теории . Согласно этой теории, электроны в металлах ведут себя как электронный газ, во многом похожий на идеальный газ. Электронный газ заполняет пространство между ионами, образующими кристаллическую решетку металла.

Из-за взаимодействия с ионами электроны могут покинуть металл, лишь преодолев так называемый потенциальный барьер . Высота этого барьера называется работой выхода . При обычных (комнатных) температурах у электронов не хватает энергии для преодоления потенциального барьера.

Свободные электроны движутся хаотично и при своем движении сталкиваются с ионами решетки. В результате таких столкновений устанавливается термодинамическое равновесие между электронным газом и решеткой. Согласно теории Друде–Лоренца, электроны обладают такой же средней энергией теплового движения, как и молекулы одноатомного идеального газа. Это позволяет оценить среднюю скорость теплового движения электронов по формулам молекулярно-кинетической теории. При комнатной температуре она оказывается примерно равной 10 5 м/с.

При наложении внешнего электрического поля в металлическом проводнике кроме теплового движения электронов возникает их упорядоченное движение (дрейф), то есть электрический ток.

Средняя скорость дрейфа:

Концентрация свободных электронов в металлах примерно равна концентрации атомов n ~ 10 28 –10 29 м –3 , модуль заряда электрона e = 1,6 * 10 19 Кл. Для проводника с площадью поперечного сечения S = 1 мм 2 = 10 -6 м 2 при силе тока I = 1 A скорость упорядоченного движения электронов равна

За 1 с электроны в проводнике перемещаются за счет упорядоченного движения меньше чем на 0,1 мм.

Таким образом, средняя скорость упорядоченного движения электронов в металлических проводниках на много порядков меньше средней скорости их теплового движения .

Малая скорость дрейфа противоречит опытному факту, что ток во всей цепи постоянного тока устанавливается практически мгновенно. Замыкание цепи вызывает распространение электрического поля со скоростью c = 3·10 8 м/с . Через время порядка l / с (l – длина цепи) вдоль цепи устанавливается стационарное распределение электрического поля и в ней начинается упорядоченное движение электронов.

В классической электронной теории металлов предполагается, что движение электронов подчиняется законам механики Ньютона. В этой теории пренебрегают взаимодействием электронов между собой, а их взаимодействие с положительными ионами сводят только к соударениям. Предполагается также, что при каждом соударении электрон передает решетке всю накопленную в электрическом поле энергию и поэтому после соударения он начинает движение с нулевой дрейфовой скоростью.

Классическая электронная теория объясняет существование электрического сопротивления металлов, законы Ома и Джоуля–Ленца. Однако в ряде вопросов классическая электронная теория приводит к выводам, находящимся в противоречии с опытом.

Например, эта теория не может объяснить, почему молярная теплоемкость металлов , также как и молярная теплоемкость диэлектрических кристаллов, равна 3R , где R – универсальная газовая постоянная (закон Дюлонга и Пти). Наличие свободных электронов не сказывается на величине теплоемкости металлов.

Классическая электронная теория не может также объяснить температурную зависимость удельного сопротивления металлов. Теория дает в то время как из эксперимента получается зависимость ρ ~ T .

Согласно классической электронной теории, удельное сопротивление металлов должно монотонно уменьшаться при охлаждении, оставаясь конечным при всех температурах.

Такая зависимость действительно наблюдается на опыте при сравнительно высоких температурах.

При более низких температурах порядка нескольких кельвинов удельное сопротивление многих металлов перестает зависеть от температуры и достигает некоторого предельного значения. Наибольший интерес представляет явление сверхпроводимости , открытое датским физиком Х. Каммерлинг-Оннесом в 1911 году. При некоторой определенной температуре T кр, различной для разных веществ, удельное сопротивление скачком уменьшается до нуля.

Критическая температура у ртути равна 4,1 К , у алюминия 1,2 К , у олова 3,7 К . Сверхпроводимость наблюдается не только у элементов, но и у многих химических соединений и сплавов. Например, соединение ниобия с оловом (Ni 3 Sn) имеет критическую температуру 18 К. Некоторые вещества, переходящие при низких температурах в сверхпроводящее состояние, не являются проводниками при обычных температурах. В то же время такие «хорошие» проводники, как медь и серебро, не становятся сверхпроводниками при низких температурах.

He -268.94°C, N(азот) -195,82°C, Н(водород) -252,77°C

В этом разделе мы приступаем к подробному изучению того, как осуществляется прохождение электрического тока в различных проводящих средах твёрдых телах, жидкостях и газах.

Напомним, что необходимым условием возникновения тока является наличие в среде достаточно большого количества свободных зарядов, которые могут начать упорядоченное движение под действием электрического поля. Такие среды как раз и называются проводниками электрического тока.

Наиболее широко распространены металлические проводники. Поэтому начинаем мы с вопросов распространения электрического тока в металлах.

Мы много раз говорили о свободных электронах, которые являются носителями свободных зарядов в металлах. Вам хорошо известно, что электрический ток в металлическом проводнике образуется в результате направленного движения свободных электронов.

3.13.1 Свободные электроны

Металлы в твёрдом состоянии имеют кристаллическую структуру: расположение атомов в пространстве характеризуется периодической повторяемостью и образует геометрически правильный рисунок, называемый кристаллической решёткой.

Атомы металлов имеют небольшое число валентных электронов, расположенных на внешней электронной оболочке. Эти валентные электроны слабо связаны с ядром, и атом легко может их потерять.

Когда атомы металла занимают места в кристаллической решётке, валентные электроны покидают свои оболочки они становятся свободными и отправляются ¾гулять¿ по всему кристаллу18 . В узлах кристаллической решётки металла остаются положительные ионы, пространство между которыми заполнено ¾газом¿ свободных электронов (рис.3.47 ).

+ + + ++

Рис. 3.47. Свободные электроны

Свободные электроны и впрямь ведут себя подобно частицам газа19 совершая тепловое движение, они хаотически снуют туда-сюда между ионами кристаллической решётки. Суммарный заряд свободных электронов равен по модулю и противоположен по знаку общему заряду положительных ионов, поэтому металлический проводник в целом оказывается электрически нейтральным.

Газ свободных электронов является ¾клеем¿, на котором держится вся кристаллическая структура проводника. Ведь положительные ионы отталкиваются друг от друга, так что кристаллическая решётка, распираемая изнутри мощными кулоновскими силами, могла бы разлететься в разные стороны. Однако в то же самое время ионы металла притягиваются к обволаки-

18 А именно, свободные электроны перемещаются по внешним орбиталям соседних атомов. Эти орбитали перекрываются друг с другом вследствие близкого расположения атомов в кристаллической решётке, так что свободные электроны оказываются ¾общей собственностью¿ всего кристалла.

19 Другой адекватный образ электронное море, которое ¾омывает¿ кристаллическую решётку.

вающему их электронному газу и, как ни в чём не бывало, остаются на своих местах, совершая лишь тепловые колебания в узлах кристаллической решётки вблизи положений равновесия.

Что произойдёт, если металлический проводник включить в замкнутую цепь, содержащую источник тока? Свободные электроны продолжают совершать хаотическое тепловое движение, но теперь под действием возникшего внешнего электрического поля они вдобавок начнут перемещаться упорядоченно. Это направленное течение электронного газа, накладывающееся на тепловое движение электронов, и есть электрический ток в металле20 . Скорость упорядоченного движения электронов в металлическом проводнике, как нам уже известно, составляет порядка 0;1 мм/с.

3.13.2 Опыт Рикке

Почему мы решили, что ток в металлах создаётся движением именно свободных электронов? Положительные ионы кристаллической решётки также испытывают на себе действие внешнего электрического поля. Может, они тоже перемещаются внутри металлического проводника и участвуют в создании тока?

Упорядоченное движение ионов означало бы постепенный перенос вещества вдоль направления электрического тока. Поэтому надо просто пропускать ток по проводнику на протяжении весьма длительного времени и посмотреть, что в итоге получится. Такого рода эксперимент и был поставлен Э. Рикке в 1901 году.

В электрическую цепь были включены три прижатых друг к другу цилиндра: два медных по краям и один алюминиевый между ними (рис. 3.48 ). По этой цепи пропускался электрический ток в течение года.

Рис. 3.48. Опыт Рикке

За год сквозь цилиндры прошёл заряд более трёх миллионов кулон. Предположим, что каждый атом металла теряет по одному валентному электрону, так что заряд иона равен элементарному заряду e = 1;6 10 19 Кл. Если ток создаётся движением положительных ионов, то нетрудно подсчитать (сделайте это сами!), что такая величина прошедшего по цепи заряда соответствует переносу вдоль цепи около 2 кг меди.

Однако после разъединения цилиндров было обнаружено лишь незначительное проникновение металлов друг в друга, обусловленное естественной диффузией их атомов (и не более того). Электрический ток в металлах не сопровождается переносом вещества, поэтому положительные ионы металла не принимают участия в создании тока.

3.13.3 Опыт Стюарта–Толмена

Прямое экспериментальное доказательство того, что электрический ток в металлах создаётся движением свободных электронов, было дано в опыте Т. Стюарта и Р. Толмена (1916 год).

20 Поэтому свободные электроны называются также электронами проводимости.

Рис. 3.49. Опыт Стюарта–Толмена

Эксперименту Стюарта–Толмена предшествовали качественные наблюдения, сделанные четырьмя годами ранее русскими физиками Л. И. Мандельштамом и Н. Д. Папалекси. Они обратили внимание на так называемый электроинерционный эффект: если резко затормозить движущийся проводник, то в нём возникает кратковременный импульс тока. Эффект объясняется тем, что в течение небольшого времени после торможения проводника его свободные заряды продолжают двигаться по инерции.

Однако никаких количественных результатов Мандельштам и Папалекси не получили, и наблюдения их опубликованы не были. Честь назвать опыт своим именем принадлежит Стюарту и Толмену, которые не только наблюдали указанный электроинерционный эффект, но и произвели необходимые измерения и расчёты.

Установка Стюарта и Толмена показана на рис. 3.49 . Катушка большим числом витков металлического провода приводилась в быстрое вращение вокруг своей оси. Концы обмотки с помощью скользящих контактов были подсоединены к специальному прибору баллистическому гальванометру, который позволяет измерять проходящий через него заряд.

После резкого торможения катушки в цепи возникал импульс тока. Направление тока указывало на то, что он вызван движением отрицательных зарядов. Измеряя баллистическим гальванометром суммарный заряд, проходящий по цепи, Стюарт и Толмен вычислили отношение q=m заряда одной частицы к её массе. Оно оказалось равно отношению e=m для электрона, которое в то время уже было хорошо известно.

Так было окончательно выяснено, что носителями свободных зарядов в металлах являются свободные электроны. Как видите, этот давно и хорошо знакомый

вам факт был установлен сравнительно поздно учитывая, что металлические проводники к тому моменту уже более столетия активно использовались в самых разнообразных экcпериментах по электромагнетизму21 .

3.13.4 Зависимость сопротивления от температуры

Опыт показывает, что при нагревании металлического проводника его сопротивление увеличивается. Как это объяснить?

Причина проста: с повышением температуры тепловые колебания ионов кристаллической решётки становятся более интенсивными, так что число соударений свободных электронов с ионами возрастает. Чем активнее тепловое движение решётки, тем труднее электронам пробираться сквозь промежутки между ионами22 . Скорость упорядоченного движения электронов уменьшается, поэтому уменьшается и сила тока (при неизменном напряжении). Это и означает увеличение сопротивления.

21 Сравните, например, с датой открытия закона Ома 1826 год. Дело, однако, заключается в том, что сам электрон был открыт лишь в 1897 году.

22 Представьте себе вращающуюся проходную дверь. В каком случае труднее проскочить через неё: когда она вращается медленно или быстро? 🙂

Как опять-таки показывает опыт, зависимость сопротивле-
ния R металлического проводника от температуры t с хорошей
точностью является линейной:
R = R0 (1 + t):
Здесь R0 сопротивление проводника при 0 C. График за-
висимости (3.68 ) является прямой линией (рис.3.50 ).

Множитель называется температурным коэффициентом сопротивления. Его значения для различных металлов и сплавов можно найти в таблицах.

Длина проводника l и его площадь поперечного сечения S при изменении температуры меняются несущественно. Выразим R и R0 через удельное сопротивление:

и подставим эти формулы в (3.68 ). Получим аналогичную зависимость удельного сопротивления от температуры:

0 (1 + t):

Коэффициент весьма мал (для меди, например, = 0;0043), так что температурной зависимостью сопротивления металла часто можно пренебречь. Однако в ряде случаев считаться с ней приходиться. Например, вольфрамовая спираль электрической лампочки раскаляется до такой степени, что её вольт-амперная характеристика оказывается существенно нелинейной.

Рис. 3.51. Вольт-амперная характеристика лампочки

Так, на рис. 3.51 приведена вольт-амперная характеристика автомобильной лампочки. Если бы лампочка представляла собой идеальный резистор, её вольт-амперная характеристика была прямой линией в соответствии с законом Ома. Эта прямая изображена синим пунктиром.

Однако по мере роста напряжения, приложенного к лампочке, график отклоняется от этой прямой всё сильнее и сильнее. Почему? Дело в том, что с увеличением напряжения ток через лампочку возрастает и больше разогревает спираль; сопротивление спирали поэтому также увеличивается. Следовательно, сила тока хотя и продолжит возрастать, но будет иметь всё меньшее и меньшее значение по сравнению с тем, которое предписывается ¾пунктирной¿ линейной зависимостью тока от напряжения.

Электрический ток в металлах – это упорядоченное движение электронов под действием электрического поля. Опыты показывают, что при протекании тока по металлическому проводнику не происходит переноса вещества, следовательно, ионы металла не принимают участия в переносе электрического заряда.

Опыт Э.Рикке В этих опытах электрический ток пропускали в течении года через три прижатых друг к другу, хорошо отшлифованных цилиндра — медный, алюминиевый и снова медный. Общий заряд, прошедший за это время через цилиндры, был очень велик (около 3,5*10 6 Кл). После окончания было установлено, что имеются лишь незначительные следы взаимного проникновения металлов, которые не превышают результатов обычной диффузии атомов в твёрдых телах. Измерения, проведённые с высокой степенью точности, показали, что масса каждого из цилиндров осталась неизменной. Поскольку массы атомов меди и алюминия существенно отличаются друг от друга, то масса цилиндров должна была бы заметно измениться, если бы носителями заряда были ионы.

Следовательно, свободными носителями заряда в металлах являются не ионы. Огромный заряд, который прошёл через цилиндры, был перенесён, очевидно, такими частицами, которые одинаковы и в меди, и в алюминии. Как известно, такие частицы входят в состав атомов всех веществ — это электроны. Естественно предположить, что ток в металлах осуществляют именно свободные электроны.

Опыт Т.Стюарта и Р.Толмена Катушка с большим числом витков тонкой проволоки приводилась в быстрое вращение вокруг своей оси. Концы катушки с помощью гибких проводов были присоединены к чувствительному баллистическому гальванометру. Раскрученная катушка резко тормозилась, и в цепи возникал кратковременных ток, обусловленный инерцией носителей заряда. Полный заряд, протекающий по цепи, измерялся по отбросу стрелки гальванометра.

6. У всех металлов с увеличением температуры растет и сопротивление. R=R 0 (1+at) где a — температурный коэффициент; R 0 – удельное сопротивление и сопротивление металлического проводника; и R – удельное сопротивление проводника и сопротивление проводника при температуре t.

В 1911 году голландский физик Камерлинг- Оннес обнаружил, что при охлаждении ртути в жидком гелии её сопротивление сначала меняется постепенно, а затем при температуре 4,2 К резко падает до нуля. Однако нулевое сопротивление не единственная отличительная черта сверхпроводимости. Ещё из теории Друде известно, что проводимость металлов увеличивается с понижением температуры, то есть электрическое сопротивление стремится к нулю.

Область применения 1. получение сильных магнитных полей; 2.мощные электромагниты со сверхпроводящей обмоткой в ускорителях и генераторах. В настоящий момент в энергетике существует большая проблема — большие потери электроэнергии при передаче ее по проводам. Возможное решение проблемы: при сверхпроводимости сопротивление проводников приблизительно равно 0 и потери энергии резко уменьшаются.

Все металлы в твердом и жидком состоянии являются проводниками электрического тока. Специально поставленные опыты показали, что при прохождении злектрического тока масса металлических проводников остается постоянной, не изменяется и их химический состав. На этом основании можно было предположить, что в создании электрического тока в металлах участвуют только электроны. Предположение об электронной природе электрического тока в металлах подтверждено опытами советских физиков Л. И. Мандельштама и Н. Д. Папалекси и американских физиков Т. Стюарта и Р. Толмена. В этих опытах было обнаружено, что при резкой остановке быстро вращающейся катушки в проводе катушки возникает электрический ток, создаваемый отрицательно заряженными частицами — электронами.

При отсутствии электрического поля свободные электроны перемещаются в кристалле металла хаотически. Под действием электрического поля свободные электроны, кроме хаотического движения, приобретают упорядоченное движение в одном направлении, и в проводнике возникает электрический ток. Свободные электроны сталкиваются с ионами кристаллической решетки, отдавая им при каждом столкновении кинетическую энергию, приобретенную при свободном пробеге под действием электрического поля. В результате упорядоченное движение электронов в металле можно рассматривать как равномерное движение с некоторой постоянной скоростью V.

Так как кинетическая энергия электронов, приобретаемая под действием электрического поля, передается при столкновении ионами кристаллической решетки, то при прохождении постоянного тока проводник нагревается.

Зависимость удельного электрического сопротивления металлов от температуры.

Удельное сопротивление металлов при нагревании увеличивается приблизительно по линейному закону (рис. 152):

где р — удельное электрическое сопротивление металла при температуре t, ро — его удельное сопротивление при О °С, а — температурный коэффициент сопротивления, особый для каждого металла,

С приближением температуры к абсолютному нулю удельное сопротивление монокристаллов становится очень малым. Этот факт свидетельствует о том, что в идеальной кристаллической решетке металла электроны перемещаются под действием электрического поля, не взаимодействуя с ионами решетки. Длина их свободного пробега при этом может достигать значений, порядка 1 см, т. е. в 107-108 раз превышает межатомные расстояния в кристалле. Электроны взаимодействуют лишь с ионами, не находящимися в узлах кристаллической решетки.

При повышении температуры возрастает число дефектов в кристаллической решетке из-за тепловых колебаний ионов, — это приводит к возрастанию удельного сопротивления кристалла.

В том, что электрическое сопротивление металлов обусловлено взаимодействиями электронов проводимости с различными дефектами решетки, убеждает и тот факт, что удельное сопротивление кристаллов металлов сильно зависит от наличия в них примесей. Например, введение 1 % примеси марганца увеличивает удельное сопротивление меди в три раза.

Сверхпроводимость.

В 1911 г. нидерландский ученый Гейке Камерлинг-Ониес (1853- 1926) обнаружил, что при понижении температуры ртути до 4,1 К ее удельное сопротивление скачком уменьшается до нуля (рис. 153). Явление уменьшения удельного сопротивления до нуля при температуре, отличной от абсолютного нуля, называется сверхпроводимостью. Материалы, обнаруживающие способность переходить при некоторых температурах, отличных от абсолютного нуля, в сверхпроводящее состояние, называются сверхпроводниками.

Прохождение тока в сверхпроводнике происходит без потерь энергии, поэтому однажды возбужденный в сверхпроводящем кольце электрический ток может существовать неограниченно долго без изменения.

Сверхпроводящие материалы уже используются в электромагнитах. Ведутся исследования, направленные на создание сверхпроводящих линий электропередачи.

Применение явления сверхпроводимости в широкой

практике может стать реальностью в ближайшие годы благодаря открытию в 1986 г. сверхпроводимости керамик — соединений лантана, бария, меди и кислорода. Сверхпроводимость таких керамик сохраняется до температур около 100 К.

Скорость упорядоченного движения электронов в проводнике.

Для определения скорости упорядоченного движения свободных электрических зарядов в проводнике нужно знать концентрацию свободных носителей заряда и силу тока . Если концентрация свободных электрических зарядов в проводнике то за промежуток времени через поперечное сечение проводника при скорости их упорядоченного движения проходит электрический заряд равный

Электрический ток в металлах — это упорядоченное движение электронов под действием электрического поля. Опыты показывают, что при протекании тока по металлическому проводнику переноса вещества не происходит, следовательно, ионы металла не принимают участия в переносе электрического заряда.

Наиболее убедительное доказательство электронной природы тока в металлах было получено в опытах с инерцией электронов. Идея таких опытов и первые качественные результаты (1913 г.) принадлежат русским физикам Л.И. Мандельштаму и Н.Д. Папалекси В 1916 году американский физик Р. Толмен и шотландский физик Б. Стюарт усовершенствовали методику этих опытов и выполнили количественные измерения, неопровержимо доказавшие, что ток в металлических проводниках обусловлен движением электронов.

Схема опыта Толмена и Стюарта показана на рис. 1.12.1. Катушка с большим числом витков тонкой проволоки приводилась в быстрое вращение вокруг своей оси. Концы катушки с помощью гибких проводов были присоединены к чувствительному баллистическому гальванометру Г . Раскрученная катушка резко тормозилась, и в цепи возникал кратковременных ток, обусловленный инерцией носителей заряда. Полный заряд, протекающий по цепи, измерялся по отбросу стрелки гальванометра.

При торможении вращающейся катушки на каждый носитель заряда e действует тормозящая сила которая играет роль сторонней силы, то есть силы неэлектрического происхождения. Сторонняя сила, отнесенная к единице заряда, по определению является напряженностью E ст поля сторонних сил:

Следовательно, в цепи при торможении катушки возникает электродвижущая сила , равная

где l — длина проволоки катушки. За время торможения катушки по цепи протечет заряд q , равный

Здесь I — мгновенное значение силы тока в катушке, R — полное сопротивление цепи, υ 0 — начальная линейная скорость проволоки.

Отсюда удельный заряд e / m свободных носителей тока в металлах равен:

Все величины, входящие в правую часть этого соотношения, можно измерить. На основании результатов опытов Толмена и Стюарта было установлено, что носители свободного заряда в металлах имеют отрицательный знак, а отношение заряда носителя к его массе близко к удельному заряду электрона, полученному из других опытов. Так было установлено, что носителями свободных зарядов в металлах являются электроны.

По современным данным модуль заряда электрона (элементарный заряд ) равен

а его удельный заряд есть

Хорошая электропроводность металлов объясняется высокой концентрацией свободных электронов, равной по порядку величины числу атомов в единице объема.

Предположение о том, что за электрический ток в металлах ответственны электроны, возникло значительно раньше опытов Толмена и Стюарта. Еще в 1900 году немецкий ученый П. Друде на основании гипотезы о существовании свободных электронов в металлах создал электронную теорию проводимости металлов. Эта теория получила развитие в работах голландского физика Х. Лоренца и носит название классической электронной теории . Согласно этой теории, электроны в металлах ведут себя как электронный газ, во многом похожий на идеальный газ. Электронный газ заполняет пространство между ионами, образующими кристаллическую решетку металла (рис. 1.12.2).

Из-за взаимодействия с ионами электроны могут покинуть металл, лишь преодолев так называемый потенциальный барьер . Высота этого барьера называется работой выхода . При обычных (комнатных) температурах у электронов не хватает энергии для преодоления потенциального барьера.

Из-за взаимодействия с кристаллической решеткой потенциальная энергия выхода электрона внутри проводника оказывается меньше, чем при удалении электрона из проводника. Электроны в проводнике находятся в своеобразной «потенциальной яме», глубина которой и называется потенциальным барьером.

Как ионы, образующие решетку, так и электроны участвуют в тепловом движении. Ионы совершают тепловые колебания вблизи положений равновесия — узлов кристаллической решетки. Свободные электроны движутся хаотично и при своем движении сталкиваются с ионами решетки. В результате таких столкновений устанавливается термодинамическое равновесие между электронным газом и решеткой. Согласно теории Друде-Лоренца, электроны обладают такой же средней энергией теплового движения, как и молекулы одноатомного идеального газа. Это позволяет оценить среднюю скорость теплового движения электронов по формулам молекулярно-кинетической теории. При комнатной температуре она оказывается примерно равной 10 5 м/с.

При наложении внешнего электрического поля в металлическом проводнике кроме теплового движения электронов возникает их упорядоченное движение (дрейф), то есть электрический ток. Среднюю скорость дрейфа можно оценить из следующих соображений. За интервал времени Δt через поперечное сечение S проводника пройдут все электроны, находившиеся в объеме

Число таких электронов равно , где n — средняя концентрация свободных электронов, примерно равная числу атомов в единице объема металлического проводника. Через сечение проводника за время Δt пройдет заряд Отсюда следует:

Концентрация n атомов в металлах составляет 10 28 -10 29 м -3 .

Оценка по этой формуле для металлического проводника сечением 1 мм 2 , по которому течет ток 10 А, дает для средней скорости упорядоченного движения электронов значение в пределах 0,6-6 мм/c. Таким образом,

средняя скорость упорядоченного движения электронов в металлических проводниках на много порядков меньше средней скорости их теплового движения

Рис. 1.12.3 дает представление о характере движения свободного электрона в кристаллической решетке.

Малая скорость дрейфа на противоречит опытному факту, что ток во всей цепи постоянного тока устанавливается практически мгновенно. Замыкание цепи вызывает распространение электрического поля со скоростью c = 3·10 8 м/с. Через время порядка l / c (l — длина цепи) вдоль цепи устанавливается стационарное распределение электрического поля и в ней начинается упорядоченное движение электронов.

В классической электронной теории металлов предполагается, что движение электронов подчиняется законам механики Ньютона. В этой теории пренебрегают взаимодействием электронов между собой, а их взаимодействие с положительными ионами сводят только к соударениям. Предполагается также, что при каждом соударении электрон передает решетке всю накопленную в электрическом поле энергию и поэтому после соударения он начинает движение с нулевой дрейфовой скоростью.

Несмотря на то, что все эти допущения являются весьма приближенными, классическая электронная теория качественно объясняет законы электрического тока в металлических проводниках.

Закон Ома . В промежутке между соударениями на электрон действует сила, равная по модулю eE , в результате чего он приобретает ускорение . Поэтому к концу свободного пробега дрейфовая скорость электрона равна

где τ — время свободного пробега, которое для упрощения расчетов предполагается одинаковым для всех электронов. Среднее значение скорости дрейфа равно половине максимального значения:

Рассмотрим проводник длины l и сечением S с концентрацией электронов n . Ток в проводнике может быть записан в виде:

где U = El — напряжение на концах проводника. Полученная формула выражает закон Ома для металлического проводника. Электрическое сопротивление проводника равно:

а удельное сопротивление ρ и удельная проводимость ν выражаются соотношениями:

Закон Джоуля-Ленца.

К концу свободного пробега электроны под действием поля приобретают кинетическую энергию

Согласно сделанным предположениям вся эта энергия при соударениях передается решетке и переходит в тепло.

За время Δt каждый электрон испытывает Δt / τ соударений. В проводнике сечением S и длины l имеется nSl электронов. Отсюда следует, что выделяемое в проводнике за время Δt тепло равно:

Это соотношение выражает закон Джоуля-Ленца.

Таким образом, классическая электронная теория объясняет существование электрического сопротивления металлов, законы Ома и Джоуля-Ленца. Однако в ряде вопросов классическая электронная теория приводит к выводам, находящимся в противоречии с опытом.

Эта теория не может, например, объяснить, почему молярная теплоемкость металлов, также как и молярная теплоемкость диэлектрических кристаллов, равна 3R , где R — универсальная газовая постоянная (закон Дюлонга и Пти, см. ч. I, § 3.10). Наличие свободных электронов на сказывается на величине теплоемкости металлов.

Классическая электронная теория не может также объяснить температурную зависимость удельного сопротивления металлов. Теория дает соотношение , в то время как из эксперимента получается зависимость ρ ~ T . Однако наиболее ярким примером расхождения теории и опытов является сверхпроводимость .

Согласно классической электронной теории, удельное сопротивление металлов должно монотонно уменьшаться при охлаждении, оставаясь конечным при всех температурах. Такая зависимость действительно наблюдается на опыте при сравнительно высоких температурах. При более низких температурах порядка нескольких кельвинов удельное сопротивление многих металлов перестает зависеть от температуры и достигает некоторого предельного значения. Однако наибольший интерес представляет удивительное явление сверхпроводимости , открытое датским физиком Х.Каммерлинг-Онесом в 1911 году. При некоторой определенной температуре T кр, различной для разных веществ, удельное сопротивление скачком уменьшается до нуля (рис. 1.12.4). Критическая температура у ртути равна 4,1 К, у аллюминия 1,2 К, у олова 3,7 К. Сверхпроводимость наблюдается не только у элементов, но и у многих химических соединений и сплавов. Например, соединение ниобия с оловом (Ni 3 Sn) имеет критическую температуру 18 К. Некоторые вещества, переходящие при низких температурах в сверхпроводящее состояние, не являются проводниками при обычных температурах. В то же время такие «хорошие» проводники, как медь и серебро, не становятся сверхпроводниками при низких температурах.

Вещества в сверхпроводящем состоянии обладают исключительными свойствами. Практически наиболее важным их них является способность длительное время (многие годы) поддерживать без затухания электрический ток, возбужденный в сверхпроводящей цепи.

Классическая электронная теория не способна объяснить явление сверхпроводимости. Объяснение механизма этого явления было дано только через 60 лет после его открытия на основе квантово-механических представлений.

Научный интерес к сверхпроводимости возрастал по мере открытия новых материалов с более высокими критическими температурами. Значительный шаг в этом направлении был сделан в 1986 году, когда было обнаружено, что у одного сложного керамического соединения T кр = 35 K. Уже в следующем 1987 году физики сумели создать новую керамику с критической температурой 98 К, превышающей температуру жидкого азота (77 К). Явление перехода веществ в сверхпроводящее состояние при температурах, превышающих температуру кипения жидкого азота, было названо высокотемпературной сверхпроводимостью . В 1988 году было создано керамическое соединение на основе элементов Tl-Ca-Ba-Cu-O с критической температурой 125 К.

В настоящее время ведутся интенсивные работы по поиску новых веществ с еще более высокими значениями T кр. Ученые надеятся получить вещество в сверхпроводящем состоянии при комнатной температуре. Если это произойдет, это будет настоящей революцией в науке, технике и вообще в жизни людей.

Следует отметить, что до настоящего времени механизм высокотемпературной сверхпроводимости керамических материалов до конца не выяснен.

Электрическая цепь. Электрический ток в металлах

На прошлом уроке мы с вами говорили об электрическом токе и источниках тока. Давайте с вами вспомним, что электрическим током называется упорядоченное движение заряженных частиц.

Также мы узнали, что для создания и поддержания тока в цепи необходимы источники тока.

Но что же такое электрическая цепь? И если это цепь, то из каких звеньев она состоит?

Электрическая цепь — это совокупность устройств и элементов, предназначенных для протекания электрического тока.

Любая электрическая цепь содержит:

1)    источник тока, создающий необходимое напряжение;

2)    нагрузку, то есть то устройство, в котором нужно создать ток. Нагрузкой может быть нагреватель или лампа накаливания, электродвигатель или звонок, различные электробытовые приборы.

Звеньями же цепи являются соединительные провода и ключ, служащий для удобства и безопасности работы.

В качестве примера рассмотрим простейшую электрическую цепь. Она состоит из источника тока, ключа, который может замыкать и размыкать цепь, лампочки и соединительных проводов. Лампочка загорается только тогда, когда ключ замкнут.

Посмотрите ещё раз на рисунок электрической цепи. Если каждый раз её зарисовывать, то работа будет слишком долгой и трудоёмкой. Поэтому ввели условные обозначения для основных звеньев электрических цепей.

Чертежи, на которых в условных обозначениях изображены соединения электрических приборов, называют схемами.

На рисунке вы видите простейшую электрическую цепь и её схему. Сравните их.

Мы уже долгое время говорим об электрическом токе, но так и не выяснили, каково его направление в электрической цепи.

За направление электрического тока в цепи принято направление, в котором движутся (или могли бы двигаться) в проводнике положительные заряды, т. е. от положительного полюса источника к отрицательному.

Это соглашение было принято условно ещё в девятнадцатом веке, когда ещё не до конца понимали природу электрического тока и считали, что перемещаться могут только положительные заряды.

Конечно, после открытия электрона, который в большинстве случаев является носителем тока, стало понятно, что выбор был сделан неудачно, но старую договорённость менять не стали.

Мы уже знаем, что электрический ток может протекать через различные вещества: металлы, электролиты, и, при определённых условиях, через газы. Как уже говорилось, для возникновения электрического тока в любом веществе необходимо, чтобы там имелись носители зарядов, которые смогут перемещаться под действием электрического поля.

Так, например, в металлах носителями свободных зарядов являются электроны. Вы знаете, что все металлы в твёрдом состоянии обладают определённой кристаллической структурой. Поэтому всякий металл надо рассматривать как пространственную кристаллическую решётку, в узлах которой расположены положительные ионы. В пространстве же между ионами хаотично движутся свободные электроны, совокупность которых называют электронным газом.

Вследствие беспорядочного характера движения электронов переноса электрического заряда в каком-либо определённом направлении не получается. Но если внутри металла создать электрическое поле, то под влиянием его сил все свободные электроны придут в упорядоченное движение в направлении действия этих сил.

Однако неправильно думать, что электроны начнут двигаться прямолинейно. Траектория их движения также останется сложной, из-за взаимодействия с другими частицами. Движение электронов в этом случае напоминает дрейф льдин во время ледохода, когда они, двигаясь беспорядочно и сталкиваясь друг с другом, дрейфуют по течению реки.

А нельзя ли непосредственно на опыте проверить, что электрический ток в металле представляет собой поток электронов?

Конечно же можно. Идея одного такого опыта заключается в следующем. Если начать очень быстро вращать кусок металла, то увлечённый кристаллической решёткой электронный газ будет вместе с ним вращаться (на подобие жидкости во вращающемся сосуде). При внезапной остановке куска металла электронный газ должен некоторое время продолжать движение по инерции, подобно тому, как продолжает ещё вращаться жидкость в сосуде после его остановки. Задача заключалась в том, чтобы найти способ обнаружить это инерционное движение электронов.

И она была решена в1913 г. русскими физиками Леонидом Исааковичем Мандельштамом и Николаем Дмитриевичем Папалекси, а также в 1916 г. американскими учёными Ричардом Толменом и Томасом Стюартом. Опыт был проведён следующим образом. Катушка с большим числом витков тонкой проволоки приводилась в быстрое вращение вокруг своей оси. Концы проволоки посредством гибких проводников соединялись с чувствительным прибором — гальванометром, который позволяет судить о наличии тока.

При резком торможении катушки в течение долей секунды гальванометр обнаруживал ток. Причём направление этого тока, а о нём судили по направлению отклонения стрелки гальванометра, показывало, что он вызван движением отрицательно заряженных частичек, то есть электронов.

Таким образом удалось доказать, что электрический ток в металлах представляет собой направленное движение электронов. Но скорость этого движения мала — всего то несколько миллиметров в секунду, что в сотни миллионов раз меньше, чем средняя скорость теплового движения электронов. Поэтому, например, за 2 ч упорядоченного движения, электрон пройдёт менее 5 м.

Хотя мы знаем, что как только мы повернём выключатель, лампа, находящаяся в нескольких метрах от него, моментально загорается. Поэтому помните: скорость распространения тока и скорость направленного движения электронов — это не одно и то же.

Когда говорят о скорости протекания тока в проводнике, то имеют в виду скорость распространения электрического поля внутри проводника, которое и приводит в направленное движение электроны. А оно распространяется со скоростью около 300 000 км/с, то есть со скоростью света.

Нечто аналогичное мы имеем в явлении движения газа в газопроводах. Например, когда в саратовском конце газопровода Москва — Саратов, наполненного газом, поднимается давление, то оно со скоростью звука в газе (а это около 500 м/с) распространяется по трубам и быстро передаётся в Москву.

Но газ, находящийся в данный момент под Саратовом, попадёт в Москву гораздо позже, так как скорость его движения по трубам значительно меньше скорости передачи давления.

Электрический ток в металлах — презентация онлайн

1. Электрический ток в металлах

Электрический ток в металлах – это
упорядоченное движение электронов
под действием электрического поля.
Опыты показывают, что при протекании
тока по металлическому проводнику не
происходит переноса вещества,
следовательно, ионы металла не
принимают участия в переносе
электрического заряда.

3. Опыт К.Рикке

В этих опытах электрический ток пропускали в течении года через три
прижатых друг к другу, хорошо отшлифованных цилиндра — медный,
алюминевый и снова медный. Общий заряд, прошедший за это время
через цилиндры, был очень велик (около 3,5*106 Кл). После окончания
было установлено, что имеются лишь незначительные следы
взаимного проникновения металлов, которые не превышают
результатов обычной диффузии атомов в твёрдых телах. Измерения,
проведённые с высокой степенью точности, показали, что масса
каждого из цилиндров осталась неизменной. Поскольку массы атомов
меди и алюминия существенно отличаются друг от друга, то масса
цилиндров должна была бы заметно измениться, если бы носителями
заряда были ионы.
Следовательно, свободными носителями заряда в металлах являются
не ионы. Огромный заряд, который прошёл через цилиндры, был
перенесён, очевидно, такими частицами, которые одинаковы и в меди,
и в алюминии. Как известно, такие частицы входят в состав атомов
всех веществ — это электроны. Естественно предположить, что ток в
металлах осуществляют именно свободные электроны.

4. Опыт Т.Стюарта и Р.Толмена

Катушка с большим числом витков тонкой
проволоки приводилась в быстрое вращение
вокруг своей оси. Концы катушки с помощью
гибких проводов были присоединены к
чувствительному баллистическому
гальванометру Г. Раскрученная катушка
резко тормозилась, и в цепи возникал
кратковременных ток, обусловленный
инерцией носителей заряда. Полный заряд,
протекающий по цепи, измерялся по отбросу
стрелки гальванометра.
Т.Стюарт и Р.Толмен определили
экспериментально удельный заряд
частиц. Он оказался равным
В начале 20 века немецкий физик П.
Друде и голландский физик Х.Лоренц
создали классическую теорию
электропроводности металлов.

7. Основные положения теории:

1.
2.
Хорошая проводимость металлов
объясняется наличием в них большого
числа электронов.
Под действием внешнего
электрического поля на
беспорядочное движение электронов
накладывается упорядоченное
движение, т.е. возникает ток.
3. Сила электрического, тока идущего по
металлическому проводнику равна:
4. Так как внутреннее строение у
разных веществ различное, то и
сопротивление тоже будет различным.
5. При увеличении хаотического
движения частиц вещества происходит
нагревание тела, т.е. выделение тепла.
Закон Джоуля-Ленца:
6. У всех металлов с увеличением
температуры растет и сопротивление.
где a — температурный коэффициент; –
удельное сопротивление и сопротивление
металлического проводника; и R – удельное
сопротивление проводника и сопротивление
проводника при температуре t.

11. Сверхпроводимость металлов и сплавов

У многих металлов и
сплавов при температурах,
близких с T=0 К,
наблюдается резкое
уменьшение удельного
сопротивления – это явление
называется
сверхпроводимостью
металлов.
P
0
Т
Оно было обнаружено голландским
физиком Х.Камерлингом – Онессом в
1911 году у ртути ( Ткр=4,2оК).
Теория сверхпроводимости была
создана лишь в 1957 году
американцами Л.Купером, Дж.
Бардином и Дж. Шриффером. Они
считали, что сверх проводимость – это
сверхтекучесть электронной жидкости.

13. Область применения:

получение сильных магнитных полей;
мощные электромагниты со сверхпроводящей
обмоткой в ускорителях и генераторах.
В настоящий момент в энергетике существует
большая проблема
— большие потери электроэнергии при передаче ее по
проводам.
Возможное решение проблемы:
при сверхпроводимости сопротивление проводников
приблизительно равно 0
и потери энергии резко уменьшаются.

14. Общие сведения

Свойством сверхпроводимости обладают около
половины металлов и несколько сотен сплавов.
Сверхпроводящие свойства зависят от типа
кристаллической структуры. Изменение её может
перевести вещество из обычного в сверхпроводящее
состояние.
Критические температуры изотопов элементов,
переходящих в сверхпроводящее состояние, связаны с
массами изотопов соотношением:
Тэ(Мэ)1/2= const (изотопический эффект)
Сильное магнитное поле разрушает эффект
сверхпроводимости. Следовательно, при помещении в
магнитное поле свойство сверхпроводимости может
исчезнуть.

[Электрический ток вокруг дентальных металлов как фактор образования аллергенных ионов металлов в полости рта]

Сообщалось, что аллергия на стоматологические металлические сплавы иногда вызывает дерматит, стоматит, красный плоский лишай и ладонный и подошвенный пустулез. Согласно закону электролиза Фарадея, когда электрический ток протекает через анод, катионные ионы металлов растворяются параллельно количеству электрического тока. Следовательно, когда пациенты с гиперчувствительностью к металлам страдали от вышеупомянутых стойких дерматозов, измерение напряжений и электрических токов вокруг стоматологических сплавов полостей рта пациента было сочтено необходимым, чтобы исследовать, были ли эти стоматологические металлы поставлялись причинным металлом. ионы пациентам.Для исследования электрохимического растворения ионов металлов; Во-первых, измерялись напряжения и электрические токи между слизистой оболочкой и стандартными наконечниками из стоматологического сплава, помещенными в полости рта каждого 15 здоровых добровольцев и пациентов. Во-вторых, такое же исследование было выполнено со слизистой оболочкой и фактически установило дентальные металлы с 158 пациентами, которые показали положительную реакцию на аллергены дентальных металлических пластырей, состоящие из 19 реагентов. Результаты были следующими: 1) Напряжение между слизистыми оболочками и стандартными металлическими пластинами, помещенными в полости рта, варьировалось в зависимости от состава зубного металла.2) Вышеупомянутые напряжения менялись, когда в ротовой полости находилась различная еда. 3) Поскольку стоматологические металлы действительно присутствуют в ротовой полости пациента с гиперчувствительностью к металлам, напряжения между соседней слизистой оболочкой и зубными металлами сильно варьируются в зависимости от конкретного пациента, а не от типов металла. Некоторые сплавы действовали как катоды для одних пациентов, но как аноды для других. 4) Амальгама и сплавы серебра показали более высокие напряжения и больший электрический ток с меньшими диапазонами изменения, чем другие виды сплавов.Оба этих сплава имели тенденцию действовать как аноды, поэтому ожидалось, что электрохимическое растворение ионов металлов будет выше, чем у других металлов. 5) Напряжение и электрические токи между слизистой оболочкой и металлами часто были выше, чем между металлами. Эти результаты показывают, что собственная слизистая оболочка пациента действует как катод для электрохимического растворения, а не стоматологические металлы. 6) Измерение напряжения и электрического тока в полости рта пациента технически просто и считается ценным, поскольку четко продемонстрирована тенденция к электрохимическому растворению ионов металлов из дентальных металлов.

«Странные металлы» выявили совершенно новый вид электрического тока

Металлический оксид лантана, стронция, меди может не иметь большого значения для большинства из нас, но для физиков он может содержать секрет разработки электроники, которая проводит электричество с почти идеальной эффективностью.

При помещении в мощное магнитное поле вещество не проводит такие свойства, как другие металлы.

Как только мы узнаем почему, мы сможем, наконец, понять, как очаровательный класс материалов, называемых высокотемпературными сверхпроводниками (ВТСП), творит свое волшебство.

В отличие от своих низкотемпературных собратьев, эти теплые материалы состоят из определенных комбинаций элементов, расположенных так, чтобы заряд мог свободно перемещаться, несмотря на прерывания грубо покачивающихся частиц.

Имейте в виду, «тепло» — довольно относительное понятие. Им по-прежнему нужны температуры ниже −135 ° C (−211 ° F). Это лучше, чем примерно –240 ° C (–405 ° F) у низкотемпературных сверхпроводников, но это не поможет выжать больше энергии из аккумулятора ноутбука.

Расширение границ высокотемпературных сверхпроводников может однажды привести нас к этому.Единственная проблема в том, что мы мало знаем о том, как они функционируют.

Группа исследователей, возглавляемая Национальной лабораторией сильного магнитного поля в Университете штата Флорида, обнаружила интересное совпадение, которое может указать путь к механизму, лежащему в основе этого явления.

Странные особенности

В большинстве металлов электроны взаимодействуют с другими частицами в своей среде, образуя так называемые квазичастицы. В большей степени, чем сумма их частей, этот объект обладает всеми характеристиками вашего обычного электрона с некоторыми изменениями.

Квазичастицы также используются для объяснения плавного движения заряда через сверхпроводники. Взаимодействуя с особенностями своего окружения, электрон меняет свое поведение, помогая ему вести себя необычным образом.

Понимание большего количества этих квазичастичных состояний кажется ключом к решению загадки того, как построить сверхпроводник, способный выдерживать некоторое количество тепла.

Оксид меди, называемый купратами, составляет одну категорию HTS. Это тонкие листы оксида меди, зажатые между другими материалами, которые помогают «легировать» проводящие слои.

При правильной температуре эта комбинация превращается в то, что материаловеды называют «странным металлом».

Странность возникает из-за странной связи между устойчивым падением температуры и величиной сопротивления, обеспечиваемой его колеблющимися атомами.

Для большинства металлов при повышении температуры каждый добавленный градус добавляет одинаковое количество сопротивления. Вся эта линейная зависимость разваливается при более низких температурах.

Не так для купратов. Пока они все еще находятся в своей холодной сверхпроводящей зоне, они продолжают демонстрировать «странную» линейную зависимость между сопротивлением и температурой.

Новые потоки

Исследователей интересовала взаимосвязь между сопротивлением и силой окружающего магнитного поля. В других исследованиях магнетизм применялся для проверки различных характеристик купратов, но ни одно из них не изучало вариации его силы.

Итак, они поместили кусок оксида меди, лантана, лантана, меди, в магнитное поле силой 80 тесла — более чем в 50 раз сильнее, чем поле, которое вы найдете в обычном медицинском сканере.

Настройка этого поля также показала линейную зависимость сопротивления, как и в «странном» состоянии с понижением температуры.

Сходство вряд ли может быть чистой случайностью.

«Обычно когда видишь такие вещи, это означает, что за этим стоит очень простой принцип», — говорит физик Аркадий Шехтер.

Обнаружение пропорционального увеличения сопротивления с ростом магнетизма также предполагает корреляцию в поведении электронов, о чем подозревали, но требовали дополнительных доказательств.

Эта корреляция между электронами исключает какую-либо роль независимых квазичастиц. Это означает, что это должно быть что-то совершенно отличное от вашей типичной проводимости.

«Здесь мы имеем ситуацию, когда ни один существующий язык не может помочь», — говорит Шехтер. «Нам нужно найти новый язык, чтобы думать об этих материалах».

С новым языком появляется возможность новых способов создания и настройки еще более необычных материалов со сверхпроводящими свойствами.

Включая — только возможно — некоторые, которым не нужен резервуар с жидким водородом для охлаждения.

Это исследование было опубликовано в журнале Science .

Какие металлы проводят электричество? (Обновление видео)

Что такое электропроводность?

Электропроводность — это измеренная величина генерируемого тока на поверхности металлической мишени. Проще говоря, это то, насколько легко электрический ток может проходить через металл.

Какие металлы проводят электричество?

Хотя все металлы могут проводить электричество, некоторые металлы используются чаще из-за их высокой проводимости.Самый распространенный пример — медь. Он обладает высокой проводимостью, поэтому он используется в электропроводке со времен телеграфа. Однако латунь, которая содержит медь, гораздо менее проводящая, потому что она состоит из дополнительных материалов, которые снижают ее проводимость, что делает ее непригодной для электрических целей.

Вы можете быть удивлены, узнав, что медь даже не является самым проводящим металлом, несмотря на то, что она используется во многих обычных приложениях (и тот факт, что она используется в качестве измерительной линейки для оценки проводимости металлов).Другое распространенное заблуждение — чистое золото — лучший проводник электричества. Хотя золото действительно имеет относительно высокий рейтинг проводимости, на самом деле оно менее проводимо, чем медь.

Какой металл лучше всего проводит электричество?

Ответ: Чистое серебро. Проблема с серебром в том, что оно может потускнеть. Эта проблема может вызвать проблемы в приложениях, где важен скин-эффект, например, с токами высокой частоты. Кроме того, он дороже меди, и небольшое увеличение проводимости не стоит дополнительных затрат.

Итак, если все металлы проводят электричество, как они все ранжируются? Взгляните на этот график:

Материал IACS (Международный стандарт отожженной меди)
Рейтинг	Металл	% Проводимость *
1	Серебро (Чистое)	105%
2	Медь	100%
3	Золото (чистое)	70%
4	Алюминий	61%
5	Латунь	28%
6	Цинк	27%
7	Никель	22%
8	Железо (чистое)	17%
9	Олово	15%
10	Фосфорная бронза	15%
11	Сталь (включая нержавеющую сталь)	3-15%
12	Свинец (чистый)	7%
13	Никель-алюминиевая бронза	7%

* Значения проводимости выражены в единицах измерения относительно меди.100% рейтинг не означает отсутствие сопротивления.

Как видите, разница в электропроводности значительно зависит от металла. Как уже упоминалось, латунь имеет очень низкий рейтинг проводимости, несмотря на то, что она содержит медь, поэтому очень важно, чтобы не делались предположения об электропроводности материала. Всегда проводите как можно больше исследований!

Для чего используется медь?

Поскольку медь является отличным проводником электричества, ее чаще всего используют в электрических целях.Многие распространенные применения также зависят от одного или нескольких полезных свойств, таких как тот факт, что он является хорошим проводником тепла или имеет низкую реакционную способность (реакция с водой и кислотами).

Некоторые из распространенных применений меди включают:

Контакты в вилке 13A — Используется, потому что это электрический проводник с низкой реактивностью и высокой прочностью.

Водопроводные трубы — Используется, потому что они пластичные (мягкие), но в то же время жесткие и прочные. Он также обладает дополнительными антибактериальными свойствами и имеет низкую реактивность.

Основание кастрюли — Используется, потому что это хороший проводник тепла с низкой реактивностью и прочность.

Электрические кабели — Используются, потому что они являются хорошими электрическими проводниками, пластичными и прочными. Это включает в себя проводку для электроники, такой как телевизионное оборудование и аксессуары.

Микропроцессоры — Аналогичны электрическим кабелям; используется, потому что это хороший электрический проводник и пластичный.

Обновление видео

Нет времени читать блог?

Посмотрите видеоблог ниже, чтобы узнать, какие металлы лучше всего проводят электричество.

Металлические Супермаркеты

Metal Supermarkets — крупнейший в мире поставщик мелкосерийного металла с более чем 100 магазинами в США, Канаде и Великобритании. Мы эксперты по металлу и обеспечиваем качественное обслуживание клиентов и продукцию с 1985 года.

В Metal Supermarkets мы поставляем широкий ассортимент металлов для различных областей применения. В нашем ассортименте: низкоуглеродистая сталь, нержавеющая сталь, алюминий, инструментальная сталь, легированная сталь, латунь, бронза и медь.

У нас в наличии широкий ассортимент форм, включая стержни, трубы, листы, пластины и многое другое. И мы можем разрезать металл в точном соответствии с вашими требованиями.

Посетите одно из наших 95 офисов по всей Северной Америке сегодня.

Электричество, протекающее по проводам, изнашивает провода? | Ребята из науки

Изнашивает ли провода электричество, протекающее по проводам, то есть теряют ли провода массу после прохождения через них электричества?

май 2002 г.

Практически все, о чем мы знаем в повседневной жизни, изнашивается.Кажется естественным для кого-то задаться вопросом, изнашиваются ли провода, по которым проходит электричество, по мере прохождения через них электричества.

Чтобы ответить на этот вопрос, сначала представьте провод как канал, по которому что-то протекает. Если канал абсолютно заполнен, всякий раз, когда некоторое количество материала течет с одного конца, равное количество материала должно вытекать с другого конца. Так обстоит дело с электричеством. Материал, протекающий по проводам, несущим электричество, — это электроны, и когда определенное количество электронов течет в провод, такое же количество должно вытекать.Проволока — это просто путь, по которому движутся электроны.

Провода изготовлены из металлов, которые являются проводниками. В проводниках есть электроны, которые довольно свободно перемещаются. Электрический ток (электричество) — это поток или движение этих электронов по проводнику. Величина протекающего тока указывается в единицах, называемых амперами. Эти электроны вынуждены двигаться из-за разницы электрических потенциалов между двумя точками провода. Эта разность потенциалов может быть создана батареей, генератором, солнечным элементом или подобным устройством и выражается в единицах, называемых вольтами.

Рассмотрим провод, подключенный к клеммам аккумулятора с заданной разностью потенциалов (напряжением). Разность потенциалов, создаваемая батареей, заставляет электроны двигаться в одном конце провода и выходить из другого в равных количествах. Представьте себе трубу диаметром с мрамор, наполненную мрамором. Если вы толкнете шарик в один конец, шарик должен выйти из другого конца. Так обстоит дело с проволокой. По мере того как электроны движутся по одному концу провода, равное количество электронов выходит из другого конца.Во время нормального протекания тока в проводе ничего не создается и не теряется. После прохождения электричества остается столько же проводов, сколько было раньше.

Теперь может возникнуть ситуация, когда через провод протекает необычно большой ток. В этом случае электроны, сталкивающиеся с атомами в проволоке, создают тепло и повышают температуру проволоки. Если через провод пропускается достаточный ток, температура может стать достаточно высокой, чтобы расплавить провод. При таких высоких температурах некоторые материалы могут испаряться или окисляться с поверхности.Так обстоит дело с нитью накаливания лампочки, крошечной вольфрамовой проволокой, которая светится при больших токах. Таким образом, нить накаливания испаряется, и темный осадок часто можно увидеть на верхней части колбы.

Однако этот тип явления возникает только при сильном токе, который приводит к высоким температурам проволоки. В том, что мы назвали бы нормальными условиями, при прохождении электричества по проводу потери материала не происходит.

Механизм протекания тока в металлическом проводнике — Учебный материал для IIT JEE

Мы знаем, что проводник — это материал, содержащий подвижные или нестатические электрические заряды.Обсудим механизм металлических проводников. В случае металлических проводников этими заряженными частицами являются электроны. Помимо этого, положительные заряды также могут быть в форме ионов, как в электролите батареи. Изоляторы — это материалы, которые имеют меньше подвижных зарядов и препятствуют прохождению тока. Таким образом, все проводники содержат электрические заряды, но эти заряды перемещаются только тогда, когда создается некоторая разность потенциалов в двух разных точках проводника. Этот поток заряда измеряется в амперах и называется электрическим током.

В большинстве материалов, как подтверждается законом Ома, постоянный ток пропорционален напряжению при условии, что форма и состояние материала не меняются, а температура также остается постоянной. Медь — очень хороший проводник и поэтому обычно используется для электропроводки. Помимо этого, существует множество неметаллических проводников, таких как графит, растворы солей и плазма.

Определение и механизм электрического тока

Проще говоря, электрический ток — это движение или поток электрически заряженных частиц, и его единица измерения — амперы.Когда электрический ток течет по проводнику, он течет как дрейф свободных электронов в металле. Электричество легко проходит через проводник, потому что электроны могут свободно перемещаться внутри объекта. Когда электроны движутся по проводнику, возникает электрический ток. Ток также можно разделить на два типа — постоянный и переменный.

Постоянный или постоянный ток — Как следует из названия, ток, который всегда течет в одном направлении и не движется вперед и назад, называется постоянным током.Самый распространенный пример постоянного тока — это аккумулятор.

AC или переменный ток — Ток, который течет вперед и назад, а не в одном направлении, называется переменным током.

Прежде чем мы фактически обсудим механизм протекания тока в проводнике, мы объясним понятие скорости дрейфа, поскольку оно потребуется при его описании.

Скорость дрейфа: Средняя скорость, достигаемая некоторой частицей, такой как электрон, из-за существования электрического поля, называется дрейфовой скоростью.Фактически предполагается, что частицы движутся вдоль некоторой плоскости, и, следовательно, скорость также может быть названа скоростью осевого дрейфа.

Механизм протекания тока в проводнике

Теперь мы обсудим усовершенствованный механизм электрического тока. Протекание тока в металлах происходит из-за преимущественного протекания свободных электронов. В отсутствие какой-либо внешней ЭДС (посредством батареи) свободные электроны беспорядочно перемещаются через металл из одной точки в другую, давая нулевой чистый ток.

При подключении к батарее свободные электроны ускоряются за счет электрического поля (созданного батареей), и они получают скорость и энергию. Однако переход не является плавным, и электроны сталкиваются с ионом решетки, в котором конечным игроком (энергии) является ион. Поскольку мы знаем, что температура тела связана с энергией колебаний этих ионов, эти столкновения приводят к увеличению температуры металла. Потеря энергии электронов при столкновении и их ускорение электрическим полем, в конечном итоге, приводит к смещению электронов в определенном направлении.(Хотя реальное движение электронов неустойчиво, общий эффект заключается в дрейфе электронов).

Таким образом, движение проводящих электронов в электрическом поле представляет собой комбинацию движения из-за случайных столкновений. Когда мы рассматриваем все свободные электроны, их случайное движение в среднем равно нулю и не влияет на скорость дрейфа. Таким образом, скорость дрейфа обусловлена ​​только воздействием электрического поля на электроны.

Посмотрите это видео, чтобы узнать больше о протекании электрического тока

askIITians предлагает исчерпывающий учебный материал, который содержит все важные темы физики IIT JEE.Все области, такие как протекание тока через металлический проводник или механизм протекания тока, также были рассмотрены в содержании. Для соискателей JEE важно твердо владеть этой темой, чтобы оставаться конкурентоспособными в JEE.

Связанные ресурсы

Чтобы узнать больше, купите учебные материалы по Current Electricity, включая учебные заметки, заметки о пересмотре, видеолекции, решенные вопросы за предыдущий год и т. Д. Также просмотрите дополнительные учебные материалы по физике здесь.

9.3: Модель проводимости в металлах

Когда электроны движутся по проводящему проводу, они не движутся с постоянной скоростью, то есть электроны не движутся по прямой с постоянной скоростью. Скорее они взаимодействуют и сталкиваются с атомами и другими свободными электронами в проводнике. Таким образом, электроны движутся зигзагообразно и дрейфуют по проволоке. Следует также отметить, что, хотя направление тока удобно обсуждать, ток является скалярной величиной.Обсуждая скорость зарядов в токе, более уместно обсудить плотность тока. Мы вернемся к этой идее в конце этого раздела.

Скорость дрейфа

Электрические сигналы передаются очень быстро. Телефонные разговоры по проводам проходят на большие расстояния без заметных задержек. Свет включается, как только переключатель света переводится в положение «включено». Большинство электрических сигналов, переносимых токами, передаются со скоростью порядка 10-8 м / с, что составляет значительную часть скорости света.{-4} м / с \). Как согласовать эти две скорости и что это говорит нам о стандартных проводниках?

Высокая скорость электрических сигналов является результатом того факта, что сила между зарядами быстро действует на расстоянии. Таким образом, когда свободный заряд вдавливается в провод, как на рисунке \ (\ PageIndex {1} \), входящий заряд толкает другие заряды впереди себя из-за силы отталкивания между подобными зарядами. Эти движущиеся заряды толкают заряды дальше по линии. Плотность заряда в системе не может быть легко увеличена, поэтому сигнал передается быстро.Возникающая в результате электрическая ударная волна движется по системе почти со скоростью света. Если быть точным, этот быстро движущийся сигнал или ударная волна представляет собой быстро распространяющееся изменение электрического поля.

Рисунок \ (\ PageIndex {1} \): Когда заряженные частицы выталкиваются в этот объем проводника, такое же количество быстро вынуждено покинуть его. Отталкивание между одноименными зарядами затрудняет увеличение количества зарядов в объеме. Таким образом, как только один заряд входит, другой почти сразу уходит, быстро передавая сигнал вперед.

Хорошие проводники имеют большое количество бесплатных зарядов. В металлах свободными зарядами являются свободные электроны. (На самом деле, хорошие электрические проводники также часто являются хорошими проводниками тепла, потому что большое количество свободных электронов может переносить тепловую энергию, а также электрический ток.) ​​Рисунок \ (\ PageIndex {2} \) показывает, как свободные электроны движутся через обычные дирижер. Расстояние, на которое может перемещаться отдельный электрон между столкновениями с атомами или другими электронами, довольно мало. Таким образом, пути электронов кажутся почти случайными, как движение атомов в газе.Но в проводнике есть электрическое поле, которое заставляет электроны дрейфовать в указанном направлении (противоположном полю, поскольку они отрицательны). Скорость дрейфа \ (\ vec {v} _d \) — это средняя скорость свободных зарядов. Скорость дрейфа довольно мала, так как свободных зарядов очень много. Если у нас есть оценка плотности свободных электронов в проводнике, мы можем вычислить скорость дрейфа для данного тока. Чем больше плотность, тем ниже скорость, необходимая для данного тока.

Рисунок \ (\ PageIndex {2} \): Свободные электроны, движущиеся в проводнике, совершают множество столкновений с другими электронами и другими частицами. Показан типичный путь одного электрона. Средняя скорость свободных зарядов называется дрейфовой скоростью \ (\ vec {v} _d \), а для электронов она движется в направлении, противоположном электрическому полю. Столкновения обычно передают энергию проводнику, требуя постоянного подвода энергии для поддержания постоянного тока.

Столкновения свободных электронов передают энергию атомам проводника.Электрическое поле действительно перемещает электроны на расстояние, но эта работа не увеличивает кинетическую энергию (или скорость) электронов. Работа передается атомам проводника, часто повышая температуру. Таким образом, для поддержания протекания тока требуется постоянная подача энергии. (Исключение составляют сверхпроводники по причинам, которые мы рассмотрим в следующей главе. Сверхпроводники могут иметь постоянный ток без непрерывной подачи энергии — большая экономия энергии.) Для проводника, который не является сверхпроводником, подача энергии может быть полезно, как в нити накаливания лампы накаливания (Рисунок \ (\ PageIndex {3} \)).Подача энергии необходима для повышения температуры вольфрамовой нити, чтобы нить светилась.

Рисунок \ (\ PageIndex {3} \): Лампа накаливания имеет простую конструкцию. Вольфрамовая нить помещена в частично вакуумированную стеклянную колбу. Один конец нити накала прикреплен к основанию винта, которое выполнено из проводящего материала. Второй конец нити накала прикреплен ко второму контакту в основании лампы. Два контакта разделены изоляционным материалом.Ток течет через нить накала, и температура нити становится достаточно большой, чтобы нить накала светилась и излучала свет. Однако эти лампы не очень энергоэффективны, что видно по теплу, исходящему от лампы. В 2012 году Соединенные Штаты, наряду со многими другими странами, начали постепенно отказываться от ламп накаливания в пользу более энергоэффективных ламп, таких как светодиодные (LED) лампы и компактные люминесцентные лампы (CFL) (право кредита) : модификация работы Сержа Сен).

Мы можем получить выражение для связи между током и скоростью дрейфа, рассмотрев количество свободных зарядов в отрезке провода, как показано на рисунке \ (\ PageIndex {4} \). Количество бесплатных зарядов на единицу объема или плотность свободных зарядов обозначается символом \ (n \), где

\ [n = \ dfrac {\ text {количество зарядов}} {\ text {volume}}. \]

Значение \ (n \) зависит от материала. Заштрихованный сегмент имеет объем \ (Av_d \, dt \), так что количество свободных зарядов в объеме равно \ (nAv_d \, dt \).{-19} \, C \).) Ток — это заряд, перемещенный за единицу времени; таким образом, если все первоначальные заряды выходят из этого сегмента за время дт , ток равен

\ [I = \ dfrac {dQ} {dt} = qn Av_d. \]

Перестановка терминов дает

\ [v_d = \ dfrac {I} {nqA} \]

где

• \ (v_d \) — скорость дрейфа,
• \ (n \) — плотность свободного заряда,
• \ (A \) — площадь поперечного сечения провода, а
• \ (I \) — ток в проводе.

Каждый носитель тока имеет заряд q и движется со скоростью дрейфа величиной \ (v_d \).

Рисунок \ (\ PageIndex {4} \): Все заряды в заштрихованном объеме этого провода перемещаются за время dt , имея скорость дрейфа величиной \ (v_d \).

Обратите внимание, что простая скорость дрейфа — это еще не все. Скорость электрона иногда намного превышает скорость его дрейфа. Кроме того, не все электроны в проводнике могут двигаться свободно, а те, которые действительно движутся, могут двигаться несколько быстрее или медленнее, чем скорость дрейфа.Итак, что мы подразумеваем под свободными электронами?

Атомы в металлическом проводнике упакованы в виде решетчатой ​​структуры. Некоторые электроны находятся достаточно далеко от ядер атомов, поэтому они не испытывают такого сильного притяжения ядер, как внутренние электроны. Это свободные электроны. Они не связаны с одним атомом, но вместо этого могут свободно перемещаться между атомами в «море» электронов. При приложении электрического поля эти свободные электроны ускоряются.При движении они сталкиваются с атомами в решетке и с другими электронами, генерируя тепловую энергию, и проводник нагревается. В изоляторе организация атомов и структура не допускают наличие таких свободных электронов.

Как вы знаете, электроэнергия обычно подается к оборудованию и приборам через круглые провода, сделанные из проводящего материала (медь, алюминий, серебро или золото), многожильные или сплошные. Диаметр провода определяет допустимую нагрузку по току — чем больше диаметр, тем больше допустимая нагрузка по току.Несмотря на то, что допустимая нагрузка по току определяется диаметром, проволока обычно не характеризуется диаметром напрямую. Вместо этого проволока обычно продается в единицах измерения, известных как «калибр». Проволока изготавливается путем пропускания материала через круглые формы, называемые «фильеры для волочения». Чтобы изготавливать более тонкие проволоки, производители протягивают проволоку через несколько матриц последовательно уменьшающегося диаметра. Исторически калибр проволоки был связан с количеством процессов волочения, необходимых для производства проволоки.По этой причине, чем больше калибр, тем меньше диаметр. В Соединенных Штатах Америки для стандартизации системы был разработан американский калибр проводов (AWG). Бытовая электропроводка обычно состоит из проводов сечением от 10 (диаметром 2,588 мм) до 14 (диаметром 1,628 мм). Устройство, используемое для измерения толщины провода, показано на рисунке \ (\ PageIndex {5} \).

Рисунок \ (\ PageIndex {5} \): Устройство для измерения толщины электрического провода. Как видите, более высокие номера калибра указывают на более тонкие провода.

Пример \ (\ PageIndex {1} \): расчет скорости дрейфа в общем проводе

Рассчитайте скорость дрейфа электронов в медной проволоке диаметром 2.8 м / с \), чем несущие его заряды.

Упражнение \ (\ PageIndex {1} \)

В примере \ (\ PageIndex {1} \) скорость дрейфа была рассчитана для медного провода диаметром 2,053 мм (калибр 12), по которому проходит ток 20 ампер. Изменится ли скорость дрейфа для провода диаметром 1,628 мм (калибр 14), по которому течет тот же ток 20 ампер?

Ответ

Диаметр проволоки 14-го калибра меньше диаметра проволоки 12-го калибра. Поскольку скорость дрейфа обратно пропорциональна площади поперечного сечения, скорость дрейфа в проводе 14-го калибра больше, чем скорость дрейфа в проводе 12-го калибра, по которому течет тот же ток.Количество электронов на кубический метр останется постоянным.

Плотность тока

Хотя часто бывает удобно поставить отрицательный или положительный знак, чтобы указать общее направление движения зарядов, ток — это скалярная величина, \ (I = \ dfrac {dQ} {dt}. \) Часто необходимо обсудите детали движения заряда, вместо обсуждения общего движения зарядов. В таких случаях необходимо обсудить плотность тока, \ (\ vec {J} \), векторную величину.Плотность тока — это поток заряда через бесконечно малую площадь, разделенный на площадь. Плотность тока должна учитывать локальную величину и направление потока заряда, которые варьируются от точки к точке. Единицей измерения плотности тока является ампер на квадратный метр, а направление определяется как направление чистого потока положительных зарядов через площадь.

Рисунок \ (\ PageIndex {6} \): Плотность тока \ (\ vec {J} \) определяется как ток, проходящий через бесконечно малую площадь поперечного сечения, деленную на площадь.Направление плотности тока — это направление чистого потока положительных зарядов, а величина равна току, деленному на бесконечно малую площадь.

Связь между током и плотностью тока можно увидеть на рисунке \ (\ PageIndex {6} \). Дифференциальный ток, протекающий через область \ (d \ vec {A} \), находится как

\ [dI = \ vec {J} \ cdot d \ vec {A} = J dA \, \ cos \, \ theta, \]

где \ (\ theta \) — угол между площадью и плотностью тока.Полный ток, проходящий через область \ (d \ vec {A} \), можно найти путем интегрирования по площади,

\ [I = \ iint_ {area} \ vec {J} \ cdot d \ vec {A}. \]

Рассмотрим величину плотности тока, которая равна силе тока, разделенной на площадь:

\ [J = \ dfrac {I} {A} = \ dfrac {n | q | Av_d} {A} = n | q | v_d. \]

Таким образом, плотность тока равна \ (\ vec {J} = nq \ vec {v} _d \). Если q положительно, \ (\ vec {v} _d \) находится в том же направлении, что и электрическое поле \ (\ vec {E} \).Если q отрицательно, \ (\ vec {v} _d \) находится в направлении, противоположном \ (\ vec {E} \). В любом случае направление плотности тока \ (\ vec {J} \) совпадает с направлением электрического поля \ (\ vec {E} \).

Пример \ (\ PageIndex {2} \): расчет плотности тока в проводе

Ток, подаваемый на лампу с лампочкой мощностью 100 Вт, составляет 0,87 ампер. Лампа подключается медным проводом диаметром 2,588 мм (калибр 10). Найдите величину плотности тока.

Стратегия

Плотность тока — это ток, проходящий через бесконечно малую площадь поперечного сечения, деленную на площадь.2}. \]

Значение

Плотность тока в токопроводящем проводе зависит от тока, проходящего через токопроводящий провод, и площади поперечного сечения провода. При заданном токе с увеличением диаметра проволоки плотность заряда уменьшается.

Упражнение \ (\ PageIndex {2} \)

Плотность тока пропорциональна току и обратно пропорциональна площади. Если плотность тока в проводящем проводе увеличится, что произойдет со скоростью дрейфа зарядов в проводе?

Ответ

Плотность тока в проводящем проводе увеличивается из-за увеличения тока.Скорость дрейфа обратно пропорциональна текущему \ (\ left (v_d = \ dfrac {nqA} {I} \ right) \), поэтому скорость дрейфа уменьшится.

Какое значение имеет плотность тока? Плотность тока пропорциональна току, а ток — это количество зарядов, которые проходят через площадь поперечного сечения в секунду. Заряды движутся по проводнику, ускоряемые электрической силой, создаваемой электрическим полем. Электрическое поле создается при приложении напряжения к проводнику.В соответствии с законом Ома мы будем использовать эту взаимосвязь между плотностью тока и электрическим полем, чтобы исследовать взаимосвязь между током через проводник и приложенным напряжением.

Авторы и авторство

• Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).

9.2 Модель проводимости в металлах — University Physics Volume 2

Учебные цели

К концу этого раздела вы сможете:

• Определите скорость дрейфа зарядов, движущихся через металл
• Определите вектор плотности тока
• Опишите работу лампы накаливания

Когда электроны движутся по проводящему проводу, они не движутся с постоянной скоростью, то есть электроны не движутся по прямой с постоянной скоростью.Скорее они взаимодействуют и сталкиваются с атомами и другими свободными электронами в проводнике. Таким образом, электроны движутся зигзагообразно и дрейфуют по проволоке. Следует также отметить, что, хотя направление тока удобно обсуждать, ток является скалярной величиной. Обсуждая скорость зарядов в токе, более уместно обсудить плотность тока. Мы вернемся к этой идее в конце этого раздела.

Скорость дрейфа

Электрические сигналы передаются очень быстро.Телефонные разговоры по проводам проходят на большие расстояния без заметных задержек. Свет включается, как только переключатель света переводится в положение «включено». Большинство электрических сигналов, переносимых токами, передаются со скоростью порядка 108 м / с · 108 м / с, что составляет значительную часть скорости света. Интересно, что отдельные заряды, составляющие ток, в среднем движутся намного медленнее, обычно дрейфуя со скоростью порядка 10-4 м / с · 10-4 м / с. Как согласовать эти две скорости и что это говорит нам о стандартных проводниках?

Высокая скорость электрических сигналов является результатом того факта, что сила между зарядами быстро действует на расстоянии.Таким образом, когда свободный заряд вдавливается в провод, как на рисунке 9.7, входящий заряд толкает другие заряды впереди себя из-за силы отталкивания между одинаковыми зарядами. Эти движущиеся заряды толкают заряды дальше по линии. Плотность заряда в системе не может быть легко увеличена, поэтому сигнал передается быстро. Возникающая в результате электрическая ударная волна движется по системе почти со скоростью света. Если быть точным, этот быстро движущийся сигнал или ударная волна представляет собой быстро распространяющееся изменение электрического поля.

Фигура 9,7 Когда заряженные частицы вдавливаются в этот объем проводника, такое же количество быстро вынуждено покинуть его. Отталкивание между одноименными зарядами затрудняет увеличение количества зарядов в объеме. Таким образом, как только один заряд входит, другой почти сразу уходит, быстро передавая сигнал вперед.

Хорошие проводники имеют большое количество бесплатных зарядов. В металлах свободными зарядами являются свободные электроны. (Фактически, хорошие электрические проводники также часто являются хорошими проводниками тепла, потому что большое количество свободных электронов может переносить тепловую энергию, а также электрический ток.На рисунке 9.8 показано, как свободные электроны движутся по обычному проводнику. Расстояние, на которое может перемещаться отдельный электрон между столкновениями с атомами или другими электронами, довольно мало. Таким образом, пути электронов кажутся почти случайными, как движение атомов в газе. Но в проводнике есть электрическое поле, которое заставляет электроны дрейфовать в указанном направлении (противоположном полю, поскольку они отрицательны). Скорость дрейфа v → dv → d — это средняя скорость свободных зарядов. Скорость дрейфа довольно мала, так как свободных зарядов очень много.Если у нас есть оценка плотности свободных электронов в проводнике, мы можем вычислить скорость дрейфа для данного тока. Чем больше плотность, тем ниже скорость, необходимая для данного тока.

Фигура 9,8 Свободные электроны, движущиеся в проводнике, совершают множество столкновений с другими электронами и другими частицами. Показан типичный путь одного электрона. Средняя скорость свободных зарядов называется дрейфовой скоростью v → dv → d, а для электронов она направлена ​​в направлении, противоположном электрическому полю.Столкновения обычно передают энергию проводнику, требуя постоянного подвода энергии для поддержания постоянного тока.

Столкновения свободных электронов передают энергию атомам проводника. Электрическое поле действительно перемещает электроны на расстояние, но эта работа не увеличивает кинетическую энергию (или скорость) электронов. Работа передается атомам проводника, часто повышая температуру. Таким образом, для поддержания протекания тока требуется постоянная подача энергии.(Исключением являются сверхпроводники по причинам, которые мы рассмотрим в следующей главе. Сверхпроводники могут иметь постоянный ток без непрерывной подачи энергии — большая экономия энергии.) Для проводника, который не является сверхпроводником, подача энергии может быть полезен, как в нити накаливания лампы накаливания (рис. 9.9). Подача энергии необходима для повышения температуры вольфрамовой нити, чтобы нить светилась.

Фигура 9.9 Лампа накаливания отличается простой конструкцией.Вольфрамовая нить помещена в частично вакуумированную стеклянную колбу. Один конец нити накала прикреплен к основанию винта, которое выполнено из проводящего материала. Второй конец нити накала прикреплен ко второму контакту в основании лампы. Два контакта разделены изоляционным материалом. Ток течет через нить накала, и температура нити становится достаточно большой, чтобы нить накала светилась и излучала свет. Однако эти лампы не очень энергоэффективны, что видно по теплу, исходящему от лампы.В 2012 году Соединенные Штаты, наряду со многими другими странами, начали постепенно отказываться от ламп накаливания в пользу более энергоэффективных ламп, таких как светодиодные (LED) лампы и компактные люминесцентные лампы (CFL) (кредитное право : модификация работы Сержа Сен).

Мы можем получить выражение для связи между током и скоростью дрейфа, рассмотрев количество свободных зарядов в отрезке провода, как показано на рисунке 9.10. Количество бесплатных зарядов на единицу объема или плотность свободных зарядов обозначается символом n , где n = количество зарядов, объем = количество зарядов, объем.Значение n зависит от материала. Заштрихованный сегмент имеет том AvddtAvddt, поэтому количество бесплатных зарядов в томе равно nAvddtnAvddt. Таким образом, заряд dQ в этом сегменте равен qnAvddtqnAvddt, где q — это количество заряда на каждом носителе. (Величина заряда электронов q = 1,60 · 10−19Cq = 1,60 · 10−19C.) Ток перемещается за единицу времени; таким образом, если все первоначальные заряды выходят из этого сегмента за время дт , ток равен

. Я = dQdt = qnAvd.Я = dQdt = qnAvd.

Перестановка терминов дает

, где vdvd — скорость дрейфа, n — плотность свободного заряда, A — площадь поперечного сечения провода, а I — ток через провод. Каждый из носителей тока имеет заряд q и движется со скоростью дрейфа величиной vdvd.

Фигура 9.10 Все заряды в заштрихованном объеме этой проволоки перемещаются за время dt , имея скорость дрейфа величиной vdvd.

Обратите внимание, что простая скорость дрейфа — это еще не все. Скорость электрона иногда намного превышает скорость его дрейфа. Кроме того, не все электроны в проводнике могут двигаться свободно, а те, которые движутся, могут двигаться несколько быстрее или медленнее, чем скорость дрейфа. Итак, что мы подразумеваем под свободными электронами?

Атомы в металлическом проводнике упакованы в виде решетчатой ​​структуры. Некоторые электроны находятся достаточно далеко от ядер атомов, поэтому они не испытывают такого сильного притяжения ядер, как внутренние электроны.Это свободные электроны. Они не связаны с одним атомом, но вместо этого могут свободно перемещаться между атомами в «море» электронов. При приложении электрического поля эти свободные электроны ускоряются. При движении они сталкиваются с атомами в решетке и с другими электронами, генерируя тепловую энергию, и проводник нагревается. В изоляторе организация атомов и структура не допускают наличие таких свободных электронов.

Как вы знаете, электроэнергия обычно подается к оборудованию и приборам через круглые провода, сделанные из проводящего материала (медь, алюминий, серебро или золото), многожильные или сплошные.Диаметр провода определяет пропускную способность по току — чем больше диаметр, тем больше пропускная способность по току. Несмотря на то, что допустимая нагрузка по току определяется диаметром, проволока обычно не характеризуется диаметром напрямую. Вместо этого проволока обычно продается в единицах измерения, известных как «калибр». Проволока изготавливается путем пропускания материала через круглые формы, называемые «фильеры для волочения». Чтобы изготавливать более тонкие проволоки, производители протягивают проволоку через несколько матриц последовательно уменьшающегося диаметра.Исторически калибр проволоки был связан с количеством процессов волочения, необходимых для производства проволоки. По этой причине, чем больше калибр, тем меньше диаметр. В Соединенных Штатах Америки для стандартизации системы был разработан американский калибр проводов (AWG). Бытовая электропроводка обычно состоит из проводов сечением от 10 (диаметром 2,588 мм) до 14 (диаметром 1,628 мм). Устройство, используемое для измерения толщины проволоки, показано на рисунке 9.11.

Фигура 9,11 Устройство для измерения толщины электрического провода.Как видите, более высокие номера калибра указывают на более тонкие провода. (Источник: Джозеф Дж. Траут)

Пример 9,3

Расчет скорости дрейфа в общем проводе

Рассчитайте скорость дрейфа электронов в медной проволоке диаметром 2,053 мм (калибр 12), по которой проходит ток 20,0 А, учитывая, что на один атом меди приходится один свободный электрон. (Бытовая электропроводка часто содержит медный провод 12-го калибра, и максимальный допустимый ток в таком проводе обычно составляет 20,0 А.) Плотность меди составляет 8.80 × 103 кг / м 38,80 × 103 кг / м3, а атомная масса меди составляет 63,54 г / моль.

Стратегия

Мы можем рассчитать скорость дрейфа, используя уравнение I = nqAvdI = nqAvd. Ток I = 20.00AI = 20.00A, а q = 1.60 · 10−19Cq = 1.60 · 10−19C — заряд электрона. Площадь поперечного сечения провода можно рассчитать по формуле A = πr2A = πr2, где r — половина диаметра. Данный диаметр составляет 2,053 мм, поэтому r составляет 1,0265 мм. Нам дана плотность меди 8,80 × 103 кг / м38.80 × 103 кг / м3, а атомная масса меди 63,54 г / моль 63,54 г / моль. Мы можем использовать эти две величины вместе с числом Авогадро, 6,02 × 1023 атома / моль, 6,02 × 1023 атома / моль, чтобы определить n , количество свободных электронов на кубический метр.

Решение

Сначала рассчитаем плотность свободных электронов в меди. На один атом меди приходится один свободный электрон. Следовательно, количество свободных электронов такое же, как количество атомов меди в м3 м3. Теперь мы можем найти n следующим образом: п = 1e − атом × 6.02 × 1023 атомсмоль × 1 моль 63,54 г × 1000 г кг × 8,80 × 103 кг1м3 = 8,34 × 1028e- / м3.n = 1e − атом × 6,02 × 1023атомсмоль × 1 моль 63,54 г × 1000 г кг × 8,80 × 103 кг1м3 = 8,34 × 1028e- / м3.

Площадь сечения провода

A = πr2 = π (2,05 · 10−3м2) 2 = 3,30 · 10−6м2. A = πr2 = π (2,05 · 10−3м2) 2 = 3,30 · 10−6м2.

Перестановка I = nqAvdI = nqAvd для изоляции скорости дрейфа дает

vd = InqA = 20,00A (8,34 × 1028 / м3) (- 1,60 × 10−19C) (3,30 × 10−6м2) = — 4,54 × 10−4 м / с. vd = InqA = 20,00A (8,34 × 1028 / м3 ) (- 1,60 × 10−19C) (3,30 × 10−6м2) = — 4,54 × 10−4 м / с.

Значение

Знак минус указывает на то, что отрицательные заряды движутся в направлении, противоположном обычному току.Небольшое значение скорости дрейфа (порядка 10-4 м / с) 10-4 м / с) подтверждает, что сигнал движется примерно в 1012 · 1012 раз быстрее (около 108 м / с) 108 м / с), чем заряды, несущие Это.

Проверьте свое понимание 9,3

Проверьте свое понимание В примере 9.4 скорость дрейфа была рассчитана для медного провода диаметром 2,053 мм (калибра 12), по которому проходит ток 20 А. Изменится ли скорость дрейфа для провода диаметром 1,628 мм (калибр 14), по которому течет тот же ток 20 ампер?

Плотность тока

Хотя часто бывает удобно поставить отрицательный или положительный знак, чтобы указать общее направление движения зарядов, ток является скалярной величиной, I = dQdtI = dQdt.Часто необходимо обсудить детали движения заряда вместо обсуждения общего движения зарядов. В таких случаях необходимо обсудить плотность тока, J → J →, векторную величину. Плотность тока — это поток заряда через бесконечно малую площадь, деленную на площадь. Плотность тока должна учитывать локальную величину и направление потока заряда, которые варьируются от точки к точке. Единицей измерения плотности тока является ампер на квадратный метр, а направление определяется как направление чистого потока положительных зарядов через площадь.

Соотношение между током и плотностью тока можно увидеть на Рисунке 9.12. Дифференциальный ток, протекающий через область dA → dA →, находится как

dI = J → · dA → = JdAcosθ, dI = J → · dA → = JdAcosθ,

где θθ — угол между площадью и плотностью тока. Полный ток, проходящий через область dA → dA →, можно найти путем интегрирования по площади,

I = areaJ → · dA → .I = areaJ → · dA →.

9,5

Рассмотрим величину плотности тока, которая равна силе тока, разделенной на площадь:

J = IA = n | q | AvdA = n | q | vd.J = IA = n | q | AvdA = n | q | vd.

Таким образом, плотность тока J → = nqv → dJ → = nqv → d. Если q положительно, v → dv → d находится в том же направлении, что и электрическое поле E → E →. Если q отрицательно, v → dv → d находится в направлении, противоположном E → E →. В любом случае направление плотности тока J → J → находится в направлении электрического поля E → E →.

Фигура 9,12 Плотность тока J → J → определяется как ток, проходящий через бесконечно малую площадь поперечного сечения, деленную на площадь.Направление плотности тока — это направление чистого потока положительных зарядов, а величина равна току, деленному на бесконечно малую площадь.

Пример 9,4

Расчет плотности тока в проводе

Сила тока, подаваемого на лампу с лампочкой мощностью 100 Вт, составляет 0,87 ампер. Лампа подключается медным проводом диаметром 2,588 мм (калибр 10). Найдите величину плотности тока.

Стратегия

Плотность тока — это ток, проходящий через бесконечно малую площадь поперечного сечения, деленную на площадь.Мы можем рассчитать величину плотности тока, используя J = IAJ = IA. Сила тока составляет 0,87 А. Площадь поперечного сечения может быть рассчитана как A = 5,26 мм2A = 5,26 мм2.

Решение

Рассчитайте плотность тока, используя заданный ток I = 0,87AI = 0,87A и площадь, которая составляет A = 5,26 мм2A = 5,26 мм2. J = IA = 0.87A5.26 × 10−6m2 = 1.65 × 105Am2. J = IA = 0.87A5.26 × 10−6m2 = 1.65 × 105Am2.

Значение

Плотность тока в проводящем проводе зависит от тока, проходящего через проводящий провод, и площади поперечного сечения провода.При заданном токе с увеличением диаметра проволоки плотность заряда уменьшается.

Проверьте свое понимание 9,4

Проверьте свое понимание Плотность тока пропорциональна току и обратно пропорциональна площади. Если плотность тока в проводящем проводе увеличится, что произойдет со скоростью дрейфа зарядов в проводе?

Какое значение имеет плотность тока? Плотность тока пропорциональна току, а ток — это количество зарядов, которые проходят через площадь поперечного сечения в секунду.Заряды движутся по проводнику, ускоряемые электрической силой, создаваемой электрическим полем. Электрическое поле создается при приложении напряжения к проводнику. В соответствии с законом Ома мы будем использовать эту взаимосвязь между плотностью тока и электрическим полем, чтобы исследовать взаимосвязь между током через проводник и приложенным напряжением.