Электрический резонанс Википедия

Эффект резонанса для разных частот внешнего воздействия и коэффициентов затухания Раскачивание человека на качелях — типичный пример резонанса. Нагруженное колебание, маятник, имеет собственную частоту колебаний, свою резонансную частоту и сопротивляется давлению с большей или меньшей скоростью.

Резона́нс (фр. resonance, от лат. resono «откликаюсь») — частотно-избирательный отклик колебательной системы на периодическое внешнее воздействие, который проявляется в резком увеличении амплитуды стационарных колебаний при совпадении частоты внешнего воздействия с определёнными значениями, характерными для данной системы^[1]. Для линейных колебательных систем значения частот резонанса совпадает с частотами собственных колебаний, а их число соответствует числу степеней свободы^[1].

Под действием резонанса, колебательная система оказывается особенно отзывчивой на действие внешней силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротностью. При помощи резонанса можно выделить и/или усилить даже весьма слабые периодические колебания.

Явление резонанса впервые было описано Галилео Галилеем в 1602 г. в работах, посвященных исследованию маятников и музыкальных струн.^[2][3]

Механика[ | ]

Школьный резонансный массовый эксперимент

Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если подталкивать качели в определённые моменты времени в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния можно найти по формуле:

f=12π

Электрический резонанс Википедия

Эффект резонанса для разных частот внешнего воздействия и коэффициентов затухания Раскачивание человека на качелях — типичный пример резонанса. Нагруженное колебание, маятник, имеет собственную частоту колебаний, свою резонансную частоту и сопротивляется давлению с большей или меньшей скоростью.

Резона́нс (фр. resonance, от лат. resono «откликаюсь») — частотно-избирательный отклик колебательной системы на периодическое внешнее воздействие, который проявляется в резком увеличении амплитуды стационарных колебаний при совпадении частоты внешнего воздействия с определёнными значениями, характерными для данной системы

[1]. Для линейных колебательных систем значения частот резонанса совпадает с частотами собственных колебаний, а их число соответствует числу степеней свободы^[1].

Под действием резонанса, колебательная система оказывается особенно отзывчивой на действие внешней силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротностью. При помощи резонанса можно выделить и/или усилить даже весьма слабые периодические колебания.

Явление резонанса впервые было описано Галилео Галилеем в 1602 г. в работах, посвященных исследованию маятников и музыкальных струн.^[2][3]

Механика

Школьный резонансный массовый эксперимент

Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если подталкивать качели в определённые моменты времени в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния можно найти по формуле:

f=12πgL{\displaystyle f={1 \over 2\pi }{\sqrt {g \over L}}},

где g — это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс. (Более точная формула довольно сложна и включает эллиптический интеграл.) Важно, что резонансная частота не зависит от массы маятника. Также важно, что раскачивать маятник нельзя на кратных частотах (высших гармониках), зато это можно делать на частотах, равных долям от основной (низших гармониках).

Резонансные явления могут приводить как к разрушению, так и к усилению устойчивости механических систем.

В основе работы механических резонаторов лежит преобразование потенциальной энергии в кинетическую и наоборот. В случае простого маятника, вся его энергия содержится в потенциальной форме, когда он неподвижен и находится в верхних точках траектории, а при прохождении нижней точки на максимальной скорости, она преобразуется в кинетическую. Потенциальная энергия пропорциональна массе маятника и высоте подъёма относительно нижней точки, кинетическая — массе и квадрату скорости в точке измерения.

Другие механические системы могут использовать запас потенциальной энергии в различных формах. Например, пружина запасает энергию сжатия, которая, фактически, является энергией связи её атомов.

Струна

Струны таких инструментов, как лютня, гитара, скрипка или пианино, имеют основную резонансную частоту, напрямую зависящую от длины, массы и силы натяжения струны. Длина волны первого резонанса струны равна её удвоенной длине. При этом, её частота зависит от скорости

v, с которой волна распространяется по струне:

f=v2L{\displaystyle f={v \over 2L}}

где L — длина струны (в случае, если она закреплена с обоих концов). Скорость распространения волны по струне зависит от её натяжения T и массы на единицу длины ρ:

v=Tρ{\displaystyle v={\sqrt {T \over \rho }}}

Таким образом, частота главного резонанса может зависеть от свойств струны и выражается следующим отношением:

f=Tρ2L=Tm/L2L=T4mL{\displaystyle f={{\sqrt {T \over \rho }} \over 2L}={{\sqrt {T \over m/L}} \over 2L}={\sqrt {T \over 4mL}}},

где T — сила натяжения, ρ — масса единицы длины струны, а m — полная масса струны.

Увеличение натяжения струны и уменьшение её массы (толщины) и длины увеличивает её резонансную частоту. Помимо основного резонанса, струны также имеют резонансы на высших гармониках основной частоты f, например, 2f, 3f, 4f^[4], и т. д. Если струне придать колебание коротким воздействием (щипком пальцев или ударом молоточка), струна начнёт колебания на всех частотах, присутствующих в воздействующем импульсе (теоретически, короткий импульс содержит

все частоты). Однако частоты, не совпадающие с резонансными, быстро затухнут, и мы услышим только гармонические колебания, которые и воспринимаются как музыкальные ноты.

Электроника

В электрических цепях резонансом называется такой режим пассивной цепи, содержащий катушки индуктивности и конденсаторы, при котором ее входное реактивное сопротивление или ее входная реактивная проводимость равны нулю. При резонансе ток на входе цепи, если он отличен от нуля, совпадает по фазе с напряжением.

В электрических цепях резонанс возникает на определённой частоте, когда индуктивная и ёмкостная составляющие реакции системы уравновешены, что позволяет энергии циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора.

Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником.

Электрическое устройство, состоящее из ёмкости и индуктивности, называется колебательным контуром. Элементы колебательного контура могут быть включены как последовательно (тогда возникает резонанс напряжений), так и параллельно (резонанс токов). При достижении резонанса, импеданс последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален. Резонансные процессы в колебательных контурах используются в элементах настройки, электрических фильтрах. Частота, на которой происходит резонанс, определяется величинами (номиналами) используемых элементов. В то же время, резонанс может быть и вреден, если он возникает в неожиданном месте по причине повреждения, недостаточно качественного проектирования или производства электронного устройства. Такой резонанс может вызывать паразитный шум, искажения сигнала, и даже повреждение компонентов.

Приняв, что в момент резонанса индуктивная и ёмкостная составляющие импеданса равны, резонансную частоту можно найти из выражения

ωL=1ωC⇒ω=1LC{\displaystyle \omega L={\frac {1}{\omega C}}\Rightarrow \omega ={\frac {1}{\sqrt {LC}}}},

где ω=2πf{\displaystyle \omega =2\pi f} ; f — резонансная частота в герцах; L — индуктивность в генри; C — ёмкость в фарадах. Важно, что в реальных системах понятие резонансной частоты неразрывно связано с полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте. Ширина полосы пропускания определяется добротностью системы.

В электронных устройствах также применяются различные электромеханические резонансные системы.

СВЧ

В СВЧ электронике широко используются объёмные резонаторы, чаще всего цилиндрической или тороидальной геометрии с размерами порядка длины волны, в которых возможны добротные колебания электромагнитного поля на отдельных частотах, определяемых граничными условиями. Наивысшей добротностью обладают сверхпроводящие резонаторы, стенки которых изготовлены из сверхпроводника и диэлектрические резонаторы с модами шепчущей галереи.

Оптика

В оптическом диапазоне самым распространенным типом резонатора является резонатор Фабри-Перо, образованный парой зеркал, между которыми в резонансе устанавливается стоячая волна. Применяются также кольцевые резонаторы с бегущей волной и оптические микрорезонаторы с модами шепчущей галереи.

Акустика

Резонанс — один из важнейших физических процессов, используемых при проектировании звуковых устройств, большинство из которых содержат резонаторы, например, струны и корпус скрипки, трубка у флейты, корпус у барабанов.

Для акустических систем и громкоговорителей резонанс отдельных элементов (корпуса, диффузора) является нежелательным явлением, так как ухудшает равномерность амплитудно-частотной характеристики устройства и верность звуковоспроизведения. Исключением являются акустические системы с фазоинвертором, в которых намеренно создаётся резонанс для улучшения воспроизведения низких частот.

Астрофизика

Орбитальный резонанс в небесной механике — это ситуация, при которой два (или более) небесных тела имеют периоды обращения, которые относятся как небольшие натуральные числа. В результате эти небесные тела оказывают регулярное гравитационное влияние друг на друга, которое может стабилизировать их орбиты.

См. также

Видеоурок: резонанс

Примечания

Литература

• Richardson LF (1922), Weather prediction by numerical process, Cambridge.
• Bretherton FP (1964), Resonant interactions between waves. J. Fluid Mech., 20, 457—472.
• Бломберген Н. Нелинейная оптика, М.: Мир, 1965. — 424 с.
• Захаров В. Е. (1974), Гамильтонов формализм для волн в нелинейных средах с дисперсией, Изв. вузов СССР. Радиофизика, 17(4), 431—453.
• Арнольд В. И. Потеря устойчивости автоколебаний вблизи резонансов, Нелинейные волны / Ред. А. В. Гапонов-Грехов. — М.: Наука, 1979. С. 116—131.
• Kaup PJ, Reiman A and Bers A (1979), Space-time evolution of nonlinear three-wave interactions. Interactions in a homogeneous medium, Rev. of Modern Phys, 51(2), 275—309.
• Haken H (1983), Advanced Synergetics. Instability Hierarchies of Self-Organizing Systems and devices, Berlin, Springer-Verlag.
• Филлипс O.М. Взаимодействие волн. Эволюция идей, Современная гидродинамика. Успехи и проблемы. — М.: Мир, 1984. — С. 297—314.
• Журавлёв В. Ф., Климов Д. М. Прикладные методы в теории колебаний. — М.: Наука, 1988.
• Сухоруков А. П.. Нелинейные волновые взаимодействия в оптике и радиофизике. — Москва: Наука, 1988. — 230 с. — ISBN 5-02-013842-8.
• Брюно А. Д. Ограниченная задача трёх тел. — М.: Наука, 1990.
• Широносов В. Г. Резонанс в физике, химии и биологии. — Ижевск: Издательский дом «Удмуртский университет», 2000. — 92 с.
• Резонанс // Музыкальная энциклопедия. — М.: Советская энциклопедия, 1978. — Т. 4. — С. 585—586. — 976 с.

Ссылки

45. Вынужденные электрические колебания

Установившиеся колебания. Вернемся к уравнениям колебательного контура:

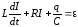или с учетом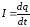

.

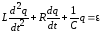Рассмотрим случай, когда в контур включена внешняя переменная ЭДС  зависящая от времени по гармоническому закону

.

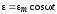Колебания, возникающие под действием внешней периодически изменяющейся ЭДС, называются вынужденными электромагнитными колебаниями.

В данном случае уравнение колебательного контура записывается как

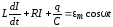или ,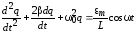

где введены обозначения:

; ,

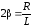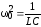где 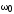— собственная частота контура; — коэффициент затухания.

Решение этого уравнения, как известно из математики, представляет собой сумму общего решения однородного уравнения (без правой части) и частного решения неоднородного уравнения.

Нас будут интересовать только установившиеся колебания, т.е. частное решение этого уравнения (общее решение однородного уравнения экспоненциально затухает, и по прошествии некоторого времени оно практически исчезает, обращается в нуль).

Это решение имеет вид

,

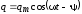где 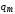— амплитуда заряда на конденсаторе; — разность фаз между колебаниями заряда и внешней ЭДС .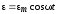

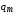и  определяются только свойствами самого контура и вынуждающей ЭДС , причем оказывается, что 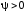, поэтомуq всегда отстает по фазе от .

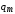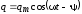Чтобы определить постоянные и, надо подставить в исходное уравнение

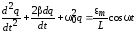
и преобразовать полученное выражение. В целях достижения большей простоты сначала найдем ток I и затем его выражение подставим в исходное уравнение

.

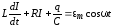Попутно будет решен и вопрос с постоянным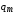и и.

Продифференцируем выражение 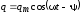поt и найдем:

.

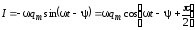Запишем это выражение так:

,

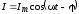где 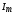— амплитуда тока; — сдвиг по фазе между током и внешней ЭДС :

; .

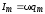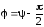Для того, чтобы найти 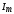и представим исходное уравнение 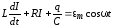в виде:

,

где слева записана сумма напряжений на индуктивности L, сопротивления R и емкости С.

Таким образом, мы видим, что сумма этих напряжений равна в каждый момент времени внешней ЭДС . Учитывая соотношения

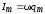и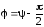

запишем:

;

;

.

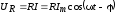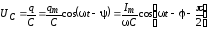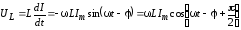Векторная диаграмма. Из последних трех формул видно, что 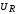находится в фазе с током I, 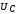отстает по фазе от тока н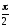а , а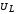опережает на 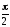. Все это можно наглядно представить с помощью векторной диаграммы, изобразив амплитуды напряжений

; ;

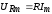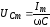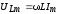
и их векторную сумму, равную, согласно

,

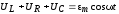вектору величины 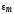(рис. 16.4)

Рис. 16.4

Из прямоугольного треугольника этой диаграммы легко получить следующие выражения для 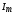и в уравнении :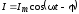

; .

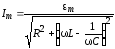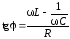46. Электрический резонанс. Резонансные кривые

Электрическим резонансом называется явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы (частоты вынуждающего переменного напряжения или внешней переменной ЭДС ) к частоте, равной или близкой собственной частоте колебательной системы. Графики зависимостей амплитуд тока I, заряда Q на конденсаторе и напряжений 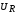,,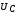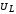от частоты внешней ЭДС  называются резонансными кривыми. Резонансные кривые для силы тока 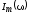показаны на рис. 16.5.

Как видно из выражения 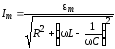, амплитуда силы тока имеет максимальное значение при.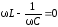

Следовательно, резонансная частота для силы тока совпадает с собственной частотой контура:

.

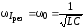Максимум при резонансе оказывается тем выше и острее, чем меньше коэффициент затухания .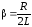

Рис. 16.5

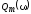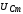Резонансные кривые для заряда на конденсаторе показаны на рис. 16.6 (резонансные кривые для напряженияна конденсаторе имеют такой же вид). Максимум амплитуды заряда достигается при резонансной частоте

,

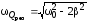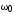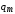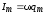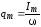которая по мере уменьшения  все больше приближается к . Для получения этого выражения надо представить, согласно, как, где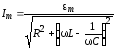, тогда.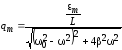

Максимум этой функции, или, что то же самое, минимум подкоренного выражения, найдем, приравняв производную по  от подкоренного выражения к нулю

.

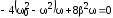Это равенство выполняется при 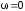,,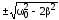 у которых только положительное значение имеет физический смысл. Следовательно, резонансная частота

.

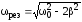Рис. 16.6

На рис. 16.7 изображено перераспределение амплитуд напряжений 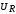,,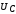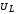в зависимости от частоты внешней ЭДС.

Рис. 16.7

Резонансные частоты для 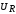,,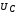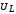определяются следующими формулами:

; ;.

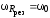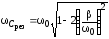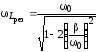Чем меньше , тем ближе резонансные частоты всех величин к значению .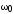

Резонансные кривые и добротность. Форма резонансных кривых определенным образом связана с добротностью Q контура. Особенно простой эта связь оказывается для случая слабого затухания, т.е. при .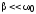

В этом случае

,

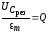где Q – добротность.

Действительно, при 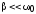, величина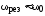и

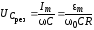или ,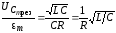

а это и есть добротность Q контура.

Таким образом, добротность контура (при 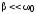) показывает во сколько раз максимальное значение амплитуды напряжения на конденсаторе (и на индуктивности) превышает амплитуду внешней ЭДС.

Добротность контура связана с другой важной характеристикой резонансной кривой – ее шириной. При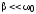

,

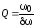где 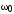— резонансная частота;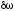— ширина резонансной кривой на «высоте», равной 0,7 от максимальной, т.е. в резонансе.

Резонанс. Таким образом, явление резонанса в случае электромагнитных колебаний – это возбуждение сильных колебаний при частоте внешней ЭДС или напряжения, равной или близкой к собственной частоте колебательного контура. Резонанс используют для выделения из сложного напряжения нужной составляющей. На этом основана вся техника радиоприема. Для того, чтобы радиоприемник принимал интересующую нас радиостанцию, его необходимо настроить, т.е. изменением емкости С и индуктивности L колебательного контура добиться совпадения его собственной частоты с частотой электромагнитных волн, излучаемых радиостанцией.

Резонанс — как источник энергии

В данной статье узнаем про резонанс — как источник энергии.

В средствах массовой информации с огромным «резонансом» говорят о РЕЗОНАНСЕ – как источнике энергии. Предлагаю разобраться с Вами, что такое электрический резонанс? Далеко ходить не будем, рассмотрим происходящие процессы в классическом LC резонансном контуре. Собственно других резонансных систем в электронике не существует. Прежде стоит отметить: бывают последовательный и параллельный колебательный (резонансный) контур. Процессы в обоих видах контуров протекают одинаково, отличие только в принципах питания.

Наиболее привлекателен, как источник энергии — параллельный колебательный контур, который все известные личности (в том числе Н. Тесла) использовали и используют в своих изобретениях и разработках. На его примере, проще рассматривать протекание тока питания и контурного тока.

Любой колебательный контур состоит из двух элементов — ёмкости С и индуктивности L. Общая ёмкость контура состоит из собственной ёмкости конденсатора входящего в состав контура, и паразитных емкостей подключенных к контуру цепей — ёмкости входной цепи, межвитковой ёмкости катушки индуктивности, ёмкости цепи нагрузки. Общая индуктивность контура состоит из собственной индуктивности катушки входящей в состав контура, и паразитных индуктивностей подключенных к контуру цепей — образуемых, как правило, длинами выводов конденсатора, транзистора, проводников цепи нагрузки. На частотах, до десятков мегагерц, паразитные ёмкости и паразитные индуктивности не значительно влияют на потери энергии резонансного контура, поэтому ими можно с достаточной уверенностью пренебречь, произведя подстройку частоты собственными элементами контура — катушкой индуктивности L , или конденсатором С.

 

Но колебательный контур обладает ещё одним параметром, оказывающим значительное влияние на потери энергии контуром — резистивным сопротивлением R , которое складывается из сопротивлений потерь в конденсаторе и катушке индуктивности, сопротивления выходного транзисторного каскада (в закрытом состоянии), и самое главное — сопротивления цепи нагрузки. Полная схема параллельного колебательного контура с резистивным сопротивлением изображена на рисунке, где C , L и R — суммарные значения ёмкостей, индуктивностей и резистивного сопротивления контура. Вообще, есть понятие – импеданс, но я не буду забивать вам голову этим понятием, а буду объяснять по простому.

Для того, чтобы понять, как C , L и R «работают» совместно, нам необходимо рассмотреть Амплитудно-частотную характеристику контура. Но сделаем мы это не на традиционном графике АЧХ, как упрощённо сделано в статье Колебательный контур. Резонанс. Изображённые ниже формулы и частотная характеристика, объясняют состояние и зависимость реактивных сопротивлений конденсатора X_C и катушки индуктивности X_L от частоты f.

На графике изображена линия зависимости реактивного сопротивления конденсатора X_C от частоты f, которая указывает, что на низких частотах реактивное сопротивление конденсатора максимально, а с повышением частоты уменьшается по экспоненте — конденсатор превращается в «проводник». Линия зависимости реактивного сопротивления катушки индуктивности X_L от частоты f, указывает, что катушка индуктивности ведёт себя наоборот, на низких частотах реактивное сопротивление катушки минимально — катушка индуктивности — «проводник», а с повышением частоты увеличивается, но не по экспоненте, а по прямой. Резистивное сопротивление контура R, никак от изменения частоты не зависит. Так как элементы контура соединены параллельно, то и складывать сопротивления конденсатора Х_C, катушки индуктивности Х_L и резистивное сопротивление контура R мы будем по формуле параллельного соединения резисторов, (подробнее в статье:Резистор).

По результирующему графику суммарного сопротивления резонансного контура мы видим, что имеется определённая частота, на которой значения сопротивления конденсатора Х_C и катушки индуктивности Х_L одинаковы, это и есть резонансная частота. Этот график фактически (но не совсем) является амплитудно-частотной характеристикой (АЧХ) контура.

Таким образом, можно сделать вывод, что элементы колебательного контура являются нагрузкой для электрического тока, могут поглощать подводимую энергию. Для подъёма АЧХ контура, необходимо увеличить общее сопротивление контура. Это можно сделать путём увеличения его составляющих — сопротивления конденсатора Х_C, катушки индуктивности Х_L и резистивного сопротивления контура R. Для повышения характеристики АЧХ и для того, чтобы частота не «уходила», необходимо одновременно увеличивая индуктивность катушки, уменьшать ёмкость конденсатора. Это следует из правила, согласно которому, на резонансной частоте величины Х_C = Х_L. Приведём формулу Томсона, получаемую из выражений зависимости Х_C и Х_L от частоты и подтверждающую это утверждение:

Из формулы Томсона следует, что на одной и той же частоте может работать множество контуров с разными величинами L и С, но с одинаковым произведением LС. Если же мы уменьшим сопротивление R , то и общее сопротивление колебательной системы так же снизится, что приведёт к потерям энергии.
Когда мы говорим о возможности получения энергии из колебательного контура, мы говорим об уменьшении сопротивления R , а это по известному закону Ома «не знаешь Ома, сиди дома», или I=U/R приводит к снижению амплитуды резонансных колебаний.

Отношение энергии, запасенной реактивными элементами контура, к энергии омических (резистивных) потерь за период, принято называть добротностью Q. Она то и зависит от вышеописанных физических величин:

Где, же дополнительная энергия резонансного контура? Всё вышеописанное ранее в этой статье, проводилось без учёта главного явления любого электрического резонансного контура – контурного тока.

 

---

 

Контурный ток

 

В связи с тем, что конденсатор и катушка индуктивности обладают реактивными свойствами, в колебательном контуре протекает контурный ток. Путь протекания этого тока проходит через конденсатор и катушку индуктивности. Направление этого тока меняется два раза за период колебаний. Этот процесс, наглядно изображён на примере простейшего транзисторного каскада на иллюстрации ниже:

Для упрощения, считаем, что транзистор работает без дополнительного смещения базы. Все переходные процессы протекания тока питания и контурного тока происходят в течение одного периода колебания, а в последующих периодах повторяются.

•Участок «0» временной характеристики, можно назвать первоначальным, когда процессы заряда и перезаряда ёмкости и индуктивности ещё не «устоялись», так как в начальный момент они разряжены. На этом этапе происходит заряд ёмкости от источника питания через открытый транзистор, при этом ток заряда сначала максимальный, а по окончании 1/4 периода падает до нуля. Ток в катушке индуктивности, обладающей инерционностью минимален. По окончании отрезка «0», контур переходит в резонансный «устоявшийся» режим.

•На участке «В» временной характеристики, когда конденсатор заряжен до напряжения источника питания, ток протекающий по пути «источник питания – катушка — открытый транзистор — источник питания» постепенно увеличивается. Когда в результате закрытия транзистора, напряжение на конденсаторе превысит потенциал, прикладываемый от источника тока, конденсатор начинает разряжаться через катушку индуктивности, к концу 1/2 периода разрядившись на неё полностью. Таким образом, в этот промежуток времени «В» через катушку индуктивности течёт два тока – ток источника питания и контурный ток разряда ёмкости.

•На участке «С» временной характеристики, когда переход транзистора закрыт, по причине инерционности катушки индуктивности происходит перезаряд конденсатора от катушки индуктивности. Катушка индуктивности полностью разряжается, а конденсатор оказывается заряженным противоположным потенциалом. Ток источника питания в этот момент «С» через элементы контура не течёт.

•На участке «D» временной характеристики, когда переход транзистора закрыт, происходит обратный разряд конденсатора на катушку индуктивности. Конденсатор полностью разряжается, а индуктивность наоборот, оказывается заряженной потенциалом противоположным источнику питания. Ток источника питания в этот момент «D» через элементы контура, по-прежнему, не течёт.

•На участке «А» временной характеристики, происходит заряд конденсатора от катушки индуктивности, а при разряде катушки до значения меньше напряжения источника питания подаваемого через открытый транзистор, конденсатор заряжается от источника питания. При этом ток заряда конденсатора сначала максимальный, а по окончании периода сигнала падает до нуля. Ток в катушке индуктивности, сначала — максимальный, а в конце временного интервала «А» становится равным нулю. В промежуток времени «А» через конденсатор течёт два тока – ток источника питания и контурный ток разряда ёмкости.

Процесс работы резонансного контура циклически повторяется по схеме: А – В – С – D – А.

Таким образом, в резонансном контуре ровно половину периода гармонического сигнала на участках А и В происходит сложение двух токов – тока источника питания и контурного тока, что в свою очередь с каждым периодом (процесса перезаряда) повышает энергию контура. Повышение энергии резонансного контура происходит только за счёт источника питания. Сколько в резонансный контур попадает энергии, столько энергии и тратится на нагрузку и потери в элементах схемы.

Почему то бытует мнение, что из электрического резонанса возможно получение «дополнительной», или «свободной» энергии, что для этого в контуре достаточно поддерживать резонанс. Выше описанные процессы, происходящие в электрическом резонансном контуре, полностью это опровергают, доказывая черезпериодное накопление энергии.

В интернете была статья, про то, что на каком-то заводе, какой-то электрик начитался статей про резонанс, и доработав понижающие трансформаторы на заводе снизил потребление энергии заводом на целый порядок.

Для учёта расхода энергии бывают счётчики активной энергии, которые стоят у нас в домах, и счётчики реактивной энергии, которые устанавливают на заводах. В чём разница? На предприятиях, как правило, имеется большое количество оборудования и станков, работающих на трёхфазных двигателях. Двигатель – это индуктивность, а наличие мощного двигателя подразумевает огромные токи. Для равномерности нагрузки мощных двигателей на трёхфазную сеть в каждый временной момент трёхфазного напряжения, в цепи питания устанавливают конденсаторы, которые совместно с обмотками двигателя образуют колебательные контура. Действие этих конденсаторов такое же, как было описано на участках А и В – во время действия сразу двух токов – тока источника питания и контурного тока. Счётчики активной энергии построены так, что заранее накопленная у потребителя энергия вносит ошибку в измерение. Как правило, это связано с «неправильным» подмагничиванием «токовой катушки». Счётчики активной энергии показывают энергию, расходованную двигателями, использующими «блоки конденсаторов», где то на одну треть меньше реально расходованной энергии. А вот счётчики реактивной энергии отлично с этим справляются. Этот «горе-электрик» не мог сделать никакой резонанс, хотя бы потому, что нагрузка потребителей на заводе в разгар дня – стабильна, а утром, в обед и вечером — величина не постоянная и скачет в широких пределах. Как было описано в этой статье, сопротивление нагрузки сильно влияет на выходную амплитуду резонансного контура. Стоило, кому ни будь на заводе, перед обеденным перерывом выключить мощный станок, то напряжение подскочило — бы и сожгло пару других станков, которые ещё не успели выключить другие рабочие. Я предполагаю, что он «химичил» со счётчиками, за что и был уволен.

 

В заключении статьи, хочу добавить для тех посетителей сайта, кто плохо учился в школе и поэтому в силу своего невежества искренне верит волшебникам:

Закон сохранения энергии никто не отменял! Вечного двигателя основанного на резонансе не бывает, и не может быть! При работе колебательного контура, происходит черезпериодное накопление энергии источника тока, поэтому в результате накопления, в определённый момент времени энергия контура может превышать подводимую к нему энергию. Энергия из «пустоты» не может появиться. «Свободная энергия» — это миф, порождённый малограмотными людьми, для людей себе подобных. Энергия присутствует во всём, что нас окружает, её только нужно правильно извлечь. Это различные химические соединения и элементы, природные явления, но не «Чудо», подобное тому, которое приписывают Тесле! И чем глупее сам «приписчик», тем «чуднее» в его голове выглядит этот выдающийся учёный. В помощь к получению энергии можно привлечь и электрический резонанс, но как вспомогательное явление, помогающее влиять на изменения свойств материалов. Не забивайте себе голову антинаучными идеями! Все, ныне существующие физические законы, никто в ближайшее время не опровергал, их только дополняли и корректировали, что с развитием техники было и всегда будет. Меньше обращайте внимание на малограмотные высказывания людей завлекающих к себе выдуманной сенсацией. Не верьте во всю чепуху, а сначала проводите анализ того, что написано в различных статьях, и что Вам излагают различные средства массовой информации.

Электрический резонанс — Большая Энциклопедия Нефти и Газа, статья, страница 1

Электрический резонанс

Cтраница 1

Электрический резонанс имеет большое практическое значение. Электрические резонансные контуры широко используются в радиотехнике, измерительной технике, телеуправлении, различных схемах автоматики, рентгеноскопии. Явления резонанса используются для изменения ( компенсации) параметров электропередач. Параллельным подключением емкостей к активно-индуктивной нагрузке ( резонанс токов) повышают коэффициенты мощности нагрузки, разгружая электрические сети от перетокрв реактивных мощностей.  [1]

Электрический резонанс широко используется в радиотехнике. Например, использование резонанса позволяет выделить радиоприемником частоту определенной передающей станции.  [2]

Электрический резонанс используется для настройки на определенную длину электромагнитной волны. В колебательном контуре индуктивность или емкость берутся переменными, что позволяет настроить контур на нужную частоту. При совпадении частоты сигнала с собственной частотой колебательного контура ток в контуре становится достаточно большим.  [3]

Электрический резонанс очень широко используется в радиотехнике.  [4]

Электрический резонанс при вынужденных колебаниях может наблюдаться как в последовательном, так и в параллельном контуре. Физические явления, происходящие при этом, хотя в общем додобны, но имеют ряд существенных особенностей. Поэтому мы рассмотрим оба указанных случая раздельно.  [5]

Электрическим резонансом называется возникающее при вынужденных колебаниях в электромагнитной системе явление, при котором обмен энергией между системой и источником вынужденных колебаний отсутствует, а поле в системе достигает максимальных значений.  [6]

Электрическим резонансом называется явление резкого возрастания амплитуды силы тока при совпадении частоты собственных колебаний контура с частотой периодически действующей вынуждающей ЭДС.  [7]

Явление электрического резонанса широко применяется в радиотехнике: настройка частоты лриемника на частоту передающей станции.  [8]

Роль электрического резонанса в технике огромна.  [10]

Что такое электрический резонанс и при каком условии он возможен.  [11]

Следовательно, электрический резонанс возникает в цепи при равенстве индуктивного и емкостного сопротивлений.  [12]

При изучении электрического резонанса ( напряжений и токов) мы рассматривали действие периодической ЭДС генератора на колебательный контур. Однако оказывается, что аналогичные явления наблюдаются и при внешних воздействиях других типов, причем возникающие колебания, так же как и при действии ЭДС, существенно зависят от частоты воздействий на контур.  [14]

Интересное применение электрического резонанса встречается в приборе, получившем название трансформатора Тесла в честь югославского физика Николы Тесла.  [15]

Страницы:      1    2    3    4

Резонанс — это… Что такое Резонанс?

Эффект резонанса для разных частот внешнего воздействия и коэффициентов затухания

Резона́нс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротность. Явление резонанса впервые было описано Галилео Галилеем в 1602 г в работах, посвященных исследованию маятников и музыкальных струн.^[1][2]

Механика

Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если вы будете подталкивать качели в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния, можно найти по формуле:

,

где g это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс. (Более точная формула довольно сложна, и включает эллиптический интеграл). Важно, что резонансная частота не зависит от массы маятника. Также важно, что раскачивать маятник нельзя на кратных частотах (высших гармониках), зато это можно делать на частотах, равных долям от основной (низших гармониках).

Резонансные явления могут вызвать необратимые разрушения в различных механических системах.

В основе работы механических резонаторов лежит преобразование потенциальной энергии в кинетическую. В случае простого маятника, вся его энергия содержится в потенциальной форме, когда он неподвижен и находится в верхних точках траектории, а при прохождении нижней точки на максимальной скорости, она преобразуется в кинетическую. Потенциальная энергия пропорциональна массе маятника и высоте подъёма относительно нижней точки, кинетическая — массе и квадрату скорости в точке измерения.

Другие механические системы могут использовать запас потенциальной энергии в различных формах. Например, пружина запасает энергию сжатия, которая, фактически, является энергией связи её атомов.

Струна

Струны таких инструментов, как лютня, гитара, скрипка или пианино, имеют основную резонансную частоту, напрямую зависящую от длины, массы и силы натяжения струны. Длина волны первого резонанса струны равна её удвоенной длине. При этом, его частота зависит от скорости v, с которой волна распространяется по струне:

где L — длина струны (в случае, если она закреплена с обоих концов). Скорость распространения волны по струне зависит от её натяжения T и массы на единицу длины ρ:

Таким образом, частота главного резонанса зависит от свойств струны и выражается следующим отношением:

,

где T — сила натяжения, ρ — масса единицы длины струны, а m — полная масса струны.

Увеличение натяжения струны и уменьшение её массы (толщины) и длины увеличивает её резонансную частоту. Помимо основного резонанса, струны также имеют резонансы на высших гармониках основной частоты f, например, 2f, 3f, 4f, и т. д. Если струне придать колебание коротким воздействием (щипком пальцев или ударом молоточка), струна начнёт колебания на всех частотах, присутствующих в воздействующем импульсе (теоретически, короткий импульс содержит все частоты). Однако частоты, не совпадающие с резонансными, быстро затухнут, и мы услышим только гармонические колебания, которые и воспринимаются как музыкальные ноты.

Электроника

В электронных устройствах резонанс возникает на определённой частоте, когда индуктивная и ёмкостная составляющие реакции системы уравновешены, что позволяет энергии циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора.

Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником.

Электрическое устройство, состоящее из ёмкости и индуктивности, называется колебательным контуром. Элементы колебательного контура могут быть включены как последовательно, так и параллельно. При достижении резонанса, импеданс последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален. Резонансные процессы в колебательных контурах используются в элементах настройки, электрических фильтрах. Частота, на которой происходит резонанс, определяется величинами (номиналами) используемых элементов. В то же время, резонанс может быть и вреден, если он возникает в неожиданном месте по причине повреждения, недостаточно качественного проектирования или производства электронного устройства. Такой резонанс может вызывать паразитный шум, искажения сигнала, и даже повреждение компонентов.

Приняв, что в момент резонанса индуктивная и ёмкостная составляющие импеданса равны, резонансную частоту можно найти из выражения

,

где  ; f — резонансная частота в герцах; L — индуктивность в генри; C — ёмкость в фарадах. Важно, что в реальных системах понятие резонансной частоты неразрывно связано с полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте. Ширина полосы пропускания определяется добротностью системы.

СВЧ

В СВЧ электронике широко используются объёмные резонаторы, чаще всего цилиндрической или тороидальной геометрии с размерами порядка длины волны, в которых возможны добротные колебания электромагнитного поля на отдельных частотах, определяемых граничными условиями. Наивысшей добротностью обладают сверхпроводящие резонаторы, стенки которых изготовлены из сверхпроводника и диэлектрические резонаторы с модами шепчущей галереи.

Оптика

В оптическом диапазоне самым распространенным типом резонатора является резонатор Фабри-Перо, образованный парой зеркал, между которыми в резонансе устанавливается стоячая волна. Применяются также кольцевые резонаторы с бегущей волной и оптические микрорезонаторы с модами шепчущей галереи.

Акустика

Резонанс — один из важнейших физических процессов, используемых при проектировании звуковых устройств, большинство из которых содержат резонаторы, например, струны и корпус скрипки, трубка у флейты, корпус у барабанов.

Астрофизика

Орбитальный резонанс в небесной механике — это ситуация, при которой два (или более) небесных тела имеют периоды обращения, которые относятся как небольшие натуральные числа. В результате эти небесные тела оказывают регулярное гравитационное влияние друг на друга, которое может стабилизировать их орбиты.

Резонансный метод разрушения льда

Известно, что при движении нагрузки по ледяному покрову развивается система изгибных гравитационных волн (ИГВ). Это сочетание изгибных колебаний пластины льда и связанных с ними гравитационных волн в воде. Когда скорость нагрузки близка к минимальной фазовой скорости от ИГВ, вода прекращает поддержку ледяного покрова и поддержка осуществляется только упругими свойствами льда. Амплитуда ИГВ резко возрастает, и с достаточной нагрузкой, начинается разрушения. Потребляемая мощность в несколько раз ниже (в зависимости от толщины льда) по сравнению с ледоколами и ледокольными навесными оборудованиями. Этот метод разрушения льда известен как резонансный метод разрушения льда^[3][4] Ученый Козин, Виктор Михайлович получил экспериментальные теоретические кривые, которые показывают возможности своего метода^[5].

Примечания

См. также

Литература

• Richardson LF (1922), Weather prediction by numerical process, Cambridge.
• Bretherton FP (1964), Resonant interactions between waves. J. Fluid Mech., 20, 457—472.
• Бломберген Н. Нелинейная оптика, М.: Мир, 1965. — 424 с.
• Захаров В. Е. (1974), Гамильтонов формализм для волн в нелинейных средах с дисперсией, Изв. вузов СССР. Радиофизика, 17(4), 431—453.
• Арнольд В. И. Потеря устойчивости автоколебаний вблизи резонансов, Нелинейные волны / Ред. А. В. Гапонов-Грехов. — М.: Наука, 1979. С. 116—131.
• Kaup PJ, Reiman A and Bers A (1979), Space-time evolution of nonlinear three-wave interactions. Interactions in a homogeneous medium, Rev. of Modern Phys, 51(2), 275—309.
• Haken H (1983), Advanced Synergetics. Instability Hierarchies of Self-Organizing Systems and devices, Berlin, Springer-Verlag.
• Филлипс O.М. Взаимодействие волн. Эволюция идей, Современная гидродинамика. Успехи и проблемы. — М.: Мир, 1984. — С. 297—314.
• Журавлёв В. Ф., Климов Д. М. Прикладные методы в теории колебаний. — М.: Наука, 1988.
• Сухоруков А.П Нелинейные волновые взаимодействия в оптике и радиофизике. — М.: Наука, 1988. — 232 с.
• Брюно А. Д. Ограниченная задача трёх тел. — М.: Наука, 1990.

Ссылки

Резонанс — это… Что такое Резонанс?

Эффект резонанса для разных частот внешнего воздействия и коэффициентов затухания

Резона́нс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротность. Явление резонанса впервые было описано Галилео Галилеем в 1602 г в работах, посвященных исследованию маятников и музыкальных струн.^[1][2]

Механика

Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если вы будете подталкивать качели в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния, можно найти по формуле:

,

где g это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс. (Более точная формула довольно сложна, и включает эллиптический интеграл). Важно, что резонансная частота не зависит от массы маятника. Также важно, что раскачивать маятник нельзя на кратных частотах (высших гармониках), зато это можно делать на частотах, равных долям от основной (низших гармониках).

Резонансные явления могут вызвать необратимые разрушения в различных механических системах.

В основе работы механических резонаторов лежит преобразование потенциальной энергии в кинетическую. В случае простого маятника, вся его энергия содержится в потенциальной форме, когда он неподвижен и находится в верхних точках траектории, а при прохождении нижней точки на максимальной скорости, она преобразуется в кинетическую. Потенциальная энергия пропорциональна массе маятника и высоте подъёма относительно нижней точки, кинетическая — массе и квадрату скорости в точке измерения.

Другие механические системы могут использовать запас потенциальной энергии в различных формах. Например, пружина запасает энергию сжатия, которая, фактически, является энергией связи её атомов.

Струна

Струны таких инструментов, как лютня, гитара, скрипка или пианино, имеют основную резонансную частоту, напрямую зависящую от длины, массы и силы натяжения струны. Длина волны первого резонанса струны равна её удвоенной длине. При этом, его частота зависит от скорости v, с которой волна распространяется по струне:

где L — длина струны (в случае, если она закреплена с обоих концов). Скорость распространения волны по струне зависит от её натяжения T и массы на единицу длины ρ:

Таким образом, частота главного резонанса зависит от свойств струны и выражается следующим отношением:

,

где T — сила натяжения, ρ — масса единицы длины струны, а m — полная масса струны.

Увеличение натяжения струны и уменьшение её массы (толщины) и длины увеличивает её резонансную частоту. Помимо основного резонанса, струны также имеют резонансы на высших гармониках основной частоты f, например, 2f, 3f, 4f, и т. д. Если струне придать колебание коротким воздействием (щипком пальцев или ударом молоточка), струна начнёт колебания на всех частотах, присутствующих в воздействующем импульсе (теоретически, короткий импульс содержит все частоты). Однако частоты, не совпадающие с резонансными, быстро затухнут, и мы услышим только гармонические колебания, которые и воспринимаются как музыкальные ноты.

Электроника

В электронных устройствах резонанс возникает на определённой частоте, когда индуктивная и ёмкостная составляющие реакции системы уравновешены, что позволяет энергии циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора.

Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником.

Электрическое устройство, состоящее из ёмкости и индуктивности, называется колебательным контуром. Элементы колебательного контура могут быть включены как последовательно, так и параллельно. При достижении резонанса, импеданс последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален. Резонансные процессы в колебательных контурах используются в элементах настройки, электрических фильтрах. Частота, на которой происходит резонанс, определяется величинами (номиналами) используемых элементов. В то же время, резонанс может быть и вреден, если он возникает в неожиданном месте по причине повреждения, недостаточно качественного проектирования или производства электронного устройства. Такой резонанс может вызывать паразитный шум, искажения сигнала, и даже повреждение компонентов.

Приняв, что в момент резонанса индуктивная и ёмкостная составляющие импеданса равны, резонансную частоту можно найти из выражения

,

где  ; f — резонансная частота в герцах; L — индуктивность в генри; C — ёмкость в фарадах. Важно, что в реальных системах понятие резонансной частоты неразрывно связано с полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте. Ширина полосы пропускания определяется добротностью системы.

СВЧ

В СВЧ электронике широко используются объёмные резонаторы, чаще всего цилиндрической или тороидальной геометрии с размерами порядка длины волны, в которых возможны добротные колебания электромагнитного поля на отдельных частотах, определяемых граничными условиями. Наивысшей добротностью обладают сверхпроводящие резонаторы, стенки которых изготовлены из сверхпроводника и диэлектрические резонаторы с модами шепчущей галереи.

Оптика

В оптическом диапазоне самым распространенным типом резонатора является резонатор Фабри-Перо, образованный парой зеркал, между которыми в резонансе устанавливается стоячая волна. Применяются также кольцевые резонаторы с бегущей волной и оптические микрорезонаторы с модами шепчущей галереи.

Акустика

Резонанс — один из важнейших физических процессов, используемых при проектировании звуковых устройств, большинство из которых содержат резонаторы, например, струны и корпус скрипки, трубка у флейты, корпус у барабанов.

Астрофизика

Орбитальный резонанс в небесной механике — это ситуация, при которой два (или более) небесных тела имеют периоды обращения, которые относятся как небольшие натуральные числа. В результате эти небесные тела оказывают регулярное гравитационное влияние друг на друга, которое может стабилизировать их орбиты.

Резонансный метод разрушения льда

Известно, что при движении нагрузки по ледяному покрову развивается система изгибных гравитационных волн (ИГВ). Это сочетание изгибных колебаний пластины льда и связанных с ними гравитационных волн в воде. Когда скорость нагрузки близка к минимальной фазовой скорости от ИГВ, вода прекращает поддержку ледяного покрова и поддержка осуществляется только упругими свойствами льда. Амплитуда ИГВ резко возрастает, и с достаточной нагрузкой, начинается разрушения. Потребляемая мощность в несколько раз ниже (в зависимости от толщины льда) по сравнению с ледоколами и ледокольными навесными оборудованиями. Этот метод разрушения льда известен как резонансный метод разрушения льда^[3][4] Ученый Козин, Виктор Михайлович получил экспериментальные теоретические кривые, которые показывают возможности своего метода^[5].

Примечания

См. также

Литература

• Richardson LF (1922), Weather prediction by numerical process, Cambridge.
• Bretherton FP (1964), Resonant interactions between waves. J. Fluid Mech., 20, 457—472.
• Бломберген Н. Нелинейная оптика, М.: Мир, 1965. — 424 с.
• Захаров В. Е. (1974), Гамильтонов формализм для волн в нелинейных средах с дисперсией, Изв. вузов СССР. Радиофизика, 17(4), 431—453.
• Арнольд В. И. Потеря устойчивости автоколебаний вблизи резонансов, Нелинейные волны / Ред. А. В. Гапонов-Грехов. — М.: Наука, 1979. С. 116—131.
• Kaup PJ, Reiman A and Bers A (1979), Space-time evolution of nonlinear three-wave interactions. Interactions in a homogeneous medium, Rev. of Modern Phys, 51(2), 275—309.
• Haken H (1983), Advanced Synergetics. Instability Hierarchies of Self-Organizing Systems and devices, Berlin, Springer-Verlag.
• Филлипс O.М. Взаимодействие волн. Эволюция идей, Современная гидродинамика. Успехи и проблемы. — М.: Мир, 1984. — С. 297—314.
• Журавлёв В. Ф., Климов Д. М. Прикладные методы в теории колебаний. — М.: Наука, 1988.
• Сухоруков А.П Нелинейные волновые взаимодействия в оптике и радиофизике. — М.: Наука, 1988. — 232 с.
• Брюно А. Д. Ограниченная задача трёх тел. — М.: Наука, 1990.

Ссылки