ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ — это… Что такое ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ?
- ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ
- ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ
-
(e0) (по старой терминологии — диэлектрич. проницаемость вакуума), физ. постоянная, входящая в ур-ния законов электрич. поля (см. КУЛОНА ЗАКОН) при записи этих ур-ний в рационализованной форме, в соответствии с к-рой образованы электрич. и магн. ед. Международной системы единиц. e0=(m0с2)-1=(107/4pc2) Ф•м-1=8,85418782(7) •10-12 Ф•м-1, где m0— магнитная постоянная. В отличие от диэлектрич. проницаемости e (зависящей от типа в-ва, темп-ры, давления и др. параметров), e0 зависит только от выбора системы ед. В СГС системе единиц (гауссовой) e0=1.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ
-
(e0) -физ постоянная, входящая в ур-ния законов электрич. поля (напр., в Кулона закон )при записи этих ур-ний в рационализованной форме, в соответствии с к-рой образованы электрич. и магн. единицы Международной системы единиц; по старой терминологии Э. п. называется диэлектрич. проницаемостью вакуума.



Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
- ЭЛЕКТРИЧЕСКАЯ ИНДУКЦИЯ
- ЭЛЕКТРИЧЕСКАЯ ПРОЧНОСТЬ
Смотреть что такое «ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ» в других словарях:
ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ — коэффициент пропорциональности ?о в законе Кулона определяющем (в единицах СИ) силу взаимодействия F двух находящихся на расстоянии r точечных электрических зарядов q1 и q2; ?о = (?оc2) 1 Ф/м = 8,854187817.10 12 Ф/м, где ?о магнитная постоянная.… … Большой Энциклопедический словарь
электрическая постоянная — Коэффициент, применяемый при записи ряда соотношений в СИ, равный величине, обратной произведению магнитной постоянной на квадрат скорости света в пустоте. Примечание — Электрическая постоянная приблизительно равна 8,85419 • 10 12 Ф/м … Справочник технического переводчика
ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ — (см.) … Большая политехническая энциклопедия
электрическая постоянная — электрическая постоянная; отрасл. диэлектрическая проницаемость пустоты Скалярная величина, характеризующая электрическое поле в пустоте, равная отношению суммарного электрического заряда, заключенного внутри некоторой замкнутой поверхности, к… … Политехнический терминологический толковый словарь
Электрическая постоянная — 14. Электрическая постоянная Постоянная, равная в системе СИ величине, обратной произведению магнитной постоянной на квадрат скорости света в пустоте. П .р и м е ч а н и е. Электрическая постоянная приблизительно равна 8,35*4 • 10 12 Ф/м Источник … Словарь-справочник терминов нормативно-технической документации
электрическая постоянная — коэффициент пропорциональности ε0 в законе Кулона , определяющем (в единицах СИ) силу взаимодействия F двух находящихся на расстоянии r точечных электрических зарядов q1 и q2; ε0 = (μ0c2) 1Ф/м = 8,854187817·10 12Ф/м, где μ0 магнитная постоянная … Энциклопедический словарь
Электрическая постоянная — (ранее также носила название диэлектрической постоянной) физическая константа, скалярная величина, определяющая напряжённость электрического поля в вакууме; входящая в выражения некоторых законов электромагнетизма, в том числе закона Кулона … Википедия
электрическая постоянная — elektrinė konstanta statusas T sritis automatika atitikmenys: angl. electric constant; permittivity constant; permittivity of free space; permittivity of vacuum vok. dielektrische konstante, f; Dielektrizitätskonstante, f; elektrische… … Automatikos terminų žodynas
электрическая постоянная — elektrinė konstanta statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. electric constant; permittivity of vacuum vok. absolute Dielektrizitätskonstante, f;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
электрическая постоянная — elektrinė konstanta statusas T sritis fizika atitikmenys: angl. permittivity constant; permittivity of free space; permittivity of vacuum vok. Dielektrizitätskonstante, f; elektrische Feldkonstante, f; Verschiebungskonstante, f rus. абсолютная… … Fizikos terminų žodynas
Электрическая постоянная — Википедия
Материал из Википедии — свободной энциклопедии
Электри́ческая постоя́нная (ранее также носила название диэлектрической постоянной) — физическая константа, скалярная величина, входящая в выражения некоторых законов электромагнетизма, в том числе закона Кулона, при записи их в рационализованной форме, соответствующей Международной системе единиц (СИ)
Иногда, используя устаревшую терминологию, называют электрической (или диэлектрической) проницаемостью вакуума[2]. Измеряется в фарадах, делённых на метр.
Определение
По определению электрическая постоянная ε0{\displaystyle \varepsilon _{0}} связана со скоростью света c{\displaystyle c} и магнитной постоянной μ0{\displaystyle \mu _{0}} соотношением[1]
- ε0=1μ0c2.{\displaystyle \varepsilon _{0}={\frac {1}{\mu _{0}c^{2}}}.}
Поскольку в СИ для магнитной постоянной справедливо точное равенство μ0=4π × 10−7 {\displaystyle \mu _{0}=4\pi \ \times \ 10^{-7}\ }Гн/м, то для электрической постоянной выполняется соотношение
- ε0=14πc2×107{\displaystyle \varepsilon _{0}={\frac {1}{4\pi c^{2}}}\times 10^{7}}м/Гн,[3]
также являющееся точным.
Видео по теме
Численное значение
Учитывая, что скорости света в СИ приписано точное значение, по определению равное 299 792 458 м/с, из последнего соотношения следует численное значение ε0{\displaystyle \varepsilon _{0}} в СИ:
- ε0=14π× 2997924582×10−7{\displaystyle \varepsilon _{0}={\frac {1}{4\pi \times \ 299792458^{2}\times 10^{-7}}}} Ф/м ≈8,85418781762039×10−12{\displaystyle \approx 8,85418781762039\times 10^{-12}} Ф·м−1.
Или, выражая то же через основные единицы СИ,
- ε0≈8,85418781762039×10−12{\displaystyle \varepsilon _{0}\approx 8,85418781762039\times 10^{-12}} м−3·кг−1·с4·А2.
В системе СГСМ μ0=1{\displaystyle \mu _{0}=1} и потому ε0=1c2≈1,11265005605362×10−21{\displaystyle \varepsilon _{0}={\frac {1}{c^{2}}}\approx 1,11265005605362\times 10^{-21}} с2·см−2.
Некоторые уравнения электродинамики в СИ
В материальных уравнениях, в вакууме, через электрическую постоянную связаны вектор электрической индукции D{\displaystyle \mathbf {D} } и вектор напряжённости электрического поля E{\displaystyle \mathbf {E} }:
- D=ε0 E.{\displaystyle \mathbf {D} =\varepsilon _{0}\ \mathbf {E} .}
Она также входит в запись закона Кулона (тоже в вакууме):
- F12=14πε0⋅q1q2r122r12r12.{\displaystyle \mathbf {F} _{12}={\frac {1}{4\pi \varepsilon _{0}}}\cdot {\frac {q_{1}q_{2}}{r_{12}^{2}}}{\frac {\mathbf {r} _{12}}{r_{12}}}.}
При использовании СИ произведение электрической постоянной на относительную диэлектрическую проницаемость называют абсолютной диэлектрической проницаемостью.
Предполагаемое переопределение
В 2011 году XXIV Генеральная конференция по мерам и весам (ГКМВ) приняла резолюцию[4], в которой, в частности, предложено в будущей ревизии Международной системы единиц (СИ) переопределить несколько основных единиц, включая ампер, таким образом, чтобы они были основаны не на созданных человеком артефактах, а на фундаментальных физических постоянных или свойствах атомов.
Предполагается, что в СИ величине элементарного электрического заряда e будет приписано точное значение, равное 1,602 17X·10−19Кл[5], а новое определение ампера будет основано на этом точном значении элементарного заряда, выраженного в c·А.
Следствием такого подхода к определению ампера станет изменение статуса электрической постоянной: после предполагаемого переопределения ампера значение электрической постоянной будет равно 14π× 2997924582× 10−7{\displaystyle {\frac {1}{4\pi \times \ 299792458^{2}\times \ 10^{-7}}}} Ф/м, но это значение приобретёт погрешность (неопределённость) и в дальнейшем будет определяться экспериментально[4].
См. также
Примечания
Диэлектрическая проницаемость — Википедия
Диэлектри́ческая проница́емость — коэффициент, входящий в математическую запись закона Кулона для силы взаимодействия точечных зарядов q1{\displaystyle q_{1}} и q2{\displaystyle q_{2}}, находящихся в однородной изолирующей (диэлектрической) среде на расстоянии r12{\displaystyle r_{12}} друг от друга:
- F=14πεa⋅|q1q2|r122{\displaystyle F={\frac {1}{4\pi \varepsilon _{a}}}\cdot {\frac {|q_{1}q_{2}|}{r_{12}^{2}}}},
а также в уравнение связи вектора электрической индукции с напряжённостью электрического поля:
- D=εaE{\displaystyle \mathbf {D} =\varepsilon _{a}\mathbf {E} }
в рассматриваемой среде[1]. Вводятся абсолютная (а) и относительная (r, от англ. relative — относительный) проницаемости:
- εa=ε0εr{\displaystyle \varepsilon _{a}=\varepsilon _{0}\varepsilon _{r}},
где ε0{\displaystyle \varepsilon _{0}} — электрическая постоянная[2]. Cам термин «диэлектрическая проницаемость» применяется и для εr{\displaystyle \varepsilon _{r}}, и для εa{\displaystyle \varepsilon _{a}}; ради краткости, одну из этих величин (в российской литературе чаще εr{\displaystyle \varepsilon _{r}}, в англоязычной εa{\displaystyle \varepsilon _{a}}) переобозначают как ε{\displaystyle \varepsilon } (из контекста всегда ясно, о чём идёт речь). Величина εr{\displaystyle \varepsilon _{r}} безразмерна, а εa{\displaystyle \varepsilon _{a}} по размерности совпадает с ε0{\displaystyle \varepsilon _{0}} (в Международной системе единиц (СИ): фарад на метр, Ф/м).
Проницаемость εr{\displaystyle \varepsilon _{r}} показывает, во сколько раз сила взаимодействия двух электрических зарядов в конкретной среде меньше, чем в вакууме, для которого εr=1{\displaystyle \varepsilon _{r}=1}. Отличие проницаемости от единицы обусловлено эффектом поляризации диэлектрика под действием внешнего электрического поля, в результате которой создаётся внутреннее противоположно направленное поле. В области низких частот ω{\displaystyle \omega } значение проницаемости реальных сред εr>1{\displaystyle \varepsilon _{r}>1}, обычно оно лежит в диапазоне 1—100, но для сегнетоэлектриков составляет десятки и сотни тысяч. Как функция частоты электрического поля величина εr(ω){\displaystyle \varepsilon _{r}(\omega )} слегка возрастает на участках вне линий поглощения данного материала, однако вблизи линий резко спадает, из-за чего высокочастотная диэлектрическая проницаемость ниже статической. Имеет место связь проницаемости и показателя преломления вещества: для немагнитной непоглощающей среды n2(ω)=εr(ω){\displaystyle n^{2}(\omega )=\varepsilon _{r}(\omega )}.
Относительная диэлектрическая проницаемость εr{\displaystyle \varepsilon _{r}} является одним из «электромагнитных параметров» среды, влияющих на распределение компонент напряжённости электромагнитного поля в пространстве и описывающих среду в материальных уравнениях электродинамики (уравнениях Максвелла).
 Схематическое изображение ориентации диполей в диэлектрической среде под воздействием электрического поля
Схематическое изображение ориентации диполей в диэлектрической среде под воздействием электрического поляАбсолютная диэлектрическая проницаемость вакуума[править | править код]
Электрическая постоянная, она же «абсолютная диэлектрическая проницаемость вакуума», в системе единиц СИ равна ε0≈8,85⋅10−12{\displaystyle \varepsilon _{0}\approx 8{,}85\cdot 10^{-12}} Ф/м (имеет размерность L−3M−1T4I2). В системе СГС эта же постоянная составляет ε0=1/4π{\displaystyle \varepsilon _{0}=1/4\pi }, однако часто в СГС вообще не задействуют ε0{\displaystyle \varepsilon _{0}}, надлежащим образом адаптируя формулы (скажем, закон Кулона: F=εr−1⋅|q1q2|/r122{\displaystyle F=\varepsilon _{r}^{-1}\cdot |q_{1}q_{2}|/r_{12}^{2}}). Электрическая постоянная связана с магнитной постоянной и скоростью света в вакууме:
- ε0μ0=c−2{\displaystyle \varepsilon _{0}\mu _{0}=c^{-2}}
Ниже все формулы приводятся для СИ, а символ ε{\displaystyle \varepsilon } используется как замена εr{\displaystyle \varepsilon _{r}} (εa=ε0ε{\displaystyle \varepsilon _{a}=\varepsilon _{0}\varepsilon }).
Эффект поляризации диэлектрика и проницаемость[править | править код]
Под воздействием электрического поля в диэлектрике имеет место поляризация — явление, связанное с ограниченным смещением зарядов или поворотом электрических диполей. Данное явление характеризует вектор электрической поляризации P{\displaystyle \mathbf {P} }, равный дипольному моменту единицы объёма диэлектрика. В отсутствие внешнего поля диполи ориентированы хаотично (см. верхний рис.), за исключением особых случаев спонтанной поляризации в сегнетоэлектриках. При наличии поля диполи в большей или меньшей степени поворачиваются (нижний рис.), в зависимости от восприимчивости χ(ω){\displaystyle \chi (\omega )} конкретного материала, а восприимчивость, в свою очередь, определяет проницаемость ε(ω){\displaystyle \varepsilon (\omega )}. Помимо дипольно-ориентационного, имеются и другие механизмы поляризации. Поляризация не изменяет суммарного заряда в любом макроскопическом объёме, однако она сопровождается появлением связанных электрических зарядов на поверхности диэлектрика и в местах неоднородностей. Эти связанные заряды создают в диэлектрике дополнительное макроскопическое поле, как правило, направленное против внешнего наложенного поля. В итоге тот факт, что εa≠ε0{\displaystyle \varepsilon _{a}\neq \varepsilon _{0}}, является следствием электрической поляризации материалов.
Роль диэлектрической проницаемости среды в физике[править | править код]
Относительная диэлектрическая проницаемость ε{\displaystyle \varepsilon } среды, наряду с её относительной магнитной проницаемостью μ{\displaystyle \mu } и удельной электропроводностью σ{\displaystyle \sigma }, влияет на распределение напряжённости электромагнитного поля в пространстве и используется при описании среды в системе уравнений Максвелла. Среду со значениями μ=1{\displaystyle \mu =1} и σ=0{\displaystyle \sigma =0} называют идеальным диэлектриком (диэлектриком без поглощения, диэлектриком без потерь), для неё ε{\displaystyle \varepsilon } определяет такие вторичные параметры, как коэффициент преломления среды, скорость распространения, фазовую скорость и коэффициент укорочения длины электромагнитной волны в среде, волновое сопротивление среды. Относительная диэлектрическая проницаемость реальных диэлектриков (диэлектриков с потерями, диэлектриков с поглощением, для которых σ>0{\displaystyle \sigma >0}) также влияет на значение тангенса угла диэлектрических потерь и погонное затухание электромагнитной волны в среде. Относительная диэлектрическая проницаемость среды влияет на электрическую ёмкость расположенных в ней проводников: увеличение ε{\displaystyle \varepsilon } приводит к увеличению ёмкости. При изменении ε{\displaystyle \varepsilon } в пространстве (то есть если ε{\displaystyle \varepsilon } зависит от координат) говорят о неоднородной среде, зависимость ε{\displaystyle \varepsilon } от частоты электромагнитных колебаний — одна из возможных причин дисперсии электромагнитных волн, зависимость ε{\displaystyle \varepsilon } от напряженности электрического поля — одна из возможных причин нелинейности среды. Если среда является анизотропной, то в материальном уравнении ε{\displaystyle \varepsilon } будет не скаляром, а тензором. При использовании метода комплексных амплитуд в решении системы уравнений Максвелла и наличии потерь в среде (σ>0{\displaystyle \sigma >0}) оперируют комплексной диэлектрической проницаемостью.
Таким образом, ε{\displaystyle \varepsilon } является одним из важнейших «электромагнитных параметров» соответствующей среды.
Диэлектрическая проницаемость непоглощающей среды[править | править код]
Проницаемость и связанные с ней величины[править | править код]
Применительно к диэлектрической среде без потерь действует цепочка соотношений:
- D=ε0E+P=ε0(1+χ)E=ε0εE{\displaystyle \mathbf {D} =\varepsilon _{0}\mathbf {E} +\mathbf {P} =\varepsilon _{0}(1+\chi )\mathbf {E} =\varepsilon _{0}\varepsilon \mathbf {E} }.
В большинстве случаев χ{\displaystyle \chi } и, соответственно, ε{\displaystyle \varepsilon } — это просто безразмерные константы конкретного материала. В вакууме χ{\displaystyle \chi } равно нулю.
Особая ситуация возникает для нелинейных сред, когда ε{\displaystyle \varepsilon } зависит от величины поля E{\displaystyle E}; такое возможно в сравнительно сильных полях. В сегнетоэлектриках возможно появление спонтанной поляризации, а именно сохранение P≠0{\displaystyle \mathbf {P} \neq 0} после снятия ранее наложенного внешнего поля.
Распределение электрического поля в пространстве с различными диэлектриками находится из численного решения уравнения Максвелла
- ∇⋅D(r)=ρ(r){\displaystyle {\boldsymbol {\nabla }}\cdot \mathbf {D(r)} =\rho (\mathbf {r} )}
или уравнения Пуассона для электрического потенциала φ{\displaystyle \varphi }
- ∇(ε(r)∇φ(r))=−ε0−1ρ(r){\displaystyle {\boldsymbol {\nabla }}\left(\varepsilon (\mathbf {r} ){\boldsymbol {\nabla }}\varphi (\mathbf {r} )\right)=-\varepsilon _{0}^{-1}\rho (\mathbf {r} )},
где ρ(r){\displaystyle \rho (\mathbf {r} )} обозначает плотность свободных зарядов. На незаряженной границе двух диэлектрических сред отношение нормальных компонент напряжённости поля En{\displaystyle E_{n}} с обеих сторон равно обратному отношению значений проницаемости сред.
В ситуации однородного диэлектрика его наличие приводит к снижению электрического поля E(r){\displaystyle \mathbf {E} (\mathbf {r} )} в ε{\displaystyle \varepsilon } раз, по сравнению со случаем вакуума при том же распределении свободных зарядов. Помимо закона Кулона, практически важным примером является конденсатор любой геометрии, заряд (не разность потенциалов!) обкладок которого фиксирован.
Проницаемость в оптическом диапазоне частот[править | править код]
Диэлектрическая проницаемость, совместно с магнитной, определяют фазовую скорость распространения электромагнитной волны в рассматриваемой среде, а именно:
- ε0ε(ω)μ0μ(ω)=vph−2{\displaystyle \varepsilon _{0}\varepsilon (\omega )\mu _{0}\mu (\omega )=v_{ph}^{-2}}.
Показатель преломления диэлектрика без потерь можно выразить как квадратный корень из произведения его магнитной и диэлектрической проницаемостей:
- n(ω)=μ(ω)⋅ε(ω){\displaystyle n(\omega )={\sqrt {\mu (\omega )\cdot \varepsilon (\omega )}}}
Для немагнитных сред μ=1{\displaystyle \mu =1}. Значения ε{\displaystyle \varepsilon } для актуального в данном контексте оптического диапазона могут очень сильно отличаться от статических значений: как правило, ε{\displaystyle \varepsilon } намного ниже, чем для статического поля. Однако, если рассматривать оптический диапазон частот сам по себе, то в нём с ростом ω{\displaystyle \omega } величина ε{\displaystyle \varepsilon } (а значит, и n{\displaystyle n}) чаще всего возрастает. Такое поведение показателя преломления («синий свет преломляется сильнее красного») является случаем так называемой нормальной дисперсии. С противоположной ситуацией аномальной дисперсии можно столкнуться вблизи полос поглощения, но такой случай не может рассматриваться как случай без потерь.
Тензор проницаемости анизотропных сред[править | править код]
Диэлектрическая проницаемость связывает электрическую индукцию D{\displaystyle \mathbf {D} } и напряжённость электрического поля E{\displaystyle \mathbf {E} }. В электрически анизотропных средах компонента вектора напряжённости Ei{\displaystyle E_{i}} может не только влиять на ту же самую компоненту вектора электрической индукции Di{\displaystyle D_{i}}, но и порождать другие его компоненты Dj(j≠i){\displaystyle D_{j}(j\neq i)}. В общем случае проницаемость является тензором, определяемым из следующего соотношения (в записи использовано соглашение Эйнштейна):
- Di=ε0εijEj{\displaystyle D_{i}=\varepsilon _{0}\varepsilon _{ij}E_{j}}
или, иначе,
- D=εaE{\displaystyle \mathbf {D} ={\boldsymbol {\varepsilon }}_{a}\mathbf {E} }
где жирный шрифт использован для векторных и тензорных величин, а
- E=E1e1+E2e2+E3e3{\displaystyle \mathbf {E} =E_{1}\mathbf {e} _{1}+E_{2}\mathbf {e} _{2}+E_{3}\mathbf {e} _{3}} — вектор напряжённости электрического поля,
- D=D1e1+D2e2+D3e3{\displaystyle \mathbf {D} =D_{1}\mathbf {e} _{1}+D_{2}\mathbf {e} _{2}+D_{3}\mathbf {e} _{3}} — вектор электрической индукции,
- εa=ε0εij{\displaystyle {\boldsymbol {\varepsilon }}_{a}=\varepsilon _{0}\varepsilon _{ij}} — тензор абсолютной диэлектрической проницаемости.
В изотропном случае любая компонента вектора напряженности Ei{\displaystyle E_{i}} влияет только на Di{\displaystyle D_{i}}, при этом εij= δijε{\displaystyle \varepsilon _{ij}=~\delta _{ij}\varepsilon }, где δij{\displaystyle \delta _{ij}} — символ Кронекера, поэтому уравнения Максвелла могут быть записаны с использованием скалярной диэлектрической проницаемости (ε{\displaystyle \varepsilon } — просто коэффициент в уравнении).
Статическая проницаемость некоторых диэлектриков[править | править код]
Значение ε{\displaystyle \varepsilon } вакуума равно единице, для реальных сред в статическом поле ε>1{\displaystyle \varepsilon >1}. Для воздуха и большинства других газов в нормальных условиях значение ε{\displaystyle \varepsilon } близко к единице в силу их низкой плотности. В статическом электрическом поле для большинства твёрдых или жидких диэлектриков значение ε{\displaystyle \varepsilon } лежит в интервале от 2 до 8, для жидкой воды значение ε{\displaystyle \varepsilon } достаточно высокое, 88 при 0∘{\displaystyle 0^{\circ }}. А у твердого льда ε{\displaystyle \varepsilon } больше и составляет 97 при 0∘{\displaystyle 0^{\circ }}. Это объясняется тем, что переход атома Н от одного О-атома к другому вызывает перестройку ковалентных и водородных связей у обоих этих О-атомов и в их в окрестности. В результате вся сеть ковалентных и водородных связей во льду сильно флуктуирует, и это приводит к аномально высокой поляризуемости льда, превосходя диэлектрическую проницаемость жидкой воды[3]. Значение ε{\displaystyle \varepsilon } велико для веществ с молекулами, обладающими большим электрическим дипольным моментом. Значение ε{\displaystyle \varepsilon } сегнетоэлектриков составляет десятки и сотни тысяч.
Электрическая постоянная — Википедия
Материал из Википедии — свободной энциклопедии
Электри́ческая постоя́нная (ранее также носила название диэлектрической постоянной) — физическая константа, скалярная величина, входящая в выражения некоторых законов электромагнетизма, в том числе закона Кулона, при записи их в рационализованной форме, соответствующей Международной системе единиц (СИ)[1].
Иногда, используя устаревшую терминологию, называют электрической (или диэлектрической) проницаемостью вакуума[2]. Измеряется в фарадах, делённых на метр.
Определение
По определению электрическая постоянная ε0{\displaystyle \varepsilon _{0}} связана со скоростью света c{\displaystyle c} и магнитной постоянной μ0{\displaystyle \mu _{0}} соотношением[1]
- ε0=1μ0c2.{\displaystyle \varepsilon _{0}={\frac {1}{\mu _{0}c^{2}}}.}
Поскольку в СИ для магнитной постоянной справедливо точное равенство μ0=4π × 10−7 {\displaystyle \mu _{0}=4\pi \ \times \ 10^{-7}\ }Гн/м, то для электрической постоянной выполняется соотношение
- ε0=14πc2×107{\displaystyle \varepsilon _{0}={\frac {1}{4\pi c^{2}}}\times 10^{7}}м/Гн,[3]
также являющееся точным.
Численное значение
Учитывая, что скорости света в СИ приписано точное значение, по определению равное 299 792 458 м/с, из последнего соотношения следует численное значение ε0{\displaystyle \varepsilon _{0}} в СИ:
- ε0=14π× 2997924582×10−7{\displaystyle \varepsilon _{0}={\frac {1}{4\pi \times \ 299792458^{2}\times 10^{-7}}}} Ф/м ≈8,85418781762039×10−12{\displaystyle \approx 8,85418781762039\times 10^{-12}} Ф·м−1.
Или, выражая то же через основные единицы СИ,
- ε0≈8,85418781762039×10−12{\displaystyle \varepsilon _{0}\approx 8,85418781762039\times 10^{-12}} м−3·кг−1·с4·А2.
В системе СГСМ μ0=1{\displaystyle \mu _{0}=1} и потому ε0=1c2≈1,11265005605362×10−21{\displaystyle \varepsilon _{0}={\frac {1}{c^{2}}}\approx 1,11265005605362\times 10^{-21}} с2·см−2.
Некоторые уравнения электродинамики в СИ
В материальных уравнениях, в вакууме, через электрическую постоянную связаны вектор электрической индукции D{\displaystyle \mathbf {D} } и вектор напряжённости электрического поля E{\displaystyle \mathbf {E} }:
- D=ε0 E.{\displaystyle \mathbf {D} =\varepsilon _{0}\ \mathbf {E} .}
Она также входит в запись закона Кулона (тоже в вакууме):
- F12=14πε0⋅q1q2r122r12r12.{\displaystyle \mathbf {F} _{12}={\frac {1}{4\pi \varepsilon _{0}}}\cdot {\frac {q_{1}q_{2}}{r_{12}^{2}}}{\frac {\mathbf {r} _{12}}{r_{12}}}.}
При использовании СИ произведение электрической постоянной на относительную диэлектрическую проницаемость называют абсолютной диэлектрической проницаемостью.
Предполагаемое переопределение
В 2011 году XXIV Генеральная конференция по мерам и весам (ГКМВ) приняла резолюцию[4], в которой, в частности, предложено в будущей ревизии Международной системы единиц (СИ) переопределить несколько основных единиц, включая ампер, таким образом, чтобы они были основаны не на созданных человеком артефактах, а на фундаментальных физических постоянных или свойствах атомов.
Предполагается, что в СИ величине элементарного электрического заряда e будет приписано точное значение, равное 1,602 17X·10−19Кл[5], а новое определение ампера будет основано на этом точном значении элементарного заряда, выраженного в c·А.
Следствием такого подхода к определению ампера станет изменение статуса электрической постоянной: после предполагаемого переопределения ампера значение электрической постоянной будет равно 14π× 2997924582× 10−7{\displaystyle {\frac {1}{4\pi \times \ 299792458^{2}\times \ 10^{-7}}}} Ф/м, но это значение приобретёт погрешность (неопределённость) и в дальнейшем будет определяться экспериментально[4].
См. также
Примечания
Электрическая постоянная Википедия
Электрическая постоянная (ранее также носила название диэлектрической постоянной) — физическая константа, скалярная величина, входящая в выражения некоторых законов электромагнетизма, в том числе закона Кулона, при записи их в рационализованной форме, соответствующей Международной системе единиц (СИ)[1].
Иногда, используя устаревшую терминологию, называют электрической (или диэлектрической) проницаемостью вакуума[2]. Измеряется в фарадах, делённых на метр.
Содержание
- 1 Определение
- 2 Численное значение
- 2.1 В Международной системе единиц
- 2.1.1 До изменения СИ 2018—2019 годов
- 2.1.2 После изменений СИ 2018—2019 годов
- 2.2 В системе СГС
- 2.1 В Международной системе единиц
- 3 Некоторые уравнения электродинамики в СИ
- 4 См. также
- 5 Примечания
Определение[ | ]
По определению в СИ электрическая постоянная ε0{\displaystyle \varepsilon _{0}} связана со скоростью света c{\displaystyle c} и магнитной постоянной μ0{\displaystyle \mu _{0}} соотношением[1]
- ε0=1μ0c2.{\displaystyle \varepsilon _{0}={\frac {1}{\mu _{0}c^{2}}}.}
Численное значение[ | ]
В Международной системе единиц[ | ]
До изменения СИ 2018—2019 годов[ | ]
Поскольку в СИ для магнитной постоянной было справедливо точное равенство μ0=4π × 10−7 {\displaystyle \mu _{0}=4\pi \ \times \ 10^{-7}\ }Гн/м
Электрическая постоянная — это… Что такое Электрическая постоянная?
- Электрическая постоянная
- коэффициент пропорциональности ε0 в Кулона законе, определяющем силу взаимодействия двух покоящихся точечных электрических зарядов. В Международной системе единиц (См. Международная система единиц) (СИ)
 ф/м = (8.85418782 ± 0,00000007) ф/м. В СГС системе единиц (См. СГС система единиц) (гауссовой) ε0 принимают равной единице (безразмерной). В отличие от диэлектрической проницаемости (См. Диэлектрическая проницаемость) ε (зависящей от типа вещества, температуры, давления и других параметров) ε0 зависит только от выбора системы единиц.
ф/м = (8.85418782 ± 0,00000007) ф/м. В СГС системе единиц (См. СГС система единиц) (гауссовой) ε0 принимают равной единице (безразмерной). В отличие от диэлектрической проницаемости (См. Диэлектрическая проницаемость) ε (зависящей от типа вещества, температуры, давления и других параметров) ε0 зависит только от выбора системы единиц.
Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.
- Электрическая печь сопротивления
- Электрическая прочность
Смотреть что такое «Электрическая постоянная» в других словарях:
ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ — (e0) (по старой терминологии диэлектрич. проницаемость вакуума), физ. постоянная, входящая в ур ния законов электрич. поля (см. КУЛОНА ЗАКОН) при записи этих ур ний в рационализованной форме, в соответствии с к рой образованы электрич. и магн. ед … Физическая энциклопедия
ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ — коэффициент пропорциональности ?о в законе Кулона определяющем (в единицах СИ) силу взаимодействия F двух находящихся на расстоянии r точечных электрических зарядов q1 и q2; ?о = (?оc2) 1 Ф/м = 8,854187817.10 12 Ф/м, где ?о магнитная постоянная.… … Большой Энциклопедический словарь
электрическая постоянная — Коэффициент, применяемый при записи ряда соотношений в СИ, равный величине, обратной произведению магнитной постоянной на квадрат скорости света в пустоте. Примечание — Электрическая постоянная приблизительно равна 8,85419 • 10 12 Ф/м … Справочник технического переводчика
ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ — (см.) … Большая политехническая энциклопедия
электрическая постоянная — электрическая постоянная; отрасл. диэлектрическая проницаемость пустоты Скалярная величина, характеризующая электрическое поле в пустоте, равная отношению суммарного электрического заряда, заключенного внутри некоторой замкнутой поверхности, к… … Политехнический терминологический толковый словарь
Электрическая постоянная — 14. Электрическая постоянная Постоянная, равная в системе СИ величине, обратной произведению магнитной постоянной на квадрат скорости света в пустоте. П .р и м е ч а н и е. Электрическая постоянная приблизительно равна 8,35*4 • 10 12 Ф/м Источник … Словарь-справочник терминов нормативно-технической документации
электрическая постоянная — коэффициент пропорциональности ε0 в законе Кулона , определяющем (в единицах СИ) силу взаимодействия F двух находящихся на расстоянии r точечных электрических зарядов q1 и q2; ε0 = (μ0c2) 1Ф/м = 8,854187817·10 12Ф/м, где μ0 магнитная постоянная … Энциклопедический словарь
Электрическая постоянная — (ранее также носила название диэлектрической постоянной) физическая константа, скалярная величина, определяющая напряжённость электрического поля в вакууме; входящая в выражения некоторых законов электромагнетизма, в том числе закона Кулона … Википедия
электрическая постоянная — elektrinė konstanta statusas T sritis automatika atitikmenys: angl. electric constant; permittivity constant; permittivity of free space; permittivity of vacuum vok. dielektrische konstante, f; Dielektrizitätskonstante, f; elektrische… … Automatikos terminų žodynas
электрическая постоянная — elektrinė konstanta statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. electric constant; permittivity of vacuum vok. absolute Dielektrizitätskonstante, f;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
электрическая постоянная — elektrinė konstanta statusas T sritis fizika atitikmenys: angl. permittivity constant; permittivity of free space; permittivity of vacuum vok. Dielektrizitätskonstante, f; elektrische Feldkonstante, f; Verschiebungskonstante, f rus. абсолютная… … Fizikos terminų žodynas
Диэлектрическая постоянная Википедия
Электрическая постоянная (ранее также носила название диэлектрической постоянной) — физическая константа, скалярная величина, входящая в выражения некоторых законов электромагнетизма, в том числе закона Кулона, при записи их в рационализованной форме, соответствующей Международной системе единиц (СИ)[1].
Иногда, используя устаревшую терминологию, называют электрической (или диэлектрической) проницаемостью вакуума[2]. Измеряется в фарадах, делённых на метр.
Определение
По определению в СИ электрическая постоянная ε0{\displaystyle \varepsilon _{0}} связана со скоростью света c{\displaystyle c} и магнитной постоянной μ0{\displaystyle \mu _{0}} соотношением[1]
- ε0=1μ0c2.{\displaystyle \varepsilon _{0}={\frac {1}{\mu _{0}c^{2}}}.}
Численное значение
В Международной системе единиц
До изменения СИ 2018—2019 годов
Поскольку в СИ для магнитной постоянной было справедливо точное равенство μ0=4π × 10−7 {\displaystyle \mu _{0}=4\pi \ \times \ 10^{-7}\ }Гн/м, то для электрической постоянной выполнялось соотношение
- ε0=14πc2⋅107{\displaystyle \varepsilon _{0}={\frac {1}{4\pi c^{2}}}\cdot 10^{7}}м/Гн,[3]
также являвшееся точным.
Учитывая, что скорости света в СИ приписано точное значение, по определению равное 299 792 458 м/с, из последнего соотношения следует численное значение ε0{\displaystyle \varepsilon _{0}} в СИ:
- ε0=14π⋅ 2997924582×10−7{\displaystyle \varepsilon _{0}={\frac {1}{4\pi \cdot \ 299792458^{2}\times 10^{-7}}}} Ф/м ≈ 8,85418781762039 · 10−12 Ф·м−1.
Или, выражая то же через основные единицы СИ,
- ε0 ≈ 8,85418781762039 · 10−12 м−3·кг−1·с4·А2.
После изменений СИ 2018—2019 годов
С 2019 года вступили в силу изменения в СИ, включающие, в частности, переопределение ампера на основе фиксации численного значения элементарного заряда. Это привело к тому, что значение электрической постоянной стало экспериментально определяемой величиной, хотя численно её значение осталось прежним с высокой точностью. Значение электрической постоянной, рекомендованное CODATA[4]:
- ε0 = 8,8541878128(13)· 10−12 м−3·кг−1·с4·А2, или Ф·м−1.
В системе СГС
В системе СГС электрическая постоянная как коэффициент, связывающий напряжённость и индукцию электрического поля в вакууме, также может быть введена. При этом в различных вариантах системы СГС электрическая постоянная имеет разную размерность и значение. Конкретно, Гауссова система единиц и система СГСЭ построены так, что электрическая постоянная безразмерна и равна 1, а в системе СГСМ она равна ε0 = 1/c2 ≈ 1,11265005605362 · 10−21 с2·см−2.
Некоторые уравнения электродинамики в СИ
В материальных уравнениях, в вакууме, через электрическую постоянную связаны вектор электрической индукции D{\displaystyle \mathbf {D} } и вектор напряжённости электрического поля E{\displaystyle \mathbf {E} }:
- D=ε0 E.{\displaystyle \mathbf {D} =\varepsilon _{0}\ \mathbf {E} .}
Она также входит в запись закона Кулона (тоже в вакууме):
- F12=14πε0⋅q1q2r122r12r12.{\displaystyle \mathbf {F} _{12}={\frac {1}{4\pi \varepsilon _{0}}}\cdot {\frac {q_{1}q_{2}}{r_{12}^{2}}}{\frac {\mathbf {r} _{12}}{r_{12}}}.}
При использовании СИ произведение электрической постоянной на относительную диэлектрическую проницаемость называют абсолютной диэлектрической проницаемостью.




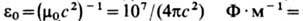
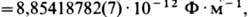
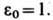
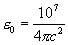 ф/м = (8.85418782 ± 0,00000007) ф/м. В СГС системе единиц (См. СГС система единиц) (гауссовой) ε0 принимают равной единице (безразмерной). В отличие от диэлектрической проницаемости (См. Диэлектрическая проницаемость) ε (зависящей от типа вещества, температуры, давления и других параметров) ε0 зависит только от выбора системы единиц.
ф/м = (8.85418782 ± 0,00000007) ф/м. В СГС системе единиц (См. СГС система единиц) (гауссовой) ε0 принимают равной единице (безразмерной). В отличие от диэлектрической проницаемости (См. Диэлектрическая проницаемость) ε (зависящей от типа вещества, температуры, давления и других параметров) ε0 зависит только от выбора системы единиц.