Открытая Физика. Электрический ток в металлах

Электрический ток в металлах – это упорядоченное движение электронов под действием электрического поля. Опыты показывают, что при протекании тока по металлическому проводнику переноса вещества не происходит, следовательно, ионы металла не принимают участия в переносе электрического заряда.

Наиболее убедительное доказательство электронной природы тока в металлах было получено в опытах с инерцией электронов. Идея таких опытов и первые качественные результаты (1913 г.) принадлежат русским физикам Л. И. Мандельштаму и Н. Д. Папалекси. В 1916 году американский физик Р. Толмен и шотландский физик Б. Стюарт усовершенствовали методику этих опытов и выполнили количественные измерения, неопровержимо доказавшие, что ток в металлических проводниках обусловлен движением электронов.

Схема опыта Толмена и Стюарта показана на рис. 1.12.1. Катушка с большим числом витков тонкой проволоки приводилась в быстрое вращение вокруг своей оси. Концы катушки с помощью гибких проводов были присоединены к чувствительному

баллистическому гальванометру Г. Раскрученная катушка резко тормозилась, и в цепи возникал кратковременных ток, обусловленный инерцией носителей заряда. Полный заряд, протекающий по цепи, измерялся по отбросу стрелки гальванометра.

Схема опыта Толмена и Стюарта

При торможении вращающейся катушки на каждый носитель заряда e действует тормозящая сила F=-mdυdt, которая играет роль сторонней силы, то есть силы неэлектрического происхождения. Сторонняя сила, отнесенная к единице заряда, по определению является напряженностью E_ст поля сторонних сил: Eст=-medυdt.

Следовательно, в цепи при торможении катушки возникает электродвижущая сила ℰ, равная ℰ=Eстl=-medυdtl, где

l – длина проволоки катушки. За время торможения катушки по цепи протечет заряд q, равный q=∫I dt=1R∫ℰdt=melυ0R.

Здесь I – мгновенное значение силы тока в катушке, R – полное сопротивление цепи, υ₀ – начальная линейная скорость проволоки.

Отсюда удельный заряд e / m свободных носителей тока в металлах равен: em=lυ0Rq.

Все величины, входящие в правую часть этого соотношения, можно измерить. На основании результатов опытов Толмена и Стюарта было установлено, что носители свободного заряда в металлах имеют отрицательный знак, а отношение заряда носителя к его массе близко к удельному заряду электрона, полученному из других опытов. Так было установлено, что носителями свободных зарядов в металлах являются электроны.

По современным данным модуль заряда электрона (элементарный заряд) равен e=1,60218ċ10-19 Кл, а его удельный заряд есть em=1,75882ċ1011 Кл/кг.

Хорошая электропроводность металлов объясняется высокой концентрацией свободных электронов, равной по порядку величины числу атомов в единице объема.

Предположение о том, что за электрический ток в металлах ответственны электроны, возникло значительно раньше опытов Толмена и Стюарта. Еще в 1900 году немецкий ученый П. Друде на основании гипотезы о существовании свободных электронов в металлах создал электронную теорию проводимости металлов. Эта теория получила развитие в работах голландского физика Х. Лоренца и носит название классической электронной теории. Согласно этой теории, электроны в металлах ведут себя как электронный газ, во многом похожий на идеальный газ. Электронный газ заполняет пространство между ионами, образующими кристаллическую решетку металла (рис. 1.12.2).

Газ свободных электронов в кристаллической решетке металла. Показана траектория одного из электронов

Из-за взаимодействия с ионами электроны могут покинуть металл, лишь преодолев так называемый потенциальный барьер. Высота этого барьера называется работой выхода. При обычных (комнатных) температурах у электронов не хватает энергии для преодоления потенциального барьера.

Из-за взаимодействия с кристаллической решеткой потенциальная энергия выхода электрона внутри проводника оказывается меньше, чем при удалении электрона из проводника. Электроны в проводнике находятся в своеобразной «потенциальной яме», глубина которой и называется потенциальным барьером.

Как ионы, образующие решетку, так и электроны участвуют в тепловом движении. Ионы совершают тепловые колебания вблизи положений равновесия – узлов кристаллической решетки. Свободные электроны движутся хаотично и при своем движении сталкиваются с ионами решетки. В результате таких столкновений устанавливается термодинамическое равновесие между электронным газом и решеткой. Согласно теории Друде–Лоренца, электроны обладают такой же средней энергией теплового движения, как и молекулы одноатомного идеального газа. Это позволяет оценить среднюю скорость υ¯т теплового движения электронов по формулам молекулярно-кинетической теории. При комнатной температуре она оказывается примерно равной 10

5 м/с.

При наложении внешнего электрического поля в металлическом проводнике кроме теплового движения электронов возникает их упорядоченное движение (дрейф), то есть электрический ток. Среднюю скорость υ¯д дрейфа можно оценить из следующих соображений. За интервал времени Δt через поперечное сечение

S проводника пройдут все электроны, находившиеся в объеме Sυ¯дΔt.

Число таких электронов равно nSυ¯дΔt, где n – средняя концентрация свободных электронов, примерно равная числу атомов в единице объема металлического проводника. Через сечение проводника за время Δt пройдет заряд Δq=enSυ¯дΔt. Отсюда следует: I=ΔqΔt=enSυ¯д. или υ¯д=IenS

Концентрация n атомов в металлах находится в пределах 10²⁸–10²⁹ м^–3.

Оценка по этой формуле для металлического проводника сечением 1 мм², по которому течет ток 10 А, дает для средней скорости υ¯д упорядоченного движения электронов значение в пределах 0,6–6 мм/c. Таким образом,

средняя скорость υ&macr;д упорядоченного движения электронов в металлических проводниках на много порядков меньше средней скорости υ&macr;т их теплового движения (υ&macr;д<<υ&macr;т). Рис. 1.12.3 дает представление о характере движения свободного электрона в кристаллической решетке.

Движение свободного электрона в кристаллической решетке: а – хаотическое движение электрона в кристаллической решетке металла; b – хаотическое движение с дрейфом, обусловленным электрическим полем. Масштабы дрейфа υ&macr;дΔt сильно преувеличены

Малая скорость дрейфа на противоречит опытному факту, что ток во всей цепи постоянного тока устанавливается практически мгновенно. Замыкание цепи вызывает распространение электрического поля со скоростью c = 3ċ10⁸ м/с. Через время порядка l / c (l – длина цепи) вдоль цепи устанавливается стационарное распределение электрического поля и в ней начинается упорядоченное движение электронов.

В классической электронной теории металлов предполагается, что движение электронов подчиняется законам механики Ньютона. В этой теории пренебрегают взаимодействием электронов между собой, а их взаимодействие с положительными ионами сводят только к соударениям. Предполагается также, что при каждом соударении электрон передает решетке всю накопленную в электрическом поле энергию и поэтому после соударения он начинает движение с нулевой дрейфовой скоростью.

Несмотря на то, что все эти допущения являются весьма приближенными, классическая электронная теория качественно объясняет законы электрического тока в металлических проводниках.

Закон Ома. В промежутке между соударениями на электрон действует сила, равная по модулю eE, в результате чего он приобретает ускорение emE. Поэтому к концу свободного пробега дрейфовая скорость электрона равна υд=(υд)max=eEmτ, где τ – время свободного пробега, которое для упрощения расчетов предполагается одинаковым для всех электронов. Среднее значение скорости дрейфа υ&macr;д равно половине максимального значения: υ&macr;д=12(υд)max=12eEmτ.

Рассмотрим проводник длины l и сечением S с концентрацией электронов n. Ток в проводнике может быть записан в виде: I=enSυ&macr;д=12e2τnSmE=e2τnS2mlU, где U = El – напряжение на концах проводника. Полученная формула выражает закон Ома для металлического проводника. Электрическое сопротивление проводника равно: R=2me2nτlS, а удельное сопротивление ρ и удельная проводимость ν выражаются соотношениями: ρ=2me2nτ;   ν=1ρ=e2nτ2m.

Закон Джоуля–Ленца. К концу свободного пробега электроны под действием поля приобретают кинетическую энергию 12m(υд)max2=12e2τ2mE2.

Согласно сделанным предположениям вся эта энергия при соударениях передается решетке и переходит в тепло.

За время Δt каждый электрон испытывает Δt / τ соударений. В проводнике сечением S и длины l имеется nSl электронов. Отсюда следует, что выделяемое в проводнике за время Δt тепло равно: ΔQ=nSlΔtτe2τ22mE2=ne2τ2mSlU2Δt=U2RΔt.

Это соотношение выражает закон Джоуля–Ленца.

Таким образом, классическая электронная теория объясняет существование электрического сопротивления металлов, законы Ома и Джоуля–Ленца. Однако в ряде вопросов классическая электронная теория приводит к выводам, находящимся в противоречии с опытом.

Эта теория не может, например, объяснить, почему молярная теплоемкость металлов, также как и молярная теплоемкость диэлектрических кристаллов, равна 3R, где R – универсальная газовая постоянная (закон Дюлонга и Пти, см. ч. I, § 3.10). Наличие свободных электронов на сказывается на величине теплоемкости металлов.

Классическая электронная теория не может также объяснить температурную зависимость удельного сопротивления металлов. Теория дает соотношение ρ~T, в то время как из эксперимента получается зависимость ρ ~ T. Однако наиболее ярким примером расхождения теории и опытов является сверхпроводимость.

Согласно классической электронной теории, удельное сопротивление металлов должно монотонно уменьшаться при охлаждении, оставаясь конечным при всех температурах. Такая зависимость действительно наблюдается на опыте при сравнительно высоких температурах. При более низких температурах порядка нескольких кельвинов удельное сопротивление многих металлов перестает зависеть от температуры и достигает некоторого предельного значения. Однако наибольший интерес представляет удивительное явление сверхпроводимости, открытое датским физиком Х. Каммерлинг-Оннесом в 1911 году. При некоторой определенной температуре T_кр, различной для разных веществ, удельное сопротивление скачком уменьшается до нуля (рис. 1.12.4). Критическая температура у ртути равна 4,1 К, у аллюминия 1,2 К, у олова 3,7 К. Сверхпроводимость наблюдается не только у элементов, но и у многих химических соединений и сплавов. Например, соединение ниобия с оловом (Ni₃Sn) имеет критическую температуру 18 К. Некоторые вещества, переходящие при низких температурах в сверхпроводящее состояние, не являются проводниками при обычных температурах. В то же время такие «хорошие» проводники, как медь и серебро, не становятся сверхпроводниками при низких температурах.

Зависимость удельного сопротивления ρ от абсолютной температуры T при низких температурах: a – нормальный металл; b – сверхпроводник

Вещества в сверхпроводящем состоянии обладают исключительными свойствами. Практически наиболее важным их них является способность длительное время (многие годы) поддерживать без затухания электрический ток, возбужденный в сверхпроводящей цепи.

Классическая электронная теория не способна объяснить явление сверхпроводимости. Объяснение механизма этого явления было дано только через 60 лет после его открытия на основе квантово-механических представлений.

Научный интерес к сверхпроводимости возрастал по мере открытия новых материалов с более высокими критическими температурами. Значительный шаг в этом направлении был сделан в 1986 году, когда было обнаружено, что у одного сложного керамического соединения T_кр = 35 K. Уже в следующем 1987 году физики сумели создать новую керамику с критической температурой 98 К, превышающей температуру жидкого азота (77 К). Явление перехода веществ в сверхпроводящее состояние при температурах, превышающих температуру кипения жидкого азота, было названо высокотемпературной сверхпроводимостью. В 1988 году было создано керамическое соединение на основе элементов Tl–Ca–Ba–Cu–O с критической температурой 125 К.

В настоящее время ведутся интенсивные работы по поиску новых веществ с еще более высокими значениями T_кр. Ученые надеятся получить вещество в сверхпроводящем состоянии при комнатной температуре. Если это произойдет, это будет настоящей революцией в науке, технике и вообще в жизни людей.

Следует отметить, что до настоящего времени механизм высокотемпературной сверхпроводимости керамических материалов до конца не выяснен.

Применение электрического тока в металлах

Практически все металлы можно рассматривать, как проводники электрического тока. Это обусловлено их строением, представляющим собой кристаллическую пространственную решетку. Узлы этой решетки совпадают с центрами положительных ионов, вокруг которых наблюдается хаотическое движение свободных электронов. Этим объясняется явление проводимости, благодаря которому применение электрического тока в металлах получило наиболее широкое распространение.

Физические свойства металлов

Свойства металлов полностью зависят от их внутреннего строения. Твердое состояние металлов представляет собой кристаллическую решетку пространственного типа, где кристаллы расположены упорядоченно. Как уже было отмечено, между узлами кристаллической решетки наблюдается движение свободных электронов.

Абсолютное значение их отрицательных зарядов совпадает с положительным зарядом всех ионов, расположенных в узлах кристаллической решетки. Когда через проводник пропускается электрический ток, ионы остаются на своем месте. Происходит перемещение свободных электронов, одинаковых в любом веществе.

Электрический ток в металлах: применение

То, что в металлах существуют электроны, проводящие ток, было доказано очень давно. Прежде всего, эти полезные свойства используются при передаче электроэнергии от источника к потребителям. В основе работы генераторов и электродвигателей также используются физические свойства металлов. Они применяются и в нагревательных приборах всех типов, предназначенных для промышленного производства и домашних условий.

Таким образом, электрический ток в металлах является упорядоченным движением свободных электронов, на которые воздействует электрическое поле. При его отсутствии, движение электронов становится хаотичным, подобно движению молекул жидкостей или газов. Однако, при наличии в проводнике электрического поля, происходит смещение электронов к положительному полюсу источника тока, то есть их движение становится упорядоченным.

Сами электроны в проводнике перемещаются с невысокой скоростью, в отличие от электрического поля, которое перемещается в проводнике со скоростью, приближающейся к скорости света. Именно эта величина служит показателем скорости распространения в проводнике электрического тока.

Электрический ток в металле: электронная проводимость

Электрический ток в металлах. Сверхпроводимость

Электрический ток в металлах. Сверхпроводимость

Электрическая проводимость ( электропроводность) — — это физическая величина , обратная сопротивлению, характеризует свойство вещества проводить электрический ток.
R — сопротивление
1/ R — электрическая проводимость

ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ

Носители свободных зарядов в металлах — свободные электроны, которые упорядоченно перемещаются вдоль проводника под действием эл.поля с постоянной средней скоростью (из-за тормозного действия положительно заряженных ионов кристаллической решетки).
Металлы обладают электронной проводимостью.

Зависимость сопротивления проводника R от температуры:

При нагревании размеры проводника меняются мало, а в основном меняется удельное сопротивление.
Удельное сопротивление проводника зависит от температуры:

где ро — удельное сопротивление при 0 градусов, t — температура,

— температурный коэффициент сопротивления
( т.е. относительное изменение удельного сопротивления проводника при нагревании его на один градус)

Для металлов и сплавов

Обычно для чистых металлов принимается

Таким образом, для металлических проводников с ростом температуры

увеличивается удельное сопротивление, увеличивается сопротивление проводника и уменьшается эл.ток в цепи.

Сопротивление проводника при изменении температуры можно рассчитать по формуле:

R = Ro ( 1 +

где Ro — сопротивление проводника при 0 градусов Цельсия
t — температура проводника

— температурный коэффициент сопротивления

Явление сверхпроводимости

Открытие низкотемпературной сверхпроводимости: 1911г. — голландский ученый Камерлинг — Оннес
наблюдается при сверхнизких температурах (ниже 25 К) во многих металлах и сплавах;
при таких температурах удельное сопротивление этих веществ становится исчезающе малым.

В 1957 г. дано теоретическое объяснение явления сверхпроводимости: Купер (США), Боголюбов (СССР)

1957г. опыт Коллинза: ток в замкнутой цепи без источника тока не прекращался в течение 2,5 лет.

В 1986 г. открыта (для металлокерамики) высокотемпературная сверхпроводимость (при 100 К).

Трудность достижения сверхпроводимости:
— необходимость сильного охлаждения вещества

Область применения:
— получение сильных магнитных полей;
— мощные электромагниты со сверхпроводящей обмоткой в ускорителях и генераторах.

В настоящий момент в энергетике существует большая проблема
— большие потери электроэнергии при передаче ее по проводам.

Возможное решение проблемы: при сверхпроводимости сопротивление проводников приблизительно равно 0 и потери энергии резко уменьшаются.

___

Вещество с самой высокой температурой сверхпроводимости
В 1988 г. США, при температуре –148°С было получено явление сверхпроводимости. Проводником служила смесь оксидов таллия, кальция, бария и меди.

Электрический ток в различных средах — Класс!ная физика

Электронная проводимость металлов. Зависимость сопротивления проводника от температуры. Сверхпроводимость — Электрический ток в полупроводниках. Р-n переход. Полупроводниковые приборы — Электрический ток в вакууме. Вакуумный диод. Электронно-лучевая трубка — Электрический ток в жидкостях. Закон электролиза — Электрический ток в газах — Контрольные вопросы к зачету по теме: Электрический ток в различных средах

Физический класс | Законы постоянного тока. Электрический ток в металлах «

Понять природу электрического тока не так-то просто. Изучение этой темы позволит вам получить общие представления о постоянном электрическом токе, его законах. Вы научитесь собирать электрические цепи, выполнять измерения и простейшие расчеты.

 

Электрическим током считается любое упорядоченное движение заряженных частиц. В металлах такими частицами являются свободные электроны. Но, чтобы электроны заставить двигаться в определенном направлении, нужно в проводнике создать электрическое поле.

 

До открытия электрона в 1890 г. направление тока условно  рассматривалось как направление перемещения положительного заряда. Под действием электрического поля заряды начинают двигаться в область меньшего потенциала.  Движение зарядов длится до тех пор, пока потенциалы на концах проводника не станут равными. Хотя известно, что электрический ток в металлах создают свободные электроны, но до сих пор существует соглашение, в соответствии с которым за направление тока принято движение положительных зарядов.

 

Чтобы электрический ток не прекращался длительное время, цепь должна содержать источник тока и быть замкнутой. Благодаря источнику тока, электродвижущая сила (ЭДС) обеспечивает постоянную разность потенциалов в цепи. Таким образом, в замкнутой цепи именно ЭДС поддерживает направленное движение зарядов.

 

Электрический ток характеризуется физической величиной – силой тока, а работа электрического поля на участке цепи – напряжением. Зависимость между силой тока и напряжением для металлов экспериментально установил в 1826 году Г. Ом.

 

При наличии источника тока закон Ома для замкнутой цепи записывается с учетом ЭДС, внешнего сопротивления цепи и внутреннего сопротивления источника тока.

 

 

Содержание

 

Условия существования электрического тока —>

Электронная теория проводимости металлов —>

Схема электрической цепи —>

Закон Ома для участка цепи —>

Закон Ома для замкнутой цепи —>

Закон Джоуля-Ленца —>

Закономерности последовательного и параллельного соединения проводников —>

Зависимость сопротивления металлов от температуры —>

Определение ЭДС и внутреннего сопротивления источника тока —>

Изучение последовательного и параллельного соединения проводников —>

 

Урок физики по теме «Электрический ток в металлах». 11-й класс

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цели урока:

— раскрыть понятие физической природы электрического тока в металлах, опытное подтверждение электронной теории;

— продолжить формирование естественно-научных представлений по изучаемой теме

— создать условия для формирования познавательного интереса, активности учащихся

— формированию навыков;

— формированию коммуникативного общения.

Оборудование: интерактивный комплекс SMART Board Notebook, локальная сеть компьютеров, интернет.

Метод ведения урока: комбинированный.

Эпиграф урока:

Науку все глубже постигнуть стремись,
Познанием вечного жаждой томись.
Лишь первых познаний блеснет тебе свет,
Узнаешь: предела для знания нет.

Фирдоуси
(Персидский и таджикский поэт, 940-1030 гг.)

План урока.

I. Оргмомент

II. Работа в группах

III. Обсуждение итогов, монтаж презентации

IV. Рефлексия

V. Домашнее задание

Ход урока

— Здравствуйте, ребята! Садитесь. Сегодня наша работа будет проходить по группам.

Задания группам:

I. Физическая природа зарядов в металлах.

II. Опыт К.Рикке.

III. Опыт Стюарта, Толмена. Опыт Мандельштама, Папалекси.

IV. Теория Друде.

V. Вольт-амперная характеристика металлов. Закон Ома.

VI. Зависимость сопротивления проводников от температуры.

VII. Сверхпроводимость.

Содержание заданий, выполненных в группах.

1. Электрическая проводимость представляет собой способность веществ проводить электрический ток под действием внешнего электрического поля.

По физической природе зарядов – носителей электрического тока, электропроводность подразделяют на:

А) электронную,

Б) ионную,

В) смешанную.

2. Для каждого вещества при заданных условиях характерна определенная зависимость силы тока от разности потенциалов.

По удельному сопротивлению вещества принято делить на:

А) проводники (p < 10^-2 Ом*м)

Б) диэлектрики (p > 10^-8 Ом*м)

В) полупроводники (10^-2 Ом*м> p>10^-8 Ом*м)

Однако такое деление условно, т. к. под воздействием ряда факторов (нагревания, облучения, примеси) удельное сопротивление веществ и их вольт — амперная характеристика изменяются, и иногда очень существенно.

3. Носителями свободных зарядов в металлах являются электроны. Доказано классическими опытами К. Рикке (1901 г.) – немецкий физик; Л.И. Мандельштамом и Н. Д. Папалекси (1913 г.) – наши соотечественники; Т. Стюартом и Р. Толменом (1916 г.) – американские физики.

К. Рикке

Опыт К. Рикке

Три предварительно взвешенных цилиндра (два медных и один алюминиевый) Рикке сложил отшлифованными торцами так, что алюминиевый оказался между медными. Затем цилиндры были включены в цепь постоянного тока: через них в течение года проходил большой ток. За то время через электрические цилиндры прошел электрический заряд, равный приблизительно 3.5 млн Кл. Вторичное взаимодействие цилиндров, проводившееся с до 0.03 мг, показало, что масса цилиндров в результате опыта не изменилась. При исследовании соприкасавшихся торцов под микроскопом было установлено, что имеются лишь незначительные следы проникновения металлов, которые не превышают результатов обычной диффузии атомов в твердых телах. Результаты опыта свидетельствовали о том, что в переносе заряда в металлах ионы не участвуют.

Л.И. Мандельштам

Н. . Папалекси

Опыт Л. И. Мандельштама и Н. Д. Папалекси

Русские ученые Л. И. Мандельштам (1879—1949; основатель школы радиофизиков) и Н. Д. Папалекси (1880—1947; крупнейший советский физик, академик, председатель Всесоюзного научного совета по радиофизике и радиотехнике при АН СССР) в 1913 году поставили оригинальный опыт. Взяли катушку с проводом и стали крутить ее в разные стороны.

Раскрутят, к примеру, по часовой стрелке, потом резко остановят и — назад.

Рассуждали они примерно так: если электроны и вправду обладают массой, то, когда катушка внезапно останавливается, электроны еще некоторое время должны двигаться по инерции. Движение электронов по проводу — электрический ток. Как задумали, так и получилось. Подсоединили к концам провода телефон и услышали звук. Раз в телефоне слышен звук, следовательно, через него ток протекает.

Т. Стюарт

Опыт Т. Стюарта и Р. Толмен

Возьмём катушку, которая может вращаться вокруг своей оси. Концы катушки с помощью скользящих контактов замкнуты на гальванометр. Если находящуюся в быстром вращении катушку резко затормозить, то свободные электроны в проволоке продолжат двигаться по инерции, в результате чего гальванометр должен зарегистрировать импульс тока.

П. Друде

Теория Друде

Электроны в металле рассматриваются как электронный газ, к которому можно применить кинетическую теорию газов. Считается, что электроны, как и атомы газа в кинетической теории, представляют собой одинаковые твердые сферы, которые движутся по прямым линиям до тех пор, пока не столкнутся друг с другом. Предполагается, что продолжительность отдельного столкновения пренебрежимо мала, и что между молекулами не действует никаких иных сил, кроме возникающих в момент столкновения. Так как электрон — отрицательно заряженная частица, то для соблюдения условия электронейтральности в твердом теле также должны быть частицы другого сорта — положительно заряженные. Друде предположил, что компенсирующий положительный заряд принадлежит гораздо более тяжелым частицам (ионам), которые он считал неподвижными. Во времена Друде не было ясно, почему в металле существуют свободные электроны и положительно заряженные ионы, и что эти ионы из себя представляют. Ответы на эти вопросы смогла дать только квантовая теория твердого тела. Для многих веществ, однако, можно просто считать, что электронный газ составляют слабо связанные с ядром внешние валентные электроны, которые в металле «освобождаются» и получают возможность свободно передвигаться по металлу, тогда как атомные ядра с электронами внутренних оболочек (атомные остовы) остаются неизменными и играют роль неподвижных положительных ионов теории Друде.

Электрический ток в металлах

Все металлы являются проводниками электрического тока и состоят из пространственной кристаллической решетки, узлы которой совпадают с центрами положительных ионов, а вокруг ионов хаотически движутся свободные электроны.

Основные положения электронной теории проводимости металлов.

1. Металл можно описать следующей моделью: кристаллическая решетка ионов погружена в идеальный электронный газ, состоящий из свободных электронов. У большинства металлов каждый атом ионизирован, поэтому концентрация свободных электронов приблизительно равна концентрации атомов 10²³— 10²⁹м^-3 и почти не зависит от температуры.
2. Свободные электроны в металлах находятся в непрерывном хаотическом движении.
3. Электрический ток в металле образуется только за счет упорядоченного движения свободных электронов.
4. Сталкиваясь с ионами, колеблющимися в узлах кристаллической решетки, электроны отдают им избыточную энергию. Вот почему при прохождении тока проводники нагреваются.

Электрический ток в металлах.

Где v – средняя скорость направленного движения заряженных частиц, S – площадь поперечного сечения проводника, n – концентрация электронов проводимости.

Оценка скорости движения свободных электронов в проводнике при S= 1 м , I = 10 A

Отметим, что скорость распространения тока в проводнике равна скорости распространения электромагнитных волн в вакууме c = 3*10⁸

Из закона Ома для участка цепи следует, что вольт-амперная характеристика металлов – прямая линия

Напомним, что , где p – удельное сопротивление, l – длина, S – площадь поперечного сечения проводника.

Сверхпроводимость

Явление уменьшения удельного сопротивления до нуля при температуре, отличной от абсолютного нуля, называется сверхпроводимостью. Материалы обнаруживающие способность переходить при некоторых температурах, отличных от абсолютного нуля, в сверхпроводящее состояние, называются сверхпроводниками.

Прохождение тока в сверхпроводнике происходит без потерь энергии, поэтому однажды возбужденный в сверхпроводящем кольце электрический ток может существовать неограниченно долго без изменения.

Сверхпроводящий материалы уже используются в электромагнитах. Ведутся исследования, направленные на создание сверхпроводящих линий электропередачи.

Применение явления сверхпроводимости в широкой практике может стать реальностью в ближайшие годы благодаря открытию в 1986 г. Сверхпроводимости керамик – соединений лантана, бария, меди и кислорода. Сверхпроводимость таких керамик сохраняется до температур около 100 К.

Молодцы, ребята! С работой справились отлично. Получилась хорошая презентация. Спасибо за урок!

Литература.

1. Горбушин Ш.А. Опорные конспекты для изучения физики за курс средней общеобразовательной школы. – Ижевск “Удмуртия”, 1992.
2. Ланина И.Я. Формирование познавательных интересов учащихся на уроках физики: Книга для учителя. – М.: Просвещение, 1985.
3. Урок физики в современной школе. Творческий поиск учителей: Книга для учителя /Сост. Э.М.Браверман/ Под редакцией В.Г. Разумовского.- М.: Просвещение, 1993
4. Дигелев Ф.М. Из истории физики и жизни ее творцов: Книга для учащихся.- М.: Просвещение, 1986.
5. Карцев В.Л. Приключения великих уравнений.- 3-е издание – М.: Знание, 1986. (Жизнь замечательных идей).

Конспект урока по физике «Электрический ток в металлах»

Тема. Электрический ток в металлах

Цели урока: сформировать понятие о природе электрического тока в металлах и его направлении; выяснить, какие действия способен совершать электрический ток; показать практическую направленность изучаемого материала; формировать научно-материалистическое мировоззрение, развивать логическое мышление, формировать представление о процессе научного познания; вырабатывать умение слушать и быть услышанным, прививать культуру умственного труда, воспитывать чувства гордости и уважения к людям, внесшим вклад в развитие науки

Тип урока: урок усвоения новых знаний

Ход урока

1. Организационный момент в виде слайд – шоу под стихотворение В. Шефнера

Я еще не устал удивляться

Чудесам, что есть на земле, —

Телевизору, голосу раций

И компьютеру на столе.

Самолеты летят сквозь тучи,

Ходят по морю корабли, —

Как до этих вещей могучих

Домечтаться люди смогли?

Как придумать могли такое,

Что кассета нам песню поет,

Что на кнопку нажмешь рукою –

И средь ночи день настает.

Я вверяю себя трамваю,

Я гляжу на экран кино.

Эту технику понимая,

Изумляюсь я все равно.

Ток по проволоке струится,

Спутник ходит по небесам…

Человеку стоит дивиться

Человеческим чудесам.

2. Актуализация опорных знаний

1. Что такое электрический ток?

2. Перечислите условия существования электрического тока.

3. Какие вещества называют проводниками электричества?

4. Что такое источник тока? Каково его назначение?

3. Изложение нового материала

Все металлы являются проводниками электрического тока и в твердом состоянии имеют кристаллическое строение.

Из курса химии вам известно, что валентные электроны в металлах легко покидают свой атом и становятся свободными. В узлах кристаллической решётки металлов расположены положительные ионы, а в пространстве между ними движутся электроны. Электроны не связаны с ядрами своих атомов и движутся беспорядочно, поэтому их называют свободными. В свою очередь, свободные электроны в металлах называют электронным газом.

В металлах электронная проводимость

Отрицательный заряд всех свободных электронов по абсолютному значению равен положительному заряду всех ионов решётки. Поэтому в обычных условиях металл электрически нейтрален.

Если в металлах создать электрическое поле, то свободные электроны продолжат двигаться хаотически и будут смещаться в сторону положительного полюса источника тока. Затем движение электронов становится направленным и возникает электрический ток.

Электрический ток в металлах – это упорядоченное движение свободных электронов

Опыт русских учёных Мандельштама и Папалекси, проведенный ими в 1913 году, экспериментально показал, что проводимость металлов обусловлена движением свободных электронов.

Л. И. Мандельштам (1879—1949; основатель школы радиофизиков) и Н. Д. Папалекси (1880 — 1947; крупнейший советский физик, академик, председатель Всесоюзного научного совета по радиофизике и радиотехнике при АН СССР) в 1913 году поставили оригинальный опыт по установлению природы тока в металлах.

Взяли катушку с проводом и стали крутить ее в разные стороны. Раскрутят, к примеру, по часовой стрелке, потом резко остановят и — назад.

Рассуждали они примерно так: если металлический проводник привести в быстрое движение, а затем резко остановить, то, когда катушка внезапно останавливается, электроны еще некоторое время должны двигаться по инерции. В результате в проводнике возникнет кратковременный ток, который можно зафиксировать гальванометром. По отклонению стрелки прибора можно установить знак заряда движущихся частиц, а по отношению заряда частиц к их массе – установить, какие именно частицы создают ток.

Движение электронов по проводу — электрический ток. Как задумали, так и получилось. Подсоединили к концам провода телефон и услышали звук. Раз в телефоне слышен звук, следовательно, через него ток протекает.

Опыт Мандельштама и Папалекси в 1916 году повторили американские ученые Толмен и Стюарт. Они тоже крутили катушку, но вместо телефона к ее концам подсоединили прибор для измерения заряда. Им удалось измерить массу частицы. Данные Толмена и Стюарта потом много раз проверялись и уточнялись другими учеными, и теперь вы знаете, что масса электрона

m_e = 9, 1 ∙ 10^-31 кг

Удельный заряд электрона, то есть заряд, приходящийся на единицу массы,

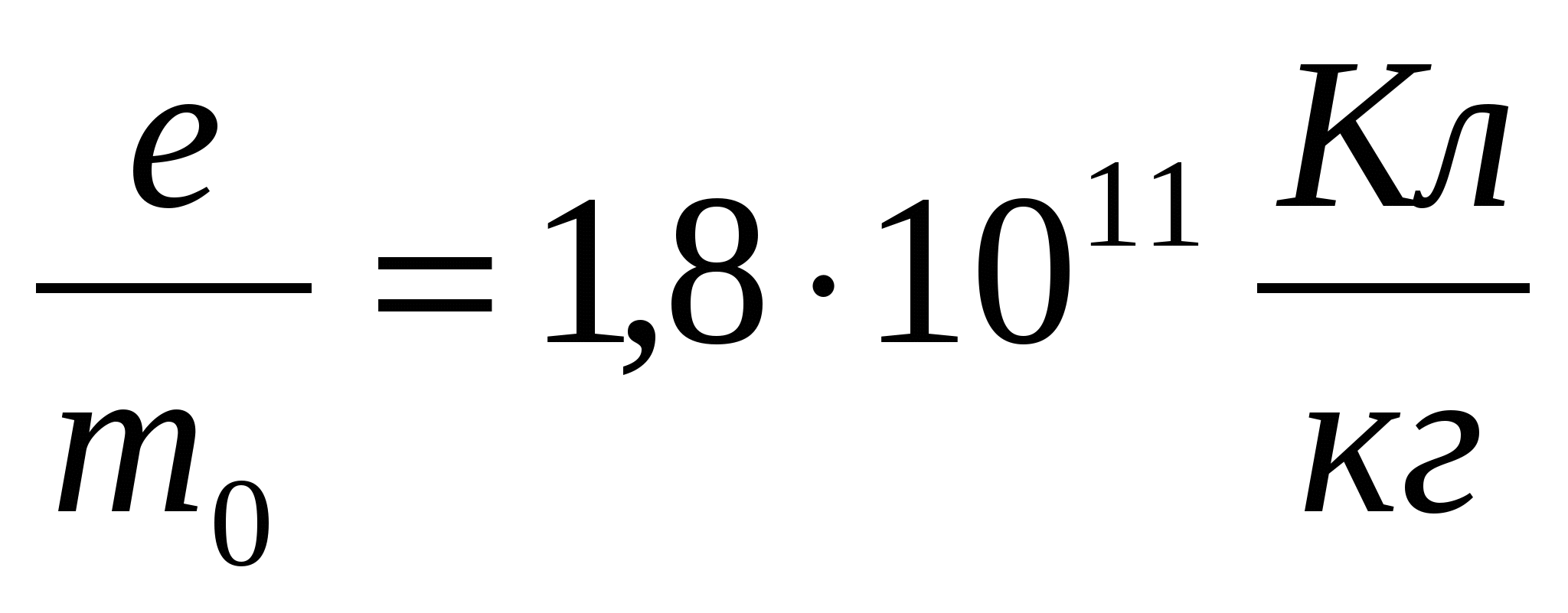
Скорость движения самих электронов в проводнике под действием электрического поля мала (несколько мм в секунду).

Но почему при замыкании электрической цепи лампочка загорается практически мгновенно?

Оказывается электрическое поле распространяется с огромной скоростью (близкой к с = 300 000 км/с) по всей длине проводника. Под действием электрического поля в упорядоченное движение приходят свободные электроны, находящиеся не только в подводящих проводниках, но и в спирали самой лампы.

Поэтому, когда говорят о скорости распространения электрического тока в проводнике, то имеют в виду скорость распространения по проводнику электрического поля.

Основные характеристики тока в металлах (проводниках):

а) сила тока в проводнике

I = envS где e = 1,6 ∙ 10^-19 Кл – модуль

заряда электрона

n – концентрация электронов

v ≈ 10⁴ 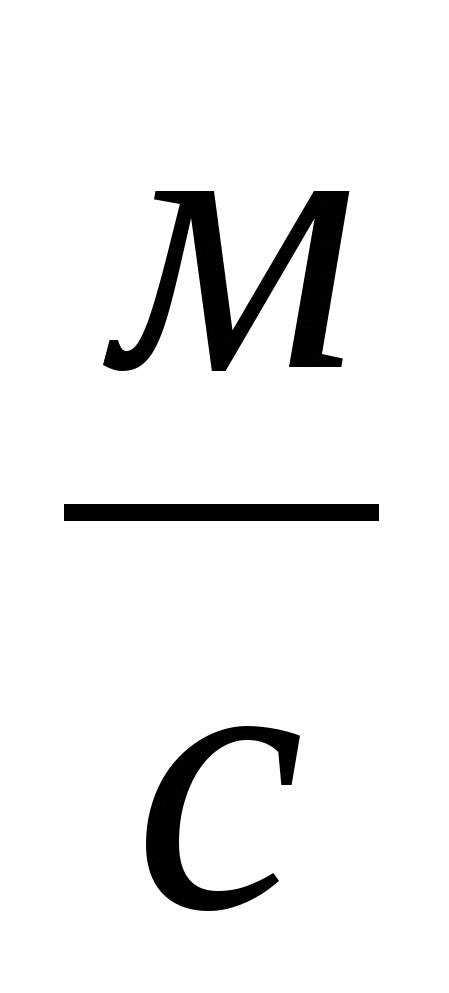— cредняя скорость

электронов

S — площадь поперечного

сечения проводника

б) вольт-амперная характеристика (зависимость силы тока в

проводнике от напряжения)

I =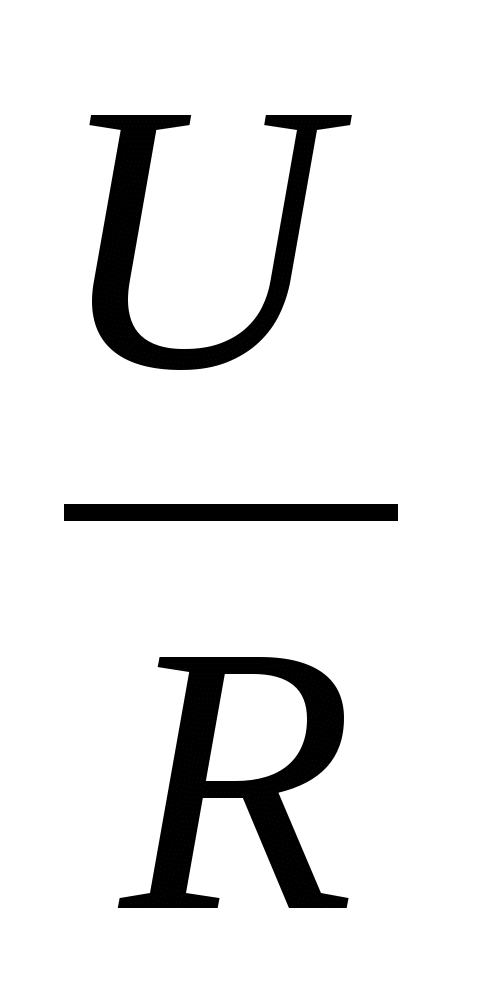

в) зависимость сопротивления проводника от температуры

В опыте, о котором мы сегодня говорили, после остановки проводника направленное движение частиц быстро прекращается, потому что проводник оказывает току сопротивление. Сопротивление металлического проводника зависит не только от его геометрических размеров и вещества, но и от температуры. Это можно подтвердить таким опытом. Если соединить стальную спираль с источником тока и постепенно нагревать её, то при постоянном напряжении сила тока будет уменьшаться. Это говорит о том, что сопротивление спирали возрастает.

R = R₀ (1 + t) где R₀ – сопротивление до

нагревания

— изменение температуры

α -температурный коэффициент

сопротивления

Если провести этот же опыт с другими спиралями, то можно заметить, что при увеличении температуры сопротивление этих спиралей тоже увеличивается, но его изменение будет другим.

Зная, как зависит сопротивление металлического проводника от температуры, измеряв сопротивление, можно определить температуру проводника. Этот факт положен в основу работы так называемых термометров сопротивления.

Вопрос учащимся:

• Где применяется электрический ток в металлах? (Проводники для передачи электроэнергии на расстояние, сердечник трансформатора для преобразования электрической энергии, трубы для предотвращения коррозии, спираль лампы для освещения, спираль ТЭНа для нагрева, и т. д.)

4. Работа с учебником (стр. 103 п.3)

5. Итог урока

• Каков характер движения электронов в металлах при отсутствии электрического поля?

• А при наличии электрического поля?

• Что представляет собой электрический ток в металлах?

• Как была доказана природа электрического тока в металлах?

• От чего зависит сопротивление металлов?

6. Домашнее задание: § 18 (читать)

Электрический ток в металлах — Мегаобучалка

Электрический ток в металлах – это упорядоченное движение электронов под действием электрического поля. Опыты показывают, что при протекании тока по металлическому проводнику не происходит переноса вещества, следовательно, ионы металла не принимают участия в переносе электрического заряда.

Наиболее убедительное доказательство электронной природы тока в металлах было получено в опытах с инерцией электронов.

Идея таких опытов и первые качественные результаты принадлежат русским физикам Л. И. Мандельштаму и Н. Д. Папалекси (1913 г.). В 1916 году американский физик Р. Толмен и шотландский физик Б. Стюарт усовершенствовали методику и выполнили количественные измерения, доказав, что ток в металлических проводниках обусловлен движением электронов.

Хорошая электропроводность металлов объясняется высокой концентрацией свободных электронов.

В 1900 году немецкий ученый П. Друде на основе гипотезы о существовании свободных электронов в металлах создал электронную теорию проводимости металлов. Эта теория получила развитие в работах голландского физика Х. Лоренца и носит название классической электронной теории. Согласно этой теории, электроны в металлах ведут себя как электронный газ, во многом похожий на идеальный газ. Электронный газ заполняет пространство между ионами, образующими кристаллическую решетку металла.

Из-за взаимодействия с ионами электроны могут покинуть металл, лишь преодолев так называемый потенциальный барьер. Высота этого барьера называется работой выхода. При обычных (комнатных) температурах у электронов не хватает энергии для преодоления потенциального барьера.

Свободные электроны движутся хаотично и при своем движении сталкиваются с ионами решетки. В результате таких столкновений устанавливается термодинамическое равновесие между электронным газом и решеткой. Согласно теории Друде–Лоренца, электроны обладают такой же средней энергией теплового движения, как и молекулы одноатомного идеального газа. Это позволяет оценить среднюю скорость теплового движения электронов по формулам молекулярно-кинетической теории. При комнатной температуре она оказывается примерно равной 10⁵ м/с.

При наложении внешнего электрического поля в металлическом проводнике кроме теплового движения электронов возникает их упорядоченное движение (дрейф), то есть электрический ток.

Средняя скорость дрейфа:

Концентрация свободных электронов в металлах примерно равна концентрации атомов n ~ 10²⁸–10²⁹ м^–3, модуль заряда электрона e = 1,6 * 10¹⁹ Кл. Для проводника с площадью поперечного сечения S = 1 мм² = 10^-6 м² при силе тока I = 1 A скорость упорядоченного движения электронов равна

За 1 с электроны в проводнике перемещаются за счет упорядоченного движения меньше чем на 0,1 мм.

Таким образом, средняя скорость упорядоченного движения электронов в металлических проводниках на много порядков меньше средней скорости их теплового движения .

Малая скорость дрейфа противоречит опытному факту, что ток во всей цепи постоянного тока устанавливается практически мгновенно. Замыкание цепи вызывает распространение электрического поля со скоростью c = 3·10⁸ м/с. Через время порядка l / с (l – длина цепи) вдоль цепи устанавливается стационарное распределение электрического поля и в ней начинается упорядоченное движение электронов.

В классической электронной теории металлов предполагается, что движение электронов подчиняется законам механики Ньютона. В этой теории пренебрегают взаимодействием электронов между собой, а их взаимодействие с положительными ионами сводят только к соударениям. Предполагается также, что при каждом соударении электрон передает решетке всю накопленную в электрическом поле энергию и поэтому после соударения он начинает движение с нулевой дрейфовой скоростью.

Классическая электронная теория объясняет существование электрического сопротивления металлов, законы Ома и Джоуля–Ленца. Однако в ряде вопросов классическая электронная теория приводит к выводам, находящимся в противоречии с опытом.

Например, эта теория не может объяснить, почему молярная теплоемкость металлов, также как и молярная теплоемкость диэлектрических кристаллов, равна 3R, где R – универсальная газовая постоянная (закон Дюлонга и Пти). Наличие свободных электронов не сказывается на величине теплоемкости металлов.

Классическая электронная теория не может также объяснить температурную зависимость удельного сопротивления металлов. Теория дает в то время как из эксперимента получается зависимость ρ ~ T.

Согласно классической электронной теории, удельное сопротивление металлов должно монотонно уменьшаться при охлаждении, оставаясь конечным при всех температурах.

Такая зависимость действительно наблюдается на опыте при сравнительно высоких температурах.

При более низких температурах порядка нескольких кельвинов удельное сопротивление многих металлов перестает зависеть от температуры и достигает некоторого предельного значения. Наибольший интерес представляет явление сверхпроводимости, открытое датским физиком Х. Каммерлинг-Оннесом в 1911 году. При некоторой определенной температуре T_кр, различной для разных веществ, удельное сопротивление скачком уменьшается до нуля.

Критическая температура у ртути равна 4,1 К, у алюминия 1,2 К, у олова 3,7 К. Сверхпроводимость наблюдается не только у элементов, но и у многих химических соединений и сплавов. Например, соединение ниобия с оловом (Ni₃Sn) имеет критическую температуру 18 К. Некоторые вещества, переходящие при низких температурах в сверхпроводящее состояние, не являются проводниками при обычных температурах. В то же время такие «хорошие» проводники, как медь и серебро, не становятся сверхпроводниками при низких температурах.

He -268.94°C, N(азот) -195,82°C, Н(водород) -252,77°C