Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Главная → Примеры решения задач ТОЭ → Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Основными законами, определяющими расчет электрической цепи, являются законы Кирхгофа.

На основе законов Кирхгофа разработан ряд практических методов расчета электрических цепей постоянного тока, позволяющих сократить вычисления при расчете сложных схем.

Существенно упростить вычисления, а в некоторых случаях и снизить трудоемкость расчета, возможно с помощью эквивалентных преобразований схемы.

Преобразуют параллельные и последовательные соединения элементов, соединение «звезда» в эквивалентный «треугольник» и наоборот. Осуществляют замену источника тока эквивалентным источником ЭДС. Методом эквивалентных преобразований теоретически можно рассчитать любую цепь, и при этом использовать простые вычислительные средства. Или же определить ток в какой-либо одной ветви, без расчета токов других участков цепи.

В данной статье по теоретическим основам электротехники рассмотрены примеры расчета линейных электрических цепей постоянного тока с использованием метода эквивалентных преобразований типовых схем соединения источников и потребителей энергии, приведены расчетные формулы.

Решение задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований

---

Задача 1. Для цепи (рис. 1), определить эквивалентное сопротивление относительно входных зажимов a−g, если известно: R

1 = R₂ = 0,5 Ом, R₃ = 8 Ом, R₄ = R₅ = 1 Ом, R₆ = 12 Ом, R₇ = 15 Ом, R₈ = 2 Ом, R₉ = 10 Ом, R₁₀= 20 Ом.

Рис. 1

Решение

Начнем эквивалентные преобразования схемы с ветви наиболее удаленной от источника, т.е. от зажимов a−g:

---

Задача 2. Для цепи (рис. 2, а), определить входное сопротивление если известно: R₁ = R₂ = R₃ = R₄= 40 Ом.

Рис. 2

Решение

Исходную схему можно перечертить относительно входных зажимов (рис. 2, б), из чего видно, что все сопротивления включены параллельно. Так как величины сопротивлений равны, то для определения величины эквивалентного сопротивленияможно воспользоваться формулой:

где R – величина сопротивления, Ом;

n – количество параллельно соединенных сопротивлений.

---

Задача 3. Определить эквивалентное сопротивление относительно зажимов a–b, если R₁ = R₂ = R₃ = R₄ = R₅ = R

₆ = 10 Ом (рис. 3, а).

Рис. 3

Решение

Преобразуем соединение «треугольник» f−d−c в эквивалентную «звезду». Определяем величины преобразованных сопротивлений (рис. 3, б):

По условию задачи величины всех сопротивлений равны, а значит:

На преобразованной схеме получили параллельное соединение ветвей между узлами e–b, тогда эквивалентное сопротивление равно:

И тогда эквивалентное сопротивление исходной схемы представляет последовательное соединение сопротивлений:

---

Задача 4. В заданной цепи (рис. 4, а) определить методом эквивалентных преобразований

входные сопротивления ветвей a−b, c–d и f−b, если известно, что: R₁ = 4 Ом, R₂ = 8 Ом, R₃ =4 Ом, R₄ = 8 Ом, R₅ = 2 Ом, R₆ = 8 Ом, R₇ = 6 Ом, R₈ =8 Ом.

Решение

Для определения входного сопротивления ветвей исключают из схемы все источники ЭДС. При этом точки c и d, а также b и f соединяются накоротко, т.к. внутренние сопротивления идеальных источников напряжения равны нулю.

Рис. 4

Ветвь a−b разрывают, и т.к. сопротивление

R_a–b = 0, то входное сопротивление ветви равно эквивалентному сопротивлению схемы относительно точек a и b (рис. 4, б):

Аналогично методом эквивалентных преобразований определяются входные сопротивления ветвей R_cd и R_bf. Причем, при вычислении сопротивлений учтено, что соединение накоротко точек a и b исключает ( «закорачивает») из схемы сопротивления R₁, R₂, R₃, R₄ в первом случае, и R₅, R₆, R₇, R₈ во втором случае.

---

Задача 5. В цепи (рис. 5) определить методом эквивалентных преобразований токи I₁, I₂, I₃ и составить баланс мощностей, если известно: R₁ = 12 Ом, R₂ = 20 Ом, R₃ = 30 Ом, U = 120 В.

Рис. 5

Решение

Эквивалентное сопротивлениедля параллельно включенных сопротивлений:

Эквивалентное сопротивление всей цепи:

Ток в неразветвленной части схемы:

Напряжение на параллельных сопротивлениях:

Токи в параллельных ветвях:

Баланс мощностей:

---

Задача 6. В цепи (рис. 6, а), определить методом эквивалентных преобразований показания амперметра, если известно: R₁ = 2 Ом, R₂ = 20 Ом, R₃ = 30 Ом, R₄ = 40 Ом, R₅ = 10 Ом, R₆ = 20 Ом, E = 48 В. Сопротивление амперметра можно считать равным нулю.

Рис. 6

Решение

Если сопротивления R₂, R₃, R₄, R₅

заменить одним эквивалентным сопротивлением R_Э, то исходную схему можно представить в упрощенном виде (рис. 6, б).

Величина эквивалентного сопротивления:

Преобразовав параллельное соединение сопротивлений R_Э и R₆ схемы (рис. 6, б), получим замкнутый контур, для которого по второму закону Кирхгофа можно записать уравнение:

откуда ток I₁:

Напряжение на зажимах параллельных ветвей U_ab выразим из уравнения по закону Ома для пассивной ветви, полученной преобразованием R_Э

и R₆:

Тогда амперметр покажет ток:

---

Задача 7. Определить токи ветвей схемы методом эквивалентных преобразований (рис. 7, а), если R₁ = R₂ = R₃ = R₄ = 3 Ом, J = 5 А, R₅ = 5 Ом.

Рис. 7

Решение

Преобразуем «треугольник» сопротивлений R₁, R₂, R₃ в эквивалентную «звезду» R₆, R₇, R₈ (рис. 7, б) и определим величины полученных сопротивлений:

Преобразуем параллельное соединение ветвей между узлами 4 и 5

Ток в контуре, полученном в результате преобразований, считаем равным току источника тока J, и тогда напряжение:

И теперь можно определить токи I₄ и I₅:

Возвращаясь к исходной схеме, определим напряжение U₃₂ из уравнения по второму закону Кирхгофа:

Тогда ток в ветви с сопротивлением R₃ определится:

Величины оставшихся неизвестными токов можно определить из уравнений по первому закону Кирхгофа для узлов 3 и 1:

---

Электронная версия статьи Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Примеры решения задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Расчет электрических цепей постоянного тока методом эквивалентных преобразований

---

Метод эквивалентных преобразований 

02.09.2011, 253623 просмотра.

Параллельное соединение сопротивлений в электрической цепи. Параллельное соединение конденсаторов и катушек.

Определение параллельного соединения

Параллельное соединение электрических элементов (проводников, сопротивлений, емкостей, индуктивностей) — это такое соединение, при котором подключенные элементы цепи имеют два общих узла подключения.

Другое определение: сопротивления подключены параллельно, если они подключены одно и той же паре узлов. 

Графическое обозначение схемы параллельного соеднинения

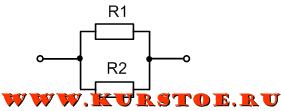
На приведенном рисунке показана схема параллельное подключения сопротивлений R1, R2, R3, R4. Из схемы видно, что все эти четыре сопротивления имеют две общие точки (узла подключения). 

  

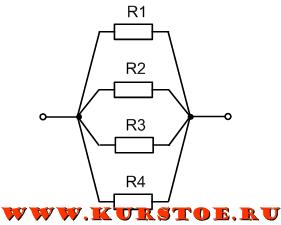
В электротехнике принято, но не строго требуется, рисовать провода горизонтально и вертикально. Поэтому эту же схему можно изобразить, как на рисунке ниже. Это тоже параллельное соединение тех же самых сопротивлений.

 

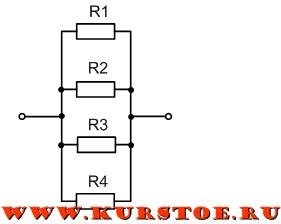
Формула для расчета параллельного соединения сопротивлений

При параллельном соединении обратная величина от эквивалентного сопротивления равна сумме обратных величин всех параллельно подключенных сопротивлений. Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.

 

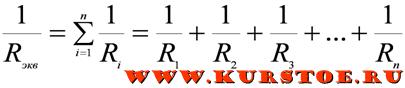
Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:

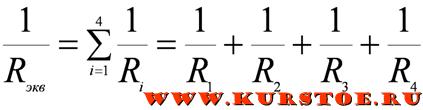
В частном случае при подключении параллельно двух сопротивлений:

Эквивалентное сопротивление цепи определяется по формуле:

 

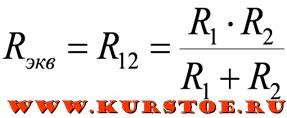
 В случае подключения «n» одинаковых сопротивлений, эквивалентное сопротивление можно рассчитать по частной формуле:

 

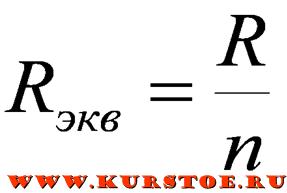
Формулы для частного рассчета вытекают из основной формулы. 

Формула для расчета параллельного соединения емкостей (конденсаторов)

При параллельном подключении емкостей (конденсаторов) эквивалентная емкость равна сумме параллельно подключенных емкостей:

 

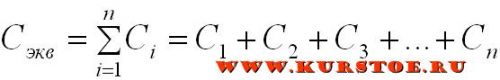
Формула для расчета параллельного соединения индуктивностей

При параллельном подключении индуктивностей, эквивалентная индуктивность рассчитывается так же, как и эквивалентное сопротивление при параллельном соединении: 

 

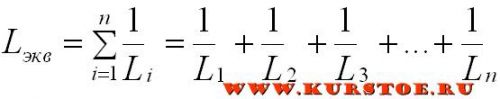
Необходимо обратить внимание, что в формуле не учтены взаимные индуктивности.

Пример свертывания параллельного сопротивления  

Для участка электрической цепи необходимо найти параллельное соединение сопротивлений выполнить их преобразование до одного.

 

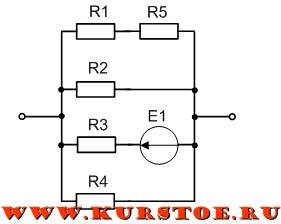
Из схемы видно, что параллельно подключены только R2 и R4. R3 не параллельно, т.к. одним концом оно подключено к источнику ЭДС E1. R1 — одним концом подключено к R5, а не к узлу. R5 — одним концом подключено к R1, а не к узлу. Можно так же говорить, что последовательное соединение сопротивлений R1 и R5 подключено параллельно с R2 и R4.

Рассчитать эквивалентное сопротивлений R14 можно по формуле для двух сопротивлений.

Ток при параллельном соединении

При параллельном соединении сопротивлений ток через каждое сопротивление в общем случае разный. Величина тока обратно пропорциональна величине сопротивления.

Напряжение при параллельном соединении 

При параллельном соединении разность потенциалов между узлами, объединяющими элементы цепи, одинакова для всех элементов.

Применение параллельного соединения

1. В промышленности изготавливаются сопротивления определенных величин. Иногда необходимо получить значение сопротивления вне данных рядов. Для этого можно подключить несколько сопротивлений параллельно. Эквивалентное сопротивление всегда будет меньше самого большого номинала сопротивления.

2. Делитель токов.

Эквивалентное сопротивление онлайн

Эквивалентное сопротивление при последовательном соединении

Альтернативное отображение

Эквивалентное сопротивление при паралельном соединении

Альтернативное отображение

Последовательное соединение

Что же такое эквивалентное сопротивление?

Все знаем что такое эквивалент. Это вещь или объект которое по своим характеристикам повторяет  оригинал.  В электротехнике эквивалент сопротивления это замена части схемы состоящей из нескольких резисторов — одним элементом(эквивалентом)

Сложные схемы соединений пока рассматривать не будем, а рассмотрим две самые простые схемы расчета эквивалентного сопротивления: последовательное и паралельное соединение

Вид последовательного соединения резисторов показан на рисунке ниже

 

И формула расчета эквивалентного сопротивления  выглядит так

 

Параллельное СОЕДИНЕНИЕ

Паралельное соединение нескольних резисторов (сопротивлений) выглядит так, как показано на рисунке

 

А формула превращается в такую

 

Стоит обратить внимание, что по таким же формулам считается эквивалентное сопротивление индуктивностей, но совершенно другой прицип будет при расчете эквивалентной ёмкости конденсаторов

 

Синтаксис

Он очень прост 

calc_e  список сопротивлений с размерностями через запятую.

В ответе мы получим эквививалентное значение  сопротивления  при последовательном и паралельных соединениях.

Важное замечание: размерности нужно писать на русском языке. Для пользователей сайта, не знающих русский язык, можем по запросу добавить обработку англоязычных наименований приставок и размерностей. Это не сложно.

Примеры

Рассчитать эквивалентное сопротивление трех резисторов  следующих номиналов: 10 Ом, 0.2кОм и 344кОм

В запросе так и пишем calc_e 10 Ом, 0.2кОм, 344кОм

Ответ не заставит себя долго ждать и выглядит вот так

Эквивалентное сопротивление при последовательном соединении

344.21килоОм

Альтернативное отображение

Эквивалентное сопротивление при паралельном соединении

9.5235458597492Ом

Альтернативное отображение

Удачи в расчетах!

Расчет электрических цепей методом эквивалентных сопротивлений (метод свертывания цепи)

⇐ ПредыдущаяСтр 3 из 3

Метод эквивалентных сопротивлений применяется для расчета таких электрических цепей, в которых имеются пассивныеэлементы, включенные между собой последовательно, параллельно или по смешанной схеме. Метод заключается в последовательной замене отдельных групп сопротивлений одним эквивалентным до получения самой простой схемы (см. рис. 13г). Затем определяется каждый ток в цепи.

 

 

Рисунок 13. Метод свертывания цепи

Определение эквивалентных сопротивлений

Обратимся к схеме, приведенной на рисунке 13а. Сопротивления 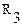и 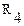соединены последовательно. Поэтому 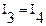. Эти два сопротивления можно заменить одним (эквивалентным) 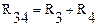, тогда схема упростится (рисунок 13б).

Сопротивления 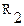и включены параллельно и их можно тоже заменить одним эквивалентным: .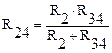

Тогда схема еще упростится ( рисунок 13в).

 

В схеме на рисунке 13в сопротивления , 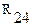и включены последовательно и могут быть заменены одним эквивалентным . Схема еще более упростится (рисунок 13г).

Подобными преобразованиями схему смешанного соединения пассивных элементов с одним источником энергии в большинстве случаев можно привести к простейшей схеме (рисунок 13г). В более сложных схемах методом эквивалентных сопротивлений достигается упрощение, которое значительно облегчает дальнейший расчет.

Определение токов

Определение начинается с простейшей схемы (рисунок 13г).

По закону Ома: 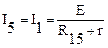т.к. ; .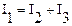

Зная 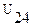легко найти 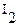и . .

Задача 1

= 20 Ом , =30 Ом, 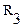= 12 Ом, 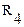= 8 Ом, 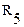= 1,5 Ом, = 160 В, = 0,5 Ом. Определить токи во всех элементах схемы и КПД источника (рисунок 13а).

 

 

Задача 2

Ток = 3 А. Величины сопротивления те же. Определить ЭДС и мощность источника (рисунок 13а).

 

Метод преобразования треугольника и звезды сопротивлений

Пассивные элементы в электрических цепях соединяются не только последовательно и параллельно. В ряде схем можно выделить группы из трех элементов, образующих треугольник или звезду сопротивлений, которые не могут быть рассчитаны методом свертывания.

При расчете подобных цепей сначала проводят преобразование треугольника сопротивлений в эквивалентную звезду или наоборот, а потом к преобразованной схеме применяют метод свертывания.

Рассмотрим схему измерителя величины сопротивлений (рисунок 14а). В этой схеме нет элементов, соединенных последовательно или параллельно, но имеются замкнутые контуры из трех сопротивлений (треугольники сопротивлений).

К узловым точкам a,b,c присоединен треугольниксопротивлени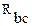й и 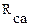. Его можно заменить по определенным правилам эквивалентной трехлучевой звездой, присоединенной к тем же точкам a,b,c (рисунок 14б).

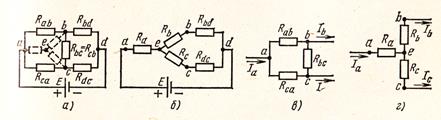
Рисунок 14. Преобразование треугольника и звезды сопротивлений

 

Преобразование треугольника сопротивлений в эквивалентную звезду

Замена треугольника сопротивлений эквивалентной звездой и наоборот осуществляется при условии, что такая замена не изменит потенциалов узловых точек a, b, c и режим работы остальной части схемы не изменится (не изменятся токи, напряжения и мощности).

Рассмотрим схемы на рисунках 14в) и 14г). Эти схемы должны быть эквивалентны для всех случаев, и в частности для тока 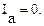При этом в схеме треугольника между точками b и c включены две параллельные ветви с сопротивлениями 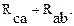Общее сопротивление между этими точками: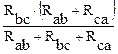

В схеме звезды между точками b и c включены последовательно сопротивления 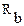и .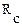

Поэтому: .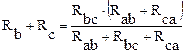

Полагая 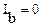, а затем аналогично получим:

;

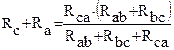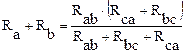
Решив эту систему из трех уравнений, получим: ;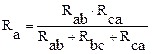

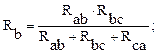
Преобразование звезды сопротивлений в эквивалентный треугольник

В той же исходной схеме заменим звезду, образованную сопротивлениям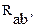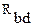и и 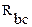на треугольник проводимости (рисунок 15а).

Рисунок 15. Преобразование звезды сопротивлений в эквивалентный треугольник

 

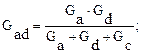
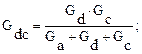
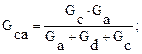
Задача

Определить токи в схеме, изображенной на рисунке 15а), если

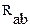= 12 Ом, 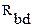= 18 Ом, = 6 Ом, 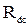=18 Ом, 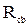=18 Ом, 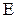=132 В.

 

Контрольные вопросы

1. В чем состоит метод свертывания электрической цепи?

2. Расскажите о преобразовании треугольника сопротивлений в эквивалентную звезду сопротивлений.

3. Расскажите о преобразовании звезды сопротивлений в эквивалентный треугольник сопротивлений.

 

Пример расчета схемы с определением потенциалов ее точек относительно произвольно выбранной

«общей точки» («земли»).

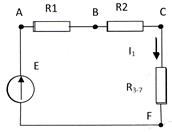
Расчет схемы предполагает кроме определение всех токов, протекающих в схеме, вычисление потенциала каждой точки схемы относительно «общей точкой» (ОТ). Иногда ОТ называют еще «землей» или «заземлением». В электрической схеме одна из точек схемы выбирается ОТ, т.е. потенциал ее условно принимается равным нулю. Обычно эта точка соединяется с корпусом прибора или с нулевым проводом электрической сети. В начале расчета не всегда ясно, какую именно точку схемы следует выбрать ОТ и в процессе расчета приходится неоднократно определять потенциалы всех точек относительно той или иной ОТ. Рассмотрим, как нужно поступать, чтобы минимизировать вычисления.

Например, нужно рассчитать схему, приведенную на рисунке 16, т.е. определить токи, протекающие во всех ветвях и определить потенциалы всех точек схемы относительно ОТ, которой в данном примере может быть выбрана либо точка F , либо точка D.

 

 

 

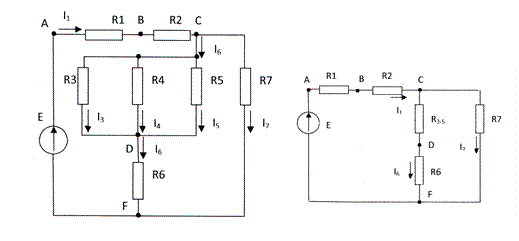
Рисунок 16. Исходная схема Рисунок 17

 

Исходные данные для расчета: R1=1 Ом; R2= R3=2 Ом;

R4=3 Ом; R5=1,2 Ом; R6=1,4 Ом; R7=6 Ом; Е=4,5 В.

Расчет токов осуществим методом эквивалентных сопротивлений и первым шагом заменим сопротивления R3, R4 и R5 одним эквивалентным сопротивлением R_3-5 (Рисунок 17).

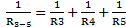; R_3-5=0,6 Ом.

Включенные последовательно сопротивления R_3-5 и R6 заменим эквивалентным R_3-6 (Рисунок 18). R_3-6= R_3-5 + R6=2 Ом.

Включенные параллельно сопротивления R_3-6 и R7 заменим эквивалентным R_3-7 (Рисунок 19). R_3-7=

 

 

 

Рисунок 18 Рисунок 19

 

Рассчитаем величины токов в схеме, используя схемы на рисунках 16-19.

Ток I₁ (Рисунок 19): I₁=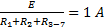

Напряжения:

Токи (Рисунок 18):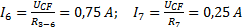

Напряжение (Рисунок 17)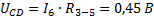

Токи (Рисунок 16):

.

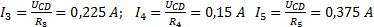Вычислять потенциалы точек легко в схеме, элементы которой включены последовательно (Рисунок 19). Вычислим потенциалы точек схемы в предположении, что ОТ является точка F, т.е. 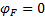. Тогда при обходе контура по направлению протекания тока I₁ получим:

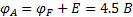
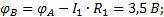
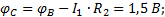
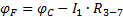=0.

Потенциал точки D вычисляется по схеме рисунка 17:

.

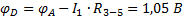По результатам расчетов построим потенциальную диаграмму (рисунок 20). По вертикали отложим вычисленные потенциалы, а по горизонтали – величины сопротивлений в порядке, показанном на рисунке 20.

 

 

Рисунок 20. Потенциальные диаграммы точек схемы

 

Потенциальная диаграмма представляет собой прямую линию ABCF, тангенс угла наклона которой к оси сопротивлений представляет собой (по закону Ома для участка цепи) ток I₁ (рисунок 19). Потенциальная диаграмма участка схемы, по которому протекает ток I₆ (рисунок 18), представлен линией CDF.

Если теперь принять точку D общей ( , то согласно рисунку 17, потенциалы всех точек относительно ее:

;

.

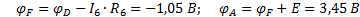
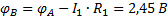Потенциальная диаграмма точек схемы рисунка 19 в этом случае будет представлять собой прямую линию A¹B¹C¹F¹ на рисунке 20, имеющую тот же наклон.

Как следует из расчетов и графиков, при изменении ОТ с F на D потенциалы всех точек меняются на одну и ту же величину разности потенциалов 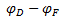между этими точками (в данном примере на 1,05 В).

Таким образом, для получения новых величин потенциалов точек схемы после изменении ОТ, необходимо:

— либо вычесть из потенциала каждой точки полученную разность потенциалов ,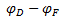

-либо перенести горизонтальную ось (ось сопротивлений) потенциальной диаграммы так, чтобы она прошла через вновь выбранную ОТ. Тогда в прежнем масштабе можно определить потенциалы других точек относительно вновь принятой ОТ.

 

 



1. Законы электрических цепей постоянного тока

1.1 Определения.

Законы электрических цепей постоянного тока подробно изучаются в школьном и вузовском курсах физики, поэтому в данном учебном пособии излагаются кратко. Приведем лишь некоторые определения и формулировки основных законов.

Узлом электрической цепи называется точка, в которой соединяется не менее трех проводников. Однородный участок цепи – это такой участок, на котором не действуют сторонние силы.

Эквивалентным сопротивлением участка цепи называется сопротивление, которым можно заменить все сопротивления рассматриваемого участка, при этом параметры других участков цепи не изменятся.

1.2 Основные законы.

Закон Ома для участка цепи:

Сила тока на участке цепи прямо пропорциональна напряжению на этом участке и обратно пропорциональна его эквивалентному сопротивлению.

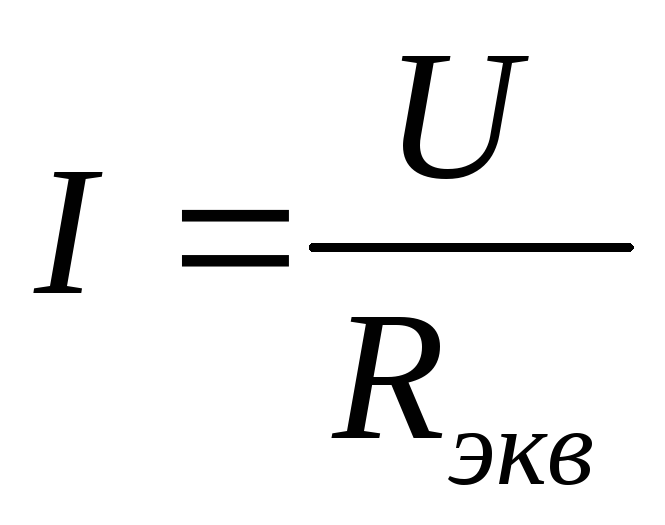(1.1)

Закон Ома для полной цепи:

Сила тока прямо пропорциональна электродвижущей силе (э.д.с.) источника тока и обратно пропорциональна полному сопротивлению этой цепи : 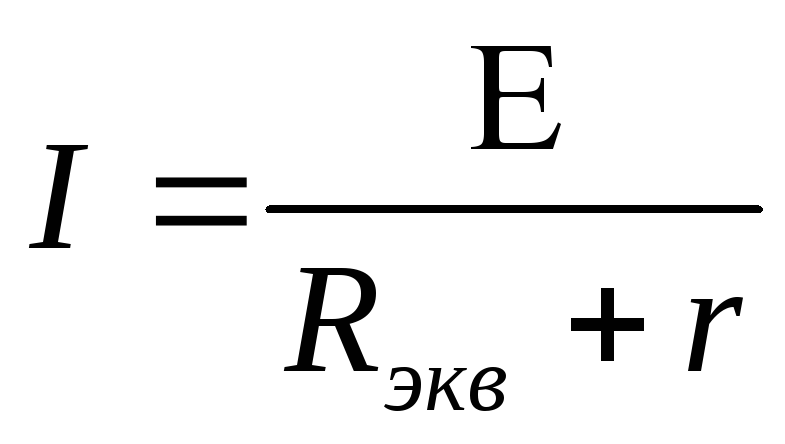. (1.2)

Здесь r – внутреннее сопротивление источника тока.

Рассчитать электрическую цепь – значит определить токи и падения напряжения на всех ее участках. Часто при расчете электрических цепей применяют законы Кирхгофа.

1-й закон Кирхгофа: Алгебраическая сумма токов, сходящихся в узле электрической цепи, равна нулю:

ΣI_k = 0 (1.3)

При этом токи, входящие в узел, и выходящие из него, берутся с разными знаками.

Другая формулировка этого закона: Сумма входящих в узел токов равна сумме токов, выходящих из него.

2-й закон Кирхгофа: Алгебраическая сумма э.д.с., входящих в замкнутый контур, равна сумме падений напряжений на элементах этого контура:

ΣЕ_k = ΣU_k (1.4)

При этом э.д.с., совпадающие по направлению с обходом контура, берутся со знаком «+», а противоположного направления – со знаком «-».

Закон баланса мощности электрической цепи: Алгебраическая сумма мощностей, генерируемых источниками напряжения, равна сумме мощностей, потребляемых приемниками электрической энергии:

ΣР_ист= ΣР_пр (1.5)

Закон баланса мощности являются универсальным инструментом, с помощью которого можно проверить правильность расчета электрической цепи.

1.3 Правила расчета эквивалентных сопротивлений.

Рассмотрим различные схемы соединения электрических элементов.

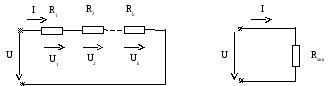
1. Последовательное соединение элементов.

Последовательное соединение элементов изображено на рис.1.1.

Цепь, через все элементы которой протекают один и тот же ток, называется неразветвленной.

Эквивалентное сопротивление последовательно соединенных элементов равно сумме сопротивлений этих элементов:

R_экв= ΣR_{k ,} (1.6)

или : R_экв=R₁ + R₂ +…+ R_k (1.7)

Падение напряжения на любом из k элементов может быть найдено по формуле:

U_k=I· R_k (1.8)

а) б)

Рис.1.1 Схема последовательного соединения (а)

и ее эквивалентная схема (б)

Применив 2-й закон Кирхгофа и закон баланса мощности, можно проверить правильность расчета электрической цепи с

последовательным соединением элементов. Должны выполняться соотношения (1.4) и (1.5) в следующем виде :

U_ист = ΣU_к =U₁ + U₂ +…+U_k (1.9)

и

Р_ист =I·U_ист= ΣР_{пр к} = Р₁+Р₂+…+Р_k (1.10)

здесь Р_{пр к}= I_k²·R_{k —} мощность, потребляемая k-тым приемником;

Р_ист – мощность источника тока.

Формула расчета реактивного сопротивления проводника: калькулятор расчетов

Реактивное сопротивление относится к числу явлений, наблюдаемых в цепях переменного тока. Тем, кто занимается ремонтом и эксплуатацией таких цепей, будет полезно знать, как определяется эта величина, и каким образом она влияет на процессы, происходящие в электросети.

Соленоид – устройство, обладающее индуктивностью

Понятие реактивного сопротивления

Данная разновидность репрезентирует взаимоотношение электротока и напряжения на определенных типах подключенных в сеть нагрузок (дросселях, конденсаторных компонентах), не сопряженное с объемами электроэнергии, используемыми потребителем. Измерительной единицей, как и для других разновидностей, выступает ом. Рассматриваемое явление обнаруживает себя только при переменном электротоке. В расчетах оно обозначается латинской литерой Х.

Различия между активным и реактивным сопротивлением

Разница между активным и реактивным сопротивлением состоит в том, что при прохождении электротока по компонентам цепи, несущим активную нагрузку, имеют место мощностные потери в виде выделения тепла, которое не может быть снова превращено в электрическую энергию. В качестве наглядного примера можно привести конфорку электроплиты, выделяющую тепловую энергию. Такими свойствами обладают и осветительные устройства, электрические двигатели, различные кабели. Фазы проходящих через такие компоненты напряжения и электротока будут совпадать.

Реактивные нагрузки отличаются наличием емкостных свойств либо способностью к индукции. В первом случае величина рассматриваемого сопротивления зависит от емкости, во втором – от электродвижущей силы самоиндукции.

Важно! Величина, в противоположность активной, может иметь плюсовой и минусовой знаки. Это зависит от того, в какую сторону идет фазовый сдвиг. При опережении электрическим током напряжения будет иметь место отрицательный показатель, в обратном случае – положительный.

Виды и свойства реактивного сопротивления

Данная величина может иметь две формы:

• емкостную – присущую конденсаторным элементам;
• индуктивную – характерную для катушек, соленоидов и обмоток.

Важно! Если к трансформатору подключить активную нагрузку, реактивное сопротивление понизится, так как упадет значение того типа мощности, который его вызывает. В некоторых цепях с несколькими индуктивными или емкостными нагрузками имеет место взаимоуничтожение фазовых сдвигов, приходящихся на разные детали, тогда комплексная величина будет равной нулю.

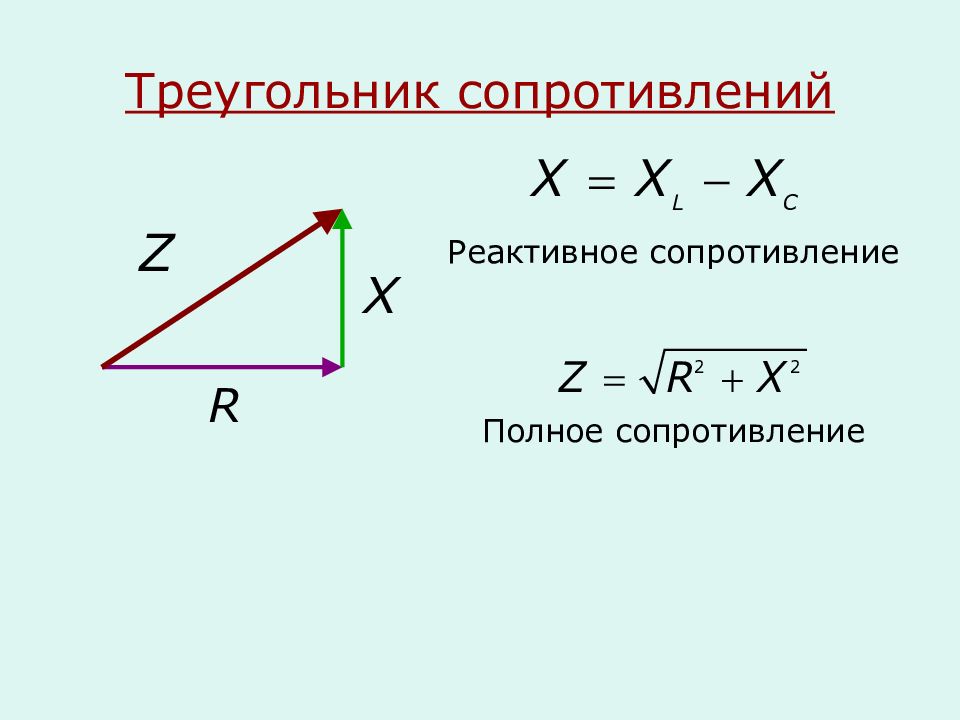
Треугольник сопротивлений

Виды пассивных элементов

Данные устройства характеризуются тем, что вместо рассеивания энергии склонны к ее накоплению. Разные типы таких деталей создают различные формы сопротивления.

Катушка индуктивности

Это радиокомпонент, представляющий собой проводниковый элемент спиральной или винтообразной формы, покрытый изоляцией. В схемах катушки используют для нивелирования помех и искажений, снижения величины переменного тока, генерации магнитного поля. Длинные тонкие элементы носят название соленоидов. Катушки отличаются небольшими величинами активной сопротивляемости и емкости, но обладают индуктивностью, генерируя электродвижущую силу.

Подключение катушки в электрическую цепь

Емкостной элемент

Примером этого вида деталей является конденсатор. Он включает в себя две проводящие обкладки, между которыми находится диэлектрический материал. Протекание электротока обусловлено накоплением и отдачей обкладками своего заряда.

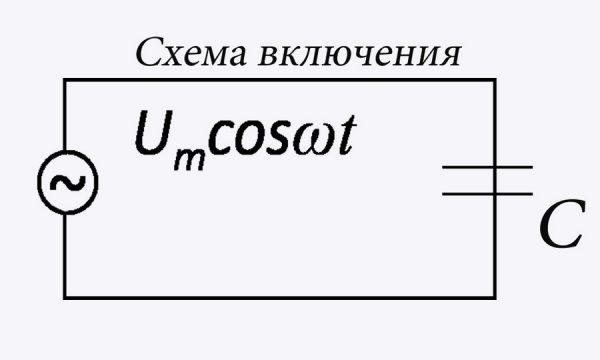
Подсоединение конденсатора в электроцепь

Конденсатор в цепи переменного тока

Конденсаторные устройства характеризуются неспособностью пропускать константный электроток. Так что если устройство подсоединить последовательно к источнику такого тока, в цепи электроток идти не будет. В переменных цепях дело обстоит иначе. Если цепочка содержит только емкостной компонент, в ней будет проходить ток, обгоняющий по фазе напряжение на 90°.

Важно! Величина электротока определяется его частотой и емкостной характеристикой использованного конденсатора.

Реактивное сопротивление конденсатора

Его можно узнать, воспользовавшись формулой:

Х=1/(C*w).

Здесь С – емкостная величина рассматриваемой детали, а w – угловая частота. При параллельном подключении элементов будет справедлива формула:

1/Хобщ = 1/Х1 + 1/Х2 +…

Если конденсаторы объединены последовательно, для нахождения комплексного показателя системы потребуется сложить значения для всех компонентов:

Хобщ = Х1 + Х2 +…

Катушка индуктивности в цепи переменного тока

В отличие от предыдущего случая, при подключении катушечного элемента идущий по нему электроток будет отставать от напряжения. Однако величина фазового сдвига будет аналогичной – 90°. При этом за препятствование быстрому увеличению тока ответственна ЭДС. Элемент способен играть роль безваттного резистора.

Реактивное сопротивление катушки индуктивности

В его расчете поможет выражение:

X = L*w.

Здесь L – показатель индуктивности подсоединенного элемента. При последовательном включении в сеть серии катушек индуктивная компонента сопротивления такой композиции может быть выражена как сумма таковых для всех деталей. Если применено параллельное соединение, справедливым будет выражение:

1/Хобщ = 1/Х1 + 1/Х2 +…

Как для катушки, так и для конденсаторных деталей будет верной запись закона Ома:

X = U/I, в которой U – величина падения напряжения на элементе.

Почему не сгорает первичная обмотка трансформатора

Иногда при эксплуатации трансформаторов возникает вопрос, почему не происходит сгорание обмотки, если ее сопротивляемость оказывается малой. Обмоточный компонент по своему устройству может быть приравнен к катушке. Соответственно, искомый показатель может быть вычислен с помощью выражения:

X = 2*π*L*F, где L – частота, F – индуктивность.

Поскольку последняя у трансформатора оказывается достаточно большой, таковым будет и итоговое число.

Мощность в цепи с реактивными радиоэлементами

При подключении таких элементов в цепь в четных четвертях периода мощность будет иметь отрицательное значение (в это время компонент направляет накопленную энергию в источник напряжения). В итоге использование энергии элементом за весь цикл оказывается равным нулю. Это означает, что на нем не происходит выделения энергии, так что на электросхемах такие детали изображаются холодными. На деле положение вещей может быть немного иным (это зависит от параметров конкретного элемента), бывает, что небольшие тепловые потери на конденсаторе или соленоиде все-таки имеют место. Но они не будут значительными, измеряющимися в кв.

Компенсация реактивной мощности

При подключении большого числа индуктивных компонентов генерируемая ими реактивная мощность создает избыточную нагрузку на трансформаторы и в целом ведет к бесполезной потере энергии. Чтобы это нивелировать, параллельно можно подсоединить конденсатор. Если правильно подобрать номинал, можно скомпенсировать фазовый сдвиг, что сильно снизит энергетические потери. Емкость этого устройства С равна 1/(2*π*f*X), где Х – параметр сопротивляемости подключенной нагрузки, равный U2/Q (Q – реактивная мощность).

Формула расчета реактивного сопротивления

В общем случае для деталей катушечного типа применяются выражения:

X = L*w = 2* π*f*L.

Для конденсаторов применяют формулы:

X = 1/(w*C)= 1/(2* π*f*C).

Для конкретного элемента, нужные параметры которого известны, величина может быть вычислена с использованием онлайн калькулятора. В форму потребуется ввести нужные данные и нажать на кнопку, инициирующую расчеты.

Умение рассчитывать данную составляющую сопротивляемости поможет узнать величину тепловых потерь на используемых нагрузках. При параллельном подсоединении конденсатора с подходящей емкостью можно решить проблему энергетических потерь на индуктивных нагрузках.

Видео

Практическая работа по дисциплине Электротехника. название Расчёт цепи постоянного тока методом эквивалентного сопротивления.

ПРАКТИЧЕСКАЯ РАБОТА №4

Наименование работы: Расчёт цепи постоянного тока методом эквивалентного сопротивления.

Цель работы: Определить общий ток и токи в ветвях при смешанном соединении приемников электрической энергии. Определить эквивалентное сопротивление. Проверить баланс мощности рассматриваемой цепи.

Пояснения к работе.

Неразветвленная электрическая цепь это последовательное соединение приемников электрической энергии.

R₁ R₂ R₃

I U₁ U₂ U₃

U I

Последовательным называется такое соединение приемников электрической энергии, при котором по всем элементам протекает один и тот же ток.

U = U₁ + U₂ + U₃

Эквивалентное сопротивление цепи равно сумме сопротивлений последовательно включенных резисторов : R_экв = R₁ + R₂ + R₃

Эквивалентным называется такое сопротивление, которое будучи включенным вместо данных резисторов, не изменяет режима работы электрической цепи.

Закон Ома для всей замкнутой цепи имеет вид:

I = U/ (R₁ + R₂ + R₃) I = U/R_экв

Р = Р₁ + Р₂ + Р₃ – уравнение баланса мощностей.

Общая мощность равна сумме мощностей последовательно включенных резисторов.

Мощности на последовательно включенных резисторах распределяются прямо пропорционально сопротивлениям резисторов.

Напряжение на последовательно включенных резисторах распределяется прямо пропорционально сопротивлениям резисторов.

Разветвленная электрическая цепь это параллельное соединение приемников электрической энергии.

I₁ R₁

I I₂ R₂ I

I₃ R₃

U

Параллельным называется такое соединение приемников электрической энергии, при котором на зажимах всех элементов имеется одно и то же напряжение.

U = U₁ = U₂ = U₃

Согласно первого закона Кирхгофа: I = I₁ + I₂ + I₃

Обратная величина эквивалентного сопротивления равна сумме обратных величин сопротивлений резисторов, включенных параллельно: 1/R_экв = 1/R₁ + 1/R₂ + 1/R₃

Величина обратная сопротивлению является проводимостью.

G_экв = 1/R_экв G_экв = G₁ + G₂ + G₃

Эквивалентное сопротивление двух резисторов, включенных параллельно, определяется по формуле: R_экв = R₁•R₂ /(R₁ + R₂)

Смешанное соединение – это такое соединение, при котором в электрической схеме имеются одновременно участки с последовательно и параллельно включенными элементами. К этим участкам применяются формулы последовательного и параллельного соединения приемников электрической энергии, а данный метод называется методом эквивалентного сопротивления или методом «свертывания».

Задание:

1. В практической работе необходимо определить общий ток и токи в ветвях при смешанном соединении приемников электрической энергии. Определить эквивалентное сопротивление. Проверить баланс мощности рассматриваемой цепи.

2. Начертить принципиальную схему своего варианта.

варианты № 4, 8, 12, 16 варианты № 3, 7, 11, 15

R₁ R₅ R₁

R₂ R₂ R₄

R₆

U U

_{R3 R4 R6 R3 R5}

варианты № 1, 5, 9, 13 варианты № 2, 6, 10, 14

R₁

R₂ R₃ R₁ R₃

R₅ R₅

U U

R₄ R₆ R₆ R₂ R₄

варианты № 20, 24, 28, 32 варианты № 19, 23, 27, 31

R₁ R₁

R₂ R₄ R₂ R₃ R₅

U U

R₃ R₅ R₆ R₄ R₆

варианты № 17, 21, 25, 29 варианты № 18, 22, 26, 30

R₁ R₁

R₂ R₄ R₅ R₂ R₄

R₅

U U

R₃ R₆ R₆ R₃

3. Переписать из таблицы данные своего варианта.

4. Выполнить расчет, в соответствии с предлагаемым методом, применяя следующие формулы: последовательное соединение — U = U₁ + U₂ + U₃ ; R_экв = R₁ + R₂ + R₃ ; Р = Р₁ + Р₂ + Р₃ ; I = U/R_экв; параллельное соединение —U = U₁ = U₂ = U₃; I = I₁ + I₂ + I₃;

1/R_экв = 1/R₁ + 1/R₂ + 1/R₃ ; G_экв = 1/R_экв ; G_экв = G₁ + G₂ + G₃ ; R_экв = R₁R₂ /(R₁ + R₂).

5. Исходные данные.

Определить все токи цепи, R_экв, U. Составить баланс мощностей.

А

A

B

B

B

B

Вт

Вт

Ом

Ом

Ом

Ом

Ом

Ом

1,2,3,4

0,3

10

20

80

24

50

70

5,6,7,8

10

12

150

100

40

10

50

9,10,11, 12

18

10

60

40

36

20

10

13,14,15,16

20

20

20

60

35

25

50

17,18,19,20

0,1

20

300

100

300

100

25

21,22,23,24

0,4

14

10

80

50

75

30

25,26,27,28

24

10

15

10

30

60

80

29,30,31,32

9

5

15

5

80

120

12

Образец решения задачи (вариант №32).

I₁ R₁ Дано: R₁ = 5 Ом; R₂ = 15 Ом; R₃ = 5 Ом;

_{R4 = 80 Ом; R5 = 120 Ом; R6 = 12 Ом;}

R₂ R₄ I₄ U₂ = 9 В.

I₂= I₃ Определить: I₁, I₂ = I₃, I₄, I₅, I₆, U, R_экв.

U

R₃ I₅ R₅ R₆ I₆

1. R₅₆ = R₅∙R₆ /(R₅ + R₆) = 120∙12 / (120 +12) = 10,9 Ом

2. R₂₃ = R₂ + R₃ = 15 +5 = 20 Ом

I₁ R₁

_R4

U R₂₃ I₂₃ I₄= I₅₆

R₅₆

I₁= I₂₃+ I₄ I₄ = I₅ + I₆ = I₅₆

3. R ₄₅₆ = R ₄ + R₅₆ = 80 + 10,9 = 90,9 Ом

I₁ R₁

U R₂₃ I₂₃ R₄₅₆ I₄= I₅₆= I₄₅₆

4. R₂₃₄₅₆ = R₂₃∙R₄₅₆ /(R₂₃ + R₄₅₆) = 20∙90,9 / (20 + 90,9) = 16,4 Ом

I₁ R₁

U R₂₃₄₅₆ I₁= I₂₃ + I₄₅₆

5. R_экв = R₁ + R₂₃₄₅₆ = 5 + 16,4 = 21,4 Ом

6. I₂ = U₂ / R₂ = 9/15= 0,6 A I₃ = I₂ = 0,6 A

7. U₃ = I₃ ∙ R₃ = 0,6∙ 5 = 3 B

8. U₂₃ = U₂ + U₃ = 9 + 3 = 12 B U₂₃ = U₄₅₆ = 12 B

9. I₄ = U₄₅₆ / R₄₅₆ = 12/ 90,9 = 0,13 A

10. U₄ = I₄ ∙ R₄ = 0,13 ∙ 80 = 10,6 B

11. U₅₆ = U₄₅₆ – U₄ = 12 – 10,6 = 1,4 B

U₅ = U₆ = U₅₆ = 1,4 B

12. I₅ =U₅ / R₅ = 1,4/120 = 0,01 A

13. I₆ = U₆/ R₆ = 1,4/ 12 = 0,12 A

I₄ = I₅ + I₆ = 0,01 + 0,12 = 0,13 A

14. I₁ = I₂ + I₄ = 0,6 + 0,13 = 0,73 A

15. U₁ = I₁ ∙ R₁ = 0,73 ∙ 5 = 3,7 B

16. U = U₁ + U₂₃ = 3,7 + 12 = 15,7 B

Проверить баланс мощности:

P₁ = U₁ ∙ I₁ = 3,7 ∙ 0,73 = 2,7 Вт;

P₂ = U₂ ∙ I₂ = 9 ∙ 0,6 = 5,4 Вт;

P₃ = U₃ ∙ I₃ = 3 ∙ 0,6 = 1,8 Вт;

P₄ = U₄ ∙ I₄ = 10,6 ∙ 0,13 = 1,4 Вт;

P₅ = U₅ ∙ I₅ = 1,4 ∙ 0,01 = 0,014 Вт;

P₆ = U₆ ∙ I₆ = 1,4 ∙ 0,12 = 0,168 Вт;

P = U∙I = 15,7∙0,73 = 11,46 ≈ 11,5 Вт

P = P₁ + P₂ + P₃ + P₄ + P₅ + P₆ .

11,5 Вт = 2,7 + 5,4 + 1,8 + 1,4 + 0.01 + 0,17 = 11,48 ≈ 11,5 Вт.

11,5 Вт = 11,5 Вт.

Работа на занятии.

1. В соответствии с принципиальной схемой своего варианта, используя исходные данные, произвести расчет токов во всех ветвях цепи, определить эквивалентное сопротивление. Проверить баланс мощности рассматриваемой цепи.

2. При решении применить предлагаемые формулы и образец решения подобной задачи.

Содержание отчета.

1. Цель работы.

2. Принципиальная электрическая схема.

3. Исходные данные

4. Формулы, необходимые для расчета.

5. Решение задачи.

6. Вывод по работе.

Литература.

1. 1. 1. 1. 1. Ф.Е. Евдокимов. Теоретические основы электротехники.- М.: Высшая школа, 2004.

стр. 64-65, 68-69, 75-76.

1. 1. 1. 1. 2. Конспект лекций. Тема: «Электрические цепи постоянного тока».