Эффект Холла
Описание сути явления
Возникновение разности потенциалов в проводнике с током под воздействием магнитного поля называют эффектом Холла.
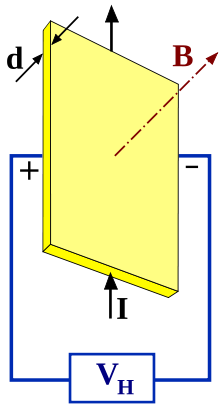
Электропроводность металлов зависит от концентрации электронов проводимости (n) и их подвижности (b). Данные величины являются весьма важными характеристиками металла и определяются опытным путем. Так, для измерения концентрации электроном используют эффект Холла. Рассмотрим проводник в виде прямоугольной пластины, в которой течет ток плотности $\overrightarrow{j.}$ Эквипотенциальными поверхностями внутри этой пластины являются плоскости, перпендикулярные направлению тока, следовательно, разность потенциалов на рис.1 между точками (1 и 2) равна нулю.

Рис. 1
Если в металле создать магнитное поле, которое будет перпендикулярно току, то между точками 1 и 2 (рис.1) возникнет разность потенциалов, которая говорит о том, что при наличии магнитного поля эквипотенциальные поверхности в пластинке отклоняются от первоначального положения. В возникновении поперечной разности потенциалов заключается эффект Холла.
Сущность эффекта Холла
Эффект Холла является следствием существования силы Лоренца. На движущиеся в магнитном поле заряды действует сила Лоренца. Под ее действием электрон отклоняется от первоначального направления движения к одной из граней. В результате одна из граней проводника заряжается отрицательно, следовательно, другая становится положительно заряженной. Внутри металла появляется поперечное электрическое поле ($\overrightarrow{E_x}$).
Сущность этого явления заключена в том, что электропроводимость проводника во внешнем магнитном поле является тензорной величиной (не скаляром). Напряженность поперечного электрического поля, которое называют холловским, добавляется к напряженности электрического поля, которое вызывает ток в отсутствии магнитного поля. В результате $\overrightarrow{E}$ поля образует с плотностью тока угол, который называют углом Холла (направление вектора $\overrightarrow{E}$ и направление вектора $\overrightarrow{j\ }\ $ не совпадают). Связь напряжённости и плотности тока имеет вид:
где ${\sigma }_{ik}$ — тензор электропроводимости. Эффект Холла относят к гальваномагнитным эффектам (эффектам, которые происходят в веществе под действие магнитного поля).
Эмпирически получено, что поперечная разность потенциалов (U), возникающая в эффекте Холла в слабых магнитных полях, может быть рассчитана как:
где $R=\frac{1}{nq_e}$- постоянная Холла, $q_e$ — заряд электрона. Разность потенциалов измеряется, остальные величины в формуле (1) известны. Так находится концентрация зарядов. По знаку разности потенциалов определяют знак носителей тока.
Значение и применение эффекта Холла
Результаты измерений показали, что в металлах ток происходит как движение отрицательных зарядов (электронов). Концентрация их изменяется в пределах равенства концентрации атомов. То есть на один атом вещества приходится, в среднем, один свободный электрон. У металлов концентрация атомов около $n\sim {10}^{28}м^{-3}.$
Эффект Холла наблюдается не только в металлах, но и например, в полупроводниках. Опыты по изучению эффекта Холла в разных веществах показали, что он не всегда является результатом движения отрицательных зарядов. Если измерение разности потенциалов в эффекте Холла показывает, что движутся положительные заряды, то такой эффект называют аномальным.
Эффект Холла используют создавая так называемые датчики Холла. Они используются для определения параметров магнитных полей, нахождения местоположения объектов.
Данный эффект используют для изучения энергетического спектра носителей заряда в металлах и полупроводниках.
На эффекте Холла основано действие магнитных насосов для стимулирования циркуляции жидких металлов и других проводящих жидкостей и магнитодинамических генераторов энергии.
Для измерения постоянной Холла часто применяют компенсационный метод. Составляют цепь, которая изображена на рис.2. По пластинке А течет ток, к ней подведены два контакта 1 и 2. G — гальванометр, K — компенсатор, который создает напряжение противоположное напряжению Холла. Изменяют напряжение с помощью компенсатора добиваются того, чтобы ток через гальванометр обратился в ноль. Получают, что разность потенциалов на компенсаторе и напряжение холла совпали. Используя формулу (2) рассчитывают постоянную $R$. В справочных материалах иногда приводят две постоянных Холла расчетную и экспериментальную. Расхождения объясняются тем, что в расчетах предполагается, что число электронов проводимости в точности равно количеству валентных электронов. $R$ может быть как положительной так и отрицательной. Постоянная Холла считается положительной, если векторы $\overrightarrow{j},\ \overrightarrow{B},\ {\overrightarrow{E}}_x$ образуют правовинтовую систему.
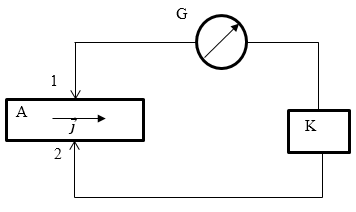
Рис. 2
Пример 1
Задание: Рассчитайте холловскую разность потенциалов для золотой ленты толщины $l={10}^{-4}$ м, по которой течет ток 10 А. Магнитное поле $1Тл.$
Решение:
Для решения задачи используем формулу:
\[U=RdjB\ \left(1.1\right),\]где экспериментальное значение постоянной Холла $R_{Au}$=-0,7$\cdot {10}^{-11}\frac{м^3}{Кл}$. Плотность тока ($j$) найдем как:
\[j=\frac{I}{ld}\left(1.2\right).\]Подставим (1.2) в (1.1), получим:
\[U=R\frac{I}{l}B.\]Проведем вычисления:
\[U=-7,4\cdot {10}^{-11}\frac{10}{{10}^{-4}}\cdot 1=-7,4\cdot {10}^{-6}\left(В\right).\]Ответ: Холловская разность потенциалов весьма мала, и составляет $U=7,4\cdot {10}^{-6}В.$
Пример 2
Задание: Получите выражение для постоянной Холла, считая, что проводник с током, помещен в магнитное поле. Следует допустить, что электрон движется равномерно.
Решение:
Сила Лоренца, которая действует на электрон в магнитном поле, движущийся со скорость $\overrightarrow{v}$ равна:
\[\overrightarrow{F}=q_e\overrightarrow{E}+q_e\left[\overrightarrow{v}\overrightarrow{B}\right]\left(2.1\right).\]В равновесии $\overrightarrow{F}=0$ тогда можно записать, что:
\[q_e\overrightarrow{E}={-q}_e\left[\overrightarrow{v}\overrightarrow{B}\right]\to \overrightarrow{E}=-\left[\overrightarrow{v}\overrightarrow{B}\right]\left(2.2\right).\]Плотность тока в проводнике можно выразить как:
\[\overrightarrow{j}=-q_en\overrightarrow{v}\left(2.3\right),\]где $n$ — концентрация электронов. Из $\left(2.3\right)$ выразим скорость:
\[\overrightarrow{v}=-\frac{\overrightarrow{j}}{nq_e}\left(2.4\right).\]Кроме того разность потенциалов между точками 1- 2 (рис.1) равна:
\[d\cdot \overrightarrow{E}=U\left(2.5\right).\]Подставим в (2.5) выражение для напряженности (2.2) и скорость из (2.4), получим:
\[U=d\left[\frac{\overrightarrow{j}}{nq_e}\overrightarrow{B}\right]=\frac{d}{nq_e}\left[\overrightarrow{j}\overrightarrow{B}\right]\left(2.6\right).\]Выражение для разности потенциалов в эффекте Холла имеет выражение:
\[U=RdjB\left(2.7\right).\]Получаем, что постоянная Холла равна:
\[R=\frac{1}{nq_e}.\]Ответ: $R=\frac{1}{nq_e}.$
Обсуждение:Квантовый эффект Холла — Википедия
Материал из Википедии — свободной энциклопедии
To IgorIvanov
Было бы неплохо включить сюда твою статью из «теорфизики для малышей».
- Мне кажется, в ней слишком частная вещь обсуждается. Хотя основную её мысль можно упомянуть и тут. Igorivanov 02:39, 9 Авг 2004 (UTC)
Квантовый эффект Холла можно было бы написать подробно, поскольку это как-раз слабо включено в стандартные энциклопедии. Begemotv2718
Локализованные состояния[править код]
По поводу того, что «частицы в магнитном поле в пространстве ограничены только по одному измерению». (я так понимаю, что речь идет о плоской задаче.) С одной стороны, при решении уравнения в полярных координатах с векторным потенциалом виде [r x B]/2 получается радиальная в.ф., затухающая на бесконечности, т.е. частица получается локализованная. С другой стороны, если решать с потенциалом типа A_x = yB, то получается локализованная только по одному измерению (но спектр все равно дискретный!). Связано это с бесконечнократным вырождением спектра, из-за чего можно формально из локализованных собственных функций составить одну делокализованную. Поэтому, как мне кажется, более корректно говорить, что в магнитном поле появляются «локализованные состояния» заряженных частиц, а потому их спектр дискретен. Igorivanov 08:55, 9 января 2006 (UTC)
- Это к чему? Одно дело наличие внешней потенциальной ямы, другое дело —локализация волновой функции. Я понимаю под «ограниченными в пространстве» частицами частицы во внешнем ограничивающем потенциале. Со мной что-то не так?—Begemotv2718 02:06, 10 января 2006 (UTC)
- Дык и однородное магнитное поле имеет (в некотором смысле) ограничивающий потенциал, который в подходящей калибровке есть аксиально симметричный двумерный осциллятор. Поэтому существуют и решения с радиальной частью, затухающей на бесконечности. Igorivanov 08:25, 10 января 2006 (UTC)
- Ну, казалось бы, уважающий себя ограничивающий потенциал хотя бы нарушает трансляционную инвариантность. Про магнитное поле такого не скажешь. —Begemotv2718 17:03, 10 января 2006 (UTC)
- Дык и однородное магнитное поле имеет (в некотором смысле) ограничивающий потенциал, который в подходящей калибровке есть аксиально симметричный двумерный осциллятор. Поэтому существуют и решения с радиальной частью, затухающей на бесконечности. Igorivanov 08:25, 10 января 2006 (UTC)
Рецензия с 29 апреля по 11 июня 2007 г.[править код]
Хочу доработать до хорошей и поэтому выслушаю предложения. Ququ 16:22, 29 апреля 2007 (UTC)
- Расширить введение. Также желательно указать источники информации. Если возможно, при помощи тега <references /> Wind 20:18, 29 апреля 2007 (UTC)
- викифицировать, прежде всего. Рисунок может какой придумаете в начало. В введении сперва про эффект Холла кратко, а уж потом про квантовый, а наиболее важную часть из введения, про нобелевскую премию в первые строки. —Bopox
- Нужно викифицировать, вычитать на наличие опечаток типа «Эквипотенциали в образце» (видимо из украинской книги). К тому же крайне необходимо для адекватного понимания дать ссылки на отечественные статьи по данной теме (на рус. яз.).—Assedo 15:43, 19 мая 2007 (UTC)
- Вводится понятие «Плато» — повидимому, постоянство (или неизменность) поперечного сопротивления в зависимости от величины Магнитной индукции, наблюдаемое на графическом представлении этой зависимости (по моим догадкам ИМХО), или это — плато, (в статье сделал правку взял в кавычки). Если «плато» термин, — то не плохо бы в статьях (в том числе и в ст. Дробный квантовый эффект Холла дать определение, или сделать примечание).—Ss novgorod 21:48, 7 июня 2007 (UTC)
- В этой и ещё в ряде статей идёт речь о так называемом Холловском сопротивления:
- Квант электрического сопротивления
- Квантовый эффект Холла
- Дробный квантовый эффект Холла
- Магнетосопротивление (это оно или нет?)
- Графен здесь есть раздел Графен#Квантовый эффект Холла на верное здесь должна быть ссылка на эту статью как оснавную?
- Эффект Холла — в статье указывается, что это такое
—Ss novgorod 21:48, 7 июня 2007 (UTC)
- Спасибо за ваши замечания. Просто я уже наверное месяц не нахожу времени исправлять это copyvio. Но как только появится буду переписывать. Ququ 21:54, 7 июня 2007 (UTC)
- Это не надо делать это совершенно разные эффекты. Ququ 21:54, 7 июня 2007 (UTC)
- В статье Квантовый эффект Холла присутствует описание Дробный квантовый эффект Холла, а в статье Дробный квантовый эффект Холла неупоминаются другие подобные эффекты, поэтому (ИМХО), неплохо бы статьи оъединить под общим названием Квантовые эффекты Холла… —Ss novgorod 22:07, 7 июня 2007 (UTC)
- Подправил Дробный квантовый эффект Холла, шаблон Объединить снял, извиняюсь погорячился ;)—Ss novgorod 22:31, 7 июня 2007 (UTC)
- немного подправил вводную часть (в части последовательности Квантовый эффект Холла >Целочисленный Квантовый эффект Холла> Дробный Квантовый эффект Холла), в том числе дал определение для «плато»—Ss novgorod 22:59, 7 июня 2007 (UTC)
- Тоже чуть подправил ваше определение, теперь более правильно звучит. Ququ 20:37, 11 июня 2007 (UTC)
Холла эффект — это… Что такое Холла эффект?

Эффе́кт Хо́лла — явление возникновения поперечной разности потенциалов (называемой также Холловским напряжением) при помещении проводника с постоянным током в магнитное поле. Открыт Э. Холлом в 1879 году в тонких пластинках золота.
Свойства
В простейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через металлический брус в слабом магнитном поле B течет электрический ток под действием напряженности E. Магнитное поле будет отклонять носители заряда (для определенности электроны) от их движения вдоль или против электрического поля к одной из граней бруса. При этом критерием малости будет служить условие, что при этом электрон не начнет двигаться по спирали.
Таким образом, сила Лоренца приведет к накоплению отрицательного заряда возле одной грани бруска и положительного возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое поле зарядов
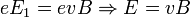 Скорость электронов v можно выразить через плотность тока:
Скорость электронов v можно выразить через плотность тока: 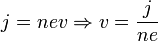 , где n — концентрация носителей заряда. Тогда
, где n — концентрация носителей заряда. Тогда 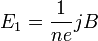
Коэффициент 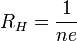 пропорциональности между E1 и jB называется коэффициентом (константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определять их тип для большого числа металлов. Для некоторых металлов (в сильных полях), таких как алюминий, цинк, железо, кобальт, наблюдается положительный знак RH, что объясняется в полуклассической и квантовой теориях твердого тела.
пропорциональности между E1 и jB называется коэффициентом (константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определять их тип для большого числа металлов. Для некоторых металлов (в сильных полях), таких как алюминий, цинк, железо, кобальт, наблюдается положительный знак RH, что объясняется в полуклассической и квантовой теориях твердого тела.
Аномальный эффект Холла
Случай появления напряжения (электрического поля) в образце перпендикулярного направлению пропускаемого через образец тока, наблюдающегося в отсутствие приложенного постоянного магнитного поля, то есть явление полностью аналогичное
Необходимым условием для наблюдения аномального эффекта Холла является нарушение инвариантности по отношению к обращению времени в системе. Например, аномальный эффект Холла может наблюдаться в образцах с намагниченностью.
Датчики на основе эффекта Холла получили очень большое распространение в вентильных двигателях (сервомоторах). Они закрепляются непосредственно на статоре двигателя и выступают в роли ДПР (датчика положения ротора). ДПР реализует обратную связь по положению ротора, выполняет ту же функцию, что и коллектор в ДПТ.
Квантовый эффект Холла
В сильных магнитных полях в плоском проводнике (то есть в квази-двумерном электронном газе) в системе начинают сказываться квантовые эффекты, что приводит к квантовому эффекту Холла: квантованию холловского сопротивления. В ещё более сильных магнитных полях проявляется дробный квантовый эффект Холла, который связан с кардинальной перестройкой внутренней структуры двумерной электронной жидкости.
Магнитосопротивление
Холл проводил опыты в надежде обнаружить возрастание сопротивления проводника в магнитном поле, но в слабых полях не зарегистрировал его. Также оно не следует из теории металлов Друде, расчеты по которой приводились выше. Однако при более строгих расчетах и в сильных полях магнитосопротивление проявляется достаточно хорошо.
Применение

Датчик Холла, используемый для измерения силы тока в проводнике.
Эффект Холла, в некоторых случаях, позволяет определить тип носителей заряда (электронный или дырочный) в металле или полупроводнике, что делает его незаменимым методом исследования свойств полупроводников.
На основе эффекта Холла работают датчики Холла: приборы, измеряющие напряжённость магнитного поля.
См. также
Ссылки
- Эффект Холла — описание на Effects.ru.
- Абрикосов А.А. Основы теории металлов. М., «Наука», главная редакция физико-математической литературы. — 1987.
- Н. Ашкрофт, Н. Мермин. Физика твердого тела.
Wikimedia Foundation. 2010.
Эффект Холла Википедия
В простейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через проводящий брусок в слабом магнитном поле с индукцией B{\displaystyle B} течёт электрический ток с плотностью j{\displaystyle j} под действием напряжённости E{\displaystyle E}. Магнитное поле будет отклонять носители заряда к одной из граней бруса от их движения вдоль или против электрического поля. При этом критерием малости[1] будет служить условие, что при этом носители заряда не начнут двигаться по циклоиде.
Таким образом, сила Лоренца приведёт к накоплению отрицательного заряда возле одной грани бруска, и положительного — возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое поле зарядов E1{\displaystyle E_{1}} не скомпенсирует силу Лоренца:
- eE1=evB⇒E1=vB.{\displaystyle eE_{1}=evB\Rightarrow E_{1}=vB.}
- где e{\displaystyle e} — электрический заряд электрона.
Скорость электронов v{\displaystyle v} можно выразить через плотность тока j{\displaystyle j}:
- j=nev⇒v=jne,{\displaystyle j=nev\Rightarrow v={\frac {j}{ne}},}
Дробный квантовый эффект Холла — Википедия
Материал из Википедии — свободной энциклопедии
Дро́бный ква́нтовый эффе́кт Хо́лла — одно из проявлений квантового эффекта Холла, когда при дробных числах заполнения уровней Ландау в двумерном электронном газе на графической зависимости холловского сопротивления от величины магнитной индукции наблюдаются участки с неизменным поперечным сопротивлением — «плато».
Дробный квантовый эффект Холла наблюдается в магнитных полях, ещё более сильных, чем поля, необходимые для обычного, целочисленного квантового эффекта Холла.
Дробный квантовый эффект Холла был открыт в 1982 году, когда Даниэль Цуи и Хорст Штёрмер заметили, что «плато» в холловском сопротивлении наблюдаются не только при целых значениях n, но и (в существенно более сильных магнитных полях) при n=1/3. В дальнейшем были обнаружены «плато» электрического сопротивления и при других дробных значениях n, например при n=2/5, 3/7…
Природа дробного квантового эффекта Холла[править | править код]
Природа дробного квантового эффекта Холла была объяснена Робертом Лафлином в 1983 году. Он принял во внимание то, что частично заполненные электронные зоны представляют собой сильно коррелированную систему. Поведение отдельных электронов в этом случае нельзя считать независимым, поскольку взаимодействие между электронами кардинально меняет характер системы. В такой системе вместо отдельных электронов возникают новые, коллективные степени свободы — квазичастицы.
Как правило, поведение сильно коррелированной системы столь сложно, что обычно не удаётся не только проследить её эволюцию, но и даже понять, каковы будут правильные квазичастицы. Тем не менее, Лафлину удалось угадать такой вид коллективной волновой функции электронного газа. Из этого выражения следовало, что квазичастицы обладают дробным электрическим зарядом, что и приводит к дробному квантовому эффекту Холла.
Особенности поведения электронной жидкости в сильном магнитном поле[править | править код]
Стоит пояснить, почему вообще Лафлин смог угадать приближённое решение задачи, которую, как правило, решить не удаётся.
Ключевым является следующее наблюдение: если электроны «плавают» в сильном внешнем магнитном поле, то им практически «всё равно», какие ещё силы на них действуют. «Практически всё равно» означает, что волновая функция всей электронной жидкости не зависит от наличия притяжения или отталкивания между электронами, или же вообще нет никакого взаимодействия. От этого меняется, конечно, энергия жидкости, но не сама её «форма».
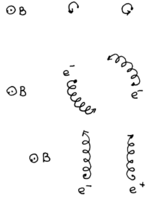 Поведение двух заряженных частиц в сильном магнитном поле.
Поведение двух заряженных частиц в сильном магнитном поле.Как это можно понять? Рассмотрим два электрона, находящихся в сильном магнитном поле. Если пренебречь взаимодействием электронов, то каждый из них под действием силы Лоренца вращался бы по окружности (см. верхний рисунок). «Сильное» магнитное поле в нашем примере означает то, что радиус орбиты во много раз меньше, чем расстояние между электронами.
«Включим» теперь электростатическое отталкивание между электронами. В пустом пространстве, электроны разлетелись бы прочь друг от друга. Однако, в нашем случае магнитное поле не допустит разлёта. Вместо этого электроны начнут медленно дрейфовать друг вокруг друга (см. средний рисунок). Если же у нас был бы электрон и позитрон, то есть, притягивающиеся частицы, то и они начали бы дрейфовать, но только параллельно друг другу (см. нижний рисунок).
Заметьте, что во всех трёх случаях две частицы образуют связанное состояние. Характер движения этого связанного состояния несколько разный, но само наличие связанного состояния — явление универсальное, не зависящее ни от силы, ни от знака, ни вообще от наличия взаимодействия.
Дальнейшие исследования дробного квантового эффекта Холла[править | править код]
В 1998 году Цуи, Штёрмер и Лафлин получили Нобелевскую премию по физике за открытие и объяснение этого явления.
- University of Cambridge, Semiconductor Physics Group Research.
- D.C. Tsui, H.L. Störmer, and A.C. Gossard, Phys. Rev. Lett. 48, 1559 (1982) DOI:10.1103/PhysRevLett.48.1559
- R.B. Laughlin, Phys. Rev. Lett. 50, 1395 (1983) DOI:10.1103/PhysRevLett.50.1395
- G. Timp, P. deVegvar, R. Behringer, J. E. Cunningham, R. Howard, H. U. Baranger and J. K. Jain, «Suppression of the Aharonov Bohm Effect in the Quantized Hall Regime» // Phys. Rev. B 39, 6227 — 6230 (1989)
- J. K. Jain, «Composite fermion approach for the fractional quantum Hall effect» // Phys. Rev. Lett. 63, 199—202 (1989)
Холла эффект — это… Что такое Холла эффект?

Эффе́кт Хо́лла — явление возникновения поперечной разности потенциалов (называемой также Холловским напряжением) при помещении проводника с постоянным током в магнитное поле. Открыт Э. Холлом в 1879 году в тонких пластинках золота.
Свойства
В простейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через металлический брус в слабом магнитном поле B течет электрический ток под действием напряженности E. Магнитное поле будет отклонять носители заряда (для определенности электроны) от их движения вдоль или против электрического поля к одной из граней бруса. При этом критерием малости будет служить условие, что при этом электрон не начнет двигаться по спирали.
Таким образом, сила Лоренца приведет к накоплению отрицательного заряда возле одной грани бруска и положительного возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое поле зарядов E1 не скомпенсирует магнитную составляющую силы Лоренца: 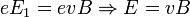 Скорость электронов v можно выразить через плотность тока:
Скорость электронов v можно выразить через плотность тока: 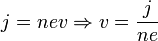 , где n — концентрация носителей заряда. Тогда
, где n — концентрация носителей заряда. Тогда 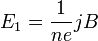 .
.
Коэффициент 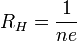 пропорциональности между E1 и jB называется коэффициентом (константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определять их тип для большого числа металлов. Для некоторых металлов (в сильных полях), таких как алюминий, цинк, железо, кобальт, наблюдается положительный знак RH, что объясняется в полуклассической и квантовой теориях твердого тела.
пропорциональности между E1 и jB называется коэффициентом (константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определять их тип для большого числа металлов. Для некоторых металлов (в сильных полях), таких как алюминий, цинк, железо, кобальт, наблюдается положительный знак RH, что объясняется в полуклассической и квантовой теориях твердого тела.
Аномальный эффект Холла
Случай появления напряжения (электрического поля) в образце перпендикулярного направлению пропускаемого через образец тока, наблюдающегося в отсутствие приложенного постоянного магнитного поля, то есть явление полностью аналогичное эффекту Холла, но наблюдающееся без внешнего постоянного магнитного поля — называется Аномальный эффект Холла.
Необходимым условием для наблюдения аномального эффекта Холла является нарушение инвариантности по отношению к обращению времени в системе. Например, аномальный эффект Холла может наблюдаться в образцах с намагниченностью.
Датчики на основе эффекта Холла получили очень большое распространение в вентильных двигателях (сервомоторах). Они закрепляются непосредственно на статоре двигателя и выступают в роли ДПР (датчика положения ротора). ДПР реализует обратную связь по положению ротора, выполняет ту же функцию, что и коллектор в ДПТ.
Квантовый эффект Холла
В сильных магнитных полях в плоском проводнике (то есть в квази-двумерном электронном газе) в системе начинают сказываться квантовые эффекты, что приводит к квантовому эффекту Холла: квантованию холловского сопротивления. В ещё более сильных магнитных полях проявляется дробный квантовый эффект Холла, который связан с кардинальной перестройкой внутренней структуры двумерной электронной жидкости.
Магнитосопротивление
Холл проводил опыты в надежде обнаружить возрастание сопротивления проводника в магнитном поле, но в слабых полях не зарегистрировал его. Также оно не следует из теории металлов Друде, расчеты по которой приводились выше. Однако при более строгих расчетах и в сильных полях магнитосопротивление проявляется достаточно хорошо.
Применение

Датчик Холла, используемый для измерения силы тока в проводнике.
Эффект Холла, в некоторых случаях, позволяет определить тип носителей заряда (электронный или дырочный) в металле или полупроводнике, что делает его незаменимым методом исследования свойств полупроводников.
На основе эффекта Холла работают датчики Холла: приборы, измеряющие напряжённость магнитного поля.
См. также
Ссылки
- Эффект Холла — описание на Effects.ru.
- Абрикосов А.А. Основы теории металлов. М., «Наука», главная редакция физико-математической литературы. — 1987.
- Н. Ашкрофт, Н. Мермин. Физика твердого тела.
Wikimedia Foundation. 2010.
ХОЛЛА ЭФФЕКТ — это… Что такое ХОЛЛА ЭФФЕКТ?
— возникновение в твёрдом проводнике с током плотностью j, помещённом в магн. поле Н, элек-трич. поля в направлении, перпендикулярном j и Н. Напряжённость электрич. поля (п о л я Х о л л а)

Здесь a — угол между векторами Н и j(a<180°). Если H | j, то поле Холла Е Н максимально: EH = RHj. Коэф. R, наз. п о с т о я н н о й Х о л л а (к о э ф. Х о л л а), является основной количеств. характеристикой X. э. Знак R положителен, если j, Н, ЕH образуют правовинтовую систему координат.
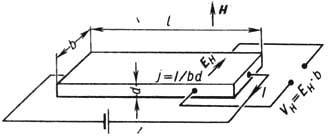
X. э. открыт Э. Г. Холлом (Е. Н. Hall) в 1879 в тонких пластинках Аu. Для наблюдения X. э. прямоуг. пластины из исследуемых веществ длиной l, значительно большей ширины b и толщины d, вдоль к-рых течёт ток I=jbd, помещают в магн. поле Н, перпендикулярное плоскости пластинки (рис.). На середине боковых граней перпендикулярно току расположены электроды, между к-рыми измеряется эдс Холла
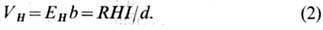
X. э. объясняется взаимодействием носителей заряда (электронов проводимости и дырок) с магн. полем. В магн. поле на электроны действует Лоренца сила F=e[Hu](u = =j/пе- ср. скорость направленного движения носителей в электрич. поле, п — концентрация носителей, е — их заряд), под действием к-рой частицы отклоняются в направлении, перпендикулярном j и Н. В результате на боковой грани пластины происходит накопление зарядов и возникает поле Холла. В свою очередь поле Холла действует на заряды и уравновешивает силу Лоренца. При равновесии eEH = eHu, откуда

Знак R совпадает со знаком носителей заряда. Для металлов, у к-рых n~1022 см -3, R~10-3 см 3/Кл, у полупроводников R~10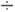 105 см 3/Кл.
105 см 3/Кл.
Коэф. Холла может быть выражен через подвижность носителей зарядаm =u др/E (дрейфовая скорость носителей u др = -eEt/m, где т — эффективная масса,t — время между двумя последоват. соударениями с рассеивающими центрами) и уд. электропроводность s=j/E=enu др/E:
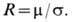
Сказанное справедливо для изотропных проводников, в частности для поликристаллов. Для анизотропных кристаллов R = r/en, где коэф. r — величина, близкая к 1, зависящая от направления Н относительно кристаллографич. осей. В области сильных магн. полей r=1. Критерий сильного поля w сt>1, где w с — циклотронная частота носителей.
В полупроводниках в электропроводимости участвуют одновременно электроны проводимости и дырки. При этом постоянная Холла выражается через парциальные проводимости электронов s э и дырок s д и их концентрации п э и n д. В случае слабых полей

Для сильных полей

При п э = п д для всех значений магнитного поля R == (1/ еn)(s э-s д)/(s э + s д), а знак R соответствует знаку осн. носителей.
Для металлов величина R зависит от зонной структуры, т. е. формы ферми-поверхности. Для замкнутых поверхностей Ферми и в сильных магн. полях постоянная Холла изотропна, а выражения для R совпадают с (3) и (4). Для открытых поверхностей Ферми R — тензор. Однако если направление Н относительно кристаллографич. осей выбрано так, что не возникает открытых сечений поверхности Ферми, то выражения для R также аналогичны (3) и (4).
X. э.- один из наиболее эфф. методов изучения энерге-тич. спектра носителей заряда в металлах и полупроводниках. Зная R, можно определить знак носителей заряда и оценить их концентрацию, что позволяет сделать заключение о кол-ве примесей в полупроводниках. Линейная зависимость R от Н используется для измерения напряжённости магн. поля (см. Магнитометры), а также для усиления пост. токов, в аналоговых вычислит. машинах, в измерит. технике и др. (Холла датчик).
При изучении X. э. в двумерном электронном газе кремниевого полевого транзистора, помещённого в квантующее магн. поле, К. фон Клитцинг (К. von Klitzing) в 1980 обнаружил, что холловское сопротивление (RH=VH/I), к-рое в условиях обычного X. э., как следует из ф-л (2) и (3), обратно пропорционально п, при изменении п то остаётся постоянным, то резко изменяется, переходя с одного уровня на другой. Вместо монотонного убывания в зависимости RH(n )наблюдались «ступеньки». При этом высота ступенек определяется такими фундам. константами, как постоянная Планка и заряд электрона, и не зависит от свойств вещества. Это явление получило назв. квантового Холла эффекта. Ю. П. Гайдуков.
При описании X. э. в магнетиках следует вместо поля Н рассматривать магн. индукцию В= Н+4p М, где М— намагниченность. Поле Холла в поликристаллич. ферромагнетиках может быть записано в виде
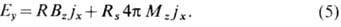
Здесь x, у, z — координатные оси. Первое слагаемое описывает нормальный X. э. Вклад в поле Холла, пропорциональный намагниченности М, наз. ферромагнитным, спонтанным или аномальным X. э. Т. к. этот вклад существует в ферро-, ферри- и антиферромагн. металлах и полупроводниках, парамагнетиках и др., то термин «а н о м а л ь н ы й X. э.» является наиб. общим. Коэф. Rs в ферромагнетиках на 1-2 порядка больше R и обладает сильной (по сравнению с R )зависимостью от темп-ры. В сплавах величина и знак Rs зависят от концентрации компонент, причём в общем случае знак Rs может не совпадать со знаком R. В монокристаллах Rs также является тензорной величиной. Роль внеш. магн. поля в создании аномального X. э. сводится только к намагничиванию образца, в частности в однодоменных образцах аномальный X. э. наблюдается и без поля.
Аномальный X. э. обусловлен спин-орбитальным взаимодействием, к-рое пропорц. намагниченности и создаёт асимметрию рассеяния. носителей заряда, приводящую к холловскому «закручиванию» в отсутствие поля.
А. Б. Грановский.
Лит. см. при статьях Гальвано магнитные явления, Квантовый Холла эффект. Магнетизм.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.



