Взаимоиндукция

В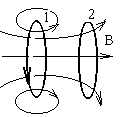озьмем два параллельных контура. Если в контуре 1 проходит ток, то он создает магнитный поток Ф₂₁, пронизывающий второй контур: Ф₂₁ = М₂₁i₁, М₂₁ – коэффициент взаимоиндукции, зависит от размеров и формы обоих контуров, их взаимного расположения и магнитной проницаемости среды.

При изменении тока в контуре 1 будет изменяться магнитный поток Ф₂₁, пронизывающий контур 2, и в нем будет возникать ЭДС индукции. Явление возникновения ЭДС индукции в одном контуре при изменении тока в другом контуре называется взаимоиндукцией.

ЭДС взаимоиндукции:

.

Это явление широко используется в технике: при передаче электроэнергии – трансформаторы, для получения чистых металлов.

Индукционные токи могут возбуждаться и в сплошных массивных проводниках. Их называют токами Фуко. Сопротивление массивного проводника мало, поэтому токи Фуко могут достигать больших значений. Тепловое действие токов Фуко используется в индукционных печах для плавления металлов. Плавление металлов в вакууме позволяет получать материалы высокой чистоты.

Токи Фуко имеют такое направление, чтобы своим действием препятствовать причине, их вызывающей. Поэтому движущиеся в сильном магнитном поле хорошие проводники испытывают сильное торможение, обусловленное взаимодействием токов Фуко с магнитным полем. Это используется для демпфирования (успокоения) подвижных частей гальванометров, сейсмографов и других приборов.

Энергия магнитного поля

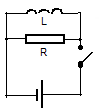Рассмотрим схему, состоящую из источника тока, катушки индуктивности и сопротивления. При замкнутом ключе в катушке индуктивности установится ток I, который создает магнитное поле, сцепленное с витками катушки индуктивности.

Если ключ разомкнуть, то через сопротивление R некоторое время будет протекать ток, обусловленный ЭДС самоиндукции. Работа, совершаемая при этом, будет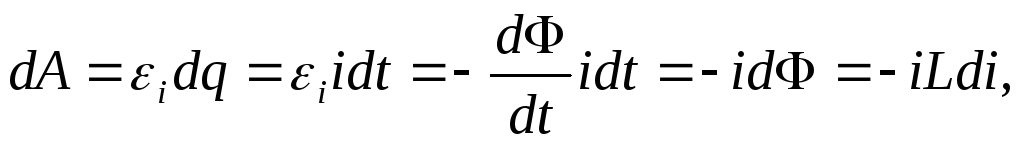

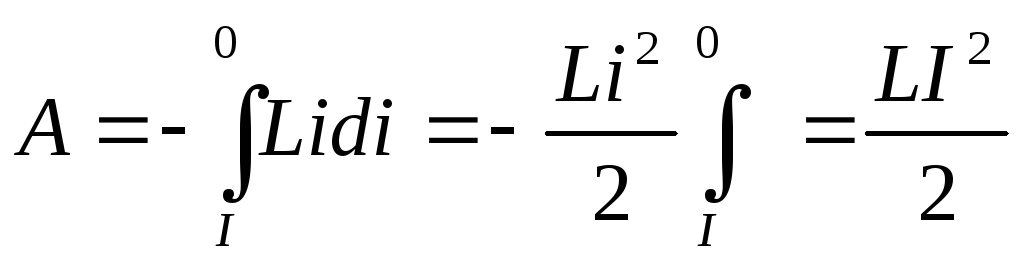. Эта работа идет на изменение внутренней энергии сопротивления. Совершение этой работы сопровождается исчезновением магнитного поля. Следовательно, магнитное поле является носителем энергии, за счет которой и совершается работа. Выразим энергию магнитного поля через величины, характеризующие само поле.

, здесь N – число витков катушки, n — число витков на единице длины катушки, l – длина катушки, V- объем катушки.

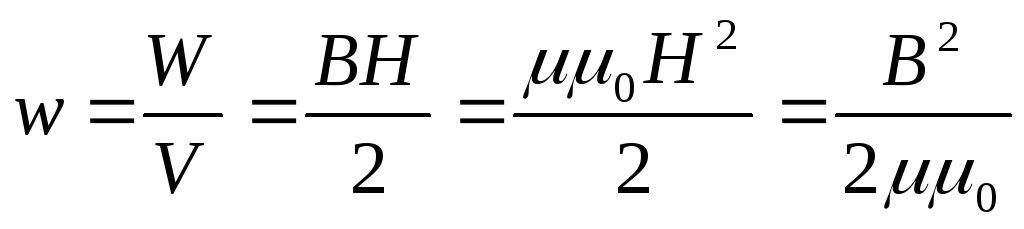— объемная плотность энергии магнитного поля.

Зная плотность энергии в каждой точке, можно найти энергию магнитного поля, заключенную в любом объеме.

.

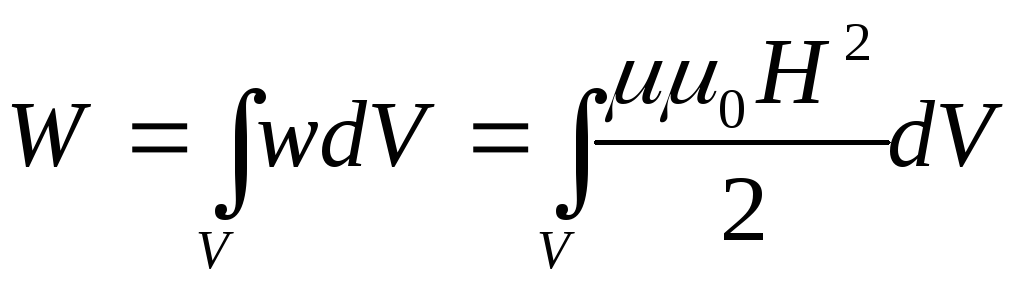Процессы в колебательном контуре

Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных между собой. Колебания в контуре можно вызвать зарядив конденсатор или возбудив ток в индуктивности с помощью внешнего магнитного поля. Рассмотрим первый случай.

З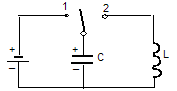арядим конденсатор, поставив переключатель в положение 1. Между пластинами конденсатора появится электрическое поле, которое будет иметь определенную энергию.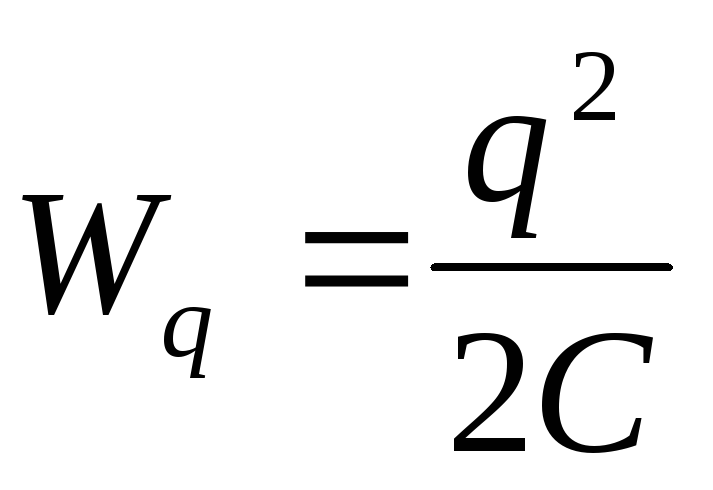

Замкнем конденсатор на катушку индуктивности, поставив переключатель в положение 2. Конденсатор начнет разряжаться и электрическое поле в нем будет уменьшаться. Ток разряда, проходя через катушку индуктивности, будет наводить в ней ЭДС самоиндукции, которая, по правилу Ленца, будет препятствовать быстрому нарастанию тока, поэтому ток в ней будет нарастать постепенно.

Через некоторое время конденсатор разрядится и энергия электрического поля в нем станет равной 0, а ток разряда достигнет максимума. Следовательно, и энергия магнитного поля станет максимальной: 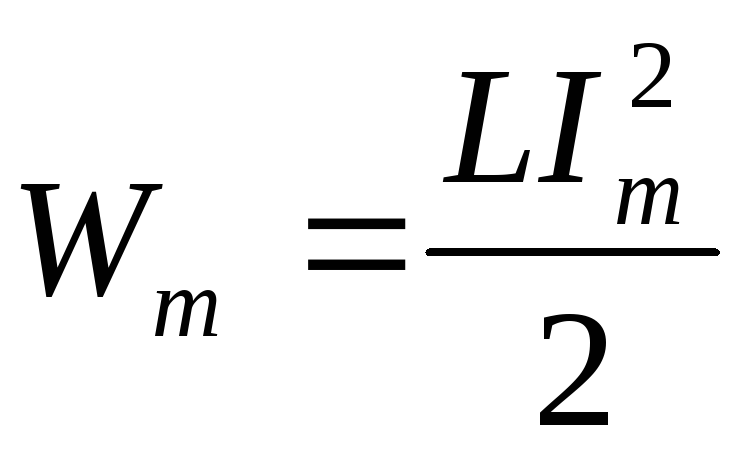, т.е., энергия электрического поля конденсатора превратилась в энергию магнитного поля катушки индуктивности.

Так как конденсатор разрядился, следовательно, ток разряда должен прекратиться. Но как только ток разряда начнет уменьшаться, это вызовет ЭДС самоиндукции и ток самоиндукции, который, в соответствии с правилом Ленца, будет стремиться поддержать ток разряда и, следовательно, будет направлен также как и ток разряда. Поэтому конденсатор начнет перезаряжаться и между его пластинами появится электрическое поле противоположного направления.

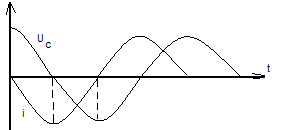
Через некоторое время ток прекратится, магнитное поле исчезнет, а конденсатор перезарядится. Энергия магнитного поля превратилась в энергию электрического поля. Далее конденсатор опять начнет разряжаться и все процессы повторятся. Если активное сопротивление контура равно 0, то процесс периодического превращения энергии электрического поля в энергию магнитного поля и обратно будет продолжаться неограниченно долго, и мы получим незатухающие электромагнитные колебания.

Электромагнитные колебания, происходящие под действием процессов в самом колебательном контуре, называются свободными.

Найдем уравнение колебаний в идеальном контуре (R = 0).

П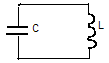о второму закону Кирхгофа сумма ЭДС в контуре равна сумме напряжений на всех участках контура.

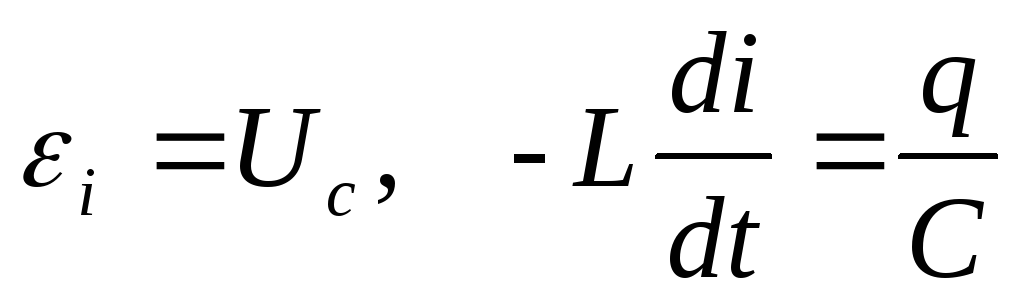. Перенесем все члены уравнения в одну сторону и разделим на L, учтем также, что i = q^‘.

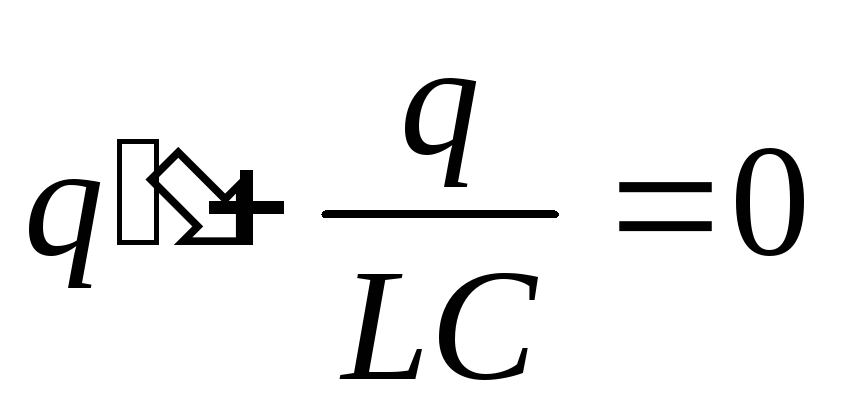
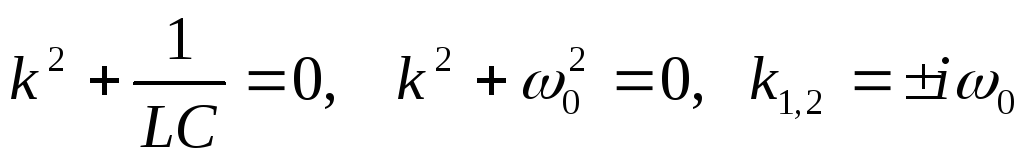
— получили дифференциальное уравнение 2-го порядка с постоянными коэффициентами. Для решения дифференциального уравнения нужно найти корни характеристического уравнения

корни характеристического уравнения получились мнимые, следовательно, решение уравнения имеет вид , где

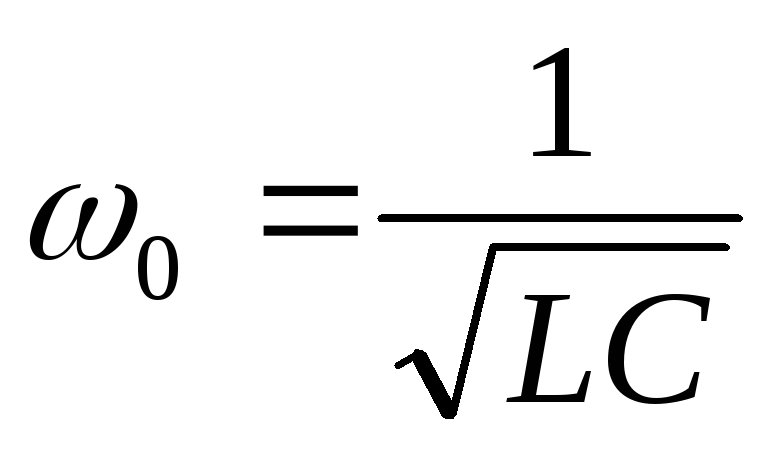
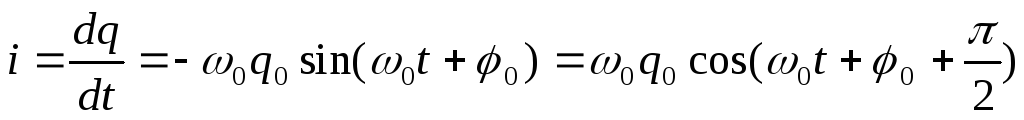— собственная частота колебаний контура. Ток в контуре:, а напряжение на конденсаторе: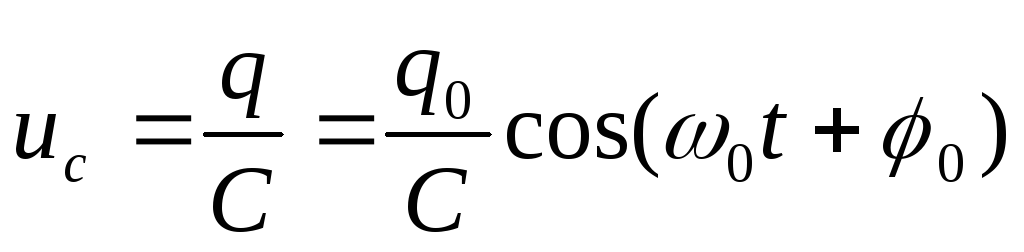— колебания тока и напряжения сдвинуты по фазе на.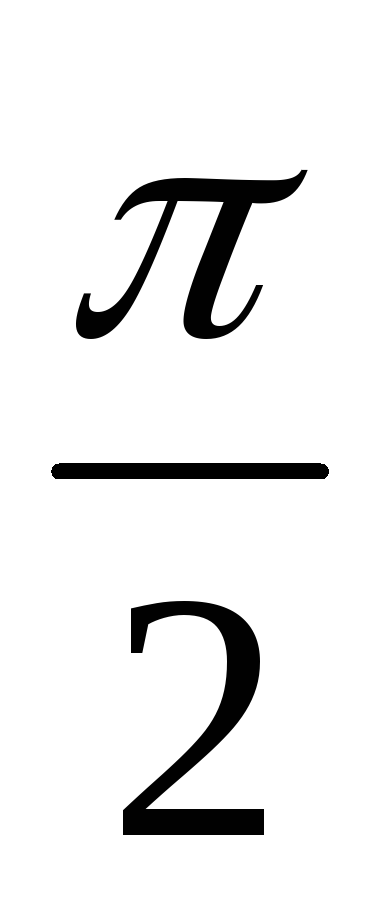

Лекция 14

Явление взаимной индукции

Пусть имеются два близко расположенных контура. При протекании по одному из них тока изменяется индукция магнитного поля и, следовательно, магнитный поток, пронизывающий второй контур. В результате во втором контуре возникает ЭДС индукции, называемая в данном случае ЭДС взаимоиндукции.

Возникновение ЭДС индукции в одном из двух контуров, связанных магнитной связью, при изменении тока в другом, называется явлением взаимной индукции.

Количественно степень магнитной связи контуров (или любых электрических цепей) характеризуется взаимной индуктивностью.

Пусть ток I₁ течет по первому контуру. Часть данного магнитного потока Ф₁₂ пронизывает второй контур (рис. 3). Величина Ф₁₂

также будет пропорциональна току I₁ , т.е.

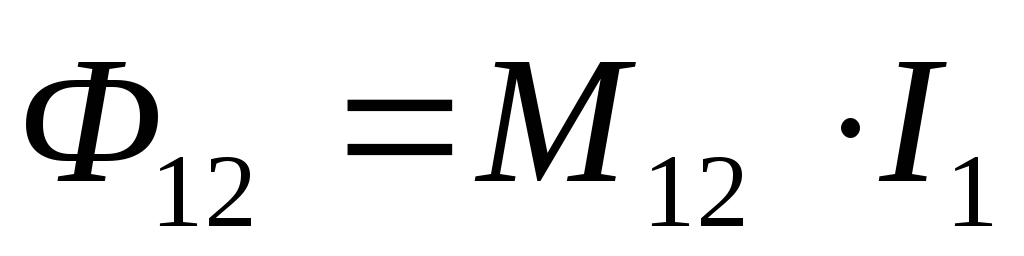, (9)

где 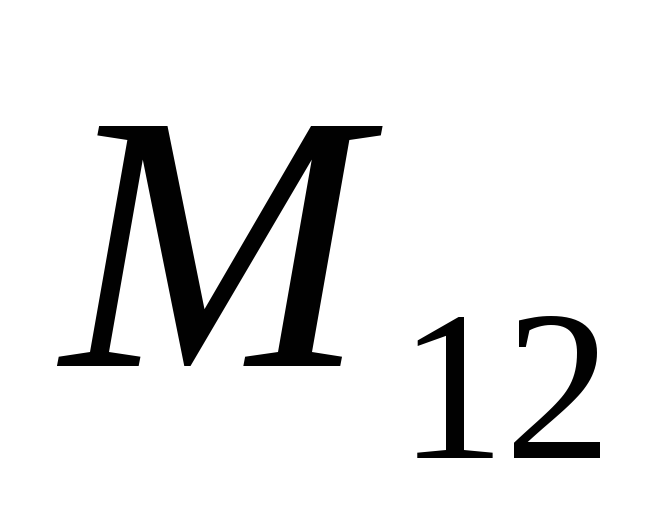— коэффициент, характеризующий влияние первого контура на второй.

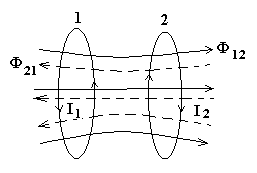
Рис.3. Возникновение ЭДС индукции в одном контуре при изменении тока в другом.

Пусть теперь ток I₂ течет по второму контуру (рис. 3). Рассуждая аналогично предыдущему случаю, для величины магнитного потока, создаваемого током

I₂ и пронизывающего первый контур, можно записать:

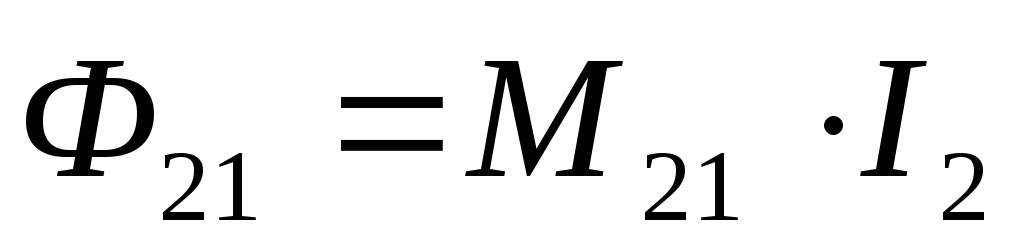
Если отсутствуют ферромагнитные сердечники, коэффициенты 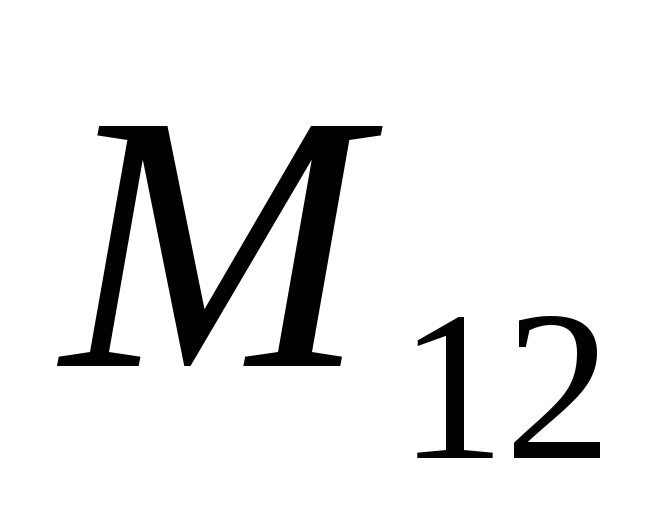и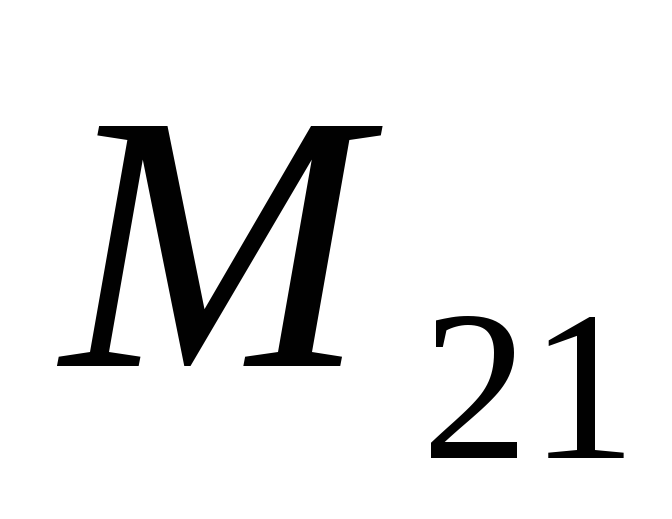тождественно равны и взаимное влияние двух контуров описывается только одним коэффициентом

= =,

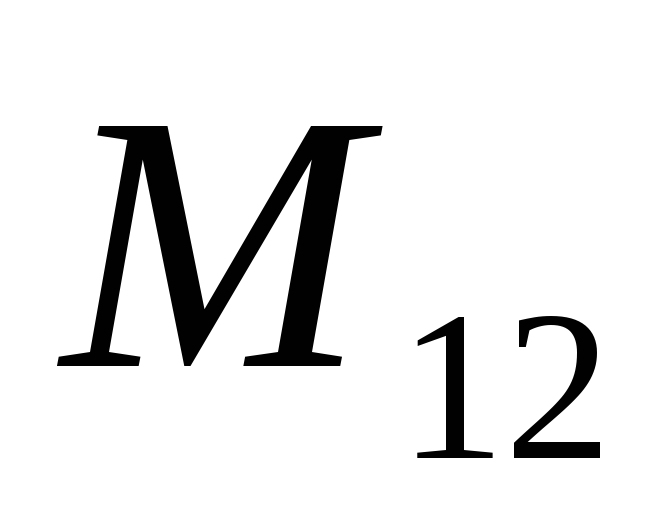который зависит от размеров и формы контуров 1 и 2, от их взаимного расположения, а также от магнитной проницаемости окружающей среды. Данный коэффициент называется взаимной индуктивностью или коэффициентом взаимной индукции контуров 1 и 2 и численно равен величине магнитного потока (в Веберах), общего для двух контуров, когда в одном из них протекает ток, равный 1 А.

При изменении тока в первом контуре, согласно закону электромагнитной индукции, в нем возникает ЭДС самоиндукции:

Ԑ_i1(10)

Во втором контуре при этом будет индицироваться ЭДС индукции:

Ԑ_i2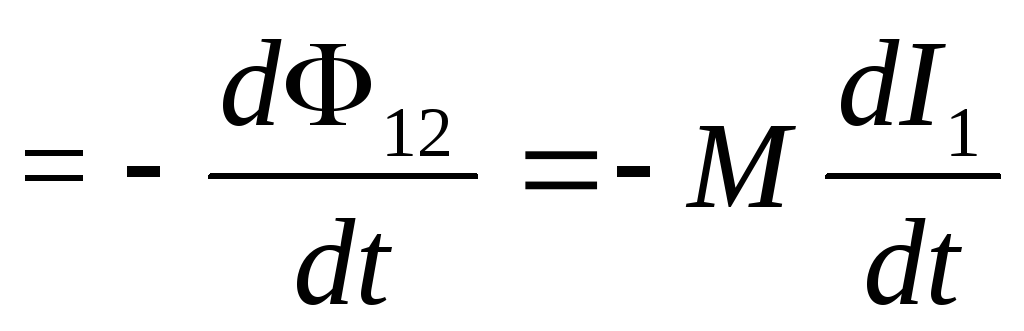(11)

Если второй контур разомкнут, то тока в нём не возникает, следовательно, обратного влияния второго контура на первый не будет. Сравнивая (10) и (11), получим:

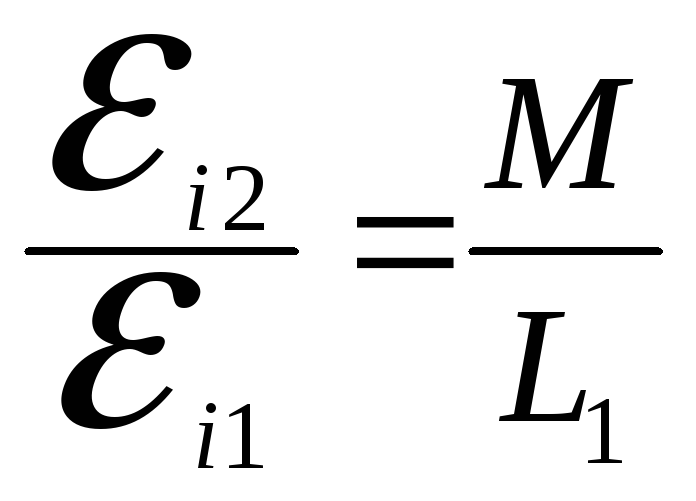(12)

Видно, что в любой момент времени отношение ЭДС, которые индуцируются в первом и во втором контуре током, протекающим по первому контуру, постоянно. Следовательно, ЭДС во втором контуре повторяет изменение ЭДС самоиндукции в первом. Это явление используется в трансформаторах для преобразования переменного напряжения в более низкое или в более высокое. Отношение М/L₁ называется КОЭФФИЦИЕНТОМ ТРАНСФОРМАЦИИ.

Описание лабораторного стенда.

Электрическая схема стенда для изучения явлений самоиндукции и взаимной индукции показана на рис.4.

Рис.4. Схема лабораторного стенда

Он представляет собой разветвлённую цепь, содержащую источник постоянного тока Ԑ₀, активные сопротивления R₁ и R₂ и две катушки индуктивности L₁ и L₂, имеющие общий ферромагнитный сердечник (т.е. катушки являются обмотками трансформатора). Катушка L₁ может отключаться при помощи переключателя Т.

Периодическое замыкание и размыкание цепи выполняется автоматически ключом К, управляемым электромагнитным реле. Реле периодически производит замыкание ключа К на время t_о и размыкание его на время t₁.

44. Индуктивность. Явление взаимоиндукции. Э.Д.С. Взаимоиндукции

ИНДУКТИВНОСТЬ (от лат. inductio — наведение, побуждение), величина, характеризующая магн. св-ва электрич. цепи. Ток, текущий в проводящем контуре, создаёт в окружающем пр-ве магн. поле, причём магнитный поток Ф, пронизывающий контур (сцепленный с ним), прямо пропорционален току I:Ф=LI. Коэфф. пропорциональности L наз. И. или коэфф. самоиндукции контура. И. зависит от размеров и формы контура, а также от магнитной проницаемости окружающей среды. В СИ И. измеряется в генри, в Гаусса системе единиц она имеет размерность длины (1 Гн=109 см).

Через И. выражается эдс самоиндукции ? в контуре, возникающая при изменении в нём тока:

(DI изменение тока за время Dt). И. определяет энергию W магн. поля тока I:

W =LI2/2.

Взаимоиндукция (взаимная индукция) — возникновение электродвижущей силы (ЭДС индукции) в одном проводнике вследствие изменения силы тока в другом проводнике или вследствие изменения взаимного расположения проводников. Взаимоиндукция — частный случай более общего явления — электромагнитной индукции. При изменении тока в одном из проводников или при изменении взаимного расположения проводников происходит изменение магнитного потока через (воображаемую) поверхность, «натянутую» на контур второго, созданного магнитным полем, порожденным током в первом проводнике, что по закону электромагнитной индукции вызывает возникновение ЭДС во втором проводнике. Если второй проводник замкнут, то под действием ЭДС взаимоиндукции в нём образуется индуцированный ток. И наоборот, изменение тока во второй цепи вызовет появление ЭДС в первой. Направление тока, возникшего при взаимоиндукции, определяется по правилу Ленца. Правило указывает на то, что изменение тока в одной цепи (катушке) встречает противодействие со стороны другой цепи (катушки).

Чем большая часть магнитного поля первой цепи пронизывает вторую цепь, тем сильнее взаимоиндукция между цепями. С количественной стороны явление взаимоиндукции характеризуется взаимной индуктивностью (коэффициентом взаимоиндукции, коэффициентом связи). Для изменения величины индуктивной связи между цепями, катушки делают подвижными. Приборы, служащие для изменения взаимоиндукции между цепями, называются вариометрами связи.

45. Свободная и принужденная составляющие переходной величины, их физический смысл. Составление уравнений электрического равновесия.

Принужденная составляющая тока (напряжения) физически представляет собой составляющую, изменяющуюся с той же частотой, что и действующая в схеме принуждающая ЭДС. Если в схеме действует принуждающая синусоидальная ЭДС частоты , то принужденная составляющая любого тока и любого напряжения в схеме является соответственно синусоидальным током (синусои­дальным напряжением) частоты.

Определяются принужденные составляющие в цепи синусоидального тока с помощью символического метода. Если в схеме действует источник постоянной ЭДС (как, например, в схеме рис. 1.2), то принужденный ток есть постоянный ток и находят его с помощью методов.

Постоянный ток через конденсатор не проходит, поэтому принужденная составляющая тока через него в цепях с источниками постоянной ЭДС равна нулю. Кроме того, напомним, что падение напряжения на индуктивной катушке от неизменного во времени тока равно нулю.

В линейных электрических цепях свободные составляющие токов и напряжений затухают во времени по показательному закону ept

Взаимоиндукция

Дата публикации: 06 марта 2015.
Категория: Электротехника.

В статье «Явление электромагнитной индукции» было дано определение взаимоиндукции. Было указано, что взаимоиндукцией называется влияние изменяющегося магнитного поля одного проводника на другой проводник, в результате чего во втором проводнике возникает индуктированная электродвижущая сила (ЭДС). Пусть мы имеем два проводника I и II (рисунок 1) или две катушки, или два контура.

Рисунок 1. Явление взаимоиндукции

Ток в первом проводнике i₁ создается источником напряжения (на чертеже не показанном). Ток i₁ образует магнитный поток Ф₁, одна часть которого Ф₁₂ пересекает второй проводник, а другая часть Ф₁₁ замыкается помимо второго проводника:

Ф₁ = Ф₁₂ + Ф₁₁ .

Если вместо проводников возьмем две катушки с числом витков w₁ и w₂, то потокосцепление второго контура будет:

ψ₁₂ = w₂ × Ф₁₂ .

Так как поток Ф₁₂ пропорционален току i₁, то зависимость между потокосцеплением ψ₁₂ и током i₁ будет:

ψ₁₂ = M₁₂ × i₁ ,

откуда

где M₁₂ – коэффициент пропорциональности, называемый коэффициентом взаимоиндукции  или взаимной индуктивностью двух катушек (или контуров).

Размерность взаимной индуктивности определяется так:

Таким образом, взаимная индуктивность M измеряется в тех же единицах, что и индуктивность L.

Взаимная индуктивность зависит от числа витков катушек, их размера, взаимного расположения катушек и магнитной проницаемости среды, в которой находятся катушки.

Если пропускать ток i₂ по второму проводнику, то по аналогии можно написать:

ψ₂₁ = w₁ × Ф₂₁ .

и

ψ₂₁ = M₂₁ × i₂ ,

откуда получим формулу взаимоиндукции для второго контура

Пользуясь законом Ома для магнитной цепи, можно доказать, что

где R_м – магнитное сопротивление замкнутого контура, по которому проходят магнитные потоки Ф₁₂ и Ф₂₁.

В выражения

подставим значения ψ₁₂, ψ₂₁, Ф₁₂, Ф₂₁.

Таким образом, M₁₂ = M₂₁ = M.

Следовательно, взаимная индуктивность двух индуктивно или магнитно-связанных цепей не зависит от того, какой цепью будет создаваться магнитный поток.

При изменении тока i₁ магнитные потоки Ф₁₁ и Ф₁₂ будут изменяться и во втором контуре возникнет индуктированная ЭДС, величина которой будет равна:

аналогично:

Эти ЭДС называются ЭДС взаимоиндукции. Если первый контур обладает сопротивлением r₁ и индуктивностью L₁, то напряжение U₁, приложенное к этому контуру, должно уравновесить ЭДС самоиндукции и взаимоиндукции, а также падение напряжения в сопротивлении r₁ контура:

Для второго контура:

Между индуктивностями L₁ и L₂ контуров и взаимной индуктивностью M существует зависимость:

Однако эта формула верна когда весь поток, создаваемый первым контуром, сцепляется с витками второго контура. На практике M меньше

, то есть

Величина k меньше единицы и называется коэффициентом связи катушек. Этот коэффициент равнялся бы единице в том случае, если бы Ф₁₂ = Ф₁ и Ф₂₁ = Ф₂.

Электромагнитная связь между двумя контурами может быть изменена, если сближать контуры или удалять их один от другого, а также если менять взаимное расположение контуров.

В технике применяют приборы, работающие по принципу взаимной индукции и служащие для изменения индуктивности цепи. Такие приборы называются вариометрами. Они состоят из двух последовательно соединенных катушек, одна из которых может вращаться внутри другой.

Пусть обе катушки расположены так, чтобы оси их были параллельны одна другой и магнитные поля катушек направлены одинаково (согласное включение). В этом случае:

где индуктивность системы

L’ = L₁ + L₂ + 2 × M .

Если повернуть внутреннюю катушку на 180°, то в этом случае магнитные потоки будут направлены навстречу один другому (встречное включение).

В этом случае:

где

L’’ = L₁ + L₂ – 2 × M .

Вращая внутреннюю катушку между первым и вторым положениями, мы можем менять индуктивность системы в пределах от L’ до L’’.

По принципу взаимной индуктивности работают трансформаторы, нашедшие весьма широкое применение в технике.

Бывает, что взаимная индукция нежелательна: две линии связи (телефонные) оказывают взаимное влияние, мешая работе одна другой. Линии сильного тока, расположенные параллельно и вблизи линии связи, индуктируют в последней токи, вызывающие шум и треск, мешающие телефонным переговорам.

Рисунок 2. Взаимоиндукция

И для вашего развития посмотрите доклад доктора технических наук Ацюковского Владимира Акимовича, о взаимоиндукции проводников:

Источник: Кузнецов М.И., «Основы электротехники» — 9-е издание, исправленное — Москва: Высшая школа, 1964 — 560с.

Взаимоиндукция — это… Что такое Взаимоиндукция?

Взаимоиндукция (взаимная индукция) — возникновение электродвижущей силы (ЭДС индукции) в одном проводнике вследствие изменения силы тока в другом проводнике или вследствие изменения взаимного расположения проводников. Взаимоиндукция — частный случай более общего явления — электромагнитной индукции. При изменении тока в одном из проводников или при изменении взаимного расположения проводников происходит изменение магнитного потока через (воображаемую) поверхность, «натянутую» на контур второго, созданного магнитным полем, порожденным током в первом проводнике, что по закону электромагнитной индукции вызывает возникновение ЭДС во втором проводнике. Если второй проводник замкнут, то под действием ЭДС взаимоиндукции в нём образуется индуцированный ток. И наоборот, изменение тока во второй цепи вызовет появление ЭДС в первой. Направление тока, возникшего при взаимоиндукции, определяется по правилу Ленца. Правило указывает на то, что изменение тока в одной цепи (катушке) встречает противодействие со стороны другой цепи (катушки).

Чем большая часть магнитного поля первой цепи пронизывает вторую цепь, тем сильнее взаимоиндукция между цепями. С количественной стороны явление взаимоиндукции характеризуется взаимной индуктивностью (коэффициентом взаимоиндукции, коэффициентом связи). Для изменения величины индуктивной связи между цепями, катушки делают подвижными. Приборы, служащие для изменения взаимоиндукции между цепями, называются вариометрами связи.

Явление взаимоиндукции широко используется для передачи энергии из одной электрической цепи в другую, для преобразования напряжения с помощью трансформатора.

Литература

• Малая Советская Энциклопедия т.2, Государственное научное издательство «Большая советская энциклопедия», 1958 г.
• Хайкин С. Э. «Словарь радиолюбителя», Госэнергоиздат, Москва 1960 г.
• Евдокимов Ф. Е. «Теоретические основы электротехники», «Высшая школа» 1981 г.

41. Явление электромагнитной индукции. Закон электромагнитной индукции. Вихревое электрическое поле. Явление взаимной индукции.

Явление электромагнитной индукции.

Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него. Электродвижущая сила, возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром.Электрический ток, вызванный этой ЭДС, называется индукционным током.

Закон электромагнитной индукции. При изменении магнитного потока в проводящем контуре возникает ЭДС индукции , равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:

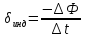
Эта формула носит название закона Фарадея.

Вихревое электрическое поле.

Электрическое поле не связано непосредственно с электрическими зарядами, и его линии напряженности не могут на них начинаться и кончаться. Они вообще нигде не начинаются и не кончаются, а представляют собой замкнутые линии, подобныe линиям индукции магнитного поля. Это так называемое вихревое электрическое поле.

 

Направление силовых линий напряженности 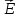совпадает с направлением индукционного тока.. Работа вихревого электрического поля при перемещении единичного положительного заряда вдоль замкнутого неподвижного проводника численно равна ЭДС индукции в этом проводнике.

Явление взаимной индукции. Взаимная индукция — возникновение электродвижущей силы (ЭДС индукции) в одном проводнике вследствие изменения силы тока в другом проводнике или вследствие изменения взаимного расположения проводников.

Направление тока, возникшего при взаимоиндукции, определяется по правилу Ленца. Правило указывает на то, что изменение тока в одной цепи (катушке) встречает противодействие со стороны другой цепи (катушки).

42. Явление самоиндукции. Индуктивность. Индуктивность соленоида. Работа перемещения проводника с током и контура с током в магнитном поле. Энергия магнитного поля соленоида.

Явление самоиндукции. В случае изменения тока в контуре в нем возникает ЭДС индукции. Это явление названо самоиндукцией.

Индуктивность. Если в пространстве, где находится контур с током I, нет ферромагнетиков, то магнитное поле, а значит и магнитный поток Ф через контур будут прямо пропорциональны току I. Тогда можно записать: Ф = LI.

L называется индуктивностью контура. По определению L > 0. Индуктивность L зависит от формы и размера контуров, а также от магнитных свойств окружающей среды. Единица измерения индуктивности – 1 Генри (Гн). 1 Гн – это индуктивность такого контура, у которого при токе 1 А магнитный поток равен 1 Веберу.

Индуктивность соленоида. Рассмотрим идеальный соленоид: длина его L гораздо больше радиуса R. В этом случае при пропускании через соленоид тока I внутри соленоида возникает однородное магнитное поле с линиями индукции, параллельными оси соленоида. Для нахождения величины магнитного поля воспользуемся теоремой о циркуляции для . Получаем: Hl = nIl, здесь n – число витков на единицу длины соленоида. Для магнитного поля B = μμ₀H = μμ₀nI. Индуктивность соленоида можно теперь определить по формуле: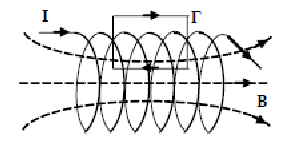

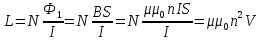
В этой формуле V – объем соленоида.

Работа перемещения проводника с током и контура с током в магнитном поле.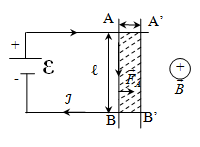

Работа, совершаемая при перемещении проводника с током в магнитном поле, определяется произведением силы тока, текущего по проводнику, на изменение магнитного потока. Работа по перемещению проводника с током совершается источником тока. Магнитное поле работу не совершает. Индукция магнитного поля в этом процессе не изменяется.

Энергия магнитного поля соленоида. Магнитное поле внутри соленоида однородно и сосредоточено внутри него, поэтому энергия заключена в объеме соленоида и имеет с ним однородное распределение с постоянной объемной плотностью.

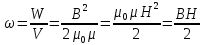
54. Эдс взаимоиндукции. Свойство взаимности для индуктивно связанных цепей.

Взаимоиндукция (взаимная индукция) — возникновение электродвижущей силы (ЭДС индукции) в одном проводнике вследствие изменения силы тока в другом проводнике или вследствие изменения взаимного расположения проводников. Взаимоиндукция — частный случай более общего явления — электромагнитной индукции. При изменении тока в одном из проводников или при изменении взаимного расположения проводников происходит изменение магнитного потока через (воображаемую) поверхность, «натянутую» на контур второго, созданного магнитным полем, порожденным током в первом проводнике, что по закону электромагнитной индукции вызывает возникновение ЭДС во втором проводнике. Если второй проводник замкнут, то под действием ЭДС взаимоиндукции в нём образуется индуцированный ток. И наоборот, изменение тока во второй цепи вызовет появление ЭДС в первой. Направление тока, возникшего при взаимоиндукции, определяется по правилу Ленца. Правило указывает на то, что изменение тока в одной цепи (катушке) встречает противодействие со стороны другой цепи (катушки).

Чем большая часть магнитного поля первой цепи пронизывает вторую цепь, тем сильнее взаимоиндукция между цепями. С количественной стороны явление взаимоиндукции характеризуется взаимной индуктивностью (коэффициентом взаимоиндукции, коэффициентом связи). Для изменения величины индуктивной связи между цепями, катушки делают подвижными. Приборы, служащие для изменения взаимоиндукции между цепями, называются вариометрами связи.

Теорема взаимности формулируется следующим образом: для любой линейной цепи ток в k-ветви, вызванный источником ЭДС Еm находящимся в m-ветви, Ik=E_mg_km равен току lm в m-ветви, вызванному источником ЭДС Ek (численно равной ЭДС Em), находящимся в k-ветви, Im=E_kg_mk.

55. Согласное и встречное включение катушек.

Последовательное соединение индуктивно связанных катушек при согласном включении.

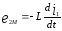
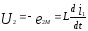то же для 1

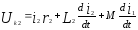
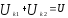
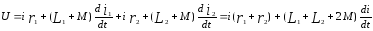
_{Переходя к синусоидальному току}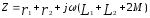

Последовательное соединение индуктивно связанных катушек при встречном включении.

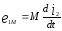
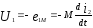
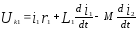то же для 2

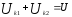
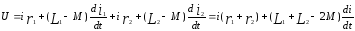
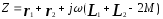
56. Последовательное соединение двух катушек. Векторная диаграмма.

Пусть две катушки, обладающие сопротивлениями R1 и R2 , индуктивностями L1 и L2 и взаимной индуктивностью M, соединены последовательно (рис. 30.1).

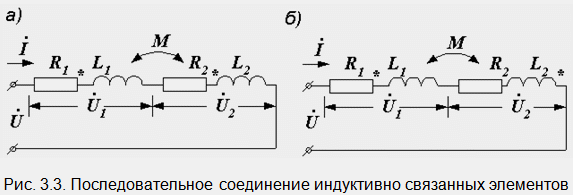
Возможны два вида их соединения – согласное и встречное. Если считать, что звездочками отмечены начала обмоток, то при согласном включении начало второй подключается к концу первой (рис. 30.1, а). Токи в обеих катушках направлены одинаково относительно одноименных зажимов: от начала к концу. При встречном включении катушек конец второй присоединяется к концу первой (рис. 30.1, б).

Напряжение на каждой из катушек содержит три составляющих: падение напряжения на активном сопротивлении, напряжение самоиндукции и напряжение взаимной индукции:

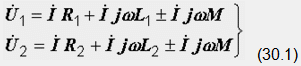
Последние имеют одинаковые знаки при согласном включении и разные при встречном. Напряжение на входе цепи равно сумме этих двух напряжений:

На рис. 30.1 изображены векторные диаграммы, построенные по уравнениям (30.1) и (30.2).