38. Вывод эдс индукции из закона сохранения энергии. Механизм возникновения эдс индукции. Вихревые токи (Токи Фуко)

Обобщая результаты своих многочисленных опытов, Фарадей пришел к количественному закону электромагнитной индукции. Он показал, что всякий раз, когда происходит изменение сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток; возникновение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой электромагнитной индукции. Значение индукционного тока, а следовательно, и э.д.с. электро­магнитной индукции 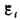 определяются только скоростью изменения магнитного потока, т. е.

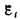
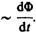
Теперь необходимо выяснить знак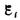 

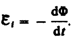
. В § 120 было показано, что знак магнитного потока зависит от выбора положительной нормали к контуру. В свою очередь, положительное направление нормали определяется правилом правого винта. Следовательно, выбирая положительное направление нормали, мы определяем как знак потока магнитной индукции, так и направление тока и э.д.с. в контуре. Пользуясь этими представлениями и выводами, можно соответственно прийти к формулировке закона электромагнитной индукции Фарадея: какова бы ни была причина изменения потока магнитной индукции, охватываемого замкнутым проводящим контуром, возникающая в контуре э. д. с.

(123.2)

Знак минус показывает, что увеличение потока вызывает э. д. с. 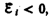 т. е. поле индукционного тока направлено навстречу потоку; уменьшение потока 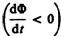вызывает  т.е. направления потока и поля индукционного тока совпадают. Знак минус в формуле (123.2) определяется правилом Ленца — общим правилом для нахождения направления индукционного тока, выведенного в 1833 г.

Механизм возникновения э.д.с. индукции можно пояснить на простом примере. Пусть изменение магнитного потока, пронизывающего контур, проис-ходит за счет изменения площади контура вследствие движения одного из проводников, составляющих контур. Пусть, например, контур образован п-образным проводником 1 и скользящей перемычкой 2 (рис. 3.12), и пусть линии индукции магнитного поля В перпендикулярны плоскости контура и направлены от нас (показаны крестиками).

П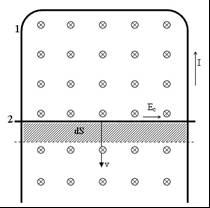ри скольжении перемычки вниз площадь контура S будет возрастать, что приведет к возрастанию магнитного потока, равного ВS. При этом, со-гласно закону Фарадея должна возникнуть э.д.с. индукции. Непосредственной физической причиной возникновения индукционного тока в контуре в данном случае является сила Лоренца. Действительно, при движении перемычки вниз со скоростью v, с той же скоростью будут перемещаться находящиеся в ней электроны. Сила Лоренца, действующая на каждый электрон, будет равна evB (где е — заряд электрона) и направлена влево. Формально эту силу можно рассматривать как проявление поля сторонних сил, имеющего напряженность Е

с. Из формулы (2.22) вытекает, что   Е_с = vB. Электродвижущая сила индукции Е _i, создаваемая полем Е_сво всей движущейся перемычке длиной l будет согласно (2.24) равна

Е_i = òЕ_сldl = Е_сl = vBl (3.25)

Скорость v движения перемычки представим как производную dx/dt. Тогда

Е_i = В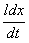= В(3.26)

В (3.26) учтено, что произведение ldx представляет со-бой приращение dS площади контура.  В свою очередь произведение BdS равно приращению dФ магнитного потока. В итоге мы получаем, что э.д.с. индукции равна производной dФ/dt от магнитного потока

Е_i = dФ/dt,(3.27)

то есть мы пришли к закону Фарадея. В проведенных рассуждениях мы для простоты оперировали модулями векторов Е_с,  v  и  В, поэтому ве-личину э.д.с. индукции в формуле (3.27)  определили также лишь по модулю.

Рассмотренное объяснение механизма возникновения э.д.с. индукции относится к случаю, когда изменение магнитного потока происходит за счет подвижных проводников. Но магнитный поток может меняться также и путем изменения величины В при неизменной геометрии контура. Тогда сила Лоренца не возникает, а ин-дукционный ток возбуждается в этом случае вихревым электрическим полем, порождае-мым меняющимся во времени магнитным полем. Этот более общий случай возникновения э.д.с. индукции будет рассмотрен в следующем разделе (тема 4).

Вихревые токи или токи Фуко́ (в честь Ж. Б. Л. Фуко) — вихревые индукционные токи, возникающие в проводниках при изменении пронизывающего их магнитного потока.

Впервые вихревые токи были обнаружены французским учёным Д.Ф Араго (1786—1853) в 1824 г. в медном диске, расположенном на оси под вращающейся магнитной стрелкой. За счёт вихревых токов диск приходил во вращение. Это явление, названное явлением Араго, было объяснено несколько лет спустя M. Фарадеем с позиций открытого им закона электромагнитной индукции: вращаемое магнитное поле наводит в медном диске токи (вихревые), которые взаимодействуют с магнитной стрелкой. Вихревые токи были подробно исследованы французским физиком 

Фуко (1819—1868) и названы его именем. Он открыл явление нагревания металлических тел, вращаемых в магнитном поле, вихревыми токами.

Токи Фуко возникают под воздействием переменного электромагнитного поля и по физической природе ничем не отличаются от индукционных токов, возникающих в линейных проводах. Они вихревые, то есть замкнуты в кольца. Электрическое сопротивление массивного проводника мало, поэтому токи Фуко достигают очень большой силы. В соответствии с правилом Ленца они выбирают внутри проводника такое направление и путь, чтобы противиться причине, вызывающей их. Поэтому движущиеся в сильном магнитном поле хорошие проводники испытывают сильное торможение, обусловленное взаимодействием токов Фуко с магнитным полем. Это свойство используется для 

демпфирования подвижных частей гальванометров, сейсмографов и др.

Тепловое действие токов Фуко используется в индукционных печах — в катушку, питаемую высокочастотным генератором большой мощности, помещают проводящее тело, в нем возникают вихревые токи, разогревающие его до плавления.

С помощью токов Фуко осуществляется прогрев металлических частей вакуумных установок для их дегазации.

Во многих случаях токи Фуко могут быть нежелательными. Для борьбы с ними принимаются специальные меры: с целью предотвращения потерь энергии на нагревание сердечников 

трансформаторов, эти сердечники набирают из тонких пластин, разделённых изолирующими прослойками. Появление ферритов сделало возможным изготовление этих проводников сплошными.

2) Вывод формулы эдс Ея якоря. Электромагнитный момент м машины постоянного тока.

Принцип работы ГПТ основан на явлении электромагнитной индукции. Если посредством первичного двигателя привести якорь машины во вращение с постоянной угловой частотой w и подать постоянное напряжение в обмотку возбуждения статора , то в каждом стержне обмотки якоря будет наводиться ЭДС

где Bcp = Фp/Sя = 2pФв/pdl — средняя магнитная индукция в зазоре под полюсом машины, Тл; Sя = pdl — площадь активной части якоря м²; p — число пар полюсов статора;

v = w(d/2) = (d/2)(2pn/60) = pdn/60,

где l и d — активная длина стержня и диаметр якоря; n и w — частота (об/мин) и угловая частота (рад/с) вращения якоря; N и 2a — число стержней и число параллельных ветвей якорной обмотки. После подстановки получим выражение ЭДС якоря

Eя= (N/2a)e1 = (pN/60a)nФв = CEnФв,

(9.1)

где CE = (pN/60a) — коэффициент ЭДС, определяемый конструктивными особенностями машины.

БИЛЕТ 26

1) Резистивный элемент (я) в цепи синусоидального тока. Активное сопротивление, активная мощность. Графики мгновенных значений тока, напряжения и мощности. Векторная диаграмма тока и напряжения.

Первое слагаемое в (3.30) есть напряжение u_R на резисторе, амплитуда которого U_mR = RI_m (I_m = U_mR/R), а сдвиг фаз между напряжением u_R и током i_R

φ = uR — iR = 0,

(3.31)

т. е. ток i_R в резисторе совпадает по фазе с напряжением u_R (рис. 3.15, б и в ).

Активная мощность цепи си­ну­соидального тока есть среднее значение общей мощности р(t) за период T. Она равна произведению действующих значений приложенного к цепи напряжения U и тока I, умноженному на cosφ, т. е.

P = UI cosφ = RI2.

Активное сопротивление — физическая величина, характеризующая сопротивление электрической цепи (или её участка) электрическому току, обусловленное необратимыми превращениями электрической энергии в другие формы (преимущественно в тепловую). Выражается в омах.

Активное сопротивление зависит от частоты переменного тока, возрастая с ее увеличением.

2) Принципиальные электрические схемы генераторов постоянного тока независимого, параллельного и смешанного возбуждений. Построить их внешние характеристики u/(I) на одном рисунке для сравнения

ГПТ независимого возбуждения

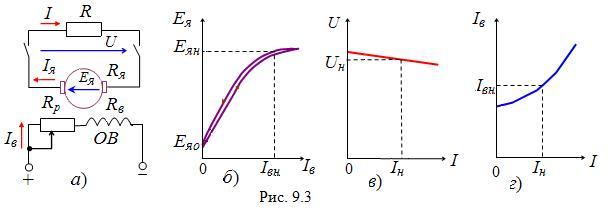
ГПТ параллельного возбуждения

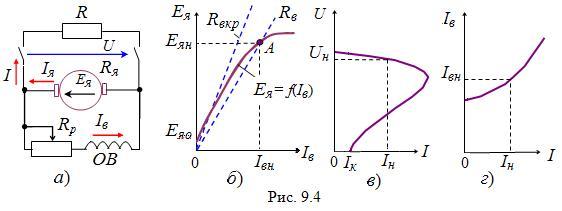
ГПТ смешанного возбуждения

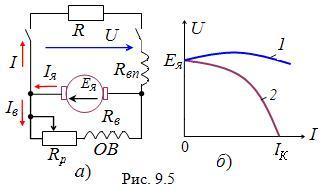
БИЛЕТ 27

1) Расчёт цепи постоянного тока с последовательным соединением нелинейного и линейного элементов (расчётно-графический метод).

При последовательном соединении нелинейных резисторов в качестве общего аргумента принимается ток, протекающий через последовательно соединенные элементы. Расчет проводится в следующей последовательности. По заданным ВАХ  отдельных резисторов в системе декартовых координат строится результирующая зависимость  . Затем на оси напряжений откладывается точка, соответствующая в выбранном масштабе заданной величине напряжения на входе цепи, из которой восстанавливается перпендикуляр до пересечения с зависимостью 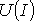 . Из точки пересечения перпендикуляра с кривой  опускается ортогональ на ось токов – полученная точка соответствует искомому току в цепи, по найденному значению которого с использованием зависимостей 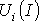 определяются напряжения 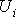 на отдельных резистивных элементах.

Применение указанной методики иллюстрируют графические построения на рис. 2,б, соответствующие цепи на рис. 2,а.

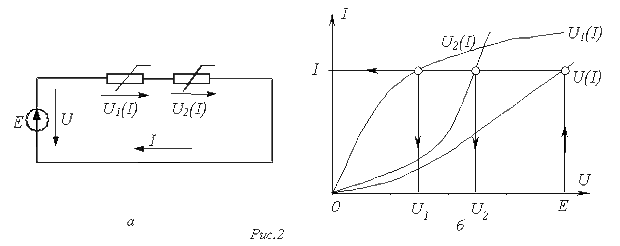
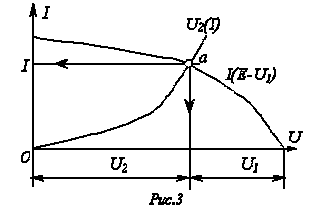
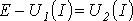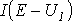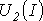Графическое решение для последовательной нелинейной цепи с двумя резистивными элементами может быть проведено и другим методом – методом пересечений. В этом случае один из нелинейных резисторов, например, с ВАХ  на рис.2,а, считается внутренним сопротивлением источника с ЭДС Е, а другой – нагрузкой. Тогда на основании соотношения  точка а (см. рис. 3) пересечения кривых  и определяет режим работы цепи. Кривая 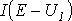 строится путем вычитания абсцисс ВАХ  из ЭДС Е для различных значений тока.

Использование данного метода наиболее рационально при последовательном соединении линейного и нелинейного резисторов. В этом случае линейный резистор принимается за внутреннее сопротивление источника, и линейная ВАХ последнего строится по двум точкам.

3.2.2. Уравнение Нернста для эдс гальванического элемента.

Электрической характеристикой электрода является потенциал, а гальванического элемента (электрохимической цепи) ‑ электродвижущая сила (ЭДС), равная алгебраической сумме скачков потенциала, возникающих на границе раздела фаз, входящих в состав цепи. ЭДС электрохимической цепи соответствует разности потенциалов правого (положительного) и левого (отрицательного) электродов и всегда положительна.

ЭДС гальванического элемента (I) равна:

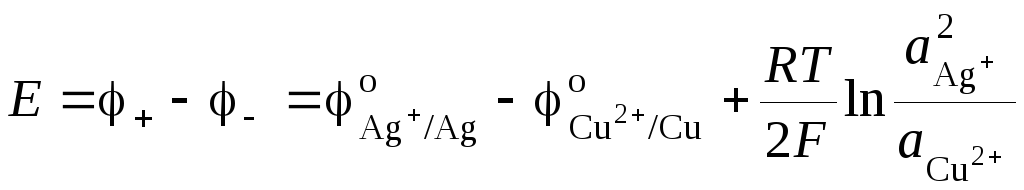(3.8)

где и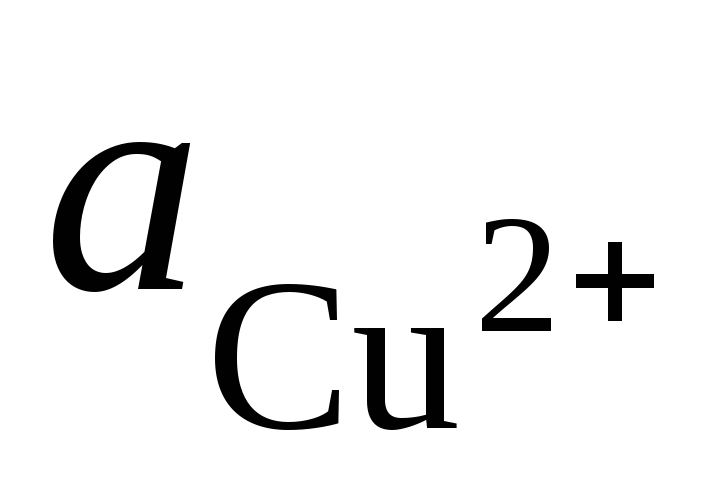– активности ионов Ag⁺ и Cu²⁺ в растворах их солей. Обозначим

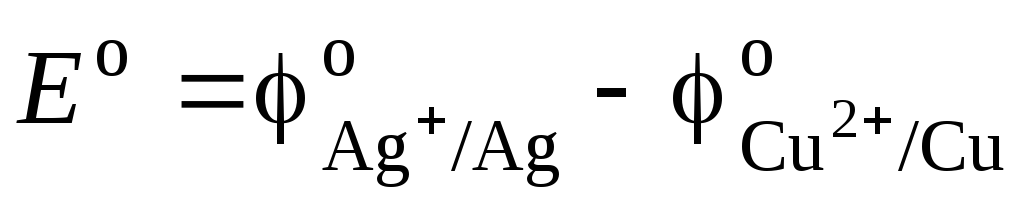, (3.9)

где Е^о – стандартная ЭДС гальванического элемента. Тогда

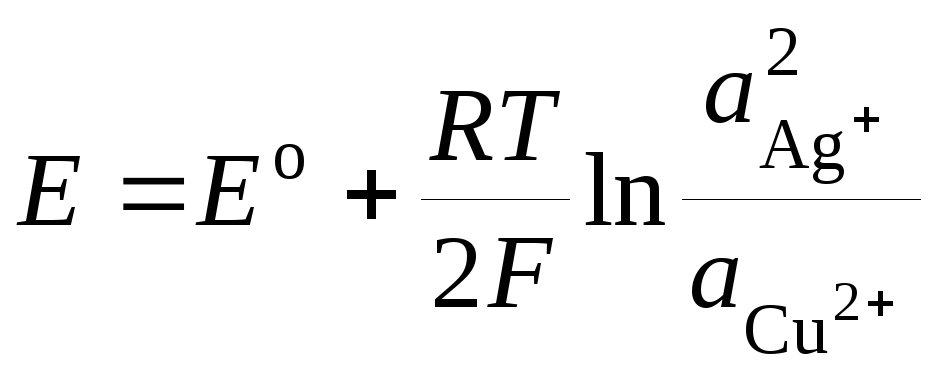. (3.10)

Следует помнить, что активность чистого твердого вещества принимается равной единице. Уравнение (3.8) носит название уравнения Нернста для ЭДС гальванического элемента.

Пусть в гальваническом элементе протекает обратимая химическая реакция

.

Максимальная полезная работа гальванического элемента при стандартных условиях равна

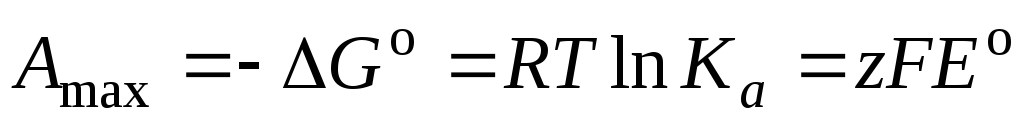, (3.11)

где z – число электронов, участвующих в элетродных реакциях (одинаковое для обоих электродов), F – постоянная Фарадея.

По уравнению изотермы Вант-Гоффа

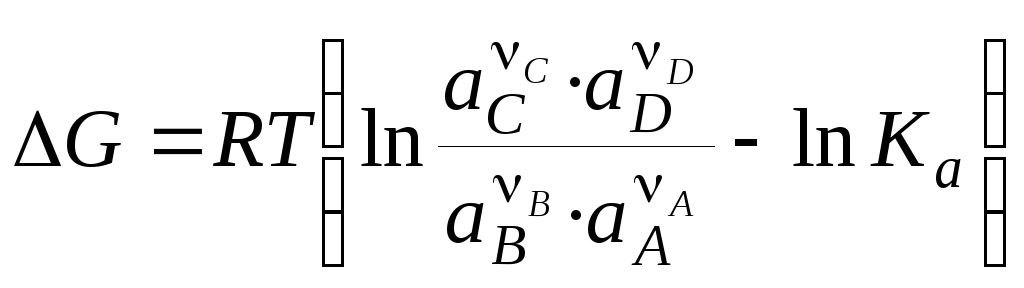, (3.12)

или

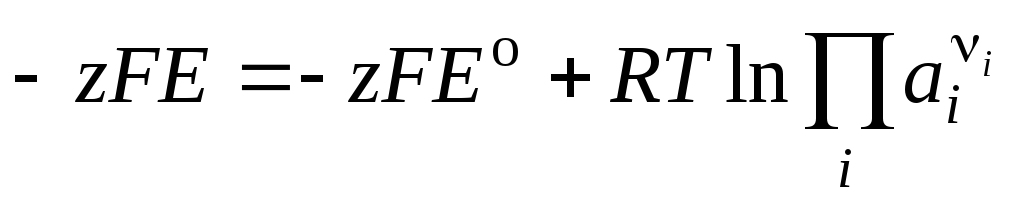. (3.13)

Следовательно,

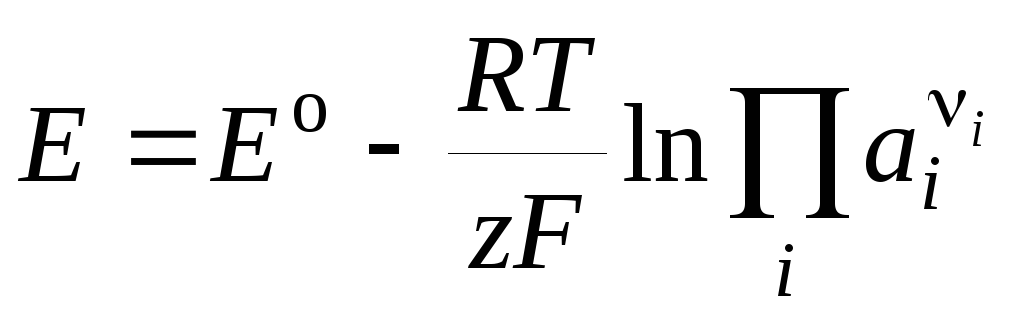. (3.14)

Уравнение Нернста в форме (3.14) применимо для расчета ЭДС любого гальванического элемента (по суммарной химической реакции) и потенциала любого электрода (по электродной реакции

3.3. Стандартный водородный электрод.

ЭЛЕКТРОДНЫЙ ПОТЕНЦИАЛ.

Можно с высокой точностью измерить ЭДС цепи, составленной из двух электродов. Однако нельзя ни измерить, ни вычислить абсолютную разность потенциалов φ на границе металл–раствор. Для практических целей достаточно иметь условные величины, характеризующие потенциалы различных электродов, отнесенные к потенциалу некоторого электрода, выбранного за стандартный.

В качестве условно-нулевого потенциала выбран потенциал стандартного водородного электрода:

,

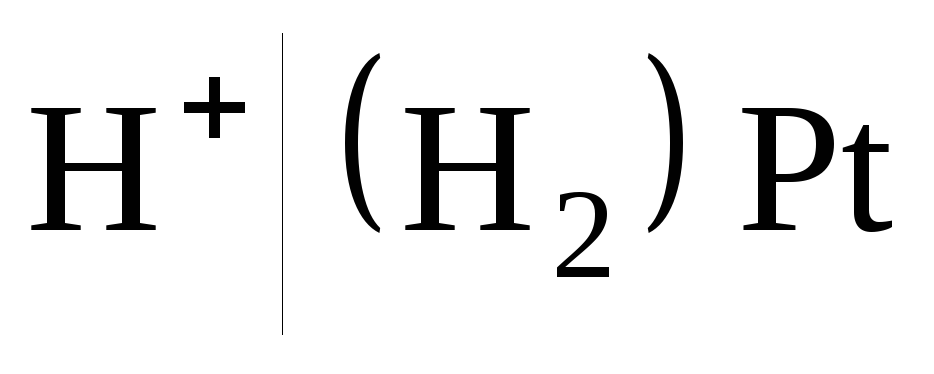в котором давление продуваемого водорода равно 1 атм, а активность ионов водорода в растворе равна 1 (рис. 7).

Электродная реакция

.

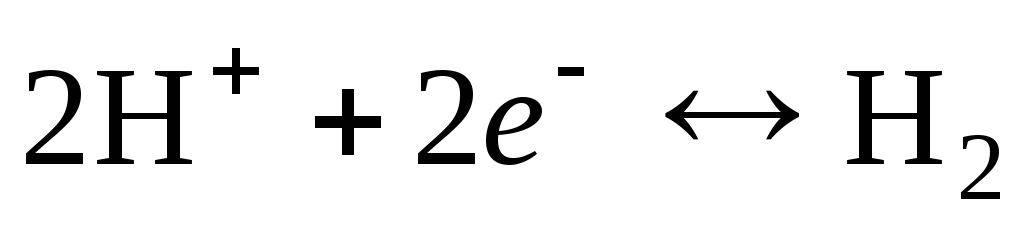Рис. 7. Общий вид водородного электрода.

Потенциал стандартного водородного электрода равен

,

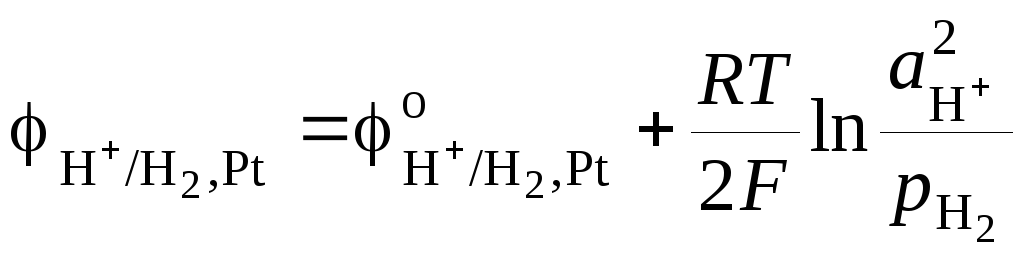С учетом того, что , R = 8.314 Дж·моль^-1·К^-1, F = 96485 Кл·моль-экв^-1,и заменяя натуральный логарифм десятичным, получаем

.

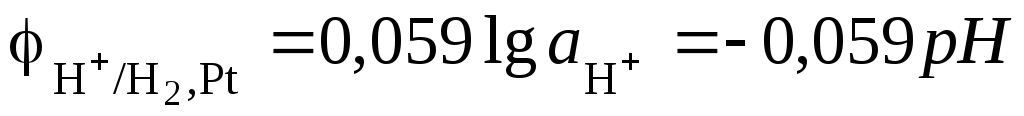Электродным потенциалом любого другого электрода называют его потенциал по отношению к стандартному водородному. Другими словами, за электродный потенциал принимают ЭДС цепи, составленной из рассматриваемого электрода и стандартного водородного электрода. При этом справа в цепи расположен рассматриваемый электрод, а слева – стандартный водородный электрод. ЭДС положительна (электродный потенциал положителен), если электрический ток внутри цепи течёт слева направо, и отрицательна – если наоборот.

Пример 3.1.

1) Составим гальванический элемент из платинового и медного электродов:

.

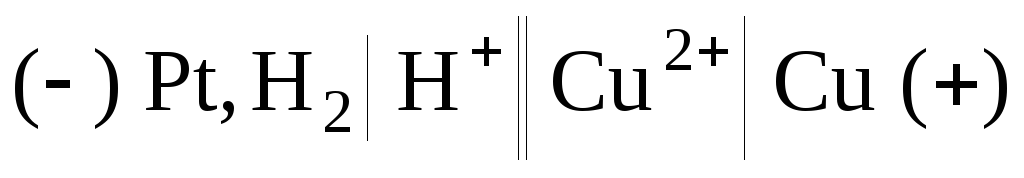Суммарная токообразующая реакция: , т.е. перенос электронов в цепи происходит слева направо (от левого электрода к правому). При стандартных условиях () .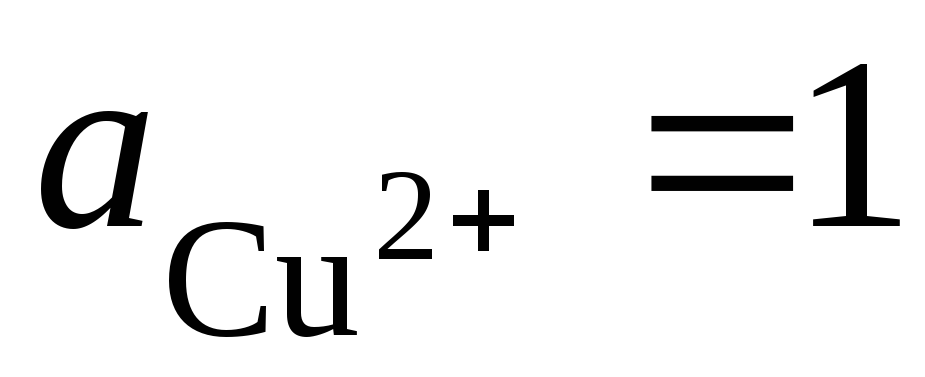

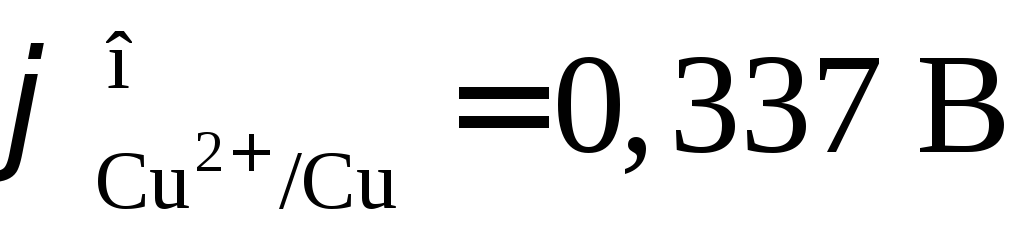2) Составим гальванический элемент из платинового и цинкового эдектродов:

.

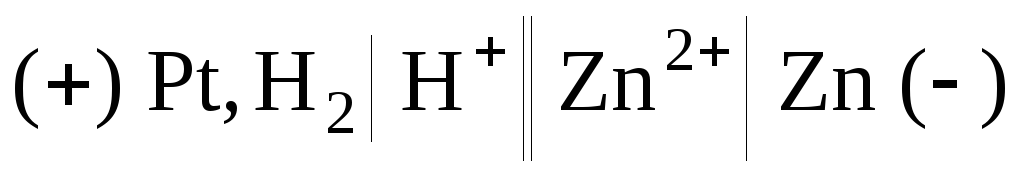Суммарная реакция: , т.е. перенос электронов в цепи происходит справа налево. При стандартных условиях () .

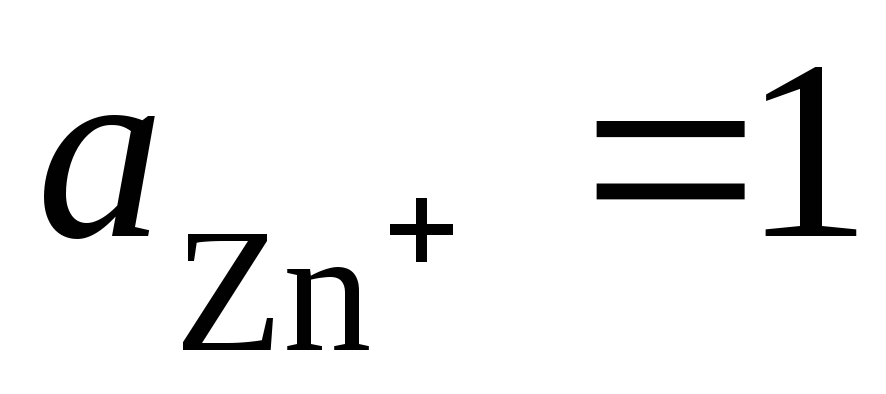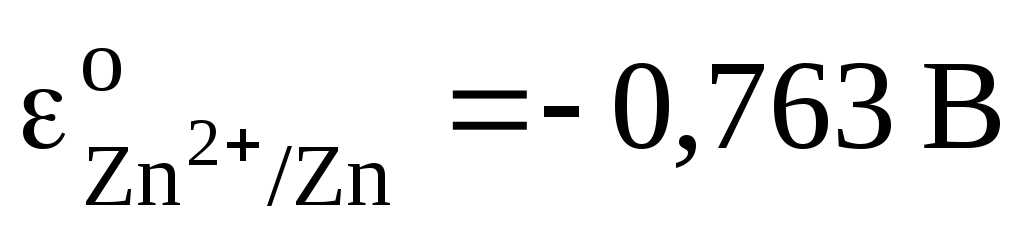Следует помнить, что ЭДС цепи всегда положительна, поэтому рассматриваемый гальванический элемент следует записать в следующем виде:

,

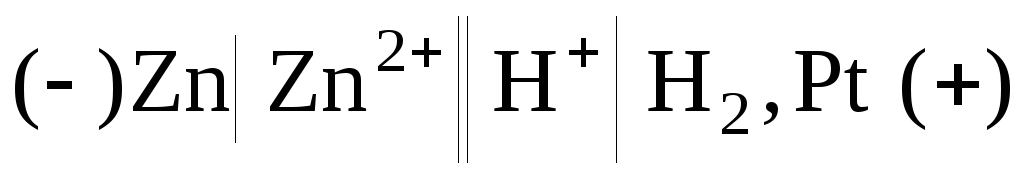при стандартных условиях .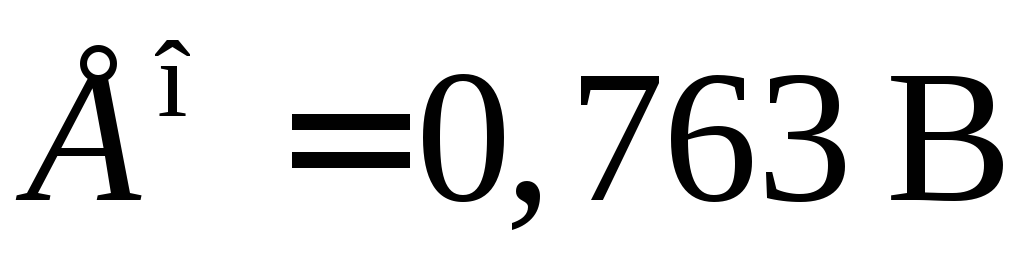

3.4. ТЕРМОДИНАМИКА ГАЛЬВАНИЧЕСКОГО ЭЛЕМЕНТА.

Гальванический элемент при работе в условиях тепловой изоляции нагревается или охлаждается. Поэтому можно предположить, что источником совершаемой электрической работы являются тепловой эффект химической реакции и энергия окружающей среды.

Рассмотрим уравнение Гиббса-Гельмгольца в следующей форме:

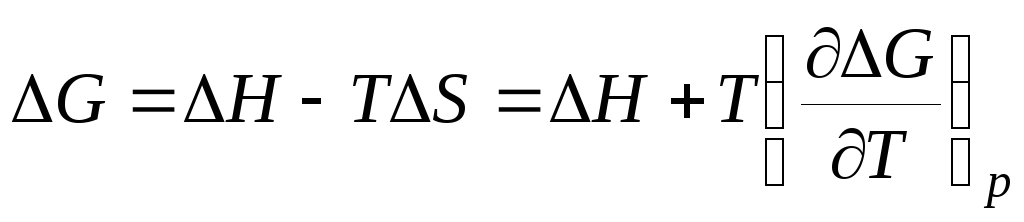, (3.15)

где ΔН и ΔS – тепловой эффект и энтропия химической реакции, протекающей в гальваническом элементе. Максимальная полезная работа электрохимической цепи равна убыли энергии Гиббса:

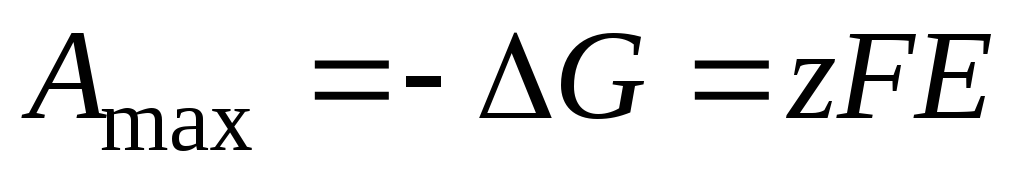, (3.16)

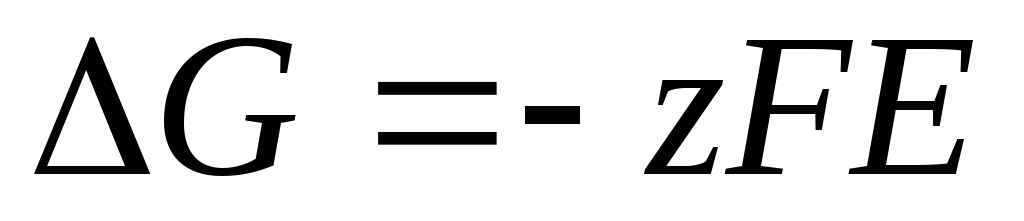. (3.17)

Тогда:

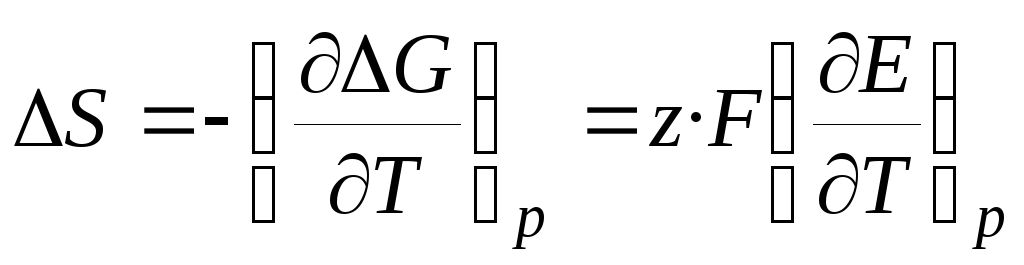, (3.18)

, (3.19)

, (3.20)

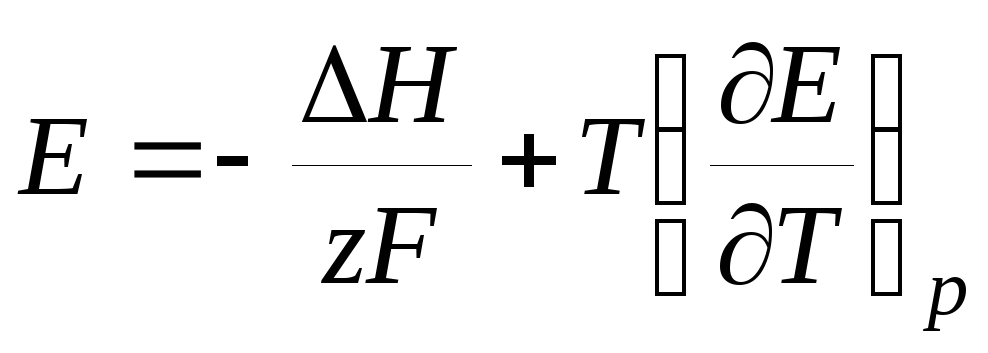, (3.21)

Следовательно,

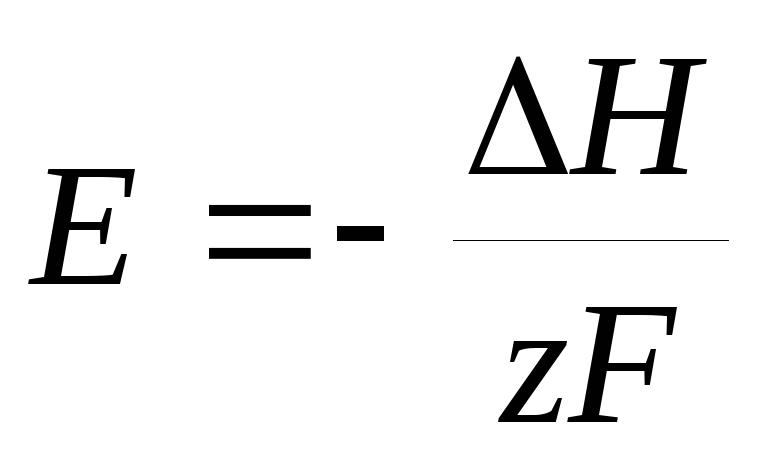, если ,

т.е. в этом случае вся электрическая работа цепи производится за счет теплового эффекта химической реакции. Если

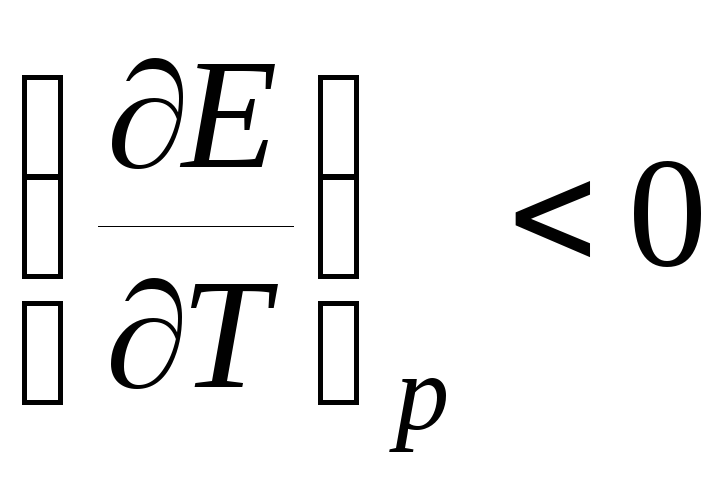, то ,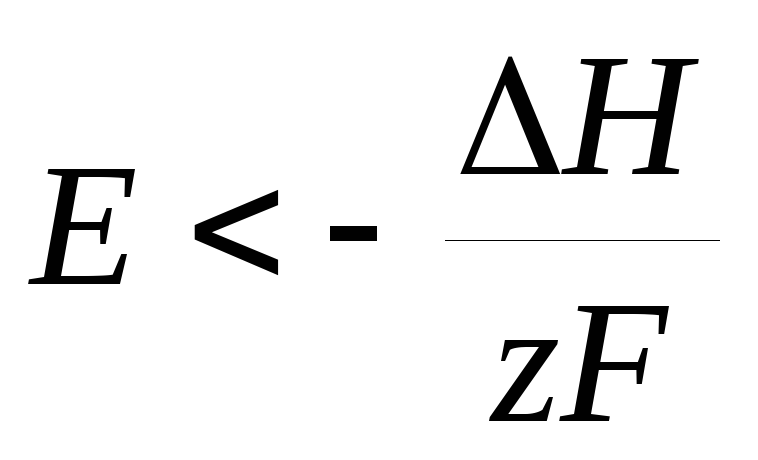

т. е. электрическая работа меньше теплового эффекта реакции. Гальванический элемент при изотермических условиях отдает теплоту в окружающую среду или нагревается в условиях тепловой изоляции. Если

, то ,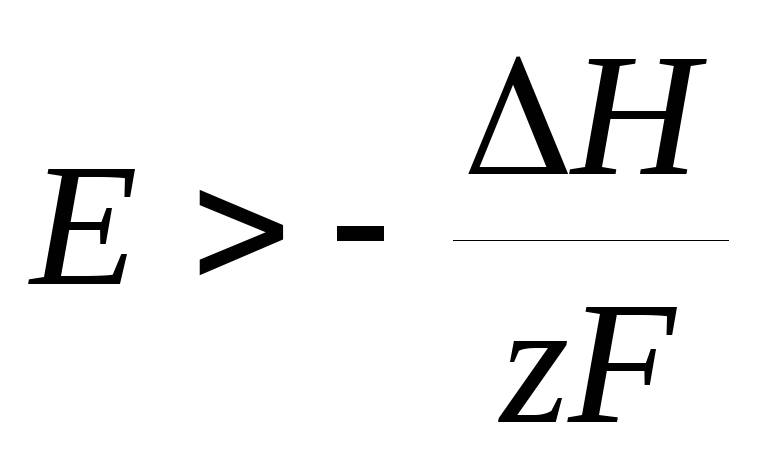

т. е. электрическая работа больше теплового эффекта реакции. Гальванический элемент при изотермических условиях поглощает теплоту из окружающей среды или охлаждается в условиях тепловой изоляции.

Измерение ЭДС обратимых гальванических элементов при различных температурах позволяет определить термодинамические характеристики химических реакций, протекающих в них, по уравнениям (3.16), (3.18) и (3.20).

3.5. КЛАССИФИКАЦИЯ ЭЛЕКТРОХИМИЧЕСКИХ ЦЕПЕЙ.

Гальванические элементы классифицируют по двум признакам:

1. По характеру суммарного процесса, лежащего в основе действия гальванического элемента. Это или химическая реакция, или процесс выравнивания концентраций двух растворов одного и того же электролита. По этому признаку элементы делятся на химические и концентрационные.

1.1. Концентрационные цепи. Концентрационные электрохимические цепи состоят из электродов с одинаковыми потенциалопределяющими реакциями. Физические и химические свойства материала электродов одинаковы, но активности одного (или нескольких) участников реакции на каждом из электродов различны. ЭДС цепи определяется отношением активностей (по уравнению Нернста):

, .

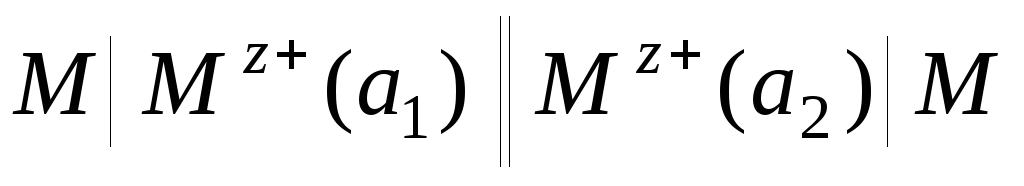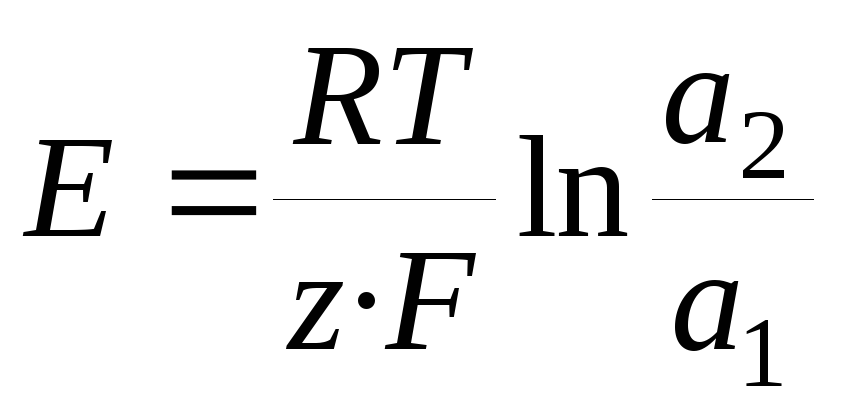В уравнение Нернста для ЭДС цепи не входят стандартные электродные потенциалы, так как они одинаковы. По результатам измерений ЭДС такой цепи и известной активности компонента в одном электроде можно рассчитать активность компонента в другом электроде. Примером концентрационной цепи может служить следующий гальванический элемент (а₂ > a₁): .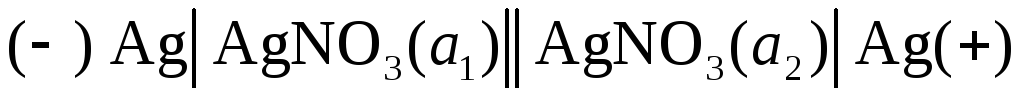

1.2. Химические цепи. Химические цепи состоят из электродов, потенциалопределяющие реакции которых различны. Электроды в таких системах отличаются и по физическим, и по химическим свойствам. Электрическая энергия возникает за счет энергии суммарной химической реакции, для которой справедливы ранее установленные соотношения между ЭДС и тепловым эффектом реакции, а также между стандартной ЭДС и константой равновесия реакции. Химические цепи разнообразны по природе и свойствам электродов, из которых они состоят. Примером такой цепи может служить серебряно-цинковый элемент: .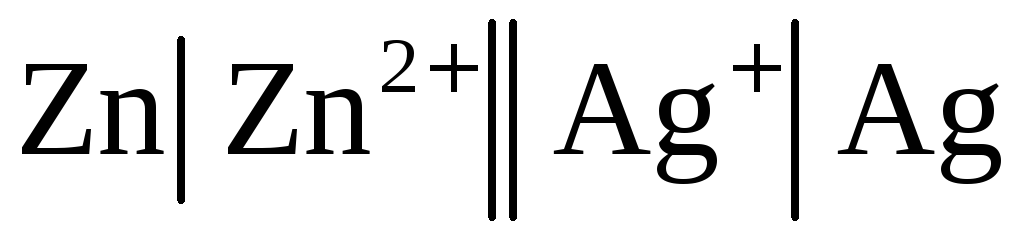

Чтобы решить вопрос о направлении суммарной химической реакции, протекающей в элементе, прежде всего следует определить полярности электродов. Катодом (положительно заряженным, правым) всегда является электрод с более положительным потенциалом. Так как

,

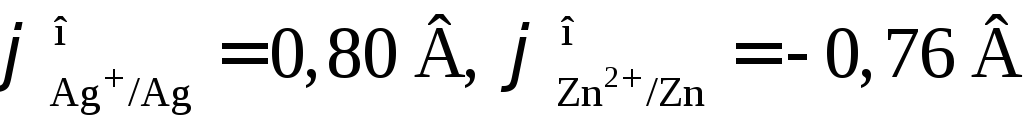то в стандартных условиях серебряный электрод будет катодом, а цинковый электрод ‑ анодом. Стандартная ЭДС элемента равна

.

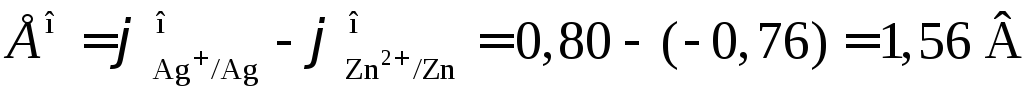Уравнения потенциалопределяющих реакций:

, .

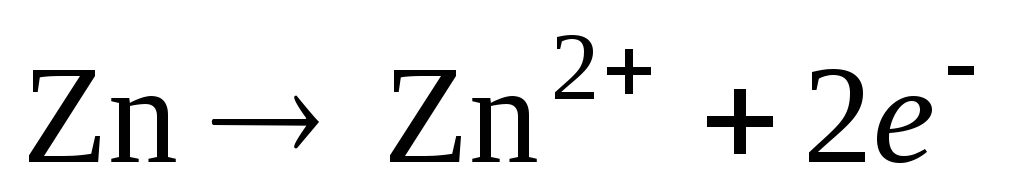Суммарная реакция в цепи

электронейтральна (электродные реакции уравнены по числу электронов и участвующих в них веществ). ЭДС элемента по уравнению Нернста равна

.

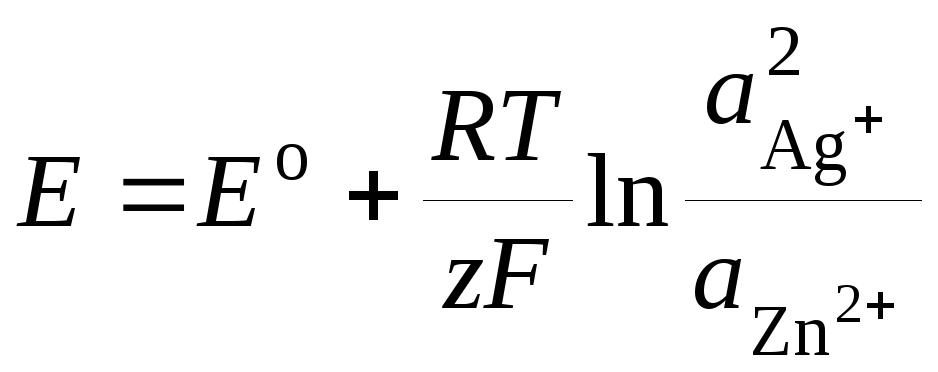Важным частным случаем химических цепей являются цепи, в которых хотя бы один из электродов является окислительно–восстановительным. Электрический ток в таких цепях возникает за счет реакций окисления и восстановления, протекающих в растворе. Примером такой цепи является цепь, составленная из стандартного водородного электрода и железного окислительно–восстановительного (редокс) электрода:

.

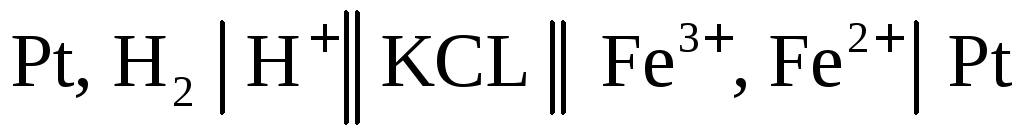2. По наличию или отсутствию жидкостного соединения между двумя растворами гальванического элемента. По этому признаку элементы делят на цепи с переносом и цепи без переноса ионов.

2.1. Цепь с переносом – это цепь с жидкостной границей. Например, цепь вида

.

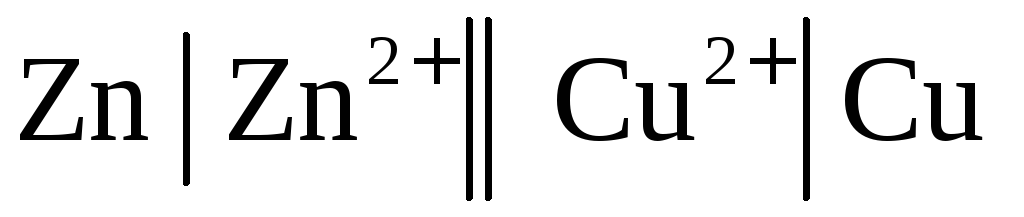В состав цинкового и медного электродов входят растворы различной природы. Контакт между двумя растворами обеспечивается с помощью специальных приспособлений, например, солевым мостиком, состоящим из трубки, заполненной смесью влажного желеобразного вещества агар-агара с солью сильного электролита (КСl). Диффузионный потенциал на границе раздела раствор-раствор элиминирован.

2.2. Цепь без переноса – это цепь без жидкостной границы. Например, цепь вида

,

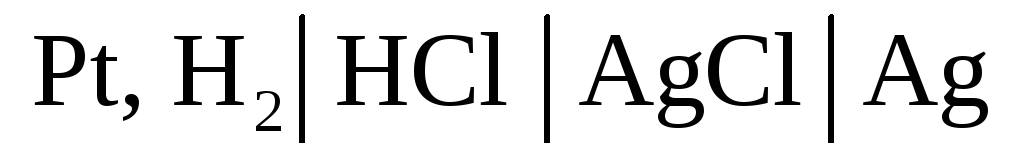в которой оба электрода погружены в один и тот же раствор.

3.6. КЛАССИФИКАЦИЯ Обратимых ЭЛЕКТРОДОВ.

Классификация обратимых электродов основана на свойствах веществ, участвующих в потенциалопределяющих процессах.

3.6.1. Электроды первого рода.

Это металлические электроды, обратимые относительно катионов (в том числе амальгамные) и металлоидные, обратимые относительно анионов (например, Se^2-/Se). В таких электродах восстановленной формой является металл, а окисленной – ион этого металла.

Если электрод обратим относительно катиона, то

, .

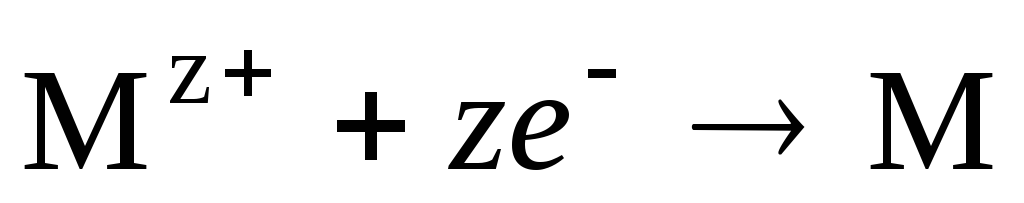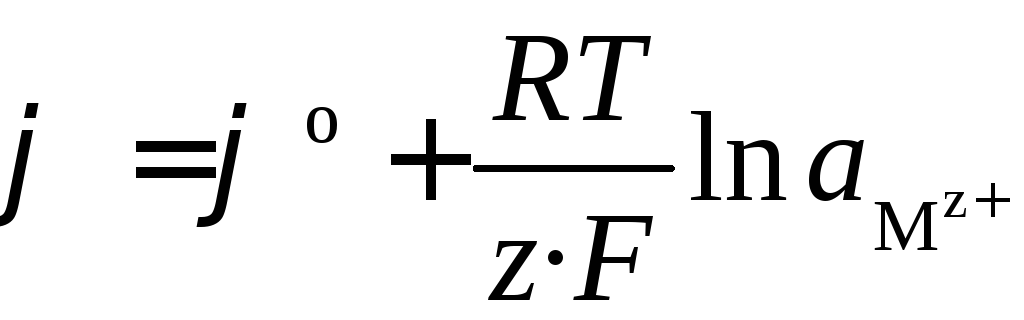Если электрод обратим относительно аниона, то

, .

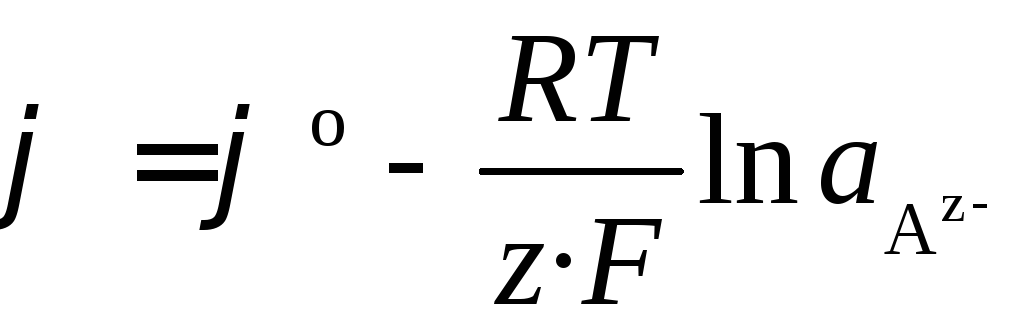К электродам первого рода относятся также газовые электроды (водородный, кислородный, хлорный). Они могут быть обратимы по отношению к катиону или аниону. Металл в газовых электродах необходим для создания электронопроводящего контакта между газом и раствором, должен быть инертен по отношению к веществам, находящимся в растворе, и способен катализировать только один потенциалопределяющий процесс. Например, водородный электрод обратим по отношению к катиону. Уравнение электродного процесса в кислой среде

может быть записано в упрощенном виде:

.

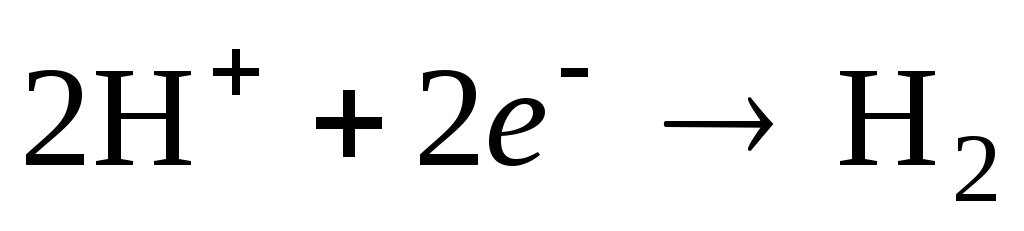Потенциал водородного электрода определяется выражением

.

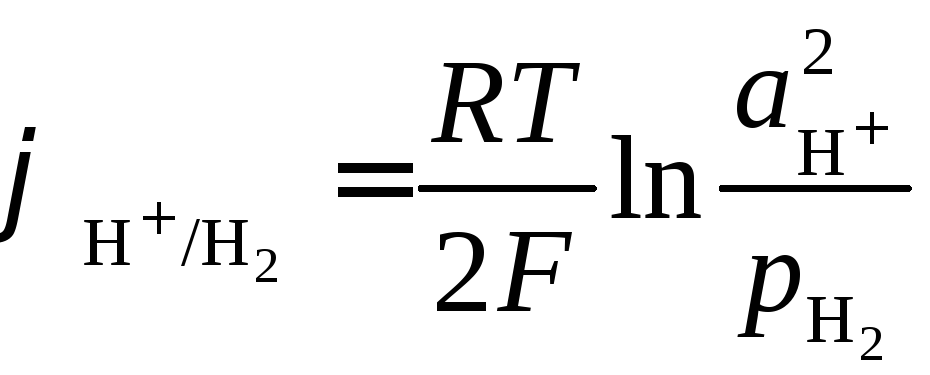Примером газового электрода, обратимым по отношению к аниону, может быть хлорный электрод с потенциалопределяющей реакцией .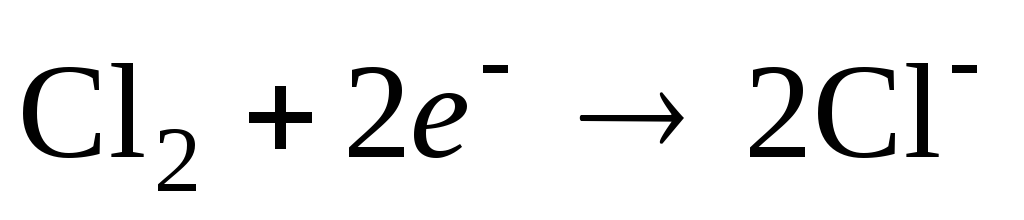

3.2. Вывод расчётной формулы

Установка состоит из двух электрически изолированных контуров: в первый контур входят генератор стандартных сигналов ГСС, катушка 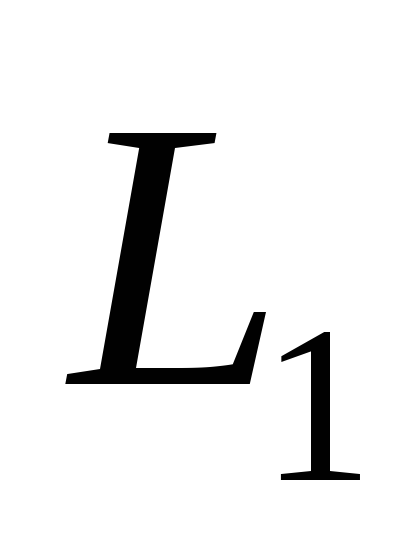, резистор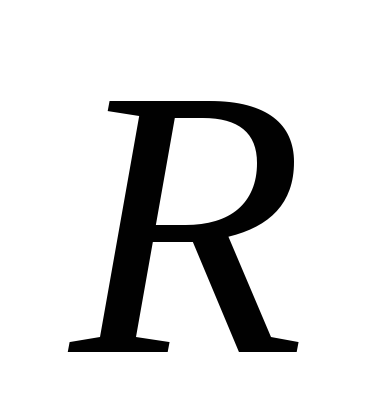и, подключенный параллельно к нему цифровой вольтметр; во второйкатушка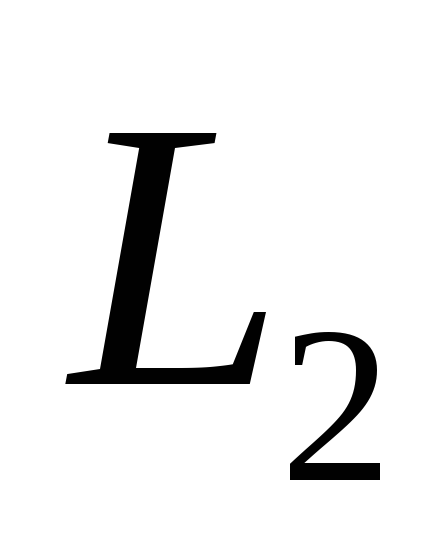и осциллограф.

ГСС генерирует в первом контуре переменное напряжение , которое можно менять по частотеи амплитуде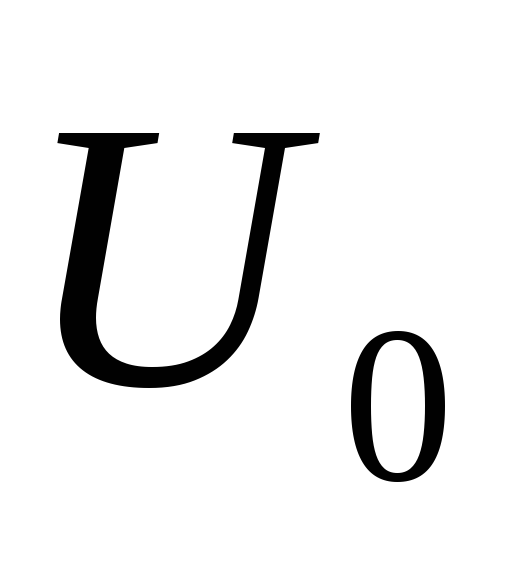и, следовательно, через первую катушку проходит переменный электрический ток, который индуцирует в ней переменный магнитный поток. Катушк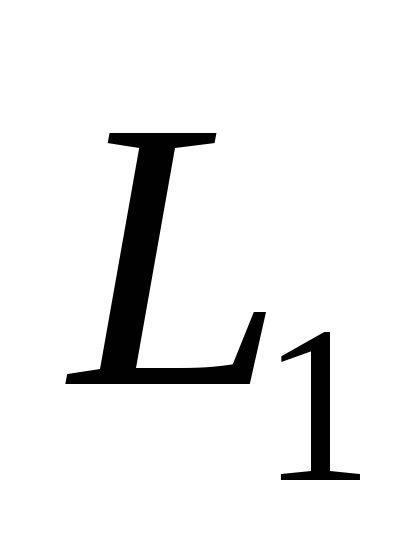ии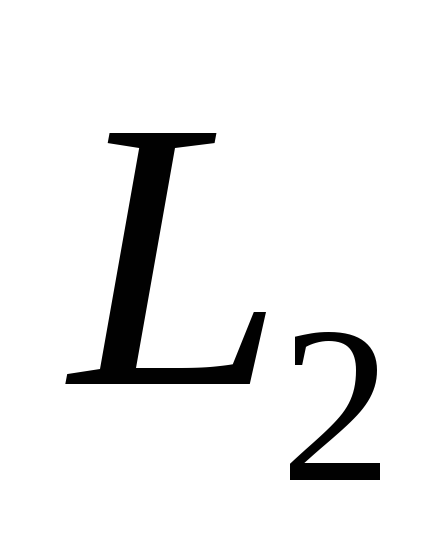находятся на близком расстоянии, поэтому магнитный поток будет пронизывать и вторую катушку. Согласно закона взаимной индукции, ЭДС индукции во второй катушке будет равна

,

(1)

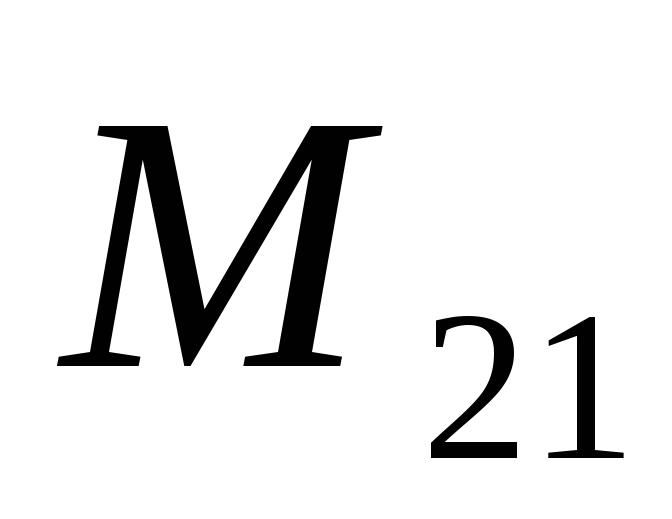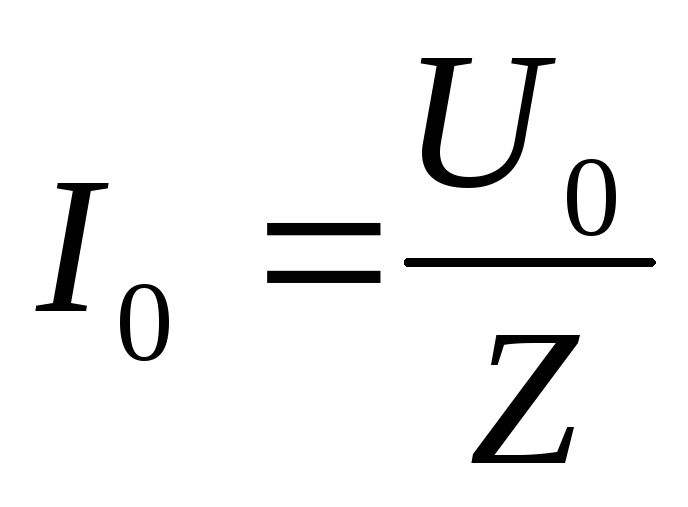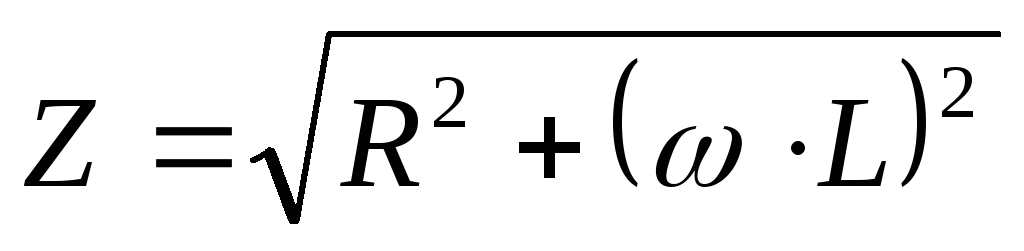где коэффициент взаимной индукции,амплитуда силы тока в первой катушке,сопротивление переменному току,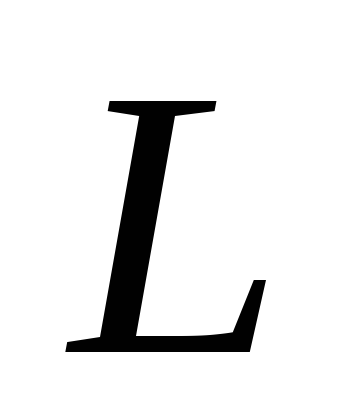коэффициент индуктивности, соответственно, первой катушки,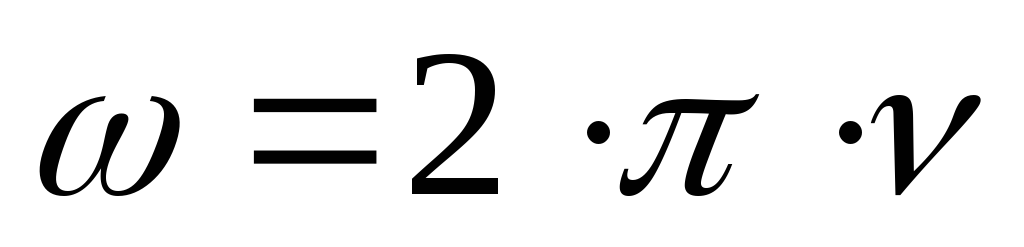циклическая частота,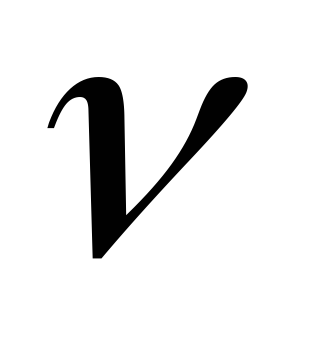частота переменного тока.

Из представленных формул следует, что амплитуда силы тока в катушке 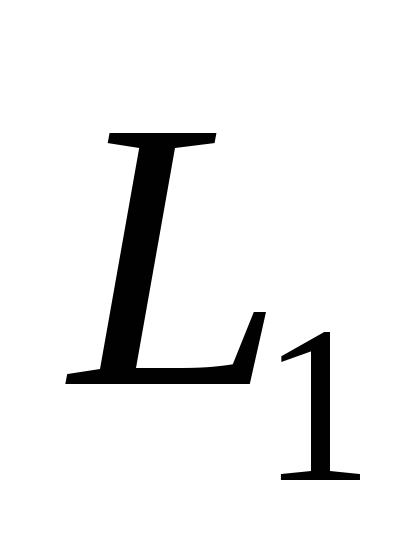является величиной зависящей от частоты подаваемого тока, что является не желательным при выполнении данной работы, поэтому последовательно к катушке подключен резистор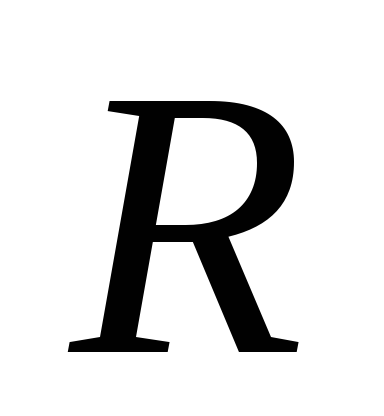, который обладает только активным сопротивлением. 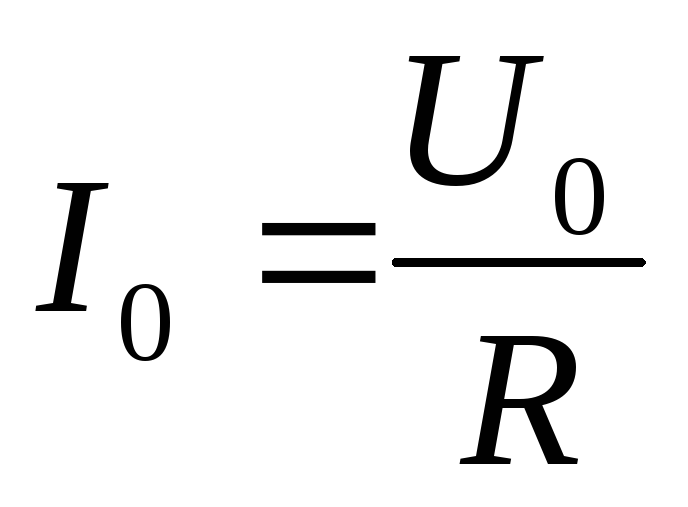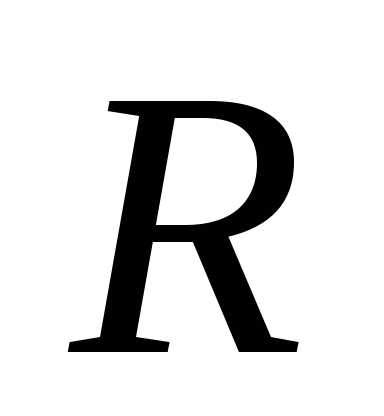По двум последовательно соединенным элементам, как известно, протекает одинаковый ток, поэтому цифровой вольтметр подключен к резистору, следовательно,амплитуда силы тока на резисторе и, соответственно, в первой катушке,сопротивление резистора,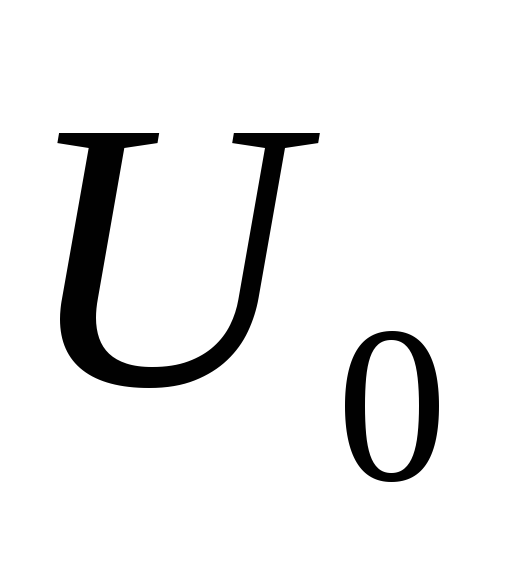амплитуда напряжения на резисторе.

ЭДС индукции во второй катушке подчиняется также гармоническому закону

,

(2)

где 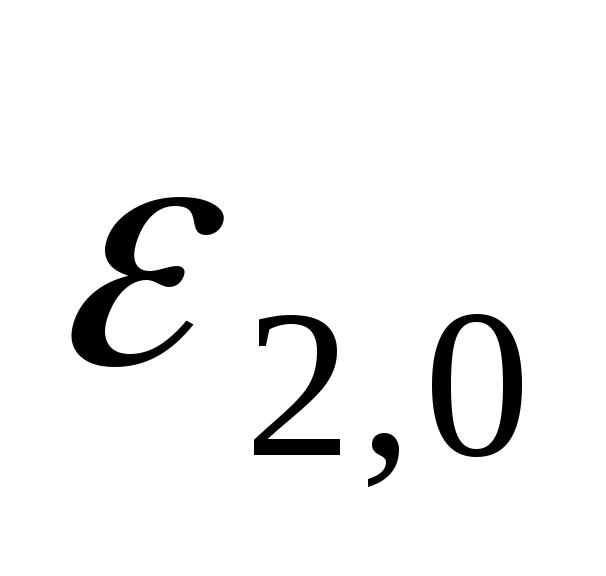амплитуда ЭДС индукции во второй катушке.

Сопоставляя формулы (1) и (2), получим

.

(3)

В данной формуле величины: 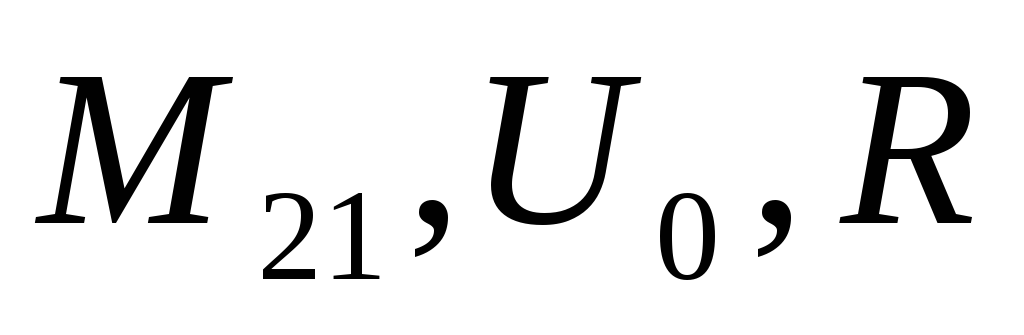, являются постоянными, поэтому из (3) следует прямо пропорциональная зависимость между амплитудой ЭДС индукции во второй катушке и частотой переменного тока подаваемого на первую катушку.

Формула для расчёта коэффициента взаимной индукции следует (3)

.

(4)

Величина коэффициента взаимной индукции, в силу выше сказанного, остаётся постоянной при неизменном расположении катушек.

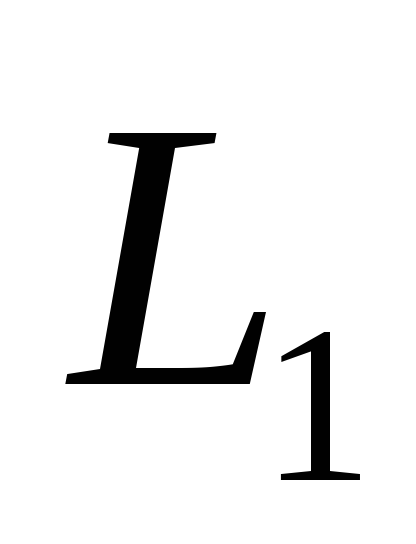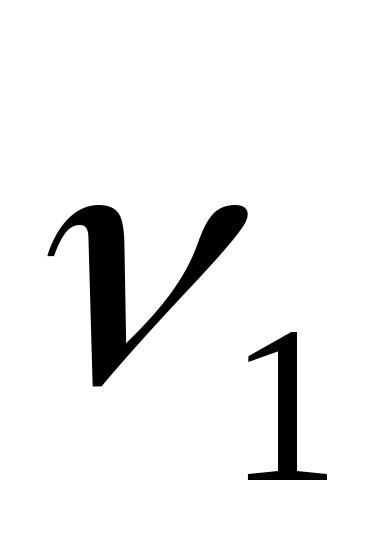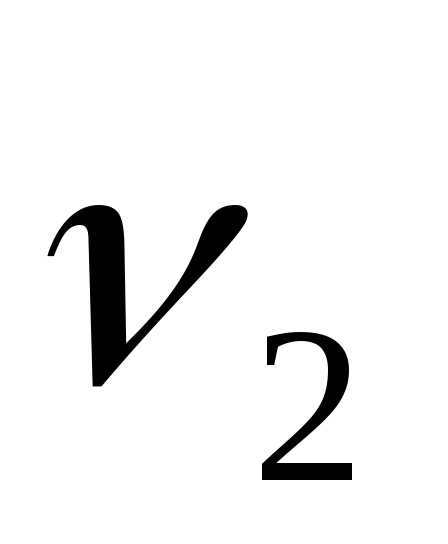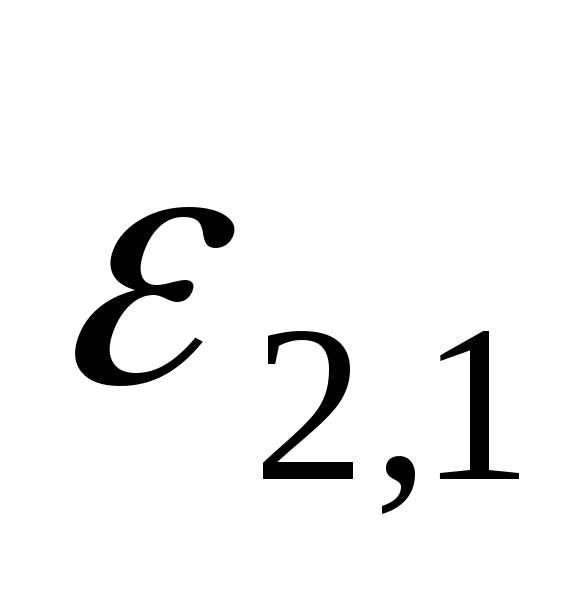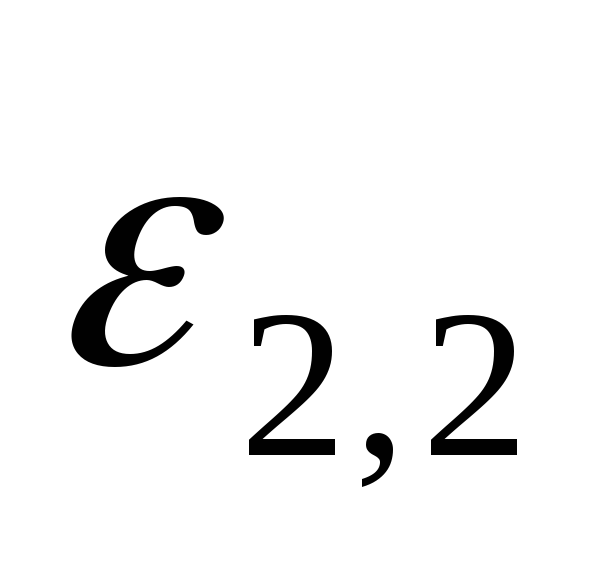При выполнении лабораторной работы при фиксированном расстоянии между катушками, на катушку подаются переменные токи с частотамии, при этом на экране осциллографа фиксируются два амплитудных значения ЭДС индукциии, т.е.

(5)

Следовательно,

.

(6)

Амплитудное значение ЭДС индукции вычисляется по формуле

,

(7)

где 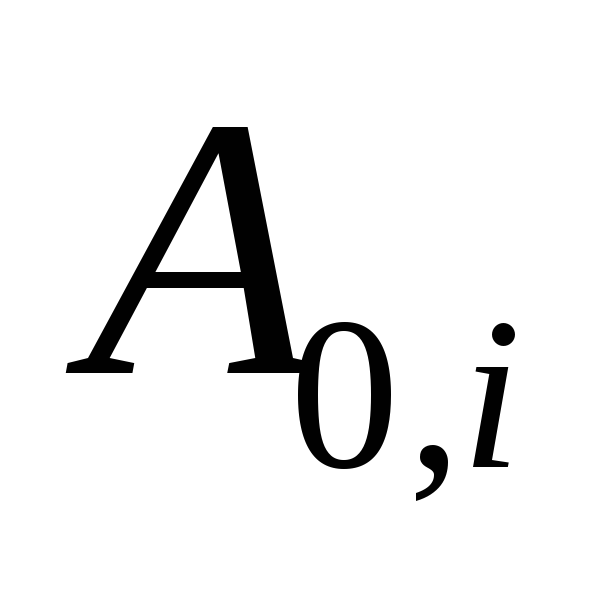амплитудное значение синусоиды на экране осциллографа в сантиметрах,калибровочный множитель, определяемый по показанию рукоятки регулировки калибровки18 (рис. 3),.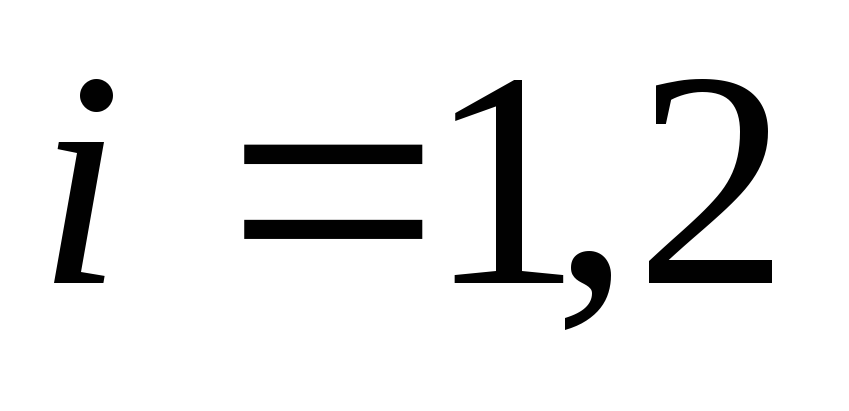

Расчётная формула, в итоге, примет вид

.

(8)

4. Описание экспериментальной установки

1. Схема экспериментальной установки приведена на рисунке 3.Общий вид установки представлен на фотографии,рис. 5.

На дюралевой скамье с метрической линейкой расположены две катушки: первичная катушка 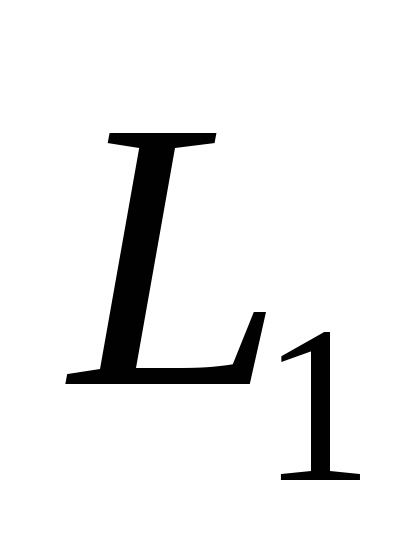зафиксирована, а вторичную катушкуможно перемещать вдоль стержня, изменяя тем самым расстояние между катушками и, следовательно, меняя коэффициент взаимной индукции.

Последовательно к 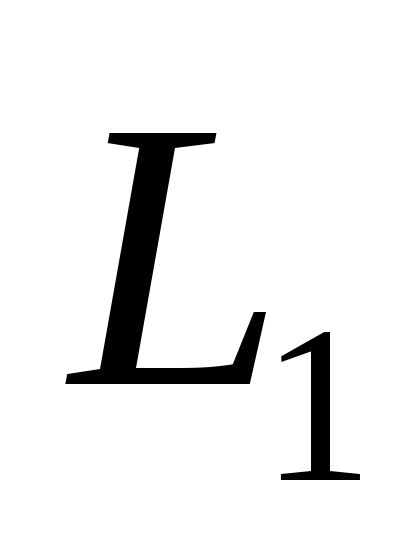подключён резистор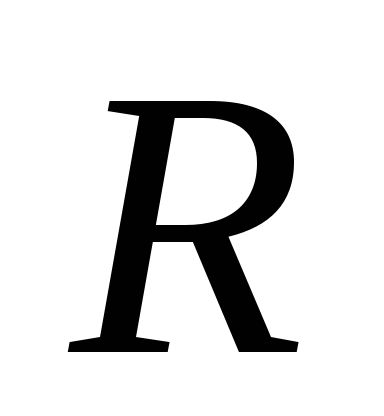, с которого с помощью цифрового вольтметра снимаются амплитудные значения переменного напряжения. На первичную катушку подаётся синусоидальный переменный ток с генератора стандартных сигналов ГСС. На вторичной катушке генерируется переменная ЭДС индукции, которая выводится на экран осциллографа.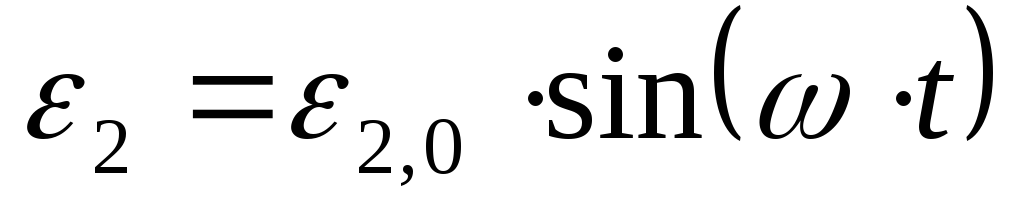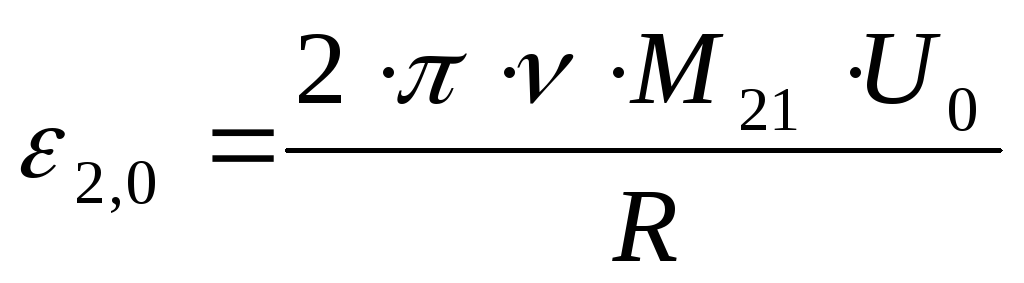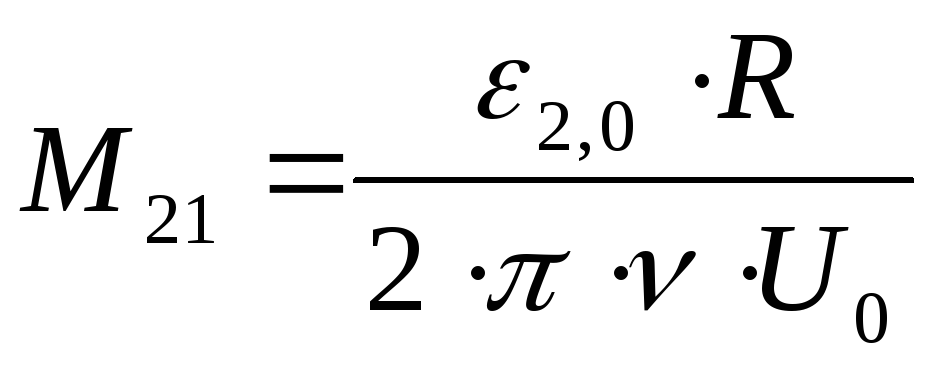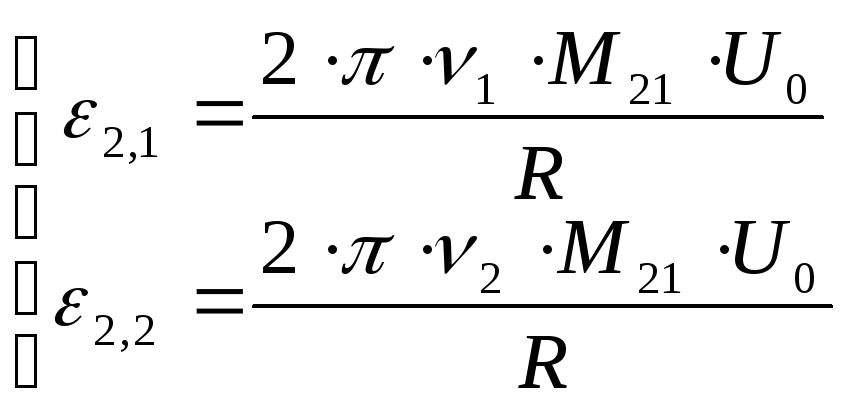