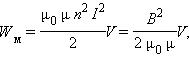ЭДС индукции в движущихся проводниках

ЭДС индукции в движущихся проводниках

Прямолинейный проводник АВ движется в магнитном поле с индукцией В по проводящим шинам, которые замкнуты на гальванометр.

На электрические заряды, перемещающиеся вместе с проводником в магнитном поле, действует сила Лоренца:

Fл = /q/vB sin a

Её направление можно определить по правилу левой руки.

Под действием силы Лоренца внутри проводника происходит распределение положительных и отрицательных зарядов вдоль всей длины проводника l.
Сила Лоренца является в данном случае сторонней силой, и в проводнике возникает ЭДС индукции, а на концах проводника АВ возникает разность потенциалов.

Причина возникновения ЭДС индукции в движущемся проводнике объясняется действием силы Лоренца на свободные заряды.

Готовимся к проверочной работе!

1. При каком направлении движения контура в магнитном поле в контуре будет возникать индукционный ток?

2. Укажите направление индукционного тока в контуре при введении его в однородное магнитное поле.

3. Как изменится магнитный поток в рамке, если рамку повернуть на 90 градусов из положения 1 в положение 2 ?

4. Будет ли возникать индукционный ток в проводниках, если они движутся так, как показано на рисунке?

5. Определить направление индукционного тока в проводнике АБ, движущемся в однородном магнитном поле.

6. Указать правильное направление индукционного тока в контурах.

Следующая страница «Самоиндукция. Индуктивность. Энергия магнитного поля. Вопросы к пр/работе»
Назад в раздел «10-11 класс»

Электромагнитное поле — Класс!ная физика

Взаимодействие токов. Магнитное поле. Вектор магнитной индукции. Сила Ампера — Действие магнитного поля на движущийся заряд.Магнитные свойства вещества — Явление электромагнитной индукции. Магнитный поток. Направление индукционного тока. Правило Ленца — ЭДС электромагнитной индукции. Вихревое электрическое поле — ЭДС индукции в движущихся проводниках
— Самоиндукция. Индуктивность. Энергия магнитного поля. Вопросы к пр/работе

ЭДС индукции в движущихся проводника

«Прежде чем решать задачу, прочитай условие!».

Жак Адамар

Данная тема посвящена решению задач на ЭДС индукции в движущихся проводниках.

Задача 1. В однородном магнитном поле движется проводник со скоростью 10 км/ч под углом 45º к вектору магнитной индукции, модуль которого равен 50 мТл. Найдите длину проводника, если при таком движении в нём возникает ЭДС индукции 0,5 В.

ДАНО:	СИ	РЕШЕНИЕ Закон электромагнитной индукции для движущихся проводников Выразим длину проводника из этой формулы

Ответ: 5 м.

Задача 2. Алюминиевый проводник с площадью поперечного сечения 5 мм² движется в магнитном поле со скоростью 8 м/с под углом 30º к вектору магнитной индукции. Найдите индукционный ток, возникающий в проводнике, если индукция поля равна 20 мТл.

ДАНО:	РЕШЕНИЕ Запишем закон электромагнитной индукции для движущихся проводников Индукционный ток можно определить по формуле Сопротивление проводника можно рассчитать по формуле С учетом последней формулы получаем, что индукционный ток равен

Ответ: 14,8 А.

Задача 3. Проводник с сопротивлением 10 Ом входит в магнитное поле со скоростью 5 м/с так, как показано на рисунке. Индукция магнитного поля равна 8×10

–4 Тл. Постройте график зависимости индукционного тока от времени, учитывая то, что длина проводника равна 10 м.

ДАНО:

РЕШЕНИЕ Закон электромагнитной индукции для движущихся проводников Индукционный ток Поскольку проводник только начал входить в магнитное поле и двигается равномерно, длина активной части будет определяться произведением скорости и времени движения Нетрудно убедиться, что уже через две секунды проводник полностью окажется в магнитном поле. Таким образом, длина активной части проводника будет линейно зависеть от времени в первые две секунды рассматриваемого промежутка времени. После этого, проводник полностью окажется в магнитном поле. Подставив данную функцию зависимости в выражение для индукционного тока, получим аналогичную функцию зависимости индукционного тока от времени. Индукционный ток в начальный момент времени равен Через 2 с индукционный ток Поскольку зависимость линейная, график представляет собой прямую, и двух точек достаточно для его построения.

 

Задача 4. Проводник длиной 40 см и сопротивлением 5 Ом помещён в магнитное поле с индукцией 50 мТл. Этот проводник подключают к источнику тока с внутренним сопротивлением 0,5 Ом. С какой скоростью нужно перемещать данный проводник перпендикулярно линиям магнитной индукции, чтобы в нём не протекал ток? Известно, что в состоянии покоя по проводнику течёт ток 0,8 А.

ДАНО:	СИ	РЕШЕНИЕ Полная ЭДС цепи определяется по формуле В цепи не будет существовать ток, если полная ЭДС цепи будет равна нулю (то есть, не будет совершаться работа по перемещению зарядов). Из этого можем заключить, что ЭДС индукции должна быть равна ЭДС источника с противоположным знаком (напомним, что отрицательная ЭДС означает, что данная ЭДС создаёт ток, направление которого противоположно направлению обхода тока). Запишем закон электромагнитной индукции Запишем закон Ома для полной цепи Тогда Выразим искомую скорость движения проводника

Ответ: 2200 м/с.

Задача 5. Проводник длиной 80 см падает в магнитном поле с индукцией 100 мТл, так, как показано на рисунке. Достигнув скорости 15 м/с, он больше не ускоряется. Если масса данного проводника равна 450 г, то каково его сопротивление?

ДАНО:	СИ	РЕШЕНИЕ Т.к. проводник движется с постоянной скоростью, то его ускорение равно нулю Запишем второй закон Ньютона Из второго закона Ньютона следует Силу Ампера можно определить по формуле Закон электромагнитной индукции имеет вид Индукционный ток В рассматриваемом случаи ток в проводнике – это индукционный ток Проверим размерности

Ответ: 20 мОм.

«ЭДС индукции в движущихся проводниках.» (11 класс)

Тема урока: ЭДС индукции в движущихся проводниках.

Тип урока: Комбинированный урок.

Цель урока: Дать понятие об энергетической характеристике индукционного электрического тока, возникающего в движущихся проводниках.

Демонстрации: Правила буравчика, правила левой руки, правила Ленца.

Используются технологии ИКТ для сопровождения изучения нового материала

Ход урока:

I. Организационный момент.

На сегодняшнем уроке мы продолжаем исследовать причины возникновения индукционного тока в замкнутом проводящем контуре. На прошлой неделе мы с вами установили тот факт, что индукционный ток в контуре возникает либо если контур покоится в переменном магнитном поле, либо если он движется в постоянном магнитном поле. Первое условие возникновения индукционного тока мы с вами уже рассмотрели, и теперь двигаемся дальше.

Тема сегодняшнего нашего урока » ЭДС индукции в движущихся проводниках».

Цель урока: познакомиться с понятием энергетической характеристики индукционного электрического тока, возникающего в движущихся проводниках.

II. Актуализация знаний.

К настоящему моменту мы с вами познакомились с рядом правил, которые используются для определения направления вектора магнитной индукции, индукционного тока, силы Ампера и Лоренца.

1. Правило буравчика.

2. Правило левой руки.

— Для движущегося участка проводника (формулировка и математическая запись закона Ампера)

— Для движущейся частицы (количественное определение силы Лоренца)

3. Правило Ленца (алгоритм применения правила к решению задач)

Все эти правила так или иначе связаны с явлением электромагнитной индукции.

— Когда и кем оно было открыто и в чем оно заключается?

(29 августа 1831 г., Майклом Фарадеем. Явление эл/м индукции заключается в возникновении электрического тока в проводящем контуре, который либо покоится в переменном магнитном поле, либо движется в постоянном магнитном поле таким образом, что число линий магнитной индукции, пронизывающих контур, меняется)

— Сформулируйте закон электромагнитной индукции.

(ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром )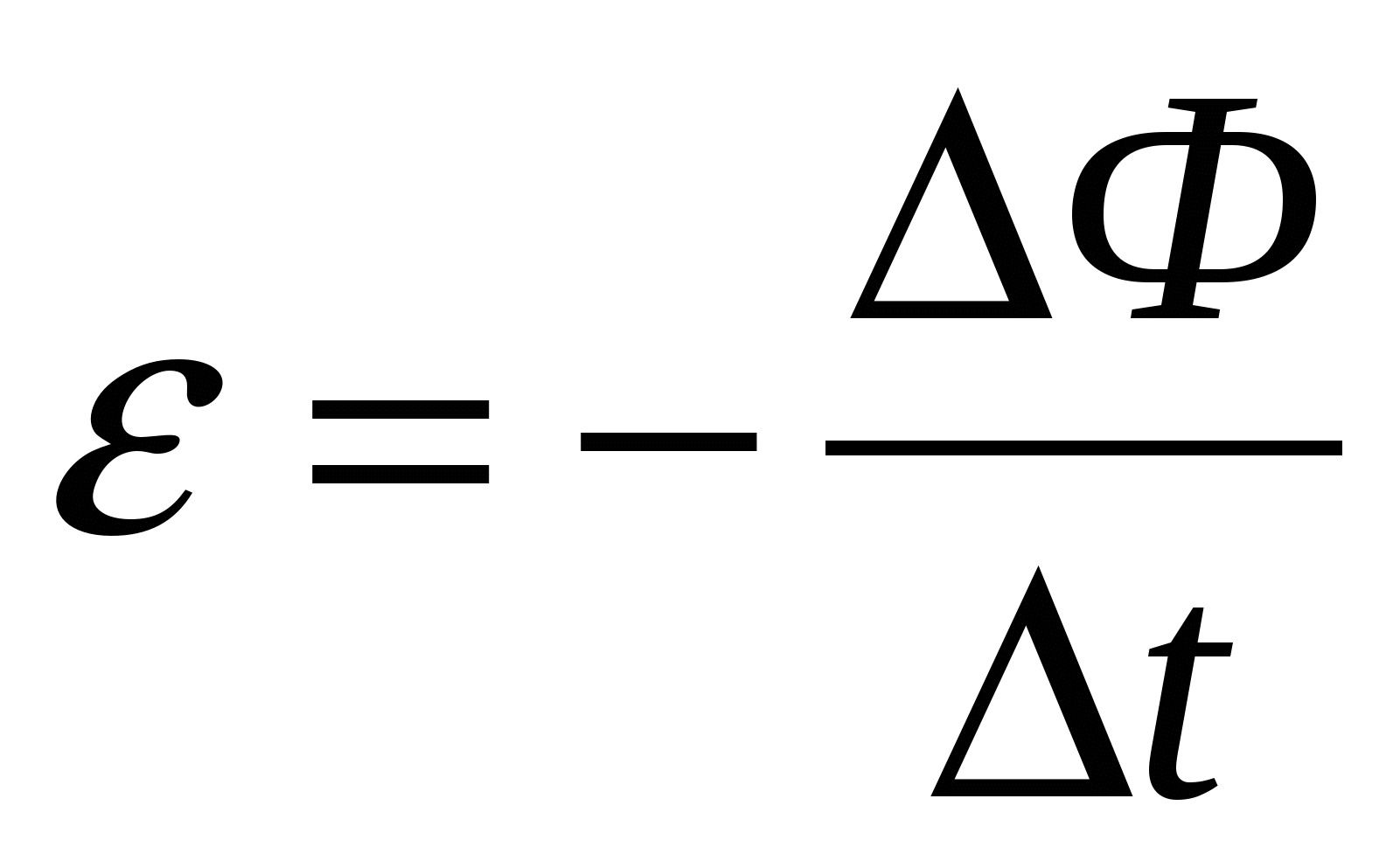

— Что является причиной возникновения индукционного тока в проводнике, покоящемся в переменном магнитном поле?

(Индукционный ток в неподвижном замкнутом контуре, находящемся в переменном магнитном поле, вызывается электрическим полем, порождаемым переменным магнитным полем, которое называется вихревым)

— Чему равна работа этого электрического поля?

(работа вихревого электрического поля при перемещении единичного положительного заряда вдоль замкнутого неподвижного проводника численно равна ЭДС индукции в этом проводнике)

III. Изучение нового материала.

1. Если проводник движется в постоянном магнитном поле, то ЭДС индукции в проводнике обусловлена не вихревым электрическим полем, которое в этом случае не может возникнуть, а другой причиной.

При движении проводника его свободные заряды движутся вместе с ним. Поэтому на них со стороны магнитного поля действует сила Лоренца. Она-то и вызывает перемещение зарядов внутри проводника. ЭДС индукции, следовательно, имеет магнитное происхождение.

Вычислим ЭДС индукции, возникающую в проводнике, движущемся в однородном магнитном поле.

Пусть сторона контура MN длиной l скользит с постоянной скоростью υ вдоль сторон NC и MD, оставаясь все время параллельной стороне CD. Вектор магнитной индукции 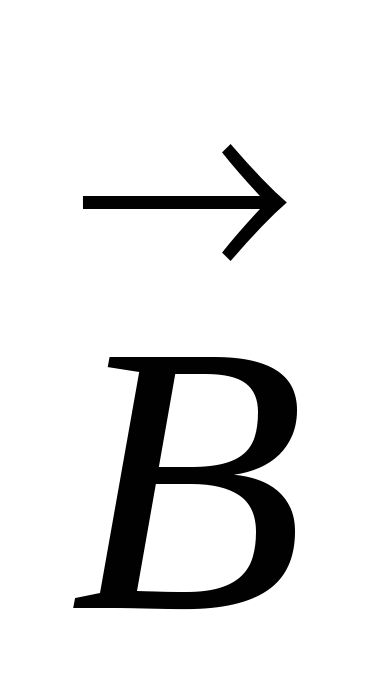однородного поля перпендикулярен проводнику и составляет угол α с направлением его скорости.

Сила, с которой магнитное поле действует на движущуюся заряженную частицу, равна по модулю .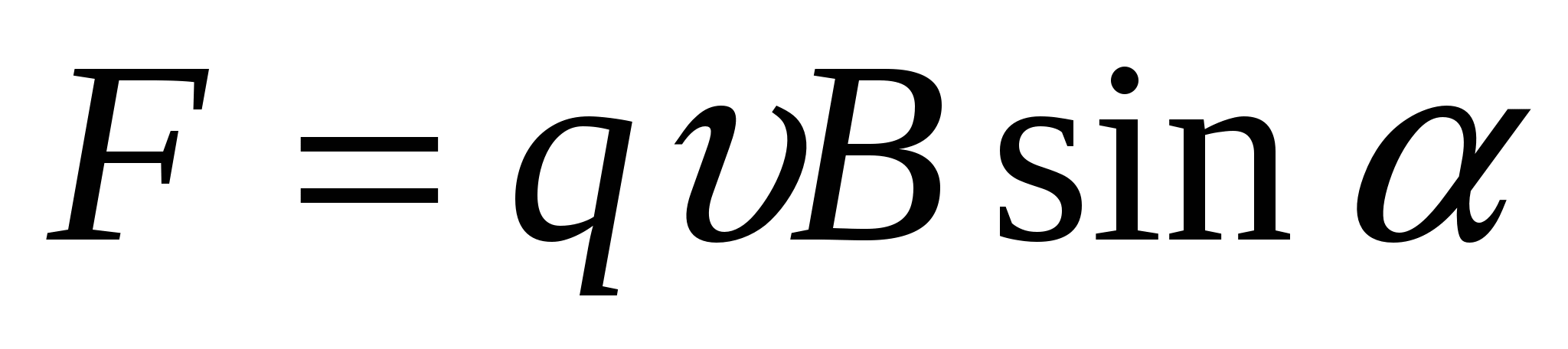

Направлена она вдоль проводника MN.

Работа данной силы на пути l положительна и равна .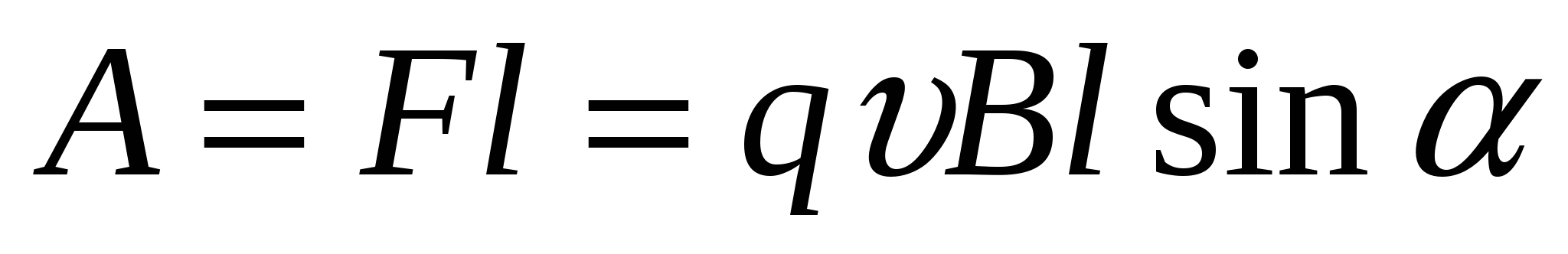

ЭДС индукции в проводнике MN равна по определению отношению работы по перемещению заряда q к этому заряду. .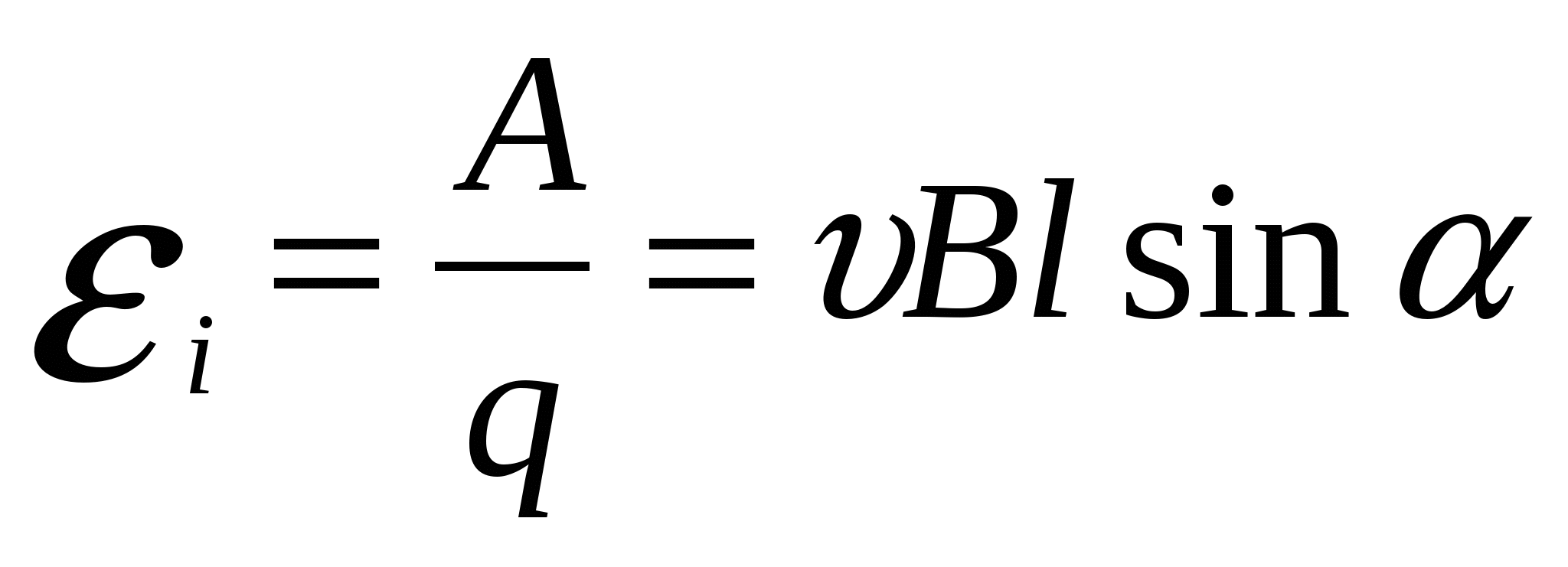

2. С другой стороны, ЭДС индукции можно вычислить с помощью закона эл/м индукции.

Магнитный поток через контур MNCD равен ,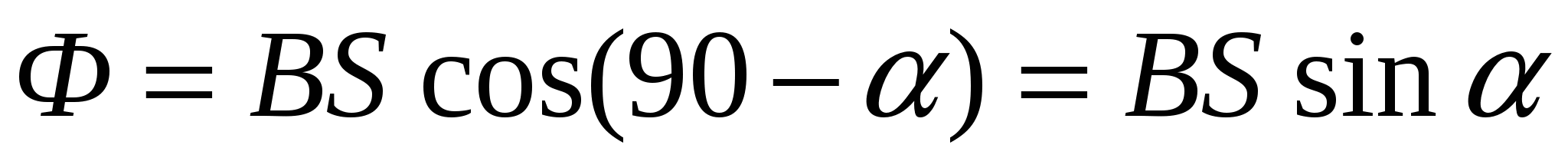

где угол 90°- есть угол между вектором 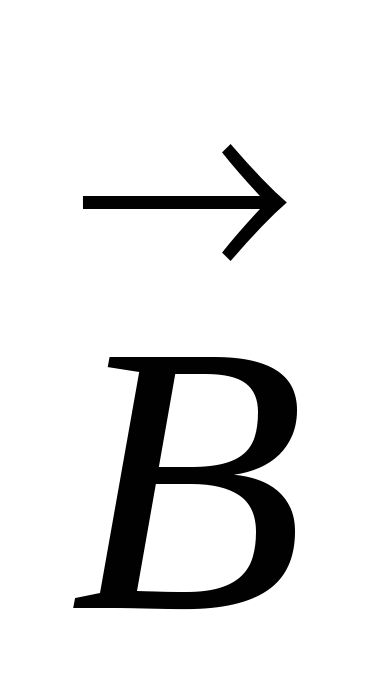и нормалью 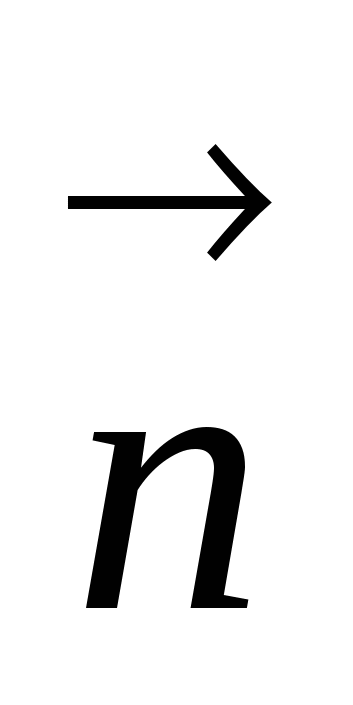к плоскости контура,

а S — площадь контура MNCD.

При перемещении проводника площадь S изменяется со временем следующим образом

За время площадь контура меняется на 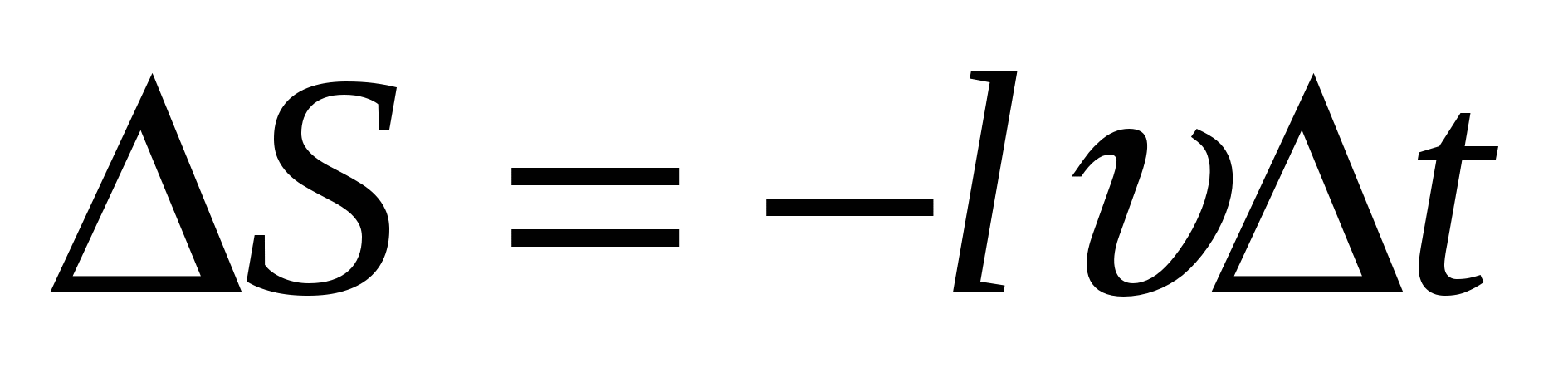. Знак минус указывает на то, что она уменьшается.

Изменение магнитного потока за это время равно .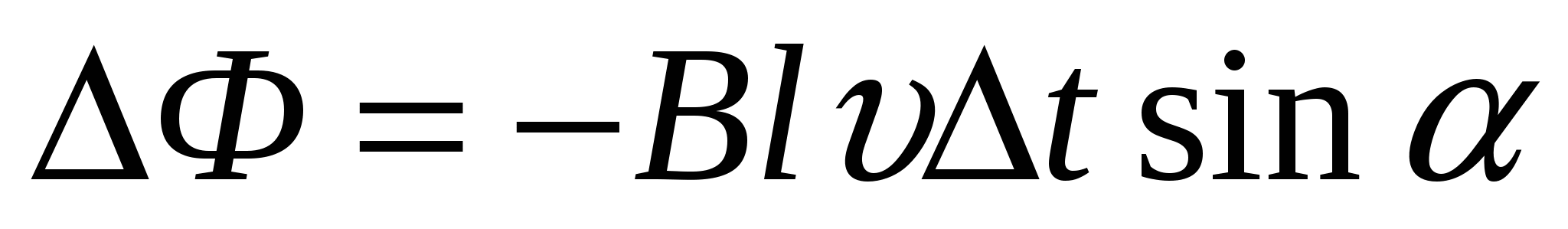

Следовательно, .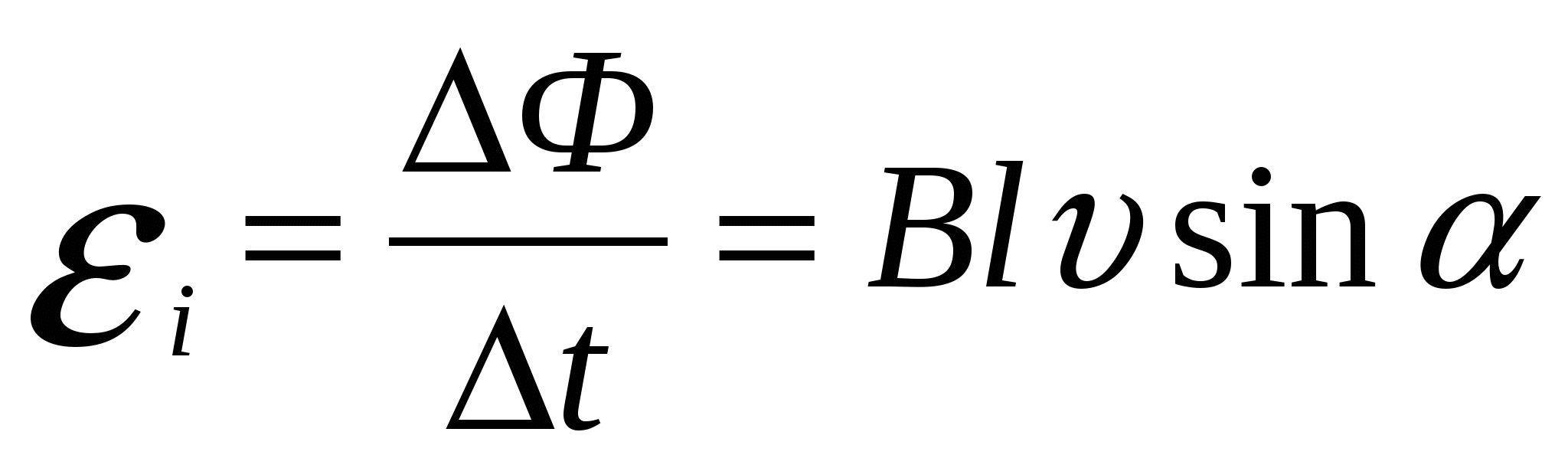

IV. Закрепление изученного.

Решение задач.

1. Найти ЭДС индукции в проводнике с длиной активной части 25 см, перемещающемся в однородном магнитном поле индукцией 8мТл со скоростью 5 м/с под углом 30° к вектору магнитной индукции. (0,005 В)

2. С какой скоростью надо перемещать проводник, длина активной части которого 1 м, под углом 60° к линиям индукции магнитного поля, чтобы в проводнике возбуждалась ЭДС индукции 1В? Индукция магнитного поля равна 0,2 Тл. (5,8 м/с)

V. Итог урока.

Итак, на сегодняшнем уроке мы с вами выяснили, что ЭДС индукции в проводниках, движущихся в постоянном магнитном поле, возникает за счет действия на свободные заряды проводника силы Лоренца.

Для количественного определения ЭДС нам необходимо знать индукцию постоянного магнитного поля, длину активной части проводника, скорость движения проводника в магнитном поле и угол между вектором магнитной индукции и вектором скорости движения.

VI. Домашнее задание.

§ 13, упр.2(9), №902(1,3)

ЭДС, возникающая в проводниках, движущихся в магнитном поле

⇐ ПредыдущаяСтр 3 из 5Следующая ⇒

ЭДС индукции возникает либо в неподвижном замкнутом проводнике, помещённом в изменяющееся во времени магнитное поле, либо в проводнике, движущемся в магнитном поле, которое может и не меняться со временем. ЭДС индукции в обоих случаях рассчитывается по формуле

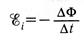
Сила Лоренца вызывает перемещение электронов в проводниках, движущихся в магнитном поле.

 

6. Вихревые поля

Причина возникновения электрического тока в неподвижном проводнике — электрическое поле.

Всякое изменение магнитного поля порождает индукционное электрическое поле независимо от наличия или отсутствия замкнутого контура, при этом если проводник разомкнут, то на его концах возникает разность потенциалов; если проводник замкнут, то в нем наблюдается индукционный ток.

Индукционное электрическое поле является вихревым.

Направление силовых линий вихревого эл. поля совпадает с направлением индукционного тока

Индукционное электрическое поле имеет совершенно другие свойства в отличии от электростатического поля.

Вихревое электрическое поле возникает в случае изменения ектора магнитной индукции внешнего поля.

 

Связь электрического и магнитного полей

Магнитное поле способно в определенных условиях порождать электрическое без помощи зарядов, а электрическое — непосредственно порождать магнитное. Именно так: магнитное поле рождает только электрическое, а электрическое — только магнитное, которое, правда, в свою очередь может породить электрическое.

 

Самоиндукция

Самоиндукция — явление возникновения ЭДС индукции в эл.цепи в результате изменения силы тока.

Возникающая при этом ЭДС называется ЭДС самоиндукции

Если ток в рассматриваемом контуре по каким-то причинам изменяется, то изменяется и магнитное поле этого тока, а, следовательно, и собственный магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока в контуре. Данное явление называется самоиндукцией, а соответствующее значение — ЭДС самоиндукции.

ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в ней

 

Индуктивность

Индуктивностью (от латинского inductio — наведение, побуждение), называется величина, характеризующая связь между изменением тока в электрической цепи и возникающей при этом ЭДС (электродвижущей силы) самоиндукции. Индуктивность обозначается большой латинской буквой «L», в честь немецкого физика Ленца. Термин индуктивности предложил в 1886 году Оливер Хевисайд.,

 

Величина магнитного потока, проходящего через контур, связана с силой тока следующим образом: Φ = LI. Коэффициент пропорциональности L называется коэффициентом самоиндукции контура или просто индуктивностью. Значение индуктивности зависит от размеров и формы контура, а также от магнитной проницаемости среды. Единицей измерения индуктивности является Генри (Гн). Дополнительные величины: мГн, мкГн.

 

Зная индуктивность, изменение силы тока и время этого изменения, можно найти ЭДС самоиндукции, которая возникает в контуре:

Через индуктивность выражают также энергию магнитного поля тока:

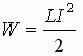
Соответственно чем больше индукция, тем больше магнитная энергия, накапливаемая в пространстве вокруг контура с током. Индуктивность является своеобразным аналогом кинетической энергии в электричестве.

 

7. Индуктивность соленоида.

L — Индуктивность (соленоида), размерность в CИ Гн

L — Длина (соленоида), размерность в СИ — м

N — Число (витков соленоида

V- Объём (соленоида), размерность в СИ — м3

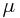— Относительная магнитная проницаемость

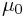— Магнитная постоянная 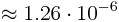Гн/м

 

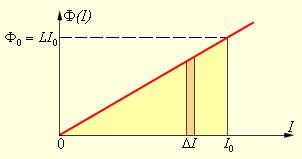Энергия магнитного поля соленоида

Энергия Wм магнитного поля катушки с индуктивностью L, создаваемого током I, равна

Применим полученное выражение для энергии катушки к длинному соленоиду с магнитным сердечником. Используя приведенные выше формулы для коэффициента самоиндукции Lμ соленоида и для магнитного поля B, создаваемого током I, можно получить: