Явление самоиндукции.Индуктивность. Энергия магнитного поля тока. Работа поля. Тесты, курсы по физике

Тестирование онлайн

• Явление самоиндукции. Индуктивность. Основные понятия

• Явление самоиндукции. Энергия магнитного поля

Явление самоиндукции

Мы уже изучили, что около проводника с током возникает магнитное поле. А также изучили, что переменное магнитное поле порождает ток (явление электромагнитной индукции). Рассмотрим электрическую цепь. При изменении силы тока в этой цепи произойдет изменение магнитного поля, в результате чего в этой же цепи возникнет дополнительный индукционный ток. Такое явление называется самоиндукцией, а ток, возникающий при этом, называется током самоиндукции.

Явление самоиндукции — это возникновение в проводящем контуре ЭДС, создаваемой вследствие изменения силы тока в самом контуре.

Индуктивность контура зависит от его формы и размеров, от магнитных свойств окружающей среды и не зависит от силы тока в контуре.

ЭДС самоиндукции определяется по формуле:

Явление самоиндукции подобно явлению инерции. Так же, как в механике нельзя мгновенно остановить движущееся тело, так и ток не может мгновенно приобрести определенное значение за счет явления самоиндукции. Если в цепь, состоящую из двух параллельно подключенных к источнику тока одинаковых ламп, последовательно со второй лампой включить катушку, то при замыкании цепи первая лампа загорается практически сразу, а вторая с заметным запаздыванием.

При размыкании цепи сила тока быстро уменьшается, и возникающая ЭДС самоиндукции препятствует уменьшению магнитного потока. При этом индуцированный ток направлен так же, как и исходный. ЭДС самоиндукции может во многом раз превысить внешнюю ЭДС. Поэтому электрические лампочки очень часто перегорают при выключении света.

Энергия магнитного поля

Энергия магнитного поля контура с током:

Индукция и индуктивность в чем разница

Когда возникает индукция? Как проходит?

Когда возникает самоиндукция?

Означает ли наличие одной из них, наличие и второй тоже или могут быть в отдельности?

Индукция – это когда изменение внешнего магнитного поля вызывает появление в замкнутом контуре эдс (закон электромагнитной индукции Фарадея).

Самоиндукция – это когда магнитное поле создаётся самим контуром, и появление эдс вызывается изменением этого собственного поля (вызванное изменением, например, тока в этом контуре). Явление самоиндукции открыто Дж. Генри.

При постоянном токе напряжение на (идеальной) катушке индуктивности равно нулю. Такая катушка представляет собой просто кусок провода. Но попытка изменить ток приводит к изменению создаваемого катушкой магнитного поля, а уж изменяющееся магнитное поле наводит эдс по фигу в чём. Вот что попало в область изменяющегося поля (в частности и сама эта катушка) – в том и наводит.

Напряжение самоиндукции определяется формулой e = L*dI/dt, где L – индуктивность контура.

Хотя индукция и самоиндукция связаны по своей физической природе (обе есть результат изменения магнитного поля), они могут существовать и по отдельности. В частности, если магнитное поле создаётся внешним источником – да хоть постоянным магнитом, движущимся относительно контура, то эдс индукции возникает, а вот самоиндукция – не обязательно. Верно и обратное. Если нет ещё одного контура, кроме того, который создаёт изменяющееся поле и в котором, стало быть, возникает самоиндукция, то и явления индукции нету.

По сути явление самоиндукции – это частный случай явления электромагнитной индукции.

Электромагнитная индукция наблюдается при любом изменение магнитного потока через замкнутый проводящий контур (рамку, катушку) и проявляется в том, что возникает индукционный ток в этом контуре.

Например, при введении постоянного магнита или катушки с током в контур или его удаления, при приближении магнита или катушки с током, при включении и выключении тока в катушке, при изменении тока реостатом. Или все то же самое, но уже движется сам контур. Обычно все эти примеры называют примерами явления электромагнитной индукции, то есть изменение магнитного потока связана с изменением внешнего магнитного поля, созданного другим объектом.

Явление электромагнитной индукции, которое происходит в одном и том же замкнутом контуре (катушке) называется самоиндукцией. Оно проявляется в том, что изменение тока в контуре (магнитного потока) замедляется (происходит с запаздыванием). Объясняется это тем, что индукционный ток возникает в том же проводнике, что и переменный ток, вызвавший его. Он всегда направлен так, что препятствует изменению магнитного потока: если ток увеличивается, то индукционный ток направлен против, если ток уменьшается, то ток направлен в ту же сторону (правило Ленца). В этом и состоит отличие в деталях, а по сути это одно и то же.

Приветствую всех на нашем сайте!

Мы продолжаем изучать электронику с самого начала, то есть с самых основ и темой сегодняшней статьи будет принцип работы и основные характеристики катушек индуктивности. Забегая вперед скажу, что сначала мы обсудим теоретические аспекты, а несколько будущих статей посвятим целиком и полностью рассмотрению различных электрических схем, в которых используются катушки индуктивности, а также элементы, которые мы изучили ранее в рамках нашего курса – резисторы и конденсаторы.

Устройство и принцип работы катушки индуктивности.

Как уже понятно из названия элемента – катушка индуктивности, в первую очередь, представляет из себя именно катушку :), то есть большое количество витков изолированного проводника. Причем наличие изоляции является важнейшим условием – витки катушки не должны замыкаться друг с другом. Чаще всего витки наматываются на цилиндрический или тороидальный каркас:

Важнейшей характеристикой катушки индуктивности является, естественно, индуктивность, иначе зачем бы ей дали такое название 🙂 Индуктивность – это способность преобразовывать энергию электрического поля в энергию магнитного поля. Это свойство катушки связано с тем, что при протекании по проводнику тока вокруг него возникает магнитное поле:

А вот как выглядит магнитное поле, возникающее при прохождении тока через катушку:

В общем то, строго говоря, любой элемент в электрической цепи имеет индуктивность, даже обычный кусок провода. Но дело в том, что величина такой индуктивности является очень незначительной, в отличие от индуктивности катушек. Собственно, для того, чтобы охарактеризовать эту величину используется единица измерения Генри (Гн). 1 Генри – это на самом деле очень большая величина, поэтому чаще всего используются мкГн (микрогенри) и мГн (милигенри). Величину индуктивности катушки можно рассчитать по следующей формуле:

Давайте разберемся, что за величину входят в это выражение:

Из формулы следует, что при увеличении числа витков или, к примеру, диаметра (а соответственно и площади поперечного сечения) катушки, индуктивность будет увеличиваться. А при увеличении длины – уменьшаться. Таким образом, витки на катушке стоит располагать как можно ближе друг к другу, поскольку это приведет к уменьшению длины катушки.

С устройством катушки индуктивности мы разобрались, пришло время рассмотреть физические процессы, которые протекают в этом элементе при прохождении электрического тока. Для этого мы рассмотрим две схемы – в одной будем пропускать через катушку постоянный ток, а в другой -переменный 🙂

Катушка индуктивности в цепи постоянного тока.

Итак, в первую очередь, давайте разберемся, что же происходит в самой катушке при протекании тока. Если ток не изменяет своей величины, то катушка не оказывает на него никакого влияния. Значит ли это, что в случае постоянного тока использование катушек индуктивности и рассматривать не стоит? А вот и нет 🙂 Ведь постоянный ток можно включать/выключать, и как раз в моменты переключения и происходит все самое интересное. Давайте рассмотрим цепь:

Резистор выполняет в данном случае роль нагрузки, на его месте могла бы быть, к примеру, лампа. Помимо резистора и индуктивности в цепь включены источник постоянного тока и переключатель, с помощью которого мы будем замыкать и размыкать цепь.

Что же произойдет в тот момент когда мы замкнем выключатель?

Ток через катушку начнет изменяться, поскольку в предыдущий момент времени он был равен 0. Изменение тока приведет к изменению магнитного потока внутри катушки, что, в свою очередь, вызовет возникновение ЭДС (электродвижущей силы) самоиндукции, которую можно выразить следующим образом:

Возникновение ЭДС приведет к появлению индукционного тока в катушке, который будет протекать в направлении, противоположном направлению тока источника питания. Таким образом, ЭДС самоиндукции будет препятствовать протеканию тока через катушку (индукционный ток будет компенсировать ток цепи из-за того, что их направления противоположны). А это значит, что в начальный момент времени (непосредственно после замыкания выключателя) ток через катушку будет равен 0. В этот момент времени ЭДС самоиндукции максимальна. А что же произойдет дальше? Поскольку величина ЭДС прямо пропорциональна скорости изменения тока, то она будет постепенно ослабевать, а ток, соответственно, наоборот будет возрастать. Давайте посмотрим на графики, иллюстрирующие то, что мы обсудили:

На первом графике мы видим входное напряжение цепи – изначально цепь разомкнута, а при замыкании переключателя появляется постоянное значение. На втором графике мы видим изменение величины тока через катушку индуктивности. Непосредственно после замыкания ключа ток отсутствует из-за возникновения ЭДС самоиндукции, а затем начинает плавно возрастать. Напряжения на катушке наоборот в начальный момент времени максимально, а затем уменьшается. График напряжения на нагрузке будет по форме (но не по величине) совпадать с графиком тока через катушку (поскольку при последовательном соединении ток, протекающий через разные элементы цепи одинаковый). Таким образом, если в качестве нагрузки мы будем использовать лампу, то они загорится не сразу после замыкания переключателя, а с небольшой задержкой (в соответствии с графиком тока).

Аналогичный переходный процесс в цепи будет наблюдаться и при размыкании ключа. В катушке индуктивности возникнет ЭДС самоиндукции, но индукционный ток в случае размыкания будет направлен в том же самом направлении, что и ток в цепи, а не в противоположном, поэтому запасенная энергия катушки индуктивности пойдет на поддержание тока в цепи:

После размыкания ключа возникает ЭДС самоиндукции, которая препятствует уменьшению тока через катушку, поэтому ток достигает нулевого значения не сразу, а по истечении некоторого времени. Напряжение же в катушке по форме идентично случаю замыкания переключателя, но противоположно по знаку. Это связано с тем, что изменение тока, а соответственно и ЭДС самоиндукции в первом и втором случаях противоположны по знаку (в первом случае ток возрастает, а во втором убывает).

Кстати, я упомянул, что величина ЭДС самоиндукции прямо пропорциональна скорости изменения силы тока, так вот, коэффициентом пропорциональности является ни что иное как индуктивность катушки:

На этом мы заканчиваем с катушками индуктивности в цепях постоянного тока и переходим к цепям переменного тока.

Катушка индуктивности в цепи переменного тока.

Рассмотрим цепь, в которой на катушку индуктивности подается переменный ток:

Давайте посмотрим на зависимости тока и ЭДС самоиндукции от времени, а затем уже разберемся, почему они выглядят именно так:

Как мы уже выяснили ЭДС самоиндукции у нас прямо пропорциональна и противоположна по знаку скорости изменения тока:

Собственно, график нам и демонстрирует эту зависимость 🙂 Смотрите сами – между точками 1 и 2 ток у нас изменяется, причем чем ближе к точке 2, тем изменения меньше, а в точке 2 в течении какого-то небольшого промежутка времени ток и вовсе не изменяет своего значения. Соответственно скорость изменения тока максимальна в точке 1 и плавно уменьшается при приближении к точке 2, а в точке 2 равна 0, что мы и видим на графике ЭДС самоиндукции. Причем на всем промежутке 1-2 ток возрастает, а значит скорость его изменения положительна, в связи с этим на ЭДС на всем этом промежутке напротив принимает отрицательные значения.

Аналогично между точками 2 и 3 – ток уменьшается – скорость изменения тока отрицательная и увеличивается – ЭДС самоиндукции увеличивается и положительна. Не буду расписывать остальные участки графика – там все процессы протекают по такому же принципу 🙂

Кроме того, на графике можно заметить очень важный момент – при увеличении тока (участки 1-2 и 3-4) ЭДС самоиндукции и ток имеют разные знаки (участок 1-2: , 0″ title=»Rendered by QuickLaTeX.com» w />, участок 3-4: 0″ title=»Rendered by QuickLaTeX.com» w />, ). Таким образом, ЭДС самоиндукции препятствует возрастанию тока (индукционные токи направлены “навстречу” току источника). А на участках 2-3 и 4-5 все наоборот – ток убывает, а ЭДС препятствует убыванию тока (поскольку индукционные токи будут направлены в ту же сторону, что и ток источника и будут частично компенсировать уменьшение тока). И в итоге мы приходим к очень интересному факту – катушка индуктивности оказывает сопротивление переменному току, протекающему по цепи. А значит она имеет сопротивление, которое называется индуктивным или реактивным и вычисляется следующим образом:

Где – круговая частота: . – это частота переменного тока.

Таким образом, чем больше частота тока, тем большее сопротивление будет ему оказывать катушка индуктивности. А если ток постоянный ( = 0), то реактивное сопротивление катушки равно 0, соответственно, она не оказывает влияния на протекающий ток.

Давайте вернемся к нашим графикам, которые мы построили для случая использования катушки индуктивности в цепи переменного тока. Мы определили ЭДС самоиндукции катушки, но каким же будет напряжение ? Здесь все на самом деле просто 🙂 По 2-му закону Кирхгофа:

Построим на одном графике зависимости тока и напряжения в цепи от времени:

Как видите ток и напряжение сдвинуты по фазе (ссылка) друг относительно друга, и это является одним из важнейших свойств цепей переменного тока, в которых используется катушка индуктивности:

При включении катушки индуктивности в цепь переменного тока в цепи появляется сдвиг фаз между напряжением и током, при этом ток отстает по фазе от напряжения на четверть периода.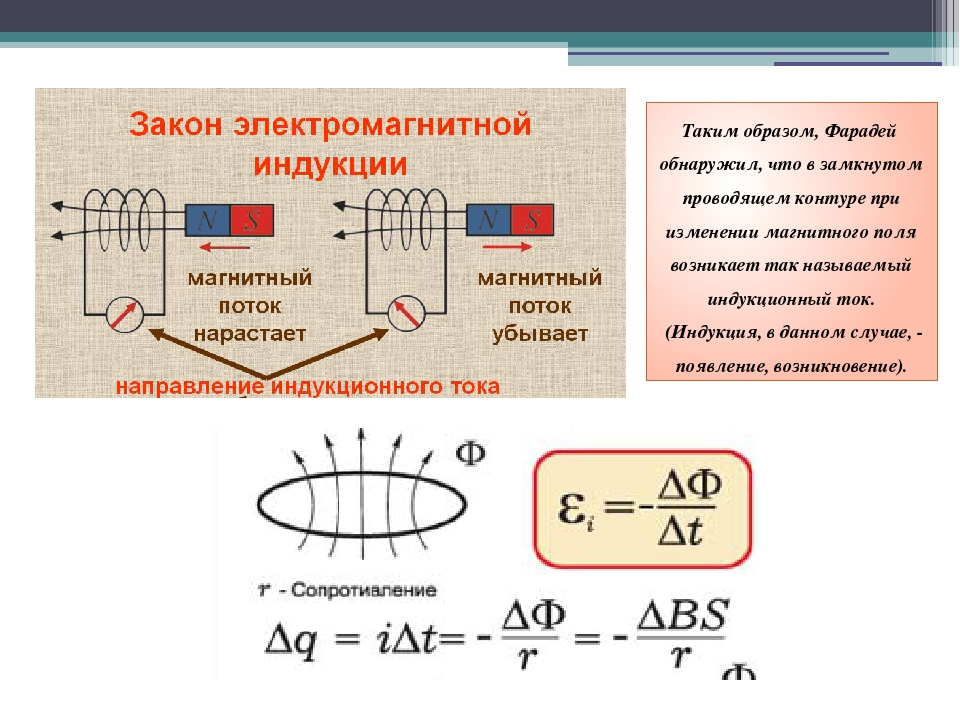

Вот и с включением катушки в цепь переменного тока мы разобрались 🙂

На этом, пожалуй, закончим сегодняшнюю статью, она получилась уже довольно объемной, поэтому дальнейший разговор о катушках индуктивности мы будем вести в следующий раз. Так что до скорых встреч, будем рады видеть вас на нашем сайте!

Чтобы задать вопрос учителю, оплатите абонемент

У вас уже есть абонемент? Войти

Волнует то, что половина формул в курсе просто взята из воздуха и никак не объясняется. Например формула для магнитной индукции с коэффициентом мю. Откуда взялся этот коэффициент? Почему 2пr в знаменателе? Почему в формуле магнитного потока не учитывается угол между нормалью к поверхности и вектором магнитной индукции? Или он по стандарту здесь считается равным нулю но нам об этом не сказали? И вообще о какой поверхности мы говорим? И так весь курс. Недосказанностей больше, чем информации. В итоге, чтобы хоть как-то решать задачи приходится просто заучивать непонятные наборы констант и переменных совсем не понимая, что за ними скрывается.

а в чом разница между самоиндукция и просто индукция

Ответ кроется в названии. Индукция в целом – возникновение электрического тока в проводнике под действием магнитного поля (изменение потока магнитного поля). А самоиндукция – вид индукции, когда действие оказывает магнитное поле созданное самим проводником.

Я правильно понял? что лампочка загорается медлинее потому что едет сопративление

Действительно, лампочка загорается медленнее, поскольку при изменении силы тока в катушке возникает так называемое «реактивное сопротивление». Но по своей природе оно отличается от сопротивления, которое присутствует в проводниках, ведь сопротивление проводников связано со столкновениями электронов с узлами кристаллической решетки. Что же касается реактивного сопротивления, то оно не изучается подробно в школьном курсе. Поэтому самоиндукцию проще представить следующим образом: при увеличении тока (замкнули цепь) в катушке возникает еще один ток, направленный в другую сторону. Таким образом, суммарный ток будет меньше. Соответственно, лампочка загорается дольше.

Вопрос, всё понятно со скоростью накала лампочек, но почему одна из них горит слабже другой?

Опыт демонстрируется в течение небольшого времени. Лампочка еще не успевает загореться. Если проводить опыт более длительное время, то накал лампочек станет практически одинаковым.

а как найти самоиндукционный ток, возникающий в катушке?

Для определения тока самоиндукции необходимо воспользоваться законом Ома и разделить ЭДС самоиндукции на сопротивление контура (катушки)

Если катушка намотана против часовой стрелки, то будет замедление, а если же я наматаю катушку по часовой стрелке?? Будет ли ускоренное зажигание лампочки??

Явление самоиндукции — определение, формулы, примеры

Магнитный поток

Прежде чем говорить об электромагнитной индукции и самоиндукции, нам нужно определить сущность магнитного потока.

Представьте, что вы взяли в руки обруч и вышли на улицу в ливень. Потоки воды будут проходить через обруч.

Если держать обруч горизонтально, то через него пройдет много воды. А если начать его поворачивать — уже меньше, потому что он расположен не под прямым углом к вертикали.

Теперь давайте поставим обруч вертикально — ни одной капли не пройдет сквозь него (если ветер не подует, конечно).

Магнитный поток очень похож на поток воды, проходящей через обруч, только считаем мы величину прошедшего через площадь магнитного поля, а не дождя.

Магнитным потоком через площадь ​S​ контура называют скалярную физическую величину, равную произведению:

• модуля вектора магнитной индукции ​B​,
• площади поверхности ​S​, которую пронизывает поток,
• и косинуса угла ​α​ между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности).

Магнитный поток Ф — магнитный поток [Вб] B — магнитная индукция [Тл] S — площадь пронизываемой поверхности [м2] n — вектор нормали (перпендикуляр к поверхности) [-]

Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.

В зависимости от угла ​α магнитный поток может быть положительным (α < 90°) или отрицательным (α > 90°). Если α = 90°, то магнитный поток равен 0.

Изменить магнитный поток можно, меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).

В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.

Электромагнитная индукция

Электромагнитная индукция — явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции открыл Майкл Фарадей в ходе серии опытов.

Опыт раз. На одну непроводящую основу намотали две катушки таким образом, что витки одной катушки были расположены между витками второй. Витки первой катушки были замкнуты на гальванометр, а второй — подключены к источнику тока.

При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.

Опыт два. Первую катушку подключили к источнику тока, а вторую — к гальванометру. При этом вторая катушка перемещалась относительно первой. При приближении или удалении катушки фиксировался ток.

Опыт три. Катушку замкнули на гальванометр, а магнит передвигали относительно катушки.

Вот что показали эти опыты:

1. Индукционный ток возникает только при изменении линий магнитной индукции.


2. Направление тока различается при увеличении числа линий и при их уменьшении.


3. Сила индукционного тока зависит от скорости изменения магнитного потока. При этом как само поле может изменяться, так и контур может перемещаться в неоднородном магнитном поле.

Почему возникает индукционный ток?

Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна электродвижущей силе (ЭДС).

Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.

Самоиндукция

Представим себе любую электрическую цепь, параметры которой можно менять. Если мы изменим силу тока в этой цепи — например, подкрутим реостат или подключим другой источник тока — произойдет изменение магнитного поля. В результате этого изменения в цепи возникнет дополнительный индукционный ток за счет электромагнитной индукции, о которой мы говорили выше. Такое явление называется самоиндукцией, а возникающий при этом ток — током самоиндукции.

Формула магнитного потока для самоиндукции Ф = LI Ф — собственный магнитный поток [Вб] L — индуктивность контура [Гн] I — сила тока в контуре [А]

Самоиндукция — это возникновение в проводящем контуре ЭДС, создаваемой вследствие изменения силы тока в самом контуре.

Самоиндукция чем-то напоминает инерцию: как в механике нельзя мгновенно остановить движущееся тело, так и ток не может мгновенно приобрести определенное значение за счет самоиндукции.

Представим цепь, состоящую из двух одинаковых ламп, параллельно подключенных к источнику тока. Если мы последовательно со второй лампой включим в эту цепь катушку, то при замыкании цепи произойдет следующее:

• первая лампа загорится практически сразу,
• вторая лампа загорится с заметным запаздыванием.

При размыкании цепи сила тока быстро уменьшается, и возникающая ЭДС самоиндукции препятствует уменьшению магнитного потока. При этом индуцированный ток направлен так же, как и исходный. ЭДС самоиндукции может во многом раз превысить внешнюю ЭДС. Поэтому электрические лампочки так часто перегорают при отключении света.

ЭДС самоиндукции ξis — ЭДС самоиндукции [В] ΔФ/Δt — скорость изменения магнитного потока [Вб/с] ΔI/Δt — скорость изменения силы тока в контуре [А/с] L — индуктивность [Гн]

Знак минуса в формуле закона электромагнитной индукции указывает на то, что ЭДС индукции препятствует изменению магнитного потока, который вызывает ЭДС.

При решении расчетных задач знак минуса не учитывается.

Индуктивность

Индуктивность — это способность накапливать магнитное поле. Она характеризует способность проводника сопротивляться электрическому току. Проще всего это делать с помощью катушки, потому что катушка состоит из витков, которые представляют собой контуры. Вспомните про магнитный поток и обруч под дождем — в контуре создается магнитный поток. Где поток, там и электромагнитная индукция.

Индуктивность контура зависит от его формы и размеров, от магнитных свойств окружающей среды и не зависит от силы тока в контуре.

Можно ли увеличивать индуктивность катушки?

Конечно! Можно увеличить число витков, например. Или поместить в центр катушки железный сердечник.

Как работает катушка

Вокруг каждого проводника, по которому протекает ток, образуется магнитное поле. Если поместить проводник в переменное поле — в нем возникнет ток.

Магнитные поля каждого витка катушки складываются. Поэтому вокруг катушки, по которой протекает ток, возникает сильное магнитное поле. При изменении силы тока в катушке будет изменяться и магнитный поток вокруг нее.

Задачка раз

На рисунке приведен график зависимости силы тока от времени в электрической цепи, индуктивность которой 1 мГн. Определите модуль ЭДС самоиндукции в интервале времени от 15 до 20 с. Ответ выразите в мкВ.

Решение

За время от 15 до 20 с сила тока изменилась от 20 до 0 мА. Модуль ЭДС самоиндукции равен:

Ответ: модуль ЭДС самоиндукции с 15 до 20 секунд равен 4 мкВ.

Задачка два

По проволочной катушке протекает постоянный электрический ток силой 2 А. При этом поток вектора магнитной индукции через контур, ограниченный витками катушки, равен 4 мВб. Электрический ток какой силы должен протекать по катушке для того, чтобы поток вектора магнитной индукции через указанный контур был равен 6 мВб?

Решение

При протекании тока через катушку индуктивности возникает магнитный поток, численно равный Ф = LI.

Отсюда индуктивность катушки равна:

Тогда для достижения значений потока вектора магнитной индукции в 6 мВб ток будет равен:

Ответ: для достижения значений потока вектора магнитной индукции в 6 мВб необходим ток в 3 А.

Электричество и магнетизм

Рассмотрим снова контур с током, но не станем его помещать на этот раз во внешнее магнитное поле. Ток сам создает свое собственное поле В, которое пронизывает контур. Это поле, как следует из закона Био — Савара — Лапласа, пропорционально силе тока

Собственное магнитное поле контура с током обуславливает наличие магнитного потока Y через поверхность, опирающуюся на этот контур, который также будет пропорционален силе тока в контуре

Введем коэффициент пропорциональности L

(8.16)

Коэффициент пропорциональности L называется индуктивностью контура. 

Индуктивность контурачисленно равна магнитному потоку, собственного магнитного поля через поверхность, опирающуюся на контур, при условии протекания в контуре единичного тока.

 

Индуктивность контура определяется формой и размерами контура, а также свойствами окружающей среды.  

В системе СИ единицей измерения индуктивности является генри (Гн)

Если в проводящем контуре протекает переменный электрический ток, то магнитное поле этого тока также меняется с течением времени. Собственный магнитный поток, создаваемый этим полем, также является переменным. Изменение магнитного потока влечет за собой возникновение ЭДС электромагнитной индукции. 

Явление возникновения ЭДС индукции в замкнутом проводящем контуре вследствие изменения тока, текущего в этом контуре, называется явлением самоиндукции.

 

Видео 8.13.  Закон Фарадея. Явление самоиндукции.

Возникающая при этом ЭДС называется ЭДС самоиндукции. Явление самоиндукции является частным случаем электромагнитной индукции.

Явление самоиндукции является, в частности, причиной явления, которое называют «экстра токи замыкания и размыкания». Оно состоит в следующем. Собственное магнитное поле в цепи постоянного тока изменяется в моменты замыкания или размыкания цепи. Это означает, что в такие моменты в цепи должна возникать ЭДС самоиндукции. Направление токов самоиндукции следует из правила Ленца. При замыкании цепи ЭДС самоиндукции вызывает ток, препятствующий увеличению основного тока в цепи, что делает конечной скорость роста силы тока, а при размыкании ток самоиндукции, препятствуя его уменьшению, делает конечной скорость убывания тока. Если бы не ЭДС самоиндукции, то при замыкании цепи ток мгновенно нарастал бы до своего стационарного значения, а при размыкании цепи, мгновенно убывал бы до нуля.  

Выведем формулу для ЭДС самоиндукции . Для этого надо продифференцировать полный магнитный поток, охватываемый проводящим контуром, по времени

(8.17)

Если контур не меняет свою форму, и рядом с контуром нет ферромагнетиков, то его индуктивность от времени не зависит. Однако, даже при неизменной форме контура, при наличии ферромагнетиков, например, ферромагнитного сердечника, индуктивность контура зависит от силы тока в нём и, тем самым, от времени, если ток переменный. Таким образом, в присутствии ферромагнетиков

,

что необходимо учитывать при дифференцировании

Подставляя это выражение в (8.17), получаем для неподвижного контура всреде

(8.18)

 

Если же индуктивность контура не зависит от силы тока в нём, то имеем

(8.19)

Мы приходим к закону самоиндукции. В этом простейшем случае: 

В отсутствие ферромагнетиков ЭДС самоиндукции в цепи прямопропорциональна скорости изменения силы тока в этой цепи.

Будем считать катушку длинной, а магнитное поле внутри нее — однородным. Пропустим через соленоид ток I. Тогда магнитная индукциявнутри соленоида равна, как мы знаем (см. (6.20)), равна

где — магнитная проницаемость сердечника, a n — число витков на единицу длины. Полное число витков в катушке равно , где l — ее длина. Пусть S — площадь поперечного сечения соленоида. Полный магнитный поток (потокосцепление) определяется как

(8.20)

где V — объем соленоида: V = Sl. Согласно определению индуктивности как коэффициента пропорциональности между  и I, получаем величину индуктивности длинного соленоида (рис. 8.31)

(8.21)

 

Рис. 8.31. Индуктивность соленоида 

При замыкании или размыкании цепи (то есть в случаях, когда ток в цепи меняется по величине) в ней вследствие явления самоиндукции возникают дополнительные токи, которые по правилу Ленца всегда направлены так, чтобы воспрепятствовать причине их вызывающей, то есть чтобы воспрепятствовать нарастанию или убыванию тока в цепи. Следовательно, как уже было сказано,при замыкании цепи ЭДС самоиндукции будет замедлять скорость нарастания тока, а при размыкании, напротив, замедлять скорость уменьшения тока в ней.

Самоиндукция простыми словами: определение, формулы, примеры

Явление электромагнитной индукции очень часто наблюдается в электротехнике. Взаимное влияние электрических и магнитных полей иногда приводит к интересным результатам. Самоиндукция – частный случай электромагнитной индукции.

Общеизвестно, что причиной порождения электрического тока является переменное магнитное поле. Именно этот принцип реализован в конструкциях современных генераторов. Природа самоиндукции также связана с электромагнетизмом, но это явление проявляется она по-другому.

Определение

Рассмотрим схему катушки, по обмоткам которой протекает электрический ток (рис. 1). Так как вокруг проводника, который находится под током, всегда существует связанное с ним магнитное поле, то силовые линии этого поля пронизывают плоскости витков. В результате такого взаимодействия соленоиды образуют собственное магнитное поле, магнитные линии которого замыкаются за его пределами.

Рис. 1. Магнитное поле катушки

Частным случаем катушки является замкнутый контур (один виток). В нём, как и в катушке, образуется собственное магнитное поле (см. рис. 2). Если ток постоянный, то в контуре никаких изменений не происходит.

Но при изменении параметров, например, в результате размыкания цепи, изменяется магнитный поток, создаваемый электрическим полем, что является причиной возникновения ЭДС индукции. Аналогичное изменение произойдёт и в случае замыкания цепи.

Изменение параметров магнитного поля вызывает появление вихревого электрического поля, что в свою очередь приводит к возбуждению индуктивной электродвижущей силы. Возникновение ЭДС индукции, в результате изменения ток в замкнутом контуре, называется самоиндукцией.

Магнитный поток, ограниченный поверхностью контура, меняется прямо пропорционально изменению тока, циркулирующего в нём.

Рис. 2. Явление самоиндукции

Направление вектора ЭДС самоиндукции не совпадает с направлением тока в период его возрастания (при замыкании цепи), но он сонаправлен с ним в период убывания (разъединения цепи). Такое действие проявляется в замедлении появления тока в соленоиде при замыкания цепи, или в его задержке на какое-то время после разрыва цепи.

Описанное явление можно наблюдать на опыте с лампочками, одна из которых подключена последовательно с индуктивностью (см. рис. 3).

Рис. 3. Схема опыта с лампочками

Как видно на рисунке слева, ток от источника питания, проходящий через лампочку 2, при замыкании контактов встретит сопротивление вихревых токов, поскольку они противоположно направлены. Поэтому зажигание этой лампочки произойдёт с задержкой.

На время включения лампочки 1 вихревые токи повлияют, но сила тока в её цепи уменьшится после зажигания лампы 2. При отключении цепи от источника питания произойдёт обратный процесс: лампочка в цепи индуктивности некоторое время будет медленно угасать, а вторая лампа потухнет сразу после разъединения контактов.

График на рисунке 4 красноречиво объясняет эффект задержки.

Рис. 4. Иллюстрация задержки изменения тока в цепи индуктивности

Обратите внимание на нелинейность изменения силы тока по времени.

Аналогичные процессы происходят в цепи, состоящей из одной катушки. На рисунке 5 изображена такая схема и график изменения силы тока.

Рис. 5. Возникновение самоиндукции

Остаётся добавить, что скорость изменение величины ЭДС зависит от количества витков соленоида. Чем больше витков, тем больше влияние вихревых токов, на параметры цепи.

В случае с переменным током амплитуда ЭДС самоиндукции пропорциональна амплитуде синусоиды питания, её частоте и индуктивности катушки.

Синусоидальный ток, проходя через катушку индуктивности, сдвигается по фазе на величину π/2. Именно этот сдвиг является причиной отставания собственного тока катушки от тока, вырабатываемого источником питания.

Формулы

Собственный магнитный поток контура (Ф) связан прямо пропорциональной зависимостью с индуктивностью (L) этого контура и величиной тока в нём (i). Данная зависимость выражается формулой: Ф = L×i. Коэффициент пропорциональности L принято называть коэффициентом самоиндукции или же просто индуктивностью контура.

При этом индуктивность контура пребывает в зависимости от его геометрии, площади плоскости ограниченной витком и магнитной проницаемости окружающей среды. Но этот коэффициент не зависит от силы тока в контуре. Если же форма, линейные размеры и магнитная проницаемость не изменяются, то для определения величины индуктивной ЭДС применяется формула:

где E_{самоинд.} – ЭДС самоиндукции, Δi – изменение силы тока за время Δt.

Индуктивность

Выше мы отметили, что индуктивность контура зависит от его геометрии и размеров, а также от магнитной проницаемости среды. Если речь идёт о катушке, то эти утверждения справедливы и для неё. На индуктивность катушки влияет её диаметр и количество витков. Индуктивность существенно повышается, если в катушку добавить ферромагнитный сердечник.

Магнитные поля отдельных витков катушки складываются. Если витков достаточно много, то ток, протекающий через катушку, образует вокруг неё сильное магнитное поле, реагирующее на изменения электрического поля. Индуктивность является той величиной, которая характеризует то, насколько сильно проводник, из которого состоят витки, противодействует электрическому току.

Чем больше индуктивность катушки и чем выше скорость прерывания её цепи, тем больший всплеск ЭДС произойдёт в цепи. При этом полярность вихревых токов на выводах катушки противоположна направлению тока источника питания.

Индуктивность (то есть коэффициент пропорциональности) является важной характеристикой катушек, дросселей и других контурных элементов. Этот параметр можно сравнить с ёмкостью конденсаторов. Тем более что действие катушки индуктивности и конденсатора в электрических цепях очень похожи. RL и RC цепочки часто используют для сглаживания всплесков напряжений в различных фильтрах.

Единицей измерения индуктивности в международной системе СИ является генри. Величина размеров в 1 Гн – это такая индуктивность, при которой ЭДС составляет 1 В, при скорости изменения тока на 1 А за секунду.

Индуктивность определяет количество энергии, выделяющейся в результате действия собственного магнитного поля при самоиндукции. Эту энергию легко рассчитать по формуле: W_м = LI²/2.

Собственная энергия катушки численно равна работе, которую необходимо выполнить источником питания при преодолении ЭДС самоиндукции.

Важно знать, что в результате резкого разрыва цепи с большой индуктивностью, энергия высвобождается в виде искры или даже с образованием дугового разряда.

Примеры использования на практике

Явление самоиндукции нашло широкое практическое применение. Автолюбители прекрасно знают, что такое катушка зажигания. Без неё карбюраторный двигатель не запустится.

Работает этот важный узел следующим образом:

1. На катушку с большой индуктивностью подаётся бортовое напряжение 12 В.
2. Электрическая цепь резко обрывается специальным прерывателем.
3. Накопленная энергия самоиндукции поступает по высоковольтным проводам на свечу и образует на её электродах мощную искру.
4. Искровой разряд зажигает топливную смесь, приводя в движение поршень.

В современных автомобилях разрыв цепи выполняет электроника, но суть от этого не меняется – для образования искры по-прежнему используется энергия самоиндукции.

Мы уже упоминали о сетевых фильтрах, в которых используется явление самоиндукции. RL цепочка реагирует на любое изменение параметров. При его возрастании она задерживает во времени пиковые скачки и заполняет собственными вихревыми токами провалы. Таким образом, происходит сглаживание напряжения в электрически цепях.

В блоках питания электронной аппаратуры таким же способом убирают:

• шумы:
• пульсации;
• нежелательные частоты.

Самоиндукция дросселей используется в люминесцентных лампах для розжига электродов. После срабатывания стартера происходит разрыв контактов, в результате чего в дросселе наводится ЭДС самоиндукции. Энергия дросселя разжигает дугу на электродах, и люминесцентная лампа начинает светиться.

Перечисленные примеры демонстрируют полезное применение самоиндукции. Однако, как это всегда бывает, индуктивная ЭДС может наносить вред. При разъединении контактов выключателей, нагрузкой которых являются цепи с большой индуктивностью, возможны дуговые разряды. Они разрушают контакты, замедляют время защиты и т.п. С целью снижения риска от негативных влияний самоиндукции автоматические выключатели оборудуют дугогасительными камерами.

В таких случаях приходится принимать меры для нейтрализации энергии ЭДС самоиндукции. Ещё большая потребность в рассеянии энергии самоиндукции возникает в полупроводниковых ключах, чувствительных к пробоям.

В промышленности и энергетике самоиндукция является серьёзной проблемой. При отключении нагруженных линий ЭДС самоиндукции может достигать опасных для жизни величин. Это требует дополнительных затрат на принятие мер предосторожности. В частности, необходимо устанавливать на линиях устройства, препятствующие молниеносному размыканию цепи.

Видео в помощь

Методы защиты устройств (датчиков, приборов, контроллеров) с транзисторными выходами от токов самоиндукции

Введение

В данной статье будет рассмотрено явление самоиндукции, проявляющееся зачастую при коммутации индуктивных нагрузок. Также будут рассмотрены способы защиты и используемое для этого оборудование.

Техника безопасности

ВНИМАНИЕ! К работам по монтажу, наладке, ремонту и обслуживанию технологического оборудования допускаются лица, имеющие техническое образование и специальную подготовку (обучение и проверку знаний) по безопасному производству работ в электроустановках с группой не ниже 2 для ремонтного персонала, а также имеющие опыт работ по обслуживанию оборудования, в конструкцию которого вносятся изменения и дополнения, либо производится модернизация. За неисправность оборудования и безопасность работников при неквалифицированном монтаже и обслуживании ООО «КИП‑Сервис» ответственности не несет.

1. Электромагнитная индукция. Определение. Физический смысл

Электромагнитная индукция — явление возникновения электрического тока, при изменении во времени магнитного поля. Изменение магнитного поля, в силу закона электромагнитной индукции, приводит к возбуждению в контуре индуктивной электродвижущей силы (ЭДС). Процесс возникновения ЭДС индукции в проводящем контуре при изменении протекающего через контур тока называется самоиндукцией. Направление ЭДС самоиндукции всегда оказывается таким, что при возрастании тока в цепи ЭДС самоиндукции препятствует этому возрастанию, а при убывании тока — препятствует убыванию. Величина ЭДС самоиндукции определяется уравнением:

E=−L×dI/dtE= -L times dI / dt

где:
E — ЭДС самоиндукции
L — индуктивность катушки
dI/dt — изменение тока во времени.

Знак «минус» означает, что ЭДС самоиндукции действует так, что индукционный ток препятствует изменению магнитного потока. Этот факт отражён в правиле Ленца:

Индукционный ток всегда имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.

Явление самоиндукции можно наблюдать при включении и последующем выключении катушек соленоидов, промежуточных реле, электромагнитных пускателей. При подаче напряжения на катушку создается электромагнитное поле, в следствии чего образуется электродвижущая сила, которая препятствует мгновенному росту тока в катушке. Согласно принципу суперпозиции, основной ток в катушке можно представить в виде суммы токов, один из которых вызван внешним напряжением и сонаправлен с основным током, а второй вызван ЭДС самоиндукции и имеет противоположное направление основному току. Скорость изменения тока через катушку ограничена и определяется индуктивностью катушки. При протекании тока катушка «запасает» энергию в своём магнитном поле. При отключении внешнего источника тока катушка отдает запасенную энергию, стремясь поддержать величину тока в цепи. Это, в свою очередь, вызывает всплеск напряжения обратной полярности на катушке. Данный всплеск может достигать значений во много раз превышающих номинальное напряжение источника питания, что может помешать нормальной работе электронных устройств, вплоть до их разрушения.

Разберем более подробно, почему скачок ЭДС самоиндукции будет иметь обратную полярность. На рисунке 1 изображены две схемы, на которых стрелками обозначено направление движения тока, а так же потенциалы на всех элементах схемы при закрытом и открытом ключе.

а — закрытый ключб — открытый ключ

Рисунок 1 — Направление тока при закрытом и открытом ключе

При закрытом ключе потенциалы на всех элементах совпадают с потенциалом источника питания (рисунок 1, а). Во время размыкания ключа, из схемы исключается источник питания, и ЭДС самоиндукции стремится поддержать ток в катушке. Для того, что бы сохранить направление тока в катушке, ЭДС меняет свой потенциал на противоположный по знаку источнику питания (рисунок 1, б). Именно поэтому всплеск ЭДС самоиндукции будет иметь обратную полярность.

Более наглядно этот всплеск показан на рисунке 2. На графике изображено напряжение источника питания Uпит, ток возникающий в катушке I, ЭДС самоиндукции.

Рисунок 2 — График изменения тока и напряжения при коммутации

2. Теоретический расчет ЭДС самоиндукции

Рассмотрим явление самоиндукции на примере работы электромагнитной катушки при пропускании через нее постоянного тока. Включение катушки происходит при помощи бесконтактного датчика. Катушку можно заменить на последовательно соединенные активное Rk и индуктивное Lk сопротивления (рисунок 3).

Рисунок 3 — Эквивалентная схема электромагнитной катушки

Тогда электрическая схема будет иметь вид, представленный на рисунке 4.

Рисунок 4 — Схема включения электромагнитной катушки

При сработавшем датчики падение напряжения U на катушке составляет 24 В. При коммутации индуктивной нагрузки в первый момент времени ток остается равным току до коммутации, а после изменяется по экспоненциальному закону. Таким образом, при переходе управляющего транзистора в закрытое состояние катушка начинает генерировать ЭДС самоиндукции, предотвращающую падение тока. Попробуем рассчитать величину генерируемого катушкой напряжения.

На рисунке 5 показано направление тока при открытом транзисторе. Переход транзистора в закрытое состояние фактически означает что цепь катушки с генерируемым ЭДС самоиндукции замыкается через подтягивающий резистор. Обозначим его Ro. По документации датчика это сопротивление составляет 5,1 кОм.

Рисунок 5 — Направление тока при открытом транзистореРисунок 6 — Направление тока после перехода транзистора в закрытое состояние

На рисунке 6 видно что ток на резисторе Ro поменял направление — это обусловлено возникновением ЭДС самоиндукции в катушке. Для полученного замкнутого контура выполняется следующее уравнение:

UR0+URk+ULk=0U_R0+U_Rk+U_Lk=0

Выражая напряжение через ток и сопротивление, получим:

I×R0+I×Rk+ULk=0I times R_0 + I times R_k +U_Lk=0 ULk=−I×(Rk+R0)U_Lk= -I times ( R_k + R_0 )

При этом ток в цепи стремится к значению тока при открытом транзисторе:

Подставим данное выражение в предыдущую формулу, получим величину генерируемого напряжения самоиндукции:

ULk=−U×(Rk+R0)/Rk=−U×(1+R0/Rk)U_Lk= -U times ( R_k + R_0 ) / R_k = -U times ( 1 + R_0 / R_k )

Все переменные из этой формулы известны:
U = 24В — напряжение питания
R_o = 5,1кОм — сопротивление подтягивающего резистора датчика
R_k = 900 Ом — активное сопротивление катушки (данные из документации).

Подставив значения в формулу, рассчитаем примерное значение напряжения самоиндукции:

ULk=−U×(1+R0/Rk)=−24×(1+5100/900)=−160ВU_Lk= -U times ( 1 + R_0/R_k ) = -24 times ( 1 + 5100 / 900 )=-160 В

Данный расчет упрощен и не учитывает индуктивность катушки, от которой так же зависит ЭДС самоиндукции. Но даже из упрощенного расчета видно, что величина генерируемого напряжения оказывается во много раз больше номинального напряжения 24В.

Воздействие ЭДС самоиндукции может повредить устройства, имеющие общие с индуктивной нагрузкой цепи питания. На рисунке 7 приведена некорректная схема, на которой от одного источника питания подключен бесконтактный датчик и катушка соленоидного клапана.

Рисунок 7 — Некорректная схема подключения

На первый взгляд, данная схема может работать без каких-либо сбоев. Однако, при выключении катушки клапана возникает всплеск напряжения в результате самоиндукции. Всплеск распространяется по цепи питания на клемму «минус» датчика. В результате, разница потенциалов между коллектором и эмиттером закрытого транзистора превышает максимальное значение, что приводит к его пробою.

3. Практическое измерение ЭДС самоиндукции

Чтобы проверить правдивость приведенных выше теоретических расчетов, проведем измерение ЭДС самоиндукции. Для проведения измерений необходимо собрать схему, для которой мы проводили расчеты. При помощи осциллографа на клеммах катушки произведем измерение напряжения (рисунок 8).

Рисунок 8 — Измерение ЭДС самоиндукции

На рисунке 9 изображена осциллограмма значений напряжения самоиндукции катушки с питанием 24 В. На графике видно, что реальный всплеск напряжения при отключении катушки в несколько раз больше напряжения питания и составляет 128 В. Как следствие, транзисторный ключ выйдет из строя. Возникающий скачок ЭДС приводит к пробою транзисторных ключей, бесконтактных датчиков, слаботочных коммутирующих элементов и другим нежелательным эффектам в схемах управления.

Рисунок 9 — ЭДС самоиндукции при выключении катушки с питанием 24 В

4. Методы и средства защиты от ЭДС самоиндукции

Для подавления ЭДС самоиндукции и предотвращения выхода из строя оборудования необходимо принимать специальные меры. Для подавления пиков напряжения на катушке во время выключения, необходимо параллельно катушке включить в схему диод (для постоянного напряжения) или варистор (для переменного напряжения). ЭДС самоиндукции будет ограничиваться этими элементами, тем самым они будут обеспечивать защиту схемы.

Диод включается параллельно катушке против напряжения питания (рисунок 10). Таким образом, в установившемся режиме он не оказывает никакого воздействия на работу схемы. Однако при отключении питания на катушке возникает ЭДС самоиндукции, имеющая полярность, противоположную рабочему напряжению. Диод открывается и шунтирует катушку индуктивности.

а — включение диода в схему PNPб — включение диода в схему NPN

Рисунок 10 — Схема включения диода для защиты от самоиндукции

Варистор также включается параллельно катушке (рисунок 11).

Рисунок 11 — Схема включения варистора для защиты от самоиндукции

При увеличении напряжения выше пороговой величины, сопротивление варистора резко уменьшается, шунтируя индуктивную нагрузку. Соответственно, при броске тока варистор быстро срабатывает и обеспечивает надежную защиту схемы.

На рисунке 12 изображен график напряжения во время включения и выключения индуктивной катушки с использованием защитного диода для напряжения 24 В.

Рисунок 12 — ЭДС самоиндукции с использованием диода

На графике видно, что использование защитных диодов сглаживает переходную характеристику напряжения.

Для защиты от ЭДС самоиндукции существует целый ряд готовых устройств. Их выбор зависит от применяемой катушки и типа напряжения питания. Для гашения ЭДС самоиндукции на катушках промежуточных реле используют модули FINDER серии 99 (рисунок 13):

Рисунок 13 — Защитный модуль Finder/99.02.9.024.99

99.02.0.230.98 Finder/ Модуль защитный(светодиод+варистор)~/=110…240

99.02.9.024.99 Finder/ Модуль защитный(светодиод+диод), =6…24В

Модули устанавливаются непосредственно на колодку реле, не требуют дополнительного изменения схемы управления.

В случае подключения катушек пускателей, либо катушек соленоидных клапанов, необходимо использовать защитные клеммники Klemsan серии WG-EKI (рисунок 14):

Рисунок 14 – Защитный клеммник WG-EKI

110 220 Клеммник WG-EKI с варистором (0,5…2,5 мм2, рабочее напряжение до 30В, рабочий ток до 10А)

110 040 Клеммник WG-EKI с защитным диодом (0,5…2,5 мм2, рабочее напряжение до 1000В, рабочий ток до 10А, ток диода 1А)

Клеммники позволяют осуществить подключение индуктивной катушки без дополнительного изменения схемы. Клеммник имеет два яруса, соединенных между собой защитным диодом либо варистором. Для осуществления защиты необходимо провести провода питания катушки через этот клеммник. При использовании клеммника с защитным диодом необходимо соблюдать полярность при подключении (рисунок 15).

Рисунок 15 — Схема подключения клеммника WG-EKI с защитным диодом

Заключение

В рамках данной статьи было рассмотрено явление самоиндукции, приведен теоретический расчет ЭДС и практическое подтверждение этого расчета. Применяя модули Finder серии 99 и клеммники Klemsan серии WG-EKI, можно избавиться от пагубного воздействия самоиндукции и сохранить целостность коммутирующих элементов цепей управления.

Инженер ООО «КИП-Сервис»
Хоровец Г.Н.

Список использованной литературы:

1. Сивухин, Д.В. Общий курс физики. Электричество. Том III / Сивухин Д.В — М.: Наука, 1977. — 724.с.
2. Калашников, С.Г. Электричество / Калашников С.Г. — 6-е изд., стереот. — М.: Физматлит, 2003.-624.с.
3. Алексеев Н.И., Кравцов А.В. Лабораторный практикум по общей физике (электричество и магнетизм). Самоиндукция / Лицей No1580 при МГТУ им. Н.Э. Баумана, 2012. — 16 с.

Читайте также:

Если через замкнутый проводник или контур будет изменяться магнитный поток Ф, а значит магнитное поле, то в нем будет возникать ЭДС индукции и электрический ток.
Источниками переменного магнитного поля являются:
а) движущийся постоянный магнит;
б)движущийся проводник с постоянным током;
в) неподвижный проводник с переменным током.
Причем, чем быстрее изменяется магнитный поток магнитного поля через контур, тем большая ЭДС индукции, а значит и сила тока возникает в нем, таким образом, величина ЭДС индукции зависит от скорости изменения магнитного потока через контур, т.е.
– это и будет законом электромагнитной индукции, для замкнутого проводника или контура:
“ЭДС индукции ?инд, возникающая в контуре прямо пропорциональна скорости изменения магнитного потока через него”.
Электромагнитная индукция – это создание ЭДС индукции в проводнике, а если он замкнут, то и электрического тока в нем, под действием переменного магнитного поля.
Закон электромагнитной индукции для катушки:
“ЭДС индукции возникающая в катушке прямо пропорциональна числу витков катушки и скорости изменения магнитного потока через нее”. Если прямолинейный проводник будет двигаться в однородном магнитном поле равномерно, то в нем будет возникать ЭДС индукции, величина которой будет определяться по формуле:
где l – длина проводника, – скорость его движения, – угол между направлением и .

“ЭДС индукции возникающая в прямолинейном проводнике равномерно движущимся в однородном магнитном поле с индукцией , прямо пропорциональна длине проводника, скорости его движения, синусу угла между направлениями магнитной индукции магнитного поля и скорости движения проводника в магнитном поле ”.
Знак «-» в законе электромагнитной индукции указывает на направление индукционного тока в замкнутом проводнике, определяемое по правилу Ленца: “Индукционный ток всегда имеет такое направление, что своим магнитным полем препятствует изменению магнитного поля, которое вызвало индукционный ток”. Если магнитное поле, вызвавшее индукционный ток нарастает или увеличивается через замкнутый проводник, то магнитное поле индукционного тока направлено ему противоположно и не будет давать ему нарастать, если же магнитное поле, вызвавшее индукционный ток убывает, то магнитное поле индукционного тока направленно также, как и убывающее магнитное поле и препятствует убыванию магнитного поля вызывающего индукционный ток.
Величина индукционного поля определяется по закону Ома: “Сила индукционного тока прямо пропорциональна ЭДС индукции возникающей в замкнутом проводнике и обратно пропорциональна сопротивлению замкнутого проводника”.
Индукционным током называется ток, полученный в замкнутом проводнике под действием переменного магнитного поля, т.е. благодаря электромагнитной индукции.
Проводник с переменным током в пространстве вокруг себя образует переменное магнитное поле, в котором будет находиться сам проводник с переменным током, поэтому в нем будет возникать ЭДС индукции, которую называют ЭДС самоиндукции, а явление электромагнитной индукции в проводнике с переменным током называют самоиндукцией.
Таким образом, самоиндукция – это частный случай электромагнитной индукции, который имеет место в проводнике с переменным током. Величина ЭДС самоиндукции, возникающая в проводнике с переменным током определяется по закону самоиндукции: “ЭДС самоиндукции, возникающая в проводнике с переменным током прямо пропорциональна скорости изменения силы тока, текущего в проводнике”.
где – скорость изменения силы тока в проводнике, характеризует быстроту изменения тока в проводнике, и показывает на сколько изменяется ток за единицу времени;
L — индуктивность проводника – это характеристика проводника по которому течет переменный ток зависит от размеров и формы проводника, и не зависит от его материала.
L показывает какая ЭДС самоиндукции возникает в проводнике при скорости изменения тока в нем равной единице или какая ?сам возникает в проводнике, если ток в нем изменяется на единицу за единицу времени.
СИ: – это индуктивность такого проводника, в котором возникает ЭДС самоиндукции равная 1 В при изменении тока на 1 А за 1 секунду.
Знак «-» в законе самоиндукции указывает на направление тока самоиндукции, определяемого по правилу Ленца. Например, при замыкании цепи ток увеличивается, возникает ЭДС самоиндукции, которая препятствует нарастанию тока; если же ток уменьшается, что происходит при размыкании цепи, то ЭДС самоиндукции будет поддерживать убывающий ток, не давая ему убывать, поэтому при размыкании цепи большой индуктивности искрит рубильник из-за большого тока самоиндукции, определяемого по закону Ома для тока самоиндукции: .
Вариант №1
1. В каком случае в катушке замкнутой на гальванометр возникает электрический ток?
2. Что определяет закон электромагнитной индукции?
3. От чего зависит ЭДС индукции, возникающая в катушке?

4. В замкнутую катушку вдвигают постоянный магнит: один раз быстро, второй медленно. В каком случае в ней возникнет больший индукционный ток?
5. Что определяют по правилу Ленца? по правилу левой руки? правого винта?
6. Из формул
а)силы Ампера выразить силу тока;
б)силы Лоренца выразить скорость движения частиц;
в) закона индукции электромагнитной индукции выразить изменение магнитного потока.
7. Что такое самоиндукция? Где она имеет место?
8. В каких единицах измеряются
а)магнитная индукция;
б)магнитный поток;
в)ЭДС индукции;
г)индуктивность проводника.
Вариант №2
1. В чем заключается явление электромагнитной индукции?
2. Какое поле создает ЭДС индукции в замкнутом проводнике? Разве может магнитное поле заставить двигаться неподвижные электрические заряды?
3. В каком случае может возникать, а в каком не возникать, ЭДС индукции в прямолинейном проводнике, движущимся в однородном магнитном поле?
4. Почему в проводнике с постоянным током не возникает ЭДС индукции, а в проводнике с переменным возникает?
5. За 3 секунды магнитный поток, пронизывающий проволочную рамку, равномерно увеличивается с 6 Вб до 9 Вб. Чему равно при этом значение ЭДС индукции в рамке?
6. Чему равна ЭДС самоиндукции в катушке индуктивностью L = 3 Гн, при равномерном уменьшении силы тока от 5 А до 1 А за 2 секунды?
Вариант №3
1. Как направлена сила Лоренца, действующая на движущуюся заряженную частицу в магнитном поле?
2. Как направлена магнитная индукция внешнего магнитного поля, в котором против часовой стрелки движется отрицательно заряженная частица?
3. Электрон влетел в магнитное поле со скоростью V перпендикулярно линиям магнитной индукции и стал двигаться по окружности радиуса R. Определите величину вектора магнитной индукции магнитного поля. (заряд электрона e, m – масса электрона)
4. Под каким углом расположен проводник с током 3 А длиной 0,1 м в однородном магнитном поле с индукцией 4 Тл, если на него действует сила Ампера равная 0,6 Н?
5. Что происходит с индукционным током в кольце, плоскость которого перпендикулярна линиям магнитной индукции, если ее величина равномерно увеличивается?
6. Чему равна индуктивность проволочной рамки, если при силе тока I = 3 А в рамке возникает магнитный поток Ф = 6 Вб?
7. Катушка сопротивлением 100 Ом, состоящая из 1000 витков площадью 5 см2, внесена в однородное магнитное поле. В течение некоторого времени индукция магнитного поля уменьшилась от 0,8 Тл до 0,3 Тл. Какой заряд будет индуцирован в проводнике за это время?

---

индуктивность | Физика

Индукция — это процесс, при котором ЭДС индуцируется изменением магнитного потока. До сих пор обсуждалось множество примеров, некоторые из которых более эффективны, чем другие. Трансформаторы, например, спроектированы так, чтобы быть особенно эффективными при наведении желаемого напряжения и тока с очень небольшими потерями энергии в другие формы. Есть ли полезная физическая величина, связанная с тем, насколько «эффективно» данное устройство? Ответ положительный, и эта физическая величина называется , индуктивность . Взаимная индуктивность — это влияние закона индукции Фарадея для одного устройства на другое, например, первичная катушка, при передаче энергии вторичной обмотке в трансформаторе. См. Рис. 1, где простые катушки индуцируют ЭДС друг в друге.

Рис. 1. Эти катушки могут вызывать ЭДС друг в друге, как неэффективный трансформатор. Их взаимная индуктивность M указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 вызывает в катушке 2 ЭДС.(Обратите внимание, что « E ₂ индуцированная» представляет наведенную ЭДС в катушке 2.)

Во многих случаях, когда геометрия устройств фиксирована, магнитный поток изменяется за счет изменения тока. Поэтому мы сконцентрируемся на скорости изменения тока, Δ I / Δ t , как причине индукции. Изменение тока I ₁ в одном устройстве, катушка 1 на рисунке, индуцирует ЭДС ₂ в другом. Мы выражаем это в форме уравнения как

[латекс] {\ text {emf}} _ {2} = — M \ frac {\ Delta {I} _ {1}} {\ Delta t} \\ [/ latex],

, где M определяется как взаимная индуктивность между двумя устройствами.Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность M , тем эффективнее связь. Например, катушки на Рисунке 1 имеют небольшой размер M по сравнению с катушками трансформатора на Рисунке 3 от Transformers. Единицами измерения для M являются (В с) / A = Ом ⋅ с, который назван генри (H) в честь Джозефа Генри. То есть 1 H = 1 Ω⋅s. Природа здесь симметрична. Если мы изменим ток I ₂ в катушке 2, мы индуцируем ЭДС ₁ в катушке 1, что равно

[латекс] {\ text {emf}} _ {1} = — M \ frac {\ Delta {I} _ {2}} {\ Delta t} \\ [/ latex],

, где M то же самое, что и для обратного процесса.Трансформаторы работают в обратном направлении с такой же эффективностью или взаимной индуктивностью M . Большая взаимная индуктивность M может быть, а может и не быть желательной. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для одежды, может вызвать опасную ЭДС на своем корпусе, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность M состоит в том, чтобы намотать катушки против ветра, чтобы нейтрализовать создаваемое магнитное поле.(См. Рисунок 2.)

Рис. 2. Нагревательные катушки электрической сушилки для одежды могут быть намотаны в противоположную сторону, так что их магнитные поля нейтрализуют друг друга, что значительно снижает взаимную индуктивность по сравнению с корпусом сушилки.

Самоиндукция , действие закона индукции Фарадея устройства на самого себя, также существует. Когда, например, увеличивается ток через катушку, магнитное поле и магнитный поток также увеличиваются, вызывая противоэдс, как того требует закон Ленца.И наоборот, если ток уменьшается, индуцируется ЭДС, которая препятствует уменьшению. Большинство устройств имеют фиксированную геометрию, поэтому изменение магнитного потока полностью связано с изменением тока Δ I через устройство. Индуцированная ЭДС связана с физической геометрией устройства и скоростью изменения тока. Выдается

[латекс] \ text {emf} = — L \ frac {\ Delta I} {\ Delta t} [/ latex],

, где L — собственная индуктивность устройства. Устройство, которое демонстрирует значительную самоиндукцию, называется катушкой индуктивности и обозначено символом на рисунке 3.

Рисунок 3.

Знак минус является выражением закона Ленца, означающего, что ЭДС препятствует изменению тока. Единицами самоиндукции является генри (Гн), как и для взаимной индуктивности. Чем больше собственная индуктивность L устройства, тем сильнее оно сопротивляется любому изменению тока через него. Например, большая катушка с множеством витков и железным сердечником имеет большой L и не позволит току быстро меняться. Чтобы избежать этого эффекта, необходимо добиться небольшого размера L , например, за счет встречной намотки катушек, как показано на рисунке 2.Катушка индуктивности 1 H — это большая катушка индуктивности. Чтобы проиллюстрировать это, рассмотрим устройство с L = 1,0 Гн, через которое протекает ток 10 А. Что произойдет, если мы попытаемся быстро отключить ток, возможно, всего за 1,0 мс? ЭДС, заданная как ЭДС = — L (Δ I / Δ t ), будет препятствовать изменению. Таким образом, ЭДС будет индуцирована ЭДС = — L (Δ I / Δ t ) = (1,0 H) [(10 A) / (1,0 мс)] = 10 000 В. Знак плюс означает, что это большое напряжение идет в том же направлении, что и ток, противодействуя его уменьшению.Такие большие ЭДС могут вызвать дуги, повредить коммутационное оборудование, и поэтому может потребоваться более медленное изменение тока. Есть применение для такого большого наведенного напряжения. Во вспышках камеры используются аккумулятор, две индуктивности, которые работают как трансформатор, и система переключения или генератор для создания больших напряжений. (Помните, что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы вызвать напряжение в другой катушке.) Система генератора будет делать это много раз, когда напряжение батареи повышается до более чем тысячи вольт.(Вы можете услышать пронзительный вой от трансформатора, когда конденсатор заряжается.) Конденсатор сохраняет высокое напряжение для последующего использования для питания вспышки. (См. Рисунок 4.)

Рис. 4. Благодаря быстрому переключению катушки индуктивности можно использовать батареи 1,5 В для индукции ЭДС в несколько тысяч вольт. Это напряжение можно использовать для хранения заряда в конденсаторе для последующего использования, например, в насадке для вспышки камеры.

Можно рассчитать L для индуктора, учитывая его геометрию (размер и форму) и зная создаваемое магнитное поле.В большинстве случаев это сложно из-за сложности создаваемого поля. Таким образом, в этом тексте индуктивность L обычно является заданной величиной. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму. Поучительно вывести уравнение для его индуктивности. Начнем с того, что наведенная ЭДС определяется законом индукции Фарадея как ЭДС = — Н (Δ Φ / Δ t ) и, по определению самоиндукции, как ЭДС = — L . (Δ I / Δ т ).Приравнивая эти доходности к

[латекс] \ text {emf} = — N \ frac {\ Delta \ Phi} {\ Delta t} = — L \ frac {\ Delta I} {\ Delta t} \\ [/ latex]

Решение для л дает

[латекс] L = N \ frac {\ Delta \ Phi} {\ Delta I} \\ [/ latex]

Это уравнение для самоиндукции L устройства всегда верно. Это означает, что самоиндукция L зависит от того, насколько эффективен ток для создания магнитного потока; чем эффективнее, тем больше Δ Φ / Δ I .Давайте воспользуемся этим последним уравнением, чтобы найти выражение для индуктивности соленоида. Поскольку площадь A соленоида является фиксированной, изменение магнитного потока составляет Δ Φ = Δ ( B A ) = A Δ B . Чтобы найти Δ B , заметим, что магнитное поле соленоида определяется выражением [латекс] B = {\ mu} _ {0} {nI} = {\ mu} _ {0} \ frac {NI} { \ ell} \\ [/ latex]. (Здесь n = N / , где N — количество катушек, а ℓ — длина соленоида.{2} A} {\ ell} \ text {(соленоид)} \\ [/ latex].

Это самоиндукция соленоида с площадью поперечного сечения A и длиной . Обратите внимание, что индуктивность зависит только от физических характеристик соленоида, в соответствии с его определением.

Пример 1. Расчет самоиндукции соленоида среднего размера

Рассчитайте самоиндукцию соленоида длиной 10,0 см и диаметром 4,00 см, который имеет 200 катушек.

Стратегия

Это прямое применение [латекса] L = \ frac {{\ mu} _ {0} {N} ^ {2} A} {\ ell} \\ [/ latex], поскольку все величины в уравнении, кроме L известны. {2} \ влево (1.{2} \ right)} {0,100 \ text {m}} \\ & = & 0,632 \ text {mH} \ end {array} \\ [/ latex].

Обсуждение

Этот соленоид среднего размера. Его индуктивность около миллигенри также считается умеренной.

Одно из распространенных применений индуктивности используется в светофорах, которые могут определить, когда автомобили ждут на перекрестке. Электрическая цепь с индуктором размещается на дороге под местом остановки ожидающей машины. Кузов автомобиля увеличивает индуктивность, и схема изменяется, посылая сигнал на светофор, чтобы изменить цвет.Точно так же металлоискатели, используемые для безопасности аэропортов, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и как приемник. Импульсный сигнал в катушке передатчика вызывает сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути. Такие детекторы могут быть настроены на чувствительность, а также могут указывать приблизительное местонахождение обнаруженного на человеке металла. (Но они не смогут обнаружить пластиковую взрывчатку, подобную той, которая была обнаружена на «бомбардировщике в нижнем белье.”) См. Рисунок 5.

Рис. 5. Знакомые ворота безопасности в аэропорту могут не только обнаруживать металлы, но и указывать их приблизительную высоту над полом. (Источник: Alexbuirds, Wikimedia Commons)

Физика для науки и техники II

из отдела академических технологий на Vimeo.

9,7 Самоиндукция

Рассмотрим две простые схемы. Катушка, которая подключена к клеммам источника питания, батареи, переключателя, и, допустим, это наша схема номер один.Мы размещаем аналогичную катушку напротив этой, и в этой схеме у нас нет источника питания. Мы можем разместить здесь гальванометр, чтобы определять ток, и назовем его схемой номер два.

Допустим, источник питания, батарея, генерирует ε вольт электродвижущей силы. Конечно, когда переключатель выключен, через эту цепь не будет протекать ток. Когда мы включаем переключатель, мы собираемся закончить тем, что определенный ток будет течь по этой цепи от положительного конца к отрицательному, так что, как только переключатель будет замкнут.

Ну, во время этого процесса, как только мы включим этот переключатель, ток будет начинаться с 0 и начнет увеличиваться до своего максимального значения. Затем он достигнет своего максимального значения и, следовательно, будет проходить через этот контур с этим постоянным значением. Но во время нарастания тока, другими словами, когда он идет от 0 до максимального значения, соответствующее магнитное поле, которое он генерирует, также будет начинаться с 0 и увеличиваться в сторону максимального значения, потому что, как вы помните, величина тока прямо пропорциональна силе создаваемого магнитного поля.

Итак, во время этого процесса, когда магнитное поле поднимается с увеличением тока, и оно будет генерировать силовые линии магнитного поля через этот первый контур, допустим, первая катушка, и эти линии будут проходить через область, окружающую вторую катушку. По мере увеличения тока это магнитное поле будет увеличиваться. Следовательно, поток через область, окруженную второй катушкой, будет увеличиваться, и в результате этого увеличения потока, согласно закону Фарадея, мы получим наведенную ЭДС и, следовательно, индуцированный ток.Этот ток появится из закона Ленца, так что он будет противодействовать своей причине, поэтому он будет генерировать магнитное поле в направлении, противоположном этому. Это магнитное поле индуцированного тока. Чтобы иметь возможность генерировать магнитное поле в этом направлении, используя правое правило, индуцированный ток должен течь против часовой стрелки по всей этой цепи.

Конечно, этот ток будет обнаружен здесь гальванометром, и стрелка гальванометра будет двигаться в одном направлении.Он отклонится от своего первоначального 0 в любой точке или в любом месте. Что ж, если мы последуем этому случаю, то магнитное поле этого индуцированного тока вдоль этой второй петли будет проходить через область, окруженную первой петлей, как это. Поскольку ток нарастает в первом, поэтому индуцированный i будет генерировать второй. Магнитное поле второй катушки пройдет через область, окруженную первой катушкой. Следовательно, он будет генерировать изменение потока через первую катушку, и этот поток будет индуцировать электродвижущую силу вдоль первой катушки и, следовательно, также ток, и этот ток будет проявляться так, что он будет противодействовать своей причине.

Если мы проследим катушки, исходные катушки, и мы вернемся к тому факту, что i индуцирован во второй катушке, чтобы появиться, и это происходит, что исходный ток i отображается как увеличивающийся от своего максимума. ценить. Следовательно, ток, возникающий в первой катушке, будет противодействовать этой причине. Другими словами, он будет пытаться противодействовать увеличению первоначального тока. Для этого он должен генерировать магнитное поле, противоположное направлению потока исходного тока.Следовательно, он должен работать в направлении, противоположном исходному току. И по этой причине мы не сможем закончить тем, что ток сразу перейдет от 0 до максимального значения. Для достижения этого значения потребуется некоторое время.

Что ж, мы можем заявить здесь, что, говоря, индуцированная электродвижущая сила также появляется в катушке, если мы изменяем ток в той же катушке. Это называется самоиндукцией, а создаваемая ЭДС, электродвижущая сила, называется «самоиндуцированной ЭДС».Итак, как только мы изменим ток в первой катушке, мы будем индуцировать ток через вторую катушку, и магнитное поле этого тока вызовет изменение потока через первую катушку. Таким образом, мы собираемся получить и , индуцированные вдоль первой катушки. И если ток увеличивается в первой катушке, этот индуцированный ток будет течь в направлении, противоположном направлению первоначального тока.

Таким образом, исходный ток сразу достигнет максимального значения.Или, если i уменьшается, если исходный ток уменьшается, от его максимального значения до 0, тогда уменьшение магнитного поля будет генерировать или индуцировать электрический ток вдоль второй катушки. Этот ток будет течь в таком направлении, что будет противодействовать своей причине, и поэтому он будет течь в таком направлении, что создаваемое им магнитное поле будет в том же направлении, что и исходное магнитное поле. Это магнитное поле, опять же, будет генерировать изменение магнитного потока через область, окруженную первой катушкой.Это вызовет наведенный ток по первому, и в этом случае, опять же, он будет появляться в противовес своей первоначальной причине, а именно уменьшению исходного тока.

Следовательно, в этом случае этот ток будет проявляться в том же направлении, что и исходный ток. Поэтому позвольте мне выключить выключатель, ток не упадет до 0 сразу, и это займет некоторое время, и мы называем эту электродвижущую силу, которая появляется в результате изменения тока так же, как самоиндуцированная. электродвижущая сила и связанный с ней ток как самоиндуцированный ток.

Хорошо. Если мы вспомним определение индуктивности для любой катушки индуктивности, мы имеем L, — это равное количество потоковых звеньев, деленное на ток. Отсюда, если мы произведем перекрестное умножение, Li будет равно N умноженному на Φ B . Что ж, по закону Фарадея индуцированная электродвижущая сила равна — Н, умноженное на количество витков, умноженное на изменение магнитного потока. Мы можем поместить это N в оператор производной, поскольку это константа, и записать это соотношение d от NΦ B к dt .Но NΦ B , из определения индуктивности, равно L time i . Следовательно, ε становится равным — d из Li по сравнению с dt .

Поскольку индуктивность постоянна, мы можем вынести ее за пределы оператора производной. Тогда наведенная ЭДС становится равной — L di по сравнению с dt , и это выражение для самоиндуцированной электродвижущей силы. Он просто говорит нам, что если ток меняется, то мы получим самоиндуцированную ЭДС через ту же катушку.Если через какой-либо индуктор протекает постоянный ток, то самоиндуцированная ЭДС будет равна 0.

Таким образом, мы можем резюмировать, сказав, что, таким образом, в любом индукторе — это может быть простой катушечный соленоид или тороид — самоиндуцированная ЭДС возникает всякий раз, когда ток изменяется со временем. Величина электродвижущей силы не влияет на индуцированную электродвижущую силу. Учитывается только скорость изменения тока. Другими словами, поскольку мы генерируем самоиндуцированную электродвижущую силу в самой первой катушке, самоиндуцированная ЭДС и связанный с ней индуцированный ток не имеют ничего общего с величиной исходного тока.Это напрямую зависит от того, насколько быстро или медленно изменяется исходный ток.

Ну, направление самоиндуцированной электродвижущей силы, опять же, определяется из закона Ленца, другими словами, самоиндуцированные действия противодействуют изменению, которое его вызывает. Таким образом, если мы добавим, мы можем сказать, что направление самоиндуцированной электродвижущей силы определяется законом Ленца. То есть противостоит своей причине.

В этом смысле, если вы посмотрите на пару интересных случаев, предполагая, что у нас есть индуктор, может быть соленоидом, тороидом или простой катушкой, и давайте предположим, что ток течет слева направо, и предположим, что i повышается.Следовательно, мы собираемся получить самоиндуцированную электродвижущую силу, и она проявится так, что будет противодействовать своей причине. Очевидно, что для протекания тока в этом направлении у нас должна быть наша оригинальная стрелка ЭДС. Он указывает вправо, чтобы ток шел слева направо. Итак, если – увеличивается, мы собираемся закончить с самоиндуцированной ЭДС вдоль этого индуктора, так что она будет противодействовать своей причине. Другими словами, он будет вести себя так, как будто у нас есть другой источник питания, противодействующий этому току.Другими словами, генерирование индуцированного тока в направлении, противоположном этому исходному току.

С другой стороны, если мы рассматриваем тот же индуктор, в этом случае ток снова уменьшается в том же направлении. Итак, снова стрелка ЭДС указывает в направлении потока тока, но теперь ток становится все меньше и меньше, поэтому мы собираемся закончить с самоиндуцированной ЭДС через этот индуктор, но эта ЭДС будет проявляться в некотором роде. что он попытается противостоять своему делу. Для этого он будет генерировать индуцированный ток, который будет течь в том же направлении, что и исходный ток.Следовательно, он будет вести себя так, как если бы у нас индуцировалась ε ‘ электродвижущей силы, и он генерирует ток в том же направлении, что и исходный. Тогда как в предыдущем случае этот индуцированный ток будет иметь направление, противоположное направлению потока исходного тока.

Хотя это не очень хорошее представление, но оно поможет вам понять, потому что, помните, мы не можем действительно использовать стрелки ЭДС из-за электродвижущей силы, генерируемой в результате индукции.Что ж, именно из-за этих причин для первого случая мы можем рассматривать этот случай как момент, когда мы включаем переключатель, чтобы ток нарастал от его, от 0 до максимального значения. В то время как во втором случае мы можем визуализировать это как момент, когда мы выключаем выключатель, так что ток уменьшается от максимального значения до 0. В обоих случаях ни максимальное значение, ни значение 0 тока не будут достигнуты сразу. Это займет некоторое время из-за самоиндуцированной электродвижущей силы.

Персонализированная обучающая платформа для учащихся K6-K12

Бесплатная Персонализированная обучающая платформа для студентов

Simply Science — это бесплатная персонализированная платформа для обучения детей в возрасте от 6 до 12 классов на основе STEM. Мы — веб-сайт открытого обучения, который побуждает детей понимать концепции и логику в удобном для них темпе, предлагая помощь с помощью интерактивной навигации. Развивайте навыки решения проблем, творческий подход к дизайну, логику и наблюдательность, не выходя из дома, бесплатно!

Обучение на основе тем

Наш контент создан специально для привлечения маленьких умов и их любопытства.Разделенные на темы, вы можете выбрать интересующую вас тему и просто узнать все, что вы хотели знать о ней. Упорядоченный, умный и интерактивный с помощью примеров, аналогий и моделирования, Simply Science гарантирует, что вы приложите максимум усилий для мышления!

Знайте свой IQ и SQ

Оцените свою способность обрабатывать информацию. Применяйте рассуждения и науку с помощью быстрого бесплатного теста IQ и SQ. Определите свои сильные и слабые стороны и сосредоточьтесь на своих интересах, чтобы построить свой научный коэффициент, который пробуждает ваше любопытство и облегчает изучение STEM.Наши IQ и SQ указывают на формирующую оценку по естествознанию и математике, которая может продвинуть вас вперед и раскрыть новый потенциал.

Технологии позволяют обучаться

Раскройте науку, математику и их загадки с помощью наших уникальных технологий, основанных на исследованиях на основе тем. Отправьтесь в новый мир с нашими темами полного погружения, наполненными забавными, увлекательными видео, викторинами и персонализированной лентой контента.

Лучшая платформа для внеклассных занятий STEM для учащихся

В то время как формальное школьное и институциональное обучение сосредоточено на языках, когнитивном развитии и многих других вещах, Simply Science является вспомогательной идеей учебной программы, обучая учащихся в 6 и 12 классах в области естественных наук, технологий, инженерии. и математика.Благодаря междисциплинарному подходу, мероприятиям и ресурсам, ориентированным на воздействие, это идеальное занятие для молодых умов после школы.

Комплексные темы обучения для детей от 9 до 18 лет

Узнавайте что-то новое каждый день, развивайте интересы и отвечайте на вопросы, которые всегда заставляли вас задуматься! Педагогика Simply Science поощряет вас исследовать, вводить новшества и применять полученные концепции в повседневной жизни, от базовых концепций до подробных бесед. Наша модель на основе темы гарантирует, что тема охватывает все темы в дисциплинах, которые она затрагивает — математику, науку и технологии, биологию и химию и все, что между ними.

Интерактивный и увлекательный контент и виртуальная помощь

Межотраслевое обучение с сокровищницей ресурсов — мы считаем, что каждый молодой ум должен иметь доступ к взаимосвязанным и равным возможностям обучения. Наука формирует мир, она всепроникающая и преобразующая. Наши материалы мирового уровня, методология и ресурсы идут рука об руку с учебной программой учебного заведения. Наши виртуальные помощники направляют студентов к ключевым навыкам в темах, чтобы развивать критическое мышление, рассуждение и дизайн.

Собственная индуктивность | Примечания по электронике

— основная информация о самоиндукции, о том, как она возникает, основная формула самоиндукции и соответствующие расчеты.

---

Индуктивность и руководство по трансформатору Включает:
Индуктивность Символы Закон Ленца Собственная индуктивность Расчет индуктивного реактивного сопротивления Теория индуктивного реактивного сопротивления Индуктивность проволоки и катушек Трансформеры

---

Самоиндукция — это эффект, который замечается, когда одна катушка испытывает влияние индуктивности.

Под действием самоиндукции и изменения тока индуцируют ЭДС или электродвижущую силу в том же проводе или катушке, создавая то, что часто называют обратной ЭДС.

Поскольку эффект наблюдается в том же проводе или катушке, которые генерируют магнитное поле, эффект известен как самоиндукция.

Определения самоиндукции

Есть различные определения, связанные с самоиндукцией, которые полезно упомянуть.

• Самоиндукция: Самоиндукция определяется как явление, при котором изменение электрического тока в цепи создает индуцированную электродвижущую силу в той же цепи.
• Блок самоиндукции: Самоиндукция катушки называется одним генри, если изменение тока в цепи на один ампер в секунду создает в цепи электродвижущую силу в один вольт.

Основы самоиндукции

Когда ток проходит по проводу, особенно когда он проходит через катушку или индуктор, индуцируется магнитное поле. Он выходит наружу от провода или индуктора и может соединяться с другими цепями.Однако он также связан с цепью, из которой он настроен.

Магнитное поле можно представить в виде концентрических контуров магнитного потока, которые окружают провод, и более крупных, которые соединяются с другими из других контуров катушки, обеспечивая самосвязь внутри катушки.

Когда ток в катушке изменяется, это вызывает индуцирование напряжения в различных контурах катушки — результат самоиндукции.

Самоиндукция

С точки зрения количественной оценки влияния индуктивности, основная формула, приведенная ниже, дает количественную оценку этого эффекта.

Где:
VL = индуцированное напряжение в вольтах
N = количество витков в катушке
dφ / dt = скорость изменения магнитного потока в веберах / секунду

Наведенное напряжение в катушке индуктивности также может быть выражено через индуктивность (в генри) и скорость изменения тока.

Самоиндукция — это способ работы одиночных катушек и дросселей. Дроссель используется в радиочастотных цепях, потому что он противодействует любому изменению, то есть радиочастотному сигналу, но допускает любое устойчивое, т.е.е. Постоянный ток течет.

Дополнительные концепции и руководства по основам электроники:
Voltage Текущий Власть Сопротивление Емкость Индуктивность Трансформеры Децибел, дБ Законы Кирхгофа Q, добротность Радиочастотный шум
Вернуться в меню «Основные понятия электроники». . .

11.2 Самоиндуктивность и индукторы — Введение в электричество, магнетизм и схемы

ЦЕЛИ ОБУЧЕНИЯ

---

К концу этого раздела вы сможете:

• Соотнесите скорость изменения тока с наведенной ЭДС, создаваемой этим током в той же цепи
• Вывести самоиндукцию цилиндрического соленоида
• Вывести самоиндукцию прямоугольного тороида

Взаимная индуктивность возникает, когда ток в одной цепи создает изменяющееся магнитное поле, которое индуцирует ЭДС в другой цепи.Но может ли магнитное поле повлиять на ток в исходной цепи, создавшей поле? Ответ положительный, и это явление называется самоиндуктивностью .

Катушки индуктивности

На рисунке 11.2.1 показаны некоторые силовые линии магнитного поля, возникающие из-за тока в кольцевой проволочной петле. Если ток постоянный, магнитный поток через контур также постоянен. Однако, если бы ток изменялся со временем — скажем, сразу после замыкания переключателя — тогда соответственно изменился бы магнитный поток.Тогда закон Фарадея говорит нам, что в цепи будет индуцирована ЭДС, где

(11.2.1)

Поскольку магнитное поле, создаваемое токоведущим проводом, прямо пропорционально току, поток, создаваемый этим полем, также пропорционален току; то есть

(11.2.2)

(рисунок 11.2.1)

Рисунок 11.2.1 Магнитное поле создается током I в контуре. Если бы он изменялся со временем, магнитный поток, проходящий через петлю, также изменился бы, и в петле была бы индуцирована ЭДС.

Это также можно записать как

(11.2.3)

, где постоянная пропорциональности известна как самоиндуктивность проволочной петли. Если петля имеет повороты, это уравнение принимает вид

.

(11.2.4)

По соглашению, положительное значение нормали к петле связано с током по правилу правой руки, поэтому на рисунке 11.2.1 нормаль направлена ​​вниз. Согласно этому соглашению, в уравнении 11.2.4 положительно, поэтому L всегда имеет положительное значение .

Для петли с витками, поэтому наведенная ЭДС может быть записана в терминах самоиндукции как

(11.2.5)

При использовании этого уравнения для определения проще всего игнорировать знаки и и вычислить как

Поскольку самоиндукция связана с магнитным полем, создаваемым током, любая конфигурация проводников обладает самоиндукцией. Например, помимо проволочной петли, длинный прямой провод имеет самоиндукцию, как и коаксиальный кабель.Коаксиальный кабель чаще всего используется в индустрии кабельного телевидения, и его также можно найти для подключения к кабельному модему. Коаксиальные кабели используются из-за их способности передавать электрические сигналы с минимальными искажениями. Коаксиальные кабели имеют два длинных цилиндрических проводника, которые обладают током и самоиндукцией, что может иметь нежелательные эффекты.

Элемент схемы, используемый для обеспечения самоиндукции, известен как индуктор. Он представлен символом, показанным на рисунке 11.2.2, который напоминает катушку с проводом, основную форму индуктора.На рисунке 11.2.3 показано несколько типов индукторов, обычно используемых в схемах.

(рисунок 11.2.2)

Рисунок 11.2.2 Символ, используемый для обозначения катушки индуктивности в цепи.

(рисунок 11.2.3)

Рисунок 11.2.3 Различные индукторы. Независимо от того, заключены ли они в капсулу, как показанные три верхних, или намотаны в катушку, как самая нижняя, каждая из них представляет собой просто относительно длинную катушку с проволокой. (кредит: Windell Oskay) Разнообразные индукторы. Независимо от того, заключены ли они в капсулу, как три верхние показанные, или намотаны в катушку, как самая нижняя, каждая из них представляет собой просто относительно длинную катушку с проволокой.(Источник: Windell Oskay)

В соответствии с законом Ленца отрицательный знак в уравнении 11.2.5 указывает, что наведенная ЭДС на катушке индуктивности всегда имеет полярность, которая противодействует изменению тока. Например, если бы ток, протекающий от до на рис. 11.2.4 (а), увеличивался, наведенная ЭДС (представленная воображаемой батареей) имела бы указанную полярность, чтобы противодействовать увеличению. Если бы ток от до уменьшался, то наведенная ЭДС имела бы противоположную полярность, опять же, чтобы противодействовать изменению тока (Рисунок 11.2.4 (б)). Наконец, если бы ток через катушку индуктивности был постоянным, в катушке не было бы индуцированной ЭДС.

(рисунок 11.2.4)

Рисунок 11.2.4 Индуцированная ЭДС на катушке индуктивности всегда противодействует изменению тока. Это можно представить себе как воображаемую батарею, заставляющую течь ток, чтобы противодействовать изменению в (а) и усиливать изменение в (б).

Одним из распространенных применений индуктивности является разрешение светофоров , определять, когда автомобили ждут на перекрестке.Электрическая цепь с индуктором размещается на дороге под местом остановки ожидающего автомобиля. Кузов автомобиля увеличивает индуктивность, и схема изменяется, посылая сигнал на светофор, чтобы изменить цвет. Аналогичным образом, металлоискатели , используемые для безопасности аэропортов, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и как приемник. Импульсный сигнал от катушки передатчика вызывает сигнал в приемнике.На самоиндукцию цепи влияет любой металлический предмет на пути (рисунок 11.2.5). Металлоискатели можно настроить на чувствительность, а также они могут определять присутствие металла на человеке.

(рисунок 11.2.5)

Рисунок 11.2.5 Знакомые ворота безопасности в аэропорту не только обнаруживают металлы, но также могут указывать их приблизительную высоту над полом. (Источник: «Alexbuirds» / Wikimedia Commons)

Высокие наведенные напряжения обнаружены в вспышках фотокамер .Во вспышках камеры используются аккумулятор, два индуктора, которые работают как трансформатор, и система переключения или генератор для создания больших напряжений. Обратите внимание, что термин «колебание» в физике определяется как колебание величины или повторяющиеся регулярные колебания величины между двумя крайними значениями вокруг среднего значения. Теперь вспомните (из «Электромагнитная индукция об электромагнитной индукции»), что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы вызвать напряжение в другой катушке.Система генератора делает это много раз, когда напряжение батареи повышается до более высокого. (Вы можете услышать пронзительный свист трансформатора, когда конденсатор заряжается.) Конденсатор сохраняет высокое напряжение для последующего использования для питания вспышки.

ПРОВЕРЬТЕ ПОНИМАНИЕ 11.2

---

Ток протекает через катушку индуктивности на рисунке 11.2.4 от до, а не от до, как показано. Увеличивается или уменьшается ток, чтобы создать ЭДС, показанную на диаграмме (а)? На диаграмме (б)?

ПРОВЕРЬТЕ ПОНИМАНИЕ 11.3

---

При изменении тока на катушке индуктивности возникает ЭДС величиной. С какой скоростью меняется ток?

Хороший подход к расчету самоиндукции катушки индуктивности состоит из следующих шагов:

---

Стратегия решения проблем: самоиндуктивность

1. Предположим, через катушку индуктивности течет ток.
2. Определите магнитное поле, создаваемое током. Если есть соответствующая симметрия, вы можете сделать это с помощью закона Ампера.
3. Получите магнитный поток,.
4. При известном магнитном потоке самоиндукция может быть найдена из уравнения 11.2.4,.

Чтобы продемонстрировать эту процедуру, мы теперь вычисляем самоиндуктивности двух катушек индуктивности.

Цилиндрический соленоид

Рассмотрим длинный цилиндрический соленоид с длиной, площадью поперечного сечения и витками провода. Мы предполагаем, что длина соленоида настолько больше, чем его диаметр, что мы можем считать, что магнитное поле распространяется по всей внутренней части соленоида, то есть мы игнорируем концевые эффекты в соленоиде.При токе, протекающем через катушки, магнитное поле внутри соленоида составляет

.

(11.2.6)

, поэтому магнитный поток на один виток равен

(11.2.7)

Используя ??, находим для самоиндукции соленоида

(11.2.8)

Если — количество витков на единицу длины соленоида, мы можем записать уравнение 11.2.8 как

(11.2.9)

где — объем соленоида.Обратите внимание, что самоиндукция длинного соленоида зависит только от его физических свойств (таких как количество витков провода на единицу длины и объема), а не от магнитного поля или тока. Это верно для индукторов в целом.

Прямоугольный тороид

Тороид прямоугольного сечения показан на рисунке 11.2.6. Внутренний и внешний радиусы тороида равны и, а — высота тороида. Применяя закон Ампера так же, как мы это делали в примере 10.4.2 для тороида с круглым поперечным сечением, мы находим, что магнитное поле внутри прямоугольного тороида также равно

(11.2.10)

где — расстояние от центральной оси тороида. Поскольку поле внутри тороида изменяется, мы должны вычислить поток путем интегрирования по поперечному сечению тороида. Используя бесконечно малый элемент площади поперечного сечения, показанный на рис. 11.2.6, получаем

(11.2.11)

(рисунок 11.2.6)

Рисунок 11.2.6 Расчет самоиндукции прямоугольного тороида.

Теперь из уравнения 11.2.11 для самоиндукции прямоугольного тороида получаем

(11.2.12)

Как и ожидалось, самоиндукция — постоянная величина, определяемая только физическими свойствами тороида.

ПРОВЕРЬТЕ ПОНИМАНИЕ 11,4

---

ПРОВЕРЬТЕ ПОНИМАНИЕ 11,5

---

(а) Каков магнитный поток через один виток соленоида самоиндукции, когда через него протекает ток? Предположим, что соленоид намотан из проволоки диаметром.(б) Какова площадь поперечного сечения соленоида?

Кандела Цитаты

Лицензионный контент CC, особая атрибуция

• Загрузите бесплатно по адресу http://cnx.org/contents/[email protected]. Получено с : http://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution

Взаимная индуктивность и самоиндукция | Формула и пример

Электромагнитная индукция возникает, когда магнитный поток, движущийся относительно одиночного проводника или катушки, индуцирует ЭДС в проводнике или катушке.Поскольку рост или уменьшение тока через катушку генерирует изменяющийся поток, ЭДС индуцируется в катушке из-за ее собственного изменения тока. Тот же эффект может вызвать ЭДС в соседней катушке. Уровень наведенной ЭДС в каждом случае зависит от самоиндукции катушки или от взаимной индуктивности между двумя катушками. Во всех случаях полярность наведенной ЭДС такова, что она противодействует первоначальному изменению, вызвавшему ЭДС.

Компоненты, называемые индукторами или дросселями, сконструированы с заданными значениями индуктивности.Индукторы могут работать последовательно или параллельно. Даже самый короткий проводник имеет индуктивность. Обычно это нежелательная величина, называемая паразитной индуктивностью.

Самоиндуктивность

Катушка и индуктивность проводника

Было показано, что ЭДС индуцируется в проводнике, движущемся через магнитное поле, и что рост тока в катушке может индуцировать ЭДС в другом магнитном поле. спаренная катушка. Катушка также может индуцировать в себе напряжение при изменении уровня тока.Это явление известно как самоиндукция, и его принцип показан на рисунке 1.

Рис.1: Токопроводящая катушка и ее площадь поперечного сечения

Магнитный поток, растущий наружу вокруг витков катушки, разрезает (или задевает) другая катушка поворачивается и индуцирует ЭДС в катушке.

Катушка и ее площадь поперечного сечения показаны на рисунке 1, концы стрелок и точки указывают направления тока в каждом витке. Каждый виток катушки имеет магнитный поток вокруг него, создаваемый током, протекающим через катушку.Однако для удобства на рисунке показано увеличение потока только вокруг одного витка катушки. Видно, что по мере роста тока поток расширяется наружу и срезает (или сметает) другие витки. Это вызывает индукцию токов в других витках, и направление индуцированных токов таково, что они создают поток, противодействующий индуцирующему их потоку.

Помня, что ток через катушку вызывает рост потока вокруг всех витков одновременно, видно, что поток от каждого витка индуцирует ток, который противодействует ему на каждом втором витке.

Чтобы установить встречные потоки, индуцированный ток в катушке должен быть противоположен току, протекающему через катушку от внешнего источника питания. Наведенный ток, конечно же, является результатом наведенной ЭДС. Таким образом, видно, что самоиндукция катушки создает наведенную ЭДС, которая противодействует внешней ЭДС, которая пропускает ток через катушку. Поскольку эта наведенная ЭДС противоположна напряжению питания, ее обычно называют противоэдс или противоэдс .Противоэдс возникает только тогда, когда ток в катушке растет или уменьшается. Когда ток достигает постоянного уровня, поток больше не меняется, и противоэдс не генерируется.

Даже один проводник имеет самоиндукцию. На рис. 2 показано, что при нарастании тока в проводнике поток может расти наружу от центра проводника. Этот поток разрезает другие части проводника и вызывает противоэдс.

Рис. 2: поперечное сечение проводника

Рост тока внутри проводника индуцирует ЭДС на других участках проводника.

На рисунке 3 показана полярность противоэдс, индуцированная в катушке, для данной полярности напряжения питания. На рисунке 3 (а) переключатель замкнут, и ток I начинает расти с нуля. Полярность противоэдс (e _L ) такова, что она противодействует росту I, поэтому она последовательно противодействует напряжению питания. Когда переключатель разомкнут (рис. 3 (b)), ток стремится к нулю. Но теперь полярность e _L такова, что противостоит закату I.это последовательно с питающим напряжением. Фактически, e _L может вызвать искрение на выводах переключателя, поскольку это зависит от индуктивности катушки.

Рис.3: Полярность наведенной ЭДС

Противоэдс, наведенная в катушке, всегда противодействует увеличению или уменьшению тока.

Единицей индуктивности в системе СИ является Генри (Гн).

Индуктивность цепи равна одному Генри, когда ЭДС 1 В индуцируется изменением тока со скоростью 1 А / с.

Таким образом, соотношение между индуктивностью, индуцированным напряжением и скоростью изменения тока будет следующим:

\ [\ begin {matrix} L = \ frac {{{e} _ {L}}} {{\ Delta i} / {\ Delta t} \;} & {} & \ left (1 \ right) \\\ end {matrix} \]

Где L — индуктивность по Генри, e _L — наведенная противоэдс в вольтах. и — скорость изменения тока в А / с. знак минус иногда ставится перед e _L , чтобы показать, что наведенная ЭДС противоположна приложенной ЭДС.Когда e _L = 1 В и = 1 А / с, L = 1H. Если скорость изменения тока составляет 2 А / с и e _L = 1 В, индуктивность составляет 0,5 Гн.

Катушка, сконструированная так, чтобы иметь определенную индуктивность, обычно называется индуктором или дросселем. Обратите внимание на графические символы для катушки индуктивности, показанные на рисунке 3.

Формула самоиндуктивности

Выражение для индуктивности может быть получено с учетом размеров катушки и количества витков [см. Рисунок 4].

Рис.4: Количество витков в катушке

Индуктивность катушки зависит от количества витков, а также от магнитного потока и изменений тока.

Из уравнения (2):

\ [\ begin {matrix} {{e} _ {L}} = N \ frac {\ Delta \ phi} {\ Delta t} & {} & \ left ( 2 \ right) \\\ end {matrix} \]

Подстановка e _L в уравнение (1) дает

\ [L = N \ frac {{\ Delta \ phi} / {\ Delta t} \ ;} {{\ Delta i} / {\ Delta t} \;} \]

или

\ [\ begin {matrix} L = N \ frac {\ Delta \ phi} {\ Delta i} & {} & \ left (3 \ right) \\\ end {matrix} \]

Также

\ [\ phi = B \ times A \]

и

$ B = {{\ mu} _ {o }} \ times {{\ mu} _ {r}} \ times H = {{\ mu} _ {o}} \ times {{\ mu} _ {r}} \ times \ frac {IN} {l} $

Следовательно,

$ \ phi = {{\ mu} _ {o}} \ times {{\ mu} _ {r}} \ times IN \ times \ frac {A} {l} $

Поскольку I — максимальный уровень тока, он также представляет изменение тока (∆i) от нуля до максимального уровня.{A} / {} _ {l} & {} & \ left (4 \ right) \\\ end {matrix} \]

Обратите внимание, что, как показано на рисунке 5, индуктивность пропорциональна поперечному сечению площадь катушки и квадрат числа витков. Он также обратно пропорционален длине катушки. Таким образом, максимальная индуктивность достигается при использовании короткой катушки с большой площадью поперечного сечения и большим количеством витков.

Рис.5: Размеры катушки

Индуктивность катушки можно рассчитать, исходя из ее размеров и проницаемости сердечника.

Уравнение (4) теперь позволяет вычислить индуктивность катушки известных размеров. В качестве альтернативы его можно использовать для определения требуемых размеров катушки с заданной индуктивностью. Однако его не так просто применить к катушкам с железным сердечником, потому что проницаемость ферромагнитного материала изменяется при изменении плотности потока. Следовательно, индуктивность катушки с железным сердечником постоянно изменяется по мере увеличения и уменьшения тока катушки.

Неиндуктивная катушка

Во многих случаях желательно иметь неиндуктивную катушку; например, прецизионные резисторы обычно не являются индуктивными.Чтобы построить такую ​​катушку, обмотка сделана из двух расположенных бок о бок проводников, как показано на рисунке 6. Каждый виток катушки имеет соседний виток, несущий ток в противоположном направлении. Магнитные поля, создаваемые соседними витками, нейтрализуют друг друга. Следовательно, противоэдс не генерируется, и катушка неиндуктивна.

Рис.6: Неиндуктивная катушка

Пример самоиндуктивности

Соленоид с 900 витками имеет общий поток 1,33 X 10 ^-7 Вт через воздушный сердечник при токе катушки 100 мА.{-3}}} = 1,6 мВ \]

Взаимная индуктивность

Когда поток от одной катушки разрезает другую соседнюю (или магнитно связанную) катушку, во второй катушке индуцируется ЭДС. Следуя закону Ленца, ЭДС, индуцированная во второй катушке, создает поток, противодействующий исходному потоку из первой катушки. Таким образом, индуцированная ЭДС снова является противоэдс, и в этом случае индуктивный эффект называется взаимной индуктивностью. На рисунке 7 показаны графические символы, используемые для катушек с взаимной индуктивностью, также называемых связанными катушками.

Рис.7: Графические символы для катушек с воздушным и железным сердечником

Как и самоиндукция, взаимная индуктивность измеряется в Генри (H) .

Формула взаимной индуктивности

Две катушки имеют взаимную индуктивность 1 Гн, когда ЭДС 1 В индуцируется в одной катушке за счет изменения тока со скоростью 1 А / с в другой катушке.

Это определение приводит к уравнению, связывающему взаимную индуктивность с наведенным напряжением и скоростью изменения тока:

\ [\ begin {matrix} M = \ frac {{{e} _ {L}}} {{{ \ Delta i} / {\ Delta t} \;} & {} & \ left (5 \ right) \\\ end {matrix} \]

Где M — взаимная индуктивность по Генри, e _L — ЭДС в вольтах, индуцированная во вторичной катушке, и представляет собой скорость изменения тока в первичной катушке в А / с.

Катушка, через которую проходит ток от внешнего источника, называется первичной, а катушка, в которой наведена ЭДС, называется вторичной.

Уравнение для ЭДС, индуцированной во вторичной катушке, можно записать как:

\ [\ begin {matrix} {{e} _ {L}} = {{N} _ {s}} \ frac {\ Delta \ phi} {\ Delta t} & {} & \ left (6 \ right) \\\ end {matrix} \]

Здесь ∆ϕ — полное изменение магнитного потока во вторичной обмотке, N _с — количество витков вторичной обмотки, а ∆t — время, необходимое для изменения магнитного потока.

Подстановка e _L из уравнения (6) в уравнение (5) дает

\ [M = {{N} _ {s}} \ frac {{\ Delta \ phi} / {\ Delta t} \ ;} {{\ Delta i} / {\ Delta t} \;} \]

Следовательно,

\ [\ begin {matrix} M = {{N} _ {s}} \ frac {\ Delta \ phi } {\ Delta i} & {} & \ left (7 \ right) \\\ end {matrix} \]

Рисунок 8 (a) иллюстрирует тот факт, что когда две катушки намотаны на один ферромагнитный сердечник, эффективно весь поток, создаваемый первичной катушкой, соединяется с вторичной катушкой.Однако, когда катушки имеют воздушный сердечник, только часть потока от первичной обмотки может соединяться с вторичной (см. Рисунок 8 (b)). В зависимости от того, какая часть первичного потока пересекает вторичную, катушки могут быть классифицированы как слабо связанные или сильно связанные. Один из способов обеспечить плотное соединение показан на Рисунке 8 (c), где каждый виток вторичной обмотки находится рядом с одним витком первичной обмотки. Катушки, намотанные таким образом, называют бифилярными.

Рис.8: Потоковые связи в первичной и вторичной обмотках

Величина магнитного потока от первичной обмотки, которая связана со вторичной, зависит от того, насколько тесно связаны катушки. Коэффициент сцепления определяет сцепление.

Величина магнитной связи между первичной обмоткой и вторичной обмоткой также определяется в терминах коэффициента связи, k. Если весь первичный поток связан с вторичным, коэффициент связи равен 1. Когда только 50% первичного потока соединяется с вторичной обмоткой, коэффициент связи равен 0.5. Таким образом,

\ [k = \ frac {flux \ text {} связей \ text {} между \ text {} primary \ text {} и \ text {} \ sec ondary} {total \ text {} fluxproduced \ text {} by \ text {} primary} \]

Возвращаясь к уравнению (7). Когда ∆ϕ — полное изменение магнитного потока в первичной обмотке, магнитная связь с вторичной обмоткой равна k∆ϕ. Следовательно, уравнение для M

\ [\ begin {matrix} M = k {{N} _ {s}} \ frac {\ Delta \ phi} {\ Delta i} & {} & \ left (8 \ right ) \\\ end {matrix} \]

Также, заменяя $ \ Delta \ phi = {{\ mu} _ {o}} \ times {{\ mu} _ {r}} \ times \ Delta i \ times N \ times \ frac {A} {l} $ в уравнение (8) дает

\ [M = \ frac {k {{N} _ {s}}} {\ Delta i} \ times {{\ mu } _ {o}} \ times {{\ mu} _ {r}} \ times \ Delta i \ times {{N} _ {p}} \ times \ frac {A} {l} \]

или

\ [\ begin {matrix} M = k \ times {{N} _ {p}} \ times {{N} _ {s}} \ times {{\ mu} _ {o}} \ times {{\ mu} _ {r}} \ times \ frac {A} {l} & {} & \ left (9 \ right) \\\ end {matrix} \]

Каждая рассматриваемая обмотка сама по себе имеет самоиндукцию, которая может рассчитывается по уравнению (4).{2}} $

или

\ [\ begin {matrix} \ sqrt {{{L} _ {1}} \ times {{L} _ {2}}} = {{N} _ {p} } \ times {{N} _ {s}} \ times {{\ mu} _ {o}} \ times {{\ mu} _ {r}} \ times \ frac {A} {l} & {} & \ left (10 \ right) \\\ end {matrix} \]

Сравнивая уравнения 9 и 10, видно, что

\ [\ begin {matrix} M = k \ sqrt {{{L} _ { 1}} \ times {{L} _ {2}}} & {} & \ left (11 \ right) \\\ end {matrix} \]

Пример взаимной индуктивности

Две одинаковые катушки намотаны железный сердечник кольцевой формы с относительной проницаемостью 500.{-2}}} \ cong 9.42mH \\\ end {align} \]

Поскольку катушки намотаны на один и тот же железный сердечник, k = 1. Уравнение (11):

$ M = k \ sqrt {{{L} _ {1}} \ times {{L} _ {2}}} = \ sqrt {9.42 \ times 9.42} = 9,42 мГн $

Взаимный | Определение самоиндуктивности | Формула

При изменении магнитного потока, связанного с катушкой (или проводником), в катушке индуцируется ЭДС. Эту ЭДС можно вызвать двумя способами:

• Путем вращения катушки в стационарном магнитном поле или вращением магнитного поля в стационарной катушке (как в генераторах переменного и постоянного тока).ЭДС, наведенная таким образом, называется динамически индуцированной ЭДС. Это так называется потому, что в этом случае движется либо магнитное поле, либо катушка.
• Магнитное поле и катушка неподвижны. Но поток, связанный с катушкой, изменяется путем изменения тока, создающего этот поток (как в трансформаторах). Наведенная таким образом ЭДС называется статически индуцированной ЭДС. Это так называется, потому что магнитное поле и катушка в этом случае неподвижны. Статически индуцированная ЭДС может быть подразделена на следующие две категории:

• Самоиндуцированная ЭДС
• Взаимно индуцированная ЭДС

Самоиндуцированная ЭДС

ЭДС, индуцированная в катушке из-за изменения магнитного потока, создаваемого ею при соединении с собственными витками, известна как самоиндуцированная ЭДС.

Рассмотрим катушку, имеющую N витков на железном сердечнике, подключенном к батарее, как показано на рисунке. Ток I протекает через катушку, он создает магнитный поток φ. Этот поток также связан со своими поворотами. Если ток, протекающий через катушку, изменяется путем изменения переменного сопротивления R, это изменяет магнитную связь с катушкой, и, следовательно, в катушке индуцируется ЭДС.

ЭДС, индуцированная таким образом, называется самоиндуцированной ЭДС. Направление наведенной ЭДС таково, что она противодействует изменению тока i.е. причина, которая его порождает (закон Ленца).

Величина самоиндуцированной ЭДС прямо пропорциональна скорости изменения магнитного потока, связанного с катушкой (закон Фарадея). Но скорость изменения магнитного потока, связанного с катушкой, прямо пропорциональна скорости изменения тока в катушке.

Следовательно, самоиндуцированная ЭДС, e α — d I / dt

Или e = — L (d I / dt) ………. (I)

Где L — константа пропорциональности и известна как коэффициент самоиндукции или самоиндукции или индуктивности катушки.

Свойство катушки противодействовать любому изменению тока, протекающего через нее, известно как самоиндукция или индуктивность катушки.

Собственная индуктивность, L = (N ₂ µ _o µ _r a) ÷ l

, где N = количество витков катушек,
a = площадь поперечного сечения магнитопровода,
l = длина магнитной цепи.
Катушка достигает этого свойства из-за самоиндуцированной ЭДС в катушке , когда ток, протекающий через нее, изменяется.

Как показано на рисунке, если ток в катушке увеличивается (путем изменения сопротивления реостата), самоиндуцированная ЭДС устанавливается в таком направлении, чтобы противодействовать нарастанию тока, т.е. -индуцированная ЭДС на противоположна приложенному напряжению.

Точно так же, если ток в катушке уменьшается, самоиндуцированная ЭДС устанавливается в таком направлении, чтобы противодействовать падению тока, то есть направление самоиндуцированной ЭДС находится в том же направлении , что и направление приложенное напряжение.

Можно отметить, что самоиндукция не предотвращает изменение тока, поскольку дополнительная энергия выдается аккумулятором для преодоления этого противодействия. Однако задерживает изменение тока через катушку .

Можно отметить, что наличие индуктивности в цепи проявляется только при изменении тока в цепи.

Например, если устойчивый (прямой) поток через катушку, имеющую индуктивность (в силу ее геометрических и магнитных свойств), не будет проявлять ее присутствие.

Однако, когда переменный (непрерывно изменяющийся) ток течет через одну и ту же катушку, он будет эффективно проявлять свое присутствие.

Единица индуктивности — Генри (Гн).

Если в уравнении (i) выше, e = 1 В и d I / dt = 1 А / секунду, то L = 1 Гн.

Следовательно, катушка (или цепь), как говорят, имеет индуктивность один Генри, если в нем индуцируется ЭДС в 1 вольт при изменении тока через него со скоростью один ампер в секунду.

Из приведенного выше выражения ясно, что индуктивность обратно пропорциональна сопротивлению магнитной цепи.Следовательно, катушка, намотанная на магнитный сердечник (с низким сопротивлением), имеет большую индуктивность, чем эквивалентная катушка с воздушным сердечником.

Взаимно индуцированная ЭДС

ЭДС, индуцированная в катушке из-за изменения магнитного потока, создаваемого другой катушкой, называется взаимно индуцированной ЭДС.

Рассмотрим катушку X, имеющую N ₁ витков, и катушку Y, имеющую N ₂ витков, намотанных на железный стержень. Когда эти катушки подключены по схеме, как показано на рисунке, ток течет через катушку X и создает магнитный поток φ ₁ .

Часть этого потока также связана с катушкой Y. Если ток, протекающий через катушку X, изменяется путем изменения переменного сопротивления R, он изменяет поток, связывающий с другой катушкой Y, и, следовательно, в катушке Y индуцируется ЭДС.

ЭДС, индуцированная таким образом, известна как взаимно индуцированная ЭДС. Направление взаимно индуцированной ЭДС таково, что она противодействует изменению тока в катушке X, то есть причине, которая его вызывает (закон Ленца).

Математически взаимно индуцированная ЭДС, e _m α — d I ₁ / dt

или e _m = — M (d I ₁ / dt)

Где M — константа пропорциональности, известная как коэффициент взаимной индуктивности или взаимной индуктивности катушки.

Взаимную индуктивность между двумя катушками можно определить как свойство второй катушки, благодаря которому она противодействует изменению тока в первой катушке. Выражения для взаимной индуктивности:

M = (N ₁ N ₂ µ _o µ _r1 a ₁ ) ÷ l ₁

M = (N ₁ N ₂ µ _o µ _r2 a ₂ ) ÷ l ₂

где, N ₁ , N ₂ = количество витков витков,
a ₁ , a ₂ = площади поперечного сечения магнитных цепей,
l ₁ , l ₂ = длины магнитных цепей.

Коэффициент сцепления

Доля магнитного потока, создаваемого током в первой катушке, которая связана со второй катушкой, называется коэффициентом связи (k) между двумя катушками.

Коэффициент связи, k = M ÷ √ (L ₁ L ₂ )

где M = взаимная индуктивность между двумя катушками,
L ₁ = собственная индуктивность первой катушки,
L ₂ = Самоиндукция второй катушки.

Значение k равно единице, если поток, создаваемый одной катушкой, полностью связан с другой. Из-за эффекта рассеяния потока значение k всегда меньше единицы. Величина взаимной индуктивности зависит от значения коэффициента связи (k). Его значение максимально при k = 1.

Электромагнетизм | Все сообщения

© http://www.yourelectricalguide.com/ Определение и формула самоиндукции.

.