В чем измеряется ЭДС индукции?

В качестве основы для решения задачи используем закон Фарадея для магнитной индукции (о явлении электромагнитной индукции см. раздел «В чем заключается явление электромагнитной индукции?»):

   

где — магнитный поток через плоскость рамки. Его величину можно найти как:

   

Зная, что наша рамка имеет форму квадрата со стороной , ее площадь () будет равна:

   

Используем уравнение изменения индукции магнитного поля, которое задано в условии задачи (), выражение для площади рамки (3), формулу (2), подставив их в (1), получим для ЭДС индукции:

   

Подставим данные из условий задачи, вычислим искомую ЭДС (учтите, что когда будете вычислять после умножения вы получите радианы, а не градусы):

   

Теперь ответим на вопрос: в чем измеряется ЭДС индукции: Как и любая другая ЭДС она измеряется в вольтах (В). Поэтому:
Ответ: В.

В чем измеряется электромагнитная индукция

Взаимосвязь электрических и магнитных полей

Электрические и магнитные явления изучались давно, вот только никому не приходило в голову каким-то образом связать эти исследования между собой. И только в 1820 году было обнаружено, что проводник с током действует на стрелку компаса. Это открытие принадлежало датскому физику Хансу Кристиану Эрстеду. Впоследствии его именем была названа единица измерения напряженности магнитного поля в системе СГС: русское обозначение Э (Эрстед), англоязычное – Oe. Такую напряженность магнитное поле имеет в вакууме при индукции в 1 Гаусс.

Это открытие наводило на мысль о том, что из электрического тока можно получить магнитное поле. Но вместе с тем возникали мысли и по поводу обратного преобразования, а именно, как из магнитного поля получить электрический ток. Ведь многие процессы в природе обратимы: из воды получается лед, который можно снова растопить в воду.

На изучение этого очевидного сейчас закона физики после открытия Эрстеда ушло целых двадцать два года. Получением электричества из магнитного поля занимался английский ученый Майкл Фарадей. Делались различной формы и размеров проводники и магниты, искались варианты их взаимного расположения. И только, видимо, случайно ученый обнаружил, что для получения на концах проводника ЭДС необходимо еще одно слагаемое – движение магнита, т.е. магнитное поле должно быть обязательно переменным.

Сейчас это никого уже не удивляет. Именно так работают все электрические генераторы, — пока его чем-то вращают, электроэнергия вырабатывается, лампочка светит. Остановили, перестали вращать, и лампочка погасла.

Электромагнитная индукция

Таким образом, ЭДС на концах проводника возникает лишь в том случае, если его определенным образом перемещать в магнитном поле. Или, точнее говоря, магнитное поле обязательно должно изменяться, быть переменным. Это явление получило название электромагнитной индукции, по-русски электромагнитное наведение: в этом случае говорят, что в проводнике наводится ЭДС. Если к такому источнику ЭДС подключить нагрузку, то в цепи будет протекать ток.

Величина наведенной ЭДС зависит от нескольких факторов: длины проводника, индукции магнитного поля B, и в немалой степени от скорости перемещения проводника в магнитном поле. Чем быстрее вращать ротор генератора, тем напряжение на его выходе выше.

Замечание: электромагнитную индукцию (явление возникновение ЭДС на концах проводника в переменном магнитном поле) не следует путать с магнитной индукцией – векторной физической величиной характеризующей собственно магнитное поле.

Три способа получения ЭДС

Индукция

Этот способ был рассмотрен в первой части статьи. Достаточно перемещать проводник в магнитном поле постоянного магнита, или наоборот перемещать (практически всегда вращением) магнит около проводника. Оба варианта однозначно позволят получить переменное магнитное поле. В этом случае способ получения ЭДС называется индукцией. Именно индукция используется для получения ЭДС в различных генераторах. В опытах Фарадея в 1831 году магнит поступательно перемещался внутри катушки провода.

Взаимоиндукция

Это название говорит о том, что в этом явлении принимают участие два проводника. В одном из них протекает изменяющийся ток, который создает вокруг него переменное магнитное поле. Если рядом находится еще один проводник, то на его концах возникает переменная же ЭДС.

Такой способ получения ЭДС называется взаимоиндукцией. Именно по принципу взаимоиндукции работают все трансформаторы, только проводники у них выполнены в виде катушек, а для усиления магнитной индукции применяются сердечники из ферромагнитных материалов.

Если ток в первом проводнике прекратится (обрыв цепи), или станет пусть даже очень сильным, но постоянным (нет никаких изменений), то на концах второго проводника никакой ЭДС получить не удастся. Вот почему трансформаторы работают только на переменном токе: если к первичной обмотке подключить гальваническую батарейку, то на выходе вторичной обмотки никакого напряжения однозначно не будет.

ЭДС во вторичной обмотке наводится только при изменении магнитного поля. Причем, чем сильнее скорость изменения, именно скорость, а не абсолютная величина, тем больше будет наведенная ЭДС.

Самоиндукция

Если убрать второй проводник, то магнитное поле в первом проводнике будет пронизывать не только окружающее пространство, но и сам проводник. Таким образом, под воздействием своего поля в проводнике наводится ЭДС, которая называется ЭДС самоиндукции.

Явления самоиндукции в 1833 году изучал русский ученый Ленц. На основании этих опытов удалось выяснить интересную закономерность: ЭДС самоиндукции всегда противодействует, компенсирует внешнее переменное магнитное поле, которое вызывает эту ЭДС. Эта зависимость называется правилом Ленца (не путать с законом Джоуля — Ленца).

Знак «минус» в формуле как раз и говорит о противодействии ЭДС самоиндукции причинам ее породившим. Если катушку подключить к источнику постоянного тока, ток будет возрастать достаточно медленно. Это очень заметно при «прозвонке» первичной обмотки трансформатора стрелочным омметром: скорость движения стрелки в сторону нулевого деления шкалы заметно меньше, чем при проверке резисторов.

При отключении катушки от источника тока ЭДС самоиндукции вызывает искрение контактов реле. В случае, когда катушка управляется транзистором, например катушка реле, то параллельно ей ставится диод в обратном направлении по отношению к источнику питания. Это делается для того, чтобы защитить полупроводниковые элементы от воздействия ЭДС самоиндукции, которая может в десятки и даже сотни раз превышать напряжение источника питания.

Для проведения опытов Ленц сконструировал интересный прибор. На концах алюминиевого коромысла закреплены два алюминиевых же кольца. Одно кольцо сплошное, а в другом был сделан пропил. Коромысло свободно вращалось на иголке.

При введении постоянного магнита в сплошное кольцо оно «убегало» от магнита, а при выведении магнита стремилось за ним. Те же самые действия с разрезанным кольцом никаких движений не вызывали. Это объясняется тем, что в сплошном кольце под воздействием переменного магнитного поля возникает ток, который создает магнитное поле. А в разомкнутом кольце тока нет, следовательно, нет и магнитного поля.

Немаловажная деталь этого опыта в том, что если магнит будет введен в кольцо и останется неподвижным, то никакой реакции алюминиевого кольца на присутствие магнита не наблюдается. Это лишний раз подтверждает, что ЭДС индукции возникает только в случае изменения магнитного поля, причем величина ЭДС зависит от скорости изменения. В данном случае просто от скорости перемещения магнита.

То же можно сказать и о взаимоиндукции и самоиндукции, только изменение напряженности магнитного поля, точнее скорость его изменения зависит от скорости изменения тока. Для иллюстрации этого явления можно привести такой пример.

Пусть через две достаточно большие одинаковые катушки проходят большие токи: через первую катушку 10А, а через вторую целых 1000, причем в обеих катушках токи линейно возрастают. Предположим, что за одну секунду ток в первой катушке изменился с 10 до 15А, а во второй с 1000 до 1001А, что вызвало появление ЭДС самоиндукции в обеих катушках.

Но, несмотря на такое огромное значение тока во второй катушке, ЭДС самоиндукции будет больше в первой, поскольку там скорость изменения тока 5А/сек, а во второй всего 1А/сек. Ведь ЭДС самоиндукции зависит от скорости возрастания тока (читай магнитного поля), а не от его абсолютной величины.

Индуктивность

Магнитные свойства катушки с током зависят от количества витков, геометрических размеров. Значительного усиления магнитного поля можно добиться введением в катушку ферромагнитного сердечника. О магнитных свойствах катушки с достаточной точностью можно судить по величине ЭДС индукции, взаимоиндукции или самоиндукции. Все эти явления были рассмотрены выше.

Характеристика катушки, которая рассказывает об этом, называется коэффициентом индуктивности (самоиндукции) или просто индуктивностью. В формулах индуктивность обозначается буквой L, а на схемах этой же буквой обозначаются катушки индуктивности.

Единица измерения индуктивности – генри (Гн). Индуктивностью 1Гн обладает катушка, в которой при изменении тока на 1А в секунду вырабатывается ЭДС 1В. Это величина достаточно большая: индуктивностью в один и более Гн обладают сетевые обмотки достаточно мощных трансформаторов.

Поэтому достаточно часто пользуются величинами меньшего порядка, а именно милли и микро генри (мГн и мкГн). Такие катушки применяются в электронных схемах. Одно из применений катушек – колебательные контура в радиоустройствах.

Также катушки используются в качестве дросселей, основное назначение которых пропустить без потерь постоянный ток при этом ослабив переменный (фильтры в источниках питания). Как правило, чем выше рабочая частота, тем меньшей индуктивности требуются катушки.

Индуктивное сопротивление

Если взять достаточно мощный сетевой трансформатор и померить мультиметром сопротивление первичной обмотки, то окажется, что оно всего несколько Ом, и даже близко к нулю. Выходит, что ток через такую обмотку будет очень большим, и даже стремиться к бесконечности. Кажется, короткое замыкание просто неизбежно! Так почему же его нет?

Одним из основных свойств катушек индуктивности является индуктивное сопротивление, которое зависит от индуктивности и от частоты переменного тока, который подведен к катушке.

Нетрудно видеть, что с увеличением частоты и индуктивности индуктивное сопротивление увеличивается, а на постоянном токе вообще становится равным нулю. Поэтому при измерении сопротивления катушек мультиметром измеряется только активное сопротивление провода.

Конструкция катушек индуктивности весьма разнообразна и зависит от частот, на которых работает катушка. Например, для работы в дециметровом диапазоне радиоволн достаточно часто используются катушки, выполненные печатным монтажом. При массовом производстве такой способ очень удобен.

Индуктивность катушки зависит от ее геометрических размеров, сердечника, количества слоев и формы. В настоящее время выпускается достаточное количество стандартных катушек индуктивности похожих на обычные резисторы с выводами. Маркировка таких катушек выполняется цветными кольцами. Также существуют катушки для поверхностного монтажа, применяемые в качестве дросселей. Индуктивность таких катушек составляет несколько миллигенри.

Поделитесь этой статьей с друзьями:

Вступайте в наши группы в социальных сетях:

В этой статье мы постараемся разобраться в том, что такое магнитная индукция, как она связана с магнитным полем, какое отношение имеет магнитная индукция к току, и как действует на ток. Вспомним основные правила, определяющие направление индукционных линий, а также отметим некоторые формулы, которые помогут в решении задач магнитостатики.

Силовой характеристикой магнитного поля в выбранной точке пространства является магнитная индукция В. Эта векторная величина определяет силу, с которой магнитное поле действует на движущуюся в нем заряженную частицу. Если заряд частицы равен q, ее скорость равна v, а индукция магнитного поля в данной точке пространства равна В, то на частицу в данной точке со стороны магнитного поля действует сила, равная:

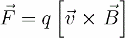
Таким образом, В — это вектор, величина и направление которого таковы, что сила Лоренца, действующая на движущийся заряд со стороны магнитного поля равна:

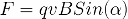
Здесь альфа — это угол между вектором скорости и вектором магнитной индукции. Вектор силы Лоренца F перпендикулярен вектору скорости и вектору магнитной индукции. Его направление для случая движения положительно заряженной частицы в однородном магнитном поле определяется правилом левой руки:

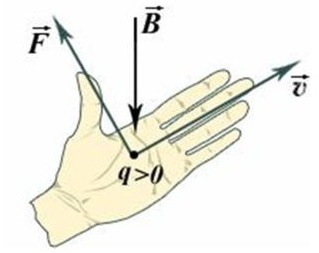
«Если левую руку расположить так, чтобы вектор магнитной индукции входил в ладонь, а четыре вытянутых пальца были направлены по направлению движения положительно заряженной частицы, то отогнутый на 90 градусов большой палец покажет направление силы Лоренца».

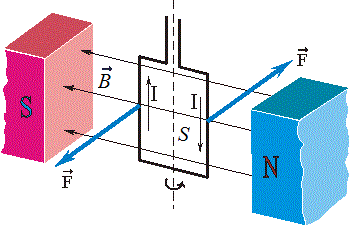
Поскольку ток в проводнике является движением заряженных частиц, то магнитную индукцию можно определить и как отношение максимального механического момента, действующего со стороны однородного магнитного поля на рамку с током, к произведению силы тока в рамке на площадь рамки:

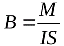
Магнитная индукция — фундаментальная характеристика магнитного поля, как напряженность для электрического поля . В системе СИ магнитная индукция измеряется в тесла (Тл), в системе СГС — в гауссах (Гс). 1 тесла = 10000 гаусс. 1 Тл — это индукция такого однородного магнитного поля, в котором на рамку площадью 1 м2, по которой течет ток в 1 А, действует максимальный вращающий механический момент сил, равный 1 Н • м.

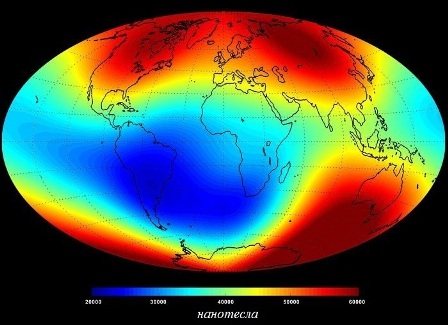
Кстати, индукция магнитного поля Земли на широте 50° в среднем составляет 0,00005 Тл, а на экваторе — 0,000031 Тл. Вектор магнитной индукции всегда направлен по касательной к магнитной силовой линии.

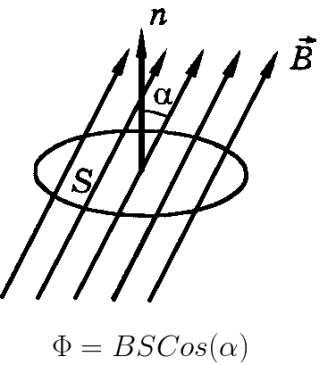
Контур, помещенный в однородное магнитное поле, пронизывается магнитным потоком Ф, — потоком вектора магнитной индукции. Величина магнитного потока Ф зависит от направления вектора магнитной индукции относительно контура, от его величины, и от площади контура, пронизываемого линиями магнитной индукции. Если вектор В будет перпендикулярен площади контура, то магнитный поток Ф, пронизывающий контур, будет максимальным.

Сам термин индукция происходит от латинского «индукцио», что означает «наведение» (например, навести на мысль – то есть вызвать мысль). Синонимы: наведение, возникновение, образование. Не путать с явлением электромагнитной индукции.

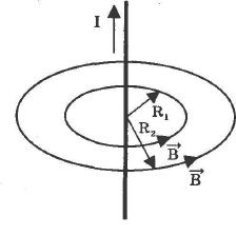
Проводник с током имеет вокруг себя магнитное поле. Открыл магнитное поле электрического тока в 1820 году датский физик Ханс Кристиан Эрстед. Для определения направления силовых линий индукции магнитного поля В электрического тока I, текущего по прямолинейному проводнику, пользуются правилом правого винта или буравчика:

«Направление вращения рукоятки буравчика показывает направление линий магнитной индукции В, а поступательное движение буравчика тогда соответствует направлению тока в проводнике.»

При этом величина магнитной индукции B на расстоянии R от проводника с током I может быть найдена про формуле:

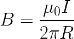
где магнитная постоянная:

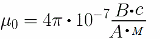
Если линии напряженности электростатического поля Е начинаясь на положительных зарядах, заканчиваются на отрицательных, то линии магнитной индукции B замкнуты всегда. В отличие от электрических зарядов, магнитных зарядов, которые бы создавали полюса подобно электрическим зарядам, в природе не обнаружено.

Теперь несколько слов о постоянных магнитах. Еще в начале 19 века, французский исследователь и физик-естествоиспытатель Андре-Мари Ампер выдвинул гипотезу о молекулярных токах. Согласно Амперу, движения электронов вокруг атомных ядер порождают элементарные токи, которые в свою очередь создают вокруг себя элементарные магнитные поля. И если кусок ферромагнетика поместить во внешнее магнитное поле, то эти микроскопические магнитики сориентируются во внешнем поле, и кусок ферромагнетика станет магнитом.

Вещества с большим значением остаточной намагниченности, такие как сплав неодим-железо-бор, позволяют сегодня получать мощные постоянные магниты. Неодимовые магниты теряют не более 1-2 % своей намагниченности за 10 лет. Но их можно легко размагнитить, нагрев до температуры +70°C и более.

Надеемся, что данная статья помогла Вам получить общее представление о том, что такое магнитная индукция и откуда на возникает.

Причиной электродвижущей силы может стать изменение магнитного поля в окружающем пространстве. Это явление называетсяэлектромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением

где — поток магнитного поля через замкнутую поверхность , ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца).

41. Индуктивность, ее единица СИ. Индуктивность длинного соленоида.

Индукти́вность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность [1] , краем которой является этот контур. [2][3][4] .

— магнитный поток, — ток в контуре, — индуктивность.

Нередко говорят об индуктивности прямого длинного провода(см.). В этом случае и других (особенно — в не отвечающих квазистационарному приближению) случаях, когда замкнутый контур непросто адекватно и однозначно указать, приведенное выше определение требует особых уточнений; отчасти полезным для этого оказывается подход (упоминаемый ниже), связывающий индуктивность с энергией магнитного поля.

Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока [4] :

.

Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.

При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током [4] :

.

Обозначение и единицы измерения

В системе единиц СИ индуктивность измеряется в генри [7] , сокращенно Гн, в системе СГС — в сантиметрах (1 Гн = 10 9 см) [4] . Контур обладает индуктивностью в один генри, если при изменении тока на один ампер в секунду на выводах контура будет возникать напряжение в один вольт. Реальный, не сверхпроводящий, контур обладает омическим сопротивлением R, поэтому на нём будет дополнительно возникать напряжение U=I*R, где I — сила тока, протекающего по контуру в данное мгновение времени.

Символ , используемый для обозначения индуктивности, был взят в честь Ленца Эмилия Христиановича (Heinrich Friedrich Emil Lenz) [ источник не указан 1017 дней ] . Единица измерения индуктивности названа в честь Джозефа Генри (Joseph Henry) [8] . Сам термин индуктивность был предложен Оливером Хевисайдом (Oliver Heaviside) в феврале 1886 года [ источник не указан 1017 дней ] .

Электрический ток, который течет в замкнутом контуре, создает вокруг себя магнитное поле, индукция которого, согласно закону Био-Савара-Лапласа, пропорциональна току. Сцепленный с контуром магнитный поток Ф поэтому прямо пропорционален току I в контуре: (1) где коэффициент пропорциональности L называетсяиндуктивностью контура. При изменении в контуре силы тока будет также изменяться и сцепленный с ним магнитный поток; значит, в контуре будет индуцироваться э.д.с. Возникновение э.д.с. индукции в проводящем контуре при изменении в нем силы тока называетсясамоиндукцией. Из выражения (1) задается единица индуктивности генри (Гн): 1 Гн — индуктивность контура, магнитный поток самоиндукции которого при токе в 1 А равен 1 Вб: 1 Гн = 1 Вб/с = 1 В

Вычислим индуктивность бесконечно длинного соленоида. Полный магнитный поток сквозь соленоид (потокосцепление) равен μ_{μ(N 2 I/l)S . Подставив в (1), найдем (2) т. е. индуктивность соленоида зависит от длиныl солениода, числа его витков N, его , площади S и магнитной проницаемости μ вещества, из которого изготовлен сердечник соленоида. Доказано, что индуктивность контура зависит в общем случае только от геометрической формы контура, его размеров и магнитной проницаемости среды, в которой он расположен, и можно провести аналог индуктивности контура с электрической емкостью уединенного проводника, которая также зависит только от формы проводника, его размеров и диэлектрической проницаемости среды. Найдем, применяя к явлению самоиндукции закон Фарадея, что э.д.с. самоиндукции равна Если контур не претерпевает деформаций и магнитная проницаемость среды остается неизменной (в дальнейшем будет показано, что последнее условие выполняется не всегда), то L = const и(3) где знак минус, определяемый правилом Ленца, говорит о том, чтоналичие индуктивности в контуре приводит к замедлению изменения тока в нем. Если ток со временем увеличивается, то (dI/dt 0 т. е. ток самоиндукции направлен навстречу току, обусловленному внешним источником, и замедляет его увеличение. Если ток со временем уменьшается, то (dI/dt>0) и ξs >1), обладающей боль­шой индуктивностью, э.д.с. самоиндукции может во много раз превышать э.д.с. источника тока, включенного в цепь. Таким образом, необходимо учитывать, что контур, содержащий индуктивность, нельзя резко размыкать, так как это (возникнове­ние значительных э.д.с. самоиндукции) может привести к пробою изоляции и выводу из строя измерительных приборов. Если в контур сопротивление вводить постепенно, то э.д.с. самоиндукции не достигнет больших значений.}

43. Явление взаимной индукции. Трансформатор.

Рассмотрим два неподвижных контура (1 и 2), которые расположены достаточно близко друг от друга (рис. 1). Если в контуре 1 протекает ток I₁, то магнитный поток, который создавается этим током (поле, создающее этот поток, на рисунке изображено сплошными линиями), прямо пропорционален I₁. Обозначим через Ф₂₁ часть потока,пронизывающая контур 2. Тогда (1) где L₂₁ — коэффициент пропорциональности.

Если ток I₁ меняет свое значение, то в контуре 2 индуцируется э.д.с. ξ_i2 , которая по закону Фарадея будет равна и противоположна по знаку скорости изменения магнитного потока Ф₂₁, который создается током в первом контуре и пронизыващет второй: Аналогичным образом, при протекании в контуре 2 тока I₂ магнитный поток (его поле изображено на рис. 1 штрихами) пронизывает первый контур. Если Ф₁₂ — часть этого потока, который пронизывает контур 1, то Если ток I₂ меняет свое значение, то в контуре 1 индуцируется э.д.с. ξ_i1 , которая равна и противоположна по знаку скорости изменения магнитного потока Ф₁₂, который создается током во втором контуре и пронизывает первый: Явление возникновения э.д.с. в одном из контуров при изменении силы тока в другом называется взаимной индукцией. Коэффициенты пропорциональности L₂₁ и L₁₂ называются взаимной индуктивностью контуров. Расчеты, которые подтверждены опытом, показывают, что L₂₁ и L₁₂ равны друг другу, т. е. (2) Коэффициенты пропорциональности L₁₂ и L₂₁ зависят от размеров, геометрической формы, взаимного расположения контуров и от магнитной проницаемости среды, окружающей контуры. Единица взаимной индуктивности та же, что и для индуктивности, — генри (Гн). Найдем взаимную индуктивность двух катушек, которые намотаны на общий тороидальный сердечник. Этот случай имеет большое практическое значение (рис. 2). Магнитная индукция поля, которое создавается первой катушкой с числом витков N₁, током I₁ и магнитной проницаемостью μ сердечника, B = μμ_{(N1I1/l) где l — длина сердечника по средней линии. Магнитный поток сквозь один виток второй катушки Ф2 = BS = μμ(N1I1/l)S}

Значит, полный магнитный поток (потокосцепление) сквозь вторичную обмотку, которая содержит N₂ витков, Поток Ψ создается током I₁, поэтому, используя (1), найдем (3) Если рассчитать магнитный поток, который создавается катушкой 2 сквозь катушку 1, то для L₁₂ получим выражение в соответствии с формулой (3). Значит, взаимная индуктивность двух катушек, которые намотаны на общий тороидальный сердечник,

Трансформа́тор (от лат. transformo — преобразовывать) — это статическое электромагнитное устройство, имеющее две или более индуктивно связанных обмоток на каком-либо магнитопроводе и предназначенное для преобразования посредствомэлектромагнитной индукции одной или нескольких систем (напряжений) переменного тока в одну или несколько других систем (напряжений) переменного тока без изменения частоты системы (напряжения) переменного тока

Электродвижущая сила индукции

Электрические токи порождают вокруг себя магнитные поля. Данная связь дала толчок к многочисленным попыткам создать электрический ток в контуре при помощи магнитного поля.

Данную задачу решил М. Фарадей в 1831 году. Ученый открыл явление электромагнитной индукции.

Электромагнитная индукция

Явление электромагнитной индукции заключается в том, что в замкнутом проводящем контуре, если изменяется поток магнитной индукции, который рассматриваемый контур охватывает, появляется электрический ток. Возникающий электрический ток называют током индукции.

Анализируя свои множественные эксперименты, М. Фарадей пришел к выводу о том, что:

1. Индукционный ток появляется всегда при изменении магнитного потока, который охватывает проводящий контур. Так, если в однородном магнитном поле проводящий замкнутый контур повернуть, то в момент разворота в нем будет течь ток индукции. В этом случае индукция магнитного поля постоянна около проводящего контура, переменным является только поток магнитной индукции, который изменяется за счет изменения площади контура.
2. Величина тока индукции не связана со способом изменения магнитного потока. Она определена только скоростью его изменения. Сила тока индукции тем больше, чем больше скорость перемещения магнита, или быстрота изменения силы тока, или скорость перемещения катушек.

Электромагнитная индукция подтверждает связь между электрическими и магнитными явлениями.

Закон Фарадея

Анализируя данные своих экспериментов, М. Фарадей предложил количественный закон, описывающий электромагнитную индукцию. Ученый доказал, что каждый раз при изменении потока магнитной индукции, который сцеплен с проводящим контуром, в проводнике появляется ток индукции. Наличие индукционного тока означает то, что в цепи присутствует электродвижущая сила (ЭДС), которую в данном случае называют электродвижущей силой электромагнитной индукции ($Ɛ_i$).

Величина тока индукции, а значит, и величина $Ɛ_i$ зависит от скорости изменения магнитного потока:

$\left|Ɛ_{i} \right|=\frac{dФ}{dt}\left( 1 \right)$.

где $Ф$ — поток магнитной индукции.

Определимся со знаком ЭДС индукции. Знак потока магнитной индукции связан с выбором положительной нормали к рассматриваемому проводящему контуру. А направление силы тока и направление нормали связывает правило правого буравчика (винта). Получается, что фиксируя направление нормали, мы устанавливаем знак магнитного потока, направление тока и $Ɛ_i$ в контуре.

Сформулируем закон электромагнитной индукции Фарадея в окончательном виде:

Определение 1

Не зависимо от причины изменения магнитного потока, который охватывает замкнутый проводящий контур, электродвижущая сила индукции, появляющаяся в этом контуре равна:

$Ɛ_{i}=-\frac{dФ}{dt}\left( 2 \right)$.

где под $\frac{dФ}{dt}$ понимают полную скорость изменения потока магнитной индукции, охватываемого проводником.

Минус в формуле (2) указывает на то, что:

• При росте потока магнитной индукции (скорость изменения магнитного потока больше нуля) ($\frac{dФ}{dt}>0)$, ЭДС индукции меньше нуля ($Ɛ_i
• При уменьшении потока магнитной индукции (скорость изменения магнитного потока меньше нуля), ЭДС индукции больше нуля ($Ɛ_i>0$). Что значит, направление потока и направление поля тока индукции совпадают.

Замечание 1

Знак минус в формуле (2) – это математическое отображение правила Ленца, которое используют для того, чтобы найти направление тока индукции.

Закон Фарадея справедлив при:

1. произвольных перемещениях замкнутого проводящего контура;
2. при любых его деформациях;
3. изменениях магнитного поля.

ЭДС индукции измеряется с Международной системе единиц (СИ) в вольтах (В).

$\left[ Ɛ_{i} \right]=\left[ \frac{dФ}{dt} \right]=\frac{Вб}{с}$=В.

Значение закона Фарадея

Закон Фарадея выражает новое физическое явление, в котором переменное магнитное поле порождает электрическое поле. Отсюда делается вывод о том, что электрическое поле может порождаться не только электрическими зарядами, но и изменяющимся магнитным полем.

Электромагнитная индукция – это всеобщий фундаментальный закон природы, реализующий связь между электрическими и магнитными полями.

Природа электродвижущей силы индукции

Если проводник перемещается в магнитном поле, то на свободные электроны его вещества действуют силы Лоренца. Эти электроны под воздействием названной силы приходят в движение относительно проводника, что означает: в проводнике появляется ток.

Рисунок 1. Проводники. Автор24 — интернет-биржа студенческих работ

Рассмотрим прямой участок $DG$ проводника на рис.1. Этот участок перемещается со скоростью $\vec v$ по проводникам $CK$ и $AL$, как по направляющим. При этом контур $AGDCA$ постоянно замкнут. Вектор индукции внешнего магнитного поля нормален плоскости рассматриваемого контура. Магнитное поле будем считать однородным. На заряды, которые перемещаются вместе с проводником, действует сила Лоренца, равная:

$\vec{F}_{L}=q\left( \vec{v}\times \vec{B} \right)\left( 3 \right)$.

где$ \vec{B}$– индукция внешнего магнитного поля. Под воздействием силы Лоренца свободные электроны проводника приходят в движение и образуют электрический ток. Направление этого тока принимают за положительный обход контура, положительная нормаль ($\vec n$) к площади контура указана на рис.1.

Наличие силы Лоренца эквивалентно тому, что в проводнике на заряды действует электрическое поле напряженность которого равна:

$\vec{E}=\frac{\vec{F}_{L}}{q}=\vec{v}\times \vec{B}\left( 4 \right)$.

Поэтому ЭДС индукции между точками 1 и 2 проводника найдем как:

$\left( Ɛ_{i} \right)_{21}=\int\limits_1^2 \vec{E} d\vec{l}=\int\limits_1^2\left( \vec{v}\times \vec{B} \right) d\vec{l}\left( 5 \right)$.

В случае, который мы рассматриваем на рис.1 точки 1 и 2 соответствуют точкам $D$ и $G$:

$\left( Ɛ_{i} \right)_{DG}=\int\limits_G^D {vBdl=vBl\, \left( 6 \right).} $

На не движущихся участках замкнутого контура, который мы рассматриваем, ЭДС не возникает. Следовательно, ЭДС контура равна ЭДС подвижного проводника $DG$, перемещающейся в магнитном поле.

$Ɛ_{i}=\int\limits_{AGDCA} {\vec{E}d\vec{l}=vBl\, \left( 7 \right).} $

Скорость перемещения проводника выразим как:

$v=\frac{dx}{dt}\left( 8 \right)$.

где $x$ — координата контактов проводника в точках $D$ и $G$ направляющими проводниками:

$Ɛ_{i}=Bl\frac{dx}{dt}\left( 9 \right)$.

Учитывая, что:

$Ф=-xlB$ (10),

где $Ф$ — поток магнитной индукции через поверхность, которую ограничивает контур $AGDCA$. Знак минус указывает на то, что направления векторов $\vec B$ и $ d\vec S$ противоположны,

окончательно имеем:

$Ɛ_{i}=-\frac{dФ}{dt}\left( 11 \right)$.

Выражение (11) мы получили, рассматривая движение части проводника. При перемещении нескольких участков проводника, ЭДС индукции находят как алгебраическую сумму ЭДС индукции, появляющихся на каждом участке.

Самоиндукция — Википедия

Самоиндукция — это явление возникновения ЭДС индукции в проводящем контуре ^[1] при изменении протекающего через контур тока.

При изменении тока в контуре пропорционально меняется^[2] и магнитный поток через поверхность, ограниченную этим контуром^[3]. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС.

Это явление и называется самоиндукцией. (Понятие родственно понятию взаимоиндукции, являясь как бы его частным случаем).

Направление ЭДС самоиндукции всегда оказывается таким, что при возрастании тока в цепи ЭДС самоиндукции препятствует этому возрастанию (направлена против тока), а при убывании тока — убыванию (сонаправлена с током). Явление самоиндукции проявляется в замедлении процессов исчезновения и установления тока^[4].

При сопоставлении силы электрического тока со скоростью в механике и электрической индуктивности с массой в механике ЭДС самоиндукции сходна с силой инерции.

Величина ЭДС самоиндукции пропорциональна скорости изменения силы тока(переменного) i{\displaystyle i}:

E=−Ldidt{\displaystyle {\mathcal {E}}=-L{\frac {di}{dt}}}.

Коэффициент пропорциональности L{\displaystyle L} называется коэффициентом самоиндукции или индуктивностью контура (катушки).

В случае синусоидальной зависимости тока, текущего через катушку, от времени, ЭДС самоиндукции в катушке отстает от тока по фазе на π/2{\displaystyle \pi /2} (то есть на 90°), а амплитуда этой ЭДС пропорциональна амплитуде тока, частоте и индуктивности (E0=LωI0{\displaystyle {\mathcal {E}}_{0}=L\omega I_{0}}). Ведь скорость изменения функции — это её первая производная, а dsin⁡ωtdt=ωcos⁡ωt=ωsin⁡(ωt+π/2){\displaystyle {\frac {d\sin \omega t}{dt}}=\omega \cos \omega t=\omega \sin(\omega t+\pi /2)}.

Для расчета более или менее сложных схем, содержащих индуктивные элементы, то есть витки, катушки и т.п. устройства, в которых наблюдается самоиндукция, (особенно, полностью линейных, то есть не содержащих нелинейных элементов^[5]) в случае синусоидальных токов и напряжений применяют метод комплексных импедансов или, в более простых случаях, менее мощный, но более наглядный его вариант — метод векторных диаграмм.

Заметим, что всё описанное применимо не только непосредственно к синусоидальным токам и напряжениям, но и практически к произвольным, поскольку последние могут быть практически всегда разложены в ряд или интеграл Фурье и таким образом сведены к синусоидальным.

В более или менее непосредственной связи с этим можно упомянуть о применении явления самоиндукции (и, соответственно, катушек индуктивности) в разнообразных колебательных контурах, фильтрах, линиях задержки и других разнообразных схемах электроники и электротехники.

За счёт явления самоиндукции в электрической цепи с источником ЭДС при замыкании цепи ток устанавливается не мгновенно, а через какое-то время. Аналогичные процессы происходят и при размыкании цепи, при этом (при резком размыкании) величина ЭДС самоиндукции может в этот момент значительно превышать ЭДС источника.

Чаще всего в обычной жизни это используется в катушках зажигания автомобилей. Типичное напряжение зажигания при напряжении питающей батареи 12В составляет 7-25 кВ. Впрочем, превышение ЭДС в выходной цепи над ЭДС батареи здесь обусловлено не только резким прерыванием тока, но и коэффициентом трансформации, поскольку чаще всего используется не простая катушка индуктивности, а катушка-трансформатор, вторичная обмотка которой как правило имеет во много раз большее количество витков (то есть, в большинстве случаев схема несколько более сложна, чем та, работа которой полностью объяснялось бы через самоиндукцию; однако физика её работы и в таком варианте отчасти совпадает с физикой работы схемы с простой катушкой).

Это явление применяется и для поджига люминесцентных ламп в стандартной традиционной схеме (здесь речь идет именно о схеме с простой катушкой индуктивности — дросселем).

Кроме того, его надо учитывать всегда при размыкании контактов, если ток течет по нагрузке с заметной индуктивностью: возникающий скачок ЭДС может приводить к пробою межконтактного промежутка и/или другим нежелательным эффектам, для подавления которых в этом случае, как правило, необходимо принимать разнообразные специальные меры.

1. ↑ Контур может быть и многовитковым — то есть, в частности, катушкой. В этом случае, так же как и в случае одиночного контура, строго говоря, контур должен быть замкнутым (например, через вольтметр, измеряющий ЭДС), но на практике при (очень) большом количестве витков различие ЭДС в полностью замкнутом контуре и в контуре с разрывом (геометрически даже большим по сравнению с размером катушки) может быть пренебрежимым.
2. ↑ Поскольку магнитный поток через контур пропорционален току в контуре. Для тонкого жесткого контура (для какового случая это утверждение и является точным) точная пропорциональность очевидна исходя из закона Био-Савара, так как исходя из него вектор магнитной индукции просто пропорционален току, а поток этого вектора (что и называется магнитным потоком) через фиксированную (она не меняется при жестком контуре) поверхность тогда тоже пропорционален току. Формально это записывается в виде равенства: магнитный поток = коэффициент самоиндукции• ток в контуре.
3. ↑ В случае сложной формы контура, например, если контур многовитковый (катушка), поверхность, ограниченная контуром (или, как говорят, «натянутая на контур») оказывается достаточно сложной, что ничуть не меняет сути описываемого явления. Для упрощения понимания случая многовитковых контуров (катушек) можно (приближенно) считать поверхность, натянутую на такой контур, состоящей из множества (стопки) поверхностей, каждая из которых натянута на свой отдельный единичный виток.
4. ↑ Калашников С. Г., Электричество, М., ГИТТЛ, 1956, гл. IX «Электромагнитная индукция», п. 107 «Исчезновение и установление тока», с. 221 — 224;
5. ↑ Сами индуктивные элементы являются линейными, то есть подчиняются линейному дифференциальному уравнению, приведенному в статье выше. Впрочем, это уравнение в реальности выполняется лишь приближенно, так что индуктивные элементы являются линейными также лишь приближенно (хотя иногда и с крайне хорошей точностью). Также в реальности встречаются отклонения от идеального уравнения, носящие линейный характер (например, связанные с упругими деформациями катушки в линейном приближении).

Электромагнитная индукция

Магнитный поток. В однородном магнитном поле, модуль вектора индукции которого равен В, помещен плоский замкнутый контур площадью S. Нормаль n к плоскости контура составляет угол a с направлением вектора магнитной индукции В (см. рис. 1).
Магнитным потоком через поверхность называется величина Ф, определяемая соотношением:

Ф = В·S·cos a.         
      
Единица измерения магнитного потока в систем СИ — 1 Вебер (1 Вб).

Электромагнитная индукция. Явление электромагнитной индукции обнаружено в 1831 г. Фарадеем. Оно выражает взаимосвязь электрических и магнитных явлений.
Рассмотрим некоторые экспериментальные факты:

постоянный магнит вставляют в катушку, замкнутую на гальванометр, или вынимают из нее. При движении магнита в контуре возникает электрический ток

Аналогичный результат будет иметь место в случае перемещения электромагнита, по которому пропускают постоянный ток, относительно первичной катушки или при изменении тока в неподвижной вторичной катушке.

рамку, замкнутую на гальванометр, помещают в однородное магнитное поле и вращают. В рамке возникает электрический ток. Если же рамка движется поступательно, не пересекая силовых линий, то ток в ней не возникает.

рамка движется  в неоднородном магнитном поле. Число линий индукции, пересекающих рамку, изменяется. В рамке возникает электрический ток

Ток, возникающий в контуре при изменении магнитного потока, называют индукционным током.
Вы знаете, что условием существования электрического тока в замкнутом контуре является наличие электродвижущей силы, поддерживающей разность потенциалов. Следовательно, при изменении магнитного потока, пронизывающего замкнутый контур, в нем возникает ЭДС, которую называют ЭДС индукции (ei).

Явление возникновения ЭДС в контуре при изменении магнитного потока, пронизывающего контур, называется электромагнитной индукцией.
Если контур замкнут, то ЭДС индукции проявляется в возникновении электрического индукционного тока
I = ei/R , где R- сопротивление контура.
Если контур разомкнут, то на концах проводника возникает разность потенциалов, равная ei.
Направление индукционного тока в контуре определяется правилом Ленца:
Индукционный ток направлен так, чтобы своим магнитным полем противодействовать изменению магнитного потока, которым он вызван.
Направление индукционного тока определяется следующим образом:

   1. установить направление внешнего магнитного поля В.
   2. определить увеличивается или уменьшается поток вектора магнитной индукции внешнего поля.
   3. по правилу Ленца указать направление вектора магнитной индукции индукционного тока Вi.
   4. по правилу правого винта определить направление индукционного тока в контуре.

ЭДС индукции в движущемся проводнике. Пусть проводник длиной L перемещается со скоростью V в однородном магнитном поле, пересекая силовые линии. Вместе с проводником движутся заряды, находящиеся в проводнике. На движущийся в магнитном поле заряд действует сила Лоренца. Свободные электроны смещаются к одному концу проводника, а на другом остаются нескомпенсированные положительные заряды. Возникает разность потенциалов, которая и представляет собой ЭДС индукции ei. Ее величину можно определить, рассчитав работу, совершаемую силой Лоренца при перемещении заряда вдоль проводника:

ei = A/q = F·L/q.

Отсюда следует, что
ei = B·V·L·sin a.

Самоиндукция является частным случаем разнообразных проявлений электромагнитной индукции.

Рассмотрим контур, подключенный к источнику тока. По контуру протекает электрический  ток I. Этот ток создает в окружающем пространстве магнитное поле. В результате контур пронизывается собственным магнитным потоком Ф. Очевидно, что собственный магнитный поток пропорционален току в контуре, создавшему магнитной поле:
Ф = L·I.

Коэффициент пропорциональности L называется индуктивностью контура. Индуктивность зависит от размеров, формы проводника, магнитных свойств среды. Единица измерения индуктивности в системе СИ — 1 Генри (Гн).
Если ток в контуре изменяется, то изменяется и собственный магнитный поток Фс. Изменение величины Фс приводит к возникновению в контуре ЭДС индукции. Данное явление называется самоиндукцией, а соответствующее значение — ЭДС самоиндукции eiс.
Из закона электромагнитной индукции следует, что
eiс = dФс/dt.

Если L = const, то eiс= — L·dI/dt.

Электромагнитная индукция

Определение электромагнитной индукции

Возникновение электрического тока в проводнике, движущемся в магнитном поле, называют явлением индукцией в движущихся проводниках. В случае движения проводника в магнитном поле, его свободные электроны приходят в движение относительно проводника под воздействием силы Лоренца. Явление электромагнитной индукции обнаружил Фарадей в 1831 г. в проводящем контуре. Он заметил, что в замкнутом проводящем контуре при изменении потока магнитной индукции через поверхность, которую ограничивает контур, появляется электрический ток. Это также явление электромагнитной индукции, возникающий ток в контуре, называют индукционным.

Итак, явление электромагнитной индукции состоит в возникновении электрического тока в замкнутом проводнике при изменении потока магнитной индукции, охватываемого контуром. При этом контур может быть неподвижным.

ЭДС индукции

Существование явления электромагнитной индукции говорит о том, что при изменении магнитного потока в контуре появляется электродвижущая сила индукции (ЭДС, ${{\mathcal E}}_i$). Величина ${{\mathcal E}}_i$ не зависит от способа изменения магнитного потока $(Ф)$, и связана со скоростью его изменения ($\frac{dФ}{dt}$). С изменением знака скорости изменения потока направление ЭДС индукции тоже изменяется:

Знак потока $Ф$ и знак ${{\mathcal E}}_i$ связывают с выбором направления нормали к плоскости контура. ${{\mathcal E}}_i$ считают положительной если ее направление образует с направлением нормали к контуру правый винт. Для рис 1. и заданном направлении нормали «от нас», перпендикулярно плоскости рисунка ($\overrightarrow{n}$) $\frac{dФ}{dt} >0,\ {{\mathcal E}}_i

Рисунок 1.

Основной единицей измерения индукционной ЭДС служит вольт $(В)$. Если скорость изменения магнитного потока равна $1\frac{Вб}{с}$ в контуре индуцируется ЭДС, равная $1 В$.

В гауссовой системе формула (1) принимает вид:

где $с$ — скорость света в вакууме. Основной единицей измерения магнитного потока в СГСЭ является максвелл $(Мкс)$, тогда ${{\mathcal E}}_i$ измеряется в СГСЭ — единицах потенциала. Для того, чтобы перевести ЭДС из системы гаусса в вольты необходимо умножить имеющееся значение на $300$. Следовательно, формулой связи системы СИ и СГСЭ можно записать выражение:

Среднее значение ЭДС индукции может быть определено как:

Поток сцепления

Если контур, в котором индуцируется ЭДС, состоит из $N$ витков (соленоид), витки соединены последовательно, ${{\mathcal E}}_i$ равна сумме ЭДС, которые индуцируются каждым витком в отдельности. Следовательно, используя формулу (1), можно записать:

Величину $\Psi$, равную:

называют потоком сцепления, или полным магнитным потоком. В том случае, если поток, который пронизывает каждый из витков, одинаковый, то можно записать, что:

В сложном контуре ${{\mathcal E}}_i$ вычисляют как:

Уравнение (8) называют основным законом электромагнитной индукции (уравнением Фарадея — Максвелла).

Частные случаи применения закона электромагнитной индукции

1. Если проводник длины $l\ $движется в однородном магнитном поле (с индукцией $В$) с постоянной скоростью $v$, то на его концах возникает разность потенциалов $U$:

где $\alpha $ — угол между направлением скорости и вектором магнитной индукции.

1. ЭДС индукции возникает в рамке, которая содержит $N$ витков, имеет площадь $S$ и вращается с постоянной угловой скоростью $\omega$ в однородном магнитном поле с индукцией $В$ и она равна:

где $\omega t$ — мгновенное значение угла между вектором магнитной индукции ($\overrightarrow{B}$) и вектором нормали к плоскости рамки ($\overrightarrow{n}$).

Пример 1

Задание: Найдите мгновенное значение ЭДС индукции рамки, которое соответствует углу поворота рамки $\alpha ,$ площадь рамки, равна $S$, она содержит $N$ витков. Рамка вращается в постоянном магнитном поле с индукцией $B$. Частота вращения рамки равна $n$.

Решение:

За основу решения задачи примем уравнение Фарадея — Максвелла:

\[{{\mathcal E}}_i=-\frac{d \Psi}{dt}\ \left(1.1\right),\]

где потокосцепление можно определить как:

\[\Psi=NФ\ \left(1.2\right),\]

где $N$ — количество витков, которые пронизывает магнитный поток $Ф$. Соответственно (1.1) примет вид:

\[{{\mathcal E}}_i=-N\frac{dФ}{dt}\ \left(1.3\right).\]

Если рамку вращать, то магнитный поток изменяется в соответствии с законом:

\[Ф=BScos\omega t\left(1.4\right),\]

где $\omega $ — угловая частота вращения. Подставим выражение (1.4) в (1.3), получим:

\[{{\mathcal E}}_i=NBS\omega sin\omega t\left(1.5\right).\]

Связь угловой частоты и часты вращения, определим как:

\[\omega =2\pi n\ \left(1.6\right),\] \[\omega t=\alpha \left(1.7\right).\]

Подставим выражения (1.6), (1.7) в формулу (1.5) получим:

\[{{\mathcal E}}_i=2\pi nNBSsin\alpha .\]

Ответ: ${{\mathcal E}}_i=2\pi nNBSsin\alpha .$

Пример 2

Задание: Определите среднее ЭДС индукции ($\left\langle {{\mathcal E}}_i\right\rangle )$, если магнитный поток, который пронизывает контур, изменяется от $Ф_1=40Вб$ до $Ф_2=0Вб$ в течении промежутка времени равного $2 с$.

Решение:

За основу решения примем формулу, определяющую среднюю ЭДС индукции:

\[\left\langle {{\mathcal E}}_i\right\rangle =-\frac{\Delta Ф}{\Delta t}\left(2.1\right).\]

Проведем вычисления:

\[\left\langle {{\mathcal E}}_i\right\rangle =-\frac{0-40}{2}=20\ \left(В\right).\]

Ответ: $\left\langle {{\mathcal E}}_i\right\rangle =20 В$.