Эдс самоиндукции
Изменение тока в катушке вызывает изменение потока сцепления самоиндукции, а следовательно возникает ЭДС.
Явление, при котором ЭДС возникает в контуре или в катушке в результате изменения тока в этом контуре или катушке, называется самоиндукцией.
ЭДС самоиндукции
обозначается  .
.

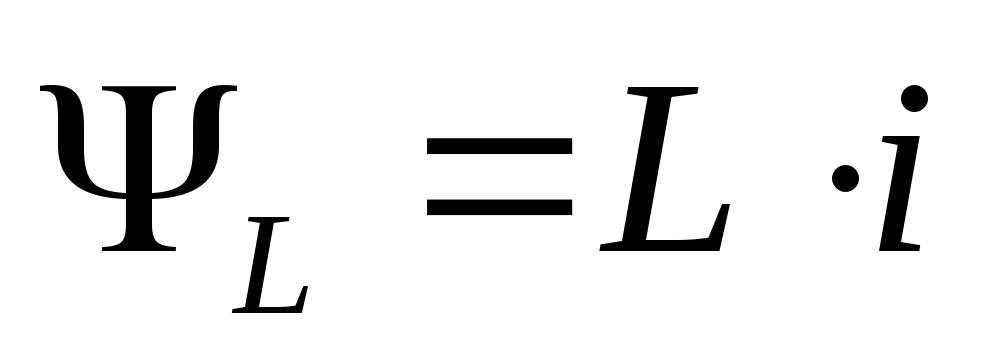

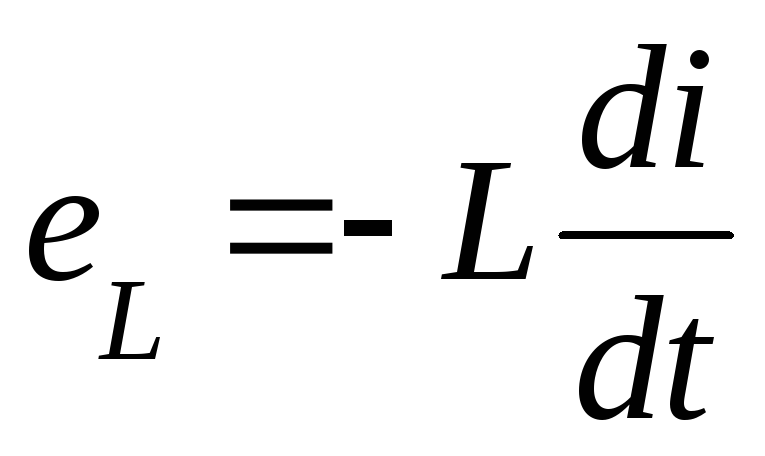
Т.о. ЭДС самоиндукции пропорциональна индуктивности катушки и скорости изменения тока в ней.
Если  (ток нарастает), то
(ток нарастает), то — отрицательна, т.е. направлена навстречу
току (противо ЭДС), если же
— отрицательна, т.е. направлена навстречу
току (противо ЭДС), если же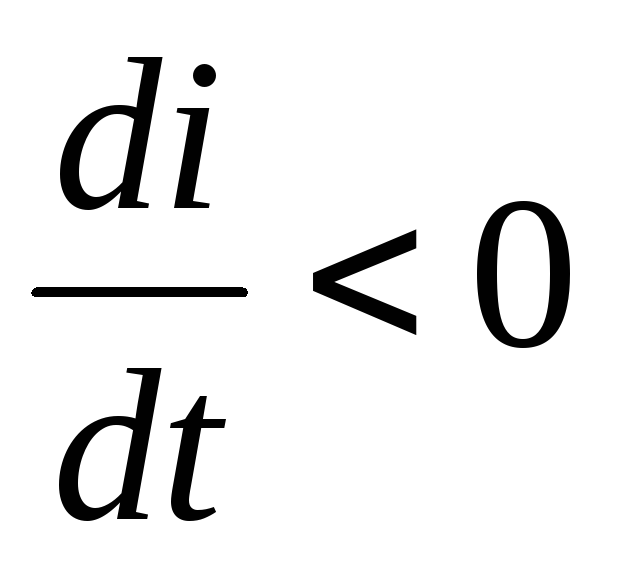 (ток убывает), то
(ток убывает), то — положительна, т.е. направлена согласно
с током.
— положительна, т.е. направлена согласно
с током.

Время нарастания и уменьшения тока характеризуется постоянным временем.
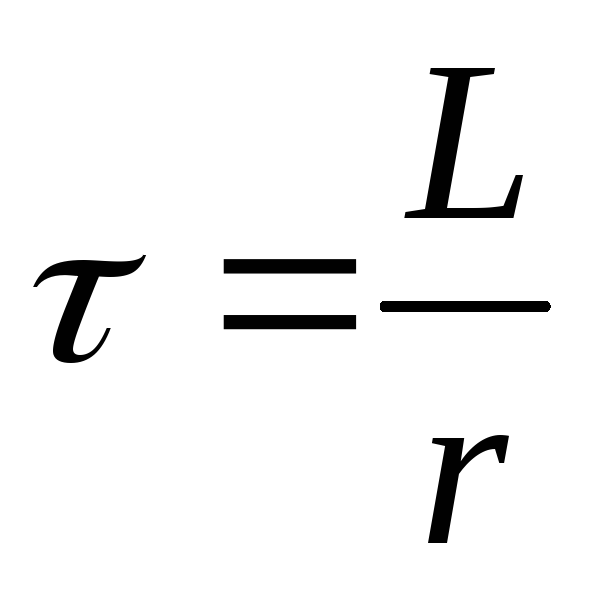
 —
«тау»
—
«тау»
При включении катушки в электрическую цепь вокруг катушки создается магнитное поле, в котором запасается часть энергии, израсходованной источниками.
Величина этой
энергии определяется как: 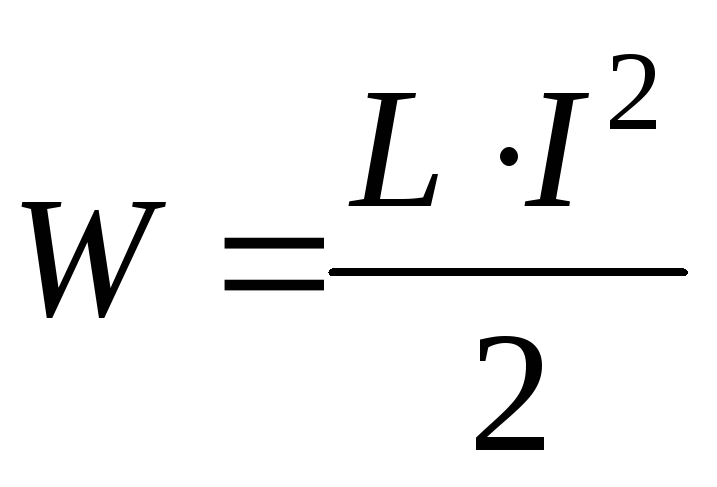
Явление взаимоиндукции
| Если две катушки с током расположены близко друг от друга, то часть магнитного потока первой катушки пронизывает витки второй и наоборот. Такие контуры и катушки называют индуктивно- или магнитосвязанными. |
Магнитный поток  ,
а следовательно и потокосцепление
,
а следовательно и потокосцепление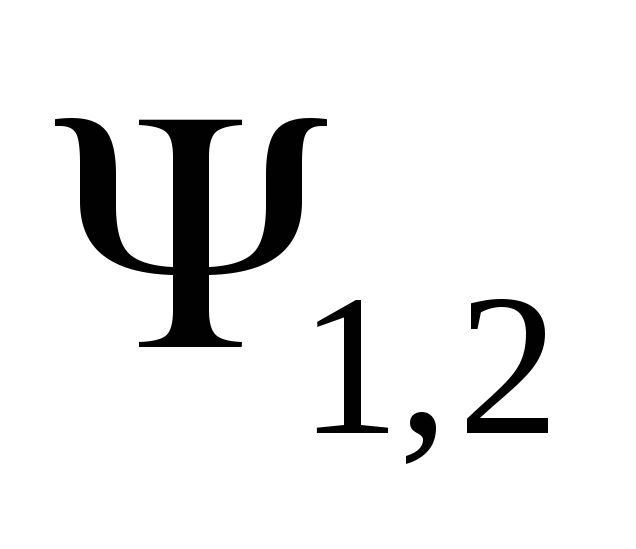
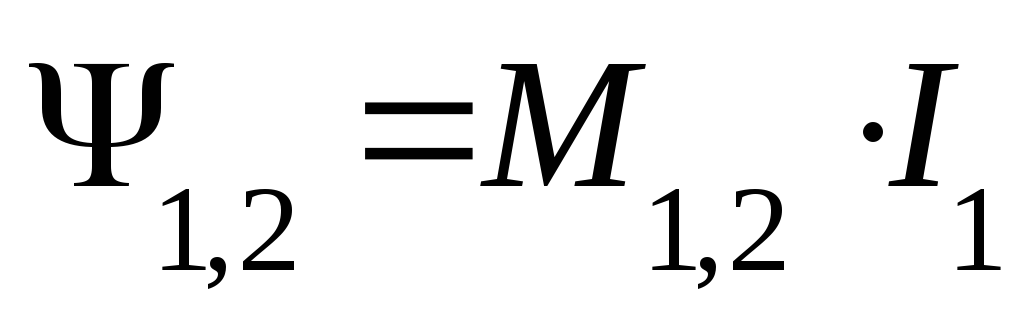

М– взаимная индуктивность двух катушек, равная отношению потокосцепления одной катушки к току другой.
ЭДС, возникающая
при этом в другой катушке будет равна: 
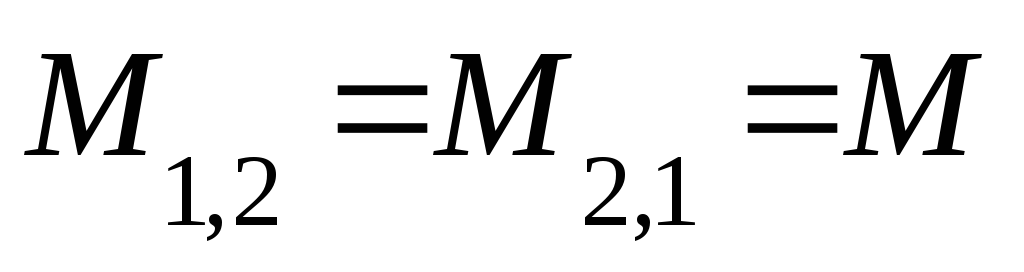

 ,
,
где K– коэффициент связи двух катушек, зависящий от взаимного их расположения (чем ближе катушка, тем большеKи наоборот).
Однофазный переменный ток
Переменнымназывают такой электрический ток, который с течением времени изменяется по величине и по направлению.
Основным достоинством переменного тока является возможность его трансформации, а также то, то электрические машины и аппараты переменного тока значительно проще и дешевле, чем постоянного тока.
Время, в течении которого ток делает полный цикл своих изменений называется периодом.
Величина, обратная
периоду и численно равная числу периодов
за секунду, называется частотой  .
.
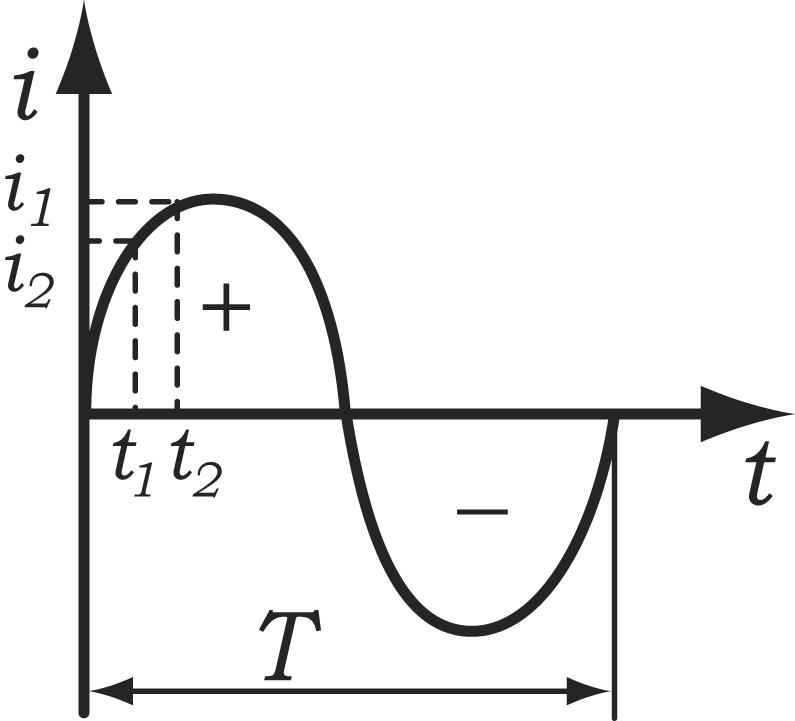
Значение переменного тока в любой момент времени называется мгновенным значением.
Наибольшее из
мгновенных значений называется максимальным, илиамплитудным 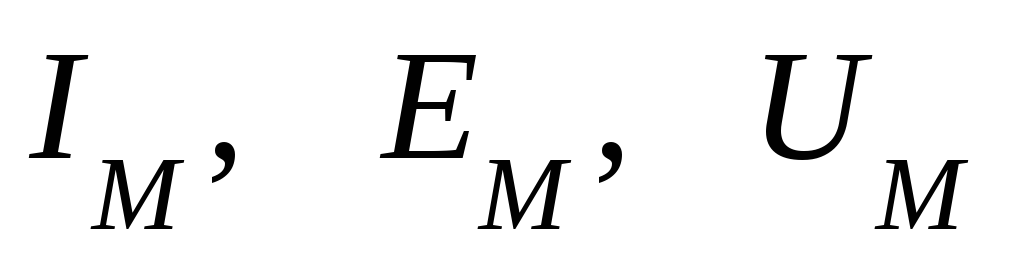
Получение синусоидальной ЭДС
Простейший генератор
переменного тока представляет собой
магнитную систему, состоящую из двух
полюсов, причем, форма полюсов такова,
что магнитная индукция в воздушном
зазоре распределяется по синусоидальному
закону, т.е. значение магнитной индукции
в любой точке 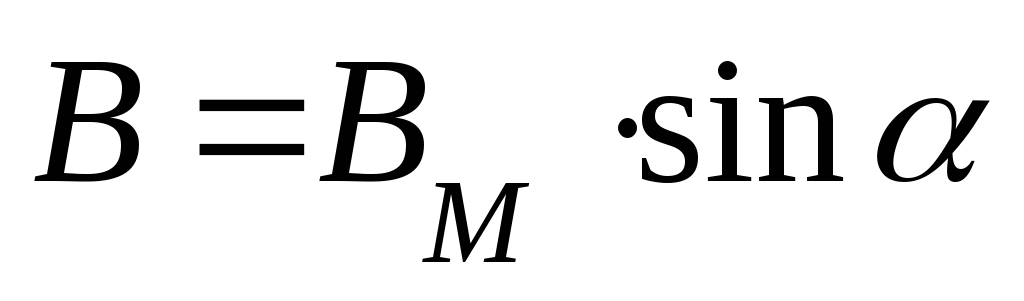 .
.

Допустим, за время tрамка развернулась
на угол, тогда
угловая скорость
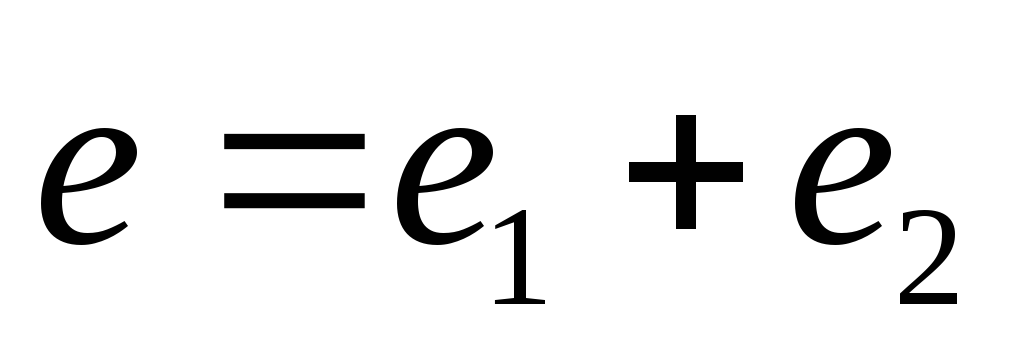



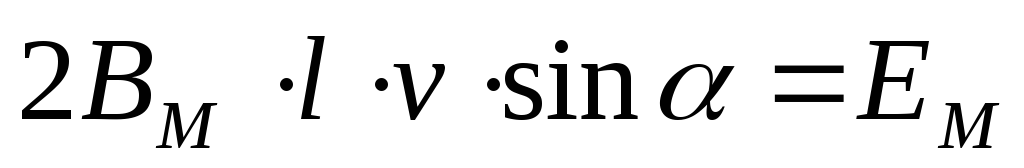


 —
угловая скорость (частота)
—
угловая скорость (частота)
За один оборот
рамка развернется на угол  ,
а время оборота – период (Т), тогда
угловая частота
,
а время оборота – период (Т), тогда
угловая частота определяется:
определяется:

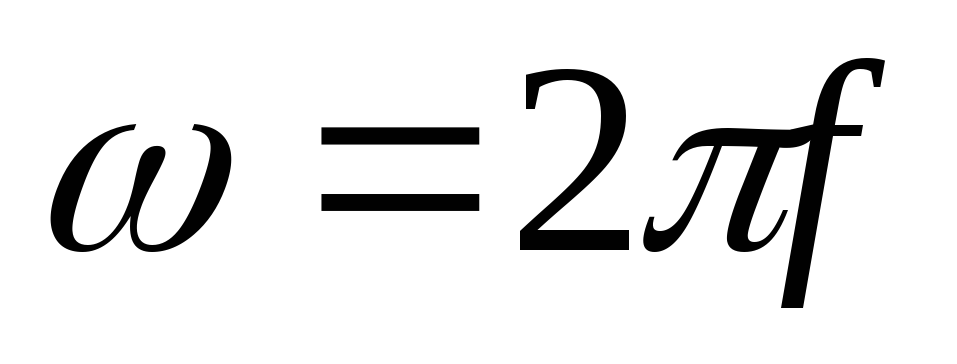
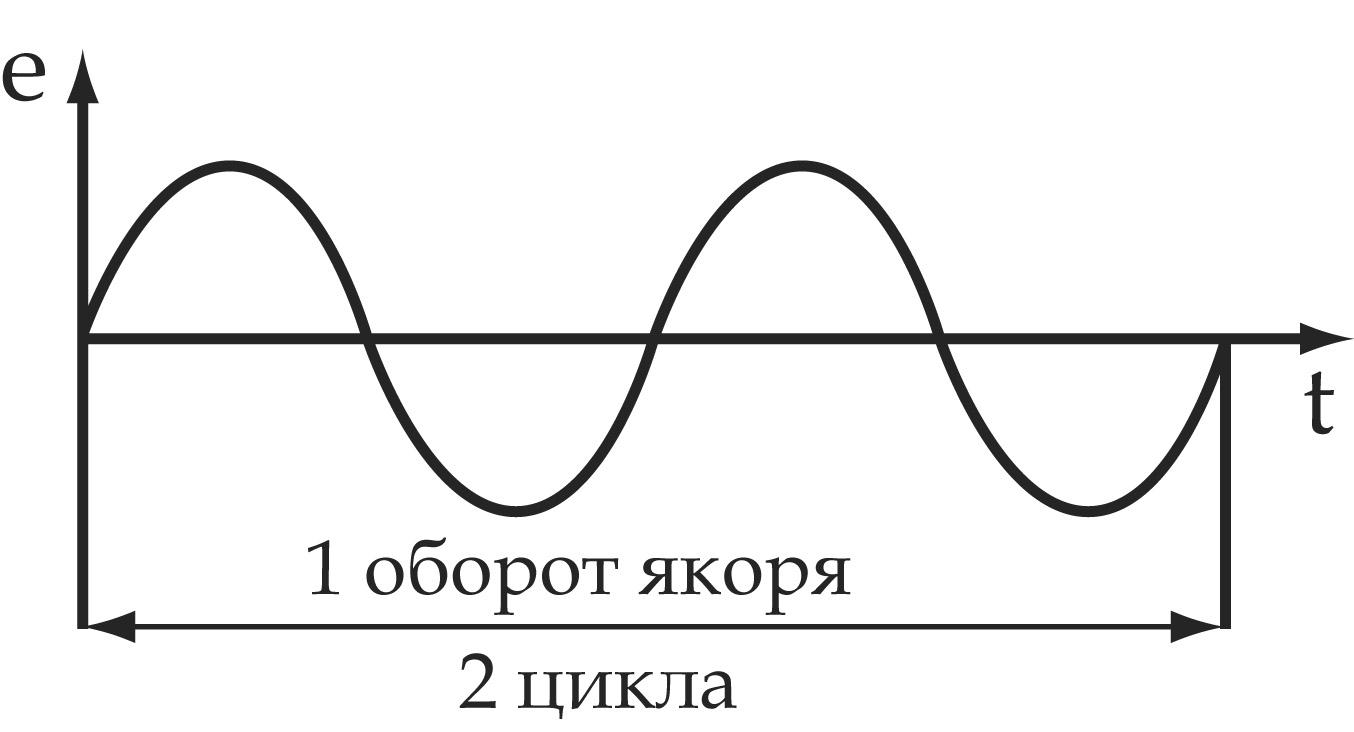
Многополюсные генераторы
| Для получения промышленной частоты 50Гц якорь двухполюсного генератора должен вращаться со скоростью 50 об/с или 3000 об/мин. Если скорость вращения меньше, то необходимо увеличить число пар полюсов. У многополюсных генераторов за 1 оборот якоря ЭДС совершает Р циклов своих |
 ,
а в секунду
,
а в секунду
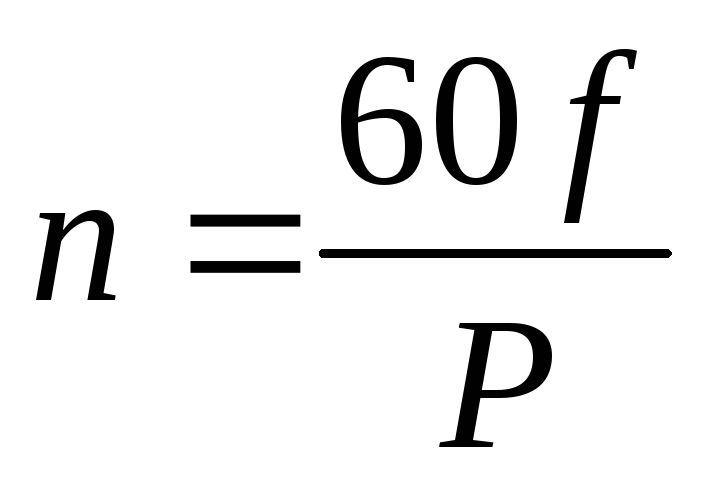
определение, формула, применение на практике
«Самоиндукция останавливает рост напряжения в индуктивных цепях». Если ваша работа или увлечение связаны с электричеством вы наверняка слышали подобные высказывания. На самом деле это явление присуще индуктивным цепям, как в явном виде, например, катушек, так и в неявном, такие как паразитные параметры кабеля. В этой статье мы простыми словами расскажем о том, что такое самоиндукция и где она применяется.
Определение
Самоиндукцией называется появление в проводнике электродвижущей силы (ЭДС), направленной в противоположную сторону относительно напряжения источника питания при протекании тока. При этом оно возникает в момент, когда сила тока в цепи изменяется. Изменяющийся электрической ток порождает изменяющееся магнитное поле, оно в свою очередь наводит ЭДС в проводнике.

Это похоже на формулировку закона электромагнитной индукции Фарадея, где сказано:
При прохождении магнитного потока через проводник, в последнем возникает ЭДС. Она пропорциональна скорости изменения магнитного потока (мат. производная по времени).
То есть:
E=dФ/dt,
Где E – ЭДС самоиндукции, измеряется в вольтах, Ф – магнитный поток, единица измерения – Вб (вебер, он же равен В/с)
Индуктивность
Мы уже сказали о том, что самоиндукция присуща индуктивным цепям, поэтому рассмотрим явление самоиндукции на примере катушки индуктивности.

Катушка индуктивности – это элемент, который представляет собой катушку из изолированного проводника. Для увеличения индуктивности увеличивают число витков или внутрь катушки помещают сердечник из магнитомягкого или другого материала.
Единица измерения индуктивности – Генри (Гн). Индуктивность характеризует то, насколько сильно проводник противодействует электрическому току. Так как вокруг каждого проводника, по которому протекает ток, образуется магнитное поле, и, если поместить проводник в переменное поле – в нем возникнет ток. В свою очередь магнитные поля каждого витка катушки складываются. Тогда вокруг катушки, по которой протекает ток, возникнет сильное магнитное поле. При изменении его силы в катушке будет изменяться и магнитный поток вокруг неё.
Согласно закону электромагнитной индукции Фарадея, если катушку будет пронизывать переменный магнитный поток, то в ней возникнет ток и ЭДС самоиндукции. Они будут препятствовать току, который протекал в индуктивности от источника питания к нагрузке. Их еще называют экстратоки ЭДС самоиндукции.
Формула ЭДС самоиндукции на индуктивности имеет вид:

То есть чем больше индуктивность, и чем больше и быстрее изменился ток – тем сильнее будет всплеск ЭДС.
При возрастании тока в катушке возникает ЭДС самоиндукции, которая направлена против напряжения источника питания, соответственно возрастание тока замедлится. То же самое происходит при убывании – самоиндукция приведет к появлению ЭДС, которое будет поддерживать ток в катушке в том же направлении, что и до этого. Отсюда следует, что напряжение на выводах катушки будет противоположным полярности источника питания.
На рисунке ниже вы видите, что при включении/отключении индуктивной цепи ток не резко возникает, а изменяется постепенно. Об этом говорят и законы коммутации.

Другое определение индуктивности звучит так: магнитный поток пропорционален току, но в его формуле индуктивность выступает в качестве коэффициента пропорциональности.
Ф=L*I
Трансформатор и взаимоиндукция
Если расположить две катушки в непосредственной близости, например, на одном сердечнике, то будет наблюдаться явление взаимоиндукции. Пропустим переменный ток по первой, тогда её переменный поток будет пронизывать витки второй и на её выводах появится ЭДС.

Это ЭДС будет зависеть от длины провода, соответственно количества витков, а также от величины магнитной проницаемости среды. Если их расположить просто около друг друга — ЭДС будет низким, а если взять сердечник из магнитомягкой стали – ЭДС будет значительно больше. Собственно, так и устроен трансформатор.
Интересно: такое взаимное влияние катушек друг на друга называют индуктивной связью.
Польза и вред
Если вам понятна теоретическая часть, стоит рассмотреть где применяется явление самоиндукции на практике. Рассмотрим на примерах того, что мы видим в быту и технике. Одно из полезнейших применений – это трансформатор, принцип его работы мы уже рассмотрели. Сейчас встречаются все реже, но ранее ежедневно использовались люминесцентные трубчатые лампы в светильниках. Принцип их работы основан на явлении самоиндукции. Её схемы вы можете увидеть ниже.

После подачи напряжения ток протекает по цепи: фаза — дроссель — спираль — стартер — спираль — ноль.
Или наоборот (фаза и ноль). После срабатывания стартера, его контакты размыкаются, тогда дроссель (катушка с большой индуктивностью) стремится поддержать ток в том же направлении, наводит ЭДС самоиндукции большой величины и происходит розжиг ламп.
Аналогично это явление применяется в цепи зажигания автомобиля или мотоцикла, которые работают на бензине. В них в разрыв между катушкой индуктивности и минусом (массой) устанавливают механический (прерыватель) или полупроводниковый ключ (транзистор в ЭБУ). Этот ключ в момент, когда в цилиндре должна образоваться искра для зажигания топлива, разрывает цепь питания катушки. Тогда энергия, запасенная в сердечнике катушки, вызывает рост ЭДС самоиндукции и напряжение на электроде свечи возрастает до тех пор, пока не наступит пробой искрового промежутка, или пока не сгорит катушка.

В блоках питания и аудиотехнике часто возникает необходимость убрать из сигнала лишние пульсации, шумы или частоты. Для этого используются фильтры разных конфигурации. Один из вариантов это LC, LR-фильтры. Благодаря препятствию роста тока и сопротивлению переменного тока, соответственно, возможно добиться поставленных целей.

Вред ЭДС самоиндукции приносит контактам выключателей, рубильников, розеток, автоматов и прочего. Вы могли заметить что, когда вытаскиваете вилку работающего пылесоса из розетки, очень часто заметна вспышка внутри неё. Это и есть сопротивление изменению тока в катушке (обмотке двигателя в данном случае).

В полупроводниковых ключах дело обстоит более критично – даже небольшая индуктивность в цепи может привести к их пробою, при достижении пиковых значений Uкэ или Uси. Для их защиты устанавливают снабберные цепи, на которых и рассеивается энергия индуктивных всплесков.

Заключение
Подведем итоги. Условиями возникновения ЭДС самоиндукции является: наличие индуктивности в цепи и изменение тока в нагрузке. Это может происходить как в работе, при смене режимов или возмущающих воздействиях, так и при коммутации приборов. Это явление может нанести вред контактам реле и пускателей, так как приводит к образованию дуги при размыкании индуктивных цепей, например, электродвигателей. Чтобы снизить негативное влияние большая часть коммутационной аппаратуры оснащается дугогасительными камерами.
В полезных целях явление ЭДС используется довольно часто, от фильтра для сглаживания пульсаций тока и фильтра частот в аудиоаппаратуре, до трансформаторов и высоковольтных катушек зажигания в автомобилях.
Напоследок рекомендуем просмотреть полезное видео по теме, на которых кратко и подробно рассматривается явление самоиндукции:
Надеемся, теперь вам стало понятно, что такое самоиндукция, как она проявляется и где ее можно использовать. Если возникли вопросы, задавайте их в комментариях под статьей!
Материалы по теме:
Вопрос 34 Электромагнитная индукция. Самоиндукция.
Электромагнитная индукция.
Электрические токи создают вокруг себя магнитное поле. 1831 г. английский физик М. Фарадей открыл явление электромагнитной индукции (заключающееся в том, что в замкнутом проводящем контуре при изменении потока магнитной индукции, охватываемого этим контуром, возникает электрический ток, получивший название индукционного). Опытным путем было также установлено, что значение индукционного тока совершенно не зависит от способа изменения потока магнитной индукции, а определяется лишь скоростью его изменения. Открытие явления электромагнитной индукции имело большое значение, так как была доказана возможность получения электрического тока с помощью магнитного поля.
Закон Фарадея и его вывод из закона сохранения энергии:
Фарадей пришел к количественному закону электромагнитной индукции. Он показал, что всякий раз, когда происходит изменение сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток; возникновение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой электромагнитной индукции. Значение индукционного тока, а следовательно, и э. д. с, электромагнитной индукции ξi определяются только скоростью изменения магнитного потока, т. е.

закона электромагнитной индукции Фарадея: какова бы ни была причина изменения потока магнитной индукции, охватываемого замкнутым проводящим контуром, возникающая в контуре э.д.с.

Знак минус показывает, что увеличение потока (dФ/dt>0) вызывает э.д.с.
ξξi<0, т. е. поле индукционного тока направлено навстречу потоку; уменьшение
потока (dФ/dt<0 ) вызывает ξi>0,
т. е. направления потока и поля индукционного тока совпадают. Знак минус в формуле (123.2) является математическим выражением правила Ленца — общего правила для нахождения направления индукционного тока, выведенного в 1833 г.
Правило Ленца: индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшего этот индукционный ток.
Закон Фарадея э.д.с. ξi электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром. Этот закон является универсальным: э.д.с. ξi не зависит от способа изменения магнитного потока.
Э.д.с. электромагнитной индукции выражается в вольтах. Действительно, учитывая, что единицей магнитного потока является вебер (Вб), получим

При вращении рамки в ней будет возникать переменная э.д.с. индукции (см. (123.2))
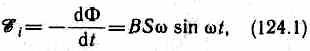
Вихревые токи (токи Фуко)
Индукционный ток возникает не только в линейных проводниках, но и в массивных сплошных проводниках, помещенных в переменное магнитное поле. Эти токи оказываются замкнутыми в толще проводника и поэтому называются вихревыми. Их также называют токами Фуко — по имени первого исследователя.
Токи Фуко, как и индукционные токи в линейных проводниках, подчиняются правилу Ленца: их магнитное поле направлено так, чтобы противодействовать изменению магнитного потока, индуцирующего вихревые токи. Индуктивность контура. Самоиндукция
Электрический ток, текущий в замкнутом контуре, создает вокруг себя магнитное поле, индукция которого, по закону Био — Савара—Лапласа (см. (110.2)), пропорциональна току. Сцепленный с контуром магнитный поток Ф поэтому пропорционален току I в контуре:
Ф=LI, (126.1)
где коэффициент пропорциональности L называется индуктивностью контура.
При изменении силы тока в контуре будет изменяться также и сцепленный с ним магнитный поток; следовательно, в контуре будет индуцироваться э.д.с. Возникновение э.д.с. индукции в проводящем контуре при изменении в нем силы тока называется самоиндукцией.
Из выражения (126.1) определяется единица индуктивности генри (Гн): 1 Гн — индуктивность такого контура, магнитный поток самоиндукции которого при токе в 1 А равен 1 Вб:
1 Гн=1 Вб/А=1В•с/А.
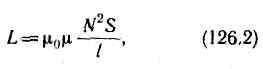
т. е. индуктивность соленоида зависит от числа витков соленоида N, его длины l, площади S и магнитной проницаемости вещества, из которого изготовлен сердечник соленоида.
Применяя к явлению самоиндукции закон Фарадея (см. (123.2)), получим, что э.д.с. самоиндукции
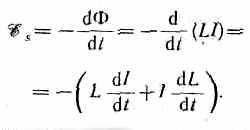
Если контур не деформируется и магнитная проницаемость среды не изменяется (в дальнейшем будет показано, что последнее условие выполняется не всегда), то L=const и
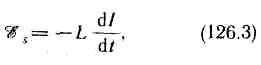
Вопрос №30
Действие магнитного поля на движущийся заряд
Опыт показывает, что магнитное поле действует не только на проводники с током (см. §111), но и на отдельные заряды, движущиеся в магнитном поле. Сила, действующая на электрический заряд Q, движущийся в магнитном поле со скоростью v, называется силой Лоренца и выражается формулой
F=Q[vB], (114.1) где В — индукция магнитного поля, в котором заряд движется.
Направление силы Лоренца определяется с помощью правила левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора v (для Q> 0 направления I и v совпадают, для Q<0—противоположны), то отогнутый большой палец покажет направление силы, действующей на положительный заряд. На рис. 169 показана взаимная ориентация векторов v, В (поле направлено к нам, на рисунке показано точками) и F для положительного заряда. На отрицательный заряд сила действует в противоположном направлении.
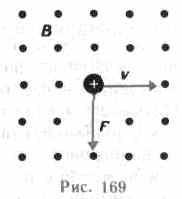
Модуль силы Лоренца (см. (114.1)) равен
F=QvBsin,
где — угол между v и В.
Отметим еще раз (см. § 109), что магнитное поле не действует на покоящийся электрический заряд. В этом существенное отличие магнитного поля от электрического. Магнитное поле действует только на движущиеся в нем заряды.
Так как по действию силы Лоренца можно определить модуль и направление вектора В, то выражение для силы Лоренца может быть использовано (наравне с другими, см. § 109) для определения вектора магнитной индукции В.
Сила Лоренца всегда перпендикулярна скорости движения заряженной частицы, поэтому она изменяет только направление этой скорости, не изменяя ее модуля. Следовательно, сила Лоренца работы не совершает. Иными словами, постоянное магнитное поле не совершает работы над движущейся в нем заряженной частицей и кинетическая энергия этой частицы при движении в магнитном поле не изменяется.
Если на движущийся электрический заряд помимо магнитного поля с индукцией В действует и электрическое поле с напряженностью Е, то результирующая сила F, приложенная к заряду, равна векторной сумме сил — силы, действующей со стороны электрического поля, и силы Лоренца:
F=QE + Q[vB].
Это выражение называется формулой Лоренца. Скорость v в этой формуле есть скорость заряда относительно магнитного поля.
Движение заряженных частиц в магнитном поле
Выражение для силы Лоренца (114.1) позволяет найти ряд закономерностей движения заряженных частиц в магнитном поле. Направление силы Лоренца и направление вызываемого ею отклонения заряженной частицы в магнитном поле зависят от знака заряда Q частицы. На этом основано определение знака заряда частиц, движущихся в магнитных полях.
Для вывода общих закономерностей будем считать, что магнитное поле однородно и на частицы электрические поля не действуют. Если заряженная частица движется в магнитном поле со скоростью v вдоль линий магнитной индукции, то угол а между векторами v и В равен 0 или . Тогда по формуле (114.1) сила Лоренца равна нулю, т. е. магнитное поле на частицу не действует и она движется равномерно и прямолинейно.
Если заряженная частица движется в магнитном поле со скоростью v, перпендикулярной вектору В, то сила Лоренца F=Q[vB] постоянна по модулю и нормальна к траектории частицы. Согласно второму закону Ньютона, эта сила создает центростремительное ускорение. Отсюда следует, что частица будет двигаться по окружности, радиус r которой определяется из условия
QvB = mv2/r,
откуда

Период вращения частицы, т. е. время Т, затрачиваемое ею на один полный оборот,
T = 2nr/v.
Подставив сюда выражение (115.1), получим
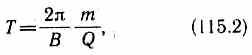
т. е. период вращения частицы в однородном магнитном поле определяется только величиной, обратной удельному заряду

(Q/m) частицы, и магнитной индукцией поля, но не зависит от ее скорости (при v << с)). На этом основано действие циклических ускорителей заряженных частиц (см. §116).
Если скорость v заряженной частицы направлена под углом а к вектору В (рис. 170), то ее движение можно представить в виде суперпозиции: 1) равномерного прямолинейного движения вдоль поля со скоростью v||=vcos; 2) равномерного движения со скоростью v┴= vsin по окружности в плоскости, перпендикулярной полю. Радиус окружности определяется формулой (115.1) (в данном случае надо заменить v на v┴=vsin). В результате сложения обоих движений возникает движение по спирали, ось которой параллельна магнитному полю (рис. 170). Шаг винтовой линии
h=v||T=vTcos.
Подставив в последнее выражение (115.2), получим
h=2mv cos/(BQ).
Направление, в котором закручивается спираль, зависит от знака заряда частицы.
Если скорость v заряженной частицы составляет угол а с направлением вектора В неоднородного магнитного поля, индукция которого возрастает в направлении движения частицы, то r и h уменьшаются с ростом В. На этом основана фокусировка заряженных частиц в магнитном поле.
Вопрос №31
Ускорителями заряженных частиц называются устройства, в которых под действием электрических и магнитных полей создаются и управляются пучки высокоэнергетичных заряженных частиц (электронов, протонов, мезонов и т.д.).
Любой ускоритель характеризуется типом ускоряемых частиц, энергией, сообщаемой частицам, разбросом частиц по энергиям и интенсивностью пучка. Ускорители делятся на непрерывные (из них выходит равномерный по времени пучок) и импульсные (из них частицы вылетают порциями — импульсами). Последние характеризуются длительностью импульса. По форме траектории и механизму ускорения частиц ускорители делятся на линейные, циклические и индукционные. В линейных ускорителях траектории движения частиц близки к прямым линиям, в циклических и индукционных — траекториями частиц являются окружности или спирали.
Рассмотрим некоторые типы ускорителей заряженных частиц.
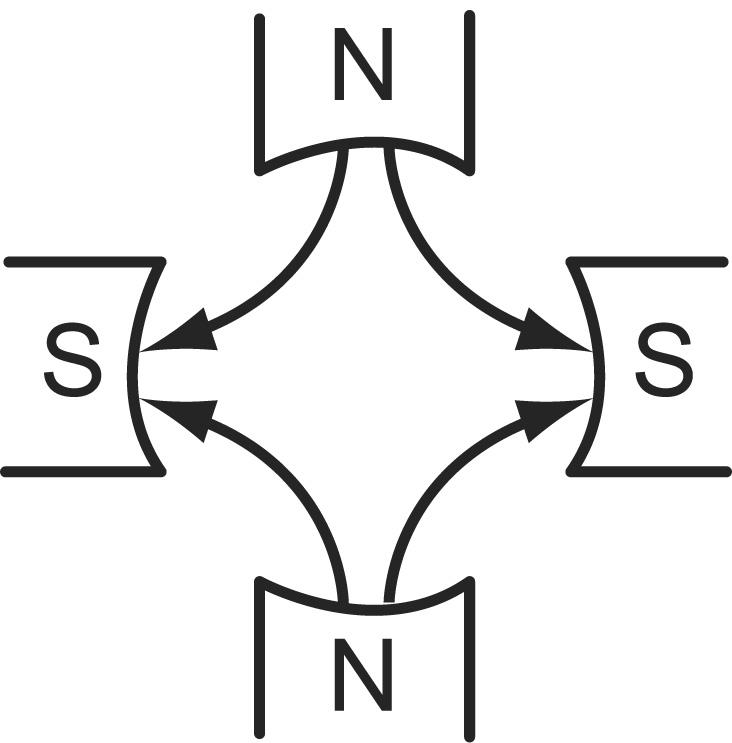
Циклотрон — циклический резонансный ускоритель тяжелых частиц (протонов, ионов). Его принципиальная схема приведена на рис. 171. Между полюсами
Фазотрон (синхроциклотрон) — циклический резонансный ускоритель тяжелых заряженных частиц (например, протонов, ионов, -частиц), в котором управляющее магнитное поле постоянно, а частота ускоряющего электрического поля медленно изменяется с периодом. Движение частиц в фазотроне, как и в циклотроне, происходит по раскручивающейся спирали. Частицы в фазотроне ускоряются до энергий, примерно равных 1 ГэВ (ограничения здесь определяются размерами фазотрона, так как с ростом скорости частиц растет радиус их орбиты).
Синхрофазотрон — циклический резонансный ускоритель тяжелых заряженных частиц (протонов, ионов), в котором объединяются свойства фазотрона и синхротрона, т. е. управляющее магнитное поле и частота ускоряющего электрического поля одновременно изменяются во времени так, чтобы радиус равновесной орбиты частиц оставался постоянным. Протоны ускоряются в синхрофазотроне до энергий 500 ГэВ.
Вопрос №32
Работа по перемещению проводника и контура с током в магнитном поле
На проводник с током в магнитном поле действуют силы, определяемые законом Ампера (см. §111). Если проводник не закреплен (например, одна из сторон контура изготовлена в виде подвижной перемычки, рис. 177), то под действием силы Ампера он будет в магнитном поле перемещаться. Следовательно, магнитное поле совершает работу по перемещению проводника с током.
Для определения этой работы рас-
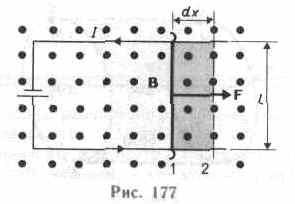
смотрим проводник длиной l с током I (он может свободно перемещаться), помещенный в однородное внешнее магнитное поле, перпендикулярное плоскости контура. При указанных на рис. 177 направлениях тока и поля сила, направление которой определяется по правилу левой руки, а значение — по закону Ампера (см. (111.2)), равна
F=IBl.
Под действием этой силы проводник переместится параллельно самому себе на отрезок Ах из положения 1 в положение 2. Работа, совершаемая магнитным полем, равна
dA=Fdx=IBldx =IBdS= IdФ,
так как ldx=dS— площадь, пересекаемая проводником при его перемещении в магнитном поле, ВdS=dФ — поток вектора магнитной индукции, пронизывающий эту площадь. Таким образом,
dA=IdФ, (121.1)
т. е. работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником. Полученная формула справедлива и для произвольного направления вектора В.
Вычислим работу по перемещению замкнутого контура с постоянным током I в магнитном поле. Предположим, что контур М перемещается в плоскости чертежа и в результате бесконечно малого перемещения займет положение М’, изображенное на рис. 178 штриховой линией. Направление тока в контуре (по часовой стрелке) и магнитного поля (перпендикулярно плоскости чертежа — за чертеж) указано на рисунке. Контур М мысленно

разобьем на два соединенных своими концами проводника: ABC и CDA.
Работа dA, совершаемая силами Ампера при рассматриваемом перемещении контура в магнитном поле, равна алгебраической сумме работ по перемещению проводников ЛВС (dA1) и СDA (dА2), т. е.
dA=dA1+dA2. (121.2)
Силы, приложенные к участку CDA контура, образуют с направлением перемещения острые углы, поэтому совершаемая ими работа dA2>0. Согласно (121.1), эта работа равна произведению силы тока I в контуре на пересеченный проводником CDA магнитный поток. Проводник CDA пересекает при своем движении поток dФ0 сквозь поверхность, выполненную в цвете, и поток dФ2, пронизывающий контур в его конечном положении. Следовательно,
dA2= I(dФ0+dФ2). (121.3)
Силы, действующие на участок ЛВС контура, образуют с направлением перемещения тупые углы, поэтому совершаемая ими работа dA1<0. Проводник ЛВС пересекает при своем движении поток dФ0 сквозь поверхность, выполненную в цвете, и поток dФ1, пронизывающий контур в начальном положении. Следовательно,
dA1=I(dФ0+dФ1). (121.4)
Подставляя (121.3) и (121.4) в (121.2), получим выражение для элементарной работы:
dA=I(dФ2 -dФ1),
где dФ2-dФ1=dФ’— изменение магнитного потока через площадь, ограниченную контуром с током. Таким образом,
dA=IdФ’. (121.5)
Проинтегрировав выражение (121.5), определим работу, совершаемую силами Ампера, при конечном произвольном перемещении контура в магнитном поле:
A=IФ, (121.6)
т. е. работа по перемещению замкнутого
контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока, сцепленного
с контуром. Формула (121.6) остается справедливой для контура любой формы в произвольном магнитном поле.
Вопрос№33
Всякое вещество является магнетиком, т. е. оно способно под действием магнитного поля приобретать магнитный момент (намагничиваться). Для понимания механизма этого явления необходимо рассмотреть действие магнитного поля на движущиеся в атоме электроны.
Ради простоты предположим, что электрон в атоме движется по круговой орбите. Если орбита электрона ориентирована относительно вектора В произвольным образом, составляя с ним угол а (рис. 188), то можно доказать, что она приходит в такое движение вокруг В, при котором вектор магнитного момента рm, сохраняя постоянным угол а, вращается вокруг на-

правления В с некоторой угловой скоростью. Такое движение в механике называется прецессией. Прецессию вокруг вертикальной оси, проходящей через точку опоры, совершает, например, диск волчка при замедлении движения.
Таким образом, электронные орбиты атома под действием внешнего магнитного поля совершают прецессионное движение, которое эквивалентно круговому току. Так как этот микроток индуцирован внешним магнитным полем, то, согласно правилу Ленца, у атома появляется составляющая магнитного поля, направленная противоположно внешнему полю. Наведенные составляющие магнитных полей атомов (молекул) складываются и образуют собственное магнитное поле вещества, ослабляющее внешнее магнитное поле. Этот эффект получил название диамагнитного эффекта, а вещества, намагничивающиеся во внешнем магнитном поле против направления поля, называются диамагнетиками.
В отсутствие внешнего магнитного поля диамагнетик немагнитен, поскольку в данном случае магнитные моменты электронов взаимно компенсируются, и суммарный магнитный момент атома (он равен векторной сумме магнитных моментов (орбитальных и спиновых) составляющих атом электронов) равен нулю. К диамагнетикам относятся многие металлы (например, Bi, Ag, Au, Cu), большинство органических соединений, смолы, углерод и т. д.
Так как диамагнитный эффект обусловлен действием внешнего магнитного поля на электроны атомов вещества, то диамагнетизм свойствен всем веществам. Однако наряду с диамагнитными веществами существуют и парамагнитные — вещества, намагничивающиеся во внешнем магнитном поле по направлению поля.
У парамагнитных веществ при отсутствии внешнего магнитного поля магнитные моменты электронов не компенсируют друг друга, и атомы (молекулы) парамагнетиков всегда обладают магнитным моментом. Однако вследствие теплового движения молекул их магнитные моменты ориентированы беспорядочно, поэтому пара-
магнитные вещества магнитными свойствами не обладают. При внесении парамагнетика во внешнее магнитное поле устанавливается преимущественная ориентация магнитных моментов атомов по полю (полной ориентации препятствует тепловое движение атомов). Таким образом, парамагнетик намагничивается, создавая собственное магнитное поле, совпадающее по направлению с внешним полем и усиливающее его. Этот эффект называется парамагнитным. При ослаблении внешнего магнитного поля до нуля ориентация магнитных моментов вследствие теплового движения нарушается и парамагнетик размагничивается. К парамагнетикам относятся редкоземельные элементы, Pt, Al и т. д. Диамагнитный эффект наблюдается и в парамагнетиках, но он значительно слабее парамагнитного и поэтому остается незаметным.
Из рассмотрения явления парамагнетизма следует, что его объяснение совпадает с объяснением ориентационной (дипольной) поляризации диэлектриков с полярными молекулами (см. §87), только электрический момент атомов в случае поляризации надо заменить магнитным моментом атомов в случае намагничения.
Подводя итог качественному рассмотрению диа- и парамагнетизма, еще раз отметим, что атомы всех веществ являются носителями диамагнитных свойств. Если магнитный момент атомов велик, то парамагнитные свойства преобладают над диамагнитными и вещество является парамагнетиком; если магнитный момент атомов мал, то преобладают диамагнитные свойства и вещество является диамагнетиком.
Подобно тому, как для количественного описания поляризации диэлектриков вводилась поляризованность (см. §88), для количественного описания намагничения магнетиков вводят векторную величину — намагниченность, определяемую магнитным моментом единицы объема магнетика:
J=pm/V=pa/V,
где pm=ра— магнитный
Согласно представлениям Вейсса, ферромагнетики при температурах ниже точки Кюри обладают спонтанной намагниченностью независимо от наличия внешнего намагничивающего поля. Спонтанное намагничение, однако, находится в кажущемся противоречии с тем, что многие ферромагнитные материалы даже при температурах ниже точки Кюри не намагничены. Для устранения этого противоречия Вейсс ввел гипотезу, согласно которой ферромагнетик ниже точки Кюри разбивается на большое число малых макроскопических областей — доменов, самопроизвольно намагниченных до насыщения.
При отсутствии внешнего магнитного поля магнитные моменты отдельных доменов ориентированы хаотически и компенсируют друг друга, поэтому результирующий магнитный момент ферромагнетика равен нулю и ферромагнетик не намагничен. Внешнее магнитное поле ориентирует по полю магнитные моменты не отдельных атомов, как это имеет место в случае парамагнетиков, а целых областей спонтанной намагниченности. Поэтому с ростом Н намагниченность
J (см. рис. 192) и магнитная индукции В (см. рис. 193) уже в довольно слабых полях растут очень быстро. Этим объясняется также увеличение ферромагнетиков до максимального значения в слабых полях (см. рис. 194). Эксперименты показали, что зависимость В от Я не является такой плавной, как показано на рис. 193, а имеет ступенчатый вид. Это свидетельствует о том, что внутри ферромагнетика домены поворачиваются по полю скачком.
При ослаблении внешнего магнитного поля до нуля ферромагнетики сохраняют остаточное намагничение, так как тепловое движение не в состоянии быстро дезориентировать магнитные моменты столь крупных образований, какими являются домены. Поэтому и наблюдается явление магнитного гистерезиса (рис.195). Для того чтобы ферромагнетик размагнитить, необходимо приложить коэрцитивную силу; размагничиванию способствуют также встряхивание и нагревание ферромагнетика. Точка Кюри оказывается той температурой, выше которой происходит разрушение доменной структуры.
ЭДС самоиндукции и индуктивность цепи
Дата публикации: .
Категория: Электротехника.
При замыкании выключателя в цепи, представленной на рисунке 1, возникнет электрический ток, направление которого показано одинарными стрелками. С появлением тока возникает магнитное поле, индукционные линии которого пересекают проводник и индуктируют в нем электродвижущую силу (ЭДС). Как было указано в статье «Явление электромагнитной индукции», эта ЭДС называется ЭДС самоиндукции. Так как всякая индуктированная ЭДС по правилу Ленца направлена против причины, ее вызвавшей, а этой причиной будет ЭДС батареи элементов, то ЭДС самоиндукции катушки будет направлена против ЭДС батареи. Направление ЭДС самоиндукции на рисунке 1 показано двойными стрелками.
Таким образом, ток устанавливается в цепи не сразу. Только когда магнитный поток установится, пересечение проводника магнитными линиями прекратится и ЭДС самоиндукции исчезнет. Тогда в цепи будет протекать постоянный ток.
 |  |
| Рисунок 1. Электродвижущая сила самоиндукции в момент замыкания цепи направлена против ЭДС источника напряжения | Рисунок 2. График постоянного тока |
На рисунке 2 дано графическое изображение постоянного тока. По горизонтальной оси отложено время, по вертикальной оси – ток. Из рисунка видно, что если в первый момент времени ток равен 6 А, то в третий, седьмой и так далее моменты времени он также и будет равен 6 А.
На рисунке 3 показано, как устанавливается ток в цепи после включения. ЭДС самоиндукции, направленная в момент включения против ЭДС батареи элементов, ослабляет ток в цепи, и поэтому в момент включения ток равен нулю. Далее в первый момент времени ток равен 2 А, во второй момент времени – 4 А, в третий – 5 А, и только спустя некоторое время в цепи устанавливается ток 6 А.
 |  |
| Рисунок 3. График нарастания тока в цепи с учетом ЭДС самоиндукции | Рисунок 4. ЭДС самоиндукции в момент размыкания цепи направлена одинаково с ЭДС источника напряжения |
При размыкании цепи (рисунок 4) исчезающий ток, направление которого показано одинарной стрелкой, будет уменьшать свое магнитное поле. Это поле, уменьшаясь от некоторой величины до нуля, будет вновь пересекать проводник и индуктировать в нем ЭДС самоиндукции.
При выключении электрической цепи с индуктивностью ЭДС самоиндукции будет направлена в ту же сторону, что и ЭДС источника напряжения. Направление ЭДС самоиндукции показано на рисунке 4 двойной стрелкой. В результате действия ЭДС самоиндукции ток в цепи исчезает не сразу.
Таким образом, ЭДС самоиндукции всегда направлена против причины, ее вызвавшей. Отмечая это ее свойство, говорят что ЭДС самоиндукции имеет реактивный характер.
Графически изменение тока в нашей цепи с учетом ЭДС самоиндукции при замыкании ее и при последующем размыкании в восьмой момент времени показано на рисунке 5.
 |  |
| Рисунок 5. График нарастания и исчезновения тока в цепи с учетом ЭДС самоиндукции | Рисунок 6. Индукционные токи при размыкании цепи |
При размыкании цепей, содержащих большое количество витков и массивные стальные сердечники или, как говорят, обладающих большой индуктивностью, ЭДС самоиндукции может быть во много раз больше ЭДС источника напряжения. Тогда в момент размыкания воздушный промежуток между ножом и неподвижным зажимом рубильника будет пробит и появившаяся электрическая дуга будет плавить медные части рубильника, а при отсутствии кожуха на рубильнике может ожечь руки человека (рисунок 6).
В самой цепи ЭДС самоиндукции может пробить изоляцию витков катушек, электромагнитов и так далее. Во избежание этого в некоторых выключающих приспособлениях устраивают защиту от ЭДС самоиндукции в виде специального контакта, который замыкает накоротко обмотку электромагнита при выключении.
Следует учитывать, что ЭДС самоиндукции проявляет себя не только в моменты включения и выключения цепи, но также и при всяких изменениях тока.
Величина ЭДС самоиндукции зависит от скорости изменения тока в цепи. Так, например, если для одной и той же цепи в одном случае в течение 1 секунды ток в цепи изменился с 50 до 40 А (то есть на 10 А), а в другом случае с 50 до 20 А (то есть на 30 А), то во втором случае в цепи будет индуктироваться втрое большая ЭДС самоиндукции.
Величина ЭДС самоиндукции зависит от индуктивности самой цепи. Цепями с большой индуктивностью являются обмотки генераторов, электродвигателей, трансформаторов и индукционных катушек, обладающих стальными сердечниками. Меньшей индуктивностью обладают прямолинейные проводники. Короткие прямолинейные проводники, лампы накаливания и электронагревательные приборы (печи, плитки) индуктивностью практически не обладают и появления ЭДС самоиндукции в них почти не наблюдается.
Магнитный поток, пронизывающий контур и индуктирующий в нем ЭДС самоиндукции, пропорционален току, протекающему по контуру:
Ф = L × I ,
где L – коэффициент пропорциональности. Он называется индуктивностью. Определим размерность индуктивности:

Ом × сек иначе называется генри (Гн).
1 генри = 103; миллигенри (мГн) = 106 микрогенри (мкГн).
Индуктивность, кроме генри, измеряют в сантиметрах:
1 генри = 109 см.
Так, например, 1 км линии телеграфа обладает индуктивностью 0,002 Гн. Индуктивность обмоток больших электромагнитов достигает нескольких сотен генри.
Если ток в контуре изменился на Δi, то магнитный поток изменится на величину Δ Ф:
Δ Ф = L × Δ i .
Величина ЭДС самоиндукции, которая появится в контуре, будет равна (формула ЭДС самоиндукции):

При равномерном изменении тока по времени выражение  будет постоянным и его можно заменить выражением
будет постоянным и его можно заменить выражением  . Тогда абсолютная величина ЭДС самоиндукции, возникающая в контуре, может быть найдена так:
. Тогда абсолютная величина ЭДС самоиндукции, возникающая в контуре, может быть найдена так:

На основании последней формулы можно дать определение единицы индуктивности – генри:

Проводник обладает индуктивностью 1 Гн, если при равномерном изменении тока на 1 А в 1 секунду в нем индуктируется ЭДС самоиндукции 1 В.
Как мы убедились выше, ЭДС самоиндукции возникает в цепи постоянного тока только в моменты его включения, выключения и при всяком его изменении. Если же величина тока в цепи неизменна, то магнитный поток проводника постоянен и ЭДС самоиндукции возникнуть не может (так как  . В моменты изменения тока в цепи ЭДС самоиндукции мешает изменениям тока, то есть оказывает ему своеобразное сопротивление.
. В моменты изменения тока в цепи ЭДС самоиндукции мешает изменениям тока, то есть оказывает ему своеобразное сопротивление.
 |
| Рисунок 7. Бифилярная обмотка катушки |
Часто на практике встречаются случаи, когда нужно изготовить катушку, не обладающую индуктивностью (добавочные сопротивления к электроизмерительным приборам, сопротивления штепсельных реостатов и тому подобные). В этом случае применяют бифилярную обмотку катушки (рисунок 7)
Как нетрудно видеть из чертежа, в соседних проводниках токи проходят в противоположных направлениях. Следовательно, магнитные поля соседних проводников взаимно уничтожаются. Общий магнитный поток и индуктивность катушки будут равны нулю. Для еще более полного уяснения понятия индуктивности приведем пример из области механики.
Как известно из физики, по второму закону Ньютона ускорение, полученное телом под действием силы, пропорционально самой силе и обратно пропорционально массе тела:

или

Сравним последнюю формулу с формулой ЭДС самоиндукции, взяв абсолютное значение ЭДС:

Если в этих формулах изменения скорости во времени  уподобить изменению тока во времени
уподобить изменению тока во времени  , механическую силу – электродвижущей силе самоиндукции, то масса тела будет соответствовать индуктивности цепи.
, механическую силу – электродвижущей силе самоиндукции, то масса тела будет соответствовать индуктивности цепи.
При равномерном прямолинейном движении a = 0, поэтому F = 0, то есть если на тело не действуют силы, его движение будет прямолинейным и равномерным (первый закон Ньютона).
В цепях постоянного тока величина тока не меняется  и поэтому eL = 0.
и поэтому eL = 0.
Источник: Кузнецов М.И., «Основы электротехники» — 9-е издание, исправленное — Москва: Высшая школа, 1964 — 560с.
1.2. Явление электромагнитной индукции и самоиндукции
(основные величины и закономерности)
Индукция
магнитного поля  – силовая характеристика магнитного
поля. Характеризует влияние магнитного
поля на движущиеся заряды и токи. Единица
измерения – тесла,
– силовая характеристика магнитного
поля. Характеризует влияние магнитного
поля на движущиеся заряды и токи. Единица
измерения – тесла, .
.
П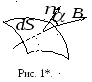 отоком вектора магнитной индукции (магнитным потоком) через площадку
отоком вектора магнитной индукции (магнитным потоком) через площадку 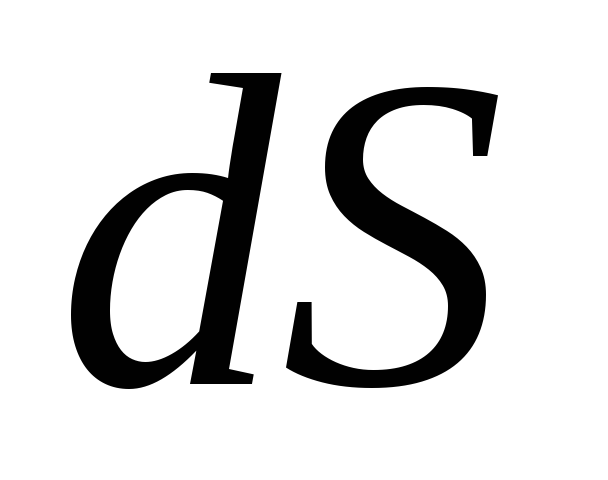 (или магнитным потоком) называется
произведение
(или магнитным потоком) называется
произведение ,
или
,
или
 ,
(8*)
,
(8*)
где 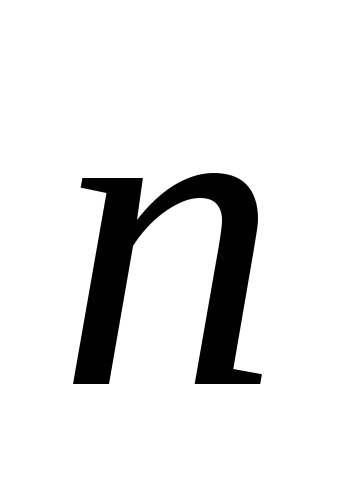 – единичный вектор – нормаль к этой
площадке,
– единичный вектор – нормаль к этой
площадке, – вектор магнитной индукции,
– вектор магнитной индукции, – угол между векторами
– угол между векторами и
и (рис. 1). (Магнитный поток можно трактовать,
как количество линий магнитной индукции,
которые пересекают поверхность
(рис. 1). (Магнитный поток можно трактовать,
как количество линий магнитной индукции,
которые пересекают поверхность ).
Единица измерения магнитного потока –
вебер:
).
Единица измерения магнитного потока –
вебер: .
.
Явление электромагнитной индукции состоит в возникновении ЭДС в замкнутом проводящем контуре при изменении магнитного потока, который пронизывает этот контур. (Например, когда в замкнутый контур (без батарейки) вносят магнит, в контуре возникает ЭДС и ток, который называют индукционным).
Закон Фарадея: ЭДС индукции, которая возникает в замкнутом проводящем контуре, равняется скорости изменения магнитного потока:

 .
(9*)
.
(9*)
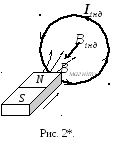
Эта ЭДС порождает индукционный ток. Знак „–” указывает на направление индукционного тока согласно правилу Ленца: при изменении магнитного потока, который пронизывает контур, в нём возникает индукционный ток такого направления, который своим магнитным полем противодействует первичному изменению магнитного потока. На рис. 2* магнитный поток, который пронизывает контур, благодаря внесению магнита, увеличивается. Поэтому индукционный ток должен иметь такое направление, чтобы его магнитное поле было противоположным полю магнита. Направление этого тока можно определить по правилу буравчика.
Если
ток проходит по замкнутому контуру, он
создает магнитное поле (и, следовательно,
магнитный поток) через этот же контур.
Когда ток в контуре меняется – меняется
и магнитный поток через этот контур,
поэтому должна возникать ЭДС индукции
(самоиндукции). То есть явление
самоиндукции состоит в возникновении ЭДС самоиндукции
в замкнутом контуре при изменении тока
в этом контуре.
Когда по контуру течет ток 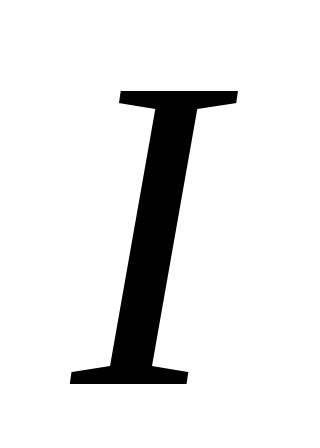 ,
то созданный им магнитный поток будет
пропорциональным силе тока:
,
то созданный им магнитный поток будет
пропорциональным силе тока: ,
где коэффициент пропорциональности
,
где коэффициент пропорциональности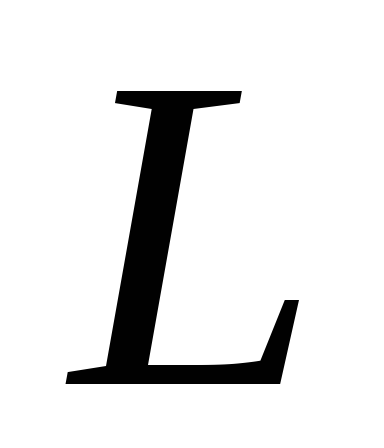 называютиндуктивностью контура. То есть индуктивность
контура численно равняется магнитному потоку,
который пронизывает контур при силе
тока
называютиндуктивностью контура. То есть индуктивность
контура численно равняется магнитному потоку,
который пронизывает контур при силе
тока 
| (10*) |
(Индуктивность
зависит от формы, размеров контура и
среды, но не зависит от силы тока). Единица
измерения индуктивности – генри: 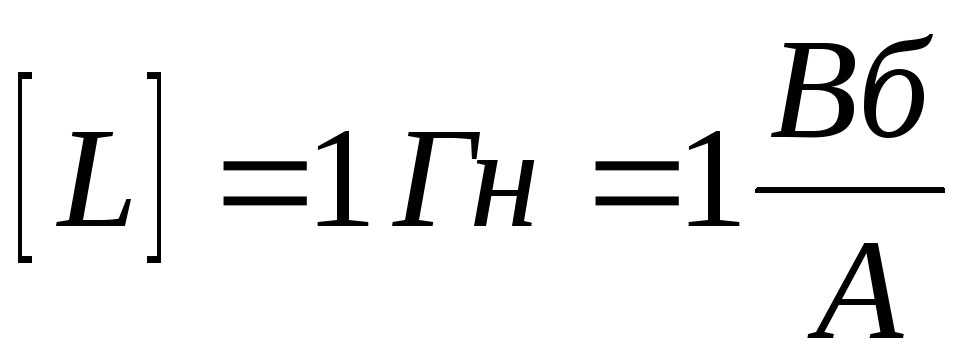 .
.
Поскольку
магнитный поток равняется  ,
то по закону Фарадея (9*) ЭДС самоиндукции
,
то по закону Фарадея (9*) ЭДС самоиндукции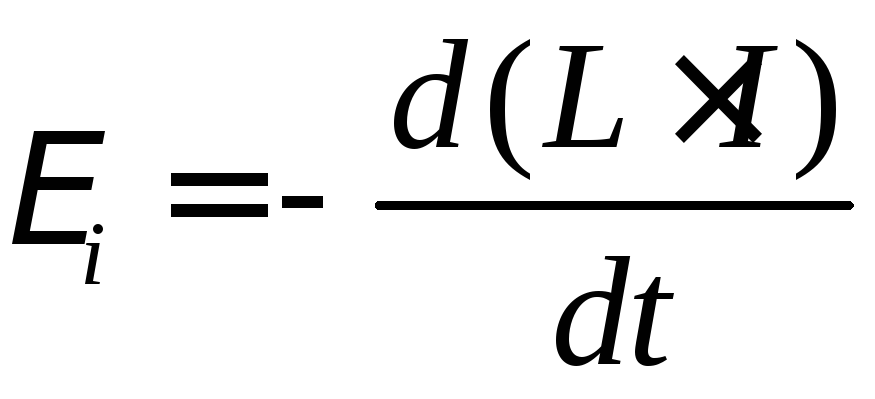 .
Если индуктивность
.
Если индуктивность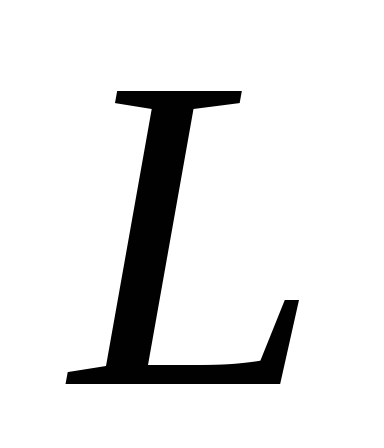 постоянная, то ее можно вынести за знак
производной. Тогда ЭДС самоиндукции
равняется
постоянная, то ее можно вынести за знак
производной. Тогда ЭДС самоиндукции
равняется
| (11*) |
Знак
„–” в этом выражении означает, что ток
самоиндукции противодействует начальному
изменению тока. (Например, когда ток  в контуре увеличивается, ток самоиндукции
в контуре увеличивается, ток самоиндукции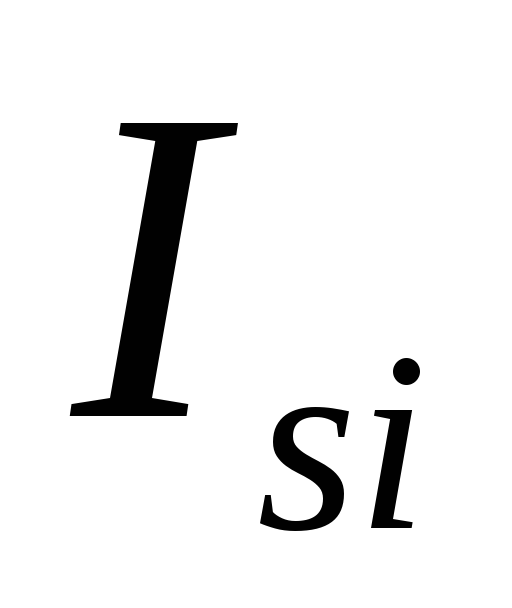 противоположен начальному току
противоположен начальному току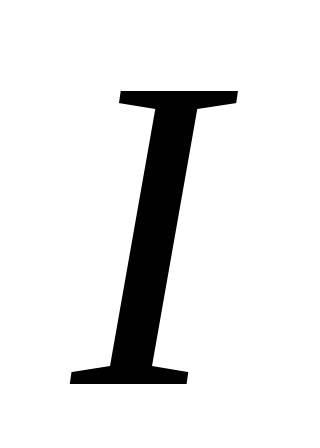 .
Когда ток
.
Когда ток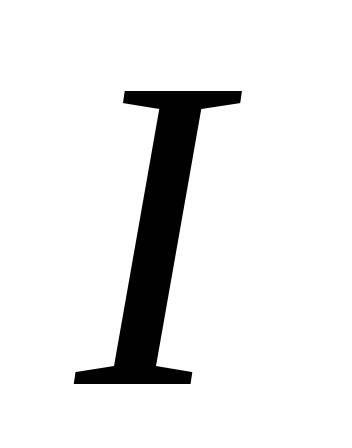 в
контуре уменьшается, то
в
контуре уменьшается, то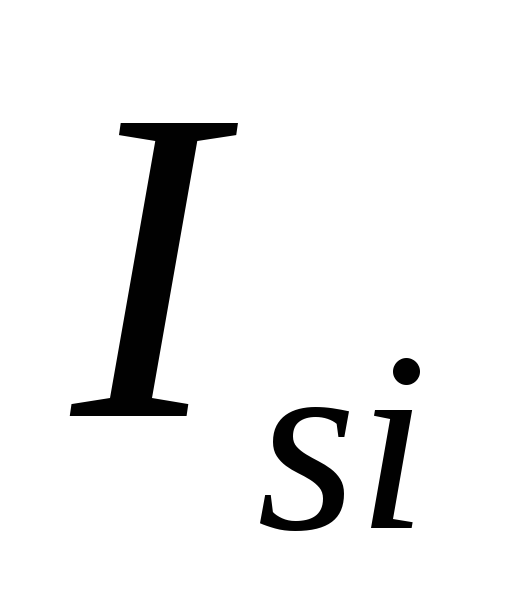 направлен в ту же сторону, что и
направлен в ту же сторону, что и ).
).
2. Индуктивность, емкость и активное сопротивление в цепи переменного тока
Р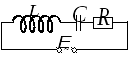 ассмотрим
контур, который включает в себя
индуктивность
ассмотрим
контур, который включает в себя
индуктивность 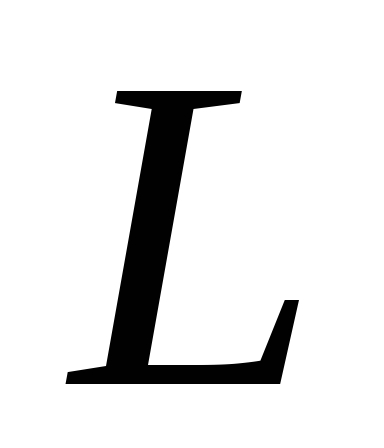 ,
емкость
,
емкость и активное сопротивление
и активное сопротивление .
Пусть в этот контур включен источник
ЭДС, которая изменяется по гармоничному
закону (синуса или косинуса) с амплитудой
.
Пусть в этот контур включен источник
ЭДС, которая изменяется по гармоничному
закону (синуса или косинуса) с амплитудой и циклической частотой
и циклической частотой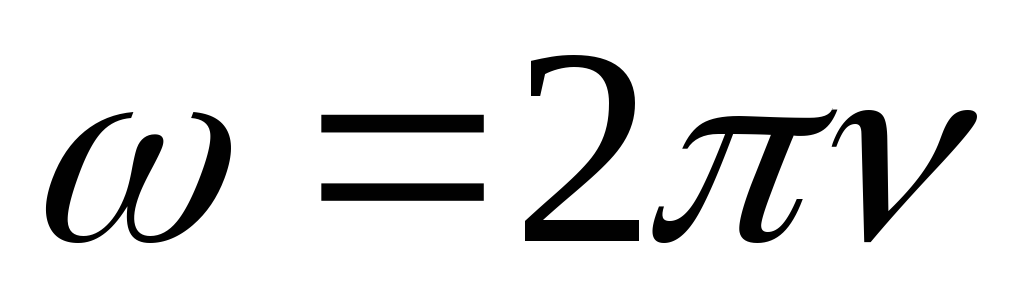 ,
где
,
где – линейная частота. Выясним, как влияют
– линейная частота. Выясним, как влияют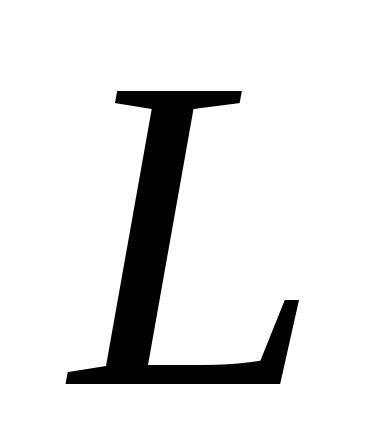 ,
, и
и отдельно и вместе на ток в этом цепи и
какие падениянапряжения будут на этих элементах. Ток на всех
элементах цепи будет одинаковым (ток
неразрывный). Пусть он меняется по закону
синуса
отдельно и вместе на ток в этом цепи и
какие падениянапряжения будут на этих элементах. Ток на всех
элементах цепи будет одинаковым (ток
неразрывный). Пусть он меняется по закону
синуса
| (1) |
где  – амплитудное значение силы тока (пока
еще неизвестное).
– амплитудное значение силы тока (пока
еще неизвестное).
2 .1.Активное
сопротивление в цепи переменного тока
.1.Активное
сопротивление в цепи переменного тока
Рассмотрим электрическую цепь, которая состоит только из источника переменного тока и активного сопротивления R. Падение напряжения на активном сопротивлении определяется из закона Ома и выражения (1)

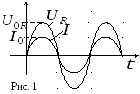 .
(2)
.
(2)
Величина 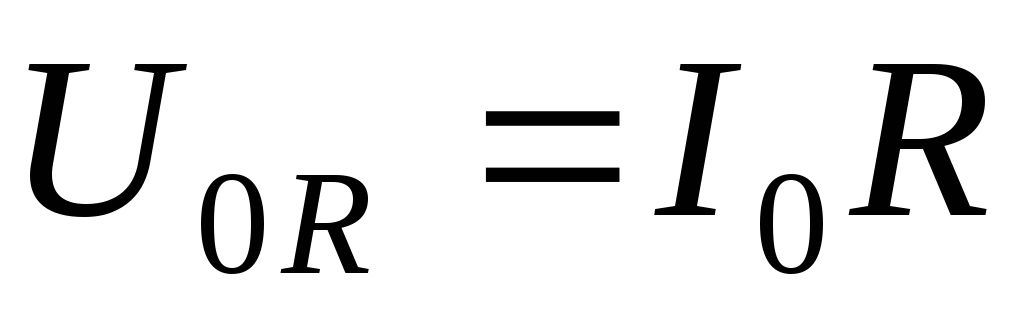 будет представлять собой амплитудное
значение напряжения на активном
сопротивлении. Сравнивая выражения (1)
и (2) видим, что колебания напряжения и
тока на активном сопротивлении происходит
с одинаковой фазой (по закону синуса,
рис.1). Заметим, что в цепи с активным
сопротивлением происходит необратимый
процесс преобразования электрической
энергии в тепловую.
будет представлять собой амплитудное
значение напряжения на активном
сопротивлении. Сравнивая выражения (1)
и (2) видим, что колебания напряжения и
тока на активном сопротивлении происходит
с одинаковой фазой (по закону синуса,
рис.1). Заметим, что в цепи с активным
сопротивлением происходит необратимый
процесс преобразования электрической
энергии в тепловую.
Явление самоиндукции
Магнитное поле контура, в котором сила тока изменяется, индуцирует ток не только в других контурах, но и в себе самом. Это явление получило название самоиндукции.
Опытным путём установлено, что магнитный поток вектора магнитной индукции поля, создаваемого текущим в контуре током, пропорционален силе этого тока:
Ф = LI, (3)
где L– индуктивность контура. Постоянная характеристика контура, которая зависит от его формы и размеров, а так же от магнитной проницаемости среды, в которой находится контур. [L] = Гн (Генри,
1Гн = Вб/А).
Если за время dtток в контуре изменится наdI, то магнитный поток, связанный с этим током, изменится наdФ =LdIв результате чего в этом контуре появится ЭДС самоиндукции:
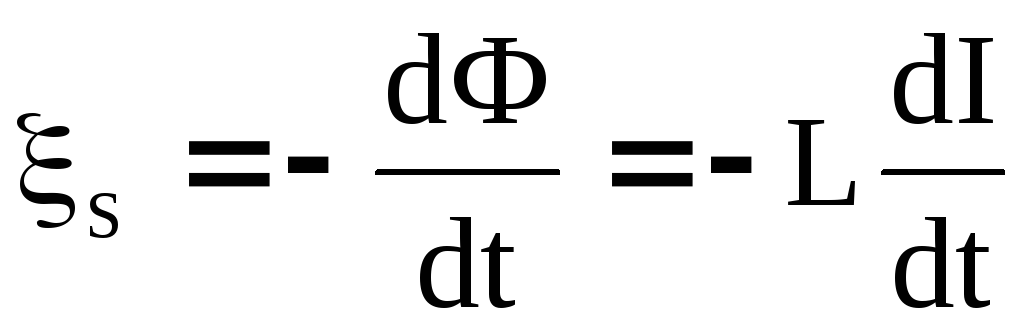 .
(4)
.
(4)
Знак минус показывает, что ЭДС самоиндукции (а, следовательно, и ток самоиндукции) всегда препятствует изменению силы тока, который вызвал самоиндукцию.
Наглядным примером явления самоиндукции служат экстратоки замыкания и размыкания, возникающие при включении и выключении электрических цепей, обладающей значительной индуктивностью.
Энергия магнитного поля
Магнитное поле обладает потенциальной энергией, которая в момент его образования (или изменения) пополняется за счёт энергии тока в цепи, совершающего при этом работу против ЭДС самоиндукции, возникающей вследствие изменения поля.
Работа dAза бесконечно малый промежуток времениdt, в течении которого ЭДС
самоиндукции и токIможно считать
постоянными, равняется:
и токIможно считать
постоянными, равняется:
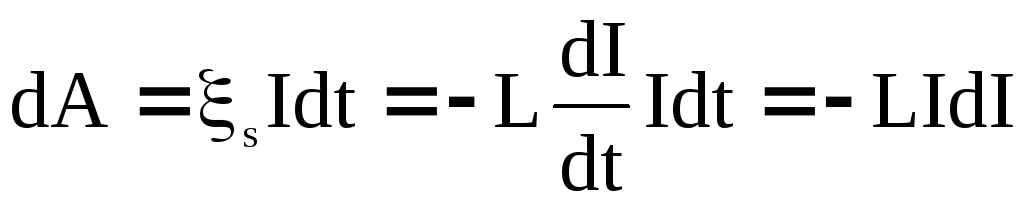 .
(5)
.
(5)
Знак минус указывает, что элементарная работа совершается током против ЭДС самоиндукции. Чтобы определить работу при изменении тока от 0 до I, проинтегрируем правую часть, получим:
 .
(6)
.
(6)
Эта работа численно равна приросту потенциальной энергии ΔWпмагнитного поля, связанного с этой цепью, т.е.A= -ΔWп.
Выразим энергию магнитного поля через его характеристики на примере соленоида. Будем считать, что магнитное поле соленоида однородно и в основном расположено внутри его. Подставим в (5) значение индуктивности соленоида, выраженное через его параметры и значение силы тока I, выраженное из формулы индукции магнитного поля соленоида:
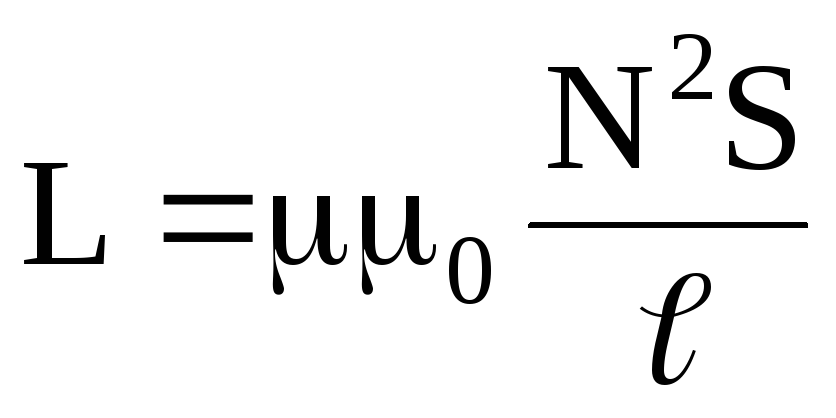 , (7)
, (7)
где N – общее число витков соленоида; ℓ – его длина; S – площадь сечения внутреннего канала соленоида.
 , (8)
, (8)
После подстановки имеем:
 . (9)
. (9)
Разделив обе части на V, получим объёмную плотность энергии поля:
 (10)
(10)
или, с учётом, что  получим,
получим, .
(11)
.
(11)
Переменный ток
2.1 Переменный ток и его основные характеристики
Переменным называется ток, изменяющийся с течением времени и по величине и по направлению. Примером переменного тока может служить потребляемый промышленный ток. Этот ток является синусоидальным, т.е. мгновенное значение его параметров меняются со временем по закону синуса (или косинуса):
i = I0sinωt, u = U0sin(ωt + φ0). (12)
П еременный
синусоидальный ток можно получить, если
вращать рамку (контур) с постоянной
скоростью
еременный
синусоидальный ток можно получить, если
вращать рамку (контур) с постоянной
скоростью
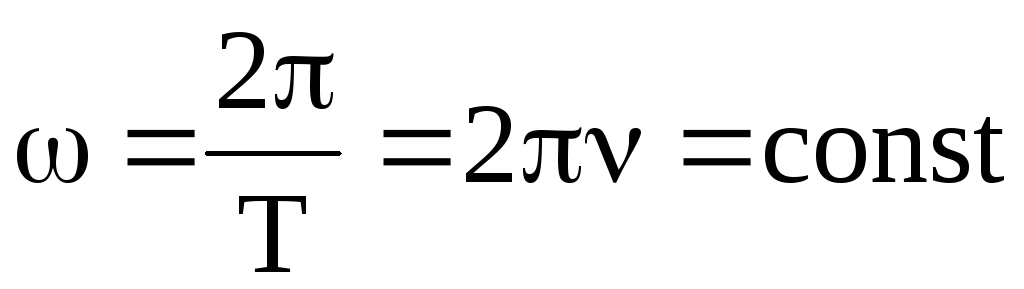
в однородном магнитном поле с индукцией B (рис.5). При этом магнитный поток, пронизывающий контур, изменяется по закону
 ,
(16)
,
(16)
где S– площадь контура, α = ωt– угол поворота рамки за время t. Изменение потока приводит к возникновению ЭДС индукции
 , (17)
, (17)
направление которой определяется по правилу Ленца.
Е сли
контур замкнут (рис.5), то по нему идёт
ток:
сли
контур замкнут (рис.5), то по нему идёт
ток:
 .
(18)
.
(18)
График изменения электродвижущей
силы и индукционного токаiпредставлен на рис.6.
и индукционного токаiпредставлен на рис.6.
Переменный
ток характеризуется периодом Т, частотой
ν = 1/Т, циклической частотой  и фазой φ = (ωt
+ φ0)
Графически значения напряжения и силы
переменного тока на участке цепи будут
представляться двумя синусоидами, в
общем случае сдвинутыми по фазе на φ.
и фазой φ = (ωt
+ φ0)
Графически значения напряжения и силы
переменного тока на участке цепи будут
представляться двумя синусоидами, в
общем случае сдвинутыми по фазе на φ.
Для характеристики переменного тока вводятся понятия действующего (эффективного) значения тока и напряжения. Эффективным значением силы переменного тока называется сила такого постоянного тока, который выделяет в данном проводнике столько же тепла за время одного периода, сколько выделяет тепла и данный переменный ток.
 ,
, . (13)
. (13)
Приборы, включенные в цепь переменного тока (амперметр, вольтметр), показывают эффективные значения тока и напряжения.
ЭДС самоиндукции — это… Что такое ЭДС самоиндукции?
- ЭДС самоиндукции
Самоиндукция — явление возникновения ЭДС индукции в проводящем контуре при изменении протекающего через контур тока.
При изменении тока в контуре меняется поток магнитной индукции через поверхность, ограниченную этим контуром, изменение потока магнитной индукции приводит к возбуждению ЭДС самоиндукции. Направление ЭДС оказывается таким, что при увеличении тока в цепи эдс препятствует возрастанию тока, а при уменьшении тока — убыванию.
Величина ЭДС пропорциональна скорости изменения силы тока I и индуктивности контура L:
 .
.
За счёт явления самоиндукции в электрической цепи с источником ЭДС при замыкании цепи ток устанавливается не мгновенно, а через какое-то время. Аналогичные процессы происходят и при размыкании цепи, при этом величина ЭДС самоиндукции может значительно превышать ЭДС источника. Чаще всего в обычной жизни это используется в катушках зажигания автомобилей. Типичное напряжение самоиндукции при напряжении питающей батареи 12В составляет 7-25кВ.
Wikimedia Foundation. 2010.
Смотреть что такое «ЭДС самоиндукции» в других словарях:
эдс самоиндукции — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN self induced emfFaraday voltageinductance voltageself induction… … Справочник технического переводчика
Самоиндукция — это явление возникновения ЭДС индукции в проводящем контуре [1]при изменении протекающего через контур тока. При изменении тока в контуре пропорционально меняется[2] и магнитный поток через поверхность, ограниченную этим контуром[3]. Изменение… … Википедия
ИНДУКТИВНОСТЬ — (от лат. inductio наведение, побуждение), величина, характеризующая магн. св ва электрич. цепи. Ток, текущий в проводящем контуре, создаёт в окружающем пр ве магн. поле, причём магнитный поток Ф, пронизывающий контур (сцепленный с ним), прямо… … Физическая энциклопедия
реактивная мощность — Величина, равная при синусоидальных электрическом токе и электрическом напряжении произведению действующего значения напряжения на действующее значение тока и на синус сдвига фаз между напряжением и током двухполюсника. [ГОСТ Р 52002 2003]… … Справочник технического переводчика
ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ — раздел физики, охватывающий знания о статическом электричестве, электрических токах и магнитных явлениях. ЭЛЕКТРОСТАТИКА В электростатике рассматриваются явления, связанные с покоящимися электрическими зарядами. Наличие сил, действующих между… … Энциклопедия Кольера
электрический трансформатор — электрический машина, не имеющая подвижных частей и преобразующая переменный ток одного напряжения в переменный ток другого напряжения. В простейшем случае состоит из магнитопровода (сердечника) и расположенных на нём двух обмоток первичной и… … Энциклопедический словарь
Импульсный стабилизатор напряжения — Импульсный стабилизатор напряжения это стабилизатор напряжения, в котором регулирующий элемент работает в ключевом режиме[1], то есть большую часть времени он находится либо в режиме отсечки, когда его сопротивление максимально, либо в… … Википедия
Катушка индуктивности — У этого термина существуют и другие значения, см. Катушка (значения). Катушка индуктивности (дроссель) на материнской плате компьютера … Википедия
Индуктивность — Размерность L2MT−2I−2 Единицы измерения СИ Гн СГС … Википедия
Диод — У этого термина существуют и другие значения, см. Диод (значения). Четыре диода и диодный мост. Диод (от др. греч … Википедия





 .
. .
. ,.
,.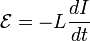 .
.