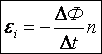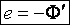Формула ЭДС индукции, E
Закон Фарадея – Максвелла для электромагнитной индукции
Основной формулой, которая определяет ЭДС индукции, является закон Фарадея – Максвелла, больше известный как основной закон электромагнитной индукции (или закон Фарадея). Этот закон утверждает, что ЭДС индукции в контуре, находящемся в переменном магнитном поле, равна по величине и противоположна по знаку скорости изменения магнитного потока () через поверхность, которую ограничивает данный контур:
где – скорость изменения магнитного потока. Полная производная в законе (1) охватывает весь спектр причин изменения магнитного потока через поверхность контура. Знак минус в формуле (1) соответствует правилу Ленца. Формула (1) для ЭДС индукции записана для системы СИ.
В случае равномерного изменения магнитного потока формулу ЭДС индукции можно записать как:
Частные случаи формул ЭДС индукции
Если контур содержит N витков, которые соединяются последовательно, то ЭДС индукции вычисляют как:
где – потокосцепление.
При движении прямолинейного проводника в однородном магнитном поле в нем возникает ЭДС индукции, которая равна:
где v – скорость движения проводника; l – длина проводника; B – модуль вектора магнитной индукции поля; .
При вращении с постоянной скоростью в однородном магнитном поле плоского контура вокруг оси, которая лежит в плоскости контура в нем возникает ЭДС индукции, равная:
где S – площадь, которую ограничивает виток; – поток самоиндукции витка; — угловая скорость; () – угол поворота контура. Следует учесть, что формула (5) справедлива, если ось вращения составляет прямой угол с направлением вектора внешнего поля .
Если во вращающейся рамке имеется N витков и самоиндукцией рассматриваемой системы можно пренебречь, то:
В стационарном проводнике, который находится в переменном магнитном поле, ЭДС индукции находят по формуле:
Примеры решения задач по теме «ЭДС индукции»
Эдс индукции
Причиной электродвижущей силы может стать изменение магнитного поля в окружающем пространстве. Это явление называетсяэлектромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением
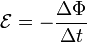
где 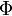
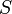 ,
ограниченную контуром. Знак «−» перед
выражением показывает, что индукционный
ток, созданный ЭДС индукции, препятствует
изменению магнитного потока в контуре
(см. правило
Ленца).
,
ограниченную контуром. Знак «−» перед
выражением показывает, что индукционный
ток, созданный ЭДС индукции, препятствует
изменению магнитного потока в контуре
(см. правило
Ленца).41. Индуктивность, ее единица СИ. Индуктивность длинного соленоида.
Индукти́вность (или коэффициент
самоиндукции) —
коэффициент пропорциональности между
электрическим током,
текущим в каком-либо замкнутом контуре,
и магнитным
потоком,
создаваемым этим током через поверхность
В формуле
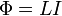
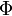 —
магнитный
поток,
—
магнитный
поток, 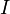 —
ток в контуре,
—
ток в контуре, 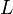 —
индуктивность.
—
индуктивность.
Нередко говорят об индуктивности прямого длинного провода(см.). В этом случае и других (особенно — в не отвечающих квазистационарному приближению) случаях, когда замкнутый контур непросто адекватно и однозначно указать, приведенное выше определение требует особых уточнений; отчасти полезным для этого оказывается подход (упоминаемый ниже), связывающий индуктивность с энергией магнитного поля.
Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока[4]:
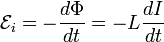 .
.
Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.
При
заданной силе тока индуктивность
определяет энергию магнитного
поля, создаваемого этим током
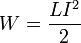 .
.
Обозначение и единицы измерения
В системе единиц СИ индуктивность измеряется в генри[7], сокращенно Гн, в системе СГС — в сантиметрах (1 Гн = 109см)[4]. Контур обладает индуктивностью в один генри, если при изменении тока на один ампер в секунду на выводах контура будет возникать напряжение в один вольт. Реальный, не сверхпроводящий, контур обладает омическим сопротивлением R, поэтому на нём будет дополнительно возникать напряжение U=I*R, где I — сила тока, протекающего по контуру в данное мгновение времени.
Символ 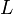
Электрический
ток, который течет в замкнутом контуре,
создает вокруг себя магнитное поле,
индукция которого, согласно закону
Био-Савара-Лапласа, пропорциональна
току. Сцепленный с контуром магнитный
поток Ф поэтому прямо пропорционален
току I в контуре: 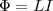
·c/А .
Вычислим
индуктивность бесконечно длинного
соленоида. Полный магнитный поток сквозь
соленоид (потокосцепление) равен
μ0μ(N2I/l)S
. Подставив в (1), найдем 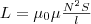 (2) т.
е. индуктивность соленоида зависит от
длиныl солениода,
числа его витков N, его , площади S и
магнитной проницаемости μ вещества, из
которого изготовлен сердечник
соленоида. Доказано, что
индуктивность контура зависит в общем
случае только от геометрической формы
контура, его размеров и магнитной
проницаемости среды, в которой он
расположен, и можно провести аналог
индуктивности контура с электрической
емкостью уединенного проводника, которая
также зависит только от формы проводника,
его размеров и диэлектрической
проницаемости среды. Найдем,
применяя к явлению самоиндукции закон
Фарадея, что э.д.с. самоиндукции
равна
(2) т.
е. индуктивность соленоида зависит от
длиныl солениода,
числа его витков N, его , площади S и
магнитной проницаемости μ вещества, из
которого изготовлен сердечник
соленоида. Доказано, что
индуктивность контура зависит в общем
случае только от геометрической формы
контура, его размеров и магнитной
проницаемости среды, в которой он
расположен, и можно провести аналог
индуктивности контура с электрической
емкостью уединенного проводника, которая
также зависит только от формы проводника,
его размеров и диэлектрической
проницаемости среды. Найдем,
применяя к явлению самоиндукции закон
Фарадея, что э.д.с. самоиндукции
равна 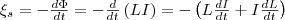
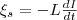 (3) где
знак минус, определяемый правилом Ленца,
говорит о том, чтоналичие
индуктивности в контуре приводит к
замедлению изменения тока в нем
(3) где
знак минус, определяемый правилом Ленца,
говорит о том, чтоналичие
индуктивности в контуре приводит к
замедлению изменения тока в нем
42. Ток при размыкании и замыкании цепи.
При всяком изменении силы тока в проводящем контуре возникает э. д. с. самоиндукции, в результате чего в контуре появляются дополнительные токи, называемые

Рассмотрим
процесс выключения тока в цепи, содержащей
источник тока с э.д.с. 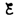
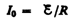
(внутренним сопротивлением источника тока пренебрегаем).
В
момент времени t=0
отключим источник тока. Ток в катушке
индуктивностью L начнет
уменьшаться, что приведет к возникновению
э.д.с. самоиндукции 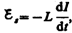 препятствующей,
согласно правилу Ленца, уменьшению
тока. В каждый момент времени ток в
цепи определяется законом Ома I=
препятствующей,
согласно правилу Ленца, уменьшению
тока. В каждый момент времени ток в
цепи определяется законом Ома I=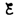 s/R, или
s/R, или
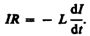 (127.1)
(127.1)
Разделив
в выражении (127.1) переменные,
получим 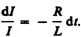 Интегрируя
это уравнение по I (от I0 до I)
и t (от
0 до t),
находим ln (I /I0)
= –Rt/L, или
Интегрируя
это уравнение по I (от I0 до I)
и t (от
0 до t),
находим ln (I /I0)
= –Rt/L, или
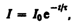 (127.2)
(127.2)
где =L/R — постоянная, называемая временем релаксации. Из (127.2) следует, что есть время, в течение которого сила тока уменьшается в е раз.
Таким образом, в процессе отключения источника тока сила тока убывает по экспоненциальному закону (127.2) и определяется кривой 1 на рис. 183. Чем больше индуктивность цепи и меньше ее сопротивление, тем больше и, следовательно, тем медленнее уменьшается ток в цепи при ее размыкании.
При
замыкании цепи помимо внешней э. д.
с. 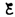 возникает
э. д. с. самоиндукции
возникает
э. д. с. самоиндукции 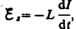 препятствующая,
согласно правилу Ленца, возрастанию
тока. По закону Ома,
препятствующая,
согласно правилу Ленца, возрастанию
тока. По закону Ома, 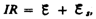 или
или
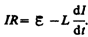
Введя
новую переменную 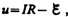 преобразуем
это уравнение к виду
преобразуем
это уравнение к виду
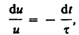
где — время релаксации.

В
момент замыкания (t=0)
сила тока I =
0 и u =
–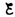 .
Следовательно, интегрируя по и (от
–
.
Следовательно, интегрируя по и (от
–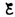 до IR–
до IR–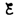 )
и t (от
0 до t),
находим ln[(IR–
)
и t (от
0 до t),
находим ln[(IR–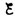 )]/–
)]/–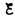 = —t/, или
= —t/, или
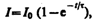 (127.3)
(127.3)
где 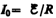 —
установившийся ток (при t).
—
установившийся ток (при t).
Таким
образом, в процессе включения источника
тока нарастание силы тока в цепи задается
функцией (127.3) и определяется кривой 2
на рис. 183. Сила тока возрастает от
начального значения I=0
и асимптотически стремится к установившемуся
значению 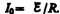 . Скорость
нарастания тока определяется тем же
временем релаксации =L/R, что
и убывание тока. Установление тока
происходит тем быстрее, чем меньше
индуктивность цепи и больше ее
сопротивление.
. Скорость
нарастания тока определяется тем же
временем релаксации =L/R, что
и убывание тока. Установление тока
происходит тем быстрее, чем меньше
индуктивность цепи и больше ее
сопротивление.
Оценим
значение э.д.с. самоиндукции 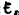 , возникающей
при мгновенном увеличении сопротивления
цепи постоянного тока от R0 до R.
Предположим, что мы размыкаем контур,
когда в нем течет установившийся ток
, возникающей
при мгновенном увеличении сопротивления
цепи постоянного тока от R0 до R.
Предположим, что мы размыкаем контур,
когда в нем течет установившийся ток 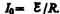 .
При размыкании цепи ток изменяется по
формуле (127.2). Подставив в нее выражение
дляI0 и ,
получим
.
При размыкании цепи ток изменяется по
формуле (127.2). Подставив в нее выражение
дляI0 и ,
получим
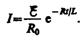
Э.д.с. самоиндукции
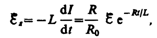
т. е. при значительном увеличении сопротивления цепи (R/R0>>1), обладающей большой индуктивностью, э.д.с. самоиндукции может во много раз превышать э.д.с. источника тока, включенного в цепь. Таким образом, необходимо учитывать, что контур, содержащий индуктивность, нельзя резко размыкать, так как это (возникновение значительных э.д.с. самоиндукции) может привести к пробою изоляции и выводу из строя измерительных приборов. Если в контур сопротивление вводить постепенно, то э.д.с. самоиндукции не достигнет больших значений.
43. Явление взаимной индукции. Трансформатор.
Рассмотрим
два неподвижных контура (1 и 2), которые
расположены достаточно близко друг от
друга (рис. 1). Если в контуре 1 протекает
ток I1,
то магнитный поток, который создавается
этим током (поле, создающее этот поток,
на рисунке изображено сплошными линиями),
прямо пропорционален I1.
Обозначим через Ф21 часть
потока,пронизывающая контур 2.
Тогда 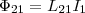 (1) где
L21 —
коэффициент пропорциональности.
(1) где
L21 —
коэффициент пропорциональности.
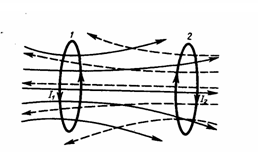
Рис.1
Если
ток I1 меняет
свое значение, то в контуре 2 индуцируется
э.д.с. ξi2 ,
которая по закону Фарадея будет равна
и противоположна по знаку скорости
изменения магнитного потока Ф21,
который создается током в первом контуре
и пронизыващет второй: 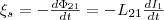 Аналогичным
образом, при протекании в контуре 2 тока
I2 магнитный
поток (его поле изображено на рис. 1
штрихами) пронизывает первый контур.
Если Ф12 —
часть этого потока, который пронизывает
контур 1, то
Аналогичным
образом, при протекании в контуре 2 тока
I2 магнитный
поток (его поле изображено на рис. 1
штрихами) пронизывает первый контур.
Если Ф12 —
часть этого потока, который пронизывает
контур 1, то 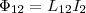 Если
ток I2 меняет
свое значение, то в контуре 1 индуцируется
э.д.с. ξi1 ,
которая равна и противоположна по знаку
скорости изменения магнитного потока
Ф12,
который создается током во втором
контуре и пронизывает первый:
Если
ток I2 меняет
свое значение, то в контуре 1 индуцируется
э.д.с. ξi1 ,
которая равна и противоположна по знаку
скорости изменения магнитного потока
Ф12,
который создается током во втором
контуре и пронизывает первый: 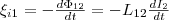 Явление
возникновения э.д.с. в одном из контуров
при изменении силы тока в другом
называется взаимной
индукцией.
Коэффициенты пропорциональности L21 и
L12 называются взаимной
индуктивностью контуров.
Расчеты, которые подтверждены опытом,
показывают, что L21 и
L12 равны
друг другу, т. е.
Явление
возникновения э.д.с. в одном из контуров
при изменении силы тока в другом
называется взаимной
индукцией.
Коэффициенты пропорциональности L21 и
L12 называются взаимной
индуктивностью контуров.
Расчеты, которые подтверждены опытом,
показывают, что L21 и
L12 равны
друг другу, т. е. 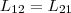 (2) Коэффициенты
пропорциональности L12 и
L21 зависят
от размеров, геометрической формы,
взаимного расположения контуров и от
магнитной проницаемости среды, окружающей
контуры. Единица взаимной индуктивности
та же, что и для индуктивности, — генри
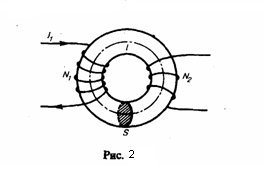
(Гн). Найдем
взаимную индуктивность двух катушек,
которые намотаны на общий тороидальный
сердечник. Этот случай имеет большое
практическое значение (рис. 2). Магнитная
индукция поля, которое создавается
первой катушкой с числом витков N1,
током I1 и
магнитной проницаемостью μ сердечника,
B = μμ0(N1I1/l)
где l —
длина сердечника по средней линии.
Магнитный поток сквозь один виток второй
катушки Ф2 =
BS = μμ0(N1I1/l)S
(2) Коэффициенты
пропорциональности L12 и
L21 зависят
от размеров, геометрической формы,
взаимного расположения контуров и от
магнитной проницаемости среды, окружающей
контуры. Единица взаимной индуктивности
та же, что и для индуктивности, — генри
(Гн). Найдем
взаимную индуктивность двух катушек,
которые намотаны на общий тороидальный
сердечник. Этот случай имеет большое
практическое значение (рис. 2). Магнитная
индукция поля, которое создавается
первой катушкой с числом витков N1,
током I1 и
магнитной проницаемостью μ сердечника,
B = μμ0(N1I1/l)
где l —
длина сердечника по средней линии.
Магнитный поток сквозь один виток второй
катушки Ф2 =
BS = μμ0(N1I1/l)S
Значит,
полный магнитный поток (потокосцепление)
сквозь вторичную обмотку, которая
содержит N2 витков, 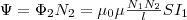 Поток
Ψ создается током I1,
поэтому, используя (1), найдем
Поток
Ψ создается током I1,
поэтому, используя (1), найдем 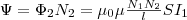 (3) Если
рассчитать магнитный поток, который
создавается катушкой 2 сквозь катушку
1, то для L12 получим
выражение в соответствии с формулой
(3). Значит, взаимная индуктивность двух
катушек, которые намотаны на общий
тороидальный сердечник,
(3) Если
рассчитать магнитный поток, который
создавается катушкой 2 сквозь катушку
1, то для L12 получим
выражение в соответствии с формулой
(3). Значит, взаимная индуктивность двух
катушек, которые намотаны на общий
тороидальный сердечник, 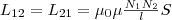
Трансформа́тор (от лат. transformo — преобразовывать) — это статическое электромагнитное устройство, имеющее две или более индуктивно связанных обмоток на каком-либо магнитопроводе и предназначенное для преобразования посредствомэлектромагнитной индукции одной или нескольких систем (напряжений) переменного тока в одну или несколько других систем (напряжений) переменного тока без изменения частоты системы (напряжения) переменного тока
что это такое, основные формулы, в чем измеряется, от чего зависит.
В материале разберемся в понятии ЭДС индукции в ситуациях ее возникновения. Также рассмотрим индуктивность в качестве ключевого параметра возникновения магнитного потока при появлении электрического поля в проводнике.
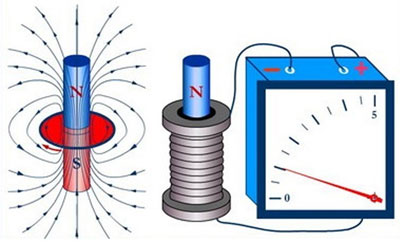

Электромагнитная индукция представляет собой генерирование электрического тока магнитными полями, которые изменяются во времени. Благодаря открытиям Фарадея и Ленца закономерности были сформулированы в законы, что ввело симметрию в понимание электромагнитных потоков. Теория Максвелла собрала воедино знания об электрическом токе и магнитных потоках. Благодаря открытия Герца человечество узнало о телекоммуникациях.
Магнитный поток
Вокруг проводника с электротоком появляется электромагнитное поле, однако параллельно возникает также обратное явление – электромагнитная индукция. Рассмотрим магнитный поток на примере: если рамку из проводника поместить в электрическое поле с индукцией и перемещать ее сверху вниз по магнитным силовым линиям или вправо-влево перпендикулярно им, тогда магнитный поток, проходящий через рамку, будет постоянной величиной.
При вращении рамки вокруг своей оси, тогда через некоторое время магнитный поток изменится на определенную величину. В результате в рамке возникает ЭДС индукции и появится электрический ток, который называется индукционным.
ЭДС индукции
Разберемся детально, что такое понятие ЭДС индукции. При помещении в магнитное поле проводника и его движении с пересечением силовых линий поля, в проводнике появляется электродвижущая сила под названием ЭДС индукции. Также она возникает, если проводник остается в неподвижном состоянии, а магнитное поле перемещается и пересекается с проводником силовыми линиями.
Когда проводник, где происходит возникновение ЭДС, замыкается на вешнюю цепь, благодаря наличию данной ЭДС по цепи начинает протекать индукционный ток. Электромагнитная индукция предполагает явление индуктирования ЭДС в проводнике в момент его пересечения силовыми линиями магнитного поля.
Электромагнитная индукция являет собой обратный процесс трансформации механической энергии в электроток. Данное понятие и его закономерности широко используются в электротехнике, большинство электромашин основывается на данном явлении.
Законы Фарадея и Ленца
Законы Фарадея и Ленца отображают закономерности возникновения электромагнитной индукции.
Фарадей выявил, что магнитные эффекты появляются в результате изменения магнитного потока во времени. В момент пересечения проводника переменным магнитным током, в нем возникает электродвижущая сила, которая приводит к возникновению электрического тока. Генерировать ток может как постоянный магнит, так и электромагнит.
Ученый определил, что интенсивность тока возрастает при быстром изменении количества силовых линий, которые пересекают контур. То есть ЭДС электромагнитной индукции пребывает в прямой зависимости от скорости магнитного потока.
Согласно закону Фарадея, формулы ЭДС индукции определяются следующим образом:
Е = — dФ/dt.
Знак «минус» указывает на взаимосвязь между полярностью индуцированной ЭДС, направлением потока и изменяющейся скоростью.
Согласно закону Ленца, можно охарактеризовать электродвижущую силу в зависимости от ее направленности. Любое изменение магнитного потока в катушке приводит к появлению ЭДС индукции, причем при быстром изменении наблюдается возрастающая ЭДС.
Если катушка, где есть ЭДС индукции, имеет замыкание на внешнюю цепь, тогда по ней течет индукционный ток, вследствие чего вокруг проводника появляется магнитное поле и катушка приобретает свойства соленоида. В результате вокруг катушки формируется свое магнитное поле.
Э.Х. Ленц установил закономерность, согласно которой определяется направление индукционного тока в катушке и ЭДС индукции. Закон гласит, что ЭДС индукции в катушке при изменении магнитного потока формирует в катушке ток направления, при котором данный магнитный поток катушки дает возможность избежать изменения постороннего магнитного потока.
Закон Ленца применяется для всех ситуаций индуктирования электротока в проводниках, вне зависимости от их конфигурации и метода изменения внешнего магнитного поля.
Движение провода в магнитном поле
Значение индуктированной ЭДС определяется в зависимости от длины проводника, пересекаемого силовыми линиями поля. При большем количестве силовых линий возрастает величина индуктируемой ЭДС. При увеличении магнитного поля и индукции, большее значение ЭДС возникает в проводнике. Таким образом, значение ЭДС индукции в движущемся в магнитном поле проводнике находится в прямой зависимости от индукции магнитного поля, длины проводника и скорости его движения.
Данная зависимость отражена в формуле Е = Blv, где Е — ЭДС индукции; В — значение магнитной индукции; I — длина проводника; v —скорость его перемещения.
Отметим, что в проводнике, который движется в магнитном поле, ЭДС индукции появляется, только когда он пересекает силовые линии магнитного поля. Если проводник движется по силовым линиям, тогда ЭДС не индуктируется. По этой причине формула применяется только в случаях, когда движением проводника направлено перпендикулярно силовым линиям.
Направление индуктированной ЭДС и электротока в проводнике определяется направлением движения самого проводника. Для выявления направления разработано правило правой руки. Если держать ладонь правой руки таким образом, чтобы в ее направлении входили силовые линии поля, а большой палец указывает направление движения проводника, тогда остальные четыре пальца показывают направление индуктированной ЭДС и направление электротока в проводнике.
Вращающаяся катушка
Функционирование генератора электротока основывается на вращении катушки в магнитном потоке, где имеется определенное количество витков. ЭДС индуцируется в электрической цепи всегда при пересечении ее магнитным потоком, на основании формулы магнитного потока Ф = B x S х cos α (магнитная индукция, умноженная на площадь поверхности, через которую проходит магнитный поток, и косинус угла, сформированный вектором направления и перпендикулярной плоскости линии).
Согласно формуле, на Ф воздействуют изменения в ситуациях:
- при изменении магнитного потока меняется вектор направления;
- изменяется площадь, заключенная в контур;
- меняется угол.
Допускается индуцирование ЭДС при неподвижном магните или неизменном токе, а просто при вращении катушки вокруг своей оси в пределах магнитного поля. В данном случае магнитный поток изменяется при смене значения угла. Катушка в процессе вращения пересекает силовые линии магнитного потока, в итоге появляется ЭДС. При равномерном вращении возникает периодическое изменение магнитного потока. Также число силовых линий, которые пересекаются ежесекундно, становится равным значениям через равные временные промежутки.
На практике в генераторах переменного электротока катушка остается в неподвижном состоянии, а электромагнит выполняет вращения вокруг нее.
ЭДС самоиндукции
При прохождении через катушку переменного электротока генерируется переменное магнитное поле, которое характеризуется меняющимся магнитным потоком, индуцирующим ЭДС. Данное явление называется самоиндукцией.
В силу того, что магнитный поток пропорционален интенсивности электротока, тогда формула ЭДС самоиндукции выглядит таким образом:
Ф = L x I, где L – индуктивность, которая измеряется в Гн. Ее величина определяется числом витков на единицу длины и величиной их поперечного сечения.
Взаимоиндукция
При расположении двух катушек рядом в них наблюдается ЭДС взаимоиндукции, которая определяется конфигурацией двух схем и их взаимной ориентацией. При возрастании разделения цепей значение взаимоиндуктивности уменьшается, поскольку наблюдается уменьшение общего для двух катушек магнитного потока.
Рассмотрим детально процесс возникновения взаимоиндукции. Есть две катушки, по проводу одной с N1 витков течет ток I1, которым создается магнитный поток и идет через вторую катушку с N2 числом витков.
Значение взаимоиндуктивности второй катушки в отношении первой:
М21 = (N2 x F21)/I1.
Значение магнитного потока:
Ф21 = (М21/N2) x I1.
Индуцированная ЭДС вычисляется по формуле:
Е2 = — N2 x dФ21/dt = — M21x dI1/dt.
В первой катушке значение индуцируемой ЭДС:
Е1 = — M12 x dI2/dt.
Важно отметить, что электродвижущая сила, спровоцированная взаимоиндукцией в одной из катушек, в любом случае прямо пропорциональна изменению электрического тока в другой катушке.
Тогда взаимоиндуктивность считается равной:
М12 = М21 = М.
Вследствие этого , E1 = — M x dI2/dt и E2 = M x dI1/dt. М = К √ (L1 x L2), где К является коэффициентом связи между двумя значениями инжуктивности.
Взаимоиндукция широко используется в трансформаторах, которые дают возможность менять значения переменного электротока. Прибор представляет собой пару катушек, которые намотаны на общий сердечник. Ток в первой катушке формирует изменяющийся магнитный поток в магнитопроводе и ток во второй катушке. При меньшем числе витков в первой катушке, чем во второй, возрастает напряжение, и соответственно при большем количестве витков в первой обмотке напряжение снижается.
Помимо генерирования и трансформации электрической энергии, явление магнитной индукции используется в прочих приборах. К примеру, в магнитных левитационных поездах, движущихся без непосредственного контакта с током в рельсах, а на пару сантиметров выше по причине электромагнитного отталкивания.
расчет электродвижущей силы по формуле
Электромагнитная индукция – генерирование электротоков магнитными полями, изменяющимися во времени. Открытие Фарадеем и Генри этого феномена ввело определенную симметрию в мир электромагнетизма. Максвеллу в одной теории удалось собрать знания об электричестве и магнетизме. Его исследования предсказывали существование электромагнитных волн перед экспериментальными наблюдениями. Герц доказал их существование и открыл человечеству эпоху телекоммуникаций.
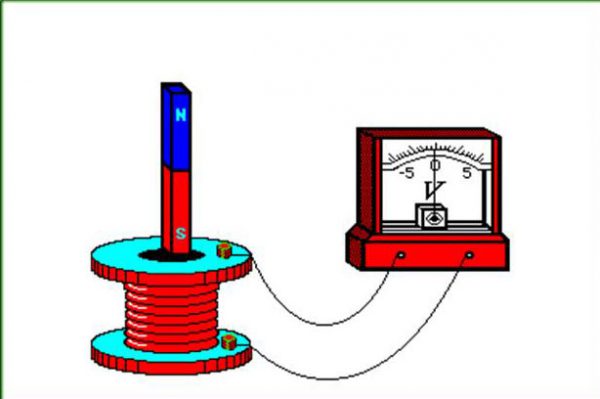
Эксперименты Фарадея
Законы Фарадея и Ленца
Электрические токи создают магнитные эффекты. А возможно ли, чтобы магнитное поле порождало электрическое? Фарадей обнаружил, что искомые эффекты возникают вследствие изменения МП во времени.
Когда проводник пересекается переменным магнитным потоком, в нем индуцируется электродвижущая сила, вызывающая электроток. Системой, которая генерирует ток, может быть постоянный магнит или электромагнит.
Явление электромагнитной индукции регулируется двумя законами: Фарадея и Ленца.
Закон Ленца позволяет охарактеризовать электродвижущую силу относительно ее направленности.
Важно! Направление индуцированной ЭДС такое, что вызванный ею ток стремится противостоять создающей его причине.
Фарадей заметил, что интенсивность индуцированного тока растет, когда быстрее изменяется число силовых линий, пересекающих контур. Другими словами, ЭДС электромагнитной индукции находится в прямой зависимости от скорости движущегося магнитного потока.
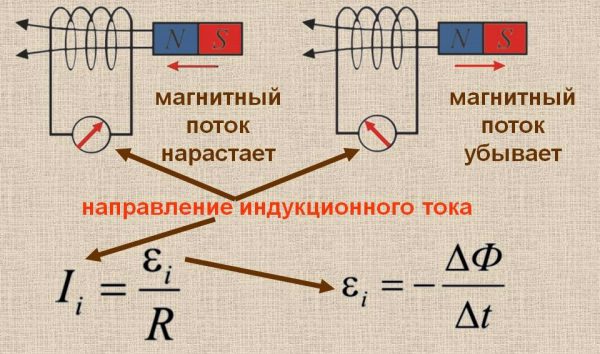
ЭДС индукции
Формула ЭДС индукции определена как:
Е = – dФ/dt.
Знак «-» показывает, как полярность индуцированной ЭДС связана со знаком потока и меняющейся скоростью.
Получена общая формулировка закона электромагнитной индукции, из которой можно вывести выражения для частных случаев.
Движение провода в магнитном поле
Когда провод длиной l движется в МП, имеющем индукцию В, внутри него будет наводиться ЭДС, пропорциональная его линейной скорости v. Для расчета ЭДС применяется формула:
- в случае движения проводника перпендикулярно направлению магнитного поля:
Е = – В x l x v;
- в случае движения под другим углом α:
Е = – В x l x v х sin α.
Индуцированная ЭДС и ток будут направлены в сторону, которую находим, пользуясь правилом правой руки: расположив руку перпендикулярно силовым линиям магнитного поля и указывая большим пальцем в сторону перемещения проводника, можно узнать направление ЭДС по оставшимся четырем распрямленным пальцам.
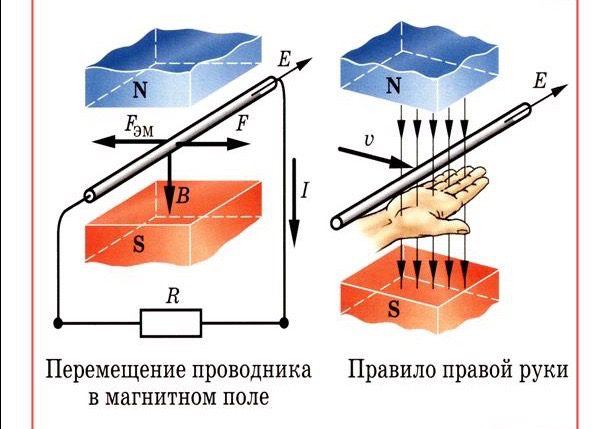
Перемещение провода в МП
Вращающаяся катушка
Работа генератора электроэнергии основана на вращении контура в МП, имеющего N витков.
ЭДС индуцируется в электроцепи всегда, когда магнитный поток ее пересекает, в соответствии с определением магнитного потока Ф = B x S х cos α (магнитная индукция, умноженная на поверхностную площадь, через которую проходит МП, и косинус угла, образованного вектором В и перпендикулярной линией к плоскости S).
Из формулы следует, что Ф подвержен изменениям в следующих случаях:
- меняется интенсивность МП – вектор В;
- варьируется площадь, ограниченная контуром;
- изменяется ориентация между ними, заданная углом.
В первых опытах Фарадея индуцированные токи были получены путем изменения магнитного поля В. Однако можно индуцировать ЭДС, не двигая магнит или не меняя ток, а просто вращая катушку вокруг своей оси в МП. В данном случае магнитный поток меняется из-за изменения угла α. Катушка при вращении пересекает линии МП, возникает ЭДС.
Если катушка вращается равномерно, это периодическое изменение приводит к периодическому изменению магнитного потока. Или количество силовых линий МП, пересекаемых каждую секунду, принимает равные значения с равными интервалами времени.
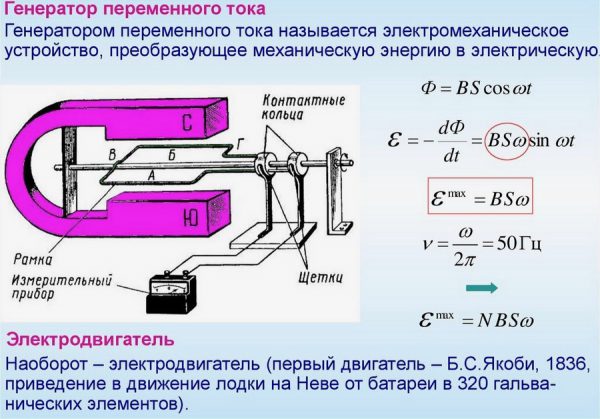
Вращение контура в МП
Важно! Наведенная ЭДС меняется вместе с ориентацией с течением времени от положительной до отрицательной и наоборот. Графическое представление ЭДС представляет собой синусоидальную линию.
Для формулы ЭДС электромагнитной индукции применяется выражение:
Е = В х ω х S x N x sin ωt, где:
- S – площадь, ограниченная одним витком или рамкой;
- N – количество витков;
- ω – угловая скорость, с которой вращается катушка;
- В – индукция МП;
- угол α = ωt.
На практике в генераторах переменного тока часто катушка остается неподвижной (статор), а электромагнит вращается вокруг нее (ротор).
ЭДС самоиндукции
Когда через катушку проходит переменный ток, он генерирует переменное МП, обладающее изменяющимся магнитным потоком, индуцирующим ЭДС. Этот эффект называется самоиндукцией.
Поскольку МП пропорционально интенсивности тока, то:
Ф = L x I,
где L – индуктивность (Гн), определяемая геометрическими величинами: количеством витков на единицу длины и размерами их поперечного сечения.
Для ЭДС индукции формула принимает вид:
Е = – L x dI/dt.
Взаимоиндукция
Если две катушки расположены рядом, то в них наводится ЭДС взаимоиндукции, зависящая от геометрии обеих схем и их ориентации относительно друг друга. Когда разделение цепей возрастает, взаимоиндуктивность снижается, так как уменьшается соединяющий их магнитный поток.
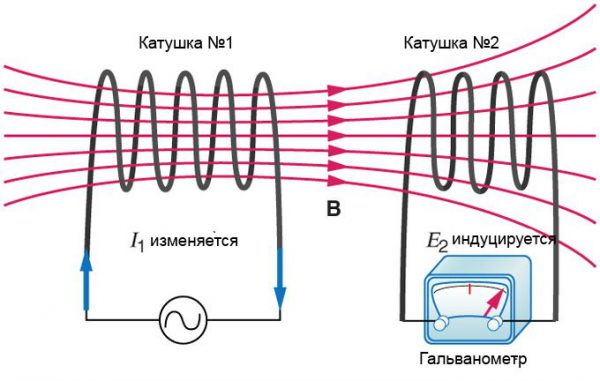
Взаимоиндукция
Пусть имеется две катушки. По проводу одной катушки, обладающей N1 витками, протекает ток I1, создающий МП, проходящее через катушку с N2 витками. Тогда:
- Взаимоиндуктивность второй катушки относительно первой:
М21 = (N2 x F21)/I1;
- Магнитный поток:
Ф21 = (М21/N2) x I1;
- Найдем индуцированную ЭДС:
Е2 = – N2 x dФ21/dt = – M21x dI1/dt;
- Идентично в первой катушке индуцируется ЭДС:
Е1 = – M12 x dI2/dt;
Важно! Электродвижущая сила, вызванная взаимоиндукцией в одной катушке, всегда пропорциональна изменению электротока в другой.
Взаимную индуктивность можно признать равной:
М12 = М21 = М.
Соответственно, E1 = – M x dI2/dt и E2 = M x dI1/dt.
М = К √ (L1 x L2),
где К – коэффициент связи между двумя индуктивностями.
Явление взаимоиндукции используется в трансформаторах – электроаппаратах, позволяющих изменить значение напряжения переменного электротока. Аппарат представляет собой две катушки, намотанные вокруг одного сердечника. Ток, присутствующий в первой, создает меняющееся МП в магнитопроводе и электроток в другой катушке. Если количество витковых оборотов первой обмотки меньше, чем другой, напряжение увеличивается, и наоборот.
Кроме генерирования, трансформации электроэнергии магнитная индукция применяется в иных устройствах. Например, в магнитных левитационных поездах, которые двигаются не в непосредственном контакте с рельсами, а на несколько сантиметров выше из-за электромагнитной силы отталкивания.
Видео
Оцените статью:| Электромагнитная индукция | |
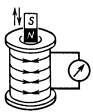
1831 г. — М. Фарадей обнаружил, что в замкнутом проводящем контуре при изменении магнитного поля возникает так называемый индукционный ток. (Индукция, в данном случае, — появление, возникновение). |
|
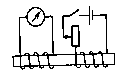
Индукционный ток в катушке возникает при перемещении постоянного магнита относительно катушки; при перемещении электромагнита относительно катушки; при перемещении сердечника относительно электромагнита, вставленного в катушку; при регулировании тока в цепи электромагнита; при замыкании и размыкании цепи |
|
Появление тока в замкнутом контуре при изменении магнитного поля, пронизывающего контур, свидетельствует о действии в контуре сторонних сил (или о возникновении ЭДС индукции). Явление возникновения ЭДС в замкнутом проводящем контуре при изменении магнитного поля (потока), пронизывающего контур, называется электромагнитной индукцией. Или: явление возникновения электрического поля при изменении магнитного поля (потока), называется электромагнитной индукцией. |
|
Закон электромагнитной индукции При всяком изменении магнитного потока через проводящий замкнутый контур в этом контуре возникает электрический ток. I зависит от свойств контура (сопротивление): ЭДС индукции в замкнутом контуре прямо пропорциональна скорости изменения магнитного потока через площадь, ограниченную этим контуром. |
|
Основные применения электромагнитной индукции: генерирование тока (индукционные генераторы на всех электростанциях, динамомашины), трансформаторы. |
|
Возникновение индукционного тока — следствие закона сохранения энергии! В случае 1: При приближении магнита, увеличении тока, замыкании цепи: В случае 2: при удалении магнита, уменьшении тока, размыкании цепи: |
|
Источником магнитного поля является ток. Поэтому: Возникающий в замкнутом контуре индукционный ток имеет такое направление, что созданный им поток магнитной индукции через площадь, ограниченную контуром, стремится компенсировать то изменение потока магнитной индукции, которое вызывает данный ток (правило Ленца). |
|
Ток в контуре имеет отрицательное направление ( Поэтому с учетом правила Ленца (знака) выражение для закона электромагнитной индукции записывается: Данная формула справедлива для СИ (коэффициент пропорциональности равен 1). В других системах единиц коэффициент другой. |
|
Если контур (например, катушка) состоит из нескольких витков, то где n – количество витков. Все предыдущие формулы справедливы в случае линейного (равномерного) изменения магнитного потока. В произвольном случае закон записывается через производную: |
|
Эдс индукции
Причиной электродвижущей силы может стать изменение магнитного поля в окружающем пространстве. Это явление называетсяэлектромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением
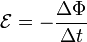
где 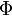 — поток
магнитного поля через
замкнутую поверхность
— поток
магнитного поля через
замкнутую поверхность 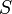 ,
ограниченную контуром. Знак «−» перед
выражением показывает, что индукционный
ток, созданный ЭДС индукции, препятствует
изменению магнитного потока в контуре
(см. правило
Ленца).
,
ограниченную контуром. Знак «−» перед
выражением показывает, что индукционный
ток, созданный ЭДС индукции, препятствует
изменению магнитного потока в контуре
(см. правило
Ленца).
41. Индуктивность, ее единица СИ. Индуктивность длинного соленоида.
Индукти́вность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность[1], краем которой является этот контур.[2][3][4].
В формуле
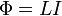
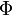 —
магнитный
поток,
—
магнитный
поток, 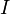 —
ток в контуре,
—
ток в контуре, 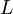 —
индуктивность.
—
индуктивность.
Нередко говорят об индуктивности прямого длинного провода(см.). В этом случае и других (особенно — в не отвечающих квазистационарному приближению) случаях, когда замкнутый контур непросто адекватно и однозначно указать, приведенное выше определение требует особых уточнений; отчасти полезным для этого оказывается подход (упоминаемый ниже), связывающий индуктивность с энергией магнитного поля.
Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока[4]:
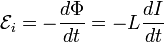 .
.
Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.
При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током[4]:
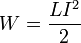 .
.
Обозначение и единицы измерения
В системе единиц СИ индуктивность измеряется в генри[7], сокращенно Гн, в системе СГС — в сантиметрах (1 Гн = 109см)[4]. Контур обладает индуктивностью в один генри, если при изменении тока на один ампер в секунду на выводах контура будет возникать напряжение в один вольт. Реальный, не сверхпроводящий, контур обладает омическим сопротивлением R, поэтому на нём будет дополнительно возникать напряжение U=I*R, где I — сила тока, протекающего по контуру в данное мгновение времени.
Символ 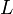 ,
используемый для обозначения индуктивности,
был взят в честь Ленца
Эмилия Христиановича (Heinrich
Friedrich Emil Lenz)[источник не указан 1017 дней].
Единица измерения индуктивности названа
в честь Джозефа
Генри (Joseph
Henry)[8].
Сам термин индуктивность был
предложен Оливером
Хевисайдом (Oliver
Heaviside) в феврале 1886
года[источник не указан 1017 дней].
,
используемый для обозначения индуктивности,
был взят в честь Ленца
Эмилия Христиановича (Heinrich
Friedrich Emil Lenz)[источник не указан 1017 дней].
Единица измерения индуктивности названа
в честь Джозефа
Генри (Joseph
Henry)[8].
Сам термин индуктивность был
предложен Оливером
Хевисайдом (Oliver
Heaviside) в феврале 1886
года[источник не указан 1017 дней].
Электрический
ток, который течет в замкнутом контуре,
создает вокруг себя магнитное поле,
индукция которого, согласно закону
Био-Савара-Лапласа, пропорциональна
току. Сцепленный с контуром магнитный
поток Ф поэтому прямо пропорционален
току I в контуре: 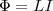 (1) где
коэффициент пропорциональности L
называетсяиндуктивностью
контура. При
изменении в контуре силы тока будет
также изменяться и сцепленный с ним
магнитный поток; значит, в контуре будет
индуцироваться э.д.с. Возникновение
э.д.с. индукции в проводящем контуре при
изменении в нем силы тока
называетсясамоиндукцией. Из
выражения (1) задается единица
индуктивности генри (Гн):
1 Гн — индуктивность контура, магнитный
поток самоиндукции которого при токе
в 1 А равен 1 Вб: 1 Гн = 1 Вб/с = 1 В
(1) где
коэффициент пропорциональности L
называетсяиндуктивностью
контура. При
изменении в контуре силы тока будет
также изменяться и сцепленный с ним
магнитный поток; значит, в контуре будет
индуцироваться э.д.с. Возникновение
э.д.с. индукции в проводящем контуре при
изменении в нем силы тока
называетсясамоиндукцией. Из
выражения (1) задается единица
индуктивности генри (Гн):
1 Гн — индуктивность контура, магнитный
поток самоиндукции которого при токе
в 1 А равен 1 Вб: 1 Гн = 1 Вб/с = 1 В
·c/А .
Вычислим
индуктивность бесконечно длинного
соленоида. Полный магнитный поток сквозь
соленоид (потокосцепление) равен
μ0μ(N2I/l)S
. Подставив в (1), найдем 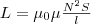 (2) т.
е. индуктивность соленоида зависит от
длиныl солениода,
числа его витков N, его , площади S и
магнитной проницаемости μ вещества, из
которого изготовлен сердечник
соленоида. Доказано, что
индуктивность контура зависит в общем
случае только от геометрической формы
контура, его размеров и магнитной
проницаемости среды, в которой он
расположен, и можно провести аналог
индуктивности контура с электрической
емкостью уединенного проводника, которая
также зависит только от формы проводника,
его размеров и диэлектрической
проницаемости среды. Найдем,
применяя к явлению самоиндукции закон
Фарадея, что э.д.с. самоиндукции
равна
(2) т.
е. индуктивность соленоида зависит от
длиныl солениода,
числа его витков N, его , площади S и
магнитной проницаемости μ вещества, из
которого изготовлен сердечник
соленоида. Доказано, что
индуктивность контура зависит в общем
случае только от геометрической формы
контура, его размеров и магнитной
проницаемости среды, в которой он
расположен, и можно провести аналог
индуктивности контура с электрической
емкостью уединенного проводника, которая
также зависит только от формы проводника,
его размеров и диэлектрической
проницаемости среды. Найдем,
применяя к явлению самоиндукции закон
Фарадея, что э.д.с. самоиндукции
равна 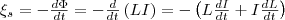 Если
контур не претерпевает деформаций и
магнитная проницаемость среды остается
неизменной (в дальнейшем будет показано,
что последнее условие выполняется не
всегда), то L = const и
Если
контур не претерпевает деформаций и
магнитная проницаемость среды остается
неизменной (в дальнейшем будет показано,
что последнее условие выполняется не
всегда), то L = const и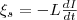 (3) где
знак минус, определяемый правилом Ленца,
говорит о том, чтоналичие
индуктивности в контуре приводит к
замедлению изменения тока в нем. Если
ток со временем увеличивается, то
(dI/dt<0) и ξs>0
т. е. ток самоиндукции направлен навстречу
току, обусловленному внешним источником,
и замедляет его увеличение. Если ток со
временем уменьшается, то (dI/dt>0) и ξs<0
т. е. индукционный ток имеет такое же
направление, как и уменьшающийся ток в
контуре, и замедляет его уменьшение.
Значит, контур, обладая определенной
индуктивностью, имеет электрическую
инертность, заключающуюся в том, что
любое изменение тока уменьшается тем
сильнее, чем больше индуктивность
контура.
(3) где
знак минус, определяемый правилом Ленца,
говорит о том, чтоналичие
индуктивности в контуре приводит к
замедлению изменения тока в нем. Если
ток со временем увеличивается, то
(dI/dt<0) и ξs>0
т. е. ток самоиндукции направлен навстречу
току, обусловленному внешним источником,
и замедляет его увеличение. Если ток со
временем уменьшается, то (dI/dt>0) и ξs<0
т. е. индукционный ток имеет такое же
направление, как и уменьшающийся ток в
контуре, и замедляет его уменьшение.
Значит, контур, обладая определенной
индуктивностью, имеет электрическую
инертность, заключающуюся в том, что
любое изменение тока уменьшается тем
сильнее, чем больше индуктивность
контура.
42. Ток при размыкании и замыкании цепи.
При всяком изменении силы тока в проводящем контуре возникает э. д. с. самоиндукции, в результате чего в контуре появляются дополнительные токи, называемые экстратоками самоиндукции. Экстратоки самоиндукции, согласно правилу Ленца, всегда направлены так, чтобы препятствовать изменениям тока в цепи, т. е. направлены противоположно току, создаваемому источником. При выключении источника тока экстратоки имеют такое же направление, что и ослабевающий ток. Следовательно, наличие индуктивности в цепи приводит к замедлению исчезновения или установления тока в цепи.

Рассмотрим
процесс выключения тока в цепи, содержащей
источник тока с э.д.с. 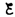 ,
резистор сопротивлением R и
катушку индуктивностью L. Под
действием внешней э. д. с. в цепи течет
постоянный ток
,
резистор сопротивлением R и
катушку индуктивностью L. Под
действием внешней э. д. с. в цепи течет
постоянный ток
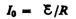
(внутренним сопротивлением источника тока пренебрегаем).
В
момент времени t=0
отключим источник тока. Ток в катушке
индуктивностью L начнет
уменьшаться, что приведет к возникновению
э.д.с. самоиндукции 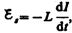 препятствующей,
согласно правилу Ленца, уменьшению
тока. В каждый момент времени ток в
цепи определяется законом Ома I=
препятствующей,
согласно правилу Ленца, уменьшению
тока. В каждый момент времени ток в
цепи определяется законом Ома I=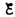 s/R, или
s/R, или
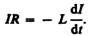 (127.1)
(127.1)
Разделив
в выражении (127.1) переменные,
получим 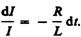 Интегрируя
это уравнение по I (от I0 до I)
и t (от
0 до t),
находим ln (I /I0)
= –Rt/L, или
Интегрируя
это уравнение по I (от I0 до I)
и t (от
0 до t),
находим ln (I /I0)
= –Rt/L, или
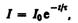 (127.2)
(127.2)
где =L/R — постоянная, называемая временем релаксации. Из (127.2) следует, что есть время, в течение которого сила тока уменьшается в е раз.
Таким образом, в процессе отключения источника тока сила тока убывает по экспоненциальному закону (127.2) и определяется кривой 1 на рис. 183. Чем больше индуктивность цепи и меньше ее сопротивление, тем больше и, следовательно, тем медленнее уменьшается ток в цепи при ее размыкании.
При
замыкании цепи помимо внешней э. д.
с. 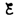 возникает
э. д. с. самоиндукции
возникает
э. д. с. самоиндукции 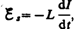 препятствующая,
согласно правилу Ленца, возрастанию
тока. По закону Ома,
препятствующая,
согласно правилу Ленца, возрастанию
тока. По закону Ома, 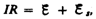 или
или
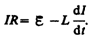
Введя
новую переменную 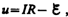 преобразуем
это уравнение к виду
преобразуем
это уравнение к виду
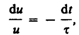
где — время релаксации.

В
момент замыкания (t=0)
сила тока I =
0 и u =
–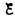 .
Следовательно, интегрируя по и (от
–
.
Следовательно, интегрируя по и (от
–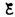 до IR–
до IR–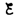 )
и t (от
0 до t),
находим ln[(IR–
)
и t (от
0 до t),
находим ln[(IR–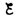 )]/–
)]/–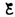 = —t/, или
= —t/, или
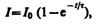 (127.3)
(127.3)
где 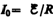 —
установившийся ток (при t).
—
установившийся ток (при t).
Таким
образом, в процессе включения источника
тока нарастание силы тока в цепи задается
функцией (127.3) и определяется кривой 2
на рис. 183. Сила тока возрастает от
начального значения I=0
и асимптотически стремится к установившемуся
значению 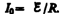 . Скорость
нарастания тока определяется тем же
временем релаксации =L/R, что
и убывание тока. Установление тока
происходит тем быстрее, чем меньше
индуктивность цепи и больше ее
сопротивление.
. Скорость
нарастания тока определяется тем же
временем релаксации =L/R, что
и убывание тока. Установление тока
происходит тем быстрее, чем меньше
индуктивность цепи и больше ее
сопротивление.
Оценим
значение э.д.с. самоиндукции 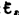 , возникающей
при мгновенном увеличении сопротивления
цепи постоянного тока от R0 до R.
Предположим, что мы размыкаем контур,
когда в нем течет установившийся ток
, возникающей
при мгновенном увеличении сопротивления
цепи постоянного тока от R0 до R.
Предположим, что мы размыкаем контур,
когда в нем течет установившийся ток 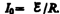 .
При размыкании цепи ток изменяется по
формуле (127.2). Подставив в нее выражение
дляI0 и ,
получим
.
При размыкании цепи ток изменяется по
формуле (127.2). Подставив в нее выражение
дляI0 и ,
получим
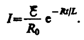
Э.д.с. самоиндукции
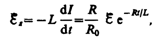
т. е. при значительном увеличении сопротивления цепи (R/R0>>1), обладающей большой индуктивностью, э.д.с. самоиндукции может во много раз превышать э.д.с. источника тока, включенного в цепь. Таким образом, необходимо учитывать, что контур, содержащий индуктивность, нельзя резко размыкать, так как это (возникновение значительных э.д.с. самоиндукции) может привести к пробою изоляции и выводу из строя измерительных приборов. Если в контур сопротивление вводить постепенно, то э.д.с. самоиндукции не достигнет больших значений.
43. Явление взаимной индукции. Трансформатор.
Рассмотрим
два неподвижных контура (1 и 2), которые
расположены достаточно близко друг от
друга (рис. 1). Если в контуре 1 протекает
ток I1,
то магнитный поток, который создавается
этим током (поле, создающее этот поток,
на рисунке изображено сплошными линиями),
прямо пропорционален I1.
Обозначим через Ф21 часть
потока,пронизывающая контур 2.
Тогда 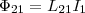 (1) где
L21 —
коэффициент пропорциональности.
(1) где
L21 —
коэффициент пропорциональности.
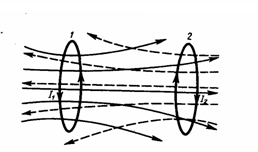
Рис.1
Если
ток I1 меняет
свое значение, то в контуре 2 индуцируется
э.д.с. ξi2 ,
которая по закону Фарадея будет равна
и противоположна по знаку скорости
изменения магнитного потока Ф21,
который создается током в первом контуре
и пронизыващет второй: 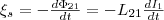 Аналогичным
образом, при протекании в контуре 2 тока
I2 магнитный
поток (его поле изображено на рис. 1
штрихами) пронизывает первый контур.
Если Ф12 —
часть этого потока, который пронизывает
контур 1, то
Аналогичным
образом, при протекании в контуре 2 тока
I2 магнитный
поток (его поле изображено на рис. 1
штрихами) пронизывает первый контур.
Если Ф12 —
часть этого потока, который пронизывает
контур 1, то 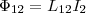 Если
ток I2 меняет
свое значение, то в контуре 1 индуцируется
э.д.с. ξi1 ,
которая равна и противоположна по знаку
скорости изменения магнитного потока
Ф12,
который создается током во втором
контуре и пронизывает первый:
Если
ток I2 меняет
свое значение, то в контуре 1 индуцируется
э.д.с. ξi1 ,
которая равна и противоположна по знаку
скорости изменения магнитного потока
Ф12,
который создается током во втором
контуре и пронизывает первый: 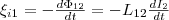 Явление
возникновения э.д.с. в одном из контуров
при изменении силы тока в другом
называется взаимной
индукцией.
Коэффициенты пропорциональности L21 и
L12 называются взаимной
индуктивностью контуров.
Расчеты, которые подтверждены опытом,
показывают, что L21 и
L12 равны
друг другу, т. е.
Явление
возникновения э.д.с. в одном из контуров
при изменении силы тока в другом
называется взаимной
индукцией.
Коэффициенты пропорциональности L21 и
L12 называются взаимной
индуктивностью контуров.
Расчеты, которые подтверждены опытом,
показывают, что L21 и
L12 равны
друг другу, т. е. 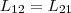 (2) Коэффициенты
пропорциональности L12 и
L21 зависят
от размеров, геометрической формы,
взаимного расположения контуров и от
магнитной проницаемости среды, окружающей
контуры. Единица взаимной индуктивности
та же, что и для индуктивности, — генри
(Гн). Найдем
взаимную индуктивность двух катушек,
которые намотаны на общий тороидальный
сердечник. Этот случай имеет большое
практическое значение (рис. 2). Магнитная
индукция поля, которое создавается
первой катушкой с числом витков N1,
током I1 и
магнитной проницаемостью μ сердечника,
B = μμ0(N1I1/l)
где l —
длина сердечника по средней линии.
Магнитный поток сквозь один виток второй
катушки Ф2 =
BS = μμ0(N1I1/l)S
(2) Коэффициенты
пропорциональности L12 и
L21 зависят
от размеров, геометрической формы,
взаимного расположения контуров и от
магнитной проницаемости среды, окружающей
контуры. Единица взаимной индуктивности
та же, что и для индуктивности, — генри
(Гн). Найдем
взаимную индуктивность двух катушек,
которые намотаны на общий тороидальный
сердечник. Этот случай имеет большое
практическое значение (рис. 2). Магнитная
индукция поля, которое создавается
первой катушкой с числом витков N1,
током I1 и
магнитной проницаемостью μ сердечника,
B = μμ0(N1I1/l)
где l —
длина сердечника по средней линии.
Магнитный поток сквозь один виток второй
катушки Ф2 =
BS = μμ0(N1I1/l)S
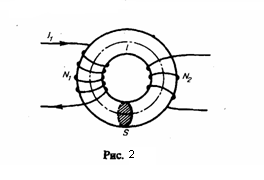
Значит,
полный магнитный поток (потокосцепление)
сквозь вторичную обмотку, которая
содержит N2 витков, 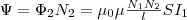 Поток
Ψ создается током I1,
поэтому, используя (1), найдем
Поток
Ψ создается током I1,
поэтому, используя (1), найдем 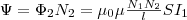 (3) Если
рассчитать магнитный поток, который
создавается катушкой 2 сквозь катушку
1, то для L12 получим
выражение в соответствии с формулой
(3). Значит, взаимная индуктивность двух
катушек, которые намотаны на общий
тороидальный сердечник,
(3) Если
рассчитать магнитный поток, который
создавается катушкой 2 сквозь катушку
1, то для L12 получим
выражение в соответствии с формулой
(3). Значит, взаимная индуктивность двух
катушек, которые намотаны на общий
тороидальный сердечник, 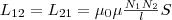
Трансформа́тор (от лат. transformo — преобразовывать) — это статическое электромагнитное устройство, имеющее две или более индуктивно связанных обмоток на каком-либо магнитопроводе и предназначенное для преобразования посредствомэлектромагнитной индукции одной или нескольких систем (напряжений) переменного тока в одну или несколько других систем (напряжений) переменного тока без изменения частоты системы (напряжения) переменного тока
феномен возникающий в индуцированном поле
Явление электромагнитной индукции – это то, что заставляет работать электрические двигатели, позволяет генераторам вырабатывать электричество. Именно его открытие в начале XIX века привело к активному развитию таких отраслей, как энергетика, станкостроение, транспорт. Также данное явление широко применяется в медицине, радиовещании, при производстве расходомеров – счетчиков учета электроэнергии.

Практическое значение электромагнитной индукции
О том, в чем суть этого явления, когда и кто его открыл, что такое индуктивность и самоиндукция, какой энергией характеризуется совокупность магнитных силовых линий, будет рассказано в этой статье.
Явление электромагнитной индукции
Классическое определение этого явления гласит, что оно представляет собой появление упорядоченного движения заряженных частиц в замкнутом проводящем ток контуре (проводнике) при изменении проходящей через него, создаваемой постоянным магнитом совокупности силовых магнитных линий.
На заметку. Впервые обнаружить описываемое в статье явление экспериментальным путем получилось в 1831 году у известного ученого-физика Майкла Фарадея. Для своих опытов он использовал железное кольцо с намотанными с двух противоположных сторон витками медного провода, которые были соединены с гальваническим элементом и магнитной стрелкой. При подключении к первой обмотке гальванического элемента стрелка некоторое время двигалась, после чего останавливалась, после его отключения – плавно возвращалась в первоначальное положение. Подобные движения стрелки позволили предположить, что упорядоченное движение носителей электрических зарядов может возникать под воздействием совокупности силовых магнитных линий, источником которых служит первая обмотка.

Майкл Фарадей
Магнитный поток
Данное явление представляет собой совокупность силовых линий, проходящих через определённое сечение проводника или замкнутого токопроводящего контура.
Рассчитывается модуль этой величины Ф по следующей формуле:
Ф= B×S×Cos α, где:
- В – модуль вектора создаваемой силовыми линиями индукции;
- S – площадь поверхности, через которую проходит поток силовых линий;
- α – угол между векторами силовых линий индукции и нормали (т.е. перпендикуляром к пронизываемой силовыми магнитными линиями плоскости).
Измеряется данная величина в Веберах (Вб).
Закон электромагнитной индукции Фарадея
Данный фундаментальный закон имеет следующую формулировку: при любых изменениях магнитного потока, проходящего через проводящий контур, происходит возникновение электродвижущей силы (сокращенно ЭДС), значение которой прямо пропорционально скорости, с которой изменяется магнитный поток.
Отображением данной закономерности является следующая формула:
Ɛi = – ΔФ/Δt, где:
- Ɛi – появляющаяся в токопроводящем контуре электродвижущая сила индукции;
- ΔФ/Δt – скорость, с которой изменяется проходящий через замкнутый контур магнитный поток.
Таким образом, сила индукционного тока, образующегося в токопроводящем замкнутом контуре при воздействии на него электродвижущей силы, будет зависеть от того, с какой скоростью изменяется проходящий через него поток силовых линий магнита.
Векторная форма
В векторной форме этот закон выражается следующей формулой:
rot E= ΔB/Δt.
Согласно этой записи, напряжённость (E) электрического поля индукционного тока возрастает при увеличении скорости изменения потока B с силовыми линиями, пересекающими замкнутый контур.
Потенциальная форма
При помощи векторного потенциала закон электромагнитной индукции имеет следующую запись:
E =ΔA/Δt, где:
- Е – напряженность электрического поля, порождаемого индукционным током;
- ΔA/Δt – изменение векторного потенциала магнитного поля, проходящего через замкнутый контур, являющийся частью замкнутой цепи проводника.
Правило Ленца
Как гласит данное правило, на направление индукционного тока влияют вызвавшие его причины (факторы). Если значение Ф возрастает, то порождаемый им ток препятствует его увеличению. Если значение Ф убывает, происходит обратное: индукционный ток меняет направление, начиная препятствовать уменьшению плотности проходящих через контур силовых линий магнитного поля. Поэтому в формуле закона Фарадея содержится знак « минус».
Взаимодействие магнита с контуром
В качестве наглядного примера взаимодействия магнита и контура в сделанную из медного провода катушку помещают магнит. Если магнит медленно вставлять внутрь катушки, происходит постепенное увеличение пересекающего ее витки создаваемого магнитом потока. Появляющееся вследствие такой манипуляции упорядоченное движение частиц в катушке будет направлено по часовой стрелке, создавая собственное магнитное поле, ослабляющее поле магнита, отталкивая его тем самым от катушки.
Если магнит отдаляют от контура, его поток уменьшается, а заряженные частицы начинают двигаться против часовой стрелки, вследствие чего возникающая совокупность силовых магнитных линий будет притягивать магнит.
На заметку. В случае с незамкнутым (открытым) контуром: металлическим или алюминиевым кольцом, имеющим прорезь; катушкой, витки которой не замкнуты через амперметр, источник питания, данная закономерность, как и правило Ленца, не работает.
Вихревое электрическое поле
Изменяющееся во времени и пространстве магнитное поле является источником появления вихревого имеющего замкнутые силовые линии электрического поля. Его воздействие объясняет упорядоченное перемещение единичных зарядов в проводнике, находящемся в (статичном) неподвижном состоянии.
Направление силовых линий электрического поля подчиняется правилу Ленца и правилу «буравчика».
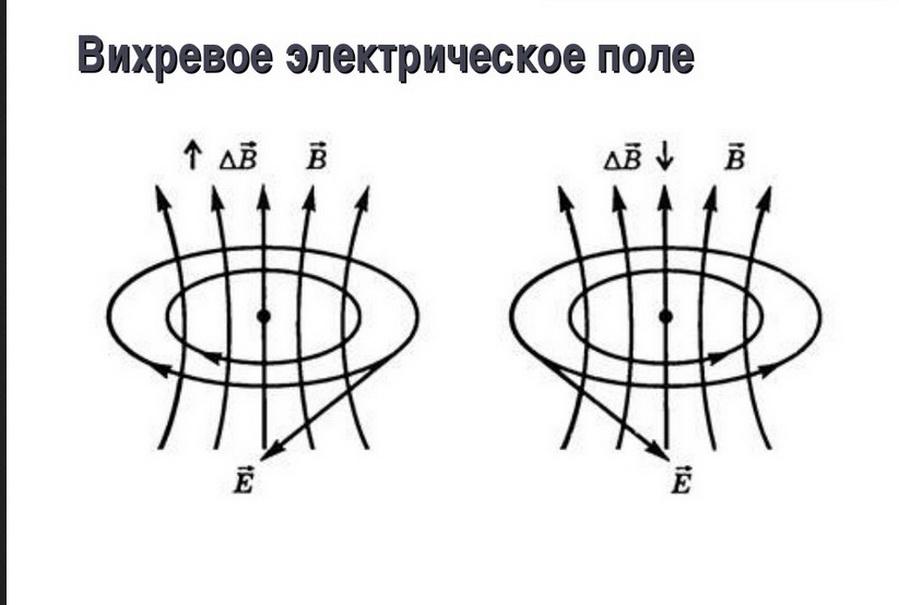
Вихревые силовые линии
Индуктивность
Проходя по контуру, электрический ток способствует образование вокруг него совокупности магнитных силовых линий. Согласно формуле Ф = L×I, создаваемый магнитом поток Ф пропорционально зависит от силы тока I.
Таким образом, под индуктивностью L понимают коэффициент соотношения магнитного потока Ф и силы тока I, протекающего по контуру. Рассчитывают данную величину по следующей формуле:
L=Ф/I.
Единицей измерения этой физической величины является Генри (Гн). 1 Гн – это индуктивность, образующаяся в замкнутом контуре, в котором сила тока изменяется на 1 Ампер, а величина напряжения в нем составляет 1 Вольт.
Самоиндукция
При изменениях значения силы тока в проводнике либо токопроводящей катушке происходит изменение магнитного потока, пронизывающего его. В результате в проводнике появляется электродвижущая сила самоиндукции, значение которой определяется по следующей формуле:
ƐiS = – ΔФ/Δt= –L(ΔI/Δt).
Энергия магнитного поля
Совокупность магнитных силовых линий имеет определенный запас энергии. Так как данное явление в контуре обусловлено протеканием по нему электрического тока, то и количество такой энергии зависит от величины затрат источников (генераторов, гальванических элементов) на создание тока. Рассчитывается эта величина (Wмаг.п) по следующей математической формуле:
Wмаг.п= (L×I2)/2.
На заметку. С практической точки зрения, значение данной величины оказывает влияние на мощность электрических агрегатов: электродвигателей, генераторов. Чем больше мощность силовых линий, образуемых обмотками или постоянными магнитами статора и ротора, тем выше крутящий момент и мощность двигателя, больше его КПД.
Основные формулы
Основные формулы для явления магнитной индукции указаны на рисунке ниже.

Основные формулы, описывающие явление электромагнитной индукции
Поняв, в чем заключается суть явления электромагнитной индукции, можно разобраться в том, как работают электродвигатели, генераторы. Эти знания, помимо большой теоретической ценности, имеет достаточно полезное практическое применение, позволяя самостоятельно находить, в ряде случаев и устранять, неисправности агрегатов, не прибегая к дорогостоящим услугам специалистов.
Видео
Более подробно и наглядно об описанном в данной статье явлении можно узнать в следующем видео.




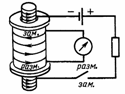

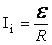 . e не зависит от свойств контура:
. e не зависит от свойств контура: 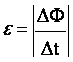 .
.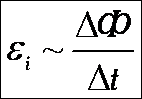
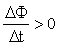 ; Магнитный поток Ф → ΔФ>0.Чтобы компенсировать это изменение (увеличение) внешнего поля, необходимо магнитное поле, направленное в сторону, противоположную внешнему полю:
; Магнитный поток Ф → ΔФ>0.Чтобы компенсировать это изменение (увеличение) внешнего поля, необходимо магнитное поле, направленное в сторону, противоположную внешнему полю: 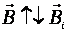 , где
, где 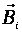 — т.н. индукционное магнитное поле.
— т.н. индукционное магнитное поле.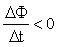 . Магнитный поток Ф → ΔФ<0. Чтобы компенсировать это изменение (уменьшение), необходимо магнитное поле, сонаправленное с внешним полем:
. Магнитный поток Ф → ΔФ<0. Чтобы компенсировать это изменение (уменьшение), необходимо магнитное поле, сонаправленное с внешним полем: 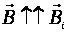 .
.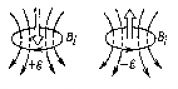
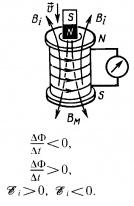
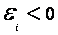 ),если
),если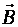 (т.е. ΔΦ>0). Ток в контуре имеет положительное направление (
(т.е. ΔΦ>0). Ток в контуре имеет положительное направление (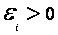 ), если
), если 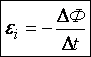 .
.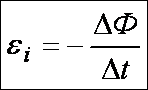
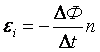 ,
,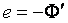 , где e – мгновенное значение ЭДС индукции.
, где e – мгновенное значение ЭДС индукции.