«Двуликая» индукция

Подмена экспериментальной зависимости Фарадея «Основным законом электромагнитной индукции» Максвелла стало поворотным пунктом в развитии электродинамики. Из процесса взаимодействия магнитного поля с электрическими зарядами электромагнитная индукция (ЭМИ) превратилась в процесс взаимодействия полей. Это было самой большой мистификацией в электродинамике, определившей все ее развитие в 20-ом веке. В частности, исследования ЭМИ пошло по двум принципиально отличным путям.

Электромагнитная индукция в движущемся проводнике

Эксперименты показывают, что ЭДС индукции возникает в любом отрезке проводника, движущемся в магнитном поле и пересекающем линии магнитной индукции. ЭДС индукции в таком «микрогенераторе» можно рассчитать с помощью схемы, представленной на Рис.1. По параллельным металлическим «рельсам», замкнутым с одной стороны проводящей перемычкой AB, в однородном поле с магнитной индукцией B с постоянной скоростью v скользит проводящий «мостик» CD длиной

l . За время dt магнитный поток, пронизывающий контур ABCD, возрастает на величину dФ = Bvl·dt, откуда

(1)

Согласно основному закону электромагнитной индукции ЭДС, индуктируемая в контуре, определяется соотношением

(2)

Так как все элементы контура, кроме «мостика», неподвижны относительно магнитного поля, то (2) — это и есть ЭДС, возникающая в движущемся проводнике.

Эта же ЭДС возникает и в незамкнутом проводящем отрезке, движущемся в магнитном поле (Рис. 2). Считается, что при перемещении проводящего отрезка в магнитном поле силой, «разделяющей» заряды q

в проводнике и создающей на концах такого «микрогенератора» индукционную ЭДС, является магнитная составляющая силы Лоренца:

(3)

Если скорость движения проводника постоянна, то и ЭДС индукции остается постоянной. В момент остановки заряды в проводнике под действием кулоновских сил «схлопываются» и микрогенератор практически мгновенно разряжается.

ЭДС в таком индукционном микрогенераторе возникает вследствие того, что проводник пересекает линии магнитного поля с некоторой скоростью v. Назовем (для краткости) такой способ генерации ЭДС электромагнитной индукции «способом пересечения». Процесс электромагнитной индукции «с пересечением» можно схематически представить так:

пересечение → возникновение силы Лоренца → перемещение зарядов → образование ЭДС

Электромагнитная индукция в замкнутом контуре

В неподвижном недеформируемом контуре пересечение линий магнитного поля проводниками отсутствует. Изменение магнитного потока, пронизывающего контур, происходит вследствие изменения магнитной индукции В. Как же возникает индукционная ЭДС в этом случае? Вот как описан этот процесс в учебнике [1]: «В этом случае объяснение возникновения ЭДС оказывается в принципе (курсив мой — К.К.) другим. Изменяющееся со временем магнитное поле порождает вихревое электрическое поле

Е… Под действием поля Е носители тока в проводнике приходят в движение — возникает индуцированный ток». Назовем такой способ генерация ЭДС «способом индукции».

Сравнивая «способ индукции» со «способом пересечения», автор [2] замечает, что «в результате изменения индукции на элементе проводника dl появляется ЭДС индукции Фарадея, которая не зависит от индукции B и скорости v движения этого элемента, а зависит только от dB/dt. Это и доказывает, что физическая природа ЭДС индукции в этих двух случаях различна». И даже так: «… оба эти явления (два механизма генерации ЭДС индукции — К.К.) … независимы друг от друга, и, тем не менее — что удивительно — ЭДС индукции в контуре всегда равна скорости изменения магнитного потока сквозь контур» [3].

Индукционный процесс по «способу индукции» можно представить так:

изменение магнитного потока → возникновение ЭДС → перемещение зарядов (индукционный ток)

Таким образом, сегодня электромагнитная индукция имеет «два лица», абсолютно непохожие друг на друга. Сравнив схематическое представление обоих процессов, можно заметить, что они в чем-то даже смотрятся «шиворот—навыворот»: в «способе пересечения» движение зарядов предшествует возникновению индукционной ЭДС, а по «способу индукции» — наоборот. Если вдуматься, то в «двуличии» индукционного процесса просматривается извечная проблема: «что первично — яйцо или курица», то есть —

заряды или поля. Попробуем решить эту вечную проблему в одном частном случае.

Многочисленные эксперименты показывают, что ЭДС индукции в замкнутом контуре не зависит от того, каким способом изменяется пронизывающий его магнитный поток. Поскольку движение относительно, то во многих случаях возникновение ЭДС в замкнутом контуре можно свести к механизму пересечения проводниками магнитного потока. Этим механизмом можно объяснить возникновение в контуре индукционной ЭДС при приближении или удалении постоянного магнита, при вращении контура в однородном (или его поступательном движении — в неоднородном) магнитном поле, при деформации контура, приводящей к изменению его площади и/или ориентации, и во многих других случаях. И только один случай не удается описать этим механизмом — возникновение ЭДС в замкнутом неподвижном и недеформируемом контуре вследствие изменения

магнитной индукции в потоке, пронизывающем контур.

Уже то обстоятельство, что только один экспериментальный факт не удается объяснить механизмом, безотказно работающим во всех остальных случаях (в том числе — и в замкнутом контуре), заставляет поискать другой способ описания процесса генерации ЭДС по «способу индукции».

Большинство авторов, по-видимому, представляет себе механизм изменения магнитного потока так: по мере увеличения магнитной индукции вновь появляющиеся линии магнитного поля как бы «расталкивают» уже существующие линии, увеличивая их плотность. Кстати, именно так представлял себе процесс возрастания магнитного потока в замкнутом контуре Максвелл: «… по мере возрастания… тока <в индукционной катушке> появляются новые линии и постепенно распространяются вовне, так что вся система развертывается изнутри» [4].

Представление магнитного поля совокупностью линий поля — это лишь модель непростого физического объекта, позволяющая дать его математическое описание. Предполагаемый механизм изменения магнитного поля — не единственный. Среди множества других вариантов описания этого процесса можно поискать и такой, который примирил бы оба способа генерации индукционной ЭДС.

На рис. 3 показан замкнутый проводящий контур в бесконечном однородном магнитном поле. Процесс увеличения магнитной индукции можно представить себе, как сгущение поля за счет поступления в поток, пронизывающий контур, новых линий поля извне — из окружающего пространства. При этом «вновь прибывающие» линии в своем движении «проникают» в контур, создавая в нем ЭДС индукции по «механизму пересечения». Такая модель сводит все случаи электромагнитной индукции к одному механизму — процессу пересечения магнитного потока проводником. Если, конечно, она не противоречит основному закону электромагнитной индукции. В этом еще нужно убедиться…

Разобьем замкнутый контур, представленный на рисунке 3, на n участков, изолированных друг от друга. При возрастании индукции в магнитном потоке по предлагаемому механизму магнитные линии, «проникая» в контур, пересекают его со скоростью v по направлению к центру. При этом выделенный на рисунке участок контура находится в тех же условиях, что и одиночный участок на рисунке 2. На каждый заряд в проводнике действует сила Лоренца F_L (3), с той лишь разницей, что скорость v — это скорость движения линий поля относительно неподвижного проводника. Как и на рисунке 2, сторонние силы «разносят» электрические заряды на концы участка, создавая на нем разность потенциалов Δ

φ_k = φ₁—φ₂. При этом на каждый заряд q действует кулоновская сила

(4)

где E_k — напряженность электрического поля на k-том участке контура. Эта сила равна по модулю и направлена навстречу силе Лоренца:

(5)

Полагая, что векторы v, B и элемент длины контура Δl_k взаимно перпендикулярны, соотношение (3) можно записать в скалярной форме:

(6)

Подставив (4) и (6) в (5), получаем

(7)

Если теперь соединить все участки в замкнутый контур, получим результирующую ЭДС в контуре

(8)

Разность потенциалов на участке определяется зависимостью

(9)

Подставляя (7) в (9) и далее в (8), получаем

(10)

В пределе (при n → ∞ и Δl_k→0) эта сумма переходит в интеграл

(11)

«Приток» линий магнитного поля в контур за время

dt составляет, очевидно,

(12)

Сравнивая (12) и (2), получаем основной закон электромагнитной индукции.

Таким образом, предлагаемый механизм не противоречит основному закону электромагнитной индукции. Но он позволяет исключить «исключения» и свести все индукционные процессы к механизму пересечения.

Должен, однако, признаться, что идея описывать процесс возникновения индукционной ЭДС в замкнутом контуре способом пересечения принадлежит не мне. Меня опередил… Майкл Фарадей! Вот что писал по этому поводу ветеран электротехнического образования профессор МГУ С. Г. Калашников:

«… если проводник находится в покое, но изменяется магнитная индукция, то при усилении поля густота линий индукции будет увеличиваться, и они будут стягиваться друг к другу, а при ослаблении поля — расходиться друг от друга. И в этом случае произойдет пересечение некоторого числа линий индукции проводником. Поэтому Фарадей заключил, что индукционный ток возникает в проводнике в том случае, если проводник или какая-либо его часть пересекает линии магнитной индукции» [5].

Разрешение «парадоксов»

Таким образом, физическая природа электромагнитной индукции («способ пересечения») — едина:

Индукционная ЭДС возникает лишь в том случае, когда электрические заряды (проводник) пересекают линии магнитного поля.

Теперь можно вернуться к «парадоксам» электромагнитной индукции.

Расчёт, приведенный выше, сделан для того, чтобы показать, что возникновение индукционной ЭДС в замкнутом контуре по методу пересечения не противоречит и «максвелловской» формулировке закона электромагнитной индукции. Но «парадоксальные» схемы, приведенные здесь, ведут себя парадоксально лишь по отношению к «максвелловской» формулировке закона. Если же оценивать результаты этих экспериментов с точки зрения закона электромагнитной индукции Фарадея, то никаких парадоксов не возникает.

Начнём с того, что только при пересечении проводником линий поля на электрические заряды действует сила (сила Лоренца), способная совершить работу (создать ЭДС) (см. далее). Когда такое пересечение отсутствует, работа не совершается, не возникает индукционный ток и не создается ЭДС индукции.

Если обратиться к тем экспериментам (схемам), которые дают «парадоксальные» результаты, то во всех этих случаях пересечение проводниками линий магнитного поля отсутствует, в чем читатель может убедиться самостоятельно.

Наиболее трудным для понимания является сам «Парадокс Геринга». Хотя цепь гальванометра остается замкнутой, магнитное поле все-таки из нее «выскальзывает». Почему же гальванометр «молчит»? Причина в том, что магнитное поле «выскальзывает» из контура… вместе с электронами на этом участке цепи (металлическом «мостике» через магнитопровод). То есть и в этом случае электроны не пересекают линии магнитного поля. Поэтому ток в цепи и не возникает.

И еще один «парадокс»

В заключение этого раздела рассмотрим еще один — классический пример, который называют «Парадоксом Фарадея». Речь идет о так называемых «униполярных генераторах», которые уже много десятилетий используются в качестве сильноточных низковольтных электрогенераторов.

После открытия электромагнитной индукции М. Фарадей предложил несколько устройств с использованием этого явления. Одним из таких устройств был индукционный генератор, получивший название «Диск Фарадея». Устройство представляло вращающийся металлический диск 1 (см. Рис. 4), который пронизывал магнитный поток от постоянного магнита 2. Электрический контур, содержавший электроизмерительный прибор (3), подключался к диску двумя скользящими контактами — на оси диска (4) и на ободе (5). При вращении диска прибор показывал в цепи постоянный ток, зависящий от скорости вращения. Возникновение индукционной ЭДС в контуре объяснялось воздействием силы Лоренца на свободные электроны вращающегося диска при пересечении ими линий магнитного поля.

В XIX веке было опробовано много вариантов «машины Фарадея». Один из них озадачил исследователей. Оказалось, что ЭДС индукции возникает в контуре и в том случае, если магнит… вращается вместе с диском. Казалось бы, при этом сила Лоренца на электроны не действует, но прибор показывал ток в контуре. На рисунке 5 схематически представлен вариант такой модификация «машины Фарадея». Конструкция отличается от «Диска Фарадея» тем, что вместо диска вращается сам цилиндрический магнит.

Этот парадоксальный результат вызвал в XIX веке оживленную дискуссию по странному вопросу: а вращается ли магнитное поле вместе с его материальным носителем — магнитом? За полтора века ученые так и не пришли к единому мнению по этому вопросу. Сегодня эта тема активно обсуждается на Интернет-форумах. Один из участников этого форума привел простой аргумент, который (по моему мнению) дает логичный и исчерпывающий ответ на этот вопрос: «Ведь никто … не сомневается, что когда мы переносим магнит из комнаты в комнату, то с ним вместе перемещается и его магнитное поле. Почему же при вращении должно быть не так?!» [6].

Согласиться с этим простым и очевидным заключением, диктуемым здравым смыслом, мешает лишь… закон ЭМИ в максвелловской формулировке. Круг замкнулся…

История науки в XX веке изобилует примерами, когда, зайдя в тупик, «научная мысль» прибегала к услугам «палочки-выручалочки» — представлениям релятивизма. В 1929 году академик И. Е. Тамм, обсуждая принцип работы униполярного генератора, писал: «В движении силовых линий <магнитного поля — К. К.>, пересекающих неподвижный проводник … усматривалась причина возникновения в этом проводнике электродвижущих сил индукции. Нечего и говорить, что такая интерпретация не выдерживает никакой критики…» [7, §112]. Но если магнитное поле неподвижно, как возникает ЭДС в контуре? Объяснить работу униполярного генератора удалось лишь с помощью… представлений теории относительности. Такое объяснение уже тогда не встретило у специалистов ни восторга, ни понимания, ни согласия.

В 1956 году С. Г. Калашников снова привел описание работы униполярного генератора [5, с. 324]. В отличие от варианта, рассмотренного И. Е. Таммом, автор считал линии магнитной индукции вращающегося магнита направленными не вдоль оси магнита, а радиально («наподобие жестких спиц»). Но магнитное поле по-прежнему предполагалось неподвижным в пространстве. И хотя это — принципиально другая конструкция, тем не менее, теория относительности объяснила работу и такого устройства! Ну чем не «палочка-выручалочка»! Такое объяснение «униполярной индукции» сегодня доказательно оспаривается участниками Интернет-форумов.

Как же работает униполярный генератор? Если признать, что магнитное поле связано с магнитом, то очевидно, что в объеме магнита никакая ЭДС возникнуть не может. Это тот же механизм, который отвечает за «Парадокс Геринга»: в обоих случаях электроны магнита движутся вместе с его магнитным полем, отсутствует пересечение линий поля электрическими зарядами, а, следовательно, и индукционная ЭДС. Где же генерируется ток в контуре? Ответ очевиден: там, где линии поля пересекают контур, то есть в проводах на участке контура АС (см. рис. 5).

Так представления о механизме электромагнитной индукции по «способу пересечения» позволяют разрешить многие «парадоксы» электромагнитного взаимодействия, в том числе и классический «Парадокс Фарадея».

Таким образом, «парадокс» в том, что уже более 100 лет ошибочно трактуется физическая природа самого процесса электромагнитной индукции. Экспериментальная зависимость Фарадея заменена ее математически тождественным выражением Максвелла, из которого исчезли главные участники процесса — электрические заряды. Почему так произошло, почему этот «парадокс» больше века оставался не замеченным? На эти вопросы отвечать не физикам, а психологам…

Чтобы понять природу электромагнитных взаимодействий, познакомимся поближе с «участниками» этих взаимодействий – магнитным и электрическим полем.

Далее: Магнитное поле.

Ссылки

[1]	Савельев И. В. Курс общей физики. Т. 2. М.: Наука, 1978. С. 178.
[2]	Матвеев А. Н. Электричество и магнетизм. М.: Высш. школа, 1956. С. 317.
[3]	Иродов И. Е. Электромагнетизм. Основные законы. М.: Лаб. Базовых Знаний, 2001. С. 248.
[4]	Максвелл Д. К. Статьи и речи. М.: Наука, 1968. С. 59.
[5]	Калашников С. К. Электричество. М.: Физматлит, 2004. С. 194.
[6]	Мисюченко И. Последняя тайна Бога. СПб.: 2009. С. 106.
[7]	Тамм И. Е. Основы теории электричества. М.: Гос. изд-во техн.-теорет. лит., 1956.

Индукции токов в движущихся проводниках. Закон электромагнитной индукции Фарадея.

Связь магнитного поля с протекающим в проводнике током обусловила эксперименты по возбуждению тока в проводящем контуре с помощью магнитного поля. Эта задача была решена в 1831 г. английским физиком Майклом Фарадеем.

Явление электромагнитной индукции – в замкнутом проводящем контуре при всяком изменении магнитного потока через поверхность, охватываемую контуром, возникает индукционный магнитный ток.

Суть классических опытов Фарадея представлена на рис.104-105. Магнитный поток через витки катушки, присоединенной к чувствительному гальванометру, можно изменять как взаимным перемещением постоянного магнита и катушки(рис.104а), так и перемещением одной катушки с током в магнитном поле другой катушки (рис.104б).

В обоих случаях возникает индукционный ток, но его направление определяется тем, убывает магнитный поток или возрастает. На рис.105 изменение магнитного потока через поверхность контура вызывается изменением тока в катушке с помощью реостата, включенного в цепь катушки.

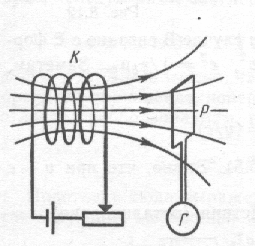
РИС.104 РИС.105

Появление индукционного тока в проводнике означает, что при изменении магнитного потока через поверхность, им ограниченную, возникает фактор, который обеспечивает направленное движение зарядов. По аналогии с цепями постоянного тока можно ввести ЭДС индукции.

Фарадей установил, что ЭДС индукции совершенно не зависит от того, каким образом изменяется магнитный поток, и определяется лишь скоростью изменения магнитного потока, а в 1845 г. Ф.Э.Нейман ввел математическую запись закона электромагнитной индукции : .

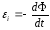Знак (-) в законе соответствует эмпирическому правилу Э.Х.Ленца: индукционный ток всегда направлен так, что создаваемое им магнитное поле противодействует изменению магнитного потока, вызвавшего появление индукционного тока.

Возникновение ЭДС индукции в контуре, перемещающимся под действием магнитного поля, было впервые обосновано Гельмгольцем в 1894 г. на основании закона сохранения энергии.

Рассмотрим замкнутый на источник контур общим сопротивлением R. Если контур неподвижен и нет преобразований в другие виды энергии, то работа источника за некоторое время, по закону Джоуля-Ленца, равна количеству теплоты выделяющейся в контуре за это время:

17. Объемная плотность энергии электрического поля. Энергия поля поверхностных зарядов. Энергия заряженных проводников.

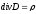, , где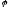— потенциал в.

, .

.

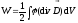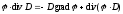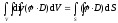И тогда для всего пространства 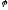пропорционален,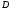пропорционален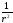,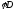пропорционально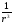, т.е. последний интеграл для всего пространства (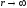) равен нулю. Т.е.

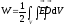, откуда энергия единицы объема

.

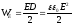Рассуждая похожим образом, находим плотность энергии магнитного поля:

.

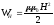Для магнитного поля еще рассматривается энергия магнитного контура с током. При увеличении силы тока источник отдает энергию на создание магнитного поля. Это есть работа на увеличение 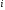от 0 до.

,

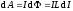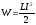— собственная энергия тока.

Энергия заряженных проводников

Учитываются только поверхностные заряды. Поэтому

.

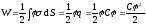Для энергии магнитных полей 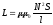(для соленоида длины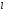),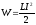— собственная энергия тока. Из таких рассуждений: для изменения тока надо совершить работу по изменению магнитного потока:

.

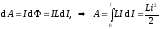Энергия заряженного конденсатора находим как произведение энергии единицы объема 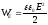на объем конденсатора.

Эдс индукции движущегося проводника

Рассмотрим модель физического эксперимента.

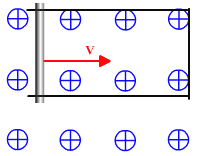
Возьмем неподвижный проволочный каркас и поместим его в магнитное поле.

Если по каркасу будет передвигаться проводник, в проводнике появится ЭДС индукции.

Изменение магнитного потока произойдет за счет изменения площади проводящего контура

Посчитаем ЭДС индукции:

П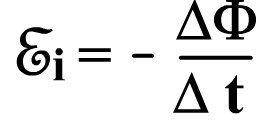о закону Фарадея

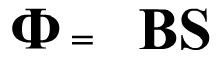
Магнитный поток в конце движения проводника

Магнитный поток в начале движения проводника

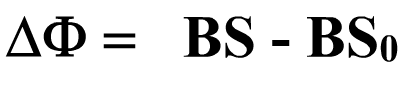
Изменение магнитного потока

Изменение площади проводящего контура связано с перемещением и со скоростью движения

Изменение магнитного потока

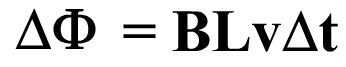
После подстановки в закон Фарадея

Э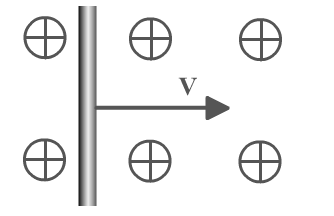тот результат получен для случая,

когда перемещение происходит под

прямым углом в силовым линиям (α = 90⁰)

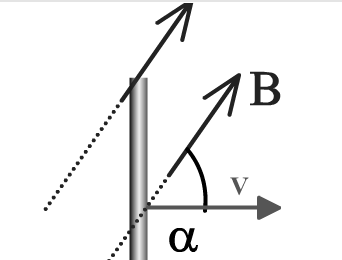
В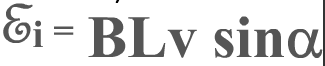 общем случае(α≠90⁰)

Если α = 0, ЭДС индукции равна нулю

При движении проводника в магнитном поле действие силы Лоренца приводит к разделению зарядов внутри проводника.

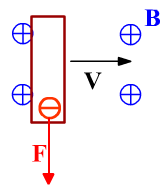
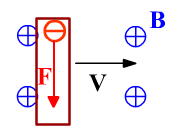
Проводник становится источником тока.

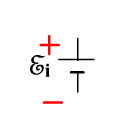
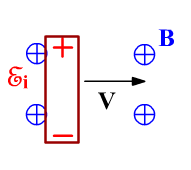
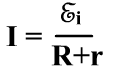
эквивалентная схема

Направление ЭДС индукции находим по правилу левой руки, как результат разделения зарядов.

Закон Ома и направление индукционного тока во внешней цепи. Если проводник замкнуть, во внешней цепи идет ток. Если не замыкать, то на концах скапливаются заряды. Знак зарядов определяется по правилу левой руки.

Причина появления ЭДС индукции в движущемся проводнике – работа силы Лоренца по разделению зарядов. Но полная работа силы Лоренца равна нулю!

Два движения: на электрон на рисунке действует сила Лоренца, направленная вниз. работа этой силы равна ЭДС индукции. Но под действием этой силы электрон начинает двигаться вдоль проводника вниз. Поэтому появляется вторая компонента силы Лоренца, направленная влево. Работа этой силы совершается против силы, которая двигает проводник (без совершения работы внешней силы проводник двигаться не может). Полная работа этих двух сил равна нулю. Механическая работа превращается в энергию электрического поля.

Самоиндукция. Индуктивность

Самоиндукция является важным частным случаем

электромагнитной индукции, когда изменяющийся

магнитный поток, вызывающий ЭДС индукции,

создается током в самом контуре.

В любом контуре, по которому протекает ток,

возникает магнитное поле. Силовые линии этого поля

пронизывают все окружающее пространство, в том числе, пересекают площадь самого контура.

Магнитный поток, который вызван током в этом самом контуре, называется собственным магнитным потоком.

Поскольку магнитный поток пропорционален индукции магнитного поля, собственный магнитный поток пропорционален силе тока в контуре

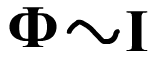
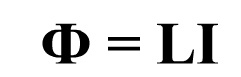
Следовательно, можно ввести коэффициент пропорциональности

Коэффициент пропорциональности L между собственным магнитным потоком в контуре и силой тока в нем называется индуктивностью контура.

Индуктивность проводника зависит от размеров, формы проводника, магнитных свойств среды.

Единица измерения индуктивности называется Генри

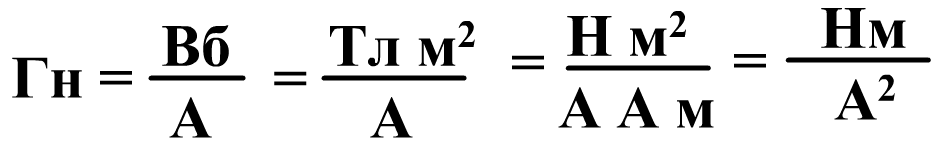
Изменение силы тока в контуре приводит к изменению собственного магнитного потока. В результате по закону электромагнитной индукции в контуре появляется ЭДС, которая называется ЭДС самоиндукции.

Явление возникновения электродвижущей сил в контуре в результате изменения силы тока в этом контуре, называется самоиндукцией.

ЭДС самоиндукции определяется из закона Фарадея

Учебно-методический материал на тему: План — конспект урока «ЭДС индукции в движущихся проводниках»

Тема урока:          ЭДС индукции в движущихся проводниках.

Тип урока:            Комбинированный урок.

Цель урока:          Дать понятие об энергетической характеристике индукционного электрического тока, возникающего в движущихся проводниках.

Демонстрации:    Правила буравчика, правила левой руки, правила Ленца.

Используются технологии ИКТ для сопровождения изучения нового материала

Ход урока:

I.   Организационный момент.

       

На сегодняшнем уроке мы продолжаем исследовать причины возникновения индукционного тока в замкнутом проводящем контуре. На прошлой неделе мы с вами установили тот факт, что индукционный ток в контуре возникает либо если контур покоится в переменном магнитном поле, либо если он движется в постоянном магнитном поле. Первое условие возникновения индукционного тока мы с вами уже рассмотрели, и теперь двигаемся дальше.

Тема сегодняшнего нашего урока » ЭДС индукции в движущихся проводниках».

Цель урока: познакомиться с понятием энергетической характеристики индукционного электрического тока, возникающего в движущихся проводниках.

II.  Актуализация знаний.

К настоящему моменту мы с вами познакомились с рядом правил, которые используются для определения  направления вектора магнитной индукции, индукционного тока, силы Ампера и Лоренца.

1. Правило буравчика.

2. Правило левой руки.

            — Для движущегося участка проводника (формулировка и математическая запись закона Ампера)

            — Для движущейся частицы (количественное определение силы Лоренца)

3. Правило Ленца (алгоритм применения правила к решению задач)

Все эти правила так или иначе связаны с явлением электромагнитной индукции.

             —  Когда  и кем оно было открыто и в чем оно заключается? 

(29 августа 1831 г., Майклом Фарадеем.  Явление эл/м  индукции заключается в возникновении электрического тока в проводящем контуре, который либо покоится в переменном магнитном поле, либо движется в постоянном магнитном поле таким образом, что число линий магнитной индукции, пронизывающих контур, меняется)

             — Сформулируйте закон электромагнитной индукции.

(ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром  )

            — Что является причиной возникновения индукционного тока в проводнике, покоящемся в переменном магнитном поле?                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                        

(Индукционный ток в неподвижном замкнутом контуре, находящемся в переменном магнитном поле, вызывается электрическим полем, порождаемым переменным магнитным полем, которое называется вихревым)

— Чему равна работа этого электрического поля?

(работа вихревого электрического поля при перемещении единичного положительного заряда вдоль замкнутого неподвижного проводника численно равна ЭДС индукции в этом проводнике)

III.   Изучение нового материала.

1.                  Если проводник движется в постоянном магнитном поле, то ЭДС индукции в проводнике обусловлена не вихревым электрическим полем, которое в этом случае не может возникнуть, а другой причиной.

При движении проводника его свободные заряды движутся вместе с ним. Поэтому на них со стороны магнитного поля действует сила Лоренца. Она-то и вызывает перемещение зарядов внутри проводника. ЭДС индукции, следовательно, имеет магнитное происхождение.

Вычислим ЭДС индукции, возникающую в проводнике, движущемся в однородном магнитном поле.

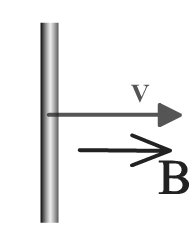
Пусть сторона контура MN длиной l скользит с постоянной скоростью υ вдоль сторон NC и MD, оставаясь все время параллельной стороне CD. Вектор магнитной индукции  однородного поля перпендикулярен проводнику и составляет угол α с направлением его скорости.

Сила, с которой магнитное поле действует на движущуюся заряженную частицу, равна по модулю .

Направлена она вдоль проводника MN.

Работа данной силы на пути l положительна и равна   .

ЭДС индукции в проводнике MN равна по определению отношению работы по перемещению заряда q к этому заряду.   .

2.                     С другой стороны, ЭДС индукции можно вычислить с помощью закона эл/м индукции.

Магнитный поток через контур MNCD равен   ,

где угол 90°- есть угол между вектором  и нормалью  к плоскости контура,

а S — площадь контура MNCD.

При перемещении проводника площадь S изменяется со временем следующим образом

За время площадь контура меняется на   . Знак минус указывает на то, что она уменьшается.

Изменение магнитного потока за это время равно .

Следовательно, .

IV.    Закрепление изученного.

Решение задач.

1. Найти ЭДС индукции в проводнике с длиной активной части 25 см, перемещающемся в однородном магнитном поле индукцией 8мТл со скоростью 5 м/с под углом 30° к вектору магнитной индукции. (0,005 В)
2. С какой скоростью надо перемещать проводник, длина активной части которого 1 м, под углом 60° к линиям индукции магнитного поля, чтобы в проводнике возбуждалась ЭДС индукции 1В? Индукция магнитного поля равна 0,2 Тл. (5,8 м/с)

V.     Итог урока.

Итак, на сегодняшнем уроке мы с вами выяснили, что ЭДС индукции в проводниках, движущихся в постоянном магнитном поле, возникает за счет действия на свободные заряды проводника силы Лоренца.

Для количественного определения ЭДС нам необходимо знать индукцию постоянного магнитного поля, длину активной части проводника, скорость движения проводника в магнитном поле и угол между вектором магнитной индукции и вектором скорости движения.

VI.    Домашнее задание.  

§ 13,  упр.2(9), №902(1,3)

ЭДС индукции в движущемся проводнике — 31 Марта 2012 — Видео- Решение задач-теория

1.      Металлический стержень и провода, по которым он скользит, находятся в однородном магнитном поле, перпендикулярном плоскости рисунка. Индукция магнитного поля 500 мТл, скорость движения проводника 2 м/с, его длина 1 м, сопротивление цепи 10 Ом. Найдите индукционный ток. Так как проводник движется в магнитном поле, то в нем возникает ЭДС индукции, равная ℰi = BLv sin α. По условию задачи α = 90°, значит ℰi = BLv. 2.      Контур с источником тока, имеющим внутреннее сопротивление 200 мОм, находится в однородном магнитном поле с индукцией 100 мТл. Найдите ток в цепи при движении перемычки со скоростью 10 м/с, если при ее движении в том же направлении со скоростью 40 м/с ток отсутствует. Сопротивлением направляющих проводников можно пренебречь. Длина перемычки 66 мм. При движении перемычки в магнитном поле, в ней возникает ЭДС индукции. Общее ЭДС может быть  равно ℰ = ℰист + ℰi или ℰ = ℰист — ℰi в зависимости от направления индукционного тока. Так как в условии задачи сказано, что при скорости 40 м/с ток отсутствует, то можно сделать вывод, что ℰ = ℰист — ℰi. Отсюда ℰист = BLv2. При скорости 10 м/с в том же направлении ℰ  = ℰист – BLv1 = BLv2 – BLv1 = BL(v2 – v1). 3.      Два параллельных вертикальных проводника, расположенные на расстоянии 1 м друг от друга, замкнуты сопротивлением 1 Ом и помещены  в однородное магнитное поле с индукцией 100 мТл, перпендикулярное плоскости проводников. По проводникам начинает вниз скользить без трения перемычка массой 100 г. Пренебрегая сопротивлением проводников и перемычки, определите максимальную скорость падения перемычки. При движении перемычки в магнитном поле, в ней возникает индукционный ток, который по правилу левой руки направлен вправо. Тогда на проводник с током магнитное поле действует силой Ампера, которая по правилу левой руки  направлена вверх. Таким образом, на перемычку действует две противоположно направленные силы – сила Ампера и сила тяжести, равнодействующая которых является причиной ускорения при движении перемычки.  Соответственно, при возрастании скорости движения перемычки будет возрастать сила Ампера. Максимальной скорости перемычка достигнет тогда, когда сила Ампера станет равной силе тяжести: mg = FA ;  mg = BIiL. 4.      По горизонтальным параллельным рельсам, расстояние между которыми 10 см, может скользить без трения параллельно самой себе проводящая перемычка, масса которой  6 г. Рельсы соединены резистором сопротивлением 6 Ом и помещены в вертикальное магнитное поле с индукцией 300 мТл. Перемычке сообщают горизонтальную параллельную рельсам скорость 1 см/с. Найдите путь, пройденный перемычкой до остановки. Электрическое сопротивление перемычки и рельс не учитывать. Так как перемычка движется, то в ней возникает ЭДС индукции ℰi = BLv. На проводник с током магнитное поле действует силой Ампера, направленная противоположно скорости по правилу левой руки и равная FA = BIL. При движении скорость уменьшается, следовательно, уменьшается и значение силы Ампера. Потому можно рассмотреть работу, выполненную силой, равной среднему значению силы Ампера: