Электромагнитная индукция — Википедия

Электромагни́тная инду́кция — явление возникновения электрического тока, электрического поля или электрической поляризации при изменении во времени магнитного поля или при движении материальной среды в магнитном поле^[1]. Электромагнитная индукция была открыта Майклом Фарадеем 29 августа 1831 года^[2]. Он обнаружил, что электродвижущая сила (ЭДС), возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина электродвижущей силы не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой ЭДС, называется индукционным током.

Согласно закону электромагнитной индукции Фарадея (в СИ):

E=−dΦBdt,{\displaystyle {\mathcal {E}}=-{{d\Phi _{B}} \over dt},}

где

E{\displaystyle {\mathcal {E}}} — электродвижущая сила, действующая вдоль произвольно выбранного контура,

ΦB{\displaystyle \Phi _{B}} =∬SB→⋅dS→{\displaystyle =\iint \limits _{S}{\vec {B}}\cdot d{\vec {S}}} — магнитный поток через поверхность, ограниченную этим контуром.

Знак «минус» в формуле отражает правило Ленца, названное так по имени российского физика Э. Х. Ленца:

Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.

Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:

E=−NdΦBdt=−dΨdt,{\displaystyle {\mathcal {E}}=-N{{d\Phi _{B}} \over dt}=-{{d\Psi } \over dt},}

где

E{\displaystyle {\mathcal {E}}} — электродвижущая сила,

N{\displaystyle N} — число витков,

ΦB{\displaystyle \Phi _{B}} — магнитный поток через один виток,

Ψ{\displaystyle \Psi } — потокосцепление катушки.

Векторная форма[править | править код]

В дифференциальной форме закон Фарадея можно записать в следующем виде:

rotE→=−∂B→∂t{\displaystyle \operatorname {rot} \,{\vec {E}}=-{\partial {\vec {B}} \over \partial t}} (в системе СИ)

или

rotE→=−1c∂B→∂t{\displaystyle \operatorname {rot} \,{\vec {E}}=-{1 \over c}{\partial {\vec {B}} \over \partial t}} (в системе СГС).

В интегральной форме (эквивалентной):

∮∂S⁡E→⋅dl→=−∂∂t∫SB→⋅ds→{\displaystyle \oint _{\partial S}{\vec {E}}\cdot {\vec {dl}}=-{\partial \over \partial t}\int _{S}{\vec {B}}\cdot {\vec {ds}}}(СИ)

или

∮∂S⁡E→⋅dl→=−1c∂∂t∫SB→⋅ds→{\displaystyle \oint _{\partial S}{\vec {E}}\cdot {\vec {dl}}=-{1 \over c}{\partial \over \partial t}\int _{S}{\vec {B}}\cdot {\vec {ds}}} (СГС).

Здесь E→{\displaystyle {\vec {E}}} — напряжённость электрического поля, B→{\displaystyle {\vec {B}}} — магнитная индукция, S {\displaystyle S\ } — произвольная поверхность, ∂S{\displaystyle \partial S} — её граница. Контур интегрирования ∂S{\displaystyle \partial S} подразумевается фиксированным (неподвижным).

Следует отметить, что закон Фарадея в такой форме, очевидно, описывает лишь ту часть ЭДС, что возникает при изменении магнитного потока через контур за счёт изменения со временем самого поля без изменения (движения) границ контура (об учете последнего см. ниже).

• В этом виде закон Фарадея входит в систему уравнений Максвелла для электромагнитного поля (в дифференциальной или интегральной форме соответственно)^[3].

Если же, скажем, магнитное поле постоянно, а магнитный поток изменяется вследствие движения границ контура (например, при увеличении его площади), то возникающая ЭДС порождается силами, удерживающими заряды на контуре (в проводнике) и силой Лоренца, порождаемой прямым действием магнитного поля на движущиеся (с контуром) заряды. При этом равенство E=−dΦ/dt{\displaystyle {\mathcal {E}}=-{{d\Phi }/dt}} продолжает соблюдаться, но ЭДС в левой части теперь не сводится к ∮⁡E→⋅dl→{\displaystyle \oint {\vec {E}}\cdot {\vec {dl}}} (которое в данном частном примере вообще равно нулю). В общем случае (когда и магнитное поле меняется со временем, и контур движется или меняет форму) последняя формула остаётся справедливой, но ЭДС в левой части в таком случае есть сумма обоих слагаемых, упомянутых выше (то есть порождается частично вихревым электрическим полем, а частично силой Лоренца и силой реакции движущегося проводника).

• Некоторые авторы, например, М. Лившиц в журнале «Квант» за 1998 год ^[4] отрицают корректность применения термина закон Фарадея или закон электромагнитной индукции и т. п. к формуле E=−dΦ/dt{\displaystyle {\mathcal {E}}=-{{d\Phi }/dt}} в случае подвижного контура (оставляя для обозначения этого случая или его объединения со случаем изменения магнитного поля, например, термин правило потока)^[5]. В таком понимании закон Фарадея — это закон, касающийся лишь циркуляции электрического поля (но не ЭДС, создаваемой с участием силы Лоренца), и в этом понимании понятие закон Фарадея в точности совпадает с содержанием соответствующего уравнения Максвелла.
• Однако возможность (пусть с некоторыми оговорками, уточняющими область применимости) совпадающей формулировки «правила потока» с законом электромагнитной индукции нельзя назвать чисто случайной. Дело в том, что, по крайней мере для определённых ситуаций, это совпадение оказывается очевидным проявлением принципа относительности. А именно, например, для случая относительного движения катушки с присоединённым к ней вольтметром, измеряющим ЭДС, и источника магнитного поля (постоянного магнита или другой катушки с током), в системе отсчёта, связанной с первой катушкой, ЭДС оказывается равной именно циркуляции электрического поля, тогда как в системе отсчёта, связанной с источником магнитного поля (магнитом), происхождение ЭДС связано с действием силы Лоренца на движущиеся с первой катушкой носители заряда. Однако та и другая ЭДС обязаны совпадать, поскольку вольтметр показывает одну и ту же величину, независимо от того, для какой системы отсчёта мы её рассчитали.

Потенциальная форма[править | править код]

При выражении магнитного поля через векторный потенциал закон Фарадея принимает вид:

E→=−∂A→∂t{\displaystyle {\vec {E}}=-{\partial {\vec {A}} \over \partial t}} (в случае отсутствия безвихревого поля, то есть тогда, когда электрическое поле порождается полностью только изменением магнитного, то есть электромагнитной индукцией).

В общем случае, при учёте и безвихревого (например, электростатического) поля имеем:

E→=−∇φ−∂A→∂t{\displaystyle {\vec {E}}=-\nabla \varphi -{\partial {\vec {A}} \over \partial t}}

Подробнее

Поскольку вектор магнитной индукции по определению выражается через векторный потенциал так:

B→=rot A→≡∇×A→,{\displaystyle {\vec {B}}=rot\ {\vec {A}}\equiv \nabla \times {\vec {A}},}

то можно подставить это выражение в

rot E→≡∇×E→=−∂B→∂t,{\displaystyle rot\ {\vec {E}}\equiv \nabla \times {\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}},}

получая

∇×E→=−∂(∇×A→)∂t,{\displaystyle \nabla \times {\vec {E}}=-{\frac {\partial (\nabla \times {\vec {A}})}{\partial t}},}

и, поменяв местами дифференцирование по времени и пространственным координатам (ротор):

∇×E→=−∇×∂A→∂t.{\displaystyle \nabla \times {\vec {E}}=-\nabla \times {\frac {\partial {\vec {A}}}{\partial t}}.}

Отсюда, поскольку ∇×E→{\displaystyle \nabla \times {\vec {E}}} полностью определяется правой частью последнего уравнения, видно, что вихревая часть электрического поля (та часть, которая имеет ротор, в отличие от безвихревого поля ∇φ{\displaystyle \nabla \varphi }) полностью определяется выражением

−∂A→∂t.{\displaystyle -{\frac {\partial {\vec {A}}}{\partial t}}.}

То есть в случае отсутствия безвихревой части можно записать

E→=−∂A→∂t,{\displaystyle {\vec {E}}=-{\frac {\partial {\vec {A}}}{\partial t}},}

а в общем случае

E→=−∇φ−dA→dt.{\displaystyle {\vec {E}}=-\nabla \varphi -{\frac {d{\vec {A}}}{dt}}.}

В 1820 году Ганс Христиан Эрстед показал, что протекающий по цепи электрический ток вызывает отклонение магнитной стрелки. Если электрический ток порождает магнетизм, то с магнетизмом должно быть связано появление электрического тока. Эта мысль захватила английского ученого М. Фарадея. «Превратить магнетизм в электричество», — записал он в 1822 году в своём дневнике. Многие годы настойчиво ставил он различные опыты, но безуспешно, и только 29 августа 1831 года наступил триумф: он открыл явление электромагнитной индукции. Установка, на которой Фарадей сделал своё открытие, состояла из кольца из мягкого железа примерно 2 см шириной и 15 см диаметром. На каждой половине кольца было намотано много витков медной проволоки. Цепь одной обмотки замыкала проволока, в её витках находилась магнитная стрелка, удаленная настолько, чтобы не сказывалось действие магнетизма, созданного в кольце. Через вторую обмотку пропускался ток от батареи гальванических элементов. При включении тока магнитная стрелка совершала несколько колебаний и успокаивалась; когда ток прерывали, стрелка снова колебалась. Выяснилось, что стрелка отклонялась в одну сторону при включении тока и в другую, когда ток прерывался. М. Фарадей установил, что «превращать магнетизм в электричество» можно и с помощью обыкновенного магнита.

В это же время американский физик Джозеф Генри также успешно проводил опыты по индукции токов, но пока он собирался опубликовать результаты своих опытов, в печати появилось сообщение М. Фарадея об открытии им электромагнитной индукции.

М. Фарадей стремился использовать открытое им явление, чтобы получить новый источник электричества.

1. ↑ Миллер М. А., Пермитин Г. В. Электромагнитная индукция // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1999. — Т. 5: Стробоскопические приборы — Яркость. — С. 537—538. — 692 с. — 20 000 экз. — ISBN 5-85270-101-7.
2. ↑ Faraday, Michael; Day, P. The philosopher’s tree: a selection of Michael Faraday’s writings (англ.). — CRC Press, 1999. — P. 71. — ISBN 978-0-7503-0570-9.
3. ↑ Это уравнение Максвелла может быть переписано в эквивалентном виде

   ∮∂S⁡E→⋅dl→=−∫S∂B→∂t⋅ds→{\displaystyle \oint _{\partial S}{\vec {E}}\cdot {\vec {dl}}=-\int _{S}{\frac {\partial {\vec {B}}}{\partial t}}\cdot {\vec {ds}}}

   (здесь просто производная по t внесена под знак интеграла). В таком виде уравнение также может быть включено в систему уравнений Максвелла, причем оговорка о неподвижности контура интегрирования теряет актуальность, так как производная теперь очевидно не действует на границу области (на пределы интегрирования), а само интегрирование в любом случае полагается «мгновенным». В принципе, в таком виде это уравнение также могут называть законом Фарадея (чтобы отличить его от других уравнений Максвелла), пусть в таком виде оно и не совпадает прямо с его обычной формулировкой (но эквивалентно ей в своей области применимости).
4. ↑ М. Лившиц. Закон электромагнитной индукции или «правило потока»? // Квант. — 1998. — № 3. — С. 37—38.
5. ↑ Такой отказ объясняется тем, что, в отличие от закона для циркуляции электрического поля, выполняющегося всегда, «правило» корректно работает лишь для случаев, когда контур, в котором вычисляется ЭДС, совпадает физически с проводником (то есть совпадает их движение; в противном же случае правило может не работать (самый известный пример — униполярная машина Фарадея; контур, который в этом случае трудно определить, но кажется довольно очевидным, что он не меняется; во всяком случае, довольно затруднительно указать разумное определение для контура, который бы в этом случае менялся), то есть проявляется парадокс, что для «закона природы» недопустимо.

Закон электромагнитной индукции Фарадея — Википедия

Зако́н электромагни́тной инду́кции Фараде́я является основным законом электродинамики, касающимся принципов работы трансформаторов, дросселей, многих видов электродвигателей и генераторов.^[1] Закон гласит:

или другими словами:

Генерируемая ЭДС пропорциональна скорости изменения магнитного потока.

При этом индукционный ток направлен таким образом, что его действие противоположно действию причины, вызвавшей этот ток (правило Ленца).^[2]

Электромагнитная индукция была обнаружена независимо друг от друга Майклом Фарадеем и Джозефом Генри в 1831 году, однако Фарадей первым опубликовал результаты своих экспериментов^[3][4].

В первой экспериментальной демонстрации электромагнитной индукции (август 1831) Фарадей обмотал двумя проводами противоположные стороны железного тора (конструкция похожа на современный трансформатор). Основываясь на своей оценке недавно обнаруженного свойства электромагнита, он ожидал, что при включении тока в одном проводе особого рода волна пройдёт сквозь тор и вызовет некоторое электрическое влияние на его противоположной стороне. Он подключил один провод к гальванометру и смотрел на него, когда другой провод подключал к батарее. В самом деле, он увидел кратковременный всплеск тока (который он назвал «волной электричества»), когда подключал провод к батарее, и другой такой же всплеск, когда отключал его.^[5] В течение двух месяцев Фарадей нашёл несколько других проявлений электромагнитной индукции. Например, он увидел всплески тока, когда быстро вставлял магнит в катушку и вытаскивал его обратно, он генерировал постоянный ток во вращающемся вблизи магнита медном диске со скользящим электрическим проводом («диск Фарадея»)^[6].

Фарадей объяснил электромагнитную индукцию с использованием концепции так называемых силовых линий. Однако, большинство учёных того времени отклонили его теоретические идеи, в основном потому, что они не были сформулированы математически.^[7] Исключение составил Максвелл, который использовал идеи Фарадея в качестве основы для своей количественной электромагнитной теории.^[7][8][9] В работах Максвелла аспект изменения во времени электромагнитной индукции выражен в виде дифференциальных уравнений. Оливер Хевисайд назвал это законом Фарадея, хотя он несколько отличается по форме от первоначального варианта закона Фарадея и не учитывает индуцирование ЭДС при движении. Версия Хевисайда является формой признанной сегодня группы уравнений, известных как уравнения Максвелла.

Эмилий Христианович Ленц сформулировал в 1834 году закон (правило Ленца), который описывает «поток через цепь» и даёт направление индуцированной ЭДС и тока в результате электромагнитной индукции.

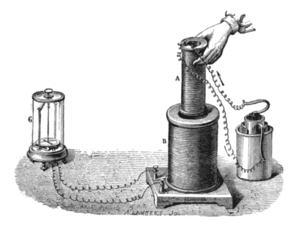Эксперимент Фарадея, показывающий индукцию между витками провода: жидкостная батарея (справа) даёт ток, который протекает через небольшую катушку (A), создавая магнитное поле. Когда катушки неподвижны, ток не индуцируется. Но когда маленькая катушка вставляется или извлекается из большой катушки (B), магнитный поток через катушку изменяется, вызывая ток, который регистрируется гальванометром (G).^[10]

Закон Фарадея как два различных явления[править | править код]

Некоторые физики отмечают, что закон Фарадея в одном уравнении описывает два разных явления: двигательную ЭДС, генерируемую действием магнитной силы на движущийся провод, и трансформаторную ЭДС, генерируемую действием электрической силы вследствие изменения магнитного поля. Джеймс Клерк Максвелл обратил внимание на этот факт в своей работе О физических силовых линиях в 1861 году. Во второй половине части II этого труда Максвелл даёт отдельное физическое объяснение для каждого из этих двух явлений. Ссылка на эти два аспекта электромагнитной индукции имеется в некоторых современных учебниках.^[11] Как пишет Ричард Фейнман:^[12]

Таким образом, «правило потока» о том, что ЭДС в цепи равна скорости изменения магнитного потока через контур, применяется независимо от причины изменения потока: то ли потому что поле изменяется, то ли потому что цепь движется (или и то, и другое)…. В нашем объяснении правила мы использовали два совершенно различных закона для двух случаев  –    v×B{\displaystyle {\stackrel {\mathbf {v\times B} }{}}}   для «движущейся цепи» и   ∇ x E = −∂ tB{\displaystyle {\stackrel {\mathbf {\nabla \ x\ E\ =\ -\partial _{\ t}B} }{}}}   для «меняющегося поля».

Мы не знаем никакого аналогичного положения в физике, когда такие простые и точные общие принципы требовали бы для своего реального понимания анализа с точки зрения двух различных явлений.

— Ричард Фейнман,   Фейнмановские лекции по физике

Отражение этой очевидной дихотомии было одним из основных путей, которые привели Эйнштейна к разработке специальной теории относительности:

Известно, что электродинамика Максвелла — как её обычно понимают в настоящее время — при применении к движущимся телам приводит к асимметрии, которая, как кажется, не присуща этому явлению. Возьмем, к примеру, электродинамическое взаимодействие магнита и проводника. Наблюдаемое явление зависит только от относительного движения проводника и магнита, тогда как обычное мнение рисует резкое различие между этими двумя случаями, в которых либо одно, либо другое тело находится в движении. Ибо, если магнит находится в движении, а проводник покоится, в окрестности магнита возникает электрическое поле с определенной плотностью энергии, создавая ток там, где расположен проводник. Но если магнит покоится, а проводник движется, то в окрестности магнита никакое электрическое поле не возникает. В проводнике, однако, мы находим электродвижущую силу, для которой не существует соответствующей энергии самой по себе, но которая вызывает — предполагая равенство относительного движения в двух обсуждаемых случаях — электрические токи по тому же направлению и той же интенсивности, как в первом случае.

Примеры подобного рода вместе с неудачной попыткой обнаружить какое-либо движение Земли относительно «светоносной среды» предполагают, что явления электродинамики, а также механики не обладают свойствами, соответствующими идее абсолютного покоя.

— Альберт Эйнштейн, К электродинамике движущихся тел^[13]

Поток через поверхность и ЭДС в контуре[править | править код]

Определение поверхностного интеграла предполагает, что поверхность Σ поделена на мелкие элементы. Каждый элемент связан с вектором dA, величина которого равна площади элемента, а направление — по нормали к элементу во внешнюю сторону. 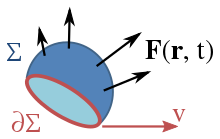Векторное поле F(r, t) определено во всём пространстве, а поверхность Σ ограничена кривой ∂Σ, движущейся со скоростью v. По этой поверхности производится интегрирование поля.

Закон электромагнитной индукции Фарадея использует понятие магнитного потока Φ_B через замкнутую поверхность Σ, который определён через поверхностный интеграл:

 :Φ=∬SBn⋅dS,{\displaystyle \Phi =\iint \limits _{S}\mathbf {B_{n}} \cdot d\mathbf {S} ,}

где dS — площадь элемента поверхности Σ(t), B — магнитное поле, а B·dS — скалярное произведение B и dS. Предполагается, что поверхность имеет «устье», очерченное замкнутой кривой, обозначенной ∂Σ(t). Закон индукции Фарадея утверждает, что когда поток изменяется, то при перемещении единичного положительного пробного заряда по замкнутой кривой ∂Σ возникает ЭДС E{\displaystyle {\mathcal {E}}}, величина которой определяется по формуле:

|E|=|dΦdt| ,{\displaystyle |{\mathcal {E}}|=\left|{{d\Phi } \over dt}\right|\ ,}

где |E|{\displaystyle |{\mathcal {E}}|} — величина электродвижущей силы (ЭДС) в вольтах, а Φ_B — магнитный поток в веберах. Направление электродвижущей силы определяется законом Ленца.

Для плотно намотанной катушки индуктивности, содержащей N витков, каждый с одинаковым магнитным потоком Φ_B, закон индукции Фарадея утверждает, что:

|E|=N|dΦBdt|,{\displaystyle |{\mathcal {E}}|=N\left|{{d\Phi _{B}} \over dt}\right|,}

где N — число витков провода, Φ_B — магнитный поток в веберах на один виток.

При выборе пути ∂Σ(t) для нахождения ЭДС заметим, что путь должен удовлетворять двум основным требованиям: (i) путь должен быть замкнутым, и (ii) путь должен охватывать относительное движение частей контура (источник происхождения t-зависимости в ∂Σ(t)). К требованиям не относится то, что путь должен совпадать с линией тока, но, конечно, ЭДС, которая находится по закону потока, будет считаться по выбранному пути. Если путь не совпадает с линией тока, то подсчитанная ЭДС, возможно, будет не та ЭДС, которая вызывает ток.

Пример 1: пространственно меняющееся магнитное поле[править | править код]

Рис. 3. Замкнутый прямоугольный провод движется вдоль оси x со скоростью v в магнитном поле, которое изменяется вдоль x.

Рассмотрим случай на рисунке 3, на котором прямоугольная замкнутая проволочная петля, расположенная в плоскости xy, перемещается в направлении оси x со скоростью v. Центр петли x_C удовлетворяет условию v = dx_C / dt. Петля имеет длину ℓ в направлении оси y и ширину w в направлении оси x. Зависящее от времени пространственно меняющееся магнитное поле B(x) показано в направлении z. Магнитное поле на левой стороне равно B(x_C − w / 2), а на правой стороне B(x_C + w / 2). Электродвижущую силу можно найти либо с помощью закона Лоренца, либо, что эквивалентно, используя вышеизложенный закон индукции Фарадея.

Закон Лоренца[править | править код]

Заряд q в проводнике на левой стороне петли испытывает силу Лоренца q v × B k = −q v B(x_C − w / 2) j   (j, k — единичные векторы в направлениях y и z; см. векторное произведение векторов), что вызывает ЭДС (работу на единицу заряда) v ℓ B(x_C − w / 2) по всей длине левой стороны петли. На правой стороне петля аналогичное рассуждение показывает, что ЭДС равна v ℓ B(x_C + w / 2). Две противоположные друг другу ЭДС толкают положительный заряд по направлению к нижней части петли. В случае, когда поле B возрастает вдоль х, сила на правой стороне будет больше, а ток будет течь по часовой стрелке. Используя правило правой руки, мы получаем, что поле B, создаваемое током, противоположно приложенному полю.^[14] ЭДС, вызывающая ток, должна увеличиваться по направлению против часовой стрелки (в отличие от тока). Складывая ЭДС в направлении против часовой стрелки вдоль петли мы находим:

E=vℓ[B(xC+w/2)−B(xC−w/2)] .{\displaystyle {\mathcal {E}}=v\ell [B(x_{C}+w/2)-B(x_{C}-w/2)]\ .}

Закон Фарадея[править | править код]

В любой точке петли магнитный поток через неё равен:

ΦB=±∫0ℓdy∫xC−w/2xC+w/2B(x)dx{\displaystyle \Phi _{B}=\pm \int _{0}^{\ell }dy\int _{x_{C}-w/2}^{x_{C}+w/2}B(x)dx}

=±ℓ∫xC−w/2xC+w/2B(x)dx .{\displaystyle \qquad =\pm \ell \int _{x_{C}-w/2}^{x_{C}+w/2}B(x)dx\ .}

Выбор знака определяется по принципу, имеет ли нормаль к поверхности в данной точке то же направление, что и B, или противоположное. Если нормаль к поверхности имеет то же направление, что и поле B наведённого тока, этот знак отрицательный. Производная по времени от потока (найденная с помощью методов дифференцирования сложной функции или по правилу Лейбница дифференцирования интеграла) равна:

dΦBdt=(−)ddxC[∫0ℓdy ∫xC−w/2xC+w/2dxB(x)]dxCdt {\displaystyle {\frac {d\Phi _{B}}{dt}}=(-){\frac {d}{dx_{C}}}\left[\int _{0}^{\ell }dy\ \int _{x_{C}-w/2}^{x_{C}+w/2}dxB(x)\right]{\frac {dx_{C}}{dt}}\ }

=(−)vℓ[B(xC+w/2)−B(xC−w/2)] ,{\displaystyle \qquad =(-)v\ell [B(x_{C}+w/2)-B(x_{C}-w/2)]\ ,}

(где v = dx_C / dt является скоростью движения петли в направлении оси х), что приводит к:

E=−dΦBdt=vℓ[B(xC+w/2)−B(xC−w/2)] ,{\displaystyle {\mathcal {E}}=-{\frac {d\Phi _{B}}{dt}}=v\ell [B(x_{C}+w/2)-B(x_{C}-w/2)]\ ,}

как и в предыдущем случае.

Эквивалентность этих двух подходов является общеизвестной, и в зависимости от решаемой задачи более практичным может оказаться либо тот, либо другой метод.

Пример 2: проводник, движущийся в постоянном магнитном поле[править | править код]

Рис. 4. Два проводника замкнутые на проводящие обода образуют «рамку» вращающуюся с угловой скоростью ω в радиальном, направленном наружу магнитном поле B фиксированной величины. Ток подается щётками, касающимися верхнего и нижнего дисков с проводящими ободами.

На рис. 4 показан шпиндель, образованный двумя дисками с проводящими ободами, и проводники, расположенные вертикально между этими ободами. ток скользящими контактами подается на проводящие обода. Эта конструкция вращается в магнитном поле, которое направлено радиально наружу и имеет одно и то же значение в любом направлении. то есть мгновенная скорость проводников, ток в них и магнитная индукция, образуют правую тройку, что заставляет проводники вращаться.

Сила Лоренца[править | править код]

В этом случае на проводники действует Сила Ампера, а на единичный заряд в проводнике Сила Лоренца — поток вектора магнитной индукции B , ток в проводниках, соединяющих проводящие обода, направлен нормально к вектору магнитной индукции, тогда сила, действующая на заряд в проводнике, будет равна

F=qBv,{\displaystyle F=qBv\,,}

где v = скорости движущегося заряда^[15]

Следовательно, сила действующая на проводники

F=IBℓ,{\displaystyle {\mathcal {F}}=IB\ell ,}

где l — длина проводников

Здесь мы использовали B как некую данность, на самом деле она зависит от геометрических размеров ободов конструкции, и это значение можно вычислить, используя Закон Био — Савара — Лапласа . Данный эффект используется и в другом устройстве, называемом Рельсотрон

Закон Фарадея[править | править код]

Интуитивно привлекательный, но ошибочный подход к использованию правила потока выражает поток через цепь по формуле Φ_B = B w ℓ, где w — ширина движущейся петли.

Ошибочность такого подхода в том, что это не рамка в обычном понимании этого слова. Прямоугольник на рисунке образован отдельными проводниками, замкнутыми на обод. Как видно на рисунке, ток по обоим проводникам течет в одном направлении, то есть здесь отсутствует понятие «замкнутый контур»

Наиболее простое и понятное объяснение этому эффекту дает понятие сила Ампера. То есть вертикальный проводник может быть вообще один, чтобы не вводить в заблуждение. Или же проводник конечной толщины может быть расположен на оси, соединяющей обода. Диаметр проводника должен быть конечным и отличаться от нуля, чтобы момент силы Ампера был ненулевой.

Рис. 6. Иллюстрация теоремы Кельвина-Стокса с помощью поверхности Σ, её границы ∂Σ и ориентации n , установленной правилом правой руки.

Переменное магнитное поле создаёт электрическое поле, описываемое уравнением Фарадея — Максвелла:

∇×E=−∂B∂t,{\displaystyle \nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}},}

где:

∇×{\displaystyle \nabla \times } обозначает ротор

E — электрическое поле

B — плотность магнитного потока.

Это уравнение присутствует в современной системе уравнений Максвелла, часто его называют законом Фарадея. Однако, поскольку оно содержит только частные производные по времени, его применение ограничено ситуациями, когда заряд покоится в переменном по времени магнитном поле. Оно не учитывает^{[уточнить]} электромагнитную индукцию в случаях, когда заряженная частица движется в магнитном поле.

В другом виде закон Фарадея может быть записан через интегральную форму теоремы Кельвина-Стокса:^[16]

∮∂Σ⁡E⋅dℓ=−∫Σ∂∂tB⋅dA.{\displaystyle \oint _{\partial \Sigma }\mathbf {E} \cdot d{\boldsymbol {\ell }}=-\int _{\Sigma }{\partial \over {\partial t}}\mathbf {B} \cdot d\mathbf {A} .}

Для выполнения интегрирования требуется независимая от времени поверхность Σ (рассматриваемая в данном контексте как часть интерпретации частных производных). Как показано на рис. 6:

Σ — поверхность, ограниченная замкнутым контуром ∂Σ, причём, как Σ, так и ∂Σ являются фиксированными, не зависящими от времени,

E — электрическое поле,

dℓ — бесконечно малый элемент контура ∂Σ,

B — магнитное поле,

dA — бесконечно малый элемент вектора поверхности Σ.

Элементы dℓ и dA имеют неопределённые знаки. Чтобы установить правильные знаки, используется правило правой руки, как описано в статье о теореме Кельвина-Стокса. Для плоской поверхности Σ положительное направление элемента пути dℓ кривой ∂Σ определяется правилом правой руки, по которому на это направление указывают четыре пальца правой руки, когда большой палец указывает в направлении нормали n к поверхности Σ.

Интеграл по ∂Σ называется интеграл по пути или криволинейным интегралом. Поверхностный интеграл в правой части уравнения Фарадея-Максвелла является явным выражением для магнитного потока Φ_B через Σ. Обратите внимание, что ненулевой интеграл по пути для E отличается от поведения электрического поля, создаваемого зарядами. Генерируемое зарядом E-поле может быть выражено как градиент скалярного поля, которое является решением уравнения Пуассона и имеет нулевой интеграл по пути.

Интегральное уравнение справедливо для любого пути ∂Σ в пространстве и любой поверхности Σ, для которой этот путь является границей.

Рис. 7. Площадь заметания элемента вектора dℓ кривой ∂Σ за время dt при движении со скоростью v.

Используя^[17]

ddt∫AB dA=∫A(∂B∂t+v div B+rot(B×v))dA{\displaystyle {\frac {\text{d}}{{\text{d}}t}}\int \limits _{A}{\mathbf {B} }{\text{ d}}\mathbf {A} =\int \limits _{A}{\left({\frac {\partial \mathbf {B} }{\partial t}}+\mathbf {v} \ {\text{div}}\ \mathbf {B} +{\text{rot}}\;(\mathbf {B} \times \mathbf {v} )\right)\;{\text{d}}}\mathbf {A} }

и принимая во внимание divB=0{\displaystyle {\text{div}}\mathbf {B} =0} (Ряд Гаусса), B×v=−v×B{\displaystyle \mathbf {B} \times \mathbf {v} =-\mathbf {v} \times \mathbf {B} } (Векторное произведение) и ∫ArotXdA=∮∂A⁡Xdℓ{\displaystyle \int _{A}{\text{rot}}\;\mathbf {X} \;\mathrm {d} \mathbf {A} =\oint _{\partial A}\mathbf {X} \;{\text{d}}{\boldsymbol {\ell }}} (теорема Кельвина — Стокса), мы находим, что полная производная магнитного потока может быть выражена

∫Σ∂B∂tdA=ddt∫ΣB dA+∮∂Σ⁡v×Bdℓ.{\displaystyle \int \limits _{\Sigma }{\frac {\partial \mathbf {B} }{\partial t}}{\textrm {d}}\mathbf {A} ={\frac {\text{d}}{{\text{d}}t}}\int \limits _{\Sigma }{\mathbf {B} }{\text{ d}}\mathbf {A} +\oint _{\partial \Sigma }\mathbf {v} \times \mathbf {B} \,{\text{d}}{\boldsymbol {\ell }}.}

Добавляя член ∮⁡v×Bdℓ{\displaystyle \oint \mathbf {v} \times \mathbf {B} \mathrm {d} \mathbf {\ell } } к обеим частям уравнения Фарадея-Максвелла и вводя вышеприведённое уравнение, мы получаем:

∮∂Σ⁡(E+v×B)dℓ=−∫Σ∂∂tBdA⏟induced emf+∮∂Σ⁡v×Bdℓ⏟motional emf=−ddt∫ΣB dA,{\displaystyle \oint \limits _{\partial \Sigma }{(\mathbf {E} +\mathbf {v} \times \mathbf {B} )}{\text{d}}\ell =\underbrace {-\int \limits _{\Sigma }{\frac {\partial }{\partial t}}\mathbf {B} {\text{d}}\mathbf {A} } _{{\text{induced}}\ {\text{emf}}}+\underbrace {\oint \limits _{\partial \Sigma }{\mathbf {v} }\times \mathbf {B} {\text{d}}\ell } _{{\text{motional}}\ {\text{emf}}}=-{\frac {\text{d}}{{\text{d}}t}}\int \limits _{\Sigma }{\mathbf {B} }{\text{ d}}\mathbf {A} ,}

что и является законом Фарадея. Таким образом, закон Фарадея и уравнения Фарадея-Максвелла физически эквивалентны.

Рис. 7 показывает интерпретацию вклада магнитной силы в ЭДС в левой части уравнения. Площадь, заметаемая сегментом dℓ кривой ∂Σ за время dt при движении со скоростью v, равна:

dA=−dℓ×vdt ,{\displaystyle d\mathbf {A} =-d{\boldsymbol {\ell \times v}}dt\ ,}

так что изменение магнитного потока ΔΦ_B через часть поверхности, ограниченной ∂Σ за время dt, равно:

dΔΦBdt=−B⋅ dℓ×v =−v×B⋅ dℓ ,{\displaystyle {\frac {d\Delta \Phi _{B}}{dt}}=-\mathbf {B} \cdot \ d{\boldsymbol {\ell \times v}}\ =-\mathbf {v} \times \mathbf {B} \cdot \ d{\boldsymbol {\ell }}\ ,}

и если сложить эти ΔΦ_B-вклады вокруг петли для всех сегментов dℓ, мы получим суммарный вклад магнитной силы в закон Фарадея. То есть этот термин связан с двигательной ЭДС.

Пример 3: точка зрения движущегося наблюдателя[править | править код]

Возвращаясь к примеру на рис. 3, в движущейся системе отсчета выявляется тесная связь между E— и B-полями, а также между двигательной и индуцированной ЭДС.^[18] Представьте себе наблюдателя, движущегося вместе с петлёй. Наблюдатель вычисляет ЭДС в петле с использованием как закона Лоренца, так и с использованием закона электромагнитной индукции Фарадея. Поскольку этот наблюдатель движется с петлей, он не видит никакого движения петли, то есть нулевую величину v × B. Однако, поскольку поле B меняется в точке x, движущийся наблюдатель видит изменяющееся во времени магнитного поля, а именно:

B=kB(x+vt) ,{\displaystyle \mathbf {B} =\mathbf {k} {B}(x+vt)\ ,}

где k  — единичный вектор в направлении z.^[19]

Закон Лоренца[править | править код]

Уравнение Фарадея-Максвелла говорит, что движущийся наблюдатель видит электрическое поле E_y в направлении оси y, определяемое по формуле:

∇×E=k dEydx{\displaystyle \nabla \times \mathbf {E} =\mathbf {k} \ {\frac {dE_{y}}{dx}}}

=−∂B∂t=−kdB(x+vt)dt=−kdBdxv  .{\displaystyle \qquad =-{\frac {\partial \mathbf {B} }{\partial t}}=-\mathbf {k} {\frac {dB(x+vt)}{dt}}=-\mathbf {k} {\frac {dB}{dx}}v\ \ .}

Применяя правило дифференцирования сложной функции:

dBdt=dBd(x+vt)d(x+vt)dt=dBdxv .{\displaystyle {\frac {dB}{dt}}={\frac {dB}{d(x+vt)}}{\frac {d(x+vt)}{dt}}={\frac {dB}{dx}}v\ .}

Решение для E_y с точностью до постоянной, которая ничего не добавляет в интеграл по петле:

Ey(x, t)=−B(x+vt) v .{\displaystyle E_{y}(x,\ t)=-B(x+vt)\ v\ .}

Источники электрического тока. Электродвижущая сила

Возьмём два проводника, заряженные разноимёнными зарядами, и соединим их другим проводником. Тогда в этом проводнике за счёт разности потенциалов на его концах возникает электрическое поле, под действием которого свободные заряды (носители тока) приходят в упорядоченное движение от положительного потенциала к отрицательному (имеется в виду движение положительных зарядов, поскольку за направление тока принимается движение именно этих зарядов), т.е. возникает электрический ток. Однако этот ток очень быстро прекращается в силу того, что протекание тока приводит к выравниванию потенциалов на концах проводника и к исчезновению внутри него электрического поля. Для непрерывного протекания тока по проводнику необходимо к его концам подключить устройство, которое бы отводило положительные заряды с конца, обладающего отрицательным потенциалом, к концу — с положительным, производя разделение зарядов и поддерживая разность потенциалов (рис. 1). Такие устройства называются источниками тока. Указанное движение зарядов внутри источника тока (движение от точки 1 к точке 2) возможно лишь в том случае, если на них со стороны источника тока действуют силы не электростатического происхождения, направленные против сил электростатического поля. Их называют сторонними силами. Природа сторонних сил может быть различной. Так, в аккумуляторах они возникают вследствие химических реакций между электродами и электролитом.

Р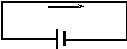

+

–

1

2



I

ис. 1

Действие сторонних сил характеризуют физической величиной, называемой электродвижущей силой (э.д.с.). Она равна работе, которую совершают сторонние силы по перемещению единичного заряда внутри источника тока, т.е. в области, где действуют сторонние силы. Если при перемещении заряда q₀ сторонние силы совершили работу A^стор, то по определению э.д.с.

(18)

Работу A^СТОР сторонних сил 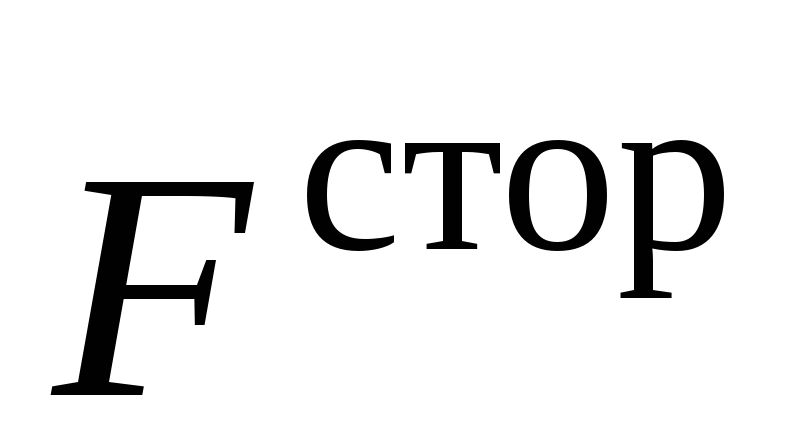можно найти по формуле механической работы:

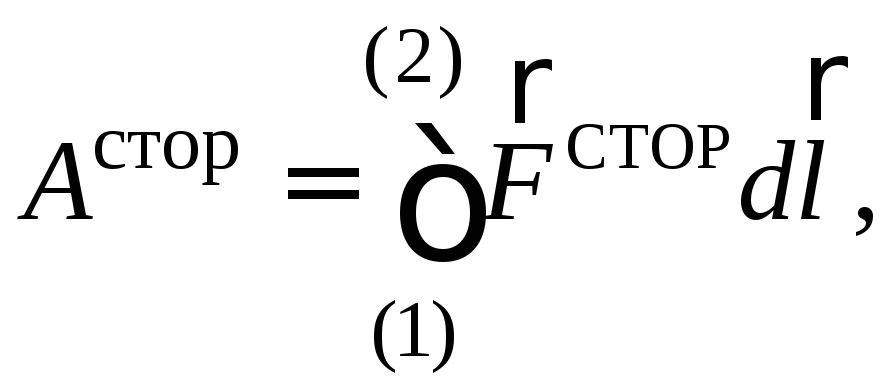(19)

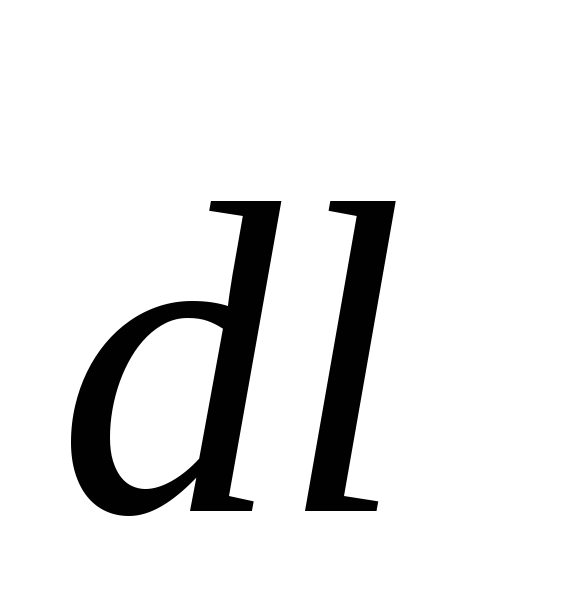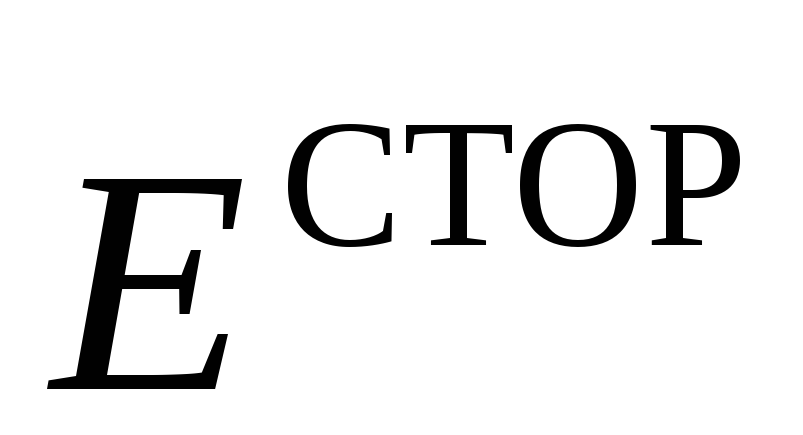где — проекция сторонней силы на элементарное перемещение . По аналогии с напряжённостью электростатического поля, т.е. напряжённостью кулоновских сил, действующих на заряды, находящиеся в этом поле, вводят понятие напряжённостисторонних сил. Тогда, согласно определению напряжённости электрического поля, запишем, что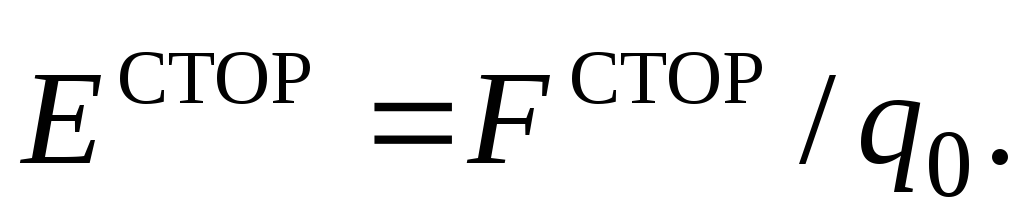ОтсюдаПодставляя это выражение в (19) и выносяq₀ за знак интеграла, находим 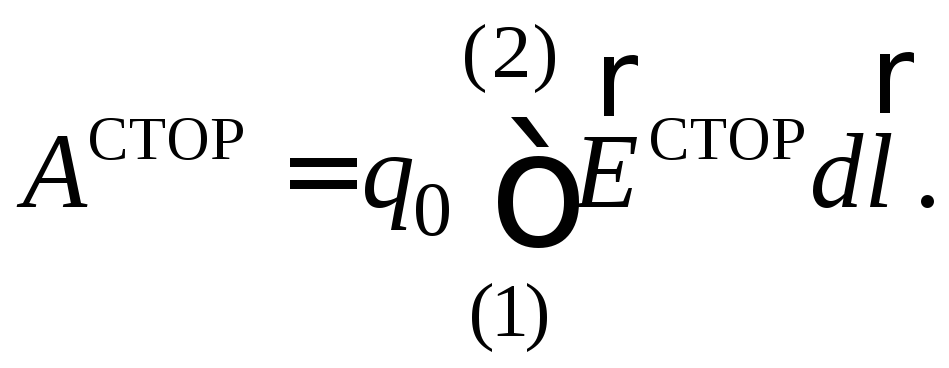Поделив обе части этого равенства наq₀ и учитывая (18), получаем 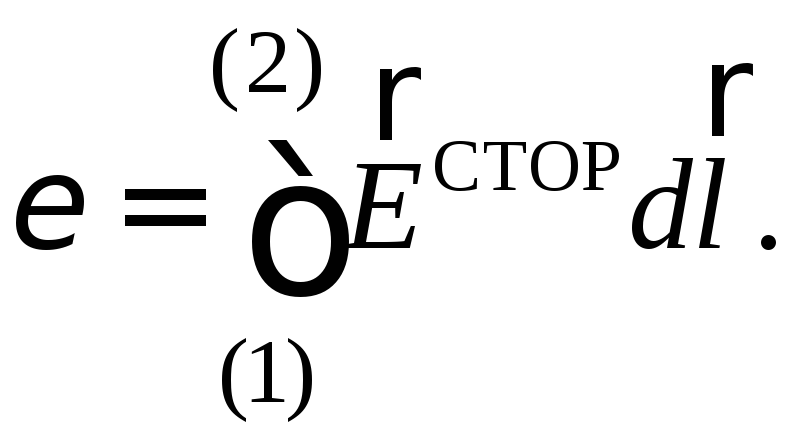Если цепь, в которой протекает ток, замкнутая (см. рис. 1), то работа сторонних сил по всей цепи равна работе этих сил внутри источника, поскольку вне источника сторонние силы не действуют. Тогда

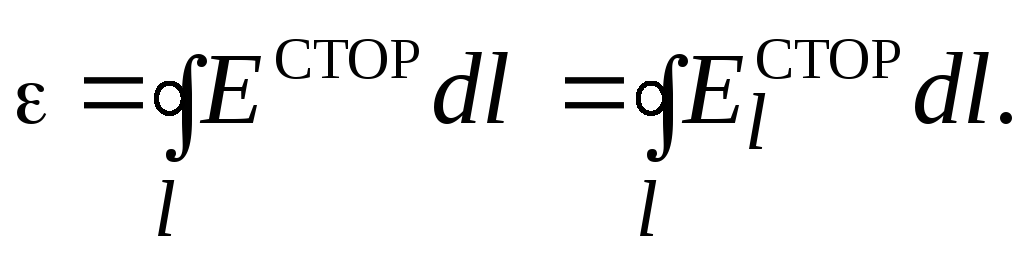(20)

Таким образом, электродвижущая сила равна циркуляции напряжённости сторонних сил.

Работа и мощность электрического тока

Работой электрического тока называется работа, которую совершают силы электрического поля, созданного в электрической цепи, при перемещении заряда по этой цепи. Пусть к концам проводника приложена постоянная разность потенциалов (напряжение) U = ₁ ₂. Тогда, совершаемая электростатическим полем по переносу заряда q за некоторое время t, равна A = q(₁₂) = qU. Величину протекшего заряда найдём, используя силу тока I: q = It. С учётом этого получаем

A = IUt . (21)

По определению мощность электрического тока равна P = A/t. Учитывая (21), получаем, что

P = IU. (22)

Источник ЭДС — Википедия

Материал из Википедии — свободной энциклопедии

Рисунок 1. Обозначение на схемах источника ЭДС (слева) и реального источника напряжения (справа). Вариант.

Исто́чник ЭДС (идеа́льный источник напряже́ния) — двухполюсник, напряжение на зажимах которого не зависит от тока, протекающего через источник и равно его ЭДС. ЭДС источника может быть задана либо постоянным, либо как функция времени, либо как функция от внешнего управляющего воздействия. В простейшем случае ЭДС определена как константа, обычно обозначаемая буквой E{\displaystyle {\mathcal {E}}}.

Идеальный источник напряжения[править | править код]

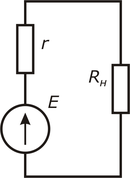Рисунок 2. Реальный источник напряжения под нагрузкой 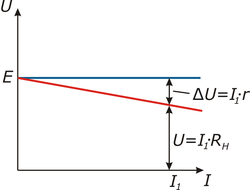Рисунок 3. Нагрузочная характеристика идеального (синий) и реального (красный) источников.

Напряжение на выводах идеального источника напряжения не зависит от нагрузки U=E=const{\displaystyle U={\mathcal {E}}={\text{const}}}. Ток определяется только сопротивлением внешней цепи R{\displaystyle R}:

I=UR.{\displaystyle I={\frac {U}{R}}.}

Модель идеального источника напряжения используется для представления реальных электронных компонентов в виде эквивалентных схем. Собственно, идеальный источник напряжения (источник ЭДС) является физической абстракцией, поскольку при стремлении сопротивления нагрузки к нулю R→0{\displaystyle R\rightarrow 0} отдаваемый ток и электрическая мощность неограниченно возрастают, что противоречит физической природе источника.

Реальный источник напряжения[править | править код]

В реальности любой источник напряжения обладает внутренним сопротивлением r{\displaystyle r}. Следует отметить, что внутреннее сопротивление — это исключительно конструктивное свойство источника. Эквивалентная схема реального источника напряжения представляет собой последовательное включение идеального источника ЭДС E{\displaystyle {\mathcal {E}}} и внутреннего сопротивления r{\displaystyle r}.

На рисунке 3 приведены нагрузочные характеристики идеального источника напряжения (синяя линия) и реального источника напряжения (красная линия).

E=Ur+UR,{\displaystyle {\mathcal {E}}=U_{r}+U_{R},}

где

Ur=I⋅r,{\displaystyle U_{r}=I\cdot r,} — падение напряжения на внутреннем сопротивлении;

UR=I⋅R,{\displaystyle U_{R}=I\cdot R,} — падение напряжения на нагрузке.

При коротком замыкании R=0{\displaystyle R=0} вся мощность источника энергии рассеивается на его внутреннем сопротивлении. В этом случае ток короткого замыкания Is.c.{\displaystyle I_{\text{s.c.}}} будет максимален. Зная напряжение холостого хода Uxx{\displaystyle U_{\text{xx}}} и ток короткого замыкания, можно вычислить внутреннее сопротивление источника напряжения:

r=UxxIs.c..{\displaystyle r={\frac {U_{\text{xx}}}{I_{\text{s.c.}}}}.}

При помощи модели источника напряжения хорошо описываются химические источники тока, батарейки, гальванические элементы, коллекторные генераторы постоянного тока с параллельным возбуждением и бытовые электросети для маломощных потребителей.

Различают источник постоянного и переменного напряжения, а также источник напряжения, управляемые напряжением (ИНУН) и источники напряжения, управляемые током (ИНУТ).

Существуют различные варианты обозначений источника напряжения. Наиболее часто встречается обозначение (a) . Вариант (c) устанавливается ГОСТ^[1] и IEC^[2]. Стрелка в кружке указывает на положительную клемму на выходе источника. При выборе обозначения нужно быть осмотрительным и использовать пояснения, чтобы не допускать путаницы с источниками тока (b), который обозначен так в статье «Источник тока».

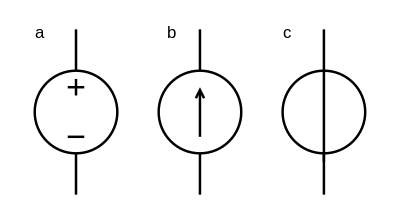Рисунок 4. Обозначения источника напряжения на схемах

Чтобы определить, который полюс источника постоянного напряжения является положительным, а какой — отрицательным, используются специальные «полюсоискатели», действие которых основано на явлении электролиза. Полюсоискатель представляет собой стеклянную ампулу, заполненную раствором поваренной соли с добавкой фенолфталеина. В ампулу снаружи введены электроды. При подключении к электродам источника напряжения начинается электролиз: на отрицательном полюсе идёт выделение водорода и образуется щелочная среда. Из-за наличия щёлочи фенолфталеин меняет свою окраску — краснеет, по красной окраске у электрода и судят о том, что он соединён с отрицательным полюсом источника напряжения^[3].

1. ↑ ГОСТ 2.721-74 Единая система конструкторской документации. Обозначения условные графические в схемах. Обозначения общего применения.
2. ↑ IEC 617-2:1996. Graphical symbols for diagrams — Part 2: Symbol elements, qualifying symbols and other symbols having general application
3. ↑ Элементарный учебник физики / Под ред. Г. С. Ландсберга. — 13-е изд.. — М.: ФИЗМАТЛИТ, 2003. — Т. 2. Электричество и магнетизм. — С. 151,152,465.

• Электротехника: Учеб. для вузов/А. С. Касаткин, М. В. Немцов.— 7-е изд., стер.— М.: Высш. шк., 2003.— 542 с.: ил. ISBN 5-06-003595-6
• Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. — М.: Гардарики, 2002. — 638 с. — ISBN 5-8297-0026-3.

Эдс-электро Ооо, Ул.космонавтов, 6

• Сельское хозяйство, продукты питания
• Химия, фармацевтика, пластмассы
• Строительство
• Энергетика, окружающая среда
• Образование, обучение, общественные институты
• Информационные технологии, компьютеры, программное обеспечение, Интернет, исследования и разработки
• Досуг, развлечения и туризм
• Электрика, электроника, оптика
• Металлы, станки, машины, металлообработка
• Розничная торговля и дистрибуция
• Бумага, печатные и издательские услуги

Что такое электрический ток: определение, характеристики, виды

Открытия, связанные с электричеством, кардинально изменили нашу жизнь. Используя электрический ток как источник энергии, человечество сделало прорыв в технологиях, которые облегчили наше существование. Сегодня электричество приводит в движение токарные станки, автомобили, управляет роботизированной техникой, обеспечивает связь. Этот список можно продолжать очень долго. Даже трудно назвать отрасль, где можно обойтись без электроэнергии.

В чём секрет такого массового использования электричества? Ведь в природе существуют и другие источники энергии, более дешевые, чем электричество. Оказывается всё дело в транспортировке.

Электрическую энергию можно доставить практически везде:

• к производственному цеху;
• квартире;
• на поле;
• в шахту, под воду и т. д.

Электроэнергию, накопленную аккумулятором, можно носить с собой. Мы пользуемся этим ежедневно, беря с собой сотовый телефон. Ни один другой вид энергии не обладает такими универсальными свойствами как электричество. Разве это не является достаточной причиной для того, чтобы глубже изучить природу и свойства электричества?

Что такое электрический ток?

Электрические явления наблюдались давно, но объяснить их природу человек смог относительно недавно. Удар молнии казался чем-то неестественным, необъяснимым. Странным казалось потрескивание некоторых предметов при их трении. Искрящаяся в темноте расчёска, после расчёсывания шерсти животных (например, кошки) вызвала недоумение, но подогревала интерес к этому явлению.

Как всё начиналось

Ещё древним грекам было известно свойство янтаря, потёртого о шерсть, притягивать некоторые мелкие предметы. Кстати, от греческого названия янтаря –«электрон» пошло название «электричество».

Когда физики вплотную занялись исследованием электризации тел, они начали понимать природу подобных явлений. А первый кратковременный электрический ток, созданный человеком, появился при соединении проводником двух наэлектризованных предметов (см. рис. 1). В 1729 году англичане Грей и Уиллер открыли проводимость зарядов некоторыми материалами. Но определения электрического тока они не смогли дать, хотя и понимали, что заряды перемещаются от одного тела к другому по проводнику.

Рис. 1. Опыт с заряженными телами

Об электрическом токе, как о физическом явлении заговорили лишь после того, как итальянец Вольта дал объяснение опытам Гальвани, а в 1794 году изобрёл первый в мире источник электричества – гальванический элемент (столб Вольта). Он обосновал упорядоченное перемещение заряженных частиц по замкнутой цепи.

Определение

В современной трактовке электрическим током называют направленное перемещение силами электрического поля заряженных частиц, Носителями зарядов металлических проводников являются электроны, а растворов кислот и солей — отрицательные и положительные ионы. Полупроводниковыми носителями зарядов являются электроны и «дырки».

Для того чтобы электрический ток существовал, необходимо всё время поддерживать электрическое поле. Должна существовать разница потенциалов, поддерживающая наличие первых двух условий. До тех пор, пока эти условия соблюдены, заряды будут упорядоченно перемещаться по участкам замкнутой электрической цепи. Эту задачу выполняют источники электричества.

Такие условия можно создать, например, с помощью электрофорной машины (рис. 2). Если два диска вращать в противоположных направлениях, то они будут заряжаться разноимёнными зарядами. На щётках, прилегающих к дискам, появится разница потенциалов. Соединив контакты проводником, мы заставим заряженные частицы двигаться упорядоченно. То есть электрофорная машина является источником электричества.

Рисунок 2. Электрофорная машина

Источники тока

Первыми источниками электрической энергии, нашедшими практическое применение, были упомянутые выше гальванические элементы. Усовершенствованные гальванические элементы (народное название – батарейки) широко применяются по сей день. Они используются для питания пультов управления, электронных часов, детских игрушек и многих других гаджетов.

С изобретением генераторов переменных токов электричество приобрело второе дыхание. Началась эра электрификации городов, а позже и всех населённых пунктов. Электрическая энергия стала доступной для всех граждан развитых стран.

Сегодня человечество ищет возобновляемые источники электроэнергии. Солнечные панели, ветряные электростанции уже занимают свои ниши в энергосистемах многих стран, включая Россию.

Характеристики

Электрический ток характеризуется величинами, которые описывают его свойства.

Сила и плотность тока

Для описания характеристики электричества часто используют термин «сила тока». Название не совсем удачное, так как оно характеризует только интенсивность движения электрических зарядов, а не какую-то силу в буквальном смысле. Тем не менее, этим термином пользуются, и он означает количество электричества (зарядов) проходящего через плоскость поперечного сечения проводника. Единицей измерения силы тока в системе СИ является ампер (А).

1 А означает то, что за одну секунду через поперечное сечение проводника проходит электрический заряд 1 Кл. (1А = 1 Кл/с).

Плотность тока  –  векторная величина. Вектор направлен в сторону движения положительных зарядов. Модуль этого вектора равен отношению силы тока на некотором перпендикулярном к направлению движения зарядов сечении проводника к площади этого сечения. В системе СИ измеряется в А/м². Плотность более ёмко характеризует электричество, однако на практике чаще используется величина «сила тока».

Разница потенциалов (напряжение) на участке цепи выражается соотношением: U = I×R, где U – напряжение, I – сила тока, а R – сопротивление. Это знаменитый закон Ома.

Мощность

Электрическими силами совершается работа против активного и реактивного сопротивления. На пассивных сопротивлениях работа преобразуется в тепловую энергию. Мощностью называют работу, выполненную за единицу времени. По отношению к электричеству применяют термин «мощность тепловых потерь». Физики Джоуль и Ленц доказали, что мощность тепловых потерь проводника равна силе тока умноженной на напряжение: P = I× U. Единица измерения мощности – ватт (Вт).

Частота

Переменный ток характеризуется также частотой. Данная характеристика показывает, как за единицу времени изменяется количество периодов (колебаний). Единицей измерения частоты является герц. 1 Гц = 1 периоду за секунду. Стандартная частота промышленного тока составляет 50 Гц.

Ток смещения

Понятие «ток смещения» ввели для удобства, хотя в классическом понимании его нельзя назвать током, так как отсутствует перенос заряда. С другой стороны, интенсивность магнитного поля пребывает в зависимости от токов проводимости и смещения.

Токи смещения можно наблюдать в конденсаторах. Несмотря на то, что при зарядке и разрядке между обкладками конденсатора не происходит перемещения заряда, ток смещения протекает через конденсатор и замыкает электрическую цепь.

Виды тока

По способу генерации и свойствам электроток бывает постоянным и переменным. Постоянный – это такой, что не меняет своего направления. Он течёт всегда в одну сторону. Переменный ток периодически меняет направление. Под переменным понимают любой ток, кроме постоянного. Если мгновенные значения повторяются в неизменной последовательности через равные промежутки времени, то такой электроток называют периодическим.

Классификация переменного тока

Классифицировать изменяющиеся во времени токи можно следующим образом:

1. Синусоидальный, подчиняющийся синусоидальной функции во времени.
2. квазистационарный – переменный, медленно изменяющийся во времени. Обычные промышленные токи являются квазистационарными.
3. Высокочастотный – частота которого превышает десятки кГц.
4. Пульсирующий – импульс которого периодически изменяется.

Различают также вихревые токи, которые возникают в проводнике при изменении магнитного потока. Блуждающие токи Фуко, как их ещё называют, не текут по проводам, а образуют вихревые контуры. Индукционный ток имеет ту же природу что и вихревой.

Дрейфовая скорость электронов

Электричество по металлическому проводнику распространяется со скоростью света. Но это не означает, что заряженные частицы несутся от полюса к полюсу с такой же скоростью. Электроны в металлических проводниках встречают на своём пути сопротивление атомов, поэтому их реальное перемещение составляет всего 0,1 мм за секунду. Реальная, упорядоченная скорость перемещения электронов в проводнике называется дрейфовой.

Если замкнуть проводником полюсы источника питания, то вокруг проводника молниеносно образуется электрическое поле. Чем больше ЭДС источников, тем сильнее проявляется напряжённость электрического поля. Реагируя на напряжённость, заряженные частицы вмиг принимают упорядоченное движение и начинают дрейфовать.

Направление электрического тока

Традиционно считают, что вектор электрического тока направлен к отрицательному полюсу источника. Но на самом деле электроны движутся к положительному полюсу. Традиция возникла из-за того, что за направление вектора было выбрано движение положительных ионов в электролитах, которые действительно стремятся к негативному полюсу.

Электроны проводимости с отрицательным зарядом в металлах были открыты позже, но физики не стали менять первоначальные убеждения. Так укрепилось утверждение, что ток направлен от плюса к минусу.

Электрический ток в различных средах

В металлах

Носителями тока в металлических проводниках являются свободные электроны, которые из-за слабых электрических связей хаотично блуждают внутри кристаллических решёток (рис. 3). Как только в проводнике появляется ЭДС, электроны начинают упорядочено дрейфовать в сторону позитивного полюса источника питания.

Рис. 3. Электрический ток в металлах

В результате прохождения тока возникает сопротивление проводников, которое препятствует потоку электронов и приводит нагреванию. При коротком замыкании выделение тепла настолько сильное, разрушает проводник.

В полупроводниках

В обычном состоянии у полупроводника нет свободных носителей зарядов.  Но если соединить два разных типа полупроводников, то при прямом подключении они превращаются в проводник. Происходит это потому, что у одного типа есть положительно заряженные ионы (дырки), а у другого – отрицательные ионы (атомы с лишним электроном).

Под напряжением электроны из одного полупроводника устремляются для замещения (рекомбинации) дырок в другом. Возникает упорядоченное движение свободных зарядов. Такую проводимость называют электронно-дырочной.

В вакууме и газе

Электрический ток возможен и в ионизированном газе. Заряд переносится положительными и отрицательными ионами. Ионизация газов возможна под действием излучения или вследствие сильного нагревания. Под действием этих факторов возбуждаются атомы, которые превращаются в ионы (рис. 4).

Рис 4. Электрический ток в газах

В вакууме электрические заряды не встречают сопротивления, поэтому. заряженные частицы движутся с околосветовыми скоростями. Носителями зарядов являются электроны. Для возникновения тока в вакууме необходимо создать источник электронов и достаточно большой положительный потенциал на электроде.

Примером может служить работа вакуумной лампы или электронно-лучевая трубка.

В жидкостях

Оговоримся сразу – не все жидкости являются проводниками. Электрический ток возможен в кислотных, щёлочных и соляных растворах. Иначе говоря – в средах, где имеются заряженные ионы.

Если опустить в раствор два электрода и подключить их к полюсам источника, то между ними будет протекать электрический ток (рис. 5). Под действием ЭДС катионы устремятся к катоду (минусу), а анионы к аноду. При этом будет происходить химическое воздействие на электроды – на них будут оседать атомы растворённых веществ. Такое явление называют электролизом.

Рис. 5. Электроток в жидкостях

Для лучшего понимания свойств электротока в разных средах, предлагаю рассмотреть картинку на рисунке 6. Обратите внимание на вольтамперные характеристики (4 столбец).

Рис. 6. Электрический ток в средах

Проводники электрического тока

Среди множества веществ, лишь некоторые являются проводниками. К хорошим проводникам относятся металлы. Важной характеристикой проводника является его удельное сопротивление.

Небольшое сопротивление имеют:

• все благородные металлы;
• медь;
• алюминий;
• олово;
• свинец.

На практике наиболее часто применяют алюминиевые и медные проводники, так как они не слишком дорогие.

Электробезопасность

Несмотря на то что электричество прочно вошло в нашу жизнь, не следует забывать об электробезопасности. Высокие напряжения опасны для жизни, а короткие замыкания становятся причиной пожаров.

При выполнении ремонтных работ необходимо строго соблюдать правила безопасности: не работать под высоким напряжением, использовать защитную одежду и специальные инструменты, применять ножи заземления и т.п.

В быту используйте только такую электротехнику, которая рассчитана на работу в соответствующей сети. Никогда не ставьте «жучки» вместо предохранителей.

Помните, что мощные электролитические конденсаторы имеют большую электрическую емкость. Накопленная в них энергия может вызвать поражение даже спустя несколько минут после отключения от сети.

Электромеханика — Википедия

Наука
Электромеханика
Тема	Электротехника
Предмет изучения	Преобразование электрической энергии в механическую и наоборот, электрические машины, электромеханические комплексы и системы.
Период зарождения	конец XIX века
Основные направления	Общая теория электромеханического преобразования энергии; Проектирование электрических машин; Анализ переходных процессов в электрических машинах.
Вспомогат. дисциплины	Механика, электродинамика, ТОЭ, электрические аппараты.
Центры исследований
Значительные учёные	Э. Арнольд, Р. Рихтер, Р. Парк, Р. А. Лютер, А. И. Важнов, А. В. Иванов-Смоленский, Л. М. Пиотровский, Д. А. Завалишин, А. И. Вольдек, И. П. Копылов

Электромеха́ника — раздел электротехники, в котором рассматриваются общие принципы электромеханического преобразования энергии^[1][2] и их практическое применение для проектирования и эксплуатации электрических машин^[3].

Предметом электромеханики является управление режимами работы и регулирование параметров обратимого преобразования электрической энергии в механическую и механической — в электрическую, включая генерирование и трансформацию электрической энергии^[4].

Электромеханика как наука рассматривает вопросы создания и совершенствования силовых и информационных устройств для взаимного преобразования электрической и механической энергии, электрических, контактных и бесконтактных аппаратов для коммутации электрических цепей и управления потоками энергии^[5].

В соответствии с общероссийским классификатором специальностей по образованию электромеханика является специальностью высшего профессионального образования, подготовка по которой осуществляется в рамках направления 140600 — «Электротехника, электромеханика и электротехнологии»^[6][7].

Одной из первых работ по электромеханике является работа, посвящённая теории и проектированию обмоток электрических машин постоянного тока, которая была опубликована в 1891 году швейцарским учёным Энгельбертом Арнольдом^[8].

В первые три десятилетия XX в. в трудах Э. Арнольда, А. Блонделя, М. Видмара, Л. Дрейфуса, М. П. Костенко, К. А. Круга и В. А. Толвинского была разработана теория установившихся режимов электрических машин.

В 1895 г. А. Блондель предложил метод двух реакций для анализа синхронных машин.

В 1929 г. Р. Парк^[en], используя метод двух реакций, вывел дифференциальные уравнения синхронной машины, названные его именем.

В 1938—1942 гг. Г. Крон создал обобщенную теорию электрических машин (дифференциальные уравнения идеализированной обобщенной электрической машины) и разработал методы тензорного и матричного анализов электрических цепей и машин.

В 1963 г. И. П. Копылов предложил математическую модель обобщенного электромеханического преобразователя для несинусоидального магнитного поля в воздушном зазоре, применимую для симметричных и несимметричных электрических машин с любым числом фаз обмоток статора и ротора и учитывающую нелинейность изменения их параметров.

Альтернативные определения электромеханики[править | править код]

Академик А. Г. Иосифьян дал общее определение электромеханики: «Электромеханика — наука о движении и взаимодействии вещественных инерциальных макроскопических и микроскопических тел, связанных с электрическими и магнитными полями»^[9]. Учитывая то, что для приведения покоящегося тела в движение требуется действие силы, определение, данное Иосифьяном А. Г., может быть приведено к следующей форме: «Электромеханика — обобщенное учение о силах, действующих в электромагнитном поле и о проблемах, связанных с проявлением этих сил»^[10].

В зарубежных источниках встречается следующее определение: «Электромеханика — технология, рассматривающая вопросы, связанные с электромеханическими компонентами, устройствами, оборудованием, системами или процессами»^[11], где под электромеханическими компонентами подразумеваются электрические машины.

Области знаний, используемые в электромеханике[править | править код]

Как правило, под законами электромеханики подразумевают следующие законы электродинамики, необходимые для анализа процессов и проектирования электромеханических преобразователей^[12].

1. Закон электромагнитной индукции Фарадея:

E=−dΦdt=B⋅ℓ⋅v,{\displaystyle {\mathcal {E}}=-{\frac {d\Phi }{dt}}=B\cdot \ell \cdot v,}

где E{\displaystyle {\mathcal {E}}} — ЭДС, Φ{\displaystyle \Phi } — магнитный поток, B{\displaystyle B} — магнитная индукция в данной точке поля, ℓ{\displaystyle \ell } — активная длина проводника в пределах равномерного магнитного поля с индукцией B{\displaystyle B}, расположенного в плоскости, перпендикулярной к направлению магнитных силовых линий, v{\displaystyle v} — скорость проводника в плоскости, нормальной к B{\displaystyle B}, в направлении, перпендикулярном к ℓ{\displaystyle \ell }.

2. Закон полного тока для магнитной цепи (1-е уравнение Максвелла в интегральной форме):

∮⁡H→⋅dl→=∑i,{\displaystyle \oint {\vec {H}}\cdot {\vec {dl}}=\sum i,}

где H→{\displaystyle {\vec {H}}} — вектор напряженности магнитного поля, dl→{\displaystyle {\vec {dl}}} — элементарное перемещение вдоль некоторого пути в магнитном поле, ∑i,{\displaystyle \sum i,} — величина полного тока, который охватывается контуром интегрирования.

3. Закон электромагнитных сил (закон Ампера).

F=B⋅I⋅ℓ.{\displaystyle F=B\cdot I\cdot \ell .}

Профессор МЭИ Копылов И. П. сформулировал три общих закона электромеханики^[13]:

1-й закон: Электромеханическое преобразование энергии не может осуществляться без потерь, его КПД всегда меньше 100 %.

2-й закон: Все электрические машины обратимы, одна и та же машина может работать как в режиме двигателя так и в режиме генератора.

3-й закон: Электромеханическое преобразование энергии осуществляется неподвижными друг относительно друга полями. Ротор может вращаться с той же скоростью, что и поле (в синхронных машинах), или с другой скоростью (в асинхронных машинах), однако поля статора и ротора в установившемся режиме неподвижны относительно друг друга.

1.Основное уравнение электрической машины^[14] — уравнение, связывающее между собой величины диаметра ротора и длины ротора с мощностью двигателя и числом оборотов в минуту:

D2⋅l⋅n1P=5,5⋅103cos⁡φ⋅k1⋅ασ⋅Bm⋅A,{\displaystyle {\frac {D^{2}\cdot l\cdot n_{1}}{P}}={\frac {5,5\cdot 10^{3}}{\cos \varphi \cdot k_{1}\cdot \alpha _{\sigma }\cdot B_{m}\cdot A}},}

где D{\displaystyle D} — диаметр ротора, l{\displaystyle l} — длина ротора, n1{\displaystyle n_{1}} — синхронная скорость вращения ротора в об/мин (равная скорости вращения первой гармоники МДС обмотки статора), P{\displaystyle P} — мощность электрической машины в кВт, cos⁡φ{\displaystyle \cos \varphi } — коэффициент мощности, k1{\displaystyle k_{1}} — обмоточный коэффициент, учитывающий влияние распределения обмотки в пазах и влияние укорочения шага обмотки, Bm{\displaystyle B_{m}} — амплитуда нормальной составляющей магнитной индукции в зазоре машины, A{\displaystyle A} — «линейная нагрузка», равная числу амперпроводников, приходящихся на 1 погонный сантиметр длины окружности статора. Правая часть основного уравнения для данного (известного) типа машины изменяются в сравнительно узких пределах и называется «машинной постоянной» или постоянной Арнольда

CA=D2⋅l⋅n1P.{\displaystyle C_{A}={\frac {D^{2}\cdot l\cdot n_{1}}{P}}.}

2.Уравнения равновесия напряжений обмоток электрической машины — уравнения, составленные для цепей обмоток на основании второго закона Кирхгофа

Для асинхронной машины с короткозамкнутым ротором уравнения равновесия напряжений имеют вид^[15]:

U˙s=Rs⋅I˙s+j⋅xσs⋅I˙s−E˙s{\displaystyle {\dot {U}}_{s}=R_{s}\cdot {\dot {I}}_{s}+j\cdot x_{\sigma s}\cdot {\dot {I}}_{s}-{\dot {E}}_{s}}

0=Rr⋅I˙r+j⋅s⋅xσr⋅I˙r−s⋅E˙r,{\displaystyle 0=R_{r}\cdot {\dot {I}}_{r}+j\cdot s\cdot x_{\sigma r}\cdot {\dot {I}}_{r}-s\cdot {\dot {E}}_{r},}

где U˙s{\displaystyle {\dot {U}}_{s}} — фазное напряжение статора, I˙s{\displaystyle {\dot {I}}_{s}} и I˙r{\displaystyle {\dot {I}}_{r}} — фазные токи статора и ротора, Rs{\displaystyle R_{s}} и Rr{\displaystyle R_{r}} — активные сопротивления обмоток статора и ротора, xσs{\displaystyle x_{\sigma s}} и xσr{\displaystyle x_{\sigma r}} — индуктивные сопротивления рассеяния статора и ротора, E˙s{\displaystyle {\dot {E}}_{s}} и E˙r{\displaystyle {\dot {E}}_{r}} — ЭДС, индуктированные в обмотках статора и ротора результирующим магнитным потоком полей статора и ротора.

3.Уравнение электромагнитного момента

Уравнение электромагнитного момента асинхронной машины имеет вид^[16]:

Me=ms⋅p⋅Us2ωs⋅Rr′/s(Rs+Rr/s)2+(ωs⋅Lk)2,{\displaystyle \mathrm {M} _{e}={\frac {m_{s}\cdot p\cdot U_{s}^{2}}{\omega _{s}}}\cdot {\frac {R_{r}’/s}{(R_{s}+R_{r}/s)^{2}+(\omega _{s}\cdot L_{k})^{2}}},}

где ms{\displaystyle m_{s}} — число фаз обмотки статора, p{\displaystyle p} — число пар полюсов, Us{\displaystyle U_{s}} — действующее значение напряжения статора, ωs{\displaystyle \omega _{s}} — частота тока статора, Rr′{\displaystyle R_{r}’} — активное сопротивление ротора, приведённое к статору, Rs{\displaystyle R_{s}} — активное сопротивление фазной обмотки статора, Lk{\displaystyle L_{k}} — индуктивное сопротивление короткого замыкания, приблизительно равное сумме индуктивности рассеяния статора и приведённой к статору индуктивности рассеяния ротора Lk≈Lsσ+L′rσ{\displaystyle L_{k}\approx Ls\sigma +L’r\sigma }.

Уравнение электромагнитного момента синхронной машины^[15] :

Me=ms⋅Us⋅Eωs⋅xd⋅sin⁡Θ+ms⋅Us22⋅ωs⋅(1xq−1xd),{\displaystyle \mathrm {M} _{e}={\frac {m_{s}\cdot U_{s}\cdot E}{\omega _{s}\cdot x_{d}}}\cdot \sin \Theta +{\frac {m_{s}\cdot U_{s}^{2}}{2\cdot \omega _{s}}}\cdot \left({\frac {1}{x_{q}}}-{\frac {1}{x_{d}}}\right),}

где E{\displaystyle E} — ЭДС, индуктируемая в обмотке статора потоком ротора, Θ{\displaystyle \Theta } — угол нагрузки (угол сдвига фаз между ЭДС и напряжением статора), xd,xq{\displaystyle x_{d},x_{q}} — продольное и поперечное синхронные индуктивные сопротивления обмотки статора.

Вопросы, рассматриваемые в электромеханике[править | править код]

В соответствии с ГОСТом^[4], определяющим содержание подготовки выпускников вузов по специальности «Электромеханика, » в электромеханике рассматриваются следующие вопросы:

Учебники по электромеханике содержат такие темы как^[12]:

1. Расчет электрических машин с нелинейными параметрами с учетом таких факторов как: насыщение, вытеснение тока, изменение момента инерции, ударные моменты нагрузки, несинусоидальнсть напряжения^[17].
2. Оптимизация электрических машин (по КПД, по отношению момента к массе и др.).

1. ↑ Уайт Д.С., Вудсон Г.Х. Электромеханическое преобразование энергии. — М.-Л.: «Энергия», 1964. — С. 7. — 528 с.
2. ↑ ^{1 2} Глава 6. Электромеханика // История электротехники / под. ред И. А. Глебова. — М.: Изд-во МЭИ, 1999. — 524 с. — ISBN 5-7046-0421-8.
3. ↑ В. В. Виноградов, Г. О. Винокур, Б. А. Ларин, С. И. Ожегов, Б. В. Томашевский, Д. Н. Ушаков. Толковый словарь русского языка: В 4 т. / Под ред. Д. Н. Ушакова. — М.: Гос. изд-во иностр. и нац. слов., 1940. — Т. 4. — 1502 с.
4. ↑ ^{1 2} В.В. Галактионов, Ю.Г. Татур, Н.С. Гудилин, Е.П. Попова. Государственный образовательный стандарт высшего профессионального образования. Государственные требования к минимуму содержания и уровню подготовки выпускника по специальности 180100 — Электромеханика. — Государственный комитет Российской федерации по высшему образованию. — М., 1995. — 26 с.
5. ↑ Высшая Аттестационная Комиссия Министерства образования и науки Российской Федерации. Справочные материалы. (неопр.) (pdf) (недоступная ссылка). Паспорта специальностей научных работников. Паспорт специальности 05.09.01 Электромеханика и электрические аппараты.. Дата обращения 17 июня 2013. Архивировано 8 июня 2013 года.
6. ↑ ОКСО 140600 — Электротехника, электромеханика и электротехнологии
7. ↑ Направления подготовки и специальности высшего профессионального образования. Электромеханика. Российское образование. Федеральный портал
8. ↑ History of the Institute of Electrical Engineering. The Institute of Electrical Engineering (ETI) of the Grand Ducal Technical University of Karlsuhe. (неопр.) (недоступная ссылка). Дата обращения 26 мая 2013. Архивировано 16 апреля 2013 года.
9. ↑ Иосифьян А. Г. Электромеханика в космосе. — «Знание», 1977. — 64 с. — («Космонавтика, астрономия»). Архивная копия от 14 июня 2013 на Wayback Machine
10. ↑ Воробьев В. Е. Основы электромеханики: Письменные лекции.. — СПб.: СЗТУ, 2003. — 79 с.
11. ↑ Steven M. Kaplan. Wiley Electrical and Electronics Engineering Dictionary. — John Wiley & Sons, Inc, 2004. — ISBN 978-0-471-40224-4.
12. ↑ ^{1 2} Гольдберг О.Д., Хелемская С.П. Электромеханика: учебник для студ. высш. учеб. заведений / под. ред. Гольдберга О.Д.. — М.: Издательский центр «Академия», 2007. — 512 с. — ISBN 978-5-7695-2886-6.
13. ↑ Копылов И. П. Математическое моделирование электрических машин. Учеб. для вузов. — 3-е изд., перераб. и доп.. — М.: Высш. шк., 2001. — 327 с.
14. ↑ Основное уравнение электрической машины (неопр.) (недоступная ссылка). Дата обращения 11 мая 2013. Архивировано 9 июня 2016 года.
15. ↑ ^{1 2} Вольдек А. И. Электрические машины. Учебн. для студ. высш. техн. учеб. заведений.. — изд. 2-е, перераб. и доп.. — Л.: Изд-во «Энергия», 1978. — 840 с.
16. ↑ Juha PyrhЁonen, Tapani Jokinen and Valґeria Hrabovcovґa. Design of Rotating Electrical Machine. — John Wiley & Sons, Ltd., 2008. — С. 330. — 512 p. — ISBN 978-0-470-69516-6.
17. ↑ Копылов И. П. Электромеханические преобразователи энергии. — М.: «Энергия», 1973. — С. 393. — 400 с.