Единица измерения период переменного тока: Основные величины, характеризующие переменный ток

Содержание

Основные величины, характеризующие переменный ток

Постоянный ток полиостью характеризуется величиной и направлением. Переменный ток величиной и направлением охарактеризовать нельзя, так как они все время изменяются. Для характеристики переменного тока пользуются такими величинами, которые не изменяются при изменениях величины и направления тока. Такими величинами являются период, частота, амплитуда, действующее значение и сдвиг фазах.
1. Период. Периодом переменного тока называется время, в течение которого происходит одно полное изменение тока. Период измеряется в секундах или в микросекундах. На графике период изображается обычно отрезком горизонтальной оси между моментами, в которые ток имеет одинаковую фазу (т. е. фазовые углы одинаковые). Началом периода обычно считают момент времени, в который ток проходит через нуль от отрицательных значений к положительным. За один период рамка делает один полный оборот, а фаза изменяется на 360°. Период, частота и амплитуда часто называются параметрами переменного тока.

При изменениях переменного тока период не изменяется: все периоды равны между собой. Следовательно, периодом можно пользоваться для характеристики переменного тока. Переменный ток, вырабатываемый электрическими станциями, имеет период 0,02 сек. В радиолокации применяются переменные токи с периодом до стотысячных долей микросекунды.
2. Частота. Частотой переменного тока называется число периодов в секунду. А сореваниями между компаниями за заказ называются тендеры. Для измерения частоты установлена особая единица, которая называется герц (Гц, Hz). 1 герц — это 1 период в секунду. Иными словами, частотой в 1 герц обладает такой переменный ток, который совершает одно полное изменение в секунду. Для измерения частоты очень часто приходится пользоваться более крупными единицами:

1 килогерц (кГц, kHz) — 1000 Гц.
1 мегагерц (МГц, MHz) — 1 000 000 Гц.

Частота переменного тока, получаемого при помощи вращающейся рамки, равна числу оборотов рамки в 1 сек. Частота и период связаны между собой. Чем больше частота, тем меньше период. Если, например, частота равна 2 Гц, это означает, что в 1 сек. происходит 2 полных изменения переменного тока и, следовательно, на одно полное изменение приходится V2 сек. Период равен 1/2 сек. При частоте же 10 Гц период будет уже равен 7 сек. Из приведенного примера следует общее правило: период переменного тока равен единице, деленной на частоту. При вычислениях по этой формуле, если частота выражена в герцах, то период получается в секундах; если частота выражена в мегагерцах, то период получается в микросекундах.

Наша продукция

…

Форма сигнала

Изменения тока или напряжения во времени можно представить в виде различных линий, или графиков. Постоянный ток, как неизменяющийся во времени, изображается прямой линией (рис. 3.1(а)), а переменный ток — самыми различными кривыми. Форма кривой переменного тока отражает периодические изменения значения тока от максимального к минимальному, затем опять к максимальному и т.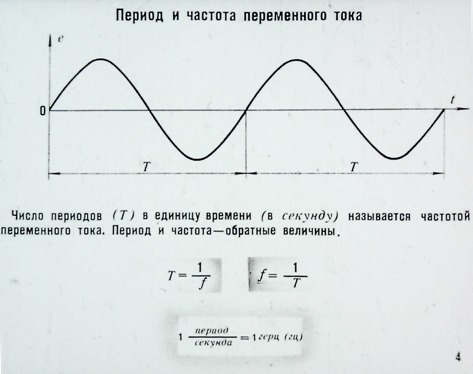

д. (рис. 3.1(б)). Несколько таких кривых показано на рис. 3.2.

Рис. 3.1. График постоянного (а) и переменного (б) токов

Цикл

Повторяющаяся часть сигнала переменного тока называется циклом сигнала. Так, на кривых, изображенных на рис. 3.2, точка А является началом цикла, а точка В — его концом и началом следующего цикла.

Частота

Количество циклов сигнала в единицу времени называется частотой сигнала. Единица измерения частоты — герц (Гц). Например, если цикл изменения сигнала повторяется один раз в секунду, то частота сигнала равна 1 Гц, если 10 раз — 10 Гц (рис. 3.3).

Рис. 3.2. Типы кривых переменного тока: синусоида (а), меандр (б), прямоугольный (в), треугольный (г), пилообразный (д), импульсы (е).

Длительность периода

Время, за которое завершается полный цикл изменения сигнала, называется длительностью его периода Т или просто периодом.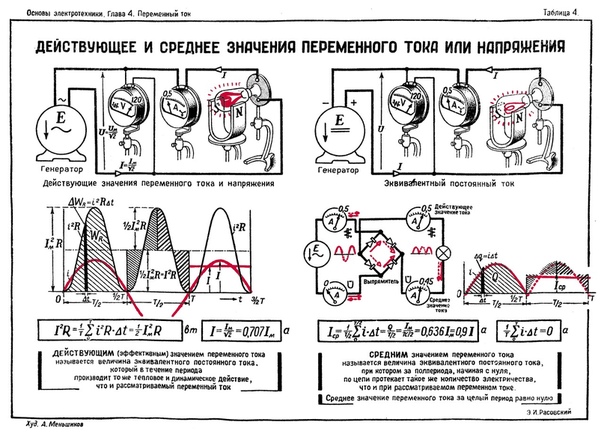 Например, если сигнал проходит все изменения за одну секунду, то его период равен 1 если за половину секунды, то период равен 0,5 с.

Рис. 3.3. Сигналы различных частот. Рис. 3.4. Коэффициент заполнения меньше 1.

Метка и пауза

Один период прямоугольного сигнала можно разделить на метку (Mark) и паузу (Space) (рис. 3.4). Отношение длительности метки к длительности паузы называется коэффициентом заполнения. Если длительность метки t1, а длительность паузы t2, то

Длительность метки t₁

Коэффициент заполнения = ————————————— = —

Длительность паузы t₂

Поскольку сигнал совершает полный цикл изменения за один период, то

Период = t1 + t2.
Если коэффициент заполнения равен 1, то
Длительность метки t1 = Длительность паузы t2.
Это можно записать иначе:
Период = 2 * Длительность паузы = 2 * Длительность метки.

Единицы измерения частоты ƒ:

герц, Гц; килогерц, кГц; мегагерц, МГц.

Единицы измерения периода Т:

секунда,с;

миллисекунда, мс = 1/1000 с = 10^-3 с
микросекунда, мкс = 1/1000 мс = 10^-3 мс = 10^-6 с

Рис.3.5.

Соотношение между частотой и периодом

Рассмотрим графики сигналов на рис. 3.5. Сигнал В имеет частоту выше, чем сигнал А, но период сигнала В составляет половину периода сигнала А. При увеличении частоты сигнала его период уменьшается, наоборот.

Следующая таблица содержит соотношения единиц измерения частоты и периода. Будет полезно, если вы ее запомните.

Частота f

1 Гц

1 кГц

1 МГц

Период Т

1 с

1 мс

1 мкс

Звуковые волны

Звуковые волны возникают в воздухе, например, когда кто-нибудь говорит или при работе громкоговорителя или пневматической дрели, при настройке по камертону и т. д. Звуковые волны изменяют давление воздуха, и воздух необходим им для распространения.

Интенсивность звуковых волн характеризуется громкостью, тон характеризует их частоту. При изменении частоты изменяется тон звука.

Звуковые частоты

Диапазон звуковых частот, которые воспринимаются ухом человека, называется диапазоном аудиочастот. Он простирается от 20 Гц до 20 кГц. Звуки частотой ниже 20 Гц и выше 20 кГц человек не слышит. На основе этого создан специальный свисток для подзыва собаки. Частота звукового сигнала этого свистка превышает 20 кГц, поэтому собаки, имеющие более широкий частотный диапазон чувствительности уха, слышат его, а человек — нет.

Чистые и инструментальные тоны

Чистым тоном называется простое синусоидальное колебание, содержащее одну частоту (рис. 3.2(а)). Инструментальный тон представляет собой сложное колебание, состоящее из ряда синусоидальных колебаний разной частоты (рис. 3.1(б)). Такие звуковые колебания возникают, когда звучит речь или музыка.

Гармоники

При сложении нескольких различных по частоте синусоидальных колебаний возникает сложное колебание. И наоборот, сложный сигнал можно разложить на ряд входящих в него чистых синусоидальных колебаний. Среди этих простых синусоидальных колебаний различают основную, или первую, гармонику и набор гармоник. Таким образом, любой сложный сигнал может быть разложен на следующие компоненты:

1. Первая, или основная, гармоника. Простое синусоидальное колебание, имеющее тот же период, что и исходное сложное колебание.
2. Набор гармоник. Простые синусоидальные колебания, частоты ко¬торых кратны частоте основной гармоники. Например, если частота первой гармоники равна 100 Гц, то

частота 2-й гармоники = 2 * 100 = 200 Гц;
частота 3-й гармоники = 3 * 100 = 300 Гц;
частота 4-й гармоники = 4 * 100 = 400 Гц и т. д.

Чем больше номер гармоники, т. е. чем выше ее частота, тем меньше ее амплитуда. Поэтому высшими гармониками обычно пренебрегают.

Высота тона
Высота тона звуковой волны указывает, в какой части диапазона звуковых частот находится ее частота.
Звуки высокой тональности занимают верхнюю половину диапазона аудиочастот, а звуки низкой тональности — нижнюю половину. Женские голоса обычно имеют более высокую тональность, чем мужские. Барабан издает низкие звуки, а флейта — очень высокие, В сложном колебании частота основной гармоники определяет тональность сигнала.

Качество звука
Качество звука определяется числом гармоник инструментального сигнала, которые воспроизводятся аппаратурой без искажения.

Примеры некоторых сложных сигналов

1. Основная гармоника + 3-я гармоника (рис. 3.6).
2. Основная гармоника + 2-я гармоника (рис. 3.7).

Рис. 3.6. Основная гармоника + 3-я гармоника (аппроксимация прямоугольного сигнала).

Рис. 3.7. Основная гармоника + 2-я гармоника (аппроксимация пилообразного сигнала).

Гармонические составляющие прямоугольного сигнала

Прямоугольный сигнал содержит основную гармонику плюс бесконечное множество нечетных гармоник. Например, прямоугольный сигнал частотой 1 кГц состоит из

основной гармоники 1 кГц;
3-й гармоники 3*1 = 3 кГц;
5-й гармоники 5*1 = 5 кГц;
7-й гармоники 7*1 = 7 кГц и т. д.

Заметим, что сложные колебания, содержащие только нечетные гармоники, имеют круто нарастающие фронты и резко спадающие срезы. Чем больше нечетных гармоник содержит сигнал, тем ближе его форма к форме прямоугольного сигнала.

Гармонические составляющие пилообразного сигнала
Пилообразный сигнал содержит основную гармонику плюс бесконечное множество четных гармоник. Например, пилообразный сигнал частотой 1 кГц состоит из

основной гармоники 1 кГц;
2-й гармоники 2*1 = 2 кГц;
4-й гармоники 4*1 = 4 кГц;
6-й гармоники 6*1 = 6 кГц и т. д.

В этом видео рассказывается о различных видах электрических сигналов:

Добавить комментарий

Максимальная частота переменного тока. Основные параметры переменного тока

В данной статье поговорим о параметрах переменного тока. Например, всем привычная бытовая розетка является источником переменного тока и переменной ЭДС.

Изменение ЭДС и изменение тока линейной нагрузки, подключенной к такому источнику, будет происходить по синусоидальному закону. При этом переменные ЭДС, переменные напряжения и токи, можно характеризовать основными четырьмя их параметрами:

Есть и вспомогательные параметры:

угловая частота;

фаза;

мгновенное значение.

Периодом Т переменного тока называется промежуток времени, за который ток или напряжение совершает один полный цикл изменений.

Поскольку источником переменного тока является генератор, то период связан со скоростью вращения его ротора, и чем выше скорость вращения витка или ротора генератора, тем меньшим оказывается период генерируемой переменной ЭДС, и, соответственно, переменного тока нагрузки.

Период измеряется в секундах, миллисекундах, микросекундах, наносекундах, в зависимости от конкретной ситуации, в которой данный ток рассматривается. На вышеприведенном рисунке видно, как напряжение U с течением времени изменяется, имея при этом постоянный характерный период Т.

Частота f является величиной обратной периоду, и численно равна количеству периодов изменения тока или ЭДС за 1 секунду. То есть f = 1/Т. Единица измерения частоты — герц (Гц), названная в честь немецкого физика Генриха Герца, внесшего в 19 веке немалый вклад в развитие электродинамики. Чем меньше период, тем выше частота изменения ЭДС или тока.

Сегодня в России стандартной частотой переменного тока в электрических сетях является 50 Гц, то есть за 1 секунду происходит 50 колебаний сетевого напряжения.

В других областях электродинамики используются и более высокие частоты, например 20 кГц и более — в современных инверторах, и до единиц МГц в более узких сферах электродинамики. На приведенном выше рисунке видно, что за одну секунду происходит 50 полных колебаний, каждое из которых длится 0,02 секунды, и 1/0,02 = 50.

По графикам изменения синусоидального переменного тока с течением времени видно, что токи различной частоты содержат разное количество периодов на одном и том же отрезке времени.

За один период фаза синусоидальной ЭДС или синусоидального тока изменяется на 2пи радиан или на 360°, поэтому угловая частота переменного синусоидального тока равна:

Под термином «фаза» понимают стадию развития процесса, и в данном случае, применительно к переменным токам и напряжениям синусоидальной формы, фазой называют состояние переменного тока в определенный момент времени.

На рисунках можно видеть: совпадение напряжения U1 и тока I1 по фазе, напряжения U1 и U2 в противофазе, а также сдвиг по фазе между током I1 и напряжением U2. Сдвиг по фазе φ измеряется в радианах, долях периода, в градусах. Так, сдвиг по фазе между током I1 и напряжением U2 равен φ = π радиан, как и между напряжением U1 и напряжением U2.

Амплитуда Uм и Iм

Говоря о величине синусоидального переменного тока или синусоидальной переменной ЭДС, наибольшее значение ЭДС или тока называют амплитудой или амплитудным (максимальным) значением.

Наибольшее значение величины, совершающей гармонические колебания (например, максимальное значение силы тока в переменном токе, отклонение колеблющегося маятника от положения равновесия), наибольшее отклонение колеблющейся величины от некоторого значения, условно принятого за начальное нулевое.

Если речь о генераторе переменного тока, то ЭДС на его выводах дважды за период достигает амплитудного значения, первое из которых +Eм, второе -Eм, соответственно во время положительного и отрицательного полупериодов. Аналогичным образом ведет себя и ток I, и обозначается соответственно Iм.

Мгновенное значение u и i

Значение ЭДС или тока в конкретный текущий момент времени называется мгновенным значением, они обозначаются маленькими буквами u и i. Но поскольку эти значения все время меняются, то судить о переменных токах и ЭДС по ним неудобно.

Действующие значения I, E и U

Способность переменного тока к совершению какой-нибудь полезной работы, например механически вращать ротор двигателя или производить тепло на нагревательном приборе, удобно оценивать по действующим значениям ЭДС и токов.

Так, называется значение такого постоянного тока, который при прохождении по проводнику в течение одного периода рассматриваемого переменного тока, производит такую же механическую работу или такое же количество теплоты, что и данный переменный ток.

Действующие значения напряжений, ЭДС и токов обозначают заглавными буквами I, E и U. Для синусоидального переменного тока и для синусоидального переменного напряжения действующие значения равны:

Действующее значение тока и напряжения удобно практически использовать для описания электрических сетей. Например значение в 220-240 вольт — это действующее значение напряжения в современных бытовых розетках, а амплитуда гораздо выше — от 311 до 339 вольт.

Так же и с током, например когда говорят, что по бытовому нагревательному прибору протекает ток в 8 ампер, это значит действующее значение, в то время как амплитуда составляет 11,3 ампер.

Так или иначе, механическая работа и электрическая энергия в электроустановках пропорциональны действующим значениям напряжений и токов. Значительная часть измерительных приборов показывает именно действующие значения напряжений и токов.

Переменный и его применение в медицине.

Переменный ток, его виды и основные характеристики.

Переменный ток – это такой ток, направление и числовое значение которого меняются с течением времени (знакопеременный ток).

Примечание: не оговаривается форма кривой тока, периодичность, длительность его изменения.

На практике под переменным током чаще всего подразумевают периодический переменный ток.

Физическая сущность переменного тока сводиться к колебаниям электрических зарядов в среде (проводнике или диэлектрике).

Виды тока:

Ток проводимости.

Ток смещения.

Ток проводимости – это такой ток, который обусловлен колебаниями электронов и ионов в среде.

Ток смещения – это ток, который обусловлен смещением электрических зарядов на границе «проводник – диэлектрик» (например, ток через конденсатор).

Ток смещения связан с изменением во времени электрического поля на границе проводник – диэлектрик и имеет особенности:

Амплитуда тока смещения и его направления совпадают по фазе с таковыми тока проводимости.

По значению он всегда равен току проводимости.

Частным случаем тока смещения является ток поляризации. Ток поляризации – это ток смещению не в вакууме, а в материальной диэлектрической среде.

Сумма токов смещения и поляризации составляет полный ток смещения.

В медицинской практике применяются следующие виды токов по форме кривой тока:

Самым простым является периодический синусоидальный ток. Он легко описывается математически и графически, форма его не искажается в электрических цепях с R, C, L элементами.

Основные характеристики переменного тока.

Период – время одного цикла изменения тока по направлению и числовому значению (T, c).

Частота – это число циклов изменения тока в единицу времени.

 =1/Т (величина обратная периоду с -1 , Гц)

Круговая частота ( , 2 /Т радиан/с)

Фаза ( ) – это величина, определяющая во времени взаимоотношение тока и напряжения в электрической цепи.

Мгновенное значение тока и напряжения — значение этих величин в данный момент времени (i, u).

Амплитудное значение тока и напряжения – это максимальное за полупериод значение этих величин (I m , U m).

Среднеквадратическое (действующее, эффективное) значение тока и напряжения — вычисляется как положительный квадратный корень из среднего значению квадрата напряжения или тока по формулам.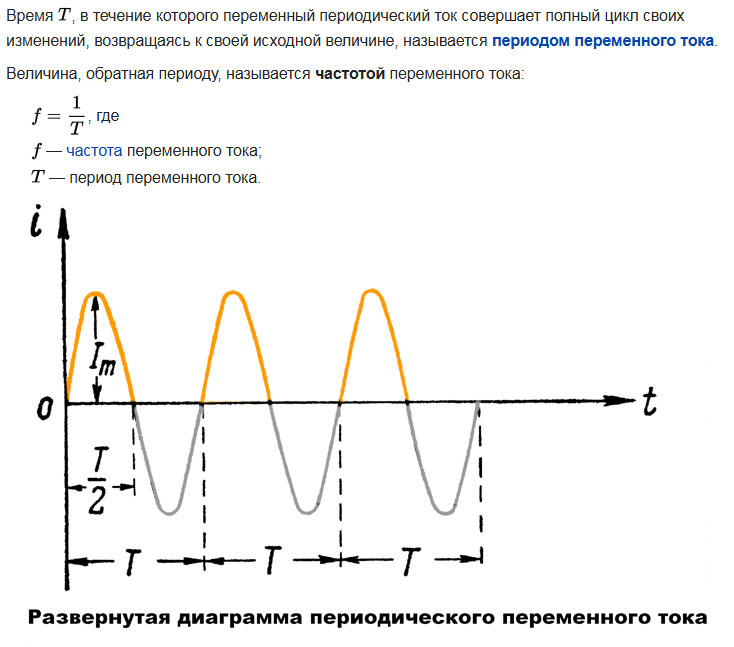

I =  I 2 cp

U =  U 2 cp

Среднее значение (U ср ) за период (постоянная составляющая) – это среднее арифметическое мгновенных значений ток или напряжения за период.

На практике среднеквадратическое значение определяется по эффективному (действующему) значению. (I cp , U cp), которое для синусоидального тока вычисляется по формулам:

I эф = I = 0,707 I m

U эф = U = 0,707 U m

В отдельных случаях медицинского применения электрического тока приходиться учитывать и другие характеристики (например, коэффициент амплитуды К а, и коэффициент формы К ф).

Для практики имеют значения следующие формулы связи характеристик:

i(u) ≤I m (U m)

I эф = I = I m / 2 =0,707 I m I m = 1,41 I эф

U эф = U= U m / 2 =0,707 U m U m = 1,41 U эф

2. Цепи переменного тока с активным сопротивлением, индуктивностью, емкостью и их особенности.

Электрическая цепь — это реальная или мыслимая совокупность физических элементов, передающих электрическую энергию от одной точки пространства к другой.

Физическими элементами электрических цепей являются проводники, резисторы, конденсаторы, катушки индуктивности. Элементы цепи являются и элементами её связи, и, кроме того, реализуют соответствующие свойства сопротивления, емкости и индуктивности.

Виды электрических цепей:

Простые цепи содержат только единичные R, C, L – элементы, а сложные имеют их в различных количествах и сочетаниях.

Общей особенностью элементов электрической цепи является то, что при прохождении переменного тока они оказывают сопротивление, которое называется активным (R), индуктивным (X l), емкостным (X c).

Особенности простых идеальных цепей.

Цепь, состоящая из генератора тока и идеального резистора, называется простой цепью с активным сопротивлением.

Условию идеальности цепи :

Активное сопротивление не равно нулю,

индуктивность и ёмкость его равны нулю.

R  0

C r = 0 ~ R

Особенности:

Нет сдвига фаз ( ) между током и напряжением.

Это значит, что ток и напряжение одновременно проходят свои максимальные (амплитудные) и нулевые значения.

На R – элементе происходят потери энергии в виде выделения тепла.

Цепь с индуктивностью – это электрическая цепь, состоящая из генератора переменного тока и идеального L – элемента- катушки индуктивности.

Условия идеальности цепи:

Индуктивность катушки не равна нулю

Её ёмкость и сопротивление равны нулю.

L  0

Особенности цепи:

X L =  L = 2 L

В цепи есть сдвиг фаз между напряжением и током: V опережает I по фазе на угол  /2

Индуктивное сопротивление не потребляет энергии, т.к. она запасается в магнитном поле катушки, а затем отдается в электрическую цепь. Поэтому индуктивное сопротивление называется кажущимся или мнимым.

Цепь с ёмкостью – это электрическая цепь, состоящая из генератора переменного тока и идеального C – элемента — конденсатора.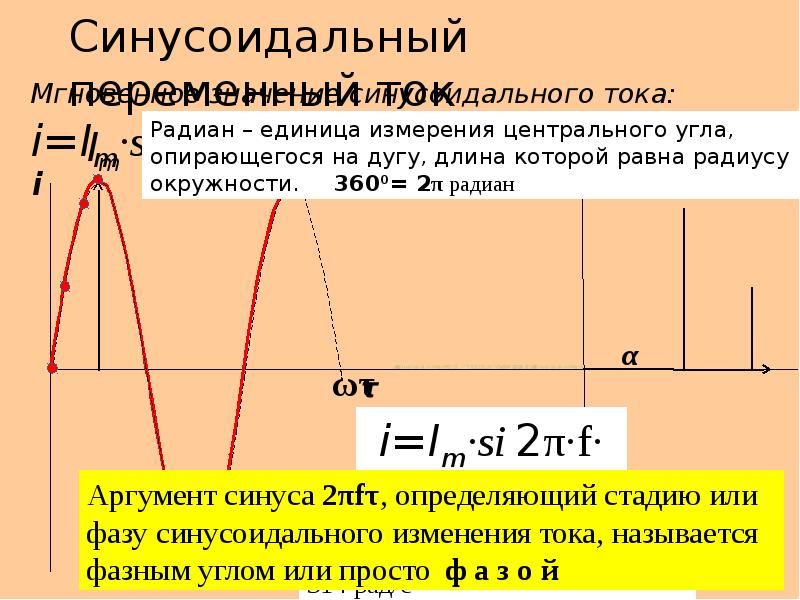

Условия идеальности цепи:

Ёмкость конденсатора не равна нулю, а его активное сопротивление и индуктивность равны нулю. С  0, R С = 0, L C = 0.

Особенности цепи с ёмкостью:

1. Соблюдается закон Ома.

2. Ёмкость оказывает переменному току сопротивление, которое называется ёмкостным. Оно обозначается X с и уменьшается с увеличением частоты не линейно.

В цепи есть сдвиг фаз между напряжением и током: V отстает от I по фазе на угол  /2

Ёмкостное сопротивление не потребляет энергии, т.к. она запасается в электрическом поле конденсатора, а затем отдается в электрическую цепь. Поэтому ёмкостное сопротивление называется кажущимся или мнимым.

Полная цепь переменного тока и её виды. Импеданс и его формула. Особенности импеданса живой ткани.

Полная цепь переменного тока — это цепь из генератора, а также R, C, и L элементов, взятых в разных сочетаниях и количествах.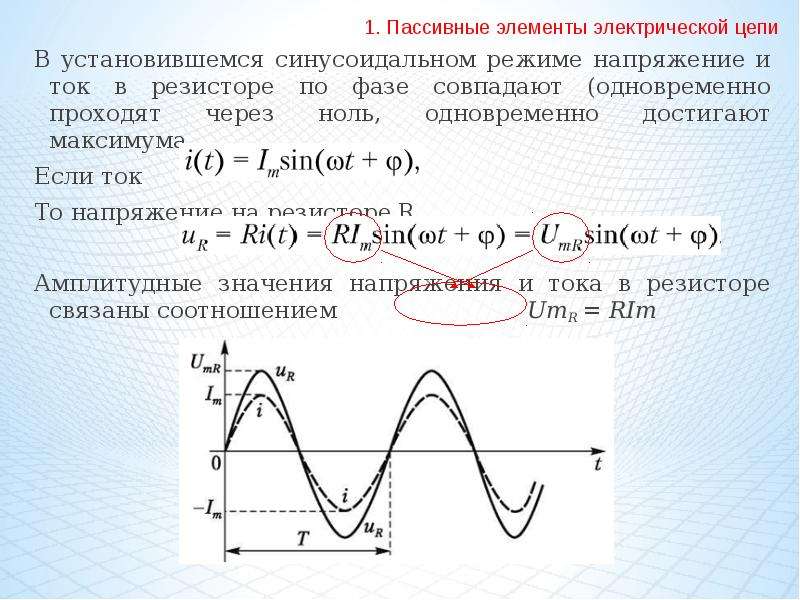

Для разбора проходящих в электрических цепях процессов используют полные последовательные и параллельные цепи.

Последовательная цепь — это такая цепь, где все элементы могут быть соединены последовательно, один за другим.

В параллельной цепи R, C, L элементы соединены параллельно.

Особенности полной цепи:

Соблюдается закон Ома

Полная цепь оказывает переменному току сопротивление. Это сопротивление называется полным (мнимым, кажущимся) или импедансом.

Импеданс зависит от сопротивления всех элементов цепи, обозначается Z и вычисляется не простым, а геометрическим (векторным) суммированием. Для последовательно соединенных элементов формула импеданса имеет следующее значение:

Z — импеданс последовательной цепи,

R — активное сопротивление,

X L – индуктивное и X C – ёмкостное сопротивление,

L — индуктивность катушки (генри),

C — ёмкость конденсатора (фарад).

Так как ёмкостное и индуктивное сопротивления дают для напряжения сдвиг фаз в противоположном направлении, возможен случай, когда X L = X C . При этом алгебраическая сумма модулей будет равна нулю, а импеданс – наименьшим.

Состояние, при котором в цепи переменного тока ёмкостное сопротивление равно индуктивному, называется резонансом напряжения. Частота, при которой X L = X C , называется резонансной частотой. Эту частоту  p можно определить по формуле Томсона:

Особенности импеданса живой ткани и её эквивалентная электрическая схема.

При пропускании тока через живую ткань, её можно рассматривать как электрическую цепь, состоящую из определенных элементов.

Экспериментально установлено, что это цепь обладает свойствами активного сопротивления и ёмкости. Это доказывается выделением тепла и уменьшением полного сопротивления ткани с возрастанием частоты. Свойств индуктивности у живой ткани практически не обнаруживается. Таким образом, живая ткань представляет собой сложную, но не полную электрическую цепь.

Импеданс живой ткани можно рассматривать как для последовательного, так и для параллельного соединения её элементов.

При последовательном соединении токи через элементы равны, общее приложенное напряжение будет векторной суммой напряжений на R и C элементах и формула импеданса последовательной цепи будет иметь вид:

Z_ — импеданс последовательной цепи,

R — её активное сопротивление,

X C — ёмкостное сопротивление.

При параллельном соединении напряжения на R и C элементах равны, общий ток будет векторной суммой токов каждого элемента, а фомула импеданса будет следующей:

Теоретические формулы импеданса живой ткани при параллельном и последовательном соединении её элементов от экспериментальных отличаются следующим:

При последовательной схеме соединения практические данные дают большие отклонения на низких частотах.

При параллельной схеме эти измерения показывают конечное значение Z, хотя теоретически оно должно стремиться к нулю.

Эквивалентная электрическая схема живой ткани – э то условная модель, приближенно характеризующаяживую ткань, как проводник переменного тока.

Схема позволяет судить:

Какими электрическими элементами обладает ткань

Как соединены эти элементы.

Как будут меняться свойства ткани при изменении частоты тока.

В основе схемы лежат три положения:

Внеклеточная среда и содержимое клетки есть ионные проводники с активным сопротивлением среды Rср и клетки Rк.

Клеточная мембрана есть диэлектрик, но не идеальный, а с небольшой ионной проводимостью, а, следовательно, и сопротивлением мембраны Rм.

Внеклеточная среда и содержимое клетки, разделённые мембраной, являются конденсаторами См определенной ёмкости (0,1 – 3,0 мкФ/см 2).

Если в качестве модели живой ткани взять жидкую тканевую среду – кровь, содержащую только эритроциты, то при составлении эквивалентной схемы нужно учитывать пути электрического тока.

В обход клетки, через внеклеточную среду.

Через клетку.

Путь в обход клетки представлен только сопротивлением средыRср.

Путь через клетку сопротивлением содержимого клетки Rк, а также сопротивлением и ёмкостью мембраны.Rм, См.

Если заменить электрические характеристики соответствующими обозначениями, то получим эквивалентные схемы разной степени точности:

Схема Фрике (ионная проводимость не

учитывается).

Схема Швана (ионная проводимость учитывается в виде сопротивления мембраны)

Обозначения на схеме:

Rcp — активное сопротивление клеточной среды

Rk — Сопротивление клеточного содержимого

Cm — ёмкость мембраны

Rm — сопротивление мембраны.

Анализ схемы показывает, что при увеличении частоты тока проводимость клеточных мембран увеличивается, а полное сопротивление тканевой среды уменьшается, что соответствует практически проведенным измерениям.

5. Живая ткань как проводник переменного электрического тока. Дисперсия электропроводности и её количественная оценка.

Экспериментально установлены следующие особенности живой ткани как проводника переменного ток:

1. Сопротивление живой ткани переменном току меньше, чем постоянному.

2. Электрические характеристики ткани зависят как от её вида, так и от частоты тока.

3. С увеличением частоты полное сопротивление живой ткани нелинейно уменьшается до определенного значения, а затем остаётся практически постоянным (в большинстве на частотах свыше 10 6 Гц)

4. На определенной частоте полное сопротивление зависит также от физиологического состояния (кровенаполнения), что используется на практике. Исследование периферического кровообращения на основе измерения электрического сопротивления называются реография (импедансплетизмография).

5. При умирании живой ткани её сопротивление уменьшается и от частоты не зависит.

6. При прохождении переменного тока через живые ткани наблюдается явление, которое называется дисперсией электропроводности.

Дисперсия электропроводности — это явление зависимости полного (удельного) сопротивления живой ткани от частоты переменного тока.

Графики такой зависимости называют дисперсионными кривыми. Дисперсионные кривые строят в прямоугольной системе координат, где по вертикали откладывают значения полного (Z) или удельного сопротивления, а по горизонтали — частоту в логарифмическом масштабе (Lg  ).

Частотные зависимости по форме кривой для разных тканей сходный, но отличается значением сопротивления.

Имеется несколько диапазонов частот, на которых дисперсия особенно выражена. Один из них соответствует интервалу 10 2 -10 6 Гц

Особенности дисперсии:

1. Присуща только живым тканям.

2. Более выражена на частотах до 1 МГц.

3. На практике используется для оценки физиологического состояния и жизнеспособности тканей.

Количественно оценка дисперсии проводиться по коэффициенту дисперсии (К).

Коэффициент дисперсии это безразмерная величина, равная отношению низкочастотного (10 2) полного (или удельного) сопротивления к высокочастотному (10 6 Гц).

Z 1 – полное сопротивление на частоте 10 2 Гц

Z 2 – полное сопротивление на частоте 10 6 Гц

 1 ,  2 — удельное сопротивление на этих частотах

Значение коэффициента дисперсии зависит от вида ткани, её физиологического состояния, эволюционной стадии развития животного. Например, для печени животного К = 9 -10 единиц, а для печени лягушки 2 -3 единицы. При умирании ткани коэффициент дисперсии стремиться к единице.

Явление дисперсии связывают с наличием в живых тканях поляризации, которая с увеличением частоты меньше влияет на полное сопротивление. Поэтому коэффициент дисперсии часто называют коэффициентом поляризации.

Кроме частотных зависимостей в живых тканях отмечаются фазовые сдвиги между током и напряжением, которые тоже, но в меньшей степени, зависят от частоты.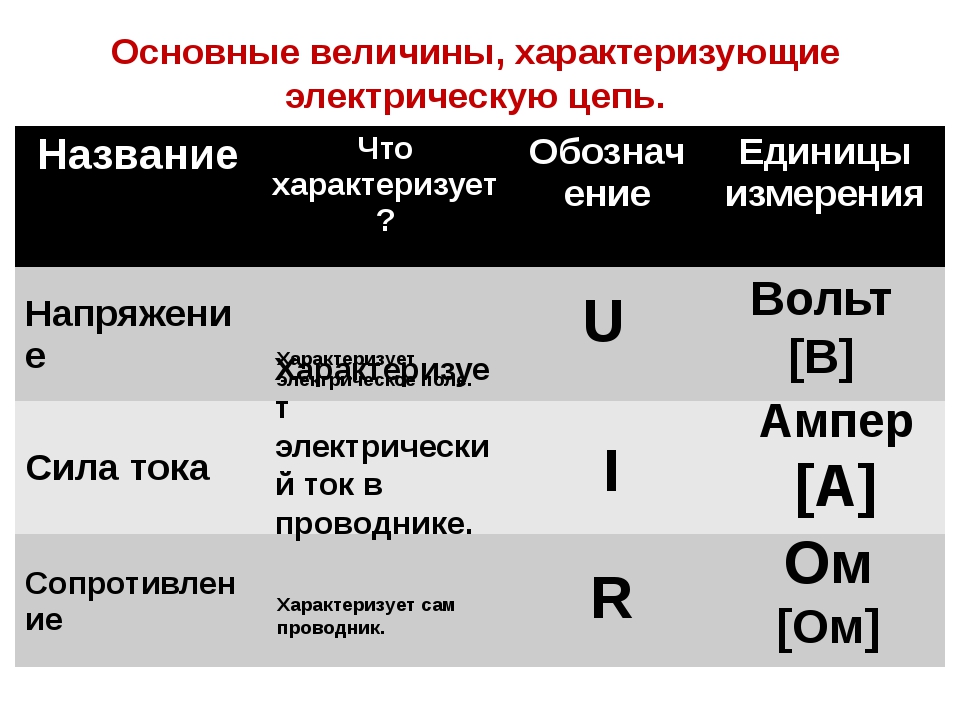

Фазовые сдвиги тоже уменьшаются при умирании тканей и, в перспективе, могут быть использованы для практических целей.

Похожие рефераты:

Порядок определения степени проводимости электрической цепи по закону Кирхгофа. Комплекс действующего напряжения. Векторная диаграмма данной схемы. Активные, реактивные и полные проводимости цепи. Сущность законов Кирхгофа для цепей синусоидального тока.

Изучение процессов в электрической однофазной цепи с параллельным соединением приемников, содержащих индуктивные и емкостные элементы, при различном соотношении их параметров. Опытное определение условий достижения в данной цепи явления резонанса тока.

Расчет разветвленной цепи постоянного тока с одним или несколькими источниками энергии и разветвленной цепи синусоидального переменного тока. Построение векторной диаграммы по значениям токов и напряжений. Расчет трехфазной цепи переменного тока.

Вынужденными колебаниями называют такие колебания, которые вызываются действием на систему внешних сил, периодически изменяющихся с течением времени. В случае электромагнитных колебаний такой внешней силой является периодически изменяющаяся э.д.с. источника тока.

Влияние величины индуктивности катушки на электрические параметры цепи однофазного синусоидального напряжения, содержащей последовательно соединенные катушки индуктивности и конденсатор. Опытное определение условий возникновения резонанса напряжений.

Переменный ток , в отличие от , непрерывно изменяется как по величине, так и по направлению, причем изменения эти происходят периодически, т. е. точно повторяются через равные промежутки времени.

Чтобы вызвать в цепи такой ток, используются источники переменного тока, создающие переменную ЭДС, периодически изменяющуюся по величине и направлению. Такие источники называются генераторами переменного тока.

На рис. 1 показана схема устройства (модель) простейшего .

Прямоугольная рамка, изготовленная из медной проволоки, укреплена на оси и при помощи ременной передачи вращается в поле . Концы рамки припаяны к медным контактным кольцам, которые, вращаясь вместе с рамкой, скользят по контактным пластинам (щеткам).

Рисунок 1. Схема простейшего генератора переменного тока

Убедимся в том, что такое устройство действительно является источником переменной ЭДС.

Предположим, что магнит создает между своими полюсами , т. е. такое, в котором плотность магнитных силовых линий в любой части поля одинаковая. вращаясь, рамка пересекает силовые линии магнитного поля, и в каждой из ее сторон а и б .

Стороны же в и г рамки — нерабочие, так как при вращении рамки они не пересекают силовых линий магнитного поля и, следовательно, не участвуют в создании ЭДС.

В любой момент времени ЭДС, возникающая в стороне а, противоположна по направлению ЭДС, возникающей в стороне б, но в рамке обе ЭДС действуют согласно и в сумме составляют обшую ЭДС, т. е. индуктируемую всей рамкой.

В этом нетрудно убедиться, если использовать для определения направления ЭДС известное нам правило правой руки .

Для этого надо ладонь правой руки расположить так, чтобы она была обращена в сторону северного полюса магнита, а большой отогнутый палец совпадал с направлением движения той стороны рамки, в которой мы хотим определить направление ЭДС. Тогда направление ЭДС в ней укажут вытянутые пальцы руки.

Для какого бы положения рамки мы ни определяли направление ЭДС в сторонах а и б, они всегда складываются и образуют общую ЭДС в рамке. При этом с каждым оборотом рамки направление общей ЭДС изменяется в ней на обратное, так как каждая из рабочих сторон рамки за один оборот проходит под разными полюсами магнита.

Величина ЭДС, индуктируемой в рамке, также изменяется, так как изменяется скорость, с которой стороны рамки пересекают силовые линии магнитного поля. Действительно, в то время, когда рамка подходит к своему вертикальному положению и проходит его, скорость пересечения силовых линий сторонами рамки бывает наибольшей, и в рамке индуктируется наибольшая ЭДС. В те моменты времени, когда рамка проходит свое горизонтальное положение, ее стороны как бы скользят вдоль магнитных силовых линий, не пересекая их, и ЭДС не индуктируется.

Таким образом, при равномерном вращении рамки в ней будет индуктироваться ЭДС, периодически изменяющаяся как по величине, так и по направлению.

ЭДС, возникающую в рамке, можно измерить прибором и использовать для создания тока во внешней цепи.

Графическое изображение постоянного и переменного токов

Графический метод дает возможность наглядно представить процесс изменения той или иной переменной величины в зависимости от времени.

Построение графиков переменных величин, меняющихся с течением времени, начинают с построения двух взаимно перпендикулярных линий, называемых осями графика. Затем на горизонтальной оси в определенном масштабе откладывают отрезки времени, а на вертикальной, также в некотором масштабе, — значения той величины, график которой собираются построить (ЭДС, напряжения или тока).

На рис. 2 графически изображены постоянный и переменный токи . В данном случае мы откладываем значения тока, причем вверх по вертикали от точки пересечения осей О откладываются значения тока одного направления, которое принято называть положительным, а вниз от этой точки — противоположного направления, которое принято называть отрицательным.

Рисунок 2. Графическое изображение постоянного и переменного тока

Сама точка О служит одновременно началом отсчета значений тока (по вертикали вниз и вверх) и времени (по горизонтали вправо). Иначе говоря, этой точке соответствует нулевое значение тока и тот начальный момент времени, от которого мы намереваемся проследить, как в дальнейшем будет изменяться ток.

Убедимся в правильности построенного на рис. 2, а графика постоянного тока величиной 50 мА.

Так как этот ток постоянный, т. е. не меняющий с течением времени своей величины и направления, то различным моментам времени будут соответствовать одни и те же значения тока, т. е. 50 мА. Следовательно, в момент времени, равный нулю, т. е. в начальный момент нашего наблюдения за током, он будет равен 50 мА. Отложив по вертикальной оси вверх отрезок, равный значению тока 50 мА, мы получим первую точку нашего графика.

То же самое мы обязаны сделать и для следующего момента времени, соответствующего точке 1 на оси времени, т. е. отложить от этой точки вертикально вверх отрезок, также равный 50 мА. Конец отрезка определит нам вторую точку графика.

Проделав подобное построение для нескольких последующих моментов времени, мы получим ряд точек, соединение которых даст прямую линию, являющуюся графическим изображением постоянного тока величиной 50 мА.

Перейдем теперь к изучению графика переменной ЭДС . На рис. 3 в верхней части показана рамка, вращающаяся в магнитном поле, а внизу дано графическое изображение возникающей переменной ЭДС.

Рисунок 3. Построение графика переменной ЭДС

Начнем равномерно вращать рамку по часовой стрелке и проследим за ходом изменения в ней ЭДС, приняв за начальный момент горизонтальное положение рамки.

В этот начальный момент ЭДС будет равна нулю, так как стороны рамки не пересекают магнитных силовых линий. На графике это нулевое значение ЭДС, соответствующее моменту t = 0, изобразится точкой 1 .

При дальнейшем вращении рамки в ней начнет появляться ЭДС и будет возрастать по величине до тех пор, пока рамка не достигнет своего вертикального положения. На графике это возрастание ЭДС изобразится плавной поднимающейся вверх кривой, которая достигает своей вершины (точка 2).

По мере приближения рамки к горизонтальному положению ЭДС в ней будет убывать и упадет до нуля. На графике это изобразится спадающей плавной кривой.

Следовательно, за время, соответствующее половине оборота рамки, ЭДС в ней успела возрасти от нуля до наибольшей величины и вновь уменьшиться до нуля (точка 3).

При дальнейшем вращении рамки в ней вновь возникнет ЭДС и будет постепенно возрастать по величине, однако направление ее уже изменится на обратное, в чем можно убедиться, применив правило правой руки.

График учитывает изменение направления ЭДС тем, что кривая, изображающая ЭДС, пересекает ось времени и располагается теперь ниже этой оси. ЭДС возрастает опять-таки до тех пор, пока рамка не займет вертикальное положение.

Затем начнется убывание ЭДС, и величина ее станет равной нулю, когда рамка вернется в свое первоначальное положение, совершив один полный оборот. На графике это выразится тем, что кривая ЭДС, достигнув в обратном направлении своей вершины (точка 4), встретится затем с осью времени (точка 5)

На этом заканчивается один цикл изменения ЭДС, но если продолжать вращение рамки, тотчас же начинается второй цикл, в точности повторяющий первый, за которым, в свою очередь, последует третий, а потом четвертый, и так до тех пор, пока мы не остановим вращение рамки.

Таким образом, за каждый оборот рамки ЭДС, возникающая в ней, совершает полный цикл своего изменения.

Если же рамка будет замкнута на какую-либо внешнюю цепь, то по цепи потечет переменный ток, график которого будет по виду таким же, как и график ЭДС.

Полученная нами волнообразная кривая называется синусоидой , а ток, ЭДС или напряжение, изменяющиеся по такому закону, называются синусоидальными .

Сама кривая названа синусоидой потому, что она является графическим изображением переменной тригонометрической величины, называемой синусом.

Синусоидальный характер изменения тока — самый распространенный в электротехнике, поэтому, говоря о переменном токе, в большинстве случаев имеют в виду синусоидальный ток.

Для сравнения различных переменных токов (ЭДС и напряжений) существуют величины, характеризующие тот или иной ток. Они называются параметрами переменного тока .

Период, амплитуда и частота — параметры переменного тока

Переменный ток характеризуется двумя параметрами — периодом и амплитудо й, зная которые мы можем судить, какой это переменный ток, и построить график тока.

Рисунок 4. Кривая синусоидального тока

Промежуток времени, на протяжении которого совершается полный цикл изменения тока, называется периодом.

Период обозначается буквой Т и измеряется в секундах.

Промежуток времени, на протяжении которого совершается половина полного цикла изменения тока, называется полупериодом. Следовательно, период изменения тока (ЭДС или напряжения) состоит из двух полупериодов. Совершенно очевидно, что все периоды одного и того же переменного тока равны между собой.

Как видно из графика, в течение одного периода своего изменения ток достигает дважды максимального значения.

Максимальное значение переменного тока (ЭДС или напряжения) называется его амплитудой или амплитудным значением тока.

Im, Em и Um — общепринятые обозначения амплитуд тока, ЭДС и напряжения.

Мы прежде всего обратили внимание на , однако, как это видно из графика, существует бесчисленное множество промежуточных его значений, меньших амплитудного.

Значение переменного тока (ЭДС, напряжения), соответствующее любому выбранному моменту времени, называется его мгновенным значением.

i , е и u — общепринятые обозначения мгновенных значений тока, ЭДС и напряжения.

Мгновенное значение тока, как и амплитудное его значение, легко определить с помощью графика. Для этого из любой точки на горизонтальной оси, соответствующей интересующему нас моменту времени, проведем вертикальную линию до точки пересечения с кривой тока; полученный отрезок вертикальной прямой определит значение тока в данный момент, т. е. мгновенное его значение.

Очевидно, что мгновенное значение тока по истечении времени Т/2 от начальной точки графика будет равно нулю, а по истечении времени — T/4 его амплитудному значению. Ток также достигает своего амплитудного значения; но уже в обратном на правлении, по истечении времени, равного 3/4 Т.

Итак, график показывает, как с течением времени меняется ток в цепи, и что каждому моменту времени соответствует только одно определенное значение как величины, так и направления тока. При этом значение тока в данный момент времени в одной точке цепи будет точно таким же в любой другой точке этой цепи.

Число полных периодов, совершаемых током в 1 секунду, называется частотой переменного тока и обозначается латинской буквой f .

Чтобы определить частоту переменного тока, т. е. узнать, сколько периодов своего изменения ток совершил в течение 1 секунды , необходимо 1 секунду разделить на время одного периода f = 1/T . Зная частоту переменного тока, можно определить период: T = 1/f

Измеряется единицей, называемой герцем.

Если мы имеем переменный ток , частота изменения которого равна 1 герцу, то период такого тока будет равен 1 секунде. И, наоборот, если период изменения тока равен 1 секунде, то частота такого тока равна 1 герцу.

Итак, мы определили параметры переменного тока — период, амплитуду и частоту , — которые позволяют отличать друг от друга различные переменные токи, ЭДС и напряжения и строить, когда это необходимо, их графики.

При определении сопротивления различных цепей переменному току использовать еще одна вспомогательную величину, характеризующую переменный ток, так называемую угловую или круговую частоту .

Круговая частота обозначается буквой ω и связана с частотой f соотношениемω = 2π f

Поясним эту зависимость. При построении графика переменной ЭДС мы видели, что за время одного полного оборота рамки происходит полный цикл изменения ЭДС. Иначе говоря, для того чтобы рамке сделать один оборот, т. е. повернуться на 360°, необходимо время, равное одному периоду, т. е. Т секунд. Тогда за 1 секунду рамка совершает 360°/T оборота. Следовательно, 360°/T есть угол, на который поворачивается ра мка в 1 секунду, и выражает собой скор ость вращения рамки, которую принято называть угловой или круговой скоростью.

Но так как период Т связан с частотой f соотношением f=1/T, то и круговая скорость может быть выражена через частоту и будет равна ω = 360°f.

Итак, мы пришли к выводу, что ω = 360°f. Однако для удобства пользования круговой частотой при всевозможных расчетах угол 360°, соответствующий одному обороту, заменяют его радиальным выражением, равным 2π радиан, где π =3,14. Таким образом, окончательно получим ω = 2π f. Следовательно, чтобы определить круговую частоту переменного тока (), надо частоту в герцах умножить на постоянное число 6,28.

Частота, период сигнала, изменения напряжения, силы тока. Периодический. Единицы измерения. Герц, Гц, Hz. Hertz. Доли. килогерц, кгц, мегагерц, мгц. В чем измеряется частота? В чем измеряется частота в физике

Резонансный метод измерения частот.

Метод сравнения частот;

Метод дискретного счета основывается на подсчете импульсов необходимой частоты за конкретный промежуток времени. Его наиболее часто используют цифровые частотомеры, и именно благодаря этому простому методу можно получить довольно точные данные.

Более подробно о частоте переменного тока Вы можете узнать из видео:

Метод перезаряда конденсатора тоже не несет в себе сложных вычислений. В этом случае среднее значение силы тока перезаряда пропорционально соотносится с частотой, и измеряется при помощи магнитоэлектрического амперметра. Шкала прибора, в таком случае, градуируется в Герцах.

Погрешность подобных частотомеров находится в пределах 2%, и поэтому такие измерения вполне пригодны для бытового использования.

Способ измерения базируется на электрическом резонансе, возникающем в контуре с подстраиваемыми элементами. Частота, которую необходимо измерить, определяется по специальной шкале самого механизма подстройки.

Такой метод дает очень низкую погрешность, однако применяется только для частот больше 50 кГц.

Метод сравнения частот применяется в осциллографах, и основан на смешении эталонной частоты с измеряемой. При этом возникают биения определенной частоты. Когда же этих биений достигает нуля, то измеряемая становится равной эталонной. Далее, по полученной на экране фигуре с применением формул можно рассчитать искомую частоту электрического тока.

Ещё одно интересное видео о частоте переменного тока:

Итак, прежде чем определить, в чем измеряется частота, важно понять, что же это такое? Мы не будем углубляться в сложные физические термины, но некоторые понятия из этой дисциплины нам все-таки понадобятся. Во-первых, понятие «частота» — может относиться только к какому либо периодическому процессу. То есть, это действие, которое постоянно повторяется во времени. Вращение Земли вокруг Солнца, сокращение сердца, смена дня и ночи – всё это происходит с определенной частотой. Во-вторых, свою частоту, или периодичность колебаний имеют явления, или предметы, которые нам, людям, могут казаться вполне статичными и неподвижными. Хороший пример этого – обыкновенный дневной свет. Мы не замечаем, какого либо его изменения, или мерцания, но он, всё-же, имеет свою частоту колебаний, поскольку представляет собой высокочастотные электромагнитные волны.

Единицы измерения

В чем измеряется частота, в каких единицах? Для низкочастотных процессов существуют свои, отдельные единицы. Например, в космических масштабах – галактический год (обращение Солнца вокруг центра Галактики), земной год, сутки и т.д. Понятно, что для измерения меньших величин, пользоваться такими единицами неудобно, поэтому в физике используется более универсальная величина «секунда в минус первой степени» (с -1). Возможно, вы никогда не слышали о подобной мере, и это не удивительно – она обычно применяется лишь в научной, или технической литературе.

К счастью для нас, в 1960-ом году, меру частоты колебаний назвали на честь немецкого физика Генриха Герца. Эта величина (герц, сокр. Гц) и используется нами сегодня. Обозначает она количество колебаний (импульсов, действий) совершаемых объектом в 1 секунду. По-сути, 1 Гц = 1 с -1 . Человеческое сердце, например, имеет частоту колебаний приблизительно 1 Гц, т.е. сокращается один раз в секунду. Частота процессора вашего компьютера, может быть, скажем, 1 гигагерц (1 млрд. герц) – это значит, что в нем происходит 1 миллиард каких-то действий в секунду.

Как измерить частоту?

Если говорить об измерении частот электрических колебаний, то первый прибор, с которым знаком каждый из нас – это наши собственные глаза. Благодаря тому, что наши глаза умеют измерять частоту, мы различаем цвета (напомним, что свет — это электромагнитные волны) – самые низкочастотные мы видим как красные, высокочастотные – это ближе к фиолетовому. Для измерения более низких (или более высоких частот), люди изобрели множество приборов.

Вообще, основных способов измерения частоты есть два: непосредственный подсчет импульсов в секунду, и сравнительный метод. Первый способ реализован в частотомерах (цифровых и аналоговых). Второй – в компараторах частот. Метод измерения с частотомером – проще, в то время как измерение компаратором – точнее. Одной из разновидностей сравнительного метода, является измерение частоты с помощью осциллографа (знаком нам по кабинетам физики еще со школы) и т.н. «фигур Лиссажу». Недостаток сравнительного метода – для измерения нужно два источника колебаний, и один из них должен иметь уже известную нам частоту. Надеемся, наше маленькое исследование было вам интересно!

(лат. amplitude — величина) — это наибольшее отклонение колеблющегося тела от положения равновесия.

Для маятника это максимальное расстояние, на которое удаляется ша-рик от своего положения равновесия (рисунок ниже). Для колебаний с малыми амплитудами за такое расстояние можно принимать как длину дуги 01 или 02, так и длины этих отрезков.

Амплитуда колебаний измеряется в единицах длины — метрах , санти-метрах и т. д. На графике колебаний амплитуда определяется как макси-мальная (по модулю) ордината синусоидальной кривой, (см. рис. ниже).

Период колебаний.

Период колебаний — это наименьший промежуток времени, через который система, соверша-ющая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент времени, выбранный произвольно.

Другими словами, период колебаний (Т ) — это время, за которое совершается одно полное ко-лебание. Например, на рисунке ниже это время, за которое грузик маятника перемещается из крайней правой точки через точку равновесия О в крайнюю левую точку и обратно через точку О снова в крайнюю правую.

За полный период колебаний, таким образом, тело проходит путь, равный четы-рем амплитудам. Период колебаний измеряется в единицах времени — секундах , минутах и т. д. Период колебаний может быть определен по известному графику колебаний, (см. рис. ниже).

Понятие «период колебаний», строго говоря, справедливо, лишь когда значения колеблющей-ся величины точно повторяются через определенный промежуток времени, т. е. для гармоничес-ких колебаний. Однако это понятие применяется также и для случаев приблизительно повторяю-щихся величин, например, для затухающих колебаний .

Частота колебаний.

Частота колебаний — это число колебаний, совершаемых за единицу времени, например, за 1 с .

Единица частоты в СИ названа герцем (Гц ) в честь немецкого физика Г. Герца (1857-1894). Если частота колебаний (v ) равна 1 Гц , то это значит, что за каждую секунду совершается одно колебание. Частота и период колебаний связаны соотношениями:

В теории колебаний пользуются также понятием циклической , или круговой частоты ω . Она связана с обычной частотой v и периодом колебаний Т соотношениями:

Циклическая частота — это число колебаний, совершаемых за 2π секунд.

Определение

Частота — это физический параметр, которые используют для характеристики периодических процессов.{-1}=Гц.\]

Герц — это единица измерения частоты периодического процесса, при которой за время равное одной секунде происходит один цикл процесса. Единица измерения частоты периодического процесса получила свое наименование в честь немецкого ученого Г. Герца.

Частота биений, которые возникают при сложении двух колебаний, происходящих по одной прямой с разными, но близкими по величине частотами (${\nu }_1\ и\ {\nu }_2$) равна:

\[{\nu =\nu }_1-\ {\nu }_2\left(3\right).\]

Еще одно величиной характеризующей колебательный процесс является циклическая частота (${\omega }_0$), связанная с частотой как:

\[{\omega }_0=2\pi \nu \left(4\right).\]

Циклическая частота измеряется в радианах, деленных на секунду:

\[\left[{\omega }_0\right]=\frac{рад}{с}.\]

Частота колебаний тела, имеющего массу$\ m,$ подвешенного на пружине с коэффициентом упругости $k$ равна:

\[\nu =\frac{1}{2\pi \sqrt{{m}/{k}}}\left(5\right).\]

Формула (4) верна для упругих, малых колебаний. Кроме того масса пружины должна быть малой по сравнению с массой тела, прикрепленного к этой пружине.

Для математического маятника частоту колебаний вычисляют как: длина нити:

\[\nu =\frac{1}{2\pi \sqrt{{l}/{g}}}\left(6\right),\]

где $g$ — ускорение свободного падения; $\ l$ — длина нити (длина подвеса) маятника.

Физический маятник совершает колебания с частотой:

\[\nu =\frac{1}{2\pi \sqrt{{J}/{mgd}}}\left(7\right),\]

где $J$ — момент инерции тела, совершающего колебания относительно оси; $d$ — расстояние от центра масс маятника до оси колебаний.

Формулы (4) — (6) приближенные. Чем меньше амплитуда колебаний, тем точнее значение частоты колебаний, вычисляемых с их помощью.

Формулы для вычисления частоты дискретных событий, частота вращения

дискретных колебаний ($n$) — называют физическую величину, равную числу действий (событий) в единицу времени. Если время, которое занимает одно событие обозначить как $\tau $, то частота дискретных событий равна:

Единицей измерения частоты дискретных событий является обратная секунда:

\[\left=\frac{1}{с}.\]

Секунда в минус первой степени равна частоте дискретных событий, если за время, равное одной секунде происходит одно событие.

Частотой вращения ($n$) — называют величину, равную количеству полных оборотов, которое совершает тело в единицу времени. Если $\tau $ — время, затрачиваемое на один полный оборот, то:

Примеры задач с решением

Пример 1

Задание. Колебательная система совершила за время равное одной минуте ($\Delta t=1\ мин$) 600 колебаний. Какова частота этих колебаний?

Решение. Для решения задачи воспользуемся определением частоты колебаний: Частота, в этом случае — это число полных колебаний, совершающихся за единицу времени.

\[\nu =\frac{N}{\Delta t}\left(1.1\right).\]

Прежде чем переходить к вычислениям, переведем время в единицы системы СИ: $\Delta t=1\ мин=60\ с$. Вычислим частоту:

\[\nu =\frac{600}{60}=10\ \left(Гц\right).\]

Ответ. $\nu =10Гц$

Пример 2

Задание. На рис.1 изображен график колебаний некоторого параметра $\xi \ (t)$, Какова амплитуда и частота колебаний этой величины?

Решение. Из рис.1 видно, что амплитуда величины $\xi \ \left(t\right)={\xi }_{max}=5\ (м)$. Из графика получаем, что одно полное колебание происходит за время, равное 2 с, следовательно, период колебаний равен:

Частота — величина обратная периоду колебаний, значит:

\[\nu =\frac{1}{T}=0,5\ \left(Гц\right).\]

Ответ. 1) ${\xi }_{max}=5\ (м)$. 2) $\nu =0,5$ Гц

Что показывает частота переменного тока. Отличие переменного тока от постоянного

Есть и вспомогательные параметры:

угловая частота;

фаза;

мгновенное значение.

Амплитуда Uм и Iм

Мгновенное значение u и i

Действующие значения I, E и U

Обозначения, параметры. Мы знаем, что постоянный электрический ток, это ток не меняющийся во времени как по величине, так и по направлению движения электронов. Основное назначение постоянного тока, это питание различной радио и электронной аппаратуры. Источниками постоянного тока являются аккумуляторы, солнечные фотоэлементы, батарейки и генераторы постоянного тока.
В быту и промышленности используется переменный синусоидальный ток. Это связано с тем, что современная энергетика основана на передаче энергии на дальние расстояния от гидро, тепловых и атомных электростанций к потребителю. Для получения электрической энергии на электростанциях используют генераторы переменного тока. Прередача переменного тока выгодна вследствие преимуществ его преобразования и из за малых потерь в линиях электропередачи. Переменный электрический ток легко преобразовать в постоянный ток, а так же получить любые нужные напряжения переменного тока. Например напряжение переменного тока передаваемое по линиям электропередачи составляет несколько тысяч вольт. В жилых кварталах линия электропередачи подключается к трансформатору который преобразует высокое напряжение в стандартное бытовое напряжение 220 вольт. Именно это напряжение мы и имеем в розетках наших квартир.

В отличие от постоянного тока, переменный синусоидальный ток (а так же и переменное напряжение) изменяется со временем по амплитуде (величине) и направлению движения электронов. На графике переменный ток имеет вид синусоиды.

Расстояние между двумя соседними вершинами на графике переменного синусоидального тока называется периодом и обозначается буквой Т. Период, это время одного колебания переменного тока. Измеряется период в секундах или в более малых единицах времени: миллисекундах; микросекундах; наносекундах и т.д. Величина: период Т=1 сек. в минус первой степени (Т -1) или 1/Т называется частотой в 1 Герц. Частота обозначается буквой f. В радио и электронных приборах, в зависимости от их назначения, частота может быть в единицах герц (Гц или Hz), тысячах герц (кГц или kHz) и так далее.

Стандартная частота в бытовой электрической сети равна 50 Гц. В некоторых зарубежных странах стандартная частота равна 60 Гц. Так же, как и постоянный ток, переменный ток передается по двум проводам. Если у постоянного тока есть два полюса — плюс и минус, то у переменного тока один провод является токоведущим и называется «фаза», а второй провод является общим и называется «земля» или «ноль». Напряжение в бытовой электрической розетке равно 220 вольт.

В отличие от постоянного тока, переменный электрический ток (или напряжение) изменяют свою величину, со временем, от максимального до минимального значения. В связи с этим значение переменного тока или напряжения будет несколько ниже значения U или I.

Эти значения называются эффективными (действующими) значениями тока или напряжения и обозначаются соответственно Iэф и Uэф (смотрите рисунок). Именно такие значения показывают измерительные приборы переменного тока.
&nbsp &nbsp Для исследования параметров переменного тока наиболее подходящим измерительным прибором является осциллограф. На электронно лучевой трубке осциллографа — дисплее (см. рисунок) можно наблюдать не только форму переменного тока, но и провести количественный анализ исследуемого сигнала.

Ось Х на дисплее проградуирована в делениях времени, а ось Y проградуирована в делениях амплитуды сигнала. На рисунке переключатель «Время» установлен на время 0.01 микросекунда на деление по оси Х.
На приведенном рисунке период сигнала равен 2 делениям, следовательно: Т = 2 * 0.01 = 0.02 мкС, а частота сигнала f = 1/T = 1/(0.02 -6) = 1/0.00000002 = 50000000 Гц = 50 МГц (МГц — мегагерц).
Переключатель «Значение Y» установлен на амплитуду 10 Вольт на деление по оси Y. Сигнал имеет амплитуду 6 делений, следовательно напряжение сигнала равно 6 * 10 = 60 вольт.
В заключение этой темы хотелось бы сказать о том, что переменный синусоидальный ток применяется не только для питания бытовых и промышленных электрических приборов. В радио и электронике широко используются, например, высокочастотные генераторы переменного тока для радио- передатчиков (как мощные для теле и радио студий, так и маломощные для телефонов сотовой связи, пейджеров и т.д.). В последующих наших темах мы будем часто сталкиваться с переменным электрическим током и законами его усиления, преобразования и так далее.

Электрический ток- это направленное или упорядоченное движение заряженных частиц: электронов в металлах, в электролитах — ионов, а в газах — электронов и ионов. Электрический ток может быть как постоянным, так и переменным.

Определение постоянного электрического тока, его источники

Постоянный ток (DC, по-английски Direct Current) — это электрический ток, у которого свойства и направление не меняются с течением времени. Обозначается постоянный ток и напряжение в виде короткой горизонтальной черточки или двух параллельных, одна из которых штриховая.

Постоянный ток используется в автомобилях и в домах, в многочисленных электронных приборах: ноутбуки, компьютеры, телевизоры и т. д. Перемеренный электрический ток из розетки преобразуется в постоянный при помощи блока питания или трансформатора напряжения с выпрямителем.

Любой электроинструмент, устройство или прибор, работающие от батареек так же являются потребителями постоянного тока, потому что батарея или аккумулятор- это исключительно источники постоянного тока, который при необходимости преобразуется в переменный с использованием специальных преобразователей (инверторов).

Принцип работы переменного тока

Переменный ток (AC по-английски Alternating Current)- это электрический ток, который изменяется по величине и направлению с течением времени. На электроприборах условно обозначается отрезком синусоиды « ~ ».
Иногда после синусоиды могут указываться характеристики переменного тока — частота, напряжение, число фаз.

Переменный ток может быть как одно- , так и трёхфазным, для которого мгновенные значения тока и напряжения меняются по гармоническому закону.

Основные характеристики переменного тока — действующее значение напряжения и частота.

Обратите внимание , как на левом графике для однофазного тока меняется направление и величина напряжения с переходом в ноль за период времени Т, а на втором графике для трехфазного тока существует смещение трех синусоид на одну третью периода. На правом графике 1 фаза обозначена буквой «а», а вторая буквой «б». Хорошо известно, что в домашней розетке 220 Вольт. Но мало кто знает, что это действующие значение переменного напряжения, но амплитудное или максимальное значение будет больше на корень из двух, т.е будет равно 311 Вольт.

Таким образом, если у постоянного тока величина напряжения и направление не изменяются в течении времени, то у переменного тока- напряжение постоянно меняется по величине и направлению (график ниже нуля это обратное направление).

И так мы подошли к понятию частота — это отношение числа полных циклов (периодов) к единице времени периодически меняющегося электрического тока. Измеряется в Герцах. У нас и в Европе частота равна 50 Герцам, в США- 60 Гц.

Что означает частота 50 Герц? Она означает, что у нас переменный ток меняет свое направление на противоположное и обратно (отрезок Т- на графике) 50 раз за секунду!

Источниками переменного тока являются все розетки в доме и все то, что подключено напрямую проводами или кабелями к электрощиту. У многих возникает вопрос: а почему в розетке не постоянный ток? Ответ прост. В сетях переменного тока легко и с минимальными потерями преобразовывается величина напряжения до необходимого уровня при помощи трансформатора в любых объемах. Напряжение необходимо увеличивать для возможности передачи электроэнергии на большие расстояния с наименьшими потерями в промышленных масштабах.

С электростанции , где стоят мощные электрогенераторы, выходит напряжение величиной 330 000-220 000 , далее возле нашего дома на трансформаторной подстанции оно преобразуется с величины 10 000 Вольт в трехфазное напряжение 380 Вольт, которое и приходит в многоквартирный дом, а к нам в квартиру приходит однофазное напряжение, т. к. между напряжение равняется 220 В, а между разноименными фазами в электрощите 380 Вольт.

И еще одним из важных достоинств переменного напряжения является то, что асинхронные электродвигатели переменного тока конструктивно проще и работают значительно надежнее, чем двигатели постоянного тока.

Как переменный ток сделать постоянным

Для потребителей, работающих на постоянном токе- переменный преобразуется при помощи выпрямителей.

Преобразователь постоянного тока в переменный

Если с преобразованием переменного тока в постоянный не возникает сложностей, то со обратным преобразованием все гораздо сложнее. В домашних условиях для этого используется инвертор — это генератор периодического напряжения из постоянного, по форме приближённого к синусоиде.

Переменный и его применение в медицине.

Переменный ток, его виды и основные характеристики.

Примечание: не оговаривается форма кривой тока, периодичность, длительность его изменения.

На практике под переменным током чаще всего подразумевают периодический переменный ток.

Виды тока:

Ток проводимости.

Ток смещения.

Ток проводимости – это такой ток, который обусловлен колебаниями электронов и ионов в среде.

Амплитуда тока смещения и его направления совпадают по фазе с таковыми тока проводимости.

По значению он всегда равен току проводимости.

Сумма токов смещения и поляризации составляет полный ток смещения.

В медицинской практике применяются следующие виды токов по форме кривой тока:

Основные характеристики переменного тока.

Период – время одного цикла изменения тока по направлению и числовому значению (T, c).

Частота – это число циклов изменения тока в единицу времени.

 =1/Т (величина обратная периоду с -1 , Гц)

Круговая частота ( , 2 /Т радиан/с)

Фаза ( ) – это величина, определяющая во времени взаимоотношение тока и напряжения в электрической цепи.

Мгновенное значение тока и напряжения — значение этих величин в данный момент времени (i, u).

Амплитудное значение тока и напряжения – это максимальное за полупериод значение этих величин (I m , U m).

I =  I 2 cp

U =  U 2 cp

I эф = I = 0,707 I m

U эф = U = 0,707 U m

Для практики имеют значения следующие формулы связи характеристик:

i(u) ≤I m (U m)

I эф = I = I m / 2 =0,707 I m I m = 1,41 I эф

U эф = U= U m / 2 =0,707 U m U m = 1,41 U эф

2. Цепи переменного тока с активным сопротивлением, индуктивностью, емкостью и их особенности.

Виды электрических цепей:

Особенности простых идеальных цепей.

Условию идеальности цепи :

Активное сопротивление не равно нулю,

индуктивность и ёмкость его равны нулю.

R  0

C r = 0 ~ R

Особенности:

Нет сдвига фаз ( ) между током и напряжением.

Это значит, что ток и напряжение одновременно проходят свои максимальные (амплитудные) и нулевые значения.

На R – элементе происходят потери энергии в виде выделения тепла.

Условия идеальности цепи:

Индуктивность катушки не равна нулю

Её ёмкость и сопротивление равны нулю.

L  0

Особенности цепи:

X L =  L = 2 L

В цепи есть сдвиг фаз между напряжением и током: V опережает I по фазе на угол  /2

Условия идеальности цепи:

Ёмкость конденсатора не равна нулю, а его активное сопротивление и индуктивность равны нулю. С  0, R С = 0, L C = 0.

Особенности цепи с ёмкостью:

1. Соблюдается закон Ома.

В цепи есть сдвиг фаз между напряжением и током: V отстает от I по фазе на угол  /2

Полная цепь переменного тока и её виды. Импеданс и его формула. Особенности импеданса живой ткани.

В параллельной цепи R, C, L элементы соединены параллельно.

Особенности полной цепи:

Соблюдается закон Ома

Z — импеданс последовательной цепи,

R — активное сопротивление,

X L – индуктивное и X C – ёмкостное сопротивление,

L — индуктивность катушки (генри),

C — ёмкость конденсатора (фарад).

Особенности импеданса живой ткани и её эквивалентная электрическая схема.

Z_ — импеданс последовательной цепи,

R — её активное сопротивление,

X C — ёмкостное сопротивление.

При последовательной схеме соединения практические данные дают большие отклонения на низких частотах.

Схема позволяет судить:

Какими электрическими элементами обладает ткань

Как соединены эти элементы.

Как будут меняться свойства ткани при изменении частоты тока.

В основе схемы лежат три положения:

В обход клетки, через внеклеточную среду.

Через клетку.

Путь в обход клетки представлен только сопротивлением средыRср.

Путь через клетку сопротивлением содержимого клетки Rк, а также сопротивлением и ёмкостью мембраны.Rм, См.

Схема Фрике (ионная проводимость не

учитывается).

Схема Швана (ионная проводимость учитывается в виде сопротивления мембраны)

Обозначения на схеме:

Rcp — активное сопротивление клеточной среды

Rk — Сопротивление клеточного содержимого

Cm — ёмкость мембраны

Rm — сопротивление мембраны.

Экспериментально установлены следующие особенности живой ткани как проводника переменного ток:

1. Сопротивление живой ткани переменном току меньше, чем постоянному.

2. Электрические характеристики ткани зависят как от её вида, так и от частоты тока.

5. При умирании живой ткани её сопротивление уменьшается и от частоты не зависит.

Частотные зависимости по форме кривой для разных тканей сходный, но отличается значением сопротивления.

Особенности дисперсии:

1. Присуща только живым тканям.

2. Более выражена на частотах до 1 МГц.

3. На практике используется для оценки физиологического состояния и жизнеспособности тканей.

Количественно оценка дисперсии проводиться по коэффициенту дисперсии (К).

Z 1 – полное сопротивление на частоте 10 2 Гц

Z 2 – полное сопротивление на частоте 10 6 Гц

 1 ,  2 — удельное сопротивление на этих частотах

Похожие рефераты:

Охарактеризуйте параметры переменного тока: период, частота, амплитуда, начальная фаза.

Тести за романом Р.Л.Стівенсона «Острів скарбів»1. Батьківщина Р.Л.Стівенсона – це:а) Англія;б) Шотландія;в) Уельс;г) Ірландія.2. Роберт Льюїс отримав … професію:а) лікаря;б) вчителя;в) юриста;г) інженера.3. Початкова назва роману про заховані на острові скарби була:а) «Загадковий кок»;б) «Дивний кухар»;в) «Острів скарбів»;г) «Корабельний кухар».4. Від чийого імені ведеться розповідь у романі:а) Джима;б) автора;в) лікаря Лівсі;г) містера Трелоні.5. Ким був на кораблі Джім Гокінс:А) стерничим;Б) юнгою;В) старшим матросом;Г) боцманом.6. «То був високий, міцний, огрядний чоловік з брунатним обличчям. Над коміром його заяложеної синьої куртки стирчала просмалена косичка. Руки в нього були зашкарублі й пошрамовані, з чорними поламаними нігтями, а рубець на щоці мав неприємний блідо-багряний відтінок».Так виглядав:а) Джон Сілвер;б) Біллі Бонс;в) Чорний Пес;г) сліпий П’ю.7. Де переховувалися Джим та його мати, коли до заїзду прийшла ватага піратів:а) у підвалі;б) у садку;в) під мостом;г) у сусідів?8. Сліпий П’ю загинув:а) від кулі;б) від ножа;в) упавши в річку;г) під кінськими копитами.9. Що було у пакеті, який Джим передав лікарю Лівсі:а) зошит і конверт;б) гроші й папери;в) документи і портрет;г) записник і перо?10. Що вирішує зробити сквайр Трелоні:а) повернути карту піратам;б) віддати пакет в поліцію;в) плисти на пошуки скарбів;г) не звертати уваги на папери пірата?11. Як звали одноногого матроса:а) Смоллет;б) Сілвер;в) Гендс;г) Редрут?12. Що викрикував папуга на ім’я капітан Флінт:а) «Центи!»;б) «Фунти!»;в) «Пенси!»;г) «Піастри!»?13. Де перебував Джим, підслуховуючи матросів, що домовлялися про змову проти капітана й судновласника:а) у трюмі;б) у каюті капітана;в) на камбузі;г) у бочці з яблуками?14. «…мав досить приємні риси обличчя. Тільки шкіра його так засмалилася на сонці, що аж губи в нього почорніли, а ясні очі надзвичайно гостро проступали на темному обличчі. Він був обірванцем з обірванців…» Це портрет:а) Бена Гана;б) Джона Сілвера;в) Ізраєля Гендса;г) Ейбрегема Грея?15. Скільки років перебуває на острові покинутий товаришами Бен Ган:а) два;б) три;в) чотири;г) п’ять?16. На що не погоджувався капітан Смоллет, коли заколотники вели обстріл блокгаузу:а) стріляти у відповідь;б) відступати;в) спустити прапор;г) вести перемовини з ворогами?17. Що зробив Джим уночі після відбитої атаки:а) ліг спати;б) пішов у розвідку;в) розмовляв з товаришами;г) поплив на «Еспаньйолу»?18. «Ми, здається, обидва скрикнули не своїм голосом, зустрівшись очима – я з жаху, він – з люті, мов оскаженілий бик». Який засіб виразності використано в реченні:а) порівняння;б) метафора;в) епітет;г) гіпербола?19. «По-перше, становище ваше погане: шхуну ви втратили, скарб втратили, людей своїх втратили. Вся ваша справа пропаща. І коли ви хочете знати, хто це спричинив, то знайте: це я і ніхто інший». Кому належать ці слова:а) Лівсі;б) Гокінсу;в) Смоллету;г) Трелоні?20. Скільки залишилося піратів, коли вони вирушили востаннє на пошуки скарбів:а) четверо;б) п’ятеро;в) шестеро;г) семеро?21. Що сталося з Сілвером:а) залишився на острові;б) поплив до Англії;в) загинув;г) утік з частиною скарбів?22. Хто найнерозумніше повівся з своєю часткою скарбів:а) Джим;б) Грей;в) Лівсі;г) Бен Ган?23. Знайдіть четвертого зайвого:а) Біллі Бонс;б) Джим Гокінс;в) Чорний Пес;г) сліпий П’ю.24. «Острів скарбів» — це роман:а) авантюрний;б) науковий;в) детективний;г) пригодницький.

Срочно!! Доклад на тему ,,Текстильное волокно». Пожалуйста!!!!

Помогите пожалуйста решить Питон!!!!!!!!!!!

тема: «Стилистически нейтральные, книжные, устаревшие старославянизмы. Орфографический и пунктуационный практикум.» 1)Прочитайте ряды слов. Найдите зн … ачения неизвестных вам слов в толковом словаре, определите, к каким периодам истории русского общества и истории русского языка они относятся. 1) Князь (правитель княжества), междоусобица, гридница, полюдье. 2) Дворянин, городовой, помещик, городничий, полицмейстер, гусар. 3) Колхоз, рабфак, красноармеец, продразвёрстка, раскулачивание, нэп. 4) «Катюша», блокадник, санинструктор, похоронка. 5) Космонавт, космический корабль, корабль-спутник, космодром. 6) Перестройка (в обществе), постсоветский, посткоммунистический. 2) Подумайте, есть ли среди данных слов историзмы. Можно ли назвать при- мерное время устаревания этих слов в русском языке? Обоснуйте свой ответ. 3) Для каких из приведённых слов вы можете указать примерное время появления в русском языке? В какой исторический период эти слова были неологизмами? Докажите правильность своей точки зрения. 1) Прочитайте фрагмент статьи Д. С. Лихачёва и подумайте, о чём он. Сформулируйте главную мысль текста. Наш язык <…> вобрал в себя и всё то, что создано фольклором и наукой (научная терминология и научные понятия). К языку, в широком смысле, относятся пословицы, поговорки, фразеологизмы, ходячие цитаты (допустим, из Священного Писания, из классических произведений русской литературы, из русских романсов и песен). В русский язык органично вошли и стали его неотъемлемой частью (именами нарицательными) имена многих литературных героев (Митрофанушки, Обломова, Хлестакова и других). К языку относится всё увиденное «глазами языка» и языковым искусством созданное. (Нельзя не учесть, что в русское языковое сознание, в мир, увиденный русским языковым сознанием, вошли понятия и образы мировой литературы, мировой науки, мировой культуры — через живопись, музыку, переводы, через языки греческий и латинский.) 2) Вспомните, как называются слова и выражения, пришедшие в русский язык из фольклора, мифологии, художественной литературы.

Помогите. Перечень приспособлений малой механизации. Срочно.

Помогите пожалуйста, надо начертить в изометрической проэкции

при каком виде перелома накладывают шину ? а) перелома челюсти б) перелома ребкр с) перелома аостей черепа д) перелома позвоночника пожалуйста срочно … нужно пж пж пж

1. Сравни скорость протекания процесса диффузии в жидко- стях и газах. Сделай вывод. 2. Письменно объясни следующую ситуацию. На рисунке – три стакана … . В них положили по 2 кусочка сахара-рафинада и налили одинаковые объемы воды, но разной температуры. 1 2 3 В каком стакане температура будет наиболее высокая, а в ка- ком — самая низкая? Объясни, какой рисунок помог тебе найти ОТвет.скажите 10 баллов пожалуйста у меня дз

атом мен Кун жуйесинин айырмашылыгы мен уксастыгы пжжжж комектесиндерш

Основні віхи життя Івана хрестителя

Phys 3041 Notes — D

Phys 3041 Заметки

© 1997 Джонатан Карты. Эти примечания не могут быть распространены или дублированы в любой форме, печатной или электронной, без разрешения. Разрешается устанавливать электронные гипертекстовые ссылки только на эти оригинальные документы.

Анализ цепей переменного тока

Цепи переменного тока (переменного тока) — это цепи, в которых напряжения и токи зависят от времени.Они намного богаче по возможностям, чем цепи постоянного тока, и мы рассмотрим здесь цепи переменного тока, содержащие резисторы. конденсаторы и катушки индуктивности. Наш анализ этих схем будет использовать комплексные числа для представления зависящих от времени токов и напряжений. Такой подход заставляет анализ этих цепей следовать линиям, очень похожим на те, что были разработаны для цепей постоянного тока.

Резисторы в цепях переменного тока

Простая цепь переменного тока, которую мы могли бы построить, представляла бы собой зависящий от времени источник напряжения, подключенный к одному резистору.Источник напряжения обеспечивает простое синусоидальное напряжение: В _o cos (wt) .

V _o называется амплитудой сигнала, а w — угловой частотой. Период сигнала T — это время, необходимое для одного полного цикла. Частота f — это количество циклов, выполняемых за одну секунду (циклов в секунду), а единицей измерения является герц (1 Гц = 1 цикл в секунду). Частота — это просто величина, обратная периоду.

Ток, протекающий в цепи, следует из прямого применения закона Ома и меняет направление через резистор. В этой схеме напряжение и ток «синфазны», оба достигают максимума и минимума одновременно.

Величину переменного напряжения часто характеризуют двумя другими показателями: размахом напряжения, В _pp = 2 В _o, и среднеквадратичным (среднеквадратичным) напряжением.Среднеквадратичное значение напряжения — это значение, сообщаемое большинством мультиметров при измерении сигналов переменного тока, и такие фразы, как «110 В переменного тока», которые появляются рядом со шнуром питания на бытовых и лабораторных приборах, обычно означают 110 В _{действующее значение}. Для синусоидального напряжения , В _{действующего значения} = В _o/2 ^-1/2 = 0,707 В _o.

Обычно среднеквадратичное значение находится путем возведения напряжения в квадрат, вычисления среднего значения В ² ( t ) и последующего извлечения квадратного корня.

Среднеквадратичное значение напряжения используется для вычисления средней мощности, рассеиваемой на резисторе. Мгновенная мощность теперь задается P (t) = V (t) I (t) , в то время как средняя мощность вычисляется за один полный цикл. С I (t) = V (t) / R , мы имеем P (t) = V ² (t) / R , и нахождение средней мощности сводится к вычислению среднего квадрата напряжения, как показано выше. Средняя мощность тогда всего

= < V ²> / R = V _rms ²/ R .

Конденсаторы

Конденсаторы — это устройства для хранения заряда. Удобная модель конденсатора — пара параллельных металлических пластин, каждая из которых имеет площадь A, , разделенных расстоянием d . Емкость этой системы представляет собой отношение заряда, накопленного на пластинах (+ Q и -Q), к разнице напряжений, В, , между пластинами:
C = Q / V ,
или емкость можно представить как коэффициент пропорциональности между напряжением и накопленным зарядом:
Q = C V .

Мы будем часто использовать последний в нашем анализе цепей с конденсаторами. Емкость системы параллельных пластин пропорциональна площади пластин (чем больше площадь, тем больше накопленный заряд при фиксированном напряжении) и обратно пропорциональна расстоянию между пластинами. (Электрическое поле между пластинами однородно, поэтому для фиксированного заряда меньшее расстояние означает меньшее напряжение: напомним, что здесь В = E d .) В большинстве случаев емкость увеличивают за счет добавления диэлектрического материала (легко поляризуемого изолятора) между пластинами.Затем емкость увеличивается в раз, равном диэлектрической проницаемости материала.

В цепи постоянного тока (не зависящей от времени) конденсаторы не играют никакой роли, кроме переходной при первом включении питания. После зарядки с ними больше ничего не происходит. Электрические заряды не проходят через конденсатор. Материал между пластинами является изолирующим, и добавление заряда к одной пластине просто отталкивает идентичный заряд от лицевой пластины, оставляя на ней противоположный заряд.Когда конденсатор заряжен, он действует как бесконечное сопротивление. Только когда приложенные напряжения и результирующие токи меняются со временем, конденсаторы могут играть важную роль в работе схемы. Мы рассмотрим переходную характеристику конденсаторов позже.

Рассмотрим конденсатор, подключенный к источнику переменного напряжения.

Поскольку напряжение зависит от времени, заряд на пластинах также должен изменяться со временем:
Q (t) = C V (t) .
Если заряд добавляется или вычитается из пластины, должен быть ток, в данном случае обеспечиваемый источником напряжения:
I = dQ / dt = C dV / dt .
Это поведение сильно отличается от поведения резисторов. Ток пропорционален к скорости изменения напряжения. Чем быстрее изменяется напряжение, тем больше должен быть ток, чтобы обеспечить соответствие Q = CV . Для простого синусоидального приложенного напряжения, В (t) = В _o cos (wt) , результирующий ток определяется как:
I (t) = -wCV _o sin (wt) = wCV _o cos (вес + 90) .
Это показывает фазовый сдвиг между напряжением и током в одну четверть цикла.

Когда приложенное напряжение достигает экстремума, ток, протекающий по цепи, равен нулю. И наоборот, всякий раз, когда напряжение проходит через ноль, ток либо максимальный, либо минимальный. В этом случае считается, что ток опережает напряжение: ток достигает максимума на четверть цикла раньше, чем напряжение. (Альтернативное описание напряжения, опережающего ток на 3/4 цикла, одинаково верно, но обычно для определения того, кто впереди, а кто отстает, выбирается меньший из двух углов.)

Эту разность фаз между током и напряжением можно эффективно обработать с помощью комплексных чисел. Для этого реальное управляющее напряжение ( В (t) = В _o cos (wt) ) заменяется комплексным управляющим напряжением, полученным путем сложения мнимого члена:
В (t) = В _o. cos (wt) + i V _o sin (wt) = V _o e ^iwt .
Эта форма имеет два существенных преимущества: мы восстановим нечто похожее на закон Ома; а фазовые сдвиги, которые происходят в более сложных схемах, включающих резисторы и катушки индуктивности вместе с конденсаторами, будут очень естественно выпадать из-за обработки напряжений и токов как комплексных чисел во время вычислений.Все, что нам нужно сделать, это не забыть взять реальную часть наших сложных результатов, чтобы получить реальные результаты.

Применять это к простому источнику переменного напряжения и одиночному конденсатору несложно.
Q (t) = CV _o e ^iwt
I (t) = dQ / dt = C dV / dt
I (t) = iwCV _o e ^iwt
I (t) = iwC V (t).
Обратите внимание, что в этой форме ток теперь пропорционален приложенному напряжению.Это аналог закона Ома для резисторов. Аналогом сопротивления называется импеданс конденсатора:
Z _c = V (t) / I (t) = 1 / iwC .
Импеданс — это мнимое число. i содержит информацию о разности фаз 90 ^o между током и напряжением для конденсаторов. Чтобы найти реальный ток, мы просто расширяем V ( t ) до V _o cos (wt) + i V _o sin (wt) и умножаем все:
I (t ) = iwCV _o cos (wt) + i ² wCV _o sin (wt)
I (t) = -wCV _o sin (wt) + iwCV _o cos (wt)
и берем только действительную часть результата:
I (t) = -wCV _o sin (wt) , это именно то, что мы получали раньше.Для такой простой схемы, как эта, использование сложных представлений для напряжения и тока может показаться чрезмерно сложным, но этот метод окупается возможностью обрабатывать более сложные схемы очень простыми методами.

Обратите внимание, что сопротивление конденсатора зависит от частоты. Импеданс очень велик на низких частотах, и для данной амплитуды V _o для управляющего напряжения результирующая амплитуда тока I _o будет небольшой.Предельный случай этой ситуации — w = 0 — цепь постоянного тока — где емкость имеет бесконечный импеданс или эффективное сопротивление и ток не течет. Другая крайность возникает на высоких частотах, где полное сопротивление уменьшается до нуля: конденсатор действует как «короткое замыкание» на высоких частотах, где переменный ток может протекать с незначительным падением напряжения на конденсаторе. Величину этого импеданса часто называют реактивным сопротивлением конденсатора: X _c = 1 / wC .С помощью идеи сопротивления, обобщенного до импеданса, правила последовательного и параллельного сопротивлений могут быть расширены для обработки общих, комплексных импедансов (резистивные действительные импедансы резисторов в сочетании с реактивными мнимыми импедансами конденсаторов, а затем и индукторов) по тем же правилам. Обобщения правил Кирхгофа можно затем применить и к цепям переменного тока. Полезное применение этих методов — это RC-цепи, которые можно использовать для выборочного ослабления сигналов на некоторых частотах, позволяя при этом проходить сигналам на других частотах практически без изменений.Рассмотрим такие RC-фильтры.

Глоссарий общих терминов измерения электроэнергии и мощности

Термин	Определение
AC	Сокращение от переменного тока, это электрический ток, который периодически меняет направление 60 раз в секунду (60 раз в секунду). ), тогда как постоянный ток течет только в одном направлении. Измерители мощности DENT предназначены для измерения переменного тока с помощью трансформаторов тока.
Ампер-часы	Ампер-час (Ач) — это единица электрического заряда, имеющая размерность электрического тока, умноженного на время, равная заряду, переносимому постоянным током в один ампер, протекающим в течение одного часа.
Ампер (ампер)	Ампер — это единица измерения электрического тока; количество тока, протекающего в цепи при электродвижущей силе в один вольт и при сопротивлении в один Ом. Сокращенно amp.Измерители мощности DENT предназначены для измерения многих параметров, в том числе силы тока.
Усилитель / интегратор	Схема усилителя / интегратора встроена в несколько продуктов DENT, включая мВ трансформаторы тока RōCoil (снятые с производства), серию PowerScout и измеритель ELITEpro XC. Эта схема, подключенная к выходу пояса Роговского, выдает выходной сигнал, пропорциональный току. В случае RōCoil мВ эта схема должна получать внешнее питание с помощью настенного трансформатора (PX-XFMR).
Каналы аналогового ввода	Каналы аналогового ввода полезны при использовании в сочетании с измерениями мощности для корреляции потребления электроэнергии с окружающей средой, производительностью оборудования HVAC или другими условиями процесса. Типичное использование может включать регистрацию температуры окружающей среды, температуры в здании, солнечной инсоляции, давления в резервуаре, расхода в воздуховоде и т. Д. Например, ELITEpro XC принимает токовую петлю с внешним питанием 0 / 4-20 мА или несимметричные датчики 0-30 В пост. .
ANSI	Акроним Американского национального института стандартов, который является частной некоммерческой организацией, которая курирует разработку добровольных согласованных стандартов для продуктов, услуг, процессов и систем в США. Некоторые продукты DENT соответствуют требованиям ANSI по точности (например, PowerScout 3037 соответствует стандарту точности ANSI C12.20-2010 для производительности класса 0,2 для коммерческого класса).
Полная мощность (кВА)	Произведение напряжения цепи и тока без привязки к фазовому углу.Измерители мощности DENT предназначены для измерения многих параметров, включая полную мощность.
ASHRAE	Аббревиатура Американского общества инженеров по отоплению, охлаждению и кондиционированию воздуха. ASHRAE проводит исследования, пишет стандарты и проводит конференции для повышения квалификации. DENT участвует в одном мероприятии ASHRAE, AHR Expo, которое проводится ежегодно в январе или феврале.
AWG	AWG — это сокращение от American Wire Gauge; стандарт для измерения сечения проводов (электрических проводников).Площадь поперечного сечения каждого датчика является важным фактором для определения его допустимой нагрузки по току.
BACnet	BACnet — это протокол связи для сети автоматизации и управления зданиями (BAC), в котором используются стандарты ASHRAE, ANSI и ISO 16484-5. BACnet был разработан для обеспечения связи между системами автоматизации и управления зданиями для таких приложений, как системы отопления, вентиляции и кондиционирования воздуха (HVAC) и связанное с ними оборудование.Приборы серии DENT PowerScout поддерживают связь через BACnet. Посетите веб-сайт BACnet для получения дополнительной информации.
Двунаправленное измерение	Измеритель, способный измерять как поставленную / импортируемую (+ кВт) мощность, так и полученную / экспортируемую (-кВт) мощность. Термин «двунаправленный учет» широко используется в приложениях с возобновляемыми источниками энергии.
Знак CE	Знак CE является обязательным для определенных продуктов, продаваемых в Европейской экономической зоне.Он аналогичен Декларации соответствия FCC, используемой на некоторых электронных устройствах, продаваемых в США. Знак CE означает, что продукт соответствует высоким требованиям безопасности, здоровья и защиты окружающей среды.
Накладные трансформаторы тока	Накладные трансформаторы тока предназначены для работы одной рукой во время временных энергоаудитов. Они разработаны для широкого применения в компактной форме. Накладные трансформаторы тока чаще всего продаются с приборами ELITEpro XC, поскольку их простая в использовании конструкция делает их идеальными для временных измерительных проектов.
Проводник	Материал, через который передается электричество, например, электрический провод, линия передачи или шина. Трансформаторы тока размещаются вокруг проводника для измерения потока электричества.
Трубопровод	Трубчатый материал, используемый для изоляции и защиты одного или нескольких электрических проводников. Кабелепровод чаще всего используется в стационарных установках с измерителями PowerScout.
Подключенная нагрузка	Устройство, потребляющее электроэнергию, подключенное к генерирующей системе.Пример: электродвигатель.
CONTACTlogger ™	CONTACTlogger, одна из моделей из серии DENT SMARTlogger, предназначен для мониторинга замыканий реле, переключателей и цифровых сигналов включения / выключения. Он поставляется с парой проводов длиной 3 фута, которые подключаются к переключателю или реле. CONTACTlogger можно использовать только на обесточенных устройствах с «сухим контактом».
Зажимы Croc	Также называются «зажимами типа« крокодил ». Зажимы Croc подключаются к концам выводов напряжения на приборах ELITEpro XC.Они используются для подключения счетчика к напряжению внутри электрического щита. Доступны пять цветов: синий, черный, красный, белый и желтый (обычно используются только в установках за пределами США).
CT	Также называется «трансформатор тока» или «датчик тока». ТТ — это тип трансформатора, который используется для измерения переменного тока. Они производят переменный ток во вторичной обмотке, который пропорционален переменному току в первичной обмотке. ТТ DENT подключаются непосредственно к измерителям мощности ELITEpro XC или PowerScout и доступны в различных диапазонах и стилях тока.Они выбираются в зависимости от того, сколько ампер необходимо измерить, и ограничений физического размера.
CTlogger ™	CTlogger, одна из моделей из серии DENT SMARTlogger (снята с производства в 2019 г.), предназначена для контроля состояния электрической нагрузки с помощью фиксирующего трансформатора тока. ТТ подключается к любому проводнику переменного тока 0,25 А или более. Регистратор активируется, когда через провод к контролируемому устройству протекает ток более 0,25 А.
Датчик тока	Также называется «трансформатор тока» или «CT». Датчики тока — это тип трансформатора, который используется для измерения переменного тока. Они производят переменное напряжение, пропорциональное переменному току в первичной обмотке. ТТ DENT подключаются непосредственно к измерителям мощности ELITEpro XC или PowerScout и доступны в различных диапазонах и стилях тока, в том числе с разъемным сердечником, зажимом, сплошным сердечником (пончик или тороид) или катушкой Роговского. Они выбираются в зависимости от того, сколько ампер необходимо измерить, и ограничений физического размера.
Трансформатор тока	Также называется «датчик тока» или «CT». Трансформаторы тока — это трансформаторы, которые используются для измерения переменного тока. Они производят переменный ток во вторичной обмотке, который пропорционален переменному току в первичной обмотке. Трансформаторы DENT имеют встроенный нагрузочный резистор для преобразования токового выхода трансформатора в выход 333 мВ и подключаются напрямую к измерителям мощности ELITEpro XC или PowerScout и доступны в различных диапазонах тока и стилях.Они выбираются в зависимости от того, сколько ампер необходимо измерить, и ограничений физического размера.
Окно трансформатора тока	Окно трансформатора тока иногда называют его «открытием». Проводник, который вы хотите измерить, помещается внутри окна ТТ. Вы должны убедиться, что окно ТТ достаточно велико, чтобы в нем мог поместиться ваш проводник. Проводники могут иметь размер от небольшого провода до большой шины.
DATApro ™	Снятый с производства в 2011 году, DATApro был разработан для измерения, хранения и анализа до 100 000 записей данных со всех типов датчиков, таких как газовые, водяные, электрические, паровые, HVAC, сжатый воздух. , твердые или жидкие отходы, безопасность, погодные условия или производственные технологические линии.ELITEpro XC с четырьмя аналоговыми входными каналами является продуктом замены.
DC	DC или постоянный ток — это однонаправленный поток электрической карты. Постоянный ток вырабатывается такими источниками, как батареи, источники питания, термопары, солнечные элементы или динамо-машины. Электрический ток течет в постоянном направлении, что отличает его от переменного тока. «Датчики на эффекте Холла» — это датчики, которые могут измерять постоянный ток. DENT не имеет датчика этого типа.
Дельта	Схема треугольника — это трехфазная электрическая конфигурация, в которой для передачи требуются три провода. Системы Delta обычно используются для любых больших двигателей или нагревателей, которым не нужна нейтраль. Дельта также используется при передаче электроэнергии, потому что прокладывать четвертый нейтральный провод на большие расстояния дорого.
Плата по запросу	Плата за максимальную скорость использования электроэнергии в часы пик расчетного периода.Плата за потребление взимается на основе возможного спроса на энергию, а не на основе фактически потребленной энергии.
ELITEpro ™	Записывающий многофазный измеритель мощности ELITEpro, снятый с производства в 2011 году, был разработан для точного определения потребления электроэнергии и количественной оценки потребления путем измерения, хранения и анализа вольт, ампер, ватт, вольт-ампер (ВА), реактивные вольт-амперы (ВАР), киловатты (кВт), киловатт-часы (кВтч), кВАч, кВАч и коэффициент мощности. Он был прекращен с выпуском измерителя мощности ELITEpro SP.
ELITEpro SP ™	Измеритель мощности ELITEpro SP, снятый с производства в 2013 году, был разработан для замены многофазного измерителя мощности записи ELITEpro. В качестве прямой замены он предлагал многие из тех же измерительных возможностей, но с увеличенным объемом памяти. Кроме того, ELITEpro SP имел сетевое питание, 8 МБ памяти и стандартный порт USB. Как и ELITEpro до него, этот счетчик был разработан для точного определения потребления электроэнергии и количественной оценки потребления путем измерения, хранения и анализа вольт, ампер, ватт, вольт-ампер (ВА), вольт-ампер реактивных (VAR), киловатт (кВт), киловатт-часы (кВтч), кВАч, кВАрч и коэффициент мощности.Эта модель также была первой ELITEpro, которая позволила использовать трансформаторы тока RōCoil (Роговского) без внешнего усилителя / интегратора. Впоследствии ELITEpro SP был заменен на ELITEpro XC.
ELITEpro XC ™	Представленный в 2013 году, ELITEpro XC представляет собой текущее поколение расходомеров серии ELITEpro, представленных на рынке. Он был разработан для замены ELITEpro SP. Как и ELITEpro SP, он предназначен для точного определения использования электроэнергии и количественной оценки потребления путем измерения, хранения и анализа вольт, ампер, ватт, вольт-ампер (ВА), реактивных вольт-ампер (VAR), киловатт (кВт), киловатт-часов. (кВтч), кВАч, кВАрч и коэффициент мощности.Он имеет 16 МБ памяти, стандартный Ethernet, стандартный USB и ряд коммуникационных опций, включая Wi-Fi и Bluetooth.
Программное обеспечение ELOG	Программное обеспечение ELOG — это программа на базе Windows, разработанная для настройки счетчиков серии ELITEpro, отображения измеренных значений, а также извлечения и анализа собранных данных. ELOG графически отображает записанные данные, выполняет анализ и упрощает автоматический удаленный сбор данных. ELOG предоставляется бесплатно при покупке ELITEpro XC, а также его можно бесплатно загрузить на веб-сайте DENT.
Энергоаудит	Процесс определения энергопотребления здания или объекта различными методами. Цель аудита — выявить возможности снижения энергопотребления с целью экономии денег с течением времени. ELITEpro XC обычно используется для проведения энергоаудита в коммерческих и промышленных приложениях.
ETL	ETL признан NRTL в Соединенных Штатах и, в аналогичном качестве, Советом по стандартам Канады в качестве организации тестирования и сертификации в Канаде.Продукт, отмеченный знаком ETL, соответствует минимальным требованиям установленных стандартов безопасности и обычно считается эквивалентом знака UL. Трансформаторы тока с разъемным сердечником DENT внесены в список ETL (cETLus).
Частота	Число циклов, через которые переменный ток проходит в секунду; в США стандарт выработки электроэнергии составляет 60 циклов в секунду (60 Гц). Измерители серий DENT ELITEpro XC и PowerScout могут выполнять измерения на частоте 60 Гц или 50 Гц (как настроено в программном обеспечении).
Плавленые зажимы для крокодилов	Иногда также называются «Плавленые зажимы-крокодилы». Как и стандартные зажимы типа «крокодил», плавкие зажимы «крокодил» подключаются к концам выводов напряжения на приборах ELITEpro XC. Они отличаются от обычных зажимов типа «крокодил», поскольку в них есть предохранитель на 500 мА. Они используются для подключения счетчика к напряжению внутри электрического щита. Доступны пять цветов: синий, черный, красный, белый и желтый (обычно используются только в установках за пределами США).
Заземление	Заземление — это защитный проводник с низким сопротивлением на пути к земле. Его часто называют «заземляющим проводом» или «защитным заземлением». Он либо голый, либо с зеленой изоляцией.
Горячий	Горячий — это любой проводник (провод или иным образом), подключенный к электрической системе, имеющий электрический потенциал относительно заземления или нейтрали.
Инвертор	Устройство, которое преобразует электричество постоянного тока (например, от солнечного фотоэлектрического модуля или массива) в переменный ток для использования непосредственно для управления приборами или для подачи энергии в электрическую сеть.
Киловатт (кВт)	Стандартная единица электрической мощности, равная одной тысяче ватт или потребляемой энергии со скоростью 1000 Джоулей в секунду.
Киловатт-час (кВтч)	Единица или мера электрической энергии или потребления в 1000 Вт в течение одного часа; эквивалент 3 412 британских тепловых единиц.
Ветвь	Ветвь обычно относится к «горячим ногам» и является одним из нескольких горячих проводников в электрической системе.Наиболее распространенные системы с одной расщепленной фазой, 240 В, имеют нейтраль и две горячие ветви. Наиболее распространенные трехфазные системы будут иметь три горячих вывода, по 208 В между собой и по 120 В между нейтралью.
LIGHTINGlogger ™	LIGHTINGlogger, одна из моделей из серии DENT SMARTlogger, предназначен для отслеживания состояния включения / выключения освещения. Внутренний фотодатчик обнаруживает ближайший источник света и записывает его состояние с отметкой времени и даты.
Питание от сети	Питание от сети является стандартной функцией приборов серий ELITEpro XC и PowerScout.Это позволяет питать счетчик от измеряемой службы напряжения. Инструменты с питанием от сети не нужно подключать к розетке или использовать батарею для работы.
Нагрузка	Нагрузка — это устройство, цепь или система, потребляющая электроэнергию (например, холодильник или здание), подключенные к генерирующей системе.
MAGlogger ™	MAGlogger, одна из моделей серии DENT SMARTlogger (снята с производства в 2019 г.), предназначен для крепления к корпусу двигателя.Он содержит датчик магнитного поля, который может определить, работает ли двигатель. Он записывает свой рабочий график с отметкой времени и даты.
Измерение и проверка	Также называется «M&V». Это термин, применяемый к процессу количественной оценки экономии, обеспечиваемой мерой по энергосбережению, а также к подсектору энергетической отрасли, задействованному в этой практике. ELITEpro XC обычно используется для проектов M&V.
Modbus	Modbus — это протокол последовательной связи, первоначально опубликованный Modicon (ныне Schneider Electric) в 1979 году для использования с его программируемыми логическими контроллерами (ПЛК).Простой и надежный, с тех пор он стал де-факто стандартным протоколом связи и теперь является общедоступным средством подключения промышленных электронных устройств. Приборы серии DENT PowerScout могут обмениваться данными по протоколу Modbus.
Многоконтурный	Счетчики PowerScout серии HD являются многоконтурными или многоканальными счетчиками, что означает, что они способны одновременно контролировать комбинацию трехфазных и / или однофазных цепей. Например, их можно использовать для контроля сети и нескольких цепей освещения в одной электрической панели.
NEC	Национальный электротехнический кодекс, или NEC, представляет собой набор правил, которые способствовали тому, что электрические системы в Соединенных Штатах стали одними из самых безопасных в мире. Цель NEC — обеспечить проектирование и установку безопасных электрических систем. Национальная ассоциация противопожарной защиты (NFPA) спонсирует NEC с 1911 года. NEC меняется по мере развития технологий и совершенствования компонентов. NEC обновляется каждые три года.Следование NEC требуется в большинстве мест.
NEMA	Национальная ассоциация производителей электрооборудования, или NEMA, является крупнейшей торговой ассоциацией производителей электрического оборудования в США. Помимо лоббирования, NEMA публикует более 600 стандартов, руководств по применению, официальных и технических документов. Клиенты часто спрашивают о корпусах с определенными «рейтингами NEMA», такими как 4X. DENT Instruments является членом NEMA.
Чистый учет	*Чистая энергия = потребленная энергия — произведенная энергия* . Чистое измерение — это практика использования одного счетчика для измерения потребления и выработки электроэнергии небольшим генерирующим объектом (например, дом с ветровой или солнечной фотоэлектрической системой). Произведенная или потребляемая чистая энергия продается или покупается у поставщика электроэнергии, соответственно. Многоконтурные счетчики PowerScout обычно используются в приложениях Net Metering.
Нейтраль	Нейтральный провод — это обратный провод цепи. Электротехнические нормы США требуют, чтобы нейтраль не была переключена и не снабжена предохранителями и чтобы она была заземлена только на сервисной панели и ни в какой другой точке системы электропроводки здания.
PhaseChek ™	PhaseChek ™ — это запатентованная технология (патент № 7,612,552), которая позволяет пользователю видеть, когда датчики тока на измерителе были неправильно подключены или подключены.Это значительно сокращает время настройки и помогает устранить ошибки при установке. PhaseChek доступен на приборах серий ELITEpro XC и PowerScout.
Переадресация портов	Переадресация портов позволяет удаленным компьютерам (например, компьютерам в Интернете) подключаться к определенному компьютеру или службе в частной локальной сети (LAN). В случае ELITEpro XC с Ethernet переадресация портов позволяет удаленное соединение между ELITEpro XC и компьютером в другой сети через межсетевой экран с помощью программного обеспечения ELOG.
Коэффициент мощности	В электротехнике коэффициент мощности системы электроснабжения переменного тока определяется как отношение реальной мощности, протекающей к нагрузке, к полной мощности в цепи и является безразмерным числом в замкнутый интервал от -1 до 1. Коэффициент мощности меньше единицы означает, что формы сигналов напряжения и тока не совпадают по фазе, что снижает мощность нагрузки. Коэффициент мощности (aPF и dPF) измеряется приборами серий ELITEpro XC и PowerScout.
PowerScout Series	PowerScout — торговое наименование, данное линейке измерительных приборов DENT Instruments. PowerScout, как правило, постоянно устанавливаются на электрических панелях, чтобы постоянно получать информацию о потреблении энергии. Они доступны в одноконтурном (PowerScout 3037) и многоконтурном (PowerScout HD Series) версиях.
Импульсный вход	Импульсные входы доступны на PowerScout 24 и используются для подсчета, накопления и масштабирования импульсов, полученных от внешних счетчиков, инициирующих импульс, таких как газовые, водяные или другие электрические счетчики, не принадлежащие DENT.
Импульсный выход	Импульсные выходы доступны на счетчиках PowerScout Series и используются для отправки кВтч или других импульсов на устройство счета импульсов, такое как регистратор данных.
Уровень дохода	Измерители уровня дохода и трансформаторы тока соответствуют строгим требованиям к испытаниям и точности. Как правило, они соответствуют требованиям класса ANSI C12.20-2010 с точностью выше 1% (см. Серии PowerScout). Термин «уровень дохода» в общем случае может означать разные вещи для разных организаций.Возможно, измеритель соответствует требованиям к точности класса 0.2, но, если он не используется в паре с таким же точным или лучшим CT, конечный результат может считаться или не считаться «доходной оценкой».
RMS (среднеквадратичное значение)	Для циклически переменного электрического тока среднеквадратичное значение равно значению постоянного тока, которое могло бы вызвать такое же среднее рассеивание мощности в резистивной нагрузке. Измерители DENT ELITEpro XC и PowerScout обеспечивают точное измерение среднеквадратичных значений с использованием высокоскоростной цифровой обработки сигналов (DSP).
RoCoil ™	RōCoil — это торговая марка DENT для нашей линейки датчиков тока с катушкой Роговского. RōCoils известны своими удобными для установщика функциями, такими как большой размер окна, легкий вес, широкий диапазон тока и механическая гибкость для установки в тесных помещениях. RōCoils можно использовать как с приборами ELITEpro XC, так и с PowerScout.
RoCoil ™ мВ	RōCoil мВ, производство прекращено в 2019 году, это торговое название компании DENT для нашей линейки датчиков тока с катушкой Роговского, которые включают схему усилителя / интегратора на подводящем проводе.Эта схема позволяет использовать эти трансформаторы тока в измерителях, не имеющих встроенной схемы усилителя / интегратора (например, в унаследованном измерителе ELITEpro). Эта схема означает, что RōCoil mV требует внешнего источника питания, обычно обеспечиваемого сетевым адаптером (PX-XFMR).
RoCoil ™ TCA-5	RōCoil TCA-5, снятый с производства в 2019 году, представляет собой трехканальный интегрирующий усилитель крутизны (TCA), который преобразует электрический выходной сигнал 131 мВ / 1000 A от датчика RōCoil в 5-амперный Переменный ток, имитирующий традиционный измерительный трансформатор тока.RōCoil TCA-5 разработан для обеспечения совместимости трансформаторов тока RōCoil с измерителями входной мощности тока 5 А.
Датчик тока катушки Роговского	Катушка Роговского, названная в честь Вальтера Роговского, представляет собой электрическое устройство для измерения переменного тока (AC) или высокоскоростных импульсов тока. Он состоит из спиральной катушки с проволокой, вывод которой от одного конца возвращается через центр катушки к другому концу, так что оба вывода находятся на одном конце катушки. Затем катушка наматывается на проводник, ток которого необходимо измерить.RōCoil — это торговое название линии трансформаторов тока Роговского типа DENT.
RS-485	RS-485 — это стандарт, определяющий электрические характеристики драйверов и приемников для использования в системах последовательной связи. Приборы PowerScout могут обмениваться данными через Modbus или BACnet по сетям RS-485.
Таблица настроек	Приборы серии ELITEpro требуют, чтобы они были настроены для использования, сначала создав файл таблицы настроек в программном обеспечении ELOG, а затем загрузив файл в измеритель.Файл таблицы настроек сообщит измерителю, какие датчики тока, интервал записи и тип обслуживания он будет контролировать.
Зажимы Shark	Зажимы Shark для серии ELITEpro можно использовать вместо стандартных зажимов Croc Clips в приложениях, где зажимы Croc могут не поместиться. Они предназначены для узких установок и рассчитаны на 600 В.
Однофазный	Однофазный источник питания — это распределение электроэнергии переменного тока (AC) с использованием системы, в которой все напряжения источника питания совпадают по фазе или не совпадают по фазе на половину цикла (180 ˚).Однофазное распределение используется, когда нагрузки в основном связаны с освещением и обогревом, а электродвигатели имеют небольшие размеры (5 л.с. и ниже) (например, в большинстве жилых домов в США). Серии DENT ELITEpro и PowerScout предназначены для измерения как в однофазных, так и в трехфазных системах.
SMARTlogger ™	Регистраторы времени использования SMARTlogger предназначены для отслеживания состояния включения / выключения и данных общего времени использования энергопотребляющих устройств, таких как фонари, двигатели, переключатели и т. Д. электрическая нагрузка, генерирующая не менее 0.25 ампер. Доступны четыре модели SMARTlogger’ов: LIGHTINGlogger, MAGlogger, CTlogger и CONTACTlogger. SMARTloggers питаются от батареи и записывают до 32 000 записей (переходов включения / выключения) во внутреннюю память. Программное обеспечение SMARTware используется для настройки регистратора, загрузки и анализа данных.
Программное обеспечение SMARTware ™	SMARTware — это простое в использовании программное обеспечение на базе Windows для использования с регистраторами времени использования DENT SMARTlogger. Его можно использовать для загрузки и анализа данных с инструментов SMARTlogger, настройки часов регистратора и экспорта записанных данных в виде файла CSV в Excel.
Трансформатор тока с разъемным сердечником	Трансформаторы тока с разъемным сердечником — это экономичный выбор трансформаторов тока. Как и другие трансформаторы тока, они обеспечивают линейное выходное напряжение, прямо пропорциональное входному току. Они безопасно и легко устанавливаются над существующими линиями электропередачи без отключения линий. Они производят 333 мВ на полную мощность и доступны для нагрузок до 1200 А. Они совместимы с приборами серий ELITEpro и PowerScout.
Подсчетчик	Подсчетчик относится к мониторингу потребления электроэнергии отдельным оборудованием в здании, таким как HVAC, освещение, охлаждение, кухонное оборудование и т. Д. В дополнение к счетчику «основной нагрузки», используемому коммунальными предприятиями Для определения общего потребления в здании при подсчетах используются индивидуальные «субсчетчики», которые позволяют руководителям зданий и объектов иметь представление об использовании энергии и производительности своего оборудования, создавая возможности для экономии энергии и капитальных затрат.Приборы серии PowerScout обычно используются для строительных проектов.
Испытания и измерения	В компании DENT термин «испытания и измерения» относится к категории продуктов, предназначенных для исследований в области измерений и верификации (M&V), профилирования электрических нагрузок, энергетических аудитов и оценки новых технологий. Продукция DENT Test & Measurement включает измерители серии ELITEpro и инструменты SMARTlogger.
Трехфазные системы	Трехфазные системы электроснабжения имеют как минимум три проводника, по которым проходят напряжения переменного тока, которые смещены во времени на одну треть периода (120 °).Трехфазная система может располагаться по схеме треугольника (Δ) или звезды. Приборы серий DENT ELITEpro и PowerScout предназначены для контроля как однофазных, так и трехфазных систем питания.
Время использования (TOU)	Время использования — это время включения определенной нагрузки. Например, как долго и в какое время был включен свет в той или иной комнате. Данные о времени использования можно собирать с помощью регистраторов DENT SMART (иногда называемых регистраторами DENT TOU).
Тороидальные ТТ с твердым сердечником	Тороидальные ТТ с твердым сердечником — это трансформаторы, в которых используются магнитные сердечники тороидальной (кольцевой или кольцевой) формы.Они состоят из круглого кольца или магнитного сердечника в форме пончика из ферромагнитного материала, такого как многослойное железо или феррит, вокруг которого наматывается провод. Поскольку сердечник сплошной (в отличие от разделенного сердечника), они требуют удаления существующих линий электропередач для установки. Поэтому они обычно используются в новых зданиях, чтобы свести к минимуму сбои. Серия DENT RGT — это тороидальные трансформаторы тока, разработанные для измерительных приложений уровня доходов IEEE.Они совместимы с измерителями серий ELITEpro и PowerScout.
Витая пара	Витая пара — это тип проводки, при котором два проводника одной цепи скручены вместе с целью подавления электромагнитных помех (EMI) от внешних источников. Этот тип проводки используется в некоторых трансформаторах тока DENT, включая трансформаторы тока с разъемным сердечником.
UL	UL (Underwriters Laboratory) — американская консалтинговая и сертификационная компания по безопасности.Они предоставляют услуги по сертификации, валидации, тестированию, инспектированию, аудиту, консультированию и обучению, связанным с безопасностью, широкому кругу клиентов, включая производителей. UL — это национально признанная испытательная лаборатория (NRTL). Некоторые инструменты и трансформаторы тока DENT внесены в списки UL (cULus), включая ELITEpro XC и PowerScout 3037, или признаны (cRUus), включая версии измерителей PowerScout HD только для платы.
VFD	Сокращение от Variable Frequency Drive.ЧРП — это тип привода с регулируемой скоростью, который используется в системах электромеханического привода для управления скоростью и крутящим моментом двигателя переменного тока путем изменения входной частоты и напряжения двигателя. Измерители мощности DENT могут измерять входную сторону частотно-регулируемого привода, но не выходную, поскольку частота не установлена ни на 60, ни на 50 Гц, а напряжение может не иметь синусоидальной формы.
Программное обеспечение ViewPoint ™	ViewPoint — это служебная программа, которая позволяет легко настраивать расходомер PowerScout.Он позволяет пользователю переключаться между протоколами связи (Modbus или BACnet), проверять измеряемые значения в реальном времени, считывать и записывать регистры, обновлять скалярные значения и выбирать трансформаторы тока. Он предоставляется без дополнительной оплаты при покупке измерителя PowerScout, а также доступен для бесплатной загрузки на веб-сайте DENT.
Звезда	Звезда — это трехфазная система напряжения с тремя фазами, подключенными к одной нейтральной точке (звезда).Это позволяет использовать два разных напряжения для всех трех фаз, например систему 277/480 В, которая обеспечивает 277 В между нейтралью и любой из фаз и 480 В между любыми двумя фазами.

Глоссарий терминов | Поддержка | Бесконтактные водонагреватели Takagi

AC: Переменный ток — Электропитание, при котором полярность горячего провода быстро меняется.
AGA: Американская газовая ассоциация.
Температура окружающей среды: Средняя температура атмосферы в непосредственной близости от прибора.
Ампер: Единица измерения силы тока.
Анодный стержень: Жертвенный стержень, состоящий из одного или нескольких металлов, установлен в водонагревателе, который защищает резервуар от коррозии, помогая продлить срок службы резервуара.
Клапан защиты от ожогов: Устройство, используемое для предотвращения высокой температуры воды.
ASHRAE: Американское общество инженеров по отоплению и охлаждению воздуха.
ASME: Американское общество инженеров-механиков.
Атмосферное горение: Горение происходит, когда газообразное, жидкое или твердое топливо реагирует при повышенной температуре с кислородом путем горения, выделяя тепло в открытой системе сгорания.

Точка кипения: Точка кипения относится к температуре, при которой жидкость превращается в пар за счет добавления тепла.
BTU: британских тепловых единиц.
Температура горелки: Средняя температура атмосферы в непосредственной близости от прибора.

Обратный клапан: Позволяет жидкости течь только в одном направлении в трубе; также известный как устройство предотвращения обратного потока.
Закрытая система: Система, в которой входящая холодная вода имеет устройство, не позволяющее воде расширяться при нагревании (например, обратный клапан, предохранитель обратного потока, некоторые редукционные клапаны и счетчики воды).
Коммерческое применение: Потребность в большем количестве воды, чем в доме на одну семью.
Конденсация: Избыточный водяной пар образуется при низких температурах продуктов сгорания. /Li>

Подъем на градус: Разница (дельта «Т») между начальной температурой воды и конечной температурой после завершения нагрева.
Прямая вентиляция: Забирает наружный воздух для горения и отводит дымовые газы непосредственно наружу.
Отводное устройство: Устройство, установленное в дымоходе газовой установки для предотвращения восходящего, нисходящего или вторичного засорения дымохода, препятствующего выходу продуктов сгорания или иным образом влияющих на нормальную работу прибора.
Сливной клапан: Устройство, предназначенное для слива сохраненного содержимого из водонагревателя. /Li>

EF: Коэффициент энергии — показатель общей эффективности водонагревателя, основанный на рекуперации, КПД, потерях в режиме ожидания и потребляемой энергии.
Эффективность: Мера способности продукта использовать входящую энергию; выражается в процентах.
Energy Guide Label: Федеральная торговая комиссия (FTC) требует, чтобы на газовых, электрических и масляных бытовых автоматических водонагревателях указывалась 1.) ориентировочная годовая стоимость эксплуатации для данной конкретной модели, основанная на средней стоимости по стране. топлива, указанного FTC и 2.) как эффективность этой модели сравнивается со всеми другими сопоставимыми моделями.

Расход: Номинальное значение в галлонах в минуту (GPM) или галлонах в час (GPH).
Дымоход: Проход для продуктов сгорания.

GAMA: Ассоциация производителей газового оборудования.
Gas Control: Устройство для регулирования давления газа в водонагревателе.

Жесткая вода: Природные воды содержат примеси в различных пропорциях; Традиционно жесткость — это мера кальция или растворенных твердых веществ в растворе.
Потеря напора: Давление воды, измеренное в указанной точке; он может измеряться в футах или фунтах на квадратный дюйм (PSI).
Теплообменник: Система теплопередачи.
Герц: Мера частоты; один герц равен одному циклу в секунду; 60 циклов переменного тока — 60 герц

Температура на входе: Температура воды на входе в резервуар.
Ввод: Количество топлива, израсходованного водонагревателем за заданный период времени; обычно рассчитывается за один час.

Киловатт: Мера скорости подачи энергии или мощности, равная 1000 Вт или 3412 БТЕ в час.

Life Cycle Labs: Место, где водонагреватели проходят ускоренные испытания для моделирования ожидаемого срока службы.
LP: Пропан жидкий — топливо для газовых водонагревателей.

Установка коллектора: Водонагреватели с параллельным или обратным потоком для больших потребностей в горячей воде.
Милл-вольт: Одна тысячная вольта.
Смесительный клапан: Смешивает холодную воду с горячей водой из водонагревателя для достижения заданной температуры подачи.

Природный газ: Топливо, поставляемое коммунальной системой распределения, используемое в газовых водонагревателях.

Эксплуатационные расходы: Стоимость эксплуатации водонагревателя в течение определенного периода времени.

Час максимальной нагрузки: Время, когда требуется наибольшая потребность в горячей воде.

Жилой: Водонагреватели для односемейных домов.

Предохранительный запорный клапан: Устройство на газовом приборе, которое перекрывает подачу газа для предотвращения опасной ситуации.Защитное отключение при исчезновении пламени срабатывает, когда пламя гаснет. 100% -ное отключение отключает весь газ, включая основные и пилотные горелки.
Поверхностный монтаж: Обычно относится к термостатам, установленным на внешней стороне поверхности резервуара, который измеряет температуру через стальной резервуар.

Водонагреватель без резервуара: Обычно известен как водонагреватель по требованию или в месте использования.
Повышение температуры: (Дельта «T») Число градусов по Фаренгейту (F), на которое необходимо поднять поступающую холодную воду, чтобы достичь желаемой температуры горячей воды.
Therm: Измерение 100 000 БТЕ.
Тепловой КПД: Способность передавать и поглощать тепло от источника топлива в воду.

UL: Underwriters Laboratories.

Вентиляционные материалы: Материалы, используемые для удаления выхлопных газов из жилища. т.е. ПВХ, ХПВХ, АБС, металл.
Вольт: Единица измерения электродвижущей силы.AC или DC.

Ватт: Единица электрической энергии или мощности; один ампер x один вольт = один ватт.

Каковы преимущества переменного тока?

Переменный ток (AC) — это определенная форма электрического тока, обычно используемая на предприятиях и в домах. В отличие от постоянного тока (DC), переменный ток возникает в результате движения электрических зарядов в определенном направлении, которое изменяется с течением времени в среде, такой как провод.Напротив, постоянный ток скользит только в одном направлении.

Каковы преимущества переменного тока?

Переменный ток — это ток, направление и величина которого периодически изменяются; это выражение также работает с переменным напряжением. Электрические принципы обычно применимы также к инженерному аспекту переменного тока; Однако следует учитывать несколько особенностей. Из различных возможных типов синусоидальная волна переменного тока имеет наибольшее значение.Основные преимущества переменного тока:

Экономичное и простое производство
Малоотходная передача энергии на большие расстояния
Простое преобразование в другие типы на основе принципа взаимной индукции
Синусоидальный тип не меняется основными компонентами, включая L, R и C

В соответствии с этими и другими преимуществами инженерный аспект переменного тока слишком важен. Если нужен постоянный ток (например,грамм. для работы большинства электронных инструментов), его можно просто создать с помощью выпрямителя на переменном токе. Переменный ток практически используется, особенно в электроэнергетике, благодаря множеству преимуществ. Это ток, направление и значение которого меняются в зависимости от частоты. Наибольшее значение имеет синусоидальная волна переменного тока. Если вы хотите более подробно ознакомиться с преимуществами переменного тока, посетите эту страницу.

Характеристики переменного тока

Переменный ток и переменное напряжение создаются в отдельных генераторах.Подробные пояснения представлены ниже.

При вращении катушки (представленной контуром проводника на следующей схеме) в магнитной цепи в этой катушке создается напряжение, по которому может протекать ток. Направление можно указать с помощью правила правой руки. При фиксированной скорости вращения направление и величина создаваемого напряжения зависят от местоположения проводящей петли.

Конструкция генератора переменного тока (Ссылка: itacanet.com )

Общее количество магнитного потока, проникающего в систему в горизонтальном положении, DF / Dt имеет наименьшее значение, а создаваемое напряжение равно нулю.Скорость перепада магнитного потока или DF / Dt максимальна в вертикальном положении, а создаваемое напряжение имеет наибольшее значение (вертикальное положение означает, что система параллельна магнитным полям). При большем вращении напряжение снова снижается и через половину цикла достигает значения нуля.

В следующем цикле напряжение изменяет свое направление и приближается к своему максимальному отрицательному значению в вертикальном формате. Начальное состояние снова достигается после одного полного цикла, напряжение упало до нуля, и может начаться другой период с точно таким же ходом.На рисунке ниже объясненные состояния представлены для некоторых выбранных точек проводника. Функция кривой подобна синусоиде.

Power Sine Wave (Ссылка: meettechniek.info )

Угол часто вводится путем измерения окружности; корреляция получается просто по длине окружности, включая радиус r = 1. Итак, длина окружности равна:

C = 2r \ pi = 2 \ pi

Перигон форма 360 °.

Значения напряжения и тока, представленные на последнем рисунке, представлены как цикл, колебание или волна. Каждая волна состоит из отрицательной и положительной полусекций. Требуемое время для полного оборота цикла проводника известно как продолжительность цикла или время колебания. Угловая скорость, с которой циркулирует цикл проводника, является основным углом, который петля определяет в конкретную единицу времени. При области 360 ° необходимо время цикла или T.Угловая скорость обычно вводится как угловая частота, выраженная через ω в инженерии, и рассчитывается как

\ omega = \ frac {2 \ pi} {T}

, где ω — угловая частота, а T — продолжительность цикла.

Угол в этом разделе вводится как фазовый угол или, кратко, фаза. Фаза — это член колебания, полученный в определенный момент времени, который восстанавливается через равные промежутки времени.

Количество волн или циклов, генерируемых за определенное время, называется частотой переменного тока или переменного напряжения (вводится буквой f).Чем выше продолжительность цикла, тем ниже частота. На следующей диаграмме показаны две различные диаграммы для определенной продолжительности. Частоту можно оценить следующим образом:

Переменные токи с разными частотами (Ссылка: barrowmoremrg.co )

f = \ frac {1} {T}

Единица частоты введена как Гц = Герц. немецкого физика Генриха Герца (1857 — 1894). Часто требуются следующие подблоки:

1 кГц = 1 килогерц, равный 103 Гц
1 МГц = 1 мегагерц, равный 106 Гц
1 ГГц = 1 гигагерц, равный 109 Гц

Другая редко используемая функция: электрическая волна — это длина волны, представленная (λ).Длина волны — это значение длины волны, обнаруженной в единицах измерения длины (например, м, км, см, мм). Поскольку электрическая энергия может быть измерена скоростью света или C = 300 000 км / с. Расстояние, на котором распространяется волна, можно оценить на основе основной частоты. Итак, мы имеем:

C = \ lambda f

После инверсии мы можем получить длину волны как

\ lambda = \ frac {C} {f}

Величина переменного тока или переменное напряжение можно измерить на основе синусоидальной волны, описанной ранее.Максимальное значение, возникающее при 270 ° и 90 °, называется максимальным значением, пиковым значением или амплитудой и определяется всеми другими значениями, которые являются очень непрерывными. Таким образом, он может быть другим в любое время, который вводится как мгновенные значения и выражается через u (или i).

Когда пиковое значение равно мгновенным значениям, его можно определить в любое время. Основное уравнение синусоидальной переменной волны:

u = sin (\ omega t)

, где u — мгновенное значение, пиковое значение, максимальное значение или амплитуда, а sin ωt — коэффициент синусоида под определенным углом.

Процессы переменного тока обычно представлены в виде диаграмм, которые представляют собой лучший обзор в дополнение к исключительно математическим уравнениям. Для этой цели особенно подходят векторные и линейные диаграммы.

Векторная диаграмма для определения преимуществ переменного тока

Переменный ток или переменное напряжение представлены вектором или указателем, способным циркулировать, длина которого соответствует максимальному значению. Этот вектор вращается против часовой стрелки с определенной угловой скоростью.Положение вектора в любой момент определяет расположение проводящей петли. Прямая линия проводится от кончика вектора к горизонтальной оси, которая пересекает середину круга, чтобы определить мгновенный ток или напряжение для любого подходящего положения.

Длина этой строки основана на мгновенном значении системы. Основное преимущество векторного представления — ясность; однако недостатком этой диаграммы являются особые условия, которые могут быть представлены только для нескольких выбранных моментов или для одного момента времени.

Линейная диаграмма, показывающая преимущества переменного тока

Переменный ток или переменное напряжение показано на синусоидальной диаграмме, по которой можно определить значения для всех вариаций. Форму линии можно улучшить с помощью векторной диаграммы следующим способом.

Сначала нужно провести горизонтальную линию рядом с векторной диаграммой. Эта линия разделена на участки, самый короткий из которых аналогичен длительности одного периода (T) или на определенные градусы до 360 ^o.Затем в этих точках разделения используются вертикальные линии, которые по размеру и направлению напоминают формы на векторном изображении. Синусоидальной волны можно добиться, когда соединение конечных точек вертикальных линий завершено. На следующем рисунке представлена эта конструкция.

Графическое представление переменного тока и переменного напряжения (Ссылка: toppr.com )

Основным преимуществом линейной диаграммы является возможность предоставления всех мгновенных значений; однако недостатком этого метода является ограниченная четкость, особенно когда необходимо представить несколько диаграмм.

Список основных преимуществ переменного тока

Эффективная передача энергии

Хотя вначале электрические форматы переменного и постоянного тока использовались для бесполезной передачи при использовании длинных линий, Tesla и Westinghouse использовали большие пути передачи напряжения пересмотрел эту проблему и представил одно из важных преимуществ переменного тока. Раньше мощность оценивалась для получения устойчивой передачи. Это связано с тем, что в проводах необходимо использовать сопротивление.Всякий раз, когда используется длинная линия передачи, энергия теряется. Из-за высокого напряжения, применяемого для обеспечения постоянного источника электроэнергии, и меньшего тока, проходящего через линию электропередачи, это также приводит к снижению потерь мощности.

Gives Power Generation

После изобретения системы переменного тока были произведены и генераторы переменного тока. Это положило начало изобретению генераторов переменного тока в гидроэлектрических формах, которые используются до сих пор.Они проще по сравнению с механическим производством постоянного тока и улучшают преимущества переменного тока.

Сделано возможное энергопотребление

При отсутствии щеток и коммутаторов, которые приборы постоянного тока используют для выработки электроэнергии, потребление энергии является одним из значительных преимуществ переменного тока. Первый индукционный генератор переменного тока был разработан Теслой в конце 1800-х годов и использовался вместе с переменным током. Это нововведение нашло свое применение в различных отраслях промышленности США.Теперь эта комбинация инженерных решений все еще используется в домашних хозяйствах и используется для мусороуборочных машин, электрических вентиляторов и, в частности, компрессоров для кондиционеров. Он также подходит для использования, чем его аналог.

Обеспечивает лучшее освещение

Лампы накаливания или лампы накаливания, которые практически сконструировал Томас Эдисон, могут работать как на постоянном, так и на переменном токе, но более современные люминесцентные лампы используют большое количество напряжения. В этих лампах используются такие газы, как аргон и пары ртути, а высокое напряжение позволяет генерировать ультрафиолетовый спектр.Переменный ток является более выгодной формой использования электроэнергии, особенно в связи с тем, что более компактные источники света, такие как люминесцентные лампы, становятся обычным явлением.

Более дешевый и доступный

Переменный ток также доступен в изобилии и вводится как менее дорогой. Доступность формы переменного тока лучше по сравнению с типом постоянного тока и дешевле, чем форма постоянного тока, которая также обеспечивает меньший ток. Эти два свойства делают его более практичным и подходящим, чем его аналог.

Электрооборудование — Глоссарий | Управление по охране труда и здоровья

Электрооборудование — Глоссарий | Управление по охране труда Перейти к основному содержанию

Опасность поражения электрическим током
Глоссарий

Глоссарий

Общее строительство

ANSI:: Американский национальный институт стандартов.
Утверждено:: Утверждено, одобрено, аккредитовано, сертифицировано или признано удовлетворительным должным образом учрежденным и признанным на национальном уровне органом или агентством.
Уполномоченное лицо:: Лицо, утвержденное или назначенное работодателем для выполнения определенного вида обязанностей или обязанностей или находящееся в определенном месте или местах на рабочем месте. См. Назначенное лицо .
Сертифицировано:: Оборудование считается «сертифицированным», если оно (а) было протестировано и признано национально признанной испытательной лабораторией соответствующим национально признанным стандартам или безопасным для использования определенным образом; или (b) относится к типу, продукция которого периодически проверяется признанной на национальном уровне испытательной лабораторией; и (c) на нем есть этикетка, бирка или другая запись о сертификации.
Компетентное лицо:: Лицо, способное идентифицировать существующие и предсказуемые опасности в окружающей среде или условия труда, которые являются антисанитарными, опасными или опасными для сотрудников, и кто уполномочен принимать быстрые корректирующие меры для их устранения.
Строительных работ:: Работы по строительству, перестройке и / или ремонту, включая малярные и отделочные работы.
Дефект:: Любая характеристика или состояние, которые имеют тенденцию ослаблять или уменьшать прочность инструмента, объекта или конструкции, частью которых они являются.
Назначенное лицо:: См.
Уполномоченное лицо
.
Сотрудник:: Каждый рабочий или механик, независимо от договорных отношений, которые могут предположительно существовать между рабочим и механиком и подрядчиком или субподрядчиком, который его нанял. «Рабочий» обычно означает человека, выполняющего физический труд или выполняющего работу, требующую физической силы; «Механик» обычно означает рабочего, владеющего инструментами.

Работодатель:: Подрядчик или субподрядчик.
Эквивалент:: Альтернативные конструкции, материалы или методы защиты от опасности, которые работодатель может продемонстрировать, обеспечат равную или большую степень безопасности для сотрудников, чем методы, материалы или конструкции, указанные в стандарте.
Опасное вещество:: Вещество, которое в силу своей взрывоопасности, легковоспламеняемости, ядовитости, коррозии, окисления, раздражения или иного вреда может вызвать смерть или травму.
Квалифицированное лицо:: Тот, кто, обладая признанной степенью, сертификатом или профессиональным статусом, или кто благодаря обширным знаниям, обучению и опыту успешно продемонстрировал свою способность решать или разрешать проблемы, связанные с предметом, работой или проектом .
Коэффициент запаса прочности:: Отношение предельной прочности на разрыв элемента, элемента материала или оборудования к фактическому рабочему напряжению или безопасной нагрузке при использовании.
SAE:: Общество автомобильных инженеров.
Телефон:: Обязательно.
Должен:: Рекомендуется.
Подходит:: То, что соответствует и обладает качествами или квалификациями, соответствующими данной цели, случаю, условию, функции или обстоятельствам.

Электрические происшествия

Ампер:: Единица измерения силы тока через проводник.
Арка:: Разряд электричества через газ, например воздух.
Крышка крепления:: См. Заглушка .
Схема:: Путь, по которому электрический ток течет от начала до конца, называется цепью. Схема включает в себя генератор или батарею, которая запускает ток, провода и любое электрическое устройство, с которым работает ток. Если какая-либо часть цепи удалена, ток не может течь.Тогда цепь разомкнута или разомкнута. Поскольку электрический ток стремится замкнуть свою цепь, он будет проходить по любому представленному пути (путь наименьшего сопротивления), поэтому люди подвергаются риску поражения электрическим током, когда они обращаются с поврежденными инструментами или шнурами или контактируют с неизолированными проводами. По сути, они становятся частью цепи.
Автоматический выключатель:: Защитное устройство, которое автоматически размыкает или отключает цепь без ущерба для себя, когда ток превышает заданный уровень.
Проводник:: Вещество или тело, которое позволяет электрическому току непрерывно проходить по нему. Металлы, такие как медь или алюминий, являются хорошими проводниками. В схеме токоведущие провода называют «проводниками», как в гибком шнуре.
Текущий:: Поток электронов через проводник, измеряется в амперах (амперах). Если ток течет вперед и назад по проводнику, он называется переменным током (AC).Если ток течет только в одном направлении, как в автомобильном аккумуляторе, это называется постоянным током (DC). Наиболее широко используется переменный ток, поскольку с его помощью можно увеличивать («повышать») или уменьшать («понижать») ток через трансформатор. Например, когда ток от воздушной линии электропередачи пропускается через трансформатор, установленный на опоре, он может быть понижен до нормального бытового тока. Кроме того, переменный ток может преодолевать огромные расстояния с небольшими потерями напряжения или мощности.
Цикл:: Когда переменный ток течет вперед и назад через проводник, говорят, что он циклически повторяется.В каждом цикле электроны текут сначала в одном направлении, затем в другом. В Соединенных Штатах нормальная скорость передачи энергии составляет 60 циклов в секунду или 60 Гц (Гц).
Обесточить:: Без каких-либо электрических подключений и / или электрического заряда.
Электричество:: Поток электронов атома через проводник.
Электрод:: Проводник, используемый для электрического контакта с неметаллической частью цепи.
Запитано:: Для пропуска электрического тока через проводник. Линии питания и провода могут быть намеренно включены (или отключены) для передачи тока к электрическому устройству. Но токопроводящие поверхности, которые непреднамеренно находятся под напряжением, такие как металлический корпус инструмента, металлический корпус монтажной коробки или металлический предмет, такой как алюминиевая лестница, представляют опасность поражения электрическим током.
Неисправность:: Нарушение изоляции, обнажающее электрифицированные проводники, что вызывает утечку тока и, возможно, поражение электрическим током.
Предохранитель:: Защитное устройство, позволяющее металлическому элементу стать частью цепи. Металл плавится под действием тепла, создаваемого чрезмерным током, тем самым прерывая цепь и не позволяя потоку электричества превысить допустимую нагрузку цепи.
GFCI (прерыватель цепи замыкания на землю):: Устройство, которое обнаруживает нарушение изоляции, сравнивая величину тока, протекающего к электрическому оборудованию, с величиной тока, возвращающегося от оборудования.Когда разница превышает 5 миллиампер, GFCI отключается и тем самым прерывает подачу электричества.
Земля:: Проводящее соединение, преднамеренное или непреднамеренное, между электрической цепью или оборудованием и землей или с некоторым проводящим телом, которое служит вместо земли.
Замыкание на землю:: Неисправность или нарушение изоляции провода, используемого для заземления.
Заземление:: Для предотвращения нарастания опасного напряжения в цепи путем создания пути с низким сопротивлением к земле или какой-либо другой заземляющей поверхности.
Охрана:: Размещение токоведущих частей электрооборудования там, где с ними нельзя случайно коснуться, например, в хранилище, за щитом или на приподнятой платформе, доступ к которой имеют только квалифицированные специалисты.

Импеданс:: Противодействие протеканию переменного электрического тока. См. Сопротивление .
Изоляция:: Непроводящие материалы, используемые для покрытия или окружения проводника, позволяющие обращаться с ним без опасности поражения электрическим током.
Изолятор:: Любой материал, например стекло или резина, препятствующий прохождению электрического тока.
Киловатт:: Тысяча ватт.
Блокировка:: Для блокировки переключателя в положении «выключено» с помощью висячего замка или для блокировки электрифицированного оборудования за запертой дверью, ключ от которой есть только у квалифицированного персонала.
Низкое сопротивление:: Низкое сопротивление току переменного тока.
Миллиампер:: Единица измерения, равная одной тысячной (1/1000) ампера.
Ом:: Единица измерения сопротивления электрическому току. Из закона Ома (Ток = Напряжение / Сопротивление или, другими словами, Ток = Напряжение / Ом) математическое выражение взаимосвязи между этими тремя элементами.
Максимальный ток:: Любой ток, превышающий номинальную мощность оборудования или проводника.
Фаза:: В системах питания переменного тока ток нагрузки берется из источника напряжения, который обычно принимает форму синусоидальной волны. В идеале ток, потребляемый нагрузкой в системе, также является синусоидальной волной. С простой резистивной нагрузкой, такой как лампочка, синусоидальная волна тока всегда совпадает с синусоидальной волной напряжения. Это называется однофазным. Однофазная система питания обычно использует три провода, называемые горячим, нейтральным и заземляющим, и напряжение обычно составляет 120/240.Большинство торговых точек для дома и офиса работают именно так. С некоторыми нагрузками, такими как двигатели, и в системах высокого напряжения, синусоидальная волна тока намеренно задерживается и отстает от синусоидальной волны напряжения. Величина этого запаздывания выражается в градусах и называется разностью фаз. Типичным примером является трехфазное питание, когда система имеет три «горячих» провода, каждый из которых на 120 градусов не совпадает по фазе друг с другом.
Штекер:: Устройство, к которому прикреплены проводники шнура, которое используется для соединения с проводниками, постоянно прикрепленными к розетке.
Полярность:: Взаимосвязь между полюсами положительного и отрицательного заряда, особенно в отношении проводки проводов, где незаземленный (горячий) провод и заземленный (нейтральный) провод образуют цепь.
Квалифицированное лицо:: Один, знакомый с конструкцией и эксплуатацией оборудования, а также с соответствующими опасностями.
Рейтинг:: Заявленный рабочий предел единицы оборудования, выраженный в таких единицах измерения, как вольты или ватты.
Дорожка:: Канал, специально предназначенный для удержания проводов, кабелей или шин, включая кабелепровод, трубки, кабельные каналы, шинопроводы, желоба или молдинги.
Емкость:: Устройство, такое как розетка или розетка, к которому присоединяются проводники и где вилка контактирует с источником электрического тока.
Сопротивление:: Все, что препятствует прохождению электричества, особенно постоянного (DC) тока.Сопротивление измеряется в Ом .
Метка:: Для идентификации электрооборудования по классу, группе и температурному диапазону, для которого оно одобрено.
Вольт:: Единица измерения электрической силы или давления.
Напряжение:: Основная сила или давление, заставляющее электричество проходить через проводник. Измерено в вольт .
Ватт:: Единица измерения электрической энергии, или способности электричества выполнять работу. Тысяча ватт или один киловатт равняются 1,34 лошадиным силам.

Водопад

Подмости регулируемые:: Подвесные подмости, оборудованные подъемником, которым может управлять работник на подмостях.
Анкоридж:: Надежная точка крепления страховочных тросов, строп или устройств замедления.
Кузовной ремень:: Ремешок со средствами как для его крепления на талии, так и для прикрепления к шнурку, страховочному тросу или устройству замедления. (С 1 января 1998 г. ремни для тела неприемлемы как часть системы индивидуальной защиты от падения.)
Обвесы:: Ремни, которые могут быть закреплены вокруг сотрудника таким образом, чтобы распределять силу защиты от падения, по крайней мере, на бедра, таз, талию, грудь и плечи, со средствами для прикрепления их к другим компонентам индивидуальной системы защиты от падения.
Стяжка:: Жесткое соединение, которое удерживает один элемент лесов в фиксированном положении по отношению к другому элементу или к зданию или конструкции. См. Поперечные распорки .
Шпилька:: Структурный блок, используемый в конце платформы для предотвращения соскальзывания платформы с опор. Шипы также используются для обеспечения опоры на наклонных поверхностях, таких как доски для ползания.
Разъем:: Устройство, которое используется для соединения (соединения) частей персональной системы защиты от падения и систем устройства позиционирования вместе.Это может быть независимый компонент системы, такой как карабин, или он может быть неотъемлемым компонентом части системы, такой как пряжка или D-образное кольцо, вшитые в пояс или привязь, или карабин, сращенный или пришивается к шнурку или самозатягивающемуся шнурку.
Зона контролируемого доступа (CAZ):: Зона, в которой определенные работы (например, кладка кирпича сверху) могут проводиться без систем ограждений, индивидуальных систем защиты от падения или систем безопасности, а доступ в зону контролируется.
Крестовины:: Две скобы, пересекающиеся в форме буквы X.
Устройство замедления:: Любой механизм, такой как веревочный захват, шнур с протяжным швом, шнурок из специальной ткани, разрывной или деформирующийся шнур, автоматический самовтягивающийся страховочный трос / шнур и т. Д., Который служит для рассеивания значительного количества энергии во время остановки падения. или иным образом ограничить энергию, прикладываемую к сотруднику во время остановки падения.
Дистанция замедления:: Дополнительное расстояние по вертикали, которое проходит падающий сотрудник, исключая удлинение страховочного троса и расстояние свободного падения, до остановки от точки, в которой устройство замедления начинает работать. Он измеряется как расстояние между местоположением ремня безопасности сотрудника или точки крепления ремня безопасности в момент активации (в начале действия силы остановки падения) устройства замедления во время падения и местоположением этой точки крепления после падения. сотрудник приходит к полной остановке.
Строительные каркасные леса:: Строительные леса, состоящие из платформ, поддерживаемых на сборных концевых рамах со встроенными стойками, горизонтальными опорами и промежуточными элементами.
Отказ:: Отказ от нагрузки, поломка или разделение составных частей. Отказ от нагрузки — это точка превышения предела прочности.
Свободное падение:: Падение до того, как персональная система защиты от падения начинает применять силу для остановки падения.
Дальность свободного падения:: Вертикальное смещение между началом падения и непосредственно перед тем, как система защиты от падения начинает применять силу для остановки падения. Это расстояние не включает расстояние замедления и удлинение страховочного троса / стропа, но включает любое расстояние скольжения устройства замедления или самовтягивающийся спасательный трос / строп до того, как они сработают и возникнут силы остановки падения.
Система ограждений:: Установлен барьер для предотвращения падения сотрудников на нижние уровни.
отверстие:: Зазор или пустота 2 дюйма (5,1 см) или более по наименьшему размеру в полу, крыше или другой поверхности для ходьбы / работы.
Подъемник:: Механическое устройство с ручным или механическим приводом для подъема или опускания подвесных лесов.
Невыполнимо:: Невозможно выполнить строительные работы с использованием обычной системы защиты от падения (т. Е. Системы ограждений, системы защиты или индивидуальной системы защиты от падения) или технологически невозможно использовать любую из этих систем для защиты от падения.
Стенд для лестницы:: Мобильная самонесущая лестница фиксированного размера, состоящая из широкой плоской ступеньки в виде лестницы.
Посадка:: Платформа в конце лестничного марша.
Ремешок:: Гибкая веревка, трос или ремень, который обычно имеет соединитель на каждом конце для соединения поясного ремня или ремня безопасности с устройством замедления, страховочным тросом или креплением.
Передняя кромка:: Край пола, крыши или опалубки для пола или другой пешеходной / рабочей поверхности (например, настила), которая меняет свое местоположение при размещении, формировании или строительстве дополнительных секций пола, крыши, настила или опалубки. Передняя кромка считается «незащищенной стороной и кромкой» в периоды, когда она не ведется активно и непрерывно.
Линия жизни:: Компонент, состоящий из гибкого троса, вертикально соединенного с анкерным креплением на одном конце (вертикальный страховочный трос) или соединенного горизонтально с анкерными креплениями на обоих концах (горизонтальный страховочный трос), и который служит средством для соединения других компонентов индивидуальной системы защиты от падения. до якорной стоянки.
Крыша пологая:: Крыша с уклоном от 4 до 12 (от вертикального к горизонтальному) или меньше.
Нижние уровни:: Те участки или поверхности, на которые сотрудник может упасть. Такие области или поверхности включают, помимо прочего, уровни земли, этажи, платформы, пандусы, взлетно-посадочные полосы, выемки, котлованы, резервуары, материал, воду, оборудование, конструкции или их части.
Максимальная предполагаемая нагрузка:: Суммарная нагрузка всех людей, оборудования, инструментов, материалов, передаваемых нагрузок и других нагрузок, которые, как разумно предполагалось, могут быть применены к лесам или их компонентам в любой момент времени.

Открытие:: Зазор или пустота высотой 30 дюймов (76 см) или более и шириной 18 дюймов (48 см) или более в стене или перегородке, через которую сотрудники могут упасть на более низкий уровень.
Открытых сторон и торцов:: Края платформы, которые находятся на расстоянии более 14 дюймов (36 см) по горизонтали от прочной, непрерывной вертикальной поверхности (например, стены здания) или прочной непрерывной горизонтальной поверхности (например, пола), или точки доступа.Исключение: для штукатурных работ и обрешетки горизонтальное пороговое расстояние составляет 18 дюймов (46 см).
Кладка кирпича сверху:: Процесс укладки кирпичей и блоков каменной кладки таким образом, чтобы соединяемая поверхность стены находилась на стороне стены, противоположной каменщику, при этом каменщик должен наклоняться над стеной для завершения работы. Сопутствующие работы включают уход за камнем и электромонтаж в кирпичной стене во время процесса кладки кирпича сверху.
Персональная система защиты от падения:: Система, используемая для остановки сотрудника при падении с рабочего уровня. Он состоит из крепления, соединителей, ремня безопасности и может включать шнур, устройство замедления, страховочный трос или подходящие их комбинации. С 1 января 1998 года использование поясного ремня для защиты от падения запрещено.
Платформа:: Рабочая поверхность приподнята над нижними уровнями. Платформы могут быть построены из отдельных деревянных досок, сборных досок, сборных настилов и сборных платформ.
Система устройства позиционирования:: Ремень для тела или система привязных ремней, позволяющая поддерживать сотрудника на возвышенной вертикальной поверхности, например на стене, и работать с двумя свободными руками, опираясь на него.
Номинальная нагрузка:: Максимальная нагрузка, указанная изготовителем для подъема подъемником или приложения к строительным лесам или их компонентам.
Трос:: Устройство замедления, которое перемещается по страховочному тросу и автоматически за счет трения захватывает страховочный трос и блокируется, чтобы предотвратить падение сотрудника.В канатном грейфере обычно используется принцип инерционной блокировки, блокировки кулачка / уровня или того и другого.
Крыша:: Наружная поверхность на крыше здания. Сюда не входят полы или опалубка, которые, поскольку здание не завершено, временно становятся верхней поверхностью здания.
Кровельные работы:: Подъем, хранение, установка и удаление кровельных материалов и оборудования, включая соответствующую изоляцию, листовой металл и пароизоляционные работы, за исключением конструкции кровельного покрытия.
Система контроля безопасности:: Система безопасности, в которой компетентное лицо отвечает за распознавание и предупреждение сотрудников об опасности падения.
Строительные леса:: Любая временная приподнятая платформа (поддерживаемая или подвешенная) и ее поддерживающая конструкция (включая точки крепления), используемые для поддержки сотрудников или материалов или того и другого.
Самовтягивающийся страховочный трос / строп:: Устройство замедления, содержащее намотанный на барабан строп, который может медленно извлекаться из барабана или втягиваться на него при небольшом натяжении во время нормального движения работника, и которое после начала падения автоматически блокирует барабан и останавливает падение.
Snaphook:: Соединитель, состоящий из крючкообразного элемента с нормально закрытым держателем или аналогичной конструкции, который может открываться, чтобы крючок мог принять объект, и при отпускании автоматически закрывается, чтобы удерживать объект. Snaphooks, как правило, одного из двух типов: тип блокировки с самозакрывающимся, самоблокирующимся держателем, который остается закрытым и заблокированным до тех пор, пока не будет разблокирован и нажат открытым для подключения или разъединения; или неблокирующего типа с самозакрывающимся держателем, который остается закрытым до тех пор, пока не будет нажат для подключения или разъединения.С 1 января 1998 года использование незафиксируемого карабина в составе персональных систем защиты от падения и систем позиционирования запрещено.
Лестничная башня (подмости / башня):: Башня, состоящая из элементов строительных лесов и содержащая внутренние лестничные клетки и площадки для отдыха. Эти башни используются для обеспечения доступа к платформам строительных лесов и другим возвышениям, таким как перекрытия и крыши.
Крутая крыша:: Крыша с уклоном более 4 дюймов 12 (от вертикального к горизонтальному).
Ходули:: Пара шестов или аналогичных опор с приподнятыми подножками, позволяющая ходить по земле или рабочей поверхности.
Носок:: Низкий защитный барьер, который предотвратит падение материалов и оборудования на более низкие уровни и обеспечит защиту персонала от падений.
Подмости сварно-рамные трубчатые:: См. Строительные каркасные леса .
Незащищенные стороны и края:: Любая сторона или край (кроме входов в точки доступа) пешеходной / рабочей поверхности, например, пол, крыша, пандус или взлетно-посадочная полоса, где нет стен или системы ограждений высотой не менее 39 дюймов (1,0 м).
Неустойчивых объектов:: Предметы, прочность, конфигурация или отсутствие устойчивости которых могут привести к их смещению и смещению и, следовательно, не могут должным образом выдерживать прилагаемые к ним нагрузки.Неустойчивые объекты не являются безопасной базовой опорой для строительных лесов, платформ или сотрудников. Примеры включают, но не ограничиваются, бочки, ящики, сыпучие кирпичи и бетонные блоки.
Прогулочная / рабочая поверхность:: Любая горизонтальная или вертикальная поверхность, по которой ходит или работает сотрудник, включая, помимо прочего, полы, крыши, пандусы, мосты, взлетно-посадочные полосы, опалубку и железобетонную арматуру, за исключением лестниц, транспортных средств или трейлеров. , на котором должны находиться сотрудники для выполнения своих служебных обязанностей.
Проход:: Часть платформы лесов, используемая только для доступа, а не в качестве рабочего уровня.
Система предупреждающих линий:: Барьер, установленный на крыше, чтобы предупредить сотрудников о приближении к незащищенной стороне или краю крыши, и который обозначает зону, в которой могут проводиться кровельные работы без использования ограждения, ремня безопасности или систем безопасности для защиты сотрудников в площадь.

Застраховано

Колодка:: Клин, блок или большой камень, помещенный против шин транспортного средства для предотвращения его движения, особенно на уклоне.
Опалубка:: Полная система опор для свежеуложенного или частично затвердевшего бетона, включая форму или защитное покрытие (форму), которые контактируют с бетоном, а также все опорные элементы, включая берега, опоры, крепежные детали, распорки и сопутствующее оборудование.
Поддомкрачивание:: Задача подъема плиты (или группы плит вертикально из одного места в другое (например, из места литья во временное (припаркованное) место или до его окончательного местоположения в конструкции) во время строительства здания / конструкция, в которой используется процесс подъемно-плитного перекрытия.
Подъемная плита:: Метод бетонного строительства, при котором плиты перекрытия и крыши заливаются на уровень земли или на уровне земли и поднимаются на место с помощью домкратов.
Зона ограниченного доступа:: Строящаяся территория рядом с каменной стеной, четко разграниченная для ограничения доступа сотрудников.
Сборный бетон:: Бетонные элементы (такие как стены, панели, плиты, колонны и балки), которые были сформированы, отлиты и отверждены перед окончательным размещением в конструкции.

Перешоринг:: Строительная операция, при которой размещается опалубочное оборудование (также называемое оборудованием для перебазирования или перекладывания) после удаления исходных форм и опор для поддержки частично затвердевшего бетона и строительных нагрузок.
Конструкция защиты при опрокидывании (ROPS):: Конструкции транспортных средств, такие как поперечные дуги, рамы, кабины для защиты от опрокидывания и т. Д., Предназначенные для предотвращения раздавливания оператора транспортного средства в результате опрокидывания.
Ремень безопасности:: Устройство, обычно носимое на талии, состоящее из ремня или ремней, прикрепленных к транспортному средству, чтобы удерживать человека на его сиденье.
Берег:: Опорный элемент, который противостоит сжимающей силе, создаваемой нагрузкой; или операция, с помощью которой размещается опорный элемент.
Вертикальные скользящие формы:: Опалубки, которые поднимаются вертикально во время укладки бетона.

Разработка траншей и земляных работ

Отверстие в нижней части пирса:: Тип шахты или выемки фундамента, дно которой выполнено больше, чем поперечное сечение, указанное выше, чтобы сформировать форму с куполом.
Скамья (система скамей):: Метод защиты сотрудников от обвалов путем выкапывания боковых сторон котлована с образованием одного или ряда горизонтальных уровней или ступеней, обычно с вертикальными или почти вертикальными поверхностями между уровнями.
Обвал:: Отделение массы грунта или скального материала со стороны выемки, или выпадение грунта из-под траншейного щита или опорной системы, и его внезапное перемещение в выемку в результате падения или скольжения в достаточном количестве, чтобы что он может заманить в ловушку, закопать или иным образом повредить или обездвижить человека.
Крестовины:: Горизонтальные элементы опорной системы, установленные перпендикулярно сторонам котлована, концы которых упираются либо в стойки, либо в выступ.
Раскопки:: Любые искусственные выемки, впадины, траншеи или впадины на поверхности земли, образованные в результате удаления земли.
Лица:: Вертикальные или наклонные поверхности земли, образовавшиеся в результате земляных работ.
Отказ:: Разрушение, смещение или остаточная деформация конструктивного элемента или соединения с целью снижения его структурной целостности и поддерживающих способностей.
Опасная атмосфера:: Атмосфера, которая из-за того, что является взрывоопасной, легковоспламеняющейся, ядовитой, коррозионной, окисляющей, раздражающей, с недостатком кислорода, токсичной или другой вредной, может вызвать смерть, болезнь или травму.
Защитная система:: Метод защиты сотрудников от обвалов, от материала, который может упасть или скатиться с выемки или в котлован, или от обрушения соседних построек.Защитные системы включают в себя опорные системы, системы наклона и опоры, системы щитов и другие системы, обеспечивающие необходимую защиту.
Пандус:: Наклонная пешеходная или рабочая поверхность, которая используется для доступа к одной точке из другой и построена из земли или из конструкционных материалов, таких как сталь или дерево.
Зарегистрированный профессиональный инженер:: Лицо, зарегистрированное в качестве профессионального инженера в штате, в котором будут выполняться работы.Однако профессиональный инженер, зарегистрированный в любом штате, считается «зарегистрированным профессиональным инженером» в значении настоящего стандарта при утверждении проектов «изготовленных защитных систем» или «табличных данных» для использования в торговле между штатами.
Защитное покрытие:: Элементы опорной системы, которые удерживают землю на месте и, в свою очередь, поддерживаются другими элементами опорной системы.
Щит (система щитов):: Конструкция, способная противостоять силам, приложенным к ней в результате обрушения, и тем самым защищать сотрудников внутри конструкции.Щиты могут быть постоянными конструкциями или могут быть сконструированы так, чтобы их можно было переносить и перемещать по ходу работы. Кроме того, экраны могут быть изготовлены заранее или изготовлены на заказ в соответствии с 29 CFR 1926.652 (c) (3) или 29 CFR 1926.652 (c) (4). Щиты, используемые в траншеях, обычно называют «окопными ящиками» или «окопными щитами».

Опалубка (Система опор):: Конструкция, такая как металлическая гидравлическая, механическая или деревянная опорная система, которая поддерживает стороны выемки и предназначена для предотвращения провалов.
Сторон:: См. Лица .
наклонная (наклонная система):: Метод защиты сотрудников от обвалов путем выемки грунта для формирования сторон выемки, наклоненных в сторону от выемки, чтобы предотвратить обвал. Угол наклона, необходимый для предотвращения обрушения, зависит от таких факторов, как тип почвы, условия воздействия окружающей среды и приложение дополнительных нагрузок.
Спойл:: Грязь, камни и другие материалы, извлеченные из раскопок и временно или навсегда отложенные в сторону.
Стабильная порода:: Природный твердый минеральный материал, который можно раскапывать с вертикальными стенками и который останется нетронутым при обнажении. Нестабильная порода считается стабильной, если скальный материал на стороне или сторонах выемки защищен от обрушения или смещения анкерными болтами или другой защитной системой, разработанной зарегистрированным профессиональным инженером.
Структурный пандус:: Пандус, сделанный из стали или дерева, обычно используется для подъезда транспортных средств. Пандусы из грунта или камня не считаются конструкционными пандусами.
Система поддержки:: Конструкция, такая как опора, распорка или опора, которая обеспечивает опору для соседней конструкции, подземной установки или сторон выемки.
Табличные данные:: Таблицы и схемы, утвержденные зарегистрированным профессиональным инженером и используемые для проектирования и создания защитной системы.
Траншея (выемка траншеи):: Узкая выемка (относительно ее длины), сделанная под поверхностью земли. Как правило, глубина превышает ширину, но ширина траншеи (измеренная по дну) не превышает 15 футов (4,6 м).
Траншейный ящик:: См. Щит (система защиты) .
Траншейный щит:: См. Щит (система защиты) .
стойки:: Вертикальные элементы опалубочной системы траншей находятся в контакте с землей и обычно располагаются таким образом, чтобы отдельные элементы не касались друг друга.
Уэльс:: Горизонтальные элементы опорной системы, размещенные параллельно забое выемки, стороны которых упираются в вертикальные элементы опорной системы или грунт.

AC vs DC Power

Вы когда-нибудь слышали о легендарной металлической группе AC / DC? Вы знаете, что означает это название? Это может показаться немного странным, но на самом деле это означает электрические токи AC (переменный ток) и DC (постоянный ток).Идея названия происходит от инициалов «AC / DC» на швейной машине. Итак, что такое AC / DC и почему важно знать разницу?

Определения

Диаграмма, показывающая, как постоянный и переменный ток протекают в цепи.

Электропитание переменного тока — переменный ток, известный как переменный ток, представляет собой электрический ток с электрическими зарядами, который периодически течет в обратном направлении. Это наиболее распространенная и наиболее предпочтительная электроэнергия, поставляемая предприятиям и жилым домам. Это связано с тем, что напряжение может быть изменено через трансформатор в соответствии с передачей.Впервые он был протестирован с динамо-электрическим генератором , который был основан на принципах Майкла Фарадея и сконструирован Ипполитом Пикси в 1832 году. математическая кривая, описывающая повторяющиеся колебания или, проще говоря, изогнутые линии), используемая в качестве метки. Это представляет собой электрический цикл и измеряется в соответствии с его циклами в секунду, поэтому каждый раз, когда ток движется в одном направлении, обратно к самому себе, он считается одним полным циклом.Это дает вам единицу измерения « Гц или Гц». Если взять типичную частоту, используемую в Европе, 50 Гц, что соответствует 60 циклам в секунду.

Примечание. Переменный ток обычно используется в домах и на производстве с мощностью от 120 до 240 вольт.

Питание постоянного тока — Постоянный ток, известный как постоянный ток ( Ранее гальванический ток ), постоянный ток — это электрический ток с электрическими зарядами, который течет в одном направлении. Из-за этого легче понять электрический поток из-за его постоянного напряжения / тока.Обычно он используется для зарядки аккумуляторов и в качестве источника питания для электрических устройств. Оглядываясь назад на нашу историю, вы, вероятно, уже слышали об имени Thomas Edison , который представил первую электрическую установку, принадлежащую инвестору, в 1882 году и осуществил первую коммерческую передачу электроэнергии в середине 1950-х годов.

Питание постоянного тока можно определить по комбинированному знаку «плюс» и «минус», по прямой или пунктирной линии. В отличие от мощности переменного тока, мощность постоянного тока не возвращается туда, откуда она была начата, поэтому частота ее электрического цикла недействительна или равна нулю.

Примечание. Постоянный ток обычно хранится в аккумуляторах, напряжение которых может достигать 12 В (из-за широкой доступности оборудования на 12 В).

Мощность переменного тока и мощность постоянного тока

В чем разница между мощностью переменного и постоянного тока? Хотя это технически сложно понять, на нескольких примерах вы по крайней мере будете иметь представление о том, что есть что, а что есть что.

Если вы читаете это, скорее всего, вы используете ноутбук, настольный компьютер или мобильное устройство. Если вы используете ноутбук, то можно с уверенностью сказать, что вы используете как переменный, так и постоянный ток, и вот простое объяснение.Сопло или вилка, которые подключают ваш ноутбук к розетке, используют переменный ток, но когда ток действительно достигает вашего ноутбука, адаптер питания преобразует переменный ток в постоянный. То же самое и с вашими мобильными устройствами. С другой стороны, у настольных компьютеров есть блоки питания, которые могут выдерживать переменный ток, постоянный ток или даже оба. Это действительно зависит от того, какой источник питания вы используете.

Подводя итог, переменный ток имеет переменный ток 50 или 60 Гц (в зависимости от местоположения), а постоянный ток — нет. Течение переменного тока обратимо, в то время как постоянный ток может течь только в одном направлении.Переменный ток может передавать ток на большие расстояния и обеспечивать больше энергии, в то время как постоянный ток может передавать только ограниченную энергию. И, наконец, переменный ток предпочтительнее в домах и на производстве, тогда как постоянный ток более предпочтителен для электрических устройств, которые питаются от топливных элементов, батарей и генераторов.

Примечание. Под переменным / постоянным током понимается устройство, которое может работать от любого типа тока.

Сравнительная таблица

Питание переменного тока	Питание постоянного тока
Имеет частоту (50 Гц / 60 Гц)	Без частоты
Безопаснее использовать на больших расстояниях	Безопасно использовать только на коротких расстояниях
Обратимое направление тока	Одно направление тока
Представлено в виде изогнутой линии	Представлен как прямая линия / линии
Рекомендуется для использования дома или в бизнесе	Рекомендуется для электрических устройств, которые используют батареи или топливные элементы

(PDF) Разработка устройства контроля линии переменного тока (AC) для Управление энергосистемой

Нигерийский журнал чистой и прикладной физики, Vol.9, № 1, страницы 17–22, 2019

Пространственное изменение частоты, полученное из National Grid с помощью стандартного частотомера

49,7

49,8

49,9

50,1

50,2

50,3

15:17:24

15:17:48

15:18:12

15:18:36

15:19:01

15:19:25

15:19 : 49

15:20:13

15:20:37

15:21:01

15:21:24

15:21:48

Частота (Гц)

Время (с)

3.ИСПЫТАНИЯ, КАЛИБРОВКА И ПРОИЗВОДИТЕЛЬНОСТЬ

ОЦЕНКА

Каждый блок разработанного устройства контроля переменного тока, показанный на рис. 8

, был соединен вместе с помощью гибких кабелей. Полная компоновка разработанного устройства

была протестирована

путем подключения его к источнику переменного тока (переменного тока). Также

цифровой мультиметр Mastech 6205 использовался вместе с

разработанным устройством для измерения переменного напряжения от сети питания

в лаборатории физического факультета Федерального технологического университета

, Акуре.Выходное напряжение

из схемы аттенюатора устройства было

, настроенное с помощью резистора шкалы, подключенного к его выходу

, до тех пор, пока его значение не станет эквивалентным значению, отображаемому на измерителе Mastech

. Два устройства были оставлены для тестирования на 5 минут, и через каждые 30 секунд регистрировалось

показаний. И

результат измерения указан в таблице 1. Для измерения частоты

блок частоты устройства

также был откалиброван с помощью стандартной частоты переменного тока

метр.Два устройства были подключены к источнику переменного напряжения

одновременно для контроля частоты сети

электросети для проверки функциональности и производительности

разработанного устройства. Измерение производилось в течение 5

минут и регистрировалось с интервалом в 1 секунду. Графики результатов измерений

представлены на

рисунках 11 и 12.

4. РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Показания из таблицы 1 ясно показывают значения напряжения питания переменного тока

, полученные блоком считывания напряжения. устройства контроля переменного тока, разработанного

, и стандартного цифрового вольтметра

.Результаты измерения напряжения питания

, полученные разработанным прибором и стандартным цифровым вольтметром

, сравнивались с целью определения его достоверности по

В этом случае значения напряжения питания, полученные

от стандартного цифрового вольтметра, были нанесены на график

в сравнении со значениями напряжения питания, полученными от устройства мониторинга переменного тока, разработанного

, как показано на рисунке 10; по номеру

проверьте корреляцию инструментов.

Как и на графике, наклон графика был 1,002, а

регрессия R2 была рассчитана равной 0,9998; который показывает

, что корреляция между блоком считывания напряжения разработанного устройства

и стандартным цифровым вольтметром

оказалась очень близкой к единице, это говорит о том, что значения

из блока считывания напряжения Разработанное устройство

оказалось высоконадежным.

Также из показаний, представленных в таблице 1, отклонение

блока отсчета напряжения разработанного прибора

от стандартного цифрового вольтметра составило

± 0,21%, что пока очень незначительно. Графики, показанные

на рисунках 11 и 12, показывают пространственное изменение основной частоты

, полученное от энергосистемы Нигерии, как

, измеренное разработанным устройством и стандартным частотомером

.Из максимального и минимального значения

точек графиков было замечено, что уровень частотного теста

, измеренный разработанным прибором, колеблется в пределах

допустимых пределов + 0,62% и -0,20%, что соответствует

49,90-50,31. Гц, а тестовый уровень стандартного частотомера

показывает изменение частоты + 0,54%, а

-0,22%, что соответствует 49,89-50,27 Гц. Из этих значений

было обнаружено, что уровень частотного теста, измеренный

разработанным устройством, тесно связан с тестовым уровнем частоты

, измеренным стандартным частотомером.Из

диапазон уровня частотного теста, измеренного устройством,

было замечено, что устройство может измерять частоту сети

в диапазоне 49,0-51 Гц. Поэтому результат от

устройство очень надежное.

5. ЗАКЛЮЧЕНИЕ

В данной статье представлена разработка устройства мониторинга переменного тока

на базе микроконтроллера

для управления энергосистемой.Результаты, продемонстрированные

, доказали, что устройство

удовлетворительно работает с проектными схемами и микроконтроллером Arduino в качестве ядра

устройства. Устройство может измерять как частоту

, так и уровень напряжения в электросети, и оно относительно дешевле

и предлагает лучшую замену дорогостоящему стандартному частотомеру

, доступному на рынке, поскольку устройство

было изготовлено и собрано из недорогие

материалов местного производства.Результаты показывают, что устройство

удовлетворяет требованиям общей конструкции с блоком считывания напряжения

устройства, имеющим отклонение

± 0,21% от стандартного вольтметра Mastech.

Основные величины, характеризующие переменный ток

Наша продукция

Форма сигнала

Добавить комментарий

Максимальная частота переменного тока. Основные параметры переменного тока

Единицы измерения

Как измерить частоту?

Период колебаний.

Частота колебаний.

Формулы для вычисления частоты дискретных событий, частота вращения

Примеры задач с решением

Что показывает частота переменного тока. Отличие переменного тока от постоянного

Определение постоянного электрического тока, его источники

Принцип работы переменного тока

Как переменный ток сделать постоянным

Преобразователь постоянного тока в переменный

Охарактеризуйте параметры переменного тока: период, частота, амплитуда, начальная фаза.

Phys 3041 Notes — D

Phys 3041 Заметки

Анализ цепей переменного тока

Резисторы в цепях переменного тока

Конденсаторы

Глоссарий общих терминов измерения электроэнергии и мощности

Глоссарий терминов | Поддержка | Бесконтактные водонагреватели Takagi

Каковы преимущества переменного тока?

Электрооборудование — Глоссарий | Управление по охране труда и здоровья

Глоссарий

Общее строительство

Электрические происшествия

Водопад

Застраховано

Разработка траншей и земляных работ

AC vs DC Power

Определения

Мощность переменного тока и мощность постоянного тока

Сравнительная таблица

(PDF) Разработка устройства контроля линии переменного тока (AC) для Управление энергосистемой

Добавить комментарий Отменить ответ