Равномерное движение по окружности
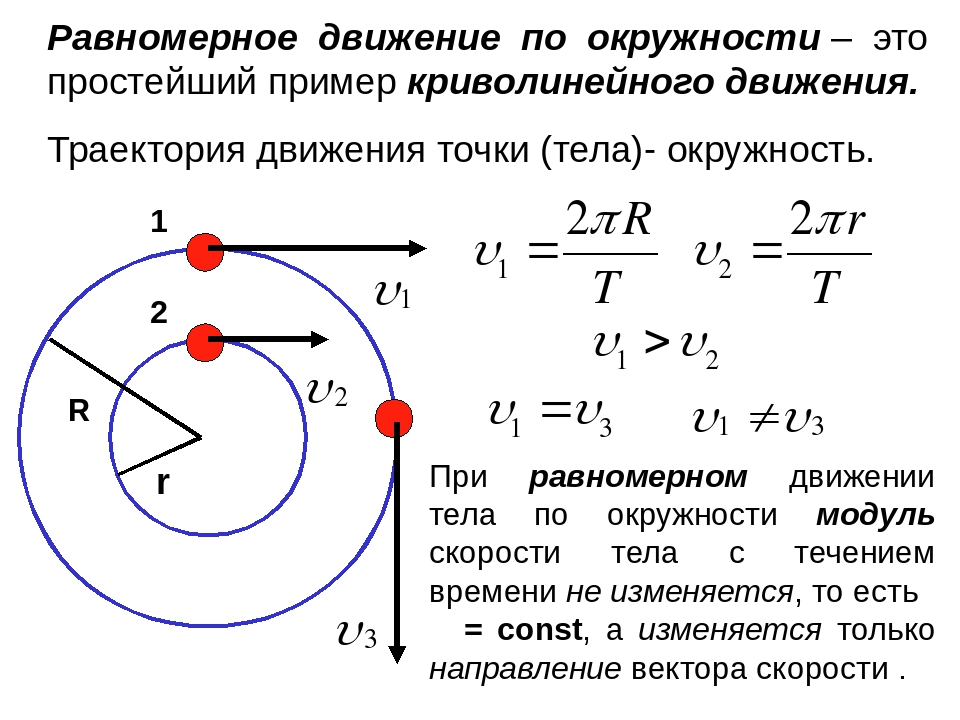
Равномерное движение по окружности – это простейший пример криволинейного движения. Например, по окружности движется конец стрелки часов по циферблату. Скорость движения тела по окружности носит название линейная скорость.
При равномерном движении тела по окружности модуль скорости тела с течением времени не изменяется, то есть v = const, а изменяется только направление вектора скорости . Тангенциальное ускорение в этом случае отсутствует (ar = 0), а изменение вектора скорости по направлению характеризуется величиной, которая называется центростремительное ускорение (нормальное ускорение) an или аЦС. В каждой точке траектории вектор центростремительного ускорения направлен к центру окружности по радиусу.
Модуль центростремительного ускорения равен
aЦС=v2 / R
Где v – линейная скорость, R – радиус окружности
Рис.
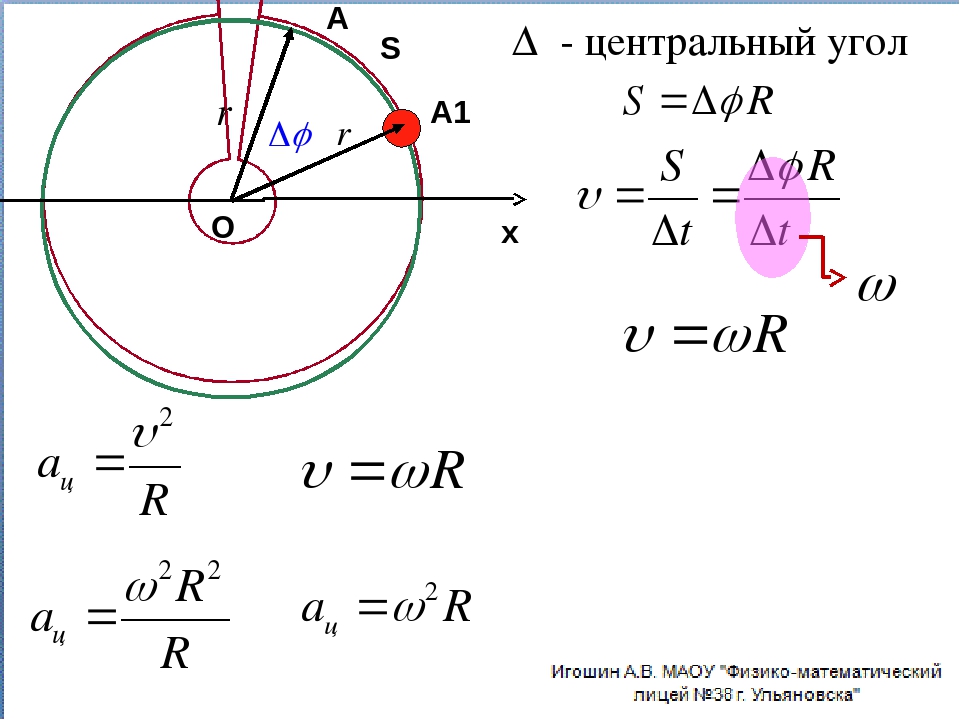
Когда описывается движение тела по окружности, используется угол поворота радиуса – угол φ, на который за время t поворачивается радиус, проведённый из центра окружности до точки, в которой в этот момент находится движущееся тело. Угол поворота измеряется в радианах. Радиан равен углу между двумя радиусами окружности, длина дуги между которыми равна радиусу окружности (рис. 1.23). То есть если l = R, то
1 радиан= l / R
Так как длина окружности равна
l = 2πR
то
360о = 2πR / R = 2π рад.
Следовательно
1 рад. = 57,2958о = 57о18’
Угловая скорость равномерного движения тела по окружности – это величина ω, равная отношению угла поворота радиуса φ к промежутку времени, в течение которого совершён этот поворот:
ω = φ / t
Единица измерения угловой скорости – радиан в секунду [рад/с]. Модуль линейной
скорости определяется отношением длины пройденного пути l к промежутку времени t:
Модуль линейной
скорости определяется отношением длины пройденного пути l к промежутку времени t:
v= l / t
Линейная скорость при равномерном движении по окружности направлена по касательной в данной точке окружности. При движении точки длина l дуги окружности, пройденной точкой, связана с углом поворота φ выражением
l = Rφ
где R – радиус окружности.
Тогда в случае равномерного движения точки линейная и угловая скорости связаны соотношением:
v = l / t = Rφ / t = Rω или v = Rω
Рис. 1.23. Радиан.
Период обращения – это промежуток времени Т, в течение которого тело (точка) совершает один оборот по окружности. Частота обращения – это величина, обратная периоду обращения – число оборотов в единицу времени (в секунду). Частота обращения обозначается буквой n.
n = 1 / T
За один период угол поворота φ точки равен 2π рад, поэтому 2π = ωT, откуда
T = 2π / ω
То есть угловая скорость равна
ω = 2π / T = 2πn
Центростремительное ускорение можно выразить через период Т и частоту обращения n:
aЦС = (4π2R) / T2 = 4π2Rn2
Лекция – 3.
 Кинематика. Часть – 3. Движение по окружности.
Кинематика. Часть – 3. Движение по окружности.1.Равномерное движение по окружности
2.Угловая скорость вращательного движения.
3.Период вращения.
4.Частота вращения.
5.Связь линейной скорости с угловой.
6.Центростремительное ускорение.
7.Равнопеременное движение по окружности.
8.Угловое ускорение в равнопеременном движении по окружности.
9.Тангенциальное ускорение.
10.Закон равноускоренного движения по окружности.
11. Средняя угловая скорость в равноускоренном движении по окружности.
12.Формулы,
устанавливающие связь между угловой
скоростью, угловым ускорением и углом
поворота в равноускоренном движении
по окружности.
1 .Равномерное движение по окружности
и называется линейной скоростью движения по окружности.
Как и в криволинейном движении вектор скорости направлен по касательной к окружности в направлении движения (Рис.25).
2. Угловая скорость в равномерном движении по окружности – отношение угла поворота радиуса ко времени поворота:
В равномерном
движении по окружности угловая скорость
постоянна. В системе СИ угловая скорость
измеряется в(рад/c).
Один радиан – рад это центральный угол,
стягивающий дугу окружности длиной
равной радиусу. Полный угол содержит радиан, т.е. за один оборот радиус
поворачивается на угол радиан.
Полный угол содержит радиан, т.е. за один оборот радиус
поворачивается на угол радиан.
3. Период вращения – интервал времени Т, в течении которого материальная точка совершает один полный оборот. В системе СИ период измеряется в секундах.
4. Частота вращения – число оборотов , совершаемых за одну секунду. В системе СИ частота измеряется в герцах ( 1Гц = 1 ) . Один герц – частота, при которой за одну секунду совершается один оборот. Легко сообразить, что
Если за время t точка совершает n оборотов по окружности то .
Зная период и частоту вращения, угловую скорость можно вычислять по формуле:
или
5 Связь линейной скорости с угловой. Длина дуги окружности равна где центральный угол, выраженный в радианах, стягивающий дугу радиус окружности. Теперь линейную скорость запишем в виде
,
где .
Ч асто бывает удобно использовать формулы: или Угловую скорость часто называют циклической частотой, а частоту линейной частотой.
6. Центростремительное ускорение. В равномерном движении по окружности модуль скорости остаётся неизменным , а направление её непрерывно меняется (Рис.26). Это значит, что тело, движущееся равномерно по окружности, испытывает ускорение, которое направлено к центру и называется центростремительным ускорением.
Пусть за промежуток времени прошло путь равный дуге окружности . Перенесём вектор , оставляя его параллельным самому себе, так чтобы его начало совпало с началом вектора в точке В. Модуль изменения скорости равен , а модуль центростремительного ускорения равен
На Рис.26 треугольники
АОВ и ДВС равнобедренные и углы при
вершинах О и В равны, как углы с взаимно
перпендикулярными сторонами АО
и
ОВ Это значит, что треугольники АОВ и ДВС
подобные.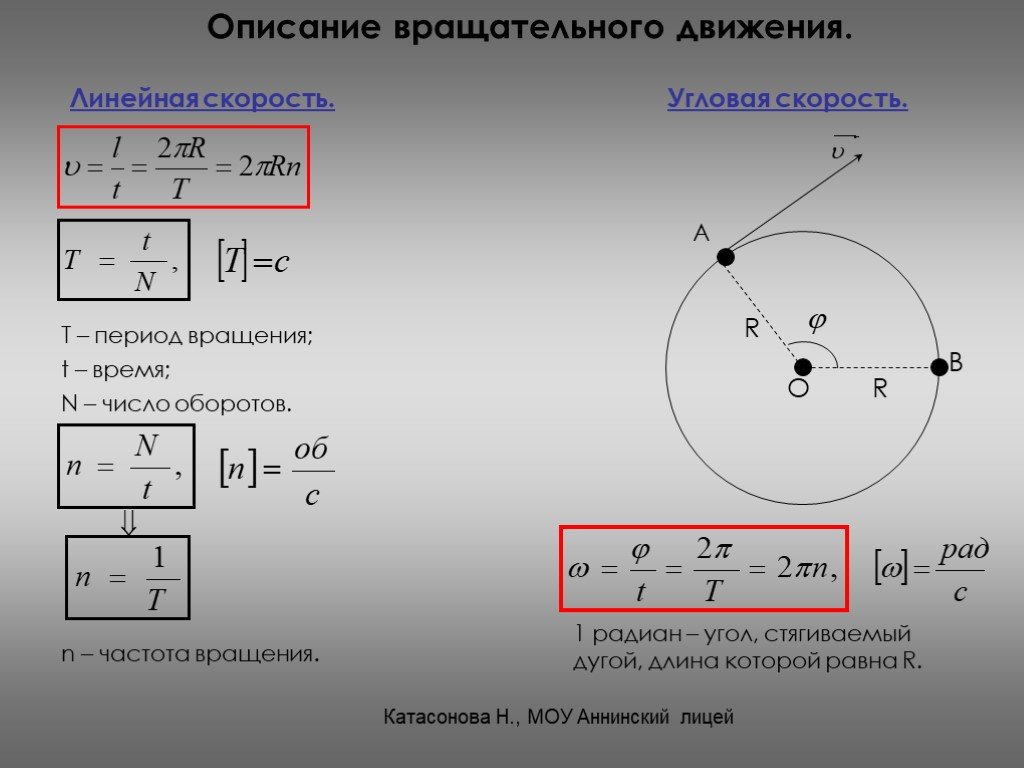 Следовательно Если то
есть интервал времени принимает сколь угодно малые значения,
то дугу можно
приближенно считать равной хорде АВ,
т.е. .
Поэтому можем записать Учитывая,
что ВД=
,
ОА=R
получим Умножая обе части последнего равенства
на ,
получим и далее выражение для модуля
центростремительного ускорения в
равномерном движении по окружности: .
Учитывая,
что получим две часто применяемые формулы:
Следовательно Если то
есть интервал времени принимает сколь угодно малые значения,
то дугу можно
приближенно считать равной хорде АВ,
т.е. .
Поэтому можем записать Учитывая,
что ВД=
,
ОА=R
получим Умножая обе части последнего равенства
на ,
получим и далее выражение для модуля
центростремительного ускорения в
равномерном движении по окружности: .
Учитывая,
что получим две часто применяемые формулы:
, .
Итак, в равномерном движении по окружности центростремительное ускорение постоянно по модулю.
Легко сообразить, что в пределе при , угол . Это значит, что углы при основании ДС треугольника ДВС стремятся значению , а вектор изменения скорости становится перпендикулярным к вектору скорости , т.е. направлен по радиусу к центру окружности.
7. Равнопеременное движение по окружности
8. Угловое ускорение в равнопеременном движении по окружности – отношение изменения угловой скорости к интервалу времени , в течении которого это изменение произошло, т.е.
,
где начальное значение угловой скорости, конечное значение угловой скорости, угловое ускорение, в системе СИ измеряется в . Из последнего равенства получим формулы для вычисления угловой скорости
и , если .
Умножая обе части этих равенств на и учитывая, что , — тангенциальное ускорение, т.е. ускорение, направленное по касательной к окружности , получим формулы для вычисления линейной скорости:
и , если .
9. Тангенциальное
ускорение численно равно изменению скорости в
единицу времени и направлено вдоль
касательной к окружности. Если >0, >0,
то движение равноускоренное. Если <0
и <0
– движение.
Если <0
и <0
– движение.
10. Закон равноускоренного движения по окружности. Путь, пройденный по окружности за время в равноускоренном движении, вычисляется по формуле:
.
Подставляя сюда , , сокращая на , получим закон равноускоренного движения по окружности:
, или , если .
Если же движение равнозамедленное, т.е. <0, то
.
1
1.Полное
ускорение в равноускоренном движении
по окружности.
В равноускоренном движении по окружности
центростремительное ускорение с
течением времени возрастает, т.к.
благодаря тангенциальному ускорению
возрастает линейная скорость. Очень
часто центростремительное ускорение
называют нормальным и обозначают как .
Так как полное ускорение в данный момент
определяют по теореме Пифагора (Рис.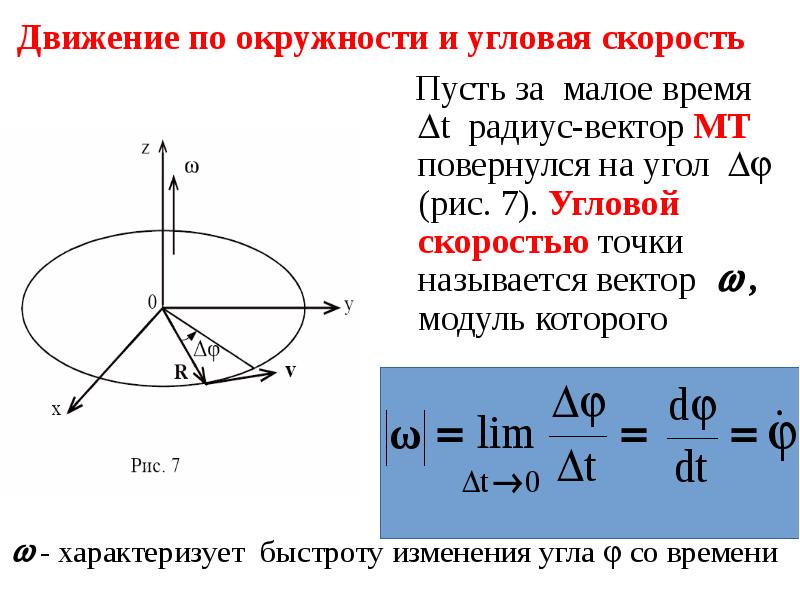 27).
27).
12. Средняя угловая скорость в равноускоренном движении по окружности. Средняя линейная скорость в равноускоренном движении по окружности равна . Подставляя сюда и и сокращая на получим
.
Если , то .
12. Формулы, устанавливающие связь между угловой скоростью, угловым ускорением и углом поворота в равноускоренном движении по окружности.
Подставляя в формулу величины , , , ,
и сокращая на , получим
.
Если , то и далее , .
Равномерное движение точки по окружности
Равномерное движение по окружности – это простейший пример криволинейного движения. Например, по окружности движется конец стрелки часов по циферблату.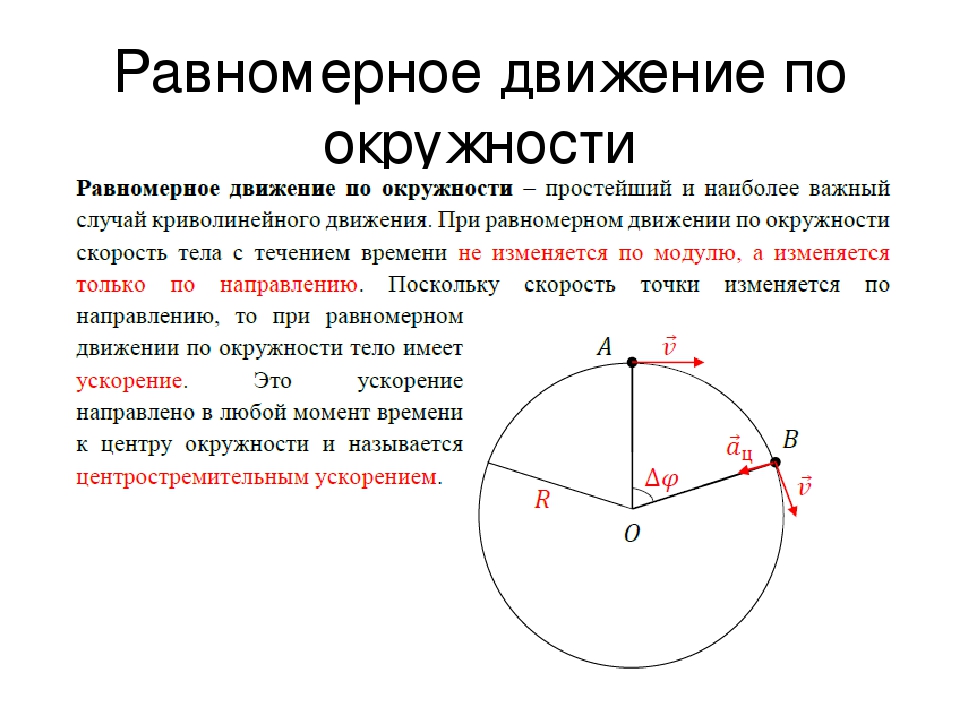 Скорость движения тела по окружности носит название линейная скорость.
Скорость движения тела по окружности носит название линейная скорость.
При равномерном движении тела по окружности модуль скорости тела с течением времени не изменяется, то есть \(v = const,\) а изменяется только направление вектора скорости. Тангенциальное ускорение в этом случае отсутствует \( (a_r = 0),\) а изменение вектора скорости по направлению характеризуется величиной, которая называется центростремительным ускорением (нормальное ускорение) \(a_n\), или \(a_{цс}\). В каждой точке траектории вектор центростремительного ускорения направлен к центру окружности по радиусу.
Модуль центростремительного ускорения равен \(a_{цс}=\frac{υ_2}{ R},\) где \(υ\) – линейная скорость, \(R\) – радиус окружности.
Когда описывается движение тела по окружности, используется угол поворота радиуса – угол \(φ\), на который за время t поворачивается радиус, проведенный из центра окружности до точки, в которой в этот момент находится движущееся тело.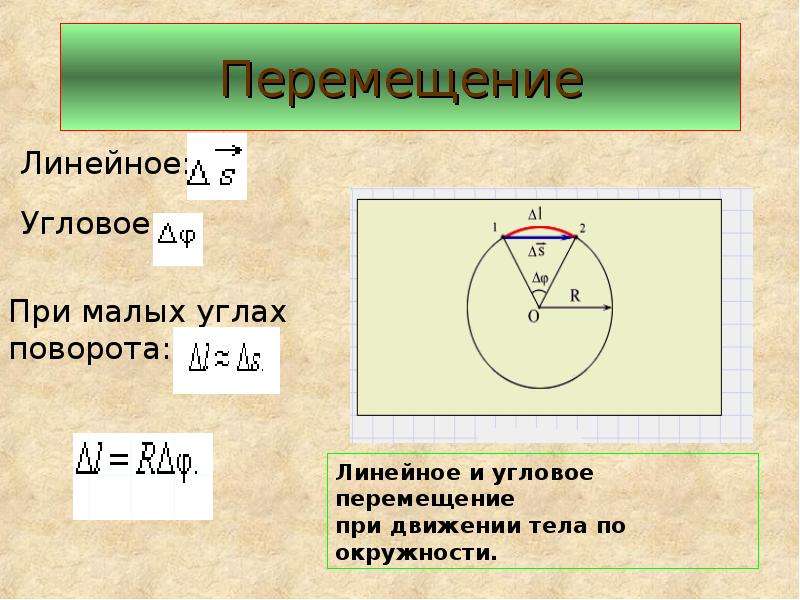 \circ18\)’ . Угловая скорость равномерного движения тела по окружности – это величина \(\omega\), равная отношению угла поворота радиуса φ к промежутку времени, в течение которого совершен этот поворот: \(ω = \frac φ t \). Единица измерения угловой скорости – радиан в секунду [рад/с]. Модуль линейной скорости определяется отношением длины пройденного пути l к промежутку времени \(t: υ= \frac l t \). Линейная скорость при равномерном движении по окружности направлена по касательной в данной точке окружности. При движении точки длина \(l\) дуги окружности, пройденной точкой, связана с углом поворота φ выражением \(l = Rφ\), где \(R\) – радиус окружности.
\circ18\)’ . Угловая скорость равномерного движения тела по окружности – это величина \(\omega\), равная отношению угла поворота радиуса φ к промежутку времени, в течение которого совершен этот поворот: \(ω = \frac φ t \). Единица измерения угловой скорости – радиан в секунду [рад/с]. Модуль линейной скорости определяется отношением длины пройденного пути l к промежутку времени \(t: υ= \frac l t \). Линейная скорость при равномерном движении по окружности направлена по касательной в данной точке окружности. При движении точки длина \(l\) дуги окружности, пройденной точкой, связана с углом поворота φ выражением \(l = Rφ\), где \(R\) – радиус окружности.
Тогда в случае равномерного движения точки линейная и угловая скорости связаны соотношением:
\(υ = \frac l t =\frac{ Rφ} t = Rω\), или \(υ = Rω\).
Период обращения – это промежуток времени Т, в течение которого тело (точка) совершает один оборот по окружности.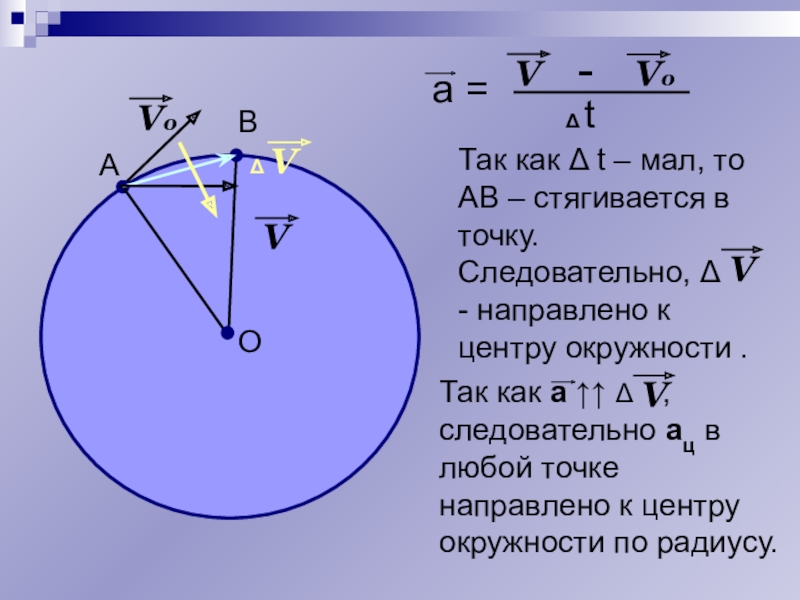 2\).
2\).
Движение по окружности с постоянной по модулю скоростью 🐲 СПАДИЛО.РУ
Понятия и определенияКриволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.
Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.
Особенности движения по окружности с постоянной по модулю скоростью:
- Траектория движения тела есть окружность.
- Вектор скорости всегда направлен по касательной к окружности.
- Направление скорости постоянно меняется под действием центростремительного ускорения.

- Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.
Период, частота и количество оборотов
Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.
Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).
t — время, в течение которого тело совершило N оборотов
За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.
Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»).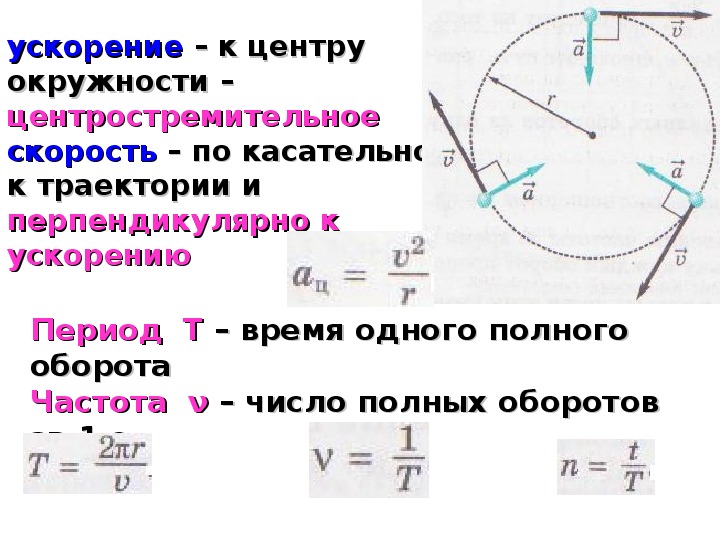 Единица измерения — Гц.
Единица измерения — Гц.
N — количество оборотов, совершенных телом за время t.
Период и частота — это обратные величины, определяемые формулами:
Количество оборотов выражается следующей формулой:
Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.
Линейная и угловая скорости
Линейная скорость
Определение и формулыЛинейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.
l — длина траектории, вдоль которой двигалось тело за время t
Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:
R — радиус окружности, по которой движется тело
Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:
Тогда формула примет вид:
Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:
Угловая скорость
Определение и формулыУгловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).
ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ
Полезные фактыРадиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.
За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:
Выражая угловую скорость через частоту, получим:
Выразив частоту через количество оборотов, формула угловой скорости примет вид:
Сравним две формулы:
Преобразуем формулу линейной скорости и получим:
Отсюда получаем взаимосвязь между линейной и угловой скоростями:
Полезные факты- У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v1 = v2.

- У вращающихся шестерен линейные скорости точек их поверхности также равны: v1 = v2.
- Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T1 = T2, ν1 = ν2, ω1 = ω2. Но v1 ≠ v2.
Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.
В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.
За каждую секунду Земля проходит расстояние, равное примерно 30 км.
Центростремительное ускорение
Определение и формулаЦентростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с2). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:
Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с2). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:
Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.
Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙103 секунд.
Радиус Земли равен 6400 км. В метрах это будет 6,4∙106. Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:
Подставляем данные в формулу:
Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:
Подставляем известные данные в формулу и вычисляем:
Ответ: 4pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17763Точка движется по окружности радиусом R с частотой обращения ν.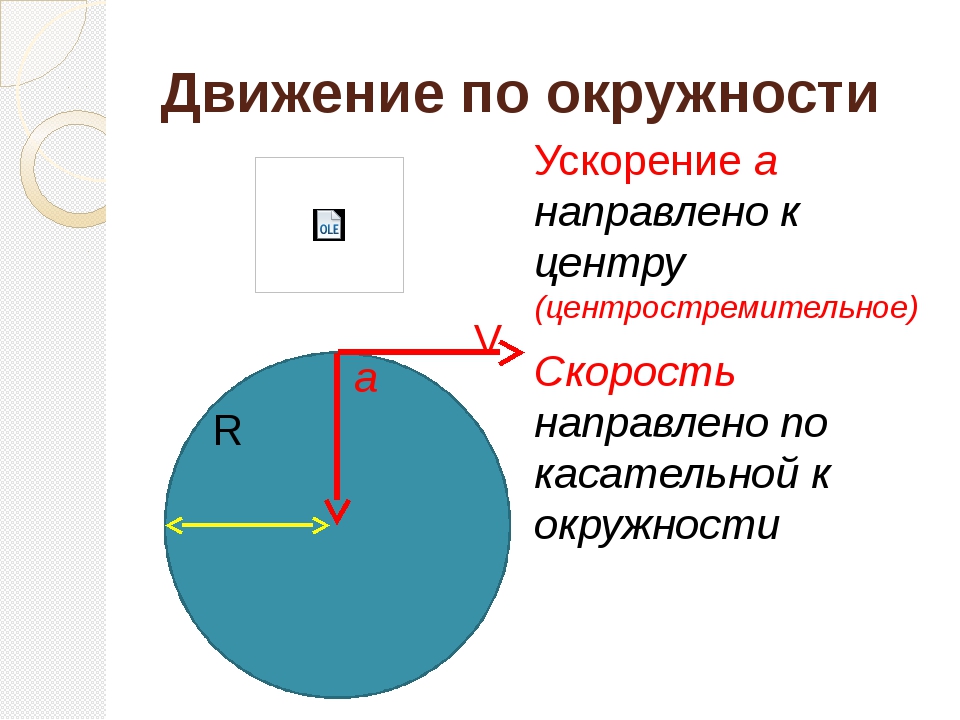 Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза
Алгоритм решения
- Записать исходные данные.
- Определить, что нужно найти.
- Записать формулу зависимости центростремительного ускорения от частоты.
- Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
- Приравнять правые части формул и найти искомую величину.
Решение
Запишем исходные данные:
- Радиус окружности R1 = R.
- Радиус окружности R2 = 4R.
- Центростремительное ускорение: aц.с. = a1 = a2.
Найти нужно ν2.
Центростремительное ускорение определяется формулой:
Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:
Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:
Произведем сокращения и получим:
Или:
Отсюда:
Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».
Верный ответ: «б».
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 6k | Оценить:
Формула угловой скорости в физике
Содержание:
Определение и формула угловой скорости
Определение
Круговым движением точки вокруг некоторой оси называют движение, при котором траекторией точки является окружность с центром, который лежит на оси вращения, при этом плоскость окружности перпендикулярна этой оси.
Вращением тела вокруг оси называют движение, при котором все точки тела совершают круговые движения около этой оси.
Перемещение при вращении характеризуют при помощи угла поворота $(\varphi)$ . Часто используют вектор элементарного поворота $\bar{d\varphi}$ , который равен по величине элементарному углу поворота тела $(d \varphi)$ за маленький отрезок времени dt и направлен по мгновенной оси вращения в сторону, откуда этот поворот виден реализующимся против часовой стрелки. Надо отметить, что только элементарные угловые перемещения являются векторами. Углы вращения на конечные величины векторами не являются.
Определение
Угловой скоростью называют скорость изменения угла поворота и обозначают ее обычно буквой $\omega$ . Математически определение угловой скорости записывают так:
$$\bar{\omega}=\frac{d \bar{\varphi}}{d t}=\dot{\bar{\varphi}}(1)$$Угловая скорость — векторная величина (это аксиальный вектор). Она имеет направление вдоль мгновенной оси вращения совпадающее с направлением поступательного правого винта, если его вращать в сторону вращения тела (рис.1).
Вектор угловой скорости может претерпевать изменения как за счет изменения скорости вращения тела вокруг оси (изменение модуля угловой скорости), так и за счет поворота оси вращения в пространстве ($\bar{\omega}$ при этом изменяет направление).
Равномерное вращение
Если тело за равные промежутки времени поворачивается на один и тот же угол, то такое вращение называют равномерным. При этом модуль угловой скорости находят как:
$$\omega=\frac{\varphi}{t}(2)$$где $(\varphi)$ – угол поворота, t – время, за которое этот поворот совершён.
Равномерное вращение часто характеризуют при помощи периода обращения (T), который является временем, за которое тело производит один оборот ($\Delta \varphi=2 \pi$). Угловая скорость связана с периодом обращения как:
$$\omega=\frac{2 \pi}{T}(3)$$С числом оборотов в единицу времени ($\nu) угловая скорость связана формулой:
$$\omega=2 \pi \nu(4)$$Понятия периода обращения и числа оборотов в единицу времени иногда используют и для описания неравномерного вращения, но понимают при этом под мгновенным значением T, время за которое тело делало бы один оборот, если бы оно вращалось равномерно с данной мгновенной величиной скорости.
Формула, связывающая линейную и угловую скорости
Линейная скорость $\bar{v}$ точки А (рис.1), которая расположена на расстоянии R от оси вращения связана с вектором угловой скорости следующим векторным произведением:
$$\bar{v}=[\bar{\omega} \bar{R}](5)$$где $\bar{R}$ – перпендикулярная к оси вращения компонента радиус-вектора точки $A (\bar{r})$ (рис.{3} \approx 20(\mathrm{rad})$$
Ответ. $\varphi = 20$ рад.
Читать дальше: Формула удельного веса.
| Криволинейное движение. | |
| При криволинейном движении вектор скорости всегда направлен по касательной к траектории движения. Любое криволинейное движение можно представить в виде суммы прямолинейных движений и движений по окружностям разных радиусов.Скорость изменяется как по величине, так и по направлению. Вектор ускорения направлен под углом к вектору скорости. | |
| РАВНОМЕРНОЕ ДВИЖЕНИЕ ТОЧКИ ПО ОКРУЖНОСТИ. | |
Равномерное движение точки по окружности — движение точки с постоянной по модулю скоростью (v=const) по траектории, представляющей собой окружность. Но, т.к. скорость всегда направлена по касательной к траектории движения, то по направлению она изменяется. Значит равномерное движение по окружности – ускоренное движение! Точка совершает перемещение с постоянной по модулю скоростью, следовательно:. В этом случае скорость точки называется линейной скоростью (ℓ–длина дуги). Вектор линейной скорости направлен по касательной к окружности в данной точке. | |
Можно характеризовать изменение положения тела с помощью углового перемещения (угла поворота) φ. Возьмем несколько концентрических окружностей и построим для всех центральный угол φ так, чтобы радиусы этих окружностей, образующие угол, накладывались друг на друга. Из рисунка видно, что одному и тому же углу φ соответствуют у одной окружности дуга ℓ и радиус r, а у другой – дуга L и радиус R. За меру угла можно принять отношение длины дуги к радиусу:. Единица измерения угла в этом случае наз. радианом(сокращение – рад). | |
Центральный угол равен одному радиану, если длина дуги равна радиусу окружности. Если точка совершила полный оборот, то длина дуги равна длине окружности. Следовательно: — полный оборот точки соответствует 2π радиан. Для перевода единиц составим пропорцию: . Следовательно: | |
Равномерное движение точки по окружности – это движение, при котором точка за любые равные промежутки времени совершает одинаковые угловые перемещения (поворачивается на одинаковые углы). Если характеризовать движение углом поворота, то удобно ввести угловую скорость: — угловая скорость показывает, на какой угол поворачивается точка при равномерном движении по окружности за единицу времени. Единица измерения в СИ — рад/с. | |
| Можно сказать, что равномерным движением по окружности наз. движение с постоянной угловой скоростью. Линейная и угловая скорости связаны между собой: , т.е. . | |
К важным характеристикам вращательного движения относятся частота и период. Период— физическая величина, показывающая, чему равно время, за которое точка совершает один полный оборот. Если обозначить N – число оборотов, а Т – период, то: . Единица измерения в СИ – с. Т.к. за период точка поворачивается на угол 2π, то . Частота – количество оборотов, которое совершила точка за единицу времени: .
Единица измерения в СИ – Гц (герц). Частота равна одному герцу, если за 1 секунду точка совершает один полный оборот (1Гц=1с-1). Частота и период – взаимно обратные величины: . Следовательно: . |
|
Равномерное движение по окружности | Физика
1. Основные характеристики равномерного движения по окружности
Движение по окружности часто встречается в природе и технике: по траекториям, близким к окружностям, движутся планеты вокруг Солнца, Луна и искусственные спутники Земли, точки колес и вращающихся деталей механизмов.
Мы ограничимся в нашем курсе равномерным движением по окружности. Напомним, что равномерным называют движение, при котором тело за любые равные промежутки времени проходит одинаковые пути.
Каковы же основные характеристики равномерного движения по окружности?
Прежде всего, это радиус окружности r и модуль скорости тела v (рис. 8.1). Далее мы увидим, что мгновенная скорость в каждой точке траектории направлена по касательной к траектории.
Следующей характеристикой равномерного движения по окружности является период обращения T. Он равен промежутку времени, в течение которого тело совершает один оборот.
? 1. Во сколько раз период обращения секундной стрелки меньше периода обращения часовой стрелки?
? 2. Докажите, что период обращения T, радиус окружности r и модуль скорости тела v связаны соотношением
T = 2πr/v. (1)
Частотой обращения ν называют число оборотов за единицу времени (секунду). Значение частоты не всегда целое число: например, если тело совершает 10 оборотов в секунду, то ν = 10 с-1, а если оно совершает пол-оборота в секунду, то ν = 0,5 с-1.
Чем больше частота обращения, тем меньше период.
? 3. Докажите, что период T и частота обращения ν связаны соотношением
ν = 1/T (2).
? 4. Чему равна частота обращения секундной стрелки, ми- К. нутной стрелки, часовой стрелки, Земли при ее суточном вращении и при ее движении вокруг Солнца?
2. Направление мгновенной скорости при движении по окружности
Поставим опыт
Затачивая инструмент с по: мощью точильного круга, можно заметить, что искры летят по касательной к кругу в точке, которой касается инструмент (рис. 8.2). Это раскаленные кусочки, оторвавшиеся от круга, поэтому их скорость в момент отрыва равна (по модулю и направлению) скорости точек диска, соприкасающихся с инструментом.
Этот опыт показывает, что при движении по окружности мгновенная скорость тела v_vec направлена по касательной к окружности в точке, где в данный момент находится тело.
Чтобы лучше осознать это, рассмотрим движение тела в течение времени Δt, малого по сравнению с периодом T. Пройденная за это время дуга окружности почти сливается с участком касательной к окружности (эта касательная показана голубой линией на рис. 8.3). А это как раз и означает, что мгновенная скорость тела направлена по касательной.
Заметим, что касательная к окружности в некоторой точке перпендикулярна радиусу окружности, проведенному в эту точку. Следовательно,
при движении по окружности мгновенная скорость тела v_vec направлена перпендикулярно радиусу, проведенному в точку, где находится тело в данный момент (см. рис. 8.1).
? 5. На рисунке 8.4 изображена траектория тела, движущегося по окружности. Перенесите рисунок в тетрадь и отметьте на нем:
а) вектор скорости тела, когда оно находится в точках А и В;
б) точку С, в которой скорость тела составляет угол 45º со скоростью тела в момент, когда оно находится в точке А.
3. Ускорение при равномерном движении по окружности
Поскольку мгновенная скорость тела направлена по касательной в каждой точке траектории, направление скорости тела при его движении по окружности изменяется. А если скорость тела изменяется любым образом (пусть даже только по направлению), то это тело движется с ускорением. Итак, при равномерном движении по окружности тело движется с ускорением.
Докажем, что
при равномерном движении тела со скоростью v по окружности радиуса r:
а) ускорение тела в каждый момент времени направлено по радиусу к центру окружности,
б) модуль ускорения a = v2/r.
Направление ускорения
Поскольку
направление вектора ускорения совпадает с направлением вектора изменения скорости Δ.
Найдем изменение скорости Δ за промежуток времени Δt, малый по сравнению с периодом T.
Обозначим 1 скорость тела в момент времени t, а 2 скорость тела в момент времени t + Δt. Тогда
Δ =2 – 1.
Обозначим Δα угол, на который повернется за время Δt радиус, проведенный в точку, где находится тело (рис. 8.5, а). Угол Δα мал, если Δt мало по сравнению с T.
На такой же угол Δα повернется за время Δt и вектор скорости тела (скорость остается все время перпендикулярной радиусу).
На рисунке 8.5, б показано, как найти изменение скорости Δ.
Векторы 1, 2 и Δ образуют равнобедренный треугольник с основанием Δ и малым углом Δα при вершине. Поэтому углы при основании этого треугольника близки к прямым углам (это следует из того, что сумма углов треугольника 180º).
Значит, изменение скорости Δ за очень малое время Δt направлено перпендикулярно скорости, то есть по радиусу, причем к центру окружности, как показано на рисунке 8.5, в. Ускорение направлено так же, как изменение скорости Δ, следовательно, ускорение тела направлено к центру окружности.
По этой причине ускорение тела при его движении по окружности часто называют центростремительным.
Из курса физики основной школы вы уже знаете, что ускорение тела обусловлено действующими на него силами. Например, при движении Земли вокруг Солнца силой, вызывающей центростремительное ускорение Земли, является сила тяготения со стороны Солнца.
? 6. Автомобиль поворачивает на 90º по дуге окружности. Изобразите на чертеже в тетради векторы скорости и ускорения автомобиля в середине дуги поворота.
Модуль ускорения
За промежуток времени Δt тело, движущееся со скоростью v, проходит по дуге окружности путь Δl = v * Δt (это красная сплошная линия на рисунке 8.6, а).
Если Δt мало по сравнению с T, эта дуга почти не отличается от отрезка прямой. Поэтому фигура, образованная двумя радиусами r и этим отрезком, представляет собой равнобедренный треугольник с основанием Δl = v * Δt.
Этот треугольник подобен равнобедренному треугольнику, образованному скоростями Δ1, Δ2 и изменением скорости Δ = * Δt (он изображен на рисунке 8.6, б), поскольку углы при вершинах этих треугольников равны. Следовательно, основания указанных двух треугольников относятся, как их боковые стороны:
(a * Δt) / (v * Δt) = v/r,
откуда получаем:
a = v2/r, (4)
Центростремительное ускорение можно выразить также через ν и r или через T и r.
? 7. Докажите, что центростремительное ускорение выражается также формулами
Подсказка. Воспользуйтесь формулами (4), (1), (2).
Можно подумать, что центростремительное ускорение, обусловленное изменением только направления скорости, не может быть значительным. Убедимся, что это не всегда так.
? 8. Чтобы космонавты без вреда для здоровья переносили большие перегрузки во время старта и посадки космического корабля, их тренируют с помощью специального аппарата – огромной центрифуги (рис. 8.7). Во время тренировки в Центре подготовки космонавтов им. Ю. А. Гагарина космонавт движется в капсуле (она изображена в левой части фотографии) по окружности радиусом 18 м.
а) С каким ускорением движется космонавт, когда центрифуга делает шесть оборотов в минуту?
б) При какой частоте обращения космонавт движется с ускорением, превышающим ускорение свободного падения в 10 раз? Чему равна при этом его линейная скорость?
Чтобы испытать на себе ощущения при движении с ускорением, в несколько раз превышающем ускорение свободного падения, можно покататься на центрифуге в парке (рис. 8.8).
? 9. Радиус колеса аттракциона 10 м. Чему равен период его обращения, когда пассажиры движутся с ускорением, в 2,5 раза превышающим ускорение свободного падения?
4. Угловая скорость
Иногда используют еще одну характеристику равномерного движения по окружности – угловую скорость ω. Ее определяют соотношением
ω = Δα/t,
где Δα – угол, на который за время t поворачивается радиус, проведенный к телу из центра окружности (рис. 8.9).
При атом угол измеряют в радианах, то есть одному полному обороту соответствует поворот на угол 2π. Единица угловой скорости совпадает с единицей частоты (1 с-1). (Напомним, что один радиан (рад) равен центральному углу, опирающемуся на дугу, длина которой равна радиусу окружности; 1 рад ≈ 57º.)
? 10. Какая скорость одинакова для всех точек минутной стрелки – линейная или угловая?
? 11. Во сколько раз угловая скорость секундной стрелки больше угловой скорости минутной стрелки?
? 12. Докажите, что угловая скорость связана с периодом обращения, частотой, радиусом окружности и скоростью соотношениями
ω = 2π/T, (7)
ω = 2πν, (8)
v = ωr. (9)
? 13.Чему равна угловая скорость движения точки поверхности Земли, обусловленная суточным вращением? Одинакова ли эта скорость для всех точек земной поверхности, находящихся: а) на одной параллели; б) на одном меридиане; в) на различных параллелях и меридианах?
? 14. Докажите, что центростремительное ускорение выражается через угловую скорость и радиус окружности формулой
a = ω2r. (10)
5. Катящееся колесо
Рассмотрим движение различных точек колеса автомобиля.
Пусть автомобиль едет со скоростью (рис. 8.10), причем его колеса катятся без проскальзывания.
Что означают слова «без проскальзывания»? Это значит, что нижняя точка колеса А покоится относительно земли (при этом шины оставляют четкие следы). Этот факт – отправная точка для нахождения скорости всех других точек колеса – например, точек В, С, D на рисунке 8.10.
Чтобы найти скорость этих точек, удобно перейти в систему отсчета, связанную с автомобилем, а потом вернуться в систему отсчета, связанную с дорогой.
В системе отсчета, связанной с автомобилем, все точки обода колеса движутся по окружности с равными по модулю скоростями. Обозначим vвр модуль этой скорости, обусловленной вращением колеса вокруг своей оси. Выясним: как связаны скорость автомобиля v и скорость вращения vвр точек его колеса? Именно тут нам и поможет тот факт, что нижняя точка колеса А покоится относительно земли.
Заметим, что скорость Aвр вращения нижней точки А направлена противоположно скорости автомобиля (рис. 8.11).
Выразим через v и vвр скорость vА точки А в системе отсчета, связанной с дорогой. Согласно правилу сложения скоростей скорость точки А относительно дороги
A = Aвр + .
Итак, скорости Aвр и направлены противоположно, а их сумма A = 0. Следовательно,
vвр = v,
то есть скорость движения точек обода колеса в системе отсчета, связанной с автомобилем, равна но модулю скорости автомобиля.
? 15.Докажите, что скорость точки С (см. рис. 8.10) относительно дороги равна 2v.
? 16. Найдите направление и модуль скорости точек В и D (см. рис. 8.10) относительно земли.
? 17. Катушка с ниткой (рис. 8.12) может катиться по горизонтальному столу без проскальзывания. Конец нити тянут в горизонтальном направлении со скоростью, равной по модулю u (рис. 8.13). Внутренний радиус катушки r, а внешний R. Докажите, что катушка будет двигаться вправо со скоростью v = u(R/(R+r)).
Подсказка. Рассмотрите движение точки А, воспользовавшись сложением скоростей, а также тем фактом, что точка катушки, касающаяся стола, покоится относительно стола.
? 18.С какой скоростью v и в каком направлении будет двигаться катушка в случае, изображенном на рисунке 8.14?
Если вы выполнили это задание правильно, ответ может показаться вам неправдоподобным. Попробуйте проверить его на опыте, проследив за тем, чтобы катушка катилась без проскальзывания.
? 19. С какой скоростью едет велосипедист, если сорвавшаяся с колеса в точке А (рис. 8.15) капелька попала снова в эту же точку? Радиус колеса 30 см.
Подсказка. Перейдите в систему отсчета, связанную с велосипедистом.
Дополнительные вопросы и задания
Необходимые для решения задач справочные данные, не приведенные в условии задачи, вы можете найти в конце учебника (под обложкой).
20. Длина минутной стрелки настенных часов 15 см, а часовой стрелки – 10 см. Какие величины можно определить из этого условия? Чему они равны?
21. Чему равна обусловленная суточным вращением скорость точек поверхности Земли, расположенных на экваторе? Длину экватора примите равной 40000 км.
22. Две шестеренки сцеплены, как показано на рисунке 8.16. Радиусы шестеренок 60 см и 30 см. Большая шестеренка вращается с частотой 2 с-1.
а) С какой скоростью движутся зубцы большой шестеренки?
б) По часовой стрелке или против нее движутся зубцы маленькой шестеренки? С какой скоростью они движутся?
в) Чему равна частота обращения маленькой шестеренки?
23. Диск радиусом 2 м равномерно вращается вокруг своей оси с периодом 0,5 с. Начертите графики зависимости скорости v и ускорения a точки диска от расстояния r до центра диска.
24. Наблюдения колец Сатурна (рис. 8.17) показали, что чем дальше от планеты находится участок кольца, тем меньше его скорость. Могут ли кольца Сатурна быть сплошными? Обоснуйте свой ответ.
Самолет летит вдоль 60-й параллели. Во время всего полета его пассажиры наблюдают Солнце в одной и той же точке небосвода. Длину экватора примите равной 40000 км.
а) В каком направлении летит самолет?
б) За какое время он совершит полный круг?
в) Какой путь самолет пролетит за это время?
г) С какой скоростью летит самолет?
26. Два тела равномерно движутся по окружностям радиусом 10 см и 1 м соответственно. У какого тела ускорение больше и во сколько раз, если:
а) скорости тел равны?
б) периоды обращения тел равны?
27. Во сколько раз ускорение точек земной поверхности на экваторе меньше ускорения свободного падения g? Во сколько раз надо было бы уменьшить продолжительность суток, чтобы оно стало равным g?
Угол поворота и угловая скорость
Цели обучения
К концу этого раздела вы сможете:
- Определите длину дуги, угол поворота, радиус кривизны и угловую скорость.
- Вычислить угловую скорость вращения колеса автомобиля.
В «Кинематике» мы изучали движение по прямой и ввели такие понятия, как смещение, скорость и ускорение. Двумерная кинематика имеет дело с движением в двух измерениях.Движение снаряда — это частный случай двумерной кинематики, в котором объект проецируется в воздух, находясь под действием силы тяжести, и приземляется на некотором расстоянии. В этой главе мы рассматриваем ситуации, когда объект не приземляется, а движется по кривой. Мы начинаем изучение равномерного кругового движения с определения двух угловых величин, необходимых для описания вращательного движения.
Угол поворота
Когда объекты вращаются вокруг некоторой оси — например, когда компакт-диск (компакт-диск) на рисунке 1 вращается вокруг своего центра — каждая точка в объекте движется по дуге окружности.Рассмотрим линию от центра компакт-диска до его края. Каждая лунка , , используемая для записи звука вдоль этой линии, перемещается под одним и тем же углом за одно и то же время. Угол поворота — это величина поворота, аналогичная линейному расстоянию. Мы определяем угол поворота Δ θ как отношение длины дуги к радиусу кривизны: [latex] \ displaystyle \ Delta \ theta = \ frac {\ Delta {s}} {r} \\ [ / латекс]
Рис. 1. Все точки на компакт-диске движутся по дугам окружности.Ямки вдоль линии от центра к краю все перемещаются на один и тот же угол Δθ за время Δt .
Рис. 2. Радиус круга повернут на угол Δθ . Длина дуги Δs описана на окружности.
Длина дуги Δs — это расстояние, пройденное по круговой траектории, как показано на рисунке 2. Обратите внимание, что r — это радиус кривизны круговой траектории.
Мы знаем, что за один полный оборот длина дуги равна длине окружности радиуса r . Окружность круга равна 2π r . Таким образом, за один полный оборот угол поворота составляет
°.[латекс] \ displaystyle \ Delta \ theta = \ frac {2 \ pi {r}} {r} = 2 \ pi \\ [/ latex].
Этот результат является основой для определения единиц, используемых для измерения углов поворота, Δ θ равными радиан, (рад), определенным так, что 2π рад = 1 оборот.
Сравнение некоторых полезных углов, выраженных как в градусах, так и в радианах, показано в таблице 1.
| Таблица 1. Сравнение угловых единиц | |
|---|---|
| Градус меры | Мера радиана |
| 30º | [латекс] \ displaystyle \ frac {\ pi} {6} \\ [/ latex] |
| 60º | [латекс] \ displaystyle \ frac {\ pi} {3} \\ [/ latex] |
| 90º | [латекс] \ displaystyle \ frac {\ pi} {2} \\ [/ latex] |
| 120º | [латекс] \ displaystyle \ frac {2 \ pi} {3} \\ [/ latex] |
| 135º | [латекс] \ displaystyle \ frac {3 \ pi} {4} \\ [/ latex] |
| 180º | π |
Рисунок 3. {\ circ}} {2 \ pi} \ приблизительно 57.{\ circ} \\ [/ латекс].
Угловая скорость
Насколько быстро вращается объект? Определим угловую скорость ω как скорость изменения угла. В символах это [латекс] \ omega = \ frac {\ Delta \ theta} {\ Delta {t}} \\ [/ latex], где угловой поворот Δ θ происходит за время Δ t . Чем больше угол поворота за заданный промежуток времени, тем больше угловая скорость. Единицы измерения угловой скорости — радианы в секунду (рад / с).
Угловая скорость ω аналогична линейной скорости v . Чтобы получить точное соотношение между угловой и линейной скоростью, мы снова рассмотрим ямку на вращающемся CD. Эта яма перемещается на длину дуги Δ с за время Δ t , поэтому она имеет линейную скорость [латекс] v = \ frac {\ Delta {s}} {\ Delta {t}} \\ [/ латекс].
Из [latex] \ Delta \ theta = \ frac {\ Delta {s}} {r} \\ [/ latex] мы видим, что Δ s = r Δ θ . Подстановка этого в выражение для v дает [latex] v = \ frac {r \ Delta \ theta} {\ Delta {t}} = r \ omega \\ [/ latex].
Мы записываем эту взаимосвязь двумя разными способами и получаем два разных вывода:
[латекс] v = r \ omega \ text {или} \ omega \ frac {v} {r} \\ [/ latex].
Первое соотношение в [latex] v = r \ omega \ text {or} \ omega \ frac {v} {r} \\ [/ latex] утверждает, что линейная скорость v пропорциональна расстоянию от центра вращения, таким образом, он является наибольшим для точки на ободе (наибольшее r ), как и следовало ожидать. Мы также можем назвать эту линейную скорость v точки на ободе тангенциальной скоростью .Вторую взаимосвязь в [latex] v = r \ omega \ text {или} \ omega \ frac {v} {r} \\ [/ latex] можно проиллюстрировать на примере шины движущегося автомобиля. Обратите внимание, что скорость точки на ободе шины такая же, как скорость v автомобиля. См. Рис. 4. Таким образом, чем быстрее движется автомобиль, тем быстрее вращается шина — большой v означает большой ω , потому что v = rω . Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью ( ω ), будет создавать для автомобиля большую линейную скорость ( v ).
Рис. 4. Автомобиль, движущийся вправо со скоростью v , имеет шину, вращающуюся с угловой скоростью ω. Скорость протектора шины относительно оси составляет v , как если бы автомобиль был поднят. Таким образом, автомобиль движется вперед с линейной скоростью v = r ω, где r — радиус шины. Чем больше угловая скорость шины, тем больше скорость автомобиля.
Пример 1. Как быстро вращается автомобильная шина?
Рассчитайте угловую скорость 0.Автомобильная шина с радиусом 300 м при движении автомобиля со скоростью 15,0 м / с (около 54 км / ч). См. Рисунок 4.
Стратегия
Поскольку линейная скорость обода шины такая же, как и скорость автомобиля, мы имеем v = 15,0 м / с. Радиус шины задан равным r = 0,300 м. Зная v и r , мы можем использовать второе соотношение в [latex] v = r \ omega \ text {или} \ omega \ frac {v} {r} \\ [/ latex] для вычисления угловой скорости .
Решение
Для вычисления угловой скорости мы будем использовать следующее соотношение: [latex] \ omega \ frac {v} {r} \\ [/ latex].
Подстановка известных,
[латекс] \ omega = \ frac {15.0 \ text {m / s}} {0.300 \ text {m}} = 50.0 \ text {rad / s} \\ [/ latex].
Обсуждение
Когда мы отменяем единицы в приведенном выше вычислении, мы получаем 50,0 / с. Но угловая скорость должна иметь единицы рад / с. Поскольку радианы на самом деле безразмерны (радианы определяются как отношение расстояний), мы можем просто вставить их в ответ для угловой скорости. Также обратите внимание, что если землеройный комбайн с гораздо большими шинами, скажем, 1.Радиус 20 м, двигался с той же скоростью 15,0 м / с, его шины вращались медленнее. У них будет угловая скорость [latex] \ omega = \ frac {15.0 \ text {m / s}} {1.20 \ text {m}} = 12.5 \ text {rad / s} \\ [/ latex].
И ω , и v имеют направления (следовательно, это угловая и линейная скорости соответственно). Угловая скорость имеет только два направления относительно оси вращения — либо по часовой стрелке, либо против часовой стрелки. Линейная скорость касается пути, как показано на рисунке 5.
Эксперимент на вынос
Привяжите какой-либо предмет к концу веревки и поверните его по горизонтальному кругу над головой (взмахнув запястьем). Поддерживайте равномерную скорость при качании объекта и измеряйте угловую скорость движения. Какая примерная скорость объекта? Определите точку рядом с вашей рукой и выполните соответствующие измерения, чтобы рассчитать линейную скорость в этой точке. Определите другие круговые движения и измерьте их угловые скорости.
Рисунок 5.Когда объект движется по кругу, например муха на краю старомодной виниловой пластинки, его мгновенная скорость всегда касается круга. Направление угловой скорости в этом случае — по часовой стрелке.
Исследования PhET: Ladybug Revolution
Присоединяйтесь к божьей коровке и исследуйте вращательное движение. {\ circ} = 1 \ text { революция} \\ [/ латекс].{\ circ} \\ [/ латекс].
Концептуальные вопросы
- Существует аналогия между вращательными и линейными физическими величинами.Какие вращательные величины аналогичны расстоянию и скорости?
Задачи и упражнения
- Грузовики с полуприцепом имеют одометр на одной ступице колеса прицепа. Ступица утяжеляется так, что она не вращается, но в ней есть шестерни для подсчета количества оборотов колеса — затем она вычисляет пройденное расстояние. Если колесо имеет диаметр 1,15 м и совершает 200 000 оборотов, сколько километров должен показывать одометр?
- Микроволновые печи вращаются со скоростью около 6 об / мин.6 \ text {m} \\ [/ latex] на его экваторе, какова линейная скорость у поверхности Земли?
- Бейсбольный питчер вытягивает руку вперед во время подачи, поворачивая предплечье вокруг локтя. Если скорость мяча в руке питчера составляет 35,0 м / с, а мяч находится на расстоянии 0,300 м от локтевого сустава, какова угловая скорость предплечья?
- В лакроссе мяч выбрасывается из сетки на конец клюшки путем вращения клюшки и предплечья вокруг локтя. Если угловая скорость мяча около локтевого сустава 30.0 рад / с и мяч находится на расстоянии 1,30 м от локтевого сустава, какова скорость мяча?
- Грузовик с шинами радиусом 0,420 м движется со скоростью 32,0 м / с. Какова угловая скорость вращающихся шин в радианах в секунду? Что это в об / мин?
- Комплексные концепции. При ударе по футбольному мячу игрок, выполняющий удар, вращает ногой вокруг тазобедренного сустава. (a) Если скорость кончика ботинка кикера составляет 35,0 м / с, а тазобедренный сустав находится на расстоянии 1,05 м от кончика ботинка, какова угловая скорость кончика ботинка? (b) Башмак находится в контакте с изначально неподвижным 0.Футбол 500 кг за 20,0 мс. Какая средняя сила прилагается к футбольному мячу, чтобы придать ему скорость 20,0 м / с? (c) Найдите максимальную дальность действия футбольного мяча, пренебрегая сопротивлением воздуха.
- Создайте свою проблему. Представьте аттракцион в парке развлечений, в котором участники вращаются вокруг вертикальной оси в цилиндре с вертикальными стенками. Как только угловая скорость достигает своего полного значения, пол опускается, и трение между стенами и пассажирами препятствует их скольжению.Постройте задачу, в которой вы вычисляете необходимую угловую скорость, которая гарантирует, что всадники не соскользнут со стены. Включите свободную диаграмму тела одного всадника. Среди переменных, которые следует учитывать, — радиус цилиндра и коэффициенты трения между одеждой гонщика и стеной.
Глоссарий
длина дуги: Δ с , расстояние, пройденное объектом по круговой траектории
яма: крошечная выемка на спиральной дорожке, отформованная в верхней части слоя поликарбоната CD
угол поворота: отношение длины дуги к радиусу кривизны на круговой траектории: [latex] \ Delta \ theta = \ frac {\ Delta {s}} {r} \\ [/ latex]
радиус кривизны: радиус круговой траектории
радиан: единица измерения угла
угловая скорость: ω, скорость изменения угла, под которым объект движется по круговой траектории
Избранные решения проблем и упражнения
1.723 км
3. 5 × 10 7 оборотов
5. 117 рад / с
7. 76,2 рад / с; 728 об / мин
8. (а) 33,3 рад / с; (б) 500 Н; (в) 40,8 м
единиц вращательной кинематики | Безграничная физика
Угловое положение, Theta
Угол поворота — это величина (угол) поворота фигуры относительно фиксированной точки — часто центра круга.
Цели обучения
Оценить взаимосвязь между радианами на обороте CD
Ключевые выводы
Ключевые моменты
- Длина дуги Δs — это расстояние, пройденное по круговой траектории.r — радиус кривизны круговой траектории.
- Угол поворота — это величина поворота, аналогичная линейному расстоянию. Угол поворота [латекс] \ Дельта \ тета [/ латекс] определяется как отношение длины дуги к радиусу кривизны: [латекс] \ Дельта \ тета [/ латекс] = Δs / r.
- За один полный оборот угол поворота составляет 2π.
Ключевые термины
- Угловое положение : угол в радианах (градусах, оборотах), на который точка или линия были повернуты в указанном направлении вокруг указанной оси.
Когда объекты вращаются вокруг некоторой оси, например, когда компакт-диск (компакт-диск) вращается вокруг своего центра, каждая точка в объекте движется по дуге окружности. Рассмотрим линию от центра компакт-диска до его края. Каждая яма, используемая для записи звука вдоль этой линии, перемещается под одним и тем же углом за одно и то же время. Угол поворота — это величина поворота, аналогичная линейному расстоянию. Мы определяем угол поворота [latex] \ Delta \ theta [/ latex] как отношение длины дуги к радиусу кривизны:
[латекс] \ Delta \ theta = \ Delta \ text {s} / \ text {r} [/ latex] (показано на).
Угол поворота : Все точки на компакт-диске перемещаются по дугам окружности. Ямки вдоль линии от центра к краю все перемещаются на один и тот же угол Δ за время Δt.
В математике угол поворота (или угловое положение) — это величина (т.е. угол), на которую фигура поворачивается относительно фиксированной точки (часто центра круга, как показано на).
Угол θ и длина дуги s : Радиус круга поворачивается на угол Δ.Длина дуги Δs указана на окружности.
Длина дуги Δs — это расстояние, пройденное по круговой траектории. r — радиус кривизны круговой траектории. Мы знаем, что за один полный оборот длина дуги равна длине окружности радиуса r. Окружность круга равна 2πr. Таким образом, за один полный оборот угол поворота составляет:
[латекс] \ Delta \ theta = (2 \ pi \ text {r}) / \ text {r} = 2 \ pi [/ latex].
Этот результат является основой для определения единиц измерения углов поворота в радианах (рад), определяемых следующим образом:
2π рад = 1 оборот.
Если [latex] \ Delta \ theta [/ latex] = 2π rad, то компакт-диск сделал один полный оборот, и каждая точка на компакт-диске вернулась в исходное положение. Поскольку в круге 360º или один оборот, отношение между радианами и градусами, таким образом, составляет 2π рад = 360º, так что:
1рад = 360º / 2π = 57,3º.
Угловая скорость, Омега
Угловая скорость ω — это скорость изменения угла, математически определяемая как ω = [latex] \ Delta \ theta [/ latex] [latex] / \ Delta \ text {t} [/ latex].
Цели обучения
Проверить, насколько быстро объект вращается на основе угловой скорости
Ключевые выводы
Ключевые моменты
- Чем больше угол поворота за заданный промежуток времени, тем больше угловая скорость.
- Угловая скорость ω аналогична линейной скорости v.
- Связь между линейной скоростью и угловой скоростью можно записать двумя разными способами: v = rω или ω = v / r.
Ключевые термины
- угловая скорость : векторная величина, описывающая объект в круговом движении; его величина равна скорости частицы, а направление перпендикулярно плоскости ее кругового движения.
Чтобы проверить, насколько быстро объект вращается, мы определяем угловую скорость ω как скорость изменения угла. В символах это
.[латекс] \ omega = \ Delta \ theta / \ Delta \ text {t} [/ latex],
, где угловой поворот Δ происходит за время Δt. Чем больше угол поворота за заданный промежуток времени, тем больше угловая скорость. Единицы измерения угловой скорости — радианы в секунду (рад / с).
Угловая скорость ω аналогична линейной скорости v.Чтобы найти точное соотношение между угловой и линейной скоростью, мы снова рассмотрим ямку на вращающемся CD. Эта яма перемещается на длину дуги Δs за время Δt, поэтому она имеет линейную скорость v = Δs / Δt.
Из [latex] \ Delta \ theta = (\ Delta \ text {s}) / \ text {r} [/ latex] мы видим, что [latex] \ Delta \ text {s} = \ text {r} \ cdot \ Дельта \ тета [/ латекс]. Подстановка этого в выражение для v дает [latex] \ text {v} = (\ text {r} \ cdot \ Delta \ theta) / (\ Delta \ text {t}) = \ text {r} (\ Delta \ theta / \ Delta \ text {t}) = \ text {r} \ omega [/ latex].
Мы можем записать это соотношение двумя разными способами: v = rω или ω = v / r.
Первое соотношение утверждает, что линейная скорость v пропорциональна расстоянию от центра вращения, таким образом, она является наибольшей для точки на ободе (наибольшее значение r), как и следовало ожидать. Мы также можем назвать эту линейную скорость v точки на ободе тангенциальной скоростью. Вторую взаимосвязь можно проиллюстрировать, рассмотрев шину движущегося автомобиля, как показано на рисунке ниже. Обратите внимание, что скорость точки в центре шины такая же, как скорость v автомобиля.Чем быстрее движется автомобиль, тем быстрее вращается шина — большой v означает большой ω, потому что v = rω. Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью (ω), будет создавать для автомобиля большую линейную скорость (v).
Угловая скорость : Автомобиль, движущийся вправо со скоростью v, имеет шину, вращающуюся с угловой скоростью ω. Скорость протектора шины относительно оси равна v, как если бы автомобиль был поднят домкратом. Таким образом, автомобиль движется вперед с линейной скоростью v = rω, где r — радиус шины.Чем больше угловая скорость шины, тем больше скорость автомобиля.
Угловое ускорение, Alpha
Угловое ускорение — это скорость изменения угловой скорости, математически выражаемая как [latex] \ alpha = \ Delta \ omega / \ Delta \ text {t} [/ latex].
Цели обучения
Объясните взаимосвязь между угловым ускорением и угловой скоростью
Ключевые выводы
Ключевые моменты
- Чем быстрее происходит изменение угловой скорости, тем больше угловое ускорение.
- При круговом движении линейное ускорение касается окружности в интересующей точке и называется касательным ускорением.
- При круговом движении центростремительное ускорение относится к изменению направления скорости, но не ее величины. Объект, совершающий круговое движение, испытывает центростремительное ускорение.
Ключевые термины
- угловое ускорение : Скорость изменения угловой скорости, часто обозначаемая α.
- тангенциальное ускорение : ускорение в направлении, касательном к окружности, в интересующей точке при круговом движении.
Угловое ускорение — это скорость изменения угловой скорости. В единицах СИ он измеряется в радианах на секунду в квадрате (рад / с 2 ) и обычно обозначается греческой буквой альфа ([латекс] \ альфа [/ латекс]).
Рассмотрим следующие ситуации, в которых угловая скорость непостоянна: когда фигуристка тянет за руки, когда ребенок запускает карусель из состояния покоя или когда жесткий диск компьютера останавливается, когда он выключен.Во всех этих случаях существует угловое ускорение, при котором изменяется [латекс] \ омега [/ латекс]. Чем быстрее происходит изменение, тем больше угловое ускорение. Угловое ускорение определяется как скорость изменения угловой скорости. В форме уравнения угловое ускорение выражается следующим образом:
[латекс] \ alpha = \ Delta \ omega / \ Delta \ text {t} [/ latex]
где [latex] \ Delta \ omega [/ latex] — это изменение угловой скорости, а [latex] \ Delta \ text {t} [/ latex] — это изменение во времени.Единицы углового ускорения: (рад / с) / с или рад / с 2 . Если [latex] \ omega [/ latex] увеличивается, тогда [latex] \ alpha [/ latex] положительно. Если [latex] \ omega [/ latex] уменьшается, то [latex] \ alpha [/ latex] отрицательно.
Полезно знать, как связаны линейное и угловое ускорение. При круговом движении ускорение составляет по касательной к окружности в интересующей точке (как показано на диаграмме ниже). Это ускорение называется тангенциальным ускорением , a t .
Касательное ускорение : При круговом движении ускорение может происходить из-за изменения величины скорости: a касается движения. Это ускорение называется тангенциальным ускорением.
Касательное ускорение относится к изменениям величины скорости, но не ее направления. При круговом движении центростремительное ускорение a c относится к изменениям направления скорости, но не ее величины. Объект, совершающий круговое движение, испытывает центростремительное ускорение (как показано на диаграмме ниже.) Таким образом, t и c перпендикулярны и независимы друг от друга. Касательное ускорение a t напрямую связано с угловым ускорением и связано с увеличением или уменьшением скорости (но не с ее направлением).
Центростремительное ускорение : Центростремительное ускорение возникает при изменении направления скорости; он перпендикулярен круговому движению. Таким образом, центростремительное и тангенциальное ускорения перпендикулярны друг другу.
6.1 Угол вращения и угловая скорость — Физика
Задачи обучения раздела
К концу этого раздела вы сможете делать следующее:
- Опишите угол поворота и свяжите его с его линейным аналогом
- Опишите угловую скорость и свяжите ее с ее линейным аналогом
- Решение задач, связанных с углом поворота и угловой скоростью
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим ученикам овладеть следующими стандартами:
- (4) Научные концепции.Учащийся знает и применяет законы движения в самых разных ситуациях. Ожидается, что студент:
- (C) анализировать и описывать ускоренное движение в двух измерениях с помощью уравнений, включая примеры снарядов и кругов.
Раздел Основные термины
| Градус меры | Меры радиана |
|---|---|
| 30∘30∘ | π6π6 |
| 60∘60∘ | π3π3 |
| 90∘90∘ | π2π2 |
| 120–120 | 2π32π3 |
| 135∘135∘ | 3π43π4 |
| 180∘180∘ | ππ |
Таблица 6.1 Обычно используемые углы в градусах и радианах
Угловая скорость
Поддержка учителя
Поддержка учителя
[BL] Проверьте смещение, скорость, скорость, ускорение.
[AL] Спросите студентов, изменяется ли скорость при равномерном круговом движении. А как насчет скорости? А как насчет разгона?
Насколько быстро вращается объект? Мы можем ответить на этот вопрос, используя понятие угловой скорости. Рассмотрим сначала угловую скорость (ω) (ω) — это скорость, с которой изменяется угол поворота.В форме уравнения угловая скорость равна
ω = ΔθΔt, ω = ΔθΔt,6,2
, что означает, что угловое вращение (Δθ) (Δθ) происходит за время ΔtΔt. Если объект поворачивается на больший угол поворота в данный момент времени, он имеет большую угловую скорость. Единицы измерения угловой скорости — радианы в секунду (рад / с).
Теперь давайте рассмотрим направление угловой скорости, а это значит, что теперь мы должны называть ее угловой скоростью. Направление угловой скорости — вдоль оси вращения.Для объекта, вращающегося по часовой стрелке, угловая скорость указывает от вас вдоль оси вращения. Для объекта, вращающегося против часовой стрелки, угловая скорость указывает на вас вдоль оси вращения.
Угловая скорость (ω) — это угловая версия линейной скорости v . Тангенциальная скорость — это мгновенная линейная скорость объекта во вращательном движении . Чтобы получить точное соотношение между угловой скоростью и тангенциальной скоростью, снова рассмотрим углубление на вращающемся компакт-диске.Эта яма перемещается по длине дуги (Δs) (Δs) за короткий промежуток времени (Δt) (Δt) , поэтому ее тангенциальная скорость равна
Из определения угла поворота, Δθ = ΔsrΔθ = Δsr, мы видим, что Δs = rΔθΔs = rΔθ. Подставляя это в выражение для v , получаем
v = rΔθΔt = rω. v = rΔθΔt = rω.Уравнение v = rωv = rω говорит, что тангенциальная скорость v пропорциональна расстоянию r от центра вращения. Следовательно, тангенциальная скорость больше для точки на внешнем крае CD (с большим r ), чем для точки ближе к центру CD (с меньшими r ).Это имеет смысл, потому что точка, находящаяся дальше от центра, должна покрывать большую длину дуги за то же время, что и точка ближе к центру. Обратите внимание, что обе точки по-прежнему будут иметь одинаковую угловую скорость, независимо от их расстояния от центра вращения. См. Рисунок 6.4.
Рисунок 6.4 Точки 1 и 2 вращаются на один и тот же угол (ΔθΔθ), но точка 2 перемещается на большую длину дуги (Δs2Δs2), потому что она дальше от центра вращения.Teacher Support
Teacher Support
[AL] Объясните, что период времени ΔtΔt в уравнении, определяющем тангенциальную скорость (v = ΔsΔtv = ΔsΔt), должен быть коротким, чтобы дуга, описываемая движущимся объектом, могла быть аппроксимирована прямой линия.Это позволяет нам определить направление касательной скорости как касательное к окружности. Это приближение становится все более точным по мере того, как ΔtΔt становится все меньше и меньше.
Теперь рассмотрим другой пример: шину движущегося автомобиля (см. Рис. 6.5). Чем быстрее вращается шина, тем быстрее движется автомобиль — большое ωω означает большое v , потому что v = rωv = rω. Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью ωω, будет создавать большую линейную (тангенциальную) скорость, v, для автомобиля.Это связано с тем, что больший радиус означает, что большая длина дуги должна касаться дороги, поэтому автомобиль должен двигаться дальше за то же время.
Рисунок 6.5 Автомобиль, движущийся со скоростью v, вправо, имеет шину, вращающуюся с угловой скоростью ωω. Скорость протектора шины относительно оси составляет v , такая же, как если бы автомобиль был поднят домкратом и колеса вращались, не касаясь дороги. Непосредственно под осью, где шина касается дороги, протектор шины движется назад по отношению к оси с тангенциальной скоростью v = rωv = rω, где r — радиус шины.Поскольку дорога неподвижна относительно этой точки шины, автомобиль должен двигаться вперед с линейной скоростью v . Большая угловая скорость шины означает большую линейную скорость автомобиля.Однако есть случаи, когда линейная скорость и тангенциальная скорость не эквивалентны, например, когда автомобиль вращает свои колеса по льду. В этом случае линейная скорость будет меньше тангенциальной скорости. Из-за отсутствия трения под шинами автомобиля на льду длина дуги, по которой движутся протекторы шин, больше, чем линейное расстояние, по которому движется автомобиль.Это похоже на бег на беговой дорожке или на велотренажере; вы буквально никуда не денетесь.
Советы для успеха
Угловая скорость ω и тангенциальная скорость v являются векторами, поэтому мы должны включить величину и направление. Направление угловой скорости — вдоль оси вращения и указывает от вас для объекта, вращающегося по часовой стрелке, и к вам для объекта, вращающегося против часовой стрелки. В математике это описывается правилом правой руки.Тангенциальная скорость обычно описывается как вверх, вниз, влево, вправо, север, юг, восток или запад, как показано на рисунке 6.6.
Рис. 6.6. Поскольку муха на краю старинной виниловой пластинки движется по кругу, ее мгновенная скорость всегда направлена по касательной к кругу. Направление угловой скорости в данном случае указано на странице.
Watch Physics
Взаимосвязь между угловой скоростью и скоростью
В этом видео рассматриваются определение и единицы угловой скорости и их связь с линейной скоростью.Здесь также показано, как преобразовать число оборотов в радианы.
Контроль захвата
Изменится ли линейная скорость объекта, движущегося по круговой траектории с постоянной угловой скоростью при увеличении радиуса траектории?
- Да, потому что тангенциальная скорость не зависит от радиуса.
- Да, потому что тангенциальная скорость зависит от радиуса.
- Нет, поскольку тангенциальная скорость не зависит от радиуса.
- Нет, потому что тангенциальная скорость зависит от радиуса.
Решение задач, связанных с углом вращения и угловой скоростью
Snap Lab
Измерение угловой скорости
В этом упражнении вы будете создавать и измерять равномерное круговое движение, а затем сравнивать его с круговыми движениями с разными радиусами.
- Одна струна (длина 1 м)
- Один предмет (резиновая пробка с двумя отверстиями) для привязки к концу
- Один таймер
Процедура
- Привяжите объект к концу строки.
- Поверните объект по горизонтальному кругу над головой (качаясь с запястья). Важно, чтобы круг был горизонтальным!
- Поддерживайте постоянную скорость вращения объекта.
- Измерьте таким образом угловую скорость объекта. Измерьте время в секундах, за которое объект совершит 10 оборотов. Разделите это время на 10, чтобы получить угловую скорость в оборотах в секунду, которую вы можете преобразовать в радианы в секунду.
- Какова приблизительная линейная скорость объекта?
- Переместите руку вверх по тетиве так, чтобы ее длина составляла 90 см.Повторите шаги 2–5.
- Переместите руку вверх по струне так, чтобы ее длина была 80 см. Повторите шаги 2–5.
- Переместите руку вверх по струне так, чтобы ее длина составила 70 см. Повторите шаги 2–5.
- Переместите руку вверх по струне так, чтобы ее длина составляла 60 см. Повторите шаги 2–5 .
- Переместите руку вверх по струне так, чтобы ее длина была 50 см. Повторите шаги 2–5 .
- Постройте графики зависимости угловой скорости от радиуса (т. Е. Длины струны) и линейной скорости от радиуса. Опишите, как выглядит каждый график.
Проверка захвата
Если вы поворачиваете объект медленно, он может вращаться со скоростью менее одного оборота в секунду. Какими были бы обороты в секунду для объекта, который совершает один оборот за пять секунд? Какова была бы его угловая скорость в радианах в секунду?
- Объект будет вращаться в \ frac {1} {5} \, \ text {rev / s}. Угловая скорость объекта будет \ frac {2 \ pi} {5} \, \ text {rad / s}.
- Объект будет вращаться в \ frac {1} {5} \, \ text {rev / s}.Угловая скорость объекта будет \ frac {\ pi} {5} \, \ text {rad / s}.
- Объект будет вращаться со скоростью 5 \, \ text {об / с}. Угловая скорость объекта будет 10 \ pi \, \ text {rad / s}.
- Объект будет вращаться со скоростью 5 \, \ text {об / с}. Угловая скорость объекта будет 5 \ pi \, \ text {rad / s}.
Теперь, когда у нас есть понимание понятий угла поворота и угловой скорости, мы применим их к реальным ситуациям с часовой башней и вращающимся колесом.
Рабочий пример
Угол поворота часовой башни
Часы на часовой башне имеют радиус 1,0 м. (а) На какой угол поворота движется часовая стрелка часов, когда она движется с 12 часов дня. до 15:00? (b) Какова длина дуги по внешнему краю часов между часовой стрелкой в эти два момента времени?
Стратегия
Мы можем вычислить угол поворота, умножив полный оборот (2π2π радиан) на долю 12 часов, покрываемых часовой стрелкой при переходе от 12 к 3.Когда у нас есть угол поворота, мы можем найти длину дуги, переписав уравнение Δθ = ΔsrΔθ = Δsr, поскольку радиус задан.
Решение для (а)
При переходе с 12 на 3 часовая стрелка покрывает 1/4 из 12 часов, необходимых для совершения полного оборота. Следовательно, угол между часовой стрелкой в точках 12 и 3 равен 14 × 2πrad = π214 × 2πrad = π2 (т.е. 90 градусов).
Решение пункта (b)
Преобразование уравнения
получаем
Вставка известных значений дает длину дуги
Δs = (1.0 м) (π2рад) = 1,6 м Δs = (1,0 м) (π2рад) = 1,6 м6,6
Обсуждение
Нам удалось отбросить радианы из окончательного решения в часть (b), потому что радианы на самом деле безразмерны. Это потому, что радиан определяется как отношение двух расстояний (радиуса и длины дуги). Таким образом, формула дает ответ в метрах, как и ожидалось для длины дуги.
Рабочий пример
Как быстро вращается автомобильная шина?
Вычислить угловую скорость 0.Автомобильная шина с радиусом 300 м при движении автомобиля со скоростью 15,0 м / с (около 54 км / ч). См. Рисунок 6.5.
Стратегия
В этом случае скорость протектора шины относительно оси шины такая же, как и скорость автомобиля относительно дороги, поэтому мы имеем v = 15,0 м / с. Радиус покрышки r = 0,300 м. Поскольку нам известны v и r , мы можем переписать уравнение v = rωv = rω, чтобы получить ω = vrω = vr и найти угловую скорость.
Решение
Чтобы найти угловую скорость, воспользуемся соотношением: ω = vrω = vr.
Вставка известных величин дает
ω = 15,0 м / с 0,300 м = 50,0 рад / с. ω = 15,0 м / с 0,300 м = 50,0 рад / с.6,7
Обсуждение
Когда мы отменяем единицы измерения в приведенном выше вычислении, мы получаем 50,0 / с (то есть 50,0 в секунду, что обычно записывается как 50,0 с −1 ). Но угловая скорость должна иметь единицы рад / с. Поскольку радианы безразмерны, мы можем вставить их в ответ для угловой скорости, потому что мы знаем, что движение является круговым. Также обратите внимание, что если землеройный трактор с гораздо большими шинами, скажем, 1.Радиус 20 м, двигался с той же скоростью 15,0 м / с, его шины вращались медленнее. У них будет угловая скорость
ω = 15,0 м / с 1,20 м = 12,5 рад / с ω = 15,0 м / с 1,20 м = 12,5 рад / с6,8
Практические задачи
1.Каков угол в градусах между часовой и минутной стрелками часов, показывающих 9:00 утра?
- 0 °
- 90 °
- 180 °
- 360 °
Каково приблизительное значение длины дуги между часовой и минутной стрелками часов, показывающих 10:00 a.м, если радиус часов 0,2 м?
- 0,1 м
- 0,2 м
- 0,3 м
- 0,6 м
Проверьте свое понимание
3.Что такое круговое движение?
- Круговое движение — это движение объекта по линейному пути.
- Круговое движение — это движение объекта по зигзагообразной траектории.
- Круговое движение — это движение объекта по круговой траектории.
- Вариант D сбивает с толку как отвлекающий
Что подразумевается под радиусом кривизны при описании вращательного движения?
- Радиус кривизны — это радиус круговой траектории.
- Радиус кривизны — это диаметр круговой траектории.
- Радиус кривизны — это длина окружности круговой траектории.
- Радиус кривизны — это площадь круговой траектории.
Что такое угловая скорость?
- Угловая скорость — это скорость изменения диаметра круговой траектории.
- Угловая скорость — это скорость изменения угла, образованного круговой траекторией.
- Угловая скорость — это скорость изменения площади круговой траектории.
- Угловая скорость — это скорость изменения радиуса круговой траектории.
Какое уравнение определяет угловую скорость ω, когда r — радиус кривизны, θ — угол, а t — время?
- \ omega = \ frac {\ Delta \ theta} {\ Delta {t}}
- \ omega = \ frac {\ Delta {t}} {\ Delta \ theta}
- \ omega = \ frac {\ Delta {r}} {\ Delta {t}}
- \ omega = \ frac {\ Delta {t}} {\ Delta {r}}
Назовите три примера объекта, совершающего круговое движение.
- искусственный спутник, вращающийся вокруг Земли, гоночный автомобиль, движущийся по круговой гоночной трассе, и волчок, вращающийся вокруг своей оси
- искусственный спутник, вращающийся вокруг Земли, гоночный автомобиль, движущийся по круговой гоночной трассе, и мяч, привязанный к веревке, вращающийся по кругу вокруг головы человека
- Земля вращается вокруг своей оси, гоночный автомобиль движется по круговой гоночной трассе, и мяч, привязанный к веревке, вращается по кругу вокруг головы человека
- Земля вращается вокруг своей оси, лопасти рабочего потолочного вентилятора и волчок, вращающийся вокруг своей оси
Какова относительная ориентация векторов радиуса и тангенциальной скорости объекта при равномерном круговом движении?
- Вектор тангенциальной скорости всегда параллелен радиусу круговой траектории, по которой движется объект.
- Вектор тангенциальной скорости всегда перпендикулярен радиусу круговой траектории, по которой движется объект.
- Вектор тангенциальной скорости всегда находится под острым углом к радиусу круговой траектории, по которой движется объект.
- Вектор тангенциальной скорости всегда находится под тупым углом к радиусу круговой траектории, по которой движется объект.
Teacher Support
Teacher Support
Используйте вопросы Check Your Understanding , чтобы оценить, усвоили ли учащиеся учебные цели этого раздела. Если учащиеся борются с определенной целью, формирующая оценка поможет определить, какая цель вызывает проблему, и направит учащихся к соответствующему содержанию.
Вращательное движение | Блог Гэри Гарбера
До сих пор в этом семестре нашего изучения классической механики мы изучали поступательное движение. Теперь мы приступим к изучению вращательного движения.
У каждой концепции, которую мы изучили до сих пор, есть вращательный аналог.
В начале года мы обсуждали, как объект может претерпеть смещение x . Мы также могли повернуть объект на угол θ.
Аналогично, скорость объекта или скорость изменения положения
имеет аналог вращения, скорость вращения, скорость изменения угла
ω = Δθ / Δt
Существует также угловое ускорение, которое представляет собой скорость изменения угловой скорости.Мы можем изучить крутящий момент, который представляет собой силу вращения. Момент инерции (или инерции вращения) — это тенденция объекта оставаться в состоянии покоя или оставаться в состоянии вращательного движения. Основываясь на этом, угловой момент — это инерция вращения в состоянии вращательного движения. У нас также может быть кинетическая энергия вращения!
Если мы предположим, что объект непрерывно вращается, то другой способ взглянуть на вращательное движение — это исследовать период вращения, T . Измеряемый в единицах времени ( миллисекунд, секунды, часы, годы, эоны …), период — это время, необходимое для одного полного оборота.Мы также могли бы описать, как часто объект вращается. Частота объекта, f , на самом деле обратно пропорциональна периоду вращения.
T = 1 / f
и
ф = 1 / т
Метрической единицей измерения частоты является герц ( Гц, ), где 1 Гц = 1 цикл / секунду . Вы, вероятно, знакомы с термином Герц по частотам на шкале радиоприемника, например, WBUR 90,9 МГц или WBZ 1030 кГц .
Пример
Представьте себе маленького мальчика, который пытается вызвать головокружение, быстро вращаясь.Если он вращается с частотой 0,8 Гц, сколько времени ему потребуется, чтобы сделать 1 оборот?
f = 0,8 Гц
T = 1 / f = 1 / 0,8 Гц = 1 / 0,8 циклов в секунду = 1,25 секунд
Другая традиционная единица измерения частоты — оборотов в минуту или оборотов в минуту . Вы можете увидеть это на старомодном проигрывателе, который мог вращаться со скоростью 33 или 45 об / мин на .
А пока рассмотрим двух маленьких человечков LEGO, стоящих на проигрывателе.Когда проигрыватель поворачивается, мы можем описать движение маленьких человечков LEGO с точки зрения их линейной скорости (метры в секунду) или скорости их вращения. Если мы установим проигрыватель на 45 об / мин, то оба LEGO-человечка будут иметь одинаковую скорость вращения. Однако у них разные линейные или тангенциальные скорости. Мы используем слово тангенциальный, потому что, если человек LEGO поскользнется и упадет, его собственная инерция заставит его отлететь от проигрывателя по линии, касательной к его круговому движению!
Мы можем рассчитать линейную скорость для каждого человека, используя уравнение
v = 2πr / Т
где r — радиус круга, а T — период вращения.Помните, что скорость — это расстояние во времени. В этом случае расстояние за один период вращения оказывается длиной окружности.
Если мужчины расположены на нашем проигрывателе на расстоянии 10 см и 4 см от центральной оси:
Пример
f = 45 об / мин
r = 12 см
Сначала вычисляем период. С 45 об / мин = 0,75 об / с
Таким образом, период вращения равен 1.33 секунд .
Таким образом, скорость будет
v = 2πr / T = 2π (10 см ) / 1,33 с = 47 см / с
У маленького человечка, стоящего в радиусе 4 см, у него гораздо меньшая линейная скорость, хотя и такая же скорость вращения.
v = 2πr / T = 2π (4 см ) / 1,33 с = 19 см / с
Существует тонкая разница между скоростью вращения и скоростью вращения, которую мы представим позже.
Мы можем определить взаимосвязь между линейной скоростью и угловой скоростью с помощью следующего уравнения
v = ω r
Обратите внимание, что ω, угловая скорость, была определена ранее как изменение угла в единицу времени.
ω = Δθ / Δt
При рассмотрении приведенного выше уравнения возникает интересный вопрос относительно единиц измерения угловой скорости. До сих пор мы использовали такие термины, как обороты в минуту или обороты в секунду. Но революцию можно было бы определить как ПОЛНЫЙ поворот на 360 °.
Вы, наверное, изучали единицы измерения углов в градусах. Но когда мы обсуждаем угловую скорость, мы обычно не говорим об целом числе оборотов. Таким образом, мы могли бы использовать такие единицы измерения, как градусы в секунду. Однако градус не является метрической единицей вращения. Стандартная единица измерения — радиан.
2π радиан = 360 °
Если мы посмотрим на изображение единичного круга, мы сможем увидеть преобразование между радианами и градусами. Это действительно одно и то же, просто разные единицы.
С одной стороны, единственная разница между частотой и угловой скоростью заключается в единицах измерения. Угловая скорость измеряется в радиан / секунду , а частота измеряется в Гц или оборотов в секунду . Таким образом, мы могли бы выразить алгебраическую связь между этими двумя терминами как
2πf = ω
Используя это, мы могли бы фактически найти угловую скорость нашего проигрывателя, который вращается со скоростью 45 об / мин .
ω = 2πf = 2π (0.75 об / с ) = 4,7 радиан / с
Пример
Давайте еще раз посмотрим на человечков LEGO на проигрывателе. Используя соотношение между линейной скоростью и угловой скоростью, находим
v = ω r
v = 4,7 радиан в секунду x 10 см = 47 см / с
и для человека ближе к центру
v = 4,7 радиан / сек x 4 см = 19 см / сек
Важно отметить, что линейная скорость увеличивается как с угловой скоростью, так и с радиусом
Период и частота — AP Physics 1
Пояснение:Мы можем начать с сохранения энергии, чтобы решить эту проблему:
Постановка задачи говорит нам, что цилиндр изначально находится в состоянии покоя, поэтому мы можем исключить начальную кинетическую энергию.Если мы предположим, что высота цилиндра при достижении периода 0,2 с имеет высоту 0, мы можем исключить конечную потенциальную энергию. Следовательно, получаем:
Расширяя эти члены и убедившись, что у нас есть линейная и вращательная составляющие кинетической энергии, мы получаем уравнение (1):
Прежде чем двигаться дальше, мы знаем, что нам нужно будет вычислить что-то, что мы сможем использовать для определения периода цилиндра. Мы знаем, что период — это время, за которое цилиндр совершает один полный оборот.Думая практически, мы можем использовать окружность цилиндра и линейную скорость для определения периода:
Используя переменные, получаем уравнение:
Преобразуя конечную скорость, мы получаем уравнение (2):
Теперь мы знаем, что период зависит от конечной линейной скорости. Вернемся к этому уравнению. Теперь мы можем вернуться к уравнению (1) и начать подставлять выражения для неизвестных переменных слева направо.Первая неизвестная переменная — это начальная высота. Однако мы можем использовать пройденное расстояние цилиндра и угол наклона:
Переставляя для начальной высоты, мы получаем уравнение (3):
Далее следующий неизвестный член — конечная скорость. Мы можем заменить уравнение (2), которое мы уже получили:
Далее следующий неизвестный член — момент инерции. Используя выражение для цилиндра, получаем уравнение (4):
Двигаясь дальше, последний неизвестный член — это конечная скорость вращения.Мы можем использовать соотношение между этим и линейной скоростью:
Теперь подставляя уравнение (2), мы получаем уравнение (5):
Теперь мы можем заменить уравнения 2, 3, 4 и 5 в уравнение (1):
Исключив массу из обеих частей уравнения и расширив каждый член:
Объединение терминов справа:
Перестановка по длине:
Проверьте свои подразделения и убедитесь, что у вас остались секунды, прежде чем двигаться дальше!
Мы знаем значения для каждой переменной, так что пора подключиться:
Как рассчитать угловую частоту
Обновлено 16 декабря 2020 г.
Автор Липи Гупта
Угловая частота ω объекта, совершающего периодическое движение, например шара на конце раскачиваемой веревки по кругу, измеряет скорость, с которой мяч проходит на полные 360 градусов, или 2π радиан.Самый простой способ понять, как рассчитать угловую частоту, — это построить формулу и посмотреть, как она работает на практике.
Формула угловой частоты
Формула для угловой частоты представляет собой частоту колебаний f (часто в герцах или колебаниях в секунду), умноженную на угол, на который движется объект. Формула угловой частоты для объекта, который совершает полное колебание или вращение:
\ omega = 2 \ pi f
Более общая формула просто:
\ omega = \ frac {\ theta} {t}
где θ — это угол, на который перемещался объект, а t — время, которое потребовалось, чтобы пройти через θ .
Помните: частота — это скорость, поэтому размеры этой величины — радианы в единицу времени. Единицы будут зависеть от конкретной проблемы. Если вы говорите о вращении карусели, вы можете говорить об угловой частоте в радианах в минуту, но угловая частота Луны вокруг Земли может иметь больше смысла в радианах в день.
Формула угловой частоты с использованием периода
Чтобы полностью понять эту величину, полезно начать с более естественной величины, периода и работать в обратном направлении.Период ( T ) колеблющегося объекта — это время, необходимое для завершения одного колебания. Например, в году 365 дней, потому что именно столько времени требуется Земле, чтобы один раз обойти вокруг Солнца. Это период движения Земли вокруг Солнца.
Но если вы хотите узнать скорость вращения, вам нужно найти угловую частоту. Частоту вращения или количество вращений, совершаемых за определенный промежуток времени, можно рассчитать по формуле:
f = \ frac {1} {T}
Для Земли один оборот вокруг Солнца занимает 365 дней, Итак, f = 1/365 дня.
Так какова угловая частота? Один оборот Земли проходит на 2π радиан, поэтому угловая частота ω = 2π / 365. На словах Земля проходит через 2π радиан за 365 дней.
Пример расчета
Попробуйте другой пример расчета угловой частоты в другой ситуации, чтобы привыкнуть к концепциям. Поездка на колесе обозрения может длиться несколько минут, за это время вы достигнете вершины поездки несколько раз. Допустим, вы сидите в верхней части колеса обозрения и замечаете, что колесо переместилось на четверть оборота за 15 секунд.Какая у него угловая частота? Есть два подхода, которые можно использовать для расчета этого количества.
Во-первых, если ¼ вращение занимает 15 секунд, полный оборот занимает 4 × 15 = 60 секунд. Следовательно, частота вращения составляет f = 1/60 с −1 , а угловая частота равна:
\ begin {align} ω & = 2πf \\ & = π / 30 \ end {выровнено }
Точно так же вы переместились через π / 2 радиан за 15 секунд, так что снова, используя наше понимание того, что такое угловая частота:
\ begin {align} ω & = \ frac {(π / 2)} {15 } \\ & = \ frac {π} {30} \ end {align}
Оба подхода дают один и тот же ответ, так что, похоже, наше понимание угловой частоты имеет смысл!
И последнее…
Угловая частота — это скалярная величина, то есть просто величина.Однако иногда мы говорим об угловой скорости, которая является вектором. Следовательно, формула угловой скорости такая же, как уравнение угловой частоты, которое определяет величину вектора.
Тогда направление вектора угловой скорости может быть определено с помощью правила правой руки. Правило правой руки позволяет нам применять соглашение, которое физики и инженеры используют для определения «направления» вращающегося объекта.
Равномерное круговое движение
Равномерное круговое движениеследующий: Центростремительное ускорение Вверх: Круговое движение Предыдущая: Введение Предположим, что объект совершает круговую орбиту радиуса с равномерной тангенциальной скоростью.Мгновенный положение объекта удобнее всего задавать в виде угол . См. Рис. 57. Например, мы могли бы решить, что соответствует в местоположение объекта, и в этом случае мы должны написать
| (245) |
где называется угловой скоростью объекта. Для равномерного вращающегося объекта, угловая скорость — это просто угол, на который объект оборачивается за одну секунду.
Рассмотрим движение объекта во временном интервале между
а также . В этом интервале объект поворачивается на угол
, и очерчивает дугу окружности длиной. См. Рис.57.
Достаточно очевидно, что длина дуги прямо пропорциональна углу
: а какова константа пропорциональности? Ну, угол
соответствует длине дуги.Следовательно, угол
должен соответствовать длине дуги
| (246) |
На этом этапе удобно определить новую угловую единицу, известную как радиан, (символ рад.). Угол измеряется в радианах, относится к углу, измеренному в градусах, через следующая простая формула:
| (247) |
Таким образом, соответствует радианам, соответствует радианам, соответствует радианам и соответствует до 1 радиана.Когда измеряется в радианах, уравнение. (246) упрощает сильно дать
| (248) |
Отныне в этом курсе все углы измеряются в радианах по умолчанию .
Рассмотрим движение объекта в коротком интервале между временами и.
В этом интервале объект поворачивается на небольшой угол и
очерчивает короткую дугу длины, где
| (249) |
Теперь ( я.е. , расстояние, пройденное за единицу времени) это просто тангенциальная скорость, тогда как (, т.е. , угол поворота за единицу времени) — это просто угловая скорость . Таким образом, разделив уравнение. (249) по, получаем
| (250) |
Обратите внимание, однако, что эта формула действительна только в том случае, если угловая скорость измеряется в радианах в секунду . Отныне в этом Конечно, все угловые скорости измеряются в радианах в секунду по умолчанию .
Объект, вращающийся с постоянной угловой скоростью, проходит сквозь
радиан за 1 секунду. Следовательно, объект поворачивается на радианы
(, то есть , он выполняет полный цикл) в
| (251) |
секунд. Здесь — период повторения кругового движения. Если объект выполняет полный цикл (, т. е. , проходит) за секунды, тогда количество циклов, выполняемых в секунду, равно
| (252) |
Здесь частота повторения , « движения измеряется в циклов в секунду — иначе известное как герц (символ Гц).
В качестве примера предположим, что объект выполняет равномерное круговое движение, радиус , с частотой
(, то есть , объект выполняет полное
вращение 50 раз в секунду). Период повторения этого движения просто
| (253) |
Кроме того, угловая частота движения определяется выражением
| (254) |
Наконец, тангенциальная скорость объекта равна
| (255) |
следующий: Центростремительное ускорение Вверх: Круговое движение Предыдущая: Введение Ричард Фицпатрик 2006-02-02 .





