Второй закон ома – Закон Ома для участка цепи и полной цепи формулы и определения

Второй закон ома определение

Второй закон ома определение

Закон ома для замкнутой цепи говорит о том что. Величина тока в замкнутой цепи, которая состоит из источника тока обладающего внутренним сопротивлением, а также внешним нагрузочным сопротивлением. Будет равна отношению электродвижущей силы источника к сумме внешнего и внутреннего сопротивлений.

Закон Ома 2

В сложных цепях встречаются соединения, которые нельзя отнести ни к последовательным, ни к параллельным. К таким соединениям относятся трехлучевая звезда и треугольник сопротивлений (рис.1.3). Их взаимное эквивалентное преобразование во многих случаях позволяет упростить схему и свести ее к схеме смешанного (параллельного и последовательного) соединения сопротивлений. При этом необходимо определенным образом пересчитать сопротивления элементов звезды или треугольника.

Закон Ома

Появление смартфонов, гаджетов, бытовых приборов и прочей электротехники коренным образом изменило облик современного человека.

Приложены огромные усилия, направленные на исследование физических закономерностей для улучшения старой и создания новой техники. Одной из таких зависимостей является закон Ома.

Закон Ома для «чайников»: понятие, формула, объяснение

Это как раз та штука, которая заставляет электроны двигаться. Электрический потенциал характеризует способность поля совершать работу по переносу заряда из одной точки в другую. Так, между двумя точками проводника существует разность потенциалов, и электрическое поле совершает работу по переносу заряда.

2 Закон ома определение

Кроме того, любой проводник, как показал Дж. Максвелл, при изменении силы тока в нём излучает энергию в окружающее пространство, и потому ЛЭП ведёт себя как антенна, что заставляет в ряде случаев наряду с омическими потерями брать в расчёт и потери на излучение.

Закон Ома для участка цепи

Расчеты, выполняемые с помощью закона Ома для участка цепи, будут правильны в том случае, когда напряжение выражено в вольтах, сопротивление в омах и ток в амперах. Если используются кратные единицы измерений этих величин (например, миллиампер, милливольт, мегаом и т. д.), то их следует перевести соответственно в амперы, вольты и омы. Чтобы подчеркнуть это, иногда формулу закона Ома для участка цепи пишут так:

Закон Ома для участка цепи

Резисторы являются пассивными элементами, которые оказывают сопротивление потоку электрического тока в цепи. Резистор, который функционирует в соответствии с законом Ома, называется омическим сопротивлением. Когда ток проходит через такой резистор, то падение напряжения на его выводах пропорционально величине сопротивления.

Закон Ома для участка цепи

Закон Ома для участка цепи — это основной закон в электротехнике. Он устанавливает связь между током, сопротивлением и напряжением. С его помощью можно изучить и рассчитать электрические цепи. Важно не просто выучить закон Ома, а понять его, как он применяется на самом деле. Так как довольно часто происходят ошибки в его применении на практике, из-за не правильного его использования.

Реферат: Закон Ома 2

В сложных цепях встречаются соединения, которые нельзя отнести ни к последовательным, ни к параллельным. К таким соединениям относятся трехлучевая звезда и треугольник сопротивлений (рис.1.3). Их взаимное эквивалентное преобразование во многих случаях позволяет упростить схему и свести ее к схеме смешанного (параллельного и последовательного) соединения сопротивлений. При этом необходимо определенным образом пересчитать сопротивления элементов звезды или треугольника.

Закон Ома

В 1826 величайший немецкий физик Георг Симон Ом публикует свою работу «Определение закона, по которому металлы проводят контактное электричество», где дает формулировку знаменитому закону. Ученые того времени встретили враждебно публикации великого физика. И лишь после того, как другой ученый – Клод Пулье, пришел к тем же выводам опытным путем, закон Ома признали во всем мире.

Закон Ома

Коэффициент r называется сопротивлением, а g — проводимостью. Оба коэффициента определяются геометрическими размерами и физическими свойствами среды, по которой протекает электрический ток. В простейшем случае протекания тока по проводнику с постоянным сечением r= r l/s , где r , l и s — соответственно удельное электрическое сопротивление проводника, его длина и площадь поперечного сечения.

Закон Ома для участка цепи

Закон Ома для замкнутой цепи гласит, что значение силы тока, который протекает в электрической цепи, имеет обратно пропорциональную зависимость в отношении сопротивления нагрузки и прямую в отношении приложенного напряжения. Это краткая формулировка, но она полностью отображает суть закона.

Школьная Энциклопедия

Чтобы в электрической цепи существовал ток, необходимо наличие в ней устройства, которое создавало бы и поддерживало разность потенциалов на участках цепи за счёт сил неэлектрического происхождения. Такое устройство называется источником постоянного тока, а силы — сторонними силами.

Что такое закон Ома

Простейшим образом создать такое поле может обыкновенная батарейка. Если на конце проводника недостаток электронов, то он обозначается знаком «+», если избыток, то «-». Электроны, имеющие всегда отрицательный заряд, естественно, устремятся к плюсу. Так в проводнике рождается электрический ток, т. е. направленное перемещение электрических зарядов. Чтобы его увеличить, необходимо усилить электрическое поле в проводнике. Или, как говорят, приложить к концам проводника большее напряжение.

Решение задач по ТОЭ, ОТЦ, Высшей математике, Физике, Программированию

v. Напpимеp, в электpонных лампах закон Стокса для силы сопpотивления, действующей на электpон, не выполняется и ускоpение электpонов в электрическом поле нельзя считать pавным нулю. Во-втоpых, необходимо, чтобы плотность носителей тока n не зависела от напpяженности поля. Напpимеp, в коpонном pазpяде пеpвое условие выполняется, но не выполняется втоpое. В этом pазpяде ток пеpеносится ионами, котоpые обpазуются в непосpедственной близости к остpию коpониpующего электpода и движутся затем чеpез весь пpомежуток.

Их плотность в этом пpомежутке существенно зависит от напpяженности поля.

russianjurist.ru

Где и когда можно применять закон Ома?

Закон Ома в упомянутой форме справедлив в достаточно широких пределах для металлов. Он выполняется до тех пор, пока металл не начнет плавиться. Менее широкий диапазон применения у растворов (расплавов) электролитов и в сильно ионизированных газах (плазме).

Работая с электрическими схемами, иногда требуется определять падение напряжения на определенном элементе. Если это будет резистор с известной величиной сопротивления (она проставляется на корпусе), а также известен проходящий через него ток, узнать напряжение можно с помощью формулы Ома, не подключая вольтметр.

Закон Ома — это… Что такое Закон Ома?

V — напряжение,
I — сила тока,
R — сопротивление.

Зако́н О́ма — физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника. Экспериментально установлен в 1826 году, и назван в честь его первооткрывателя Георга Ома.

В своей оригинальной форме он был записан его автором в виде : ,

Здесь X — показания гальванометра, т.е в современных обозначениях сила тока I, a — величина, характеризующая свойства источника тока, постоянная в широких пределах и не зависящая от величины тока, то есть в современной терминологии электродвижущая сила (ЭДС) , l — величина, определяемая длиной соединяющих проводов, чему в современных представлениях соответствует сопротивление внешней цепи R и, наконец, b параметр, характеризующий свойства всей установки, в котором сейчас можно усмотреть учёт внутреннего сопротивления источника тока r^[1].

В таком случае в современных терминах и в соответствии с предложенной автором записи формулировка Ома (1) выражает

Закон Ома для полной цепи:

, (2)

где:

Из закона Ома для полной цепи вытекают следствия:

• При r<<R сила тока в цепи обратно пропорциональна её сопротивлению. А сам источник в ряде случаев может быть назван источником напряжения
• При r>>R сила тока от свойств внешней цепи (от величины нагрузки) не зависит. И источник может быть назван источником тока.

Часто^[2] выражение:

(3)

(где есть напряжение или падение напряжения, или, что то же, разность потенциалов между началом и концом участка проводника) тоже называют «Законом Ома».

Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется:

(4)

То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника.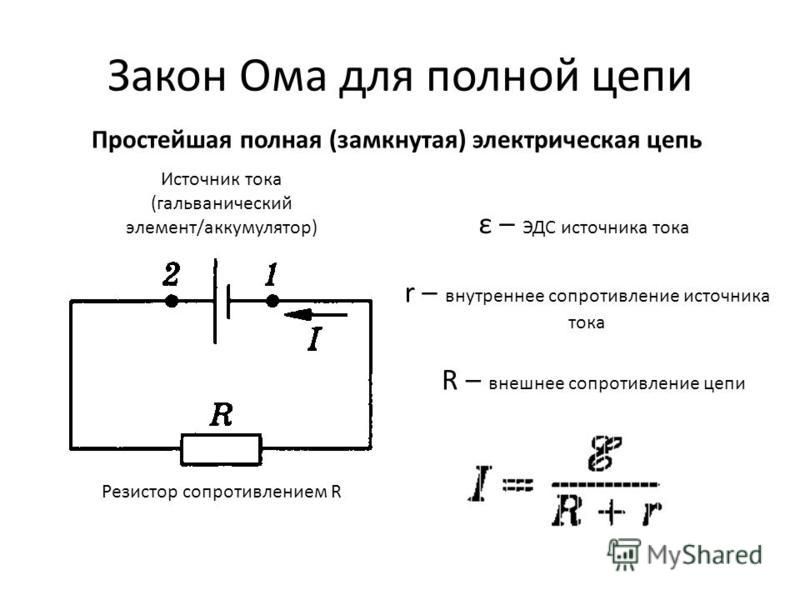 Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС.

К другой записи формулы (3), а именно:

(5)

Применима другая формулировка:

Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи.

Выражение (5) можно переписать в виде:

(6)

где коэффициент пропорциональности G назван проводимость или электропроводность. Изначально единицей измерения проводимости был «обратный Ом» — Mо^[3], впоследствии переименованный в Си́менс (обозначение: См, S).

Мнемоническая диаграмма для Закона

Схема, иллюстрирующая три составляющие закона Ома Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления

В соответствии с этой диаграммой формально может быть записано выражение:

(7)

Которое всего лишь позволяет вычислить (применительно к известному току, создающему на заданном участке цепи известное напряжение), сопротивление этого участка. Но математически корректное утверждение о том, что сопротивление проводника растёт прямо пропорционально приложенному к нему напряжению и обратно пропорционально пропускаемому через него току, физически ложно.

В специально оговорённых случаях сопротивление может зависеть от этих величин, но по умолчанию оно определяется лишь физическими и геометрическими параметрами проводника:

(8)

где:

•  — удельное сопротивление материала, из которого сделан проводник,
•  — его длина
•  — площадь его поперечного сечения

Закон Ома и ЛЭП

Одним из важнейших требований к линиям электропередач (ЛЭП) является уменьшение потерь при доставке энергии потребителю.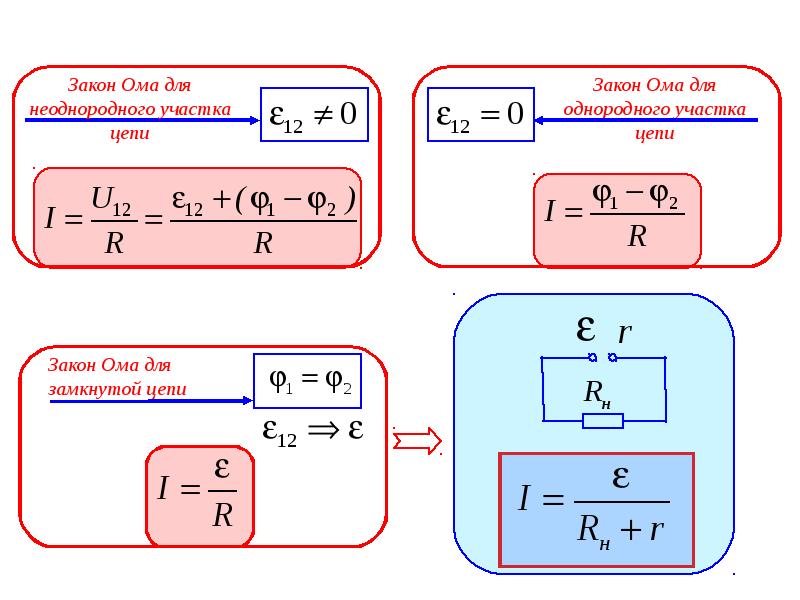 Эти потери в настоящее время заключаются в нагреве проводов, то есть переходе энергии тока в тепловую энергию, за что ответственно омическое сопротивление проводов. Иными словами задача состоит в том, чтобы довести до потребителя как можно более значительную часть мощности источника тока = при минимальных потерях мощности в линии передачи = , где , причём на этот раз есть суммарное сопротивление проводов и внутреннего сопротивления генератора, (последнее всё же меньше сопротивления линии передач).

В таком случае потери мощности будут определяться выражением:

= (9)

Отсюда следует, что при постоянной передаваемой мощности её потери растут прямо пропорционально длине ЛЭП и обратно пропорционально квадрату ЭДС. Таким образом желательно всемерное её увеличение, что ограничивается электрической прочностью обмотки генератора. И повышать напряжение на входе линии следует уже после выхода тока из генератора, что для постоянного тока является проблемой. Однако, для переменного тока эта задача много проще решается с помощью использования трансформаторов, что и предопределило повсеместное распространение ЛЭП на переменном токе.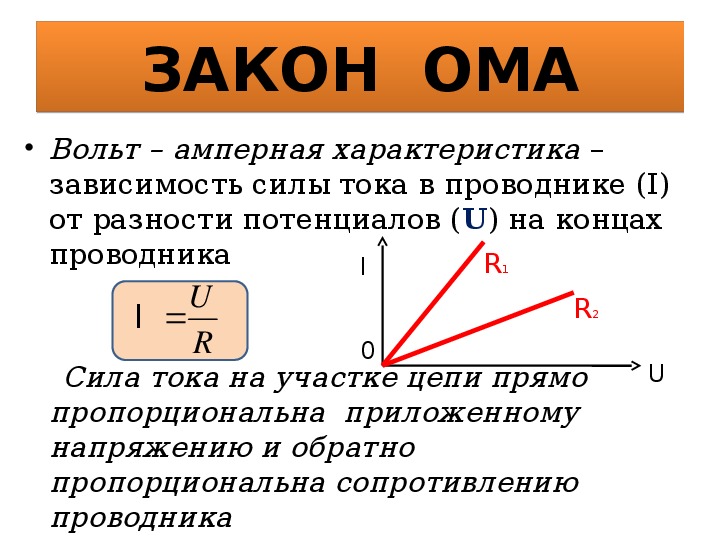 Однако при повышении напряжения в ней возникают потери на коронирование и возникают трудности с обеспечением надёжности изоляции от земной поверхности. Поэтому наибольшее, практически используемое, напряжение в дальних ЛЭП не превышает миллиона вольт.

Кроме того, любой проводник, как показал Дж. Максвелл, при изменении силы тока в нём, излучает энергию в окружающее пространство, и потому ЛЭП ведёт себя как антенна, что заставляет в ряде случаев наряду с омическими потерями брать в расчёт и потери на излучение.

Закон Ома в дифференциальной форме

Сопротивление зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника.

Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:

где:

Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1).

Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред.

Закон Ома для переменного тока

Вышеприведённые соображения о свойствах электрической цепи при использовании источника (генератора) с переменной во времени ЭДС остаются справедливыми. Специальному рассмотрению подлежит лишь учёт специфических свойств потребителя, приводящих к разновремённости достижения напряжением и током своих максимальных значений, то есть учёта фазового сдвига.

Если ток является синусоидальным с циклической частотой , а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными:

где:

• U = U₀e^iωt — напряжение или разность потенциалов,
• I — сила тока,
• Z = Re^−iδ — комплексное сопротивление (импеданс),
• R = (R_a² + R_r²)^1/2 — полное сопротивление,
• R_r = ωL − 1/(ωC) — реактивное сопротивление (разность индуктивного и емкостного),
• R_а — активное (омическое) сопротивление, не зависящее от частоты,
• δ = − arctg (R_r/R_a) — сдвиг фаз между напряжением и силой тока.

При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведён взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, подбором такой что Тогда все значения токов и напряжений в схеме надо считать как

Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо.

Также необходимо отметить, что закон Ома является лишь простейшим приближением для описания зависимости тока от разности потенциалов и от сопротивления и для некоторых структур справедлив лишь в узком диапазоне значений. Для описания более сложных (нелинейных) систем, когда зависимостью сопротивления от силы тока нельзя пренебречь, принято обсуждать вольт-амперную характеристику.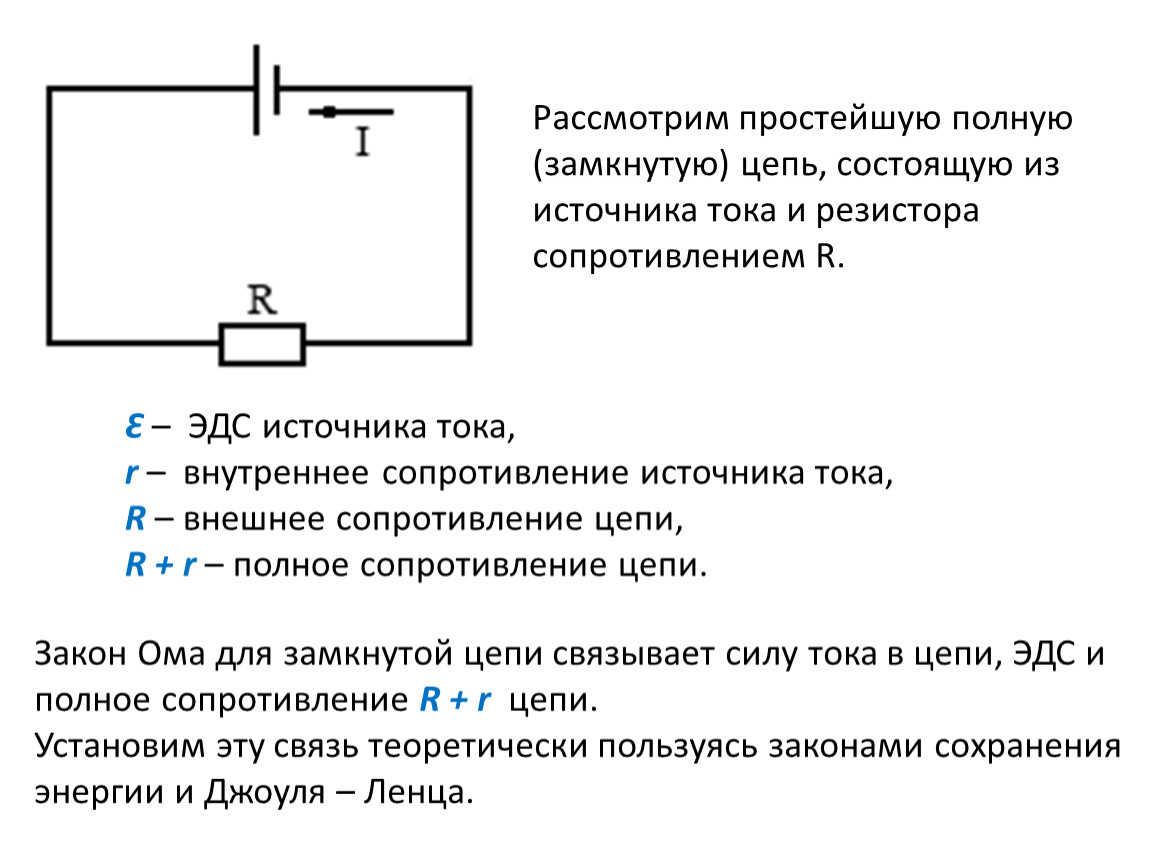 Отклонения от закона Ома наблюдаются также в случаях, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.

Трактовка закона Ома

Закон Ома можно просто объяснить при помощи теории Друде:

Здесь:

См. также

Примечания

Ссылки

Основные электрические законы. Базовые формулы и расчеты

В предыдущей статье мы познакомились с основными электрическими понятиями, такими как электрический ток, напряжение, сопротивление и мощность. Настал черед основных электрических законов, так сказать, базиса, без знания и понимания которых невозможно изучение и понимание электронных схем и устройств.

Закон Ома

Электрический ток, напряжение, сопротивление и мощность, безусловно, между собой связаны. А взаимосвязь между ними описывается, без сомнения, самым главным электрическим законом – законом Ома. В упрощенном виде этот закон называется: закон Ома для участка цепи. И звучит этот закон следующем образом:

«Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи».

Для практического применения формулу закона Ома можно представить в виде вот такого треугольника, который помимо основного представления формулы, поможет определить и остальные величины.

Работает треугольник следующим образом. Чтобы вычислить одну из величин, достаточно закрыть ее пальцем. Например:

В предыдущей статье мы проводили аналогию между электричеством и водой, и выявили взаимосвязь между напряжением, током и сопротивлением. Также хорошей интерпретацией закона Ома может послужить следующий рисунок, наглядно отображающий сущность закона:

На нем мы видим, что человечек «Вольт» (напряжение) проталкивает человечка «Ампера» (ток) через проводник, который стягивает человечек «Ом» (сопротивление). Вот и получается, что чем сильнее сопротивление сжимает проводник, тем тяжелее току через него проходить («сила тока обратно пропорциональна сопротивлению участка цепи» – или чем больше сопротивление, тем хуже приходится току и тем он меньше). Но напряжение не спит и толкает ток изо всех сил (чем выше напряжение, тем больше ток или – «сила тока в участке цепи прямо пропорциональна напряжению»).

Когда фонарик начинает слабо светить, мы говорим – «разрядилась батарейка». Что с ней произошло, что значит разрядилась? А значит это, что напряжение батарейки снизилось и оно больше не в состоянии «помогать» току преодолевать сопротивление цепей фонарика и лампочки. Вот и получается, что чем больше напряжение – тем больше ток.

Последовательное подключение – последовательная цепь

При последовательном подключении потребителей, например обычных лампочек, сила тока в каждом потребителе одинаковая, а вот напряжение будет отличаться. На каждом из потребителей напряжение будет падать (снижаться).

А закон Ома в последовательной цепи будет иметь вид:

При последовательном соединении сопротивления потребителей складываются. Формула для расчета общего сопротивления:

Параллельное подключение – параллельная цепь

При параллельном подключении, к каждому потребителю прикладывается одинаковое напряжение, а вот ток через каждый из потребителей, в случае, если их сопротивление отличается – будет отличаться.

Закон Ома для параллельной цепи, состоящей из трех потребителей, будет иметь вид:

При параллельном соединении общее сопротивление цепи всегда будет меньше значения самого маленького отдельного сопротивления. Или еще говорят, что «сопротивление будет меньше наименьшего».

Общее сопротивление цепи, состоящей из двух потребителей, при параллельном соединении:

Общее сопротивление цепи, состоящей из трех потребителей, при параллельном соединении:

Для большего числа потребителей расчет производится исходя из того, что при параллельном соединении проводимость (величина обратная сопротивлению) рассчитывается как сумма проводимостей каждого потребителя.

Электрическая мощность

Мощность – это физическая величина, характеризующая скорость передачи или преобразования электрической энергии. Рассчитывается мощность по следующей формуле:

Таким образом зная, напряжение источника и измерив потребляемый ток, мы можем определить мощность потребляемую электроприбором. И наоборот, зная мощность электроприбора и напряжение сети, можем определить величину потребляемого тока. Такие вычисления порой необходимы. Например, для защиты электроприборов используются предохранители или автоматические выключатели. Чтобы правильно подобрать средство защиты нужно знать потребляемый ток. Предохранители, применяемые в бытовой технике, как правило подлежат ремонту и для их восстановления достаточно подобрать и заменить проволоку.

Применив закон Ома, можно рассчитать мощность и по другой формуле:

При расчетах надо учитывать, что часть потребляемой электроэнергии расходуется на нагрев и преобразуется в тепло. При работе греются не только электрообогреватели, но и телевизоры, и компьютеры и другая бытовая техника.

И в завершение, в качестве бонуса, вот такая шпаргалка, которая поможет определить любой из основных электрических параметров, по уже известным.

Формула закона Ома в физике

Содержание:

Определение и формула закона Ома

Определение

Закон был получен Омом опытным путем. Построив вольт – амперную характеристику для проводника можно увидеть, что сила тока (I), текущего через проводник пропорциональна напряжению (U) на нем $(I \sim U)$.

Закон Ома для участка цепи

Если на рассматриваемом участке цепи, содержащей проводник, источников ЭДС нет $\left(U_{21}=\varphi_{1}-\varphi_{2}\right)$, то формула закона Ома является предельно простой:

$$I=\frac{U}{R}=\frac{\varphi_{1}-\varphi_{2}}{R}(1)$$

где R – сопротивление проводника (совокупности проводников, участка цепи).

Если источник тока в участок цепи включен и характеризуется при помощи ЭДС ($\varepsilon$), то формула закона Ома преобразуется к виду:

$$I=\frac{U}{R}=\frac{\varphi_{1}-\varphi_{2}+\varepsilon}{R}(2)$$

Закон Ома для замкнутой цепи

В том случае, если цепь является замкнутой, закон Ома принимает вид:

$$I=\frac{\varepsilon}{R}(3)$$

где под R=R_vnesh+r_ist понимают полное сопротивление цепи, которое включает так называемое внешнее сопротивление (R_vnesh) и сопротивление источника ЭДС (r_ist).

Формула закона Ома в дифференциальной форме

Все выше приведенные формулы закона Ома были представлены в интегральной форме. Этот закон можно записать в дифференциальной форме, которая характеризует электрическое состояние в точке.

$$\bar{j}=\sigma \bar{E}(4)$$

где $\sigma=\frac{1}{\rho}$ – удельная проводимость, $\rho$ – удельное сопротивление, $\bar{j}$ – вектор плотности тока, $\bar{E}$ – вектор напряженности электрического поля. Векторы $\bar{j}$ и $\bar{E}$ характеризуют одну точку проводящей среды. В том случае, если среда изотропна, то $\bar{j} \uparrow \uparrow \bar{E}$.

Примеры решения задач

Пример

Задание. Пространство между пластинами плоского конденсатора заполняет неоднородное плохо проводящее вещество, удельная проводимость которого изменяется в соответствии с линейным законом: $\sigma(r)=\sigma_{1}+\frac{\sigma_{2}-\sigma_{1}}{d} r$ в направлении перпендикулярном пластинам. d – расстояние между пластинами, S – площадь пластин конденсатора.{d} \frac{1}{\left(\sigma_{1}+\frac{\sigma_{2}-\sigma_{1}}{d}\right.} r\right) \frac{d r}{S}=\frac{d}{S\left(\sigma_{2}-\sigma_{1}\right)}\left[\ln \left(d \sigma_{2}\right)-\ln \left(d \sigma_{1}\right)\right]= \\ =\frac{d}{S\left(\sigma_{2}-\sigma_{1}\right)} \ln \left(\frac{\sigma_{2}}{\sigma_{1}}\right)(1.2) \end{array} $$

Подставим найденное в (1.2) сопротивление в (1.1), получим искомую силу тока:

$I=\frac{U}{\frac{d}{S\left(\sigma_{2}-\sigma_{1}\right)} \ln \left(\frac{\sigma_{2}}{\sigma_{1}}\right)}=\frac{U S\left(\sigma_{2}-\sigma_{1}\right)}{d \cdot \ln \left(\frac{\sigma_{2}}{\sigma_{1}}\right)}$

Ответ. $I=\frac{U S\left(\sigma_{2}-\sigma_{1}\right)}{d \cdot \ln \left(\frac{\sigma_{2}}{\sigma_{1}}\right)}$

Слишком сложно?

Формула закона Ома не по зубам? Тебе ответит эксперт через 10 минут!

Пример

Задание. Какой будет плотность тока в металлическом проводнике (удельное сопротивление считать равным $\rho$) постоянного сечения, имеющем длину l, если напряжение, которое приложено к проводу равно U?

Решение. Плотность тока для проводника, который имеет постоянное сечение S можно найти как:

$$j=\frac{I}{S}(2.1)$$

Силу тока можно вычислить, если использовать формулу Закона Ома для участка цепи не имеющего ЭДС:

$$I=\frac{U}{R}(2.2)$$

Сопротивление провода найдем, применяя формулу:

$$R=\rho \frac{l}{S}(2.3)$$

Подставим, необходимые величины в (2.1), получим:

$$j=\frac{U}{S R}=\frac{U S}{S \rho l}$$

Ответ. $j=\frac{U S}{S \rho l}$

Читать дальше: Формула мощности тока.

РАЗНИЦА МЕЖДУ ЗАКОНОМ ОМА И ЗАКОНОМ КИРХГОФА | СРАВНИТЕ РАЗНИЦУ МЕЖДУ ПОХОЖИМИ ТЕРМИНАМИ — ТЕХНОЛОГИЯ

Когда дело доходит до понимания электричества, очень важно понимать взаимосвязь между примитивными параметрами, напряжением и током. Основным принципом, описывающим эти отношения, является закон Ома.

Ключевое различие — закон Ома против закона Кирхгофа
 

Когда дело доходит до понимания электричества, очень важно понимать взаимосвязь между примитивными параметрами, напряжением и током. Основным принципом, описывающим эти отношения, является закон Ома. С другой стороны, закон Кирхгофа — это теория, которая описывает свойства этих параметров по отдельности. Таким образом, ключевое различие между законом Ома и законом Кирхгофа состоит в том, что Закон Ома описывает взаимосвязь между напряжением и током на резистивном элементе, в то время как Кирхгоф’s-закон описывает поведение тока и напряжения в ветви цепи.

1. Обзор и основные отличия
2. Что такое закон Ома
3. Что такое закон Кирхгофа
4. Сравнение бок о бок — закон Ома против закона Кирхгофа в табличной форме.
5. Резюме

Что такое закон Ома?

Закон Ома гласит, что ток, протекающий по проводнику, пропорционален напряжению на нем, и наоборот. Этот принцип был основан немецким физиком Георгом Омом и сформулирован следующим образом:

V = ИК

Закон Ома можно сравнить с течением воды в трубе. Разность потенциалов между двумя концами приводит в движение воду по трубе, как ток, который создается разностью напряжений на резистивном элементе. Более того, уменьшенное сопротивление, которое увеличивает ток, эквивалентно уменьшению площади поперечного сечения трубы, что уменьшает поток воды.

Что касается отдельного оборудования или цепи элементов в целом, закон Ома используется для расчета полного сопротивления элемента или цепи с измеренными током и напряжением. С помощью рассчитанного сопротивления можно определить или спрогнозировать энергопотребление цепи, если значение сопротивления изменится любым средним значением, например температурой.

Сложная форма закона Ома применима к цепям переменного тока, где V и I — комплексные переменные. В этом случае R относится к сопротивлению цепи (Z). Импеданс также является комплексным числом, в котором только действительная часть способствует рассеиванию активной мощности.

Что такое закон Кирхгофа?

Закон Кирхгофа был предложен немецким физиком Густавом Кирхгофом. Закон Кирхгофа имеет две формы: закон Кирхгофа по току (KCL) и закон Кирхгофа по напряжению (KVL). KCL и KVL описывают сохранение тока и напряжения соответственно.

Действующий закон Кирхгофа (KCL)

KCL утверждает, что общий ток, который входит в узел (точка соединения нескольких ответвленных цепей), и общий ток, вытекающий из узла, равны.

Закон напряжения Кирхгофа (KVL)

KLV, с другой стороны, утверждает, что сумма напряжений в замкнутом контуре равна нулю.

Это выражается в другой форме, поскольку сумма напряжений между двумя узлами цепи равна каждой ответвленной цепи между этими двумя узлами. Это можно изобразить, как на следующем рисунке.

Вот,

v

₁ + v₂ + v₃ — v₄ = 0

KVL и KVC чрезвычайно полезны при анализе схем. Однако закон Ома необходимо использовать вместе с ними при решении параметров схемы. Для примера такого анализа схемы дана плавная фигура.

Рассматривая узлы A и B, KCL можно применить следующим образом.

Для узла A; я₁ + Я₂ = Я₃

Для узла B; я₁ + Я₂ = Я₃

Затем КВЛ применяется к замкнутому контуру (1)

V₁ + Я₁ р₁ + Я₃ р_{3 =} 0

Затем КВЛ применяется к замкнутому контуру (2)

V₂ + Я₂ р₂+ Я₃ р_{3 =} 0

Затем КВЛ применяется к замкнутому контуру (3)

V₁ + Я₁ р₁ — я₂ р₂ — V_{2 =} 0

Решая вышеуказанные уравнения, можно найти любой неизвестный параметр схемы. Обратите внимание, что закон Ома используется при определении напряжений на резисторах.

В чем разница между законом Ома и законом Кирхгофа?

Закон Ома против закона Кирхгофа
Закон Ома описывает соотношение между напряжением и током на резистивном элементе.	Закон Кирхгофа описывает поведение тока и напряжения соответственно в ветви цепи.
Закон
Закон Ома гласит, что напряжение на проводнике пропорционально току, протекающему по нему.	KCL заявляет, что сумма текущих потоков к узлу равна нулю, в то время как KVL утверждает, что сумма напряжений в замкнутом контуре равна нулю.
Приложения
Закон Ома применим к отдельному резистивному элементу или набору резистивных цепей в целом.	KCL и KVL применимы к серии резистивных элементов в цепи.

Резюме — закон Ома против закона Кирхгофа

Законы Ома и Кирхгофа — это две фундаментальные теории в анализе электрических цепей. Они описывают свойства и соотношение напряжения и тока в отдельном проводящем элементе и ветви электрической цепи соответственно. В то время как закон Ома применим к резистивному элементу, законы Кирхгофа применяются к ряду элементов. Это наиболее важное различие между законом Ома и законом Кирхгофа. KCL и KVL обычно используются в схемном анализе вместе с законом Ома.

Скачать PDF-версию закона Ома и закона Кирхгофа

Вы можете скачать PDF-версию этой статьи и использовать ее в автономных целях в соответствии с примечаниями к цитированию. Пожалуйста, скачайте PDF-версию здесь. Разница между законом Ома и законом Кирхгофа.

Ссылки:

1. «Окружной закон Кирхгофа». Окружной закон Кирхгофа, доступен здесь. Проверено 4 сентября 2017 г.
2. «Окружные законы Кирхгофа». Википедия, Фонд Викимедиа, 1 сентября 2017 г., доступно здесь. Проверено 4 сентября 2017 г.

Изображение предоставлено:

1. «OhmsLaw» от Waveguide2 (выступление) (передано Nk / изначально загружено Waveguide2) (изначально загружено на en.wikipedia) (общественное достояние) через Commons Wikimedia
2. «Текущий закон Кирхгофа» путем индуктивной нагрузки — собственный рисунок (общественное достояние) через Commons Wikimedia
3. «Закон напряжения Кирхгофа» Квинканкс — собственная работа (CC BY-SA 3.0) через Commons Wikimedia

1. Закон Ома для участка цепи

Зависимость силы тока и напряжения Закон Ома для участка цепи. Сопротивление. Чем сильнее поле действует на частицы, тем больше будет сила тока в цепи. Электрическое поле характеризуется величиной, называемой напряжением. Следовательно, сила тока зависит от напряжения. Опытным путем удалось установить, что сила тока связана с напряжением прямо пропорционально. В случаях, когда изменяли величину напряжения в цепи, не меняя всех остальных параметров, сила тока возрастала или уменьшалась во столько же раз, во сколько меняли напряжение.  Сопротивление связано с силой тока обратно пропорционально. Если на каком-либо участке цепи изменить величину сопротивления, не меняя напряжения на концах этого участка, сила тока также изменится. Причем если мы уменьшим величину сопротивления, то сила тока возрастет во столько же раз. И, наоборот, при увеличении сопротивления сила тока пропорционально уменьшается. Формула закона Ома для участка цепи  Закон Ома для участка цепи гласит: Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению. I=U/R, где I – сила тока, U – напряжение, R – сопротивление. Применение закона Ома Закон Ома (1827)– один из основополагающих законов физики. Невозможно себе представить любой самый элементарный расчет основных электрических величин для любой цепи без использования закона Ома. Представление об этом законе – это не удел исключительно инженеров-электронщиков, а необходимая часть базовых знаний любого мало-мальски образованного человека. Недаром есть поговорка: «Не знаешь закон Ома – сиди дома». Из формулы для закона Ома можно рассчитать также величины напряжения и сопротивления участка цепи:U=IR    и    R=U/IВеличина сопротивления некоторого участка цепи есть величина постоянная, поэтому при изменении силы тока будет изменяться только напряжение и наоборот. Для изменения сопротивления участка цепи следует собрать цепь заново. Расчет же требуемой величины сопротивления при проектировании и сборке цепи можно произвести по закону Ома, исходя из предполагаемых значений силы тока и напряжения, которые будут пропущены через данный участок цепи. Урок #1 — Закон Ома и Электрический Ток Интерактивный тест Закон Ома для участка электрической цепи.. Updating… 1 3_15 закон Ома.swf (156k) Ольга Федотова, 5 янв. 2016 г., 02:16 1 определение закона Ома.swf (238k) Ольга Федотова, 5 янв. 2016 г., 02:16 2 вычислите.swf (36k) Ольга Федотова, 5 янв. 2016 г., 02:16 3_1 допиши формулы.gif (33k) Ольга Федотова, 5 янв. 2016 г., 02:16 ĉ 3_1 физический диктант закон Ома.doc (28k) Ольга Федотова, 5 янв. 2016 г., 02:16 ć 3_2 Тест к уроку Закон Ома для участка электрической цепи.ppt (101k) Ольга Федотова, 5 янв. 2016 г., 02:16 ĉ 3_3 самостоятельная работа_8-4.doc (64k) Ольга Федотова, 5 янв. 2016 г., 02:16 ĉ 3_4 реши самостоятельно задачи на сопротивление.doc (27k) Ольга Федотова, 5 янв. 2016 г., 02:16 3_4 тест Zakon OMA.rar (9k) Ольга Федотова, 5 янв. 2016 г., 02:20 3_4 тест закон OM тест.rar (236k) Ольга Федотова, 5 янв. 2016 г., 02:20 Ċ ТСК-8.2.17 зависимость.pdf (122k) Ольга Федотова, 28 февр. 2016 г., 21:14 опорный конспект Закон Ома.jpeg (91k) Ольга Федотова, 5 янв. 2016 г., 00:06

Значение закона Ома

Применяя основной закон электрической цепи (закон Ома), можно объяснить многие природные явления, которые на первый взгляд кажутся загадочными и парадоксальными. Например, всем известно, что любой контакт человека с электрическими проводами, находящимися под напряжением, является смертельно опасным. Всего лишь одно прикосновение к оборвавшемуся проводу высоковольтной линии способно убить электрическим током человека или животное. Но в то же время, мы постоянно видим, как птицы спокойно усаживаются на высоковольтные провода электропередач, и ничто не угрожает жизни этих живых существ. Тогда как же найти объяснение такому парадоксу?

А объясняется подобное явление довольно просто, если представить, что находящаяся на электрическом проводе птица – это один из участков электрической сети, сопротивление второго значительно превышает сопротивление другого участка той же цепи (то есть небольшого промежутка между лапками птицы). Следовательно, сила электрического тока, воздействующая на первый участок цепи, то есть на тело птицы, будет совершенно безопасной для неё.

Однако полная безопасность гарантирована ей только при соприкосновении с участком высоковольтного провода. Но стоит только птице, усевшейся на линию электропередач, задеть крылом или клювом провод или какой-либо предмет, находящийся вблизи от провода (например, телеграфный столб), то птица неминуемо погибнет. Ведь столб непосредственно связан с землёй, и поток электрических зарядов, переходя на тело птицы, способен мгновенно убить её, стремительно двигаясь по направлению к земле. К сожалению, по этой причине в городах гибнет немало птиц.

Для защиты пернатых от губительного воздействия электричества зарубежными учеными были разработаны специальные устройства – насесты для птиц, изолированные от электрического тока. Такие приспособления размещали на высоковольтных линиях электропередач. Птицы, усаживаясь на изолированный насест, могут без всякого риска для жизни прикасаться клювом, крыльями или хвостом к проводам, столбам или кронштейнам.

Наибольшим сопротивлением обладает поверхность верхнего, так называемого рогового слоя кожи человека. Сопротивление сухой и неповреждённой кожи может достигать 40 000 – 100 000 Ом. Роговой слой кожи очень незначителен, всего 0,05 – 0,2 мм. и легко пробивается напряжением 250 В. При этом сопротивление уменьшается в сто раз и падает тем скорее, чем дольше действует на тело человека ток. 
Резко, до 800 – 1000 Ом, уменьшают сопротивление тела человека повышенная потливость кожного покрова, переутомление, нервное возбуждение, опьянение. Этим объясняется, что порой даже небольшое напряжение может вызвать поражение электрическим током. Если, например, сопротивление тела человека равно 700 Ом, то опасным будет напряжение всего в 35 В. Именно поэтому, например, специалисты-электрики даже при работе с напряжением 36 В применяют изолирующие защитные средства – резиновые перчатки или инструмент с изолированными ручками.

Закон

Ома — Университетская физика, том 2

Цели обучения

К концу этого раздела вы сможете:

• Опишите закон Ома
• Распознавать, когда применяется закон Ома, а когда нет.

До сих пор в этой главе мы обсуждали три электрических свойства: ток, напряжение и сопротивление. Оказывается, многие материалы демонстрируют простую взаимосвязь между значениями этих свойств, известную как закон Ома.Многие другие материалы не демонстрируют эту взаимосвязь, поэтому, несмотря на то, что они называются законом Ома, они не считаются законом природы, как законы Ньютона или законы термодинамики. Но это очень полезно для расчетов с материалами, которые подчиняются закону Ома.

Описание закона Ома

Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению В, . Немецкий физик Георг Симон Ом (1787–1854) первым экспериментально продемонстрировал, что ток в металлической проволоке прямо пропорционален приложенному напряжению :

Это важное соотношение лежит в основе закона Ома.Его можно рассматривать как причинно-следственную связь, в которой напряжение является причиной, а ток — следствием. Это эмпирический закон, который означает, что это экспериментально наблюдаемое явление, подобное трению. Такая линейная зависимость возникает не всегда. Любой материал, компонент или устройство, подчиняющееся закону Ома, где ток, протекающий через устройство, пропорционален приложенному напряжению, известен как омический материал или омический компонент. Любой материал или компонент, который не подчиняется закону Ома, известен как неомический материал или неомный компонент.

Эксперимент Ома

В статье, опубликованной в 1827 году, Георг Ом описал эксперимент, в котором он измерял напряжение и ток в различных простых электрических цепях, содержащих провода различной длины. Аналогичный эксперимент показан на (Рисунок). Этот эксперимент используется для наблюдения за током через резистор, возникающим в результате приложенного напряжения. В этой простой схеме резистор включен последовательно с батареей. Напряжение измеряется вольтметром, который необходимо разместить на резисторе (параллельно резистору).Ток измеряется амперметром, который должен быть на одной линии с резистором (последовательно с резистором).

Экспериментальная установка, используемая для определения того, является ли резистор омическим или неомическим устройством. (a) Когда батарея подключена, ток течет по часовой стрелке, а вольтметр и амперметр показывают положительные значения. (b) Когда выводы батареи переключаются, ток течет против часовой стрелки, а вольтметр и амперметр показывают отрицательные показания.

В этой обновленной версии оригинального эксперимента Ома было выполнено несколько измерений тока для нескольких различных напряжений. Когда батарея была подключена, как показано на (Рисунок) (а), ток протекал по часовой стрелке, и показания вольтметра и амперметра были положительными. Изменится ли поведение тока, если ток течет в обратном направлении? Чтобы заставить ток течь в обратном направлении, выводы батареи можно переключить.При переключении выводов батареи показания вольтметра и амперметра были отрицательными, потому что ток протекал в обратном направлении, в данном случае против часовой стрелки. Результаты аналогичного эксперимента показаны на (Рисунок).

Резистор вставлен в цепь с батареей. Приложенное напряжение изменяется от -10,00 В до +10,00 В с шагом 1,00 В. На графике показаны значения напряжения в зависимости от тока, типичные для случайного экспериментатора.

В этом эксперименте напряжение, приложенное к резистору, изменяется от -10,00 до +10,00 В с шагом 1,00 В. Измеряются ток через резистор и напряжение на резисторе. Построен график зависимости напряжения от тока, и результат будет приблизительно линейным. Наклон линии — это сопротивление или напряжение, деленное на ток. Этот результат известен как закон Ома:

, где В, — напряжение, измеренное в вольтах на рассматриваемом объекте, I — ток, измеренный через объект в амперах, а R — сопротивление в единицах Ом.Как указывалось ранее, любое устройство, которое показывает линейную зависимость между напряжением и током, известно как омическое устройство. Следовательно, резистор — это омическое устройство.

Проверьте свое понимание Напряжение, подаваемое в ваш дом, изменяется как. Если к этому напряжению подключить резистор, будет ли по-прежнему действовать закон Ома?

Да, закон Ома все еще в силе. В каждый момент времени ток равен, поэтому ток также является функцией времени.

Неомные устройства не показывают линейной зависимости между напряжением и током.Одним из таких устройств является элемент полупроводниковой схемы, известный как диод. Диод — это схемное устройство, которое позволяет току течь только в одном направлении. Схема простой схемы, состоящей из батареи, диода и резистора, показана на (рисунок). Хотя мы не рассматриваем теорию диода в этом разделе, диод можно протестировать, чтобы определить, является ли он омическим или неомическим устройством.

Диод — это полупроводниковое устройство, которое пропускает ток, только если диод смещен в прямом направлении, что означает, что анод положительный, а катод отрицательный.

График зависимости тока от напряжения показан на (Рисунок). Обратите внимание, что поведение диода показано как зависимость тока от напряжения, тогда как работа резистора показана как зависимость напряжения от тока. Диод состоит из анода и катода. Когда анод находится под отрицательным потенциалом, а катод — под положительным потенциалом, как показано в части (а), говорят, что диод имеет обратное смещение. При обратном смещении диод имеет очень большое сопротивление, и через диод и резистор протекает очень небольшой ток — практически нулевой ток.По мере увеличения напряжения, приложенного к цепи, ток остается практически нулевым, пока напряжение не достигнет напряжения пробоя и диод не будет проводить ток, как показано на (Рисунок). Когда аккумулятор и потенциал на диоде меняются местами, что делает анод положительным, а катод отрицательным, диод проводит, и ток течет через диод, если напряжение больше 0,7 В. Сопротивление диода близко к нулю. (Это причина наличия резистора в цепи; если бы его не было, ток стал бы очень большим.) Из графика на (Рисунок) видно, что напряжение и ток не имеют линейной зависимости. Таким образом, диод является примером безомного устройства.

Когда напряжение на диоде отрицательное и небольшое, через диод протекает очень небольшой ток. Когда напряжение достигает напряжения пробоя, диод проводит. Когда напряжение на диоде положительное и превышает 0,7 В (фактическое значение напряжения зависит от диода), диод проводит. По мере увеличения приложенного напряжения ток через диод увеличивается, но напряжение на диоде остается приблизительно равным 0.7 В.

Закон Ома обычно формулируется как, но первоначально он был сформулирован как микроскопическое изображение с точки зрения плотности тока, проводимости и электрического поля. Этот микроскопический взгляд предполагает, что пропорциональность обусловлена ​​дрейфовой скоростью свободных электронов в металле, возникающей в результате приложенного электрического поля. Как было сказано ранее, плотность тока пропорциональна приложенному электрическому полю. Переформулировка закона Ома приписывается Густаву Кирхгофу, имя которого мы еще раз увидим в следующей главе.

(PDF) Связь закона Ома со 2-м законом Ньютона

Связь закона Ома со 2-м законом Ньютона

Jeff Yee

[email protected]

20 января 2019 г.

Резюме

Закон Ома касается напряжения (V), ток (I) и сопротивление (R) в электрических системах как V = IR. Второй закон Ньютона связывает

силы (F), массы (m) и ускорения (a) как F = ma. Хотя электрические и механические системы поддерживаются

различных уравнений для описания этих отношений сегодня, будет показано, что законы Ома и Ньютона связаны между собой и построены на той же основе, которая управляет силой частиц и всей материи. .

По своей природе электрические и механические системы действительно взаимосвязаны. Электроэнергия часто используется в механических системах

, таких как лифты или электромобили, в которых энергия передается от движущихся электронов движущимся массам большего размера.

Или наоборот, что электрическая энергия может вырабатываться механической системой. Природа связывает эти процессы, а

уравнений человечества — нет.

Связь закона Ома и закона Ньютона в единицах измерения

Основная причина того, что электрические и механические системы не связаны уравнениями, заключается в том, что компоненты

этих уравнений не используют одни и те же единицы.Например, в механических системах движение массы измеряется

как скорость [м / с], но в электрических системах движение электронов, называемое током, измеряется в амперах [A].

Проблема заключается в определении электрического заряда, который является свойством частиц в атоме, таких как электрон и

протон. Заряд измеряется в кулонах [C]. Это неправильное понимание значения заряда

, которое вызывает разделение между электрическими и механическими системами.Если заряд измеряется как амплитуда волны,

, что является расстоянием, тогда все единицы выравниваются, и уравнения могут быть объединены. Волны обладают

свойствами конструктивной и деструктивной интерференции, что позволяет объединять или нейтрализовать заряды на основе

их конструктивной интерференции волн.

Используя этот принцип, кулоновские единицы [C] для элементарного заряда (e) заменяются на единицы расстояния [м]:

Поскольку все компоненты закона Ома зависят от кулоновских единиц, они заменяются следующим образом:

Закон

Ом — обзор

ЗАКОН ОМА

Закон

Ома гласит, что электрический ток (I [амперы {Å}]) в цепи пропорционален разности электрических потенциалов (В; вольт [v]) в схема:

Константа пропорциональности, R, известна как сопротивление и измеряется в омах (В).На рисунке 4.5 показана простая электрическая цепь постоянного тока, состоящая из батареи 5 В и резистора 100 Ом. Стрелка показывает направление протекания тока в цепи. После некоторой алгебраической перестановки уравнения 4-1 мы можем использовать закон Ома для определения тока в цепи:

РИСУНОК 4.5. Простая электрическая схема, состоящая из батареи 5 В и резистора 100 Ом. Закон Ома используется для вычисления электрического тока (I), который течет от высокого (+) к низкому (-) потенциалу.

Ур.4.2I = ΔV / RI = 5V / 100ΩI = 0,05A

Что произойдет, если мы удвоим электрический потенциал в цепи до 10 В? Ответ прост; удваиваем ток в цепи.

I = ΔV / RI = 10 В / 100 Ом I = 0,10 А

Что произойдет, если мы удвоим сопротивление в цепи до 200 Ом?

I = ΔV / RI = 5V / 200ΩI = 0,025A

В этом случае ток исходной цепи уменьшается вдвое.

Закон Ома может помочь нам понять, как работают некоторые очень распространенные преобразователи. Например, многие обычные чувствительные элементы показывают изменение электрического сопротивления в ответ на изменение измеряемой величины.Когда эти резистивные чувствительные элементы правильно размещены в простых цепях постоянного тока, изменения измеряемой величины изменят сопротивление, ток и электрический потенциал в цепи.

На рисунке 4.6 показана простая электрическая схема, содержащая батарею 4 В и два резистора. Один резистор имеет постоянное сопротивление 10 000 В, тогда как второй резистор состоит из термистора, который представляет собой кусок керамического материала, который демонстрирует повторяемое изменение сопротивления в зависимости от температуры. Первый и второй столбцы таблицы 4-2 содержат данные, показывающие, как сопротивление термистора изменяется с температурой.Закон Ома может использоваться для определения тока, протекающего в цепи, и изменения напряжения, которое возникает на каждом резисторе по мере того, как ток течет по цепи. Для определения протекания тока необходимо рассчитать полное сопротивление цепи. Это получается суммой постоянного резистора R _f и переменного термистора R _t . Таким образом, для температуры 0 ° C R _f и R _t равны 10 000 и 9800 В соответственно.

РИСУНОК 4.6. Простая электрическая схема, состоящая из батареи на 4 В, постоянного резистора на 10 000- В и переменного резистора, известного как термистор. Изменения температуры изменяют общее сопротивление цепи, что приводит к изменению протекания тока и падения напряжения на обоих резисторах. По закону Ома вычисляется ток, протекающий в цепи, и результирующее напряжение падает на обоих резисторах.

ТАБЛИЦА 4.2. Пример расчета значений тока и напряжения в простой цепи термистора (рисунок 4.5) при различных температурах

9019 9019 9019 9019 9019 9019

Температура (° C)	Сопротивление термистора (R t ) (Ом)	Фиксированное сопротивление (R f ) (Ом)	Ток цепи (мА)	Напряжение на R f (В)	Напряжение на R t (В)
0	9800	10,000	0.202		9019 9019 9019 9019 9019 9019 9019 9019	7600	10 000	0.227	2,27	1,73
10	5900	10,000	0,252	2,52	1,48
15		4700	20	3750	10,000	0,291	2,91	1,09
25	3000	10,000	0,308	3.08	0,92

В столбце 2 указано сопротивление элемента термистора при температурах, представленных в столбце 1.

Ур. 4.3I = ΔV / (Rf + Rp) I = 4V / (10,000 Ом + 9800 Ом) I = 0,000202 A = 0,202 мА

Обратите внимание, что ток довольно мал. В этом случае предпочтительной единицей измерения тока являются миллиамперы (мА), а не амперы (1 мА 0,001 А). Как только известен протекание тока, можно определить падение напряжения на каждом сопротивлении в цепи. Опять же, согласно закону Ома, падение напряжения на фиксированном резисторе составляет:

Eq.4,4ΔV = I * RΔV = 0,202 мА * 10,000 ОмΔV = 0,000202 A * 10,000ΩΔV = 2,02В

А падение напряжения на термисторе составляет:

ΔV = I * RΔV = 0,000202 A * 9800ΩΔV = 1,98 В

четвертый, пятый и шестой столбцы таблицы 4.2 показывают результаты аналогичных вычислений тока и падения напряжения для других температур, перечисленных в таблице. Обратите внимание, как изменение температуры элемента термистора вызывает изменение протекания тока, что, в свою очередь, вызывает изменение падения напряжения как на фиксированном, так и на элементах сопротивления термистора.При эксплуатации температура измеряется путем подсоединения одной стороны выводных проводов к фиксированному резистору, а другую сторону выводов к входным клеммам системы DAS, предварительно настроенной для приема входного сигнала постоянного тока 0–4 В. На рис. 4.7 графически показано, как выходной сигнал цепи термистора будет изменяться в зависимости от температуры. Обратите внимание, что мы решили подключить DAS к фиксированному резистору (иногда называемому токоизмерительным резистором ) , потому что напряжение увеличивается с температурой.Напротив, падение напряжения на термисторе уменьшается с повышением температуры.

РИСУНОК 4.7. Выходное напряжение цепи термистора на Рисунке 4.5 как функция температуры.

Физика для науки и техники II

Закон 6.5 Ома от Office of Academic Technologies на Vimeo.

6,05 Закон Ома

Мы видели, что сопротивление определяется как разность потенциалов между двумя точками, деленная на количество тока, проходящего через эти точки.Кроме того, удельное сопротивление определялось как отношение электрического поля в интересующей области к плотности тока в этой области. Эти соотношения в физике известны как законы Ома.

Здесь мы можем выразить разность потенциалов между двумя точками как ток, умноженный на сопротивление. Если мы построим график разности потенциалов между двумя точками в зависимости от тока, проходящего через эти точки для различных типов компонентов типичной электрической цепи, мы можем получить два разных случая.В одном случае соотношение между разностью потенциалов и током является линейным, поэтому это соотношение, другими словами, В по сравнению с и , всегда становится постоянным.

Конечно, вторая категория — это случай, когда это соотношение не является постоянным, и в результате мы получаем кривую. Например, что-то подобное, что и в случае диодов с переходом pn . Итак, вот пример поведения резистора, например, и это случай диода с переходом pn .

Говорят, что проводящее устройство подчиняется закону Ома, если его сопротивление между любыми двумя точками не зависит от величины и полярности разности потенциалов, приложенной между этими точками. Итак, если мы констатируем это, проводящее устройство подчиняется закону Ома, если его сопротивление между любыми двумя точками не зависит от величины и полярности разности потенциалов, приложенной между этими точками. Другими словами, отношение V к i или i к V остается постоянным все время, так что наклон кривой остается постоянным.Другими словами, мы получаем прямую линию, когда строим график i против V или V против i .

Итак, V равно i , умноженному на R . Верно для всех токопроводящих устройств. Мы просто разделяем эти устройства независимо от того, подчиняются они закону Ома или нет, просто глядя на сопротивление, независимо от того, остается ли оно постоянным или нет. Другими словами, отношение В, к и , ток к разности потенциалов к току, остается постоянным или нет.

Если это соотношение остается постоянным, мы говорим, что компонент подчиняется закону Ома. Если нет, то мы говорим, что этот компонент не подчиняется закону Ома. Итак, если i по сравнению с V линейно, то это соответствует случаю подчинения закону Ома. С другой стороны, если i по сравнению с V , разность потенциалов, не является линейной, то это тот случай, который мы называем не подчиняющимся закону Ома.

Конечно, местный аналог закона Ома связан с определением удельного сопротивления, которое определялось как отношение электрического поля к плотности тока.Отсюда мы можем выразить E как ρ , умноженное на J . Конечно, это верно только для изотропных материалов. Материалы, электрические свойства которых одинаковы во всех направлениях. И здесь снова аналогичным образом, если отношение электрического поля к плотности тока остается постоянным все время, другими словами, если удельное сопротивление среды постоянно, тогда эта среда подчиняется закону Ома. С другой стороны, если это отношение электрического поля к плотности тока непостоянно или E по сравнению с J не является линейной кривой, то мы в конечном итоге говорим, что эта среда не подчиняется закону Ома.

Итак, до сих пор мы ввели два разных набора величин, в основном микроскопических величин, и это были электрические поля, плотность тока, удельное сопротивление. Эти величины важны, когда мы исследуем фундаментальное электрическое поведение материи. Итак, предположим, что они важны, когда мы ищем фундаментальные электрические свойства материи.

С другой стороны, макроскопические свойства или макроскопические величины, которые представляют собой разность потенциалов, ток и сопротивление, и эти величины важны, когда мы делаем электрические инструменты из определенных проводников.Итак, эти величины важны, когда мы делаем электрические инструменты, определенные цепи, например, на определенных проводниках.

Другими словами, всякий раз, когда мы имеем дело со схемами, мы, следовательно, имеем дело с макроскопическими величинами, а именно разностью потенциалов, током и сопротивлением. С другой стороны, если мы пытаемся понять фундаментальные электрические свойства конкретной среды, то мы будем иметь дело с электрическим полем, плотностью тока и удельным сопротивлением или проводимостью этой среды.

L3: Закон Ома — Физические вычисления

Содержание

1. Закон Ома
   1. Связь закона Ома с нашими аналогами с водой
   2. Почему \ (I \), а не \ (C \)?
2. Обязательно используйте базовые единицы
   1. Общие префиксы СИ
   2. Конвертирующие единицы
3. Давайте проанализируем некоторые схемы!
   1. Пример 1: Решить для текущего
      1. Шаг 1: Определить известные
      2. Шаг 2: Применить известные
      3. Шаг 3: Решить для тока I
   2. Пример 2: Решить для тока снова (но с другим сопротивлением)
   3. Пример 3: Найти напряжение
   4. Пример 4: Найти сопротивление
4. Упражнение: Использование симулятора цепей
5. Краткое содержание урока
6. Ресурсы
7. Следующий урок

---

В этом уроке мы узнаем о законе Ома , один из наиболее важных эмпирических законов в электрических цепях, который описывает, как связаны между собой ток , , напряжение , напряжение и сопротивление , .Хотя закон Ома невероятно полезен для анализа и понимания того, как работают схемы, как и многие «законы», он не всегда соблюдается (особенно для так называемых «неомических» устройств, таких как светодиоды или другие диоды). Но мы к этому еще вернемся.

А теперь перейдем к закону Георга Ома!

Закон Ома

В 1827 году, после многих лет экспериментов, немецкий физик Георг Симон Ом опубликовал «Гальваническая цепь , исследованная математически, », которая стала основой закона Ома.Закон Ома гласит, что ток (\ (I \) в амперах) в проводнике прямо пропорционален приложенному напряжению (\ (V \) в вольтах) против сопротивления проводника (\ (R \) в омах) :

\ [I = \ frac {V} {R} \]

Таким образом, если мы удвоим напряжение в нашей цепи, например, соединяя две батареи последовательно, то мы также удвоим ток. Закон Ома имеет большое значение для построения и использования схем с микроконтроллерами, включая делители напряжения и резистивные датчики.

Важно отметить, что вы увидите и будете использовать закон Ома во всех трех эквивалентных воплощениях (которые могут быть получены с помощью простой алгебры):

Если вы хотите найти ток в вашей схеме, вы используете: \ (I = \ frac {V} {R} \)

Чтобы найти напряжение , используйте: \ (V = I * R \)

Чтобы найти сопротивление , используйте: \ (R = \ frac {V} {I } \)

Обратите внимание, как эти уравнения соотносятся с концепциями, которые мы объясняли в нашем первом уроке по напряжению, току и сопротивлению, к которым вы, возможно, захотите вернуться.Например, \ (I = \ frac {V} {R} \) ясно демонстрирует, что для увеличения тока мы можем либо увеличить напряжение , либо уменьшить сопротивление .

Связь закона Ома с нашими аналогами с водой

Опять же, опираясь на наши гидравлические и электрические аналогии (которые мы подробно использовали в предыдущих уроках), мы можем выделить еще одно сходство. В 1840-х годах Пуазейль эмпирически показал, что скорость потока воды через трубу равна падению давления в трубе, деленному на сопротивление трубы — это называется закон Пуазейля .И это имеет смысл концептуально: большая разница давлений между двумя концами трубы создает большую силу, а меньшее сопротивление позволяет большему потоку воды.

Вам знакомо это уравнение? Должно. Это в точности закон Ома! Ток в цепи прямо пропорционален падению напряжения в цепи, деленному на ее сопротивление. См. Изображение ниже.

Рисунок. Закон Пуазейля для плавного течения жидкости и закон Ома для электрического тока аналогичны.Изображение основано на HyperPhysics в штате Джорджия и создано в PowerPoint. Изображения Пуазейля и Ома взяты из Википедии.

---

ПРИМЕЧАНИЕ:

Уравнение закона Пуазейля справедливо только для плавного (ламинарного, а не турбулентного) течения ньютоновской жидкости, такой как вода. Но такое условие не имеет отношения к электрическому току.

---

Почему \ (I \), а не \ (C \)?

Вы можете спросить: «Если \ (R \) — это сопротивление r в омах (Ом), а V — напряжение v в вольтах (В), то почему \ (I \) используется для обозначения c Ток в амперах (A), а не в \ (C \)? » Две причины: во-первых, \ (C \) уже зарезервирован для единицы СИ, состоящей из столбцов (C), которая используется в самом определении ампер (напомним, что \ (1 \ A = 1 \ C / s \)) и таким образом, можно запутаться! Во-вторых, ампер назван в честь Андре-Мари Ампера, считающегося отцом электромагнетизма, который называл силу тока « i ntensité du courant» или « i ntensité du courant».Итак, ток равен \ (I \), а не \ (C \).

Обязательно используйте базовые блоки.

Распространенная проблема при применении закона Ома — или анализе цепей в целом — это испорченные базовые блоки. В цифровых схемах мы часто имеем дело с кОм (кОм), , что составляет 1000 Ом, миллиампер (ма), , что составляет \ (\ frac {1} {1000} \) (0,001) усилителя — или даже микроампер (мкА), что составляет одну миллионную (\ (\ frac {1} {1,000,000} \) или 0,000001) усилителя, и так далее. Нам нужно преобразовать эти единицы в базовые единицы в вольтах (В), омах (Ом) и амперах (А) для выполнения нашего анализа.

Например, если схема содержит резистор 2,2 кОм с батареей 9 В, для расчета тока не следует ошибочно писать \ (I = \ frac {9V} {2.2Ω} A \), а вместо этого \ (I = \ frac {9V} {2200Ω} A \). Первый даст вам 4,1 А (большая сила тока и неправильный!), А второй дает правильное значение 0,0041 А, что составляет 4,1 мА.

Так что обязательно дважды проверяйте свои единицы!

Общие префиксы SI

Ниже мы написали несколько общих префиксов SI, большинство из которых должно быть вам знакомо по другим измеряемым величинам.{-12} \) pico n триллионная пикосекунда, пикоамп

Таблица Эта диаграмма основана на веб-странице метрических префиксов SI NIST и рисунке 2.2 в книге Бартлетта.

Преобразование единиц

Для преобразования между префиксной единицей и базовой единицей мы умножаем на коэффициент преобразования. Чтобы преобразовать базовую единицу в единицу с префиксом, мы делим на коэффициент преобразования.

Так, например, чтобы преобразовать 2.{-6}} = 37 мкА \).

Разберем схемы!

Уф, хорошо, теперь мы готовы приступить к анализу некоторых схем. Мы начнем с простой схемы и перейдем к ней. Анализируя (или даже готовясь к созданию) схем, всегда полезно взять карандаш и бумагу. Итак, сделайте это сейчас.

Кроме того, полезно иметь способ проверить нашу работу, что мы можем сделать в симуляторе схем. Мне нравится использовать CircuitJS, но я также использовал EveryCircuit и CircuitLab — последнее стоит денег.

Прежде чем мы начнем, давайте посмотрим это видео, в котором я строю простую резистивную схему в CircuitJS и вычисляю ее ток с учетом источника напряжения и резистора.

Видео Видео было создано с помощью симулятора CircuitJS. Прямая ссылка здесь.

Пример 1: Решить для тока

Представьте себе схему с батарейным питанием и одним резистором (базовым, да, но с педагогической точки зрения мощным!). Если нам заданы напряжение \ (9 В \) и сопротивление (\ (100 Ом \)), можем ли мы решить для тока \ (I \)?

Рисунок. Простая схема с питанием 9 В с одним резистором \ (100 Ом \). Можете ли вы, используя закон Ома, вычислить ток \ (I \)? Изображения сделаны в Fritzing и PowerPoint.

Шаг 1. Определите известных

Чтобы начать анализ, вам нужно определить все, что вы знаете об этой цепи.

Обратите внимание, что все провода, соприкасающиеся с положительной клеммой батареи , имеют одинаковый электрический потенциал (\ (9 В \)), который мы теперь пометили красным, и все провода, соприкасающиеся с отрицательной клеммой батареи , имеют одинаковый электрический потенциал. (\ (0V \)) — который мы отметили черным.Обратите внимание, что даже несмотря на то, что медные провода имеют некоторое сопротивление, оно настолько мало (особенно для длин в цифровой цепи), что мы можем смоделировать его как \ (0Ω \) (действительно, провода всегда предполагаются \ (0Ω \) в этом виде схемотехнического анализа).

И поскольку мы вычисляем по току, нам нужно использовать формулировку закона Ома: \ (I = \ frac {V} {R} \). Более конкретно, поскольку напряжение всегда относительное — разность электрических потенциалов — мы используем \ (I = \ frac {V_1 — V_2} {R} \)

Рис. Все провода, соприкасающиеся с плюсовой клеммой аккумулятора, имеют одинаковое напряжение (9 В). Точно так же все провода, соприкасающиеся с отрицательной клеммой аккумулятора, имеют одинаковое напряжение (0 В). Изображения сделаны в Fritzing и PowerPoint.

Шаг 2: Примените знания

Установив, что все провода наверху схемы (те, которые непосредственно подключены к положительной клемме) имеют одинаковый электрический потенциал, мы можем отметить это как один узел \ (V_1 \ ) . Точно так же все провода, соприкасающиеся с отрицательной клеммой АКБ, можно назвать узлом \ (В_2 \) .

Теперь мы можем заменить \ (9V \) на \ (V_1 \) и \ (0V \) на \ (V_2 \). И мы также знаем, что \ (R = 100Ω \), что дает нам полное уравнение: \ (I = \ frac {9V — 0V} {100Ω} \)

Рис. Мы можем назвать все провода, соприкасающиеся с положительным клеммным узлом батареи \ (V_1 \), и все провода, соприкасающиеся с отрицательным клеммным узлом \ (V_2 \). Используя эту информацию, мы можем заменить \ (9V \) на \ (V_1 \) и \ (0V \) на \ (V_2 \). Изображения сделаны в Fritzing и PowerPoint.

Шаг 3: Решите для тока I

Наконец, мы готовы решить для тока \ (I = \ frac {9V — 0V} {100Ω} \ Rightarrow 0.09A \ Rightarrow 90mA \)

Сделали. Мы успешно применили закон Ома для определения тока!

Пример 2: Снова вычислить для тока (но с другим сопротивлением)

Давайте попробуем снова вычислить для тока с помощью аналогичной схемы. На этот раз сопротивление увеличено с \ (100 Ом \) до \ (4,7 кОм \).

Прежде чем делать что-либо еще: полезно подумать о концептуально , что произойдет?

Ток уменьшается, верно? И делает это пропорционально.

Действительно, ток изменяется от \ (90 мА \) с \ (100 Ом \) до \ (I = \ frac {9V} {4700 Ом} \ Rightarrow 0.0019𝐴 \ Rightarrow 1.9𝑚𝐴 \), что не очень много!

Рисунок. Как и ожидалось, ток \ (I \) снижается, когда сопротивление \ (R \) увеличивается.

Пример 3: Решить для напряжения

Как отмечалось выше, мы можем использовать три различных формулировки закона Ома (\ (I = \ frac {V} {R} \), \ (V = I * R \), и \ (R = \ frac {V} {I} \)), чтобы помочь нам проанализировать различные неизвестные в схеме.

В этом случае давайте воспользуемся законом Ома, чтобы найти неизвестный источник напряжения . Предположим, что схема аналогична предыдущей: один источник напряжения (но неизвестного напряжения) с одним резистором размером \ (100 Ом \) и током \ (I = 50 мА \).

Поскольку мы вычисляем напряжение, мы должны использовать формулу \ (V = I * R \). Первое, что нам нужно сделать, это убедиться, что все наши измерения находятся в базовых единицах . Сила тока нет, поэтому измените его на силу тока (а не в миллиампер): \ (I = 50 мА \ Rightarrow 0.05А \).

Теперь мы можем легко найти \ (V = 0,05 A * 100 Ом = 5 В). Батарея является источником напряжения \ (5В \).

Рисунок. Используя формулировку \ (V = I * R \) закона Ома, мы можем найти напряжение при известном токе \ (I \) и известном сопротивлении \ (R \). Изображения сделаны в Fritzing и PowerPoint.

Пример 4: Решите для сопротивления

Готов поспорить, вы уже поняли это!

Наконец, вы можете использовать \ (R = \ frac {V} {I} \) для определения сопротивления, если известны \ (V \) и \ (I \).В этом случае давайте вернемся к нашей батарее \ (9 В \) и предположим, что у нас есть ток \ (1,32 мА \). Какой номинал резистора \ (R \)?

Опять же, первое, что нужно сделать, это преобразовать все единицы в базовые. Итак, \ (1.32mA \ Rightarrow 0.00132A \).

Теперь мы можем найти \ (R = \ frac {9V} {0.00132A} \ Rightarrow 6818.2Ω \ Rightarrow 6.8kΩ \)

Рис. Используя формулировку \ (R = \ frac {V} {I} \) закона Ома, мы можем найти сопротивление \ (R \) при известном напряжении \ (V \) и известном токе \ (I \ ).Изображения сделаны в Fritzing и PowerPoint.

Упражнение: Использование симулятора схем

Теперь, когда мы получили начальное понимание закона Ома, пора построить и поиграть с некоторыми схемами в симуляторе схем.

Используя CircuitJS, постройте и проанализируйте пять различных типов резистивных цепей. Вы можете создавать любые схемы с некоторыми требованиями:

• Все схемы должны иметь только один источник питания
• Вы должны использовать только резисторы
• Вы можете использовать столько резисторов на схему, сколько хотите, но дважды щелкните по провода для отображения тока / напряжения
• Для каждой схемы сделайте снимок экрана и поместите его в журнал прототипирования вместе с кратким отражением того, что вы наблюдали / узнали.

Вы можете сохранить схемы одним из двух способов: (1) загрузить их локально (Файл -> Сохранить как) или (2) экспортировать их как общую ссылку (Файл -> Экспортировать как ссылку) — используйте последний вариант. для ваших журналов по прототипированию.

В свои журналы прототипирования включите снимок экрана каждой схемы CircuitJS вместе с кратким описанием того, что вы наблюдали, и прямой ссылкой на созданную вами схему CircuitJS.

Краткое содержание урока

В этом уроке мы узнали:

• Что существует эмпирический закон, называемый законом Ома, который описывает линейную зависимость между напряжением, током и сопротивлением
• В частности, закон Ома утверждает, что ток в цепь — это полное напряжение, деленное на полное сопротивление (\ (I = \ frac {V} {R} \)).Этот закон основан на концепциях и интуиции, которые мы развили в первом уроке этой серии.
• Мы также узнали, как применить закон Ома к некоторым простым схемам, чтобы найти неизвестные токи, напряжения и сопротивления.
• Это обычная проблема. для новичков забывает преобразовать измерения в базовые единицы
• Затем мы поигрались со схемами в CircuitJS и сделали наблюдения.

Ресурсы

Следующий урок

В следующем уроке мы применим закон Ома к более сложным схемам, особенно тем, которые объединяют резисторы в серии и те, которые объединяют их в параллельно .

Предыдущая: Схема Следующая: Последовательные и параллельные резисторы

---

Все материалы с открытым исходным кодом созданы лабораторией Makeability Lab и профессором Джоном Э. Фрелихом. Нашли ошибку? Отправьте сообщение о проблеме на GitHub.

KVL, KCL и закон Ома

Принцип работы

Согласно закону Кирхгофа о напряжении (KVL), сумма всех напряжений в контуре равна нулю. При обходе контура интуитивно вы можете рассматривать источник напряжения как положительное значение, а резисторы как отрицательные значения, потребляющие напряжение.В этом моделировании входное напряжение равно сумме падений напряжения на R ₁ и R ₂ : V _в — V _R1 — V _R2 = 0. Другими словами, V _в = V _R1 + V _R2 .

Вы можете найти напряжение на R ₂ , используя правило делителя напряжения. Во-первых, используйте уравнение для определения R _eq для двух неравных резисторов из модели сети резисторов (это также применимо к резисторам равного номинала, хотя их можно решить без этого уравнения):

Затем используйте уравнение делителя напряжения, чтобы найти V _R2:

Кроме того, напряжение на R ₂ и R ₃ равно, потому что эти резисторы подключены параллельно: V _R2 = V _R3 .

Согласно закону Кирхгофа по току (KCL), сумма всех токов, входящих в узел, равна сумме всех токов, выходящих из него. Ток I _R1 в этой симуляции делится на два — I _R2 и I _R3 — и, таким образом, равен их сумме: I _R1 — I _R2 — I _R3 = 0. Другими словами, I _R1 = I _R2 + I _R3 .

По закону Ома ток через каждый резистор будет равен напряжению на резисторе, деленному на его сопротивление.Это моделирование показывает, что ток течет по пути наименьшего сопротивления (через R ₂ протекает больше тока, чем через R ₃ ): V = IR ₁ = I ₂ R ₂ = I ₃ Р ₃ .

В этой модели также указывается мощность, рассеиваемая каждым резистором. Вы можете убедиться, что рассеиваемая мощность равна току, протекающему через резистор, умноженному на напряжение на нем.

Эксперименты

• Приравнивается R ₂ и R ₃ значений.Каков ток через эти резисторы по отношению к току через R ₁ сейчас?
• Измените значение R ₂ или R ₃ на ноль Ом. Какой сейчас ток через оставшиеся два ненулевых резистора?

Закон Ома

Закон Ома

Национальная аэронавтика и Космическое управление Исследовательский центр Гленна

Образовательный продукт Учителя 9–12 классы

---

Где:

V = напряжение

I = ток

R = Сопротивление

---

Пример проблемы:

Аккумулятор на девять вольт обеспечивает питание беспроводного плойка с сопротивлением 18 Ом.Насколько ток протекает через щипцы для завивки?

Эскиз:

---

Решение:

1.) Поскольку V (напряжение) и R (сопротивление) известны, решите для I (ток), разделив обе стороны уравнение Р.

2.) Буквы R в правой части уравнения Отмена.

3.) I остается в терминах V и R.

4.) Подставьте значения для V (напряжение) и R (Сопротивление).

5.) Решите относительно I (Текущий).

---

Задача № 1

Настенная розетка на 110 В обеспечивает питание стробоскопа. свет с сопротивлением 2200 Ом. Сколько тока течет через стробоскоп?

Эскиз:

Выберите свой ответ ниже

1. 0.5 усилители
2. 2,0 усилители
3. 0,05 усилители
4. 1,0 усилители

---

Задача № 2

Проигрыватель компакт-дисков с сопротивлением 40 Ом имеет через него протекает ток 0,1 ампер.