Закон Ома для полной цепи
Закон Ома для полной цепи – эмпирический (полученный из эксперимента) закон, который устанавливает связь между силой тока, электродвижущей силой (ЭДС) и внешним и внутренним сопротивлением в цепи.
При проведении реальных исследований электрических характеристик цепей с постоянным током необходимо учитывать сопротивление самого источника тока. Таким образом в физике осуществляется переход от идеального источника тока к реальному источнику тока, у которого есть свое сопротивление (см. рис. 1).

Рис. 1. Изображение идеального и реального источников тока
Рассмотрение источника тока с собственным сопротивлением обязывает использовать закон Ома для полной цепи.
Сформулируем закона Ома для полной цепи так (см. рис. 2): сила тока в полной цепи прямо пропорциональна ЭДС и обратно пропорциональна полному сопротивлению цепи, где под полным сопротивлением понимается сумма внешних и внутренних сопротивлений.

Рис. 2. Схема закона Ома для полной цепи.
Формула закона Ома для полной цепи

- R – внешнее сопротивление [Ом];
- r – сопротивление источника ЭДС (внутреннее) [Ом];
- I – сила тока [А];
- ε– ЭДС источника тока [В].
Рассмотрим некоторые задачи на данную тему. Задачи на закон Ома для полной цепи, как правило, дают ученикам 10 класса, чтобы они могли лучше усвоить указанную тему.
I. Определите силу тока в цепи с лампочкой, сопротивлением 2,4 Ом и источником тока, ЭДС которого равно 10 В, а внутреннее сопротивление 0,1 Ом.
По определению закона Ома для полной цепи, сила тока равна:

II. Определить внутреннее сопротивление источника тока с ЭДС 52 В. Если известно, что при подключении этого источника тока к цепи с сопротивлением 10 Ом амперметр показывает значение 5 А.
Запишем закон Ома для полной цепи и выразим из него внутреннее сопротивление:

III. Однажды школьник спросил у учителя по физике: «Почему батарейка садится?» Как грамотно ответить на данный вопрос?
Мы уже знаем, что реальный источник обладает собственным сопротивлением, которое обусловлено либо сопротивлением растворов электролитов для гальванических элементов и аккумуляторов, либо сопротивлением проводников для генераторов. Согласно закону Ома для полной цепи:

следовательно, ток в цепи может уменьшаться либо из-за уменьшения ЭДС, либо из-за повышения внутреннего сопротивления. Значение ЭДС у аккумулятора почти постоянный. Следовательно, ток в цепи понижается за счет повышения внутреннего сопротивления. Итак, «батарейка» садится, так как её внутреннее сопротивление увеличивается.
2. Закон Ома для участка цепи.
I=u/R
Сила тока на участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.
Графически, данная зависимость, выглядит следующим образом:
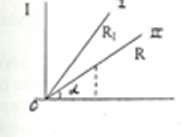
Наклон прямой I(u) определяется величиной сопротивления: чем больше R, тем меньше наклон прямой I(U). Это видно из таких соображений:
Ctg = u/I = R
Даны два графика для двух проводников с различными сопротивлениями:
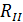 >
> 
Следствия из закона Ома:
R = u / I =>> [R] = [B/A] = [Oм]
Данная формула не дает зависимости R от u и I так как сопротивление — это электрическая характеристика проводника. Другими словами,
Сопротивление — свойство самого проводника оказывать препятствие току.
3. Правило Кирхгофа. Параллельное и последовательное соединение проводников.
Узлом называется точка, в которой сходится более чем два проводника.

Ток, текущий к узлу, считается имеющим один знак (плюс или минус), текущий от узла — имеющим другой знак (минус или плюс).
Первое правило Кирхгофа гласит: алгебраическая сумма токов, сходящихся в узле, равна нулю.

Справедливость этого утверждения вытекает из следующих соображений: если бы алгебраическая сумма токов была отлична от нуля, то в узле происходило бы накопление или уменьшение заряда, что в свою очередь привело бы к изменению потенциала узла и изменению текущих в цепи токов. Таким образом, чтобы токи в цепи были постоянными, должно выполняться условие
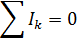
Выделим в разветвленной цепи какой-либо замкнутый контур ABCFD

К отдельным ее участкам можно применить закон Ома для участка цепи. Тогда для разности потенциалов точек А и В имеем
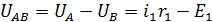
Аналогично для других участков:
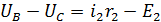


Складывая почленно эти равенства, мы найдем, что сумма левых частей равно нулю, откуда
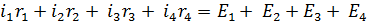
Поэтому:
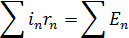
Это уравнение выражает второе правило Кирхгофа
Алгебраическая сумма произведений токов на сопротивление в ветвях замкнутого контура, равна алгебраической сумме ЭДС встречающихся в этом контуре.
Последовательное и параллельное соеденение проводников
При последовательном соединении все потребители включают в цепь поочередно друг за другом

Законы последовательного соединения:
а) Сила тока на любом участке цепи одинакова
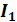 =
=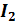 =…=
=…= =const
=const
Справедливость этого утверждения вытекает из следующих соображений: если бы на различных участках цепи сила тока была различной, то в некоторых точках цепи происходило бы накопление зарядов, чего не наблюдается.
б) Напряжение на всей цепи равно сумме напряжений на отдельных ее участках.
U
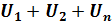
Это утверждение вытекает ю того, что работа по перемещению заряда по цепи равна сумме работ на отдельных участках:
A= 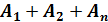
Разделив все члены этого равенства на «q», мы получим равенство из б).
в) Используя следствие из закона Ома (u = IR), равенство из б) примет вид:
I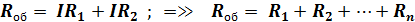
Для «n» одинаковых сопротивлений:
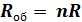
г) Напряжение на последовательно включенных проводниках прямо пропорционально их сопротивлению.

При параллельном соединении проводников, их начала и концы имеют общие точки подключения к источнику тока.

Законы параллельного соединения:
а) Так как в т. 1 заряд не накапливается, то заряд, поступающий в единицу времени в узел 1, равен заряду, уходящему из узла за это же время
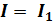 +
+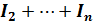
б) В этом случае выход из строя одного прибора не отражается на работе остальных (перегорела лампочка), тогда как при последовательном соединении выход из строя одного прибора размыкает цепь
U=const
в) Применив закон Ома к а), получим:
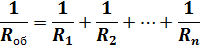
При параллельном соединении общее сопротивление уменьшается. Величина, обратная сопротивлению — проводимость => проводимость параллельного разветвления равна сумме проводимостей его ветвей
Для «n» одинаковых сопротивлений в) примет вид:
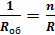 =>
=> 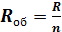
г) Сила тока при параллельном соединении разветвляется по ветвям согласно их сопротивлениям: больший ток идет через меньшее сопротивление, а меньший — через большее.

Основные законы цепей постоянного тока
Расчет и анализ электрических цепей производится с использованием закона Ома, первого и второго законов Кирхгофа. На основе этих законов устанавливается взаимосвязь между значениями токов, напряжений, ЭДС всей электрической цепи и отдельных ее участков и параметрами элементов, входящих в состав этой цепи.
Закон Ома для участка цепи
Соотношение
между током I, напряжением UR и сопротивлением
R участка аb электрической цепи (рис. 1.3)
выражается законом Ома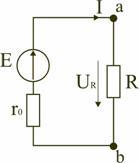
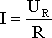
Рис.1 или UR = RI.
В этом случае UR = RI – называют напряжением
или падением напряжения на резисторе R, а – током в резисторе R.
При расчете электрических цепей иногда удобнее пользоваться не сопротивлением R, а величиной обратной сопротивлению, т.е. электрической проводимостью:
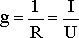 .
.
В этом случае закон Ома для участка цепи запишется в виде:
I = Uq.
Закон Ома для всей цепи
Этот закон определяет зависимость между ЭДС Е источника питания с внутренним сопротивлением r0 (рис.1), током I электрической цепи и общим эквивалентным сопротивлением RЭ = r0 + R всей цепи:
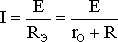 .
.
Сложная электрическая цепь содержит, как правило, несколько ветвей, в которые могут быть включены свои источники питания и режим ее работы не может быть описан только законом Ома. Но это можно выполнить на основании первого и второго законов Кирхгофа, являющихся следствием закона сохранения энергии.
Первый закон Кирхгофа
В любом узле электрической цепи алгебраическая сумма токов равна нулю
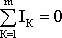 ,
,
где m – число ветвей подключенных к узлу.
При записи уравнений по первому закону Кирхгофа токи, направленные к узлу, берут со знаком «плюс», а токи, направленные от узла – со знаком «минус». Например, для узла а (см. рис. 1) I — I1 — I2 = 0.
Второй закон Кирхгофа
В любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех его участках
 ,
,
где n – число источников ЭДС в контуре; m – число элементов с сопротивлением Rк в контуре; Uк = RкIк – напряжение или падение напряжения на к-м элементе контура.
Для схемы (рис. 1) запишем уравнение по второму закону Кирхгофа:
E = UR + U1.
Если в электрической цепи включены источники напряжений, то второй закон Кирхгофа формулируется в следующем виде: алгебраическая сумма напряжений на всех элементах контура, включая источники ЭДС равна нулю
 .
.
При записи уравнений по второму закону Кирхгофа необходимо:
1) задать условные положительные направления ЭДС, токов и напряжений;
2) выбрать направление обхода контура, для которого записывается уравнение;
3) записать уравнение, пользуясь одной из формулировок второго закона Кирхгофа, причем слагаемые, входящие в уравнение, берут со знаком «плюс», если их условные положительные направления совпадают с обходом контура, и со знаком «минус», если они противоположны.
 Рис.2
Рис.2
Запишем уравнения по II закону Кирхгофа для контуров электрической схемы (рис. 2):
контур I: E = RI + R1I1 + r0I,
контур II: R1I1 + R2I2 = 0,
контур III: E = RI + R2I2 + r0I.
В действующей цепи электрическая энергия источника питания преобразуется в другие виды энергии. На участке цепи с сопротивлением R в течение времени t при токе I расходуется электрическая энергия
W = I2Rt.
Скорость преобразования электрической энергии в другие виды представляет электрическую мощность
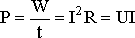 .
.
Из закона сохранения энергии следует, что мощность источников питания в любой момент времени равна сумме мощностей, расходуемой на всех участках цепи.
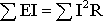 .
.
Это соотношение (1.8) называют уравнением баланса мощностей. При составлении уравнения баланса мощностей следует учесть, что если действительные направления ЭДС и тока источника совпадают, то источник ЭДС работает в режиме источника питания, и произведение E I подставляют в (1.8) со знаком плюс. Если не совпадают, то источник ЭДС работает в режиме потребителя электрической энергии, и произведение E I подставляют в (1.8) со знаком минус. Для цепи, показанной на рис. 1.2 уравнение баланса мощностей запишется в виде:
EI = I2(r0 + R) + I12R1 + I22R2.
Схемы соединения приёмников электрической цепи.
Сопротивления в электрических цепях могут быть соединены последовательно, параллельно, по смешанной схеме и по схемам «звезда», «треугольник». Расчет сложной схемы упрощается, если сопротивления в этой схеме заменяются одним эквивалентным сопротивлением Rэкв, и вся схема представляется в виде схемы на рис. 1.3, где R=Rэкв, а расчет токов и напряжений производится с помощью законов Ома и Кирхгофа.
ЗАКОН ОМА
На рисунке показана схема знакомой вам простейшей электрической цепи. Эта замкнутая цепь состоит из трех элементов: источника напряжения — батареи GB, потребителя тока — нагрузки R, которой может быть, например, нить накала электрической лампы или резистор, и проводников, соединяющих источник напряжения с нагрузкой. Между прочим, если эту цепь дополнить выключателем, то получится полная схема карманного электрического фонаря.

Нагрузка R, обладающая определенным сопротивлением, является участком цепи. Значение тока на этом участке цепи зависит от действующего на нем напряжения и его сопротивления: чем больше напряжение и меньше сопротивление, тем большим ток будет идти по участку цепи. Эта зависимость тока от напряжения и сопротивления выражается следующей формулой:
I = U/R
где I — ток, выраженный в амперах, А; U — напряжение в вольтах, В; R — сопротивление в омах, Ом. Читается это математическое выражение так: ток на участке цепи прямо пропорционален напряжению на нем и обратно пропорционален его сопротивлению. Это основной закон электротехники, именуемый законом Ома (по фамилии Г. Ома), для участка электрической цепи. Используя закон Ома, можно по двум известным электрическим величинам узнать неизвестную третью. Вот несколько примеров практического применения закона Ома.
Первый пример: На участке цепи, обладающем сопротивлением 5 Ом, действует напряжение 25 В. Надо узнать значение тока на этом участке цепи.
Решение: I = U/R = 25 / 5 = 5 А.
Второй пример: На участке цепи действует напряжение 12 В, создавая в нем ток, равный 20 мА. Каково сопротивление этого участка цепи? Прежде всего ток 20 мА нужно выразить в амперах. Это будет 0,02 А. Тогда R = 12 / 0,02 = 600 Ом.
Третий пример: Через участок цепи сопротивлением 10 кОм течет ток 20 мА. Каково напряжение, действующее на этом участке цепи? Здесь, как и в предыдущем примере, ток должен быть выражен в амперах (20 мА = 0,02 А), сопротивление в омах (10кОм = 10000Ом). Следовательно, U = IR = 0,02 х 10000 = 200 В. На цоколе лампы накаливания плоского карманного фонаря выштамповано: 0,28 А и 3,5 В. О чем говорят эти сведения? О том, что лампочка будет нормально светиться при токе 0,28 А, который обусловливается напряжением 3,5 В, Пользуясь законом Ома, нетрудно подсчитать, что накаленная нить лампочки имеет сопротивление R = 3,5 / 0,28 = 12,5 Ом. Это, подчеркиваю, сопротивление накаленной нити лампочки. А сопротивление остывшей нити значительно меньше. Закон Ома справедлив не только для участка, но и для всей электрической цепи. В этом случае в значение R подставляется суммарное сопротивление всех элементов цепи, в том числе и внутреннее сопротивление источника тока. Однако при простейших расчетах цепей обычно пренебрегают сопротивлением соединительных проводников и внутренним сопротивлением источника тока.
В связи с этим приведу еще один пример: Напряжение электроосветительной сети 220 В. Какой ток потечет в цепи, если сопротивление нагрузки равно 1000Ом? Решение: I = U/R = 220 / 1000 = 0,22 А. Примерно такой ток потребляет электрический паяльник.
Всеми этими формулами, вытекающими из закона Ома, можно пользоваться и для расчета цепей переменного тока, но при условии, если в цепях нет катушек индуктивности и конденсаторов.
Закон Ома и производные от него расчетные формулы, достаточно легко запомнить, если пользоваться вот этой графической схемой, т. н. треугольник закона Ома:
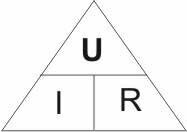
>Пользоваться этим треугольником легко, достаточно четко запомнить, что горизонтальная линия в треугольнике означает знак деления (по аналогии дробной черты), а вертикальная линия в треугольнике означает знак умножения.
Теперь рассмотрим такой вопрос: как влияет на ток резистор, включаемый в цепь последовательно с нагрузкой или параллельно ей? Разберем такой пример. У нас имеется лампочка от круглого электрического, фонаря, рассчитанная на напряжение 2,5 В и ток 0,075 А. Можно ли питать эту лампочку от батареи 3336Л, начальное напряжение которой 4,5 В? Нетрудно подсчитать, что накаленная нить этой лампочки имеет сопротивление немногим больше 30 Ом. Если же питать ее от свежей батареи 3336Л, то через нить накала лампочки, по закону Ома, пойдет ток, почти вдвое превышающий тот ток, на который она рассчитана. Такой перегрузки нить не выдержит, она перекалится и разрушится. Но эту лампочку все же можно питать от батареи 336Л, если последовательно в цепь включить добавочный резистор сопротивлением 25 Ом, как это показано на рис..

В этом случае общее сопротивление внешней цепи будет равно примерно 55 Ом, т.е. 30 Ом — сопротивление нити лампочки Н плюс 25 Ом — сопротивление добавочного резистора R. В цепи, следовательно, потечет ток, равный примерно 0,08 А, т.е. почти такой же, на который рассчитана нить накала лампочки. Эту лампочку можно питать от батареи и с более высоким напряжением и даже от электроосветительной сети, если подобрать резистор соответствующего сопротивления. В этом примере добавочный резистор ограничивает ток в цепи до нужного нам значения. Чем больше будет его сопротивление, тем меньше будет и ток в цепи. В данном случае в цепь было включено последовательно два сопротивления: сопротивление нити лампочки и сопротивление резистора. А при последовательном соединении сопротивлений ток одинаков во всех точках цепи. Можно включать амперметр в любую точку цепи, и всюду он будет показывать одно значение. Это явление можно сравнить с потоком воды в реке. Русло реки на различных участках может быть широким или узким, глубоким или мелким. Однако за определенный промежуток времени через поперечное сечение любого участка русла реки всегда проходит одинаковое количество воды.
Добавочный резистор, включаемый в цепь последовательно с нагрузкой (как, например, на рис. выше), можно рассматривать как резистор, «гасящий» часть напряжения, действующего в цепи. Напряжение, которое гасится добавочным резистором или, как говорят, падает на нем, будет тем большим, чем больше сопротивление этого резистора. Зная ток и сопротивление добавочного резистора, падение напряжения на нем легко подсчитать все по той же знакомой вам формуле U = IR, Здесь U — падение напряжения, В; I — ток в цепи, A; R — сопротивление добавочного резистора, Ом. Применительно к нашему примеру резистор R ( на рис.) погасил избыток напряжения: U = IR = 0,08 х 25 = 2 В. Остальное напряжение батареи, равное приблизительно 2,5 В, упало на нити лампочки. Необходимое сопротивление резистора можно найти по другой знакомой вам формуле R = U/I, где R — искомое сопротивление добавочного резистора, Ом; U-напряжение, которое необходимо погасить, В; I — ток в цепи, А. Для нашего примера сопротивление добавочного резистора равно: R = U/I = 2/0,075, 27 Ом. Изменяя сопротивление, можно уменьшать или увеличивать напряжение, которое падает на добавочном резисторе, и таким образом регулировать ток в цепи. Но добавочный резистор R в такой цепи может быть переменным, т.е. резистором, сопротивление которого можно изменять (см. рис. ниже).

В этом случае с помощью движка резистора можно плавно изменять напряжение, подводимое к нагрузке Н, а значит, плавно регулировать ток, протекающий через эту нагрузку. Включенный таким образом переменный резистор называют реостатом, С помощью реостатов регулируют токи в цепях приемников, телевизоров и усилителей. Во многих кинотеатрах реостаты использовали для плавного гашения света в зрительном зале. Есть, однако, и другой способ подключения нагрузки к источнику тока с избыточным напряжением — тоже с помощью переменного резистора, но включенного потенциометром, т.е. делителем напряжения, как показано на рис..
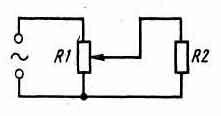
Здесь R1 — резистор, включенный потенциометром, a R2 — нагрузка, которой может быть та же лампочка накаливания или какой — то другой прибор. На резисторе R1 происходит падение напряжения источника тока, которое частично или полностью может быть подано к нагрузке R2. Когда движок резистора находится в крайнем нижнем положении, к нагрузке напряжение вообще не подается (если это лампочка, она гореть не будет). По мере перемещения движка резистора вверх мы будем подавать все большее напряжение к нагрузке R2 (если это лампочка, ее нить будет накаливаться). Когда же движок резистора R1 окажется в крайнем верхнем положении, к нагрузке R2 будет подано все напряжение источника тока (если R2 — лампочка карманного фонаря, а напряжение источника тока большое, нить лампочки перегорит). Можно опытным путем найти такое положение движка переменного резистора, при котором к нагрузке будет подано необходимое ей напряжение. Переменные резисторы, включаемые потенциометрами, широко используют для регулирования громкости в приемниках и усилителях. Резистор может быть непосредственно подключен параллельно нагрузке. В таком случае ток на этом участке цепи разветвляется и идет двумя параллельными путями: через добавочный резистор и основную нагрузку. Наибольший ток будет в ветви с наименьшим сопротивлением. Сумма же токов обеих ветвей будет равна току, расходуемому на питание внешней цепи. К параллельному соединению прибегают в тех Случаях, когда надо ограничить ток не во всей цепи, как при последовательном включении добавочного резистора, а только на каком — то участке. Добавочные резисторы подключают, например, параллельно миллиамперметрам, чтобы ими можно было измерять большие токи. Такие резисторы называют шунтирующими или шунтами. Слово шунт означает ответвление.
Спасибо lessonradio.narod.ru
Закон Ома — это… Что такое Закон Ома?
V — напряжение,I — сила тока,
R — сопротивление.
Зако́н О́ма — физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника. Экспериментально установлен в 1826 году, и назван в честь его первооткрывателя Георга Ома.
В своей оригинальной форме он был записан его автором в виде : ,
Здесь X — показания гальванометра, т.е в современных обозначениях сила тока I, a — величина, характеризующая свойства источника тока, постоянная в широких пределах и не зависящая от величины тока, то есть в современной терминологии электродвижущая сила (ЭДС) , l — величина, определяемая длиной соединяющих проводов, чему в современных представлениях соответствует сопротивление внешней цепи R и, наконец, b параметр, характеризующий свойства всей установки, в котором сейчас можно усмотреть учёт внутреннего сопротивления источника тока r[1].
В таком случае в современных терминах и в соответствии с предложенной автором записи формулировка Ома (1) выражает
Закон Ома для полной цепи:
, (2)
где:
Из закона Ома для полной цепи вытекают следствия:
- При r<<R сила тока в цепи обратно пропорциональна её сопротивлению. А сам источник в ряде случаев может быть назван источником напряжения
- При r>>R сила тока от свойств внешней цепи (от величины нагрузки) не зависит. И источник может быть назван источником тока.
Часто[2] выражение:
(3)
(где есть напряжение или падение напряжения, или, что то же, разность потенциалов между началом и концом участка проводника) тоже называют «Законом Ома».
Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется:
(4)
То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС.
К другой записи формулы (3), а именно:
(5)
Применима другая формулировка:
 | Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи. |  |
Выражение (5) можно переписать в виде:
(6)
где коэффициент пропорциональности G назван проводимость или электропроводность. Изначально единицей измерения проводимости был «обратный Ом» — Mо[3], впоследствии переименованный в Си́менс (обозначение: См, S).
Мнемоническая диаграмма для Закона
Схема, иллюстрирующая три составляющие закона Ома Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисленияВ соответствии с этой диаграммой формально может быть записано выражение:
(7)
Которое всего лишь позволяет вычислить (применительно к известному току, создающему на заданном участке цепи известное напряжение), сопротивление этого участка. Но математически корректное утверждение о том, что сопротивление проводника растёт прямо пропорционально приложенному к нему напряжению и обратно пропорционально пропускаемому через него току, физически ложно.
В специально оговорённых случаях сопротивление может зависеть от этих величин, но по умолчанию оно определяется лишь физическими и геометрическими параметрами проводника:
(8)
где:
- — удельное сопротивление материала, из которого сделан проводник,
- — его длина
- — площадь его поперечного сечения
Закон Ома и ЛЭП
Одним из важнейших требований к линиям электропередач (ЛЭП) является уменьшение потерь при доставке энергии потребителю. Эти потери в настоящее время заключаются в нагреве проводов, то есть переходе энергии тока в тепловую энергию, за что ответственно омическое сопротивление проводов. Иными словами задача состоит в том, чтобы довести до потребителя как можно более значительную часть мощности источника тока = при минимальных потерях мощности в линии передачи = , где , причём на этот раз есть суммарное сопротивление проводов и внутреннего сопротивления генератора, (последнее всё же меньше сопротивления линии передач).
В таком случае потери мощности будут определяться выражением:
= (9)
Отсюда следует, что при постоянной передаваемой мощности её потери растут прямо пропорционально длине ЛЭП и обратно пропорционально квадрату ЭДС. Таким образом желательно всемерное её увеличение, что ограничивается электрической прочностью обмотки генератора. И повышать напряжение на входе линии следует уже после выхода тока из генератора, что для постоянного тока является проблемой. Однако, для переменного тока эта задача много проще решается с помощью использования трансформаторов, что и предопределило повсеместное распространение ЛЭП на переменном токе. Однако при повышении напряжения в ней возникают потери на коронирование и возникают трудности с обеспечением надёжности изоляции от земной поверхности. Поэтому наибольшее, практически используемое, напряжение в дальних ЛЭП не превышает миллиона вольт.
Кроме того, любой проводник, как показал Дж. Максвелл, при изменении силы тока в нём, излучает энергию в окружающее пространство, и потому ЛЭП ведёт себя как антенна, что заставляет в ряде случаев наряду с омическими потерями брать в расчёт и потери на излучение.
Закон Ома в дифференциальной форме
Сопротивление зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника.
Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:
где:
Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1).
Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред.
Закон Ома для переменного тока
Вышеприведённые соображения о свойствах электрической цепи при использовании источника (генератора) с переменной во времени ЭДС остаются справедливыми. Специальному рассмотрению подлежит лишь учёт специфических свойств потребителя, приводящих к разновремённости достижения напряжением и током своих максимальных значений, то есть учёта фазового сдвига.
Если ток является синусоидальным с циклической частотой , а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными:
где:
- U = U0eiωt — напряжение или разность потенциалов,
- I — сила тока,
- Z = Re−iδ — комплексное сопротивление (импеданс),
- R = (Ra2 + Rr2)1/2 — полное сопротивление,
- Rr = ωL − 1/(ωC) — реактивное сопротивление (разность индуктивного и емкостного),
- Rа — активное (омическое) сопротивление, не зависящее от частоты,
- δ = − arctg (Rr/Ra) — сдвиг фаз между напряжением и силой тока.
При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведён взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, подбором такой что Тогда все значения токов и напряжений в схеме надо считать как
Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо.
Также необходимо отметить, что закон Ома является лишь простейшим приближением для описания зависимости тока от разности потенциалов и от сопротивления и для некоторых структур справедлив лишь в узком диапазоне значений. Для описания более сложных (нелинейных) систем, когда зависимостью сопротивления от силы тока нельзя пренебречь, принято обсуждать вольт-амперную характеристику. Отклонения от закона Ома наблюдаются также в случаях, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.
Трактовка закона Ома
Закон Ома можно просто объяснить при помощи теории Друде:
Здесь:
См. также
Примечания
Ссылки
3.2. Закон Ома в дифференциальной форме
Найдем
связь между векторами  и
и  . Для этого мысленно выделим в
окрестности некоторой точки проводника
элементарный цилиндрический объем
с образующими, параллельными векторам
. Для этого мысленно выделим в
окрестности некоторой точки проводника
элементарный цилиндрический объем
с образующими, параллельными векторам 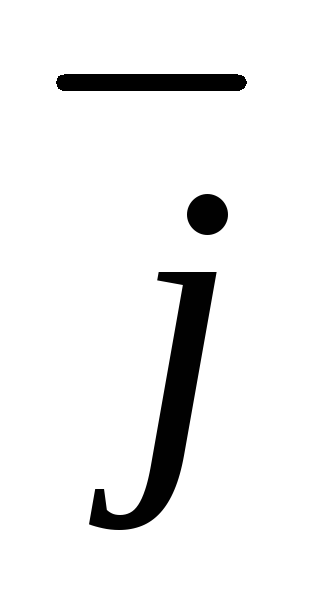 и
и  ,
(см.
рис.
4 ).
,
(см.
рис.
4 ).
Между
концами проводника длиной dl напряжение U = Edl, под действием которого через его
поперечное сечение площадью dS
течет ток I = jdS. Сопротивление цилиндрического
проводника, в нашем случае, равно R = 
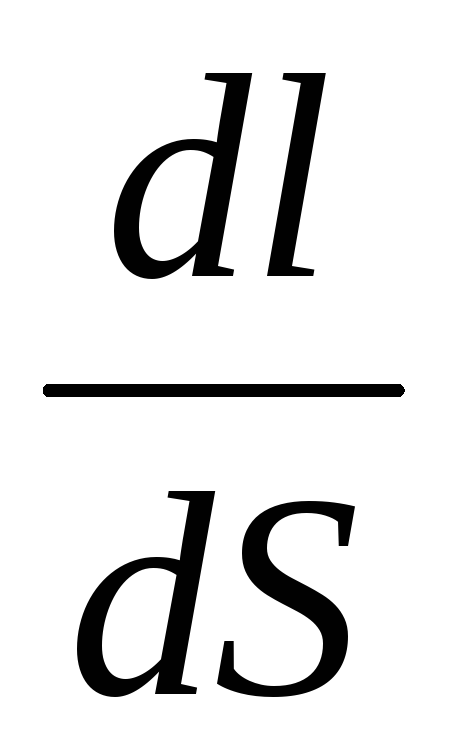 .Используя закон Ома для участка цепи
I
=
.Используя закон Ома для участка цепи
I
= 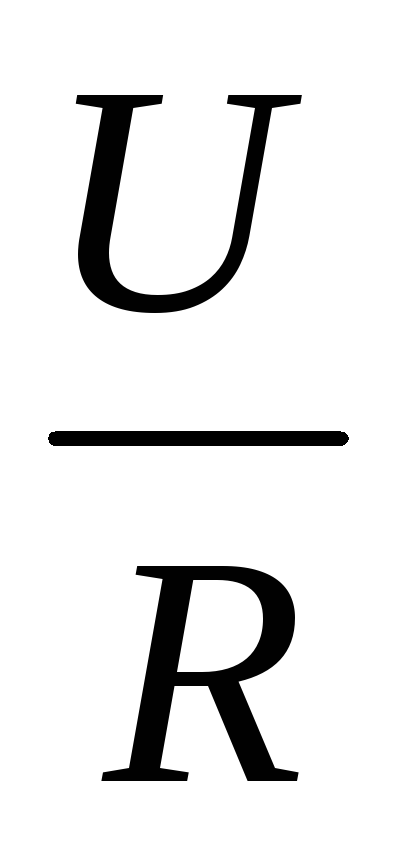 ,
находим: jdS =
,
находим: jdS =  , откуда
и получаем закон Ома в дифференциальной
форме
, откуда
и получаем закон Ома в дифференциальной
форме 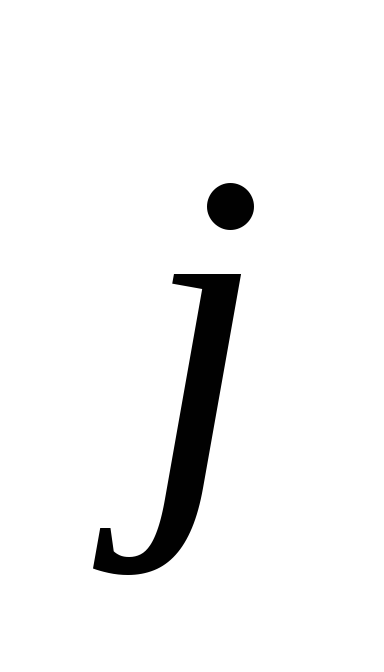 =
= 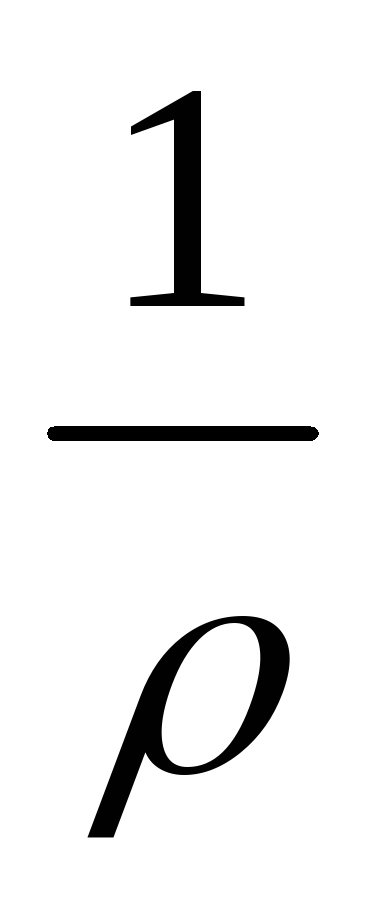
 =
=  , (16)
, (16)
где  =
=  удельная электропроводность;
[
удельная электропроводность;
[ ]
= 1 /
(Ом м)
= 1
См
/
м, где
1
См
= 1 /
Ом
–
это единица измерения электропроводности
в СИ, называемая сименс (См). Для металлов
согласно классической теории
электропроводности
]
= 1 /
(Ом м)
= 1
См
/
м, где
1
См
= 1 /
Ом
–
это единица измерения электропроводности
в СИ, называемая сименс (См). Для металлов
согласно классической теории
электропроводности  =
,
(17)
=
,
(17)
где
n
—
концентрация свободных электронов,
она может достигать 10
 10
10 электрон / м
электрон / м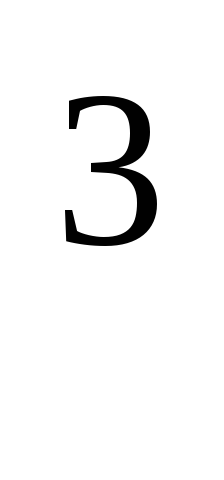 ; e—заряд
электрона, m — его масса;
<
; e—заряд
электрона, m — его масса;
<
 > — средняя длина свободного пробега
электрона; < v
> =
> — средняя длина свободного пробега
электрона; < v
> =  (18)
(18)
<
v
> —
средняя скорость теплового движения
электрона, k = 1,38 10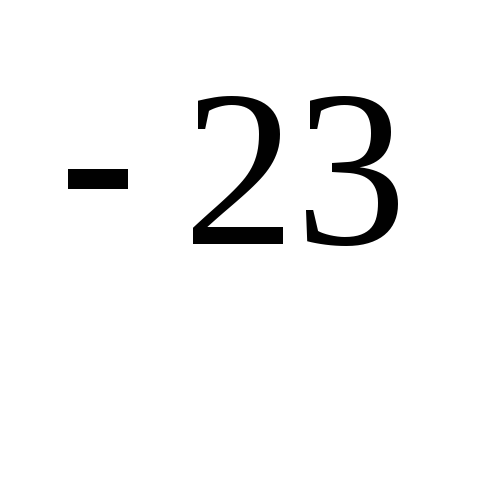 Дж/К
—
постоянная Больцмана.
Дж/К
—
постоянная Больцмана.
С
учетом
(18)
из
(17)
следует, что
~  ,
а
,
а 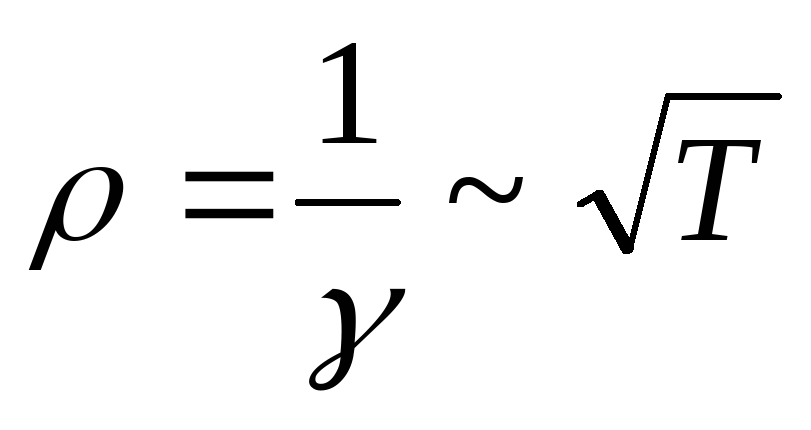 ,
тогда как опыт показывает, что
,
тогда как опыт показывает, что ~ Т .
Этот и другие недостатки классической
теории электропроводности металлов
устранила квантовая теория
электропроводности.
~ Т .
Этот и другие недостатки классической
теории электропроводности металлов
устранила квантовая теория
электропроводности.
4. Закон Ома для неоднородного участка цепи
На неоднородном участке цепи плотность тока пропорциональна сумме напряжен -ностей электростатического поля и поля сторонних сил, т.е.
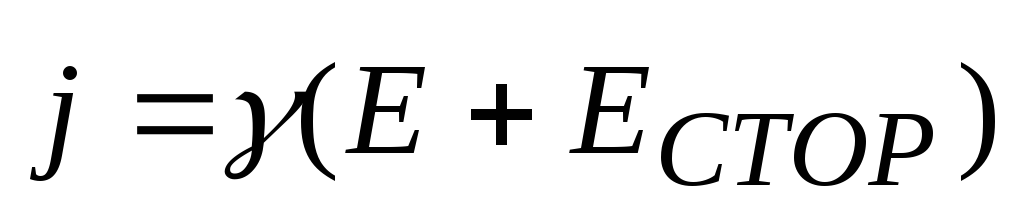 .
(19)
.
(19)
Рассмотрим цилиндрический проводник длиной / с площадью поперечного сечения S. Умножим обе части равенства (19) на перемещение dl вдоль оси проводника и проинтегрируем получившееся соотношение по длине проводника от 0 до l:
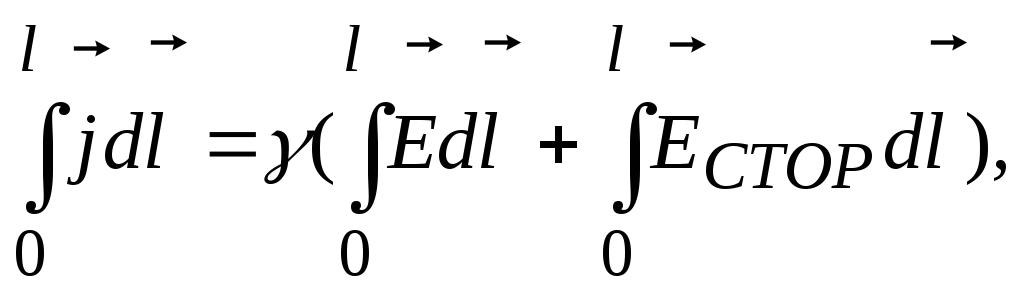
что
дает j l =  (
(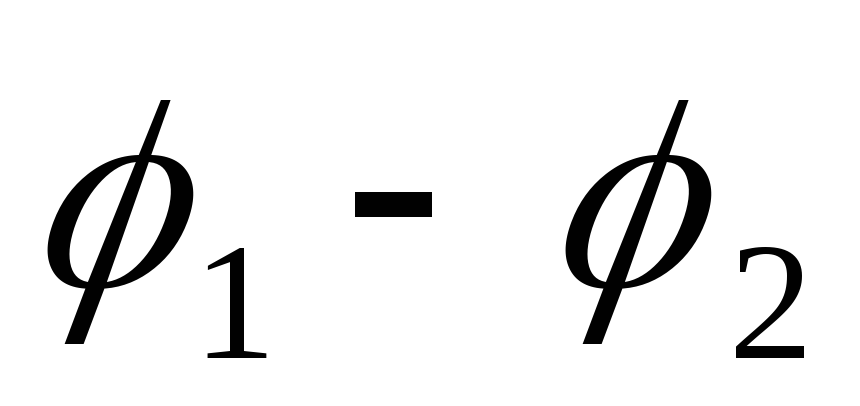 +
+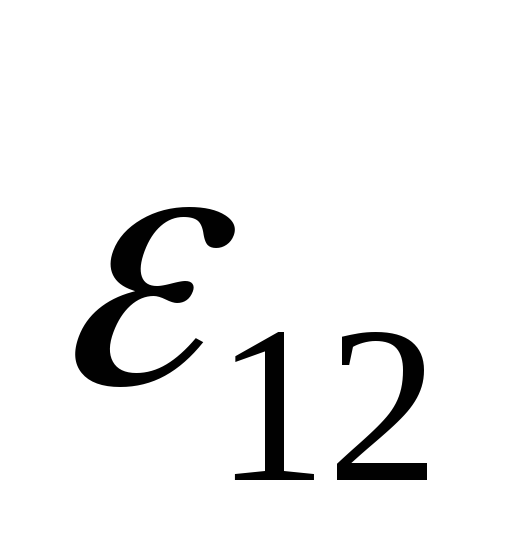 ). (20)
). (20)
Заменив j на I/S,
а  на
на 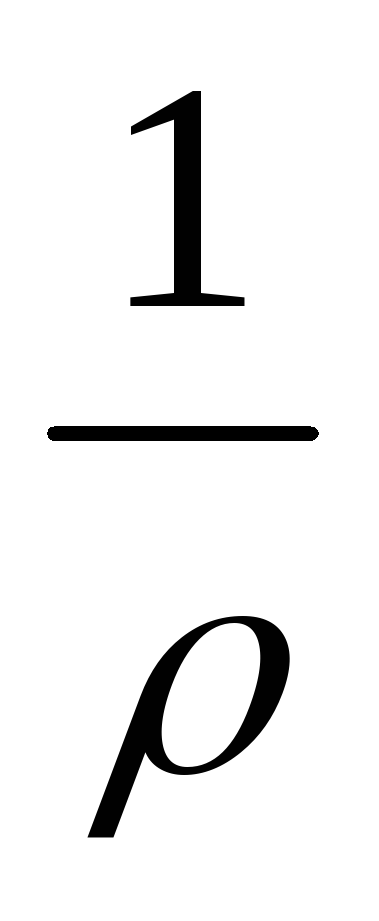 ,
из
(20)
получим I
,
из
(20)
получим I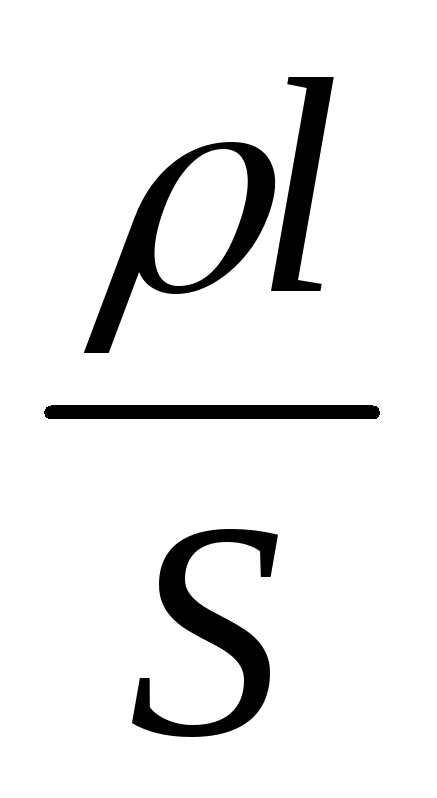 =
=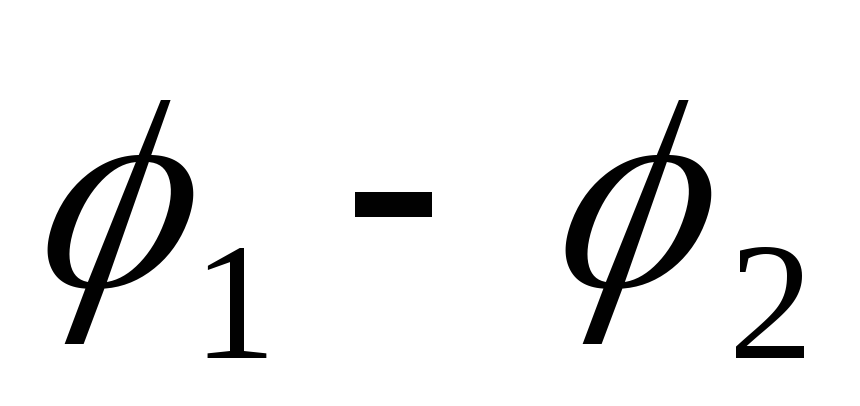 +
+  , откуда следует закон Ома для неоднородного
участка цепи I =
(
, откуда следует закон Ома для неоднородного
участка цепи I =
(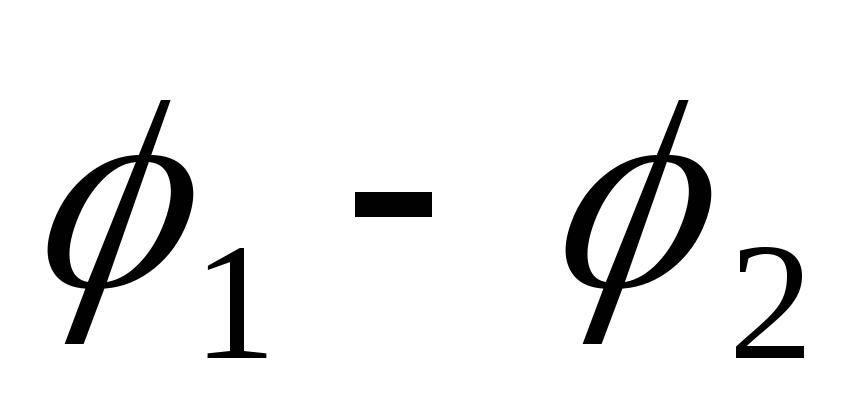 +
+ 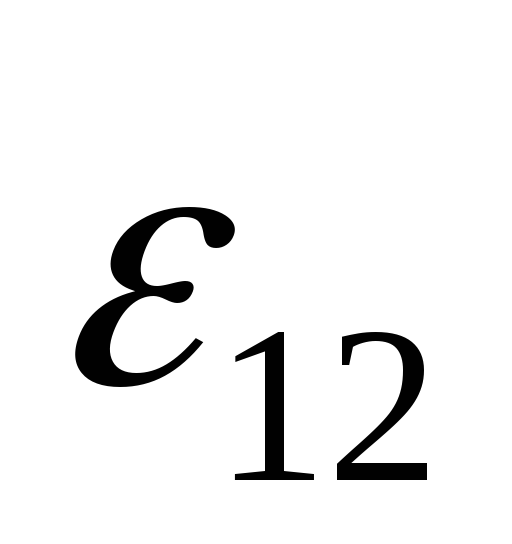 )
/ R
)
/ R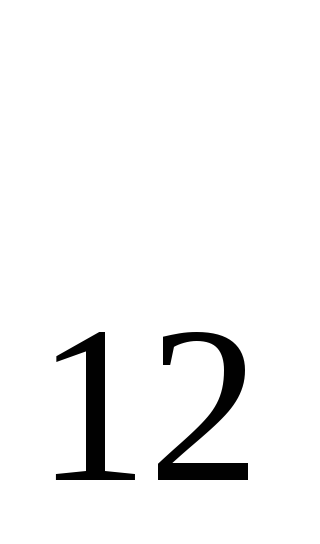 (21)
(21)
где R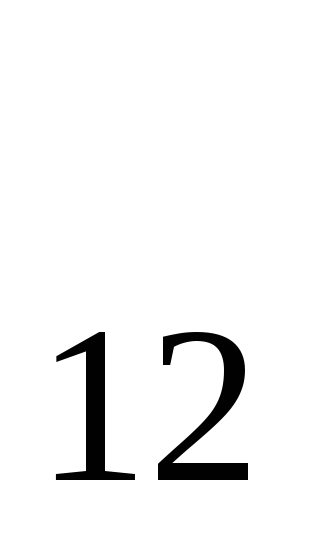 =
=  l / S — сопротивление участка цепи
12. Для
замкнутой цепи
l / S — сопротивление участка цепи
12. Для
замкнутой цепи 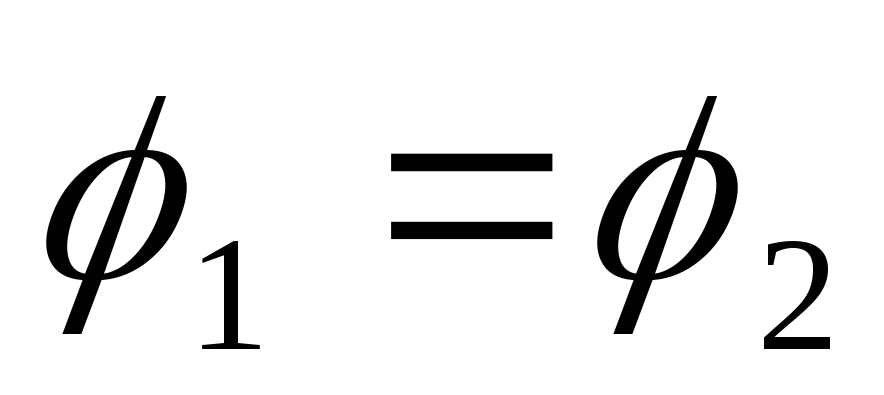 формула
(21)
запишется в виде I =
формула
(21)
запишется в виде I =  / R
/ R (22)
(22)
где R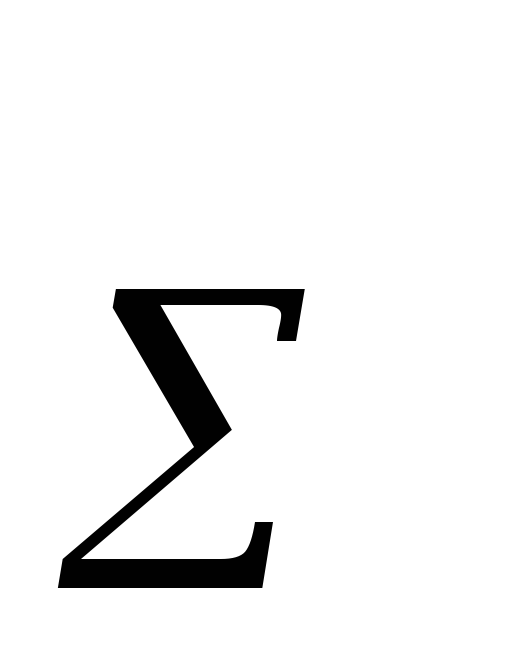 — суммарное сопротивление всей цепи;
— суммарное сопротивление всей цепи;  — ЭДС источника.
— ЭДС источника.
Пусть
замкнутая цепь состоит из источника
электрической энергии с ЭДС  и внутренним сопротивлением r ,а также внешней цепи потребителя,
имеющей сопротивление R.
Согласно
(22) I =
и внутренним сопротивлением r ,а также внешней цепи потребителя,
имеющей сопротивление R.
Согласно
(22) I =  /
(R + r). (23)
/
(R + r). (23)
Р азность
потенциалов на электродах источника,
рис. 5, равна напряжению на внешнем
участке цепи: U =
азность
потенциалов на электродах источника,
рис. 5, равна напряжению на внешнем
участке цепи: U =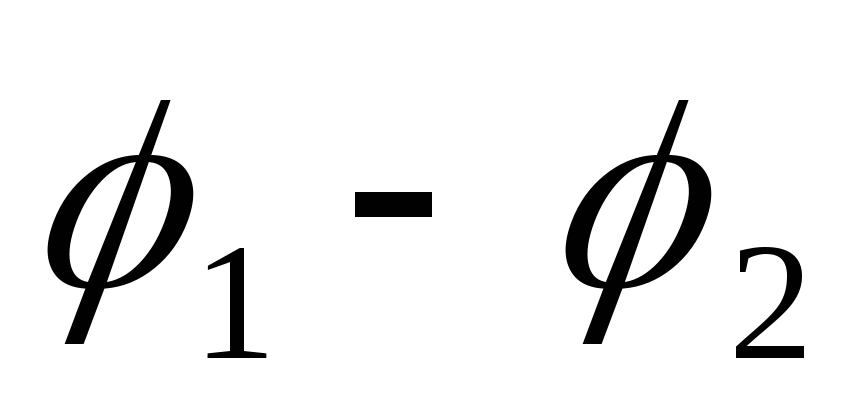 = IR =
= IR = —
Ir. (24)
—
Ir. (24)
Е  сли
цепь разомкнуть, то ток в ней прекратится
и напряжение
U
на зажимах источника станет равным его
ЭДС, т.е. U =
сли
цепь разомкнуть, то ток в ней прекратится
и напряжение
U
на зажимах источника станет равным его
ЭДС, т.е. U =  .
.
Таким
образом, напряжение на внешнем участке
цепи, рис.
5,
будет равно U = IR =  R / (R + r). (25)
R / (R + r). (25)
В
пределе, когда R 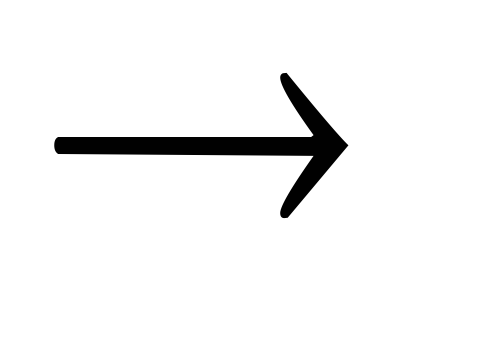 0 (источник тока замкнут накоротко), то
в этом случае, в соответствии с
(23),
ток максимален
0 (источник тока замкнут накоротко), то
в этом случае, в соответствии с
(23),
ток максимален
I =
I
=
I =
=  /
R, (26)
/
R, (26)
а напряжение во внешней цепи равно нулю.
В
противоположном предельном случае, R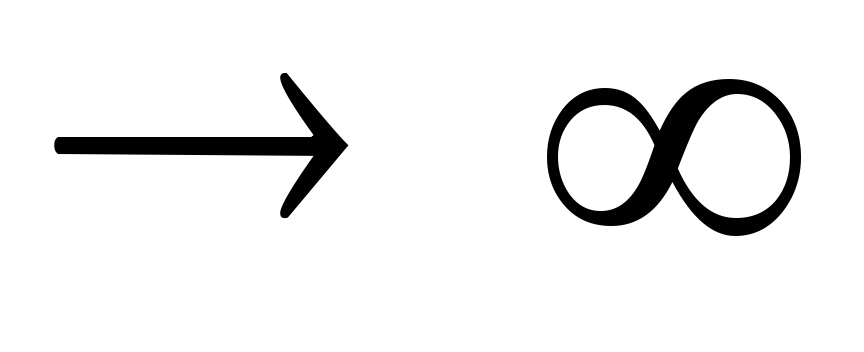 ,
цепь разомкнута и ток отсутствует: I=lim
,
цепь разомкнута и ток отсутствует: I=lim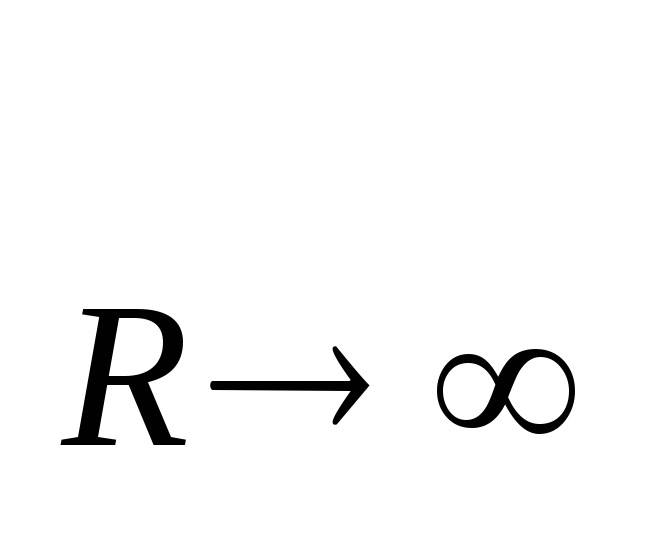 [
[ / (R+r)]=0, а
напряжение на зажимах источника
максимально и равно его ЭДС: U
/ (R+r)]=0, а
напряжение на зажимах источника
максимально и равно его ЭДС: U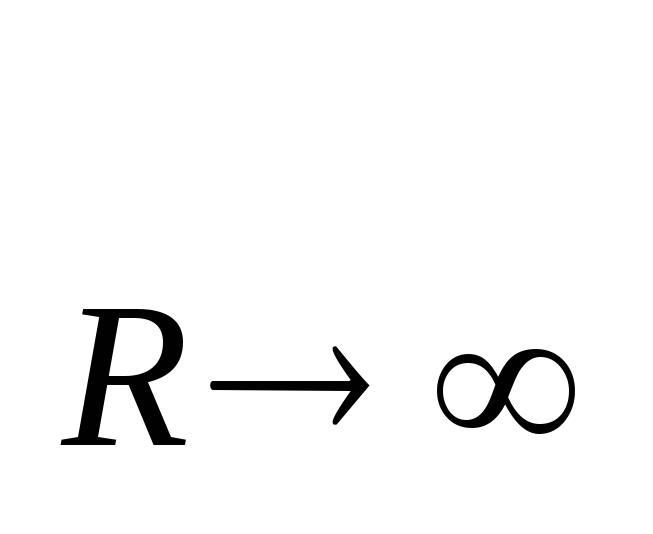 =
=  R / (R + r)=
R / (R + r)=  ,
т. к. lim
,
т. к. lim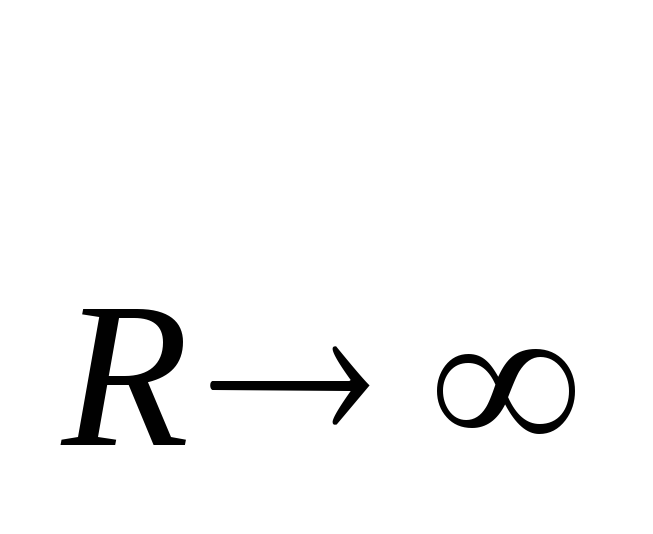 R / (R + r)
= 1. (27)
R / (R + r)
= 1. (27)
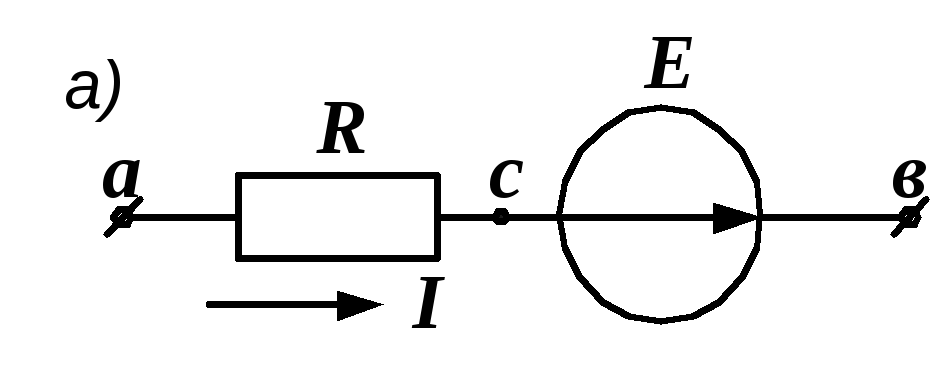
1.2. Закон Ома для участка цепи с эдс
На практике часто встречается задача, когда требуется определить ток в некоторой ветви при известных ее параметрах и потенциалах ее зажимов.
Пусть в схеме на рис. 1.8, а заданы R, E, a, b, и требуется определить ток.
| |
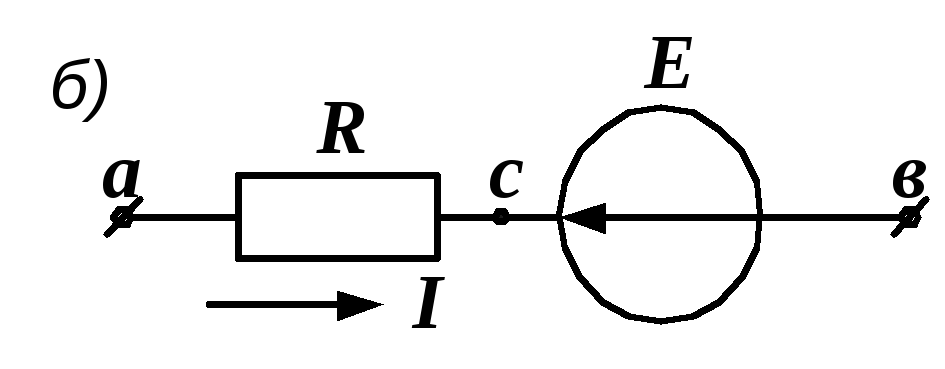
Рис. 1.8. Варианты ветви с ЭДС
Между R и E отметим промежуточную точку с и выразим ее потенциал через потенциалы точек а и b.
Так как в резисторе ток протекает слева направо, то потенциал точки а выше потенциала точки с на величину падения напряжения в активном сопротивлении:
a = с + IR. (1.4)
Точка b находится на положительном полюсе источника, а с – на отрицательном. Поэтому
b = с + E. (1.5)
Беря разность левых и правых частей выражений (1.4) и (1.5), получим
a – b = IR – Е,
откуда
 .
.
Для цепи на рис. 1.8, б после аналогичных рассуждений будем иметь
I = (a – b – E) G.
В двух последних формулах ЭДС записывается с плюсом, если ее направление на схеме совпадает с направлением тока, и с минусом – в противоположном случае.
1.3. Расчет сложных электрических цепей постоянного тока
1.3.1. Метод уравнений Кирхгофа
Этот метод сводится к решению системы уравнений, количество которых равно числу неизвестных токов (числу ветвей). Покажем его применение на примере схемы, изображенной на рис. 1.9.

Рис. 1.9. Сложная электрическая цепь
Первый закон Кирхгофа: в узле электрической цепи алгебраическая сумма токов равна нулю.
Произвольно задавшись направлениями токов в ветвях и принимая токи, подтекающие к узлу, положительными, а оттекающие от узла – отрицательными, записываем:
узел а:
узел b:
узел с:
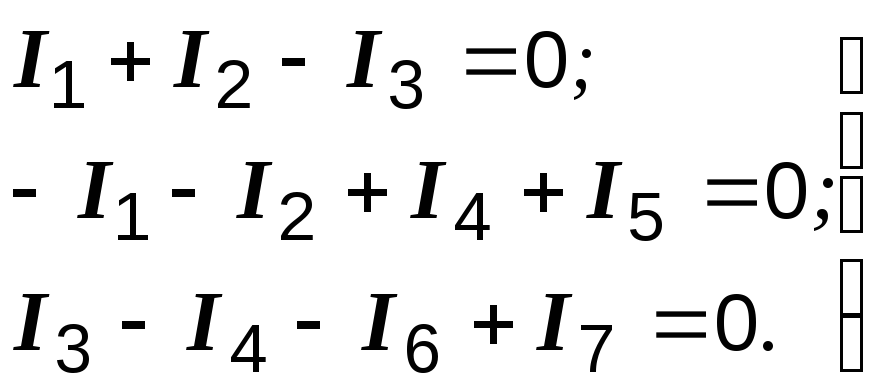 (1.6)
(1.6)Число независимых уравнений в первом законе Кирхгофа – на единицу меньше числа узлов, поэтому для последнего узла d уравнение не пишем.
В заданной схеме семь ветвей, семь неизвестных токов. Система (1.6) содержит только три уравнения. Недостающие четыре записываем по второму закону Кирхгофа.
Второй закон Кирхгофа: в замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех сопротивлениях контура.
Число уравнений, составляемых по этому закону, равно числу взаимно независимых контуров. При рассмотрении схемы каждый последующий контур является независимым относительно предыдущих, если он отличается от них хотя бы одной новой ветвью. В заданной схеме таких контуров четыре. Они отмечены пронумерованными дугообразными стрелками. Любой другой контур новых ветвей не содержит, поэтому не является независимым. Дугообразные стрелки показывают произвольно выбранные направления обхода контуров. Если направления ЭДС и токов совпадают с направлением обхода контура, то они записываются с плюсом, если не совпадают – то с минусом.
контур 1:
контур 2:
контур 3:
контур 4:
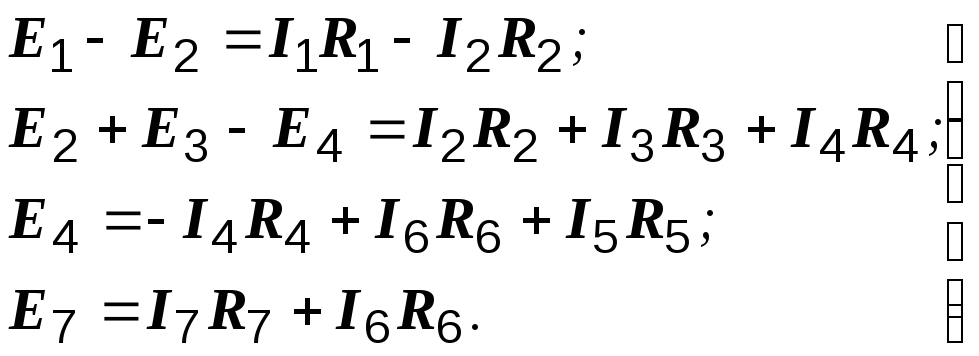 (1.7)
(1.7)Системы (1.6) и (1.7) дают достаточное количество уравнений для отыскания всех неизвестных токов.
1.3.2. Метод узловых потенциалов
Уравнения, составляемые по этому методу, называются узловыми уравнениями. В качестве неизвестных они содержат потенциалы узлов, причем один из них задается заранее – обычно принимается равным нулю. Пусть таким узлом будет узел d: d = 0. Равенство нулю какой-то точки схемы обычно показывается как ее заземление.
Запишем для каждой ветви выражение закона Ома:

 (1.8)
(1.8)
Подставляя формулы (1.8) в систему (1.6) после несложных преобразований получаем следующие уравнения, количество которых на единицу меньше числа узлов:
 (1.9)
(1.9)
При решении практических задач указанный вывод не делают, а узловые уравнения записывают сразу, пользуясь следующим правилом.
Потенциал узла, для которого составляется уравнение (например, в первом уравнении последней системы – это узел а), умножается на сумму проводимостей ветвей, присоединенных к этому узлу: а (G1+G2+G3).Это произведение записывается в левой части уравнения со знаком плюс. Потенциал каждого соседнего узла (b и с) умножается на проводимости ветвей, лежащих между этим (соседним) узлом и узлом, для которого составляется уравнение.
Эти произведения b (G1 + G2) и сG3 записываются со знаком минус. В правой части уравнения стоит алгебраическая сумма произведений ЭДС на проводимости тех ветвей, которые присоединены к рассматриваемому узлу: E1G1, E2G2 и E3G3. Эти произведения записываются с плюсом, если ЭДС направлены к узлу, и с минусом, если от узла.
Найдя из (1.9) потенциалы узлов и подставляя их в (1.8), определяем токи ветвей.