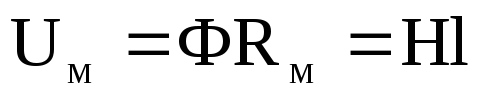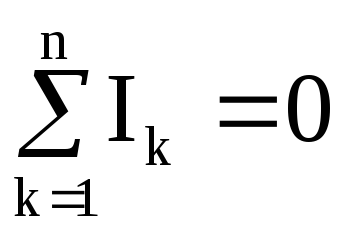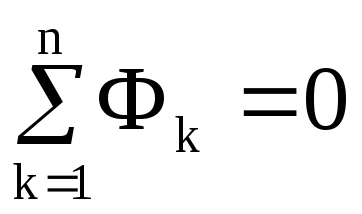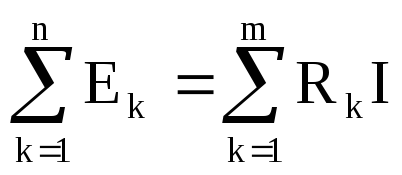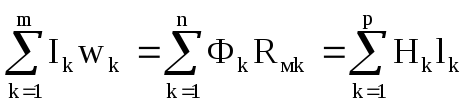3. Закони (правила) кірхгофа

Питання розрахунку електричних кіл має велике практичне значення. Такі питання розглядаються в прикладних задачах електротехніки, радіотехніки та електроніки. Крім того за допомогою електричних кіл можна моделювати ряд неелектричних процесів. Наприклад, в нафтовій справі використовується метод електрогідродинамічних аналогій, де потоки нафти моделюються струмами, а електрорушійні сили тисками, які зумовлюють рух нафти.

Найбільш просто розрахунок розгалужених електричних кіл проводиться за допомогою законів (правил) Кірхгофа.¹

Перший закон Кірхгофа стосується вузла, тобто точки електричного кола, де сходяться не менше трьох провідників і стверджує, що алгебраїчна сума струмів у вузлі дорівнює нулю.

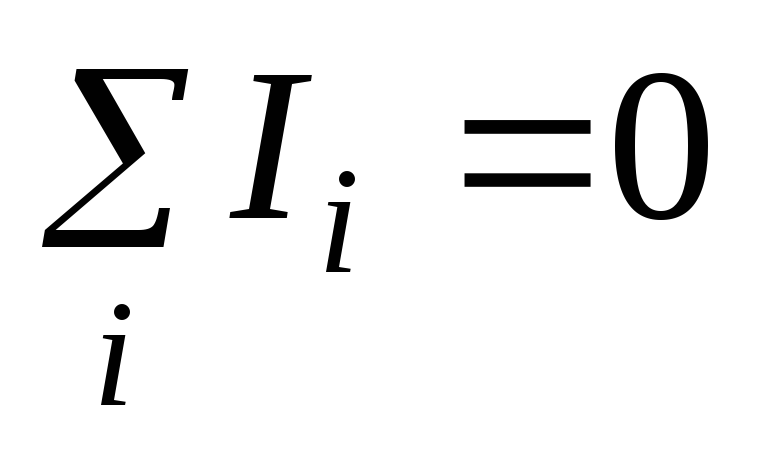
П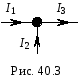ри цьому, струми, які входять в вузол вважаємо додатними, а ті, які виходять від’ємними. Перший закон Кірхгофа випливає з закону збереження електричного заряду.

На рис.40.3 наведений приклад вузла з вказаними напрямами струмів.

Для такого вузла перший закон Кірхгофа прийме вигляд:

І₁ + І₂ – І₃= 0

Застосовуючи узагальнений закон Ома для будь-якого замкнутого контуру можна сформулювати другий закон Кірхгофа; а саме:

алгебраїчна сума добутків сили струму на опори відповідних ділянок замкнутого контуру дорівнює алгебраїчній сумі ЕРС, які діють в цьому контурі.

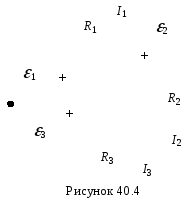
На рис. 40.4 вказана схема замкнутого електричного контуру. Для того, щоб для такого контуру записати другий закон Кірхгофа спочатку вибирають обхід контуру, наприклад за годинниковою стрілкою, тоді, струми які співпадають з заданим обходом вважаємо додатними. Тому в другому законі Кірхгофа струм I₁ буде додатнім, а струми I₂ та I₃ від’ємними. Знак ЕРС визначаться вище вказаним правилом (див. закон Ома для неоднорідної ділянки кола), тобто, якщо в напрямі обходу переходимо від від’ємного полюса джерела струму до додатного, то така ЕРС буде з знаком «+», а навпаки — знак «-«. Тому в другому законі Кірхгофа для нашого контуру перша та друга ЕРС будуть додатними, а третя – від’ємною і в результаті другий закон Кірхгофа для вказаного на рис.40.4 замкнутого контуру запишеться:

I₁R₁ — I₂R₂ — I₃R₃ = ₁ + ₂ — ₃

4. Принцип компенсаційного методу визначення ерс

Визначити ЕРС джерела струму можна різними методами. Наприклад, вимірявши силу струму І, зовнішній R та внутрішній r опори замкнутого кола, за формулою (40.3) підрахуємо ЕРС. На практиці широкого застосування набув інший метод, який полягає в тому, що невідому ЕРС компенсують рівною їй напругою. На рис. 40.5 наведена принципова схема компенсаційного методу вимірювання ЕРС. Така схема складається з двох замкнутих контурів. В контурі АВ ε А струм

І від джерела ε створює на кінцях реохорда АВ напругу U_AB, яка більша від ε_х (наприклад, U_AB = 5 B, ε_х =2 В). Тому на реохорді АВ знайдеться така ділянка АХ, напруга на кінцях якої U_AX буде рівна невідомій ЕРС ε_х. Якщо в другому контурі АСХА невідому ЕРС ε_х ввімкнути “назустріч” такій напрузі, то струм через невідомий елемент ε_х буде відсутнім – відбудеться компенсація невідомої ЕРС відомим значенням напруги U_AX на реохорді. Така компенсація досягається переміщенням вздовж реохорда рухомого контакту РК.

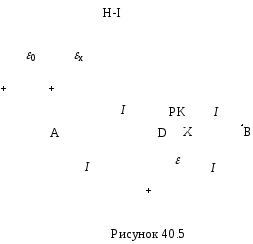Наявність або відсутність струму через невідомий елемент ε_х фіксується нуль-індикатором (Н-І).

Використовуючи другий закон Кірхгофа для контуру АСХА, умова компенсації запишеться рівнянням (40.4), де

І – сила струму через реохорд, R_AX— опір відповідної ділянки реохорда.

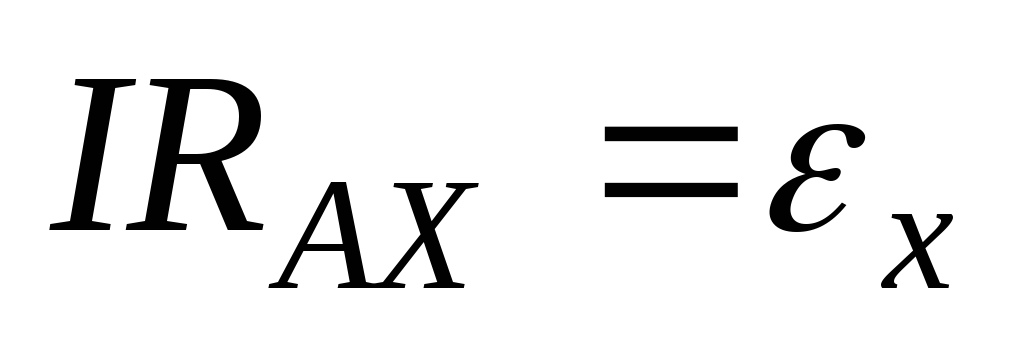(40.4)

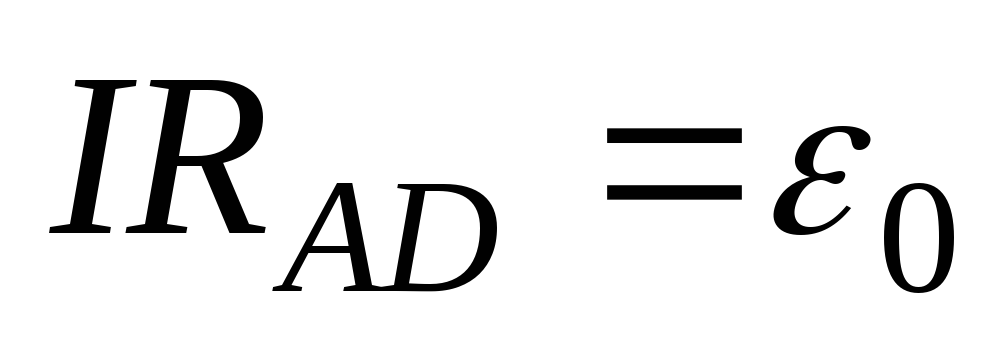(40.5)

Якщо замість невідомого джерела ε_х в контур ввімкнути відомий елемент ε₀, то умова компенсації наступить при іншому положенні рухомого контакту РК, наприклад, в точці D. Тоді другий закон Кірхгофа для контуру ACDA прийме вигляд (40.5). З рівнянь (40.4) та (40.5) маємо: невідома ЕРС визначається простим співвідношенням (40.6).

(40.6)

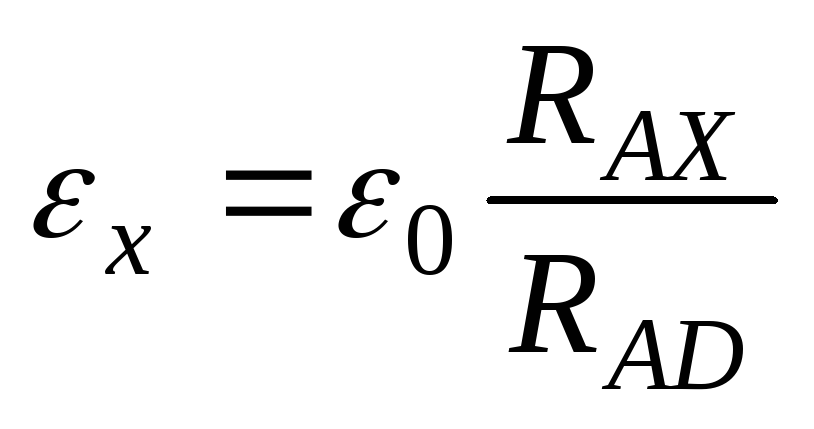
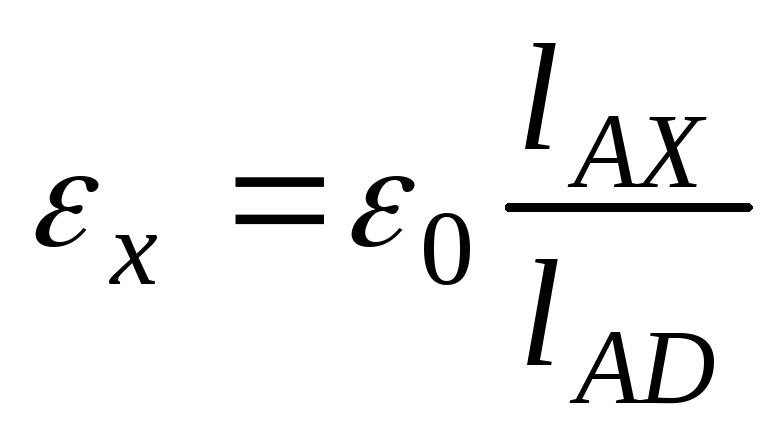(40.7)

Відношення опорів R_AX та R_AD можна замінити відношенням відповідних довжин частин реохорда l_AX та l_AD і таким чином, отримати кінцеву робочу формулу (40.7) для визначення невідомої ЕРС методом компенсації при її порівнянні з відомою ε₀ (еталонною) електрорушійною силою.

Перший і другий закони Кірхгофа

4.1 / 5 оцінка (116 голосів)

Приклад складної електричного кола ви можете подивитися на малюнку 1.

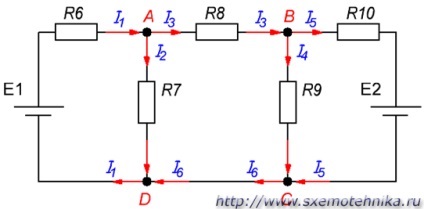
Малюнок 1. Складна електричний ланцюг.

Іноді закони Кирхгофа називають правилами Кірхгофа. особливо в старій літературі.

Перший закон Кірхгофа

Формулювання №1: Сума всіх струмів, що втікають у вузол, дорівнює сумі всіх струмів, що випливають з вузла.

Формулювання №2: Алгебраїчна сума всіх струмів в вузлі дорівнює нулю.

Поясню перший закон Кірхгофа на прикладі малюнка 2.

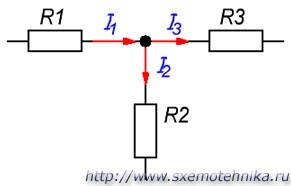
Малюнок 2. Вузол електричного кола.

Тут струм I1 — ток, впадає в вузол. а струми I2 і I3 — струми, що випливають з вузла. Тоді застосовуючи формулювання №1, можна записати:

Що б підтвердити справедливість формулювання №2, перенесемо струми I2 і I3 в ліву частину виразу (1). тим самим отримаємо:

Знаки «мінус» в вираженні (2) і означають, що струми випливають з вузла.

Знаки для втікають і випливають струмів можна брати довільно, проте в основному завжди втікає струми беруть зі знаком «+», а випливають зі знаком «-» (наприклад як вийшло в вираженні (2)).

Другий закон Кірхгофа.

Формулювання: Алгебраїчна сума ЕРС, що діють в замкнутому контурі, дорівнює алгебраїчній сумі падінь напруги на всіх резистивних елементах в цьому контурі.

Тут термін «алгебраїчна сума» означає, що як величина ЕРС так і величина падіння напруги на елементах може бути як зі знаком «+» так і зі знаком «-». При цьому визначити знак можна за наступним алгоритмом:

1. Вибираємо напрям обходу контуру (два варіанти або за годинниковою, або проти).

2. Довільно вибираємо напрямок струмів через елементи ланцюга.

3. Розставляємо знаки для ЕРС і напруг, що падають на елементах за правилами:

— ЕРС, що створюють струм в контурі, напрям якого збігається з напрям обходу контуру записуються зі знаком «+», в іншому випадку ЕРС записуються зі знаком «-».

— напруги, які падають на елементах ланцюга записуються зі знаком «+», якщо струм, що протікає через ці елементи збігається за напрямком з обходом контуру, в іншому випадку напруги записуються зі знаком «-».

Наприклад, розглянемо ланцюг, представлену на малюнку 3, і запишемо вираз згідно з другим законом Кірхгофа, обходячи контур за годинниковою стрілкою, і вибравши напрямок струмів через резистори, як показано на малюнку.

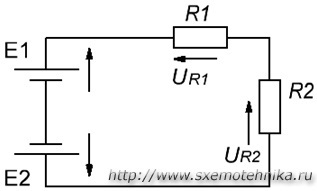
Малюнок 3. Електричне коло, для пояснення другого закону Кірхгофа.

Розрахунки електричних ланцюгів за допомогою законів Кірхгофа.

Тепер давайте розглянемо варіант складного ланцюга, і я вам розповім, як на практиці застосовувати закони Кірхгофа.

Отже, на малюнку 4 є складний ланцюг з двома джерелами ЕРС величиною E1 = 12 в і E2 = 5 ст. з внутрішнім опором джерел r1 = r2 = 0,1 Ом. працюючих на загальне навантаження R = 2 Ома. Як же будуть розподілені струми в цьому ланцюзі, і які вони мають значення, нам належить з’ясувати.

Малюнок 4. Приклад розрахунку складної електричного кола.

Тепер згідно з першим законом Кірхгофа для вузла А складаємо такий вислів:

Використовуючи другий закон Кірхгофа, запишемо ще два вирази для зовнішнього контуру і внутрішнього лівого контуру, вибравши напрямок обходу за годинниковою стрілкою.

Для зовнішнього контуру:

Для внутрішнього лівого контуру:

Отже, у нас вийшла система з трьох рівнянь з трьома невідомими:

Тепер підставимо в цю систему відомі нам величини напруг і опорів:

Далі з першого і другого рівняння висловимо струм I2

Наступним кроком прирівняємо перше і друге рівняння і отримаємо систему з двох рівнянь:

Висловлюємо з першого рівняння значення I

І підставляємо його значення в друге рівняння

Вирішуємо отримане рівняння

Тепер в вираз I = 2I1 — 70 підставимо значення

Ну, а згідно з першим закону Кирхгофа ток I2 = I — I1

Знак «мінус» для струму I2 означає, то що ми не правильно вибрали напрямок струму, тобто в нашому випадку струм I2 випливає з вузла А.

Тепер отримані дані можна перевірити на практиці або змоделювати цю схему наприклад в програмі Multisim.

Скріншот моделювання схеми для перевірки законів Кірхгофа ви можете подивитися на малюнку 5.

Малюнок 5. Порівняння результатів розрахунку і моделювання роботи ланцюга.

Ви можете абсолютно БЕЗКОШТОВНО отримати повноцінний курс з креслення схем і створення малюнків в програмі sPlan 7.0!

Якщо Ви хочете з новачка перетворитися в профессіноала, стати висококласним, конкурентним і грамотним фахівцем в області найперспективнішого напрямку мікроелектроніки, тоді вивчіть новий відокурс по мікроконтролерів!

Запевняю такого ще немає ніде!

В результаті ви навчитеся з нуля трохи Тольна розробляти власні пристрої, але і сполучати з ними різну переферію!

Схожі статті

2.2.2 Другий закон Кірхгофа.

Алгебраїчна сума ЕРС у будь-якому контурі кола дорівнює алгебраїчній сумі напруг на елементах цього контуру:

∑ E = ∑U . (2.2)

Якщо в розглянутому контурі відсутні ЕРС, то рівняння (2.2) приймає вид:

∑U = 0. (2.3)

Обхід контуру відбувається в довільно обраному напрямку. При цьому ЕРС і напруги, що збігаються з напрямком обходу, беруться з однаковими знаками, наприклад, зі знаками «+».

Наприклад, для схеми (рис. 2.2) маємо:

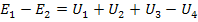
Другий закон Кірхгофа можна застосовувати й для контурів, які складаються не тільки з ділянок схеми, але й з напруг між якими-небудь крапками схеми.

Так для контуру 4-5-3-6-4, що складає з ділянки кола 4-5-3 і напруги 4-6-3, можна скласти рівняння:

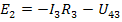
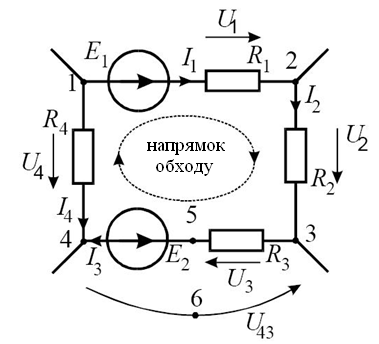
Рис. 2.2. Ілюстрація до другого закону Кірхгофа

2.3 Розподіл потенціалу уздовж електричного кола

Розглянемо нерозгалужене електричне коло постійного струму (ЕКПС), що містить резистори з опорами R і джерелами ЕРС E (рис. 2.3).

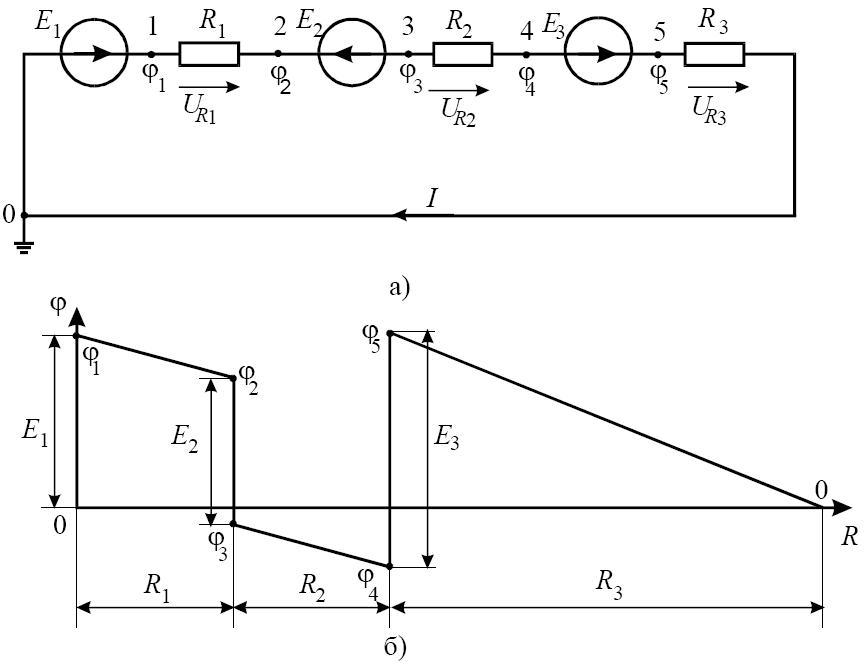
Рис. 2.3. Схема ЕКПС (а) і графік зміни потенціалу (б) уздовж цього кола (контуру).

Приймемо потенціал однієї із точок ЕКПС рівним нулю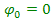. Тоді можемо знайти потенціали інших крапок схеми при відомих значеннях сили струму I , ЕРС 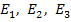і опорів :

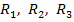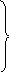
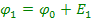
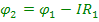
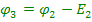
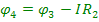(2.4)

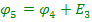
Графік зміни потенціалу відповідно до формул (2.4) представлений на рис. 2.3, б.

Цей графік служить графічною ілюстрацією другого закону Кірхгофа.

2.4 Послідовне й паралельне з’єднання резистивних елементів

2.4.1 Послідовне з’єднання.

Розглянемо коло з послідовним з’єднанням резисторів з відповідними опорами 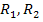(рис. 2.4)

Струм I , що протікає по цих резисторах той самий. Напруги 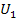і на кожному з резисторів різні.

На підставі другого закону Кірхгофа можна записати:

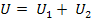(2.5)

де U – напруга джерела ЕРС, прикладене до обох резисторів, В.

Застосовуючи закон Ома, перепишемо рівняння (2.5)

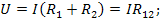(2.6)

де — загальний (еквівалентний) опір всього кола відносно затискачів 1 і 2, Ом.

Рис. 2.4. Схема ЕК із послідовним з’єднанням резисторів (а) і спрощена схема цього кола з еквівалентним опором (б)

Отримані результати можна поширити на n послідовно з’єднаних резисторів:

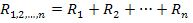(2.7)

Опір кола, що складається з декількох послідовно з’єднаних резистивних елементів, дорівнює сумі їхніх опорів.

2.4.2 Паралельне з’єднання

При паралельному з’єднанні елементів (рис. 2.5,а) до них прикладена та сама напруга.

На підставі першого закону Кірхгофа можна записати

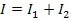
або

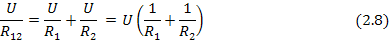
звідки

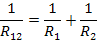
де 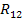— загальний еквівалентний опір кола, Ом.

Рис. 2.5. Схема ЕК із паралельним з’єднанням резисторів (а) і спрощена схема цього кола з еквівалентним опором (б)

Вираз (2.8) можна поширити на випадок n паралельно з’єднаних резистивних елементів. Тоді

Якщо замість опорів резисторів увести поняття електричной провідності, рівної 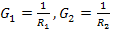і т.д., одержимо:

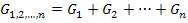, (2.10)

Загальна еквівалентна провідність 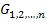електричного кола, що складається з n паралельно з’єднаних резистивних елементів, дорівнює сумі їх провідностей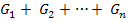

Паралельне включення — основний спосіб включення в ЕК різних приймачів (споживачів) електричної енергії.

Коло, що живить струмом який-небудь населений пункт, являє собою систему паралельно з’єднаних приймачів електричної енергії. Основна лінія розпадається на паралельні лінії, що йдуть до окремих районах населеного пункту. Ці районні лінії у свою чергу розгалужуються на більше дрібні, обслуговуючі окремі вулиці, будинки, підприємства. Але

й ці лінії розгалужуються на більше дрібні ділянки, поки, нарешті, в окремі кінцеві ділянки не виявляться включеними безпосередньо приймачі електричної енергії: електродвигуни в цехах заводів, лампи в будинках і т.д. На рис. 2.6 зображена така кінцева ділянка електричного кола, у якій паралельно включені лампи накалювання 1, нагрівальні прилади 2, електродвигун 3 і акумулятор 4, поставлений на зарядку.

ЕД

Рис. 2.6. Схема ЕК із паралельно включеними приймачами електричної енергії

1. — лампи накалювання,

2. — нагрівальні прилади,

3. — електродвигун,

4. — акумулятор.

12.2.3 Перший закон Кірхгофа для магнітних кіл

Алгебраїчна сума магнітних потоків, що збігаються в будь-якому вузлі магнітного кола, дорівнює нулю:

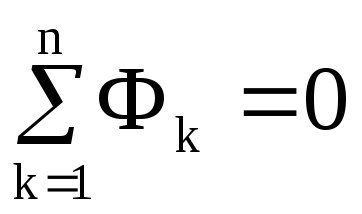(12.27)

Розглянемо вузол магнітного кола (рис.12.10), для якого маємо

Рис.12.10

,

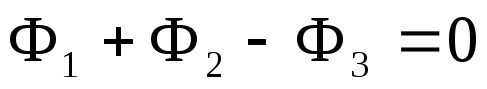або

.

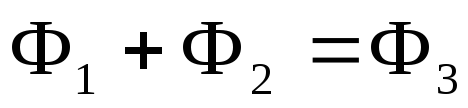Відповідно до цього закону можна стверджувати, що магнітні силові лінії завжди замкнені. Цей факт підтверджується експериментально.

12.2.4 Другий закон Кірхгофа для магнітних кіл

Аналіз магнітних кіл показує, що вони схожі (подібні) з електричними. Магнітний потік є аналогом струму в електричних колах, джерело МРС- 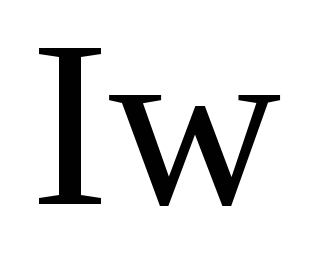— аналогом ЕРС в електричних колах. І, як зазначалося (12.26), добуток 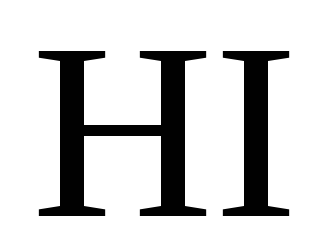є магнітною напругою. Магнітна напруга в магнітному колі є аналогом елек-тричної напруги 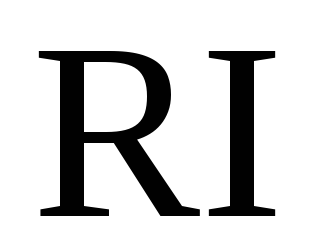в електричних колах.

Згідно із законом повного струму для нерозгалуженого магнітного кола (рис.12.7) маємо

,

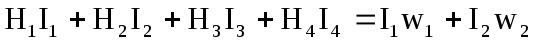або

, (12.28)

де ; 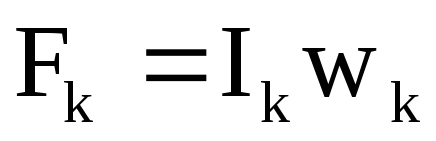,або в загальному вигляді

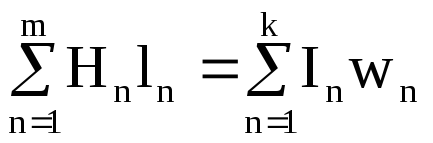(12.29)

Отже в будь-якому замкненому контурі магнітного кола алгебраїчна сума магнітних напруг дорівнює алгебраїчній сумі МРС, які діють в цьому самому контурі.

Це і є другий закон Кірхгофа для магнітних кіл. Неважко помітити, що закон повного струму (12.25) і другий закон Кірхгофа (12.29) математично мають однаковий запис .

12.2.5. Магнітний опір і магнітна провідність Закон Ома для магнітних кіл

Згідно з (12.24) запишемо закон повного струму :

.

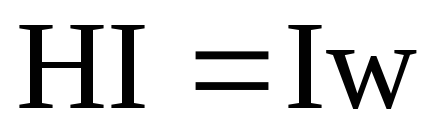Як відомо, , у свою чергу, 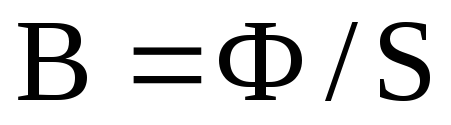, тобто .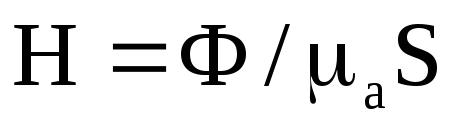

Підставимо значення 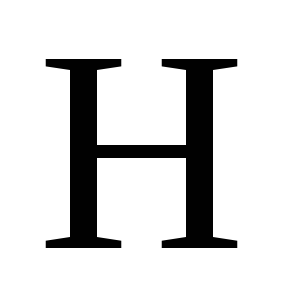у першу формулу і запишемо

.

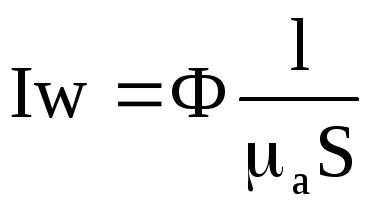або

(12.31)

або

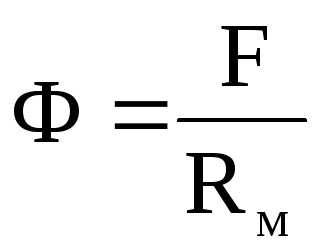. о (12.32)

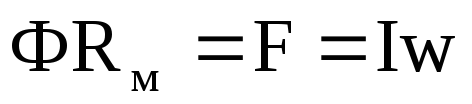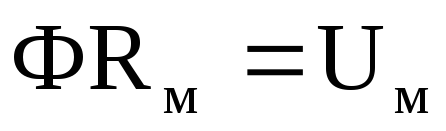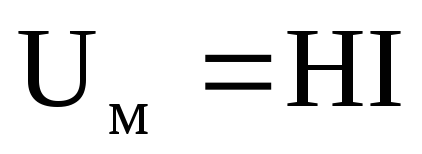З (12.32) , де . У свою чергу, . Отже, , тут 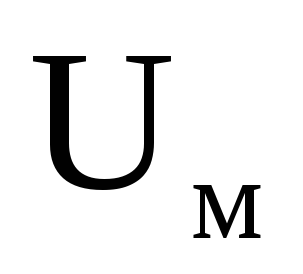— магнітна напруга, вимірюється в амперах.

Як уже згадувалось у (12.23), є аналогом струму в електричних колах, є аналогом ЕРС в електричних колах. Пригадаємо закон Ома для ділянки електричного кола 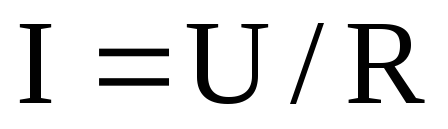. Отже, у формулі (12.31) величина 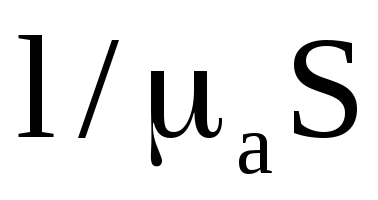має бути аналогом електричного опору . Вона називається магнітним опором :

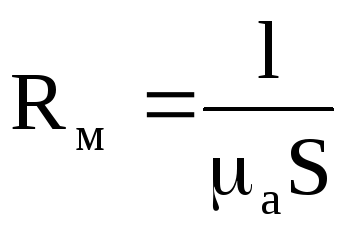(12.33) Одиниця вимірювання магнітного опору 1/Гн:

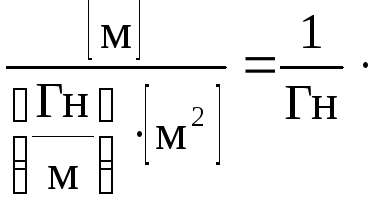
Обернена до магнітного опору величина називається магнітною провідністю, позначається буквою і вимірюється в генрі /Гн/:

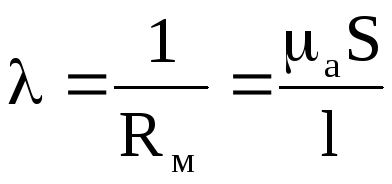(12.34)

Формули (12.31) і (12.32) виражають закон Ома для магнітного кола . Його можна записати й так:

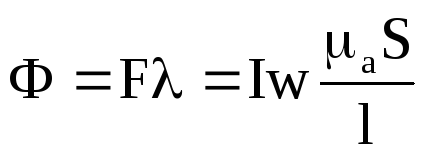(12.35)

Таблиця 12.1

Електричне коло				Магнітне коло
Параметр або закон	Позначен-ня	Одиниця вимірювання	Позначення		Одиниця вимірювання	Параметр або закон
Електричний струм		A			Вб	Магнітний потік
Електрична напруга		B			А	Магнітна напруга
Електрорушійна сила		B			А	Магніторушійна сила (н.с.)
Електричний опір		Ом			Гн-1	Магнітний опір
Електрична провідність		См			Гн	Магнітна провідність
Закон Ома для електричного кола						Закон Ома для магнітного кола
Перший закон Кірхгофа для електричного кола						Перший закон Кірхгофа для магнітного кола
Другий закон Кірхгофа для електричного кола						Другий закон Кірхгофа для магнітного кола

Закони Кирхгофа — Новини — 2020

Відносини між U і I

Два закони Кірхгофа розповідають нам про зв’язок між напруженнями та струмами в ланцюгах.

Поточний закон Кирхгофа говорить, що: алгебраїчна сума струмів на вузлі дорівнює нулю.

Для двох моментів може знадобитися додаткове пояснення:

1. Вузлом є технічний термін для з’єднання в ланцюзі, де два або більше гілок з’єднуються. На рисунку 2.1 показано вузол з чотирма гілками, з’єднаними;
2. фразу «алгебраїчна сума» нагадує нам, що при застосуванні чинного закону Кірхгофа ми повинні брати до уваги поточний напрям, а також величину.

Цей Закон використовується в аналізі схем для визначення співвідношень між струмами, що течуть у гілках схеми. Наприклад, на рис. 2.1 потоки, що течуть у чотирьох гілках, з’єднаних з вузлом, були визначені як I ₁, I ₂, I ₃, I ₄ і поточний закон Кирхгофа, дозволяє нам записати рівняння, що стосується цих струмів.

Дивлячись уважно на рис. 2.1, ми бачимо, що два струми (I ₁, I ₂ ) протікають у напрямку до вузла, тоді як два інші струми (I ₃, I ₄ ) течуть назовні. «Алгебраїчна сума» повинна враховувати цю різницю у відносному напрямку.

Щоб суворо застосувати чинне законодавство Кірхгофа, ми спочатку повинні зробити довільний вибір позитивного поточного напряму.

Припустимо, що струми, що входять в вузол (I ₁, I ₂ ), розглядаються як позитивні вклади в алгебраїчну суму (і навпаки, течії, що течуть з вузла, розглядаються як негативні вклади), тоді алгебраїчна сума струмів буде записана: + I ₁ + I ₂ — I ₃ — I ₄, і згідно з поточним законом Кірхгофа ця алгебраїчна сума дорівнює нулю:

+ I ₁ + I ₂ — I ₃ — I ₄ = 0 (2.1)

Той же результат може бути отриманий при протилежному виборі позитивного напрямку струму. Якщо струми, що течуть з вузла (I ₃, I ₄ ), розглядаються як позитивні вклади в алгебраїчну суму, тоді алгебраїчна сума струмів буде записана: — I1 — I2 + I3 + I4, прирівнюючи цю алгебраїчну суму до нуля:

— I ₁ — I ₂ + I ₃ + I ₄ = 0 (2.2)

що таке ж співвідношення, як урівень. 2.1 з усіма умовами помножене на -1.

Слід підкреслити, що вибір конвенції підписів при використанні поточного закону Кірхгофа є абсолютно довільним і, звичайно, не залежить від отриманого результату. Проте, це найкраща практика бути послідовним у вашому виборі, тому що це мінімізує шанс помилки під час написання алгебраїчної суми.

Екв. 2.1 та 2.2 можна переставити, щоб показати, що:

I ₁ + I ₂ = I ₃ + I ₄ (2.3)

і, звертаючись до рисунка 2.1, ми бачимо, що це рівняння показує, що струм, що входить у вузол, дорівнює поточному потоку. Ця формулювання природно виникає з фізичних міркувань струму як потоку заряду.

Зарядка не накопичується в вузлі, тому будь-який заряд, що входить у вузол через одну або декілька гілок, повинен витікати з вузла через інші гілки. Тому струм, що входить, дорівнює току, що виходить з вузла.

Працював приклад 2.1

Обчислити струм, який я входить у вузол.

Рішення

Вибір струмів, що течуть у вузол як позитивний і застосовуючи Кірхгофа

Поточний закон: +3 -2 + I = 0, тому I = -1 A

Потік, що входить у вузол, дорівнює -1A, який аналогічно тому, як + 1A витікає з вузла

Працював приклад 2.2

Обчислити струм, визначений на діаграмі.

Рішення

У цій задачі є два вузли, кожна з яких має три гілки. Почніть, визначивши струм, що протікає в гілці між двома вузлами. Напрямок I ‘обрано випадковим чином: це може виявити позитивне чи негативне значення. Вибір струмів, що витікають з вузлів як позитивні і застосовуючи діюче Закон Кі

Закони Кірхгофа. Методи контурних струмів та вузлових потенціалів. Електричне коло

Метод рівнянь Кірхгофа

 Метод контурних струмів та метод вузлових потенціалів широко популярні при знаходженні опорів чи струмів в електричних колах. Алгоритми розрахунків всюди описані, проте не кожен студент їх розуміє та мало живих прикладів можна знайти в інтернеті. Суть методів полягає в вираженні струмів через напруги або навпаки, складанні рівнянь КІРХГОФА, а далі перевірки, чи все правильно розраховано. 

Перший закон Кірхгофа: В кожному вузлі алгебраїчна сума струмів дорівнює нулю. При цьому струми, які входять в розгалуження й виходять із нього вважаються величинами різних знаків. Формула першого закону Кірхгофа має вигляд

Другий закон Кірхгофа: Для будь-якого замкнутого контура сума електрорушійних сил дорівнює сумі добутків сил струму на кожній ділянці контура на опір ділянки, враховуючи внутрішній опір джерел струму. Математично друге правило Кірхгофа записується формулою:

Баланс потужностей: Потужності , які генеруються джерелами енергії повинні повністью споживатися навантаженнями (резисторами).
Фізично це означає, що в електричному колі виконується баланс потужностей:
Р_дж=Р_сп.
Це наслідок закону збереження енергії.

Закони на вигляд достатньо прості якщо знати базові поняття, без яких розуміння електричних кіл неможливі.
Наведемо основні складові електричних кіл, щоб при подальшому поясненні Ви завжди могли вернутися до наведених далі підказок.
Електричним колом називають замкнутий контур, який складається з джерела струму, споживачів енергії та з’єднувальних проводів, через які проходить електричний струм. 
Електромагнітні процеси, які відбуваються в електричних колах, можна описати за допомогою електричних величин — електрорушійної сили, струму й напруги.
Електричне коло — множина сполучених між собою провідниками , джерел струму й напруги, конденсаторів, перемикачів, котушок індуктивності і ін., через яку може проходити електричний струм.

До елементів електричних кіл належать:

1. Вузол — точка в якій сходиться хоча б три струми.
2. Вітка — частина кола по якій протікає один струм між двома суміжними вузлами.
3. Контур — будь-який замкнений шлях, що проходить по кількох вітках.
4. Незалежний контур — відрізняється від інших (раніше обраних) хоч би однією віткою.

Задача 1 Розрахункова-графічна робота з дисципліни «Електротехніка, електроніка».

1. Розрахуйте напруги на всіх компонентах кола та струми через них методом контурних струмів.
   Для цього:
1. Перемалюйте задану схему.
2. Позначте умовні додатні напрямки всіх напруг і струмів, оберіть напрямки контурних струмів.
3. Складіть матричне рівняння для контурних струмів і розв’яжіть його, тобто розрахуйте контурні струми.
4. За значеннями контурних струмів розрахуйте значення струмів у всіх гілках.
5. За законом Ома розрахуйте напруги на всіх компонентах кола.
6. Нанесіть отримані значення струмів і напруг на схему кола, враховуючи умовні додатні напрямки.

1. Розрахуйте напруги на всіх компонентах кола та струми через них методом вузлових потенціалів.
   Для цього:
1. Перемалюйте задану схему.
2. Заземліть один з вузлів кола.
3. Складіть матричне рівняння для вузлових потенціалів і розв’яжіть його, тобто розрахуйте потенціали всіх вузлів.
4. За значенням вузлових потенціалів розрахуйте значення напруг на усіх гілках.
5. За законом Ома розрахуйте струми через всі компоненти кола.
6. Нанесіть отримані значення струмів і напруг на схему кола, враховуючи умовні додатні напрямки.
   Порівняйте із результатами, отриманими в п. 1 – вони повинні збігатись.

1. Розрахуйте потужності, які споживає кожний резистор, а також потужності, які виділяє кожне джерело енергії.
   Порівняйте суму виділеної і спожитої потужності.

Дано: R1=4 Ом, R2=7 Ом, R3=10 Ом, R4=12 Ом, R5=20 Ом, R6=5,5 Ом, E2=20 В, E3=10 В.

Електрична схема

1 Спосіб: Метод контурних струмів

Алгоритм розв’язання електричного кола  методом контурних струмів.
1. Спершу з’ясувати кількість незалежних контурів. Скласти рівняння за методом контурних струмів. Кількість рівнянь, які складені методом контурних струмів повинна дорівнювати кількості незалежних контурів. Бажано напрями контурних струмів задавати однаково (наприклад, за годинниковою стрілкою).
Запам’ятайте!Струми контурів із джерелами струмів вважаються відомими і для них рівняння не складається (зайва інформація).
2. Визначити власні та взаємні опори контурів і контурні ЕРС. 
3. Будь-яким відомим Вам методом розв’язати систему рівнянь і знайти контурні струми.
4. За знайденими контурними струмами визначити струми у вітках схеми.
На практиці алгоритм працює так:

У колі три незалежних контури. За методом контурних струмів потрібно скласти три рівняння:
, або
.
Запишемо власні контурні опори:
R₁₁=R₁+R₂+R₆=4+7+5,5 Ом;
R₂₂=R₂+R₄+R₅=7+12+20 =39 Ом;
R₃₃=R₃+R₄+R₆=10+12+5,5=27,5 Ом.
Взаємні контурні опори при однакових напрямках контурних струмів — від’ємні:
R₁₂=R₂₁=-R₂=-7 Ом;
R

Закони Кірхгофа

Закони Кірхгофа (або правила Кірхгофа) — співвідношення, які виконуються між струмами і напругами на ділянках будь електричного кола. Правила Кірхгофа дозволяють розраховувати будь-які електричні кола постійного та квазістаціонарного струму. ^[1] Мають особливе значення в електротехніці через свою універсальність, так як придатні для вирішення багатьох завдань теорії електричних ланцюгів. Застосування правил Кірхгофа до лінійного ланцюга дозволяє отримати систему лінійних рівнянь щодо струмів, і відповідно, знайти значення струмів на всіх гілках ланцюга. Сформульовано Густавом Кірхгофа в 1845.

1. Формулювання

Для формулювання законів Кірхгофа, в електричного кола виділяються вузли — точки з’єднання трьох і більше провідників і контури — замкнуті шляху з провідників. При цьому кожен провідник може входити в кілька контурів.

У цьому випадку закони формулюються таким чином.

1.1. Перший закон

Перший закон Кірхгофа (Закон струмів Кірхгофа, ЗТК) говорить, що алгебраїчна сума струмів в будь-якому вузлі будь ланцюга дорівнює нулю (значення випливають струмів беруться зі зворотним знаком):

Іншими словами, скільки струму втікає у вузол, стільки з нього і випливає. Даний закон випливає з закону збереження заряду. Якщо ланцюг містить p вузлів, то вона описується p — 1 рівняннями струмів. Цей закон може застосовуватися і для інших фізичних явищ (наприклад, водяні труби), де є закон збереження величини і потік цієї величини.

1.2. Другий закон

Другий закон Кірхгофа (Закон напруг Кірхгофа, ЗНК) говорить, що алгебраїчна сума падінь напружень по будь-якому замкнутому контуру кола дорівнює алгебраїчній сумі ЕРС, що діють уздовж цього ж контура. Якщо в контурі немає ЕРС, то сумарне падіння напруги дорівнює нулю:

для постійних напруг

для змінних напруг

Іншими словами, при обході ланцюга по контуру, потенціал, змінюючись, повертається до початкового значення. Якщо ланцюг містить гілок, з яких містять джерела струму гілки в кількості , То вона описується рівняннями напруг. Окремим випадком другого правила для ланцюга, що з одного контуру, є закон Ома для цього ланцюга.

Закони Кірхгофа справедливі для лінійних і нелінійних ланцюгів при будь-якому характері зміни в часі струмів і напруг.

Приклад

На цьому малюнку для кожного провідника позначений протікає по ньому струм (буквою «I») і напруга між сполучаються їм вузлами (буквою «U»)

Наприклад, для наведеної на малюнку ланцюга, відповідно до першого закону виконуються наступні співвідношення:

Зверніть увагу, що для кожного вузла має бути вибрано позитивний напрямок, наприклад тут, струми, що впадає у вузол, вважаються позитивними, а випливають — негативними.

Згідно з другим законом, справедливі співвідношення:

2. Особливості складання рівнянь для розрахунку струмів

• Закони Кірхгофа, записані для вузлів та контурів ланцюга, дають повну систему лінійних рівнянь, яка дозволяє знайти всі струми і напруги.
• Перед тим, як скласти рівняння, потрібно довільно вибрати:
  • позитивні напрямки струмів у гілках і позначити їх на схемі;
  • позитивні напрямки обходу контурів для складання рівнянь за другим законом.
• З метою однаковості рекомендується для всіх контурів позитивні напрямки обходу вибирати однаковими (напр.: за годинниковою стрілкою)
• Якщо напрямок струму збігається з напрямком обходу контуру (яке вибирається довільно), перепад напруги вважається позитивним, в іншому випадку — негативним.
• При запису лінійно незалежних рівнянь за другим законом, прагнуть, щоб у кожен новий контур, для якого складають рівняння, входила хоча б одна нова гілка, яка не увійшла в попередні контури, для яких вже записані рівняння за другим законом (достатнє, але не необхідна умова)

3. Про значення для електротехніки

Правила Кірхгофа мають прикладний характер і дозволяють поряд і в поєднанні з іншими прийомами і способами (метод еквівалентного генератора, метод контурних струмів, метод вузлових напруг, принцип суперпозиції, спосіб складання потенційної діаграми) вирішувати завдання електротехніки. Правила Кірхгофа знайшли широке застосування завдяки простій формулюванні рівнянь і можливості їх вирішення стандартними способами лінійної алгебри ( методом Крамера, методом Гаусса та ін.)

Існує думка, згідно з яким «Закони Кірхгофа» слід іменувати «Правилами Кірхгофа», бо вони не відображають фундаментальних сутностей природи (і не є узагальненням великої кількості досвідчених даних), а можуть бути виведені з інших положень і припущень.

4. Закон випромінювання

Закон випромінювання Кирхгофа — відношення випромінювальної здатності будь-якого тіла до його поглинальної здатності однакове для всіх тіл при даній температурі для даної частоти для рівноважного випромінювання і не залежить від їх форми, хімічного складу та ін.

Примітки

Література

• Матвєєв А. Н. Електрика і магнетизм — Навчальний посібник. — М .: Вища школа, 1983. — 463 с.
• Калашников С. Г. Електрика — Навчальний посібник. — М .: Физматлит, 2003. — 625 с.
• Безсонов Л. А. Теоретичні основи електротехніки. Електричні кола — 11-е видання. — М .: Гардарики, 2007.