1.4. Дрейфовый и диффузионный токи в полупроводниках
Электрический ток может возникнуть в полупроводнике только при направленном движении носителей заряда, которое создается либо под воздействием электрического поля (дрейф), либо вследствие неравномерного распределения носителей заряда по объему кристалла (диффузия). Если электрическое поле отсутствует, и носители заряда имеют в кристалле равномерную концентрацию, то электроны и дырки совершают непрерывное хаотическое тепловое движение. В результате столкновения носителей заряда друг с другом и с атомами кристаллической решетки скорость и направление их движения все время изменяются, так что тока в кристалле не будет.
Под действием приложенного к кристаллу напряжения в нем возникает электрическое поле. Движение носителей заряда упорядочивается: электроны перемещаются по направлению к положительному электроду, дырки – к отрицательному. При этом не прекращается и тепловое движение носителей заряда, вследствие которого происходят столкновения их с атомами полупроводника и примеси.

Направленное движение носителей заряда под действием сил электрического поля называют дрейфом, а вызванный этим движением ток – дрейфовым током. При этом характер тока может быть электронным, если он вызван движением электронов, или дырочным, если он создается направленным перемещением дырок.
Средняя скорость носителей заряда в электрическом поле прямо пропорциональна напряженности электрического поля:
ν = μ E
Коэффициент пропорциональности m называют подвижностью электронов (mn), или дырок (mp). Свободные электроны движутся в пространстве между узлами кристаллической решетки, а дырки – по ковалентным связям, поэтому средняя скорость, а следовательно, и подвижность электронов больше, чем дырок. У кремния подвижность носителей заряда меньше, чем у германия.
В собственных полупроводниках концентрации электронов и дырок одинаковы, но вследствие их разной подвижности электронная составляющая тока больше дырочной. В примесных полупроводниках концентрации электронов и дырок существенно отличаются, характер тока определяется основными носителями заряда: в полупроводниках р-типа – дырками, а в полупроводниках n-типа – электронами.
При неравномерной концентрации носителей заряда вероятность их столкновения друг с другом больше в тех слоях полупроводника, где их концентрация выше. Совершая хаотическое тепловое движение, носители заряда отклоняются в сторону, где меньше число столкновений, т.е. движутся в направлении уменьшения их концентрации.
Направленное движение носителей заряда из слоя с более высокой их концентрацией в слой, где концентрация ниже, называют диффузией, а ток, вызванный этим явлением, – диффузионным током. Этот ток, как и дрейфовый, может быть электронным или дырочным.
Степень неравномерности распределения носителей заряда характеризуется градиентом концентрации; его определяют как отношение изменения концентрации к изменению расстояния, на котором оно происходит. Чем больше градиент концентрации, т.е. чем резче она изменяется, тем больше диффузионный ток.
Электроны, перемещаясь из слоя с высокой концентрацией в слой с более низкой концентрацией, по мере продвижения рекомбинируют с дырками, и наоборот, диффундирующие в слой с пониженной концентрацией дырки рекомбинируют с электронами. При этом избыточная концентрация носителей заряда уменьшается.

2.3. Дрейфовый и диффузионный токи в полупроводниках.
Электрический ток может возникнуть в полупроводнике только при направленном движении носителей заряда, которое создается либо под воздействием электрического поля (дрейф), либо вследствие неравномерного распределения носителей заряда по объему кристалла (диффузия).
Если электрическое поле отсутствует и носители заряда имеют в кристалле равномерную концентрацию, то электроны и дырки совершают непрерывное хаотическое тепловое движение. В результате столкновения носителей заряда друг с другом и с атомами кристаллической решетки скорость и направление их движения все время изменяются, так что тока в кристалле не будет.
Под действием приложенного к кристаллу напряжения в нем возникает электрическое поле; движение носителей заряда упорядочивается: электроны перемещаются по направлению к положительному электроду, дырки – к отрицательному. При этом не прекращается и тепловое движение носителей заряда, вследствие которого происходят столкновения их с атомами полупроводника и примеси.
Направленное движение носителей заряда под действием сил электрического поля называют дрейфом, а вызванный этим движением ток – дрейфовым током. При этом характер тока может быть электронным, если он вызван движением электронов, или дырочным, если он создается направленным перемещением дырок.
В собственных полупроводниках концентрации электронов и дырок одинаковы, но вследствие их разной подвижности электронная составляющая тока больше дырочной. В примесных полупроводниках концентрации электронов и дырок существенно отличаются, характер тока определяется основными носителями заряда: в полупроводниках
При неравномерной концентрации носителей заряда вероятность их столкновения друг с другом больше в тех слоях полупроводника, где их концентрация выше. Совершая хаотическое тепловое движение, носители заряда отклоняются в сторону, где меньше число столкновений, т. е. движутся в направлении уменьшения их концентрации.
Направленное движение носителей заряда из слоя с более высокой их концентрацией в слой, где концентрация ниже, называют
Электроны, перемещаясь из слоя с высокой концентрацией в слой с более низкой концентрацией, по мере продвижения рекомбинируют с дырками, и наоборот, диффундирующие в слой с пониженной концентрацией дырки рекомбинируют с электронами. При этом избыточная концентрация носителей заряда уменьшается.
2.4. Полупроводниковые резисторы
Как следует из вышесказанного, полупроводники представляют собой особый класс веществ, обладающий целым рядом уникальных электрофизических свойств. На основе полупроводниковых материалов были разработаны многочисленные электронные приборы, являющиеся элементной базой современных радиоэлектронных и информационных систем. Наиболее простыми полупроводниковыми приборами, принцип действия которых основан на уникальных электрофизических свойствах полупроводников, являются
Полупроводниковыми резисторами называют приборы, принцип действия которых основан на свойствах полупроводников изменять свое сопротивление под действием температуры, электромагнитного излучения, приложенного напряжения и других факторов. Рассмотрим три наиболее распространенных типа полупроводниковых резисторов.
Терморезисторы, обладающие отрицательным температурным коэффициентом сопротивления, называют термисторами. Они нашли широкое применение в радиоэлектронном оборудовании самого различного назначения.
В полупроводниковых терморезисторах зависимость сопротивления от температуры достаточно точно описывается выражением, которое является аппроксимацией
R(T)=R0 (T0) еxp ( В/Т-В/Т0 )
Где R0 (T0) номинальное значение сопротивления при температуре Т0.=293K
Т- температура в К,
В- коэффициент постоянный для данного типа резисторов
Примерная зависимость сопротивления терморезистора от температуры представлена на рис. 2.4.2.
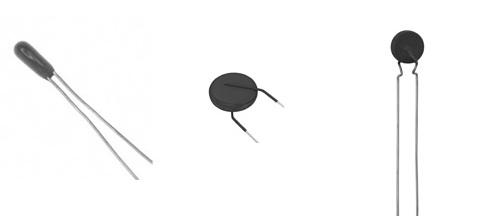
Рисунок 2.4.1. Внешний вид терморезисторов.
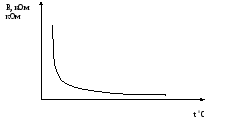
Рисунок 2.4.2. График зависимости сопротивления терморезистора от температуры.
К важнейшим параметрам термисторов относятся: холодное сопротивление — сопротивление термистора при температуре окружающей среды 20 °С; температурный коэффициент сопротивления TKС, выражающий в процентах изменение сопротивления термистора при изменении температуры на 1°С; максимальная рабочая температура — температура, при которой характеристики термистора остаются стабильными в течение установленного срока службы;
коэффициент рассеяния b – мощность, рассеиваемая термистором при разности температур термистора и окружающей среды в 1 °С; постоянная времени τ – время, в течение которого температура термистора становится равной 63 °С при перенесении его из среды с температурой 20 °С в среду с температурой 100 °С. Постоянная времени определяется как отношение теплоемкости к коэффициенту рассеяния: τ=Н/b.
В устройствах промышленной электроники термисторы применяются достаточно широко для измерения и регулирования температуры, термокомпенсации различных элементов электрических схем, работающих в широком диапазоне температур, стабилизации напряжения в цепях переменного и постоянного токов, а также в качестве регулируемых бесконтактных резисторов в цепях автоматики.
В ряде специальных устройств находят применение так называемые полупроводниковые болометры, состоящие из двух термисторов. Один из термисторов (активный) непосредственно подвергается воздействию контролируемого фактора (температуры излучения), а другой (компенсационный) служит для компенсации влияния температуры окружающей среды.
Позисторами называют полупроводниковые термисторы с положительным температурным коэффициентом сопротивления. В качестве полупроводника в них используют титанат бария со специальными примесями, сопротивление которого увеличивается при повышении температуры.
Как и для термисторов с отрицательным ТКC, для позисторов основными характеристиками являются вольтамперная и температурная. Параметры позисторов аналогичны параметрам термисторов с отрицательным TKC.
Варистор представляет собой полупроводниковый резистор, сопротивление которого зависит от приложенного напряжения. Внешний вид варисторов представлен на рис. 2.4.3. Примерный вид вольтамперной характеристики варистора приведен на рисунке 2.4.4. Симметричность характеристики позволяет использовать варистор в цепях как постоянного, так и переменного тока. К основным параметрам варисторов относятся: статическое сопротивление при постоянных значениях напряжения и тока Rст=U/I; динамическое сопротивление переменному току Rд=ΔU/ΔI; коэффициент нелинейности – отношение статического сопротивления к динамическому в данной точке характеристики р=Rст/Rд; наибольшая амплитуда импульсного напряжения и допустимая рассеиваемая мощность

Рисунок 2.4.3. Варисторы.

Рисyнок 2.4.4. Вольтамперная характеристика варистора
.
Исходя из двух последних параметров, выбирают рабочее эксплуатационное напряжение варистора.
В схемах промышленной электроники варисторы применяют для регулирования электрических величин, стабилизации токов и напряжений и для защиты приборов и элементов схем от перенапряжений.
Контрольные вопросы:
1. Какие вещества называют полупроводниками?
2. Как зависит электропроводность полупроводников от температуры?
3. Объясните следующие термины: валентная зона, зона проводимости, запрещенная зона?
4. Приведите формулу зависимости сопротивления терморезистора от температуры?
5. Какие полупроводники называют полупроводниками р-типа?
6. Какие полупроводники называют полупроводниками п-типа?
7. Приведите выражение для удельной электропроводности полупроводников.
8. Объясните термин «дырка».
9. Что такое дрейфовый ток?
10. Что такое диффузионный ток?
11. Что такое варистор?
Диффузионный и дрейфовый токи.
Диффузия (от лат. diffusio — распространение, растекание, рассеивание) — неравновесный процесс, вызываемый тепловым движением частиц, приводящий к установлению равновесия и выравниванию концентраций (при постоянстве температуры и отсутствии внешних сил). Если частицы заряжены, то их диффузионное перемещение приводит к появлению диффузионных токов.
Диффузионный поток направлен из области высокой концентрации в область низкой концентрации. Свободные носители заряжены. Следовательно любое их перемещение, в том числе и диффузионное, приводит к появлению электрических токов, которые так и будем называть диффузионными.
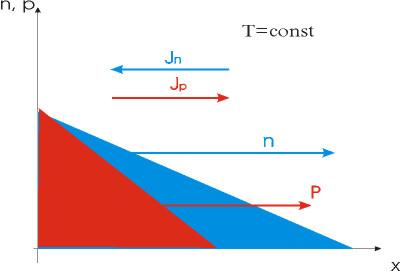
Рис. 1.25. Схема, иллюстрирующая возникновение диффузионных токов электронов и дырок.
Схема на рис. 1.25 иллюстрирует возникновение диффузионных токов электронов и дырок. Следует обратить внимание, что потоки электронов и дырок на схеме направлены в одну сторону, а токи дырочный и электронный токи в разные. Направление дырочного тока совпадает с направлением потока, электронного противоположно, поэтому токи компенсируют друг друга уменьшая общий диффузионный ток.
Скорость диффузии (диффузионный поток) пропорционален градиенту концентрации, поэтому для диффузионных токов можно записать:
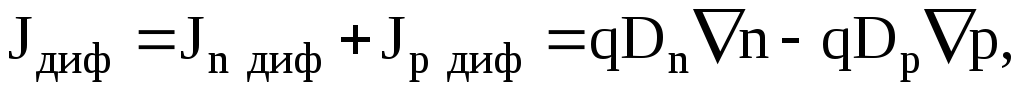 (1.61)
(1.61)
где Dnи Dpсоответственно коэффициенты диффузии электронов и дырок. Коэффициенты диффузии носителей заряда связаны с их подвижностью соотношением Эйнштейна:
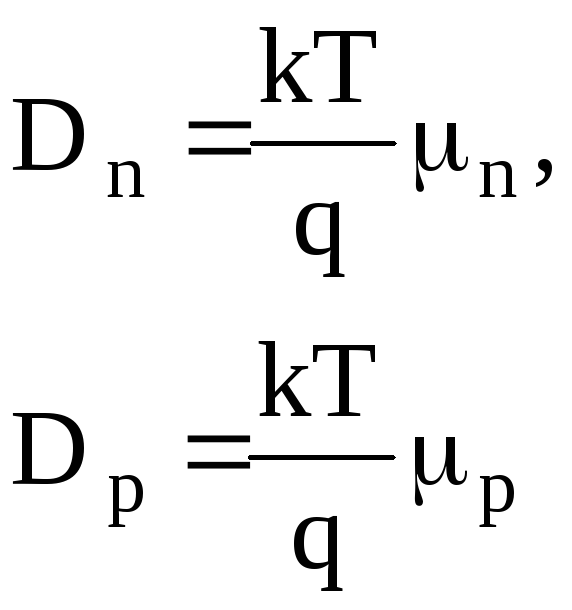 (1.62)
(1.62)
Коэффициент диффузии тем выше, чем выше подвижность носителей заряда.
Токи, возникающие во внешних полях принято называть дрейфовыми, поскольку внешнее поле не прекращая хаотического теплового движения носителей заряда заставляет их смещаться (дрейфовать) в направлении, которое зависит от знака носителя и направления внешнего поля. К дрейфовым токам можно отнести и рассмотренные ранее токи проводимости токи (их иногда называют омическими), используя (1.56) для них можно записать:
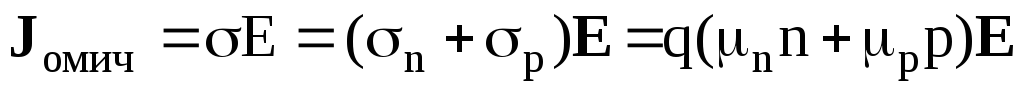 ( 1.57)
( 1.57)
Таким образом процессы, определяющие перенос зарядов в полупроводниках будут определяться четырьмя токами: дрейфовыми токами электронов и дырок, возникающими при наличии электрического поля и диффузионными токами электронов и дырок, возникающими в том случае, когда существует градиент концентрации носителей заряда.
Все четыре тока связаны между собой уравнением непрерывности (4), которой явилось следствием закона сохранения заряда.
1.2.8. Уравнение непрерывности.
Для полупроводника, в объеме которого происходит генерация и рекомбинация носителей заряда, используя (4) запишем:
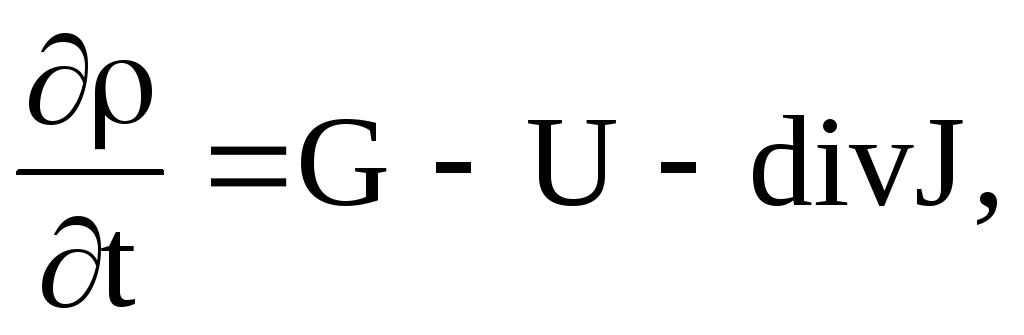 (1.58)
(1.58)
где G и U соответственно члены характеризующие скорость генерации и скорость рекомбинации носителей заряда. Используя (21) и (24) и разделив левую и правую части уравнения на величину заряда электронов получим:
 (1.59)
(1.59)
Для одномерного случая разделяя члены, относящиеся к электронам и дыркам , учитывая, что полный ток равен:
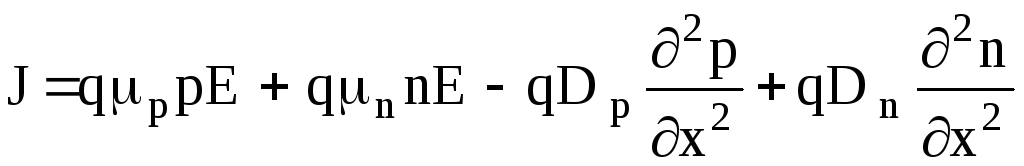 (1.60)
(1.60)
получим:
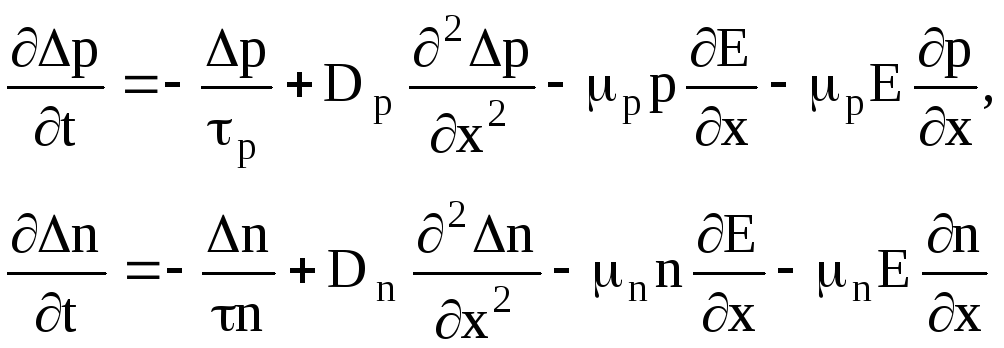 (1.61)
(1.61)
Связь между распределением заряда и электрического поля в образце устанавливается с помощью уравнения Пуассона:
 (1.63)
(1.63)
Для полупроводника близкого к собственному основными зарядами являются электроны и дырки, поэтому:
 (1.64)
(1.64)
Подставляя ∂E/∂x в (31) получим:
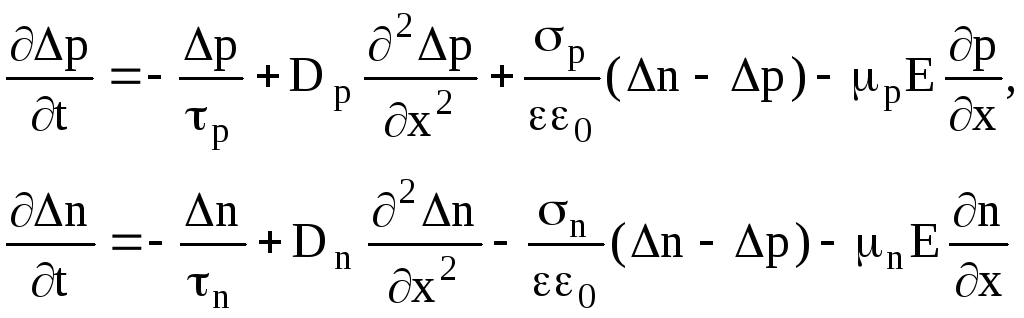 (1.65)
(1.65)
Считая, что в образце выполняется условие электронейтральности: Δp≈Δn и τp≈ τn. суммируя уравнения для электронов и дырок получим:
 (1.66)
(1.66)
где D и μ коэффициенты , характеризующие совместную диффузию и дрейф электронов и дырок, поэтому их и называют коэффициентами амбиполярной диффузии и амбиполярной подвижности:
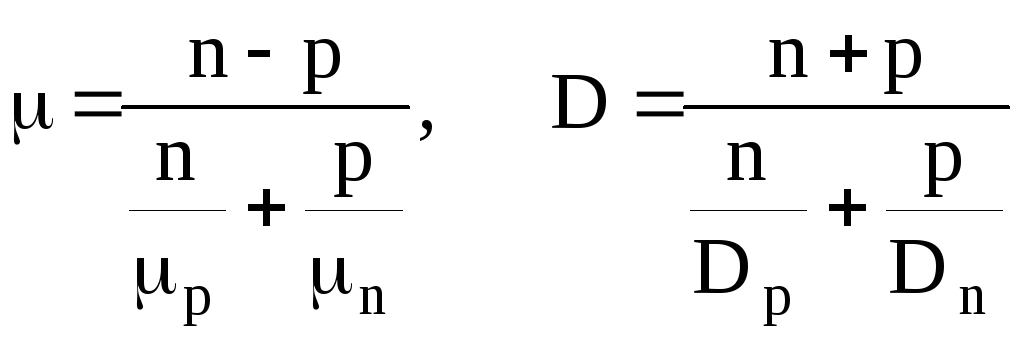 (1.67)
(1.67)
Уравнение (1.67) описывает основные изменения происходящие с носителями заряда и соответственно токами в полупроводниковых материалах и соответственно приборах на их основе. Это уравнение в правой части содержит три члена: генерационно-рекомбинационный, диффузионный и дрейфовый. Это уравнение широко используется при анализе процессов в полупроводниковых приборах, поскольку позволяет значительно упростить расчеты, по существу заменив операции с четырьмя потоками носителей операциями с одним.
Пример.
Предположим, что у нас имеется полупроводниковый образец в центре которого инжектируется избыточная концентрация электронов и дырок (Δn ≈ Δp) , такое распределение можно создать коротким лазерным импульсом с энергией квантов большей ширины запрещенной зоны. Как со временем будет изменяться этот импульс, если к образцу приложить внешнее электрическое напряжение (рис. 1.26), которое создаст в нем электрическое.
Ответ на поставленный вопрос поможет дать уравнения (1.66), (1.67) при этом не обязательно решать само уравнение, достаточно воспользоваться введенными характеристическими коэффициентами, характеризующими совместно движение электронов и дырок (36). Действительно направление движения совпадает с электрическим полем, если подвижность — положительная величина и направлено в другую сторону, если подвижность — отрицательная величина.
Допустим, что рассматриваемый полупроводник n типа, тогда n>>p и из (1.67) получим, что μ ≈μp. Следовательно перемещение импульса носителей заряда в электрическом поле будет определяться перемещением дырокvдр= μpE.
Допустим, что рассматриваемый полупроводник p типа, тогда p>> n и из (1.67) получим, что μ ≈μn. Следовательно перемещение импульса носителей заряда в электрическом поле будет определяться перемещением электронов vдр= — μnE.
В случае собственного полупроводника (n = p = ni) μ = 0 и соответственноvдр= μE.
Рассмотренные варианты проиллюстрированы на нижней диаграмме рис. 1.26.
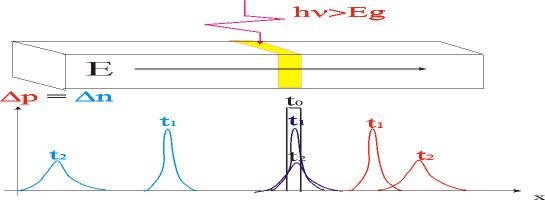
Рис. 1.26. Дрейф инжектированного светом электронно-дырочного импульса в электрическом поле.
В процессе дрейфа импульс будет расплываться за счет диффузии и общее число избыточных носителей заряда в нем будет уменьшаться в результате рекомбинации.
Приведенный пример демонстрирует эффективность уравнения (35) при анализе процессов в различных областях полупроводниковых приборов. Так биполярные полупроводниковые приборы (диоды, транзисторы, тиристоры и др) состоят из чередующихся областей p и n типа. Поэтому для анализа процессов в различных областях используются уравнения для неосновных носителей заряда.
Для p области p>>n
и соответственно будут иметь место
следующие уравнения.  (1.68)
(1.68)
Каждое из приведенных уравнений является частным случаем более общего уравнения (1.66) и используется для анализа процессов в полупроводниковых материалах и приборах именно для частных случаев, что значительно упрощает поиск возможного решения. Решение уравнения (1.66) достаточно в общем виде весьма сложно и, если это требуется по условиям задачи, то обычно выполняется численными методами с использованием соответствующих компьютерных программ.
Аналогично для n типа n>>p Для p соответственно будут иметь место
следующие уравнения:
 (1.69)
(1.69)
1.4 Дрейфовый и диффузионный токи в полупроводниках
Электрический ток может возникнуть в полупроводнике только при направленном движении носителей заряда, которое создается либо под воздействием электрического поля (дрейф), либо вследствие неравномерного распределения носителей заряда по объему кристалла (диффузия). Если электрическое поле отсутствует, и носители заряда имеют в кристалле равномерную концентрацию, то электроны и дырки совершают непрерывное хаотическое тепловое движение. В результате столкновения носителей заряда друг с другом и с атомами кристаллической решетки скорость и направление их движения все время изменяются, так что тока в кристалле не будет.
Под действием приложенного к кристаллу напряжения в нем возникает электрическое поле. Движение носителей заряда упорядочивается: электроны перемещаются по направлению к положительному электроду, дырки – к отрицательному. При этом не прекращается и тепловое движение носителей заряда, вследствие которого происходят столкновения их с атомами полупроводника и примеси.
Направленное движение носителей заряда под действием сил электрического поля называют дрейфом, а вызванный этим движением ток – дрейфовым током. При этом характер тока может быть электронным, если он вызван движением электронов, или дырочным, если он создается направленным перемещением дырок.
Средняя скорость носителей заряда в электрическом поле прямо пропорциональна напряженности электрического поля:
ν = μ E
Коэффициент пропорциональности называют подвижностью электронов (n), или дырок (p). Свободные электроны движутся в пространстве между узлами кристаллической решетки, а дырки – по ковалентным связям, поэтому средняя скорость, а следовательно, и подвижность электронов больше, чем дырок. У кремния подвижность носителей заряда меньше, чем у германия.
В собственных полупроводниках концентрации электронов и дырок одинаковы, но вследствие их разной подвижности электронная составляющая тока больше дырочной. В примесных полупроводниках концентрации электронов и дырок существенно отличаются, характер тока определяется основными носителями заряда: в полупроводниках р-типа – дырками, а в полупроводниках n-типа – электронами.
При неравномерной концентрации носителей заряда вероятность их столкновения друг с другом больше в тех слоях полупроводника, где их концентрация выше. Совершая хаотическое тепловое движение, носители заряда отклоняются в сторону, где меньше число столкновений, т.е. движутся в направлении уменьшения их концентрации.
Направленное движение носителей заряда из слоя с более высокой их концентрацией в слой, где концентрация ниже, называют диффузией, а ток, вызванный этим явлением, – диффузионным током. Этот ток, как и дрейфовый, может быть электронным или дырочным.
Степень неравномерности распределения носителей заряда характеризуется градиентом концентрации; его определяют как отношение изменения концентрации к изменению расстояния, на котором оно происходит. Чем больше градиент концентрации, т.е. чем резче она изменяется, тем больше диффузионный ток.
Электроны, перемещаясь из слоя с высокой концентрацией в слой с более низкой концентрацией, по мере продвижения рекомбинируют с дырками, и наоборот, диффундирующие в слой с пониженной концентрацией дырки рекомбинируют с электронами. При этом избыточная концентрация носителей заряда уменьшается.
1.4. Дрейфовый и диффузионный токи в полупроводниках
Электрический ток может возникнуть в полупроводнике только при направленном движении носителей заряда, которое создается либо под воздействием электрического поля (дрейф), либо вследствие неравномерного распределения носителей заряда по объему кристалла (диффузия). Если электрическое поле отсутствует, и носители заряда имеют в кристалле равномерную концентрацию, то электроны и дырки совершают непрерывное хаотическое тепловое движение. В результате столкновения носителей заряда друг с другом и с атомами кристаллической решетки скорость и направление их движения все время изменяются, так что тока в кристалле не будет.
Под действием приложенного к кристаллу напряжения в нем возникает электрическое поле. Движение носителей заряда упорядочивается: электроны перемещаются по направлению к положительному электроду, дырки – к отрицательному. При этом не прекращается и тепловое движение носителей заряда, вследствие которого происходят столкновения их с атомами полупроводника и примеси.
Направленное движение носителей заряда под действием сил электрического поля называют дрейфом, а вызванный этим движением ток –дрейфовым током. При этом характер тока может быть электронным, если он вызван движением электронов, или дырочным, если он создается направленным перемещением дырок.
Средняя скорость носителей заряда в электрическом поле прямо пропорциональна напряженности электрического поля:
ν=μE
Коэффициент пропорциональности называют подвижностью электронов (n), или дырок (p). Свободные электроны движутся в пространстве между узлами кристаллической решетки, а дырки – по ковалентным связям, поэтому средняя скорость, а следовательно, и подвижность электронов больше, чем дырок. У кремния подвижность носителей заряда меньше, чем у германия.
В собственных полупроводниках концентрации электронов и дырок одинаковы, но вследствие их разной подвижности электронная составляющая тока больше дырочной. В примесных полупроводниках концентрации электронов и дырок существенно отличаются, характер тока определяется основными носителями заряда: в полупроводниках р-типа – дырками, а в полупроводниках n-типа – электронами.
При неравномерной концентрации носителей заряда вероятность их столкновения друг с другом больше в тех слоях полупроводника, где их концентрация выше. Совершая хаотическое тепловое движение, носители заряда отклоняются в сторону, где меньше число столкновений, т.е. движутся в направлении уменьшения их концентрации.
Направленное движение носителей заряда из слоя с более высокой их концентрацией в слой, где концентрация ниже, называют диффузией, а ток, вызванный этим явлением, – диффузионным током. Этот ток, как и дрейфовый, может быть электронным или дырочным.
Степень неравномерности распределения носителей заряда характеризуется градиентом концентрации; его определяют как отношение изменения концентрации к изменению расстояния, на котором оно происходит. Чем больше градиент концентрации, т.е. чем резче она изменяется, тем больше диффузионный ток.
Электроны, перемещаясь из слоя с высокой концентрацией в слой с более низкой концентрацией, по мере продвижения рекомбинируют с дырками, и наоборот, диффундирующие в слой с пониженной концентрацией дырки рекомбинируют с электронами. При этом избыточная концентрация носителей заряда уменьшается.
1.2 Токи в полупроводниках
1.2.1 Дрейфовый ток
В
полупроводниках свободные электроны
и дырки находятся в состоянии
хаотического движения. Поэтому, если
выбрать произвольное сечение внутри
объема полупроводника и подсчитать
число носителей заряда, проходящих
через это сечение за единицу времени
слева направо и справа налево, значения
этих чисел окажутся одинаковыми. Это
означает, что электрический ток в данном
объеме полупроводника отсутствует. При
помещении полупроводника в электрическое
поле напряженностью Е на хаотическое
движение носителей зарядов накладывается
составляющая направленного движения.
Направленное движение носителей зарядов
в электрическом поле обусловливает
появление тока, называемого дрейфовым
(рис. 1.5) 
В области высоких температур концентрация электронов и дырок значительно возрастает за счет разрыва ковалентных связей и, несмотря на уменьшение их подвижности, электропроводность полупроводника увеличивается по экспоненциальному закону.
Рисунок 1.5 Дрейфовый ток в полупроводнике
1.2.2 Диффузионный ток
Кроме
теплового возбуждения, приводящего к
возникновению равновесной концентрации
зарядов, равномерно распределенных по
объему полупроводника, обогащение
полупроводника электронами до концентрации
np и дырками до концентрации pn может осуществляться его освещением,
облучением потоком заряжённых частиц,
введением их через контакт (инжекцией)
и т. д. В этом случае энергия возбудителя
передается непосредственно носителям
заряда и тепловая энергия кристаллической
решетки остается практически постоянной.
Следовательно, избыточные носители
заряда не находятся в тепловом равновесии
с решеткой и поэтому называются
неравновесными. В отличие от равновесных
они могут неравномерно распределяться
по объему полупроводника (рис. 1.6)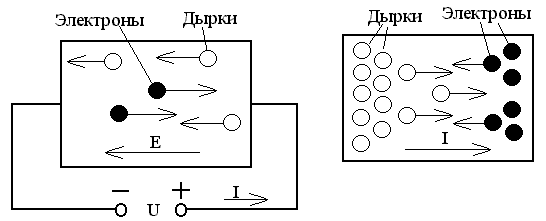
После прекращения действия возбудителя за счет рекомбинации электронов и дырок концентрация избыточных носителей быстро убывает и достигает равновесного значения.
Носители зарядов рекомбинируют в объеме полупроводника и на его поверхности. Неравномерное распределение неравновесных носителей зарядов сопровождается их диффузией в сторону меньшей концентрации. Это движение носителей зарядов обусловливает прохождение электрического тока, называемого диффузионным (рис. 1.6).
Рисунок 1.6 Диффузионный ток в полупроводнике
1.3 Контактные явления
Электронно-дырочный переход в состоянии равновесия
Принцип действия большинства полупроводниковых приборов основан на физических явлениях, происходящих в области контакта твердых тел. При этом преимущественно используются контакты: полупроводник-полупроводник; металл-полупроводник; металл-диэлектрик-полупроводник.
Если переход создается между полупроводниками n-типа и p-типа, то его называют электронно-дырочным или p-n переходом.
Электронно-дырочный переход создается в одном кристалле полупроводника с использованием сложных и разнообразных технологических операций.
Рассмотрим
p-n
переход, в котором концентрации доноров
Nд и акцепторов Na изменяются скачком на границе раздела
(рис. 1.7, а). Такой p-n
переход называют резким. Равновесная
концентрация дырок в p-области
(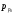 )
значительно превышает их концентрацию
вn-области
(
)
значительно превышает их концентрацию
вn-области
(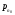 ).
Аналогично для электронов выполняется
условие
).
Аналогично для электронов выполняется
условие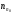 >
> .
Неравномерное распределение концентраций
одноименных носителей зарядов в кристалле
(рис. 1.7, б) приводит к возникновению
диффузии электронов изn-области
в p-область
и дырок из p-области
в n-область.
Такое движение зарядов создает
диффузионный ток электронов и дырок.
.
Неравномерное распределение концентраций
одноименных носителей зарядов в кристалле
(рис. 1.7, б) приводит к возникновению
диффузии электронов изn-области
в p-область
и дырок из p-области
в n-область.
Такое движение зарядов создает
диффузионный ток электронов и дырок.
Электроны и дырки, переходя через контакт навстречу друг другу (благодаря диффузии), рекомбинируют и в приконтактной области дырочного полупроводника образуется нескомпенсированный заряд отрицательных ионов акцепторных примесей, а в электронном полупроводнике нескомпенсированный заряд положительных донорных ионов (рис. 1.6, в). Таким образом, электронный полупроводник заряжается положительно, а дырочный — отрицательно. Между областями с различными типами электропроводности возникает собственное электрическое поле напряженностью Eсоб (рис. 1.7, а), созданное двумя слоями объемных зарядов.
Собственное электрическое поле является тормозящим для основных носителей заряда и ускоряющим для неосновных. Электроны p-области и дырки n-области, совершая тепловое движение, попадают в пределы диффузионного электрического поля, увлекаются им и перебрасываются в противоположные области, образуя ток дрейфа, или ток проводимости.
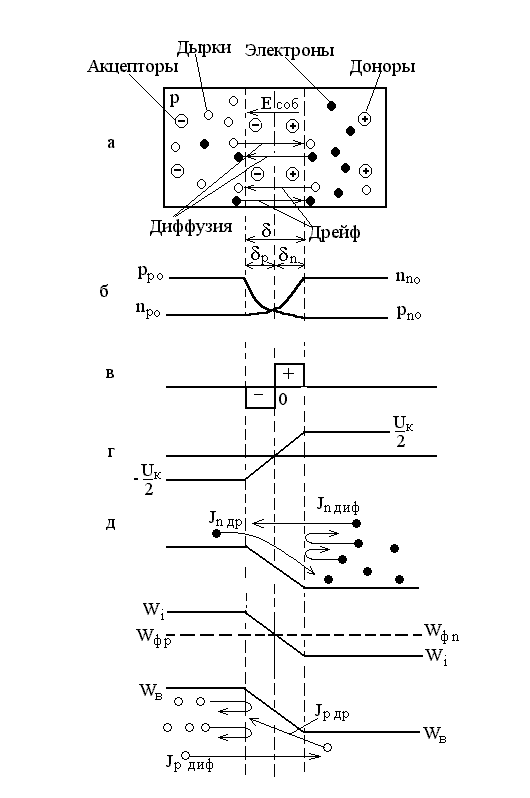
Рисунок 1.7 Равновесное состояние p-n перехода
Приконтактную область, где имеется собственное электрическое поле, называют p—n переходом. В данной области полупроводник характеризуется собственной электропроводностью и обладает по сравнению с остальным объемом повышенным сопротивлением. В связи с этим его называют запирающим слоем или областью объемного заряда.
На ширину запирающего слоя существенное влияние оказывает концентрация примесных атомов. Увеличение концентрации примесных атомов сужает запирающий слой, а уменьшение расширяет его. Это часто используется для придания полупроводниковым приборам требуемых свойств.
Диффузионный и дрейфовый токи.
Диффузия (от лат. diffusio — распространение, растекание, рассеивание) — неравновесный процесс, вызываемый тепловым движением частиц, приводящий к установлению равновесия и выравниванию концентраций (при постоянстве температуры и отсутствии внешних сил). Если частицы заряжены, то их диффузионное перемещение приводит к появлению диффузионных токов.
Диффузионный поток направлен из области высокой концентрации в область низкой концентрации. Свободные носители заряжены. Следовательно любое их перемещение, в том числе и диффузионное, приводит к появлению электрических токов, которые так и будем называть диффузионными.

Рис. 1.25. Схема, иллюстрирующая возникновение диффузионных токов электронов и дырок.
Схема на рис. 1.25 иллюстрирует возникновение диффузионных токов электронов и дырок. Следует обратить внимание, что потоки электронов и дырок на схеме направлены в одну сторону, а токи дырочный и электронный токи в разные. Направление дырочного тока совпадает с направлением потока, электронного противоположно, поэтому токи компенсируют друг друга уменьшая общий диффузионный ток.
Скорость диффузии (диффузионный поток) пропорционален градиенту концентрации, поэтому для диффузионных токов можно записать:
 (1.61)
(1.61)
где Dn и Dp соответственно коэффициенты диффузии электронов и дырок. Коэффициенты диффузии носителей заряда связаны с их подвижностью соотношением Эйнштейна:
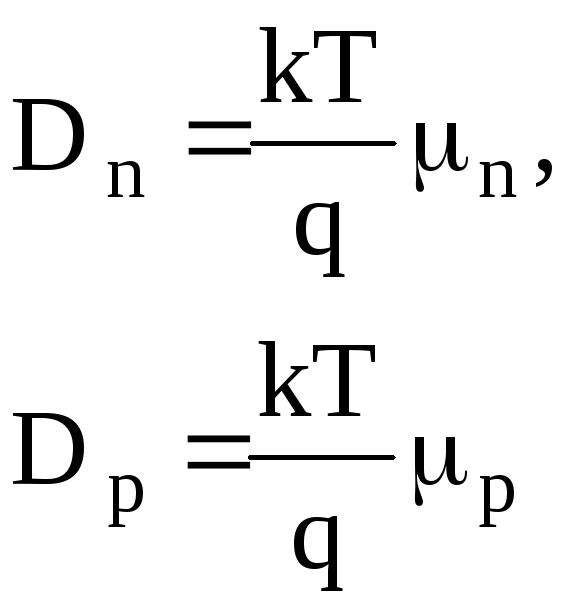 (1.62)
(1.62)
Коэффициент диффузии тем выше, чем выше подвижность носителей заряда.
Токи, возникающие во внешних полях принято называть дрейфовыми, поскольку внешнее поле не прекращая хаотического теплового движения носителей заряда заставляет их смещаться (дрейфовать) в направлении, которое зависит от знака носителя и направления внешнего поля. К дрейфовым токам можно отнести и рассмотренные ранее токи проводимости токи (их иногда называют омическими), используя (1.56) для них можно записать:
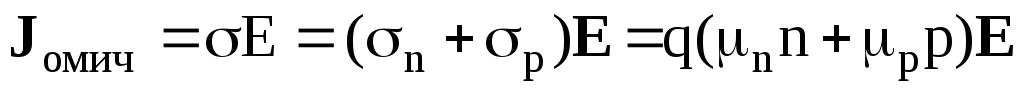 ( 1.57)
( 1.57)
Таким образом процессы, определяющие перенос зарядов в полупроводниках будут определяться четырьмя токами: дрейфовыми токами электронов и дырок, возникающими при наличии электрического поля и диффузионными токами электронов и дырок, возникающими в том случае, когда существует градиент концентрации носителей заряда.
Все четыре тока связаны между собой уравнением непрерывности (4), которой явилось следствием закона сохранения заряда.
1.2.8. Уравнение непрерывности.
Для полупроводника, в объеме которого происходит генерация и рекомбинация носителей заряда, используя (4) запишем:
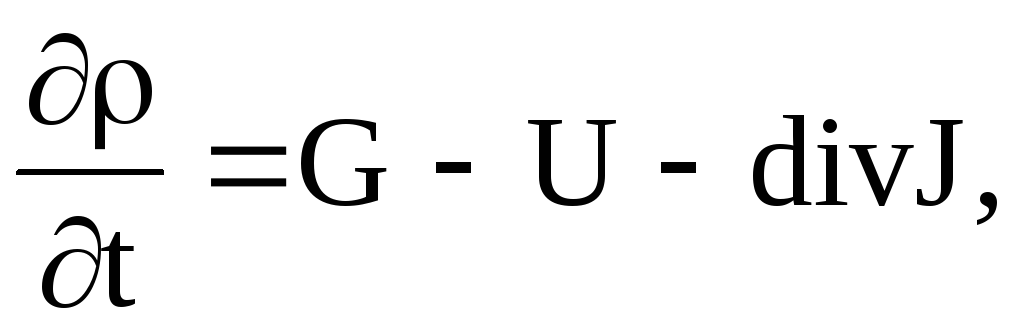 (1.58)
(1.58)
где G и U соответственно члены характеризующие скорость генерации и скорость рекомбинации носителей заряда. Используя (21) и (24) и разделив левую и правую части уравнения на величину заряда электронов получим:
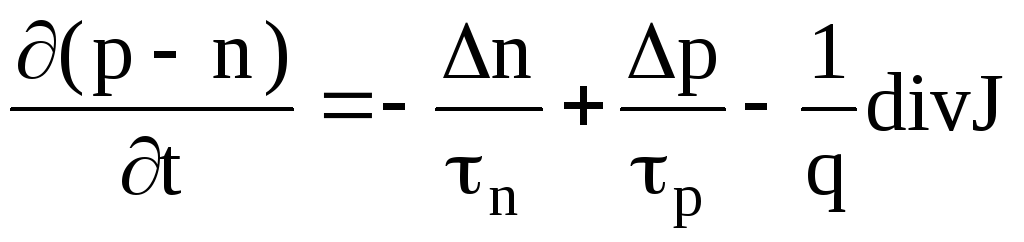 (1.59)
(1.59)
Для одномерного случая разделяя члены, относящиеся к электронам и дыркам , учитывая, что полный ток равен:
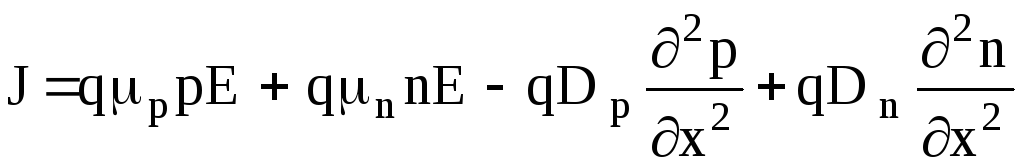 (1.60)
(1.60)
получим:
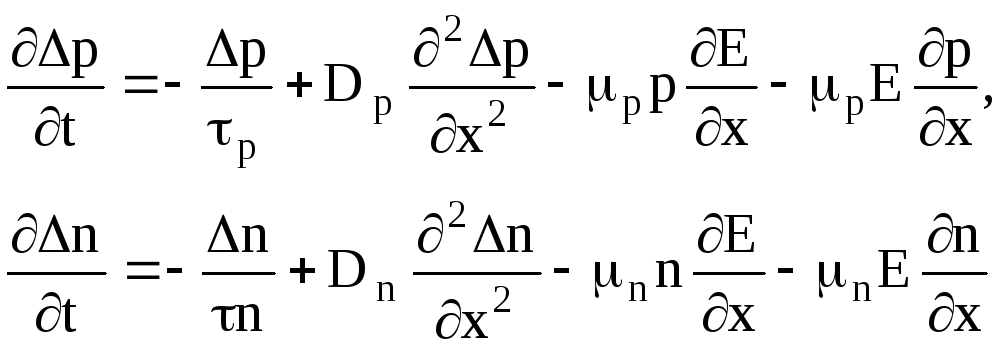 (1.61)
(1.61)
Связь между распределением заряда и электрического поля в образце устанавливается с помощью уравнения Пуассона:
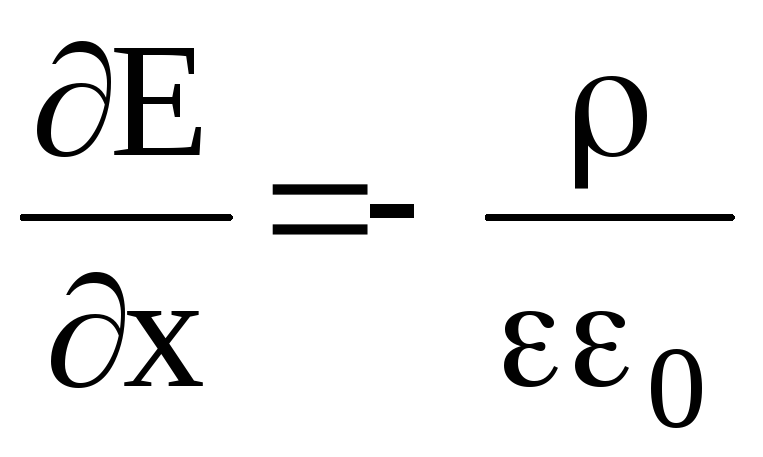 (1.63)
(1.63)
Для полупроводника близкого к собственному основными зарядами являются электроны и дырки, поэтому:
 (1.64)
(1.64)
Подставляя ∂E/∂x в (31) получим:
 (1.65)
(1.65)
Считая, что в образце выполняется условие электронейтральности: Δp≈Δn и τp ≈ τn. суммируя уравнения для электронов и дырок получим:
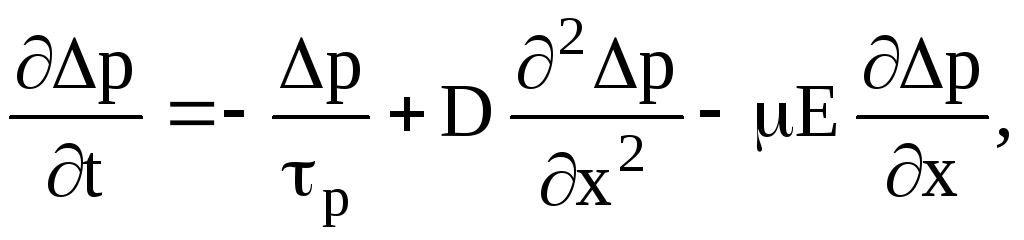 (1.66)
(1.66)
где D и μ коэффициенты , характеризующие совместную диффузию и дрейф электронов и дырок, поэтому их и называют коэффициентами амбиполярной диффузии и амбиполярной подвижности:
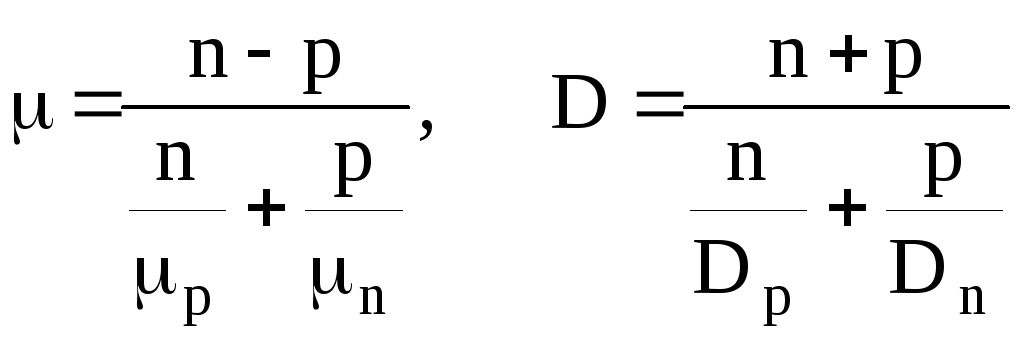 (1.67)
(1.67)
Уравнение (1.67) описывает основные изменения происходящие с носителями заряда и соответственно токами в полупроводниковых материалах и соответственно приборах на их основе. Это уравнение в правой части содержит три члена: генерационно-рекомбинационный, диффузионный и дрейфовый. Это уравнение широко используется при анализе процессов в полупроводниковых приборах, поскольку позволяет значительно упростить расчеты, по существу заменив операции с четырьмя потоками носителей операциями с одним.
Пример.
Предположим, что у нас имеется полупроводниковый образец в центре которого инжектируется избыточная концентрация электронов и дырок (Δn ≈ Δp) , такое распределение можно создать коротким лазерным импульсом с энергией квантов большей ширины запрещенной зоны. Как со временем будет изменяться этот импульс, если к образцу приложить внешнее электрическое напряжение (рис. 1.26), которое создаст в нем электрическое.
Ответ на поставленный вопрос поможет дать уравнения (1.66), (1.67) при этом не обязательно решать само уравнение, достаточно воспользоваться введенными характеристическими коэффициентами, характеризующими совместно движение электронов и дырок (36). Действительно направление движения совпадает с электрическим полем, если подвижность — положительная величина и направлено в другую сторону, если подвижность — отрицательная величина.
Допустим, что рассматриваемый полупроводник n типа, тогда n>>p и из (1.67) получим, что μ ≈μp. Следовательно перемещение импульса носителей заряда в электрическом поле будет определяться перемещением дырок vдр= μpE.
Допустим, что рассматриваемый полупроводник p типа, тогда p>> n и из (1.67) получим, что μ ≈μn. Следовательно перемещение импульса носителей заряда в электрическом поле будет определяться перемещением электронов vдр= — μnE.
В случае собственного полупроводника (n = p = ni) μ = 0 и соответственно vдр= μE.
Рассмотренные варианты проиллюстрированы на нижней диаграмме рис. 1.26.
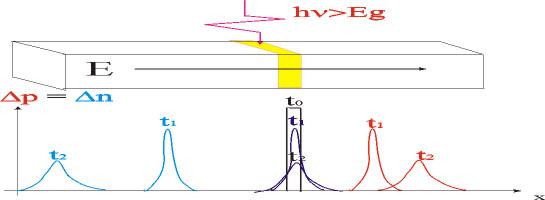
Рис. 1.26. Дрейф инжектированного светом электронно-дырочного импульса в электрическом поле.
В процессе дрейфа импульс будет расплываться за счет диффузии и общее число избыточных носителей заряда в нем будет уменьшаться в результате рекомбинации.
Приведенный пример демонстрирует эффективность уравнения (35) при анализе процессов в различных областях полупроводниковых приборов. Так биполярные полупроводниковые приборы (диоды, транзисторы, тиристоры и др) состоят из чередующихся областей p и n типа. Поэтому для анализа процессов в различных областях используются уравнения для неосновных носителей заряда.
Для p области p>>n и соответственно будут иметь место следующие уравнения.
 (1.68)
(1.68)
Каждое из приведенных уравнений является частным случаем более общего уравнения (1.66) и используется для анализа процессов в полупроводниковых материалах и приборах именно для частных случаев, что значительно упрощает поиск возможного решения. Решение уравнения (1.66) достаточно в общем виде весьма сложно и, если это требуется по условиям задачи, то обычно выполняется численными методами с использованием соответствующих компьютерных программ.
Аналогично для n типа n>>p Для p соответственно будут иметь место
следующие уравнения:
 (1.69)
(1.69)



