Методическая разработка урока «Метод контурных токов» (10 класс). Профильный уровень

Методическая разработка урока физики для профильного класса

(политехнический, физико-математический)

Урок 12/114 10 класс

Тема: Метод контурных токов.

Цели урока:

1. образовательная: научить учащихся производить расчеты сложных электрических цепей;

2. развивающая: сформировать умения анализировать, развитие логики мышления, поиска способов рационального решения физических задач;

3. воспитательная: воспитание мотивации учения.

Содержание урока:

1. Организационный момент

2. Проверка знаний.

1. Фронтальный опрос.

Вопросы:

• Дайте определение узла электрической цепи. Начертите на доске электрический узел, укажите направление электрических токов в подводящих к узлу ветвях.

• Сформулируйте первое правило Кирхгофа.

• Запишите первое правило Кирхгофа для начерченного на доске (рис. 1) узла.

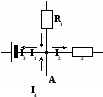
Рис. 1. Рис.2.

• Какое соединение элементов электрической цепи можно считать ветвью?

• Сформулируйте второе правило Кирхгофа, запишите второе правило Кирхгофа для предложенной схемы (рис. 2).

• Объясните, как записать второе правило Кирхгофа, если в ветви находятся несколько источников тока?

• Как влияет полярность включения источника тока в электрическую цепь на знак ЭДС в уравнении?

2. Индивидуальный опрос у доски с одновременным решением задачи № 1 в тетрадях учащихся.

ЗАДАЧА № 1.

В предложенной электрической цепи определите силу тока во всех резисторах, используя законы Кирхгофа.

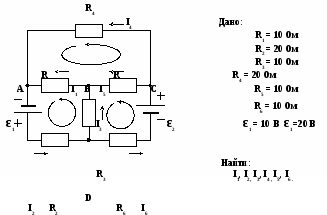
Рис. 3

Решение задачи:

Напишем 1 закон Кирхгофа для узлов А, В, С:

А: I₁ — I₂ + I₄ = 0;

В: I₅ – I₁ + I₃ = 0;

С: I₆ – I₄ – I₅ = 0.

Выберем направление обхода контуров ADBA, BDCB и ABCA и напишем 2 закон Кирхгофа для этих контуров:

ADBA: ε₁ = I₂ ^. R₂ + I₁ ^. R₁ + I₃ ^. R₃

;

BDCB: ε₂ = I₅ ^. R₅ — I₃ ^. R₃ + I₆ ^. R₆ ;

ABCA : 0 = I₄ ^. R₄ — I₁ ^. R₁ – I₅ ^. R₅ .

П

одставим численные значения сопротивлений резисторов и источников тока в полученные уравнения и объединим их систему из шести уравнений с шестью неизвестными:

Выразим из наиболее простого уравнения системы один из неизвестных токов и, подставив это неизвестное в остальные уравнения, преобразуем уравнения системы с учетом полученного выражения, и, понижая с каждым преобразованием ранг системы уравнений, найдем численные значения неизвестных, входящих в эту систему уравнений:

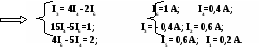
Подставим полученные значения силы тока в резисторах в уравнения Кирхгофа, убедимся в правильности расчетов:

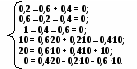
3. Изучение нового материала.

Вопросы: Расчет электрических цепей с помощью метода контурных токов.

Расчет электрической цепи методом контурных токов.

Для сравнения уровня сложности расчетов произведем расчет электрической цепи Рис. 3., предложенной в предыдущей задаче, методом контурных токов:

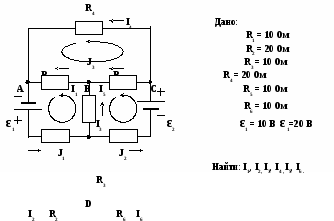
Основным достоинством, рассматриваемого метода расчета электрической цепи, метода контурных токов является то, что для вычисления силы токов в каждом элементе цепи количество уравнений в системе соответствует количеству контуров рассчитываемой электрической цепи. В нашем случае необходимо составить всего три уравнения, что в два раза меньше чем в системе уравнений рассчитываемой при использовании законов Кирхгофа.

Выберем в контурах ADBA, BDCB и ABCA произвольно направления контурных токов J₁, J₂ и J₃. Составим систему из трех уравнений:

Подставив в полученную систему уравнений численные значения резисторов и ЭДС, рассчитаем контурные токи:

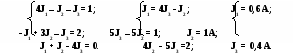
Сила тока в отдельных резисторах определяется как векторная сумма контурных токов, протекающих через эти резисторы:

I₁ = J₁ – J₃ = 0,2 А; I₂ = J₁ = 0,6 А;

I₃ = J₂ – J₁ = 0,4 А; I₄ = J₃ = 0,4 А;

I₅ =

J₂ – J₃ = 0,6 А; I₆ = J₂ = 1А.

Результаты расчета проверяются с помощью законов Кирхгофа.

4. Закрепление изученного материала.

У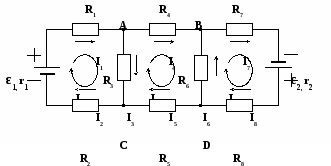чащимся предлагается самостоятельно записать уравнения, необходимые для расчета следующей электрической цепи (рис. 4) методом контурных токов:

Рис. 4.

Для предложенной электрической цепи выберем 3 контура:

1 – контур: С, R₂ ,ε_1,R₁, А, R₃, С

2 – контур: С, R₃, А, R₄, В, R₆, D, R₅, С

3 – контур: D, R₆, В, R₇, ε_2, R₈, D

Составим уравнения согласно второму правилу Кирхгофа для выбранных контуров:

ε₁= J₁ ^. (R₁ + R₂ + R₃ + r₁) – J₂ ^. R₃ (1).

0 = J₂ ^. (R₃ + R₄ + R₅ + R₆) – J₁ ^. R₃ – J₃ ^. R₆ (2).

ε ₂= J₃ ^. (R₆ + R₇ + R₈ + r₂) – J₂ ^. R₆ (3).

После решения системы трех уравнений с тремя неизвестными найдем токи в элементах цепи:

I₁ = I₂ =J₁, I₃ =J₁ – J₂,

I₄ = I₅ =J₂, I₃ =J₁ – J₂,

I₆ = J₂ – J₃, I₇ = I₈ =J₃.

5. Самостоятельная работа учащихся по решению задач.

Используя метод контурных токов, вычислите численные значения силы тока в каждом элементе, найдите падение напряжения на всех резисторах, предложенной электрической цепи:

ЗАДАЧА № 2.

Рассчитайте электрическую цепь методом контурных токов:

Дано:

ε₁ = 50 В

ε₂ = 40 В

R₁ = 7 Ом

R₂ = 10 Ом

R₃ = 6 Ом

r₁ = 3 Ом

r₂ = 4 Ом.

Определить:

I₁ , I₂ , I₃,

U₁, U₂, U₃.

РЕШЕНИЕ:

В цепи два простых контура. Выберем направление контурных токов J₁ и J₂ с учетом полярности ЭДС источников тока.

Для контура C,ε_1, r_1, R₁, A, R₂,C: ε₁= J₁ ^. (R₁ + R₂ + r₁) + J₂ ^. R₂ (1).

Для контура C, R₂, A, R₃ , ε_1, r_1, ,C: ε₂= J₂ ^. (R₃ + R₂ + r₂) + J₁ ^. R₂ (2).

Подставляя в выражения (1) и (2) численные значения сопротивления резисторов и ЭДС источников тока, получаем систему из двух уравнений:

50 = J₁ ^. (7 + 10 + 3) + J₂ ^. 10, 5 = 2J₁ + J₂ , J₁ = 2 А;

40 = J₂ ^. (6 + 10 + 4) + J₁ ^. 10. 4 = 2J₂ + J₁. J₂ = 1 А.

Рассчитаем токи в отдельных резисторах: I₁ = J₁ = 2А; I₂ = J₁ + J₂ = 3А; I₃ = J₂ = 1А.

Рассчитаем падение напряжения на резисторах: U₁ = I₁ ^. R₁ = 2 ^. 7 = 14 B, U₂ = I₂ ^. R₂ = 3 ^. 10 = 30 B, U₃ = I₃ ^. R₃ = 1 ^. 6 = 6 B.

Ответ: I₁ = 2А; I₂ = 3А; I₃ = 1А. U₁ = 14 B, U₂ = 30 B, U₃ = 6 B.

6. Подведение итогов урока.

7. Задание на дом.

Рассчитайте методом контурных токов электрические цепи:

ЗАДАЧА № 1.

Д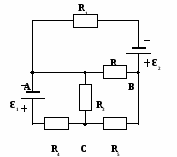ано:

ε₁ = 20 В

ε₂ = 30 В

R₁ = 16 Ом

R₂ = 10 Ом

R₃ = 20 Ом

R₄ = 7 Ом

R₅ = 10 Ом

r₁ = 3 Ом

r₂ = 4 Ом.

Определить:

I₁ , I₂ , I₃, I₄ , I₅ ,

U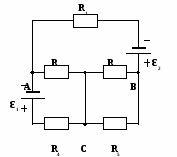₁, U₂, U_3, U₄, U₅.

ЗАДАЧА № 2.

Дано:

ε₁ = 20 В

ε₂ = 30 В

R₁ = 16 Ом

R₂ = 10 Ом

R₃ = 20 Ом

R₄ = 8 Ом

R₅ = 20 Ом

r₁ = 2 Ом

r₂ = 4 Ом.

Определить:

I₁ , I₂ , I₃, I₄ , I₅ ,

U₁, U₂, U_3, U₄, U₅.

З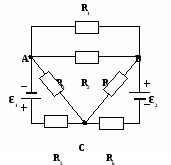АДАЧА № 3.

Дано:

ε₁ = 100 В

ε₂ = 50 В

R₁ = 20 Ом

R₂ = 30 Ом

R₃ = 20 Ом

R₄ = 20 Ом

R₅ = 75 Ом

R₆ = 78 Ом

r₁ = 5 Ом

r₂ = 2 Ом.

Определить:

I₁ , I₂ , I₃, I₄ , I₅ , I₆,

U₁, U₂, U_3, U₄, U_5, U₆.

Метод прямого использования законов Кирхгофа — КиберПедия

В основу метода положено то, что для каждого независимого узла электрической схемы можно составить уравнение по первому закону Кирхгофа (узловые уравнения), а для каждого независимого контура – по второму закону Кирхгофа (контурные уравнения).

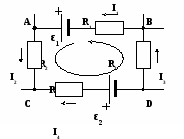
Рассмотрим схему (рис. 3.3).

 

Выберем условно положительные направления токов. Если в простых цепях обычно можно определить истинные направления токов, то в сложных цепях это сделать не всегда возможно, так как источники действуют в разных направлениях и могут компенсировать друг друга, поэтому направления токов выбираем произвольно. Если в ветви есть источник ЭДС, то часто направление тока задают совпадающим с направлением источника, но это не обязательно.

Определяем количество независимых узлов и контуров.

В рассматриваемой схеме пять ветвей т = 5 и три узла п = 3(один фиктивный), следовательно, количество независимых узлов N = п – 1 = 3 – 1 = 2; количество независимых контуров К = т – (п – 1) = 5 – (3 – 1) = 3.

Таким образом, для данной схемы можно составить два узловых и три контурных уравнения.

Составим уравнения для узлов 1 и 2, считая положительными токи, текущие от узла,

;

.

Для расчета пяти токов необходимо иметь пять уравнений. Недостающие три уравнения составляем по второму закону Кирхгофа для контуров:

Е₁ – R₂ – R₁; R₂ – R₃ – R₄ – E₂; R₄ – R₅ – R₆ – E₃ – E₂,

выбрав направление обхода контуров по часовой стрелке.

;

;

.

Итак, мы получили пять уравнений с пятью неизвестными. Решая их любым известным в математике способом, находим токи в ветвях.

Достоинством этого метода является то, что уравнения составляются непосредственно для искомых величин, в результате не требуется определения промежуточных или фиктивных параметров.

К недостаткам следует отнести то, что при расчете этим методом составляется большое количество уравнений, каждое из которых включает в себя только часть токов. В результате получается система с большим количеством нулевых членов, что затрудняет применение матричных методов.

 

Метод контурных токов

Метод контурных токов позволяет уменьшить число уравнений, составляемых по законам Кирхгофа до числа независимых контуров.

Метод контурных токов основан на том свойстве, что ток в каждой ветви может быть представлен в виде алгебраической суммы независимых контурных токов, протекающих в этой ветви.

Рассмотрим электрическую цепь (рис. 3.4), аналогичную той, что рассматривали в предыдущем случае.

Определим число независимых контуров:

К = т – (п – 1) = 5 – (3 – 1) = 3.

Считаем, что в каждом контуре протекает свой, независимый от других контуров, ток. Направление контурных токов обозначаем круговой стрелкой. Выберем направление контурных токов по часовой стрелке и запишем для каждого контура уравнение по второму закону Кирхгофа с использованием контурных токов, считая положительным направлением для каждого контура направление контурного тока:

.

 

Эту систему уравнений можно привести к следующему виду:

.

При расчете цепей методом контурных токов удобнее пользоваться готовой математической моделью, которая представляет собой систему линейных алгебраических уравнений:

Здесь R₁₁, R₂₂, R₃₃ – собственные сопротивления контуров, равные сумме всех сопротивлений, входящих в контур:

;

;

.

Все остальные сопротивления являются взаимными:

R₁₂ = R₂₁ = R₂ – взаимное сопротивление между первым и вторым контурами;

R₂₃ = R₃₂ = R₄ – взаимное сопротивление между вторым и третьим контурами;

R₁₃ = R₃₁ = 0; – взаимное сопротивление между первым и третьим контурами.

Из схемы можно видеть, что первый и третий контуры не имеют общей ветви, а граничат только через узел, поэтому их взаимное сопротивление равно нулю

Е₁₁ = Е₁; Е₂₂ = –Е₂; Е₃₃ = Е₃ +Е₂ – контурные ЭДС.

Если действие э.д.с. совпадает с направлением контурного тока, то ЭДС имеет знак «плюс», если не совпадает – «минус».

При использовании математической модели следует направления всех контурных токов выбирать одинаковыми. В этом случае члены, расположенные по главной диагонали и содержащие собственные сопротивления контуров, будут положительны, а члены, содержащие взаимные сопротивления, – отрицательны.

Если число уравнений больше двух, то систему удобнее решать матричным методом.

Составим главный определитель системы

.

Частные определители получим, заменяя соответствующие столбцы матриц столбцами свободных членов

.

Контурные токи находим из выражений:

; ; .

Для того чтобы определить истинные токи в ветвях, следут пользоваться следующими правилами. Если в ветви протекает только один контурный ток, то истинный ток равен этому контурному току, причем, если условно положительное направление истинного тока совпадает с направлением контурного тока, то ставим знак контурного тока, если не совпадает – противоположный. Если в ветви протекает два контурных тока, то за положительный принимаем тот, направление которого совпадает с направлением истинного тока. Для заданной схемы истинные токи определятся выражениями:

; ; ; ; .

Достоинством этого метода по отношению к предыдущему является то, что количество уравнений, составляемых по законам Кирхгофа, уменьшается.

К недостаткам можно отнести введение в расчеты фиктивных величин – контурных токов, через посредство которых находят истинные токи.

 

Метод узловых потенциалов

Метод узловых потенциалов заключается в том, что сначала находят потенциалы всех узлов схемы, а потом по известным потенциалам, используя обобщенный закон Ома, определяют токи в ветвях.

Количество уравнений, составляемых по методу узловых потенциалов, определяется числом независимых узлов N = n – 1.

Заземляем один из узлов. Как правило, заземляется узел, в котором сходится больше ветвей. Заземлим узел 3 (рис. 3.4), то есть полагаем .

Выразим токи в ветвях через потенциалы.

; ;

; ; .

Здесь

; ; ; ; – проводимости ветвей.

Для узлов 1 и 2 составим уравнения по первому закону Кирхгофа:

;

;

Подставим в эти уравнения выражения для токов, раскрывая скобки:

;

.

Преобразуем выражения:

;

.

Эту систему уравнений можно записать в общем виде и при расчетах сразу использовать готовую модель:

Здесь и – собственные проводимости узлов, они определяются суммой проводимостей всех ветвей, сходящихся в данном узле;

– взаимные проводимости, то есть проводимости ветвей, расположенных между соответствующими узлами;

; – узловые токи.

Для того чтобы рассчитать узловые токи, из всех ветвей, сходящихся в данном узле, выбираем те, которые содержат источники, умножаем ЭДС каждого источника на проводимость ветви, в которой он находится. Если в одном узле сходятся несколько ветвей с источниками, как, например, в узле 2, то находим их алгебраическую сумму. Если источник направлен к узлу, то узловой ток берем со знаком «плюс», если от узла – «минус».

Решая полученную систему любым способом, находим потенциалы узлов 1 и 2, и, подставляя их в полученные выражения для токов, находим токи.

Достоинство данного метода состоит в том, что он позволяет свести количество уравнений в схеме к минимуму.

Недостаток состоит в следующем. Рассчитывая цепь методом узловых потенциалов, мы работаем с проводимостями ветвей. Проводимость – величина обратная сопротивлению, и при больших значениях сопротивлений проводимости малы. Отсюда точность метода узловых потенциалов ниже, чем у метода контурных токов, поэтому метод узловых потенциалов целесообразно применять тогда, когда число уравнений, составляемых по методу узловых потенциалов, меньше, чем по методу контурных токов, как в нашем случае.

 

Метод двух узлов

Метод двух узлов является частным случаем метода узловых потенциалов. Этот метод применяется в том случае, когда в схеме имеется несколько ветвей, присоединенных к одной паре узлов. В частности, этот метод позволяет определить напряжение, подаваемое на нагрузку, если она питается от нескольких источников, соединенных параллельно.

Рассмотрим схему, в которой три источника работают на одну нагрузку R₄ (рис. 3.5).

Воспользуемся методом узловых потенциалов. Выразим потенциал точки а через потенциал точки b вдоль каждой ветви:

.

Перенесем потенциал в левую часть. Разность потенциалов точек a и b представляет собой напряжение между узлами U_ab:

;

;

;

.

Отсюда выразим токи:

; ;

; .

Запишем первый закон Кирхгофа для узла а:

.

Подставим сюда выражения для токов, раскрывая скобки,

или

.

Отсюда

.

Эта формула позволяет определить напряжение между двумя узлами при наличии нескольких параллельных ветвей с источниками. При этом справедливо правило: если ЭДС направлена в сторону узла а, то она положительна, если от узла – отрицательна.

 

Метод наложения

В основу метода положен принцип наложения: ток в любой ветви разветвленной линейной электрической цепи с несколькими источниками может быть получен как алгебраическая сумма токов, вызываемых в этой ветви каждым источником в отдельности.

Метод расчета токов в электрической цепи, основанный на определении токов в одной и той же ветви при поочередном воздействии всех ЭДС и последующем алгебраическом сложении этих токов называется методом наложения.

При расчете методом наложения электрической цепи с реальными источниками следует учитывать внутренние сопротивления источников ЭДС.

Как правило, метод наложения используется в том случае, если в цепи имеется два источника.

Рассмотрим применение этого метода на примере схемы (рис. 3.6).

 

 

Задача состоит в том, чтобы найти токи в ветвях I₁, I₂, I₃ методом наложения.

Задаемся условно положительными направлениями токов в ветвях.

1. Исключаем источник Е₂, тогда в цепи будет действовать только один источник Е₁, и схема примет вид (рис. 3.7)

Так как в цепи действует только один источник, мы можем задать истинные для данной схемы направления частичных токов I₁^’, I₂^’, I₃^’.

Для расчета этих токов используем любой метод расчета простых цепей, например, метод эквивалентных преобразований.

Находим эквивалентное сопротивление цепи

.

Зная величины Е₁ и R_эк, находим ток источника

.

Для определения токов I₂^’ и I₃^’ найдем напряжение между точками a и b.

.

Используя найденное напряжение, по закону Ома находим токи I₂^’ и I₃^’

; .

2. Исключаем источник Е₁, тогда в цепи будет действовать только один источник Е₂ и схема примет вид (рис. 3.8).

Зададимся истинными направлениями частичных токов в ветвях для данной схемы I₁^’’, I₂^’’, I₃^’’ и выполним расчеты, аналогичные предыдущим.

Находим эквивалентное сопротивление цепи

.

Зная величины Е₂ и R”_эк, находим ток источника

.

Для определения токов I₁^” и I₃^” найдем напряжение между точками a и b

.

Находим токи I₁^” и I₃^”:

; .

3. Находим истинные токи в ветвях как алгебраическую сумму токов, создаваемых каждым источником:

; ; .

При этом частичный ток берется положительным, если его направление совпадает с выбранным условно положительным направлением истинного тока, и отрицательным, если его направление противоположно.

 

А что такое контурный ток? В чем смысл метода контурных токов?

Это чистой воды второй закон Кирхгоффа для цепи из нескольких контуров (ну и плюс закон Ома, очевидно), он разобран подробно в каждом учебнике и сети.

Обычная система уравнений (матрица)…

Контурный ток = току, протекающему в данном контуре. В соседнем контуре протекает другой контурный ток. В общем проводе протекает алгебраическая сумма обоих контурных токов.

Контурный ток, если он течет по элементу, входящему в другой контур (а) — это удобная для расчетов абстракция, если он течет по элементу, не входящему в другой контур (а) — это истинный ток. Метод контурных токов позволяет очень просто записать систему уравнений для контурных токов, которая так же просто может быть решена матричным методом. Истинные токи находятся элементарно. Метод контурных токов отличается компактностью и на его основе созданы простые алгоритмы и программы для расчета сложных электрических схем.

Это вроде-бы условная величина, принимаемая для расчётов в данном методе. Модифицированный закон Кирхгофа

9. Метод контурных токов

     Метод непосредственного применения законов Кирхгофа громоздок. Имеется возможность уменьшить количество совместно решаемых уравнений системы. Число уравнений, составленных по методу контурных токов, равно количеству уравнений, составляемых по второму закону Кирхгофа.         Метод контурных токов заключается в том, что вместо токов в ветвях определяются, на основании второго закона Кирхгофа, так называемые контурные токи, замыкающиеся в контурах.         На рис. 4.2 в качестве примера изображена двухконтурная схема, в которой I₁₁ и I₂₂ — контурные токи.

      Токи в сопротивлениях R₁ и R₂ равны соответствующим контурным токам. Ток в сопротивлении R₃, являющийся общим для обоих контуров, равен разности контурных токов I₁₁ и I₂₂, так как эти токи направлены в ветви с R₃ встречно.

В нашем случае эти токи направлены по часовой стрелке. Направление обхода контура совпадает с направлением контурных токов. Уравнения для этих контуров имеют следующий вид:

       Перегруппируем слагаемые в уравнениях

(4.4)

     Суммарное сопротивление данного контура называется собственным сопротивлением контура.       Собственные сопротивления контуров схемы

,     

     Сопротивление R₃, принадлежащее одновременно двум контурам, называется общим сопротивлением этих контуров.

,

      E₁₁ = E₁ и E₂₂ = E₂ — контурные ЭДС.         В общем виде уравнения (4.4) и (4.5) записываются следующим образом: ,.

       Собственные сопротивления всегда имеют знак «плюс».         Ветви схемы, по которым протекает один контурный ток, называются внешними, а ветви, по которым протекают несколько контурных токов, называются общими. Ток во внешней ветви совпадает по величине и по направлению c контурным. Ток в общей ветви равен алгебраической сумме контурных токов, протекающих в этой ветви. 

.

10. Метод узловых потенциалов

    Метод узловых потенциалов позволяет составить систему уравнений, по которой можно определить потенциалы всех узлов схемы. По известным разностям узловых потенциалов можно определить токи во всех ветвях. В схеме на рисунке 4.3 имеется четыре узла. Потенциал любой точки схемы можно принять равным нулю. Тогда у нас останутся неизвестными три потенциала. Узел, величину потенциала которого выбирают произвольно, называют базисным. Укажем в схеме произвольно направления токов. Примем для схемы φ₄ = 0.    Запишем уравнение по первому закону Кирхгофа для узла 1.

(4.6)

     В соответствии с законами Ома для активной и пассивной ветви

,     где — проводимость первой ветви.

,     где — проводимость второй ветви.

     Подставим выражения токов в уравнение (4.6).

(4.7)

     где g₁₁ = g₁ + g₂ — собственная проводимость узла 1.

     Собственной проводимостью узла называется сумма проводимостей ветвей, сходящихся в данном узле.       g₁₂ = g₂ — общая проводимость между узлами 1 и 2.       Общей проводимостью называют проводимость ветви, соединяющей узлы 1 и 2.      — сумма токов источников, находящихся в ветвях, сходящихся в узле 1.      Если ток источника направлен к узлу, величина его записывается в правую часть уравнения со знаком «плюс», если от узла — со знаком «минус».        По аналогии запишем для узла 2:

       для узла 3:

        Решив совместно уравнения (4.7), (4.8), (4.9), определим неизвестные потенциалы φ₁, φ₂, φ₃, а затем по закону Ома для активной или пассивной ветви найдем токи.         Если число узлов схемы — n, количество уравнений по методу узловых потенциалов —   (n — 1).

4.2. Метод контурных токов

Метод непосредственного применения законов Кирхгофа громоздок. Имеется возможность уменьшить количество совместно решаемых уравнений системы. Число уравнений, составленных по методу контурных токов, равно количеству уравнений, составляемых по второму закону Кирхгофа.

Метод контурных токов заключается в том, что вместо токов в ветвях определяются, на основании второго закона Кирхгофа, так называемые контурные токи, замыкающиеся в контурах.

На рис. 4.2 в качестве примера изображена двухконтурная схема, в которой I₁₁и I₂₂— контурные токи.

Рис. 4.2

Токи в сопротивлениях R₁и R₂равны соответствующим контурным токам. Ток в сопротивлении R₃, являющийся общим для обоих контуров, равен разности контурных токов I₁₁и I₂₂, так как эти токи направлены в ветви с R₃ встречно.

Порядок расчета

Выбираются независимые контуры, и задаются произвольные направления контурных токов.

В нашем случае эти токи направлены по часовой стрелке. Направление обхода контура совпадает с направлением контурных токов. Уравнения для этих контуров имеют следующий вид:

Перегруппируем слагаемые в уравнениях

     (4.4)

     (4.5)

Суммарное сопротивление данного контура называется собственным сопротивлением контура.

Собственные сопротивления контуров схемы

,     .

Сопротивление R₃, принадлежащее одновременно двум контурам, называется общим сопротивлением этих контуров.

,

где R₁₂— общее сопротивление между первым и вторым контурами;

R₂₁— общее сопротивление между вторым и первым контурами.

E₁₁= E₁и E₂₂= E₂— контурные ЭДС.

В общем виде уравнения (4.4) и (4.5) записываются следующим образом:

,

.

Собственные сопротивления всегда имеют знак «плюс».

Общее сопротивление имеет знак «минус», если в данном сопротивлении контурные токи направлены встречно друг другу, и знак «плюс», если контурные токи в общем сопротивлении совпадают по направлению.

Решая уравнения (4.4) и (4.5) совместно, определим контурные токи I₁₁и I₂₂, затем от контурных токов переходим к токам в ветвях.

Ветви схемы, по которым протекает один контурный ток, называются внешними, а ветви, по которым протекают несколько контурных токов, называются общими. Ток во внешней ветви совпадает по величине и по направлению c контурным. Ток в общей ветви равен алгебраической сумме контурных токов, протекающих в этой ветви.

В схеме на рис. 4.2

.

Рекомендации

1. Контуры выбирают произвольно, но целесообразно выбрать контуры таким образом, чтобы их внутренняя область не пересекалась ни с одной ветвью, принадлежащей другим контурам.

2. Контурные токи желательно направлять одинаково (по часовой стрелке или против).

3. Если нужно определить ток в одной ветви сложной схемы, необходимо сделать его контурным.

4. Если в схеме имеется ветвь с известным контурным током, этот ток следует сделать контурным, благодаря чему количество уравнений становится на единицу меньше.

4.3. Метод узловых потенциалов

Метод узловых потенциалов позволяет составить систему уравнений, по которой можно определить потенциалы всех узлов схемы. По известным разностям узловых потенциалов можно определить токи во всех ветвях. В схеме на рисунке 4.3 имеется четыре узла. Потенциал любой точки схемы можно принять равным нулю. Тогда у нас останутся неизвестными три потенциала. Узел, величину потенциала которого выбирают произвольно, называют базисным. Укажем в схеме произвольно направления токов. Примем для схемы φ₄= 0.

Запишем уравнение по первому закону Кирхгофа для узла 1.

Рис. 4.3

(4.6)

В соответствии с законами Ома для активной и пассивной ветви

,

где — проводимость первой ветви.

,

где — проводимость второй ветви.

Подставим выражения токов в уравнение (4.6).

(4.7)

где g₁₁= g₁+ g₂— собственная проводимость узла 1.

Собственной проводимостью узла называется сумма проводимостей ветвей, сходящихся в данном узле.

g₁₂= g₂— общая проводимость между узлами 1 и 2.

Общей проводимостью называют проводимость ветви, соединяющей узлы 1 и 2.

— сумма токов источников, находящихся в ветвях, сходящихся в узле 1.

Если ток источника направлен к узлу, величина его записывается в правую часть уравнения со знаком «плюс», если от узла — со знаком «минус».

По аналогии запишем для узла 2:

    (4.8)

для узла 3:

    (4.9)

Решив совместно уравнения (4.7), (4.8), (4.9), определим неизвестные потенциалы φ₁, φ₂, φ₃, а затем по закону Ома для активной или пассивной ветви найдем токи.

Если число узлов схемы — n, количество уравнений по методу узловых потенциалов —   (n — 1).

Замечание.

Если в какой-либо ветви содержится идеальный источник ЭДС, необходимо один из двух узлов, между которыми включена эта ветвь, выбрать в качестве базисного, тогда потенциал другого узла окажется известным и равным величине ЭДС. Количество составляемых узловых уравнений становится на одно меньше.

14. Применение метода контурных токов и метода узловых напряжений при наличии в цепи непреобразуемых источников.

Для решения задачи по МКТ необходимо, чтобы в цепи действовали только источники напряжения. Если в исходной цепи были источники тока, то перед началом анализа их нужно преобразовать в эквивалентные источники напряжения. Но могут быть и непреобразуемые источники тока.

Нужно так выбирать контурные токи, чтобы через непреобразуемый источник проходил только один контурный ток, тогда он будет ему и равен

а) i₁^r=i₀

б)

Для определения правых частей уравнений по МУН в цепи должны действовать только ИТ. Если имеются ИН, то перед началом надо преобразовать их в эквивалентные источники тока.

а)

Если такой источник один, то нужно выбирать не любой узел в качестве базисного, а один из узлов, подключённых к непреобразуемому ИН.

U₁^у=U₀

б)Если источников несколько, то тяжёло решить эту проблему и нужно преобразовывать следующим образом:

15. Метод наложения. Принцип взаимности (обратимости).

Для произвольной цепи определим например первый контурный ток по методу контурных токов.

Метод наложения:

I₁^к=aU₀₁+bU₀₂+cU₀₃+…=I₁^’+I₂^’’+I₃^’’’+…

U₁^к-сумма источников напряжения

U₂^к-сумма ИН

I₁^’-ток, вызв. действием только U_{01, а} U₀₂= U₀₃=…=0

I₂^’’-ток, вызв. действием только U_{02, а} U₀₁= U₀₃=…=0

G_2-1= I₁^к/ U₂^к | U₁^к =U₃^к=…= U_n^к=0 –передаточная проводимость между 1м и 2м контурами при наличии источника только во 2м контуре.

G_1-1= I₁^к/ U₁^к | U₂^к =U₃^к=…= U_n^к=0 – Входная проводимость короткого замыкания.

Теорема взаимности.

Пусть имеется один единственный источник, находящийся во втором контуре, а ток будем определять первого контура т.е. U₂^к = U₀, а U₁^к =U₃^к=…= U_n^к=0

Пусть тот же самый источник U₀ будет в первом контуре, а ток будем определять второго контура.

Из математики известно, что для определителей симметричных относительно главной диагонали минор D₂₁=D₁₂, значит G_2-1=G_1-2 – теорема взаимности или обратимости.

Если единственный источник, находящийся в первом контуре вызывает некоторый ток во втором, то, будучи перенесенным, во второй контур, где находился раньше, вызовет точно такой же ток i₁=i₂.

13. Метод эквивалентногоисточника напряжения (теорема Теневена) и эквивалентного источника тока (теорема Нортона).

Этот метод удобно применять тогда, когда интересуются током только в одной ветви. Суть метода заключается в следующем: действие всей цепи на исследуемую ветвь заменяют действием эквивалентного источника напряжения или источника тока.

Различают два метода:

1)Метод эквивалентного ИН (теорема Теневена)

2)Метод эквивалентного ИТ (теорема Нортона)

МЭИН

Док-во: ничего не изменится, если в k-ую ветвь включить два ИН одинаковой величины, но противоположной полярности. U^’=U^’’

i_k= i_k1+ i_k2, где i_k1-ток вызванный всеми источниками цепи и источником U^’’, а i_k2-ток вызванный только источником U^’.

Выберем такое U^’’, чтобы i_k1=0_, но если ток равен нулю, то можно разомкнутьветвь, в которой ток не течёт. При отсутствии токаi_k1 U_аб есть ничто иное, как напряжение холостого хода. U_аб=U_хх.=>U^’’= U^’= U_хх.

Таким образом, ток любой ветви может быть найден, как , где

U_хх-напряжение на разомкнутых зажимах исследуемой ветви. R₀-сопротивление всей цепи при закороченных и разомкнутых ИТ относительно зажимов исследуемой ветви.

МЭИТ – в этом методе действие всей цепи по отношению к k-ой ветви заменяем ИТ с проводимостью по отношению к ветви. G_k=1/R_k; U_k=U_аб=i_o/G₀+G_k; i_k=U_k/R_k; i₀=?, G₀=?

Можно провести аналогичное предыдущему доказательство этой теоремы. Теорема Теневена доказана.

i₀=U_хх/R₀; G₀=1/R₀

i₀=i_кз=U_хх/R₀

Таким образом ток каждой i-ой ветви можно найти U_k=i_кз/G₀+G_k, i_кз-ток через короткозамкнутые зажимы исследуемой ветви.

Билет 17

Приобразование звезды в треугольник и обратно

Полезно упрощать цепь перед решением

Исчезает (0) узле. Для звезды сумма токов в узле 0

Выражая тотже ток из треугольника

Тогда получаем

Преобразование в треугольник – удаление из цепи одного узла. Число уравнений МИН на 1 меньше, мостовая цепь -> лесничная

Соединение звездой и треугольником дуальны->результат можно получить на дуальной основе. Число уравнений МКТ на 1 меньше, мост в лестницу

Билет 18

Принцип непрерывности заряда во времени

Если через С-элемент в какой то момент времени возникает конечный по величины ток то заряд в этот момент времени должен изменяться непрерывно (не скачком).

Билет 19

Принцип непрерывности потокосцепления во времяни

Если к L-элементу в какой то момент времяни например при t=0 приложено конечное по величене напряжение то потокосцепление в этот момент времени должно изменяться непрерывно (не скачком)

Билет 20

ДУRLC цепи и общие свойства их решения

Определим i(t)

Для параллельного соединения элементов

В общем случае требуется решить уравнения n-порядка с n начальными условиями – задача Каши

Классический метод

Решение уравнения = общее решение однородного уравнения + частное решение не однородного

Общее решение = свободная составляющая частное решение = вынужденная составляющая

Решение однородного ду в общем случае для цепиn порядка есть где pk корень характеристического уравнения Ак – постоянная интегрирования, причем предполагается что нету кратных корней

Процессы в цепи к бесконечности затухают

Либо отрицательной должна быть вещественная часть если корни комплексные

Корни характеристич. уравнений часто называют частными собственных колебания

Вынужденная составляющая ищется в форме правой части. Если воздействие const или периодич то в цепи устанавливается постоянный или периодический. При постоянном или периодическом воздействии при любом изменении цепи (например подключении ИТ или ИН обрыве итд ) происходит переход из одного уст состояния в другое – это и есть основная задача расчета переходного процесса (бывают аварийные и нормальные)

Билет 21

Переходный процесс при включенииRL цепи

Начальные условия

Решение

Характеристическое уравнение

Определение вынужденной составляющей

a)из ду в форме правой части

б) из цепи в установившемся режиме. Заменяем индуктивность проводником, тк устанавливается постоянный

Коэф. А определяется из начальных условий

Билет 22

Переходный процесс при включенииRC цепи

Решение

RCp+1=0

RCp+1=0

Определение вынужденной составляющей

Вынужденная составляющая будет константой так как правая часть константа

8) Метод контурных токов

Этот метод позволяет уменьшить ко­личество уравнений системы, составляемых по законам Кирхгофа, до

где n_в– число ветвей цепи;

n_y– число узлов цепи;

n_m– число источников тока цепи.

Он основан на том, что ток в любой ветви цепи можно предста­вить в виде алгебраической суммы контурных токов, протекающих по этой ветви. При использовании метода перед расчётом выбирают на­правления и путь протекания контурных токов — по любой ветви дол­жен протекать хотя бы один выбранный контурный ток. Общее число неизвестных контурных токов определяется величиной k (1). Причём, из пути их протекания следует исключить ветви с источниками тока.

Пример:

Исходные данные:

R₁=24 Ом;R₂=70 Ом;R₃=44 Ом;R₄=12 Ом;R₅=20 Ом; R₆=30 Ом; Е₂=40 В; Е₃=19,6 В;J_K2=0 А;J_K3=0,1 А.

При расчёте этой схемы методом контурных токов возможны два пути:

1) Преобразование исходной схемы не производится.

2) Предусматривает преобразование реальных источников тока в эквивалентную э.д.с.

Для расчёта данной схемы выбираем второй путь и при этом учтём, что

J_K2=0 А. ПреобразуемJ_K3 вE₃^*. Пользуясь законом Ома, получаемE₃^*=J_K3R₃=4,4B.

Схема, полученная после преобразования представлена на рисунке 2.

Рисунок 2 – Преобразованная схема

E₃^’=E₃+E₃^*=19,6+4,4=24(B)

После упрощения исходной схемы можно непосредственно перейти к реализации метода контурных токов. Для этого нужно определить количество контурных токов. Сделать это можно по формуле:

где n_в– число ветвей цепи;

n_y– число узлов цепи;

n_m– число источников тока цепи.

В рассматриваемой схеме n_в=6,n_y=4; n_m=0.

Итак, зная количество контурных токов, нужно выбрать их направления.

Схема с направлениями контурных токов представлена на рисунке 3.

Рисунок 3 – Преобразованная схема с направлениями контурных токов

Составим систему уравнений по второму закону Кирхгофа для определения неизвестных контурных токов (порядок системы равен k):

Составим матрицу:

Отсюда выразим матрицу контурных токов:

Зная значения контурных токов, можно найти реальные токи. Они будут равны комбинации контурных токов.

Используя контурные токи, мы получили токи конкретные.

10) Метод узловых напряжений (потенциалов)

11) Представление схем в виде графов. Топологические понятия

Электрическая цепь характеризуется совокупностью элементов, из которых она состоит, и способом их соединения. Соединение элементов электрической цепи наглядно отображается ее схемой. Рассмотрим для примера две электрические схемы (рис. 1, 2), введя понятие ветви и узла.

Ветвьюназывается участок цепи, обтекаемый одним и тем же током.

Узел– место соединения трех и более ветвей.

Представленные схемы различны и по форме, и по назначению, но каждая из указанных цепей содержит по 6 ветвей и 4 узла, одинаково соединенных. Таким образом, в смысле геометрии (топологии) соединений ветвей данные схемы идентичны.

Топологические (геометрические) свойства электрической цепи не зависят от типа и свойств элементов, из которых состоит ветвь. Поэтому целесообразно каждую ветвь схемы электрической цепи изобразить отрезком линии. Если каждую ветвь схем на рис. 1 и 2 заменить отрезком линии, получается геометрическая фигура, показанная на рис. 3.

Условное изображение схемы, в котором каждая ветвь заменяется отрезком линии, называется графом электрической цепи. При этом следует помнить, что ветви могут состоять из каких-либо элементов, в свою очередь соединенных различным образом.

Отрезок линии, соответствующий ветви схемы, называется ветвью графа. Граничные точки ветви графа называютузлами графа. Ветвям графа может быть дана определенная ориентация, указанная стрелкой. Граф, у которого все ветви ориентированы, называетсяориентированным.

Подграфомграфа называется часть графа, т.е. это может быть одна ветвь или один изолированный узел графа, а также любое множество ветвей и узлов, содержащихся в графе.

В теории электрических цепей важное значение имеют следующие подграфы:

1. Путь– это упорядоченная последовательность ветвей, в которой каждые две соседние ветви имеют общий узел, причем любая ветвь и любой узел встречаются на этом пути только один раз. Например, в схеме на рис. 3 ветви2-6-5; 4-5; 3-6-4; 1образуют пути между одной и той же парой узлов1и3. Таким образом, путь – это совокупность ветвей, проходимых непрерывно.

2. Контур– замкнутый путь, в котором один из узлов является начальным и конечным узлом пути. Например, для графа по рис. 3 можно определить контуры, образованные ветвями2-4-6; 3-5-6; 2-3-5-4. Если между любой парой узлов графа существует связь, то граф называют связным.

3. Дерево– это связный подграф, содержащий все узлы графа, но ни одного контура. Примерами деревьев для графа на рис. 3 могут служить фигуры на рис. 4.

Рис.4

4. Ветви связи (дополнения дерева)– это ветви графа, дополняющие дерево до исходного графа.

Если граф содержит mузлов иnветвей, то число ветвей любого дерева, а числа ветвей связи графа.

5. Сечение графа– множество ветвей, удаление которых делит граф на два изолированных подграфа, один из которых, в частности, может быть отдельным узлом.

Сечение можно наглядно изобразить в виде следа некоторой замкнутой поверхности, рассекающей соответствующие ветви. Примерами таких поверхностей являются для нашего графа на рис. 3 S₁иS₂. При этом получаем соответственно сечения, образованные ветвями6-4-5 и 6-2-1-5.

С понятием дерева связаны понятия главных контуров и сечений:

• главный контур– контур, состоящий из ветвей дерева и только одной ветви связи;

• главное сечение – сечение, состоящее из ветвей связи и только одной ветви дерева.