Реферат на тему: Закон Ампера

🔊 Слушать текст

Закон Ампера показывает, с какой силой действует магнитное поле на помещенный в него проводник. Эту силу также называют силой Ампера.
Формулировка закона: сила, действующая на проводник с током, помещенный в однородное магнитное поле, пропорциональна длине проводника, вектору магнитной индукции, силе тока и синусу угла между вектором магнитной индукции и проводником.

Если размер проводника произволен, а поле неоднородно, то формула выглядит следующим образом:

Направление силы Ампера определяется по правилу левой руки.
Правило левой руки:если расположить левую руку так, чтобы перпендикулярная составляющая вектора магнитной индукции входила в ладонь, а четыре пальца были вытянуты по направлению тока в проводнике, то отставленный на 90

°большой палец, укажет направление силы Ампера.

МП движущего заряда. Действие МП на движущийся заряд. Сила Ампера, Лоренца.

Любой проводник с током создает в окружающем пространстве магнитное поле. При этом электрический же ток является упорядоченным движением электрических зарядов. Значит можно считать, что любой движущийся в вакууме или среде заряд порождает вокруг себя магнитное поле. В результате обобщения многочисленных опытных данных был установлен закон, который определяет поле В точечного заряда Q, движущегося с постоянной нерелятивистской скоростью v. Этот закон задается формулой

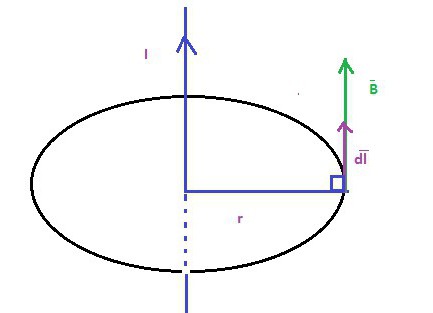
(1)
где r — радиус-вектор, который проведен от заряда Q к точке наблюдения М (рис. 1). Согласно (1), вектор В направлен перпендикулярно плоскости, в которой находятся векторы v и r: его направление совпадает с направлением поступательного движения правого винта при его вращении от v к r.

Рис.1
Модуль вектора магнитной индукции (1) находится по формуле

(2)
где α — угол между векторами v и r. Сопоставляя закон Био-Савара-Лапласа и (1), мы видим, что движущийся заряд по своим магнитным свойствам эквивалентен элементу тока: Idl = Qv
Действие МП на движущийся заряд.
Из опыта известно, что магнитное поле оказывает действие не только на проводники с током, но и на отдельные заряды, которые движутся в магнитном поле. Сила, которая действует на электрический заряд Q, движущийся в магнитном поле со скоростью v, называется силой Лоренца и задается выражением: F = Q где В — индукция магнитного поля, в котором заряд движется.
Чтобы определить направление силы Лоренца используем правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора v (для Q>0 направления I и v совпадают, для Q На рис. 1 продемонстрирована взаимная ориентация векторов v, В (поле имеет направление на нас, на рисунке показано точками) и F для положительного заряда. Если заряд отрицательный, то сила действует в противоположном направлении.

Модуль силы Лоренца, как уже известно, равенF = QvB sin a; где α — угол между v и В.
МП не оказывает действия на покоящийся электрический заряд. Этим магнитное поле существенно отличается от электрического. Магнитное поле действует только на движущиеся в нем заряды.

Зная действие силы Лоренца на заряд можно найти модуль и направление вектора В, и формула для силы Лоренца может быть применена для нахождения вектора магнитной индукции В.
Поскольку сила Лоренца всегда перпендикулярна скорости движения заряженной частицы, то данная сила может менять только направление этой скорости, не изменяя при этом ее модуля. Значит, сила Лоренца работы не совершает.
В случае, если на движущийся электрический заряд вместе с магнитным полем с индукцией В действует еще и электрическое поле с напряженностью Е, то суммарная результирующая сила F, которая приложена приложенная к заряду, равна векторной сумме сил — силы, действующей со стороны электрического поля, и силы Лоренца: F = QE + Q[v,B]
Сила Ампера, Лоренца.
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера.
Сила действия однородного маг­нитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником:
F = B.I.l. sin α — закон Ампера.
Сила, действующая на заряженную движущуюся частицу в магнитном поле, называется силой Лоренца:

Явление электромагнитной индукции. Закон Фарадея. ЭДС индукции в движущихся проводниках. Самоиндукция.

Фарадейпредположил, что если вокруг проводника с током существует магнитное поле, то естественно ожидать, что должно происходить и обратное явление – возникновение электрического тока под действием магнитного поля. И вот в 1831 г. Фарадей публикует статью, где сообщает об открытии нового явления – явления электромагнитной индукции.
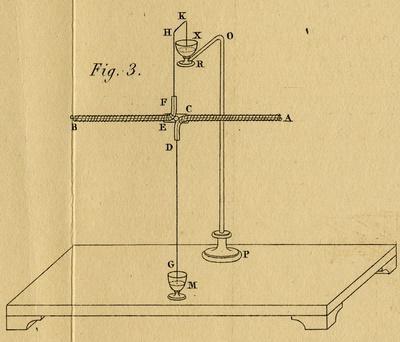
Опыты Фарадея были чрезвычайно просты. Он присоединял гальванометр G к концам катушки L и приближал к ней магнит. Стрелка гальванометра отклонялась, фиксируя появление тока в цепи. Ток протекал, пока магнит двигался. При отдалении магнита от катушки гальванометр отмечал появление тока противоположного направления. Аналогичный результат отмечался, если магнит заменяли катушкой с током или замкнутым контуром с током.

Движущиеся магнит или проводник с током создают через катушку L переменное магнитное поле. В случае их неподвижности создаваемое ими поле постоянно. Если вблизи замкнутого контура поместить проводник с переменным током, то в замкнутом контуре также возникнет ток. На основе анализа опытных данных Фарадей установил, что ток в проводящих контурах появляется при изменении магнитного потока через площадь, ограниченную этим контуром.
Этот ток был назван индукционным.Открытие Фарадея было названо явлением электромагнитной индукции и легло в дальнейшем в основу работы электрических двигателей, генераторов, трансформаторов и подобных им приборов.
Итак, если магнитный поток через поверхность, ограниченную некоторым контуром, изменяется, то в контуре возникает электрический ток. Известно, что электрический ток в проводнике может возникнуть только под действием сторонних сил, т.е. при наличии э.д.с.. В случае индукционного тока э.д.с., соответствующая сторонним силам, называется электродвижущей силой электромагнитной индукции εi.
Э.д.с. электромагнитной индукции в контуре пропорциональна скорости изменения магнитного потока Фm сквозь поверхность, ограниченную этим контуром:

где к – коэффициент пропорциональности. Данная э.д.с. не зависит от того, чем вызвано изменение магнитного потока – либо перемещением контура в постоянном магнитном поле, либо изменением самого поля.
Итак, направление индукционного тока определяется правилом Ленца: При всяком изменении магнитного потока сквозь поверхность, ограниченную замкнутым проводящим контуром, в последнем возникает индукционный ток такого направления, что его магнитное поле противодействует изменению магнитного потока.
Обобщением закона Фарадея и правила Ленца является закон Фарадея – Ленца: Электродвижущая сила электромагнитной индукции в замкнутом проводящем контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную контуром:

Это выражение представляет собой основной закон электромагнитной индукции.
При скорости изменения магнитного потока 1Вб/с в контуре индуцируется э.д.с. в 1 В.
Пусть контур, в котором индуцируется э.д.с., состоит не из одного, а из N витков, например, представляет собой соленоид. Соленоид – это цилиндрическая катушка с током, состоящая из большого числа витков. Так как витки в соленоиде соединяются последовательно, εi в данном случае будет равна сумме э.д.с., индуцируемых в каждом из витков по отдельности

:

Величину Ψ = ΣΦm называют потокосцеплением или полным магнитным потоком. Если поток, пронизывающий каждый из витков, одинаков (т.е. Ψ = NΦm), то в этом случае

Немецкий физик Г. Гельмгольц доказал, что закон Фарадея-Ленца является следствием закона сохранения энергии. Пусть замкнутый проводящий контур находится в неоднородном магнитном поле. Если в контуре течет ток I, то под действием сил Ампера незакрепленный контур придет в движение. Элементарная работа dA, совершаемая при перемещении контура за время dt, будет составлять

dA = IdФm,
где dФm – изменение магнитного потока сквозь площадь контура за время dt. Работа тока за время dt по преодолению электрического сопротивления R цепи равна I2Rdt. Полная работа источника тока за это время равна εIdt. По закону сохранения энергии работа источника тока затрачивается на две названные работы, т.е.
εIdt = IdФm + I2Rdt.
Разделив обе части равенства на Idt, получим

Следовательно, при изменении магнитного потока, сцепленного с контуром, в последнем возникает электродвижущая сила индукции

Электромагнитные колебания. Колебательной контур.

Электромагнитные колебания — это колебания таких величин, индуктивность, как сопротивление, ЭДС, заряд, сила тока.
Колебательный контур — это электрическая цепь, которая состоит из последовательно соединенных конденсатора, катушки и резистора.Изменение электрического заряда на обкладке кон- денсатора с течением времени описывается дифференциальным уравнением:

Электромагнитные волны и их свойства.

В колебательном контуре происходит процесс перехода электрической энергии конденсатора в энергию магнитного поля катушки и наоборот. Если в определенные моменты времени компенсировать потери энергии в контуре на сопротивление за счет внешнего источника, то получим незатухающие электрические колебания, которые через антенну могут быть излучены в окружающее пространство.
Процесс распространения электромагнитных колебаний, периодических изменений напряженностей электрического и магнитных полей, в окружающем пространстве называется электромагнитной волной.
Электромагнитные волны охватывают большой спектр длин волн от 105 до 10 м и по частотам от 104 до 1024 Гц. По названию электромагнитные волны разделяются на радиоволны, инфракрасное, видимое и ультрафиолетовое излучения, рентгеновские лучи и -излучение. В зависимости от длины волны или частоты свойства электромагнитных волн меняются, что является убедительным доказательством диалектико-материалистического закона перехода количества в новое качество.
Электромагнитное поле материальное и обладает энергией, количеством движения, массой, перемещается в пространстве: в вакууме со скоростью С, а в среде со скоростью: V= , где = 8,85 ;
Объемная плотность энергии электромагнитного поля . Практическое исполь­зование электромагнитных явлений весьма широкое. Это – системы и средства связи, радиовещания, телевидения, электронно-вычислительная техника, системы управления различного назна­чения, измерительные и медицинские приборы, бытовая электро- и радиоаппаратура и другие, т.е. то, без чего невозможно представить себе современное общество.
Как действует на здоровье людей мощное электромагнитное излучение, точных научных данных почти нет, есть только неподтвержденные гипотезы и, в общем-то, небезосновательные опасение, что все неестественное действует губительно. Доказано, что ультрафиолетовое, рентгеновское и -излучение большой интенсивности во многих случаях наносят реальный вред всему живому.

Геометрическая оптика. Законы ГО.

Геометрическая (лучевая) оптика использует идеализированное представление о световом луче – бесконечно тонком пучке света, распространяющемся прямолинейно в однородной изотропной среде, а также представления о точечном источнике излучения, равномерно светящем во все стороны. λ – длина световой волны, – характерный размер
предмета, находящегося на пути волны. Геометрическая оптика является предельным случаем волновой оптики и ее принципы выполняются при соблюдении условия:
h/D << 1 т. е. геометрическая оптика, строго говоря, применима лишь к бесконечно коротким волнам.
В основе геометрической оптики лежит так же принцип независимости световых лучей: лучи при перемещении не возмущают друг друга. Поэтому перемещения лучей не мешают каждому из них распространяться независимо друг от друга.
Для многих практических задач оптики можно не учитывать волновые свойства света и считать распространение света прямолинейным. При этом картина сводится к рассмотрению геометрии хода световых лучей.
Основные законы геометрической оптики.
Перечислим основные законы оптики, следующие из опытных данных:
1) Прямолинейное распространение.
2) Закон независимости световых лучей, то есть два луча, пересекаясь, никак не мешают друг другу. Этот закон лучше согласуется с волновой теорией, так как частицы в принципе могли бы сталкиваться друг с другом.
3) Закон отражения. луч падающий, луч отраженный и перпендикуляр к поверхности раздела, восстановленный в точке падения луча, лежат в одной плоскости, называемой плоскостью падения; угол падения равен углу
Отражения.
4) Закон преломления света.
Закон преломления: луч падающий, луч преломленный и перпендикуляр к поверхности раздела, восстановленный из точки падения луча, лежат в одной плоскости – плоскости падения. Отношение синуса угла падения к синусу угла отражения равно отношению скоростей света в обеих средах.
Sin i1/ sin i2 = n2/n1 = n21
где – относительный показатель преломления второй среды относительно первой среды. n21
Если вещество 1 – пустота, вакуум, то n12 → n2 – абсолютный показатель преломления вещества 2. Можно легко показать, что n12 = n2 /n1 , в этом равенстве слева относительный показатель преломления двух веществ (например, 1 – воздух, 2 – стекло), а справа – отношение их абсолютных показателей преломления.
5) Закон обратимости света (его можно вывести из закона 4). Если направить свет в обратном направлении, он пройдёт по тому же пути.
Из закона 4) следует, что если n2 > n1 , то Sin i1 > Sin i2 . Пусть теперь у нас n2 < n1 , то есть свет из стекла, например, выходит в воздух, и мы постепенно увеличиваем угол i1.
Тогда можно понять, что при достижении некоторого значения этого угла (i1)пр окажется, что угол i2 окажется равным π /2 (луч 5). Тогда Sin i2 = 1 и n1 Sin (i1)пр = n2 . Итак Sin
(i1)пр = n2 / n1 .

Дополнительная информация из Википедии по теме: Закон Ампера

Классическая электродинамика

Электричество · Магнетизм

Электростатика Закон Кулона Теорема Гаусса Электрический дипольный момент Электрический заряд Электрическая индукция Электрическое поле Электростатический потенциал

Магнитостатика Закон Био — Савара — Лапласа Закон Ампера Магнитный момент Магнитное поле Магнитный поток Магнитная индукция

Электродинамика Векторный потенциал Диполь Потенциалы Лиенара — Вихерта Сила Лоренца Ток смещения Униполярная индукция Уравнения Максвелла Электрический ток Электродвижущая сила Электромагнитная индукция Электромагнитное излучение Электромагнитное поле

Электрическая цепь Закон Ома Законы Кирхгофа Индуктивность Радиоволновод Резонатор Электрическая ёмкость Электрическая проводимость Электрическое сопротивление Электрический импеданс

Ковариантная формулировка Тензор электромагнитного поля Тензор энергии-импульса 4-потенциал 4-ток

Известные учёные Генри Кавендиш Майкл Фарадей Никола Тесла Андре-Мари Ампер Густав Роберт Кирхгоф Джеймс Клерк Максвелл Оливер Хевисайд Генрих Рудольф Герц Альберт Абрахам Майкельсон Роберт Эндрюс Милликен

См. также: Портал:Физика

Зако́н Ампе́ра  — закон взаимодействия электрических токов. Впервые был установлен Андре Мари Ампером в 1820 для постоянного тока. Из закона Ампера следует, что параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Сила оказывается линейно зависимой как от тока, так и от магнитной индукции B{\displaystyle B} . Выражение для силы dF→{\displaystyle d{\vec {F}}} , с которой магнитное поле действует на элемент объёма dV{\displaystyle dV} проводника с током плотности j→{\displaystyle {\vec {j}}} , находящегося в магнитном поле с индукцией B→{\displaystyle {\vec {B}}} , в Международной системе единиц (СИ) имеет вид:

dF→=j→×B→dV.{\displaystyle d{\vec {F}}={\vec {j}}\times {\vec {B}}dV.}

Если ток течёт по тонкому проводнику, то j→dV=Idl→{\displaystyle {\vec {j}}dV=Id{\vec {l}}} , где dl→{\displaystyle d{\vec {l}}}  — «элемент длины» проводника — вектор, по модулю равный dl{\displaystyle dl} и совпадающий по направлению с током. Тогда предыдущее равенство можно переписать следующим образом:

Направление силы dF→{\displaystyle d{\vec {F}}} определяется по правилу вычисления векторного произведения, которое удобно запомнить при помощи правила левой руки.

Модуль силы Ампера можно найти по формуле:

dF=IBdlsin⁡α,{\displaystyle dF=IBdl\sin \alpha ,}

где α{\displaystyle \alpha }  — угол между вектором магнитной индукции и направлением, вдоль которого течёт ток.

Сила F{\displaystyle F} максимальна, когда проводник с током расположен перпендикулярно линиям магнитной индукции (α=90∘,sin⁡α=1{\displaystyle \alpha =90^{\circ },\sin \alpha =1} ):

F=BLI{\displaystyle F=BLI} , где L{\displaystyle L}  — длина проводника.

Смотри полный текст на Wikipedia

Читайте также:

Навигация по записям

Реферат Закон Ампера

скачать

Реферат на тему:

Зако́н Ампе́ра  — закон взаимодействия постоянных токов. Установлен Андре Мари Ампером в 1820. Из закона Ампера следует, что параллельные проводники с постоянными токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Сила , с которой магнитное поле действует на элемент объёма dV проводника с током плотности , находящегося в магнитном поле с индукцией :

.

Если ток течёт по тонкому проводнику, то , где  — «элемент длины» проводника — вектор, по модулю равный dl и совпадающий по направлению с током. Тогда предыдущее равенство можно переписать следующим образом:

Направление силы определяется по правилу вычисления векторного произведения, которое удобно запомнить при помощи правила левой руки.

Модуль силы Ампера можно найти по формуле:

,

где α — угол между векторами магнитной индукции и тока.

Сила dF максимальна когда элемент проводника с током расположен перпендикулярно линиям магнитной индукции ():

.

Два параллельных проводника

Два бесконечных параллельных проводника в вакууме

Наиболее известным примером, иллюстрирующим силу Ампера, является следующая задача. В вакууме на расстоянии r друг от друга расположены два бесконечных параллельных проводника, в которых в одном направлении текут токи I₁ и I₂. Требуется найти силу, действующую на единицу длины проводника.

Бесконечный проводник с током I₁ в точке на расстоянии r создаёт магнитное поле с индукцией:

(по закону Био — Савара — Лапласа).

Теперь по закону Ампера найдём силу, с которой первый проводник действует на второй:

По правилу буравчика, направлена в сторону первого проводника (аналогично и для , а значит, проводники притягиваются).

Модуль данной силы (r — расстояние между проводниками):

Интегрируем, учитывая только проводник единичной длины (пределы l от 0 до 1):

Электроизмерительные приборы. Применение закона Ампера

Тема урока: «Электроизмерительные приборы. Применение закона Ампера. Громкоговоритель».

Тип урока: формирование новых знаний.

Цель урока: показать практическую применимость закона Ампера.

Ход урока.

1. Организационный момент.

2. Проверка домашнего задания.

Задача№1

Горизонтальные рельсы находятся в вертикальном однородном магнитном поле на расстоянии l = 0,3 м друг от друга. На рельсах лежит стержень, перпендикулярный им. Какой должна быть индукция магнитного поля, для того чтобы стержень начал равномерно двигаться вдоль рельсов, если по нему пропускать ток силой I = 50А? Коэффициент трения стержня о рельсы μ = 0,2, масса стержня m = 0,5 кг.

Дано: Решение:

l = 0,3м при пропускании тока по стержню (сделать подр. чертеж)

μ = 0,2 на него действует сила Ампера,

I = 50А модуль которой и сила трения

m = 0,5 кг

B-? стержень будет двигаться равномерно,

если модули этих сил равны:

Отсюда,

Ответ: .

Задача№2

Рамка площадью s=25 см², содержащая n=100 витков провода, помещена в однородное магнитное поле так что индукция B параллельна плоскости рамки. При величине тока в каждом витке I=1А на рамку со стороны магнитного поля действует момент силы M=5*10^-3 Н*м. Определите величину B вектора индукции магнитного поля.

Дано: Решение:

S=25 см²=25*10^-4м² Механический момент, действующий на рамку с током в N=100 магнитном поле

I=1A ,

α=90⁰ (угол м/у нормалью к поверхности рамки и направлением магнитного поля)

M=5*10^-3Н*м Магнитный момент рамки с током (короткой катушки)

B-? ,

получаем, , значит

=

Ответ: В=.

Задача№3

Прямолинейный проводник с током помещен в однородное магнитное поле с индукцией B=0,2 Тл. Найдите величину силы, действующую на проводник, если его длина l=10 см, величина тока I = 3 А, а направление тока составляет с направлением вектора индукции магнитного поля α = 45⁰.

Дано: Решение:

В=0,2Тл

l=0,1м

I=3A

α = 45⁰

F_A-?

Ответ:.

1. Изучение нового материала.

Ориентирующее действие магнитного поля на контур с током (см. § 2) используют в электроизмерительных приборах магнитоэлектрической системы — амперметрах и вольтметрах.

Измерительный прибор магнитоэлектрической системы устроен следующим образом (рис. 1.20). На легкую алюминиевую рамку 2 прямоугольной формы с прикрепленной к ней стрелкой 4 намотана катушка. Рамка укреплена на двух полуосях ОО’. В положении равновесия ее удерживают две тонкие спиральные пружины 3. Силы упругости со стороны пружин, возвращающие катушку в положение равновесия, пропорциональны углу отклонения стрелки от положения равновесия. Катушку помещают между полюсами постоянного магнита М с наконечниками специальной формы. Внутри катушки расположен цилиндр 1 из железа. Такая конструкция обеспечивает радиальное направление линий магнитной индукции в той области, где находятся витки катушки (рис. 1.21). В результате при любом положении катушки силы, действующие на нее со стороны магнитного поля, максимальны и при неизменной силе тока постоянны. Векторы F и —F изображают силы, действующие на катушку со стороны магнитного поля и поворачивающие ее. Катушка с током поворачивается до Рис. 1.20 тех пор, пока силы упругости со стороны пружин не уравновесят силы, действующие на рамку со стороны магнитного поля. Увеличивая силу тока в 2 раза, мы обнаружим, что стрелка поворачивается на угол, вдвое больший, и т. д. Это происходит потому, что силы, действующие на катушку со стороны магнитного поля, прямо пропорциональны силе тока: Рис. 1.21 Fm ~ I. Благодаря этому можно определить силу тока по углу поворота катушки, если проградуировать прибор. Для этого надо установить, каким углам поворота стрелки соответствуют известные значения силы тока.

Такой же прибор может измерять и напряжение. Для этого нужно градуировать прибор так, чтобы угол поворота стрелки соответствовал определенным значениям напряжения. Кроме того, сопротивление вольтметра должно быть много больше сопротивления амперметра.

ГРОМКОГОВОРИТЕЛЬ

Зная направление и модуль силы, действующей на любой участок проводника с током, можно вычислить суммарную силу, действующую на весь замкнутый проводник. Для этого надо найти сумму сил, действующих на каждый участок проводника с током.

Закон Ампера используют для расчета сил, действующих на проводники с током, во многих технических устройствах. В частности — в электродвигателях, с которыми вы ознакомились в предыдущих классах.

Разберем устройство громкоговорителя.

Громкоговоритель служит для возбуждения звуковых волн под действием переменного электрического тока, меняющегося со звуковой частотой. В электродинамическом громкоговорителе (динамике) используется действие магнитного поля постоянного магнита на переменный ток в подвижной катушке.

Схема устройства громкоговорителя показана на рисунке 1.22, а. Звуковая катушка ЗК располагается в зазоре кольцевого магнита М. С катушкой жестко связан бумажный конус — диафрагма D. Диафрагма укреплена на упругих подвесах, позволяющих ей совершать вынужденные колебания вместе с подвижной катушкой.

По катушке проходит переменный электрический ток с частотой, равной звуковой частоте сигнала с микрофона или с выхода радиоприемника, проигрывателя, магнитофона. Под действием силы Ампера катушка колеблется вдоль оси громкоговорителя ОО₁ (см. рис. 1.22, а) в такт с колебаниями тока. Эти колебания передаются диафрагме, и поверхность диафрагмы излучает звуковые волны.

Первоклассные громкоговорители воспроизводят без значительных искажений звуковые колебания в диапазоне 40—15 ООО Гц. Но такие устройства очень сложны. Поэтому обычно применяют системы из нескольких громкоговорителей, каждый из которых воспроизводит звук в определенном небольшом интервале частот. Общим недостатком всех громкоговорителей является их малый КПД. Они излучают лишь 1—3% подводимой энергии.

Звук в радиоприемнике, проигрывателе и магнитофоне возникает в результате движения катушки с током в поле постоянного магнита.

Наряду с электромеханическими громкоговорителями в настоящее время широкое применение получили громкоговорители, основанные на пьезоэлектрическом эффекте. Этот эффект проявляется в виде деформации некоторых типов кристаллов в электростатическом поле. Две пьезопластинки склеивают. Пластинки подбирают так, что одна из них увеличивается по длине под действием поля, а другая уменьшается (см. рис. 1.22, б). В результате получают элемент, который сильно изгибается под действием поля и при переменном электрическом поле создает акустическую волну. Пьезогромкоговорители очень удобны в изготовлении и могут быть совсем маленькими. Вследствие этого они нашли широкое применение в радиотелефонах, мобильных телефонах, ноутбуках и микрокомпьютерах.

1. Закрепление изученного.

— Как устроен измерительный прибор магнитоэлектрической системы?

— Почему магнитные силы, действующие на проводники катушки прибора, не зависят от угла поворота катушки?

— Что удерживает рамку от вращения в магнитном поле?

— Чем амперметр отличается от вольтметра?

— Из чего состоит громкоговоритель?

— Какие громкоговорители вы можете назвать?

1. Решение задач. Решение заданий ЕГЭ.

Задача №1 (уровень С4).

По прямому горизонтальному проводнику длиной 1 м с площадью поперечного сечения 1,25 •10^-5 м², подвешенному с помощью двух одинаковых невесомых пружинок жесткостью 100 Н/м, течет ток I=10А (см. рисунок). Какой угол а составляют оси пружинок с вертикалью после включения вертикального магнитного поля с индукцией В=0,1 Тл, если абсолютное удлинение каждой из пружинок при этом составляет

7•10^-3м? (Плотность материала проводника 8•10³ кг/м³.)

Дано: Решение:

I=10А Условие механического равновесия проводника приводит к системе l=1 м уравнений:

k=100 Н/м Поделим второе равенство на первое:

В=0,1 Тл

S=1,25 •10^-5м²

Δl=7•10^-3м

=8•10³ кг/м³

α-?

.

(у задачи возможны еще два варианта решения: через синус угла и через косинус)

Задача №2 (уровень С4).

Горизонтальный проводящий стержень прямоугольного сечения поступательно движется с ускорением вверх по гладкой наклонной плоскости в вертикальном однородном магнитном поле (см. рисунок). По стержню протекает ток I= 4А. Угол наклона плоскости α = 30°. Отношение массы стержня к его длине m/l = 0,1 кг/м. Модуль индукции магнитного поля В = 0,2 Тл. Определите ускорение, с которым движется стержень.

Дано: Решение:

α = 30° На рисунке показаны силы, действующие на стержень:

I= 4А – сила тяжести mg,;

m/l = 0,1 кг/м – сила реакции опоры N;

а-? – сила Ампера Fа;

Спроецируем эти силы на ось ох, получим:

1. Домашнее задание: §4,5; упр.1 стр 26 (з.3)

Используемые материалы:

• Универсальные поурочные разработки по физике 11 класс. – М.: Вако, 2009. – 464 с. – (В помощь школьному учителю), Волков В.А

• Решение задач по физике_Савченко_1988 -479с

• ЕГЭ. Физика. Полн. курс А,В,С. Самост. подг_Громцева_2013 -368с

• Физика. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни / Г. Я. Мякишев, Б. Б. Буховцев, В. М. Чаругин; под ред. В. И. Николаева, Н. А. Парфентьевой. — 19-е изд. — М.: Просвещение, 2010. — 399 с.

Сила Ампера и ее применение

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать её на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: [email protected]

Мы в социальных сетях

Социальные сети давно стали неотъемлемой частью нашей жизни. Мы узнаем из них новости, общаемся с друзьями, участвуем в интерактивных клубах по интересам

ВКонтакте >

Что такое Myslide.ru?

Myslide.ru — это сайт презентаций, докладов, проектов в формате PowerPoint. Мы помогаем учителям, школьникам, студентам, преподавателям хранить и обмениваться своими учебными материалами с другими пользователями.

---

Для правообладателей >

Закон Ампера.

В 21 веке, казалось бы, открыты все законы природы. Магнетизм, электричество, молекулярный и атомный мир являют собой открытую книгу. При этом многие законы, открытые сто с лишним лет назад, не теряют актуальности и по сей день, являясь основой работы многих привычных нам предметов. В первую очередь, речь идет об электричестве. Имя Андре Ампера, французского физика-изобретателя не только дало название физическому закону, но и широко известно физикам и школьникам по всему миру благодаря описанному им явлению.

В 1820 году, основываясь на описанном Эрстедом взаимодействии магнитной стрелки и электрического тока, текущего по проводу, Ампер совершил важнейшее открытие, получившее название Закон Ампера. Формулировка его вкратце звучит следующим образом:

пропускание электрического тока в одном направлении через двух проводников, расположенных параллельно друг другу, ведет к их взаимоотталкиванию. Пропускание его в разных направлениях при прочих равных вызывает взаимное притяжение двух проводников.

Помимо этих заключений, видимых невооруженных глазом, Закон Ампера включает в себя ряд понятий, открытых тем же исследователем в то же время.

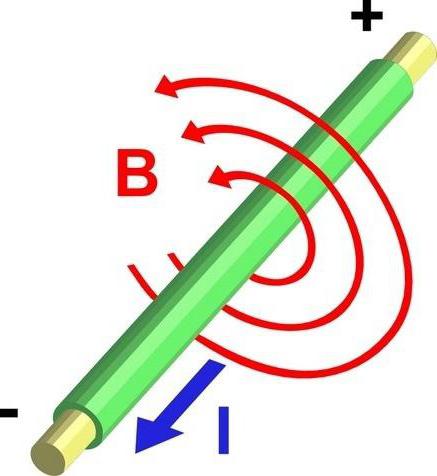
Сделав вывод о поведении двух проводников при пропускании через них тока в разных направлениях, французский ученый стал исследовать силы, обеспечивающие их таковое поведение. Логика его рассуждений была проста: электрический ток, пропущенный через проводник, создает магнитное поле. Образно его можно представить в качестве концентрических кругов, обрамляющих сечение проводника. Другой проводник, при условии, что он параллелен первому и расстояние между ними невелико, попадает в область воздействия магнитного поля, в результате чего образуется сила, воздействующая на атомы проводника и приводящая их в движение. Закон Ампера также позволяет объяснить возникшие наблюдения:

• Магнитное поле является результатом протекания любого электрического тока;
• Магнитное поле оказывает воздействие на движущиеся электрические заряды.

Основываясь на проделанном эксперименте и полученных результатах, Андре Ампер связал силы и явления, воздействующие на проводники в момент проведения через них электрического тока, поэтому Закон Ампера может быть представлен формулой:

F = IBl sin a.

Где F — сила Ампера, т.е. сила, воздействующая на проводник с током, находящийся в магнитном поле;

I — сила тока;

l— длина проводника;

B— модуль вектора магнитной индукции;

sin a — синус угла, образовавшегося между вектором магнитной индукции и проводником.

Сила Ампера — векторная величина, т.е. имеющая направление. Определить его можно с помощью так называемого «Правила левой руки»:

• четыре пальца левой руки направлены в сторону направления протекания электрического тока, вектор магнитной индукции (B) при этом входит в ладонь перпендикулярно. Тогда направление силы тока будет указывать отогнутый в плоскости ладони большой палец.

В современной науке применение Закона Ампера, в основном, приходится на производство электротехники. В частности, речь идет о громкоговорителях и динамиках. Принцип работы громкоговорителя, например, заключается в преобразовании электрической энергии в акустическую. Катушка — основа любого динамика или громкоговорителя — пропускает через себя переменный ток, частота которого соответствует частоте микрофона или динамика. Как гласит Закон Ампера, катушка начинает колебаться под действием тока, колебания передаются параллельно оси громкоговорителя диафрагме устройства. В результате излучаются звуковые волны, которые мы и слышим.

Кроме того, что создал Закон Ампера, изобретатель известен тем, что оставил свое имя в физике на века, поскольку оно было присвоено единице измерения силы тока.

формулировка и применение :: SYL.ru

Закон Ампера, формулировка которого известна любому физику, является одним из четырех уравнений Максвелла, которые в своей совокупности образуют фундамент всей теории классической электродинамики.

Уравнения Максвелла

Часть закона Ампера о том, как электрические токи, источники магнитного поля, относятся к самому полю. Другими словами, это (в совокупности с законом Гаусса для магнетизма) точно описывает картину, в которой электрические токи порождают магнитные поля. Поправочная часть Максвелла является значимой, поскольку она говорит, что магнитные поля появляются, когда электрические поля изменяются во времени. Это также важно, поскольку уравнения Максвелла не согласуются без него. С коррекцией термина можно вывести формулы сохранения электрического заряда и предсказать существование электромагнитных волн, которые перемещаются со скоростью.

В доходчивой форме закон Ампера принимает участие соответственно линейности уравнений Максвелла и, следовательно, всей теории классической электродинамики. Если взять два токовых распределителя и их совместить, тогда магнитное поле будет представлять собой сумму магнитных полей, производимых каждой конфигурацией.

Регулировочный элемент Максвелла является еще линейным, и, следовательно, электромагнитные волны являются линейными тоже. Они мешают друг другу согласно принципу суперпозиции и проходят прямо сквозь друг друга без рассеяния.

Как объяснить закон Ампера простым языком?

Простейшим объяснением является то, что провод переносит ток. Если игнорировать магнитное поле Земли, можно представить, что вертикальный провод с электрическим током идет вверх.

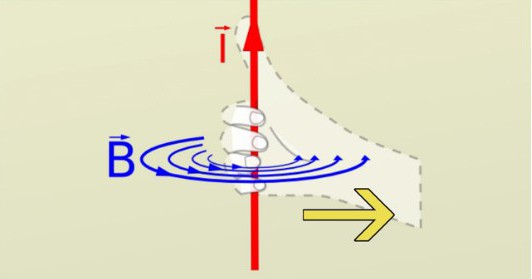
Люди склонны говорить об электромагнетизме, но электричество отдельно от магнетизма, поскольку установлено, что электричество и магнетизм влияют друг на друга и могут быть объединены в систему уравнений. В частности, в случае токоведущих проводов электрический ток производит магнитное поле. Ориентация этих полей не очень понятна, но это заметно. Магнитные компасы могут быть размещены вокруг токоведущих проводов, а направления поля можно увидеть в направлениях игловых точек.

Есть возможность рассмотреть это из-за простой симметрии. Ток в проводе производит магнитное поле, но что должно произойти с узором в этих полях, если провод остается вертикальным и поворачивается на некоторый угол около этой вертикальной оси? Дело в том, что ток не меняется в любом случае на такой поворот. Он по-прежнему идет прямо. Следовательно, это вращение не может изменить картину магнитного поля, которое производится.

Структуры

Есть только две возможные структуры, которые работали бы от этого. Либо поля направлены радиально в сторону или подальше от провода, или вокруг провода. Первая возможность — это то, что люди получают от электрически заряженного провода электрическое поле. Вторая возможность — это то, что можно получить магнитное поле, создаваемое током, через провода.

Для одиночного проводника формы поля имеют круговые структуры по центру провода, и сила поля убывает с расстоянием. Как шаблон, это очень похоже на рябь, которая образуется при падении камня в воду. Существует два основных различия между прудом и картиной магнитного поля. Первый – это то, что магнитное поле остается неизменным на заданном расстоянии. Оно не будет расти, а будет уменьшаться в заданной точке. Второй заключается в том, что магнитное поле имеет направление к каждой точке касания окружности.

Сила тока и расстояние

Следующая часть закона Ампера гласит, что сила магнитного поля зависит от силы тока и расстояния от провода. В результате получается, что, если умножить силу магнитного поля на окружность круга, этот продукт будет пропорционален силе электрического тока. То есть, если удвоить расстояние от провода, линия окружности удваивается, а величина магнитного поля падает в 2 раза.

Но закон Ампера позволяет разобраться с токами, которые производятся в системах более сложных, чем одиночный провод. Но все эти случаи эквивалентны. Это означает, что идея магнитной напряженности поля, умноженной на длину пути, остается полезной и по-прежнему зависит от суммы всех токов внутри контура, который образует путь.

Как можно понять закон в практическом смысле?

Это влечет за собой некоторые векторные исчисления, которые можно объяснить интуитивно понятным способом:

• Магнитные поля создаются электрическими токами.
• Магнитные поля «накручены» на ток, который их производит в заданном направлении.
• Чем больше ток, тем сильнее создается магнитное поле. Напряженность магнитного поля пропорциональна току.

Закон Ампера связывает вместе эти понятия в одной из двух математических формул. Поле становится более интенсивным по мере приближения к проводу.

Пропорциональность суммарному току

В интегральной форме закона Ампера используется понятие линейного интеграла. В принципе, можно выбрать определенный цикл (т. е. замкнутый путь через космос) и пройтись вдоль петли, сложить составляющие магнитного поля. Это покажет, насколько магнитное поле вьется вокруг поверхности, ограниченной петлей. Утверждение, что эта величина пропорциональна суммарному току, который ограничен петлей, верно.

Чтобы понять это, нужно рассмотреть контур, ограничивающий провод. Если выполнить петлю вокруг провода, магнитное поле всегда идет к точке в том же направлении, что означает, что общая сумма криволинейного интеграла будет положительной. Это говорит, что можно пройти вокруг тока! Кроме того, можно определить направление тока, используя правило правой руки. Если поток тока пошел в другом направлении, значение криволинейного интеграла переворачивается.

Теперь можно предположить, что взят цикл, в котором не подкладывают проволоку, но делают круг против часовой стрелки над проводом. Если пройтись вокруг нижней части петли, в большинстве случаев направление будет идти против течения, поэтому вклад в интеграл будет отрицательным. Но когда направление проходит вокруг верхней части петли, в большинстве случаев оно будет такое же, что и ток, так что вклад будет положительным. Это говорит, что нет ничего внутри цикла (либо нет тока вообще, или течения токов в противоположных направлениях компенсируют друг друга).

Дифференциал

В дифференциальной форме применение закона Ампера происходит в концепции завитков векторной области. Локон — это количественное измерение, векторное поле — это «керлинг» вокруг данной точки. Если брать все меньшие и меньшие циклы вокруг точки и вычислить криволинейный интеграл, результат должен стать примерно пропорциональным площади петли. Коэффициентом пропорциональности является завиток.

Если взять цикл, который не содержат провода, криволинейный интеграл всегда будет равен нулю. Если петли все дальше и дальше, он всегда будет равен нулю. Коэффициент пропорциональности будет равен нулю, и ротор будет равен нолю (если быть точным, то нулевой вектор). Но если находиться внутри провода, то, независимо от того, какие петли, он будет получать ток, протекающий через него. Идея заключается в том, что для бесконечно малого контура только плотность тока в этот момент будет «внутри» него, а так только плотность тока в этой точке будет определять значение криволинейного интеграла. Поэтому ротор должен быть пропорционален плотности тока в данной точке, так как он соотносится по значению криволинейного интеграла по бесконечно малой петле.

Заключение

В дифференциальной и интегральной формах закон Ампера эквивалентен, он может быть показан путем применения теоремы Стокса. По существу, дифференциальная форма является бесконечно малой версией второго уравнения в «интегральной форме». Но теорема Стокса — это тема другого исследования.

Закон Ампера и его применение

Урок 3. Закон Ампера и его применение

Цель: сформулировать закон Ампера и показать его практическую применимость.

Ход урока

I. Организационный момент

II. Актуализация знаний

— Опишите опыт Эрстеда.

— Каким является магнитное поле?

— Что можно сказать об основных линиях магнитного поля?

— Что такое соленоид?

— Сформулируйте правила для определения направлений силовых линий магнитного поля?

— Что можно сказать о магнитных монополях?

III. Выполнение лабораторной работы

Лабораторная работа по теме «Изучение свойств постоянных магнитов»

Цели: получить картины силовых линий магнитного поля вокруг постоянных магнитов.

Оборудование: магнит полюсовой (2 шт.), магнит подковообразный, магнитная стрелка, скрепки, медный провод, ластик, железные опилки.

Ход работы

1. Найдите северный полюс стрелки, установите полюса полюсового магнита и подковообразного. Обозначьте северный и южный полюса магнитов.

2. Положите лист картона на полюсовой магнит и равномерно посыпьте его железными опилками. Не двигая магнит и картонку, осторожно постучите по картонке, чтобы опилки могли перемещаться. Обратите внимание, как выстроились опилки на листе. Сделайте рисунок в тетради.

3. Получите картину магнитного поля двух полюсовых магнитов, расположенных параллельно друг другу, и подковообразного магнита.

4. Что можно сказать о линиях магнитной индукции?

IV. Изучение нового материала

1. Проведение эксперимента.

По двум параллельным проводникам пропускаем электрический ток. В том случае, если ток направлен в одну сторону, наблюдается притяжение проводников, если в разные стороны, то отталкивание.

Притяжение или отталкивание электрически нейтральных проводников при пропускании через них электрического тока называют магнитным взаимодействием токов.

На проводник с током в магнитном поле действует сила, которая получила название силы Ампера. Направление этой силы можно найти при помощи правила левой руки. Математическая запись имеет следующий вид:

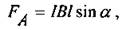
где I — сила тока в проводнике; В — магнитная индукция; l — длина проводника; α — угол между направлением проводника и направлением вектора магнитной индукции.

2. Работа с учебником.

Учащиеся открывают с. 900 учебника, читают § 64 и отвечают на следующие вопросы:

— Как устроен измерительный прибор магнитоэлектрической системы?

— Каково устройство электродвигателя постоянного тока?

— От чего зависит вращающийся магнит электродвигателя постоянного тока?

— Как можно изменить направление вращения якоря электродвигателя?

— Как можно изменить скорость вращения якоря электродвигателя?

V. Решение задач

1. Какая сила действует на каждый метр длины воздушных проводов троллейбусной линии, расположенных на расстоянии 52 м друг от друга, если сила тока в проводах — 2000 А? (Ответ: 1,5 Н.)

2. Вычислите индукцию магнитного поля на расстоянии 10 м от длинного прямого проводника при силе тока в проводнике 20 А. (Ответ: 4 · 10^-5 Тл.)

3. Вычислите индукцию магнитного поля внутри цилиндрической катушки длиной 10 м, содержащей 200 витков провода, при силе тока в катушке 5 А. (Ответ: 1,3 · 10^-2 Тл.)

Задачи повышенной сложности:

1. В вертикально однородном магнитном поле на двух тонких лентах горизонтально подвешен проводник длиной 20 см и массой 20,4 г. Индукция магнитного поля равна 0,5 Тл. На какой угол от вертикали отклонятся ленты, если сила тока в проводнике равна 2 А. (Ответ: 45°.)

2. Прямолинейный проводник массой 2 кг и длиной 50 см помещен в однородное магнитное поле перпендикулярно линиям индукции. Индукция поля равна 15 Тл. Какой силы ток должен проходить по нему, чтобы он висел не падая? (Ответ: 2,7 Тл.)

3. Проводящий стержень лежит на горизонтальной поверхности перпендикулярно однородному горизонтальному магнитному полю с индукцией 0,2 Тл. Какую силу в горизонтальном направлении нужно приложить перпендикулярному проводнику для его равномерного поступательного движения? Сила тока в проводнике — 10 А, масса — 100 г, длина — 25 см, коэффициент трения — 0,1. (Ответ: 0,548 Н или 0,402 Н.)

VI. Подведение итогов урока

Дополнительный материал Андре-Мари Ампер

Андре-Мари Ампер родился 20 января 1775 г. в Лионе в семье образованного коммерсанта. Отец его вскоре переселился с семьей в имение Полемье, расположенное в окрестностях Лиона, и лично руководил воспитанием сына. Уже к 14 годам Ампер прочитал все 20 томов знаменитой «Энциклопедии» Дидро и д’Аламбера. Проявляя с детства большую склонность к

математическим наукам, Ампер к 18 годам в совершенстве изучил основные труды Эйлера, Бернулли и Лагранжа. К тому времени он хорошо владел латынью, греческим и итальянским языками. Иными словами, Ампер получил глубокое и энциклопедическое образование.

В 1793 г. в Лионе вспыхнул контрреволюционный мятеж. Отец Ампера — жирондист, исполнявший обязанности судьи при мятежниках, после подавления мятежа был казнён как сообщник аристократов. Имущество его было конфисковано. Юный Ампер начал свою трудовую деятельность с частных уроков. В 1801 г. он занял должность преподавателя физики и химии центральной школы в городе Бурге. Здесь он написал первый научный труд, посвященный теории вероятности «Опыт математической теории игры». Эта работа привлекла внимание д’Аламбера и Лапласа. И Ампер стал преподавать математику и астрономию в Лионском лицее. В 1805 г. Ампер был назначен репетитором по математике в знаменитой Политехнической школе в Париже и с 1809 г. заведовал кафедрой высшей математики и механики. В этот период Ампер публикует ряд математических трудов по теории рядов. В 1813 г. его избирают членом Института (т. е. Парижской Академии наук) на место скончавшегося Лагранжа. Вскоре после избрания Ампер представил в Академию свое исследование о преломлении света. К этому же времени относится его знаменитое «Письмо к г. Бертолле», в котором Ампер сформулировал открытый им независимо от Авогадро химический закон, именуемый ныне законом Авогадро-Ампера.

В 1816 г. Ампер опубликовал свою классификацию химических элементов, первую в истории химии серьезную попытку расположить химические элементы по их сходству между собой.

Открытие Эрстедом в 1820 г. действия электрического тока на магнитную стрелку привлекает внимание Ампера к явлениям электромагнетизма. Ампер ставит многочисленные опыты, изобретает для этой цели сложные приборы, которые изготавливает за свой счет, что сильно подрывает его материальное положение.

С 1820 по 1826 г. Ампер опубликовал ряд теоретических и экспериментальных трудов по электродинамике и почти еженедельно выступал с докладами к Академии наук.

В 1822 г. он выпустил «Сборник наблюдений по электромагнетизму», в 1823 г. — «Конспект теории электродинамических явлений» и, наконец, в 1826 г. — знаменитую «Теорию электродинамических явлений, выведенных исключительно из опыта». Ампер получает всемирную известность как выдающийся физик.