Онлайн калькулятор: Скорость и длина волны
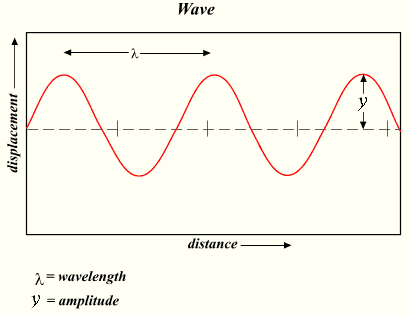
Если бросить камень в воду, то в месте его падения частицы воды начинают колебаться, двигаясь вверх и вниз. Соседние частицы, связанные с ними силами сцепления, также приходят в колебание. Однако для передачи колебания соседним частицам требуется некоторое время. То есть, чем дальше отстоят частицы от места, где начались колебания, тем позже эти частицы будут вовлечены в колебательное движение. Таким образом, от места падения камня волна бежит во все стороны с определенной скоростью, которая называется скоростью распространения волны. Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней. Если считать скорость волны постоянной, то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней:
,
то можно получить формулу, выражающую связь длины волны с ее скоростью и частотой:
Калькулятор ниже позволяет по двум известным параметрам формулы посчитать неизвестный.

Скорость и длина волны
ВычислитьДлину волны по скорости и периодуДлину волны по скорости и частотеПериод волны по скорости и длинеСкорость волны по длине и периодуСкорость волны по длине и частотеЧастоту волны по скорости и длинеТочность вычисленияЗнаков после запятой: 3
Скорость волны, м/с
Длина волны, м
Период волны, с
Частота волны, Гц
save Сохранить share Поделиться extension Виджет
Длина волны ⟷ частота — 3G-aerial
Частота ⟷ Длина волны:
Калькулятор позволяет рассчитать длину волны по известной частоте или частоту по известной длине волны.
Расчет ведется по простейшей формуле, связывающей между собой длину волны, частоту и скорость света: λ = с/f
| № | Диапазон | Условное обозначение диапазона частот | Наименование по длине волны | |
|---|---|---|---|---|
| частот | длин волн | |||
| 1 | 3-30Гц | 105-104км | КНЧ (ELF) — крайне низкие частоты | Декаметрические |
| 2 | 30-300Гц | 104-103км | Мегаметрические | |
| 3 | 300-3000Гц | 103-102км | УНЧ (ULF) — ультра низкие частоты | Гектокилометровые |
| 4 | 3-30кГц | 100-10км | ОНЧ (VLF)- очень низкие частоты | Сверхдлинные (мириаметровые) |
| 5 | 30-300кГц | НЧ (LF) — низкие частоты | Длинные (километровые) | |
| 6 | 300-3000кГц | 1000-100м | СЧ (MF) — средние частоты | Средние (гектометровые) |
| 7 | 3-30МГц | 100-10м | ВЧ (HF) — высокие частоты | Короткие (декаметровые) |
| 8 | 30-300МГц | 10-1м | ОВЧ (VHF) — очень высокие частоты | Метровые, ультра короткие |
| 9 | 300-3000МГц | 100-10см | УВЧ (UHF) — ультра высокие частоты | Дециметровые |
| 10 | 3-30ГГц | 10-1см | СВЧ (SHF) — сверх высокие частоты | Сантиметровые |
| 11 | 30-300ГГц | 10-1мм | КВЧ (EHF)- крайне высокие частоты | Миллиметровые |
| 12 | 300-3000ГГц | 1-0,1мм | ГВЧ — гипервысокие частоты | Субмиллиметровые |
| 13 | Оптические диапазоны волн. (начиная с инфракрасного) | |||
ДЛИНА ВОЛНЫ и частота (формула и онлайн-расчет)
Расчет
Введите данные в какое-либо поле, остальные параметры будут расчитаны автоматически.
Если в какой-либо области изменения данных, другие автоматически пересчитываются.
Обнаруженны NaN, проверьте, что вы ввели в поле
корректные данные, то есть без букв и других символов.
Коэффициент укорочения
Для расчета петель симметризационных и окурки коаксиального кабеля должны быть приняты во внимание коэффициент укорочения k.
Для коаксиальный кабель с пеной диэлектрика
k = 0,81 и для кабеля с полиэтиленовым диэлектриком составляет k = 0,66.
Коэффициент укорочения не может быть равен нулю.
Если вы не понимаете антенная технологии, оставить укорочение фактора всегда 1.
Точность расчета
Расчет зависит от скорости распространения электромагнитных волн = скорость света.
Для иллюстративных целей, расчет подсчитывает только округленное значение (в вакууме)
c = 300 000 000 m/s
Для точных расчетов распространения в вакууме должны ввести:
c = 299 792 458 m/s
Скорость распространения электромагнитных волн различных материалов ниже.
Формулы
| Длина волны (лямбда) | λ = | 300 / f | [m] |
| Частота | f = | 300 / λ | [MHz] |
λ … длина одной волны
T … время
Длина волны и частота
Дополнительная информация для расчета длины волны и частоты. можно найти в Википедии в соответствующих паролей (см ссылки ниже)
Расчет длины волны онлайн
Ссылки
Калькулятор Частота волны | Преобразование единиц частоты волны
Частота — это количество повторений за определенную единицу времени, часто ее называют «временная частота» В физике и инженерных дисциплинах: оптика, радио и акустика, частота обычно обозначается латинской буквой «f» или греческой буквой «v» (Ню). Частота синусоидальной волны является расстоянием, над которым повторяется форма волны. Обычно она определяется, учитывая расстояние между последовательностью соответствующих точек той же фазы, как, например, нулевых переходов, гребней, впадин. Как правило, любая картина волны может быть описана в условиях синусоидальных компонентов. Для периодических волн частота имеет обратную связь с длиной волны. Единица СИ частоты – Герц, символ — Гц, который назван в честь немецкого физика Генриха Герца. Единица СИ длины волны — метр.
Конвертер частоты волны
Переводим из
Переводим в
| Основные единицы | |
| Гигагерц | ГГц |
| Герц | Гц |
| Килогерц | кГц |
| Мегагерц | МГц |
| Миллигерц | мГц |
| Петагерц | ПГц |
| Терагерц | ТГц |
| Другие единицы | |
| Аттогерц | aHz |
| Сантигерц | сГц |
| Цикл в секунду | cyc./s |
| Децигерц | dHz |
| Декагерц | daHz |
| Эксагерц | EHz |
| Фемтогерц | fHz |
| Гектогерц | hHz |
| Микрогерц | µHz |
| Наногерц | nHz |
| Пикогерц | pHz |
| Сантиметровая длина Волны | w.l. cm |
| Декаметровая длина Волны | w.l. dam |
| Дециметровая длина Волны | w.l. dm |
| Эксаметровая длина Волны | w.l. Em |
| Гигаметровая длина Волны | w.l. Gm |
| Гектометровая длина Волны | w.l. Hm |
| Километровая длина Волны | w.l. Km |
| Мегаметровая длина Волны | w.l. Mm |
| Метровая длина Волны | w.l. m |
| Микрометровая длина Волны | w.l. µm |
| Миллиметровая длина Волны | w.l. mm |
| Петаметровая длина Волны | w.l. Pm |
| Тераметровая длина Волны | w.l. Tm |
| Основные единицы | |
| Гигагерц | ГГц |
| Герц | Гц |
| Килогерц | кГц |
| Мегагерц | МГц |
| Миллигерц | мГц |
| Петагерц | ПГц |
| Терагерц | ТГц |
| Другие единицы | |
| Аттогерц | aHz |
| Сантигерц | сГц |
| Цикл в секунду | cyc./s |
| Децигерц | dHz |
| Декагерц | daHz |
| Эксагерц | EHz |
| Фемтогерц | fHz |
| Гектогерц | hHz |
| Микрогерц | µHz |
| Наногерц | nHz |
| Пикогерц | pHz |
| Сантиметровая длина Волны | w.l. cm |
| Декаметровая длина Волны | w.l. dam |
| Дециметровая длина Волны | w.l. dm |
| Эксаметровая длина Волны | w.l. Em |
| Гигаметровая длина Волны | w.l. Gm |
| Гектометровая длина Волны | w.l. Hm |
| Километровая длина Волны | w.l. Km |
| Мегаметровая длина Волны | w.l. Mm |
| Метровая длина Волны | w.l. m |
| Микрометровая длина Волны | w.l. µm |
| Миллиметровая длина Волны | w.l. mm |
| Петаметровая длина Волны | w.l. Pm |
| Тераметровая длина Волны | w.l. Tm |
Результат конвертации:
Волны и ветер. Расчет характеристик волны
Пользователь оставил нам на сайте запрос — калькулятор штормовых баллов морской волны, где попросил создать калькулятор «Расчет по высоте волны и промежутками между волнами(частота)?».
Интуиция подсказывала, что какая-то зависимость между силой ветра и волнами есть. Так как я в теории волн не силен, пришлось вопрос слегка изучить.
Результат изучения в виде калькулятора чуть ниже, а под ним мои рассуждения на тему, родившиеся в результате копания в разных источниках, то есть немного теории. Сразу скажу, что калькулятор не рассчитывает, а точнее говоря, не прогнозирует высоту волны — это отдельная тема, которая рассмотрена здесь — Волны и ветер. Статистическое прогнозирование высоты волны.

Расчет характеристик волны
Точность вычисленияЗнаков после запятой: 2
Относительная глубина
Длина волны (метры)
Угловая частота (рад/с)
Волновое число
Фазовая скорость (м/с)
Групповая скорость (м/с)
save Сохранить share Поделиться extension Виджет
Теория
Достаточно очевидно, что волны на море не могут быть описаны одной синусоидой, так как образуются в результате наложения множества волн с разными периодами и фазами. Для примера можно посмотреть на картинку ниже, которая показывает волну, полученную в результате наложения трех разных синусоид.
 «Wave disp» by Kraaiennest — Own work. Licensed under GFDL via Wikimedia Commons — http://commons.wikimedia.org/wiki/File:Wave_disp.gif#mediaviewer/File:Wave_disp.gif
«Wave disp» by Kraaiennest — Own work. Licensed under GFDL via Wikimedia Commons — http://commons.wikimedia.org/wiki/File:Wave_disp.gif#mediaviewer/File:Wave_disp.gifИсточник: «Wave disp» by Kraaiennest — Own work. Licensed under GFDL via Wikimedia Commons — http://commons.wikimedia.org/wiki/File:Wave_disp.gif#mediaviewer/File:Wave_disp.gif
Поэтому для анализа состояния моря обычно строят энергетический спектр, то есть откладывают по оси Y единицы энергии, а по оси X — частоту, получая таким образом плотность энергии — количество энергии, переносимой волнами с соответствующим диапазоном частот. И, как оказалось, под действием ветра, форма энергетического спектра меняется, причем чем сильнее ветер, тем более ярко на спектре выражен пик — волны определенных частот, переносящие наибольшее количество энергии. На картинке ниже как умел нарисовал, как это примерно выглядит.
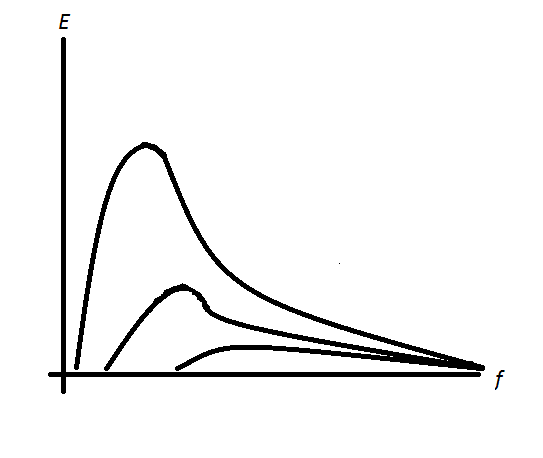 Распределение энергии по спектру частот в зависимости от силы ветра
Распределение энергии по спектру частот в зависимости от силы ветраЧастоты, где наблюдается пик, называют доминантными. Соответственно, можно облегчить себе жизнь и рассчитать характеристики волны только для доминантной частоты. Как показала практика, это будет давать достаточно хорошее приближение к реальности.
Ну а что касается характеристик волны, на помощь приходит линейная теория волн, а именно, расчет гравитационных волн в линеаризованном приближении. Чтобы было понятнее о чем речь дальше, приведем несколько определений из Википедии:
Волны на поверхности жидкости — название разнообразных волн, возникающих на поверхности раздела между жидкостью и газом или жидкостью и жидкостью. Нижняя часть волны называется подошвой, верхняя — гребнем.
Гравитационные волны на воде — разновидность волн на поверхности жидкости, при которых сила, возвращающая деформированную поверхность жидкости к состоянию равновесия, есть просто сила тяжести, связанная с перепадом высот гребня и впадины в гравитационном поле.
Дисперсия волн — в теории волн различие фазовых скоростей линейных волн в зависимости от их частоты. То есть волны разной длины (соответственно, разной частоты) имеют разные скорости в среде, что убедительно демонстрирует опыт с преломлением света в призме. Это важно понимать для дальнейших рассуждений.
Волновое число — это отношение 2π радиан к длине волны: . Волновое число можно представить как разность фазы волны (в радианах) в один и тот же момент времени в пространственных точках на расстоянии единицы длины (одного метра), либо количество пространственных периодов (гребней) волны, приходящееся на 2π метров.
Используя определение волнового числа можно записать следующие формулы:
Длина волны
Фазовая скорость (Скорость гребня)
Период волны (выраженный через угловую частоту)
Картинка для привлечения внимания — красная точка показывает фазовую скорость, зеленая — групповую скорость (скорость пакета волн).
 «Wave group» by Kraaiennest — Own work. Licensed under GFDL via Wikimedia Commons — http://commons.wikimedia.org/wiki/File:Wave_group.gif#mediaviewer/File:Wave_group.gif
«Wave group» by Kraaiennest — Own work. Licensed under GFDL via Wikimedia Commons — http://commons.wikimedia.org/wiki/File:Wave_group.gif#mediaviewer/File:Wave_group.gifИсточник: «Wave group» by Kraaiennest — Own work. Licensed under GFDL via Wikimedia Commons — http://commons.wikimedia.org/wiki/File:Wave_group.gif#mediaviewer/File:Wave_group.gif
Закон дисперсии
Ключевым моментом в расчете характеристик волны является понятие закона дисперсии или дисперсионного уравнения (соотношения) .
Закон дисперсии или дисперсионное уравнение (соотношение) в теории волн — это связь частоты и волнового вектора (волнового числа) волны.
В общем виде это соотношение записывается как
.
Это соотношение для воды выведено в линейной теории волн для так называемой свободной поверхности, то есть поверхности жидкости, не ограниченной стенками сосуда или русла, и выглядит следующим образом:
,
где
g — ускорение свободного падения,
k — волновое число,
tanh — гиперболический тангенс,
h — расстояние от поверхности жидкости до дна.
Можно провести дальнейшее упрощение формулы, исходя из графика гиперболического тангенса. Заметим, что при kh, стремящемся к нулю, гиперболический тангенс может быть аппроксимирован своим аргументом, т. е. значением kh, а при kh, стремящемся к бесконечности, гиперболический тангенс kh стремится к единице. Последний случай, очевидно, относится к очень большим глубинам. Можно ли оценить, насколько они должны быть большие? Если взять гиперболический тангенс числа Пи, то его значение равно примерно 0.9964, что уже довольно близко к единице (число Пи взято для удобства работы с формулой). Тогда
.
То есть для расчета характеристик волны воду можно считать глубокой, если глубина больше хотя бы половины длины волны, и в большинстве мест мирового океана это условие соблюдается.
Вообще, исходя из графика гиперболического тангенса, используется следующая классификация волн по относительной глубине (соотношению глубины к длине волны).
1. Волны на глубокой воде
Глубина больше половины длины волны, гиперболический тангенс аппроксимируется единицей:
2. Волны на переходных глубинах
Глубина от одной двадцатой до одной второй длины волны, гиперболический тангенс не аппроксимируется:
3. Волны на мелкой воде
Глубина меньше одной двадцатой длины волны, гиперболический тангенс аппроксимируется своим аргументом:
Рассмотрим соотношения для этих случаев
Случай мелкой воды
Уравнение приобретает вид
,
откуда
Групповая скорость для случая мелкой воды
То есть, в соответствии с теорией, на мелкой воде волны не должны иметь дисперсии, так как фазовая скорость не зависит от частоты. Однако надо учитывать, что на мелкой воде начинают работать нелинейные эффекты, связанные с повышением амплитуды волны. Нелинейные эффекты сказываются, когда амплитуда волны становится сравнимой с её длиной. Одним из характерных эффектов в этом режиме является появление изломов на вершинах волн. Кроме того, появляется возможность опрокидывания волны — всем известный прибой. Эти эффекты пока не поддаются точному аналитическому расчёту.
Случай переходных глубин
Уравнение не упрощается, и тогда:
Групповая скорость для случая переходных глубин:
Заметим, что уравнение длины волны является трансцендентным, и находить его решение нужно численными методами. Например, используя Метод итераций (метод последовательных приближений).
Случай глубокой воды
Уравнение приобретает вид
,
откуда
Групповая скорость для случая глубокой воды:
Итак, измерив период волны, мы с достаточной точностью можем вычислить фазовую скорость, групповую скорость и длину волны. А измерение периода волны можно провести, например, засекая секундомером время прохождения гребней, то есть период — это наиболее доступная вещь, которую можно измерить без специальных приборов. Если вы где-то вблизи берега — надо представлять себе глубину, если глубины заведомо большие, то можно пользоваться формулами для глубокой воды, в которые глубина, как параметр, не входит. Так как у нас под рукой вычислительная мощь компьютера, калькулятор использует не упрощенные формулы, находя длину волны методом итераций (метод будет сходиться, так как производная функции меньше единицы).
Теперь возвращаемся к ветру. Собственно, постоянно дующий в одном направлении ветер это и есть то, что формирует волны, то, что сообщает волнам энергию.
И, довольно очевидно, для того чтобы сообщать волнам энергию, ветер должен дуть быстрее, или хотя бы со скоростью, равной фазовой скорости волны.
Здесь вводится определение полностью сформированной волны (fully developed sea). Полностью сформированная волна — волна, достигнувшая максимальных характеристик при данном ветре. То есть волна находится в состоянии равновесия по энергии — сколько сообщается энергии ветром, столько и уходит на движение. Не каждая волна достигает такого состояния, так как требуется, чтобы ветер постоянно дул над всей поверхностью, которую проходит волна в течении некоторого времени. И чем сильнее ветер, тем больше времени и больше расстояния требуется для формирования такой волны. Но зато уж если она сформировалась, ее фазовая скорость догонит скорость ветра.



