Список литературы

[1] Гоноровский И.С. Радиотехнические цепи и сигналы Москва, Советское радио, 1977, 608 c.

[2] Баскаков, С.И. Радиотехнические цепи и сигналы Москва, ЛЕНАНД, 2016, 528 c. ISBN 978-5-9710-2464-4

[3] Bracewell, R. The Fourier Transform and Its Applications McGraw-Hills, 1986, 474 c. ISBN 0-07-007-015-6

© Бахурин Сергей 2015 — 2019. Все права защищены. Любое копирование материалов сайте без разрешения автора запрещено.

Виды сигналов: аналоговый, цифровой, дискретный

Каждый день люди сталкиваются с использованием электронных приборов. Без них невозможна современная жизнь. Ведь речь идет о телевизоре, радио, компьютере, телефоне, мультиварке и прочем. Раньше, еще несколько лет назад, никто не задумывался о том, какой сигнал используется в каждом работоспособном приборе. Сейчас же слова «аналоговый», «цифровой», «дискретный» уже давно на слуху. Некоторые виды сигналов из перечисленных являются качественными и надежными.

Цифровая передача стала использоваться намного позже, чем аналоговая. Это связано с тем, что такой сигнал намного проще обслуживать, да и техника на тот момент не была настолько усовершенствована.

С понятием «дискретность» сталкивается каждый человек постоянно. Если переводить это слово с латинского языка, то означать оно будет «прерывистость». Углубляясь далеко в науку, можно сказать, что дискретный сигнал представляет собой метод передачи информации, который подразумевает изменение во времени среды-переносчика. Последняя принимает любое значение из всех возможных. Сейчас дискретность уходит на второй план, после того, как было принято решение производить системы на чипе. Они являются целостными, а все компоненты тесно взаимодействуют друг с другом. В дискретности же все с точностью наоборот – каждая деталь завершена и связана с другими за счет специальных линий связи.

Сигнал

Сигнал представляет собой специальный код, который передается в пространство одной или несколькими системами. Эта формулировка является общей.

В сфере информации и связи сигналом назван специальный носитель каких-либо данных, который используется для передачи сообщений. Он может быть создан, но не принят, последнее условие не обязательно. Если же сигнал является сообщением, то его «ловля» считается необходимой.

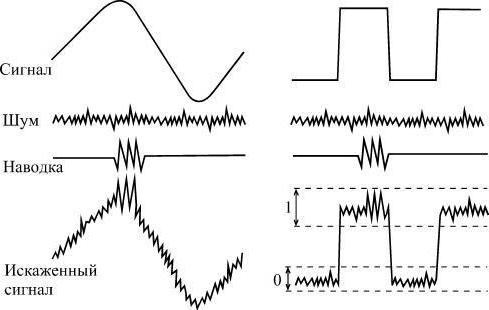
Описываемый код передачи данных задается математической функцией. Она характеризует все возможные изменения параметров. В радиотехнической теории эта модель считается базовой. В ней же аналогом сигнала был назван шум. Он представляет собой функцию времени, которая свободно взаимодействует с переданным кодом и искажает его.

В статье охарактеризованы виды сигналов: дискретный, аналоговый и цифровой. Также коротко дана основная теория по описываемой теме.

Виды сигналов

Существует несколько типов классификации имеющихся сигналов. Рассмотрим, какие бывают виды.

1. По физической среде носителя данных разделяют электрический сигнал, оптический, акустический и электромагнитный. Имеется еще несколько видов, однако они малоизвестны.
2. По способу задания сигналы делятся на регулярные и нерегулярные. Первые представляют собой детерминированные методы передачи данных, которые задаются аналитической функцией. Случайные же формулируются за счет теории вероятности, а также они принимают любые значения в различные промежутки времени.
3. В зависимости от функций, которые описывают все параметры сигнала, методы передачи данных могут быть аналоговыми, дискретными, цифровыми (способ, который является квантованным по уровню). Они используются для обеспечения работы многих электрических приборов.

Теперь читателю известны все виды передачи сигналов. Разобраться в них не составит труда любому человеку, главное — немного подумать и вспомнить школьный курс физики.

Для чего обрабатывается сигнал?

Сигнал обрабатывается с целью передачи и получения информации, которая в нем зашифрована. Как только она будет извлечена, ее можно использовать различными способами. В отдельных ситуациях ее переформатируют.

Существует и другая причина обработки всех сигналов. Она заключается в небольшом сжатии частот (чтобы не повредить информацию). После этого ее форматируют и передают на медленных скоростях.

В аналоговом и цифровом сигналах используются особенные методы. В частности, фильтрация, свертка, корреляция. Они необходимы для восстановления сигнала, если он поврежден или имеет шум.

Создание и формирование

Зачастую для формирования сигналов необходим аналого-цифровой (АЦП) и цифро-аналоговый (ЦАП) преобразователи. Чаще всего они оба используются лишь в ситуации с применением DSP-технологий. В остальных случаях подойдет только использование ЦАП.

При создании физических аналоговых кодов с дальнейшим применением цифровых методов полагаются на полученную информацию, которая передается со специальных приборов.

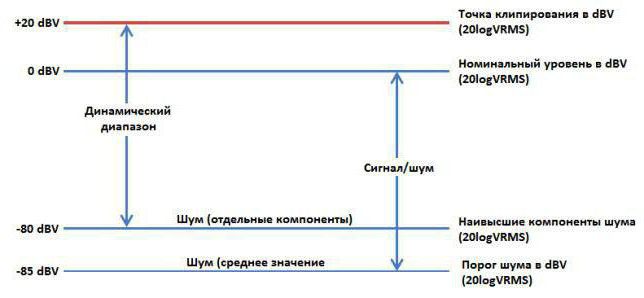
Динамический диапазон

Диапазон сигнала вычисляется разностью большего и меньшего уровня громкости, которые выражены в децибелах. Он полностью зависит от произведения и особенностей исполнения. Речь идет как о музыкальных треках, так и об обычных диалогах между людьми. Если брать, например, диктора, который читает новости, то его динамический диапазон колеблется в районе 25-30 дБ. А во время чтения какого-либо произведения он может вырастать до 50 дБ.

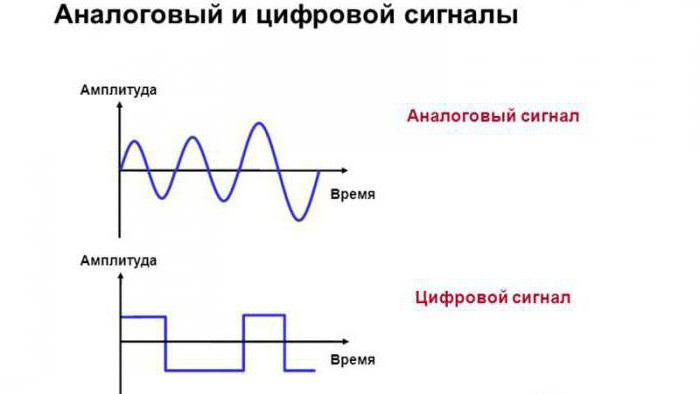
Аналоговый сигнал

Аналоговый сигнал является непрерывным во времени способом передачи данных. Недостатком его можно назвать присутствие шума, который иногда приводит к полной потере информации. Очень часто возникают такие ситуации, что невозможно определить, где в коде важные данные, а где обычные искажения.

Именно из-за этого цифровая обработка сигналов приобрела большую популярность и постепенно вытесняет аналоговую.

Цифровой сигнал

Цифровой сигнал является особым потоком данных, он описывается за счет дискретных функций. Его амплитуда может принять определенное значение из уже заданных. Если аналоговый сигнал способен поступать с огромным количеством шумов, то цифровой отфильтровывает большую часть полученных помех.

Помимо этого, такой вид передачи данных переносит информацию без лишней смысловой нагрузки. Через один физический канал может быть отправлено сразу несколько кодов.

Виды цифрового сигнала не существуют, так как он выделяется как отдельный и самостоятельный метод передачи данных. Он представляет собой двоичный поток. В наше время такой сигнал считается самым популярным. Это связано с простотой использования.

Применение цифрового сигнала

Чем же отличается цифровой электрический сигнал от других? Тем, что он способен совершать в ретрансляторе полную регенерацию. Когда в оборудование связи поступает сигнал, имеющий малейшие помехи, он сразу же меняет свою форму на цифровую. Это позволяет, например, телевышке снова сформировать сигнал, но уже без шумового эффекта.

В том случае, если код поступает уже с большими искажениями, то, к сожалению, восстановлению он не подлежит. Если брать в сравнении аналоговую связь, то в аналогичной ситуации ретранслятор может извлечь часть данных, затрачивая много энергии.

Обсуждая сотовую связь разных форматов, при сильном искажении на цифровой линии разговаривать практически невозможно, так как не слышны слова или целые фразы. Аналоговая связь в таком случае более действенна, ведь можно продолжать вести диалог.

Именно из-за подобных неполадок цифровой сигнал ретрансляторы формируют очень часто для того, чтобы сократить разрыв линии связи.

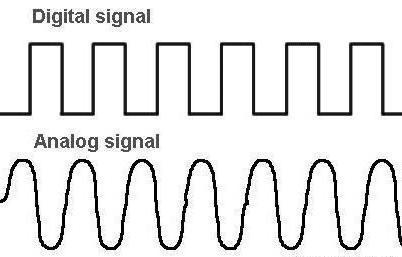
Дискретный сигнал

Сейчас каждый человек пользуется мобильным телефоном или какой-то «звонилкой» на своем компьютере. Одна из задач приборов или программного обеспечения – это передача сигнала, в данном случае голосового потока. Для переноса непрерывной волны необходим канал, который имел бы пропускную способность высшего уровня. Именно поэтому было предпринято решение использовать дискретный сигнал. Он создает не саму волну, а ее цифровой вид. Почему же? Потому что передача идет от техники (например, телефона или компьютера). В чем плюсы такого вида переноса информации? С его помощью уменьшается общее количество передаваемых данных, а также легче организуется пакетная отправка.

Понятие «дискретизация» уже давно стабильно используется в работе вычислительной техники. Благодаря такому сигналу передается не непрерывная информация, которая полностью закодирована специальными символами и буквами, а данные, собранные в особенные блоки. Они являются отдельными и законченными частицами. Такой метод кодировки уже давно отодвинулся на второй план, однако не исчез полностью. С помощью него можно легко передавать небольшие куски информации.

Сравнение цифрового и аналогового сигналов

Покупая технику, вряд ли кто-то думает о том, какие виды сигналов использованы в том или другом приборе, а об их среде и природе уж тем более. Но иногда все же приходится разбираться с понятиями.

Уже давно стало ясно, что аналоговые технологии теряют спрос, ведь их использование нерационально. Взамен приходит цифровая связь. Нужно понимать, о чем идет речь и от чего отказывается человечество.

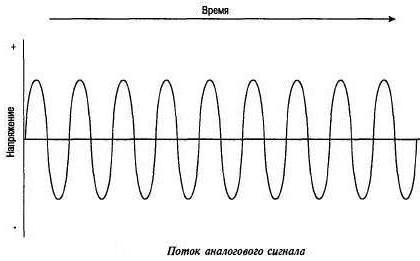
Если говорить коротко, то аналоговый сигнал – способ передачи информации, который подразумевает описание данных непрерывными функциями времени. По сути, говоря конкретно, амплитуда колебаний может быть равна любому значению, находящемуся в определенных границах.

Цифровая обработка сигналов описывается дискретными функциями времени. Иначе говоря, амплитуда колебаний этого метода равна строго заданным значениям.

Переходя от теории к практике, надо сказать о том, что аналоговому сигналу характерны помехи. С цифровым же таких проблем нет, потому что он успешно их «сглаживает». За счет новых технологий такой метод передачи данных способен своими силами без вмешательства ученого восстановить всю исходную информацию.

Говоря о телевидении, можно уже с уверенностью сказать: аналоговая передача давно изжила себя. Большинство потребителей переходят на цифровой сигнал. Минус последнего заключается в том, что если аналоговую передачу способен принимать любой прибор, то более современный способ – только специальная техника. Хоть и спрос на устаревший метод уже давно упал, все же такие виды сигналов до сих пор не способны полностью уйти из повседневной жизни.

Дискретность. Принципы и применение. Сигнал и работа.Особенности

Дискретность в переводе с латинского языка обозначает прерывистость. Данное понятие применяется в различных отраслях науки, в частности электронике, физике, биологии, математике и так далее. В электронике существует понятие дискретного сигнала, предусматривающее передачу информации в условиях изменения возможных значений передающей среды. Кроме этого прерывистость используется и в других более щепетильных сферах, к примеру, в микроэлектронике. В частности при разработке дискретных схем представляющих собой элементы линий связи.

Как применяется дискретность в электронике

Существующие современные технологии связи, в том числе и разработанные для этого компьютерные программы, обеспечивают передачу голоса, являющегося звуковым потоком. При этом разработчики подобного оборудования и программного обеспечения сталкиваются с тем, что голосовой поток это непрерывная волна, передача которой возможна только на канале с высокой пропускной способностью. Его применение слишком затратно как в плане ресурсов, так и финансово. Эта проблема решается использованием принципов дискретности.

Дискретный сигнал представляет собой вместо стандартной непрерывной волны специальное цифровое выражение, способное ее описать. С установленной частотой параметры волны конвертируются в цифровую информацию и отправляются для приема. Фактически, получается обеспечить связь с минимальным применением ресурсов и энергии.

Дискретность позволяет существенно уменьшить суммарный поток данных, формируя из него пакетную передачу. При этом благодаря тому, что соблюдается выборка волны с промежутками между работой и паузами, то исключается вероятность искажения. Создается гарантия, что отправленная часть пакетных данных будет доставлена по предназначению, а за ней уже передастся следующая часть. В случае же с обыкновенными волнами, возможность помех намного выше.

Примеры простейшей дискретности

Учебники по физике для объяснения понятия дискретности при применении его к сигналу зачастую приводят аналогию с печатной книгой. Так, при ее чтении воспринимается непрерывный поток изложенной информации. При этом фактически вся изложенная в ней информация это код, состоящий из набора букв, пробелов и знаков препинания. Изначально способ общения человека – это голос, но посредством письма возможно записать звук с помощью буквенного кода. При этом, если рассматривать в плане емкости в килобайтах или мегабайтах, то объем напечатанного текста будет занимать меньше места, чем его звуковая запись.

Возвращаясь к примеру с книгой получается, что ее автор создает определенный дискретный сигнал, разбивая звуковой поток на блоки и излагая их определенным способом кодирования, то есть письменным языком. Сам читатель открывающий книгу посредством своих знаний в кодировании и мысли объединяет дискретные буквы в непрерывный информационный поток. Данный пример весьма удачно помогает упрощенным языком объяснить зачем нужна дискретность и почему она так тесно связана с сигналами, применяемыми в электронике.

Простым примером визуальной дискретности можно назвать старые рисованные мультфильмы. Их кадр состоял из десятков картинок, которые шли друг за другом с небольшими паузами. Каждая последующая картинка немного изменяется, поэтому глазу человека кажется, что персонажи на экране двигаются. Именно благодаря дискретности вообще возможно формировать движущееся изображение.

Пример с рисованными мультфильмами отображает лишь часть свойства дискретности. Аналогичная технология применяется и при создании видео. Стоит вспомнить диафильмы или старые кинопленки, когда на одной длинной ленте идет множество маленьких картинок, при изменении которых создается эффект движения на экране. Хотя современные технологии и отошли от материальных носителей кадров такого плана, но по-прежнему используется принцип дискретности, хотя и видоизмененный.

Дискретный сигнал

Данное понятие позволяет отобразить противоположное явления непрерывному сигналу. При использовании непрерывности одним из проявлений выступает звуковая волна с определенной амплитудой и частотой, которая транслируется постоянно без пауз. Хотя и существует несколько вполне эффективных способов обработки непрерывного или так называемого аналогового сигнала, позволяющих уменьшить объем информационного потока, но они не так действенны. Использование дискретной переработки позволяет делать оборудование менее объемным и отказаться от дорогостоящих коммуникаций. В электронике понятие дискретный и цифровой сигнал это практически одно и то же.

К неоспоримым достоинствам дискретного сигнала можно отнести:

• Возможность избежать искажения информации.
• Обеспечение высокой помехоустойчивости, что возможно в результате применения кодирования информации.
• Возможность архивирования данных для сохранения ресурсов носителей.
• Обеспечение возможности трансляции информации из различных источников по единому каналу.
• Наличие упрощенного математического описания.

Не лишена дискретность и недостатков. При ее использовании требуется применение высоких технологий, в связи с чем ответственные детали электронных механизмов теряют возможность проведения кустарного ремонта. При серьезной поломке требуется замена отдельных агрегатов. Кроме этого возможна частичная потеря информации, которая заключена в дискретном сигнале.

Способы реализации дискретности при работе с сигналами

Как уже было выяснено, дискретный сигнал представляет собой последовательность цифровых закодированных значений. Существуют различные способы кодирования, но одним из самых популярных считаются двоичные цифровые сигналы. Они используются практически во всех электронных устройствах, поскольку легко кодируются и декодируются.

Дискретный цифровой сигнал имеет два значения «1» и «0». Для передачи данных создается импульсное напряжение. После генерации импульса принимающее его устройство воспринимает часть сигнала как «1», а последующую после этого паузу как «0». Декодирующая аппаратура оценивает частоту подаваемых импульсов и проводит их восстановление в изначальные данные. Если рассматривать график дискретного сигнала, можно увидеть, что переход между нулевым и максимальным значением происходит мгновенно. График состоит из прямоугольных углов, когда линия между верхним и нижним значением не имеет плавного перехода. Благодаря этому принимающая аппаратура считывает информацию четко, тем самым исключаются помехи, поскольку даже слабо принятый импульс будет читаться как максимум, то есть «1», а пауза как «0».

Хотя дискретность и способна значительно уменьшить образование помех, но не может исключить их полное отсутствие. Если имеется большой уровень шума цифрового потока, то восстановить данные из полученных сигналов невозможно. В случае же с непрерывными аналоговыми сигналами можно применять различные фильтры, чтобы убрать искажения и восстановить информацию. Именно поэтому принцип дискретности применяется далеко не всегда.

Техническая реализация принципов дискретности

Дискретные сигналы используются для записи на известные носители, такие как CD, DVD и так далее. Их читают цифровые проигрыватели, мобильные телефоны, модемы и практически любое техническое оборудование, которым все пользуются ежедневно. Все мультимедийные технологии состоят из устройств сжатия, кодировки и декодировки, что и позволяет работать с дискретными сигналами.

Даже те сферы, которые изначально использовали непрерывные технологии передачи данных, начинают отказываться от такого способа и внедряют дискретность. Вся современная аудиотехника работает именно по такому способу. Также происходит постепенный отказ от аналового телевещания. Отсутствие резкого перехода с одной технологии на вторую наблюдается благодаря тому, что дискретный сигнал можно обратно конвертировать в аналоговый. Это обеспечивает определенную совместимость разных систем.

Если рассматривать еще примеры оборудования, где применяются принципы дискретности, то к таким примерам можно отнести:

• Звуковые карты.
• Электронные музыкальные инструменты.
• Навигаторы.
• Цифровые фотоаппараты.

Сфера применения принципа дискретности очень обширна. В связи с этим оборудование, где он внедряется, значительно прогрессирует, при этом удобство применения такой аппаратуры многократно возрастает.

Похожие темы:

Курс лекций «Основы цифровой обработки сигналов» / Habr

Часто ко мне обращаются люди с вопросами по задачам из области цифровой обработки сигналов (ЦОС). Я подробно рассказываю нюансы, подсказываю нужные источники информации. Но всем слушателям, как показало время, не хватает практических задач и примеров в процессе познания этой области. В связи с этим я решил написать краткий интерактивный курс по цифровой обработке сигналов и выложить его в открытый доступ.

Большая часть обучающего материала для наглядного и интерактивного представления реализована с использованием Jupyter Notebook. Предполагается, что читатель имеет базовые знания из области высшей математики, а также немного владеет языком программирования Python.

Список лекций

Для пользователей MATLAB (GNU Octave) освоение материала с точки зрения программного кода не составит труда, поскольку основные функции и их атрибуты во многом идентичны и схожи с методами из Python-библиотек.

Все материалы сгруппированы по основным тематикам цифровой обработки сигналов:

1. Сигналы: аналоговые, дискретные, цифровые. Z-преобразование,
2. Преобразование Фурье: амплитудный и фазовый сигнала, ДПФ и БПФ,
3. Свертка и корреляция. Линейная и циклическая свертка. Быстрая свёртка
4. Случайные процессы. Белый шум. Функция плотности вероятностей
5. Детерминированные сигналы. Модуляция: АМ, ЧМ, ФМ, ЛЧМ. Манипуляция
6. Фильтрация сигналов: БИХ, КИХ фильтры
7. Оконные функции в задачах фильтрации. Детектирование слабых сигналов.
8. Ресемплинг: децимация и интерполяция. CIC-фильтры, фильтры скользящего среднего

Список лекций — достаточный но, разумеется, неполный для вводного знакомства с областью ЦОС. При наличии свободного времени я планирую поддерживать и развивать этот проект.

Где найти?

Ниже приводится очень краткое описание разделов курса с небольшими пояснениями, терминами и определениями. Основная информация доступна в исходных лекциях, здесь представлен лишь краткий обзор!

Сигналы. Z-преобразование

Все сигналы по способу представления на множестве можно разделить на четыре группы:

• аналоговые — описываются непрерывными во времени функциями,
• дискретные — прерываются во времени с шагом заданным дискретизации,
• квантованные — имеют набор конечных уровней (как правило, по амплитуде),
• цифровые — комбинация свойств дискретных и квантованных сигналов.

Для правильного восстановления аналогового сигнала из цифрового без искажений и потерь используется теорема отсчетов, известная как Теорема Котельникова (Найквиста-Шеннона).

Любой непрерывный сигнал с ограниченным спектром может быть восстановлен однозначно и без потерь по своим дискретным отсчетам, взятым с частотой строго больше удвоенной верхней частоты спектра непрерывного сигнала.

Также в этом разделе описывается Z-преобразование и его свойства, показывается представление дискретных последовательностей в Z-форме.

Пример конечной дискретной последовательности:

x(nT) = {2, 1, -2, 0, 2, 3, 1, 0}

X(z) = 2 + z^-1 — 2z^-2 + 2z^-4 + 3z^-5 + 1z^-6

Преобразование Фурье. Свойства. ДПФ и БПФ

В частности, в этом разделе описывается Python пакет scipy.ffpack для вычисления различных преобразований Фурье (синусное, косинусное, прямое, обратное, многомерное, вещественное).

Преобразование Фурье позволяет представить любую функцию в виде набора гармонических сигналов! Преобразование Фурье лежит в основе методов свертки и проектировании цифровых корреляторов, активно применяется при спектральном анализе, используется при работе с длинными числами.

Особенности спектров дискретных сигналов:
1. Спектральная плотность дискретного сигнала – периодическая функция с периодом, равным частоте дискретизации.
2. Если дискретная последовательность вещественная, то модуль спектральной плотности такой последовательности есть четная функция, а аргумент – нечетная функция частоты.

Спектр гармонического сигнала:

Сравнение эффективности ДПФ и БПФ

Любой сигнал произвольной формы можно представить в виде набора гармонических сигналов разных частот. Иными словами, сигнал сложной формы во временной области имеет набор комплексных отсчетов в частотной области, которые называются *гармоники*. Эти отсчеты выражают амплитуду и фазу гармонического воздействия на определенной частоте. Чем больше набор гармоник в частотной области, тем точнее представляется сигнал сложной формы.

Свертка и корреляция

В реальных задачах часто ставится вопрос о степени похожести одного процесса на другой или же о независимости одного процесса от другого. Иными словами, требуется определить взаимосвязь между сигналами, то есть найти корреляцию. Методы корреляции используются в широком диапазоне задач: поиск сигналов, компьютерное зрение и обработка изображений, в задачах радиолокации для определения характеристик целей и определения расстояния до объекта. Кроме того, с помощью корреляции производится поиск слабых сигналов в шумах.

Свертка описывает взаимодействие сигналов между собой. Если один из сигналов — импульсная характеристика фильтра, то свертка входной последовательности с импульсной характеристикой есть ни что иное, как реакция цепи на входное воздействие. Иными словами, результирующий сигнал отражает прохождение сигнала через фильтр.

Автокорреляционная функция (АКФ) находит применение в кодировании информации. Выбор кодирующей последовательности по параметрам длины, частоты и формы во многом обусловлен корреляционными свойствами этой последовательности. Наилучшая кодовая последовательность обладает наименьшим значением вероятности ложного обнаружения или срабатывания (для детектирования сигналов, для пороговых устройств) или ложной синхронизации (для передачи и приема кодовых последовательностей).

В этом разделе представлена таблица сравнения эффективности быстрой свертки и свертки, вычисляемой по прямой формуле (по числу вещественных умножений).

Как видно, для длин БПФ до 64, быстрая свёртка проигрывает у прямого метода. Однако, при увеличении длины БПФ результаты меняются в обратную сторону — быстрая свертка начинает выигрывать у прямого метода. Очевидно, чем больше длина БПФ, тем лучше выигрыш частотного метода.

Случайные сигналы и шум

Случайным сигналом называют функцию времени, значения которой заранее неизвестны и могут быть предсказаны лишь с некоторой вероятностью. К основным характеристикам случайных сигналов относятся:

• закон распределения (относительное время пребывания значения сигнала в определенном интервале),
• спектральное распределение мощности сигнала.

В задачах ЦОС случайные сигналы делятся на два класса:

• шумы — беспорядочные колебания, состоящие из набора разных частот и амплитуд,
• сигналы, несущие информацию, для обработки которых требуется прибегать к вероятностным методам.

С помощью случайных величин можно моделировать воздействие реальной среды на прохождение сигнала от источника к приёмнику данных. При прохождении сигнала через какое-то шумящее звено, к сигналу добавляется так называемый белый шум. Как правило, спектральная плотность такого шума равномерно (одинаково) распределена на всех частотах, а значения шума во временной области распределены нормально (Гауссовский закон распределения). Поскольку белый шум физически добавляется к амплитудам сигнала в выбранные отсчеты времени, он называется аддитивный белый гауссовский шум (AWGN — Additive white Gaussian noise).

Сигналы, модуляция и манипуляция

Для удобства на языке Python создан набор функций, осуществляющих перечисленные виды модуляции. Пример реализации ЛЧМ-сигнала:

def signal_chirp(amp=1.0, freq=0.0, beta=0.25, period=100, **kwargs):
    """
    Create Chirp signal

    Parameters
    ----------
    amp : float
        Signal magnitude
    beta : float
        Modulation bandwidth: beta < N for complex, beta < 0.5N for real
    freq : float or int
        Linear frequency of signal
    period : integer
        Number of points for signal (same as period)
    kwargs : bool
        Complex signal if is_complex = True
        Modulated by half-sine wave if is_modsine = True
    """
    is_complex = kwargs.get('is_complex', False)
    is_modsine = kwargs.get('is_modsine', False)

    t = np.linspace(0, 1, period)
    tt = np.pi * (freq * t + beta * t ** 2)
    
    if is_complex is True:
        res = amp * (np.cos(tt) + 1j * np.sin(tt))
    else:
        res = amp * np.cos(tt)

    if is_modsine is True:
        return res * np.sin(np.pi * t)
    return res

Также в этом разделе из теории передачи дискретных сообщений описаны виды цифровой модуляции — манипуляции. Как и в случае с аналоговыми сигналами, цифровые гармонические последовательности могут быть манипулированы по амплитуде, фазе и частоте (либо по нескольким параметрам сразу).

Цифровые фильтры — БИХ и КИХ

В разделе перечислены основные преимущества и недостатки цифровых фильтров (в сравнении с аналоговыми). Вводится понятие импульсной и передаточной характеристик фильтра. Рассматривается два класса фильтров — с бесконечной импульсной характеристикой (БИХ) и конечной импульсной характеристикой (КИХ). Показан способ проектирования фильтров по канонической и прямой форме. Для КИХ фильтров рассматривается вопрос о способе перехода к рекурсивной форме.

Для КИХ фильтров показан процесс проектирования фильтра от стадии разработки технического задания (с указанием основных параметров), до программной и аппаратной реализации — поиска коэффициентов фильтра (с учетом формы представления числа, разрядности данных и т.д.). Вводятся определения симметричных КИХ фильтров, линейной ФЧХ и её связи с понятием групповой задержки.

Оконные функции в задачах фильтрации

Чем сильнее подавление боковых лепестков спектра, тем шире главный лепесток спектра и наоборот.

Одно из применений оконных функций: обнаружение слабых сигналов на фоне более сильных путём подавления уровня боковых лепестков. Основные оконные функции в задачах ЦОС — **треугольное, синусоидальное, окно Ланцоша, Ханна, Хэмминга, Блэкмана, Харриса, Блэкмана-Харриса, окно с плоской вершиной, окно Наталла, Гаусса, Кайзера** и множество других. Большая часть из них выражена через конечный ряд путём суммирования гармонических сигналов с определенными весовыми коэффициентами. Такие сигналы отлично реализуются на практике на любых аппаратных устройствах (программируемые логические схемы или сигнальные процессоры).

Ресемплинг. Децимация и интерполяция

Децимация (прореживание) – понижение частоты дискретизации. Интерполяция – повышение частоты дискретизации.

Также в разделе рассматривается класс однородных КИХ фильтров, которые называются интегрально-гребенчатыми фильтрами (CIC, Cascaded integrator–comb). Показана реализация, основные свойства и особенности CIC фильтров. В силу линейности математических операций, происходящих в CIC фильтре возможно каскадное соединение нескольких фильтров подряд, что дает пропорциональное уменьшение уровня боковых лепестков, но также увеличивает «завал» главного лепестка амплитудно-частотной характеристики.

График АЧХ фильтра в зависимости от коэффициента децимации:

Также в этом разделе обсуждается вопрос увеличения разрядности данных на выходе CIC фильтра в зависимости от его параметров. Это особенно важно в задачах программной реализации, в частности на ПЛИС.

Для практической реализации CIC фильтров на Python разработан отдельный класс CicFilter, реализующий методы децимации и интерполяции. Также показаны примеры изменения частоты дискретизации с помощью встроенных методов из scipy пакета Python.

class CicFilter:
    """
    Cascaded Integrator-Comb (CIC) filter is an optimized class of
    finite impulse response (FIR) filter.
    CIC filter combines an interpolator or decimator, so it has some
    parameters:

    R - decimation or interpolation ratio,
    N - number of stages in filter (or filter order)
    M - number of samples per stage (1 or 2)*

    * for this realisation of CIC filter just leave M = 1.

    CIC filter is used in multi-rate processing. In hardware
    applications CIC filter doesn't need multipliers, just only
    adders / subtractors and delay lines.

    Equation for 1st order CIC filter:
    y[n] = x[n] - x[n-RM] + y[n-1].


    Parameters
    ----------
    x : np.array
        input signal
    """

    def __init__(self, x):
        self.x = x

    def decimator(self, r, n):
        """
        CIC decimator: Integrator + Decimator + Comb

        Parameters
        ----------
        r : int
            decimation rate
        n : int
            filter order
        """

        # integrator
        y = self.x[:]
        for i in range(n):
            y = np.cumsum(y)

        # decimator

        y = y[::r]
        # comb stage
        return np.diff(y, n=n, prepend=np.zeros(n))

    def interpolator(self, r, n, mode=False):
        """
        CIC inteprolator: Comb + Decimator + Integrator

        Parameters
        ----------
        r : int
            interpolation rate
        n : int
            filter order
        mode : bool
            False - zero padding, True - value padding.
        """

        # comb stage
        y = np.diff(self.x, n=n,
                    prepend=np.zeros(n), append=np.zeros(n))

        # interpolation
        if mode:
            y = np.repeat(y, r)
        else:
            y = np.array([i if j == 0 else 0 for i in y for j in range(r)])

        # integrator
        for i in range(n):
            y = np.cumsum(y)

        if mode:
            return y[1:1 - n * r]
        else:
            return y[r - 1:-n * r + r - 1]

Наконец, в этом разделе приведен особый класс фильтров — скользящего среднего. Показано три способа реализации: через свертку сигналов, с помощью КИХ-фильтра и БИХ-фильтра.

Заключение

Дополнительно к этому материалу я поддерживаю и развиваю свой проект по основным модулям ЦОС (на языке Python). Он содержит пакет генерации различных сигналов, класс CIC фильтров для задач децимации и интерполяции, алгоритм расчета коэффициентов корректирующего КИХ-фильтра, фильтр скользящего среднего, алгоритм вычисления сверх-длинного БПФ через методы двумерного преобразования (последнее очень пригодилось в работе при аппаратной реализации на ПЛИС).

Спасибо за внимание!

Цифровой сигнал — Википедия

Материал из Википедии — свободной энциклопедии

Цифровой сигнал — сигнал, который можно представить в виде последовательности дискретных (цифровых) значений. В наше время наиболее распространены двоичные цифровые сигналы (битовый поток) в связи с простотой кодирования и используемостью в двоичной электронике. Для передачи цифрового сигнала по аналоговым каналам (например, электрическим или радиоканалам) используются различные виды манипуляции (модуляции).

Важным свойством цифрового сигнала, определившего его доминирование в современных системах связи, является его способность к полной регенерации в ретрансляторе (до некоторого порогового отношения сигнал/шум). Когда в ретранслятор приходит сигнал с небольшими помехами, он преобразуется в цифровую форму, и ретранслятор заново формирует сигнал, полностью убирая искажения. Аналоговый же сигнал удаётся усилить лишь вместе с наложившимися на него шумами.

С другой стороны, если цифровой сигнал приходит с большими помехами, восстановить его невозможно (эффект крутой скалы (англ.)), в то время как из искаженного аналогового сигнала можно извлечь часть информации, хотя и с трудом. Если сравнивать сотовую связь аналогового формата (AMPS, NMT) с цифровой связью (GSM, CDMA), то при помехах на цифровой линии из разговора выпадают порой целые слова, а на аналоговой можно вести разговор, хотя и с помехами.

Выход из данной ситуации — чаще регенерировать цифровой сигнал, вставляя регенераторы в разрыв линии связи, или уменьшать длину линии связи (например, уменьшать расстояние от сотового телефона до базовой станции, что достигается более частым расположением базовых станций на местности).

Использование в цифровых системах алгоритмов проверки и восстановления цифровой информации позволяет существенно увеличить надёжность передачи информации.

что общего, в чём отличие типов сигнала

Вся информация в окружающем нас мире передаётся в виде сигналов: цифровых, аналоговых и дискретных. При этом разница между двумя последними для многих понятна не совсем и в этой статье мы попытаемся дать полные определения обоим типам передачи данных, а также выявить их сходства и различия.

Аналоговый сигнал

Для начала вспомним, что сигнальные данные – это коды, использующиеся для обмена какими-либо сообщениями в информационных или управленческих сферах деятельности. В электронике аналоговый тип кода используется при передаче электричества: при этом определённым величинам амплитуды и частоты звука, яркости цвета и света соответствуют определённые значения напряжения. Из-за этих соответствий данный тип передачи данных и прозвали аналоговым.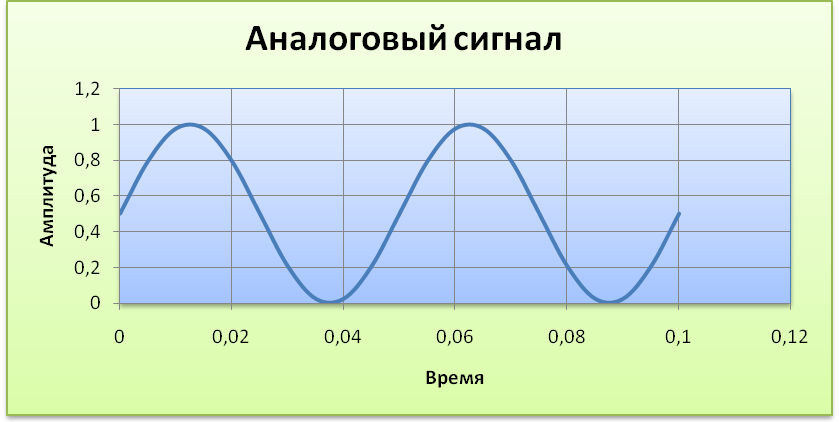

Интересно! Наш с вами мозг и нейронные связи в нём также работают с электричеством, а это значит, что обоняние, зрение, слух и запах мы можем чувствовать именно благодаря обработке мозгом аналоговых сигналов, поступающих к нему от органов чувств. По этому же принципу работает мозг и у животных.

В мире физики передачу данных при помощи сигнала можно отразить графически. В данном случае график будет представлять собой постоянно «скачущую» то вверх, то вниз кривую, не имеющую прямых углов. Похожие графики большинство из нас часто рисовало в школе на уроках физики и математики.

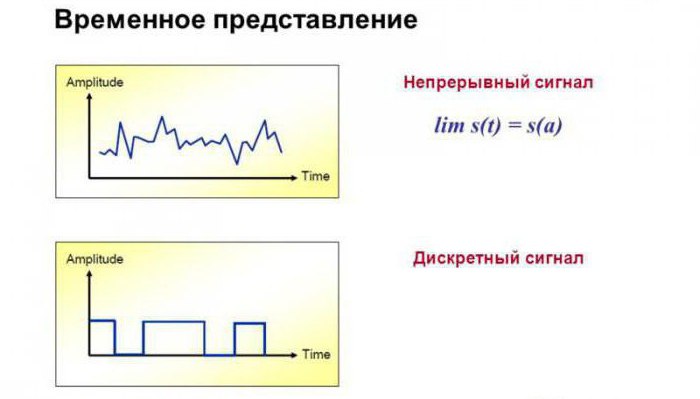
Дискретный сигнал

Латинская лексема discretus переводится на великий и могучий примерно как «разделённый», что даёт нам ключ к пониманию принципа работы дискретного кода. Если говорить о тех же графиках, то изображение дискретного сигнала будет сродни изображению аналогового, с той лишь разницей, что у первого кривая превратится в ступенчатую линию с прямыми углами и собственной амплитудой.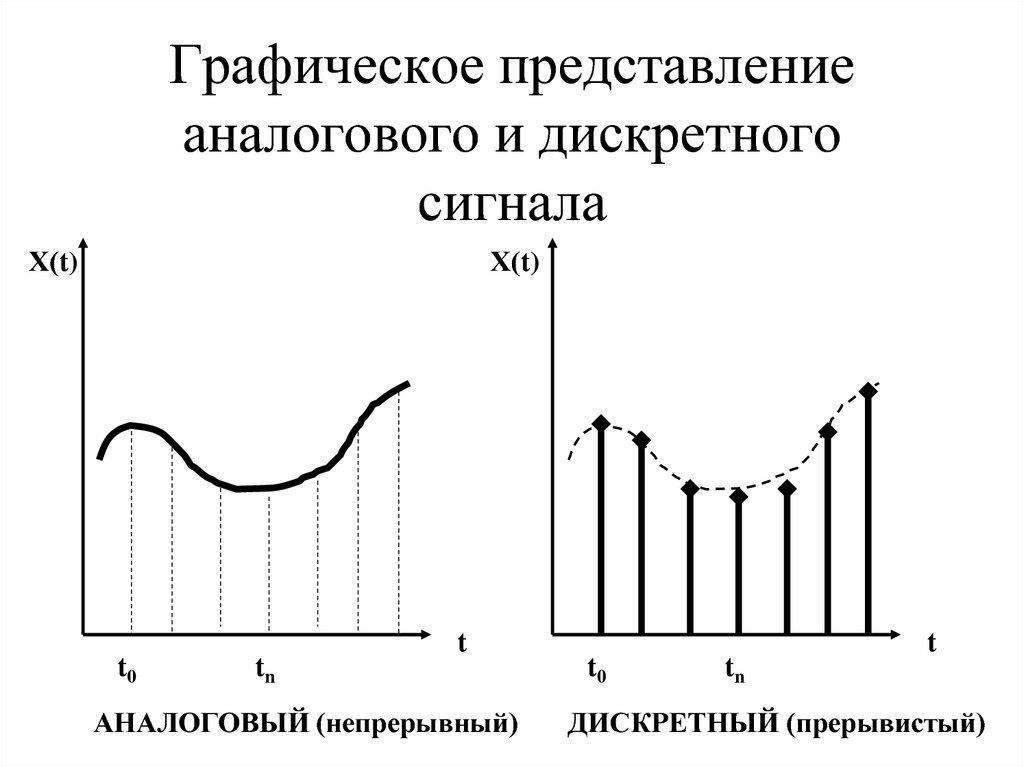

Дискретный способ передачи информации подразумевает либо изменение во времени при постоянной величине, либо, напротив, изменения по уровню без перерыва по времени.

Пример. В период, равный одной миллисекунде, дискретный сигнал равен какой-либо величине. По истечении этого времени сигнал резко изменяется в какую-либо сторону и остаётся неизменным ещё одну миллисекунду, после чего цикл повторяется.

Многие специалисты уточняют, что данный тип кода – промежуточное звено между аналоговым и цифровым способами передачи данных. Отчасти это так и есть, и многие из тех, кто родился раньше «нулевых» помнят, как в своё время все пользователи повально переходили на цифровое телевещание.

Что общего

Оба рассматриваемых нами в рамках данной статьи типа передачи данных служат одной общей цели: доставке какой-либо закодированной информации из одной точки физического пространства в другую. Также, если отразить «аналог» и «дискрет» графически, то их графики по амплитуде будут весьма похожи, если не принимать во внимание то, что дискретный будет состоять из ломаной кривой линии.

В чём отличие типов сигнала

Ключевая разница между двумя этими кодами заключается в том, что аналоговый сигнал никогда не прерывается по времени, в отличие от дискретного. Из этого различия вытекают и большинство преимуществ и недостатков одного кода перед другим. К примеру, дискретный тип:

• помехоустойчив и имеет небольшое количество значений;
• довольно просто и быстро расшифровывается принимающим оборудованием;
• пригоден к кодировке больших объёмов данных для их хранения либо передачи на большие расстояния.

При всех этих преимуществах у него есть один серьёзный недостаток: достаточной большой уровень помех в системе может спровоцировать обрыв, при котором первоначальный вид потока данных восстановить без специальных устройств уже не удастся.

Внимание! Цифровой тип передачи данных ни в коем случае не стоит путать с дискретным: цифровой способ используется как отдельный и самостоятельный метод передачи информации.

Если же говорить об аналоговом сигнале, то к его преимуществам относят простоту формирования и небольшую стоимость оборудования, которое с ним работает. Минусов у данного типа сигнала гораздо больше: он содержит большое количество лишней информации, которая фильтруется при приёме, обладает слабой помехоустойчивостью и часто поступает с искажениями (что особенно плохо в случае с передачей видеосигнала), а также его легко перехватить и расшифровать любым доступным устройством.

Справка! Современные технологии позволяют без особых усилий преобразовывать один тип кода в другой. Осуществляется данная процедура при помощи специальных преобразователей (например, аналогово-цифрового в звукозаписывающем оборудовании).

Если не вдаваться в особенности и нюансы, то можно заключить, что разница между аналоговым и цифровым сигналом заключается в их прерывности/непрерывности, разном графическом воплощении и в различающихся свойствах переданной информации.