Аналоговый, дискретный, цифровой сигналы

Понятие стыка цифровых АТС

ЦСК должна обеспечивать интерфейс (стык) с аналоговыми и цифровыми абонентскими линиями (АЛ) и системами передачи.

Стыком называется граница между двумя функциональными блоками, которая задается функциональными характеристиками, общими характеристиками физического соединения, характеристиками сигналов и другими характеристиками в зависимости от специфики.

Стык обеспечивает одноразовое определение параметров соединения между двумя уст­ройствами. Эти параметры относятся к типу, количеству и функциям соединительных цепей, а также к типу, форме и последовательности сигналов, которые передаются по этим цепям.

Точное определение типов, количества, формы и последовательности соединений и взаимосвязи между двумя функциональными блоками на стыке между ними задается спе­цификацией стыка.

Стыки цифровой АТС можно разделить на следующие

— аналоговый абонентский стык;

— цифровой абонентский стык;

— абонентский стык ISDN;

— сетевые (цифровые и аналоговые) стыки.

Кольцевые соединители

Кольцевые структуры находят применение в целом ряде областей связи. Прежде всего это кольцевые системы передачи с временным группообразованием, которые по существу имеют конфигурацию последовательно соединенных однонаправленных линий, образую­щих замкнутую цепь или кольцо. При этом в каждом узле сети реализуются две основные функции:

1) каждый узел работает как регенератор, чтобы восстановить входящий цифровой сиг­нал и передать его заново;

в узлах сети опознается структура цикла временного группообразования и осуществ­ляется связь по кольцу посредством

2) удаления и ввода цифрового сигнала в определенных канальных интервалах, приписанных к каждому узлу.

Возможность перераспределения канальных интервалов между произвольными парами узлов в кольцевой системе с временным группообразованием означает, что кольцо является распределенной системой передачи и коммутации. Идея одновременности передачи и ком­мутации в кольцевых структурах была распространена на цифровые коммутационные поля.

В такой схеме с помощью единственного канала между любыми двумя узлами может быть установлено дуплексное соединение. В этом смысле кольцевая схема выполняет про­странственно-временное преобразование координат сигнала и может быть рассмотрена как один из вариантов построения S/T-ступени.

В системах электросвязи информация передается с помощью сигналов. Международный союз электросвязи дает следующее определение сигнала:

Сигналом систем электросвязи называется совокупность электромагнитных волн, ко­торая распространяется по одностороннему каналу передачи и предназначена для воздей­ствия на приемное устройство.

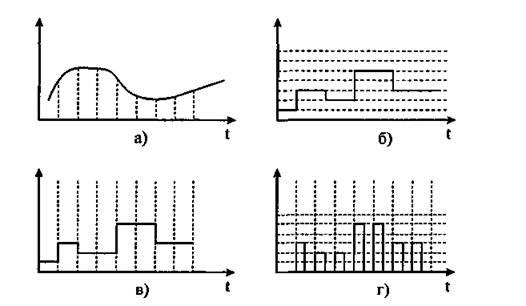
1) аналоговый сигнал — сигнал у которого каждый представляющий параметр задается функцией непрерывного времени с непрерывным множеством возможных значений

2) дискретный по уровню сигнал — сигнал, у которого значения представляющих пара­метров задается функцией непрерывного времени с конечным множеством возможных зна­чений. Процесс дискретизации сигнала по уровню носит название

квантования;

3) дискретный по времени сигнал — сигнал, у которого каждый представляющий пара­метр задается функцией дискретного времени с непрерывным множеством возможных зна­чений

4) цифровой сигнал — сигнал, у которого значения представляющих параметров задается функцией дискретного времени с конечным множеством возможных значений

 

 

Модуляция 

— это преобразование одного сигнала в другой путем изменения па­раметров сигнала-переносчика в соответствии с преобразуемым сигналом. В качестве сиг­нала-переносчика используют гармонические сигналы, периодические последовательности импульсов и т.д.

 

 

Например, при передаче по линии цифрового сигнала двоичным кодом может появиться постоянная составляющая сигнала за счет преобладания единиц во всех кодовых словах.

Отсутствие же постоянной составляющей в линии позволяет использовать согласующие трансформаторы в линейных устройствах, а также обеспечить дистанционное питание реге­нераторов постоянным током. Чтобы избавиться от нежелательной постоянной составляющей цифрового сигнала, перед посылкой в линию двоичные сигналы преобразуются с помощью специальных кодов. Для первичной цифровой системы передачи (ЦСП) принят код HDB3.

Кодирование двоичного сигнала в модифицированный квазитроичный сигнал с ис­пользованием кода HDB3 производится по следующим правилам (рис. 1.5).

 

 

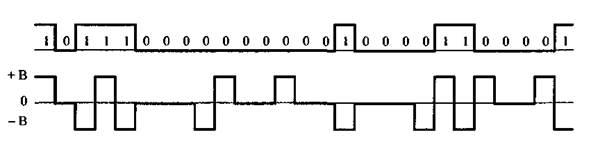
Рис. 1.5. Двоичный и соответствующий ему HDB3 коды

Импульсно-кодовая модуляция

Преобразование непрерывного первичного аналогового сигнала в цифровой код называется импульсно-кодовой модуляцией (ИКМ). Основными операциями при ИКМ являются операции дискретизации по времени, квантова­ния (дискретизации по уровню дискретного по времени сигнала) и кодирования.

Дискретизацией аналогового сигнала по времени называется преобразование, при кото­ром представляющий параметр аналогового сигнала задается совокупностью его значений в дискретные моменты времени, или, другими словами, при котором из непрерывного анало­гового сигнала c(t) (рис. 1.6, а) получают выборочные значения с„ (рис. 1.6, б). Значения представляющего параметра сигнала, полученные в результате операции дискретизации по времени, называются отсчетами.

Наибольшее распространение получили цифровые системы передачи, в которых при­меняется равномерная дискретизация аналогового сигнала (отсчеты этого сигнала произво­дятся через одинаковые интервалы времени). При равномерной дискретизации используют­ся понятия: 

интервал дискретизации At (интервал времени между двумя соседними отсче­тами дискретного сигнала) и частота дискретизации Fd (величина, обратная интервалу дискретизации). Величина интервала дискретизации выбирается в соответствии с теоремой Котельникова.

Согласно теореме Котельникова, аналоговый сиг­нал с ограниченным спектром и бесконечным интерва­лом наблюдения можно без ошибок восстановить из дискретного сигнала, полученного дискретизацией ис­ходного аналогового сигнала, если частота дискретиза­ции в два раза больше максимальной частоты спектра аналогового сигнала:

 

Теорема Котельникова

Теоре́ма Коте́льникова (в англоязычной литературе — теорема Найквиста-Шеннона) гласит, что, если аналоговый сигнал x(t) имеет ограниченный спектр, то он может быть восстановлен однозначно и без потерь по своим дискретным отсчѐтам, взятым с частотой более удвоенной максимальной частоты спектра Fmax.

дискретизация, квантование, кодирование. 5. Цифровые системы передачи. Основы построения телекоммуникационных систем и сетей

В настоящее время во всём мире развивается цифровая форма передачи сигналов: цифровая телефония, цифровое кабельное телевидение, цифровые системы коммутации и системы передачи, цифровые сети связи. Качество цифровой связи значительно выше, чем аналоговой, так как цифровые сигналы гораздо более помехоустойчивы: нет накопления шумов, легко обрабатываются, цифровые сигналы можно «сжимать», что позволяет в одной полосе частот организовать больше каналов с высокой скоростью передачи и отличным качеством.

Цифровой сигнал – это последовательность импульсов. Общепринято импульсную последовательность представлять как чередование двух символов: 0 и 1. «Binary Digit» – «двоичная цифра». Отсюда и пошло понятие бит, то есть одна позиция в цифровом сигнале есть 1 бит; это может быть либо 0, либо 1. Восемь позиций в цифровом сигнале определяется понятием байт [1].

При передаче цифровых сигналов вводится понятие скорости передачи – это количество бит, передаваемых в единицу времени (в секунду).

Для передачи непрерывных сообщений цифровыми методами необходимо произвести преобразование этих сообщений в дискретные, которое осуществляется путём дискретизации непрерывных сигналов во времени и квантования их по уровню, и преобразования квантованных отсчётов в цифровой сигнал [6].

Дискретизация сигналов заключается в замене непрерывного сообщения u_к(t) последовательностью его отсчётов, то есть последовательностью импульсов, модулированных по амплитуде (смотри рисунок 5.1, а). Частота дискретизации F_д выбирается из условия (4.4.1). Полученный аналоговый АИМ сигнал u

АИМ(iT_д), где i = 1, 2, 3 …, приведённый на рисунке 5.1, а, затем подвергается операции квантования, которая состоит в замене отсчётов мгновенных значений сигнала u_АИМ (iT_д) дискретными значениями u₀, u₁, u₂ … u₇ разрешённых уровней u_кв (iT_д). В процессе квантования мгновенные значения АИМ сигнала уровней u_АИМ(iT_д) заменяются ближайшими разрешёнными уровнями сигнала u_кв(iT_д) (смотри рисунок 5.1, а).

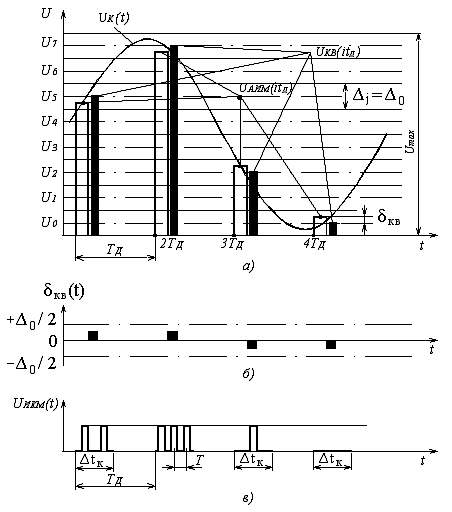
Рисунок 5.1. Принцип ИКМ: а – дискретизация; б – ошибка квантования; в – цифровой сигнал с ИКМ

Такое преобразование первичных сигналов можно называть квантованной амплитудно-импульсной модуляцией (КАИМ). Особенностью такого сигнала является то, что все его уровни можно пронумеровать и тем самым свести передачу КАИМ-сигнала к передаче последовательностей номеров уровней, которые этот сигнал принимает в моменты i∙t_д.

Расстояние между ближайшими разрешёнными уровнями квантования (u₀ … u₇ на рисунке 5.1, а) ∆ называется шагом квантования. Шкала квантования называется равномерной, если все шаги квантования равны между собой ∆_j = ∆₀ [5].

Если в момент взятия i-го отсчёта мгновенное значение непрерывного сообщения u_к(t_i) удовлетворяет условию

u_j – ∆_j/2 ≤ u_АИМ(iT_д) ≤ u_j + ∆_j/2, (5.1)

то квантованному импульсу u_кв(iT_д) присваивается амплитуда разрешённого u_j уровня квантования (смотри рисунок 5.1, а). При этом возникает ошибка квантования δ_кв, представляющая разность между передаваемой квантованной величиной u_кв(iT_д) и истинным значением непрерывного сигнала в данный момент времени u_АИМ(iT_д) (смотри рисунок 5.1, б):

δ_кв(iT_д) = u_кв(iT_д) – u_АИМ(iT_д). (5.2)

Как следует из рисунков 5.1, б и (5.1), ошибка квантования лежит в пределах

–∆₀/2 ≤ δ_кв ≤ ∆₀/2. (5.3)

Амплитудная характеристика квантующего устройства при равномерной шкале квантования приведена на рисунке 5.2, а. Она имеет ступенчатую форму, и при изменении непрерывного сообщения u_к(t) и соответствующего ему АИМ сигнала u_АИМ(iT_д) в пределах одной ступени выходной сигнал остаётся постоянным, а при достижении границы этой ступени изменяется скачком на величину шага квантования. При этом ошибка квантования зависит от u_к(t) и имеет вид, изображённый на рисунке 5.2, б.

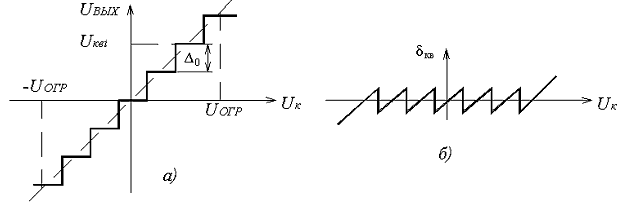
Рисунок 5.2. Амплитудная характеристика квантователя (а) и зависимость ошибки квантования от амплитуды импульсов (б)

Как следует из рисунка 5.2, б, из-за нелинейности амплитудной характеристики квантователя ошибка квантования δ_кв представляет собой функцию с большим числом резких скачков, частота следования которых существенно выше частоты исходного сообщения u_к(t), то есть при квантовании происходит расширение спектра сигнала. При этом соседние боковые полосы будут накладываться друг на друга и в полосу пропускания ФНЧ на выходе канала попадут составляющие спектра искажений от квантования, распределение которых в полосе ФНЧ считается равномерным. Поскольку практически все дискретные значения непрерывного сообщения находятся в пределах зоны квантования от –u_огр до +u_огр, то при равномерной шкале квантования ∆_j = ∆₀ и тогда:

Ркв = (1/12) ∆²₀. (5.4)

Из выражения (5.4) видно, что при равномерной шкале квантования мощность шума квантования не зависит от уровня квантуемого сигнала и определяется только шагом квантования ∆₀.

Рассмотрим теперь кодирование и декодирование сигналов. Следующий шаг в преобразовании сигнала состоит в переводе квантованного АИМ-сигнала в цифровой. Эта операция называется кодированием АИМ-сигнала. Кодом называется закон, устанавливающий соответствие между квантованной амплитудой и структурой кодовой группы [8].

Различают равномерный и неравномерный коды. Если все кодовые группы состоят из равного числа символов, то код называется равномерным. Если же кодовые группы состоят из различного числа символов, то код называется неравномерным. В системах передачи с импульсно-кодовой модуляцией, как правило, используется равномерный двоичный код.

Для определения структуры двоичной кодовой комбинации на выходе кодера в простейшем случае необходимо в двоичном коде записать амплитуду АИМ отсчётов, выраженную в шагах квантования

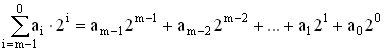, (5.5)

где a_i = {0,1} – состояние соответствующего разряда комбинации; 2ⁱ – вес соответствующего разряда в шагах квантования.

Если в десятичной системе «вес» каждой позиции числа равен числу десять в некоторой степени, то в двоичной системе вместо числа десять используют число два. «Веса» первых тринадцати позиций двоичного числа имеют следующие значения:

Таблица – 5.1

212	211	210	29	28	27	26	25	24	23	22	21	20
4096	2048	1024	512	256	128	64	32	16	8	4	2	1

По принципу действия кодеры делятся на кодеры счётного типа, матричные, взвешивающего типа и другие. Наиболее часто используются кодеры взвешивающего типа, простейшим из которых является кодер поразрядного взвешивания (рисунок 5.3), реализующий функцию (5.5) с формирования натурального двоичного кода [5]. Принцип работы такого кодера заключается в уравновешивании кодируемых АИМ отсчётов суммой эталонных напряжений. Схема линейного кодера поразрядного взвешивания содержит восемь ячеек (при m = 8), обеспечивающих формирование значения коэффициента а_i соответствующего разряда (5.5). В состав каждой ячейки (за исключением последней, соответствующей младшему по весу разряду) входит схема сравнения СС и схема вычитания СВ.

Схема сравнения обеспечивает сравнение амплитуды поступающего АИМ сигнала с эталонными сигналами, амплитуды которых равны весам соответствующих разрядов

U_эт8 = 2⁷∆ = 128∆; U_эт7 = 2⁶∆ = 64∆; … U_эт1 = 2⁰∆ = 1∆.

Если на входе СС_i амплитуда поступающего АИМ сигнала равна или превышает U_этi, то на выходе схемы сравнения формируется «1», а в СВ_i из входного сигнала вычитается U_этi, после чего он поступает на вход следующей ячейки. Если же амплитуда АИМ сигнала на входе СС_i меньше U_этi, то на выходе СС_i формируется «0» и АИМ сигнал проходит через СВ_i без изменений. После окончания процесса кодирования текущего отсчёта на выходе кодера получается восьмиразрядный параллельный код, кодер устанавливается в исходное состояние и начинается кодирование следующего отсчёта.

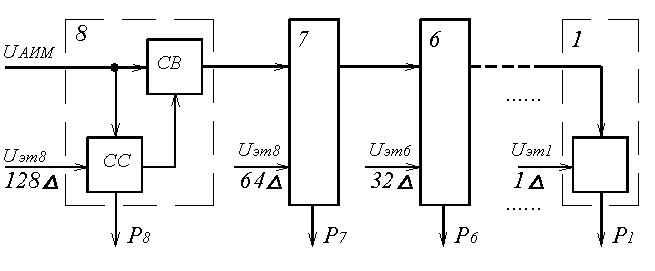
Рисунок 5.3. Линейный кодер поразрядного действия

Если, например, на вход кодера поступил АИМ отсчёт с амплитудой U_АИМ = 185∆, то СС₈ формирует Р₈ = 1 и на вход седьмой ячейки поступил сигнал с амплитудой U_АИМ = 185∆ – 128∆ = 57∆. На выходе СС₇ сформируется Р₇ = 0 и на вход шестой ячейки кодера поступит сигнал с той же амплитудой U_АИМ = 57∆. На выходе СС₆ сформируется Р₆ = 1 и на вход следующей ячейки поступит сигнал с амплитудой U_АИМ = 57∆ – 32∆ = 25∆ и так далее. В результате будет сформирована кодовая комбинация 10111001.

В процессе декодирования сигнала m – разрядные кодовые комбинации преобразуются в АИМ отсчёты соответствующей амплитуды [4]. Сигнал на выходе декодера получается в результате суммирования эталонных сигналов U_этi тех разрядов кодовой комбинации, значения которых равно 1 (рисунок 5.4). Так, если на вход декодера поступила кодовая комбинация 10111001, то амплитуда АИМ отсчёта на его выходе будет равна U_АИМ = 128∆ + 32∆ + 16∆ + 8∆ + 1∆ = 185∆.

В линейном декодере (рисунок 5.4) под воздействием управляющих сигналов, поступающих от генераторного оборудования, в регистр сдвига записывается очередная восьмиразрядная кодовая комбинация. В момент прихода импульса считывания замыкаются только те ключи Кл₁ … Кл₈, которые соответствуют разрядам, имеющим значения «1». В результате в сумматоре объединяются соответствующие эталонные напряжения и на его выходе получается соответствующая амплитуда АИМ отсчёта.

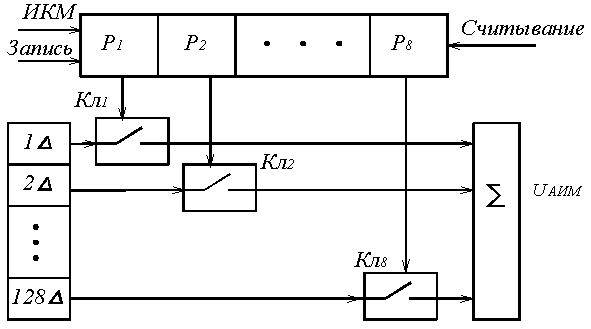
Рисунок 5.4. Линейный декодер взвешивающего типа

Рассмотренная схема кодера (рисунок 5.3) поразрядного взвешивания содержит большое число схем сравнения, которые являются относительно сложными устройствами. На практике чаще используется кодер взвешивающего типа с одной схемой сравнения и цепью обратной связи, содержащей декодер. Как следует из выражения (5.4), мощность шума квантования при линейном кодировании будет равной при различных амплитудах квантованных сигналов. Для синусоидальных сигналов отношение сигнал/шум квантования, рассчитывается по формуле:

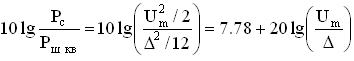, (5.6)

где U_m – амплитуда квантуемого сигнала.

Из формулы видно, что для слабых входных сигналов это отношение гораздо хуже, чем для сигналов большой амплитуды. Для устранения этого недостатка было предложено использовать неравномерное квантование, то есть изменять шаг квантования пропорционально изменению амплитуды входного сигнала.

Для кодирования с неравномерной шкалой квантования могут быть использованы:

• прямое нелинейное кодирование, при котором кодер сочетает в себе функции аналого-цифрового преобразования (АЦП) и компрессора;
• аналоговое компандирование, при котором компрессирование сигнала осуществляется перед линейным кодером и экспандирование сигнала после линейного декодера;
• преобразование на основе линейного кодирования, при котором кодирование сигнала осуществляется в линейном кодере с большим числом разрядов с последующим цифровым компандированием [5].

Переменную величину шага квантования можно получить с помощью устройства с нелинейной амплитудной характеристикой (рисунок 5.5) (которая называется компрессором, поскольку сжимает динамический диапазон входного сигнала) и равномерного квантователя (смотри рисунок 5.2). На приёмной стороне осуществляется расширение динамического диапазона экспандером, имеющим характеристику, противоположную компрессору, что обеспечивает линейность системы передачи. Совокупность операций сжатия динамического диапазона компрессором и расширение его экспандером называется компадированием сигнала.

В настоящее время в системах ВРК с ИКМ применяется характеристика компадирования типа А (рисунок 5.5).

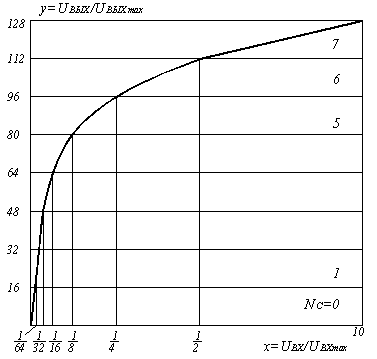
Рисунок 5.5. Характеристика компрессирования типа А

На этом рисунке сегментированная характеристика компрессии типа А для положительных сигналов (для отрицательных сигналов характеристика имеет аналогичный вид). Общее число сегментов характеристики N_с = 16, однако четыре центральных сегмента (по два в положительной и отрицательной областях) имеют одинаковый шаг квантования и фактически образуют один сегмент, вследствие чего число сегментов равно N_с = 13. Поэтому такая характеристика получила название типа А = 87.16/13. В центральном сегменте (N_с =1 или 2) значение ∆₀ минимально (то есть равно ∆₀) и соответствует равномерной двенадцатиразрядной шкале (m = 12), а в каждом последующем сегменте к краям характеристики шаг квантования увеличивается вдвое.

Представление ИКМ сигнала восьмиразрядными кодовыми комбинациями использует формат «знак – абсолютное значение», где один разряд отображает полярность АИМ сигнала П, а остальные – определяют его абсолютное значение. Семь разрядов, отображающих абсолютное значение, подразделяются на определитель номера сегмента С из трёх разрядов и определитель шага квантования К из четырёх разрядов (рисунок 5.6).

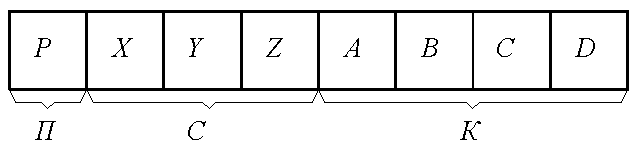
Рисунок 5.6. Формат восьмиразрядной ИКМ комбинации

Для реализации такого кодера необходимо задать величины эталонных напряжений для нижней границы каждого сегмента и при кодировании внутри сегмента (таблица 5.2).

Схемы и принцип действия нелинейных кодеков взвешивающего типа в основном те же, что и у линейных кодеков. Отличие заключается в последовательности включения эталонных напряжений в процессе кодирования исходного сигнала [5].

Таблица 5.2. Эталонные напряжения для нелинейного кодека

Номер сегмента Nс	Эталонное напряжение нижней границы сегмента	Эталонные напряжения при кодировании в пределах сегмента
		8∆i(A)	4∆i(B)	2∆iI(С)	∆i(D)
0	0	8∆0	4∆0	2∆0	1∆0
1	16∆0	8∆0	4∆0	2∆0	1∆0
2	32∆0	16∆0	8∆0	4∆0	2∆0
3	64∆0	32∆0	16∆0	8∆0	4∆0
4	128∆0	64∆0	32∆0	16∆0	8∆0
5	256∆0	128∆0	64∆0	32∆0	16∆0
6	512∆0	256∆0	128∆0	64∆0	32∆0
7	1024∆0	512∆0	256∆0	128∆0	64∆0

Таким образом, максимальный шаг квантования (в седьмом сегменте) в 64 раза превышает минимальный шаг квантования, а отношение сигнал/шум квантования (для максимального значения синусоидального сигнала) может быть определено по выражению (5.6) и составит: для второго сегмента

Р_с – Р_шкв = 7.78 + 20lg(А/∆) = 7.78 + 20 lg(32∆₀/∆₀) = 37.88 дБ;

Для седьмого сегмента

Р_с – Р_шкв = 7.78 + 20 lg(2048∆₀/64∆₀) = 37.88 дБ.

Зависимость отношения сигнал/шум квантования от уровня входного сигнала при компадировании по закону А = 87.6/13 приведена на рисунке 5.7. Для сигналов в пределах нулевого и первого сегментов осуществляется равномерное квантование с шагом ∆₀, поэтому Р_с – Р_шкв увеличивается с ростом р_с. При переходе ко второму сегменту шаг квантования увеличивается в два раза, вследствие чего Р_с – Р_шкв резко уменьшается на 6 дБ, а затем в пределах данного сегмента возрастает с ростом р_с, поскольку внутри сегмента осуществляется равномерное квантование. После попадания сигнала в зону ограничения отношение сигнал/шум резко уменьшается за счёт перегрузки кодера.

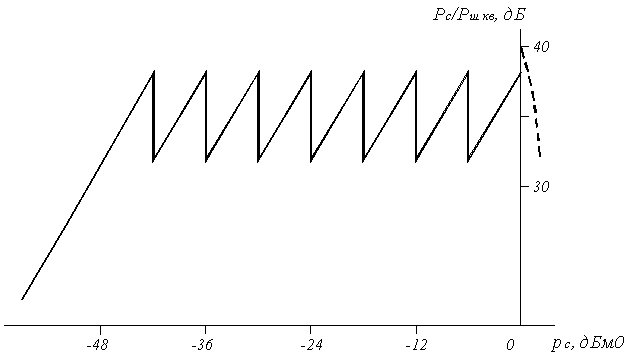
Рисунок 5.7. Зависимость Р_с/Р_{ш кв} = f(р_с)

На рисунке 5.8 представлена упрощённая схема нелинейного кодера взвешивающего типа, реализующего прямое кодирование АИМ сигнала.

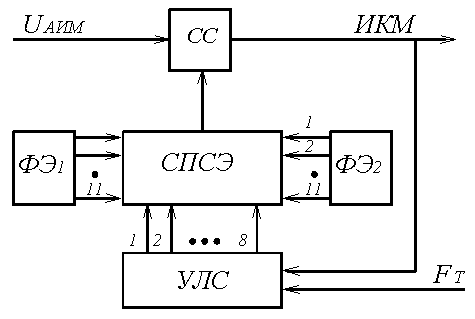
Рисунок 5.8. Нелинейный кодер взвешивающего типа

Кодирование осуществляется за восемь тактовых интервалов, в каждом из которых формируется один из символов кодовой комбинации (рисунок 5.6). В первом такте определяется знак поступившего на вход кодера отсчёта. Если отсчёт положительный, то в знаковом разряде формируется «1» и к схеме переключения и суммирования эталонов СПСЭ подключается формирователь положительных эталонных напряжений ФЭ₁, в противном случае формируется «0» и к схеме подключается ФЭ₂. Затем происходит формирование кода номера сегмента методом деления их числа пополам (рисунок 5.9).

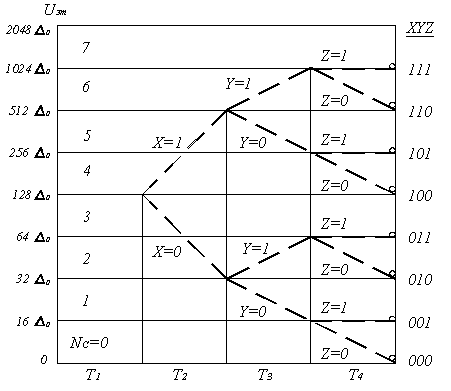
Рисунок 5.9. Алгоритм формирования кода номера сегмента

Во втором такте управляющая логическая схема УЛС и СПСЭ обеспечивают подачу на вход схемы сравнения эталонного сигнала U_эт = 128 ∆₀, соответствующего нижней границе четвёртого (среднего) сегмента. Если амплитуда отсчёта U_АИМ ≥ U_эт = 128 ∆₀, то принимается решение, что амплитуда отсчёта попадёт в один из четырёх вышележащих сегментов и формируется очередной символ X = 1, который по цепи обратной связи поступает на вход УЛС. В противном случае принимается решение, что амплитуда отсчёта попадает в один из нижележащих сегментов и формируется X = 0.

В третьем такте в зависимости от значения предыдущего символа X уточняется номер сегмента, в который попадает амплитуда кодируемого отсчёта. Если X = 1, то УЛС и СПСЭ подают на вход СС эталонное напряжение U_эт = 512 ∆₀, соответствующего нижней границе шестого сегмента. При этом, если U_АИМ ≥ U_эт = 512 ∆₀ то принимается решение, что отсчёт попадает в один из двух вышележащих сегментов и формируется очередной символ Y = 1. В противном случае, если U_АИМ ≤ U_эт = 512 ∆₀, принимается решение, что отсчёт попадает в два нижележащих сегмента и формируется Y = 0.

Если же X = 0, то УЛС с помощью СПСЭ обеспечивает подачу на вход СС эталонного напряжения U_эт = 32 ∆₀, соответствующего нижней границе второго сегмента. Если U_АИМ ≥ U_эт = 32 ∆₀, то принимается решение, что отсчёт попадает во второй и третий сегменты и формируется Y = 1. Если U_АИМ ≤ U_эт = 32 ∆₀, то принимается решение, что отсчёт попадает в два нижележащих сегмента и формируется Y = 0.

В четвёртом такте аналогичным образом формируется символ Z и окончательно формируется код номера сегмента. В результате, после четырёх тактов кодирования, сформируется четыре символа восьмиразрядной кодовой комбинации PXYZ (рисунок 5.6) и к СС подключается одно из восьми эталонных напряжений, соответствующих нижней границе сегмента, в котором находится кодируемый отсчёт.

В оставшихся четырёх тактах последовательно формируются символы ABCD кодовой комбинации, значения которых зависят от номера шага квантования внутри сегмента, соответствующего амплитуде кодируемого отсчёта. Поскольку внутри любого сегмента осуществляется равномерное квантование, то процесс кодирования реализуется, как и в линейных кодерах взвешивающего типа, путём последовательного включения эталонных напряжений соответствующих данному сегменту (таблица 5.2).

Практикум на применение нелинейного кодера при компадировании по закону А = 87.6/13:

Например, если на вход кодера поступил положительный отсчёт с амплитудой U_АИМ = 889 ∆₀, то после первых четырёх тактов сформируются символы PXYZ = 1110 и к СС подключится эталонное напряжение U_эт = 512 ∆₀, соответствующее нижней границе шестого сегмента, поскольку кодируемый сигнал находится в этом сегменте. В пятом такте к этому эталонному сигналу добавляется максимальное эталонное напряжение U_эт = 256 ∆₀, соответствующее символу А в определителе шага квантования К (рисунок 5.6) шестого сегмента (таблица 5.2). Так как U_АИМ > U_эт = (512 +256) ∆₀, то формируется символ А = 1 и это эталонное напряжение остаётся включенным. В шестом такте подключается эталонное напряжение соответствующее символу В в определителе шага квантования U_эт = 128 ∆₀ и так как U_АИМ > U_эт = (512 +256 + 128) ∆₀, то на выходе СС формируется символ В = 1 и это эталонное напряжение остаётся включенным. В седьмом такте подключается эталонное напряжение соответствующее символу С в определителе шага квантования U_эт = 64 ∆₀ и так как U_АИМ < U_эт = (512 +256 + 128 + 64) ∆₀, то на выходе СС формируется символ С = 0. В восьмом такте вместо U_эт = 64 ∆₀ подключается эталонное напряжение соответствующее символу D в определителе шага квантования U_эт = 32 ∆₀ и так как U_АИМ < U_эт = (512 +256 + 128 + 32) ∆₀, то на выходе СС формируется символ D = 0 и это эталонное напряжение отключается и на этом процесс кодирования очередного отсчёта заканчивается. При этом на выходе кодера сформирована кодовая комбинация PXYZABCD = 11101100, соответствующая амплитуде уравновешивающего АИМ сигнала на входе СС U_АИМ = 896 ∆₀. Разница между входным и уравновешивающим АИМ сигналами на входах СС представляет ошибку квантования δ_кв = U_АИМ – U_АИМ = 7∆₀.

Цифровая обработка сигналов — Википедия

Материал из Википедии — свободной энциклопедии

Цифрова́я обрабо́тка сигна́лов (ЦОС, DSP — англ. digital signal processing) — способы обработки сигналов на основе численных методов с использованием цифровой вычислительной техники.^[1][2]

Любой непрерывный (аналоговый) сигнал s(t){\displaystyle s(t)} может быть подвергнут дискретизации по времени и квантованию по уровню (оцифровке), то есть представлен в цифровой форме. Если частота дискретизации сигнала Fd{\displaystyle F_{d}} не меньше, чем удвоенная наивысшая частота в спектре сигнала Fmax{\displaystyle F_{max}} (то есть Fd≥2⋅Fmax{\displaystyle F_{d}\geq 2\cdot F_{max}}, см. теорему Найквиста — Шеннона — Котельникова), то полученный дискретный сигнал s(k){\displaystyle s(k)} эквивалентен сигналу s(t){\displaystyle s(t)} в том смысле, что s(t){\displaystyle s(t)} может быть в точности восстановлен из s(k){\displaystyle s(k)}.

При помощи математических алгоритмов s(k){\displaystyle s(k)} преобразуется в некоторый другой сигнал s1(k){\displaystyle s_{1}(k)}, имеющий требуемые свойства. Процесс преобразования сигналов называется фильтрацией, а устройство, выполняющее фильтрацию, называется фильтром. Поскольку отсчёты сигналов поступают с постоянной скоростью Fd{\displaystyle F_{d}}, фильтр должен успевать обрабатывать текущий отсчёт до поступления следующего, то есть обрабатывать сигнал в реальном времени. Для обработки сигналов (фильтрации) в реальном времени применяют специальные вычислительные устройства — цифровые сигнальные процессоры.

Всё это полностью применимо не только к непрерывным сигналам, но и к прерывистым, а также к сигналам, записанным на запоминающие устройства. В последнем случае скорость обработки непринципиальна, так как при медленной обработке данные не будут потеряны.

Различают методы обработки сигналов во временной (англ. time domain) и в частотной (англ. frequency domain) области. Эквивалентность частотно-временных преобразований однозначно определяется через преобразование Фурье.

Обработка сигналов во временной области широко используется в современной электронной осциллографии и в цифровых осциллографах. Для представления сигналов в частотной области используются цифровые анализаторы спектра. Для изучения математических аспектов обработки сигналов используются пакеты-расширения (чаще всего под именем Signal Processing) систем компьютерной математики MATLAB, Octave, Mathcad, Mathematica, Maple и др.

В последние годы при обработке сигналов и изображений широко используется новый математический базис представления сигналов с помощью «коротких волночек» — вейвлетов. С его помощью могут обрабатываться нестационарные сигналы, сигналы с разрывами и иными особенностями, сигналы в виде пачек.

• Линейная фильтрация — селекция (выбор) сигнала в частотной области; синтез (создание) фильтров, согласованных с сигналами; частотное разделение каналов; цифровые преобразователи Гильберта (Lⁿ(a, b)) и дифференциаторы; корректоры характеристик каналов.
• Спектральный анализ — обработка речевых, звуковых, сейсмических, гидроакустических сигналов; распознавание образов.
• Частотно-временной анализ — компрессия (сжатие) изображений, гидро- и радиолокация, разнообразные задачи обнаружения сигнала.
• Адаптивная фильтрация — распознавание речи, изображений, распознавание образов, подавление шумов, адаптивные антенные решётки.
• Нелинейная обработка — вычисление корреляций, медианная фильтрация; синтез амплитудных, фазовых, частотных детекторов, обработка речи, векторное кодирование.
• Многоскоростная обработка — интерполяция (увеличение) и децимация (уменьшение) частоты дискретизации в многоскоростных системах телекоммуникации, аудиосистемах.
• Свёртка традиционных типов.
• Секционная свёртка.
• Обнаружение сигнала — задача обнаружения сигнала на фоне шумов и помех.^[3]
• Различение сигнала — задача распознавания сигнала на фоне других сигналов, с подобными характеристиками.^[3]
• Оценивание сигнала — задача определения характеристик сигнала (амплитуда, частота, фаза).^[3]

Цифровая обработка сигнала в передатчике^[4]

Распространение сигналов по каналу связи

Цифровая обработка сигнала в приёмнике^[4]

1. ↑ Арбузов С. М., Гук И., Соловьева И., Солонина А. И., Улахович Д. А. Основы цифровой обработки сигналов. Курс лекций. — СПб.: БХВ-Петербург, 2003. — 576 с. — ISBN 5-94157-388-X.
2. ↑ Глинченко, А. С. Цифровая обработка сигналов. — Красноярск. — ISBN 978-5-7638-1271-8.
3. ↑ ^{1 2 3} Богданович В. А., Вострецов А. Г. Теория устойчивого обнаружения, различения и оценивания сигналов. — 2-е изд., испр.. — М.: Физматлит, 2004. — 320 с. — ISBN 5-9221-0505-8.
4. ↑ ^{1 2} Скляр Б. Цифровая связь. Теоретические основы и практическое применение. Пер. с англ. — М.: Издательский дом «Вильямс», 2003. — 1104 с. — С. 33. — ISBN 5-8459-0497-8

• Ричард Лайонс Цифровая обработка сигналов: Второе издание. Пер. с англ. — М.: Бином-Пресс, 2006 г. — 656 с.: ил.
• Солонина А. И., Клионский Д. М., Меркучева Т. В., Перов С. Н., Цифровая обработка сигналов и MATLAB, 2013 г.
• Стивен Смит Цифровая обработка сигналов. Практическое руководство для инженеров и научных работников. Додэка XXI, 2008. — 720 с. ISBN 978-5-94120-145-7, ISBN 0-750674-44-X
• Юкио Сато Без паники! Цифровая обработка сигналов. Додэка XXI, 2010. — 176 с. ISBN 978-5-94120-251-5, ISBN 4-274-08674-7
• Сергиенко А. Б. Цифровая обработка сигналов. — 2-е. — СПб.: Питер, 2007. — С. 751. — ISBN 5-469-00816-9.
• Гольденберг Л. М. и др. Цифровая обработка сигналов. Справочник. — М.: Радио и связь, 1985. — 312 с.
• Гольденберг Л. М. и др. Цифровая обработка сигналов. Учебное пособие для вузов. — М.: Радио и связь, 1990. — 256 с.
• Оппенгейм А., Шафер Р. Цифровая обработка сигналов. Изд. 2-е, испр. — М.: Техносфера, 2007. — 856 с. ISBN 978-5-94836-135-2
• Оппенгейм А. В., Шафер Р. В. Цифровая обработка сигналов. — М.: Связь, 1979. — 416 с.
• Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов. — М.: Мир, 1978. — 848 с.
• Глинченко А. С. Цифровая обработка сигналов. В 2 ч. — Красноярск: Изд-во КГТУ, 2001. — 383 с.
• Блейхут Р. Быстрые алгоритмы цифровой обработки сигналов. — М.: Мир, 1989. — 448 с.
• Даджион Д., Мерсеро Р. Цифровая обработка многомерных сигналов. — М.: Мир, 1988. — 488 с.
• Макс Ж. Методы и техника обработки сигналов при физических измерениях. В 2-х тт. — М.: «Мир», 1983.
• Марпл-мл. С. Л. Цифровой спектральный анализ и его приложения. — М.: МИР, 1990. — С. 584.
• Хемминг Р. В. Цифровые фильтры. — М.: Недра, 1987. — 221 с.
• Дьяконов В. П. MATLAB 6.5 SP1/7.0 + Simulink 5/6/ Обработка сигналов и проектирование фильтров. — М.: СОЛОН-Пресс, 2005. — 676 с.
• Дьяконов В. П. Вейвлеты. От теории к практике. Изд.е 2-ое дополненное и переработанное. — М.: СОЛОН-Пресс, 2005. — 400 с.
• Дьяконов В. П. Современная осциллография и осциллографы. — М.: СОЛОН-Пресс, 2004. — 320 с.
• Афонский А. А., Дьяконов В. П. Измерительные приборы и массовые электронные измерения / Под ред. проф. В. П. Дьяконова. — М.: СОЛОН-Пресс, 2007. — 544 с.
• Афонский А. А., Дьяконов В. П. Цифровые анализаторы спектра, сигналов и логики / Под ред. проф. В. П. Дьяконова. — М.: СОЛОН-Пресс, 2009. — 248 с.
• Богданович В. А., Вострецов А. Г. Теория устойчивого обнаружения, различения и оценивания сигналов. 2-е изд., испр. — М.: Физматлит, 2004. — 320 с. — ISBN 5-9221-0505-8.

Что такое дискретный сигнал?

С дискретностью каждый из нас сталкивается ежедневно. Это одно из свойств, присущее материи. В дословном переводе с латинского языка слово discretus означает прерывистость. Например, дискретный сигнал — это способ передачи информации, когда среда-переносчик изменяется во времени, принимая любое из существующего списка допустимых значений.

Конечно, термин «дискретность» применяется в более широком смысле. В частности, сейчас прогресс в микроэлектронике направлен на создание и развитие технологии SOC – «Система на чипе». Предполагается, что все составляющие устройство компоненты между собой тесно интегрированы на единой подложке. Противоположность такого подхода – дискретные схемы, когда элементы сами являются завершенными изделиями, соединяясь линиями связи.

Пожалуй, сейчас невозможно найти человека, который бы не пользовался мобильным телефоном или программой Скайп на компьютере. Одна из их задач – это передача звукового потока (в частности, голоса). Но так как такой звук представляет собой непрерывную волну, для его непосредственной передачи потребовался бы канал с высокой пропускной способностью. Для решения этого вопроса было предложено использовать дискретный сигнал. Формирует он не волну, а ее цифровое представление (помните, речь идет о мобильных телефонах и компьютерах). С волны через определенные промежутки времени выполняются выборки значений данных. То есть, создается дискретный сигнал. Его преимущество очевидно: меньший суммарный поток данных и возможность организации пакетной передачи. Целевое приемное устройство объединяет все выборки в единый блок, генерируя исходную волну. Чем больше промежутки между выборками, тем выше вероятность искажения исходной волны. Дискретизация широко используется в вычислительной технике.

Говоря о том, что такое дискретный сигнал, нельзя не воспользоваться замечательной аналогией с обычной печатной книгой. Человек, читая ее, получает непрерывный поток информации. В то же время, содержащиеся в ней данные «закодированы» в виде определенных последовательностей букв – слов – предложений. Получается, что автор из неделимой мысли формирует своеобразный дискретный сигнал, так как выражает ее разбиением на блоки, используя тот или иной способ кодировки (алфавит, язык). Читатель в данном примере получает возможность воспринимать идею автора только после мысленного объединения слов в поток информации.

Наверняка, вы читаете эту статью с экрана компьютера. А ведь даже экран монитора может служить примером, где проявляется дискретность и непрерывность. Вспомним старые модели, основанные на ЭЛТ. В них изображение формировалось последовательностью кадров, которые необходимо было «отрисовывать» несколько десятков раз в секунду. Очевидно, что данное устройство использует дискретный способ построения картинки.

Дискретный сигнал является полной противоположностью непрерывному. Последний представляет собой функцию интенсивности от времени (если представить его на декартовой плоскости). Как уже указывалось, одним из примеров может служить звуковая волна. Она характеризуется частотой и амплитудой, однако естественным образом нигде не прерывается. Большинство природных процессов описываются именно таким способом. Несмотря на то, что, все-таки, существует несколько способов обработки непрерывного (или аналогового) сигнала, позволяющих уменьшить поток данных, в современных цифровых системах распространен именно дискретный. Отчасти благодаря тому, что его можно достаточно просто преобразовать в исходный, независимо от конфигурации последнего. Кстати, стоит отметить, что термины «дискретный» и «цифровой» практически равнозначны.

Что такое цифровой и аналоговый сигнал?

Сегодня попытаемся разобраться, что такое аналоговый и цифровой сигналы? Их преимущества и недостатки. Не будем кидаться различными научными терминами и определениями, а попытаемся разобраться в ситуации на пальцах.

Что такое аналоговый сигнал?

Аналоговый сигнал основан на аналогии электрического сигнала (значений тока и напряжения) значению исходного сигнала (цвету пикселя, частоте и амплитуде звука и т.п). Т.е. определенные значения тока и напряжения соответствуют передаче определенного цвета пикселя или звукового сигнала.

Приведу пример на аналоговом видеосигнале.

Напряжение на проводе 5 вольт соответствует синему цвету, 6 вольт – зеленому, 7 вольт красному.

Для того чтобы на экране появились красные, синие и зеленые полосы нужно поочередно подавать на кабель напряжения 5, 6, 7 вольт. Чем быстрее мы проводим смену напряжений, тем тоньше полоски получаются у нас на мониторе. Сократив интервал между сменой напряжений до минимума, мы получим уже не полоски, а чередующиеся друг за другом цветные точки.

Важной особенностью аналогового сигнала является то обстоятельство, что он передается строго от передатчика к приемнику (например, от антенны к телевизору), обратной связи нет. Поэтому если в передачу сигнала вмешается помеха (например, вместо шести вольт придет четыре), цвет пикселя исказится, и на экране появится рябь.
Аналоговый сигнал непрерывен.
Что такое цифровой сигнал?

Передача данных осуществляется также с помощью электрического сигнала, но значений этих сигналов всего два и они соответствуют 0 и 1. Т.е. по проводам передается последовательность из нулей и единиц. Примерно так: 01010001001 и т. д. Для того чтобы приемное устройство (например, телевизор) не запутался в передаваемых данных, цифры передаются пачками. Это происходит примерно так: 10100010 10101010 10100000 10111110. Каждая такая пачка несет какую-нибудь информацию, например — цвет пикселя. Важной особенностью цифрового сигнала, является то, что передающие и принимающее устройство могут общаться между собой и исправлять друг за другом ошибки, которые могут возникнуть при передаче.

Примеры передачи цифрового и аналогового сигналов

Для цифрового сигнала передача происходит примерно так:

• Видеомагнитофон: Эй, телевизор, цвет пикселя с координатами 120х300 — зеленый.
• Помеха: АААААААААААААА!
• Телевизор: Какой? Не слышу!
• Видеомагнитофон: Зеленый!
• Телевизор: Ага, понял! Рисую зеленый.
• Видеомагнитофон: Следующий цвет красный!
• Телевизор: Прошу подтвердить, что цвет красный.
• Видеомагнитофон: подтверждаю.
• Телевизор: Ок! рисую.

и. т. д.

Передача для аналогового сигнала:

• Видеомагнитофон: Эй, телевизор, цвет пикселя с координатами 120х300 — зеленый.
• Помеха: АААААААААААААА!
• Телевизор: Какой? Не слышу! Блин, нарисую синий.
• Видеомагнитофон: Следующий цвет красный!
• Помеха: БАХ! БУМ!
• Телевизор: Красный вроде! Рисую.
• Видеомагнитофон: Лопата!
• Помеха: ПШШШШШШ!
• Телевизор: ?!. Надо что-то рисовать ?! Пусть будет лопата!

Преимущества и недостатки цифрового и аналогового сигналов

Из вышесказанного можно сделать вывод, что при прочих равных условиях качество передачи информации с помощью цифры будет выше, чем при аналоговом представлении сигнала. В то же время при хорошей помехозащищенности две технологии могут конкурировать на равных.