Устройство сбора дискретных сигналов УСДД-24.01

Купить Устройство сбора дискретных сигналов УСДД-24.01 от производителя с доставкой по России

Устройство сбора дискретных сигналов УСДД-24.01 производит сбор и обработку показаний, которые поступают от с 10-ти дискретных и 16-ти потенциальных входов модуля. Полученные сведения отправляются в сеть при помощи интерфейса RS-485 при появлении соответствующего запроса от другого устройства. Управление устройством сбора сигналов реализовано через программу-конфигуратор (настройка передачи данных по RS-485, тестовые опросы входов, проведение инверсии входных данных).

УСДД-24.01 используется в АИИС КУЭ, интеллектуальных системах мониторинга и управления жизнеобеспечением загородных домов и прочих систем умного дистанционного управления. Устройство обеспечивает заявленные параметры при следующих условиях окружающей среды:

• температура окружающего воздуха –20°С..+40°С;
• влажность воздуха при +25°С (30..80)%;
• атмосферное давление (84..100) кПа.

Особенности:

Питание устройства осуществляется подачей необходимого напряжения на контакты “+48V”, “–48V”. При этом на контактах “+12V”, “–12V” появляется напряжение +12V, которое может быть использовано для питания внешних устройств, например УСДД-24АС.01. Другим вариантом питания устройства является подача необходимого напряжения на контакты “+12V”, “–12V”. При этом подача напряжения на контакты “+48V”, “–48V”

недопустима.

Порядок установки:

ВНИМАНИЕ: Если к устройству подключаются сигналы, имеющие опасное напряжение, необходимо все монтажные работы производить при отключенном питании.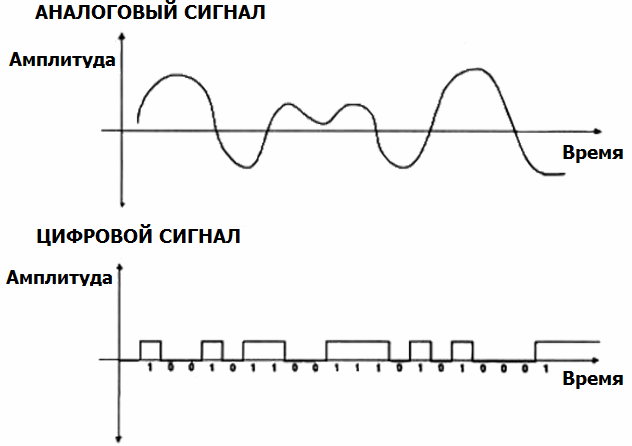

• При проведении монтажных и пусконаладочных работ необходимо пользоваться проектной документацией на систему мониторинга.
• Установить устройство на DIN-рейку.
• Связь прибора по интерфейсу RS-485 выполнять по двухпроводной схеме. Подключение следует осуществлять витой парой проводов, соблюдая полярность. Провод А подключается к выводу А прибора, аналогично соединяются между собой выводы В. Подключение необходимо производить при отключенном питании обоих устройств.
• Соединить входы устройства с дискретными датчиками (сухие контакты) и/или с потенциальными контактами (мокрые контакты), руководствуясь проектной документацией на систему мониторинга.
• Подключить датчик температуры согласно рисунку 2 руководства по эксплуатации.

Купить УСДД-24.01​ от компании IcbCom

Мы предлагаем приобрести устройство сбора дискретных сигналов УСДД-24.01 по выгодным ценам. «АйСиБиКом» — это гарантия качества и долговечности продукции.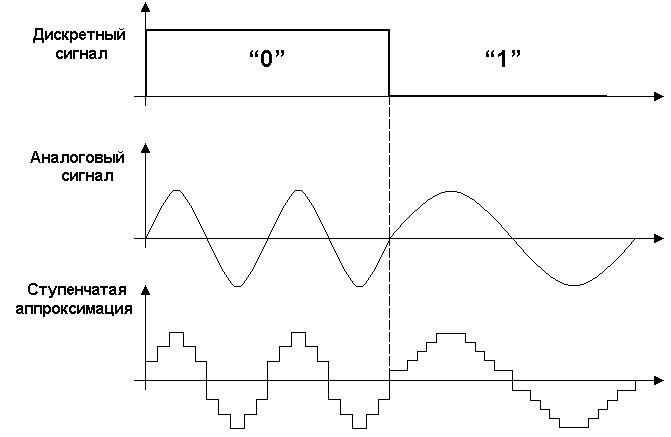

Доставка осуществляется по Москве и другим городам России. Более подробную информацию (точную стоимость, способ доставки, условия сотрудничества) вы можете узнать у наших менеджеров по телефону 8-800-775-19-75 или сделав запрос на коммерческое предложение через сайт. ​

Наименование характеристики	Значение
Рабочий диапазон температур	от — 20 до + 40 °С
Напряжение	– вариант1: на контактах “+48V”, “–48V +18,0…+72,0В – вариант2: на контактах “+12V”, “–12V”
Интерфейс	RS-485
Скорость передачи данных по интерфейсу	9600 бит/с
Потребляемый ток	не более 20 мА
Допустимое напряжение для потенциальных входов	0…50 В
Монтаж	на DIN рейку 35мм.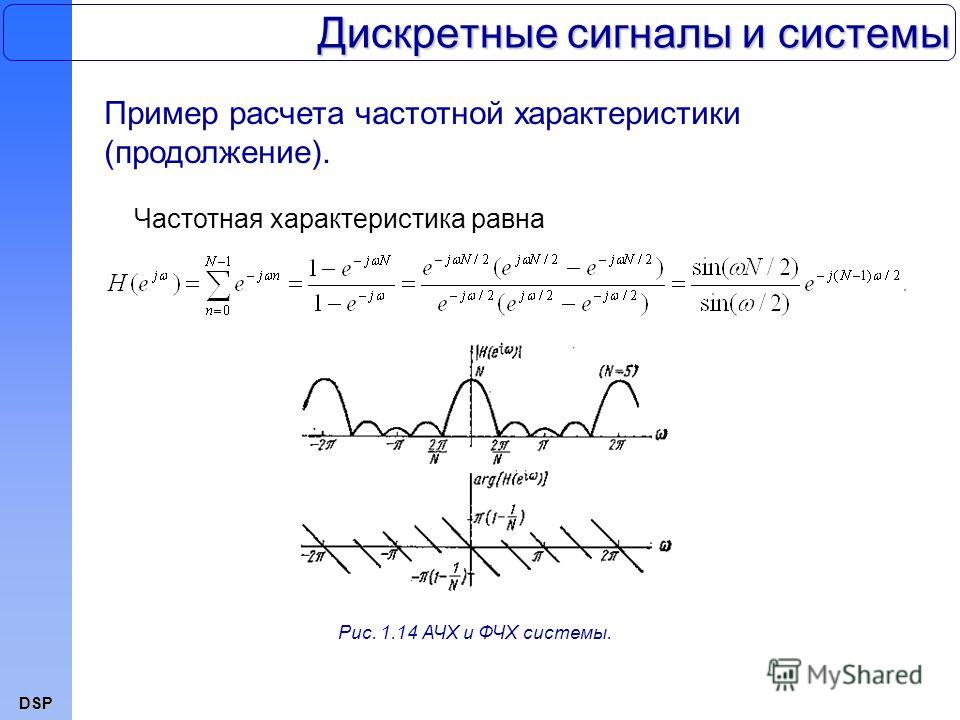 Положение в пространстве произвольное.
Средняя наработка на отказ	не менее 150000 ч
Срок службы	20 лет
Масса устройства	не более 0,25 кг

Сопутствующие товары

Ваше сообщение успешно отправлено!

МОДУЛЬ ДИСКРЕТНЫХ СИГНАЛОВ. 4 ВХОДА И 2 РЕЛЕЙНЫХ ВЫХОДА. НАПРЯЖЕНИЕ ВХОДОВ DC 24V. БИСТАБИЛЬНЫЕ РЕЛЕЙНЫЕ ВЫХОДЫ. МАКСИМАЛЬНО ВОЗМОЖНО 2 МОДУЛЯ ДИСКРЕТНЫХ СИГНАЛОВ ДЛЯ ОДНОГО БАЗОВОГО МОДУЛЯ 2

Код товара 1464708

Артикул 3UF7310-1AB00-0

Страна Германия

Наименование МОДУЛЬ ДИСКРЕТНЫХ СИГНАЛОВ.

4 ВХОДА И 2 РЕЛЕЙНЫХ ВЫХОДА. НАПРЯЖЕНИЕ ВХОДОВ DC 24V. БИСТАБИЛЬНЫЕ РЕЛЕЙНЫЕ ВЫХОДЫ. МАКСИМАЛЬНО ВОЗМОЖНО 2 МОДУЛЯ ДИСКРЕТНЫХ СИГНАЛОВ ДЛЯ ОДНОГО БАЗОВОГО МОДУЛЯ 2

Упаковки  

Сертификат RU C-DE.АЖ26.B03033-01

Масса, кг 0.146

Степень защиты IP20

Характеристики

Код товара 1464708

Артикул 3UF7310-1AB00-0

Страна Германия

Наименование МОДУЛЬ ДИСКРЕТНЫХ СИГНАЛОВ.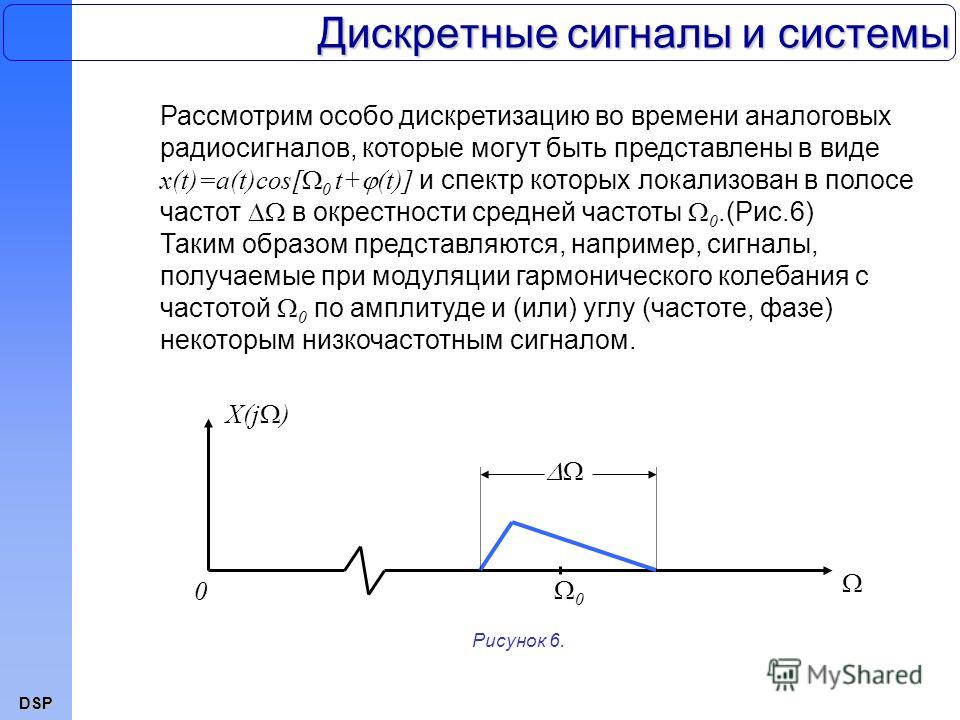 4 ВХОДА И 2 РЕЛЕЙНЫХ ВЫХОДА. НАПРЯЖЕНИЕ ВХОДОВ DC 24V. БИСТАБИЛЬНЫЕ РЕЛЕЙНЫЕ ВЫХОДЫ. МАКСИМАЛЬНО ВОЗМОЖНО 2 МОДУЛЯ ДИСКРЕТНЫХ СИГНАЛОВ ДЛЯ ОДНОГО БАЗОВОГО МОДУЛЯ 2

Упаковки  

Сертификат RU C-DE.АЖ26.B03033-01

Масса, кг 0.146

Степень защиты IP20

Всегда поможем:
Центр поддержки
и продаж

Скидки до 10% +

баллы до 10%

Доставка по городу
от 150 р.

Получение в 150
пунктах выдачи

К-3201 Модуль ввода дискретных сигналов

	Цена: по запросу
	Модуль ввода дискретных сигналов К-3201 обеспечивает ввод дискретных сигналов, и вывод данных по интерфейсу RS-485.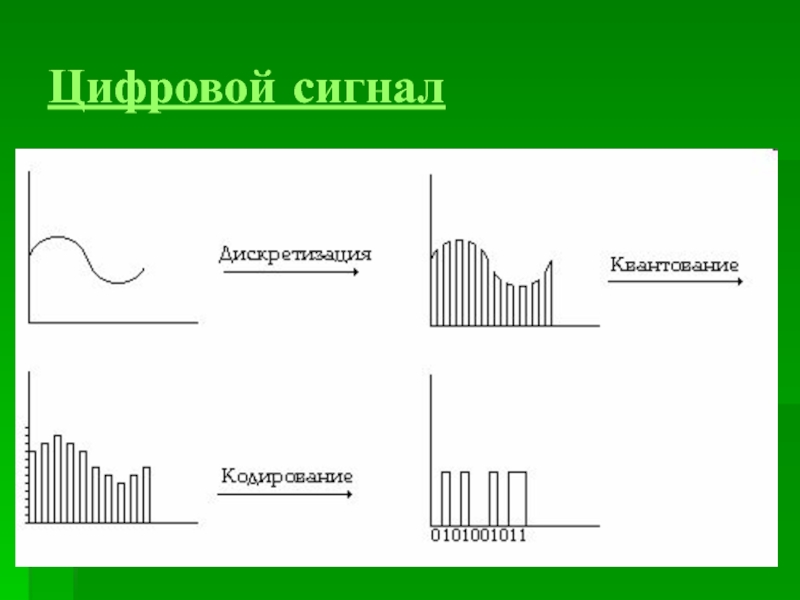

Назначение: 

Модуль К-3201 предназначен для выполнения функций ввода дискретных сигналов, и вывод данных по интерфейсу RS-485.
Модуль К-3201 предназначен для встраивания в состав шкафов автоматики и стоек технических средств контроля, сигнализации, управления и защиты, объединенных в сеть интерфейсами RS-485 с аппаратурой верхнего ровня.

Технические характеристики: 

Кол-во входов дискретных сигналов	16
Количество групп входов	4
Количество входов в группе	4
Номинальное напряжение входных сигналов	24 В
Диапазон тока входных сигналов	10-20 мА
Напряжение срабатывания, В, не менее	21
Напряжение отпускания, В, не более	17
Настройка входного фильтра, сек	Откл; 0,5; 1; 2
Интерфейс	RS-485
Протокол	Modbus RTU
Скорость обмена, бод	2400-230400
Гальваническая развязка	500 В
Номинальное напряжение питания	24 В
Диапазон напряжения питания	18. ..36 В
Потребляемая мощность, не более	3 Вт
Диапазон температур эксплуатации	— 40..70°С
Габаритные размеры, не более	150x80x40 мм
Масса, не более	0,4 кг

Техническая документация: 

Паспорт на модуль К-3201
Руководство по эксплуатации на модуль К-3201

Смежные продукты:

Комплекс технических средств автоматизации КТС СА
Комплекс технических средств охранно-пожарной сигнализации и управления пожаротушением КТС-2000
Контроллер К-2000/М

Аналоговые и дискретные сигналы: вжух! и в облаке!

Быстрая и надежная передача аналоговых и дискретных сигналов
ввода/вывода в облако

Все больше и больше полевых устройств подключаются к промышленному Интернету вещей (IIot), в связи с чем появилась необходимость обеспечения стабильного подключения этих «вещей» к Интернету. Поэтому была сделана ставка на те сетевые устройства, которые могут оставаться подключенными к сети, и, в случае неожиданного сбоя, могут восстановить связь без непосредственного вмешательства персонала. Хотя сами данные являются самым важным аспектом любого приложения ввода/вывода, прежде чем их можно будет использовать, они должны быть получены со всех промышленных датчиков и устройств. Устройства Moxa серии ioThinx 4500 представляют собой модульные контроллеры и модульные системы ввода/вывода аналоговых и дискретных сигналов для приложений IIoT, при этом главными особенностями ioThinx являются поддержка различных языков программирования, работа с облачными сервисами, высокая вычислительная мощность для точного управления и высокий уровень кибербезопасности в масштабе всей системы. Устройства ioThinx разработаны для того, чтобы помочь IIoT-системам быстро и безопасно передавать данные с устройств ввода/вывода в облако.

Контроллеры IIoT серии ioThinx 4533

Процессор	NXP i. MX7D 1ГГц
Рабочее напряжение	Питание устройства: 12 ~ 48 В пост. Питание исполнительных устройств: 12/24 В пост.
Макс. кол-во модулей ввода/вывода	64
Операционная система	Linux kernel 4.4 (CIP, PREEMPT_RT), Debian 9
ОЗУ	512 MB DDR3
Встроенная flash-память	8 Гб eMMC (6 Гб свободны для пользователя)
Поддержка языков программирования	C/C++, Python
Рабочая температура	Стандартные модели: -20/+60°C Модели с расширенным диапазоном температур: -40/+75°C

Подключение к облаку	Язык программирования	Точность управления	Кибербезопасность системы
Сохраняйте информацию с устройства сбора данных в облаке с помощью встроенных библиотек Azure/AWS/Alibaba SDK.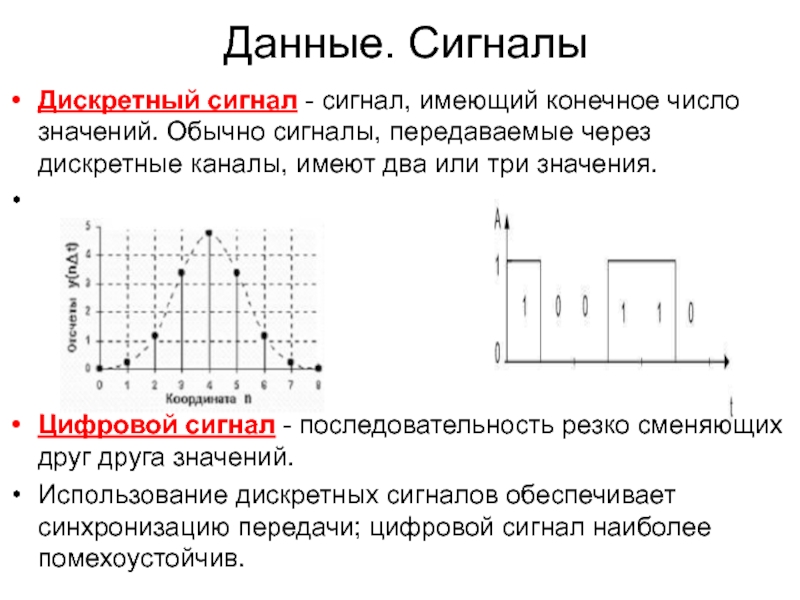 Упростите свою работу благодаря совместимости протокола OPC UA со SCADA-системами.	Поддержка различных языков программирования.	Используйте операционную систему реального времени для управления и проведения вычислений на одном устройстве, установив приоритеты в настройках	Функция Systematic Security Protection поможет пользователям снизить угрозу безопасности.

Модули удаленного ввода/вывода IIoT серии ioThinx 4510

Рабочее напряжение	Питание устройства: 12 ~ 48 В пост. Питание исполнительных устройств: 12/24 В пост.
Макс. кол-во модулей ввода/вывода	32
Протоколы IT	SNMPv1/v2c/v3, RESTful API, MQTT
Протоколы АСУ ТП	Modbus/TCP Server (slave)
Функции шлюза	Modbus/RTU Master в Modbus/TCP, SNMP, RESTful API, MQTT
Рабочая температура	Стандартные модели: -20/+60°C Модели с расширенным диапазоном температур: -40/+75°C

Подключение к облаку	Авто реконфигурация	Кибербезопасность
Устройства серии ioThinx 4510 поддерживают протокол MQTT, с помощью которого можно легко подключиться к облаку.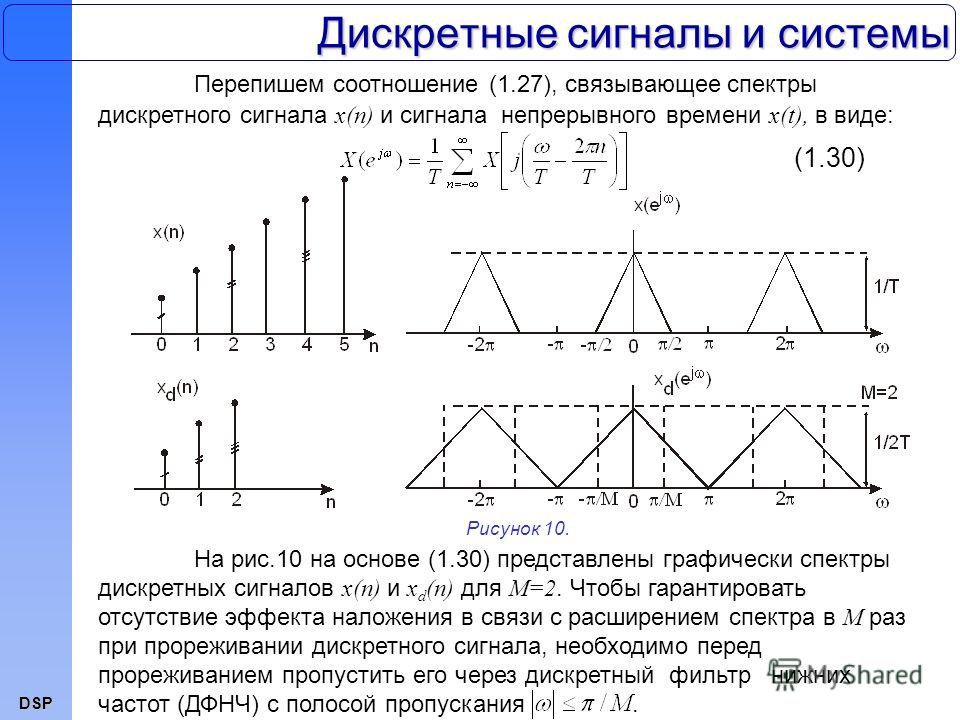 Если вы используете web-интерфейс HMI или NMS для контроля данных в частном облаке, можно установить соединение, используя протоколы RESTful API или SNMP, соответственно.	Можно произвести изменения (добавить/удалить/переместить модули) без необходимости перенастройки. Просто настройте модули, которые хотите изменить, не изменяя настройки остальных.	Устройства серии ioThinx 4510 соответствуют стандарту МЭК 62443 уровня 1. Конфиденциальность Авторизация: Управление учетными записями, Политики входа в систему, Управление сеансами Целостность Контроль доступа: Контроль доступа на основе ролей, Белый список IP-адресов Доступность Защита интерфейса: Защита сетевого порта (данный сервис по умолчанию отключен)

Брошюра Контроллеры и системы сбора данных для приложений IIoT Скачать

Брошюра Возможность связи с полевыми устройствами по протоколу MQTT в приложениях IIoT Скачать

Модуль вывода дискретных сигналов SM 322 для Simatic S7-300, 32 дискретных транзисторных выхода 1х32DO = 24В/ 0,5А, SIEMENS, 6ES73221BL000AA0

Артикул:

6ES73221BL000AA0

Производитель:

EAN код:

4025515060932

Код заказа:

6ES7322-1BL00-0AA0

Страна производства:

Германия

Технические характеристики товара:

SimaticS7-300 SM322 Модуль вывода дискретных сигналов, 32вых. DC24V/0,5A

Актуальная серия:

Единицы измерения:

шт

Есть на складе

Дополнительная информация о «6ES73221BL000AA0»

Напряжение питания:

24В DC

Назначение модулей расширения:

Модули вывода дискретных сигналов

Тип фронтального разъема:

40 клемм

Аналоги «6ES73221BL000AA0»

Артикул:

6ES73225GH000AB0

Производитель:

SIEMENS

Серия:

Simatic S7-300

55606 руб/шт

Артикул:

6ES73221FH000AA0

Производитель:

SIEMENS

Серия:

Simatic S7-300

39694 руб/шт

Артикул:

6ES73221BH010AA0

Производитель:

SIEMENS

Серия:

Simatic S7-300

25952 руб/шт

Артикул:

6ES73221Bh200AA0

Производитель:

SIEMENS

Серия:

Simatic S7-300

31425 руб/шт

Артикул:

6ES73228BF000AB0

Производитель:

SIEMENS

Серия:

Simatic S7-300

43624 руб/шт

Артикул:

6ES73221FL000AA0

Производитель:

SIEMENS

Серия:

Simatic S7-300

73609 руб/шт

Артикул:

6ES73221BF010AA0

Производитель:

SIEMENS

Серия:

Simatic S7-300

20990 руб/шт

Артикул:

6ES73221FF010AA0

Производитель:

SIEMENS

Серия:

Simatic S7-300

27398 руб/шт

Артикул:

6ES73225FF000AB0

Производитель:

SIEMENS

Серия:

Simatic S7-300

33237 руб/шт

Артикул:

6ES73221BP500AA0

Производитель:

SIEMENS

Серия:

Simatic S7-300

72834 руб/шт

Артикул:

6ES73221BP000AA0

Производитель:

SIEMENS

Серия:

Simatic S7-300

72834 руб/шт

Артикул:

6ES73225SD000AB0

Производитель:

SIEMENS

Серия:

Simatic S7-300

45758 руб/шт

Артикул:

6ES73225RD000AB0

Производитель:

SIEMENS

Серия:

Simatic S7-300

45758 руб/шт

Артикул:

6ES73228Bh200AB0

Производитель:

SIEMENS

Серия:

Simatic S7-300

95494 руб/шт

Артикул:

6ES72221BF320XB0

Производитель:

SIEMENS

Серия:

Simatic S7-1200

10559 руб/шт

Артикул:

6ES72221Bh420XB0

Производитель:

SIEMENS

Серия:

Simatic S7-1200

16750 руб/шт

Популярные товары раздела «Модули расширения»

Артикул:

6ED10551FB100BA2

Производитель:

SIEMENS

9105 руб/шт

Артикул:

6ES72314HF320XB0

Производитель:

SIEMENS

Серия:

Simatic S7-1200

35221 руб/шт

Артикул:

6ES73211BL000AA0

Производитель:

SIEMENS

Серия:

Simatic S7-300

37628 руб/шт

Артикул:

6ED10551FB000BA1

Производитель:

SIEMENS

Цена по запросу

Обработка и подготовка дискретных сигналов

X20CM1201	Комбинированный модуль Х20, 1 инкрементальный энкодер AB, 24 В, 4 дискретных входа 24 В, 4 канала 24 В, настраиваемых как входы или выходы, настраиваемая логическая схема цифрового управления
X20DC1073	Модуль с функцией дискретного счетчика X20, 1 счетчик Sin/Cos, 1 Vss, входная частота 400 кГц, мониторинг энкодера, модуль NetTime
X20DS1119	Модуль X20 с многофункциональным процессором дискретных сигналов, 3 дискретных канала 5 В (симметричный сигнал), настраиваются как входы или выходы, 2 дискретных входных канала 24 В (несимметричный сигнал), до 2 счетчиков импульсов, 1 универсальный двухканальный счетчик, настраивается как счетчик A/B или реверсивный счетчик, генератор линейного перемещения (A/B, направление/частота) с 1 опорным импульсом, 1 абсолютный энкодер SSI, функция NetTime
X20DS1319	Модуль X20 с многофункциональным процессором дискретных сигналов, 4 дискретных входа, 4 дискретных канала, настраиваемых как входы или выходы, 2 счетчика импульсов, 1 универсальный двухканальный счетчик, настраивается как A/B или реверсивный счетчик, генератор линейного перемещения (A/B, направление/частота), до 2 опорных импульсов, абсолютный энкодер SSI, функция NetTime
X20DS1828	Модуль дискретных сигналов X20, 1 интерфейс HIPERFACE, функция NetTime
X20DS1928	Модуль дискретных сигналов X20, 1 интерфейс EnDat 2. 1/2.2, функция NetTime
X20DS4389	Модуль дискретных сигналов X20, 4 дискретных входа, 24 В пост. тока, 4 дискретных выхода, 24 В пост. тока, 0,1 А, функция избыточной дискретизации ввода/вывода, функции ввода/вывода со срабатыванием по времени, функция NetTime

Модуль ввода дискретных сигналов ОВЕН МВ110-16ДН

Отгрузка осуществляется в любой город России, а также: Белгород, Алексеевка, Беловское, Северный, Октябрский, Разумное, Стрелецкое, Таврово, Борисовка, Валуйки, Вейделевка, Волоконовка, Головчино, Губкин, Мелихово, Бехтеевка, Короча, Погореловка, Алексеевка, Красное, Бирюч, Ливенка, Красная Яруга, Новый Оскол, Прохоровка, Беленихино, Пролетарский, Сумовский, Ракитное, Ровеньки, Старый Оскол, Чернянка, Шебекино, Маслова Пристань, Яковлево, Строитель, Томаровка, Ржевка

Прибор для сбора данных со встроенных дискретных входов с передачей их в сеть RS-485

• Счетчик импульсов частотой до 1 кГц
• Работа в сети RS-485
• Протоколы: ОВЕН, ModBus-RTU, ModBus-ASCII, DCON

Госповерка: не требуется

Прибор предназначен для сбора данных со встроенных дискретных входов с передачей их в сеть RS-485. Встроенные дискретные входы могут работать в режиме счетчиков импульсов частотой до 1 кГц. МВ110 работает в сети RS-485 по протоколам ОВЕН, ModBus-RTU, ModBus-ASCII, DCON. МВ110 не является Мастером сети, поэтому сеть RS-485 должна иметь Мастер сети – например, ПК с запущенной на нем SCADA-системой, контроллер или регулятор. К МВ110 предоставляются бесплатный ОРС-драйвер и библиотека стандарта WIN DLL, которые рекомендуется использовать при подключении прибора к SCADA-системам и контроллерам других производителей. Конфигурирование МВ110 осуществляется на ПК через адаптер интерфейса RS-485/RS-232 или RS-485/USB (например ОВЕН АСЗ-М или АС4) с помощью программы «Конфигуратор М110», входящей в комплект поставки. Прибор отвечает требованиям по устойчивости к воздействию помех в соответствии с ГОСТ Р 51522 для оборудования класса А.

Особенности:

• 16 каналов дискретного ввода, без изоляции – модификация Д, групповая изоляция – модификация ДН
• Типы входных сигналов: сигналы =24В, транзисторные ключи p-n-p, n-p-n типа
• Частота измерений: до 1 кГц, минимальная длительность импульса 0. 5 мс
• Счетчик импульсов для каждого канала
• Напряжение питания: ~220В и =24В (универсальный источник питания)

Основные технические характеристики:

Параметр	Значение
Напряжение питания: МВ110-220.16Д(ДН)   МВ110-24.16Д(ДН)   МВ110-224.16Д(ДН)	90…264В переменного тока (номинальное напряжение 220В) частотой 47…63 Гц 18…29В постоянного тока (номинальное напряжение 24В) 90…264В переменного тока (номинальное напряжение 220В) частотой 47…63 Гц или 20…375В постоянного тока (номинальное напряжение 24В)
Потребляемая мощность	6ВА
Количество дискретных входов	16
Интерфейс связи с компьютером	RS-485
Максимальная скорость обмена по интерфейсу RS-485	115 200 бит/с
Степень защиты корпуса	IP20
Габаритные размеры	(63×110×73) ± 1 мм
Вес	0,5 кг

 

Discrete Signal — обзор

Periodic-Discrete

Это дискретные сигналы, которые периодически повторяются от отрицательной до положительной бесконечности. Этот класс преобразования Фурье иногда называют дискретным рядом Фурье, но чаще всего его называют дискретным преобразованием Фурье .

Вы могли подумать, что названия, данные этим четырем типам преобразований Фурье, сбивают с толку и плохо организованы. Ты прав; имена эволюционировали довольно бессистемно за 200 лет.Вы ничего не можете сделать, кроме как запомнить их и двигаться дальше.

Все эти четыре класса сигналов простираются до положительной и отрицательной бесконечности . Вы говорите, держитесь! Что, если у вас есть только конечное количество выборок, хранящихся в вашем компьютере, скажем, сигнал, сформированный из 1024 точек. Нет ли версии преобразования Фурье, которая использует сигналы конечной длины? Нет, нет. Волны синуса и косинуса определены как как простирающиеся от отрицательной бесконечности до положительной бесконечности. Вы не можете использовать группу бесконечно длинных сигналов, чтобы синтезировать что-то конечной длины. Чтобы решить эту дилемму, нужно сделать так, чтобы конечные данные выглядели как — сигнал бесконечной длины. Это делается путем представления, что сигнал имеет бесконечное количество выборок слева и справа от фактических точек. Если все эти «воображаемые» выборки имеют нулевое значение, сигнал выглядит дискретным и апериодическим , и применяется дискретное временное преобразование Фурье. В качестве альтернативы воображаемые образцы могут быть дублированием реальных 1024 точек. В этом случае сигнал выглядит дискретным и периодическим с периодом 1024 отсчета.Это требует использования дискретного преобразования Фурье.

Как оказалось, для синтеза сигнала апериодического требуется бесконечное количество синусоид . Это делает невозможным вычисление дискретного преобразования Фурье в компьютерном алгоритме. По исключению единственный тип преобразования Фурье, который может использоваться в DSP, — это DFT. Другими словами, цифровые компьютеры могут работать только с информацией, длина которой составляет дискретных и конечных длины. Когда вы боретесь с теоретическими проблемами, решаете домашние задания и размышляете над математическими загадками, вы можете обнаружить, что используете первых трех членов семейства преобразований Фурье. Когда вы садитесь за компьютер, вы будете использовать только DFT. Мы кратко рассмотрим эти другие преобразования Фурье в следующих главах. А пока сконцентрируйтесь на понимании дискретного преобразования Фурье.

Вернитесь к примеру разложения ДПФ на рис. 8-1. На первый взгляд, это сигнал из 16 точек, разложенный на 18 синусоид, каждая из которых состоит из 16 точек.Говоря более формально, 16-точечный сигнал, показанный на (а), следует рассматривать как один период бесконечно длинного периодического сигнала. Аналогично, каждая из 18 синусоид, показанных на (b), представляет собой сегмент из 16 точек из бесконечно длинной синусоиды. Имеет ли значение, рассматриваем ли мы это как 16-точечный сигнал, синтезируемый из 16-точечных синусоид, или как бесконечно длинный периодический сигнал, синтезируемый из бесконечно длинных синусоид? Ответ: обычно нет, но иногда да . В следующих главах мы встретимся со свойствами ДПФ, которые кажутся сбивающими с толку, если рассматривать сигналы как конечные, но станут очевидными, если учесть периодический характер.Ключевым моментом для понимания является то, что эта периодичность вызывается для использования математического инструмента , то есть ДПФ. Обычно это бессмысленно с точки зрения того, где возник сигнал или как он был получен.

Каждое из четырех преобразований Фурье можно разделить на реальных и комплексных версий. Реальная версия является самой простой, с использованием обычных чисел и алгебры для синтеза и разложения. Например, рис. 8-1 представляет собой пример реального ДПФ .Сложные версии четырех преобразований Фурье намного сложнее и требуют использования комплексных чисел и . Это такие числа, как: 3+ 4j , где j равно -1 (инженеры-электрики используют переменную j , а математики используют переменную i ). Сложная математика может быстро стать непосильной даже для тех, кто специализируется на DSP. Фактически, основная цель этой книги — представить основы DSP без использования сложных математических вычислений, что позволит более широкому кругу ученых и инженеров понять материал.Сложные преобразования Фурье — это область деятельности тех, кто специализируется на DSP и готов погрузиться по шею в болото математики. Если вы так склонны, главы 30–3330313233 доставят вас туда.

Математический термин преобразование широко используется в цифровой обработке сигналов, такой как преобразование Фурье, преобразование Лапласа, преобразование Z, преобразование Гильберта, дискретное косинусное преобразование и т. Д. Что такое преобразование? Чтобы ответить на этот вопрос, вспомните, что такое функция .Функция — это алгоритм или процедура, которые изменяют одно значение на другое значение. Например, y = 2 x + 1 — это функция. Вы выбираете какое-то значение для x , вставляете его в уравнение, и выдает значение y . Функции также могут преобразовывать несколько значений в одно значение, например: y = 2 a + 3 b + 4 c , где a, b и c заменяются на y .

Преобразования

являются прямым продолжением этого, позволяя как входу, так и выходу иметь нескольких значений .Предположим, у вас есть сигнал, состоящий из 100 выборок. Если вы разработаете какое-то уравнение, алгоритм или процедуру для преобразования этих 100 выборок в другие 100 выборок, у вас есть преобразование. Если вы считаете, что он достаточно полезен, у вас есть полное право прикрепить к нему свою фамилию и изложить его достоинства своим коллегам. (Это лучше всего работает, если вы выдающийся французский математик 18 века.) Преобразования не ограничиваются каким-либо конкретным типом или количеством данных. Например, у вас может быть 100 выборок дискретных данных для входа и 200 выборок дискретных данных для выхода.Точно так же у вас может быть непрерывный сигнал для входа и непрерывный сигнал для выхода. Также разрешены смешанные сигналы, дискретные входящие и непрерывные выходящие и наоборот. Короче говоря, преобразование — это любая фиксированная процедура, которая преобразует один фрагмент данных в другой. Давайте посмотрим, как это применимо к рассматриваемой теме: дискретное преобразование Фурье.

Разница между цифровым сигналом и дискретным сигналом

В электротехнике термины «дискретный сигнал» и «сигнал с дискретным временем» используются периодически для обозначения одного и того же, последний термин более общий и более точный.Формулировка «сигнал с дискретным временем» до некоторой степени объясняется сама собой.

Многие инженеры и теоретики приравнивают и приравнивают цифровую обработку сигналов к обработке сигналов квантованных сигналов дискретного времени. Однако есть тонкости. Теоретико-информационная концепция сигнала слишком сложна, чтобы ее можно было втиснуть в «простое» объяснение, я предлагаю вам сначала узнать, что такое «цифровая форма волны». Форма волны не является сигналом, но может представлять сигнал в ваших проектах блоков обработки.Для новичка в изучении DSP знание того, что такое цифровой сигнал, является практически полезным знанием, обещающим помочь вам в свое время продвинуться в тонкостях теоретико-информационной концепции.

Цифровой сигнал — это напряжение или ток, который изменяется со временем между значениями, называемыми «логическими уровнями», эти уровни определяются дисциплиной «цифровая абстракция» ( http://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-002-circuits-and-electronics-spring-2007/video-lectures/6002_l4.pdf). Изменяющиеся значения напряжения или тока не всегда попадают в пределы, предписанные правилами цифровой абстракции для значений сигналов на логических уровнях: при переключении между уровнями напряжение или ток, будучи непрерывной функцией, проходит «запрещенные» диапазоны. Та же самая дисциплина цифровой абстракции предписывает учитывать ограничения не только для значений логических уровней, но и для параметров синхронизации, из которых очень важными являются время установки и удержания — защитные временные интервалы стабильности сигнала, окружающие фронт утверждения тактового сигнала.См. Хорошее руководство по цифровым сигналам на http://www.ni.com/white-paper/3299/en/. Примечательно, что в этом руководстве цифровые сигналы называются цифровыми сигналами.

Говоря (относительно простыми) словами, цифровой сигнал — это форма сигнала с логическими уровнями сигнала и параметрами синхронизации, соответствующими правилам цифровой абстракции для данной конструкции. То, что является допустимым цифровым сигналом для одного дизайна, может оказаться неподходящим для другого.

Периодичность суммы дискретных сигналов

Это общепринятое (но не обязательно повсеместное) соглашение, согласно которому квадратные скобки, как в $ x [n] $ означает сигналы с дискретным временем, где $ n $ — целое число (в соответствии с общепринятым соглашением, что переменные, обозначаемые буквами $ i, j, k, l, m, n $ или $ I, J, K, L, N $ (или имена переменных, начинающиеся с этих букв) обычно используются для целочисленных переменных (хотя $ j $ часто зарезервировано для квадратного корня из $ -1 $ в кругах DSP).Таким образом, $ x [n] $ — это $ n $ -й элемент (помните, что $ n $ — целое число) последовательности $ x $, где $ x $ понимается как отображение из $ \ mathbb Z $ в $ \ mathbb R $ или в $ \ mathbb C $.

Говорят, что последовательность $ x $ имеет период $ N $ (или является периодической с периодом $ N $), если существует положительное целое число $ N $ такое, что $$ x [n + N] = x [n] ~ \ text {для всех} ~ n \ in \ mathbb Z. \ tag {1} $$

Теперь, если $ x $ имеет период $ N $, то также можно сказать, что он имеет период $ kN $, где $ k $ — положительное целое число.Наименьшее целое число, которое является периодом периодической последовательности, называется основным периодом последовательности, а все другие возможные периоды обязательно являются целыми числами, кратными основного периода.

Таким образом, если $ x $ и $ y $ — периодические последовательности с фундаментальными периодами $ N_1 $ и $ N_2 $ соответственно, то их сумма $ z $ (то есть $ z [n] = x [n] + y [n ] $ для всех $ n \ in \ mathbb Z $) также является периодической последовательностью с периодом, равным наименьшему общему кратному $ \ operatorname {lcm} (N_1, N_2) $ для $ N_1 $ и $ N_2 $.

---

Самое интересное начинается, когда люди начинают думать о , о выборке сигналов непрерывного времени $ x (t) $ и $ y (t) $ один раз каждые $ T_s $ секунд и вызове значений выборки $ x [n] $ и $ y [n] $, например

$$ x [n] = x (nT_s), ~ y [n] = y (nT_s), ~ \ text {для всех} ~ n \ in \ mathbb Z. \ tag {2} $$

Теперь сигнал $ x (t) $ непрерывного времени называется периодическим с периодом $ T_0 $, если существует положительное действительное число $ T_0 $ такое, что $ x (t + T_0) = x (t) $ для всех $ t \ in \ mathbb R $, и, как и в случае с последовательностями, мы можем определить основной период периодического сигнала как наименьший из всех возможных периодов сигнала (а все другие периоды кратны основной период).Но,

Если $ x (t) $ — периодический непрерывный сигнал с фундаментальным периодом $ T_0 $, то не обязательно , чтобы дискретизированная последовательность $ x $ (где $ x [n] = x (nT_s) $) — периодическая последовательность.

Каноническим примером является $ \ cos (t) $, который представляет собой непрерывный сигнал с фундаментальным периодом $ 2 \ pi $, дискретизируемый один раз в секунду, чтобы дать $ \ cos [n] $, который является , а не периодической последовательностью. (Он распадается прямо при $ n = 0 $, не существует целого числа $ N $ такого, что $ \ cos [0 + N] = \ cos (N) $ равно $ \ cos [0] = \ cos (0 ) = 1 $).«Но, но, но, — бормочете вы, — вы не делаете выборку на уровне Найквиста или выше!» Ну, частота Найквиста не имеет никакого отношения к делу, поскольку мы не заинтересованы в реконструкции или идеальном представлении и т. Д., Но вы можете взять любой рациональный интервал выборки $ \ ll 1 $, который вам нравится, и вы все равно не получите периодическая последовательность вне $ \ cos (t) $ (или любой другой непрерывный периодический сигнал, если на то пошло), если только отношение $ T_0 / T_s $ периода сигнала $ T_0 $ к интервалу дискретизации $ T_s $ не равно рациональное число .

2.4: Сигналы в дискретном времени — Engineering LibreTexts

Цели обучения

• Сигналы могут быть представлены дискретными величинами, а не функцией непрерывной переменной.
• Эти дискретные временные сигналы не обязательно должны принимать действительные числовые значения.
• Многие свойства непрерывнозначных сигналов передаются почти напрямую в дискретную область.

До сих пор мы рассматривали так называемые аналоговые сигналы и системы .Математически аналоговые сигналы — это функции, имеющие в качестве независимых переменных непрерывные величины, такие как пространство и время. Сигналы дискретного времени — это функции, определенные на целых числах; это последовательности. Один из фундаментальных результатов теории сигналов детализирует условия, при которых аналоговый сигнал может быть преобразован в сигнал с дискретным временем и получить без ошибки . Этот результат важен, потому что дискретными сигналами времени можно управлять с помощью систем, созданных как компьютерные программы.Последующие модули описывают, как практически вся обработка аналоговых сигналов может выполняться с помощью программного обеспечения.

Какими бы важными ни были такие результаты, сигналы с дискретным временем носят более общий характер и включают в себя сигналы, полученные из аналоговых сигналов и , которые таковыми не являются. Например, символы, образующие текстовый файл, образуют последовательность, которая также является сигналом дискретного времени. Мы также должны иметь дело с такими символически значимыми сигналами и системами.

Как и в случае с аналоговыми сигналами, мы ищем способы разложения сигналов дискретного времени с действительным знаком на более простые компоненты.Благодаря этому подходу, ведущему к лучшему пониманию структуры сигнала, мы можем использовать эту структуру для представления информации (создавать способы представления информации с помощью сигналов) и для извлечения информации (извлекать информацию, представленную таким образом). Для сигналов с символическими значениями используется другой подход: мы разрабатываем общее представление всех сигналов с символическим значением, чтобы объединить содержащуюся в них информацию. С точки зрения представления информации, наиболее важным вопросом становится эффективность как для сигналов с действительным, так и для символических значений; Каков наиболее экономичный и компактный способ представления информации для последующего извлечения.

Сигналы с действительными и комплексными значениями

Сигнал с дискретным временем представлен символически как с (n), , где n = {…, — 1,0,1 …}. Обычно мы рисуем сигналы с дискретным временем в виде основных графиков, чтобы подчеркнуть тот факт, что это функции, определенные только для целых чисел. Мы можем задержать дискретный сигнал на целое число, как и с аналоговыми. Отсроченная единичная выборка имеет выражение

δ (n − m) δ (n − m) \ [\ delta (n-m) \]

и равняется единице, если n = m .{i2 \ pi fn} \]

Синусоиды

Синусоиды дискретного времени имеют очевидную форму

\ [s (n) = A \ cos (2 \ pi fn + \ varphi) \]

В отличие от аналоговых комплексных экспонент и синусоид, частота которых может быть любой действительной величиной, частоты их аналогов в дискретном времени дают уникальные формы сигнала только , когда f лежит в интервале (-½, ½). Это свойство можно легко понять, заметив, что добавление целого числа к частоте комплексной экспоненты с дискретным временем не влияет на значение сигнала.{i2 \ pi fn} \]

Этот вывод следует из того, что комплексная экспонента, вычисленная как целое, кратное 2π , равна единице.

Единица Образец

Второй по важности сигнал дискретного времени — это единичная выборка , которая определена как

.

\ [\ delta (n) = 1 \; если\; п = 0 \\ \ дельта (п) = 0 \; в противном случае \]

Рис. 2.4.2. Единичная выборка

Исследование графика дискретного сигнала, аналогичного графику косинусоидального сигнала, показанного на рис.{\ infty} s (m) \ delta (n-m) \]

Этот вид разложения уникален для сигналов с дискретным временем и впоследствии окажется полезным.

Системы с дискретным временем могут воздействовать на сигналы с дискретным временем таким же образом, как и в аналоговых сигналах и системах. Из-за роли программного обеспечения в системах с дискретным временем можно представить и «сконструировать» гораздо больше различных систем с помощью программ, чем с помощью аналоговых сигналов. Фактически, особый класс аналоговых сигналов может быть преобразован в сигналы с дискретным временем, обработан с помощью программного обеспечения и преобразован обратно в аналоговый сигнал, и все это без появления ошибки.Для таких сигналов системы могут быть легко созданы в программном обеспечении с эквивалентными аналоговыми реализациями, которые сложно, если не невозможно, спроектировать.

Символьные сигналы

Другой интересный аспект сигналов с дискретным временем состоит в том, что их значения не обязательно должны быть действительными числами. У нас есть действительные сигналы с дискретным временем, такие как синусоида, но у нас также есть сигналы, которые обозначают последовательность символов, набранных на клавиатуре. Такие символы определенно не являются действительными числами, и как набор возможных значений сигналов они имеют небольшую математическую структуру, кроме того, что они являются членами набора.Более формально, каждый элемент символьного сигнала s (n) принимает одно из значений {a ₁ , …. a _K } , которые составляют алфавит A . Эта техническая терминология не означает, что мы ограничиваем символы только членами английского или греческого алфавита. Они могут представлять символы клавиатуры, байты (8-битные величины), целые числа, передающие суточную температуру. Независимо от того, управляются ли они программным обеспечением или нет, системы с дискретным временем в конечном итоге состоят из цифровых схем, которые состоят из полностью аналоговых схемных элементов.Кроме того, передача и прием сигналов с дискретным временем, таких как электронная почта, осуществляется с помощью аналоговых сигналов и систем. Понимание того, как взаимосвязаны дискретные и аналоговые сигналы и системы, возможно, является основной целью этого курса.

Обработка сигналов в дискретном времени | edX

6.341x разработан для обеспечения как глубокого, так и интуитивного понимания теории, лежащей в основе современных систем и приложений обработки сигналов с дискретным временем. Курс начинается с обзора и расширения основ обработки сигналов, включая обсуждение систем с групповой задержкой и минимальной фазой, а также использования систем с дискретным временем (DT) для обработки сигналов с непрерывным временем (CT).В рамках курса разрабатываются структуры блок-схемы и блок-схемы, включая решетчатые фильтры для реализации систем DT, а также методы проектирования фильтров DT. Обсуждаются и разрабатываются параметрическое моделирование сигналов и эффективная реализация многоскоростных систем DT и систем преобразования частоты дискретизации. Представлено углубленное развитие ДПФ и его вычислений, а также его использование для спектрального анализа и фильтрации. Этот компонент курса включает в себя тщательную и проницательную разработку взаимосвязи между зависящим от времени преобразованием Фурье и использованием банков фильтров как для спектрального анализа, так и для кодирования сигналов.

6.341x состоит из одиннадцати разделов, каждый из которых обычно состоит из двух-четырех тем. Исходный материал для изучения каждой темы включает предлагаемые чтения в тексте курса, поясняющие примечания, прочую связанную литературу и отрывки из видео, а также будет включать интерактивный дискуссионный форум в режиме онлайн. Текст курса — это широко используемый текст Оппенгейма и Шафера (третье издание). Видеосегменты адаптированы на основе видеозаписей в реальном времени курса обучения в Массачусетском технологическом институте.

Каждая тема включает в себя набор автоматически оцениваемых упражнений для самооценки и помощи в усвоении и понимании основ темы, а в некоторых случаях и для предварительного просмотра тем.Типичная часть курса завершается набором более обширных задач, которые помогают интегрировать темы и развивать более глубокое понимание. Будет предоставлена ​​автоматическая оценка ваших ответов на эти проблемы, а также решения.

6.341x и эта свободно доступная версия были разработаны при поддержке и поддержке Департамента электротехники и информатики Массачусетского технологического института, Управления цифрового обучения Массачусетского технологического института и Исследовательской лаборатории электроники Массачусетского технологического института.

Этот курс можно цитировать: Алан В. Оппенгейм и Томас А. Баран, Обработка сигналов в дискретном времени 6.341x, на edX, лето 2016. https://www.edx.org/course/discrete-time-signal- processing-mitx-6-341x-1

Знакомство с сигналами

Знакомство с сигналами

• Определение сигналов
  • Типы сигналов
  • Свойства сигнала
• Пример сигналов
  • Различные сигналы
  • Свойство периодичности
  • Разница между системами CT и DT
• Дельта функция

Свойства и типы сигналов

Управление сигналами

• разворот времени
• сдвиг во времени
• замедление / замедление времени
  • Разница между CT и DT

Составление сигналов

Почему цифровая обработка сигналов?

Если вы работаете на компьютере или используете компьютер для манипулирования данными, вы почти наверняка работаете с цифровыми сигналами.Все манипуляции с данными являются примерами цифровой обработки сигналов (для нашей цели обработка сигналов с дискретным временем как экземпляры цифровой обработки сигналов). Примеры использования DSP:

• Фильтрация: устранение шума из сигналов, таких как речевые сигналы и другие аудиоданные, астрономические данные, сейсмические данные, изображения.
• Синтез и манипуляции: например, синтез речи, синтез музыки, графика.
• Анализ: сейсмические данные, атмосферные данные, анализ фондового рынка.
• Голосовая связь: обработка, кодирование и декодирование для хранения и пересылки.
• Кодирование голоса, звука и изображений для сжатия.
• Активное шумоподавление: наушники, глушители в автомобилях
• Обработка изображений, компьютерное зрение
• Компьютерная графика
• Промышленное применение: анализ вибрации, химический анализ
• Biomed: МРТ, сканирование кошек, визуализация, анализы, ЭКГ, ЭМГ и т. Д.
• Радар, Эхолот
• Сейсмология.

Определение сигналов

Что такое сигнал?

Сигнал — это способ передачи информации. Жесты, семафоры, изображения, звук — все может быть сигналами.

Технически — функция времени, пространства или другой переменной наблюдения, которая передает информацию

Распишем 3 форм сигналов:

• Непрерывный / аналоговый сигнал
• Сигнал дискретного времени
• Цифровой сигнал

Непрерывный (CT) / аналоговый сигнал

конечная , действительная , гладкая функция $ s (t) $ переменной t , которая обычно представляет время.И s , и t в $ s (t) $ являются непрерывными

Почему с действительной стоимостью ?

Обычно явления реального мира имеют реальную ценность.

Почему конечный ?

Реальные сигналы обычно имеют ограниченную энергию просто потому, что нам не доступен бесконечный источник энергии.
В качестве альтернативы, особенно когда они характеризуют долговременные явления (например, солнечное излучение), они будут ограничены по мощности.
Реальные сигналы также будут ограничены по амплитуде — их значения ни в коем случае не будут бесконечными.

Чтобы утверждать, что сигнал «конечен», нам нужна некоторая характеристика его «размера». Утверждать, что сигнал конечен, значит утверждать, что размер сигнала ограничен — он никогда не стремится к бесконечности.2 (\ тау), д \ тау. $

Амплитуда = $ max | s (t) | $ 90 167

Почему гладкий ?

Реальные сигналы никогда не меняются резко / мгновенно. Чтобы быть более техническим, у них конечная пропускная способность .

Обратите внимание, что хотя мы сделали предположения о сигналах (конечность, реальные, гладкие), при фактическом анализе и разработке методов обработки сигналов эти соображения обычно игнорируются.

Дискретный сигнал (DT)

Сигнал с дискретным временем — это ограниченная последовательность с непрерывными значениями $ s [n] $. С другой стороны, его можно рассматривать как непрерывную функцию от дискретного индекса $ n $. 2 [n].$

Амплитуда = $ max | s [n] | $ 90 167

Гладкость не применяется.

Цифровой сигнал

Мы будем работать с с цифровыми сигналами, но будем развивать теорию в основном вокруг сигналов с дискретным временем .

Цифровые компьютеры работают с сигналами цифровых , а не с сигналами дискретного времени.Цифровой сигнал представляет собой последовательность $ s [n] $, где index значения $ s [n] $ не только конечны, но могут принимать только конечный набор значений. Например, в цифровом сигнале, где отдельные числа $ s [n] $ хранятся с использованием 16-битных целых чисел, $ s [n] $ может принимать одно из 2 ¹⁶ значений.

В числовом ряду $ s [n] $ значения s могут принимать только фиксированный набор значений.

Цифровые сигналы — это сигналы с дискретным временем, полученные после «оцифровки». Цифровые сигналы также обычно получают путем измерения от явления реального мира. Однако, в отличие от принятой нормы для аналоговых сигналов, цифровые сигналы могут принимать комплексные значения.

Выше представлены некоторые критерии для реальных сигналов. Теоретические сигналы не ограничены

реальный — это часто нарушается; работаем с комплексными числами

конечное / ограниченное

энергия — ВСЕГДА нарушается

. Сигналы, которые имеют бесконечную временную протяженность, , то есть , которые простираются от $ — \ infty $ до $ \ infty $, могут иметь бесконечную энергию.

мощность — почти никогда: почти все сигналы, с которыми мы столкнемся, имеют ограниченную мощность

гладкость — это часто нарушается многими из рассматриваемых нами сигналов непрерывного времени.

Примеры «стандартных» сигналов

Мы перечисляем некоторые основные типы сигналов, которые часто встречаются в DSP. Мы перечисляем их версии для непрерывного и дискретного времени. Обратите внимание, что аналог аналогов непрерывного времени версии некоторых из этих сигналов являются искусственными конструкциями — они нарушают некоторые из условий, которые мы указано выше для сигналов реального мира и фактически не может быть реализовано.

Типы сигналов

Мы можем классифицировать сигналы по их свойствам, и все это повлияет на наш анализ этих сигналов позже.

Периодические сигналы

Сигнал является периодическим, если он повторяется ровно через некоторый промежуток времени. Однако значение периодичности различается для сигналов с непрерывным и дискретным временем.Мы рассмотрим каждый из них по очереди.

Сигналы непрерывного времени Таким образом, в непрерывном времени сигнал, если он называется периодическим, если существует какое-либо значение $ T $ такое, что \ [ s (t) = s (t + MT), ~~~~~ — \ infty \ leq M \ leq \ infty, ~~ \ text {integer} ~ M \] Наименьшее значение $ T $, для которого указанное выше соотношение удерживает период сигнала.

Дискретные сигналы времени

Определение периодичности для сигналов с дискретным временем аналогично определению для сигналов с непрерывным временем с одним ключевым отличием: период должен быть целым числом.Как мы увидим, это приводит к некоторым неинтуитивным выводам.

Дискретный сигнал времени $ x [n] $ называется периодическим, если существует положительное целое значение $ N $ такое, что \ [ x [n] = x [n + MN] \] для всех целых $ M $. Наименьшее значение $ N $, для которого справедливо указанное выше, является периодом сигнала.

Четные и нечетные сигналы

Симметический сигнал и — это сигнал, который зеркально отражается в момент времени $ t = 0 $.Сигнал считается, даже если он обладает следующим свойством: \ [ \ text {Непрерывное время:} ~ s (t) = s (-t) \\ \ text {Дискретное время:} ~ s [n] = s [-n] \]

Сигнал является нечетным симметическим сигналом, если он имеет следующее свойство: \ [ \ text {Непрерывное время:} ~ s (t) = -s (-t) \\ \ text {Дискретное время:} ~ s [n] = -s [-n] \]

На рисунке ниже показаны примеры четных и нечетных симметричных сигналов.Например, косинус даже симметричен, поскольку $ \ cos (\ theta) = \ cos (- \ theta) $, что приводит к $ \ cos (\ omega t) = \ cos (\ omega (-t)) $ . С другой стороны, синус нечетно симметричен, поскольку $ \ sin (\ theta) = — \ sin (- \ theta) $, что приводит к $ \ sin (\ omega t) = — \ sin (\ omega (-t) ) $.

Разложение сигнала на четные и нечетные составляющие Любой сигнал $ x [n] $ может быть выражен как сумма четного и нечетного сигналов следующим образом. \ [ x [n] = x_ {четное} [n] + x_ {нечетное} [n] \] куда \ [ x_ {даже} [n] = 0.5 (х [п] + х [-n]) \\ x_ {odd} [n] = 0,5 (x [n] — x [-n]) \]

Управляющие сигналы

Сигналы могут быть составлены путем манипулирования и комбинирования других сигналов. Кратко рассмотрим эти манипуляции.

Масштабирование

Простое масштабирование сигнала вверх или вниз по коэффициенту усиления.

Непрерывное время: $ y (t) = a x (t) $

Дискретное время: $ y [n] = a x [n] $

$ a $ может быть реальным / мнимым, положительным / отрицательным. Когда $ a отрицательно, сигнал переворачивается по оси y.

Разворот времени

Переворот сигнала слева направо.

Непрерывное время: $ y (t) = x (-t) $

Дискретное время: $ y [n] = x [-n] $

Сдвиг во времени

Сигнал смещен вдоль оси индента на $ \ tau $ (или N для дискретного времени). Если $ \ tau $ положительно, сигнал задерживается, а если $ \ tau $ отрицательный сигнал продвигается.

Непрерывное время: $ y (t) = x (t- \ tau) $

Дискретное время: $ y [n] = x [n — N] $

Расширение

Саму временную ось можно масштабировать на $ \ alpha $.

Непрерывное время: $ y (t) = x (\ alpha t) $

Дискретное время: $ y [n] = x [/ alpha n] $

Расширение DT отличается от расширения CT, потому что $ x [n] $ определяется ТОЛЬКО для целого числа n, поэтому для существования $ y [n] = x [\ alpha n] $ «an» должно быть целым числом.

Однако $ x [\ alpha n] $ для $ a \ neq 1 $ проигрывает некоторым выборкам. Вы никогда не сможете полностью восстановить x [n] из него. Этот процесс часто называют дециминкацией .

Для сигналов DT $ y [n] = x [\ alpha n] $ для $ \ alpha интерполировать нули для неопределенных значений, если $ an $ не является целым числом.

Составные сигналы

Сигналы могут быть составлены путем манипулирования и комбинирования других сигналов. Есть несколько способов комбинирования сигналов, и мы рассматриваем следующие два:

ПРИЛОЖЕНИЕ

Непрерывное время: $ y (t) = x_1 (t) + x_2 (t) $ Дискретное время: $ y [n] = x_1 [n] + x_2 [n] $

УМНОЖЕНИЕ

Непрерывное время: $ y (t) = x_1 (t) x_2 (t) $ Дискретное время: $ y [n] = y_1 [n] y_2 [n] $

$ x_1 [n] $ и $ x_2 [n] $ сами могут быть получены путем манипулирования другими сигналами.{\ alpha t} u (t) $ для $ \ alpha

На самом деле односторонние сигналы могут быть получены умножением на u [n] (или сдвинутые / обращенные во времени версии u [n] или u (t)).

Получение базовых сигналов друг от друга

Можно получить один сигнал из другого просто с помощью математических манипуляций.{\ infty} u [k] \ delta [n-k] $

На этом завершается введение в сигналы. В обзоре мы обсудили важность DSP, типы сигналов и их свойства, манипуляции с сигналами, и состав сигнала. Далее мы обсудим системы.

В чем разница между аналоговыми и дискретными сигналами?

Разница между аналоговыми и дискретными сигналами подобна разнице между переключателем света и переключателем света с диммером.

В этой статье мы ответим на основной вопрос, касающийся электрической связи: в чем разница между аналоговыми и дискретными сигналами?

Valve Automation on the Rise

Для все большего числа производителей автоматизация клапанов оказывается выгодным вложением средств.Kimray предлагает несколько продуктов, которые работают с помощью электроэнергии, и знания, чтобы заставить их работать.

Типы связи

В современной нефтегазовой отрасли существует два основных типа электронной связи: дискретная и аналоговая.

Понимание того, как они взаимодействуют с PLC (программируемым логическим контроллером), RTU (Remote Terminal Unit) и другой электроникой, поможет вам выбрать правильное оборудование для вашего приложения.

Дискретные сигналы

Дискретные сигналы либо включены, либо выключены, как выключатель света.

Приложения и процессы, которые вы хотите автоматизировать, будут определять типы дискретных устройств, которые вы выбираете.

Существует множество устройств, используемых для отправки и приема дискретных сигналов включения / выключения. К ним относятся:

Аналоговые сигналы

Аналоговые сигналы — это сигналы, которые могут изменяться или изменяться, как выключатель света с диммером. Диммер будет изменять сопротивление в линии, заставляя свет тускнеть или становиться ярче по вашему выбору.

Уровень жидкости, температура, положение, давление и расход — это лишь некоторые из измерений, которые аналоговые устройства могут предоставить системе управления.

Как что-то физическое, например давление, становится аналоговым сигналом?

Устройства мониторинга, такие как преобразователи, используются для преобразования физических свойств в электрический сигнал. Некоторые преобразователи используют физические свойства для управления сопротивлением в электрической цепи. Вот два примера:

• RTD — RTD (датчик температуры сопротивления) будет изменять значение сопротивления в зависимости от температуры. С увеличением температуры увеличивается и сопротивление в цепи, изменяя подаваемое напряжение или ток.
• Датчик давления — То же самое верно и для датчиков давления, в которых используются тензодатчики. По мере увеличения давления на тензодатчике сопротивление в цепи увеличивается, а уровень напряжения или тока изменяется.

Выходные сигналы, которые выдают преобразователи, могут быть основаны на напряжении или токе. Самыми популярными сигналами преобразователей в нефтегазовой отрасли являются 4-20 мА (миллиампер) и 0-10 В постоянного тока (постоянный ток вольт).

Аналоговые устройства используются в таких приложениях, как управление давлением, управление потоком и других приложениях, где изменяющийся сигнал используется для дросселирования или управления положением устройства.

Чтобы обсудить со специалистом электрические опции для вашей работы, обратитесь в местный магазин Kimray или к авторизованному дистрибьютору.

.