Закон Ома в дифференциальной форме
Закон Ома в интегральной форме для однородного участка цепи (не содержащего ЭДС)
| (7.6.1) |
Для однородного линейного проводника выразим R через ρ:
| , | (7.6.2) |
ρ – удельное объемное сопротивление; [ρ] = [Ом·м].
Найдем связь между и в бесконечно малом объеме проводника – закон Ома в дифференциальной форме.
В изотропном проводнике (в данном случае с постоянным сопротивлением) носители зарядов движутся в направлении действия силы, т.е. вектор плотности тока и вектор напряженности поля коллинеарны (рис. 7.6).
Исходя из закона Ома (7.6.1), имеем:
А мы знаем, что или . Отсюда можно записать
| , | (7.6.3) |
это запись закона Ома в дифференциальной форме.
Здесь – удельная электропроводность.
Размерность σ – [].
Плотность тока можно выразить через заряд электрона е, количество зарядов n и дрейфовую скорость :
.
| (7.6.4) |
Теперь, если удельную электропроводность σ выразить через е, n и b: то вновь получим выражение закона Ома в дифференциальной форме:
.
Закон Ома для неоднородного участка цепи Работа и мощность тока. Закон Джоуля – Ленца
Закон ома в дифференциальной форме
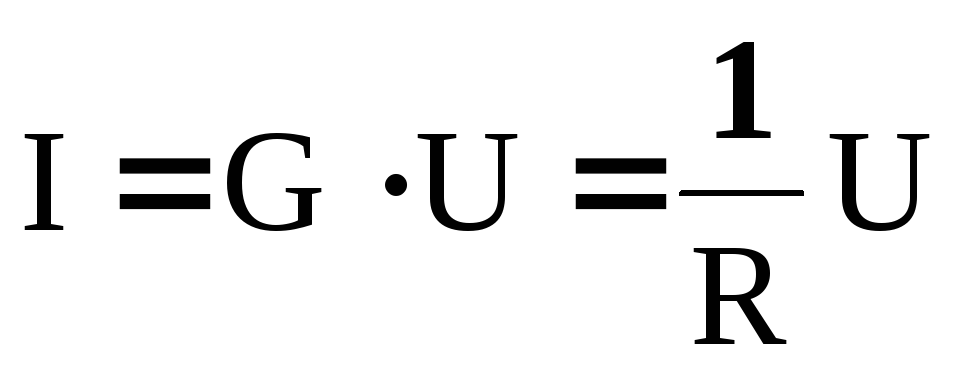 , (11)
, (11)
где коэффициент пропорциональности G = 1 / R и называется электрической проводимостью проводника. Для линейных проводников с постоянным поперечным сечением
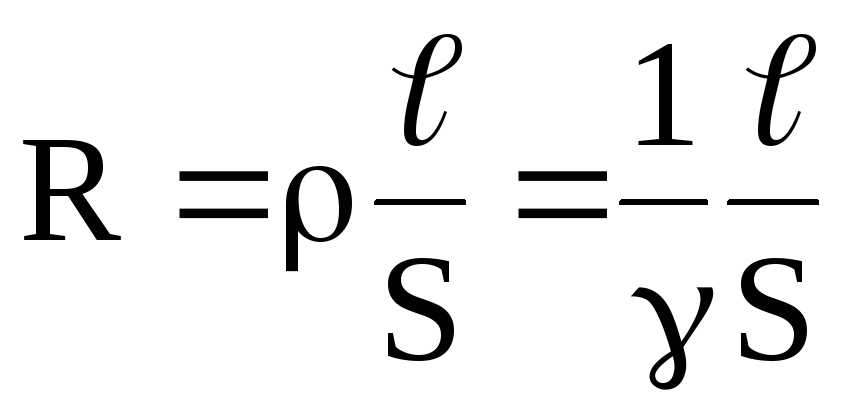 , (12)
, (12)
где γ = 1 / ρ – удельная электропроводность материала
 – его длина. Тогда для изотропного
проводника выражение (11) с учётом (12)
примет вид:
– его длина. Тогда для изотропного
проводника выражение (11) с учётом (12)
примет вид:  . (13)
. (13)
Теперь
для плотности тока (2) с учётом, что 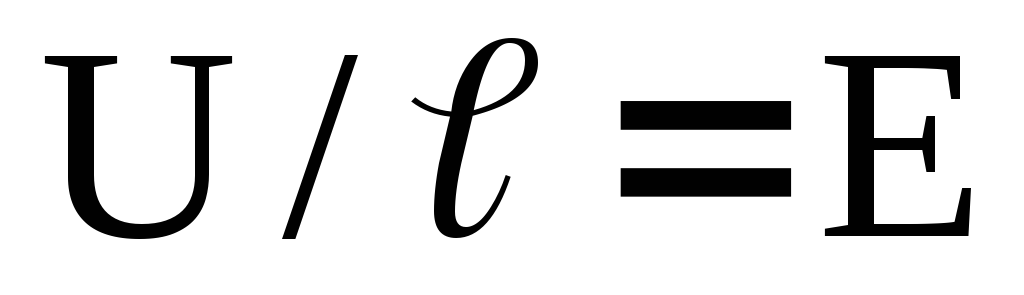 – напряжённость поля в проводнике,
получим:
– напряжённость поля в проводнике,
получим:
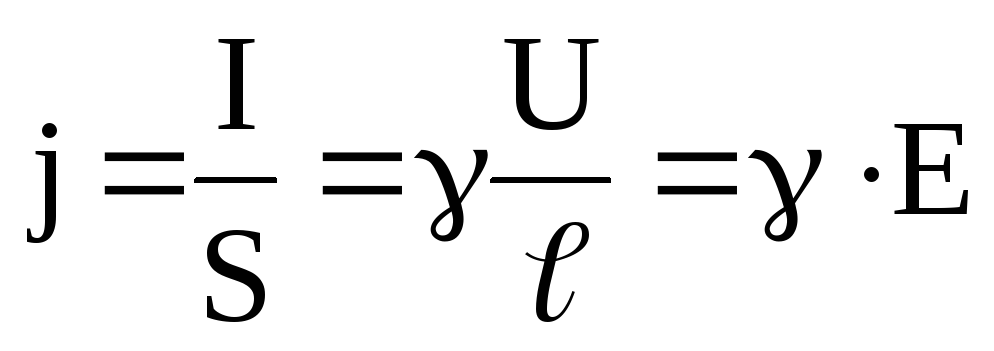
Выражение (14) в векторной форме это закон Ома в дифференциальной форме:
 . (15)
. (15)
Получим в
дифференциальной форме закон Джоуля-Ленца.
Количество теплоты, выделяющееся в
элементе проводника, объёмом  за времяdt:
за времяdt:
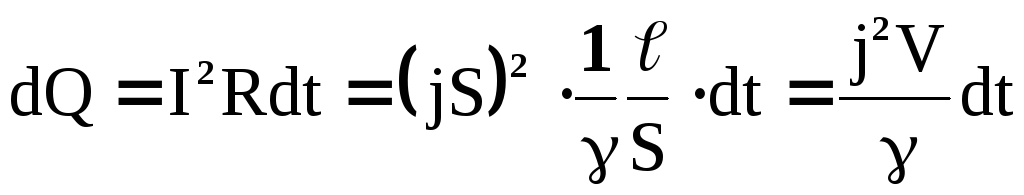 . (16)
. (16)
Теперь, количество теплоты, которое выделяется в единице объема проводника за единицу времени, будет:
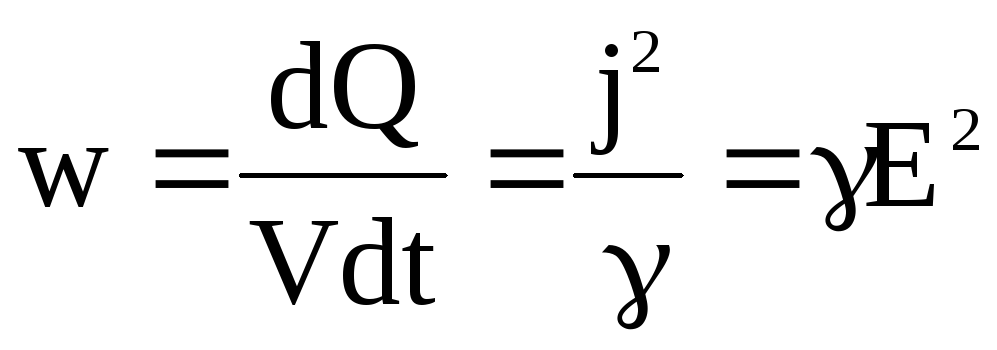 . (17)
. (17)
Эта величина называется удельной тепловой мощностью тока.
Э л е к т р и ч е с к и й т о к в м е т а л л а х
 Ток
в металлах представляет собой движение
не связанных с ионами кристаллической
решеткой электронов. Первое опытное
подтверждение того, что в создании тока
в металлах ионы участия не принимают,
было получено еще в 1901 г. в опыте немецкого
ученого К. Рикке (1845 – 1915). В течение года
ток пропускали через три последовательно
составленных и тщательно пришлифованных
цилиндраAl
– Cu
– Al.
При этом в телах не было обнаружено даже
мизерного переноса вещества или
каких-либо химических изменений. Т.е.
Ток
в металлах представляет собой движение
не связанных с ионами кристаллической
решеткой электронов. Первое опытное
подтверждение того, что в создании тока
в металлах ионы участия не принимают,
было получено еще в 1901 г. в опыте немецкого
ученого К. Рикке (1845 – 1915). В течение года
ток пропускали через три последовательно
составленных и тщательно пришлифованных
цилиндраAl
– Cu
– Al.
При этом в телах не было обнаружено даже
мизерного переноса вещества или
каких-либо химических изменений. Т.е.
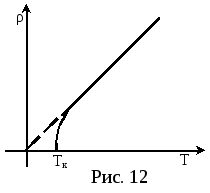
Сопротивление чистых металлических проводников при не очень низких температурах:
R = R0 (1+ α·t0C), откуда
R = α R0T, (18)
где α = 1/273 К-1 – температурный коэффициент сопротивления, R0 – сопротивление проводника при 00 С.
В области низких температур (Т < 20 К) сопротивление многих металлов (Al, Pb, Zn) и их сплавов резко падает до нуля. Это явление сверхпроводимости.
Электрический ток в электролитах и расплавах
Если в электролит или расплав ввести две твердотельных пластинки (электроды) и подать на них напряжение, то возникает электрический ток, который создаётся направленным движением ионов. Достигнув соответствующих электродов, ионы отдают или приобретают электроны и превращаются в нейтральные атомы или молекулы. В результате химических реакций вторичные продукты либо оседают на электродах, либо переходят в раствор. Явление осаждения составных частей электролита на электродах получило название электролиза. Материалы, в которых при прохождении тока происходят химические превращения, относятся к проводникам второго рода. Т.е.
Количественно электролиз описывается законами Фарадея:
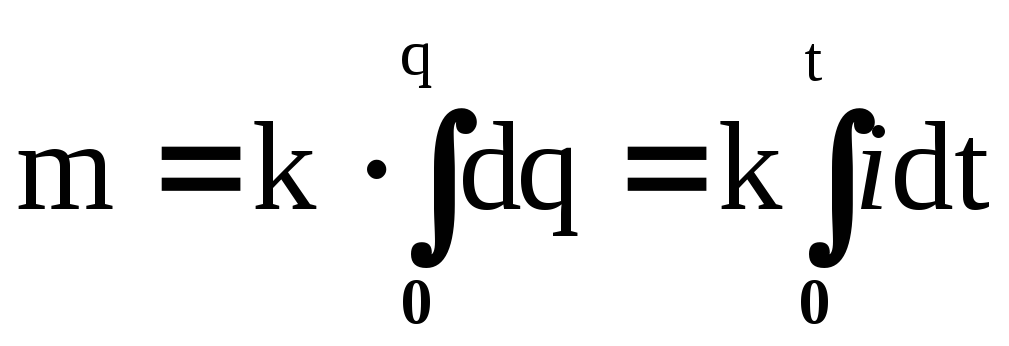 ,
,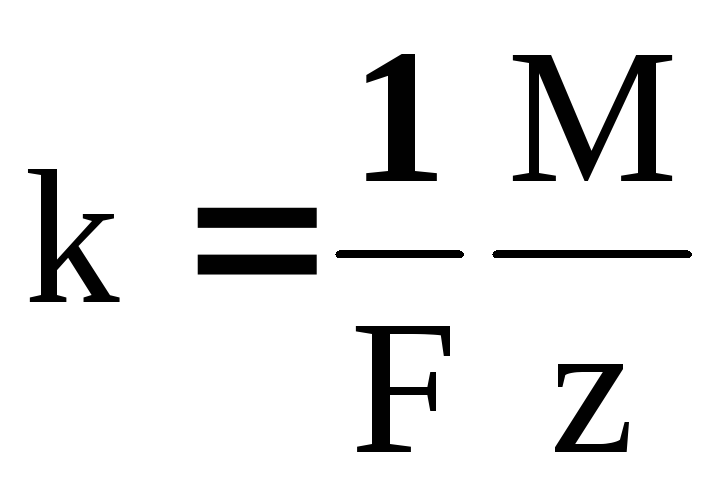 , (19)
, (19)
где m – масса осевшего на электроде вещества, k – его электрохимический эквивалент, i = f(t) – сила тока, t – время его протекания, F – число Фарадея (F = 96,497∙106 Кл/моль.), М – молярная масса вещества, z – валентность, F/z – называется химическим эквивалентом вещества.
Если величина тока I в процессе электролиза не меняется, то (18) принимает вид:
 (20)
(20)
Ионы, как носители электрического заряда в электролитах, образуются в растворах солей, щелочей или кислот в воде и некоторых других жидкостях в результате электролитической диссоциации.
В растворе каждая
полярная молекула растворенного вещества
окружена дипольными молекулами
растворителя. Причем к положительно
заряженной части молекулы растворенного
вещества молекулы растворителя повернуты
своими «отрицательными» концами, а к
отрицательно заряженной соответственно
«положительными». Это ослабляет силы
электростатического притяжения ионов,
образующих молекулу растворенного
вещества. В результате теплового движения
может произойти разрыв связи. Образующиеся
ионы
(анионы и
катионы)
начинают странствовать по раствору.
При сближении на достаточно малое
расстояние анион и катион могут снова
соединится. Этот процесс называется
рекомбинация (или молизация). В растворе
процессы диссоциации и рекомбинации
идут параллельно. В конечном итоге в
растворе при постоянных внешних условиях
устанавливается динамическое равновесие.
Этому состоянию соответствует определенная
степень диссоциации, которую принято
характеризовать коэффициентом диссоциации
– α, который показывает долю распавшихся
молекул растворенного вещества – α =
n
При невысоких температурах ионы бывают окружены облепившими их ионами растворителя. Это явление получило название сольватации (для водных растворов – гидратации), а сам комплекс из иона и удерживаемой его силовым полем оболочки из молекул растворителя называют сольватом.
Рассмотрим механизм электролитической проводимости. При наложении электрического поля на электролит на каждый ион будет действовать кулоновская сила Fк
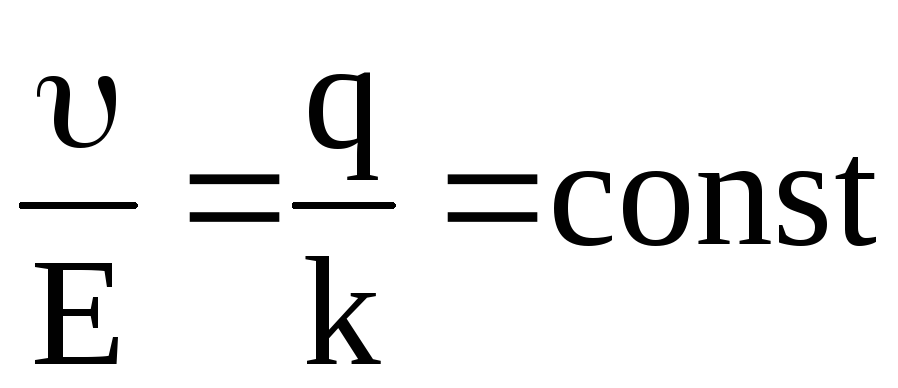 ,
т.к. для данного раствора k =const
и q = const.
Отношение
,
т.к. для данного раствора k =const
и q = const.
Отношение  (21)
(21)
называется подвижностью ионов, которая представляет среднюю
скорость дрейфа заряженных частиц в поле с напряженностью 1 В/м). [b] = м2 / (В·с). Подвижность ионов b зависит от их природы, свойств растворителя и температуры. При комнатной температуре для водных растворов подвижность по порядку величины равна 10-8 – 10-7 м2/В∙с.
Для установившегося движения, в соответствии с (5) и учетом (20) плотность тока в электролите будет:
j = (n+ q+ b+ + n— q— b—)Е (22)
Величина в скобках не зависит от напряженности поля – Е. Это значит, ток в электролитах подчиняется закону Ома. Если каждая молекула диссоциирует на два иона, то
 j
= αnq(b+ + b—)Е.
(23)
j
= αnq(b+ + b—)Е.
(23)
Выражение
γ = αnq(b+ + b—) (24)
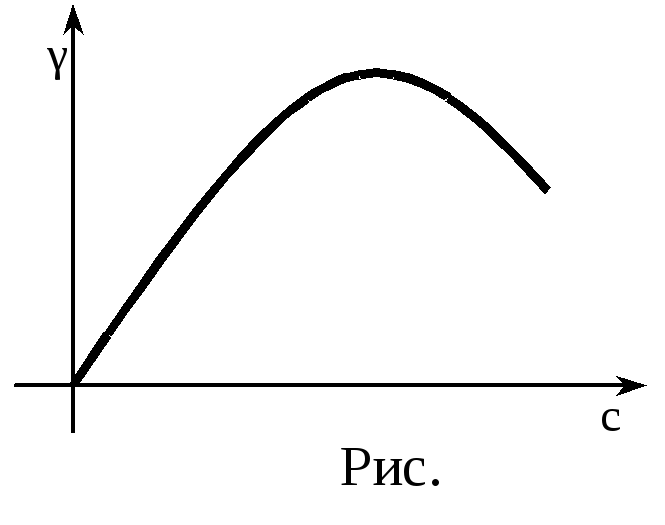
представляет собой электропроводность электролита. Как видно из выражения (23), проводимость электролитов растет с повышением температуры, т.к. при этом увеличивается коэффициент диссоциации и подвижность ионов. Зависимость γ от концентрации довольно сложная (рис.): Для слабых растворов, когда α ≈ 1, γ растет пропорционально с. В дальнейшем с увеличением концентрации коэффициент диссоциации α убывает, поэтому рост проводимости замедляется, а затем даже начинает уменьшаться.
Электрофорез – направленное движение заряженных частиц (ионов, капелек жидкости, взвешенных и коллоидных части) под воздействием электрического поля в какой-то среде. Скорость упорядоченного движения при электрофорезе определяется уравнением Смолуховского:
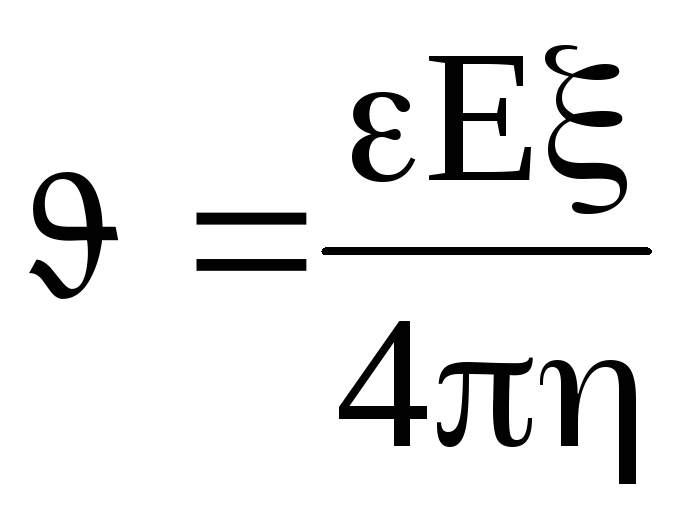 ,
(25)
,
(25)
где ε – диэлектрическая проницаемость среды, Е – напряженность электрического поля, η – вязкость среды, ξ – электрокинетический (дзета) потенциал. (Более подробно материал изложен в лабораторной работе «Электрофорез»)
Интегральные и дифференциальные форма закона Ома: содержание и формулы
Обычно для расчётов электрического тока пользуются законом Ома для участка цепи: I=U/R, где I – ток в цепи, U – напряжение, R – суммарное сопротивление. Ток в этой цепи может протекать через различные участки из разных проводов. Поэтому для расчётов силы тока в определённом участке проводника лучше применить закон Ома в дифференциальной форме. Так как плотность тока Ī – векторная величина, то формула закона имеет вид: Ī = γĒ, где γ – удельная проводимость, обратная удельному сопротивлению γ=1/R, а Ē – напряжённость электрического поля. Может выражаться закон Ома также в интегральных формах.

Закон Ома
Действие электродвижущих сил
Электродвижущая сила (ЭДС) является скалярной величиной, характеризующей работу не электрических сил, заставляющих производить разность потенциалов на выходе.
Дополнительная информация. Скалярная величина – это когда она может быть выражена только определённым значением. В отличие от векторной величины, которая определяется не только значением, но и направлением.
Используется ЭДС в генераторах, преобразующих какую либо работу А (джоуль) в электрическую. Для этого могут быть использованы такие виды энергии по их происхождению:
- Механическая индукционная. Вывод ЭДС возникает при пересечении проводником линий магнитного поля;
- Механическая пьезоэлектрическая. Возникновение ЭДС происходит при деформации некоторых веществ;
- Световая энергия. Здесь ЭДС появляется в полупроводниках при действии на них световых лучей;
- Термическая энергия. ЭДС образуется, когда контакты из разнородных проводников находятся под разными температурами;
- Химическая энергия. Возникновение ЭДС происходит вследствие химических реакций.
В зависимости от характера энергии и устройства генератора ЭДС может возникать как переменная, так и постоянная. Переменная может быть как синусоидальная (магнитные индукционные генераторы), так и импульсная (пьезозажигалки). Постоянную ЭДС преобразуют в основном из химической (элементы питания, аккумуляторы), световой (фотоэлементы) энергий и температуры (элементы Пельтье).

Генераторы тока
ЭДС образует на разноименных проводниках разность потенциалов. Если не соединять проводником клеммы, на которых имеется разность потенциалов, то тока в цепи не будет. Следовательно, никакой энергии не будет израсходовано. На клеммах будет оставаться разность потенциалов. Работу для поддержания этой разности совершать не надо.
Если к клеммам с разностью потенциалов подключить проводник с нагрузкой, то через него будет протекать электрический ток, выполняя работу в нагрузке. При этом разность потенциалов на клеммах будет стремиться к 0, что приведёт к падению тока до 0. Для поддержания разности потенциалов стабильной величиной необходимо, чтобы ЭДС получала энергию. Эта энергия затрачивает работу, равную той, которая совершается в нагрузке.
Движение тока по неоднородным проводникам
Разность потенциалов, вызванная ЭДС, будет производить напряжение на клеммах генератора. ЭДС – это скалярная величина. При подключении к клеммам проводника через него потечёт ток, плотность которого выражается, например, Ī. Это уже векторная величина. Если ток создан только разностью потенциалов на клеммах, то векторы потенциала и плотности тока будут совпадать. Такой проводник называют однородным. Закон Ома для однородного участка цепи:
I=U/R.
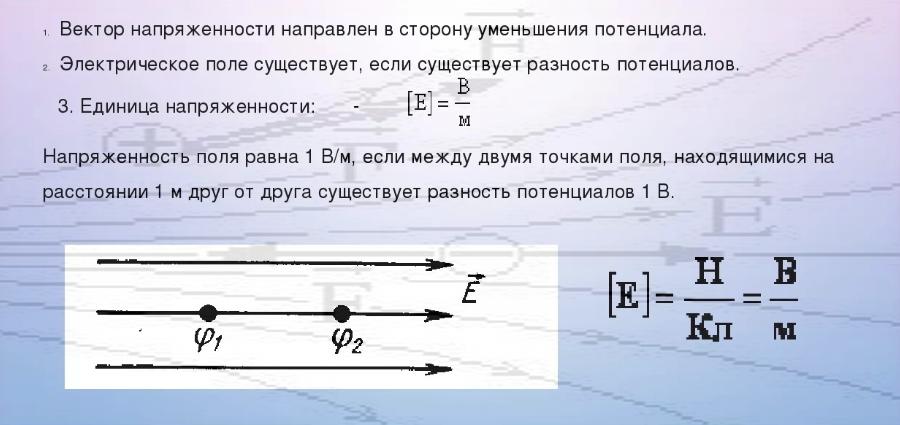
Вектор напряжённости
Неоднородный проводник, кроме сил, которые образованы разностями потенциалов, имеет сторонние силы. Для определения плотности тока Ī пользуются законом Ома в дифференциальной форме для неоднородных проводников:
Ī=γ(E+Ē₁+ Ē₂+ Ēn).
Векторы и каждый участок проводника складываются, E – напряжённость, созданная разностью потенциалов на клеммах проводника (скалярная величина). Ē₁, Ē₂, Ēn – векторные величины напряжённости первой, второй и энной сторонних сил.
Так как γ – удельная проводимость проводника, обратная сопротивлению, ϕ₁ – потенциал на 1-ой точке, ϕ₂ – потенциал на 2-ой точке, то закон Ома для неоднородного участка цепи от 1-ой до 2-ой точки будет записываться так:
Ī =(ϕ₁ – ϕ₂+ Ē)/R.
Для ознакомления металлы и их удельное сопротивление:
- Серебро – 1,6×10ˉ⁸Ом×м;
- Медь – 1,72×10ˉ⁸ Ом×м;
- Алюминий – 2,6×10ˉ⁸ Ом×м;
- Латунь – 3…7,0×10ˉ⁸ Ом×м;
- Бронза – 8,0×10ˉ⁸ Ом×м;
- Железо – 9,8×10ˉ⁸ Ом×м;
- Свинец – 2.0×10ˉ⁶Ом×м;
- Графит – 3…5,0×10ˉ⁵Ом×м.
Трактовка и пределы применимости закона Ома
Если необходимо определить одну из величин: ток, напряжение или сопротивление для однородной цепи, то пользуются формулой, формулировка которой изображена на рисунке.
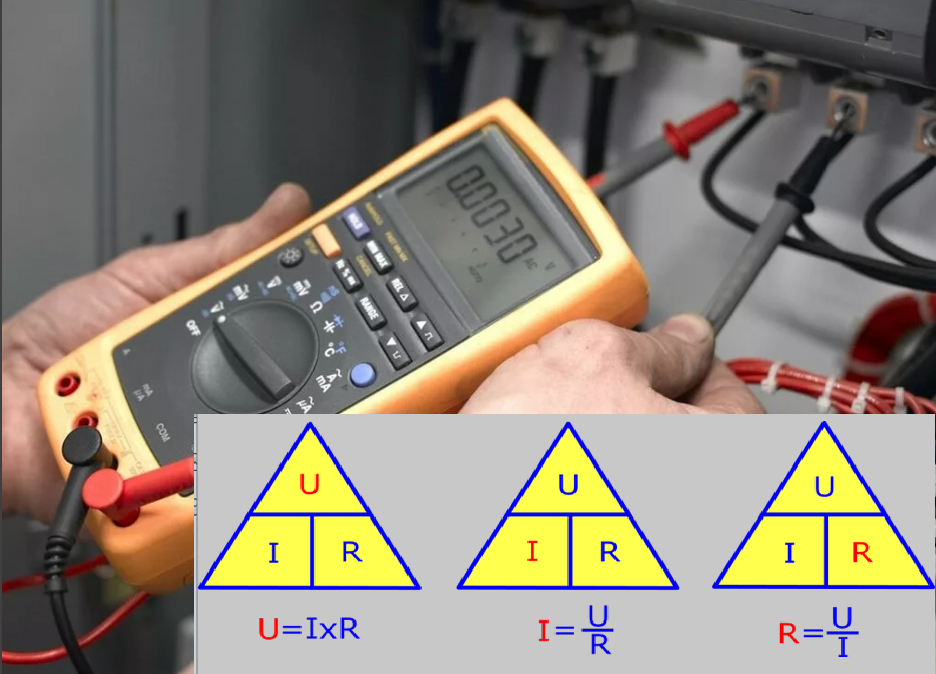
Закон Ома в треугольнике
Для удобства решения тождества величины изображены в треугольнике. Теперь, пользуясь первой формулой, зная сопротивление цепи и ток, можно высчитать напряжение, которое действует на замкнутый контур. Зная напряжение и сопротивление цепи, можно определить ток по 2-ой формуле. По 3-ей формуле высчитывают сопротивление нагрузки, зная напряжение и ток.
Существуют исключения, когда закон Ома не соблюдается. Примеры:
- В переменных ЭДС, если нагрузка имеет индукционный или ёмкостный характер. При повышении частоты из-за инерционности носителей заряда вступают в силу законы электродинамики. Конденсаторы и катушки индуктивности в качестве сопротивления для переменного тока, колебательный контур.
- Для веществ, обладающих сверхпроводимостью при низких температурах. Датчики измерительных приборов высокой точности, сверхпроводящие соленоиды, сверхпроводящие кабели с током 5 000 А.
- При высоких температурах, когда проводник начинает проявлять нелинейную характеристику сопротивления. Вольфрамовая нить лампы накаливания, спирали нагревательных элементов.
- При высоких напряжениях, когда происходит пробой диэлектрика. Свечи зажигания карбюраторных двигателей, наконечники для защиты от тлеющего разряда высоковольтных ЛЭП.
- В наполненных газом люминесцентных и вакуумных лампах. Люминесцентные лампы, вакуумные индикаторы, индикаторы тлеющего разряда.
- В полупроводниковых приборах с p-n переходами и в нелинейных полупроводниках. Это светодиоды, стабилитроны, транзисторы, электронные приборы.
Интересно. Используется закон Ома в дифференциальной форме, когда имеется несколько ЭДС, или цепь проводников находится под воздействием сторонних сил. К примеру, при зарядке аккумуляторов солнечными батареями или другими ЭДС, также в генераторах с обмотками возбуждения, если их дифференцировать.

Измерительный мост
Материалы проводников, к которым применяется закон Ома, названы оммическими или линейными проводниками. Те, у которых сопротивление имеет функциональную зависимость от интенсивности тока, – нелинейными. Так могут вести себя металлы при крайне низких или высоких температурах.
Видео
Закон Ома в дифференциальной форме
При детальном изучении силы тока в сильно неоднородном проводнике закон Ома в обычной форме не подходит, так как он не учитывает локальные параметры проводника. Рассмотрим, например, проводник у которого вдоль оси значительно изменяется электрическое сопротивление и его поперечное сечение. Очевидно, что такой проводник можно представить, как один резистор с интегральным сопротивлением (такое, которое одновременно учитывает все неравномерности), однако если встает вопрос как именно течет ток в таком резисторе, то обычная формулировка закона Ома не применима.
Давайте выведем закон Ома в дифференциальной форме. Рассмотрим проводник с переменным поперечным сечением и сопротивлением вдоль оси z (см. рисунок 1). Разделим этот проводник по середине на две части. Затем полученные два кусочка разделим ещё на две части. Заметим, что при разбиении, каждая часть становится более однородной, нежели проводник в совокупности (см. рис. 2).

Рис.1. Проводник с переменным поперечным сечением и сопротивлением вдоль оси

Рис. 2. Разбиение неоднородного проводника на части
А теперь, внимание! Делим полученные кусочки на две части и так далее до бесконечности! Т.е. проводник теперь состоит из бесконечного числа бесконечно малых проводников. Интерес представляет такой бесконечно малый кусочек, ведь он строго однороден. У него постоянная толщина и постоянное сопротивление. Вообще такой кусочек проводника разумно было бы показать в виде тонкой вертикальной линии, но для наглядности покажем, что проводник толщину имеет хоть она бесконечно мала (см. рис. 3).

Рис. 3. Бесконечно малый проводник
Итак, закон Ома в дифференциальной форме связывает плотность тока, с удельной проводимостью и напряженностью для бесконечно малого участка проводника.
Строгая формулировка закона Ома в дифференциальной может быть записана так: плотность тока прямо пропорциональной напряжённости и удельной проводимости для бесконечно малого участка проводника.
Выведем формулу закона Ома в дифференциальной форме. Запишем связь между потенциальном и напряжённостью
Закон Ома в дифференциальной форме.
Р ассмотрим
небольшой участок однородного проводника
постоянного сечения, находящегося под
напряжением
ассмотрим
небольшой участок однородного проводника
постоянного сечения, находящегося под
напряжением .
Поделив напряжение на сопротивление
участка и, учитывая, что
.
Поделив напряжение на сопротивление
участка и, учитывая, что
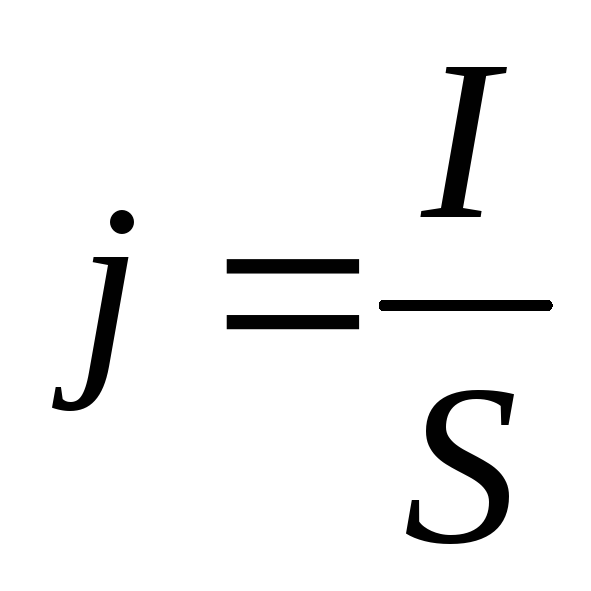 ,
, 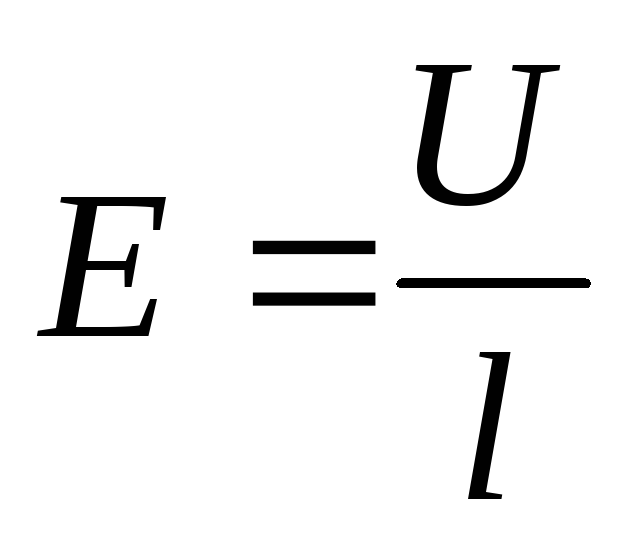 ,
,
находим
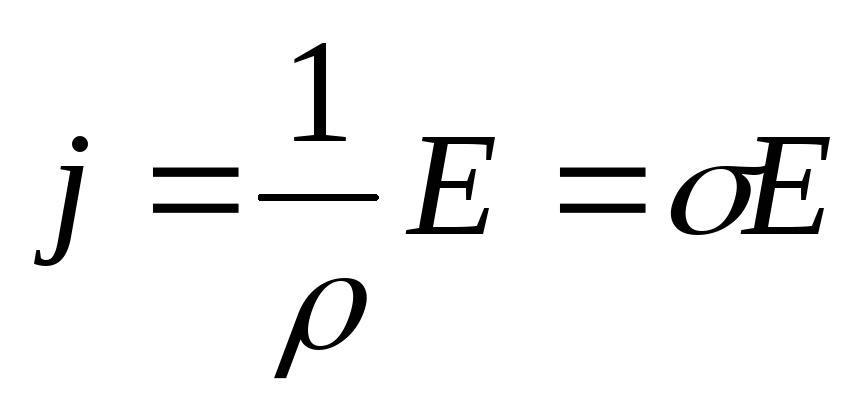 ,
,
 .
.
Плотность тока в каждой точке проводника пропорциональна напряжённости электрического поля. Полученное соотношение выражает локальный закон Ома и называется законом Ома в дифференциальной форме.
Отметим, что в случае постоянноготока избыточный заряд внутриоднородногопроводника равен нулю. Действительно, при постоянном токе, заряд, входящий в выделенный объём, равен заряду, выходящему из объема, т.е.
 ,
,
откуда следует
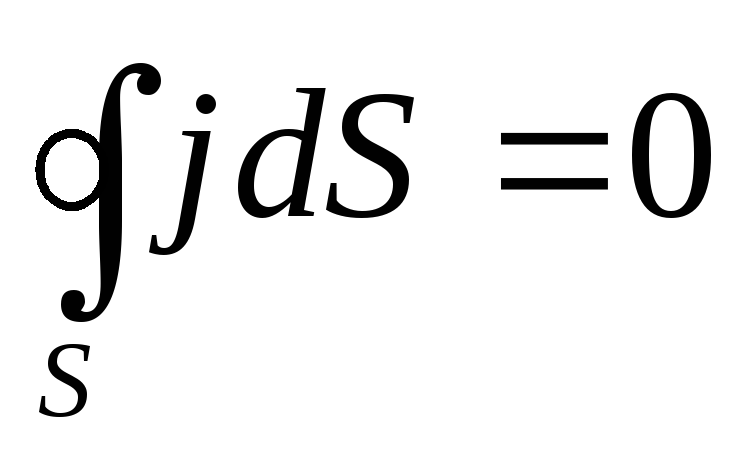 .
.
Учитывая, что
 ,
,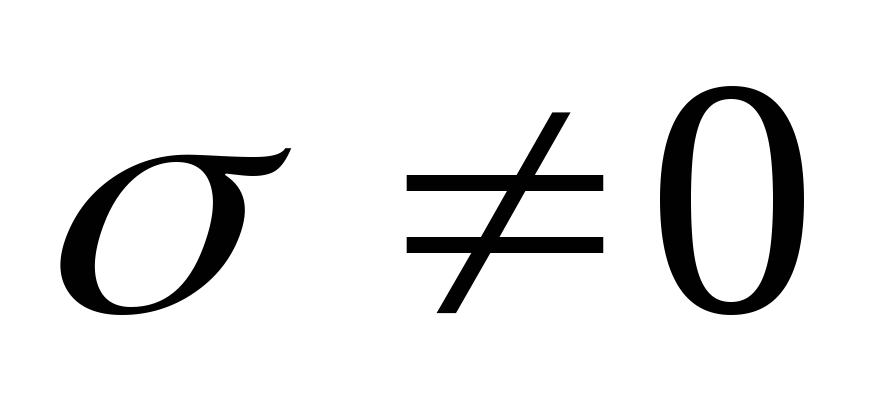 ,
,
 ,
,
т.е.  .
.
Избыточный заряд может появиться только на поверхности однородного проводника, где проводник имеет неоднородность.
В проводнике при постоянном токе распределение зарядов не изменяется с течением времени, хотя и происходит движение зарядов, так как в каждой точке на место уходящих зарядов непрерывно поступают новые. Эти движущиеся заряды создают электрическое поле аналогичноеполю неподвижных зарядов той же конфигурации, т.е. является потенциальным.
Закон Ома для участка, содержащего сторонние силы.
Сторонниминазывают силы не электростатического происхождения. Они могут быть обусловлены химической и физической неоднородностью проводника, например, таковы силы, возникающие при соприкосновении разнородных проводников (гальванические элементы, аккумуляторы) или проводников различной температуры (термоэлементы) и др.
Постоянный ток возможен только при наличии сторонних сил, так как одни электростатические силы могут вызвать только кратковременный ток.
Сторонние силы должны переносить положительные носители на участках своего действия в сторону возрастания потенциала, компенсируя действие электростатических сил.
Для количественной характеристики сторонних сил вводят понятие поля сторонних сил и его напряженность аналогично полю электрических сил:
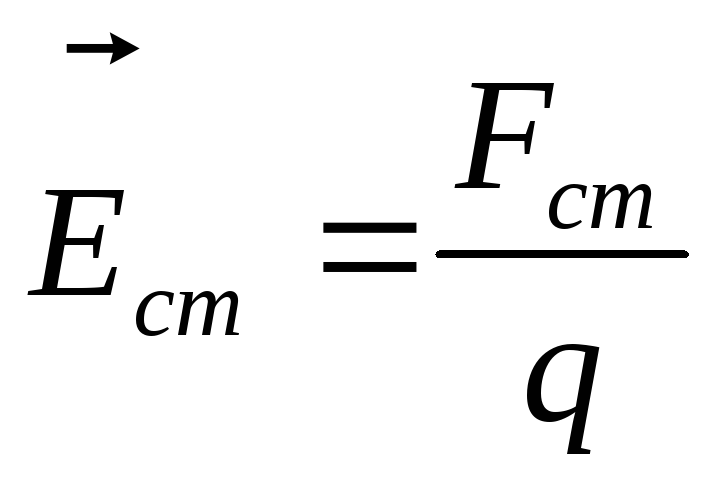 .
.
Очевидно, плотность тока в местах, где существуют электрические и сторонние силы определяется соотношением:
 ,
,
которое называется обобщенным законом Ома в дифференциальной форме.
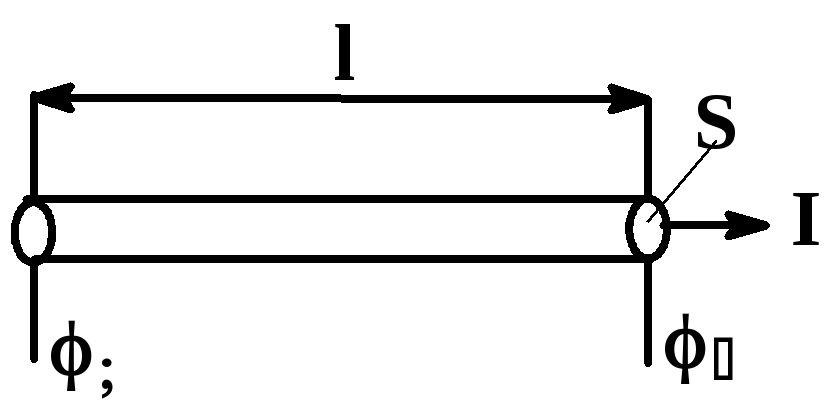
Закон Ома в интегральной форме для участка, содержащего источник тока.
Д ля
простоты рассмотрим участок проводника
в форме цилиндра (см. рисунок), к торцам
которого приложена разность потенциалов
ля
простоты рассмотрим участок проводника
в форме цилиндра (см. рисунок), к торцам
которого приложена разность потенциалов и в пределах которого действуют сторонние
силы.
и в пределах которого действуют сторонние
силы.
Умножим выражение локального закона Ома:

скалярно на вектор перемещения вдоль линии тока и проинтегрируем от точки 1 до точки 2:
 .
.
После интегрирования получаем:
 ,
,
где 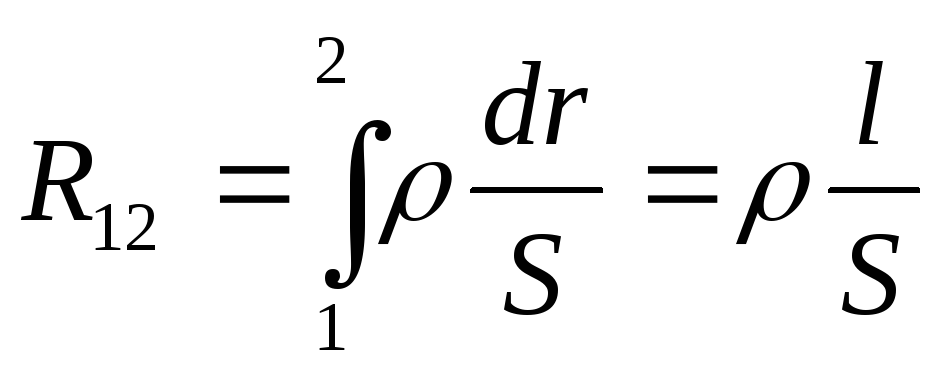 — сопротивление участка цепи между
сечениями 1 и 2,
— сопротивление участка цепи между
сечениями 1 и 2, – сила тока на участке,
– сила тока на участке,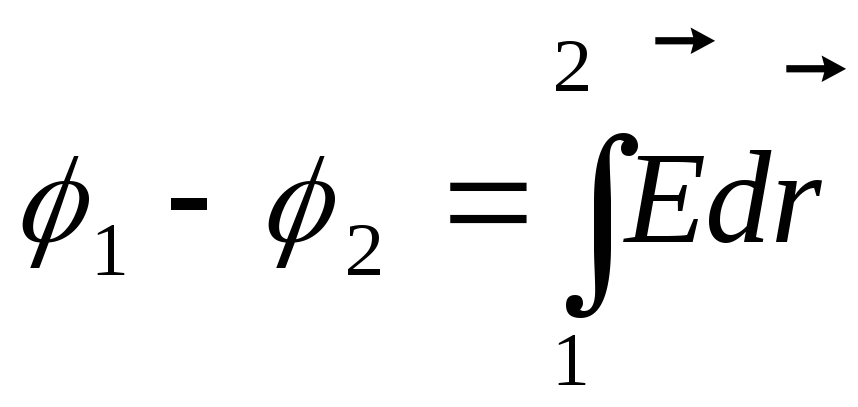 — разность потенциалов,
— разность потенциалов, —
электродвижущая сила (э.д.с.), действующая
на данном участке цепи, равная работе
сторонних сил по перемещению единичного
положительного заряда. Произведение
—
электродвижущая сила (э.д.с.), действующая
на данном участке цепи, равная работе
сторонних сил по перемещению единичного
положительного заряда. Произведение называютпадениемнапряжения на
участке.
называютпадениемнапряжения на
участке.
Э.д.с., как и сила тока  и соответственно падение напряжения,
является величиной алгебраической:
если э.д.с. способствует движению
положительных носителей в выбранном
направлении, то
и соответственно падение напряжения,
является величиной алгебраической:
если э.д.с. способствует движению
положительных носителей в выбранном
направлении, то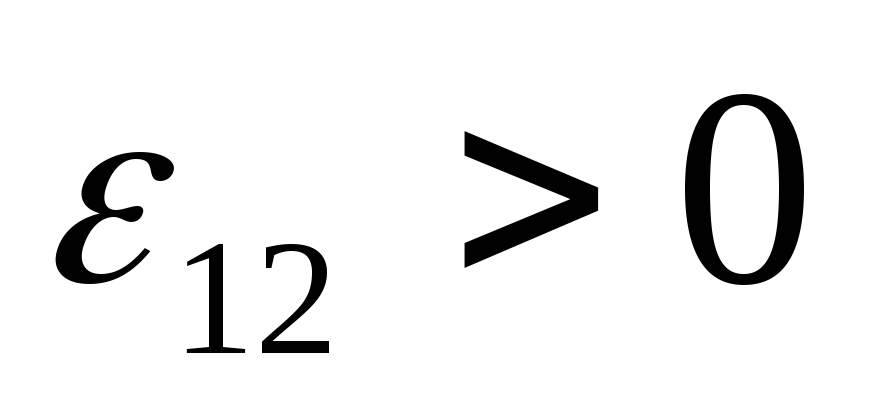 ,
если же препятствует, то
,
если же препятствует, то .
.
Полученное соотношение выражает интегральную форму закона Ома для участка, содержащего сторонние силы.
О бычно
сторонние силы действуют на ограниченном
участке, которые называют источником
постоянного тока. Условно источник
обозначают двумя вертикальными
черточками, короткой и длинной. Короткая
относится к отрицательному полюсу,
длинная – к положительному. Э.д.с.
направлена от минуса к плюсу, так как
сторонние силы в источнике всегда
действуют против электрических сил.
бычно
сторонние силы действуют на ограниченном
участке, которые называют источником
постоянного тока. Условно источник
обозначают двумя вертикальными
черточками, короткой и длинной. Короткая
относится к отрицательному полюсу,
длинная – к положительному. Э.д.с.
направлена от минуса к плюсу, так как
сторонние силы в источнике всегда
действуют против электрических сил.
Пример.
Рассмотрим участок, содержащий источник и сопротивление (см. рисунок).
В ыразим
разность потенциалов:
ыразим
разность потенциалов:
 .
.
В нашем примере  .
.
Пусть ток на участке течёт от 1 и 2 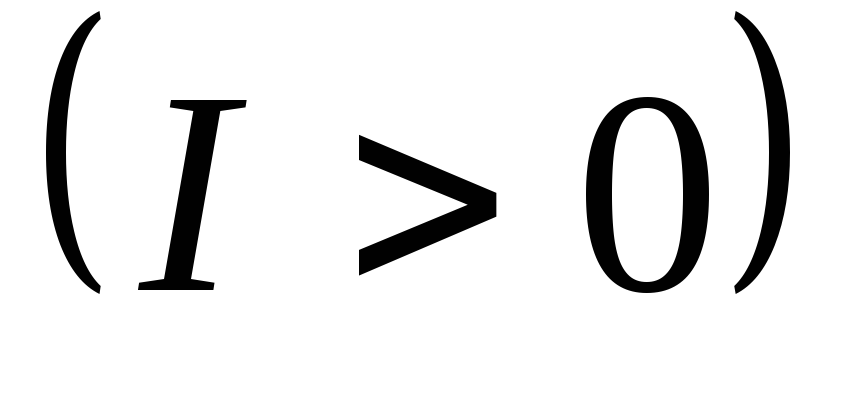 .
Алгебраическая сумма в правой части
может оказаться отрицательной.
Следовательно
.
Алгебраическая сумма в правой части
может оказаться отрицательной.
Следовательно ,
т.е. ток течёт в сторону повышения
потенциала. Это возможно потому, что на
участке действует э.д.с. в положительном
направлении (от 1 и 2). Если
,
т.е. ток течёт в сторону повышения
потенциала. Это возможно потому, что на
участке действует э.д.с. в положительном
направлении (от 1 и 2). Если ,
то
,
то ,
т.е. э.д.с. источника равна разности
потенциалов между полюсами источника.
,
т.е. э.д.с. источника равна разности
потенциалов между полюсами источника.
Закон Ома. Закон Ома в дифференциальной форме
Закон Ома. Закон Ома в дифференциальной форме.
Зако́н О́ма — физический закон, определяющий связь электродвижущей силы источникаили электрического напряжения с силой тока и сопротивлением проводника. Экспериментально установлен в 1826 году, и назван в честь его первооткрывателя Георга Ома.
В своей оригинальной форме
он был записан его автором в виде :  ,
,
Здесь X —
показания гальванометра,
т.е в современных обозначениях сила
тока I, a —
величина, характеризующая свойства
источника тока, постоянная в широких
пределах и не зависящая от величины
тока, то есть в современной терминологии
электродвижущая сила (ЭДС)  , l —
величина, определяемая длиной соединяющих
проводов, чему в современных представлениях
соответствует сопротивление внешней
цепи R и,
наконец, b параметр,
характеризующий свойства всей установки,
в котором сейчас можно усмотреть учёт
внутреннего сопротивления источника
тока r[1].
, l —
величина, определяемая длиной соединяющих
проводов, чему в современных представлениях
соответствует сопротивление внешней
цепи R и,
наконец, b параметр,
характеризующий свойства всей установки,
в котором сейчас можно усмотреть учёт
внутреннего сопротивления источника
тока r[1].
В таком случае в современных терминах и в соответствии с предложенной автором записи формулировка Ома (1) выражает
Закон Ома для полной цепи:
 ,
(2)
,
(2)
где:
 — ЭДС источника
напряжения(В),
— ЭДС источника
напряжения(В), — сила
тока в
цепи (А),
— сила
тока в
цепи (А), — сопротивление всех
внешних элементов цепи (Ом),
— сопротивление всех
внешних элементов цепи (Ом), — внутреннее
сопротивление источника
напряжения (Ом).
— внутреннее
сопротивление источника
напряжения (Ом).
Из закона Ома для полной цепи вытекают следствия:
При r<<R сила тока в цепи обратно пропорциональна её сопротивлению. А сам источник в ряде случаев может быть назван источником напряжения
При r>>R сила тока от свойств внешней цепи (от величины нагрузки) не зависит. И источник может быть назван источником тока.
Часто[2] выражение:
 (3)
(3)
(где  есть напряжение или падение
напряжения,
или, что то же, разность
потенциалов между
началом и концом участка проводника)
тоже называют «Законом Ома».
есть напряжение или падение
напряжения,
или, что то же, разность
потенциалов между
началом и концом участка проводника)
тоже называют «Законом Ома».
Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется:
 (4)
(4)
То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС.
К другой записи формулы (3), а именно:
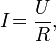 (5)
(5)
Применима другая формулировка:
| Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи. |
|
Выражение (5) можно переписать в виде:
 (6)
(6)
где коэффициент пропорциональности G назван проводимость или электропроводность. Изначально единицей измерения проводимости был «обратный Ом» — Mо[3], впоследствии переименованный в Си́менс (обозначение: См, S).
| (7.6.3) |
|
это запись закона Ома в дифференциальной форме.
Здесь 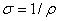 – удельная
электропроводность.
– удельная
электропроводность.
Размерность σ – [ ].
].
Плотность
тока можно выразить через заряд
электрона е,
количество зарядов n и
дрейфовую скорость 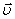 :
:
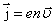 .
.
Обозначим 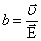 ,
тогда
,
тогда  ;
;
|
| (7.6.4) |
|
Теперь, если удельную
электропроводность σ выразить
через е, n и b: 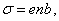 то
вновь получим выражение закона
Ома в дифференциальной форме:
то
вновь получим выражение закона
Ома в дифференциальной форме:
 .
.
3.2.2. Закон Ома в интегральной и дифференциальной форме
| Пусть по проводнику длиной l и сечением S течет ток I. В проводнике создается электрическое поле напряженности E, а 1 и 2 – потенциалы на концах проводника. В случае однородного проводника величину 1 — 2 = U можно назвать падением напряжения на участке проводника. |
Закон Ома: сила тока, текущего по однородному участку проводника, прямо пропорциональна падению напряжения на проводнике:

— закон Ома в интегральной форме
где R – электрическое сопротивление проводника.
Размерность сопротивления в СИ: [R] = В/А = Ом.
Ом – сопротивление такого проводника, в котором при напряжении в 1 В течет ток 1А.
Сопротивление зависит от геометрических размеров и формы проводников, материала и температуры проводников. Для цилиндрического проводника

где — удельное сопротивление проводника.
Удельное сопротивление численно равно сопротивлению проводника длиной 1 м и площадью поперечного сечения 1 м2. Размерность удельного сопротивления в СИ: [] = Омм.
Величина, обратная сопротивлению, называется проводимостью.
Величина, обратная удельному сопротивлению, называется удельной проводимостью:
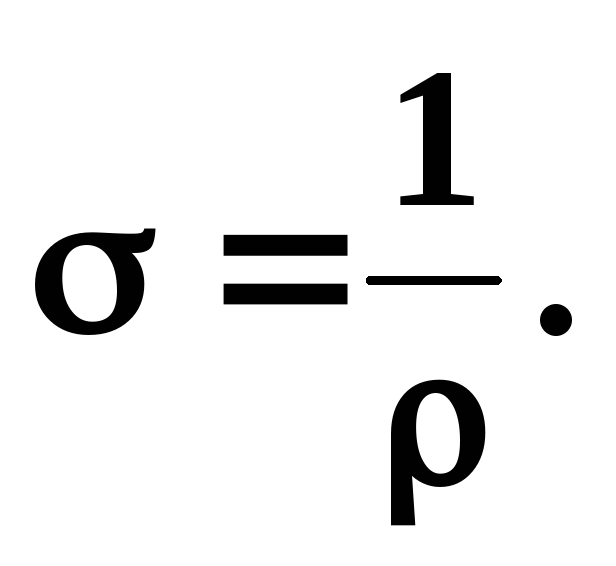
Единица, обратная Ом, называется Сименсом [См].
Учитывая выше
написанные уравнения, а также 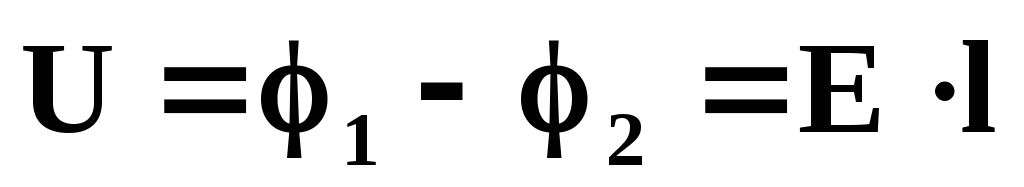 ,
получим:
,
получим:


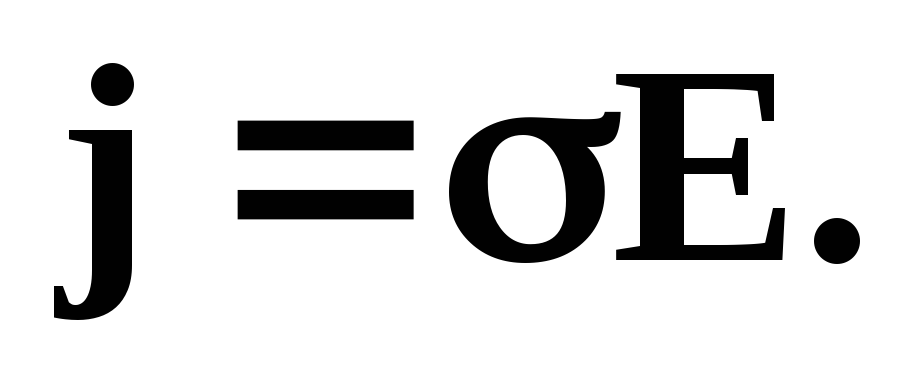
– закон Ома в дифференциальной форме.
3.2.3. Сторонние силы. Закон Ома для цепи, содержащей эдс
Для возникновения и существования электрического тока необходимо:
наличие свободных носителей тока – заряженных частиц, способных перемещаться упорядоченно;
наличие электрического поля, энергия которого должна каким-то образом восполняться.
| Соединим проводником два тела с зарядами +q и –q. Кулоновские силы заставляют электроны перемещаться по проводнику. Возникнет ток. Однако тела при этом будут разряжаться, разность потенциалов уменьшится, ток быстро прекратится. |
Т.е. если в цепи действуют только силы электростатического поля, то происходит перемещение носителей таким образом, что потенциалы всех точек цепи выравниваются и электростатическое поле исчезает.
Следовательно, поле кулоновских сил не может являться причиной постоянного электрического тока.
Ток в проводнике нейтрализует заряды на его концах. Для поддержания постоянного тока необходимо поддерживать постоянную разность потенциалов, следовательно, разделять заряды. Электрические силы разделять заряды не могут.
Силы, разделяющие заряды, имеют неэлектрическую природу и называются сторонними силами.
Устройство, в котором действуют сторонние силы, называется источником тока.
Сторонние силы заставляют заряды двигаться внутри источника тока против сил поля. Благодаря этому в цепи поддерживается постоянная разность потенциалов.
Перемещая заряды, сторонние силы совершают работу за счет энергии, затраченной в источнике тока. Например, в электрофорной машине разделение зарядов происходит за счет механической работы, в гальваническом элементе – за счет энергии химических реакций и т.д.
Величина, равная работе сторонних сил по перемещению единичного положительного заряда, называется электродвижущей силой (ЭДС).
Обозначим 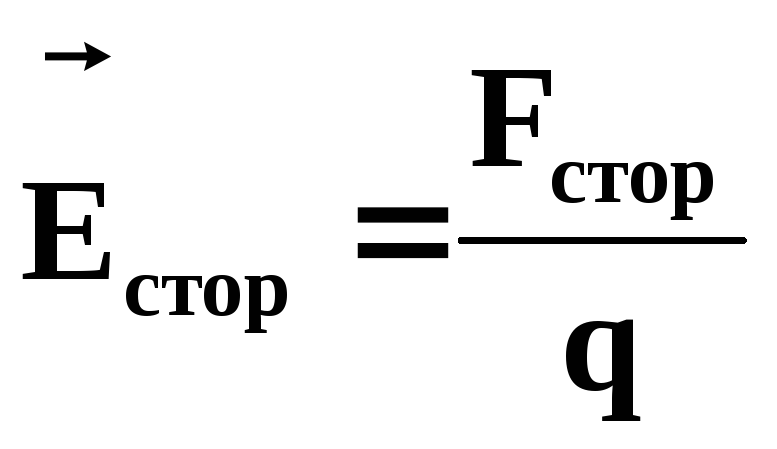 — вектор напряженности поля сторонних
сил.
— вектор напряженности поля сторонних
сил.
Результирующее поле, действующее на заряды в проводнике, в общем случае
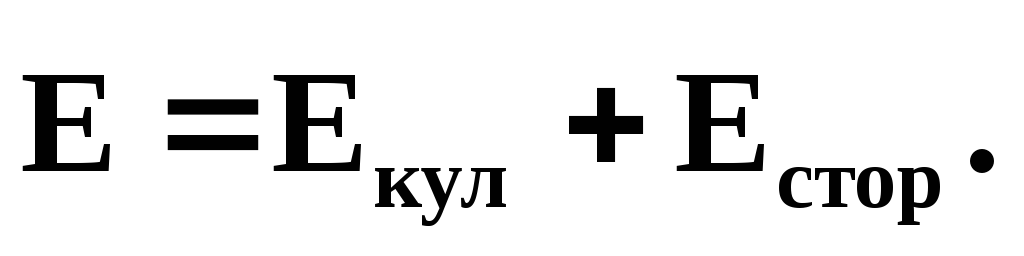
Плотность тока в цепи
 .
.
– закон Ома в дифференциальной форме для цепи, содержащей ЭДС.
| Рассмотрим участок AB замкнутой цепи, содержащей ЭДС (рис.3.18). Выделим мысленно малый элемент dl. |
Плотность тока
на этом участке опишется уравнением  .
Умножим скалярно обе части этого
равенства на
.
Умножим скалярно обе части этого
равенства на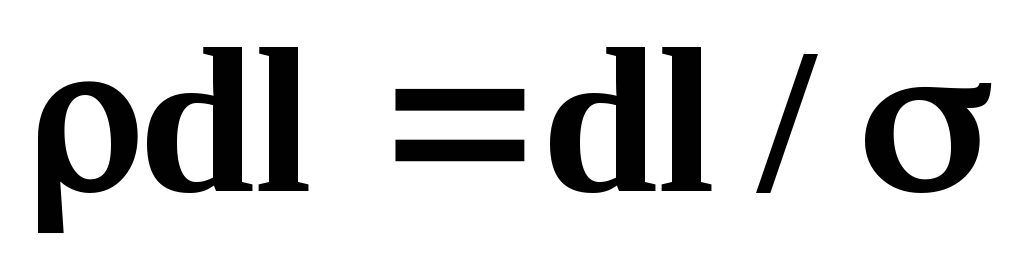 и проинтегрируем по участкуAB:
и проинтегрируем по участкуAB:

Рассмотрим каждый интеграл в отдельности:
а)
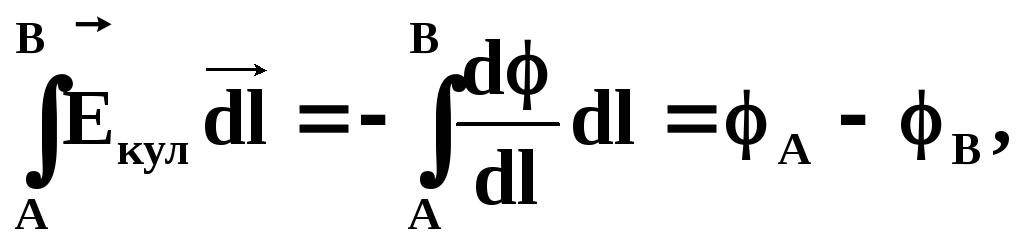
где А — В – разность потенциалов между точками A и B.
Разность потенциалов численно равна работе кулоновских сил по перемещению единичного положительного заряда из т.A в т.B;
б)
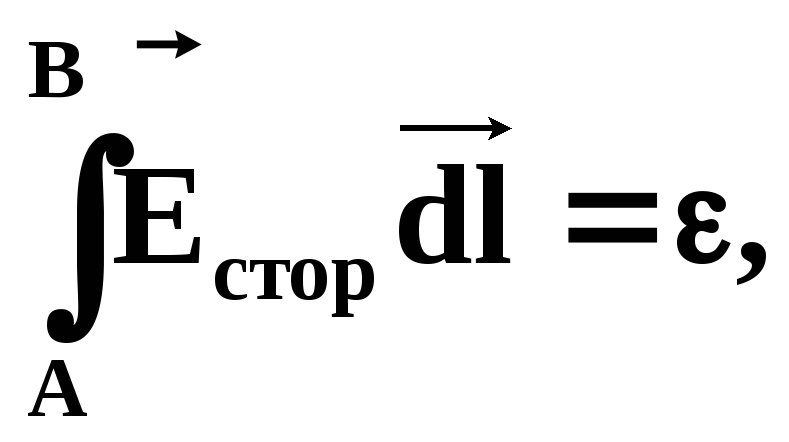
где — ЭДС.
ЭДС, действующая на участке цепи, численно равна работе сторонних сил по перемещению единичного положительного заряда из т.A в т.B;
в)

где RAB – сопротивление участка AB.
С учетом выше сказанного можно получить:

— закон Ома для участка цепи с ЭДС.

Частные случаи:
если на данном участке цепи источник тока отсутствует, то получаем закон Ома для однородного участка цепи:

если цепь замкнута (=0), то получим закон Ома для замкнутой цепи:
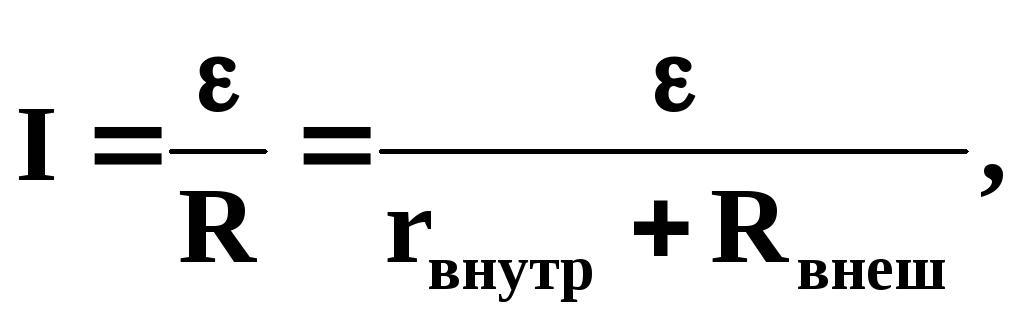
где — ЭДС, действующая в цепи, R – суммарное сопротивление всей цепи, rвнутр – внутреннее сопротивление источника тока, Rвнеш – сопротивление внешней цепи;
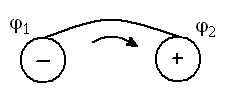
если цепь разомкнута, то I = 0 и 12 = 2 — 1, т.е. ЭДС, действующая в разомкнутой цепи равна разности потенциалов на ее концах.
В случае короткого замыкания сопротивление внешней цепи Rвнеш = 0 и сила тока
 в этом случае ограничивается только
величиной внутреннего сопротивления
источника тока.
в этом случае ограничивается только
величиной внутреннего сопротивления
источника тока.
Величина IRAB = UAB называется падением напряжения на участке AB.
Падение напряжения на участке AB численно равно работе кулоновских и сторонних сил по перемещению единичного положительного заряда из т.A в т.B.
Если цепь замкнута, то 1 = 2 и
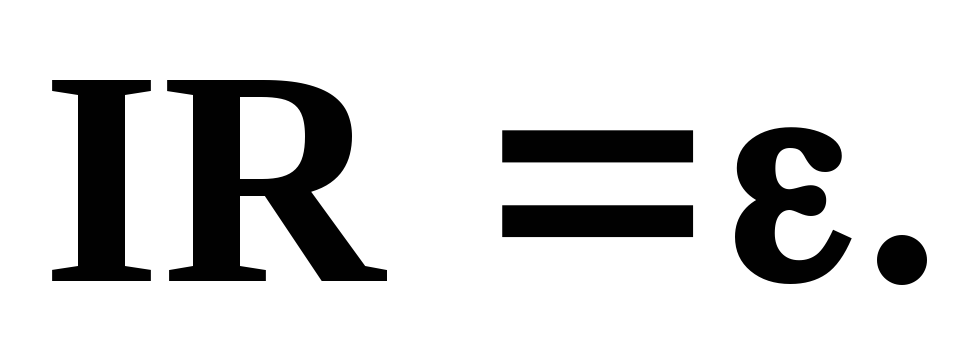
– закон Ома для замкнутой цепи.
Если участок цепи не содержит ЭДС, то





 — ЭДС источника
напряжения(В),
— ЭДС источника
напряжения(В),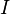 — сила
тока в
цепи (А),
— сила
тока в
цепи (А), — сопротивление всех
внешних элементов цепи (Ом),
— сопротивление всех
внешних элементов цепи (Ом), — внутреннее
сопротивление источника
напряжения (Ом).
— внутреннее
сопротивление источника
напряжения (Ом).

 ,
,

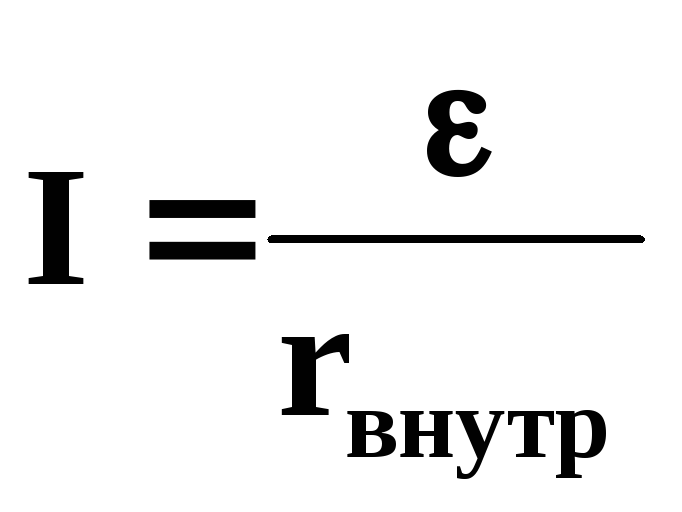 в этом случае ограничивается только
величиной внутреннего сопротивления
источника тока.
в этом случае ограничивается только
величиной внутреннего сопротивления
источника тока.