Диаметр — это… Что такое Диаметр?
Диаметр в изначальном значении это отрезок, соединяющий две точки на окружности и проходящий через центр окружности, а также длина этого отрезка. Диаметр равен двум радиусам.
Диаметр геометрических фигур
Диаметр окружности, круга, сферы, шара
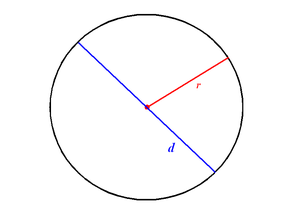 Радиус (r) и диаметр (d) окружности
Радиус (r) и диаметр (d) окружностиДиаметр — это хорда (отрезок, соединяющий две точки) на окружности (сфере, поверхности шара), и проходящий через центр этой окружности (сферы, шара). Также диаметром называют длину этого отрезка. Диаметр окружности является хордой, проходящей через её центр; такая хорда имеет максимальную длину. По величине диаметр равен двум радиусам.
Символ диаметра
Символ диаметра «⌀» (может не отображаться в некоторых браузерах) схож начертанием со строчной перечёркнутой буквой «o». В Юникоде он находится под десятичным номером 8960 или шестнадцатеричным номером 2300 (может быть введён в HTML-код как ⌀ или %%c (буква c — латинская) или \U+2205 в текстовой строке.
Во многих случаях символ диаметра может не отображаться, так как он редко включается в шрифты — например, он присутствует в Arial Unicode MS (поставляется с Microsoft Office, при установке именуется «Универсальный шрифт»), DejaVu (свободный), Code2000 (условно-бесплатный) и некоторых других.
Следует отличать символ диаметра «⌀» от других похожих на него символов:
Вариации и обобщения
Понятие диаметра допускает естественные обобщения на некоторые другие геометрические объекты.
- Под диаметром конического сечения понимается прямая проходящая через середины двух параллельных хорд.
- Под диаметром метрического пространства понимается точная верхняя грань расстояний между парами его точек. В частности:
- Диаметр графа — это максимальное из расстояний между парами его вершин. Расстояние между вершинами определяется как наименьшее число рёбер, которые необходимо пройти, чтобы добраться из одной вершины в другую. Иначе говоря, это расстояние между двумя вершинами графа, максимально удаленными друг от друга.
- Диаметр геометрической фигуры — максимальное расстояние между точками этой фигуры.
- Диаметром множества , лежащего в метрическом пространстве с метрикой , называется величина . Например, диаметр n-размерного гиперкуба со стороной s равен
- .
См. также
Литература
Диаметр — Википедия. Что такое Диаметр
Материал из Википедии — свободной энциклопедииДиа́метр в изначальном значении термина — отрезок, соединяющий две точки на окружности и проходящий через центр окружности, а также длина этого отрезка. Диаметр равен двум радиусам.
Диаметр геометрических фигур
 Радиус (r) и диаметр (d) окружности
Радиус (r) и диаметр (d) окружностиДиаметр — это хорда (отрезок, соединяющий две точки) на окружности (сфере, поверхности шара), проходящая через центр этой окружности (сферы, шара). Также диаметром называют длину этого отрезка. Диаметр окружности является хордой, проходящей через её центр; такая хорда имеет наибольшую длину. По величине диаметр равен двум радиусам.
Символ диаметра
Символы со сходным начертанием:Символ диаметра «⌀» (может не отображаться в некоторых браузерах) схож начертанием со строчной перечёркнутой буквой «o». В Юникоде он находится под десятичным номером 8960 или шестнадцатеричным номером 2300 (может быть введён в HTML-код как ⌀ или ⌀). Этот символ не присутствует в стандартных раскладках, поэтому для его ввода при компьютерном наборе необходимо использовать вспомогательные средства — например, приложение «Таблица символов» в Windows, программу «Таблица символов» (ранее gucharmap) в GNOME, команду «Вставка» → «Символ…» в программах Microsoft Office и т. д. Специализированные программы могут предоставлять пользователю свои способы ввода этого символа: к примеру, в САПР AutoCAD для ввода символа диаметра используется сочетание символов c — латинская) или \U+2205 в текстовой строке.
Во многих случаях символ диаметра может не отображаться, так как он редко включается в шрифты — например, он присутствует в Arial Unicode MS (поставляется с Microsoft Office, при установке именуется «Универсальный шрифт»), DejaVu (свободный), Code2000 (условно-бесплатный) и некоторых других.
Сопряжённые диаметры эллипса и гиперболы
Сопряжённые диаметры эллипса

- Диаметром эллипса называют произвольную хорду, проходящую через его центр. Сопряжёнными диаметрами эллипса называют пару его диаметров, обладающих следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре.
На рисунке представлена пара сопряженных диаметров (красный и синий). Если в точках пересечения диаметра с эллипсом провести прямую, параллельную сопряжённому диаметру, то прямая будет касательной к эллипсу, и четыре таких касательных ко всем четырём концам пары сопряжённых диаметров эллипса образуют описанный около эллипса параллелограмм (зеленые линии на рисунке).
- Расстояния r1{\displaystyle r_{1}} и r2{\displaystyle r_{2}} от каждого из фокусов до данной точки на эллипсе называются фокальными радиусами в этой точке.
- Радиус эллипса в данной точке (расстояние от его центра до данной точки) вычисляется по формуле r=abb2cos2φ+a2sin2φ=b1−e2cos2φ{\displaystyle r={\frac {ab}{\sqrt {b^{2}\cos ^{2}\varphi +a^{2}\sin ^{2}\varphi }}}={\frac {b}{\sqrt {1-e^{2}\cos ^{2}\varphi }}}}, где φ{\displaystyle \varphi } — угол между радиус-вектором данной точки и осью абсцисс.
Сопряжённые диаметры гиперболы
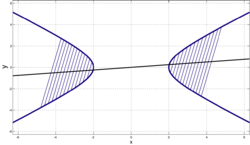 Диаметры гиперболы
Диаметры гиперболы- Диаметром гиперболы, как и всякого конического сечения, является прямая, проходящая через середины параллельных хорд. Каждому направлению параллельных хорд соответствует свой сопряжённый диаметр. Все диаметры гиперболы проходят через её центр. Диаметр, соответствующий хордам, параллельным мнимой оси, есть действительная ось; диаметр соответствующий хордам, параллельным действительной оси, есть мнимая ось.
- Угловой коэффициент k{\displaystyle k} параллельных хорд и угловой коэффициент k1{\displaystyle k_{1}} соответствующего диаметра связан соотношением
- k⋅k1=ε2−1=b2a2{\displaystyle k\cdot k_{1}=\varepsilon ^{2}-1={\frac {b^{2}}{a^{2}}}}
 Для произвольного угла φ показаны диаметры и сопряженные им диаметры для окружностей и равнобочных гипербол.
Для произвольного угла φ показаны диаметры и сопряженные им диаметры для окружностей и равнобочных гипербол.
- Если диаметр гипербол a делит пополам хорды, параллельные диаметру b, то диаметр b делит пополам хорды, параллельные диаметру a. Такие диаметры называются взаимно сопряжёнными.
- Главными диаметрами гипербол называются взаимно сопряжённые и взаимно перпендикулярные диаметры. У гиперболы есть только одна пара главных диаметров — действительная и мнимая оси.
- В случае гипербол с асимптотами, образующими прямой угол, её сопряженные гиперболы получатся при её зеркальном отражении относительно одной из асимптот. При таком зеркальном отражении её диаметр перейдет в сопряженный диаметр, который будет просто диаметром сопряженной гиперболы (см. рис.). Также. как наблюдается перпендикулярность сопряженных диаметров на окружности (на рис. слева), аналогичная ортогональность наблюдается для сопряженных диаметров гиперболы со взаимно перпендикулярными асимптотами (на рис. справа).
Вариации и обобщения
Понятие диаметра допускает естественные обобщения на некоторые другие геометрические объекты.
- Под диаметром конического сечения понимается прямая проходящая через середины двух параллельных хорд.
- Под диаметром метрического пространства понимается точная верхняя грань расстояний между парами его точек. В частности:
- Диаметр графа — это максимальное из расстояний между парами его вершин. Расстояние между вершинами определяется как наименьшее число рёбер, которые необходимо пройти, чтобы добраться из одной вершины в другую. Иначе говоря, это расстояние между двумя вершинами графа, максимально удаленными друг от друга.
- Диаметр геометрической фигуры — максимальное расстояние между точками этой фигуры.
- Диаметром множества M{\displaystyle M}, лежащего в метрическом пространстве с метрикой ρ{\displaystyle \rho }, называется величина (supx,y∈Mρ(x,y)){\displaystyle (\sup _{x,y\in M}\rho (x,y))}. Например, диаметр n-размерного гиперкуба со стороной s равен
- d=s⋅n{\displaystyle d=s\cdot {\sqrt {n}}}.
Некоторые окружности, построенные в треугольнике на одном отрезке, как на диаметре
См. также
Литература
Ответы Mail.ru: что такое диаметр круга
Диаметр в изначальном значении термина — отрезок, соединяющий две точки на окружности и проходящий через центр окружности, а также длина этого отрезка. Диаметр равен двум радиусам. Диаметр — это хорда (отрезок, соединяющий две точки) на окружности (сфере, поверхности шара), проходящая через центр этой окружности (сферы, шара). Также диаметром называют длину этого отрезка. Диаметр окружности является хордой, проходящей через её центр; такая хорда имеет наибольшую длину. По величине диаметр равен двум радиусам. Понятие диаметра допускает естественные обобщения на некоторые другие геометрические объекты. Под диаметром конического сечения понимается прямая проходящая через середины двух параллельных хорд. Под диаметром метрического пространства понимается точная верхняя грань расстояний между парами его точек. В частности: Диаметр графа — это максимальное из расстояний между парами его вершин. Расстояние между вершинами определяется как наименьшее число рёбер, которые необходимо пройти, чтобы добраться из одной вершины в другую. Иначе говоря, это расстояние между двумя вершинами графа, максимально удаленными друг от друга. Диаметр геометрической фигуры — максимальное расстояние между точками этой фигуры. Источник: Интернет
Максимальное расстояние его габарита.
тебя в гугле забанили?
диаметр это 2 радиуса. <img src=»//otvet.imgsmail.ru/download/46ec7c4b87618b3462399388f2755dbe_i-6.jpg»>
представь что круг это угол и проведи биссектрису
Диаметр — это <a rel=»nofollow» href=»https://ru.wikipedia.org/wiki/Хорда_(геометрия)» title=»Хорда (геометрия)» target=»_blank» >хорда</a> (<a rel=»nofollow» href=»https://ru.wikipedia.org/wiki/Отрезок» title=»Отрезок» target=»_blank» >отрезок</a>, соединяющий две точки) на <a rel=»nofollow» href=»https://ru.wikipedia.org/wiki/Окружность» title=»Окружность» target=»_blank» >окружности</a> (<a rel=»nofollow» href=»https://ru.wikipedia.org/wiki/Сфера» title=»Сфера» target=»_blank» >сфере</a>, поверхности <a rel=»nofollow» href=»https://ru.wikipedia.org/wiki/Шар_(стереометрия)» title=»Шар (стереометрия)» target=»_blank» >шара</a>), проходящая через<a rel=»nofollow» href=»https://ru.wikipedia.org/wiki/Центр» title=»Центр» target=»_blank» >центр</a> этой окружности (сферы, шара) . Также диаметром называют длину этого отрезка. Диаметр окружности является<a rel=»nofollow» href=»https://ru.wikipedia.org/wiki/Хорда_(геометрия)» title=»Хорда (геометрия)» target=»_blank» >хордой</a>, проходящей через её центр; такая хорда имеет наибольшую длину. По величине диаметр равен двум<a rel=»nofollow» href=»https://ru.wikipedia.org/wiki/Радиус» title=»Радиус» target=»_blank» >радиусам</a>.
Отрезок, проходящий через центр круга с концами на границах окружности<img src=»//otvet.imgsmail.ru/download/289afb4b1cd27022623f96a94ae6fcb3_i-197.jpg»>
ДИАМЕТР (от греч. diametros — поперечник) окружности, отрезок прямой, соединяющий две точки окружности и проходящий через ее центр.
диаметр это 2 радиуса
Отрезок который соединяет две точки окружности и проходит через центр называют диаметром.
отрезок проходящий через центр окружности
Условный проход — Википедия
Материал из Википедии — свободной энциклопедии
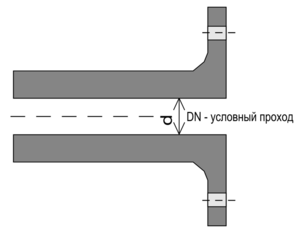
Условный проход, номинальный диаметр — номинальный параметр, применяемый при описании трубопроводных систем как характеризующий признак при монтаже и подгонке друг к другу деталей трубопровода (труб, фитингов, арматуры).
Условный проход примерно соответствует внутреннему диаметру элемента трубопровода, выраженному в миллиметрах. Он не имеет единицы измерения и указывается, например, как DN 100, (Ду 100 в прошлом).
Градуировка условных проходов рассчитана таким образом, чтобы пропускная способность трубопровода при переходе от одного прохода к следующему возрастала на 60—100 %. Условный проход рассчитывается при проектировании таким образом, чтобы обеспечить требуемую пропускную способность трубопровода.
Согласно ГОСТ 28338-89 «Соединения трубопроводов и арматура. Номинальные диаметры. Ряды», значения условного прохода (номинального диаметра) выбираются из ряда:
| 2,5 | 3 | 4 | 5 | 6 | 10 | 12 |
| 15 | 16[1] | 20 | 25 | 32 | 40 | 50 |
| 63[1] | 65 | 80 | 100 | 125 | 150 | 160[1] |
| 175[2] | 200 | 250 | 300 | 350 | 400 | 450 |
| 500 | 600 | 700 | 800 | 900 | 1000 | 1200 |
| 1400 | 1600 | 1800 | 2000 | 2200 | 2400 | 2600[2] |
| 2800 | 3000 | 3200[2] | 3400 | 3600[2] | 3800[2] | 4000 |
Альтернативное пояснение понятия «условный проход» («диаметр условного прохода»)[править | править код]
Чтобы сохранить для всех элементов трубопровода (труб, арматуры и соединительных частей) значение проходного сечения, обеспечивающее расчётные условия для прохода жидкости, пара или газа, введено понятие условного прохода.
Под условным проходом труб, арматуры и соединительных деталей понимают (округленный вверх или вниз до значений стандартного ряда) внутренний диаметр труб (в свету). Условный проход обозначают буквами DN (Ду в прошлом) с добавлением величины условного прохода в миллиметрах: например, условный проход диаметром 150 мм обозначают DN 150 (Ду 150 в прошлом).
Истинный внутренний диаметр труб обычно не равен (за редким исключением) диаметру условного прохода. Так, например, у труб с наружным диаметром 159 мм при толщине стенки 8 мм истинный внутренний диаметр составляет 143 мм, а при толщине стенки 5 мм — 149 мм, однако в обоих случаях условный проход принимается равным 150.
Величины условных проходов арматуры, соединительных частей, а также всех деталей технологического оборудования приборов, к которым присоединяют трубы или арматуру, установлены ГОСТ 28338-89.
Фактический внутренний диаметр каждой трубы зависит от толщины её стенок. Часто диаметр условного прохода (условный проход, номинальный диаметр) и фактический внутренний диаметр не равны. Обычно размеры водогазопроводных труб обозначают по внутренним диаметрам, а остальных типов — по наружным.
Стальные трубы по условиям технологии их производства имеют постоянные наружные диаметры. Для обеспечения прочности трубопроводов, работающих при повышенных или высоких давлениях, увеличивают толщину их стенки, поэтому внутренние диаметры труб отличаются от условных проходов. Так, трубопровод наружным диаметром 273 мм с толщиной стенки 9 мм имеет фактический внутренний диаметр (без учета допусков) 255 мм, а условный проход принимают по ближайшему значению стандартной шкалы — 250 мм.
Соответствие другим номинальным размерам[править | править код]
На практике условным проходам труб соответствуют номиналы труб и фитингов, выраженных по другим параметрам.
| Условный проход (DN) трубы, в мм | Резьба (G), в дюймах | Наружный диаметр, трубы, в мм | ||
|---|---|---|---|---|
| Стальная шовная труба, водо- и газопроводная | Бесшовная стальная труба | Полимерная труба | ||
| 10 | 3/8″ | 17 | 16 | 16 |
| 15 | 1/2″ | 21,3 | 20 | 20 |
| 20 | 3/4″ | 26,8 | 26 | 25 |
| 25 | 1″ | 33,5 | 32 | 32 |
| 32 | 1 1/4″ | 42,3 | 42 | 40 |
| 40 | 1 1/2″ | 48 | 45 | 50 |
| 50 | 2″ | 60 | 57 | 63 |
| 65 | 2 1/2″ | 75,5 | 76 | 75 |
| 80 | 3″ | 88,5 | 89 | 90 |
| 90 | 3 1/2″ | 101,3 | 102 | 110 |
| 100 | 4″ | 114 | 108 | 125 |
| 125 | 5″ | 140 | 133 | 140 |
| 150 | 6″ | 165 | 159 | 160 |
- ↑ 1 2 3 Допускается применять только для гидравлических и пневматических устройств.
- ↑ 1 2 3 4 5 Для арматуры общего назначения применять не допускается.
Диаметр что это? Значение слова Диаметр
Значение слова Диаметр по Ефремовой:
Диаметр — 1. Отрезок прямой, соединяющий две точки окружности и проходящий через центр (в математике).
2. Поперечник любого круглого или кажущегося круглым тела, пространства.
Значение слова Диаметр по Ожегову:
Диаметр — Отрезок прямой линии, соединяющий две точки окружности и проходящий через ее центр
Диаметр Длина этого отрезка
Диаметр в Энциклопедическом словаре:
Диаметр — (от греч. diametros — поперечник) окружности — отрезок прямой, соединяющий две точки окружности и проходящий через ее центр.
Значение слова Диаметр по словарю Ушакова:
ДИАМЕТР, диаметра, м. (греч. diametros). Прямая линия, проходящая через центр кривой фигуры и ограниченная ее контуром (мат.). Большой диаметр эллипсиса. || Поперечник круга, расстояние по прямой линии между его крайними точками. Труба имеет в диаметре десять сантиметров.
Значение слова Диаметр по словарю Даля:
Диаметр
м. греч. поперечник, говоря о круге или шаре. Истинный диаметр светила, астроном. поперечник планеты в линейной мере. видимый диаметр, поперечник в градусах и в долях его, служащий мерою угла, под которым планета видна. Диаметральный, поперечный. поперек супротивный: толщина веревок меряется по окру ясности, а толщина бревен и деревьев диаметрально, в отрубе, в поперечнике.
Значение слова Диаметр по словарю Брокгауза и Ефрона:
Диаметр (геом.) — прямая линия, проходящая через центр кривой фигуры (круга, эллипса, гиперболы, параболы и др.). В круге все Д. равны и делят круг и все перпендикулярные хорды пополам. В эллипсе лишь два Д.: самый большой и самый малый перпендикулярные между собой делят эллипс пополам. В шаре, сфероиде, эллипсоиде и т. п. Д. = плоскость, проходит через центр и делит фигуры все перпендикулярные плоскости пополам.
Определение слова «Диаметр» по БСЭ:
Диаметр (от греч. diбmetros — поперечник)
окружности (круга), хорда, проходящая через центр окружности. Кроме того, Д. окружности называется длина этой хорды, равная двум радиусам.
В аналитической геометрии под Д. конического сечения (или кривой второго порядка) понимается прямая, проходящая через середины параллельных хорд. Для центральных кривых второго порядка (окружности, эллипса, гиперболы) это — прямая, проходящая через центр кривой. В случае параболы все Д. параллельны её оси.
Понятие Д. окружности как длины отрезка распространяется на др. геометрические фигуры и на множества более общей природы. Именно Д. фигуры (или множества в метрическом пространстве) называется верхняя грань расстояний между всевозможными парами точек этой фигуры (см. Верхняя и нижняя грани). В этом смысле Д. эллипса равен длине большой оси, а Д. квадрата равен длине его диагонали.


Диаметр — Большая советская энциклопедия
Диа́метр
(от греч. diámetros — поперечник)
окружности (круга), хорда, проходящая через центр окружности. Кроме того, Д. окружности называется длина этой хорды, равная двум радиусам.
В аналитической геометрии под Д. конического сечения (См. Конические сечения) (или кривой второго порядка) понимается прямая, проходящая через середины параллельных хорд. Для центральных кривых второго порядка (окружности, эллипса, гиперболы) это — прямая, проходящая через центр кривой. В случае параболы все Д. параллельны её оси.
Понятие Д. окружности как длины отрезка распространяется на др. геометрические фигуры и на множества более общей природы. Именно Д. фигуры (или множества в метрическом пространстве) называется верхняя грань расстояний между всевозможными парами точек этой фигуры (см. Верхняя и нижняя грани). В этом смысле Д. эллипса равен длине большой оси, а Д. квадрата равен длине его диагонали.
Источник: Большая советская энциклопедия на Gufo.me
Значения в других словарях
- диаметр — диаметр I м. Отрезок прямой линии, соединяющий две точки окружности и проходящий через центр (в математике). II м. Поперечник любого круглого или кажущегося круглым тела, пространства. Толковый словарь Ефремовой
- диаметр — ДИАМЕТР м. греч. поперечник, говоря о круге или шаре. Истинный диаметр светила, астроном. поперечник планеты в линейной мере; видимый диаметр, поперечник в градусах и в долях его, служащий мерою угла, под которым планета видна. Толковый словарь Даля
- диаметр — сущ., м., употр. сравн. часто (нет) чего? диаметра, чему? диаметру, (вижу) что? диаметр, чем? диаметром, о чём? о диаметре; мн. что? диаметры, (нет) чего? диаметров, чему? диаметрам, (вижу) что? диаметры, чем? диаметрами, о чём? о диаметрах… Толковый словарь Дмитриева
- Диаметр — 1) Д. линии второго порядка — прямая, проходящая через середины параллельных хорд. Д. наз. сопряженным относительно хорд (а также направлений хорд), к-рые он делит пополам. Математическая энциклопедия
- диаметр — • максимальный ~ Словарь русской идиоматики
- диаметр — орф. диаметр, -а Орфографический словарь Лопатина
- диаметр — ДИАМЕТР, а, м. В математике: отрезок прямой линии, соединяющий две точки окружности и проходящий через её центр, а также длина этого отрезка. | прил. диаметральный, ая, ое. Толковый словарь Ожегова
- Диаметр — (геом.) — прямая линия, проходящая чрез центр кривой фигуры (круга, эллипса, гиперболы, параболы и др.). В круге все Д. равны и делят круг и все перпендикулярные хорды пополам. В эллипсе лишь два… Энциклопедический словарь Брокгауза и Ефрона
- диаметр — Диаметр, диаметры, диаметра, диаметров, диаметру, диаметрам, диаметр, диаметры, диаметром, диаметрами, диаметре, диаметрах Грамматический словарь Зализняка
- диаметр — ДИАМЕТР -а; м. [от греч. diametros — поперечник] Отрезок прямой, соединяющий две точки окружности и проходящий через центр. Д. шара. Д. круга. Определить д. // Поперечник любого круглого или кажущегося круглым тела, вместилища, пространства. Д. колеса. Д. бревна. Полметра в диаметре. Толковый словарь Кузнецова
- диаметр — ДИ’АМЕТР, диаметра, ·муж. (·греч. diametros). Прямая линия, проходящая через центр кривой фигуры и ограниченная ее контуром (мат.). Большой диаметр эллипсиса. | Поперечник круга, расстояние по прямой линии между его крайними точками. Труба имеет в диаметре десять сантиметров. Толковый словарь Ушакова
- диаметр — -а, м. Отрезок прямой, соединяющий две точки окружности и проходящий через центр (мат.). || Поперечник любого круглого или кажущегося круглым тела, вместилища, пространства. Ствол дерева диаметром в метр. Малый академический словарь
- ДИАМЕТР — ДИАМЕТР (от греч. diametros — поперечник) окружности, отрезок прямой, соединяющий две точки окружности и проходящий через ее центр. Большой энциклопедический словарь
- диаметр — диа́метр впервые в Уст. морск. 1720 г.; см. Смирнов 109. Через франц. diamètre из лат. diametrus, греч. διάμετρος «поперечник»; см. Дорнзайф 22; Горяев, ЭС 446; диаметра́льный из нем. или франц. diamétral – то же. Этимологический словарь Макса Фасмера
- диаметр — Диа́метр/. Морфемно-орфографический словарь
- диаметр — Диаметра, м. [греч. diametros]. Прямая линия, проходящая через центр кривой фигуры и ограниченная ее контуром (мат.). Большой диаметр эллипсиса. || Поперечник круга, расстояние по прямой линии между его крайними точками. Труба имеет в диаметре десять сантиметров. Большой словарь иностранных слов
- диаметр — ДИАМЕТР а, м. diamètre m., Diameter. — Лекс. Нордстет 1780: диаметр; САР-1: диаметр. Словарь галлицизмов русского языка
- диаметр — сущ., кол-во синонимов: 2 калибр 6 поперечник 10 Словарь синонимов русского языка

Диаметр | Наука | Fandom
Диаметр окружности, круга, сферы, шара — отрезок, соединяющий две точки на окружности (сфере) и проходящий через центр окружности (или сферы), а также длина этого отрезка. Диаметр равен двум радиусам. Под диаметром геометрической фигуры понимается максимальное расстояние между точками этой фигуры.
Диаметр геометрических фигур Править
Диаметр окружности, круга, сферы, шара Править
Радиус (r) и диаметр (d) окружности
Диаметр — это хорда (отрезок, соединяющий две точки) на окружности (сфере, поверхности шара), и проходящий через центр этой окружности (сферы, шара). Также диаметром называют длину этого отрезка. Диаметр окружности является хордой, проходящей через её центр; такая хорда имеет максимальную длину. По величине диаметр равен двум радиусам.
Диаметр гиперболы Править
Диаметры гиперболы
Диаметром гиперболы называют произвольную хорду, проходящую через её центр. Сопряжёнными диаметрами гиперболы называют пару её диаметров, обладающих следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре.
Диаметр эллипса Править
Сопряженные диаметры эллипса. Пунктирами обозначены главные полуоси
Диаметром эллипса называют произвольную хорду, проходящую через его центр. Сопряжёнными диаметрами эллипса называют пару его диаметров, обладающих следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре. Если эллипс является образом окружности при аффинном преобразовании, то его сопряжённые диаметры являются образами двух перпендикулярных диаметров этой окружности.
Диаметр, перпендикулярный к сопряжённым ему хордам, называется главной осью и является осью симметрии фигуры.
Диаметром множества $ M $, лежащего в метрическом пространстве с метрикой $ d $, называется величина $ \sup_{x,y \in M}d(x, y) $. Например, диаметр n-размерного гиперкуба со стороной s равен
- $ d=s\sqrt{n} $
Диаметр графа — это максимум расстояния между вершинами для всех пар вершин. Расстояние между вершинами — наименьшее число рёбер, которые необходимо пройти, чтобы добраться из одной вершины в другую.
Связанные определения Править
- Сопряжённые диаметры — диаметры, обладающие следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре. Если эллипс является образом окружности при аффинном преобразовании, то его сопряжённые диаметры являются образами двух перпендикулярных диаметров этой окружности.
Символ диаметра Править
Символ диаметра «⌀» (может не отображаться в некоторых браузерах) схож начертанием со строчной перечёркнутой буквой «o». В Юникоде он находится под десятичным номером 8960 или шестнадцатеричным номером 2300 (может быть введён в HTML-код как ⌀ или ⌀). Этот символ не присутствует в стандартных раскладках, поэтому для его ввода при компьютерном наборе необходимо использовать вспомогательные средства — например, приложение «Таблица символов» (в Windows), программу Таблица символов Юникода (gucharmap) в GNOME, команду «Вставка» → «Символ…» в программах Microsoft Office и т. д. Кроме того, во многих случаях символ диаметра не будет отображаться, так как он редко включается в шрифты — например, он присутствует в Arial Unicode MS (поставляется с Microsoft Office), DejaVu (свободный), Code2000 (условно бесплатный) и некоторых других.
Следует отличать символ диаметра «⌀» от других похожих на него символов:
Также иногда диаметр обозначается буквой «d», однако в Интернациональной Системе (СИ) он обозначен как «⌀».
В



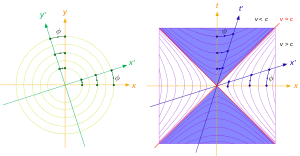 Для произвольного угла φ показаны диаметры и сопряженные им диаметры для окружностей и равнобочных гипербол.
Для произвольного угла φ показаны диаметры и сопряженные им диаметры для окружностей и равнобочных гипербол.