Расчёт делителя напряжения на резисторах онлайн
Р/л технология
Схема такого делителя предназначена для получения заданного выходного напряжения, которое будет ниже, чем входное. Например, источник напряжения 24 Вольта, в нужно получить 6 Вольт. Самым простым способом решить этот вопрос – это применить делитель напряжения, состоящий из двух споротивлний.
Он применяется, как при проектировании схем, так и по прямому назначению. Для его расчета используются формулы, которые основаны на законе Ома. Эти формулы позволяют подобрать нужный номинал сопротивлений. Потребуется лишь знать сопротивление нагрузки, входное и выходное напряжения. От этого сопротивления зависит, насколько точно удастся рассчитать весь делитель и получить точно указанное выходное напряжение. Как правило, сопротивление нагрузки выше, чем сопротивление делителя напряжения.
Если неизвестно выходное напряжение, но известно сопротивление и входное напряжения, то неизвестную величину можно вычислить по указанной формуле.
Для того чтобы не считать постоянно по формулам эти величины, были придуманы онлайн-калькуляторы, которые позволяют точно определить значения резисторов или выходного напряжения. Потребуется лишь внести известные величины. Такой расчет можно производить, как на компьютере, с доступом в сеть Интернет, так и при помощи смартфона. Это значительно экономит время и дает стабильную точность расчетов.
Стоит отметить, что современные калькуляторы-онлайн могут рассчитать и мощность, на которую должен быть установлен резистор.
В радиоэлектронике делители напряжения представлены и в готовых конструктивных решениях. Ими служат, к примеру, переменные резисторы и фоторезисторы, которые имеют возможность менять значение сопротивления, при повороте ручки потенциометра или попадании света. В переменном резисторе присутствуют три вывода, с которых можно получить два сопротивления.
Автор: RadioRadar
Мнения читателей
Нет комментариев.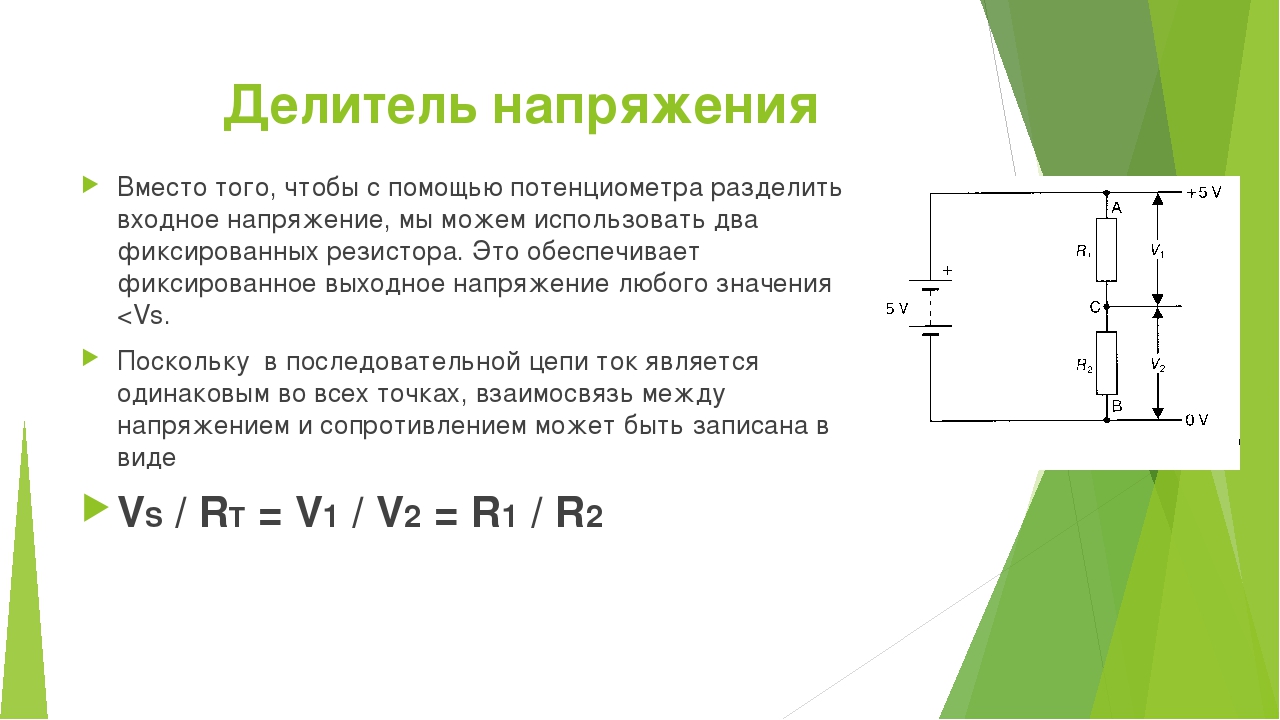 Ваш комментарий будет первый.
Ваш комментарий будет первый.
Вы можете оставить свой комментарий, мнение или вопрос по приведенному выше материалу:
Поля, обязательные для заполнения
Добавить
Очистить
Делитель напряжения
Делитель напряжения применяют с целью получения части напряжения, для отдельных компонентов схемы, используя всего один источник питания.
Принципиальная схема делителя напряжения до элементарного проста и состоит всего из двух резисторов. Главным в ее сборке остается правильный расчет сопротивления резисторов, необходимый для получения конкретного напряжения, и мощности, проходящей через них.
К примеру, для делителя напряжения возьмем сопротивлением исходя из расчетов:
Расчет резисторов для делителя напряжения происходит с конца схемы, а именно имеем изначальные данные: Нагрузка устройства (части компонентов на схеме), для которого рассчитываем делитель напряжения (I) – 20 mA; необходимо получить ток (Uout) – 5 v.
R2 = Uout / I = 5 v / 0.02A = 250 Om;
Зная сопротивление резистора R2, можем найти сопротивление резистора R1:
R1 = Uin / I – R2 = 12 v / 0.02A – 250 Om = 350 Om;
Расчет делителя напряжения окончен, но не все на практике так хорошо, как в теории. Так как нагрузка на выходе делителя напряжения имеет свое сопротивление, расчет необходимо производить с поправкой на это.
Помним, что нагрузка у нас составляет 20 mA, исходя из этого, по закону Ома, рассчитываем сопротивление нагрузки:
Rнагр = U / I = 5 v / 0.02 A = 250 Om;
Как видно, данный расчет мы уже производили выше для резистора R2 делителя напряжения.
В данном случае нагрузка служит параллельным сопротивлением резистору R2, и все расчеты следует поправить, иначе мы потеряем почти 2v:
Rобщ(Rнагр и R2) = Rнагр * R2 / (Rнагр + R2) = 250 * 250 / 250 + 250 = 125 Om;
Uout = Uin ( Rобщ / (R1 + Rобщ ) ) = 12 v ( 125 Om / ( 350 Om + 125 Om) ) = 3,16 v;
Исходя из этого, сопротивление резистора R1 необходимо рассчитывать по формуле:
R1 = Uin / Uout * Rобщ – Rобщ = 12 v / 5 v * 125 Om – 125 Om = 175 Om;
Делаем проверку:
Uout = Uin ( Rобщ / (R1 + Rобщ ) ) = 12 v ( 125 Om / ( 175 Om + 125 Om) ) = 5 v;
Расчет резисторов необходимых для нашего делителя напряжения закончен, осталось выяснить тип резистора, способный выдержать нагрузку. Рассчитываем мощность, проходящую через резистор делителя напряжения:
Рассчитываем мощность, проходящую через резистор делителя напряжения:
P = Uin2 / R1 = 12 v * 12 v / 175 Om ≈ 0,823 Watt;
Делаем вывод, что нам подойдут резисторы, например МЛТ-1 – мощностью не менее 1 Watt.
Применять такого типа делители напряжения можно, только если подключаемая нагрузка потребляет от долей до нескольких десятков миллиампер тока. Данный делитель напряжения никак нельзя использовать для питания мощных приборов, таких как ламп, двигателей и т.д.
Также в качестве эксперимента можно произвести масштабируемость сопротивлений делителя напряжения. Но помните, что чем меньше сопротивление в резисторах делителя напряжения, тем больше на них нагрузка и больше расход энергии.
Делители напряжения удачно подходят для преобразования сигнала с датчиков на основе резисторов. Такие резисторы как фоторезисторы, терморезисторы, тензорезисторы и т.д. способны изменять свое сопротивление в ходе воздействия на них окружающей среды. Подключение такого сенсора к выходу делителя напряжения или вместо одного из резисторов R1 и R2 и вольтметра к точке Uout можно снимать показания.
Подключение такого сенсора к выходу делителя напряжения или вместо одного из резисторов R1 и R2 и вольтметра к точке Uout можно снимать показания.
Практическая работа «Расчёт резистивного делителя напряжения»
Практическая работа № 1
Расчёт резистивного делителя напряжения
Цель: Уметь рассчитывать элементы схемы; знать принципы соотношений между значениями показателей сигналов; уметь применять полученные данные для построения временной диаграммы.
1 Задание
1.1 Начертить схему резистивного делителя напряжения.
1.2 Рассчитать сопротивления резисторов для получения коэффициента передачи.
1.3 Округлить найденное сопротивление до стандартного номинала.
1.4 Определить полученный коэффициент передачи, сравнить его с заданным, оценить погрешность и сделать выводы к её допуску.
1. 5 Определить амплитуду выходного напряжения.
5 Определить амплитуду выходного напряжения.
1.6 Рассчитать мощность, которую рассеивают резисторы и обозначить на схеме номиналы мощностей резисторов.
1.7 Показать в масштабе эпюры входного и выходного напряжений, обращая внимание на фазу сигналов (вверху входное напряжение, внизу – выходное). Внимание! Размещение эпюр в разных столбцах или на разных страницах не разрешается.
2 Исходные данные
2.1 Входное сопротивление Rвх ≥ 1 кОм.
2.2 Амплитуда входного напряжения Um вх = 10 + M, В.
Здесь и дальше: М – предпоследняя, а N – последняя цифры зачётной книжки.
3 Методические указания к решению задания
3.1 Привести схему резистивного делителя напряжения.
Рисунок 3.1 – Схема резисторного делителя напряжения
3. 2 Рассчитать заданный коэффициент передачи делителя.
2 Рассчитать заданный коэффициент передачи делителя.
Согласно условию задания
Rвх ≥ 1 кОм
А так как в данном случае резисторы соединены последовательно, то входное сопротивление цепи равно:
Rвх (1.1)
Из данной формулы видно, что коэффициент передачи будет равным:
Как видно по рисунку 1 и формуле 1.1 входное сопротивление зависит как от сопротивления резистора R1, так и от сопротивления резистора R2. Для выполнения условия задачи можно задать сопротивление одного из этих резисторов равным 1 кОм. Если задать R2 = 1 кОм, то в таком случае Rвх > 1кОм.
Тогда значение резистора R1
R1 =((10+N)-1) . 1000, Ом
3.3 Из Приложения найти ближайшую стандартную величину R1.
3.4 Рассчитать коэффициент передачи делителя с новыми значениями.
Крас =
Определить погрешность коэффициента передачи:
∆К = Крас – К
δ% =
Так как в реальности нельзя изготовить идеальный резистор, все резисторы имеют шкалу допуска разброса параметров. Необходимо выбрать тип резистора из Рядов номинальных значений сопротивлений с ближайшим допустимым отклонением от номинала. Соответственно погрешность δ% будет равна номинальному отклонению.
3.5 Определить амплитуду выходного напряжения
Um вых = Крас
3.6 Рассчитать мощности, которые рассеивают резисторы по формуле:
P = U . I = U2 / R = I2 . К (1.4)
Также используйте формулу:
Um вх = Um R1 + Um R2 = Um R1 + Um вых (1. 5)
5)
Выберите номинальные величины мощностей резисторов.
3.7 На графике покажите эпюры входного и выходного напряжений.
4 Пример расчета (для М =1, N=4)
4.1 Приведем схему резистивного делителя напряжения.
Рисунок 4.1 – Схема резистивного делителя напряжения
4.2 Рассчитаем заданный коэффициент передачи делителя.
Согласно условию задания
Rвх ≥ 1 кОм
А так как в данном случае резисторы соединены последовательно, то входное сопротивление цепи равно:
Rвх (1.1)
(1.2)
Как видно по рисунку 3.1 и формуле 1.1 входное сопротивление зависит как от сопротивления резистора R1, так и от сопротивления резистора R2. Для выполнения условия задачи можно задать сопротивление одного из этих резисторов равным 1 кОм. Если задать R2 = 1 кОм, то в таком случае Rвх > 1кОм.
Для выполнения условия задачи можно задать сопротивление одного из этих резисторов равным 1 кОм. Если задать R2 = 1 кОм, то в таком случае Rвх > 1кОм.
Тогда значение резистора R1
R1 =((10+ -1) . 1000=(14-1) . 1000=13000, Ом
4.3 Из Приложения находим ближайшую стандартную величину R1=13кОм.
4.4 Рассчитать коэффициент передачи делителя с новыми значениями.
Крас
Определить погрешность коэффициента передачи:
∆К = Крас – К=0,071 – 0,071=0
δ% = = . 100%= 0%
Но так как в реальности нельзя изготовить идеальный резистор, все резисторы имеют шкалу допуска разброса параметров. Мы выбрали тип резистора из ряда Е24, для которого допустимые отклонения от номинала составляет ± 5% . Соответственно δ% = 5% .
Полученное значение погрешности не превышает 5%, что удовлетворяет условию.
4.5 Определим амплитуду выходного напряжения
Um вых = Крас . Um вх (1.3)
4.6 Рассчитаем мощности, которые рассеивают резисторы по формуле:
P = U . I = U2 / R = I2 . К (1.4)
Um вх = 10 + M = 10 + 1 = 11 В
Um вых = 0,071 . 11 = 0,781 В
Так как Um вх = U
Um R1 = Um вх — Um вых = 11 – 0,781 = 10,219, В
PR2 = U2m вых / R2 = 0,7812 / 1000 = 6,1 . 10-4, Вт
10-4, Вт
PR
Выбираем номинальные величины мощностей резисторов.
PR1 = 0,125 Вт; PR2 = 0,125 Вт.
4.7 На графике покажем эпюры входного и выходного напряжений.
Рисунок 4.2 – Эпюры входного и выходного напряжений делителя
Приложение
Ряды номинальных значений сопротивлений, емкостей и индуктивностей с допуском ±5 % и более
Е3 Е6
Е12
Е24
Е3
Е6
Е12
Е24
Е3
Е6
Е12
Е24
1
1
1
1
2.
 2
22.2
2.2
2.2
4.7
4.7
4.7
4.7
1.1
2.4
5.1
1.2
1.2
2.7
2.7
5.6
5.6
1.
 3
33
6.2
1.5
1.5
1.5
3.3
3.3
3.3
6.8
6.8
6.8
1.6
3.6
7.5
1.
 8
81.8
3.9
3.9
8.2
8.2
2
4.3
9.1
Номиналы соответствуют числам, приведенным в таблице и числам, полученным умножением на 10n, где n — целое положительное или отрицательное число.
Ряд Е3 соответствует отклонению от номинального значения ±50%
Ряд Е6 соответствует отклонению от номинального значения ±20%
Ряд Е12 соответствует отклонению от номинального значения ±10%
Ряд Е24 соответствует отклонению от номинального значения ±5%.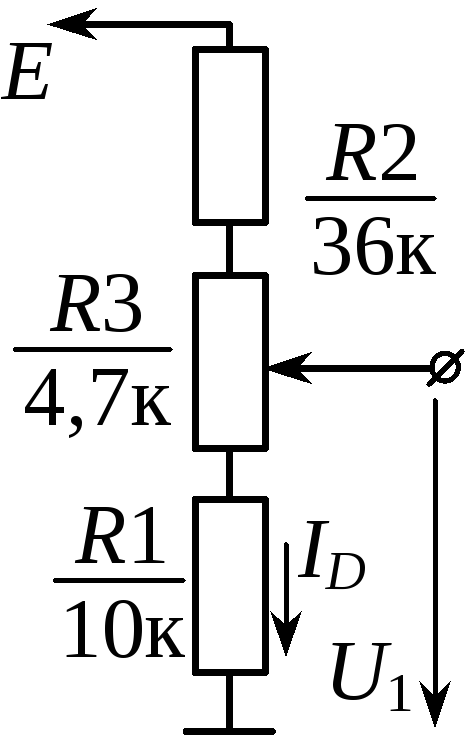
Делитель напряжения
При последовательном подключении нескольких резисторов, на каждом из них происходит падение напряжения. Таким образом, подключенные последовательно компоненты, как бы делят напряжение между собой. Каким именно образом будет происходить деление напряжения, можно рассчитать, используя закон Ома для участка цепи.
РАСЧЁТ ПРОПОРЦИИ
Сила тока, протекающая через резисторы одинакова, т.к. они соединены последовательно, и по закону Ома может быть рассчитана как:
По тому же закону Ома можно вычислить напряжение Vout, которое падает на резисторе R2:
Из полученной формулы видно, что чем больше R2 относительно R1, тем большее напряжение падает на нём.
СЧИТЫВАНИЕ РЕЗИСТИВНЫХ СЕНСОРОВ
Если вместо R2 использовать не постоянный резистор, а датчик, который меняет своё сопротивление, Vout будет зависеть от измеряемого значения.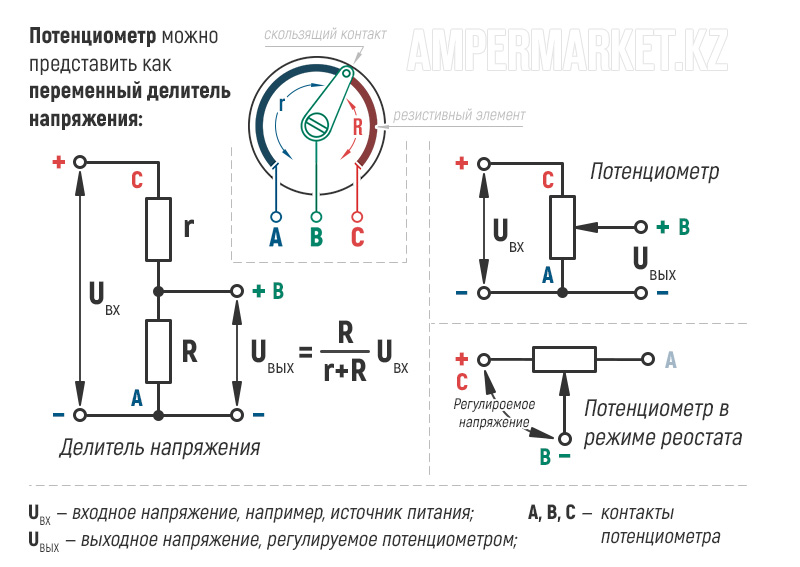
Микроконтроллер умеет измерять напряжение. Таким образом, мы можем использовать свойства делителя напряжения для получения показаний от сенсора. Датчики же, в свою очередь, способны менять своё сопротивление в зависимости от внешних условий. Для одного датчика это — поворот ручки, для другого — изменение освещённости. Ниже приведены примеры резистивных датчиков, которые без особых проблем можно «подружить» с Arduino.
ТЕРМИСТОР
Термистор изменяет своё сопротивление в зависимости от собственной температуры.
ФОТОРЕЗИСТОР
Фоторезистор (англ. Light Dependent Resistor или сокращённо LDR) изменяет своё сопротивление в зависимости от силы света, попадающего на его керамическую «змейку».
ПОТЕНЦИОМЕТР
Потенциометр ещё называют переменным резистором, триммером.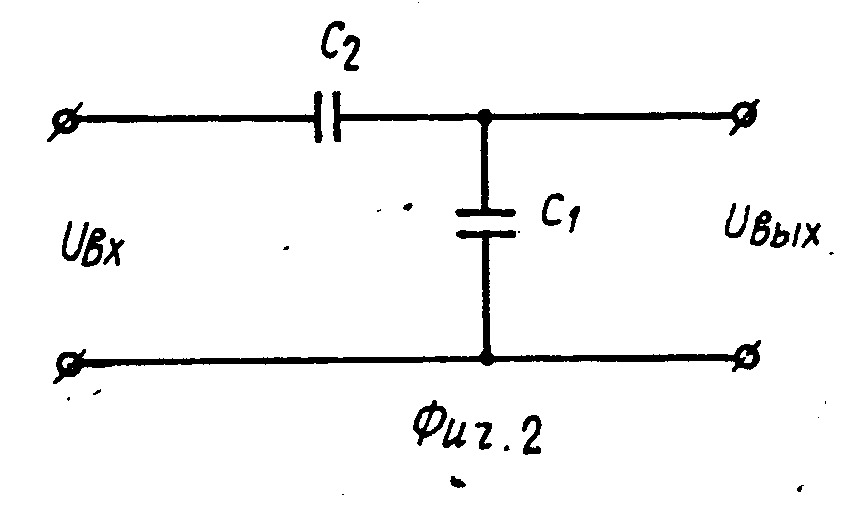 Это делитель из двух резисторов в одном корпусе. Поэтому у него 3 ноги: питание, выход, земля.
Это делитель из двух резисторов в одном корпусе. Поэтому у него 3 ноги: питание, выход, земля.
Соотношение R1 и R2 меняется поворотом ручки. От 100% в пользу R1 до 100% в пользу R2.
С оригиналом статьи вы можете ознакомиться на сайте Amperka.ru
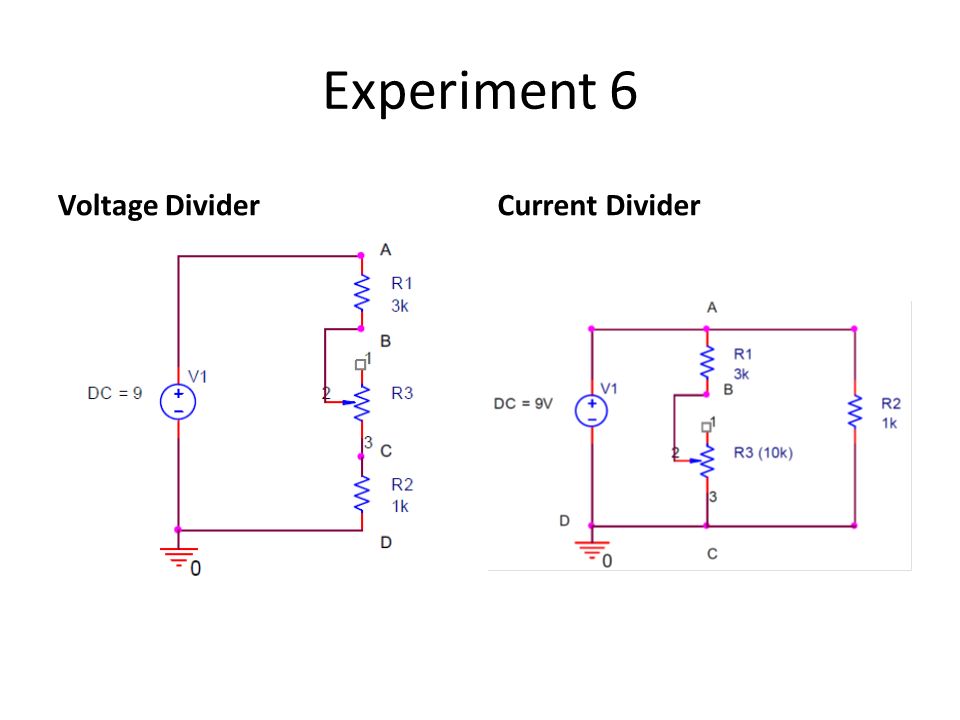
Расчет сети делителя напряжения — UbuntuGeeks
Схема может быть перерисована (всегда хорошая идея) следующим образом:
имитировать эту схему — схема, созданная с использованием CircuitLab
Существует несколько подходов к решению значения напряжения для контакта 3. Вероятно, тот, который изучался ранее, будет использовать процесс применения эквивалентов Тевенина. Давайте сделаем это:
имитировать эту схему
Здесь \ $ V_ \ text {TH} = 9 \: \ text {V} \ frac {R_ {83} + R_ {85}} {R_ {83} + R_ {85} + R_ {113} } \ $ и \ $ R_ \ text {TH} = \ frac {R_ {113} \ cdot \ left (R_ {83} + R_ {85} \ right)} {R_ {83} + R_ {85} + R_ {113}} \ $.
На данный момент это простой делитель напряжения. Давайте на секунду остановимся и посмотрим на это более внимательно, прежде чем перейти к следующему шагу. Здесь вы можете видеть, что за \ $ R_ \ text {TH} \ $ следует резистор \ $ 1 \: \ text {M} \ Omega \ $. Поскольку \ $ R_ \ text {TH} \ $ не может быть очень большим по сравнению (несколько тысяч Ом, но не близко к значению \ $ R_ {114} \ $), мы можем легко увидеть даже при этом Отметим, что потенциометр может лишь немного изменить напряжение на контакте 3. Я думаю, это уже ясно.
Выше был шаг 1. Но есть еще один шаг, необходимый для получения напряжения на контакте:
$$ \ {начать выравнивать *} V_ \ text {pin 3} & amp; = V_ \ text {TH} \ frac {R_ {86}} {R_ \ text {TH} + R_ {114} + R_ {86}} \ tag {Шаг 2} \\ \\ & Амп; = 9 \: \ текст {V}, \ CDOT \ гидроразрыва {R_ {83} + R_ {85}} {R_ {83} + R_ {85} + R_ {113}} \ CDOT \ гидроразрыва {R_ {86 }} {\ гидроразрыва {R_ {113} \ CDOT \ влево (R_ {83} + R_ {85} \ справа)} {R_ {83} + R_ {85} + R_ {113}} + R_ {114} + R_ {86}} \\\\ & amp; = 9 \: \ text {V} \ cdot R_ {86} \ cdot \ frac {R_ {83} + R_ {85}} {R_ {113} \ cdot \ left (R_ {83} + R_ {85 } \ справа) + \ влево (R_ {114} + {R_ 86} \ справа) \ CDOT \ влево (R_ {83} + R_ {85} + R_ {113} \ справа)} \\\\ & amp; = 9 \: \ text {V} \ cdot \ frac {R_ {86}} {R_ {113} + \ left (R_ {114} + R_ {86} \ right) \ cdot \ left (1+ \ гидроразрыва {R_ {113} {} R_ {83} + R_ {85}} \ справа)} \ {метка} Final \ Конец {выравнивать *} $$
Этот последний шаг на самом деле очень полезен, потому что он изолирует потенциометр \ $ R_ {83} \ $ и позволяет вам лучше увидеть, какое влияние он оказывает на всю структуру ответа.
Другой подход заключается в использовании узлового анализа и решении одновременных уравнений (два из них). Но результат будет таким же, и вышеупомянутое опирается на ограниченное знание менее мощных инструментов (если, возможно, еще некоторую алгебру.)
Я также хотел бы услышать о том, что вы обнаружите в процессе отслеживания проблемы. Пожалуйста, дайте нам знать, что вы найдете.
Калькулятор делителя напряжения| Контур X, код
Введение в делители напряженияРезисторы в серии , когда через них протекает одинаковый ток. Следовательно, по закону Ома полное напряжение в цепи последовательных резисторов является суммой отдельных падений на резисторах.
Другими словами, каждый резистор вносит свой вклад в общее напряжение в цепи.
Обычно для определения падения напряжения на отдельном резисторе необходимо знать ток.Каждый резистор способствует падению напряжения, и это падение пропорционально его сопротивлению. Таким образом, любое падение напряжения в последовательной цепи, учитывая только сопротивление и общее напряжение, разрешимо.
Таким образом, любое падение напряжения в последовательной цепи, учитывая только сопротивление и общее напряжение, разрешимо.
Узел напряжения V O в приведенной выше схеме представляет собой напряжение на R 2 .
Вот способ найти напряжение V O :
Так как в последовательной цепи общий ток равен току в каждом резисторе,
А так,
наконец,
Вышеприведенное уравнение известно как делитель напряжения .
Вы можете легко изменить это уравнение, чтобы найти напряжение на R 1 : просто замените R 2 в числителе на R 1 .
Делители напряжения обычно используются для снижения напряжения до безопасного уровня. Например, датчик с диапазоном напряжения от 0 до 9 В повреждает большинство микроконтроллеров.
Схема делителя напряжения между датчиком и микроконтроллером, предпочтительно два резистора равного номинала, может решить эту проблему.Почему две равные ценности? потому что, если два резистора равны в делителе напряжения, выходное напряжение составляет половину входного напряжения.
Сопротивление преобразованию напряженияЕще одно прекрасное применение делителя напряжения — это преобразование сопротивления в напряжение. Рассмотрим фотоэлемент, сопротивление которого зависит от силы света. Микроконтроллер не сможет напрямую считывать сопротивление фотоэлемента. Но если фотоэлемент подключен как одна из ветвей делителя напряжения, его сопротивление преобразуется в напряжение.
Калькулятор делителя напряжения Этот онлайн-калькулятор рассчитает выходное напряжение в приведенной ниже схеме делителя напряжения. Поместите значение входного или общего напряжения, значения сопротивления и нажмите «Вычислить».
Проверьте также
CD4013 — это интегральная схема, состоящая из двух триггеров D-типа.Имеет номер…
.Делитель потенциала — онлайн-калькулятор
Делитель потенциала — это самый простой способ получения источника с более низкой ЭДС. от источника с более высокой э.д.с.
Выходное напряжение делителя потенциала можно рассчитать как
U out = U дюйм R 2 / (R 1 + R 2 ) (1)
где
U out = выходное напряжение (В)
R = сопротивление (Ом, Ом)
U in = входное напряжение (В)
Пример — Делитель потенциала — Высокое энергопотребление
Выходное напряжение от делителя потенциала с двумя резисторами R 1 = 10 Ом и R 2 = 20 Ом и входное напряжение 12 В можно рассчитать как
U выход = (12 В) (20 Ом) / ((10 Ом) + (20 Ом))
= 8 (В)
Ток через делитель потенциала R 1 и 900 рандов 19 2 (напр.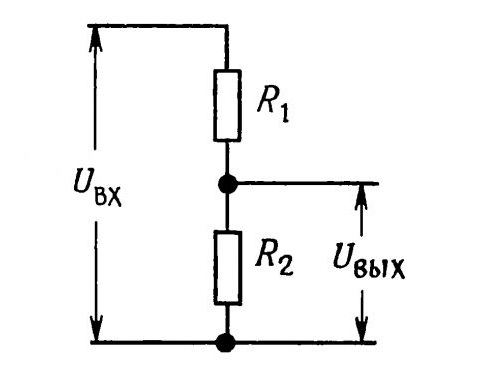 выходной ток) можно рассчитать по закону Ома
выходной ток) можно рассчитать по закону Ома
I = U / R
= (12 В) / ((10 Ом) + (20 Ом))
= 0,4 А
можно рассчитать потребляемую мощность делителя
P = UI
= (12 В) (0,4 A)
= 4,8 Вт
Пример — Делитель потенциала — меньшее энергопотребление
Выходное напряжение от делителя потенциала с двумя резисторами R 1 = 1000 Ом и R 2 = 2000 Ом и входное напряжение 12 В можно рассчитать как
U out = (12 В) ( 2000 Ом) / ((1000 Ом) + (2000 Ом))
= 8 (В)
Ток через делитель потенциала R 1 и R 2 (пример.выходной ток) можно рассчитать по закону Ома
I = U / R
= (12 В) / ((1000 Ом) + (2000 Ом))
= 0,004 А
можно рассчитать потребляемую мощность делителя
P = UI
= (12 В) (0,004 A)
= 0,048 Вт
Потребляемую мощность в потенциальном делителе можно уменьшить за счет увеличения сопротивления .
Делитель потенциала — Калькулятор
входное напряжение U дюйм (вольт)
резистор R 1 (ом)
резистор R 2 (ом)
om
Номограмму ниже можно использовать для оценки потенциального делителя.
Загрузите и распечатайте Номограмму делителя потенциала!
Значения по умолчанию на приведенной ниже номограмме для U в = 12 В , R 2 = 47 Ом и U на выходе = 3,3 В . Так как сумма сопротивлений (R 1 + R 2 ) по номограмме составляет примерно 170 Ом — сопротивление R 1 можно рассчитать как
R 1 ≈ ( 170 Ом — 47 Ом)
≈ 123 Ом.
Формула правила делителя напряжения, список и полное объяснение
Правило делителя напряжения — одна из наиболее распространенных концепций в проектировании электронных схем.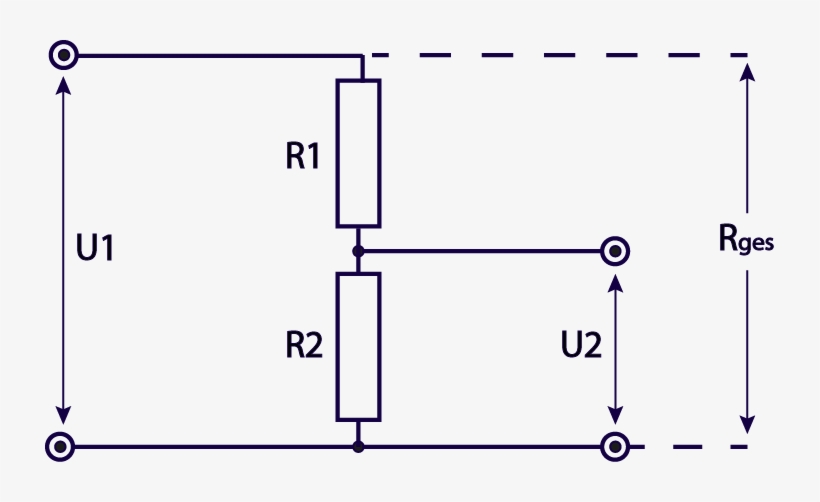 Итак, сегодня мы подробно обсудили формулу делителя напряжения, откуда она взята, а также некоторые практические примеры. Мы также объяснили, как спроектировать схему делителя напряжения для требуемого выхода.
Итак, сегодня мы подробно обсудили формулу делителя напряжения, откуда она взята, а также некоторые практические примеры. Мы также объяснили, как спроектировать схему делителя напряжения для требуемого выхода.
Изучая основы электроники, мы сталкиваемся с множеством трудностей, изучая формулы, правила и шаги по их реализации.Приведенные ниже темы охватывают простой метод изучения формул, а также приемы их запоминания.
Что такое правило делителя напряжения?
Правило делителя напряжения также называется правилом делителя потенциала, правилом деления потенциала или правилом деления напряжения.
Короче говоря, он присвоен как VDR.
Правила делителя напряжения дают представление о принципиальной схеме и применимой формуле и ее выводе, чтобы помочь с различными требованиями к напряжению при проектировании схемы.
Определение делителя напряжения:
Он определяется как схема, которая используется для уменьшения большого значения напряжения до меньшего значения.
Он дает необходимое выходное напряжение как долю входного напряжения, которой можно управлять с помощью формулы.
Схема делителя напряжения — это схема, которая делит одно значение напряжения на несколько выходных значений.
Тип схемы:
Пассивный по своей природе (так как не имеет активных элементов)
Линейное поведение (выход линейно пропорционален входу)
Схема делителя напряжения:
Рис (a), Рис ( б) и рис (в) представляют собой принципиальные схемы делителя напряжения.Почему три схемы ниже для одного и того же правила?
Итак, ответ, это всего лишь одна схема с разным расположением и символом источника. Просто упростите их, и вы обнаружите, что они одинаковы в электрических соединениях.
Анализ и формула правила делителя напряжения:
Рисунок, показывающий базовую схему цепи делителя напряжения с двумя резисторами:
Это основная принципиальная схема, которая показывает VDR и его формулу. Это очень прикладная схема, и формула обычно используется для расчета выходного напряжения повсюду при анализе цепей
Это очень прикладная схема, и формула обычно используется для расчета выходного напряжения повсюду при анализе цепей
Вывод делителя напряжения:
Здесь источник напряжения В подключен последовательно с резистором r1 и r2 .
И ток « i» протекает через них, вызывая падение напряжения на v1 на r1 и падение напряжения на v2 на r2 .
Поскольку это замкнутый контур, текущий ток будет таким же.
Для получения формул выходного напряжения нам необходимо применить закон Ома к каждому резистору и поместить значения в уравнение, полученное с помощью KCL (закон Куррента Кирхгофа), как показано ниже, шаг за шагом:
Согласно закону Ома мы получаем
v1 = i ☓r1 ———- (I)
v2 = i☓r2 ———– (II)
Применение KVL в приведенной выше схеме
V — v1 — v2 = 0
т.е. V = v1 + v2
Положив значение v1 и v2 в приведенном выше уравнении,
получаем,
V = i☓r1 + i☓r2
∴ V = i☓ (r1 + r2)
Следовательно,
i = V / (r1 + r2)
Подставляя значение «i» в (I) и (II)
мы получаем,
v1 = r1☓ (V / (r1 + r2))
v2 = r2☓ (V / (r1 + r2))
(регулируя переменных)
Также
v1 = V☓ (r1 / (r1 + r2))
v2 = V☓ (r2 / (r1 + r2)) → (примечание: v2 = Vout) → (III)
(путем настройки переменных для условий, где нам нужно найти номиналы резисторов)
Опять же,
r1 = (v1☓ (r1 + r2)) / V
r2 = (v2☓ (r1 + r2)) / V
Вывод по схеме делителя напряжения:
- Из уравнения → (III) можно сказать, что выход напряжение равно , падение напряжения на выходном резисторе (резистор, через который мы принимаем выходной сигнал)
(проверьте схему с 3 последовательно включенными резисторами, вы получите точку) - Значения резистора в знаменателе не что иное, как резистор эквивалентный из r1 и r2, это может быть r1 + r2 + r3 +… + rn, где n количество резисторов.

Рисунок, показывающий делитель напряжения с 3 резисторами и его эквиваленты:
В этой схеме (согласно приведенному выше выводу из выводов):
→ Как на рис. 1 Vout1 — это напряжение на резисторе R2 и R3
∴ взяты эквивалентные последовательные сопротивления R2 и R3 .
то же, что и на рис.1 (а)
→ На рис.1 Vout2 — это напряжение только на резисторе R3
∴ взято эквивалентное последовательное сопротивление R3 .
То же, что и на рис. 1 (b)
Практический пример схемы делителя напряжения (VDR) / FAQ:
Разработайте делитель напряжения, чтобы получить выходное напряжение 1,5 В для разработки усилителя смещение. Заданное напряжение источника 5В.
Дано → Vo = 1,5 В и Vin = 5 В
из уравнения → (III) или по упрощенной формуле (ищите 1-е изображение сообщения)
у нас есть, Vo = Vin. (R2 / (R1 + R2))
(R2 / (R1 + R2))
Допустим, R1 = 1 кОм
поместите все значения в формулу : 1.5 = 5. (R2 / (1K + R2))
Получаем, R2 = 0,428 кОм
Теперь спроектируйте схему, как показано выше !!!
Разработайте делитель напряжения, чтобы выдавать различное выходное напряжение 3 вольт и 6 вольт для компаратора, учитывая, что источник входного напряжения имеет разность потенциалов 9 вольт.
Как одинаковый последовательно включенный резистор обеспечивает одинаковое падение напряжения на каждом резисторе.
∴ согласно вопросу,
Vin = 9 Вольт, Vout1 = 6Volts и Vout2 = 3Volts
Из этого мы можем сделать вывод, что наименьший выход составляет 3 вольта, а другое необходимое выходное напряжение — 6 вольт.
Затем мы можем использовать три резистора с одинаковыми номиналами. (Скажем, 1 кОм )
∴ R1 = R2 = R3 = 1 кОм проектирование завершено.
Разработайте делитель напряжения, чтобы выходное напряжение было равным половине входного. Заданное напряжение источника — 12 В.
Дано → Vo = 1 / 2Vin и Vin = 12 В
используя упрощенную формулу:
мы имеем, Vo = Vin. (R2 / (R1 + R2))
Предположим, R1 = 10 кОм
положить все значения в формуле ∴ 6 = 12. (R2 / (10K + R2))
Получаем, R2 = 10KΩ
Теперь спроектируйте схему с этими компонентами !!
Можно ли применить правило делителя напряжения в параллельных цепях?
Нет, вы, , не можете применить деления напряжения по правилу в параллельной цепи , поскольку это применимо только к последовательным резисторам.Только причина того, что VDR — это модификация закона Ома.
Применяется ли правило делителя напряжения только к резисторам?
Нет, его можно применить к любому пассивному элементу, например, конденсатору и катушке индуктивности. Единственное, что вы должны предположить, это их импеданс (Z).
Единственное, что вы должны предположить, это их импеданс (Z).
Вместо резистора в правиле делителя напряжения необходимо использовать импеданс вместе с модифицированной формулой уравнений импеданса.
Zr для резистора, Zc для конденсатора, Zl для индуктора.
Применение правила делителя напряжения / цепи:
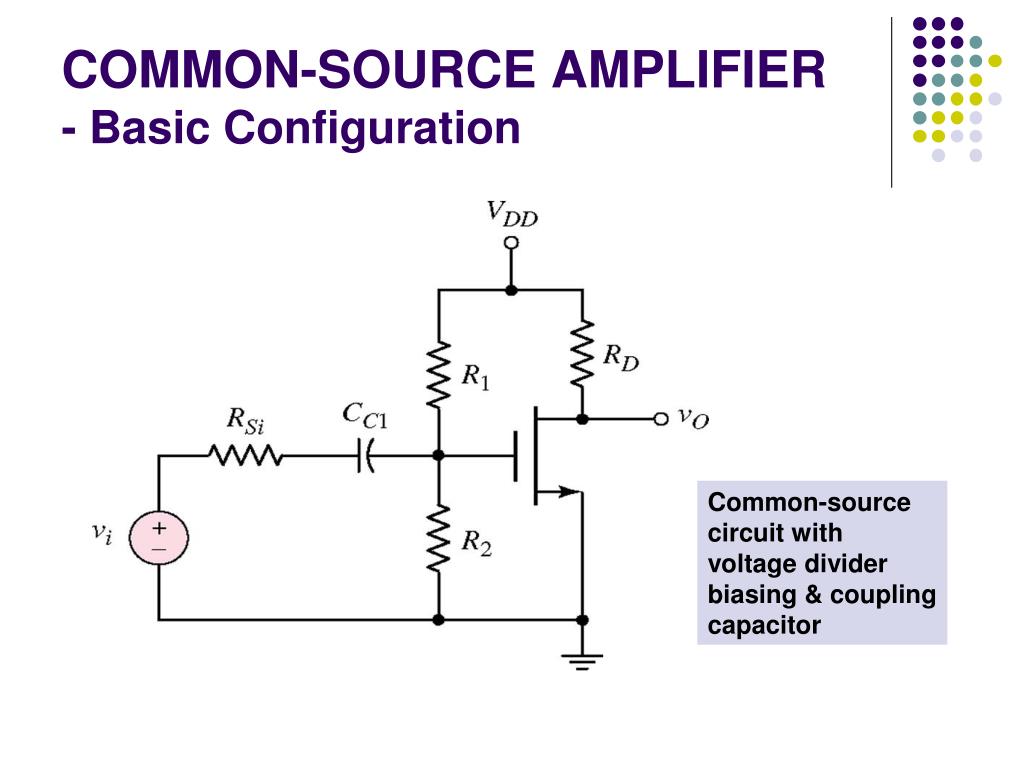
1) Он используется в качестве цепи смещения в усилителе BJT.
2) Схема обратной связи в операционном усилителе использует правило делителя напряжения для управления входом и управления усилением напряжения.
3) Это важная схема компаратора, которая используется для сравнения различных напряжений, независимо от того, больше или меньше конкретное напряжение, чем опорное напряжение.
4) Сдвиг логического уровня использует формулу делителя напряжения.
Бонусные подсказки:
- Когда резисторы R1 и R2 одинаковы, т.е. того же значения, то выходное напряжение составляет ровно половину (50%) исходного входного.

- Кроме того, эта схема подразумевает, что она полезна там, где у нас нет источника более низкого напряжения.
- Его можно использовать в качестве замены трансформатора (только и только если нагрузка имеет большой резистивный импеданс, мы должны использовать резисторы высокой мощности, скажем 3 Вт / 5 Вт, он практически не используется, так как он обладает риском поражения электрическим током. )
- Вы заметили тестер электрических линий (тестер проводов под напряжением), это не что иное, как делитель напряжения с резистором R1 и резистором R2, который заменен световым индикатором с низким сопротивлением, потребляющим ток.
Из приведенного выше содержания мы узнали:
Что такое правило делителя напряжения?
Делитель напряжения на 3 резистора.
Вывод правила делителя напряжения.
Пример решения делителя напряжения / решенные проблемы.
Калькулятор делителя напряжения
Инструкция
Эта утилита вычисляет любую из четырех переменных, входящих в простой двухрезисторный
делитель напряжения, заданные значения для каждой из трех других переменных. Переменные:
Переменные:
- В в — (входное) напряжение, которое появляется в верхней части делителя, измерено в верхней части R 1 относительно заземления цепи.
- R 1 — Сопротивление (в Ом) верхнего резистора
- R 2 — Сопротивление (в Ом) нижнего резистора
- V out — Напряжение, которое появляется на стыке R 1 и R 2 , измеряется относительно заземления цепи.
Пример
Обычно требуется вычислить одно из двух сопротивлений, при заданном V на , желаемом V на выходе и на одном из двух сопротивлений. В этом случае вы вводите два напряжения и известный резистор и утилита найдет неизвестный резистор
Однако рассмотрим следующий случай:
Вы устраняете неисправность в цепи и обнаруживаете, что V на выходе делителя напряжения на 5 Вольт
V в , рассчитанный на два резистора по 10 кОм, только измерительный. 45 В (вы ожидали увидеть 2,5 В).
45 В (вы ожидали увидеть 2,5 В).
В этом случае вы подозреваете, что использовали неверное значение резистора. Вы должны ввести одно из рассчитанных значений резистора, ввести два напряжения и найти номинал резистора. Изучив рассчитанное значение, можно предположить, что вы неправильно считали резистор. Например, в делителе напряжения, состоящем из двух резисторов 22,1 кОм для деления 5 В на 2,5 В, вы обнаружите, что на самом деле результат был 0.45 В. Вы думаете, что у вас неверное значение для одного из резисторов. Итак, вы вводите 5 В и 0,45 В (как V в и V из , соответственно), установите R 1 равным расчетным 22 100 Ом и решите для R 2 , и, вуаля! — вы получаете значение 2100 Ом для R 2 , предполагая, что вы могли ошибочно заменить резистор 2,21 кОм для резистора 22,1 кОм!
Калькулятор
Делитель напряжения| CE Distribution
Что такое делитель напряжения?
Делитель напряжения — это распространенная и полезная схема, которую можно найти во многих устройствах. Фактически, большинство регуляторов громкости в гитарах и усилителях работают как делители напряжения. Они создают выходное напряжение, составляющее часть входного напряжения. Эта часть входного напряжения пропорциональна соотношению двух резисторов, используемых в цепи. Используемые четыре переменные — это входное напряжение (~ V _ {\ text {in}} ~), выходное напряжение (~ V _ {\ text {out}} ~) и два резистора ~ R_1 ~ и ~ R_2 ~. С тремя известными переменными мы можем использовать уравнение делителя напряжения, чтобы найти четвертую.
Фактически, большинство регуляторов громкости в гитарах и усилителях работают как делители напряжения. Они создают выходное напряжение, составляющее часть входного напряжения. Эта часть входного напряжения пропорциональна соотношению двух резисторов, используемых в цепи. Используемые четыре переменные — это входное напряжение (~ V _ {\ text {in}} ~), выходное напряжение (~ V _ {\ text {out}} ~) и два резистора ~ R_1 ~ и ~ R_2 ~. С тремя известными переменными мы можем использовать уравнение делителя напряжения, чтобы найти четвертую.
Это уравнение получено из закона Ома.Применяя закон Ома к входному напряжению, мы знаем, что
$$ V _ {\ text {in}} = I_1 \ times R $$В случае ~ V _ {\ text {in}} ~,
$$ R = (R_1 + R_2) $$, поэтому
$$ V _ {\ text {in}} = I_1 \ times (R_1 + R_2) $$Для ~ V _ {\ text {out}} ~ мы знаем, что
$$ V _ {\ text {out}} = I_2 \ times R_2 $$ ~ I_1 ~ предполагается равным ~ I_2 ~.
Решая для ~ I_1 ~, находим, что
$$ I_1 = \ frac {V _ {\ text {in}}} {(R_1 + R_2)} $$Решая для ~ I_2 ~, получаем
$$ I_2 = \ frac {V _ {\ text {out}}} {R_2} $$Объединяя эти уравнения, получаем
$$ \ frac {V _ {\ text {out}}} {R_2} = \ frac {V _ {\ text {in}}} {(R_1 + R_2)} $$Решение для ~ V _ {\ text {out} } ~ мы получаем уравнение делителя напряжения
$$ V _ {\ text {out}} = V _ {\ text {in}} \ times \ frac {R_2} {(R_1 + R_2)} $$Выше мы упоминали, что ~ I_1 ~ предполагается равным ~ I_2 ~.Это очень важно при рассмотрении использования делителя напряжения. Давайте попробуем этот пример. У нас есть входное напряжение 10В. Мы будем использовать два резистора 10 кОм как ~ R_1 ~ и ~ R_2 ~, что даст нам выходное напряжение 5 В. Мы хотим применить 5V к нагрузке 100k, которая будет выглядеть так:
Мы видим, что ~ R_2 ~ работает параллельно нашей нагрузке 100 кОм, изменяя наш делитель напряжения. ~ I_1 ~ больше не равно ~ I_2 ~, поскольку ток делится между ~ R_2 ~ и нагрузкой.Используя значения резисторов в уравнении параллельного сопротивления, мы находим, что
~ I_1 ~ больше не равно ~ I_2 ~, поскольку ток делится между ~ R_2 ~ и нагрузкой.Используя значения резисторов в уравнении параллельного сопротивления, мы находим, что
Когда мы используем этот результат с нашим По формуле делителя напряжения мы можем увидеть изменение выходного напряжения с делителя.
$$ 10 \ text {V} × \ frac {9 {,} 090.91Ω} {(10 {,} 000Ω + 9 {,} 090.91Ω)} = 4.76 \ text {V} $$ 4.76V соответствует 4.8 % отличия от ожидаемого выходного напряжения 5 В. Вам нужно будет подумать, является ли это изменение критичным для контура, который вы проектируете.При использовании более высокой нагрузки делитель будет более точным, а более низкая нагрузка приведет к еще менее точному выходному напряжению, чем в нашем примере. Это одна из причин, по которой делители напряжения не следует использовать для подачи энергии вместо таких компонентов, как регуляторы напряжения или другие цепи питания. Операционный усилитель с единичным усилением может использоваться после делителя напряжения в схемах, требующих более точного выходного напряжения.
Операционный усилитель с единичным усилением может использоваться после делителя напряжения в схемах, требующих более точного выходного напряжения.
Обратите внимание, что информация, представленная в этой статье, предназначена только для справки.CE Distribution не делает никаких заявлений, обещаний или гарантий относительно точности, полноты или адекватности содержания этой статьи и прямо отказывается от ответственности за ошибки или упущения со стороны автора. В отношении содержания этой статьи не дается никаких гарантий, подразумеваемых, выраженных или установленных законом, включая, помимо прочего, гарантии ненарушения прав третьих лиц, права собственности, товарной пригодности или пригодности для определенной цели. или его ссылки на другие ресурсы.
| Новости Проэкт Технология РобоСпатиум Делать вклад Предметный указатель Скачать Ответы Игры Советы по покупкам Контакт <<< RC-схема операционного усилителя >>> youtube.com/embed/6KwvX32B6Ek» allowfullscreen=»» frameborder=»0″/> Постоянное сопротивлениеРисунок 1:В главе о сетях постоянного сопротивления мы познакомились с теорией делителей напряжения.Теперь я хотел бы представить некоторые практические преимущества этих простых сетей. Делители напряжения очень полезны, если вам нужна фиксированная часть напряжения питания для специального устройства в электронной схеме. Например, в главе о схемах усиления мы приложили напряжение смещения к выводу базы биполярного переходного транзистора. Напряжение смещения составляло около 0,67 В, в то время как номинальное напряжение использованной батареи составляло 12 В. Таким образом, соотношение напряжений составляет 0,67 В: 12,00 В. При использовании резистора 1 кОм значение второго составляет: R 2 = (1 кОм * 0.67 В) / (12,00 В — 0,67 В) = 59 Ом. Что произойдет, если изменится выходное напряжение батареи? Конечное напряжение заряда свинцово-кислотных аккумуляторов 12 В составляет 14 В, и вы должны прекратить их разряжать при напряжении 11,2 В, поэтому падение напряжения при R 2 варьируется в пределах U max = 14,0 В * 59 Ом / (59 Ом + 1000 Ом.  ) = 0,78 В и U мин. = 11,2 В * 59 Ом / (59 Ом + 1000 Ом) = 0,62 В. Поэтому, если вы собираетесь создать высококачественный усилитель, вам следует позаботиться о более постоянном входном напряжении, чем может обеспечить свинцово-кислотная батарея. ) = 0,78 В и U мин. = 11,2 В * 59 Ом / (59 Ом + 1000 Ом) = 0,62 В. Поэтому, если вы собираетесь создать высококачественный усилитель, вам следует позаботиться о более постоянном входном напряжении, чем может обеспечить свинцово-кислотная батарея. Рисунок 2: Выходное сопротивлениеПри использовании делителя напряжения в качестве источника напряжения для специального устройства следует учитывать сдвиг напряжения при подключении нагрузки параллельно одному из резисторов. Из главы об электронных переключателях мы узнали, что базового напряжения 0,75 В на BD135 достаточно для включения электродвигателя. Делитель напряжения 2.7 кОм и сопротивление 180 Ом обеспечивают это напряжение, если никакая нагрузка не подключена параллельно к R 2 . При подключении транзистора к схеме падение напряжения на R 2 уменьшается всего до 0,68 В, что недостаточно для переключения электродвигателя. Сопротивление линии эмиттер-база транзисторов составляет примерно 1800 Ом.Чтобы получить более стабильное выходное напряжение, необходимо уменьшить общее сопротивление делителя напряжения. При использовании резистора 495 Ом и 33 Ом (см. Пример выше) падение напряжения на R 2 равно 0.  75В без нагрузки и 0,74В при подключении транзистора к сети. Недостатком уменьшения общего сопротивления является то, что большая часть входного напряжения тратится в виде тепла. 256 мВт рассеивается при R 1 и 17 мВт при R 2 , в то время как на транзисторе потребляется всего 375 мкВт. 75В без нагрузки и 0,74В при подключении транзистора к сети. Недостатком уменьшения общего сопротивления является то, что большая часть входного напряжения тратится в виде тепла. 256 мВт рассеивается при R 1 и 17 мВт при R 2 , в то время как на транзисторе потребляется всего 375 мкВт. ПотенциометрРисунок 3:В принципе, потенциометр — это регулируемый делитель напряжения. Обычно они состоят из резистивного элемента, образованного дугой окружности, немного меньше полного витка.Выходное напряжение на скользящем контакте находится между нулем вольт и входным напряжением делителя. Кусок резистивного провода с зажимом, используемый в качестве скользящего контакта, можно использовать как очень простую конструкцию линейного потенциометра. Выходное напряжение делителя может использоваться как входное значение схемы управления, следовательно, потенциометры могут использоваться в качестве датчиков для целей позиционирования.  Сервоприводы обычно используют однооборотные потенциометры для управления вращательным движением.Соответственно, выходное напряжение линейного скользящего потенциометра может использоваться для определения соответствующей регулировки линейного движения. Сервоприводы обычно используют однооборотные потенциометры для управления вращательным движением.Соответственно, выходное напряжение линейного скользящего потенциометра может использоваться для определения соответствующей регулировки линейного движения. Рисунок 4: Н мостикРисунок 5:Н-мост — это электронная схема, которая позволяет приложить напряжение к нагрузке в любом направлении. Очень простой мост H состоит из двух потенциометров с нагрузкой, подключенной к двум скользящим контактам.  Если выходное напряжение потенциометра номер один равно выходному напряжению потенциометра номер два (например, оба находятся в их среднем положении), на нагрузку не подается напряжение. Рисунок 6: Если выходное напряжение потенциометра номер два более положительное, чем выходное напряжение потенциометра номер один, положительный вывод находится на правой стороне нагрузки. Рисунок 7: Если выходное напряжение потенциометра номер два меньше положительного, чем выходное напряжение потенциометра номер один, положительный вывод находится на левой стороне нагрузки. ДиодыРисунок 8:Вольт-амперная характеристика полупроводникового диода отличается от характеристики омического резистора. Сопротивление кремниевого диода с прямым смещением значительно уменьшается при падении напряжения примерно на 0.6В. При замене R 2 на диод с прямым смещением падение напряжения не превышает 0,6 В, даже если входное напряжение явно выше.  При последовательном включении двух или более диодов с прямым смещением падение напряжения кратно 0,6 В. Например, результирующее падение напряжения составляет примерно 1,8 В при использовании трех диодов. Рисунок 9: Переменное сопротивлениеРисунок 10:Сопротивление некоторых устройств значительно зависит от температуры или света. В качестве датчика можно использовать делитель напряжения с одним постоянным и одним переменным резистором. Падение напряжения на переменном резисторе зависит от наблюдаемой физической величины. На чертеже фототранзистор и постоянный резистор используются для преобразования переменной силы света в переменное падение напряжения. Пока светится фототранзистор, падение напряжения на устройстве уменьшается. <<< RC-схема операционного усилителя >>> Новости Проэкт Технология РобоСпатиум Делать вклад Предметный указатель Архивы Скачать Ответы Игры Ссылки Советы по покупкам Контакт Отпечаток |
Как работают делители напряжения | CircuitBread
Прежде чем мы углубимся в делители напряжения, важно хорошо понимать, что происходит с параллельными и последовательными резисторами. Как только вы поймете, как падает напряжение на резисторе, вы примерно на полпути к пониманию делителя напряжения. Если вам нужно напряжение в вашей цепи ниже, чем напряжение, обеспечиваемое вашим источником питания, вы можете использовать делитель напряжения. При этом используются два (или более!) Резистора, подключенных последовательно, и узлы между резисторами будут иметь более низкое напряжение, чем входное. Напряжение зависит от номинала различных резисторов по сравнению с между собой.
Как только вы поймете, как падает напряжение на резисторе, вы примерно на полпути к пониманию делителя напряжения. Если вам нужно напряжение в вашей цепи ниже, чем напряжение, обеспечиваемое вашим источником питания, вы можете использовать делитель напряжения. При этом используются два (или более!) Резистора, подключенных последовательно, и узлы между резисторами будут иметь более низкое напряжение, чем входное. Напряжение зависит от номинала различных резисторов по сравнению с между собой.
Что такое делитель напряжения?
Схема делителя напряжения Я уже говорил об этом, но скажу еще раз.Делитель напряжения — это буквально два последовательно соединенных резистора. Но самая важная часть заключается в том, что вы измеряете напряжение между этими резисторами (V OUT ), и оно будет меньше входного напряжения (V IN ). Чтобы точно определить, что это за выходной сигнал, учитывая номиналы резисторов, вы используете следующее уравнение.
Если проделать это медленно, математика приобретет большой смысл.
- Во-первых, в знаменателе вы вычисляете полное сопротивление двух резисторов R1 + R2.
- Во-вторых, в числителе у вас есть номинал резистора, на котором вы хотите измерить напряжение, R2. По сути, вы устанавливаете процент сопротивления R2 от общего R1 + R2.
- В-третьих, вы умножаете этот процент на V IN .
Из этого следует отметить две вещи:
- Если вы понимаете концепцию работы с двумя и понимаете, как / почему это представляет математика, очень легко увеличить количество резисторов, которые используются вместе.Все дело в процентах.
- Если R1 = R2, то V OUT просто V IN /2. Делайте вещи простыми и красивыми.
Если вы хотите еще раз проверить свою работу или сократить путь, мы создали инструмент, который поможет с делителями напряжения.
Что еще мне следует учесть?
Реальность сложна.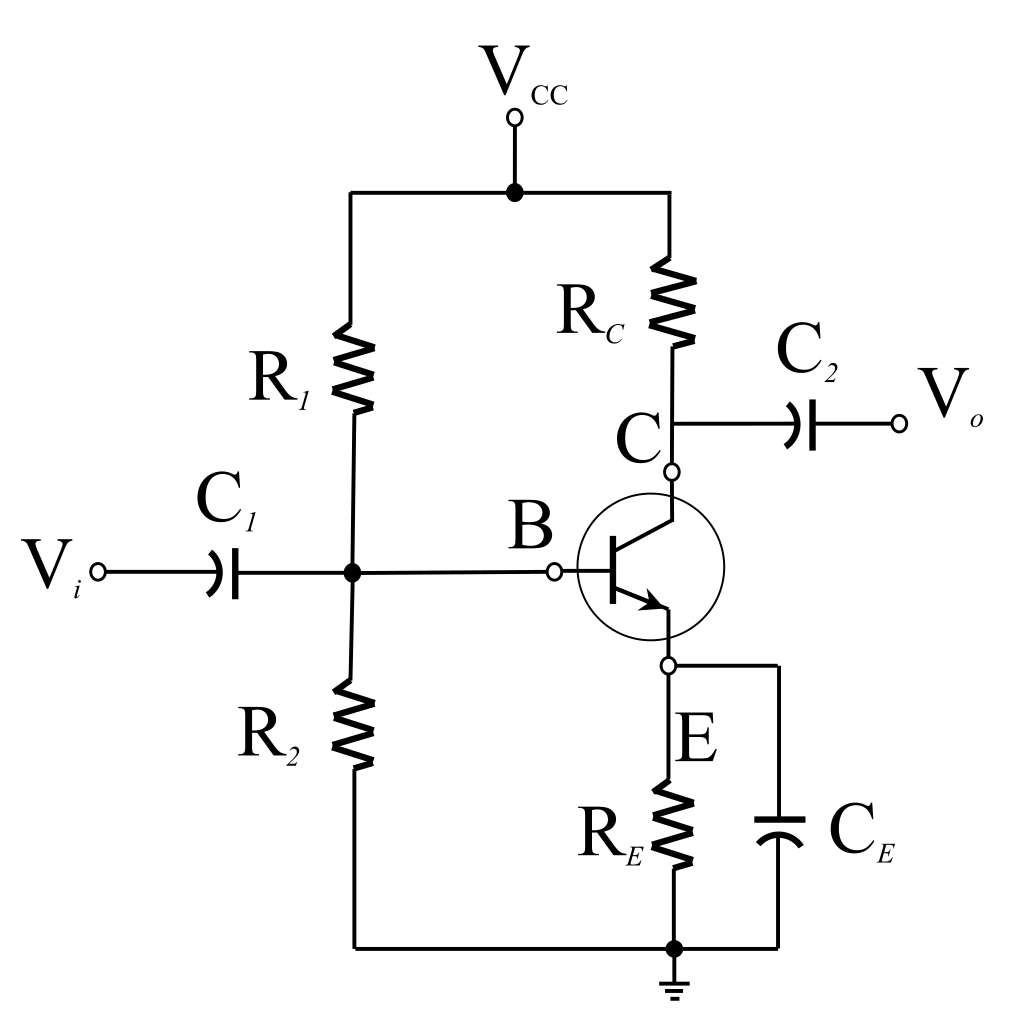 Или, по крайней мере, с нюансами. Так да.
Или, по крайней мере, с нюансами. Так да.
Самая большая проблема
Давайте представим, что у нас есть источник питания 5 В и два последовательно соединенных резистора по 10 кОм каждый, что делает напряжение между двумя резисторами равным 2.5В.
Инструмент делителя напряжения Снимок экранаТеперь у нас есть устройство, которое требует 2,5 В и в идеале потребляет 2,5 мА или имеет эквивалентное сопротивление 1 кОм. Кидаем на делитель напряжения и не работает. Почему? Схема делителя напряжения
с напряжением 0,42 ВЭто потому, что мы полностью изменили схему с нашей нагрузкой! Вместо двух последовательно соединенных резисторов 10 кОм, это резистор 10 кОм, соединенный последовательно с эквивалентным резистором 909 Ом. Для источника 5 В это означает, что фактически напряжение составляет ~ 0.42В, на 2В меньше, чем ожидалось.
Инструмент параллельной эквивалентности Снимок экрана Инструмент делителя напряжения с 10 Ом Снимок экрана Эту проблему можно обойти, используя резисторы меньшего номинала.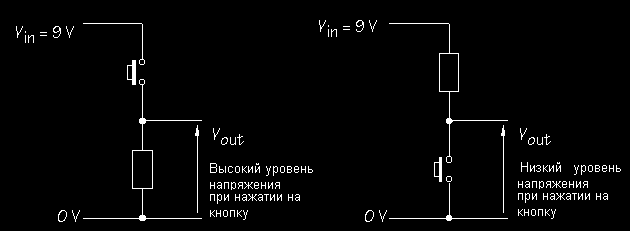 Вместо 10 кОм вы можете использовать резисторы 10 Ом, что при нагрузке 1 кОм даст вам около 2,487 В, что всего на 0,013 В от идеальных 2,5 В. Но теперь у нас есть другая проблема.
Вместо 10 кОм вы можете использовать резисторы 10 Ом, что при нагрузке 1 кОм даст вам около 2,487 В, что всего на 0,013 В от идеальных 2,5 В. Но теперь у нас есть другая проблема.
С двумя резисторами 10 Ом, один из которых подключен параллельно нагрузке 1 кОм, мы имеем эквивалент 19.9 Ом между нашим источником напряжения и землей. Это 0,2513 ампер, или общая рассеиваемая мощность 1,257 Вт! Когда на самом деле нашему устройству нужно всего 2,5 В и 2,5 мА, или 6,25 милливатт. Это означает, что наша вымышленная схема тратит ~ 1,25 Вт или имеет КПД всего около 0,5%. Итак, это компромисс между использованием больших и малых резисторов для делителя напряжения. Эффективность против жесткости.
Некоторые другие проблемы
В зависимости от вашего приложения, если вам нужно точное напряжение, вам также понадобится очень точный, точный и стабильный вход напряжения, а также очень точный резистор.Таким образом, ваши затраты могут быть выше, чем предполагалось изначально.
Кроме того, вы можете получить более стабильное напряжение, используя стабилитрон. Мы не будем вдаваться в подробности, но стабилитроны — еще один относительно недорогой способ получить более низкое напряжение. У него есть свои недостатки, но это еще одна альтернатива для простого и недорогого регулирования напряжения.
Наконец, в реальной жизни потенциометр — это делитель напряжения, который изменяет значения сопротивления в зависимости от того, где заканчивается ручка. Вы можете подключить микроконтроллер к потенциометру, и микроконтроллер периодически измеряет выходное напряжение, давая вам возможность вручную подавать вход на этот контроллер.Это очень часто. Но он также страдает от баланса между жесткостью и потерями мощности.
Ну черт возьми. Есть ли польза от использования делителя напряжения?
Несмотря на эти недостатки, есть приложения, в которых делитель напряжения — это именно то, что вам нужно. Делители напряжения чрезвычайно просты, и, если вы знаете, какое у вас входящее напряжение, вы можете легко и недорого получить точное напряжение, которое вам нужно. Пока оно ниже входящего напряжения. Используя два резистора, которые в большом количестве могут стоить вам меньше копейки, вы можете избежать использования надоедливого и дорогого источника питания.
Пока оно ниже входящего напряжения. Используя два резистора, которые в большом количестве могут стоить вам меньше копейки, вы можете избежать использования надоедливого и дорогого источника питания.
Одно из наиболее распространенных применений — установка опорного напряжения для АЦП. Если вы хотите взять образцы и хотите сузить диапазон выборки для увеличения разрешения, вы можете установить опорное напряжение ниже, чем напряжение питания.
Резюме
Делители напряжения могут быть очень полезными, но они более ограничены в использовании, чем можно было бы ожидать, когда впервые задумались об этом. Но это не умаляет важности изучения и понимания того, как они работают, поскольку они часто появляются в проектах, намеренно или как побочный эффект какой-либо другой особенности дизайна.
Плюсы:
Минусы:
- Не очень стабильный
- Не очень жесткий
- Излишнее или чрезмерное рассеивание мощности
- Множество других опций