Коэффициент мощности cos φ: определение, назначение, формула
Коэффициент мощности – это скалярная физическая величина, показывающая насколько рационально потребителями расходуется электрическая энергия. Другими словами, коэффициент мощности описывает электроприемники с точки зрения присутствия в потребляемом токе реактивной составляющей.
В этой статье мы рассмотрим физическую сущность и основные методы определения cos φ.
Математически cos φ
Математически cos φ определяется как отношение активной мощности к полной или равен отношению косинуса этих величин (отсюда и название параметра).
Величина коэффициента мощности может изменяться в интервале 0 — 1 (либо в диапазоне 0 — 100%). Чем ближе его величина к 1, тем лучше, поскольку при величине cos φ = 1 – потребителем реактивная мощность не потребляется (равняется 0), следовательно, меньше потребляемая полная мощность в общем.
Низкий cos φ указывает на то, что на внутреннем сопротивлении потребителя выделяется повышенная реактивная мощность.
Когда токи / напряжения являются идеальными сигналами синусоидальной формы, то коэффициент мощности составляет 1.
Васильев Дмитрий Петрович
Профессор электротехники СПбГПУ
В энергетике для коэффициента мощности используются следующие обозначения cos φ либо λ. В случае если для определения коэффициента мощности используется λ, его значение выражают в %.
Геометрически коэффициент мощности можно изобразить, как косинус угла на векторной диаграмме между током, напряжением между током, напряжением. В связи с чем при синусоидальной форме токов и напряжений величина cos φ совпадает с косинусом угла, от которого отстают эти фазы.
Короткое видео о кратким объяснением, что такое коэффициент мощности:
Повышение коэффициента мощности
Значение коэффициента мощности рассчитывают при проектировании сетей. Поскольку низкое его значение является следствием увеличения величины общих потерь электроэнергии. Для его увеличения в сетях используют различные способы коррекции, повышая его значение до 1.
Поскольку низкое его значение является следствием увеличения величины общих потерь электроэнергии. Для его увеличения в сетях используют различные способы коррекции, повышая его значение до 1.
Повышение cos φ преследует 3 основные задачи:
- снижение потерь электроэнергии;
- рациональное использование цветных металлов на создание электропроводящей аппаратуры;
- оптимальное использование установленной мощности трансформаторов, генератор и прочих машин переменного тока.
Технически коррекция реализуется в виде введения различных дополнительных схем на вход устройств. Эта техника требуется для равномерного использования мощности фазы, устранения перегрузок нулевого провода 3-х-фазной сети, и является обязательной для импульсных источников питания, установленной мощностью 100 Вт и более.
Абрамян Евгений Павлович
Доцент кафедры электротехники СПбГПУ
Помимо этого, компенсация позволяет обеспечить отсутствие всплесков потребляемого тока на пике синусоиды, равномерную нагрузку на питающую линию.
Основные способы коррекции cos φ
1. Коррекция реактивной составляющей мощности производится путём включения реактивного элемента, имеющего противоположное действие. К примеру, для компенсации работы асинхронной машины, обладающей высокой индуктивной реактивной составляющей мощности, в параллель включается конденсатор.
2. Корректировка нелинейности электропотребления. При потреблении тока нагрузкой непропорционально основной гармонике напряжения, для повышения коэффициента мощности в схему вводят пассивный (активный) корректор коэффициента мощности. Наиболее простым примером пассивного корректора cos φ является дроссель с высокой индуктивностью, подключаемый последовательно с нагрузкой. Дроссель производит сглаживание импульсного потребления нагрузки и создание низшей, основной гармоники тока.
3. Корректировка естественным способом, не предусматривающая установку дополнительных устройств, предполагает упорядочение технологического процесса, рациональное распределение нагрузок, ведущее к улучшению режима потребления электроэнергии оборудованием, повышению коэффициента мощности.
Подробное видео с объяснением, что такое cosφ :
Косинус фи — простое объяснение в 3-х словах. Таблицы коэффициента мощности для различных потребителей.
Многие из вас наверняка видели на электроинструментах, двигателях, а также люминесцентных лампах, лампах ДРЛ, ДНАТ и других, такие надписи как косинус фи — cos ϕ.
Однако люди далекие от электротехники и позабывшие школьные уроки физики, не совсем понимают, что же означает данный параметр и зачем он вообще нужен.
Когда ток отстает от напряжения
Предположим перед вами есть 2 проводника. Один из этих проводников имеет потенциал. Не суть важно какой именно — отрицательный (минус) или положительный (плюс).
Один из этих проводников имеет потенциал. Не суть важно какой именно — отрицательный (минус) или положительный (плюс).
У другого провода вообще нет никакого потенциала. Соответственно между этими двумя проводниками будет разность потенциалов, т.к. у одного он есть, а у другого его нет.
Эту разность потенциалов как раз таки и принято называть напряжением.
Если вы соедините кончики двух проводов не непосредственно между собой, а через лампочку накаливания, то через ее вольфрамовую нить начнет протекать ток. От одного провода к другому.
В какой-то момент он его достигает и держится на этом уровне постоянно. То же самое будет, если подключить не одну, а две, три лампочки и т.д.
А что случится, если вместе с лампой последовательно включить катушку, намотанную из множества витков проволоки?
Изменится ли как-то процесс нарастания тока? Конечно, да.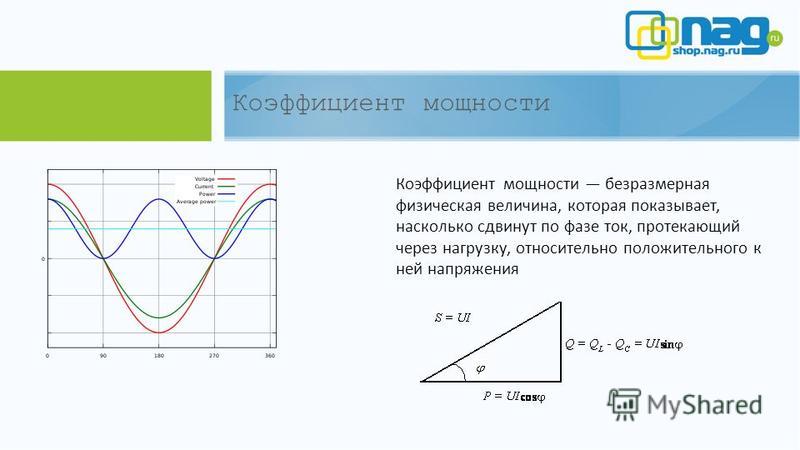
Данная катушка индуктивности, заметно затормозит время увеличения тока от нуля до максимума. Фактически получится, что максимальное напряжение (разность потенциалов) на лампе уже есть, а вот ток поспевать за ним не будет.
Его нарастание слишком медленное. Из-за чего это происходит и кто виноват? Виноваты витки катушки, которые оказывают влияние друг на друга и тормозят ток.
Если у вас напряжение постоянное, например как в аккумуляторах или в батарейках, ток относительно медленно, но все-таки успеет дорасти до своего номинального значения.
А далее, ток будет вместе с напряжением идти, что называется «нога в ногу».
А вот если взять напряжение из розетки, с переменной синусоидой, то здесь оно не постоянно и будет меняться. Сначала U какое-то время положительная величина, а потом — отрицательная, причем одинаковое по амплитуде. На рисунке это изображается в виде волны.
Эти постоянные колебания не дают нашему току, проходящему сквозь катушку, достигнуть своего установившегося значения и догнать таки напряжение. Только он будет подбираться к этой величине, а напряжение уже начинает падать.
Только он будет подбираться к этой величине, а напряжение уже начинает падать.
Поэтому в этом случае и говорят, что ток отстает от напряжения.
Причем, чем больше в катушке намотано витков, тем большим будет это самое запаздывание.
Как же это все связано с косинусом фи — cos ϕ?
Что такое коэффициент мощности
А связано это таким образом, что данное отставание тока измеряется углом поворота. Полный цикл синусоиды или волны, который она проходит от нуля до нуля, вместив в себя максимальное и минимальное значение, измеряется в градусах. И один такой цикл равен 360 градусов.
А вот угол отставания тока от напряжения, как раз таки и обозначается греческой буквой фи. Значение косинуса этого угла опаздывания и есть тот самый cos ϕ.
Таким образом, чем больше ток отстает от напряжения, тем большим будет этот угол. Соответственно косинус фи будет уменьшаться.
По научному, ток сдвинутый от напряжения называется фазовым сдвигом. При этом почему-то многие уверены, что синусоида всегда идеальна. Хотя это далеко не так.
При этом почему-то многие уверены, что синусоида всегда идеальна. Хотя это далеко не так.
В качестве примера можно взять импульсные блоки питания.
Не идеальность синусоиды выражается коэфф. нелинейных искажений — КНИ. Если сложить две эти величины — cos ϕ и КНИ, то вы получите коэффициент мощности.
Однако, чтобы все не усложнять, чаще всего под понятием коэфф. мощности имеют в виду только лишь один косинус фи.
На практике, данный коэффициент мощности рассчитывают не при помощи угла сдвига фаз, а отношением активной мощности к полной.
Активная и реактивная мощность
Существует такое понятие как треугольник мощностей. Сам косинус — это тригонометрическая функция, которая и появилась при изучении свойств прямоугольных треугольников.
Она здорово помогает производить определенные вычисления с ними. Например, наглядно показывает отношение длин прилежащего катета (P-активная мощность) к гипотенузе (S-полная мощность).
То есть, зная угол сдвига, можно узнать, сколько активной мощности содержится в полной.
Только не путайте cos ϕ с КПД. Это разные понятия. Реактивная составляющая не расходуется, а «возвращается» на подстанцию в сеть, т.е. фактически потери ее нет. Только небольшая ее часть может тратиться на нагрев проводов.
В КПД все более четко — полезная мощность используется на нагрев — охлаждение — механическую работу, остальное уходит безвозвратно. Эта разница и показывается в КПД.
Более подробно, с графиками, рисунками и простыми словами, без особых научных формулировок обо всем этом говорится в ролике ниже.
Низкий коэффициент мощности и его последствия
Рассмотренное запаздывание тока относительно напряжения — это не хорошее явление. Как оно может сказаться на ваших лампочках или проводке?
- во-первых, это повышенное потребление электроэнергии
Часть энергии будет просто «болтаться» в катушке, при этом не принося никакой пользы. Правда не пугайтесь, ваш бытовой счетчик реактивную энергию не считает и платить вы за нее не будете.
Правда не пугайтесь, ваш бытовой счетчик реактивную энергию не считает и платить вы за нее не будете.
Например, если вы включите в розетку инструмент или светильник с полной мощностью 100Ва, на блоке питания которого будет указано cos ϕ=0,5. То прибор учета накрутит вам только на половину от этой величины, то есть 50Вт.
Зато по проводам питания будет проходить вся нагрузка, разогревая их бесполезной работой.
- величина тока в проводке увеличится
Вот известное наглядное видео, демонстрирующее последствия этого для проводки.
- для эл.станций и трансформаторов оно вредно перегрузкой
Казалось бы, выбрось катушку и вся проблема исчезнет. Однако делать этого нельзя.

Катушки просто необходимы как функциональная часть всей схемы и избавиться от них не получится. Например в тех же дроссельных лампах ДРЛ, ДНАТ, люминесцентных и т.п.
Поэтому характеристика коэфф. мощности, здесь больше относится к блоку питания, нежели к самой лампе. Данный cos ϕ может принимать значение от ноля до единицы.
Ноль означает, что полезная работа не совершается. Единица — вся энергия идет на совершение полезной работы.
Чем выше коэффициент мощности, тем ниже потери электроэнергии. Вот таблица косинуса фи для различных потребителей:
Как измерить коэффициент мощности
Если вы не знаете точный коэфф. мощности своего прибора, или его нет на бирке, можно ли измерить косинус фи в домашних условиях, не прибегая к различным формулам и вычислениям? Конечно можно.
Для этого достаточно приобрести широко распространенный инструмент — цифровой ваттметр в розетку.
Подключая любое оборудование через него, можно легко без замеров и сложных вычислений, узнать фактический cos ϕ.
Зачастую, фактические данные могут быть даже точнее, чем написанные на шильдике, которые рассчитаны для идеальных условий.
Если он слишком низкий, что делать, чтобы привести его значение как можно ближе к единице? Можно это дело определенным образом компенсировать. Например, с помощью конденсаторов.
Однако это тема совсем другой статьи.
Описание параметра «Компенсация (cos ϕ)»
Коэффициент мощности (cos φ) — физическая величина, являющаяся энергетической характеристикой электрического тока. Коэффициент мощности характеризует приёмник электроэнергии переменного тока, а именно — степень линейности нагрузки. Равен отношению потребляемой электроприёмником активной мощности к полной мощности. Активная мощность расходуется на совершение работы. Полная мощность — геометрическая сумма активной и реактивной мощностей (в случае синусоидальных тока и напряжения).
Коэффициент мощности математически можно интерпретировать как косинус угла между векторами тока и напряжения. Поэтому в случае синусоидальных напряжения и тока величина коэффициента мощности совпадает с косинусом угла, на который отстают соответствующие фазы.
Коэффициент мощности позволяет судить о нелинейных искажениях, вносимых нагрузкой в электросеть. Чем он меньше, тем больше вносится нелинейных искажений. Кроме того, при одной и той же активной мощности нагрузки мощность, бесполезно рассеиваемая на проводах, обратно пропорциональна квадрату коэффициента мощности. Таким образом, чем меньше коэффициент мощности, тем ниже качество потребления электроэнергии.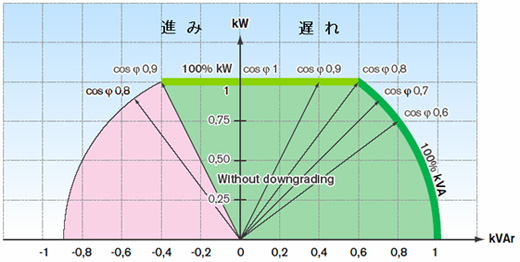 Для повышения качества электропотребления применяются различные способы коррекции коэффициента мощности, т. е. его повышения до значения, близкого к единице.
Для повышения качества электропотребления применяются различные способы коррекции коэффициента мощности, т. е. его повышения до значения, близкого к единице.
| Значение коэффициента мощности | Высокое | Хорошее | Удовлетворительное | Низкое | Неудовлетворительное |
|---|---|---|---|---|---|
| cos φ | 0,95…1 | 0,8…0,95 | 0,65…0,8 | 0,5…0,65 | 0…0,5 |
Описание параметра «Компенсация (cos ϕ)»
Коэффициент мощности (cos φ) — физическая величина, являющаяся энергетической характеристикой электрического тока. Коэффициент мощности характеризует приёмник электроэнергии переменного тока, а именно — степень линейности нагрузки. Равен отношению потребляемой электроприёмником активной мощности к полной мощности. Активная мощность расходуется на совершение работы. Полная мощность — геометрическая сумма активной и реактивной мощностей (в случае синусоидальных тока и напряжения). В общем случае полную мощность можно определить как произведение действующих (среднеквадратических) значений тока и напряжения в цепи. Полная мощность равна корню квадратному из суммы квадратов активной и неактивной мощностей. В качестве единицы измерения полной мощности принято использовать вольт-ампер (ВА) вместо ватта (Вт).
Активная мощность расходуется на совершение работы. Полная мощность — геометрическая сумма активной и реактивной мощностей (в случае синусоидальных тока и напряжения). В общем случае полную мощность можно определить как произведение действующих (среднеквадратических) значений тока и напряжения в цепи. Полная мощность равна корню квадратному из суммы квадратов активной и неактивной мощностей. В качестве единицы измерения полной мощности принято использовать вольт-ампер (ВА) вместо ватта (Вт).
Коэффициент мощности математически можно интерпретировать как косинус угла между векторами тока и напряжения. Поэтому в случае синусоидальных напряжения и тока величина коэффициента мощности совпадает с косинусом угла, на который отстают соответствующие фазы.
Коэффициент мощности позволяет судить о нелинейных искажениях, вносимых нагрузкой в электросеть. Чем он меньше, тем больше вносится нелинейных искажений. Кроме того, при одной и той же активной мощности нагрузки мощность, бесполезно рассеиваемая на проводах, обратно пропорциональна квадрату коэффициента мощности. Таким образом, чем меньше коэффициент мощности, тем ниже качество потребления электроэнергии. Для повышения качества электропотребления применяются различные способы коррекции коэффициента мощности, т. е. его повышения до значения, близкого к единице.
Таким образом, чем меньше коэффициент мощности, тем ниже качество потребления электроэнергии. Для повышения качества электропотребления применяются различные способы коррекции коэффициента мощности, т. е. его повышения до значения, близкого к единице.
| Значение коэффициента мощности | Высокое | Хорошее | Удовлетворительное | Низкое | Неудовлетворительное |
|---|---|---|---|---|---|
| cos φ | 0,95…1 | 0,8…0,95 | 0,65…0,8 | 0,5…0,65 | 0…0,5 |
Коэффициент мощности (cos φ, косинус фи ), Полная (кажущаяся), активная и реактивная мощность электродвигателя=электромотора и не только его. Коэффициент мощности для трехфазного электродвигателя.
Коэффициент мощности (cos φ, косинус фи ), Полная (кажущаяся), активная и реактивная мощность электродвигателя=электромотора и не только его. Коэффициент мощности для трехфазного электродвигателя.
Коэффициент мощности для трехфазного электродвигателя.
На шильдиках многих электромоторов (электродвигателей и др. устройств) указывают активную мощность в Вт и cosφ / или λ /или PF. Что тут к чему см. ниже.
Подразумеваем,что переменное напряжение в сети синусоидальное — обычное, хотя все рассуждения ниже верны и для всех гармоник по отдельности других периодических напряжений.
Полная, или кажущаяся мощность S (apparent power) измеряется в вольт-амперах (ВА или VA) и определяется произведением переменных напряжения и тока системы. Удобно считать, что полная мощность в цепи переменного тока выражается комплексным числом таким, что активная мощность является его действительной частью, реактивная мощность — мнимой.
|
Активная мощность P (active power = real power =true power) измеряется в ваттах (Вт, W) и это та мощность, которая потребляется электрическим сопротивлением системы на тепло и полезную работу. Для сетей переменного тока:
- P=U*I*cosφ, где U и I — действующие=эффективные=среднеквадратичные значения напряжения и тока, а φ- сдвиг фаз между ними
Реактивная мощность Q (reactive power) измеряется в вольт-амперах реактивных (вар, var) и это электромагнитная мощность, которая запасается и отдается обратно в сеть колебательным контуром системы. Реактивная мощность в идеале не выполняет работы, т.е. название вводит в заблуждение. Легко догадаться глядя на рисунок, что:
Реактивная мощность в идеале не выполняет работы, т.е. название вводит в заблуждение. Легко догадаться глядя на рисунок, что:
- P=U*I*sinφ, где U и I — действующие=эффективные=среднеквадратичные значения напряжения и тока, а φ- сдвиг фаз между ними
Сама концепция активной и реактивной мощности актуальна для устройств (приемников) переменного тока. Она малоактуальна=никогда не упоминатеся для приемников постоянного тока в силу малости (мизерности) соответствующих эффектов, связанных только с переходными процессами при включении/выключении.
Любая система, как известно, имеет емкость и индуктивность = является неким колебательным контуром. Переменный ток в одной фазе накачивает электромагнитное поле этого контура энергией а в противоположной фазе эта энергия уходит обратно в генератор ( в сеть). Это вызывает в РФ 3 проблемы (для поставщика энергии!)
- Хотя теоретически, при нулевых сопротивлениях передачи, на выработку реактивной мощности не тратится мощность генератора, но практически для передачи реактивной мощности по сети требуется дополнительная, активная мощность генератора (потери передачи).

- Сеть должна пропускать и активные и реактивные токи, т.е иметь запас по пропускным характеристикам.
- Генератор мог бы, выдавая те же ток и напряжение, поставлять потребителю электроэнергии больше активной мощности.
попробуем догадаться, что делает поставщик электроэнергии? Правильно, пытается навязать Вам различные тарифы для разлиных значений cos φ. Что можно сделать: можно заказать компенсацию реактивной мощности ( т.е. установку неких блоков конденсаторов или катушек), которые заставят реактивную нагрузку колебаться внутри Вашего предприятия/устройства. Стоит ли это делать? Зависит от стоимости установки, наценок за коэффициент мощности и очень даже часто не имеет экономического смысла. В некоторых странах качество питающего напряжения тоже может пострадать от избытка реактивной мощности, но в РФ проблема неактуальна в силу изначально очень низкго качества в питающей сети.
Естественно, хотелось бы ввести величину, которая характеризовала бы степень линейности нагрузки. И такая величина вводится под названием коэффициент мощности («косинус фи», power factor, PF), как отношение активной мощности к полной, естественно сразу в 2-х видах, в РФ это:
И такая величина вводится под названием коэффициент мощности («косинус фи», power factor, PF), как отношение активной мощности к полной, естественно сразу в 2-х видах, в РФ это:
- λ=P/S*100% — то есть, если в %, то это лямбда, P в (Вт), S в (ВА)
- cosφ=P/S — более распространенная величина , P в (Вт), S в (ВА)
Коэффициент мощности для трехфазного асинхронного (обычного) электродвигателя.
cosφ = P / (√3*U*I)
где
cosφ = косинус фи
√3 = квадратный корень из трех
P = активная мощность (Вт)
U = Напряжение (В)
I = Ток (А)
Что такое cos f в электричестве. Определение коэффициента мощности
Как мы уже знаем из предыдущих лекций по электротехнике электрическая цепь может иметь чисто активную, реактивную и смешанную нагрузку.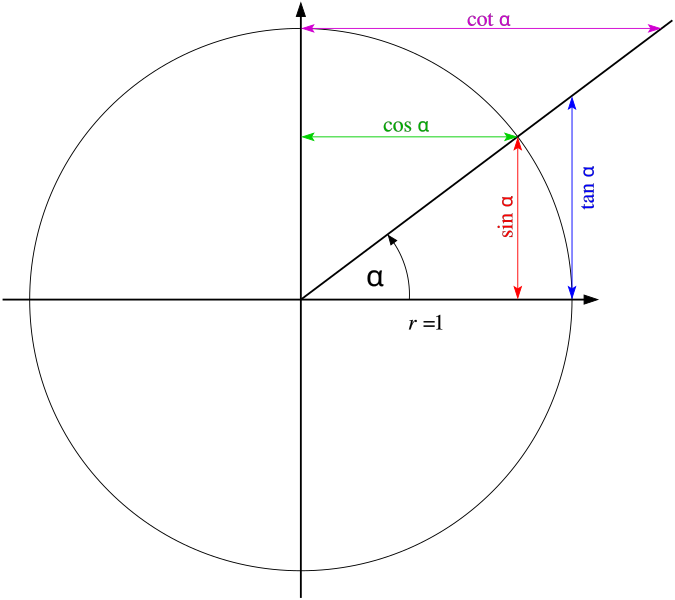 Угол сдвига между напряжением и током – это и есть угол φ. А косинус фи принято называть коэффициентом мощности.
Угол сдвига между напряжением и током – это и есть угол φ. А косинус фи принято называть коэффициентом мощности.
При чисто активной нагрузке, например при подсоединенной лампы накаливания, косинус фи (cosφ) будет равен единице, так как угол φ равен нулю. При емкостном характере в нагрузке, протекающий ток будет опережать напряжение, а при индуктивной наоборот. Если в электрическую цепь поставить идеальную индуктивность, то угол между протекающим током и напряжением составит 90 градусов.
В рассмотренном выше примере понятие коэффициента мощности возникает из-за индуктивной нагрузки. На практике чисто индуктивная нагрузка невозможна в принципе, должно быть хоть какое-то небольшое активное сопротивление, то есть в реальных условиях нужно рассматривать смешанную нагрузку.
Коэффициент мощности в виде формулы можно записать, как отношение активной мощности (P ) к полной (S ):
Если косинус фи равен единице, то это идеальный показатель при чисто активной нагрузке, cosφ=0,9 считается очень хорошим значением, а на предприятиях пытаются достичь cosφ=0,8.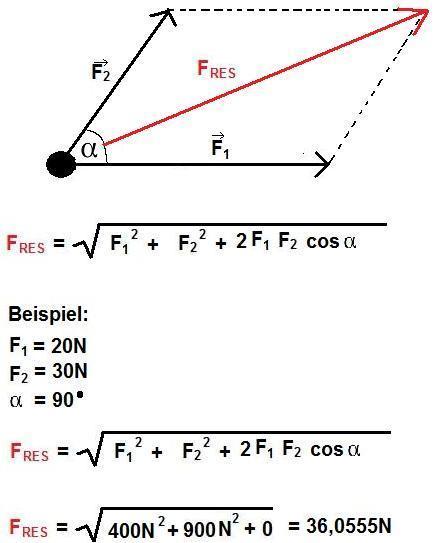
Чего пытаются достичь повышая косинус «фи» |
Повышая коэффициент мощности пытаются добиться следующих основных целей:
Сокращение расходов на электрическую энергию
Экономию цветных металлов за счет уменьшения диаметра медных проводов
Максимум применения заданной мощности трансформаторов, генераторов и электродвигателей переменного тока.
Так, например, от одного и того же трансформатора можно получить больше активной мощности потребителей, при большем значении величины косинуса фи. Так, от трансформатора с номинальной по паспорту мощностью S н =1000 кВа при соsφ = 0,7 можно достичь активной мощности Р 1 = S н cosφ = 1000 0,7=700 кВт , а при cosφ = 0,95 активная мощность будет равна Р 2 = S н φ= 1000 0,95 = 950 кВт.
Причем в обоих примерах трансформатор будет нагружен полностью до 1000 кВа. Причиной малого коэффициента мощности на производствах являются недогруженные трансформаторы и асинхронные электродвигатели.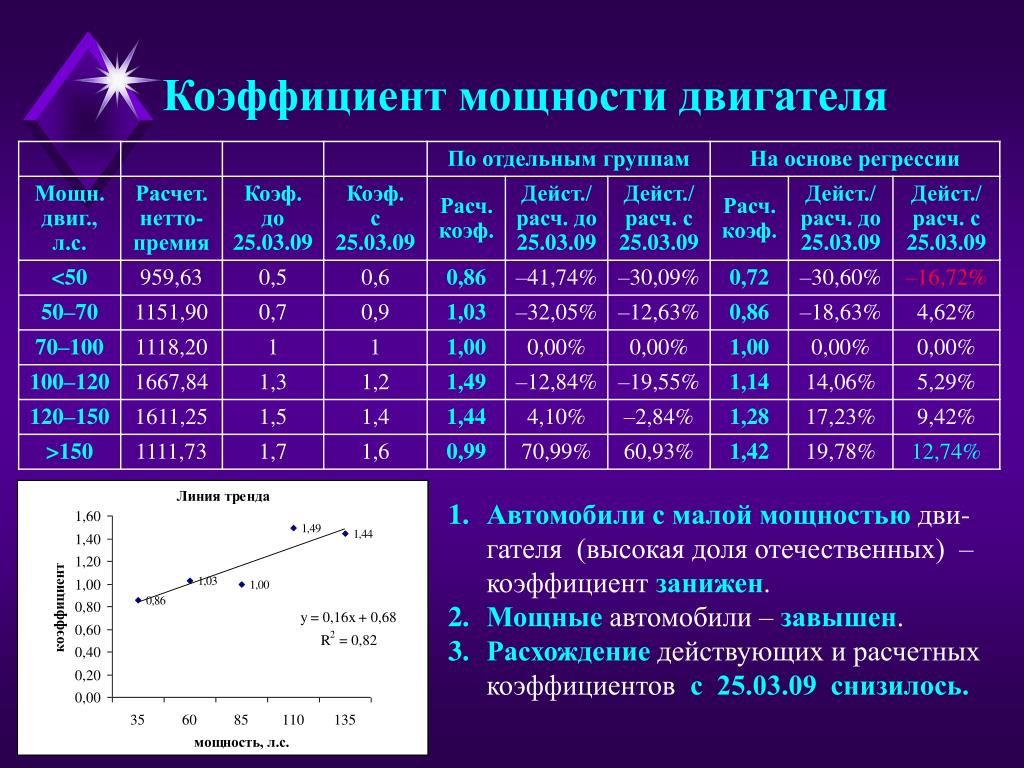 Допустим, асинхронный двигатель при ХХ имеет cosφ хх равный 0,2, тогда как при загрузке до своей номинальной мощности его соsφ н = 0,85.
Допустим, асинхронный двигатель при ХХ имеет cosφ хх равный 0,2, тогда как при загрузке до своей номинальной мощности его соsφ н = 0,85.
Для наглядности рассмотрим приближенный рисунок треугольника мощности для асинхронного двигателя. При XX асинхронный двигатель потребляет реактивную мощность, равную 30% номинальной мощности, тогда как потребляемая активная мощность составляет около 15%. Коэффициент мощности в данном случае достаточно мал. С ростом нагрузки активная мощность также растет, а реактивная меняется совсем немного и поэтому cosφ возрастает.
Основным мероприятием, повышающим cosφ, является работа совершаемая на полную производственную мощность. В данном случае асинхронные ЭД будут работать с cosφ, близкими к номинальным величинам.
Мероприятия по повышению cosφ можно условно поделить на два основных типа:
К первому типу относятся мероприятия не требующие установки компенсирующих схем и целесообразные во всех случаях. К ним можно отнести упорядочение технологического процесса, ведущее к улучшению энергетического режима оборудования и повышению cosφ, использование синхронных ЭД вместо асинхронных.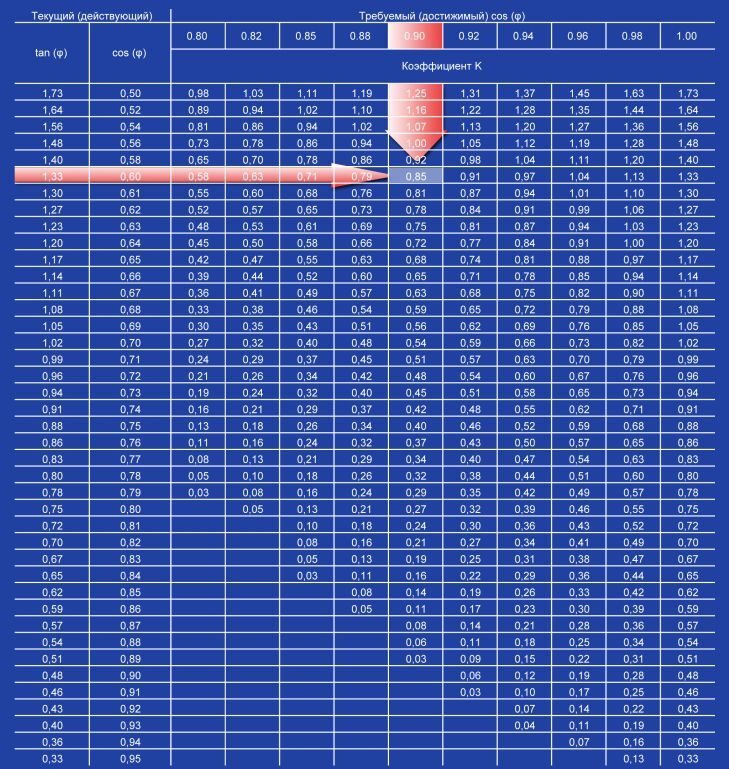 Ко второй группе относятся мероприятия связанные с использованием компенсирующих устройств и схем (искусственные методы).
Ко второй группе относятся мероприятия связанные с использованием компенсирующих устройств и схем (искусственные методы).
Видеоурок по теме коэффициент мощности |
Коэффициентом мощности, или «косинусом фи» (cos φ ), цепи называется отношение к полной мощности.
В общем случае активная мощность меньше полной мощности, то есть у этой дроби числитель меньше знаменателя, и поэтому меньше единицы.
Только в случае чисто активной нагрузки, когда вся мощность является активной мощностью, числитель и знаменатель этой дроби равны между собой, и поэтому коэффициент мощности равен единице.
Реактивная энергия потребляется нагрузкой и, если не принимать специальных мер, она будет загружать линию, идущую от генератора к нагрузке. Нельзя лишить реактивной энергии цепь, содержащую индуктивную нагрузку, но разгрузить генератор от реактивной мощности необходимо.
Чем большую часть полной мощности составляет активная мощность, тем меньше числитель отличается от знаменателя дроби и тем ближе коэффициент мощности к единице. Задача состоит в том, чтобы заставить протекать по линии к потребителю только минимально необходимую величину реактивной энергии.
Задача состоит в том, чтобы заставить протекать по линии к потребителю только минимально необходимую величину реактивной энергии.
Cos φ , или коэффициент мощности, измеряется особым прибором фазометром.
Пример 1. Амперметр показывает ток 10 А, вольтметр — 120 В, ваттметр — 1 кВт. Определить cos φ потребителя.
S = I × U = 10 × 120 = 1200 ВА,
Пример 2. Определить активную мощность, отдаваемую генератором однофазного в сеть, если вольтметр на щите генератора показывает 220 В, амперметр — 20 А и фазометр 0,8.
P = I × U × cos φ = 20 × 220 × 0,8 = 3520 Вт = 3,52 кВт.
Полная мощность.
S = I × U = 20 × 220 = 4400 ВА = 4,4 кВА.
Пример 3. Вольтметр, установленный на щитке электродвигателя показывает 120 В, амперметр — 450 А, ваттметр — 50 кВт. Определить z , r , x L , S , cos φ , Q .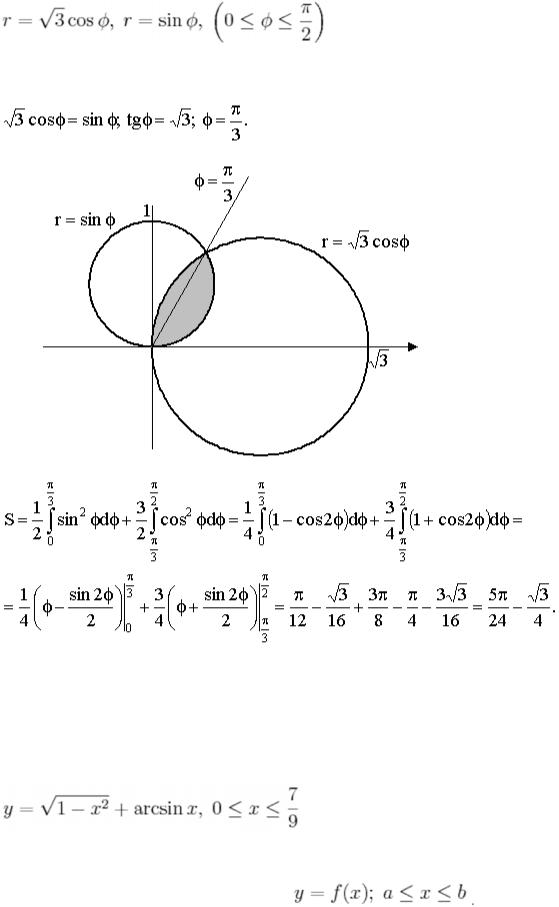
Так как P = I 2 × r , то
S = I × U = 450 × 120 = 54000 ВА = 54 кВА,
Из построения треугольников сопротивлений, напряжений и мощностей для определенной цепи видно, что эти треугольники подобны один другому, так как их стороны пропорциональны. Из каждого треугольника можно найти «косинус фи» цепи, как показано на рисунке 1. Этим можно воспользоваться для решения самых разнообразных задач.
Пример 4. Определить z , x L , U , U а, U L , S , P , Q , если I = 6 А, r = 3 Ом, cos φ = 0,8 и ток отстает от по
Уменьшается пропорционально нагрузке. В то же время реактивная мощность изменяется меньше. Поэтому чем меньше нагрузка двигателя, тем с меньшим коэффициентом мощности он работает.
Так, например, асинхронный двигатель в 400 кВт при 1000 оборотах в минуту имеет «косинус фи», равный при полной нагрузке 0,83. При ¾ нагрузки тот же двигатель имеет cos φ = 0,8. При ½ нагрузке cos φ = 0,7 и при ¼ нагрузки cos φ = 0,5.
При ¾ нагрузки тот же двигатель имеет cos φ = 0,8. При ½ нагрузке cos φ = 0,7 и при ¼ нагрузки cos φ = 0,5.
Двигатели, работающие вхолостую, имеют «косинус фи», равный от 0,1 до 0,3 в зависимости от типа, мощности и скорости вращения.
Неправильный выбор типа электродвигателя
Двигатели быстроходные и большой мощности имеют более высокий «косинус фи», чем тихоходные и маломощные двигатели. Двигатели закрытого типа имеют cos φ ниже, чем двигатели открытого типа. Двигатели, неправильно выбранные по типу, мощности и скорости, понижают cos φ .
Повышение напряжения в сети
В часы малых нагрузок, обеденных перерывов и тому подобного напряжение сети на предприятии увеличивается на несколько вольт. Это ведет к увеличению намагничивающего тока индивидуальных потребителей (реактивной составляющей их полного тока), что в свою очередь вызывает уменьшение cos φ предприятия.
Неправильный ремонт двигателя
При перемотке электродвигателей обмотчики вследствие неправильного подбора проводов иногда не заполняют пазы машины тем количеством проводников, которое было в фабричной обмотке. При работе такого двигателя, вышедшего из ремонта, увеличивается рассеяния, что приводит к уменьшению cos φ двигателя.
При работе такого двигателя, вышедшего из ремонта, увеличивается рассеяния, что приводит к уменьшению cos φ двигателя.
При сильном износе подшипников ротор двигателя может задевать при вращении за статор. Вместо того чтобы сменить подшипники, обслуживающий персонал иногда идет по неправильному и вредному пути и подвергает ротор обточке.
Увеличение воздушного зазора между ротором и статором вызывает увеличение намагничивающего тока и уменьшение cos φ двигателя.
Способы увеличения «косинуса фи»
Вышеперечисленные последствия низкого cos φ с достаточной убедительностью говорят о том, что необходимо вести борьбу за высокий cos φ . К мерам увеличения cos φ относятся:
- Правильный выбор типа, мощности и скорости вновь устанавливаемых двигателей;
- Увеличение загрузки двигателей;
- Недопущение работы двигателей вхолостую продолжительное время;
- Правильный и высококачественный ремонт двигателей;
- Применение статических (то есть неподвижных, невращающихся) .

Малый вес конденсаторов, отсутствие вращающихся частей, незначительные потери энергии в них, легкость обслуживания, безопасность и надежность в работе дают возможность широкого применения статических конденсаторов для повышения cos φ двигателей.
Отрезок ос , представляющий активную слагающую тока I 1 , равен:
ос = I 1 × cos φ 1 = оа × cos φ 1 .
На бирках (шильдиках) электродвигателей обязательно указана его мощность, измеряемая в ваттах, и вот такой значок «cosφ». Что обозначает косинус фи в электротехнике – это коэффициент мощности. И определяется он соотношением мощности активной к полной. При этом чем выше данный коэффициент, то есть приближается к единице, тем лучше. Потому что в данном случае реактивная мощность будет равна нулю, а, значит, будет уменьшаться потребляемое значение, что приведет к экономии электроэнергии.
Поэтому чтобы разобраться в косинусе фи, необходимо сначала разобраться со всеми этими мощностями.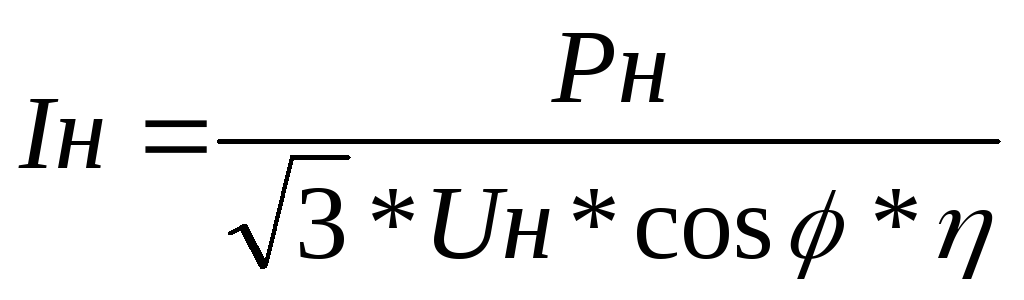
Мощности в электродвигателе
Итак, полная мощность с единицей измерения вольт-ампер (ВА) – это комплексная величина, состоящая из активной мощности (действительной) и реактивной (мнимой). Если рассматривать полный показатель по формуле, то можно это отобразить вот так:
N=√Nа²+Nр²
Или вот так:
Теперь рассмотрим составляющие первой формулы. Активная мощность действует только на активных сопротивлениях, то есть она присутствует при определенных нагрузках, а, точнее сказать, когда электрический двигатель работает. Вычисляется она вот по этой формуле:
Что значит активное сопротивление? Здесь необходимо понимать, что в цепях переменного тока сопротивление выше, чем в цепях постоянного тока. Это связано со многими факторами. К примеру, это вихревые токи, которые образуются в цепи, это электромагнитное поле, это близость расположения проводников и так далее. Именно поэтому сопротивление в сетях переменного тока называют активным, а в сетях постоянного тока омическим.
Теперь, что касается реактивной мощностной составляющей. Во-первых, эта величина измеряется в вольт ампер реактивный (вар). Во-вторых, это своеобразная накопительная мощность, которая накапливается в проводниковых сетях, а потом отдается обратно в сеть. Кстати, эта величина может быть положительной или отрицательной.
Причинами появления реактивной составляющей могут быть приборы, которые выдают емкостную или индуктивную нагрузку. Рассчитывают этот показатель вот по этой формуле:
Если рассматривать полезность реактивной мощности, то она не расходуется на прямые нужды потребителя. К примеру, в электрических двигателях она не преобразуется из электрической в механическую. И хотя полезной нагрузки эта мощность не несет, без нее не может быть осуществлена полезная работа. И все же производители стараются данный показатель уменьшить, потому что повышение активной составляющей приводит к снижению реактивной, отсюда и низкий КПД оборудования или сети.
Косинус фи
Как уже было сказано выше, значение косинуса фи в электротехнике – это величина, характеризующая степень линейности нагрузки.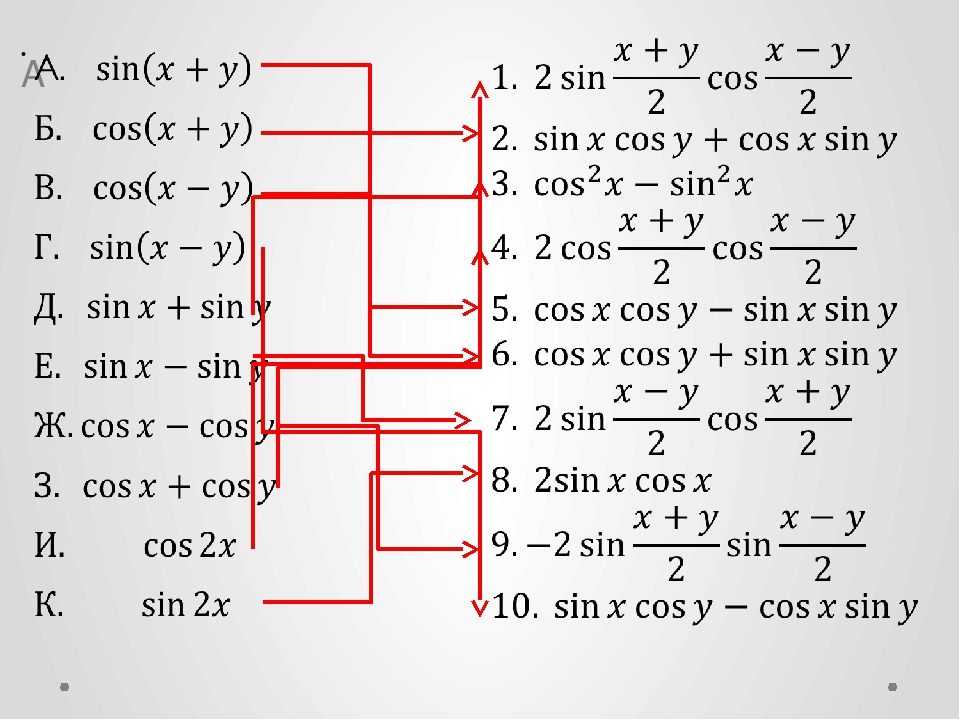 Для нее тоже существует формула:
Для нее тоже существует формула:
cos φ = N а / (√3*U*I).
Что касается величины «cosφ», то ее увеличение преследует несколько целей.
- Основная цель – экономия потребления электрического тока.
- Соответственно экономия цветных металлов, которые используются в обмотках электромотора.
- Максимальное использование полезной мощности агрегата.
Хотелось бы отметить вот какой момент – производственные электрические сети всегда находятся в недогруженном состоянии. Почему? Все дело в том, что не все электродвигатели постоянно работают под нагрузкой. Любой асинхронный двигатель на холостом ходе имеет косинус фи, равный приблизительно значению 0,2. При нагрузке косинус фи увеличивается до 0,85. Почему так происходит? Все опять упирается в активную и реактивную мощности. Первая при холостом ходе мотора приблизительно составляет 30%, вторая 15%. Как только нагрузка на электрический двигатель увеличивается, тут же поднимается активная составляющая, а реактивная снижается практически до нуля. Поэтому основное требование увеличения «cos
φ»
– это работа предприятия с полной нагрузкой.
Поэтому основное требование увеличения «cos
φ»
– это работа предприятия с полной нагрузкой.
Мероприятия по увеличению косинуса фи
Чтобы увеличить косинус фи, можно воспользоваться двумя способами:
- Естественным путем без установки компенсирующих приборов и устройств.
- Искусственным путем с установкой компенсирующих агрегатов.
Очень многих впервые столкнувшихся с электротехникой обывателей пугают страшные и непонятные аббревиатуры. Таких в данной сфере превеликое множество. В данной статье мы поподробнее остановимся на одной из таких аббревиатур. Итак, представляем вашему вниманию cos φ или по другому коэффициент мощности. Также вместо этой аббревиатуры можно увидеть символ λ . Отличие между ними в том, что если указано λ , значит значение будет выражено в процентах.
cos φ
или коэффициент мощности указывает на наличие или отсутствие реактивной составляющей мощности у потребителя электрической энергии. При наличии такой составляющей переменный ток и напряжение не совпадают во времени по фазе. Ток или опережает напряжение или отстает от него, в зависимости от того, какая нагрузка — емкостная или индуктивная. Емкостная нагрузка возникает при наличии в электроустановке потребителя статических конденсаторов, выпрямителей и т. д. Индуктивная нагрузка возникает при наличии в электроустановке потребителя различных катушек, пускателей, электродвигателей. В общем, большинство электроустановок, которые находятся в пользовании потребителей приводят к возникновению реактивной мощности. Чем больше угол сдвига, тем больше доля реактивной энергии в электроустановке потребителя.
Ток или опережает напряжение или отстает от него, в зависимости от того, какая нагрузка — емкостная или индуктивная. Емкостная нагрузка возникает при наличии в электроустановке потребителя статических конденсаторов, выпрямителей и т. д. Индуктивная нагрузка возникает при наличии в электроустановке потребителя различных катушек, пускателей, электродвигателей. В общем, большинство электроустановок, которые находятся в пользовании потребителей приводят к возникновению реактивной мощности. Чем больше угол сдвига, тем больше доля реактивной энергии в электроустановке потребителя.
Для того, чтобы понять что такое коэффициент мощности, поговорим подробнее о том, что же это за мощность, из чего она состоит и как находится.
Итак, в цепи постоянного тока определить мощность потребителя не составляет большого труда. Зная напряжение и протекающий ток, мы просто умножаем эти величины.
В цепи переменного тока все немного сложнее. Как уже говорилось ранее, как правило, при синусоидальном переменном токе изменение напряжения и тока не совпадают во времени, то есть между ними происходит сдвиг по фазе. Только в частном случае, когда вся нагрузка полностью активная, напряжение и ток совпадают по фазе. При этом угол сдвига ( φ
)=0°, следовательно cos 0° = 1
. Получается, что вся энергия совершает полезную работу. Конечно это идеальный вариант. На самом деле, в подавляющем большинстве случаев электроприборы содержат в себе различные катушки, конденсаторы и т. д. В таких устройствах полная мощность раскладывается на активную и реактивную. Измеряется полная мощность в вольтамперах (ВА). Найти полную мощность можно путем умножения действующего значения напряжения на действующее значение тока.
Только в частном случае, когда вся нагрузка полностью активная, напряжение и ток совпадают по фазе. При этом угол сдвига ( φ
)=0°, следовательно cos 0° = 1
. Получается, что вся энергия совершает полезную работу. Конечно это идеальный вариант. На самом деле, в подавляющем большинстве случаев электроприборы содержат в себе различные катушки, конденсаторы и т. д. В таких устройствах полная мощность раскладывается на активную и реактивную. Измеряется полная мощность в вольтамперах (ВА). Найти полную мощность можно путем умножения действующего значения напряжения на действующее значение тока.
Полная мощность определяет фактические нагрузки на систему электроснабжения, по этому пропускная способность линий электропередач, мощность трансформаторов, генераторов, стабилизаторов и т. д. указывается именно в вольтамперах, а не в ваттах.
В свою очередь полная мощность состоит из активной мощности ( Р
) и реактивной мощности ( Q
). Активная мощность – это та часть электрической энергии, которая расходуется непосредственно на совершение полезной работы (подогрев электроплиты, нагрев нити в лампе накаливания, вращение вала электродвигателя).
В этой формуле мы как раз и видим cos φ
Чем меньше угол сдвига между напряжением током, тем больше электрической энергии осуществляет полезную работу, то есть совершают нагрев воды в электрическом чайнике, или вращение вала электродвигателя. Повторимся еще раз, что в идеале угол сдвига φ = 0° , следовательно = 1 . Однако, чаще всего для нормального функционирования электроустановок, в их составе присутствуют различные катушки, конденсаторы, обмотки. Характеристикой таких потребителей является реактивная мощность.
Реактивная мощность измеряется в вольтамперах реактивных (Вар)
. Данная энергия не совершает непосредственно полезную работу, но необходима для нормальной работы таких приборов, как пускатели, трансформаторы, электрические двигатели. Например, в работе трансформатора электрическая энергия с первичной обмотки передается на вторичную через электромагнитное поле. Для создания электромагнитного поля и используется реактивная энергия. При полностью индуктивной нагрузке (например, работа трансформатора в режиме холостого хода), угол сдвига фаз напряжения и тока равен 90°
. Следовательно cos φ = cos = 90° = 0
. Это означает, что активная мощность будет тоже равна нулю. Получается, что никакой полезной работы не производится. При этом, вследствие потерь в магнитопроводах, на нагрев, электрическая энергия все равно расходуется, значит расходуется сырье на электростанциях, нагружаются сети, трансформаторы и генераторы.
При полностью индуктивной нагрузке (например, работа трансформатора в режиме холостого хода), угол сдвига фаз напряжения и тока равен 90°
. Следовательно cos φ = cos = 90° = 0
. Это означает, что активная мощность будет тоже равна нулю. Получается, что никакой полезной работы не производится. При этом, вследствие потерь в магнитопроводах, на нагрев, электрическая энергия все равно расходуется, значит расходуется сырье на электростанциях, нагружаются сети, трансформаторы и генераторы.
Условно считается, что потребители, которые имеют обмотки на магнитопроводах, то есть представляют собой индуктивность, потребляют положительную реактивную мощность. О приборах, в которых имеются конденсаторы, принято говорить, что они генерируют отрицательную реактивную мощность. Синхронные генераторы, двигатели, компенсаторы способны как производить, так и потреблять реактивную мощность, то есть они способны вести себя относительно электрической сети и как емкость и как индуктивность.
Примерное значение cos φ
для различных электроустановок переменного тока: 0,05-0,1 – трансформаторы в режиме холостого хода; до 1 – для нагревательных приборов и ламп накаливания; для асинхронных электродвигателей 0,7-0,9 при номинальной нагрузке.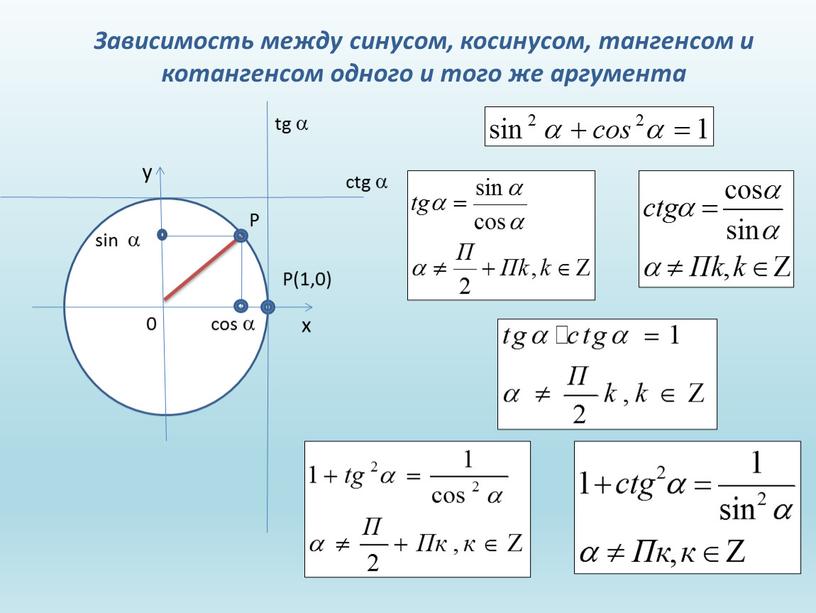 С уменьшением нагрузки электродвигателя cos φ
уменьшается.
С уменьшением нагрузки электродвигателя cos φ
уменьшается.
Для того, чтобы уменьшить влияние реактивной мощности на электросеть, прибегают к искусственному завышению cos φ . Для этого непосредственно у потребителя электрической энергии устанавливаются батареи статических конденсаторов. Более подробно на способах компенсации реактивной энергии можно будет ознакомиться в следующих статьях.
| Чем ближе cos фи к единице — тем лучше. Если, например, на электроприборе указан cos фи 0,7 и мощность 1 тыс. ватт (1 Квт.), это означает, что прибор потребляет в реальности 1,4 Квт. Это необходимо учитывать при установке розетки, подключении удлинителя, сетевого фильтра или стабилизатора. Это значение важно только для предприятий, которые платят за активную и реактивную мощность. Частникам (читай для квартир) это не сильно критично, с точки зрения оплаты за электроэнергию. Если на лампе указана мощность, например, в 10 Вт (активная мощность), cos фи равен 0,9, то потребляемая светильником «полная мощность» будет 10/0,9=11,11 Вт, таким образом, предприятие будет платить за полную мощность за 11,11, а квартирант только за 10 Вт. Под понятием «полная мощность» подразумевается вся та мощность, которая потребляется электроприбором и включает в себя активную (мощность) составляющую и реактивную (мощность) составляющую. Активная (мощность) составляющая — энергия, которая превращается в полезную работу и трансформируется, например, в свет. Реактивная (мощность) составляющая — энергия, которая идет на нагрев проводников (проводов), фактически ее можно характеризовать еще, как потери на передачу энергии. Сos фи — это отношение полной мощности электроприбора к активной мощности. Чем выше cos фи потребителя, тем меньше будут потери мощности в линии и дешевле обойдётся передача электроэнергии потребителю. Сos фи показывает нам насколько эффективно используется рабочая мощность потребителя.
Рекомендуем почитать: Обозначение ламп Какие светодиодные лампы лучше?
|
cos, cosf, cosl — cppreference.com
float cosf (float arg); | (1) | (с C99) |
двойной соз (двойной аргумент); | (2) | |
long double cosl (длинный двойной аргумент); | (3) | (с C99) |
# определить cos (arg) | (4) | (с C99) |
1-3) Вычисляет косинус arg (измеряется в радианах).
cosl . В противном случае, если аргумент имеет целочисленный тип или тип double, вызывается cos . В противном случае вызывается cosf . Если аргумент сложный, то макрос вызывает соответствующую сложную функцию (ccosf, ccos, ccosl).[править] Параметры
| аргумент | — | значение с плавающей запятой, представляющее угол в радианах |
[править] Возвращаемое значение
Если ошибок нет, косинус arg (cos (arg)) находится в диапазоне [-1; +1], возвращается.
Результат может иметь незначительное значение или не иметь никакого значения, если величина | (до C ++ 11) |
Если возникает ошибка домена, возвращается значение, определяемое реализацией (NaN, если поддерживается).
Если ошибка диапазона возникает из-за недостаточного заполнения, возвращается правильный результат (после округления).
[править] Обработка ошибок
Сообщения об ошибках указаны в math_errhandling.
Если реализация поддерживает арифметику с плавающей запятой IEEE (IEC 60559),
- если аргумент равен ± 0, результат равен 1.0
- если аргумент равен ± ∞, возвращается NaN и повышается FE_INVALID
- если аргумент — NaN, возвращается NaN
[править] Примечания
Случай, когда аргумент бесконечен, не указан как ошибка домена в C, но он определен как ошибка домена в POSIX.
[править] Пример
#include#include #include #include #pragma STDC FENV_ACCESS ON int main (пусто) { двойной пи = acos (-1); // типичное использование printf ("cos (pi / 3) =% f \ n", cos (pi / 3)); printf ("cos (pi / 2) =% f \ n", cos (pi / 2)); printf ("cos (-3 * pi / 4) =% f \ n", cos (-3 * pi / 4)); // специальные значения printf ("cos (+0) =% f \ n", cos (0.0)); printf ("cos (-0) =% f \ n", cos (-0. 0)); // обработка ошибок feclearexcept (FE_ALL_EXCEPT); printf ("cos (БЕСКОНЕЧНОСТЬ) =% f \ n", cos (БЕСКОНЕЧНОСТЬ)); if (fetestexcept (FE_INVALID)) put ("FE_INVALID поднят"); }
Возможный выход:
cos (пи / 3) = 0,500000
cos (пи / 2) = 0,000000
соз (-3 * пи / 4) = -0,707107
соз (+0) = 1.000000
cos (-0) = 1.000000
cos (БЕСКОНЕЧНОСТЬ) = -nan
FE_INVALID поднял [править] Ссылки
- Стандарт
- C11 (ISO / IEC 9899: 2011):
- 7.12.4.5 Функции cos (стр: 239)
- 7.25 Типовая математика
(p: 373-375)
- 7.25 Типовая математика
- F.10.1.5 Функции cos (стр: 519)
- Стандарт
- C99 (ISO / IEC 9899: 1999):
- 7.12.4.5 Функции cos (стр: 220)
- 7.22 Типовой тип math
(p: 335-337)
- 7.22 Типовой тип math
- F.9.
 1.5 Функции cos (стр: 456)
1.5 Функции cos (стр: 456)
- F.9.
- Стандарт C89 / C90 (ISO / IEC 9899: 1990):
[править] См. Также
Функция косинуса
Функция косинуса — это периодический функция, которая очень важна в тригонометрии.
Самый простой способ понять функцию косинуса — использовать единичную окружность. Для заданного угла измерения θ , нарисуйте единичный круг на координатной плоскости и нарисуйте угол с центром в начале координат, с одной стороной в качестве положительного Икс -ось.В Икс -координата точки, где другая сторона угла пересекает круг, равна потому что ( θ ) , а у -координата грех ( θ ) .
Есть несколько значений косинуса, которые следует запомнить, исходя из
30
°
—
60
°
—
90
°
треугольники
а также
45
°
—
45
°
—
90
°
треугольники
.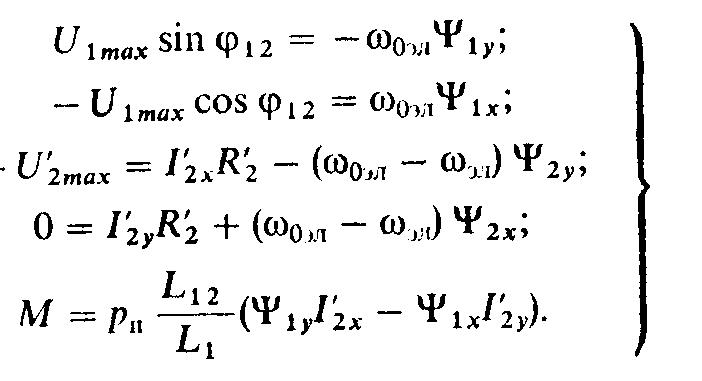
Зная эти значения, вы можете получить много других значений для функции косинуса. Помните, что cos \ theta; положительно в квадрантах я а также я V и отрицательные в квадрантах я я а также я я я .
Вы можете нанести эти точки на координатную плоскость, чтобы показать часть функции косинуса, часть между 0 а также 2 π .
Для значений θ меньше, чем 0 или больше чем 2 π вы можете найти ценность потому что ( θ ) с помощью опорный угол .
График функции в более широком интервале показан ниже.
Обратите внимание, что функция — это вся реальная линия, а диапазон — — 1 ≤ у ≤ 1 .
В
период
из
ж
(
Икс
)
знак равно
потому что
(
Икс
)
является
2
π
. То есть форма кривой повторяется каждые
2
π
-единичный интервал на
Икс
-ось.
То есть форма кривой повторяется каждые
2
π
-единичный интервал на
Икс
-ось.
В амплитуда из ж ( Икс ) знак равно потому что ( Икс ) является 1 , то есть высота волны.
Модифицированная функция у знак равно а потому что ( б Икс ) имеет амплитуду а и период 2 π / б .
тригонометрических функций
тригонометрических функцийПроизвольные углы и единичная окружность
До сих пор мы использовали единичный круг для определения тригонометрических функций для острых углов. В следующем разделе, где мы рассмотрим наклонные треугольники, нам понадобится нечто большее, чем острые углы.Некоторые наклонные треугольники являются тупыми, и нам нужно знать синус и косинус тупых углов. Пока мы делаем это, мы также должны определять триггерные функции для углов, превышающих 180 °, и для отрицательных углов. Сначала нам нужно четко определить, что это за углы.
Пока мы делаем это, мы также должны определять триггерные функции для углов, превышающих 180 °, и для отрицательных углов. Сначала нам нужно четко определить, что это за углы.Древнегреческие геометры считали углы только между 0 ° и 180 °, и они не считали ни прямой угол 180 °, ни вырожденный угол 0 ° углами. Эти частные случаи полезно не только рассматривать как углы, но и включать в них углы от 180 ° до 360 °, которые иногда называют «углами отражения».«С применением тригонометрии к предметам исчисления и дифференциальных уравнений, углы, превышающие 360 °, и отрицательные углы также стали приемлемыми.
Рассмотрим единичную окружность. Обозначьте его центр (0,0) как O, и обозначьте точку (1,0) на нем как A. В качестве движущейся точки B движется по единичной окружности, начиная с A и двигаясь по против часовой стрелки, угол AOB как угол 0 ° и увеличивается. Когда B прошел весь путь по окружности и вернулся к A, , тогда угол AOB будет углом 360 °. Конечно, это тот же угол, что и угол 0 °, поэтому мы можем идентифицировать эти два угла. Поскольку B продолжает второй раз по кругу, мы получаем углы в диапазоне от 360 ° до 720 °. Это те же углы, которые мы видели в первый раз, но у нас есть разные названия. Например, прямой угол обозначается как 90 ° или 450 °. Каждый раз по кругу мы получаем другое название угла. Таким образом, 90 °, 450 °, 810 ° и 1170 ° — это один и тот же угол.
Конечно, это тот же угол, что и угол 0 °, поэтому мы можем идентифицировать эти два угла. Поскольку B продолжает второй раз по кругу, мы получаем углы в диапазоне от 360 ° до 720 °. Это те же углы, которые мы видели в первый раз, но у нас есть разные названия. Например, прямой угол обозначается как 90 ° или 450 °. Каждый раз по кругу мы получаем другое название угла. Таким образом, 90 °, 450 °, 810 ° и 1170 ° — это один и тот же угол.
Если B начинается в той же точке A и движется по часовой стрелке, то мы получим отрицательные углы, или, точнее, названия в отрицательных градусах для тех же углов.Например, если вы проедете четверть круга по часовой стрелке, угол AOB будет назван как –90 °. Конечно, это то же самое, что и угол 270 °.
Таким образом, любой угол имеет бесконечное количество имен, но все они отличаются друг от друга на 360 °.
Синусы и косинусы произвольных углов
Теперь, когда мы указали произвольные углы, мы можем определить их синусы и косинусы. Пусть угол расположен так, чтобы его вершина находилась в центре единичной окружности O = (0,0), и пусть первая сторона угла расположена вдоль оси x .Пусть вторая сторона угла пересекает единичную окружность в точке B. Тогда угол равен углу AOB , где A равно (1,0). Мы используем координаты B , чтобы определить косинус угла и синус угла. В частности, координата x точки B является косинусом угла, а координата y точки B является синусом угла. Это определение расширяет определения синуса и косинуса, данные ранее для острых углов.
Пусть угол расположен так, чтобы его вершина находилась в центре единичной окружности O = (0,0), и пусть первая сторона угла расположена вдоль оси x .Пусть вторая сторона угла пересекает единичную окружность в точке B. Тогда угол равен углу AOB , где A равно (1,0). Мы используем координаты B , чтобы определить косинус угла и синус угла. В частности, координата x точки B является косинусом угла, а координата y точки B является синусом угла. Это определение расширяет определения синуса и косинуса, данные ранее для острых углов.Свойства синусов и косинусов, вытекающие из этого определения
Есть несколько свойств, которые мы можем легко вывести из этого определения. Некоторые из них обобщают тождества, которые мы уже видели для острых углов.- Синус и косинус являются периодическими функциями периода 360 °, то есть периода 2 π . Это потому, что синусы и косинусы определяются в терминах углов, и вы можете добавить кратные 360 ° или 2 π , и это не изменит угол.
 Таким образом, для любого угла θ , sin ( θ + 360 °) = sin θ, и
Таким образом, для любого угла θ , sin ( θ + 360 °) = sin θ, иcos ( θ + 360 °) = cos θ.
Многие из современных приложений тригонометрии вытекают из использования тригонометрии в исчислении, особенно в тех приложениях, которые имеют дело непосредственно с тригонометрическими функциями. Итак, мы должны использовать радиан, когда думаем о триггерах с точки зрения триггерных функций. В радианах последняя пара уравнений читается как
sin ( θ + 2 π ) = sin θ, иcos ( θ + 2 π ) = cos θ.
- Синус и косинус дополняют друг друга: cos θ = sin ( π /2 — θ )
sin θ = cos ( π /2 — θ )
Мы видели это раньше, но теперь у нас есть это для любого угла θ. Это правда, потому что, когда вы отражаете плоскость через диагональную линию y = x, угол заменяется его дополнением.
- Пифагорейское тождество синусов и косинусов следует непосредственно из определения.
 Поскольку точка B лежит на единичной окружности, ее координаты x и y удовлетворяют уравнению x 2 + y 2 = 1. Но координаты — это косинус и синус, поэтому делаем вывод sin 2 θ + cos 2 θ = 1.
Поскольку точка B лежит на единичной окружности, ее координаты x и y удовлетворяют уравнению x 2 + y 2 = 1. Но координаты — это косинус и синус, поэтому делаем вывод sin 2 θ + cos 2 θ = 1.Теперь мы готовы рассмотреть синус и косинус как функции.
- Синус — нечетная функция, а косинус — четная функция.Возможно, вы не встречали этих прилагательных «нечетный» и «четный» применительно к функциям, но их важно знать. Функция f называется нечетной функцией , если для любого числа x, f (- x ) = — f ( x ). Функция f называется функцией четных , если для любого числа x, f (- x ) = f ( x ). Большинство функций не являются ни нечетными, ни четными, но некоторые из наиболее важных функций являются теми или иными.Любой многочлен только с членами нечетной степени является нечетной функцией, например, f ( x ) = x 5 + 8 x 3 -2 x.
 (Обратите внимание, что все степени x являются нечетными числами.) Точно так же любой многочлен только с членами четной степени является четной функцией. Например, f ( x ) = x 4 — 3 x 2 — 5. (Константа 5 равна 5 x 0 , а 0 — четное число.)
(Обратите внимание, что все степени x являются нечетными числами.) Точно так же любой многочлен только с членами четной степени является четной функцией. Например, f ( x ) = x 4 — 3 x 2 — 5. (Константа 5 равна 5 x 0 , а 0 — четное число.)Синус — нечетная функция, а косинус — четная
sin (- θ ) = –sin θ, иcos (- θ ) = cos θ.
Эти факты вытекают из симметрии единичной окружности относительно оси x . Угол — т. — тот же угол, что и т. , за исключением того, что он находится с другой стороны оси x . Переворачивание точки ( x, y ) на другую сторону оси x превращается в ( x, –y ), поэтому координата y инвертируется, то есть синус инвертируется , но координата x осталась прежней, то есть косинус не изменился.
- Очевидным свойством синусов и косинусов является то, что их значения лежат в диапазоне от –1 до 1.
 Каждая точка на единичной окружности находится на расстоянии 1 единицы от начала координат, поэтому координаты любой точки также находятся в пределах 1 от 0.
Каждая точка на единичной окружности находится на расстоянии 1 единицы от начала координат, поэтому координаты любой точки также находятся в пределах 1 от 0.
Графики функций синуса и косинуса
Давайте возьмем t как переменный угол. Вы можете думать о t и как об угле, и как о времени. Для людей хороший способ понять функцию — это посмотреть на ее график.Начнем с графика sin t. Возьмите горизонтальную ось за ось t (а не за ось x , как обычно), возьмите вертикальную ось за ось y и изобразите уравнение y = sin t . Похоже на это. Во-первых, заметим, что он периодичен с периодом 2 π . Геометрически это означает, что если вы возьмете кривую и сдвинете ее 2 π влево или вправо, кривая снова упадет на себя.Во-вторых, обратите внимание, что график находится в пределах одной единицы оси t . Мало что еще является очевидным, кроме случаев, когда оно увеличивается и уменьшается.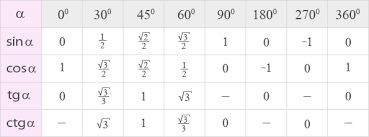 Например, sin t увеличивается от 0 до π /2, поскольку координата y точки B увеличивается с увеличением угла AOB от 0 до π /2.
Например, sin t увеличивается от 0 до π /2, поскольку координата y точки B увеличивается с увеличением угла AOB от 0 до π /2.
Теперь давайте посмотрим на график косинуса. Опять же, возьмите горизонтальную ось за ось t , а теперь возьмите вертикальную ось за ось x и изобразите уравнение x = cos t.
Обратите внимание, что он выглядит так же, как график sin t , за исключением того, что он сдвинут влево на π /2. Это из-за тождества cos t = sin ( π /2 + t ). Хотя мы раньше не сталкивались с этим тождеством, оно легко следует из уже рассмотренных: cos t = cos — t = sin ( π /2 — (- t )) = sin ( π /2 + т ).
Графики функций тангенса и котангенса
График касательной функции имеет вертикальную асимптоту при x = π /2. Это потому, что касательная приближается к бесконечности, когда t приближается к π /2. (На самом деле, она приближается к минус бесконечности, поскольку t приближается к π /2 справа, как вы можете видеть на графике.
(На самом деле, она приближается к минус бесконечности, поскольку t приближается к π /2 справа, как вы можете видеть на графике.Вы также можете видеть, что тангенс имеет период π ; также есть вертикальные асимптоты через каждые π единиц слева и справа.Алгебраически эта периодичность выражается как tan ( t + π ) = tan t.
График котангенса очень похож.
Это сходство просто потому, что котангенс t является тангенсом дополнительного угла π — t.
Графики функций секанса и косеканса
Секанс — это величина, обратная косинусу, а поскольку косинус принимает только значения от –1 до 1, секанс принимает только значения выше 1 или ниже –1, как показано на графике.2x`Изучите анимацию этих функций и их производных здесь:
Интерактивный апплет дифференцирования — тригонометрические функции.
На словах можно сказать:
ВАЖНО:Производная sin x равна cos x ,
Производная cos x равна −sin x (обратите внимание на отрицательный знак!) И
Производная tan x равна sec 2 х .2 + 3)`.2 + 3) `
cos x 2 + 3
не равно
cos ( x 2 + 3).
Кронштейны имеют большое значение. У многих студентов с этим возникают проблемы.
Вот графики y = cos x 2 + 3 (зеленый) и y = cos ( x 2 + 3) (показаны синим).
Первый, y = cos x 2 + 3 или y = (cos x 2 ) + 3, означает взять кривую y = cos x 2 и переместите его на «3» вверх.2sin x`
6. Найдите производную неявной функции
x cos 2 y + sin x cos y = 1.
Ответ
Неявная функция:
`x \ cos 2y + sin x \ cos y = 1`
Мы дифференцируем каждый термин слева направо:
`x (-2 \ sin 2y) ((dy) / (dx))` `+ (cos 2y) (1)` `+ sin x (-sin y (dy) / (dx))` `+ cos у \ соз х`
`= 0`
Так
`(-2x \ sin 2y-sin x \ sin y) ((dy) / (dx))` = -cos 2y-cos y \ cos x`
Решение для dy / dx дает:
`(dy) / (dx) = (- cos 2y-cos y \ cos x) / (- 2x \ sin 2y-sin x \ sin y)`
`= (cos 2y + cos x \ cos y) / (2x \ sin 2y + sin x \ sin y)`
7. 2`
2`
Когда x = 0,15 (конечно, в радианах), это выражение (которое дает нам наклон) равен «-2,65».
Вот график нашей ситуации. Показана касательная к кривой в точке, где x = 0,15. Его наклон равен «-2,65».
8. Ток (в амперах) в цепи усилителя как функция времени t (в секундах) равен
`i = 0.10 cos (120πt + π / 6)`.
Найдите выражение для напряжения на 2.{k-m} \ binom {m} {k} \ phi_ {1/2} (k-1, z) $$
Мы интерполируем от первой целой точки, где значение является действительным, то есть от x = -1.
Теперь мы получаем аппроксимацию другого полупотока cos x, взяв arccos на вышеуказанную функцию:
$$ \ phi_ {2} (x, z) = \ arccos (\ phi_ {1} (x + 1, z)) $$
Мы знаем, что поток cos (x) должен совпадать с первой функцией в четных целых числах и со второй функцией в нечетных целых числах.
Итак, мы делаем заглушку потока, следуя этим знаниям (мы также хотим, чтобы его абсолютное значение было монотонным). {[n]} (\ phi (x + n, z)) $$
{[n]} (\ phi (x + n, z)) $$
Численно этот предел сходится довольно быстро. Если предел существует, он по определению удовлетворяет уравнению
$$ \ cos (\ Phi (x, z)) = \ Phi (x + 1, z) $$
так что это правда сток.
Сказанное выше можно проиллюстрировать графическим изображением:
Здесь верхний полупоток (поток cos (cos z))) синий, нижний полупоток красный, реальная часть потока желтая, воображаемая часть потока зеленая. Все потоки принимаются за точку z = 1.
После этого мы можем построить график полу-итерации косинуса $ \ Phi (1/2, z) $:
Здесь синий — действительная часть, а красный — мнимая часть.
Мы можем проверить, что полу-итерация повторяется дважды $ \ Phi (1/2, \ Phi (1/2, z)) $ (синий) довольно хорошо следует за косинусом (красный) на положительных полупериодах и в любом месте конуса положительно (то есть на мнимой оси тоже):
Я думаю, это совпадает с ответом Джеральда Эдгара выше. Модифицированная функция, повторенная дважды, дает косинус по всем действительным осям:
Модифицированная функция, повторенная дважды, дает косинус по всем действительным осям:
Это истинная половина итерация косинуса, которая работает по всей действительной оси, производя точно косинус:
Но, как было отмечено выше Джоэлом Дэвидом Хэмкинсом, существует бесконечное количество таких решений, ни одно из которых не работает для всех комплексных чисел.
Эту функцию можно рассматривать как истинное решение на комплексной плоскости, если ее интерпретировать как многозначную функцию.(х + 1) + 1) / 2) FL [x_, z_]: = Nest [ArcCos, Flow2 [x + a, z], a] График [{Semi1 [x, 1], Semi2 [x, 1], Re [FL [x, 1]], Im [FL [x, 1]]}, {x, -5, 5}, AspectRatio -> Automatic, PlotRange -> 3] График [{Re [FL [0,5, x]], Im [FL [0,5, x]]}, {x, -5, 5}, AspectRatio -> Automatic, PlotRange -> 3] График [{Re [FL [0,5, FL [0,5, x]]], Cos [x]}, {x, -5, 5}, AspectRatio -> Automatic, PlotRange -> 3] HalfCos [z_]: = Если [Im [z] == 0, Знак [Re [Cos [z]]]] * FL [0,5, z], Знак [Re [z]] * FL [0,5, z]] График [{Re [HalfCos [x]], Im [HalfCos [x]]}, {x, -5, 5}, AspectRatio -> Automatic, PlotRange -> 3] График [{Re [HalfCos [HalfCos [x]]], Cos [x]}, {x, -5, 5}, AspectRatio -> Automatic, PlotRange -> 3] Расчет
— Рассмотрим функцию g (x) = cos (f (x)) и ее производную.
 Как g ′ (x) и f ′ (x) связаны друг с другом? исчисление — Рассмотрим функцию g (x) = cos (f (x)) и ее производную. Как g ′ (x) и f ′ (x) связаны друг с другом? — Обмен математическими стеками
Как g ′ (x) и f ′ (x) связаны друг с другом? исчисление — Рассмотрим функцию g (x) = cos (f (x)) и ее производную. Как g ′ (x) и f ′ (x) связаны друг с другом? — Обмен математическими стекамиСеть обмена стеков
Сеть Stack Exchange состоит из 177 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
Посетить Stack Exchange- 0
- +0
- Авторизоваться Зарегистрироваться
Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях. Регистрация займет всего минуту.
Регистрация займет всего минуту.
Кто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 250 раз
$ \ begingroup $Найти производную функции:
$$ f (x) = \ left (\ arccos \ left (\ sqrt {1-x ^ 2} \ right) \ right) $$
Хорошо, для этого я бы использовал правило цепочки, чтобы получить $ f ‘(x) = \ frac {x} {\ sqrt {x ^ 2} \ sqrt {1-x ^ 2}} $
Однако вопрос говорит так:
Подсказка: рассмотрите функцию $ g (x) = cos (f (x)) $ и ее производную. Как связаны друг с другом $ g ‘(x) $ и $ f’ (x) $?
Как связаны друг с другом $ g ‘(x) $ и $ f’ (x) $?
Я не понимаю этой части, что они означают? Означает ли это, что я не могу использовать цепное правило для получения производной?
Создан 22 окт.
Наочи11777 бронзовых знаков
$ \ endgroup $ 2 $ \ begingroup $Хорошо, это глупо, но я думаю, что это то, что ваш вопрос «пытается» показать.2}}. $$ Полагаю, преимущество состоит в том, чтобы показать, что вы можете решить проблему, не зная явно, как различать $ \ arccos {x} $.
Создан 22 окт. 2}
2}
Теперь найдите $ g ‘(x) $ и сравните его со своим $ f’ (x) $
Создан 22 окт.
$ \ endgroup $ $ \ begingroup $Я полагаю, они имеют в виду неявную дифференциацию.2}}. \ End {align} $$
Создан 22 окт.
Фаррухота29.6k22 золотых знака1515 серебряных знаков4848 бронзовых знаков
$ \ endgroup $ $ \ begingroup $$$ f (x) = \ arccos \ left (\ sqrt {1-x ^ 2} \ right) $$ $$ \ sqrt {1-x ^ 2} = \ cos \ left (f (x) \ right) $$ так: $$ g (x) = \ sqrt {1-x ^ 2} $$ $$ g ‘(x) = \ frac {x} {\ sqrt {1-x ^ 2}} $$ так: $$ \ frac {x} {\ sqrt {1-x ^ 2}} = — f ‘(x) \ sin \ left (f (x) \ right) $$
Создан 22 окт.
10.2k33 золотых знака1010 серебряных знаков2828 бронзовых знаков
$ \ endgroup $ Mathematics Stack Exchange лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie Настроить параметры
Дифференциальная топология.
 Докажите, что существует гладкое отображение $ g \ Colon R \ to R $ такое, что $ f (\ cos (t), \ sin (t)) = (\ cos (g (t)), \ sin (g (t))) $ и такое, что $ g (2π) = g (0) +2 \ pi q $.
Докажите, что существует гладкое отображение $ g \ Colon R \ to R $ такое, что $ f (\ cos (t), \ sin (t)) = (\ cos (g (t)), \ sin (g (t))) $ и такое, что $ g (2π) = g (0) +2 \ pi q $.Возьмите конкретное значение $ t $; вычислить $ (\ cos (t), \ sin (t)) $. Оцените $ f $ в этой точке, чтобы получить новую точку $ (\ cos u, \ sin u) $, где $ u $ определяется только с точностью, кратной $ 2 \ pi $. Теперь предварительно определим $ g (t) = u $. Это дает определение, но оно не обязательно непрерывно, верно? (Или гладкий). Но это основная идея: $ g (t) $ — это угол для $ f (\ cos t, \ sin t) $. А $ q $ — это целое число, которое вам, возможно, придется добавить, чтобы все работало гладко в конечных точках интервала.1: x \ to (\ cos x, \ sin x) $ — универсальное накрывающее отображение. (Это из-за теоремы о подъеме пути.)
Теперь составьте $ H $ с картой $ u \ mapsto u \ bmod 2 \ pi $, чтобы получить карту
$$
K: I \ к \ mathbb R: u \ mapsto H (u \ bmod 2 \ pi)
$$
которое, очевидно, тоже непрерывно. $ K $ — это карта $ g $, которую вы ищете.
$ K $ — это карта $ g $, которую вы ищете.
Теперь вам нужно показать, что все работает хорошо, но это довольно просто. Число $ 2 \ pi q $, которое вы ищете, — это просто $ H (2 \ pi) — H (0) $, которое является целым кратным $ 2 \ pi $ из-за выводов теоремы о подъеме пути, одно из которых состоит в том, что $ p (H (0)) = p (H (2 \ pi)) $.
Для сглаживания у вас есть несколько карт, которые являются композициями друг друга, и две из каждых трех известны как сглаженные; Нетрудно сделать вывод, что и третье тоже.
.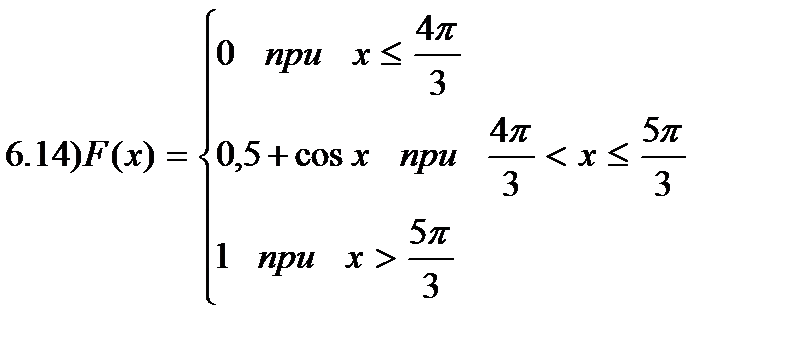





 Величина sin φ для значений φ от 0 до -90° является отрицательной величиной
Величина sin φ для значений φ от 0 до -90° является отрицательной величиной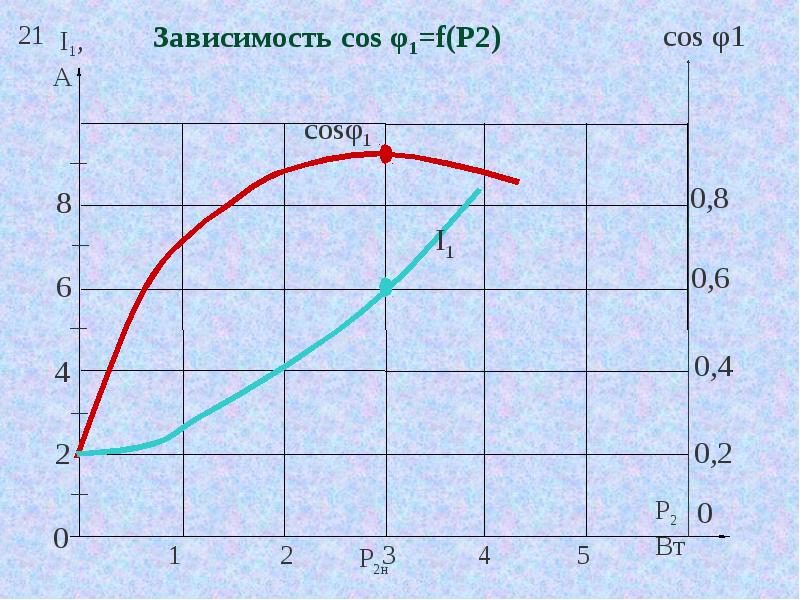

 »»»»Теплый свет лампы
»»»»Холодный свет лампы
»»»Аналоги ламп накаливания до 100 Вт.
»»»»Теплый свет лампы
»»»»Холодный свет лампы
»»»Аналоги ламп накаливания до 500 Вт.
»»»»Теплый свет лампы
»»Лампы накаливания
»»Лампы люминесцентные
»»»Лампы Т4 люминесцентные
»»»Лампы Т5 люминесцентные
»»»Лампы Т8 люминесцентные
»»Лампы галогенные
»»»Лампы галогенные декоративные
»»»Лампы галогенные G4, GU 5.3, GU10
»»»Блоки защиты галогенных ламп
»»Лампы металлогалогенные
»»Лампы ртутные и натриевые
»Светильники
»»Светодиодные светильники LED
»»»Потолочные светодиодные светильники
»»»»Светодиодный светильник под Армстронг
»»»»Встраиваемые светодиодные светильники
»»»»Накладные светодиодные светильники
»»»»Точечные светодиодные светильники
»»»»Крепления для потолочных светильников
»»»Настольные светодиодные светильники
»»»Прожекторы светодиодные
»»»Светодиодные светильники уличного освещения
»»»Для ЖКХ
»»Для дома
»»»Потолочные светильники, люстры
»»»»Светильники под лампу накаливания
»»»»Люстры
»»»»Люминесцентные светильники
»»»Настенные светильники, бра
»»»»Светильники под лампу накаливания
»»»»Люминесцентные светильники
»»»Ночники
»»»Для ванной и туалета
»»»Для кухни
»»»Точечные светильники
»»»Настольные светильники
»»Светильники лофт
»»Диско шар
»»Для дачи
»»Для теплицы
»»Для бани и сауны
»»Для гаража и подвала
»»Для производства
»»Для офиса
»»Для склада и производства
»»Для улицы
»»»Кронштейны для уличных светильниов
»»Светильники для сада и парка
»»Для подсветки
»»Для спортивного зала
»»Для магазина
»»Переносные светильники
»»Аварийные светильники
»»Аккумуляторные светильники
»»Патроны к светильникам
»Светодиодная подсветка
»»Светодиодная подсветка потолка
»»»Светодиодная гибкая лента для помещений на самоклеющейся основе ULS-3528
»»» Светодиодная гибкая лента для помещений на самоклеющейся основе ULS-5050
»»»Светодиодная гибкая герметичная лента ULS-3528
»»»Светодиодная гибкая герметичная лента ULS-5050
»»»Драйверы для светодиодов
»»»Контроллеры для управления светодиодными источниками света
»»Светодиодная подсветка шкафа
»»Электронные трансформаторы
»Стабилизаторы напряжения
»»Однофазные стабилизаторы напряжения
»»Стабилизаторы напряжения напольные, электронные
»»Стабилизаторы напряжения настенные, релейные
»»Стабилизаторы напряжения настольные
»»Стабилизаторы напряжения электромеханические
»Низковольтная аппаратура
»»Автоматические выключатели
»»»Автоматы для проводов сечением до 25мм.
»»»»Теплый свет лампы
»»»»Холодный свет лампы
»»»Аналоги ламп накаливания до 100 Вт.
»»»»Теплый свет лампы
»»»»Холодный свет лампы
»»»Аналоги ламп накаливания до 500 Вт.
»»»»Теплый свет лампы
»»Лампы накаливания
»»Лампы люминесцентные
»»»Лампы Т4 люминесцентные
»»»Лампы Т5 люминесцентные
»»»Лампы Т8 люминесцентные
»»Лампы галогенные
»»»Лампы галогенные декоративные
»»»Лампы галогенные G4, GU 5.3, GU10
»»»Блоки защиты галогенных ламп
»»Лампы металлогалогенные
»»Лампы ртутные и натриевые
»Светильники
»»Светодиодные светильники LED
»»»Потолочные светодиодные светильники
»»»»Светодиодный светильник под Армстронг
»»»»Встраиваемые светодиодные светильники
»»»»Накладные светодиодные светильники
»»»»Точечные светодиодные светильники
»»»»Крепления для потолочных светильников
»»»Настольные светодиодные светильники
»»»Прожекторы светодиодные
»»»Светодиодные светильники уличного освещения
»»»Для ЖКХ
»»Для дома
»»»Потолочные светильники, люстры
»»»»Светильники под лампу накаливания
»»»»Люстры
»»»»Люминесцентные светильники
»»»Настенные светильники, бра
»»»»Светильники под лампу накаливания
»»»»Люминесцентные светильники
»»»Ночники
»»»Для ванной и туалета
»»»Для кухни
»»»Точечные светильники
»»»Настольные светильники
»»Светильники лофт
»»Диско шар
»»Для дачи
»»Для теплицы
»»Для бани и сауны
»»Для гаража и подвала
»»Для производства
»»Для офиса
»»Для склада и производства
»»Для улицы
»»»Кронштейны для уличных светильниов
»»Светильники для сада и парка
»»Для подсветки
»»Для спортивного зала
»»Для магазина
»»Переносные светильники
»»Аварийные светильники
»»Аккумуляторные светильники
»»Патроны к светильникам
»Светодиодная подсветка
»»Светодиодная подсветка потолка
»»»Светодиодная гибкая лента для помещений на самоклеющейся основе ULS-3528
»»» Светодиодная гибкая лента для помещений на самоклеющейся основе ULS-5050
»»»Светодиодная гибкая герметичная лента ULS-3528
»»»Светодиодная гибкая герметичная лента ULS-5050
»»»Драйверы для светодиодов
»»»Контроллеры для управления светодиодными источниками света
»»Светодиодная подсветка шкафа
»»Электронные трансформаторы
»Стабилизаторы напряжения
»»Однофазные стабилизаторы напряжения
»»Стабилизаторы напряжения напольные, электронные
»»Стабилизаторы напряжения настенные, релейные
»»Стабилизаторы напряжения настольные
»»Стабилизаторы напряжения электромеханические
»Низковольтная аппаратура
»»Автоматические выключатели
»»»Автоматы для проводов сечением до 25мм. »»»»Для дома, характеристика B
»»»»Для дома, характеристика C
»»»»Для производства, характеристика D
»»»Автоматы для проводов сечением до 35мм.
»»»»Для дома, характеристика C
»»»»Для производства, характеристика D
»»»Автоматы для проводов сечением до 50мм.
»»»»Для дома, характеристика C
»»»»Для производства, характеристика D
»»»Автоматы промышленные ВА88
»»УЗО
»»Дифференциальные автоматы
»»»Серия АВДТ 63
»»»Серия АВДТ 64 с защитой
»»»Дифавтоматы АД12, АД14
»»»Серия DX
»»Разрядники, ограничители импульсных перенапряжений
»»Выключатель нагрузки (мини-рубильник)
»»Предохранители
»»»Плавкие вставки цилиндрические ПВЦ
»»»Предохранители автоматические резьбовые ПАР
»»»Предохранители ППНН
»»Контакторы
»»»Контакторы модульные серии КМ63
»»»Контакторы малогабаритные КМН
»»»Контакторы КМН в оболочке IP54
»»Пускатели ручные
»Электроустановочные изделия
»»Выключатели
»»»Выключатели внутренние
»»»Выключатели накладные
»»Розетки
»»»Розетки внутренние
»»»»Серия INARI
»»»»Серия LARIO
»»»»Серия VATTERN
»»»»Серия MELAREN
»»»»Розетки, выключатели Legrand Valena
»»»Розетки накладные
»»»»Серия SUNGARY
»»»»Серия BALATON
»»»»Серия SAIMA
»»Коробки монтажные, подрозетники
»»»Монтажные коробки для открытой проводки
»»»Монтажные коробки для скрытой проводки
»»Удлинители электрические
»»»Удлинители бытовые
»»»Удлинители силовые
»»Сетевые фильтры
»»Тройники электрические
»»Вилки электрические
»»Силовые разъёмы
»»»Вилки переносные
»»»Розетки стационарные
»»»Розетки переносные
»»»Розетки стационарные для скрытой установки
»»»Вилки стационарные
»Щитовое оборудование
»»Корпуса к щитам электрическим
»»»Для помещения
»»»»Пластиковые боксы
»»»»»Боксы пластиковые навесные
»»»»»Боксы пластиковые встраиваемые
»»»»»Бокс КМПн
»»»»Металлические корпуса
»»»»»Щиты распределительные
»»»»»Щиты учётно-распределительные
»»»»»Щиты с монтажной панелью
»»»»»Щиты этажные
»»»»Шкафы напольные
»»»»»Сборно-разборные шкафы
»»»»»Моноблочные шкафы
»»»»»Аксессуары к шкафам
»»»Для улицы IP65
»»Электрощиты в сборе
»»»Ящики с понижающим трансформатором (ЯТП)
»»»Ящики с рубильником и предохранителями (ЯРП)
»»»Ящики с блоком «рубильник-предохранитель» (ЯБПВУ)
»»»Щитки осветительные (ОЩВ)
»»Аксессуры для шкафов и щитов
»»»Шина нулевая
»»»Шина нулевая на DIN-рейку в корпусе
»»»Шина N нулевая с изолятором на DIN-рейку
»»»Шина N нулевая, в изоляторе
»»»Шина N нулевая на угловых изоляторах
»»»Шина соединительная
»»»DIN-рейки
»Фонарики
»»Фонарики налобные
»»Фонари прожекторы
»»Фонари ручные
»»Фонари кемпинговые
»»Фонари с зарядкой от сети
»»Фонари для охоты
»Провод, Кабель
»»Кабель
»»»Кабель медный NYM (3-я изоляция, еврост.
»»»»Для дома, характеристика B
»»»»Для дома, характеристика C
»»»»Для производства, характеристика D
»»»Автоматы для проводов сечением до 35мм.
»»»»Для дома, характеристика C
»»»»Для производства, характеристика D
»»»Автоматы для проводов сечением до 50мм.
»»»»Для дома, характеристика C
»»»»Для производства, характеристика D
»»»Автоматы промышленные ВА88
»»УЗО
»»Дифференциальные автоматы
»»»Серия АВДТ 63
»»»Серия АВДТ 64 с защитой
»»»Дифавтоматы АД12, АД14
»»»Серия DX
»»Разрядники, ограничители импульсных перенапряжений
»»Выключатель нагрузки (мини-рубильник)
»»Предохранители
»»»Плавкие вставки цилиндрические ПВЦ
»»»Предохранители автоматические резьбовые ПАР
»»»Предохранители ППНН
»»Контакторы
»»»Контакторы модульные серии КМ63
»»»Контакторы малогабаритные КМН
»»»Контакторы КМН в оболочке IP54
»»Пускатели ручные
»Электроустановочные изделия
»»Выключатели
»»»Выключатели внутренние
»»»Выключатели накладные
»»Розетки
»»»Розетки внутренние
»»»»Серия INARI
»»»»Серия LARIO
»»»»Серия VATTERN
»»»»Серия MELAREN
»»»»Розетки, выключатели Legrand Valena
»»»Розетки накладные
»»»»Серия SUNGARY
»»»»Серия BALATON
»»»»Серия SAIMA
»»Коробки монтажные, подрозетники
»»»Монтажные коробки для открытой проводки
»»»Монтажные коробки для скрытой проводки
»»Удлинители электрические
»»»Удлинители бытовые
»»»Удлинители силовые
»»Сетевые фильтры
»»Тройники электрические
»»Вилки электрические
»»Силовые разъёмы
»»»Вилки переносные
»»»Розетки стационарные
»»»Розетки переносные
»»»Розетки стационарные для скрытой установки
»»»Вилки стационарные
»Щитовое оборудование
»»Корпуса к щитам электрическим
»»»Для помещения
»»»»Пластиковые боксы
»»»»»Боксы пластиковые навесные
»»»»»Боксы пластиковые встраиваемые
»»»»»Бокс КМПн
»»»»Металлические корпуса
»»»»»Щиты распределительные
»»»»»Щиты учётно-распределительные
»»»»»Щиты с монтажной панелью
»»»»»Щиты этажные
»»»»Шкафы напольные
»»»»»Сборно-разборные шкафы
»»»»»Моноблочные шкафы
»»»»»Аксессуары к шкафам
»»»Для улицы IP65
»»Электрощиты в сборе
»»»Ящики с понижающим трансформатором (ЯТП)
»»»Ящики с рубильником и предохранителями (ЯРП)
»»»Ящики с блоком «рубильник-предохранитель» (ЯБПВУ)
»»»Щитки осветительные (ОЩВ)
»»Аксессуры для шкафов и щитов
»»»Шина нулевая
»»»Шина нулевая на DIN-рейку в корпусе
»»»Шина N нулевая с изолятором на DIN-рейку
»»»Шина N нулевая, в изоляторе
»»»Шина N нулевая на угловых изоляторах
»»»Шина соединительная
»»»DIN-рейки
»Фонарики
»»Фонарики налобные
»»Фонари прожекторы
»»Фонари ручные
»»Фонари кемпинговые
»»Фонари с зарядкой от сети
»»Фонари для охоты
»Провод, Кабель
»»Кабель
»»»Кабель медный NYM (3-я изоляция, еврост. )
»»»Кабель медный силовой ВВГ-нг
»»»Кабель медный силовой ВВГ
»»»Кабель алюминиевый АВВГ, АВВГп
»»»Кабель бронированный
»»Провод
»»»Провод медный
»»»Провод медный осветительный ПУНП, ПУГНП
»»»Провод монтажный
»»»Провод медный гибкий соединительный ПВС
»»»Провод медный гибкий соединительный ШВВП (ПГВВП)
»»»Провод медный установочный ПВ
»»»Провод водопогружной ( ВВП)
»»»Провод алюминиевый
»»»Провод телефонный
»»»Провод ВВП
»Звонки дверные
»»Звонки беспроводные
»»»1 звонок + 1 кнопка
»»»1 звонок + 2 кнопки
»»»2 звонка + 1 кнопка
»»»1 звонок (вилка 220В) + 1кнопка (батарейка А23)
»»Звонки проводные
»Системы для прокладки кабеля
»»Кабельные каналы
»»Гофрированные трубы
»»»Аксессуары для труб
»»Металлорукав
»»»Аксессуары для металлорукава
»»»Металлорукав в ПВХ-изоляции
»»Труба ПВХ
»»»Аксессуары для труб
»»Лотки металлические
»Климатическое оборудование
»»Тепловые пушки и вентиляторы
»»»Тепловые пушки
»»»Масляные радиаторы
»»»Тепловентиляторы электрические
»»»»Керамические обогреватели
»»»»Спиральные обогреватели
»»Охлаждаемся, климатическое оборудование
»»»Кондиционеры напольные
»Инструмент, расходные материалы
»»Инструмент
»»Изоляция
»»»Термоусаживаемая трубка ТУТнг
»»»Изолента
»»Клеммы, зажимы
»»»Строительно-монтажная клемма КБМ
»»»Зажим винтовой ЗВИ
»»»Соединительный изолирующий зажим СИЗ
»»Хомуты, скобы
»»»Лента спиральная монтажная пластиковая ЛСМ
»»»Хомут нейлон
»»»Хомут полиамид
»»»Кабельный хомут с горизонтальным замком
»»»Скоба плоская
»»»Скоба круглая
»Умный дом
»»Датчики движения
»»Дистанционное управление
»»Фотореле
)
»»»Кабель медный силовой ВВГ-нг
»»»Кабель медный силовой ВВГ
»»»Кабель алюминиевый АВВГ, АВВГп
»»»Кабель бронированный
»»Провод
»»»Провод медный
»»»Провод медный осветительный ПУНП, ПУГНП
»»»Провод монтажный
»»»Провод медный гибкий соединительный ПВС
»»»Провод медный гибкий соединительный ШВВП (ПГВВП)
»»»Провод медный установочный ПВ
»»»Провод водопогружной ( ВВП)
»»»Провод алюминиевый
»»»Провод телефонный
»»»Провод ВВП
»Звонки дверные
»»Звонки беспроводные
»»»1 звонок + 1 кнопка
»»»1 звонок + 2 кнопки
»»»2 звонка + 1 кнопка
»»»1 звонок (вилка 220В) + 1кнопка (батарейка А23)
»»Звонки проводные
»Системы для прокладки кабеля
»»Кабельные каналы
»»Гофрированные трубы
»»»Аксессуары для труб
»»Металлорукав
»»»Аксессуары для металлорукава
»»»Металлорукав в ПВХ-изоляции
»»Труба ПВХ
»»»Аксессуары для труб
»»Лотки металлические
»Климатическое оборудование
»»Тепловые пушки и вентиляторы
»»»Тепловые пушки
»»»Масляные радиаторы
»»»Тепловентиляторы электрические
»»»»Керамические обогреватели
»»»»Спиральные обогреватели
»»Охлаждаемся, климатическое оборудование
»»»Кондиционеры напольные
»Инструмент, расходные материалы
»»Инструмент
»»Изоляция
»»»Термоусаживаемая трубка ТУТнг
»»»Изолента
»»Клеммы, зажимы
»»»Строительно-монтажная клемма КБМ
»»»Зажим винтовой ЗВИ
»»»Соединительный изолирующий зажим СИЗ
»»Хомуты, скобы
»»»Лента спиральная монтажная пластиковая ЛСМ
»»»Хомут нейлон
»»»Хомут полиамид
»»»Кабельный хомут с горизонтальным замком
»»»Скоба плоская
»»»Скоба круглая
»Умный дом
»»Датчики движения
»»Дистанционное управление
»»Фотореле

 0));
// обработка ошибок
feclearexcept (FE_ALL_EXCEPT);
printf ("cos (БЕСКОНЕЧНОСТЬ) =% f \ n", cos (БЕСКОНЕЧНОСТЬ));
if (fetestexcept (FE_INVALID)) put ("FE_INVALID поднят");
}
0));
// обработка ошибок
feclearexcept (FE_ALL_EXCEPT);
printf ("cos (БЕСКОНЕЧНОСТЬ) =% f \ n", cos (БЕСКОНЕЧНОСТЬ));
if (fetestexcept (FE_INVALID)) put ("FE_INVALID поднят");
} 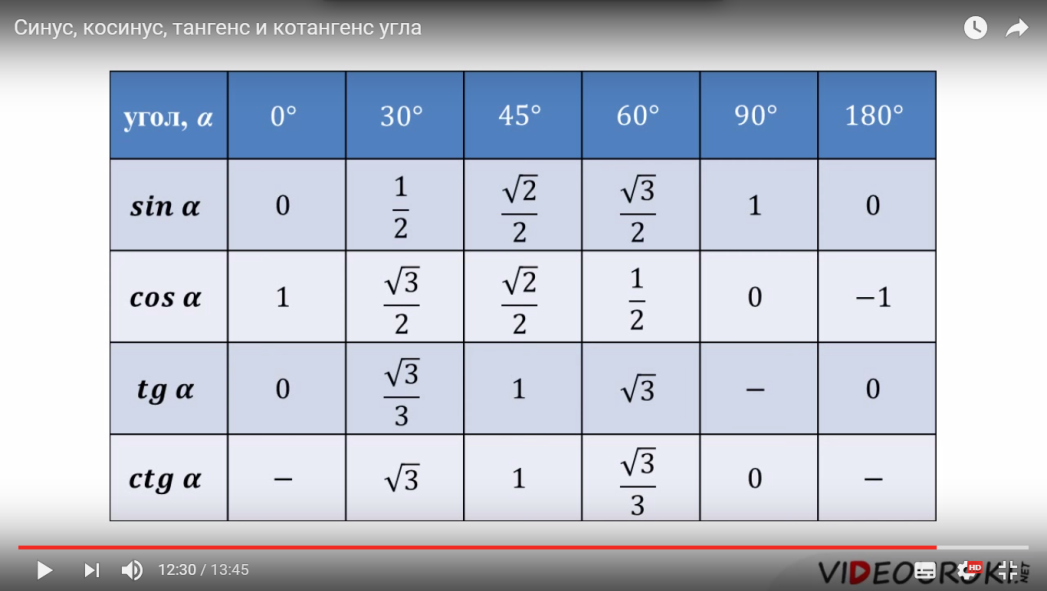 1.5 Функции cos (стр: 456)
1.5 Функции cos (стр: 456)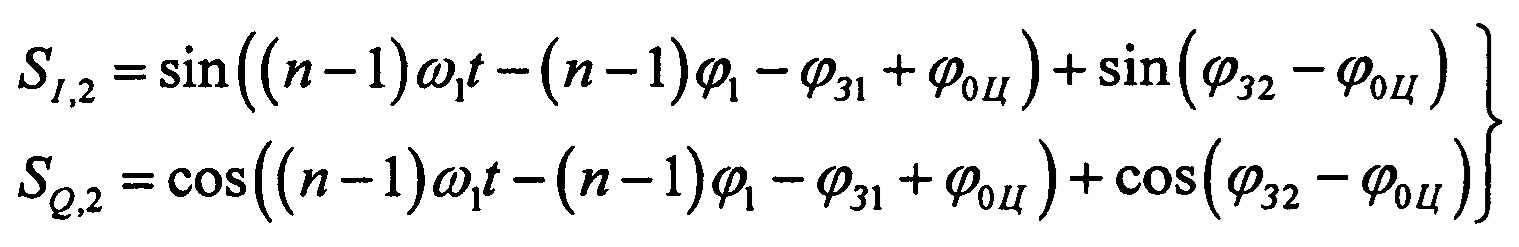 Таким образом, для любого угла θ , sin ( θ + 360 °) = sin θ, и
Таким образом, для любого угла θ , sin ( θ + 360 °) = sin θ, и Поскольку точка B лежит на единичной окружности, ее координаты x и y удовлетворяют уравнению x 2 + y 2 = 1. Но координаты — это косинус и синус, поэтому делаем вывод sin 2 θ + cos 2 θ = 1.
Поскольку точка B лежит на единичной окружности, ее координаты x и y удовлетворяют уравнению x 2 + y 2 = 1. Но координаты — это косинус и синус, поэтому делаем вывод sin 2 θ + cos 2 θ = 1. (Обратите внимание, что все степени x являются нечетными числами.) Точно так же любой многочлен только с членами четной степени является четной функцией. Например, f ( x ) = x 4 — 3 x 2 — 5. (Константа 5 равна 5 x 0 , а 0 — четное число.)
(Обратите внимание, что все степени x являются нечетными числами.) Точно так же любой многочлен только с членами четной степени является четной функцией. Например, f ( x ) = x 4 — 3 x 2 — 5. (Константа 5 равна 5 x 0 , а 0 — четное число.) Каждая точка на единичной окружности находится на расстоянии 1 единицы от начала координат, поэтому координаты любой точки также находятся в пределах 1 от 0.
Каждая точка на единичной окружности находится на расстоянии 1 единицы от начала координат, поэтому координаты любой точки также находятся в пределах 1 от 0. 2 + 3)`.2 + 3) `
2 + 3)`.2 + 3) `