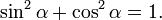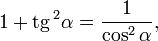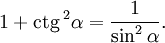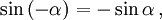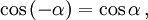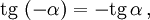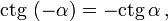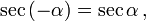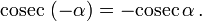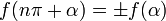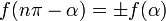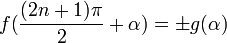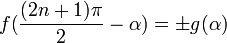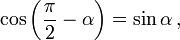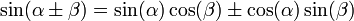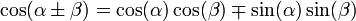Косинус — это… Что такое Косинус?

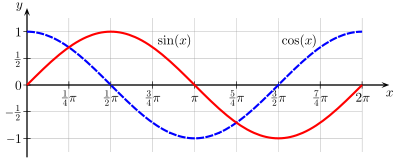
Рис. 1
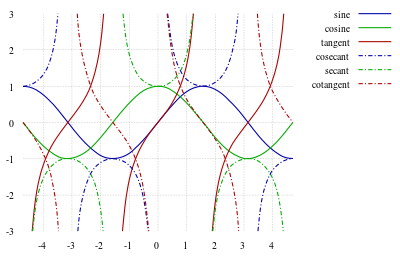
Графики тригонометрических функций: синуса, косинуса, тангенса, секанса, косеканса, котангенса
Тригонометрические функции — вид элементарных функций. Обычно к ним относят синус (sin x), косинус (cos x), тангенс (tg x), котангенс (ctg x), секанс (sec x) и косеканс (cosec x), последняя пара функций в настоящее время сравнительно малоупотребительна (про ещё менее употребляемые функции см. здесь). В англоязычной литературе тангенс, котангенс и косеканс обозначаются tan x, cot x, csc x. Обычно тригонометрические функции определяются геометрически, но можно определить их аналитически через суммы рядов или как решения некоторых дифференциальных уравнений, что позволяет расширить область определения этих функций на комплексные числа.
Способы определения
Геометрическое определение
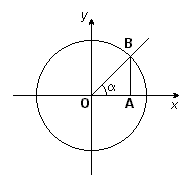
Рис. 2
Определение тригонометрических функций
Обычно тригонометрические функции определяются геометрически. Пусть дана декартова система координат на плоскости и построена окружность радиуса R с центром в начале координат O. Будем измерять углы как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначим xB, ординату обозначим yB (см. рисунок.)
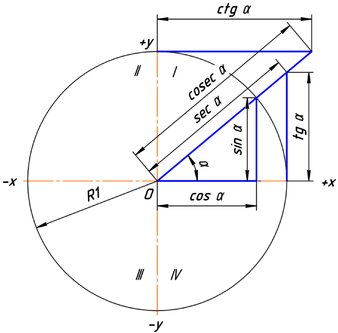
Рис. 3.
Ясно, что значения тригонометрических функций не зависят от величины радиуса окружности R в силу свойств подобных фигур. Часто этот радиус принимают равным величине единичного отрезка, тогда синус равен просто ординате yB, а косинус — абсциссе xB. На рисунке 3 показаны величины тригонометрических функций для единичной окружности.
Если α — действительное число, то синусом α в математическом анализе называется синус угла, радианная мера которого равна α, аналогично для прочих тригонометрических функций.
Определение тригонометрических функций для острых углов
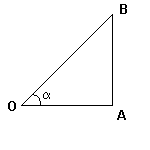
Рис. 4.
Тригонометрические функции острого угла
Во многих учебниках элементарной геометрии до настоящего времени тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника. Пусть OAB — треугольник с углом α. Тогда:
- Синусом α называется отношение AB/OB (противолежащего катета к гипотенузе)
- Косинусом α называется отношение ОА/OB (прилежащего катета к гипотенузе)
- Тангенсом α называется отношение AB/OA (отношение противолежащего катета к прилежащему)
- Котангенсом α называется отношение ОА/AB (отношение прилежащего катета к противолежащему)
- Секансом α называется отношение ОB/OA (гипотенузы к прилежащему катету)
- Косекансом α называется отношение ОB/AB (гипотенузы к противолежащему катету)
Построив систему координат с началом в точке O, направлением оси абсцисс вдоль OA и в случае необходимости изменив ориентацию (перевернув) треугольник так, чтобы он находился в первой четверти системы координат, и затем, построив окружность с радиусом, равным гипотенузе, сразу находим, что такое определение функций приводит к тому же результату, что и предыдущее. Данное определение имеет некоторое педагогическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач про тупоугольные треугольники (см. Теорема синусов, Теорема косинусов).
Определение тригонометрических функций как решений дифференциальных уравнений
Функции косинус и синус можно определить как чётное (косинус) и нечётное (синус) решение дифференциального уравнения
с начальными условиями cos(0) = sin'(0) = 1, то есть как функций одной переменной, вторая производная которых равна самой функции, взятой со знаком минус:
Определение тригонометрических функций как решений функциональных уравнений
Функции косинус и синус можно определить как непрерывные решения (f и g соответственно) системы функциональных уравнений: 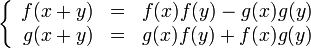
Определение тригонометрических функций через ряды
Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу и что производная косинуса равна минус синусу. Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде суммы степенны́х рядов:
Пользуясь этими формулами, а также уравнениями 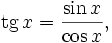
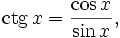
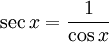 и
и 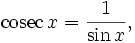 можно найти разложения в ряд Тейлора и других тригонометрических функций:
можно найти разложения в ряд Тейлора и других тригонометрических функций:
 где Bn — числа Бернулли.
где Bn — числа Бернулли. где En — числа Эйлера.
где En — числа Эйлера.
Значения тригонометрических функций для некоторых углов
Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице.
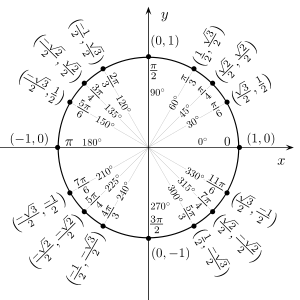
Значения косинуса и синуса на окружности.
Значения тригонометрических функций нестандартных углов
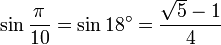
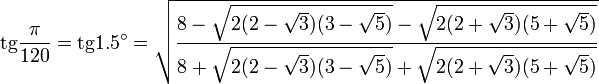
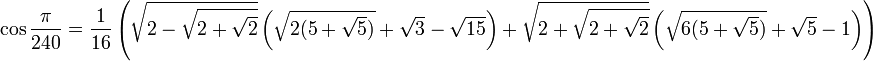
Свойства тригонометрических функций
Простейшие тождества
Так как синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α то, согласно уравнению единичной окружности или теореме Пифагора, имеем:
Деля это уравнение на квадрат косинуса и синуса соответственно имеем далее:
Чётность
Косинус и секанс — чётные. Остальные четыре функции — нечётные, то есть:
Периодичность
Функции y = sin α, y = cos α, y = sec α, y = cosec α — периодические с периодом 2π. Функции: y = tg α, y = ctg α — c периодом π
Формулы приведения
Здесь f — любая тригонометрическая функция, g — соответствующая ей другая функция из пары (то есть косинус для синуса, синус для косинуса и аналогично для остальных функций). Нужный знак в правой части равенства определяется следующим образом: предположим что угол α находится в первой четверти, тогда определяем знаки значений функций в левой и правой части равенства и в случае их несовпадения перед правой частью пишем знак -, например:
Формулы сложения
Другие тригонометрические тождества.
Однопараметрическое представление
Все тригонометрические функции можно выразить через тангенс половинного угла.
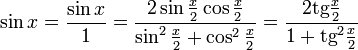
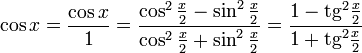
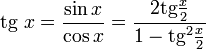
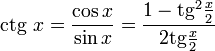
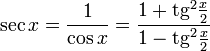
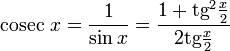
Производные и интегралы
Все тригонометрические функции непрерывно дифференцируемы на всей области определения:
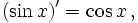
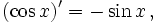
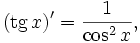
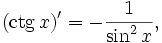
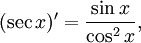
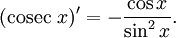
Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом:
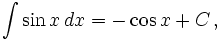
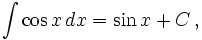
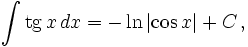
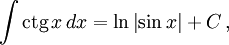
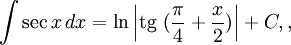
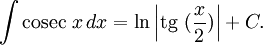
- См. также Список интегралов от тригонометрических функций
История
Линия синуса у индийских математиков первоначально называлась «арха-джива» («полутетива»), затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские переводчики не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали арабскими буквами и стали называть линию синуса «джиба». Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.
Современное обозначение синуса sin и косинуса cos введено Леонардом Эйлером в XVIII веке.
Термины «тангенс» (от лат. tangens — касающийся) и «секанс» (лат. secans — секущий) были введены датским математиком Томасом Финке (1561—1656) в его книге «Геометрия круглого» (Geometria rotundi, 1583)
Сам термин тригонометрические функции введён Клюгелем в 1770.
См. также
Ссылки
Wikimedia Foundation. 2010.
Тригонометричні функції — Вікіпедія
Матеріал з Вікіпедії — вільної енциклопедії.
Тригонометри́чні фу́нкції — функції кута. Вони можуть бути визначені як відношення двох сторін та кута трикутника або як відношення координат точок кола. Відіграють важливу роль при дослідженні періодичних функцій та багатьох об’єктів. Наприклад, при дослідженні рядів, диференційних рівнянь.
Наведемо шість базових тригонометричних функцій. Останні чотири визначаються через перші дві. Іншими словами, вони є означеннями, а не самостійними сутностями.
- синус (sin α)
- косинус (cos α)
- тангенс (tg α = sin α / cos α)
- котангенс (ctg α = cos α / sin α)
- секанс (sec α = 1 / cos α)
- косеканс (cosec α = 1 / sin α)
Геометричне визначення[ред. | ред. код]
 Визначення кутів за допомогою прямокутного трикутника.
Визначення кутів за допомогою прямокутного трикутника. 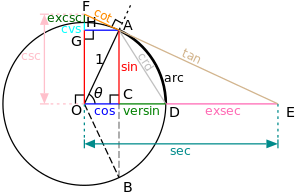 Визначення тригонометричних функцій на одиничному колі.
Визначення тригонометричних функцій на одиничному колі.Тригонометричні функції можна визначити розглянувши прямокутний трикутник.
Косинусом кута називається відношення довжини прилеглого катета до довжини гіпотенузи:
- cosα=ACAB=bc, cosβ=BCAB=ac .{\displaystyle \cos \alpha ={\frac {AC}{AB}}={\frac {b}{c}},~~~\cos \beta ={\frac {BC}{AB}}={\frac {a}{c}}~.}
Синусом кута називається відношення довжини протилежного катета до довжини гіпотенузи:
- sinα=BCAB=ac, sinβ=ACAB=bc .{\displaystyle \sin \alpha ={\frac {BC}{AB}}={\frac {a}{c}},~~~\sin \beta ={\frac {AC}{AB}}={\frac {b}{c}}~.}
Тангенсом кута називається відношення довжини протилежного катета до довжини прилеглого катета:
- tg α=BCAC=ab, tg β=ACBC=ba .{\displaystyle {\mbox{tg}}~\alpha ={\frac {BC}{AC}}={\frac {a}{b}},~~~{\mbox{tg}}~\beta ={\frac {AC}{BC}}={\frac {b}{a}}~.}
Котангенсом кута називається відношення довжини прилеглого катета до довжини протилежного катета:
- ctg α=ACBC=ba, ctg β=BCAC=ab .{\displaystyle {\mbox{ctg}}~\alpha ={\frac {AC}{BC}}={\frac {b}{a}},~~~{\mbox{ctg}}~\beta ={\frac {BC}{AC}}={\frac {a}{b}}~.}
Аналогічним чином можна визначити тригонометричні функції на колі з одиничним радіусом.
sinx{\displaystyle \sin \,x} та cosx{\displaystyle \cos \,x} це періодичні функції із періодом 2π,{\displaystyle \ 2\pi ,}
tgx{\displaystyle \operatorname {tg} \,x} та ctgx{\displaystyle \operatorname {ctg} \,x} мають період π.{\displaystyle \ \pi .}
Співвідношення, наведені нижче, дозволяють виразити значення тригонометричних функцій від довільного дійсного арґументу через значення функцій для аргументу із інтервалу [0,π2]{\displaystyle [0,{\pi \over 2}]}
- sinx=cos(π2−x){\displaystyle \sin x=\cos \left({\pi \over 2}-x\right)}
- cosx=sin(π2−x){\displaystyle \cos x=\sin \left({\pi \over 2}-x\right)}
- tgx=ctg(π2−x){\displaystyle \operatorname {tg} x=\operatorname {ctg} \left({\pi \over 2}-x\right)}
- ctgx=tg(π2−x){\displaystyle \operatorname {ctg} x=\operatorname {tg} \left({\pi \over 2}-x\right)}
Основні співвідношення[ред. | ред. код]
Наступне співвідношення випливає із теореми Піфагора:
- sin2x+cos2x=1{\displaystyle ~\sin ^{2}x+\cos ^{2}x=1}
Теореми додавання та формули для кратних кутів[ред. | ред. код]
Формули для функцій суми кутів[ред. | ред. код]
Із основного співвідношення
- sin(α+β)=sinαcosβ+cosαsinβ{\displaystyle \sin {\left(\alpha +\beta \right)}=\sin \alpha \cos \beta +\cos \alpha \sin \beta }
отримуємо
| sin(α±β)=sinαcosβ±cosαsinβ,{\displaystyle \sin {\left(\alpha \pm \beta \right)}=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta ,} |
| cos(α±β)=cosαcosβ∓sinαsinβ,{\displaystyle \cos {\left(\alpha \pm \beta \right)}=\cos \alpha \cos \beta \mp \sin \alpha \sin \beta ,} |
| tg(α±β)=tgα±tgβ1∓tgαtgβ, ctg(α±β)=ctgαctgβ∓1ctgβ±ctgα{\displaystyle \operatorname {tg} {\left(\alpha \pm \beta \right)}={{\operatorname {tg} \alpha \pm \operatorname {tg} \beta } \over {1\mp \operatorname {tg} \alpha \operatorname {tg} \beta }},~~~\operatorname {ctg} {\left(\alpha \pm \beta \right)}={{\operatorname {ctg} \alpha \operatorname {ctg} \beta \mp 1} \over {\operatorname {ctg} \beta \pm \operatorname {ctg} \alpha }}} |
Формули для функцій подвійних кутів[ред. | ред. код]
| sin2α=2sinαcosα{\displaystyle \sin {2\alpha }=2\sin \alpha \cos \alpha } |
| cos2α=cos2α−sin2α=2cos2α−1=1−2sin2α{\displaystyle \cos {2\alpha }=\cos ^{2}\alpha -\sin ^{2}\alpha =2\cos ^{2}\alpha -1=1-2\sin ^{2}\alpha } |
| tg2α=2tgα1−tg2α , ctg2α=ctg2α−12ctgα=12(ctgα−tgα){\displaystyle \operatorname {tg} {2\alpha }={{2\operatorname {tg} \alpha } \over {1-\operatorname {tg} ^{2}\alpha }}~,~~~\operatorname {ctg} {2\alpha }={{\operatorname {ctg} ^{2}\alpha -1} \over {2\operatorname {ctg} \alpha }}={1 \over 2}{\left(\operatorname {ctg} \alpha -\operatorname {tg} \alpha \right)}} |
Формули для функцій потрійних кутів[ред. | ред. код]
| sin3α=3sinα−4sin3α , cos3α=4cos3α−3cosα{\displaystyle \sin {3\alpha }=3\sin \alpha -4\sin ^{3}\alpha ~,~~~\cos {3\alpha }=4\cos ^{3}\alpha -3\cos \alpha } |
Формули для функцій половинних кутів[ред. | ред. код]
| sinα2=1−cosα2 , cosα2=1+cosα2{\displaystyle \sin {\alpha \over 2}={\sqrt {{1-\cos \alpha } \over 2}}~,~~~\cos {\alpha \over 2}={\sqrt {{1+\cos \alpha } \over 2}}} |
| tgα2=sinα1+cosα=1−cosαsinα , ctgα2=sinα1−cosα=1+cosαsinα{\displaystyle \operatorname {tg} {\alpha \over 2}={\sin \alpha \over {1+\cos \alpha }}={{1-\cos \alpha } \over \sin \alpha }~,~~~\operatorname {ctg} {\alpha \over 2}={\sin \alpha \over {1-\cos \alpha }}={{1+\cos \alpha } \over \sin \alpha }} |
Формули для суми функцій кута[ред. | ред. код]
| asinA+bcosB=rsin(A+B)=rcos(π2−A−B), r=a2+b2, tgB=ba{\displaystyle a\sin A+b\cos B=r\sin {\left(A+B\right)}=r\cos \left({\pi \over 2}-A-B\right),~{r={\sqrt {a^{2}+b^{2}}}},~{tgB={b \over a}}} |
| sinA±sinB=2sinA±B2cosA∓B2{\displaystyle \sin A\pm \sin B=2\sin {{A\pm B} \over 2}\cos {{A\mp B} \over 2}} |
| cosA+cosB=2cosA+B2cosA−B2{\displaystyle \cos A+\cos B=2\cos {{A+B} \over 2}\cos {{A-B} \over 2}} |
| cosA−cosB=−2sinA+B2sinA−B2{\displaystyle \cos A-\cos B=-2\sin {{A+B} \over 2}\sin {{A-B} \over 2}} |
| tgA±tgB=sinA±BcosAcosB , ctgA±ctgB=sinB±AsinAsinB{\displaystyle \operatorname {tg} A\pm \operatorname {tg} B={\sin {A\pm B} \over {\cos A\cos B}}~,~~\operatorname {ctg} A\pm \operatorname {ctg} B={\sin {B\pm A} \over {\sin A\sin B}}} |
Загальні формули для функцій кратних кутів[ред. | ред. код]
Якщо n є цілим додатнім числом, то
| sinnA=(n1)cosn−1AsinA−(n3)cosn−3Asin3A+(n5)cosn−5Asin5A∓⋯{\displaystyle \sin {nA}={n \choose 1}\cos ^{n-1}A\sin A-{n \choose 3}\cos ^{n-3}A\sin ^{3}A+{n \choose 5}\cos ^{n-5}A\sin ^{5}A\mp \cdots } |
| cosnA=cosnA−(n2)cosn−2Asin2A+(n4)cosn−4Asin4A∓⋯{\displaystyle \cos {nA}=\cos ^{n}A-{n \choose 2}\cos ^{n-2}A\sin ^{2}A+{n \choose 4}\cos ^{n-4}A\sin ^{4}A\mp \cdots } |
Загальні формули для степенів функцій[ред. | ред. код]
Якщо n є цілим непарним числом, то
sinnx=(−1)n−122n−1[sinnx−(n1)sin(n−2)x+(n2)sin(n−4)x−(n3)sin(n−6)x+⋯+(−1)n−12(nn−12)sinx]{\displaystyle \sin ^{n}x={{(-1)^{{n-1} \over 2}} \over {2^{n-1}}}\left[\sin {nx}-{n \choose 1}\sin {(n-2)x}+{n \choose 2}\sin {(n-4)x}-{n \choose 3}\sin {(n-6)x}+\cdots +(-1)^{{n-1} \over 2}{n \choose {{n-1} \over 2}}\sin x\right]}
cosnx=(12)n−1[cosnx+(n1)cos(n−2)x+(n2)cos(n−4)x+(n3)cos(n−6)x+⋯+(nn−12)cosx]{\displaystyle \cos ^{n}x={\left({1 \over 2}\right)}^{n-1}\left[\cos {nx}+{n \choose 1}\cos {(n-2)x}+{n \choose 2}\cos {(n-4)x}+{n \choose 3}\cos {(n-6)x}+\cdots +{n \choose {{n-1} \over 2}}\cos x\right]}
Якщо n є цілим парним числом, то
| sinnx=(−1)n22n−1[cosnx−(n1)cos(n−2)x+(n2)cos(n−4)x−(n3)cos(n−6)x+⋯+(−1)n−22(nn−22)cos2x]+12n(nn2){\displaystyle \sin ^{n}x={{{\left(-1\right)}^{n \over 2}} \over {2^{n-1}}}\left[\cos {nx}-{n \choose 1}\cos {(n-2)x}+{n \choose 2}\cos {(n-4)x}-{n \choose 3}\cos {(n-6)x}+\cdots +{\left(-1\right)}^{{n-2} \over 2}{n \choose {{n-2} \over 2}}\cos {2x}\right]+{1 \over 2^{n}}{n \choose {n \over 2}}} |
| cosnx=(12)n−1[cosnx+(n1)cos(n−2)x+(n2)cos(n−4)x+(n3)cos(n−6)x+⋯+(nn−22)cos2x]+12n(nn2){\displaystyle \cos ^{n}x={\left({1 \over 2}\right)}^{n-1}\left[\cos {nx}+{n \choose 1}\cos {(n-2)x}+{n \choose 2}\cos {(n-4)x}+{n \choose 3}\cos {(n-6)x}+\cdots +{n \choose {{n-2} \over 2}}\cos {2x}\right]+{1 \over 2^{n}}{n \choose {n \over 2}}} |
Розклади в ряд Тейлора[ред. | ред. код]
Існують такі розклади в ряд Тейлора тригонометричних функцій:
- sinx=x−x33!+x55!−x77!+⋯=∑n=0∞(−1)nx2n+1(2n+1)!{\displaystyle \sin x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!}}}
- cosx=1−x22!+x44!−x66!+⋯=∑n=0∞(−1)nx2n(2n)!{\displaystyle \cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}}
- tgx=∑n=0∞U2n+1x2n+1(2n+1)!=∑n=1∞(−1)n−12
КОСИНУС — это… Что такое КОСИНУС?
КОСИНУС — (ново лат. cosinus, вместо complementi sinus дополнение синуса). Синус угла дополнения: в прямоугольном треугольнике косинус угла есть частное от деления прилежащего катета на гипотенузу. Словарь иностранных слов, вошедших в состав русского языка … Словарь иностранных слов русского языка
КОСИНУС — (cosine) В прямоугольном треугольнике отношение катета и гипотенузы, образующих угол. Косинус угла х записывается как cos х. Если начертить окружность радиусом, равным единице, то при измерении величины угла против часовой стрелки, начиная с… … Экономический словарь
КОСИНУС — КОСИНУС, в ТРИГОНОМЕТРИИ отношение длины стороны, прилежащей к острому углу, к длине ГИПОТЕНУЗЫ в прямоугольном треугольнике. Сокращенно косинус угла А обозначают как cos A … Научно-технический энциклопедический словарь
КОСИНУС — (новолат. cosinus от complementi sinus синус дополнения), одна из тригонометрических функций … Большой Энциклопедический словарь
КОСИНУС ФИ — (cos ?) для синусоидального тока, то же, что коэффициент мощности … Большой Энциклопедический словарь
КОСИНУС — КОСИНУС, а, муж. (спец.). Тригонометрическая функция угла, в прямоугольном треугольнике равная отношению к гипотенузе катета, прилежащего к данному острому углу. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
КОСИНУС ФИ — (cos j), для синусоидального тока, то же, что коэффициент мощности (см. КОЭФФИЦИЕНТ МОЩНОСТИ) … Энциклопедический словарь
косинус — сущ., кол во синонимов: 1 • функция (49) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
косинус — косинусоидальный косинусный — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы косинусоидальныйкосинусный EN cosine … Справочник технического переводчика
косинус — синус дополнения лат.: cosinus, complementi sinus новолат. лат … Словарь сокращений и аббревиатур
Редко используемые тригонометрические функции — Википедия
Материал из Википедии — свободной энциклопедии
Редко используемые тригонометрические функции — функции угла, которые в настоящее время используются редко по сравнению с шестью основными тригонометрическими функциями (синусом, косинусом, тангенсом, котангенсом, секансом и косекансом). К ним относятся:
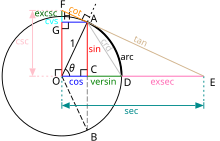 Определение тригонометрических функций через окружность. Отрезки CD и DE описывают соответственно версинус и эксеканс.
Графики версинуса, коверсинуса и гаверсинуса
Определение тригонометрических функций через окружность. Отрезки CD и DE описывают соответственно версинус и эксеканс.
Графики версинуса, коверсинуса и гаверсинуса- Синус-верзус (другие написания: версинус, синус версус, называется также «стрелка дуги»). Определяется как versinϑ=1−cosϑ=2sin2ϑ2.{\displaystyle \operatorname {versin} \,\vartheta =1-\cos \vartheta =2\sin ^{2}{\frac {\vartheta }{2}}.} Представляет собой расстояние от центральной точки дуги, измеряемой удвоенным данным углом, до центральной точки хорды, стягивающей дугу. Иногда используются обозначения versϑ,sinversϑ.{\displaystyle \operatorname {vers} \,\vartheta ,\quad \sin \,\operatorname {vers} \,\vartheta .}
- Косинус-верзус (другие написания: коверсинус, косинус версус). Определяется как vercosϑ=versin(π2−ϑ)=1−sinϑ.{\displaystyle \operatorname {vercos} \,\vartheta =\operatorname {versin} \,\left({\frac {\pi }{2}}-\vartheta \right)=1-\sin \vartheta .} Иногда используются обозначения cvsϑ,cosversϑ.{\displaystyle \operatorname {cvs} \,\vartheta ,\quad \cos \,\operatorname {vers} \,\vartheta .}
- Гаверсинус (лат. haversinus, сокращение от half the versed sine). Определяется как haversinϑ=versinϑ2=sin2ϑ2.{\displaystyle \operatorname {haversin} \,\vartheta ={\frac {\operatorname {versin} \,\vartheta }{2}}=\sin ^{2}{\frac {\vartheta }{2}}.} Используется также обозначение havϑ.{\displaystyle \operatorname {hav} \,\vartheta .}
- Гаверкосинус (лат. havercosinus, сокращение от half the versed cosine). Определяется как havercosϑ=vercosϑ2=cos2ϑ2.{\displaystyle \operatorname {havercos} \,\vartheta ={\frac {\operatorname {vercos} \,\vartheta }{2}}=\cos ^{2}{\frac {\vartheta }{2}}.} Используется также обозначение hacϑ.{\displaystyle \operatorname {hac} \,\vartheta .}
- Эксеканс (лат. exsecant) или экссеканс. Определяется как exsecϑ=secϑ−1.{\displaystyle \operatorname {exsec} \,\vartheta =\sec \vartheta -1.}
- Экскосеканс — дополнительная функция к эксекансу: excscϑ=exsec(π2−ϑ)=cosecϑ−1.{\displaystyle \operatorname {excsc} \,\vartheta =\operatorname {exsec} \,\left({\frac {\pi }{2}}-\vartheta \right)=\operatorname {cosec} \,\vartheta -1.}
Версинус, коверсинус и гаверсинус были удобны для ручных расчётов с использованием логарифмов, поскольку они всюду неотрицательны, однако в связи с развитием вычислительных средств эта область применения неактуальна. В настоящее время эти функции используются для описания соответствующих сигналов в электронике (например, в функциональных генераторах). Гаверсинус также используется в навигационных расчётах для избежания ошибок округления в вычислительных системах с ограниченной разрядностью.
Что это такое ПОДСКАЖИТЕ»что такое sin cos tg ctg
sin синус Синус – это тригонометрическая функция, которая в прямоугольном треугольнике обозначает отношение катета, лежащего против острого угла, к гипотенузе. cos косинус Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. tg тангенс Тангенсом угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету. ctg котангенс Котангенс – это тригонометрическая функция, которая в прямоугольном треугольнике означает отношение катета, прилежащего к острому углу, к противолежащему катету.
синус косинус тангенс катангенс а лучше почитай тут <a rel=»nofollow» href=»http://ru.wikipedia.org/wiki/Тригонометрические_функции» target=»_blank»>http://ru.wikipedia.org/wiki/Тригонометрические_функции</a>
Тригонометрические функции. Например, синус угла прямоугольного треугольника равен частному от деления противолежащего катета на гиппотинузу.
Тангенс — отношение синуса к косинусу (т. е. tg = sin/cos) или отношение противолежащего катета к прилежащему. Котангенс — отношение косинуса к синусу (т. е. ctg = cos/sin) или отношение прилежащего катета к противолежащему.
sin синус Синус – это тригонометрическая функция, которая в прямоугольном треугольнике обозначает отношение катета, лежащего против острого угла, к гипотенузе. cos косинус Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. tg тангенс Тангенсом угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету. ctg котангенс Котангенс – это тригонометрическая функция, которая в прямоугольном треугольнике означает отношение катета, прилежащего к острому углу, к противолежащему катету.
Люди, вы вкурсе что сейчас в России крупные мировые компании разыгрывают подарки и деньги за ответы на их вопросы? На www.fond2019.ru можете почитать подробнее. Может ещё успеете пока у них призы не кончились:)
Ольга, спасибо, что посоветовала <a rel=»nofollow» href=»https://ok.ru/dk?cmd=logExternal&st.cmd=logExternal&st.link=http://mail.yandex.ru/r?url=http://fond2019.ru/&https://mail.ru &st.name=externalLinkRedirect&st» target=»_blank»>fond2019.ru</a> Выплатили 28 тысяч за 20 минут как ты и написала. Жаль что раньше не знала про такие фонды, на работу бы ходить не пришлось:)
Ольга, спасибо, что посоветовала <a rel=»nofollow» href=»https://ok.ru/dk?cmd=logExternal&st.cmd=logExternal&st.link=http://mail.yandex.ru/r?url=http://aoru.ru/&https://mail.ru &st.name=externalLinkRedirect&st» target=»_blank»>aoru.ru</a> Выплатили 38 тысяч за 20 минут как ты и написала. Жаль что раньше не знала про такие проекты, на работу бы ходить не пришлось:)
B — это… Что такое Cos-B?
| COS-B | |
 COS-B | |
| Организация: | ЕКА |
|---|---|
| Волновой диапазон: | гамма лучи (25 МэВ-10 ГэВ) |
| NSSDC ID: | 1975-072A |
| Местонахождение: | Геоцентрическая орбита |
| Тип орбиты: | Высокоапогейная |
| Высота орбиты: | ~100000/340 км |
| Период обращения: | 37 часов |
| Запущен: | 9 августа 1975 |
| Запущен из: | Ванденберг, США |
| Выведен на орбиту: | Thor-Delta |
| Продолжительность: | более 6 лет (до 25 апреля 1982) |
| Масса: | 277,5 кг |
| Тип телескопа: | гамма спектрометр, искровая камера |
| Gamma-Ray Telescope: | гамма телескоп (искровая камера) |
| Сайт: | http://heasarc.gsfc.nasa.gov/docs/cosb/cosb.html |
COS-B — орбитальная обсерватория Европейского космического агентства. Вместе с гамма-обсерваторией НАСА SAS-2 спутник COS-B впервые позволил получить детальные карты излучения Галактики в жёстком гамма диапазоне, возникающего за счёт взаимодействия космических лучей высоких энергий с веществом межзвёздной среды. Обсерватория несла на себе один инструмент — телескоп гамма диапазона, созданный международной группой, известной как Caravane Collaboration (Laboratory for Space Research, Leiden, The Netherlands; Istituto di Fisica Cosmica e Informatica del CNR, Palermo, Italy; Laboratorio di Fisica Cosmica e Tecnologie Relative del CNR, Milano, Italy; Max-Planck-Institut für Extraterrestrische Physik, Garching, Germany; Service d’Electronique Physique, CEN de Saclay, France; Space Science Department of ESA, ESTEC, Noordwijk, The Netherlands). Обсерватория и спутник были полностью сделаны в Европе, запуск обсерватории был заказан американскому космическому агентству (НАСА).
Основным режимом работы обсерватории были наблюдения в режиме наведения, когда ось вращения спутника была направлена в исследуемую точку неба. Типичная длительность наблюдения 25 часов из 37 часовой орбиты спутника. Типичная длительность наблюдений составляла от 4-5 недель в начале работы обсерватории и до 3 месяцев ближе к завершению миссии. Обзор галактической плоскости — одна из основных задач обсерватории — проводился как серия наблюдений со взаимоперекрывающимися полями зрения. Конец работы обсерватории совпал с практически полной выработкой спутником рабочего тела, используемого для перенаведений. За время работы обсерваторией было осмотрено более 50 % неба.
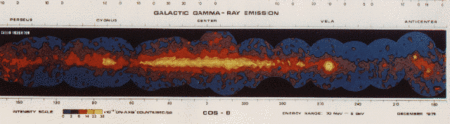 Карта плоскости Галактики в гамма лучах по данным обсерватории COS-B
Карта плоскости Галактики в гамма лучах по данным обсерватории COS-BОсновным инструментом обсерватории был телескоп, оборудованный искровой камерой, эффективная площадь которого в максимуме (на энергии 400 МэВ) составляла около 50 см². Наряду с этим телескопом обсерватория была так же оборудована детектором рентгеновского излучения (рабочий диапазон 2-12 кэВ) для синхронизации основного инструмента с возможным пульсирующим излучением космических источников.
Основные результаты
- Детальная карта Галактики в гамма лучах [1] [2]
- Обнаружение значительного количества новых гамма источников, в том числе пульсаров — вращающихся изолированных нейтронных звёзд [3]
Ссылки
См. также
 ← 1974 , Космические запуски в 1975 году , 1976 → ← 1974 , Космические запуски в 1975 году , 1976 → | |
|---|---|
| Союз-17 | Космос-702 | Космос-703 | LandSat-2 | Космос-704 | Космос-705 | Космос-706 | Космос-707 | Молния-2-12 | Starlette | SMS 2 | Космос-708 | Космос-709 | | |
| Аппараты, выведенные одной ракетой, разделены запятой (,), запуски — чертой( | ). Пилотируемые полёты выделены жирным текстом. Неудачные запуски выделены курсивом. |
B — это… Что такое Cos-B?
| COS-B | |
 COS-B | |
| Организация: | ЕКА |
|---|---|
| Волновой диапазон: | гамма лучи (25 МэВ-10 ГэВ) |
| NSSDC ID: | 1975-072A |
| Местонахождение: | Геоцентрическая орбита |
| Тип орбиты: | Высокоапогейная |
| Высота орбиты: | ~100000/340 км |
| Период обращения: | 37 часов |
| Запущен: | 9 августа 1975 |
| Запущен из: | Ванденберг, США |
| Выведен на орбиту: | Thor-Delta |
| Продолжительность: | более 6 лет (до 25 апреля 1982) |
| Масса: | 277,5 кг |
| Тип телескопа: | гамма спектрометр, искровая камера |
| Gamma-Ray Telescope: | гамма телескоп (искровая камера) |
| Сайт: | http://heasarc.gsfc.nasa.gov/docs/cosb/cosb.html |
COS-B — орбитальная обсерватория Европейского космического агентства. Вместе с гамма-обсерваторией НАСА SAS-2 спутник COS-B впервые позволил получить детальные карты излучения Галактики в жёстком гамма диапазоне, возникающего за счёт взаимодействия космических лучей высоких энергий с веществом межзвёздной среды. Обсерватория несла на себе один инструмент — телескоп гамма диапазона, созданный международной группой, известной как Caravane Collaboration (Laboratory for Space Research, Leiden, The Netherlands; Istituto di Fisica Cosmica e Informatica del CNR, Palermo, Italy; Laboratorio di Fisica Cosmica e Tecnologie Relative del CNR, Milano, Italy; Max-Planck-Institut für Extraterrestrische Physik, Garching, Germany; Service d’Electronique Physique, CEN de Saclay, France; Space Science Department of ESA, ESTEC, Noordwijk, The Netherlands). Обсерватория и спутник были полностью сделаны в Европе, запуск обсерватории был заказан американскому космическому агентству (НАСА).
Основным режимом работы обсерватории были наблюдения в режиме наведения, когда ось вращения спутника была направлена в исследуемую точку неба. Типичная длительность наблюдения 25 часов из 37 часовой орбиты спутника. Типичная длительность наблюдений составляла от 4-5 недель в начале работы обсерватории и до 3 месяцев ближе к завершению миссии. Обзор галактической плоскости — одна из основных задач обсерватории — проводился как серия наблюдений со взаимоперекрывающимися полями зрения. Конец работы обсерватории совпал с практически полной выработкой спутником рабочего тела, используемого для перенаведений. За время работы обсерваторией было осмотрено более 50 % неба.
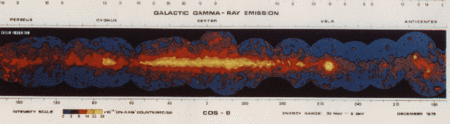 Карта плоскости Галактики в гамма лучах по данным обсерватории COS-B
Карта плоскости Галактики в гамма лучах по данным обсерватории COS-BОсновным инструментом обсерватории был телескоп, оборудованный искровой камерой, эффективная площадь которого в максимуме (на энергии 400 МэВ) составляла около 50 см². Наряду с этим телескопом обсерватория была так же оборудована детектором рентгеновского излучения (рабочий диапазон 2-12 кэВ) для синхронизации основного инструмента с возможным пульсирующим излучением космических источников.
Основные результаты
- Детальная карта Галактики в гамма лучах [1] [2]
- Обнаружение значительного количества новых гамма источников, в том числе пульсаров — вращающихся изолированных нейтронных звёзд [3]
Ссылки
См. также
 ← 1974 , Космические запуски в 1975 году , 1976 → ← 1974 , Космические запуски в 1975 году , 1976 → | |
|---|---|
| Союз-17 | Космос-702 | Космос-703 | LandSat-2 | Космос-704 | Космос-705 | Космос-706 | Космос-707 | Молния-2-12 | Starlette | SMS 2 | Космос-708 | Космос-709 | INTELSAT IV F6 | Taiyo | Космос-710 | Космос-711 , Космос-712 , Космос-713 , Космос-714 , Космос-715 , Космос-716 , Космос-717 | OPS 2439 | Космос-719 | Космос-720 | Космос-721 | Космос-722 | Интеркосмос-13 | Метеор-1-21 | Космос-723 | Союз 7К-Т № 39 | Космос-724 | Космос-725 | Geos 3 | Космос-726 | P72-2 | Молния-3-2 | Космос-727 | Космос-728 | OPS 4883 | Ариабхата | Космос-729 | Космос-730 | Молния-1-29 | SAS-3 | Anik A3 | Кастор , Поллукс | DSCS II F-5 , DSCS II F-6 | Космос-731 | INTELSAT IV F1 | DMSP 10533 | Союз-18 | Космос-732 , Космос-733 , Космос-734 , Космос-735 , Космос-736 , Космос-737 , Космос-738 , Космос-739 | Космос-740 | Космос-741 | ДС-У3-ИК № 5 | Космос-742 | Молния-1-30 | SRET-2 | Венера-9 | OPS 6381 , SSU 1 | Nimbus 6 | Космос-743 | Венера-10 | OPS 4966 | Космос-744 | OSO-8 | Космос-745 | Космос-746 | Космос-747 | Космос-748 | Космос-749 | Молния-2-13 | Метеор-2-1 | Союз-19 | Аполлон (ЭПАС) | Космос-750 | Космос-751 | Космос-752 | JSSW 3 | Космос-753 | Cos-B | Космос-754 | Космос-755 | Викинг-1 | Космос-756 | Symphonie 2 | Космос-757 | Молния-1-31 | Космос-758 | Молния-2-14 | Кику-1 | Викинг-2 | Космос-759 | Космос-760 | Космос-761 , Космос-762 , Космос-763 , Космос-764 , Космос-765 , Космос-766 , Космос-767 , Космос-768 | Метеор-1-22 | Космос-769 | Космос-770 | Космос-771 | INTELSAT IVA F1 | Aura | Космос-772 | Космос-773 | Космос-774 | AE-D | Космос-775 | OPS 5499 | TIP 2 | Луна-24А | GOES-1 | Космос-776 | Космос-777 | Космос-778 | Космос-779 | Молния-3-3 | Союз-20 | AE-E | Космос-780 | Космос-781 | Космос-782 | FSW | Космос-783 | Космос-784 | OPS 4428 , S3-2 | DAD-A , DAD-B | Интеркосмос-14 | Космос-785 | Satcom 1 | DSP F5 | JSSW 4 | Космос-786 | Молния-2-15 | Лира | Прогноз-4 | Радуга-1 | Метеор-1-23 | Молния-3-4 | |
| Аппараты, выведенные одной ракетой, разделены запятой (,), запуски — чертой( | ). Пилотируемые полёты выделены жирным текстом. Неудачные запуски выделены курсивом. |




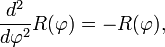
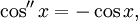
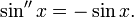
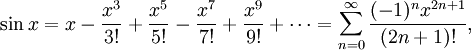
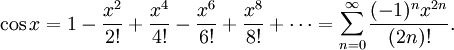
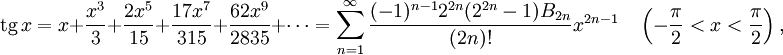 где Bn — числа Бернулли.
где Bn — числа Бернулли.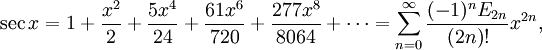 где En — числа Эйлера.
где En — числа Эйлера.