Циклическая частота колебаний, теория и онлайн калькуляторы

Определение

Мерой колебательного движения служит циклическая (или угловая, или круговая) частотой колебаний.

Это скалярная физическая величина.

Циклическая частота при гармонических колебаниях

Пусть колебания совершает материальная точка. При этом материальная точка через равные промежутки времени проходит через одно и то же положение.

Самыми простыми колебаниями являются гармонические колебания. Рассмотрим следующую кинематическую модель. Точка M с постоянной по модулю скоростью ($v$) движется по окружности радиуса A. В этом случае ее угловую скорость обозначим ${\omega }_0$, эта скорость постоянна (рис.1).

Проекция точки $M$ на диаметр окружности (точка $N$), на ось X, выполняет колебания от $N_1$ до $N_2\ $и обратно. Такое колебание N ,будет гармоническим. Для описания колебания точки N необходимо записать координату точки N, как функцию от времени ($t$). Пусть при $t=0$ радиус OM образует с осью X угол ${\varphi }_0$. Через некоторый промежуток времени этот угол изменится на величину ${\omega }_0t$ и будет равен ${\omega }_0t+{\varphi }_0$, тогда:

\[x=A{\cos \left({\omega }_0t+{\varphi }_0\right)\ }\left(1\right).\]

Выражение (1) является аналитической формой записи гармонического колебания точки N по диаметру $N_1N_2$.

Обратимся к выражению (1). Величина $A$ — это максимальное отклонение точки, совершающей колебания, от положения равновесия (точки О — центра окружности), называется амплитудой колебаний.

Параметр ${\omega }_0$ — циклическая частота колебаний. $\varphi =({\omega }_0t+{\varphi }_0$) — фаза колебаний; ${\varphi }_0$ — начальная фаза колебаний.

Циклическую частоту гармонических колебаний можно определить как частную производную от фазы колебаний по времени:

\[{\omega }_0=\frac{?\varphi }{\partial t}=\dot{\varphi }\left(2\right).\]

При ${\varphi }_0=0$, уравнение колебаний (1) преобразуется к виду:

\[x=A{\cos \left({\omega }_0t\right)\ }\left(3\right).\]

Если начальная фаза колебаний равна ${\varphi }_0=\frac{\pi }{2}$ , то получим уравнение колебаний в виде:

\[x=A{{\rm s}in \left({\omega }_0t\right)\ }\left(4\right).\]

Выражения (3) и (4) показывают, что при гармонических колебаниях абсцисса $x$ — это функция синус или косинус от времени. При графическом изображении гармонических колебаний получается косинусоида или синусоида. Форма кривой определена амплитудой колебаний и величиной циклической частоты. Положение кривой зависит от начальной фазы.

Циклическую частоту колебаний можно выразить через период (T) колебаний:

\[{\omega }_0=\frac{2\pi }{T}\left(5\right).\]

Циклическую час

Циклическая частота — Википедия

Материал из Википедии — свободной энциклопедии

Углова́я частота́ (синонимы: радиальная частота, циклическая частота, круговая частота, частота вращения) — скалярная физическая величина, мера частоты вращательного или колебательного движения. В случае вращательного движения угловая частота равна модулю вектора угловой скорости. В Международной системе единиц (СИ) и системе СГС угловая частота выражается в радианах в секунду, её размерность обратна размерности времени (радианы безразмерны).

Угловая частота является производной по времени от фазы колебания:

ω=∂φ/∂t.{\displaystyle \omega =\partial \varphi /\partial t.}

Другое распространённое обозначение ω=φ˙.{\displaystyle \omega ={\dot {\varphi }}.}

Угловая частота связана с частотой ν соотношением^[1]

ω=2πν.{\displaystyle \omega ={2\pi \nu }.}

В случае использования в качестве единицы угловой частоты градусов в секунду связь с обычной частотой будет следующей:

ω=360∘ν.{\displaystyle \omega ={360^{\circ }\nu }.}

В случае вращательного движения угловая частота численно равна углу, на который повернется вращающееся тело за единицу времени (то есть равна модулю вектора угловой скорости), в случае колебательного движения — приращению полной фазы колебания за единицу времени. Численно угловая (циклическая) частота равна числу циклов (колебаний, оборотов) за 2π единиц времени.

Введение циклической частоты (в её основной размерности — радианах в секунду) позволяет упростить многие формулы в теоретической физике и электронике. Так, резонансная циклическая частота колебательного LC-контура равна ωLC=1/LC,{\displaystyle \omega _{LC}=1/{\sqrt {LC}},} тогда как обычная резонансная частота νLC=1/(2πLC).{\displaystyle \nu _{LC}=1/(2\pi {\sqrt {LC}}).}

В то же время ряд других формул усложняется. Решающим соображением в пользу циклической частоты стало то, что переводные множители 2π и 1/(2π), появляющиеся во многих формулах при использовании радианов для измерения углов и фаз, исчезают при введении циклической частоты.

См. также[ | ]

Примечания[ | ]

1. ↑ Угловая частота (неопр.). Большой энциклопедический политехнический словарь. Проверено 27 октября 2016.

Циклическая частота Википедия

Углова́я частота́ (синонимы: радиальная частота, циклическая частота, круговая частота, частота вращения) — скалярная физическая величина, мера частоты вращательного или колебательного движения. В случае вращательного движения угловая частота равна модулю вектора угловой скорости. В Международной системе единиц (СИ) и системе СГС угловая частота выражается в радианах в секунду, её размерность обратна размерности времени (радианы безразмерны).

Угловая частота является производной по времени от фазы колебания:

ω=∂φ/∂t.{\displaystyle \omega =\partial \varphi /\partial t.}

Другое распространённое обозначение ω=φ˙.{\displaystyle \omega ={\dot {\varphi }}.}

Угловая частота связана с частотой ν соотношением^[1]

ω=2πν.{\displaystyle \omega ={2\pi \nu }.}

В случае использования в качестве единицы угловой частоты градусов в секунду связь с обычной частотой будет следующей:

ω=360∘ν.{\displaystyle \omega ={360^{\circ }\nu }.}

В случае вращательного движения угловая частота численно равна углу, на который повернется вращающееся тело за единицу времени (то есть равна модулю вектора угловой скорости), в случае колебательного движения — приращению полной фазы колебания за единицу времени. Численно угловая (циклическая) частота равна числу циклов (колебаний, оборотов) за 2π единиц времени.

Введение циклической частоты (в её основной размерности — радианах в секунду) позволяет упростить многие формулы в теоретической физике и электронике. Так, резонансная циклическая частота колебательного LC-контура равна ωLC=1/LC,{\displaystyle \omega _{LC}=1/{\sqrt {LC}},} тогда как обычная резонансная частота νLC=1/(2πLC).{\displaystyle \nu _{LC}=1/(2\pi {\sqrt {LC}}).}

В то же время ряд других формул усложняется. Решающим соображением в пользу циклической частоты стало то, что переводные множители 2π и 1/(2π), появляющиеся во многих формулах при использовании радианов для измерения углов и фаз, исчезают при введении циклической частоты.

См. также[ | ]

Примечания

Циклическая частота Википедия

Углова́я частота́ (синонимы: радиальная частота, циклическая частота, круговая частота, частота вращения) — скалярная физическая величина, мера частоты вращательного или колебательного движения. В случае вращательного движения угловая частота равна модулю вектора угловой скорости. В Международной системе единиц (СИ) и системе СГС угловая частота выражается в радианах в секунду, её размерность обратна размерности времени (радианы безразмерны).

Угловая частота является производной по времени от фазы колебания:

ω=∂φ/∂t.{\displaystyle \omega =\partial \varphi /\partial t.}

Другое распространённое обозначение ω=φ˙.{\displaystyle \omega ={\dot {\varphi }}.}

Угловая частота связана с частотой ν соотношением^[1]

ω=2πν.{\displaystyle \omega ={2\pi \nu }.}

В случае использования в качестве единицы угловой частоты градусов в секунду связь с обычной частотой будет следующей:

ω=360∘ν.{\displaystyle \omega ={360^{\circ }\nu }.}

В случае вращательного движения угловая частота численно равна углу, на который повернется вращающееся тело за единицу времени (то есть равна модулю вектора угловой скорости), в случае колебательного движения — приращению полной фазы колебания за единицу времени. Численно угловая (циклическая) частота равна числу циклов (колебаний, оборотов) за 2π единиц времени.

Введение циклической частоты (в её основной размерности — радианах в секунду) позволяет упростить многие формулы в теоретической физике и электронике. Так, резонансная циклическая частота колебательного LC-контура равна ωLC=1/LC,{\displaystyle \omega _{LC}=1/{\sqrt {LC}},} тогда как обычная резонансная частота νLC=1/(2πLC).{\displaystyle \nu _{LC}=1/(2\pi {\sqrt {LC}}).}

В то же время ряд других формул усложняется. Решающим соображением в пользу циклической частоты стало то, что переводные множители 2π и 1/(2π), появляющиеся во многих формулах при использовании радианов для измерения углов и фаз, исчезают при введении циклической частоты.

См. также

Примечания

1. ↑ Угловая частота (неопр.). Большой энциклопедический политехнический словарь. Дата обращения 27 октября 2016.

Угловая частота — это… Что такое Угловая частота?

Углова́я частота́ (синонимы: радиальная частота, циклическая частота, круговая частота) — скалярная физическая величина, мера частоты вращательного или колебательного движения. В случае вращательного движения, угловая частота равна модулю вектора угловой скорости. В системах СИ и СГС угловая частота выражается в радианах в секунду, её размерность обратна размерности времени (радианы безразмерны). Угловая частота является производной по времени от фазы колебания:

Другое распространённое обозначение

Угловая частота в радианах в секунду выражается через частоту f (выражаемую в оборотах в секунду или колебаниях в секунду), как

В случае использования в качестве единицы угловой частоты градусов в секунду связь с обычной частотой будет следующей:

Численно циклическая частота равна числу циклов (колебаний, оборотов) за 2π секунд. Введение циклической частоты (в её основной размерности — радианах в секунду) позволяет упростить многие формулы в теоретической физике и электронике. Так, резонансная циклическая частота колебательного LC-контура равна тогда как обычная резонансная частота В то же время ряд других формул усложняется. Решающим соображением в пользу циклической частоты стало то, что множители 2π и 1/(2π), появляющиеся во многих формулах при использовании радианов для измерения углов и фаз, исчезают при введении циклической частоты.

См. также

1.5.1 Гармонические колебания. Амплитуда и фаза колебаний

Видеоурок: Гармонические колебания — Физика в опытах и экспериментах

Лекция: Гармонические колебания. Амплитуда и фаза колебаний

Гармонические колебания

Во время колебаний все состояния системы повторяются с некоторой периодичностью. 

Если данную периодичность можно описать законами синуса или косинуса, то такие колебания называются гармоническими.

Уравнения гармонических колебаний имеют следующий вид:

Данная зависимость позволит определить положение тела или состояние системы относительно начального состояния в любой момент времени.

Характеристика гармонических колебаний

1. Амплитуда — максимальное отклонение от начального положения. Обозначается [Хмак] = 1м.

2. Период — ФВ, характеризующая время одного полного колебания. Основная единица измерений — секунда (с).

 

t — все время движения

N — количество колебаний

В СИ период колебаний выражается в секундах [T]=c

3.  Частота — ФВ, определяющая количество колебаний, совершенных в единицу времени. Основной единицей измерения являются Герцы (Гц).

v — частота — число колебаний за 1 сек.

t — все время движения

N — количество колебаний
[v] = [Гц]

Частота и период связаны друг с другом обратной зависимостью.

4. Фаза — ФВ, определяющая временные рамки, на протяжении которых рассматриваются колебания системы. В уравнении колебаний фаза — аргумент функции. Измеряется в радианах (рад). Начальная фаза — это положение переменных величин в начальный момент времени.

ф — фаза колебаний
w — циклическая частота

 

5. Циклическая частота — это количество колебаний тела за 2п секунд. Измеряется в рад/с. В уравнении колебаний находится в аргументе функции перед временем.

Находится по формуле:

6. Скорость и ускорение колебаний. Так как скорость — первая производная от координаты, а ускорение — вторая производная, то, чтобы определить скорость и ускорение в любой момент времени следует воспользоваться следующей функцией:

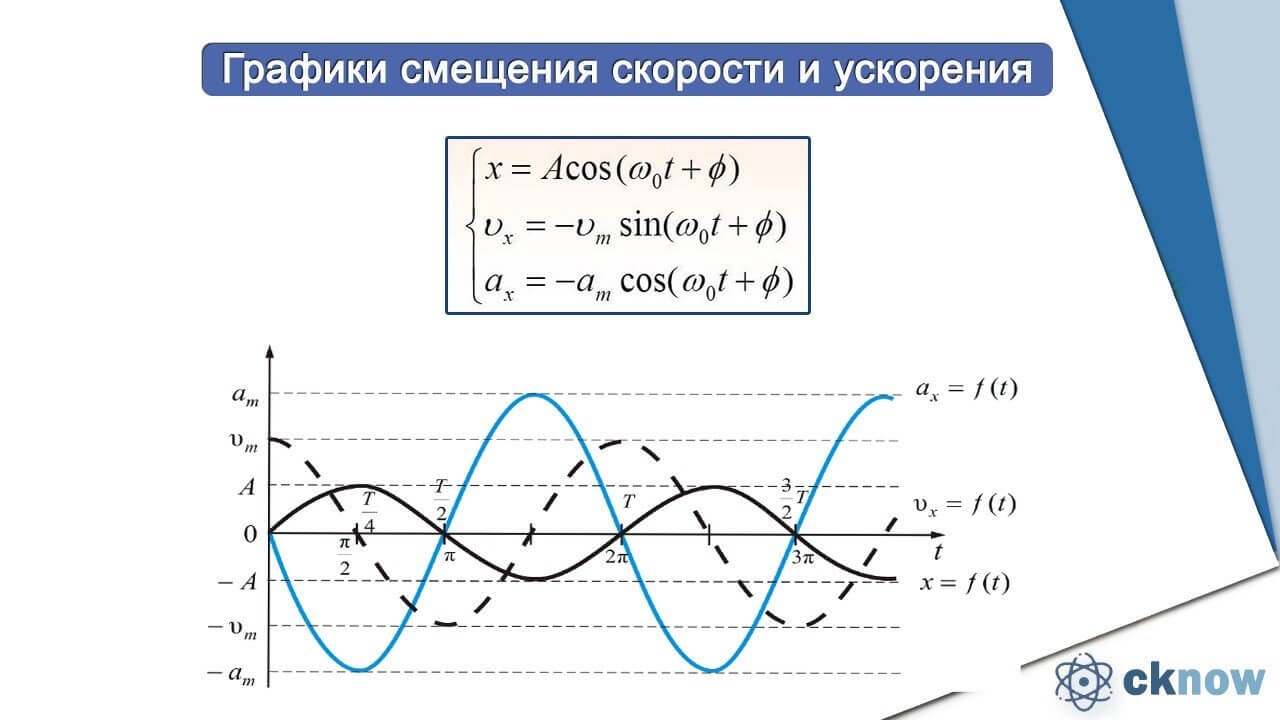
 7. Сила, приводящая к гармоническим колебаниям:

Превращение энергии гармонических колебаний

Во время совершения гармонических колебаний справедлив закон сохранения энергии.

Вся механическая энергия, сумма потенциальной и кинетической энергии, во время гармонических колебаний остается неизменной.

В самой нижней точке, в начальном положении математического маятника, кинетическая энергия достигает своего максимума, так как в этой точке значение скорости максимальное.

В точке, где маятник достигает максимальной амплитуды, тело достигает максимальное значение потенциальной энергии.

В промежуточных значениях механическая энергия состоит из суммы кинетической и потенциальной энергии.

Е = Ек + Еп = Ек.мах = Еп.мах.

Эти же правила справедливы и для пружинного маятника.

Частота | Virtual Laboratory Wiki

Частота́ — физическая величина, характеристика периодического процесса, равная числу полных циклов, совершённых за единицу времени. Стандартные обозначения в формулах — $ ~{\nu} $, $ ~f $ или $ ~F $. Единицей частоты в Международной системе единиц (СИ) в общем случае является герц (

Гц, Hz). Величина, обратная частоте, называется периодом.

Мгновенная частота и частоты спектральных составляющих

Периодический сигнал характеризуется мгновенной частотой, являющейся скоростью изменения фазы, но тот же сигнал можно представить в виде суммы гармонических спектральных составляющих, имеющих свои частоты. Свойства мгновенной частоты и частоты спектральной составляющей различны, подробнее об этом можно прочитать, например, в книге Финка.

Циклическая частота


В теории электромагнетизма, теоретической физике, а также в некоторых прикладных электрорадиотехнических расчётах удобно использовать дополнительную величину — циклическую (круговую, радиальную, угловую) частоту (обозначается $ ~ {\omega} $). Циклическая частота связана с частотой колебаний соотношением $ ~\omega = 2\pi f $. В математическом смысле циклическая частота — это первая производная полной фазы колебаний по времени. Единица циклической частоты — радиан в секунду (

рад/с, rad/s) .

В механике при рассмотрении вращательного движения аналогом циклической частоты служит угловая скорость.

Частота дискретных событий

Частота дискретных событий (частота импульсов) — физическая величина, равная числу дискретных событий, происходящих за единицу времени. Единица частоты дискретных событий секунда в минус первой степени (

с⁻¹, s⁻¹), однако на практике для выражения частоты импульсов обычно используют герц.

Частота вращения

Частота вращения — физическая величина, равная числу полных оборотов за единицу времени. Единица частоты вращения — секунда в минус первой степени (с⁻¹, s⁻¹), оборот в секунду. Часто используются такие единицы, как оборот в минуту, оборот в час и т. д.

Другие величины, связанные с частотой

Метрологические аспекты

Измерения

Эталоны

Литература

Ссылки

См. также

---

Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: Частота. Список первоначальных авторов статьи можно посмотреть в

истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .

---