Сумматоры и цифровые компараторы: принцип работы, схемы
 Сумматоры — это комбинационные устройства, предназначенные для сложения чисел. Рассмотрим сложение двух одноразрядных двоичных чисел, для чего составим таблицу сложения (таблицу истинности), в которой отразим значения входных чисел А и В, значение результата суммирования S и значение переноса в старший разряд P (см. рис. 3.48).
Сумматоры — это комбинационные устройства, предназначенные для сложения чисел. Рассмотрим сложение двух одноразрядных двоичных чисел, для чего составим таблицу сложения (таблицу истинности), в которой отразим значения входных чисел А и В, значение результата суммирования S и значение переноса в старший разряд P (см. рис. 3.48).
Цифровые сумматоры
Работа устройства, реализующего таблицу истинность (рис. 3.48), описывается следующими уравнениями
S = А·В + А·В
Р = А·В
Очевидно, что по отношении: к столбцу S реализуется логическая функция «исключающее ИЛИ», т. е. S = А + В. Устройство, реализующее таблицу (рис. 3.48), называют полусумматором, и оно имеет логическую структуру, изображенную на рис. 3.49.

Поскольку полусумматор имеет только два входа, он может использоваться для суммирования лишь в младшем разряде.
При суммировании двух многоразрядных чисел для каждого разряда (кроме младшего) необходимо использовать устройство, имеющее дополнительный вход переноса. Такое устройство (рис. 3.50) называют полным сумматором и его можно представить как объединение двух полусумматоров (Рвх — дополнительный вход переноса). Сумматор обозначают через SM.

Цифровые компараторы
Цифровые компараторы выполняют сравнение двух чисел, заданных в двоичном коде. Они могут определять равенство двух двоичных чисел A и B с одинаковым количеством разрядов либо вид неравенства A> B или A < B. Цифровые компараторы имеют три выхода.
Схема одноразрядного компаратора представляет собой структуру логического элемента «исключающее ИЛИ-НЕ» (рис. 3.51).

Из анализа схемы следует, что если A= B, то F = 1, в противном случае, т. е. при А ≠ В, F = 0. Если А > В, т. е. А = 1, В = 0, то С = 1, а если А < В, т. е. А = 0, В = 1, то D = l.
Если попарно равны между собой все разряды двух n-разрядных двоичных чисел, то равны и эти два числа А и В. Применяя цифровой компаратор для каждого разряда, например, четырехзначных чисел, и определяя значения F1, F2, F3, F4 логических переменных на выходах компараторов, факт равенства А = В установим в случае, когда F = F1 · F2 · F3 · F4 = 1. Если же F = 0, то А ≠ В.
Неравенство А > В обеспечивается (для четырехразрядного числа) в четырех случаях: или А4 > В4, или А4 = В4 и А3 > В3, или А4 = В4, А3 = В3 и А2 > В2, или А4 = В4, А3 = В3, А2 = В2 и A1 > В1 (где А4 и В4 — старшие разряды чисел А и В). Очевидно, что если поменять местами А1 и B1, то будет выполняться неравенство А < В.
Цифровые компараторы выпускают, как правило, в виде самостоятельных микросхем. Так, микросхема К564ИП2 (рис. 3.52) является четырехразрядным компаратором, в котором каждый из одноразрядных компараторов аналогичен рассмотренной ранее схеме. Данная микросхема имеет расширяющие входы А < В, А = В, А > В, что позволяет наращивать разрядность обоих чисел. Для этого компараторы соединяют каскадно или параллельно (пирамидально).
 Рассмотрим каскадное соединение компараторов К564ИП2 для сравнения двух восьмиразрядных чисел (рис. 3.53). При этом соединении выходы А = В и А < В предыдущей микросхемы (младшие разряды) подключают к соответствующим входам последующей. На входы А < В, А = В, А > В микросхемы младших разрядов подают соответственно потенциалы U0 и U1 (U0 соответствует логическому 0, a U1 — «1»). В последующих микросхемах на входах А > В поддерживают потенциал логической единицы U1.
Рассмотрим каскадное соединение компараторов К564ИП2 для сравнения двух восьмиразрядных чисел (рис. 3.53). При этом соединении выходы А = В и А < В предыдущей микросхемы (младшие разряды) подключают к соответствующим входам последующей. На входы А < В, А = В, А > В микросхемы младших разрядов подают соответственно потенциалы U0 и U1 (U0 соответствует логическому 0, a U1 — «1»). В последующих микросхемах на входах А > В поддерживают потенциал логической единицы U1.
Цифровой компаратор — это… Что такое Цифровой компаратор?
Цифровой компаратор или компаратор амплитуд является электронным устройством, берущим два числа в двоичном виде и определяющим, является ли первое число меньшим, большим или равным второму числу.
Компараторы используются в центральных процессорах и микроконтроллерах. Примерами цифровых компараторов являются КМОП — 4063 и 4585, ТТЛ — 7485 и 74682-89.
Аналоговым эквивалентом цифрового компаратора является компаратор напряжений. Некоторые микроконтроллеры имеют аналоговые компараторы на некоторых своих входах, которые могут быть считаны или включать прерывание.
Таблица истинности компаратора
Действие однобитного цифрового компаратора может быть выражено таблицей истинности:
Действие двухцифрового компаратора может быть выражено таблицей истинности:
Выражения
Рассмотрим два 4-х битных числа A и B
Здесь каждая буква с цифрой представляет одну из цифр в числе.
- Равенство (эквивалентность)
Двоичные числа A и B будут равны, если все пары значащих цифр обоих чисел равны, т.е.,
, , и
Так как числа являются двоичными, то цифры являются или 0 или 1. Булева функция для равенства любых двух цифр и может быть выражена как
.
равна 1 только если и равны.
Для равенства A и B, все функции (для i=0,1,2,3) должны быть равны 1.
Состояние равенства A и B может быть выражено используя операции И, как
Двоичная функция (A=B) равна 1 только если все пары цифр двух чисел равны.
- Неравенство (неэквивалентность)
Чтобы определить наибольшее из двух двоичных чисел, мы рассмотрим отношение величин пар значащих цифр, начиная с наиболее значащих битов, последовательно продвигаясь к младшим значащим битам до нахождения неравенства. Когда неравенство найдено, то, если соответствующий бит A равен 1 и такой же бит B равен 0, то мы считаем, что A>B.
Это последовательное сравнение может быть выражено логически как:
(A>B) и (A < B) — выходные двоичные переменные, которые равны 1 когда A>B или A<B соответственно.
См. также
- 4000 серия
- 7400 серия
Ссылки
27.3 Цифровые компараторы
Цифровые компараторы – это КЦУ, предназначенные для сравнения двух двоичных чисел.
Обычно компаратор имеет входы наращивания разрядности, куда подключаются выходы результатов сравнения от другого компаратора. Это позволяет увеличивать разрядность сравниваемых чисел. УГО типичного цифрового компаратора приведено на рисунке 27.4. Работу цифрового компаратора можно представить следующим словесным описанием:
– если число А больше числа В, то активный уровень присутствует на выходе «А>В»;
– если число А меньше числа В, то активный уровень присутствует на выходе «А<В»;
– если число А равно числу В, то активный уровень без изменения копируется с одного из входов результата сравнения («А>В», «А=В» или «А<В») на одноимённый выход. При этом активный уровень должен присутствовать только на одном из этих входов.

Рисунок 27.4 – УГО цифрового компаратора
Если используется одиночная микросхема, то для ее правильной работы достаточно подать единицу на вход A = B, а состояния входов A<B и A>B не важны, на них можно подать как нуль, так и единицу. Если микросхемы компараторов кодов каскадируются (объединяются) для увеличения числа разрядов сравниваемых кодов, то надо выходные сигналы микросхемы, обрабатывающей младшие разряды кода, подать на одноименные входы микросхемы, обрабатывающей старшие разряды кода (рисунок 27.5).
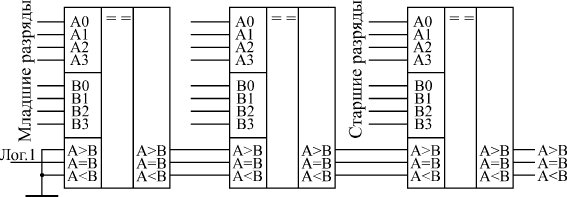
Рисунок 27.5 – Схема увеличения разрядности цифрового компаратора
Одно из основных применений компараторов кодов состоит в селектировании входных кодов. В этом случае достаточно иметь информацию только о совпадении кодов на входах компаратора, а не о соотношении их величин. Интересующий нас код (эталонный) подается на один вход компаратора, а изменяющийся код (входной) – на другой вход. Используется только выход равенства кодов А = В.
Микросхемы, выполняющие функции цифрового компаратора, кодируются буквами СП.
27.4 Схема проверки на чётность/нечётность
Схема проверки на чётность/нечётность – это КЦУ, сигнал на выходе которого будет активным, если количество единиц в поданном на вход двоичном наборе чётно/нечётно.
УГО типичной схемы проверки на чётность/нечётность приведено на рисунке 27.6. Описание работы схемы проверки на чётность/нечётность в таблице 27.3.
Наиболее важным применением схем проверки на четность/нечетность является проверка ситуации когда полученные с линии или извлеченные из памяти данные искажены ошибкой и использовать их нельзя. Общая схема организации контроля показана на рисунке 27.7.

Рисунок 27.6 – УГО Схемы проверки на четность/нечетность
Таблица 27.3 – Таблица истинности схемы проверки на четность/нечетность
Входы | Выход чётности | |||
D0 | D1 | D2 | Q0 | |
0 | 0 | 0 | 0 | 1 |
0 | 0 | 0 | 1 | 0 |
0 | 0 | 1 | 0 | 0 |
0 | 0 | 1 | 1 | 1 |
0 | 1 | 0 | 0 | 0 |
0 | 1 | 0 | 1 | 1 |
0 | 1 | 1 | 0 | 1 |
0 | 1 | 1 | 1 | 0 |
1 | 0 | 0 | 0 | 0 |
1 | 0 | 0 | 1 | 1 |
1 | 0 | 1 | 0 | 1 |
1 | 0 | 1 | 1 | 0 |
1 | 1 | 0 | 0 | 1 |
1 | 1 | 0 | 1 | 0 |
1 | 1 | 1 | 0 | 0 |
1 | 1 | 1 | 1 | 1 |
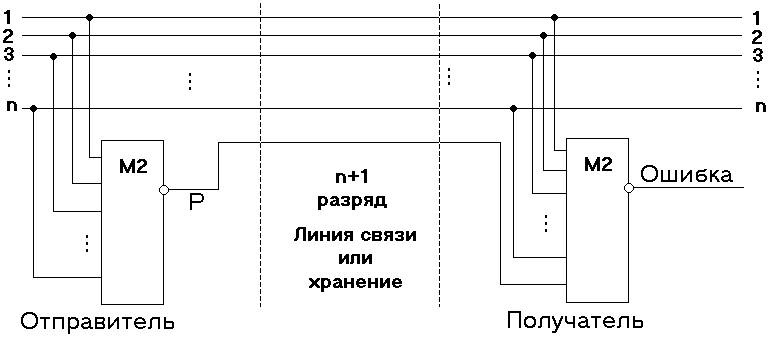
Рисунок 27.7 – Схема организации контроля линии связи
На приемном конце линии или после чтения из памяти от полученного (n+1)-разрядного слова снова берется свертка по четности. Если значение этой свертки равно 1, то или в передаваемом слове, или в контрольном разряде при передаче или хранении произошла ошибка. Столь простой контроль не позволяет исправить ошибку, но он, по крайней мере, дает возможность при обнаружении ошибки исключить неверные данные, затребовать повторную передачу и т.д.
Контроль по четности – самый дешевый по аппаратурным затратам вид контроля, и применяется он очень широко. Практически любой канал передачи цифровых данных или запоминающее устройство, если они не имеют какого-либо более сильного метода контроля, защищены контролем по четности.
Микросхемы, выполняющие функции схемы проверки на чётность/нечётность кодируются буквами ИП.
Лекция № 28
СУММАТОРЫ
Цифровой компаратор — Википедия. Что такое Цифровой компаратор
Цифрово́й компара́тор или компара́тор ко́дов логическое устройство с двумя словарными входами, на которые подаются два разных двоичных слова равной в битах длины и обычно с тремя двоичными выходами, на которые выдаётся признак сравнения входных слов, — первое слово больше второго, меньше или слова равны. При этом выходы «больше», «меньше» имеют смысл, если входные слова кодируют числа в том или ином машинном представлении.
Часто цифровые компараторы не имеют выходов «больше», «меньше», а только выход «равно».
Может быть построен на логических элементах, работа которых основана на самых различных физических принципах, но современные компараторы обычно представляют собой полупроводниковые электронные устройства работающие в двоичной логике.
Промышленностью компараторы выпускаются в виде законченных компонентов — микросхем с разной длиной сравниваемых слов и других параметров. Примеры микросхем цифровых компараторов: КМОП-логика — 4063 и 4585, ТТЛ — 7485 и 74682-89 и многие другие.
Компараторы широко используются в вычислительной технике, измерительной технике, радио- и проводной связи, бытовых приборах. Например, цифровые часы с будильником содержат цифровой компаратор, при совпадении текущего времени с заданным, подается звуковой сигнал.
Аналоговым эквивалентом цифрового компаратора является аналоговый компаратор напряжений или токов. Некоторые микроконтроллеры имеют входные встроенные аналоговые компараторы, состояние выходов которых может быть считано программой контроллера или вызывать её прерывание подпрограммой.
Логические функции
Для примера рассмотрим два 4-х битных слова A{\displaystyle A} и B{\displaystyle B}, пусть эти слова представляют собой некоторые натуральные числа, представленные в двоичном виде, причем 3-й разряд будет старшим:
- A=A3,A2,A1,A0{\displaystyle A=A_{3},A_{2},A_{1},A_{0}},
- B=B3,B2,B1,B0{\displaystyle B=B_{3},B_{2},B_{1},B_{0}}
Здесь каждая буква с нижним цифровым индексом представляет один из битов в числах.
- Равенство (эквивалентность)
Двоичные числа A{\displaystyle A} и B{\displaystyle B} будут равны, если все пары соответственных битов обоих чисел равны, то есть:
- A3=B3{\displaystyle A_{3}=B_{3}}, A2=B2{\displaystyle A_{2}=B_{2}}, A1=B1{\displaystyle A_{1}=B_{1}} и A0=B0{\displaystyle A_{0}=B_{0}}.
В двоичной записи чисел их цифры это или 0, или 1. Булева функция для равенства любых двух цифр Ai{\displaystyle A_{i}} и Bi{\displaystyle B_{i}} (здесь логическая операция «ИЛИ» обозначена символом +{\displaystyle +}, а «И» символом точки) может быть выражена как:
- xi=Ai⋅Bi+A¯i⋅B¯i{\displaystyle x_{i}=A_{i}\cdot B_{i}+{\overline {A}}_{i}\cdot {\overline {B}}_{i}}.
При этом xi{\displaystyle x_{i}} равна 1 только если Ai{\displaystyle A_{i}} и Bi{\displaystyle B_{i}} равны.
Для равенства Ai{\displaystyle A_{i}} и Bi{\displaystyle B_{i}}, все функции xi{\displaystyle x_{i}} (для i = 0, 1, 2, 3) должны быть равны 1.
Поэтому признак равенства Ai{\displaystyle A_{i}} и Bi{\displaystyle B_{i}} записывается в виде логической функции как
- (A=B)=x3⋅x2⋅x1⋅x0{\displaystyle \ (A=B)=x_{3}\cdot x_{2}\cdot x_{1}\cdot x_{0}}.
Двоичная функция (A=B){\displaystyle (A=B)} равна 1 только если все пары цифр двух чисел равны.
- Неравенство (неэквивалентность)
Чтобы определить наибольшее из двух двоичных чисел, мы рассмотрим отношение величин пар значащих цифр, начиная со старших битов к младшим битам до нахождения неравенства в некоторой позиции. Когда неравенство найдено, то, если соответствующий бит A{\displaystyle A} равен 1 и такой же бит B{\displaystyle B} равен 0, то мы считаем, что A>B{\displaystyle A>B}.
Это последовательное сравнение может быть выражено логическими выражениями как:
- (A>B)=A3⋅B¯3+x3⋅A2⋅B¯2+x3⋅x2⋅A1⋅B¯1+x3⋅x2⋅x1⋅A0⋅B¯0{\displaystyle (A>B)=A_{3}\cdot {\overline {B}}_{3}+x_{3}\cdot A_{2}\cdot {\overline {B}}_{2}+x_{3}\cdot x_{2}\cdot A_{1}\cdot {\overline {B}}_{1}+x_{3}\cdot x_{2}\cdot x_{1}\cdot A_{0}\cdot {\overline {B}}_{0}},
- (A<B)=A¯3⋅B3+x3⋅A¯2⋅B2+x3⋅x2⋅A¯1⋅B1+x3⋅x2⋅x1⋅A¯0⋅B0{\displaystyle (A<B)={\overline {A}}_{3}\cdot B_{3}+x_{3}\cdot {\overline {A}}_{2}\cdot B_{2}+x_{3}\cdot x_{2}\cdot {\overline {A}}_{1}\cdot B_{1}+x_{3}\cdot x_{2}\cdot x_{1}\cdot {\overline {A}}_{0}\cdot B_{0}}.
(A>B){\displaystyle (A>B)} и (A<B){\displaystyle (A<B)} — выходные двоичные переменные, которые равны 1 когда A>B{\displaystyle A>B} или A<B{\displaystyle A<B} соответственно.
Таблицы истинности компаратора
Для примеров приведены таблицы истинности тривиального однобитового и двухбитового компараторов.
Логическая функция однобитового цифрового компаратора описывается таблицей истинности:
Таблица истинности двухбитового компаратора:
См. также
Ссылки
Цифровой компаратор — Википедия
Цифрово́й компара́тор или компара́тор ко́дов логическое устройство с двумя словарными входами, на которые подаются два разных двоичных слова равной в битах длины и обычно с тремя двоичными выходами, на которые выдаётся признак сравнения входных слов, — первое слово больше второго, меньше или слова равны. При этом выходы «больше», «меньше» имеют смысл, если входные слова кодируют числа в том или ином машинном представлении.
Часто цифровые компараторы не имеют выходов «больше», «меньше», а только выход «равно».
Может быть построен на логических элементах, работа которых основана на самых различных физических принципах, но современные компараторы обычно представляют собой полупроводниковые электронные устройства работающие в двоичной логике.
Промышленностью компараторы выпускаются в виде законченных компонентов — микросхем с разной длиной сравниваемых слов и других параметров. Примеры микросхем цифровых компараторов: КМОП-логика — 4063 и 4585, ТТЛ — 7485 и 74682-89 и многие другие.
Компараторы широко используются в вычислительной технике, измерительной технике, радио- и проводной связи, бытовых приборах. Например, цифровые часы с будильником содержат цифровой компаратор, при совпадении текущего времени с заданным, подается звуковой сигнал.
Аналоговым эквивалентом цифрового компаратора является аналоговый компаратор напряжений или токов. Некоторые микроконтроллеры имеют входные встроенные аналоговые компараторы, состояние выходов которых может быть считано программой контроллера или вызывать её прерывание подпрограммой.
Логические функции
Для примера рассмотрим два 4-битных слова A{\displaystyle A} и B{\displaystyle B}, пусть эти слова представляют собой некоторые натуральные числа, представленные в двоичном виде, причем 3-й разряд будет старшим:
- A=A3,A2,A1,A0{\displaystyle A=A_{3},A_{2},A_{1},A_{0}},
- B=B3,B2,B1,B0{\displaystyle B=B_{3},B_{2},B_{1},B_{0}}
Здесь каждая буква с нижним цифровым индексом представляет один из битов в числах.
- Равенство (эквивалентность)
Двоичные числа A{\displaystyle A} и B{\displaystyle B} будут равны, если все пары соответственных битов обоих чисел равны, то есть:
- A3=B3{\displaystyle A_{3}=B_{3}}, A2=B2{\displaystyle A_{2}=B_{2}}, A1=B1{\displaystyle A_{1}=B_{1}} и A0=B0{\displaystyle A_{0}=B_{0}}.
В двоичной записи чисел их цифры это или 0, или 1. Булева функция для равенства любых двух цифр Ai{\displaystyle A_{i}} и Bi{\displaystyle B_{i}} (здесь логическая операция «ИЛИ» обозначена символом +{\displaystyle +}, а «И» символом точки) может быть выражена как:
- xi=Ai⋅Bi+A¯i⋅B¯i{\displaystyle x_{i}=A_{i}\cdot B_{i}+{\overline {A}}_{i}\cdot {\overline {B}}_{i}}.
При этом xi{\displaystyle x_{i}} равна 1 только если Ai{\displaystyle A_{i}} и Bi{\displaystyle B_{i}} равны.
Для равенства Ai{\displaystyle A_{i}} и Bi{\displaystyle B_{i}}, все функции xi{\displaystyle x_{i}} (для i = 0, 1, 2, 3) должны быть равны 1.
Поэтому признак равенства Ai{\displaystyle A_{i}} и Bi{\displaystyle B_{i}} записывается в виде логической функции как
- (A=B)=x3⋅x2⋅x1⋅x0{\displaystyle \ (A=B)=x_{3}\cdot x_{2}\cdot x_{1}\cdot x_{0}}.
Двоичная функция (A=B){\displaystyle (A=B)} равна 1 только если все пары цифр двух чисел равны.
- Неравенство (неэквивалентность)
Чтобы определить наибольшее из двух двоичных чисел, мы рассмотрим отношение величин пар значащих цифр, начиная со старших битов к младшим битам до нахождения неравенства в некоторой позиции. Когда неравенство найдено, то, если соответствующий бит A{\displaystyle A} равен 1 и такой же бит B{\displaystyle B} равен 0, то мы считаем, что A>B{\displaystyle A>B}.
Это последовательное сравнение может быть выражено логическими выражениями как:
- (A>B)=A3⋅B¯3+x3⋅A2⋅B¯2+x3⋅x2⋅A1⋅B¯1+x3⋅x2⋅x1⋅A0⋅B¯0{\displaystyle (A>B)=A_{3}\cdot {\overline {B}}_{3}+x_{3}\cdot A_{2}\cdot {\overline {B}}_{2}+x_{3}\cdot x_{2}\cdot A_{1}\cdot {\overline {B}}_{1}+x_{3}\cdot x_{2}\cdot x_{1}\cdot A_{0}\cdot {\overline {B}}_{0}},
- (A<B)=A¯3⋅B3+x3⋅A¯2⋅B2+x3⋅x2⋅A¯1⋅B1+x3⋅x2⋅x1⋅A¯0⋅B0{\displaystyle (A<B)={\overline {A}}_{3}\cdot B_{3}+x_{3}\cdot {\overline {A}}_{2}\cdot B_{2}+x_{3}\cdot x_{2}\cdot {\overline {A}}_{1}\cdot B_{1}+x_{3}\cdot x_{2}\cdot x_{1}\cdot {\overline {A}}_{0}\cdot B_{0}}.
(A>B){\displaystyle (A>B)} и (A<B){\displaystyle (A<B)} — выходные двоичные переменные, которые равны 1 когда A>B{\displaystyle A>B} или A<B{\displaystyle A<B} соответственно.
Таблицы истинности компаратора
Для примеров приведены таблицы истинности тривиального однобитового и двухбитового компараторов.
Логическая функция однобитового цифрового компаратора описывается таблицей истинности:
Таблица истинности двухбитового компаратора:
См. также
Ссылки
Глава 5. Цифровые компараторы
F< = a3b3 + a3 Å b3 ×a2b2 +
+ a3 Å b3 ×a2 Å b2 ×a1b1 + (5.9) + a3 Å b3 ×a2 Å b2 ×a1 Å b1 × a0b0 +
+ a3 Å b3 ×a2 Å b2 ×a1 Å b1 × a0 Å b0 × f<.
Отношение F= будет выполняться, когда все разряды сравниваемых чисел равны:
F= = | a3 Å b3 | × | a2 Å b2 | × | a1 Å b1 | × | a0 Å b0 | × f= , | (5.10) |
где f= — отношение А = В для всей оставшейся части младших разрядов сравниваемых чисел. Выражение для F> может быть записано либо по форме, аналогичной уравнению (5.9), а именно:
F> = a3b3 + a3 Å b3 ×a2 b2 +
+ a3 Å b3 ×a2 Å b2 ×a1b1 + (5.11) + a3 Å b3 ×a2 Å b2 ×a1 Å b1 ×a0 b0 +
+ a3 Å b3 ×a2 Å b2 ×a1 Å b1 ×a0 Å b0 × f> ,
где f> — отношение А > B для всей оставшейся части младших разрядов сравниваемых чисел, либо в виде (см. выражение (5.6))
|
|
|
|
|
|
|
|
|
|
|
|
F> = | F | < × | F | = × f> = | F< + F= | × f> = F< + F= + | f | > . | (5.12) | ||
Применяя формальные методы минимизации, для функций F< и F> можно получить следующие выражения:
F< = a3b3 + a3b3 ×a2b2 +
+ a3b3 × a2b2 ×a1b1 + (5.13)
+a3b3 × a2b2 ×a1b1 ×a0b0 +
+a3b3 × a2b2 ×a1b1 ×a0 b0 × f< ,
F> = a3b3 + a3b3 ×a2b2 +
|
|
|
|
|
|
|
|
|
|
|
|
+ | a | 3b3 × | a | 2b2 | ×a1 | b | 1 | + | |||
|
|
|
|
|
|
|
|
|
|
| (5.14) |
+a3b3 × a2b2 ×a1b1 ×a0 b0 +
+a3b3 × a2b2 ×a1b1 ×a0b0 × f>.
Итак, зная четыре старших разряда сравниваемых многоразрядных чисел и сигналы отношения f<, f= и f> для всей оставшейся части младших разрядов этих чисел, можно легко вычислить окончательные
отношения F<, F= и F>.
Если теперь требуется увеличить разрядность сравниваемых чисел в сторону старших разрядов на четыре (см. числа A′ и B′ в верхней части рис.5.1), то и в этом случае можно записать те же уравнения (5.9) — (5.14), причём в качестве f<, f= и f> в них будут фигурировать отношения F<, F= и F>, полученные для нижней части рис.5.1. Ясно, что таким образом можно увеличивать разрядность сравниваемых чисел до любой величины, причём не требуется никаких дополнительных логических элементов.
Входы ai и bi принято называть информационными, а входы f<, f= и f> — расширительными или каскадными. Примерами таких изделий могут служить интегральные схемы типа 134СП1 (74L85), К555СП1 (SN74LS85N), 564ИП2 (CD4585AK), CD4063B и др. Хотя в функциональном отношении все эти интегральные схемы близки друг другу, нужно знать, что они выполняют несколько различающиеся функции, т.е. не являются полностью взаимозаменяемыми. Различия определяются прежде всего тем, по каким конкретно уравнениям реализуются отношения F<, F= и F> этих микросхем. Именно последнее будет определять, как выполняются в них другие важные требования, предъявляемые к наращиваемым компараторам, а именно:
•если для четырёх информационных разрядов отдельно взятой микросхемы выполняется отношение А
<B или А > В, то её соответствующие выходные сигналы не должны зависеть от сигналов f<, f= и f>;
Компараторы цифровых сигналов
Сравнение кодированных сигналов осуществляется с помощью цифровых компараторов. Цифровые компараторы выполняют сравнение двух чисел, заданных в двоичном (двоично-десятичном) коде. В зависимости от схемного исполнения компараторы могут определять равенство А = В (А и В – независимые числа с равным количеством разрядов) либо определять вид неравенства: А < В или А > В. Результат сравнения отображается соответствующим логическим уровнем на выходе.
Цифровые компараторы широко применяются для выявления нужного числа (слова) в потоке цифровой информации, для отметки времени в часовых приборах, для выполнения условных переходов в вычислительных устройствах, реализации программно управляемых приоритетов в системах прерывания компьютеров и т. д.
Ниже приведены схемы одноразрядного (рис. 11.11) и двухразрядного компараторов (рис. 11.12).

Рис. 11.11. схема сравнения одноразрядных чисел

Рис. 11.12. схема определения неравенства двухразрядных чисел
Многоразрядные компараторы строятся на базе одноразрядных. Применяют два способа построения многоразрядных компараторов. При первом способе сравнение идет последовательно разряд за разрядом. При появлении неравенства в каком-либо из разрядов, сравнение прекращается и выдается результат сравнения. Если неравенство оказывается в последнем разряде, то должна быть выполнена операция сравнения для всех разрядов. Это занимает много времени.
Схема сравнения многоразрядных чисел по первому способу представлена на рис. 11.13. Более быстрый способ – сравнение во всех разрядах одновременно и анализ результатов поразрядного сравнения.
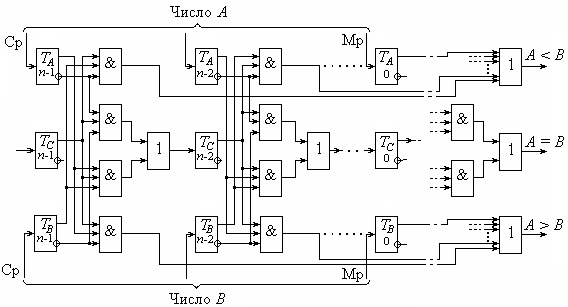
Рис. 11.13. Схема сравнения многоразрядных чисел
Нашей промышленностью выпускаются компараторы ТТЛ 555СП1, 531СП1, КМОП 561ИП2 и др. Компаратор 555СП1 – четырехразрядный, имеет 11 входов (рис. 11.14). Четыре пары входов принимают для анализа два четырехразрядных слова А0-А3 и В0-В3. Три входа (A < В), (A = В), (A > В) нужны для создания схемы наращивания, т. е. увеличения емкости компаратора. Компаратор имеет три выхода результатов анализа: A > В, A < В, A = В.
Соотношения входных и выходных сигналов компаратора представлены в табл. 11.6. Шесть последних строк таблицы отражают режим наращивания каскадов, который может быть последовательным или параллельным. При последовательном наращивании выходы A > В, A < В, A = В от схемы, анализирующей младшие разряды, следует присоединить к одноименным входам последующего каскада (рис. 11.15). Этим способом при двух компараторах СП1 можно сравнить два восьмиразрядных слова. Нетрудно подсчитать число каскадов для любой большей длины слова. Однако каждый последующий каскад увеличит общее время задержки распространения сигнала на 15 нс.
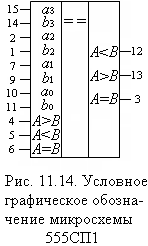
Рис. 11.14 Условное графическое обозначение микросхемы 555 СП1
Таблица 11.6
№ п.п. | Сравниваемые данные | Входы наращивания каскадов | Выходы | |||||||
а3, b3 | а2, b2 | аb, b1 | а0, b0 | A>B | A<B | A=B | A>B | A<B | A=B | |
1 | а3>b3 | X | X | X | X | X | X | 1 | 0 | 0 |
2 | а3<b3 | X | X | X | X | X | X | 0 | 1 | 0 |
3 | а3=b3 | а2>b2 | X | X | X | X | X | 1 | 0 | 0 |
4 | а3=b3 | а2<b2 | X | X | X | X | X | 0 | 1 | 0 |
5 | « | а2=b2 | a1>b1 | X | X | X | X | 1 | 0 | 0 |
6 | « | а2=b2 | a1<b1 | X | X | X | X | 0 | 1 | 0 |
7 | « | « | a1=b1 | а0>b0 | X | X | X | 1 | 0 | 0 |
8 | « | « | a1=b1 | а0<b0 | X | X | X | 0 | 1 | 0 |
9 | « | « | « | а0=b0 | 1 | 0 | 0 | 1 | 0 | 0 |
10 | « | « | « | а0=b0 | 0 | 1 | 0 | 0 | 1 | 0 |
11 | « | « | « | « | 0 | 0 | 1 | 0 | 0 | 1 |
12 | « | « | « | « | X | X | 1 | 0 | 0 | 1 |
13 | « | « | « | « | 1 | 1 | 0 | 0 | 0 | 0 |
14 | « | « | « | « | 0 | 0 | 0 | 1 | 1 | 1 |
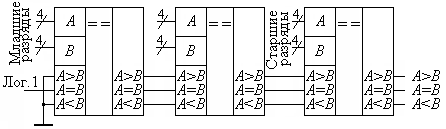
Рис. 11.15. Последовательная схема объединения компараторов
Девятая и десятая строки табл. 11.6 говорят о том, что входы A > В и A < В могут служить пятой парой разрядных входов. Тогда одиночный компаратор можно использовать как пятиразрядный.
При применении компараторов надо учитывать, что при каскадировании задержки микросхем суммируются, и объединенный компаратор, состоящий из n микросхем, будет в n раз медленнее одиночного.
Если важен только факт равенства или неравенства сравниваемых кодов, то увеличить быстродействие при параллельном объединении компараторов можно, путём подачи их выходных сигналов A = В на логический элемент И (рис. 11.16). В этом случае суммарная задержка схемы составит задержку одного компаратора плюс задержку логического элемента И. Более подробные сведения о многокаскадных компараторах можно посмотреть, например, в [9, 11].
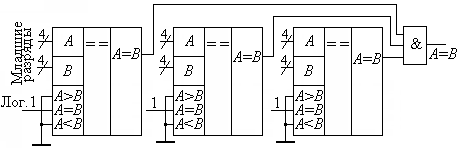
Рис. 11.16. Параллельная схема увеличения разрядности для оценки
равенства чисел
Компаратор КМОП серии 561ИП2 имеет несколько отличных режимов работы: например при всех низких уровнях входных сигналов A > В, A = В, A < В выходные A > В, A = В, A < В также низкие (у 555СП1 A > В и A < В высокие), т. е. для анализа работы компаратора надо использовать другую таблицу.



