КУЛОНА ЗАКОН — это… Что такое КУЛОНА ЗАКОН?
— один из осн. законов электростатики, определяющий величину и направление силы взаимодействия между двумя неподвижными точечными зарядами. Экспериментально с достаточной точностью впервые доказан около 1773 Г. Кавендишем (Н. Cavendish), использовавшим метод сферич. конденсатора: отсутствие поля внутри заряж. сферы доказывает, что сила эл.-статич. взаимодействия меняется обратно пропорционально квадрату расстояния; однако результаты Кавендиша не были опубликованы. В 1785 закон был установлен Ш. О. Кулоном (Ch. A. Coulomb) с помощью спец. крутильных весов. Согласно К. з., два точечных заряда взаимодействуют друг с другом в вакууме с силой, пропорциональной произведению величин зарядов e1 и е2 и обратно пропорциональной квадрату расстояния г между ними: F=ke1e2/r2, где k — коэф. пропорциональности, зависящий от выбора единиц измерений. В Гаусса системе единиц k
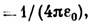
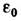 — электрическая постоянная. Сила взаимодействия направлена по прямой, соединяющей заряды, причём одноимённые заряды отталкиваются, а разноимённые притягиваются. Силы, определяемые К. з., подчиняются принципу суперпозиции. В однородном диэлектрике сила взаимодействия между точечными зарядами уменьшается в
— электрическая постоянная. Сила взаимодействия направлена по прямой, соединяющей заряды, причём одноимённые заряды отталкиваются, а разноимённые притягиваются. Силы, определяемые К. з., подчиняются принципу суперпозиции. В однородном диэлектрике сила взаимодействия между точечными зарядами уменьшается в 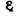 раз: где
раз: где 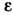 — диэлектрич. проницаемость.
— диэлектрич. проницаемость.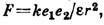
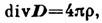 где D — вектор электрич. индукции,
где D — вектор электрич. индукции,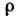 — плотность заряда. Для макроскопич. расстояний с помощью экспериментов в земных условиях, проведённых по методу Кавендиша, доказано (1971), что показатель степени для г в К. з. не может отличаться от -2 более чем на 6 *10
— плотность заряда. Для макроскопич. расстояний с помощью экспериментов в земных условиях, проведённых по методу Кавендиша, доказано (1971), что показатель степени для г в К. з. не может отличаться от -2 более чем на 6 *10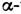 частиц следует, что К. з. не нарушается вплоть до расстояний
частиц следует, что К. з. не нарушается вплоть до расстояний 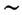 10 -12 см. Впрочем, для описания взаимодействия заряж. частиц на таких расстояниях понятия, с помощью к-рых формулируется К. з., в частности понятия силы и положения частицы, вообще говоря, неприменимы. В этой области пространственных масштабов действуют законы квантовой физики. К. з. можно считать одним из предельных следствий квантовой электродинамики (КЭД), в рамках к-рой взаимодействие заряж. частиц обусловлено обменом фотонами. Вследствие этого эксперименты по проверке выводов КЭД можно рассматривать как опыты по проверке К. з. Так, опыты по аннигиляции электронов и позитронов показали, что отклонений от законов КЭД не наблюдается вплоть до расстояний ~10
10 -12 см. Впрочем, для описания взаимодействия заряж. частиц на таких расстояниях понятия, с помощью к-рых формулируется К. з., в частности понятия силы и положения частицы, вообще говоря, неприменимы. В этой области пространственных масштабов действуют законы квантовой физики. К. з. можно считать одним из предельных следствий квантовой электродинамики (КЭД), в рамках к-рой взаимодействие заряж. частиц обусловлено обменом фотонами. Вследствие этого эксперименты по проверке выводов КЭД можно рассматривать как опыты по проверке К. з. Так, опыты по аннигиляции электронов и позитронов показали, что отклонений от законов КЭД не наблюдается вплоть до расстояний ~10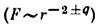 от -2 позволяет определить верх. предел возможной массы покоя фотона
от -2 позволяет определить верх. предел возможной массы покоя фотона 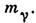
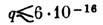 соответствует кг.
соответствует кг. К. з. наз. также закон, определяющий 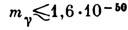 силу взаимодействия двух магн. полюсов:
силу взаимодействия двух магн. полюсов: 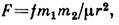 где m1 и m2 — т. н. магн. заряды,
где m1 и m2 — т. н. магн. заряды, 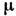 — магн. проницаемость среды, f — коэф. пропорциональности, зависящий от выбора системы единиц и в общем случае не равный
— магн. проницаемость среды, f — коэф. пропорциональности, зависящий от выбора системы единиц и в общем случае не равный
Лит.: Тамм И. Е., Основы теории электричества, 9 изд., М., 1976, гл. 1; Ландау Л. Д., Лифшиц Е. М., Теория поля, 7 изд., М., 1988, гл. 5; Сивухин Д. В., Общий курс физики, 2 изд., т. 3 — Электричество, М., 1983.
С. Р. Филонович,
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
Кулона закон — это… Что такое Кулона закон?
основной закон электростатики, определяющий силу взаимодействия F двух неподвижных точечных электрических зарядов. Согласно закону Кулона, F прямо пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между ними. Открыт Ш. Кулоном в 1785.
КУЛО́НА ЗАКО́Н, один из основных законов электростатики (см. ЭЛЕКТРОСТАТИКА), определяющий величину и направление силы взаимодействия между двумя неподвижными точечными электрическими зарядами. Установлен Ш. О. Кулоном (см. КУЛОН Шарль Огюстен) в 1785 г.В своих опытах Кулон измерял силы притяжения и отталкивания заряженных шариков с помощью крутильных весов (
На основании многочисленных опытов Кулон установил следующий закон:
Сила взаимодействия неподвижных зарядов, находящихся в вакууме, прямо пропорциональна произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними:
F = k .(Q1Q2/r2)
Сила F направлена по прямой, соединяющей взаимодействующие заряды, т. е. является центральной. Кулоновские силы могут быть как силами притяжения, так и силами отталкивания. Если F 0 для одноименных зарядов, то между зарядами действует сила отталкивания. Эта сила называется кулоновской силой.
Закон Кулона справедлив для точечных заряженных тел в вакууме, а так же для шаров, радиусы которых соизмеримы с расстояниями между их центрами (заряды распределены равномерно). Практически закон Кулона хорошо выполняется, если размеры заряженных тел много меньше расстояния между ними.
F = (1/4peo).(Q1Q2/r2)
(1/4peo) = 9.109 м/Ф.
Если взаимодействующие заряды находятся в однородной и изотропной среде, то кулоновская сила:
F =(1/4peo).(Q1Q2/r2),
e — диэлектрическая проницаемость (см. ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ) среды, безразмерная величина, показывающая, во сколько раз сила взаимодействия между зарядами в данной среде меньше силы их взаимодействия в вакууме.
Опыт показывает, что силы кулоновского взаимодействия подчиняются принципу суперпозиции (см. СУПЕРПОЗИЦИИ ПРИНЦИП).
Если заряженное тело взаимодействует одновременно с несколькими заряженными телами, то результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других заряженных тел.
Закон Кулона служит одним из экспериментальных оснований классической электродинамики; его обобщение приводит, в частности, к теореме Гаусса (см. ГАУССА ТЕОРЕМА).
Законом Кулона называется также закон, определяющий силу взаимодействия двух магнитных полюсов:
Этот закон установлен Ш. О. Кулоном практически одновременно с законом взаимодействия электрических зарядов, но не имеет такого общего характера, как закон для электрических сил, так как носит условный характер в связи с тем, магнитные заряды в природе не существуют.
Закон Кулона и его полевая трактовка
Историческая справка
Закон Кулона входит в число основных экспериментальных фактов, находящихся в основании теории б электричестве. Этот закон для определения силы взаимодействия точечных зарядов $q_1\ $ и $q_2$, которые находятся на расстоянии $r$, имеет вид:
где ${\varepsilon }_0=8,8\cdot {10}^{-12}\frac{Ф}{м}$.
Этот закон установлен Ш. Кулоном в 1785 г. экспериментально. Кулон измерял силы взаимодействия заряженных тел. Точность опытов была плохой, только аналогии с силами тяготения дала уверенность в том, что закон в виде (1) справедлив. С результатами эксперимента, обычно сравнивают следствия из закона Кулона, и на этой основе делается вывод о точности и границах применения данного закона. Первая проверка закона была проведена Кавендишем за 13 лет до Кулона. Кавендиш работ не публиковал, но надо отметить, что его метод был более точным, чем эксперименты Кулона. Позднее опыты по проверке закона Кулона проводил Максвелл. Эти опыты подтвердили справедливость закона Кулона с большой точностью. В соответствии с современными представлениями электромагнитные взаимодействия осуществляются посредством фотонов. Вследствие чего вопрос о справедливости закона Кулона сводится к вопросу о равенстве массы фотона нулю. Все частицы обладают корпускулярными и волновыми свойствами. Энергия фотона (${\varepsilon }_{\nu }=h\nu $) и ${\varepsilon }_{\nu }=m_{\nu }c^2$, где $m_{\nu }$ — масса фотона, $h$ — постоянная Планка. Масса $m_{\nu}$ больше массы покоя, если у фотона масса отлична от нуля. Следовательно, если найти верхний предел для $m_{\nu }$, получим ограничение для массы покоя фотона. Если существование электромагнитных волн с большой длиной волны (а лучше бесконечной) доказать, то можно утверждать, что $m_{\nu }$ очень мало. Наиболее длинные электромагнитные волны, которые удалось наблюдать на сегодняшний момент, образуются в виде стоячих волн в пространстве между поверхностью Земли и ионосферой. Они носят имя Шумана, а точнее называются резонансами Шумана. Минимальный резонанс Шумана соответствует частоте $\nu $=8Гц. С учетом расстояния от поверхности Земли было получено, что $m_{\nu }
Для малых расстояний закон Кулона проверяется в экспериментах, связанных с элементарными частицами. Уже опыты Резерфорда доказали, что закон Кулона справедлив с большой точностью на расстоянии ${10}^{-15}м$.
До работ Фарадея закон Кулона трактовался с позиций дальнодействия, то есть считалось, что одно тело действует на другое без посредников (действие на расстоянии). В первой половине 18 века сложился другой взгляд на механизм взаимодействия, в соответствии с которым существует посредник, осуществляющий непрерывную передачу сил.(теория близкодействия). Поначалу таким посредником назначили, так называемый Мировой эфир. Состояние которого характеризовали некоторыми механическими свойствами. Попытка математического описания механической картины передачи электрических взаимодействий была сделана Максвеллом. Он пытался представить электромагнитные силы в виде механических сил, которые вызываются натяжением и давлением в эфире. Позже Максвелл перешел к феноменологической формулировке взаимодействия и охарактеризовал состояние среды с помощью векторов: напряженности электростатического поля ($\overrightarrow{E}$), электрического смещения ($\overrightarrow{D}$), напряженности магнитного поля ($\overrightarrow{H}$), магнитной индукции ($\overrightarrow{B}$), которым не дал никакой механической интерпретации. В 1864 г. Максвелл сформулировал уравнения электромагнитного поля (уравнения Максвелла). Надежда на механическое толкование электромагнитных взаимодействий умерла. Поле стало основной сущностью, посредством которого осуществляется электромагнитное взаимодействие. Оно характеризуется величинами, которые не могут интерпретироваться в рамках механики. После того как Герц записал уравнения Максвелла в современном виде стало очевидно, что поле существует в пространстве и времени наряду с материей.
Полевая трактовка закона Кулона
Пусть мы имеем два точечных заряда $q_1\ (точка\ 1)\ $ и $q_2$(точка 2).Тогда ${\overrightarrow{F}}_{12}$- сила, с которой заряд $q_1$ действует на заряд $q_2$. ${\overrightarrow{F}}_{21}$- сила, с которой заряд $q_2$ действует на заряд $q_1$. ${\overrightarrow{r}}_{12}$- вектор из точки (1) в точку (2), ${\overrightarrow{r}}_{21}$ — вектор из точки (2) в точку (1). Исходя из принятых нами обозначений, запишем закон Кулона:
По своему физическому содержанию формулы (2) и (3) различны. Они определяют силы, которые действуют на второй (2) и первый (3) заряды, то есть описывают силы в разных точках пространства. Механизм же возникновения этих сил одинаков. Заряды вокруг себя создают электрическое поле. Это поле принято характеризовать напряженностью ($\overrightarrow{E}$). Напряженностью электрического поля является физическая величина, которая равна отношению силы, с которой действует поле на положительный заряд, помещенный в данную точку поля к заряду. Соответственно, с учетом (2,3), запишем:
Соответственно:
Формула (4) описывает напряженность электрического поля, которое образуется зарядом $q_1.$ Формула (5) характеризует силу, с которой поле с напряженностью ${\overrightarrow{E}}_2$ действует на заряд, который находится в точке поля. Действие одного заряда на другой делится на:
- Точечный заряд создает вокруг себя электрическое поле, напряженность которого равна: \[\overrightarrow{E}=\frac{1}{4\pi {\varepsilon }_0}\frac{q}{r^2}\frac{\overrightarrow{r}}{r}\ \left(8\right),\]
- На точечный заряд q, который находится в точке поля с напряженностью $\overrightarrow{E}$, действует сила равная: \[\overrightarrow{F}=q\overrightarrow{E}\ \left(9\right).\]
где $\overrightarrow{r}$- радиус — вектор, проведенный из точки нахождения заряда до точки, в которой определяется напряженность.
Эти два утверждения дают полевую трактовку Закона Кулона.
Если имеется несколько источников поля (количество зарядов $N$), то результирующую силу, действующую на пробный заряд $q$ можно найти как:
\[\overrightarrow{F}=\sum\limits^N_{i=1}{\overrightarrow{F_{ia}}}\left(10\right),\]где $\overrightarrow{F_{ia}}$ — сила, с которой N зарядов действуют на заряд $q$.
Закон Кулона в формуле (1) записан для вакуума, если мы имеем дело с какой-то средой, ее диэлектрические свойства характеризует диэлектрическая проницаемость среды ($\varepsilon $), тогда уравнение (1) примет вид:
\[\overrightarrow{F}=\frac{1}{4\pi {\varepsilon \varepsilon }_0}\frac{q_1q_2\overrightarrow{r}}{r^3}\ \left(11\right).\]Пример 1
Задание: Три одинаковых точечных заряда величиной $q$ поместили в вершинах равностороннего треугольника. Найдите величину точечного заряда $Q$, который надо поместить в центр масс треугольника, чтобы система находилась в состоянии равновесия.
Решение:

Рис. 1
Для определенности допустим, что заряды в вершинах треугольника отрицательные, тогда на пересечении медиан (в центре масс) положительный.
Рассмотрим силы, которые действуют на заряд ${-q}_1$. Это будут три силы Кулона, две — отталкивания, со стороны зарядов в вершинах и одна — притяжения со стороны «центрального». Тогда условие равновесия сил запишем в виде:
\[\overrightarrow{F_{12}}+\overrightarrow{F_{13}}+\overrightarrow{F_{10}}=0\ \left(1.1\right).\]Выберем ось OX, как указано на рис.1, найдем проекцию уравнения (1) на эту ось:
\[F_{12}{cos \left(\frac{\alpha }{2}\right)\ }+F_{13}{cos \left(\frac{\alpha }{2}\right)\ }-F_{10}=0\ \left(1.2\right),\]где $\alpha $- угол треугольника (так как треугольник равносторонний, следовательно, $\alpha =60{}^\circ $).
Так как по условию задачи треугольник равносторонний, заряды в вершинах одинаковые и равны q, то $F_{12}=F_{13}$, а по закону Кулона:
\[F_{12}=F_{13}=\frac{q^2}{4 \pi \varepsilon \varepsilon_0a^2}\ \left(1.3\right),\]где a — сторона треугольника. Для силы $F_{10}$ по закону Кулона получим:
\[F_{10}=\frac{qQ}{4\pi \varepsilon \varepsilon_0r^2}\ \left(1.4\right).\]В таком случае выражение (1.2) запишем в виде:
\[\frac{2q^2}{4\pi {\varepsilon \varepsilon }_0a^2}{cos \left(\frac{\alpha }{2}\right)\ }=\frac{qQ}{4\pi {\varepsilon \varepsilon }_0r^2}\ \left(1.5\right),\]где точка пересечения медиан делит их в соотношении 2:1, если считать от вершины, следовательно:
\[r=\frac{2}{3}{acos \left(\frac{\alpha }{2}\right)\ }\left(1.6\right).\]Подставляем (1.6) в (1.5) выражаем $Q$, получаем:
\[Q=\frac{8qcos^3\left(\frac{б}{2}\right)}{9}\]Ответ: $Q=\frac{8qcos^3\left(\frac{\alpha }{2}\right)}{9}$ (Кл).
Пример 2
Задание: Положительный точечный заряд 1 Кл находится на плоскости XOY в точке, которая определена радиус — вектором$\overrightarrow{{\ r}_1}=4\overrightarrow{i}+6\overrightarrow{j}$,(м) где $i$ и $j$ — орты осей. Найдите модуль напряженности электрического поля E в точке с радиус-вектором $\overrightarrow{{\ r}_2}=16\overrightarrow{i}-\overrightarrow{j}\ (м)$.
Решение:
Найдем разность векторов $\overrightarrow{{\ r}_2}$-$\overrightarrow{{\ r}_1}$, получим:
\[\overrightarrow{{\ r}_2}-\overrightarrow{{\ r}_1}=12\overrightarrow{i}-\overrightarrow{7j}\ \left(2.1\right).\]Из закона Кулона выражение для напряженности электростатического поля может быть записано как:
\[E=\frac{1}{4\pi {\varepsilon }_0}\frac{q}{r^2}=k\frac{q}{r^2}\ \left(2.2\right),\]где $k=9•{10}^9\frac{Нм^2}{{Кл}^2}$
Найдем $r$, получим:
\[r=\left|\overrightarrow{{\ r}_2}-\overrightarrow{{\ r}_1}\right|=\sqrt{{12}^2+7^2}\approx 13,89\ (м)\]Вычислим напряженность (модуль), получим:
\[E=9\cdot {10}^9\frac{1}{193}\approx 4,7{\cdot 10}^7\ \left(\frac{В}{м}\right).\]Ответ: Напряженность поля в заданной точке $4,7{\cdot 10}^7\frac{В}{м}$.
Закон Кулона (механика) — это… Что такое Закон Кулона (механика)?
- Закон Кулона (механика)
Закон Амонтона-Кулона — сила трения при скольжении тела о поверхность не зависит от площади соприкосновения тела с поверхностью, но зависит от силы нормальной реакции этого тела и от состояния окружающей среды.
Сила трения скольжения возникает при скольжении данного тела по поверхности другого тела.

где
 — коэффициент трения для данных поверхностей (табулированная справочная величина),
— коэффициент трения для данных поверхностей (табулированная справочная величина),  — сила нормального давления ( силы реакции опоры , но не давления , т.к. давление зависит от площади )
— сила нормального давления ( силы реакции опоры , но не давления , т.к. давление зависит от площади )Литература
- Иродов. Механика — основные законы (учебник).
Wikimedia Foundation. 2010.
- Карпаччо
- Хамон
Смотреть что такое «Закон Кулона (механика)» в других словарях:
Закон Кулона — О законе сухого трения см. Закон Амонтона Кулона Классическая электродинамика … Википедия
Закон Амонтона — Кулона — сила трения при скольжении тела о поверхность не зависит от площади соприкосновения тела с поверхностью, но зависит от силы нормальной реакции этого тела и от состояния окружающей среды. Сила трения скольжения возникает при скольжении данного… … Википедия
Закон Амонтона — Кулона — Трение процесс взаимодействия твёрдых тел при их относительном движении (смещении) либо при движении твердого тела в жидкой или газообразной среде. По другому называется фрикционным взаимодействием (англ. friction). Изучением процессов трения… … Википедия
Закон Амонтона — Закон Амонтона Кулона эмпирический закон, устанавливающий связь между поверхностной силой трения, возникающей при относительном скольжении тела, с силой нормальной реакции, действующей на тело со стороны поверхности. Сила трения,… … Википедия
КВАНТОВАЯ МЕХАНИКА — фундаментальная физическая теория динамического поведения всех элементарных форм вещества и излучения, а также их взаимодействий. Квантовая механика представляет собой теоретическую основу, на которой строится современная теория атомов, атомных… … Энциклопедия Кольера
КВАНТОВАЯ МЕХАНИКА — (волновая механика), теория, устанавливающая способ описания и законы движения микрочастиц (элем. ч ц, атомов, молекул, ат. ядер) и их систем (напр., кристаллов), а также связь величин, характеризующих ч цы и системы, с физ. величинами,… … Физическая энциклопедия
Квантовая механика — волновая механика, теория устанавливающая способ описания и законы движения микрочастиц (элементарных частиц, атомов, молекул, атомных ядер) и их систем (например, кристаллов) а также связь величин, характеризующих частицы и системы, с… … Большая советская энциклопедия
Беспорядочное течение — Механика сплошных сред Сплошная среда Классическая механика Закон сохранения массы · Закон сохранения импульса … Википедия
Турбулентный поток — Механика сплошных сред Сплошная среда Классическая механика Закон сохранения массы · Закон сохранения импульса … Википедия
Турбуленция — Механика сплошных сред Сплошная среда Классическая механика Закон сохранения массы · Закон сохранения импульса … Википедия
Закон Амонтона — Кулона — это… Что такое Закон Амонтона — Кулона?
- Закон Амонтона — Кулона
Закон Амонтона — Кулона
Закон Амонтона-Кулона — сила трения при скольжении тела о поверхность не зависит от площади соприкосновения тела с поверхностью, но зависит от силы нормальной реакции этого тела и от состояния окружающей среды.
Сила трения скольжения возникает при скольжении данного тела по поверхности другого тела.
где — коэффициент трения для данных поверхностей (зависит от рода трущихся поверхностей, качества их обработки, в меньшей степени — от их температуры, относительной скорости тел и др., не зависит от площади соприкасающихся поверхностей), — сила нормального давления (сила реакции опоры, но не давление, т.к. давление зависит от площади).
Литература
- Иродов. Механика — основные законы (учебник).
См. также
Wikimedia Foundation. 2010.
- Закон о трёх колосках
- Закон Вакернагеля
Смотреть что такое «Закон Амонтона — Кулона» в других словарях:
Закон Амонтона — Кулона — Трение процесс взаимодействия твёрдых тел при их относительном движении (смещении) либо при движении твердого тела в жидкой или газообразной среде. По другому называется фрикционным взаимодействием (англ. friction). Изучением процессов трения… … Википедия
Закон Амонтона — Закон Амонтона Кулона эмпирический закон, устанавливающий связь между поверхностной силой трения, возникающей при относительном скольжении тела, с силой нормальной реакции, действующей на тело со стороны поверхности. Сила трения,… … Википедия
Закон Кулона (механика) — Закон Амонтона Кулона сила трения при скольжении тела о поверхность не зависит от площади соприкосновения тела с поверхностью, но зависит от силы нормальной реакции этого тела и от состояния окружающей среды. Сила трения скольжения возникает при… … Википедия
Закон Кулона — О законе сухого трения см. Закон Амонтона Кулона Классическая электродинамика … Википедия
Закон кулона — О законе сухого трения см. Закон Амонтона Кулона Классическая электродинамика Магнитное поле соленоида Электричество · Магнетизм Электростатика … Википедия
Кулона закон — О законе сухого трения см. Закон Амонтона Кулона Классическая электродинамика Магнитное поле соленоида Электричество · Магнетизм Электростатика … Википедия
Трение — У этого термина существуют и другие значения, см. Радиационное трение. Трение процесс взаимодействия тел при их относительном движении (смещении) либо при движении тела в газообразной или жидкой среде. По другому называется фрикционным… … Википедия
Коэффициент трения — Трение процесс взаимодействия твёрдых тел при их относительном движении (смещении) либо при движении твердого тела в жидкой или газообразной среде. По другому называется фрикционным взаимодействием (англ. friction). Изучением процессов трения… … Википедия
Амонтон, Гийом — Амонтон Гийом Guillaume Amontons Род деятельности: механик, физик, математик, изобретатель Дата рождения: 31 августа 1663(1663 08 31) … Википедия
Теория механизмов и машин — Теория машин и механизмов (ТММ) это научная дисциплина об общих методах исследования, построения, кинематики и динамики механизмов и машин и о научных основах их проектирования. Содержание 1 История развития дисциплины 2 Основные понятия … Википедия
Закон Амонтона — Кулона — Википедия
Материал из Википедии — свободной энциклопедии
Зако́н Амонто́на — Куло́на — эмпирический закон, устанавливающий линейную связь между поверхностной силой трения, возникающей при относительном скольжении тел, и силой нормальной реакции, действующей на тело со стороны поверхности.
Сила трения скольжения одного тела по поверхности другого тела (опоры) равна
- F=μN{\displaystyle F=\mu N}
и направлена тангенциально к общей границе между двумя телами в сторону, противоположную перемещению. Здесь μ{\displaystyle \mu } — коэффициент трения для данных поверхностей (зависит от материала трущихся поверхностей, качества обработки их поверхностного слоя, в меньшей степени — от температуры и относительной скорости перемещения и не зависит от площади соприкасающихся поверхностей), N{\displaystyle N} — сила нормальной реакции опоры (зависит от площади пятна контакта и давления).
Согласно третьему закону Ньютона, указанная выше сила трения действует и со стороны опоры на тело, и со стороны тела на опору.
В настоящее время установлено, что коэффициент трения в разной степени зависит от трех факторов:
- материала трущихся тел и характера смазки, плёнки, имеющейся на поверхности;
- конструкции фрикционного сочленения: размера поверхности, геометрического очертания, в основном от отношения площадей трения контактирующих деталей — коэффициента взаимного перекрытия;
- режима работы: температуры, скорости, нагрузки, в основном температурного поля, возникающего в тонком поверхностном слое.
Впервые понятие о коэффициенте трения ввел Леонардо да Винчи[1] (1508), позже Амонтон (1699). Часто приведённую выше формулу называют законом (формулой) Кулона (или Амонтона — Кулона). Шарль Кулон в 1785 году подтвердил закон и предложил обобщённую формулу (см. приведённую литературу):
- F=A+μN{\displaystyle F=A+\mu N},
где A{\displaystyle A} — характеристика сцепления (за счёт молекулярного сцепления), не зависящая от нагрузки. Это была первая формула, в которой учитывалось два вида тангенциального сопротивления — зависящее и не зависящее от внешней нагрузки.
- Сивухин Д. В. Общий курс физики. — М.: Наука, 1979. — Т. I. Механика. — С. 101—102. — 520 с.
- Справочник по триботехнике / Под ред. М.Хебды, А. В. Чичинадзе. Т.1. — М.: Машиностроение, 1989. С.19, 118.
- Крагельский И. В., Виноградова И. Э. Коэффициенты трения. Справочное пособие. — М.: Машгиз, 1962. С.9, 11.
- Словарь-справочник по трению, износу и смазке деталей машин / В. Д. Зозуля, Е. Л. Шведков, Д. Я. Ровинский, Э. Д. Браун. АН УССР. Ин-т проблем материаловедения. — 2-е изд., пере-раб. и доп. — Киев : Наук, думка, 1990. С. 66.
- Первозванский А. А. Трение — сила знакомая, но таинственная. Соросовский образовательный журнал, 1998, № 2, с. 129—134.
- Минаков А. П. Немного о трении. ИТФВестник № 2. http://myreset.narod.ru
Сила Кулона, закон Кулона, границы применимости, напряженность электростатического поля, принцип суперпозиции.
⇐ ПредыдущаяСтр 3 из 9Следующая ⇒
Опыты по притяжению и отталкиванию наэлектризованных тел позволяют предположить, что эл.заряды взаимодействуют. Причем взаимодействие зависит от расстояния (чем ближе – тем сильнее). Предположение – заряд передается через воздух. Опыт – заряженный электроскоп поместили под колокол, воздух откачали, а листочки электроскопа по-прежнему отталкивались. В результате исследований было установлено, что эл.заряды окружены эл.полем.
Электрическое поле (часть эл.магнитного) – особый вид материи, который создается эл.зарядами, неразрывно с ними связан и воздействует на заряды одинаково, независимо от того, двигаются они или покоятся в данной инерциальной системе отсчета.
Электрическое поле, создаваемое неподвижными зарядами – электростатическое. Его характеристиками являются напряженность и потенциал.
Электрическое поле взаимодействует с зарядом. Энергия этого взаимодействия — потенциальная.
Потенциал электрического поля – скалярная величина, энергетическая характеристика, равная отношению потенциальной энергии пробного заряда к величине этого заряда. 
Пробным называют тот заряд, который существенно не меняет поле, с которым взаимодействует (элементарный заряд –равный 1,6*10-19 Кл ).
Напряженность (силовая характеристика)в данной точке электростатического поля — векторная физическая величина, равная отношению силы, действующей в данной точке поля, на точечный пробный заряд, к этому заряду. E = F/q. (E = F при q = 1). Ед. измерения 1 В/м = 1 Дж/(м*Кл) = 1Н/м или Н/кл
В каждой точке поля напряженность имеет определенное значение и зависит от координат. В случае переменных полей она зависит и от времени.
Направление вектора Е совпадает с направлением силы, действующей на «+» заряд. Если поле создается «-» зарядом, то вектор Е направлен к заряду и противонаправлен силе. Линии напряженности начинаются у «+» зарядов (или в бесконечности) и оканчиваются у «-» зарядов. По густоте линий можно судить о величине Е 


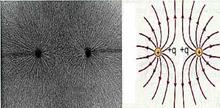

Разные заряды одноименные заряды пластина
 Картина будет более наглядной, если рисовать не векторы в отдельных точках, а непрерывные линии, касательные к которым в каждой точке совпадают с направлением вектора напряженности. Эти линии называются линиями напряженности или силовыми линиями электрического поля. За направление силовых линий принимается направление вектора Е.
Картина будет более наглядной, если рисовать не векторы в отдельных точках, а непрерывные линии, касательные к которым в каждой точке совпадают с направлением вектора напряженности. Эти линии называются линиями напряженности или силовыми линиями электрического поля. За направление силовых линий принимается направление вектора Е.
Напряженность поля увеличивается по мере приближения к заряду, а силовые линии при этом сгущаются.
Линии напряженности электростатических полей не замкнуты. Отметим, что напряженность поля в диэлектрике меньше, чем в вакууме из-за явления поляризации и, следовательно, густота силовых линий в диэлектрике меньше. Отношение напряженности поля в вакууме к напряженности в данной среде называют диэлектрической проницаемостью вещества. Eвак./E.
Напряженность электростатического поля в металле равняется нулю, так как поле свободных зарядов, существующих в нем, через достаточно короткий промежуток времени уравновесит внешнее поле и ток в металле будет равен нулю. Поэтому силовые линии в металл не проникают.
Однородным называется электростатическое поле, во всех точках которого напряженность одинакова по величине и направлению
Электрическая сила (Кулоновская) – сила, с которой электрическое поле действует на внесенный в него электрический заряд независимо от того, двигается он или покоится в данной инерциальной системе отсчета.
Подносим заряженную «+» палочку к заряженной «-» гильзе. По мере приближения палочки угол отклонения гильзы будет увеличиваться. Следовательно, чем ближе расположены тела, тем сильнее действие поля.
Закон взаимодействия электрических зарядов (закон Кулона) – два точечных неподвижных заряда взаимодействуют в вакууме с силой, прямопропорциональной произведению их зарядов и обратнопропорциональной квадрату расстояния между ними, 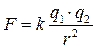 где
где 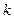 —коэффициент пропорциональности,
—коэффициент пропорциональности, 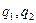 — заряды,
— заряды, 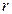 — расстояние между ними.
— расстояние между ними.
Границы применимости закона Кулона –
1. Заряженные тела должны быть точечными. Если же размеры и расстояния соизмеримы, то необходимо мысленно «разбить» тело на такие малые объемы, чтобы каждый из них отвечал условию точечности. Суммирование сил, действующих между элементарными объемами заряженных тел, дает возможность определить электрическую силу.
2. Заряженные тела должны быть неподвижными, т.к. при движении заряженных тел проявляется действие магнитного поля, возникающего в результате этого движения.
Принцип суперпозиции
Если на тело действует несколько сил, то по законам механики Ньютона результирующая сила равна их геометрической сумме. В нашем случае – телом является электрический заряд. На электрические заряды действуют силы со стороны поля. Если при наложении в пространстве полей от нескольких зарядов эти поля не влияют друг на друга, то результирующая сила со стороны всех полей на заряд должна быть равна геометрической сумме сил со стороны каждого поля. Это означает, что напряженности полей складываются геометрически, так как напряженности прямо пропорциональны силам.
 Т.о. принцип суперпозиции или принцип независимого наложения полей – если в данной точке пространства различные заряды создают электрические поля, напряженность которых
Т.о. принцип суперпозиции или принцип независимого наложения полей – если в данной точке пространства различные заряды создают электрические поля, напряженность которых  ,
,  ,
, 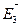 и т.д., то результирующая напряженность поля в этой точке равна
и т.д., то результирующая напряженность поля в этой точке равна 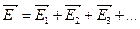
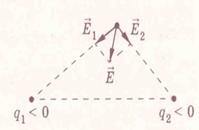 На рисунке показано, как геометрически определять напряженность поля, созданного двумя зарядами.
На рисунке показано, как геометрически определять напряженность поля, созданного двумя зарядами.
Для определения напряженности поля надо мысленно разделить на маленькие элементы, каждый из которых можно считать точечным. Определить заряды всех этих элементов и найти напряженности полей, созданных всеми ими в заданной точке. После этого геометрически сложить напряженности от всех элементов и найти результирующую.
Поля, удовлетворяющие этому принципу, называют линейными. Т.е. у них нет взаимодействия между отдельными участками, поле не действует само на себя. Гравитационное поле – нелинейно, как и поля взаимодействия кварков.




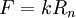
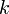 — коэффициент трения для данных поверхностей (табулированная справочная величина),
— коэффициент трения для данных поверхностей (табулированная справочная величина), 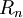 — сила нормального давления ( силы реакции опоры , но не давления , т.к. давление зависит от площади )
— сила нормального давления ( силы реакции опоры , но не давления , т.к. давление зависит от площади )