Скольжение асинхронного двигателя — Википедия

Материал из Википедии — свободной энциклопедии

Скольжение асинхронного двигателя — относительная разность скоростей вращения ротора и изменения переменного магнитного потока, создаваемого обмотками статора двигателя переменного тока. Скольжение может измеряться в относительных единицах и в процентах.

s=(n1−n)/n1{\displaystyle s=(n_{1}-n)/n_{1}},

где n{\displaystyle n} — скорость вращения ротора асинхронного двигателя, об/мин

n1{\displaystyle n_{1}} — скорость циклического изменения магнитного потока статора, называется синхронной скоростью двигателя.

n1=60×f/p{\displaystyle n_{1}=60\times f/p},

где f — частота сети переменного тока, Гц

p — число пар полюсов обмотки статора (число пар катушек на фазу).

Из последней формулы видно, что скорость вращения двигателя n практически определяется значением его синхронной скорости, а последняя при стандартной частоте 50 Гц зависит от числа пар полюсов: при одной паре полюсов — 3000 об/мин, при двух парах — 1500 об/мин, при трёх парах — 1000 об/мин и т. д.

Режим холостого хода

Холостой ход асинхронного двигателя имеет место в том случае, если на валу отсутствует нагрузка в виде рабочего органа или редуктора. При сборке нового двигателя всегда проводится испытания холостого хода, для того чтобы определить потери в подшипниках, вентиляторе и магнитопроводе, а также узнать значения намагничивающего тока. Во время холостого хода скольжение составляет: S=0,01÷0,08.

Следует заметить, что так же существует режим идеального холостого хода, при котором n₂=n₁, что практически реализовать невозможно, даже если учесть, что нет силы трения в подшипниках. На самом деле суть заключается в том, что асинхронному двигателю необходимо, чтобы ротор отставал от магнитного вращающегося поля статора. При отставании поле статора индуцирует магнитное поле в ротор, что заставляет его вращаться за полем статора.

Критическое скольжение

Если постепенно повышать нагрузку двигателя, то скольжение будет расти (ротор будет все сильнее отставать от вращающегося магнитного поля), при этом пропорционально скольжению будет расти ток, наводимый в роторе, а пропорционально ему будет расти и момент. Поэтому при малых нагрузках можно считать, что момент пропорционален скольжению. Но при росте скольжения возрастают активные потери в роторе, которые снижают ток ротора, поэтому момент растет медленнее чем скольжение, и при определенном скольжении момент достигает максимума, а потом начинает снижаться. Скольжение, при котором момент достигает максимума, называется критическим.

Видео по теме

Литература

• Хомяков Н. М., Денисов В. В., Панов В. А. Электротехника и электрооборудование судов. — Ленинград: Издательство «Судостроение», 1971. — 368 с.

Скольжение асинхронного двигателя — Википедия

Материал из Википедии — свободной энциклопедии

Скольжение асинхронного двигателя — относительная разность скоростей вращения ротора и изменения переменного магнитного потока, создаваемого обмотками статора двигателя переменного тока. Скольжение может измеряться в относительных единицах и в процентах.

s=(n1−n)/n1{\displaystyle s=(n_{1}-n)/n_{1}},

где n{\displaystyle n} — скорость вращения ротора асинхронного двигателя, об/мин

n1{\displaystyle n_{1}} — скорость циклического изменения магнитного потока статора, называется синхронной скоростью двигателя.

n1=60×f/p{\displaystyle n_{1}=60\times f/p},

где f — частота сети переменного тока, Гц

p — число пар полюсов обмотки статора (число пар катушек на фазу).

Из последней формулы видно, что скорость вращения двигателя n практически определяется значением его синхронной скорости, а последняя при стандартной частоте 50 Гц зависит от числа пар полюсов: при одной паре полюсов — 3000 об/мин, при двух парах — 1500 об/мин, при трёх парах — 1000 об/мин и т. д.

Режим холостого хода

Холостой ход асинхронного двигателя имеет место в том случае, если на валу отсутствует нагрузка в виде рабочего органа или редуктора. При сборке нового двигателя всегда проводится испытания холостого хода, для того чтобы определить потери в подшипниках, вентиляторе и магнитопроводе, а также узнать значения намагничивающего тока. Во время холостого хода скольжение составляет: S=0,01÷0,08.

Следует заметить, что так же существует режим идеального холостого хода, при котором n₂=n₁, что практически реализовать невозможно, даже если учесть, что нет силы трения в подшипниках. На самом деле суть заключается в том, что асинхронному двигателю необходимо, чтобы ротор отставал от магнитного вращающегося поля статора. При отставании поле статора индуцирует магнитное поле в ротор, что заставляет его вращаться за полем статора.

Критическое скольжение

Если постепенно повышать нагрузку двигателя, то скольжение будет расти (ротор будет все сильнее отставать от вращающегося магнитного поля), при этом пропорционально скольжению будет расти ток, наводимый в роторе, а пропорционально ему будет расти и момент. Поэтому при малых нагрузках можно считать, что момент пропорционален скольжению. Но при росте скольжения возрастают активные потери в роторе, которые снижают ток ротора, поэтому момент растет медленнее чем скольжение, и при определенном скольжении момент достигает максимума, а потом начинает снижаться. Скольжение, при котором момент достигает максимума, называется критическим.

Литература

• Хомяков Н. М., Денисов В. В., Панов В. А. Электротехника и электрооборудование судов. — Ленинград: Издательство «Судостроение», 1971. — 368 с.

Скольжение асинхронного двигателя — Вики

Скольжение асинхронного двигателя — относительная разность скоростей вращения ротора и изменения переменного магнитного потока, создаваемого обмотками статора двигателя переменного тока. Скольжение может измеряться в относительных единицах и в процентах.

s=(n1−n)/n1{\displaystyle s=(n_{1}-n)/n_{1}},

где n{\displaystyle n} — скорость вращения ротора асинхронного двигателя, об/мин

n1{\displaystyle n_{1}} — скорость циклического изменения магнитного потока статора, называется синхронной скоростью двигателя.

n1=60×f/p{\displaystyle n_{1}=60\times f/p},

где f — частота сети переменного тока, Гц

p — число пар полюсов обмотки статора (число пар катушек на фазу).

Из последней формулы видно, что скорость вращения двигателя n практически определяется значением его синхронной скорости, а последняя при стандартной частоте 50 Гц зависит от числа пар полюсов: при одной паре полюсов — 3000 об/мин, при двух парах — 1500 об/мин, при трёх парах — 1000 об/мин и т. д.

Режим холостого хода

Холостой ход асинхронного двигателя подразумевает отсутствие на валу нагрузки в виде рабочего органа или редуктора. В режиме холостого хода скольжение составляет

s=(n1−n1)/n1=0{\displaystyle s=(n_{1}-n_{1})/n_{1}=0}.

В режиме холостого хода ротор вращается с частотой лишь немного меньшей синхронной частоты вращения n1{\displaystyle n_{1}} и скольжение весьма мало отличается от нуля.

Следует заметить, что так же существует режим идеального холостого хода, при котором n=n1{\displaystyle n=n_{1}}, что практически реализовать невозможно, даже если учесть отсутствие силы трения в подшипниках. Сам принцип работы асинхронного двигателя подразумевает отставание ротора от вращающегося магнитного поля статора. При s=0{\displaystyle s=0} поле статора не пересекает обмотки ротора и не может индуцировать в нём ток, а значит не создаётся магнитное поле ротора

Генераторный режим

Если обмотку статора включить в сеть, а ротор посредством приводного двигателя вращать в направлении вращения магнитного поля с частотой n>n1{\displaystyle n>n_{1}}, то направление движения ротора относительно поля статора изменится на обратное (по сравнению с двигательным режимом), так как ротор будет обгонять поле статора. При этом скольжение станет отрицательным, а ЭДС, наведенная в обмотке ротора изменит свое направление. Таким образом, в генераторном режиме скольжение может изменяться в диапазоне −∞<s<0{\displaystyle -\infty <s<0}, то есть оно может принимать любые отрицательные значения.

Режим торможения противовключением

В режиме электромагнитного торможения частота вращения ротора является отрицательной, поэтому скольжение принимает положительные значения больше единицы

s=[n1−(−n)]/

Особенности асинхронного электродвигателя

В современной электроэнергетике почти повсеместно пе­ременный ток вытесняет постоянный. Это объясняется многими преимуществами машин переменного тока в сравнении с ма­шинами постоянного тока. В частности, у машин переменного тока вес, габариты и стоимость меньше, а к. п. д. выше; они проще в обслуживании, долговечнее и надежнее машин посто­янного тока. Правда, электродвигатели переменного тока хуже поддаются регулировке, они развивают значительно меньшие пусковые моменты. Поэтому, если от электродвигателей требу­ются высокие регулировочные качества и повышенные пусковые моменты, применяют электродвигатели постоянного тока.

Привод механизмов портовых подъемно-транспортных машин чаще всего осуществляется асинхронными электродвига­телями трехфазного переменного тока, получившими наибольшее распространение в электроэнергетике. Зависимости от исполнения ротора, различают асин­хронные электродвигатели с короткозамкнутым ротором и с фазным ротором (с контактными кольцами). Принципиальная схема включения этих электродвигателей приведена на рис. 40..

Из курса электротехники известно, что принцип действия асинхронных электродвигателей основан на использовании так называемого вращающегося магнитного поля. При подаче трехфазного тока в обмотке статора создается магнитное поле, вращающееся со скоростью

где f— частота тока в обмотке статора;

р — число пар полюсов обмотки статора.

Эта скорость называется синхронной. Магнитное поле статора, (пересекая обмотку ротора, наводит в ней э. д. с., ко­торая создает в цепи ротора ток. Последний, взаимодействуя с магнитным полем статора, образует вращающий момент, заставляющий ротор вращаться в ту же сторону, что и магнит­ное поле статора. При нормальной работе асинхронного электродвигателя его ротор вращается со скоростью п₂<п₁. Если бы скорость вращения ротора была равна скорости, с которой вращается магнитное поле статора, то последнее относительно ротора было бы неподвижным. В этом случае э. д. с. и ток в обмотке ротора были бы равны нулю и никакого вращающего момента не возникло бы.

Величиной, характеризующей работу асинхронного электро­двигателя, является скольжение s:

где n₁—синхронная скорость;

n₂ — скорость вращения ротора.

Зная скольжение, нетрудно определить скорость вращения электродвигателя

При работе электродвигателя без нагрузки скорость его близка к синхронной, а скольжение очень мало.

Двигательный режим асинхронного электродвигателя имеет место при скольжениях, изменяющихся в пределах от 0 до 1, при этом число оборотов ротора изменяется от n₁ до 0. Номинальная величина скольжения асинхронного электродви­гателя составляет 0,03—0,1, причем первая цифра относится к более мощным, а вторая — к менее мощным электродвигателям (до 10—20 квт).

Очевидно, s = 0 в том случае, когда ротор вращается с син­хронной скоростью n₁. Можно считать, что на холостом ходу электродвигателя его ротор вращается с этой скоростью, если не учитывается трение.

Величина скольжения s =1, когда ротор электродвигателя не вращается при включенной обмотке статора. Этот режим называют режимом короткого замыкания электродвигателя (или режимом стоянки под током). Получить режим короткого замыкания можно, искусственно затормозив ротор или пере­грузив электродвигатель до полной остановки его. Пуск асин­хронного электродвигателя также начинается именно с этого режима.

Выражение (81) показывает, что скольжение может изме­няться гораздо в больших пределах, чем указано выше. Дей­ствительно, ротор электродвигателя под действием посторон­него источника механической энергии (например, под действи­ем опускающегося груза) может вращаться со скоростью больше синхронной. В этом случае скольжение будет отрицательным (s<0). Отрицательное скольжение имеет место при работе асинхронного электродвигателя в генераторном режиме, когда, например, под действием опускающегося груза ротор вращается в ту же сторону, что и магнитное поле статора со скоростью n₂>n₁.

Можно также представить, что ротор электродвигателя под действием опускающегося груза вращается в направлении, противоположном направлению вращения магнитного поля ста­тора. В этом случае s>1, так как в выражение (81) величи­ну п₂ нужно подставить с отрицательным знаком. Такой ре­жим называется режимом противовключения.

Таким образом, теоретически скольжение асинхронного электродвигателя может изменяться в пределах от —? до + ?. Практически же скольжение асинхронного электродви­гателя при работе последнего в двигательном и тормозных режима« изменяется в пределах от —2 до +2.

Из курса электрических машин известно, что для асинхрон­ного электродвигателя может быть составлена схема замеще­ния, с помощью которой производится анализ работы электродвигателя и исследуются режимы его работы. На рис. 41 при­ведена упрощенная схема замещения асинхронного электро­двигателя, в которой приняты следующие обозначения:

U₁ — фазное напряжение обмотки статора, в;

I₁ — фазный ток обмотки статора, а;

I₀ — фазный ток холостого хода электродвигателя, а;

I₂ — приведенный фазный ток обмотки ротора, а;

r₁ и х₁ — активное и индуктивное сопротивления фазы обмотки статора, ом;

r₂’ и х₂‘ — приведенные активное и индуктивное сопротивления фазы обмотки ротора, ом.

Для приведенных величин могут быть выведены следующие соотношения:

где т₁ и т₂ — число фаз обмоток статора и ротора;

к = U_1н / E_2н — коэффициент трансформации э. д. с. (U_1н — номи­нальное фазное напряжение обмотки статора; E_2н — фазная э. д. с. обмотки ротора при разом­кнутых контактных кольцах).

Мощность Р₁ забираемая электродвигателем из сети, опре­деляется напряжением сети U₁, током статора I₁ зависящим от нагрузки, и коэффициентом  мощности cos? т.е.

Мощность на валу электродвигателя зависит от его к. п. д.? и может быть вычислена по формуле

Если пренебречь механическими и вентиляционными поте­рями, которые незначительны, то можно считать, что механи­ческая мощность асинхронного электродвигателя (мощность на валу) равна, потерям мощности в сопротивлении схемы замещения, приведенной на рис. 41, т. е.

где т₂ = т₁ — приведенное число фаз обмотки ротора.

Между токами асинхронного электродвигателя, согласно схеме замещения, существует зависимость

Ток статора асинхронных электродвигателей I₁ очень велик даже при отсутствии нагрузки на валу. Это объясняется тем, что намагничивающий ток этих электродвигателей составляет 50—70% номинального тока статора.

Принципы построения систем частотного управления. Законы частотного управления. Абсолютное скольжение. Схема замещения асинхронного двигателя при частотном управлении

3. Принципы построения систем

частотного управления

3.1. Законы частотного управления

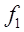Под законами частотного управления принято понимать зависимости между действующим напряжением на статоре  и частотой , поддерживаемые в установившихся режимах так, что  при изменении 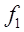 с целью изменения скорости вращения магнитного поля двигателя одновременно изменяется и .

Как известно, свойства двигателя в установившихся режимах работы можно описать с использованием схемы замещения.

Введем в рассмотрение относительную частоту , где  – номинальное  значение  частоты. Любому текущему значению частоты 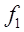    питающего напряжения соответствует угловая скорость вращения магнитного поля и всех результирующих (обобщенных) векторов, равная , где – число пар полюсов. Номинальной частоте  соответствует номинальная скорость поля .

В теории частотного управления асинхронным двигателем вместо понятия «скольжение» используется понятие «абсолютное скольжение».

Так как скольжение S равно , где – механическая угловая скорость вращения вала двигателя, то можно осуществить преобразование:

.

Абсолютным скольжением bназывается величина

.

Следовательно, между скольжением S и абсолютным скольжением b существует соотношение . С учетом введенных обозначений схему замещения двигателя можно представить в виде рис. 3.1.

Возможно двухзонное частотное регулирование скорости, т. е. как    в сторону уменьшения частоты, так и в сторону ее повышения по отношению к номинальной.

Во второй зоне регулирования (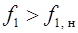) частота напряжения изменяется при условии поддержания напряжения на неизменном уровне, равном номинальному.

Рис. 3.1. Схема замещения асинхронного двигателя

при частотном управлении

В первой зоне регулирования () одновременно со снижением частоты ниже номинального значения  возникает необходимость снижения напряжения. Это следует из уравнения

, где 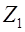 – сопротивление статорных обмоток,  – ток статора,  – число витков фазных обмоток статора,  – обмоточный коэффициент, 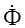 – магнитный поток.

При незначительном () диапазоне регулирования скорости        в первой зоне относительное значение падения напряжения в первичной цепи невелико:

.

Из последнего выражения следует, что при  снижение частоты приводит к увеличению потока двигателя.

Существенное увеличение магнитного потока нежелательно, т. к. это вызывает насыщение магнитной цепи, значительное увеличение тока намагничивания. Так, уже изменение 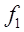 на 10 % приводит к увеличению намагничивающего тока на 20–30 %. Изменение частоты в более широких пределах приводит к более существенному увеличению 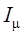. Отмеченное обстоятельство ведет к интенсивному нагреванию двигателя, снижению его энергетических показателей и срока службы.

Нежелательно также существенное снижение магнитного потока,     т. к. при этом снижается перегрузочная способность двигателя  с одновременным перегревом двигателя, что следует из выражения

, где k– конструктивный коэффициент,  – ток ротора, 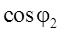 – коэффициент мощности вторичной цепи.

В связи с изложенным при построении систем частотного регулирования скорости асинхронного двигателя вниз от основной скорости () стремятся поддерживать магнитный поток примерно на том же уровне, который обеспечивается при номинальном режиме работы двигателя. При этом используется один из следующих законов регулирования:

                                                                                      (3.1)

                                                                                        (3.2)

                                                                                     (3.3)

                                                                                     (3.4)

Наиболее простой закон (3.1) используется при необходимости регулирования скорости в небольшом диапазоне, когда падение напряжения в обмотках статора мало влияет на величину тока намагничивания.

Исходя из баланса активной мощности в роторе [9]

.

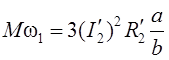Определяя ток ротора  из схемы замещения (рис. 3.1) и пренебрегая сопротивлением  статорной обмотки, можно получить следующее приближенное выражение для электромагнитного момента двигателя:

.

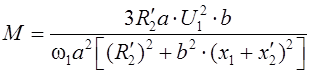Определив из (3.5) известными способами критическое значение абсолютного скольжения  и учитывая, что 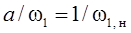, получим следующее выражение для критического момента:

. 

Следовательно, при рассмотренных условиях во всем диапазоне регулирования скорости поддерживается постоянство перегрузочной способности двигателя, под которой понимают величину

.

Системы частотного регулирования, реализующие закон регулирования (3. 1), обеспечивают диапазон регулирования скорости до  при статизме механической характеристики в пределах 5–10 %.

Для момента сопротивления , зависящего от скорости, закон регулирования (3.4) можно заменить следующими законами [9]:

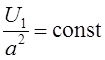 при ,

 при ,

 при .

Однако, как показано в [1], во всех случаях удовлетворительные результаты обеспечивает закон (3.4).

2.7. Зависимость электромагнитного момента от скольжения

Выражение для электромагнитного момента (*) справедливо для любого режима работы и может быть использовано для построения зависимости момента от скольжения при изменении последнего от +∞ до −∞ (рис. 2.14).

Рассмотрим часть этой характеристики, соответствующая режиму двигателя, т.е. при скольжении, изменяющемся от 1 до 0. Обозначим момент, развиваемый двигателем при пуске в ход (S=1) как M_пуск. Скольжение, при котором момент достигает наибольшего значения, называют критическим скольжением S_кр, а наибольшее значение момента – критическим моментом M_кр. Отношение критического момента к номинальному называют перегрузочной способностью двигателя

M_кр/M_н=λ=2÷3.

Из анализа формулы (*) на максимум можно получить соотношения для M_кр и S_кр

Mкр=Cм	U12	;     Sкр≈	R2	.
	2X2		X2

Критический момент не зависит от активного сопротивления ротора, но зависит от подведенного напряжения. При уменьшении U₁ снижается перегрузочная способность асинхронного двигателя.

Из выражения (*), разделив M на M_кр, можно получить формулу, известную под названием «формула Клосса», удобную для построения M=f(S).

	M	=	2
	Mкр		S/Sкр+Sкр/S

Если в эту формулу подставить вместо M и S номинальные значения момента и скольжения (M_н и S_н), то можно получить соотношение для расчета критического скольжения.

.

Участок характеристики (рис. 2.14), на котором скольжение изменяется от 0 до S_кр, соответствует устойчивой работе двигателя. На этом участке располагается точка номинального режима (M_н, S_н). В пределах изменения скольжения от 0 до S_кр изменение нагрузки на валу двигателя будет приводить к изменению частоты вращения ротора, изменению скольжения и вращающего момента. С увеличением момента нагрузки на валу частота вращения ротора станет меньше, что приведет к увеличению скольжения и электромагнитного (вращающего) момента. Если момент нагрузки превысит критический момент, то двигатель остановится.

Участок характеристики, на котором скольжение изменяется от S_кр до 1, соответствует неустойчивой работе двигателя. Этот участок характеристики двигатель проходит при пуске в ход и при торможении.

2.8. Механическая характеристика асинхронного двигателя

Под механической характеристикой принято понимать зависимость частоты вращения ротора в функции от электромагнитного момента n=f(M). Эту характеристику (рис. 2.15) можно получить, используя зависимость M=f(S) и пересчитав частоту вращения ротора при разных значениях скольжения.

Рис. 2.15

Так как S=(n₀−n)/n₀, отсюда n=n₀(1−S). Напомним, что n₀=(60f)/p – частота вращения магнитного поля.

Участок 1-3 соответствует устойчивой работе, участок 3-4 – неустойчивой работе. Точка 1 соответствует идеальному холостому ходу двигателя, когда n=n₀. Точка 2 соответствует номинальному режиму работы двигателя, ее координаты M_н и n_н. Точка 3 соответствует критическому моменту M_кр и критической частоте вращения n_кр. Точка 4 соответствует пусковому моменту двигателя M_пуск. Механическую характеристику можно рассчитать и построить по паспортным данным. Точка 1:

n₀=(60f)/p,

где: p – число пар полюсов машины; f – частота сети.

Точка 2 с координатами n_н и M_н. Номинальная частота вращения n_н задается в паспорте. Номинальный момент рассчитывается по формуле:

здесь: P_н – номинальная мощность (мощность на валу).

Точка 3 с координатами M_крn_кр. Критический момент рассчитывается по формуле M_кр=M_нλ. Перегрузочная способность λ задается в паспорте двигателя n_кр=n₀(1−S_кр), 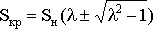,S_н=(n₀−n_н)/n₀ – номинальное скольжение.

Точка 4 имеет координаты n=0 и M=M_пуск. Пусковой момент вычисляют по формуле

M_пуск=M_нλ_пуск,

где: λ_пуск – кратность пускового момента задается в паспорте.

Асинхронные двигатели имеют жесткую механическую характеристику, т.к. частота вращения ротора (участок 1–3) мало зависит от нагрузки на валу. Это одно из достоинств этих двигателей.