Особенности цепи при резонансе напряжений:

1. Электрическая цепь обладает резистивным (активным) характером: ток совпадает с напряжением (ток и напряжение синфазны), сдвиг фаз в цепи φ = 0 , Z = R и схема замещения содержит только один резистивный элемент:

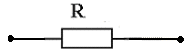
2. Коэффициент мощности сos φ = 1 – вся поступающая в цепь электрическая энергия преобразуется в работу, как полезную, так и различного рода потери.

3. Полное сопротивление цепи минимально: и равно активному сопротивлению цепи: X _L – X _C= 0  Z = R = min .

 

4. Ток в цепи максимален: I = U/ Z = U/ R = max и при малой величине активного сопротивления может достигать очень больших и опасных для цепи значений.

5. Цепь потребляет от сети максимальную и только активную мощность, равную полной мощности: P= I² R = I U сos φ = IU= S = max.

  6. Цепь не потребляет от сети реактивную мощность Q = I U sin φ = 0 — обмена реактивной энергией между источником электрической энергии и цепью не происходит. Однако в самой цепи существует реактивная мощность и между реактивными элементами (катушкой и конденсатором) происходит обмен реактивной энергией. При этом индуктивная и ёмкостная составляющие реактивной мощности в цепи могут быть очень большими, поскольку при резонансе напряжений происходит их взаимная компенсация.

 

7. При резонансе напряжений (Х _L= Х _C) или при условиях близких к резонансу (Х _L≈ Х _C) возможно возникновение явления перенапряжений на реактивных элементах, когда напряжение на катушке и конденсаторе может превысить приложенное к цепи напряжение.

 Явление перенапряжений возникает всегда при условии: Х _L = Х _C

> R , а также может возникать при условии: Х _L ≈ Х _C > R .

13. Расчет параллельной цепи переменного тока. Последовательная эквивалентная схема замещения. Резонанс токов. Особенности цепи.

При расчете разветвлённой электрической цепи обычно известны приложенное напряжение и сопротивления элементов цепи, а в результате расчёта необходимо определить токи в ветвях и в неразветвлённой части цепи, параметры эквивалентной последовательной схемы замещения и построить векторную диаграмму.

 Разветвлённая цепь переменного тока в общем случае может содержать несколько различных по характеру ветвей с различной комбинацией последовательно включенных реальных и идеализированных элементов. В отличие от расчета последовательной цепи в расчете параллельной цепи обычно используется

метод проводимостей.

 Любой элемент (участок) электрической цепи характеризуется параметрами –

комплексным сопротивлением [Ом] или обратной величиной – комплексной проводимостью Y [См]:

.

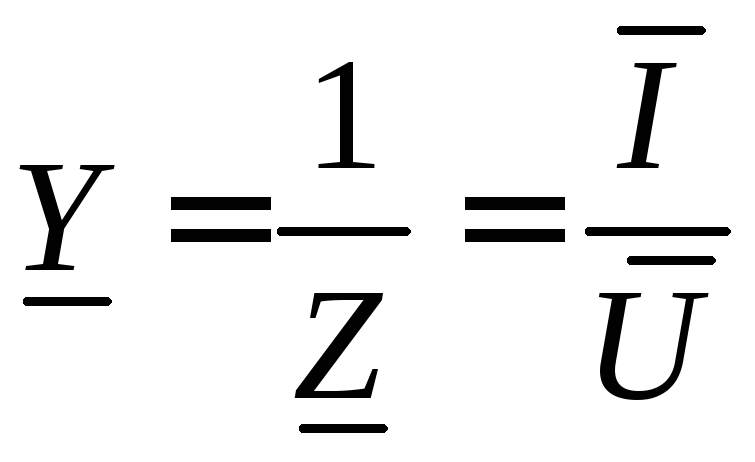
Комплексная проводимость , как и всякая комплексная величина, может быть представлена в алгебраическом виде: ,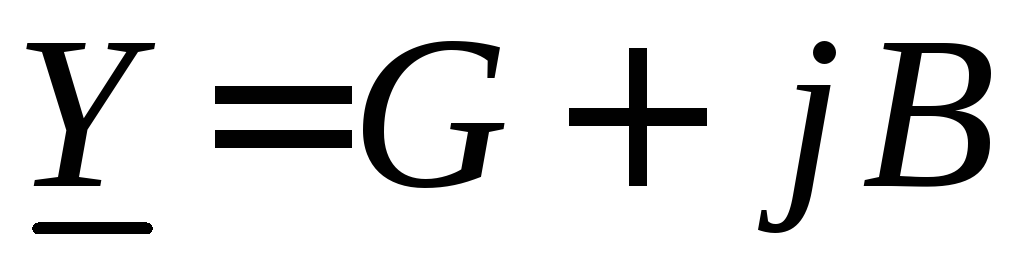

Здесь Y = [ ] = 1/ Z — модуль комплексной проводимости — полная проводимость,

G — действительная составляющая комплексной проводимости — активная проводимость

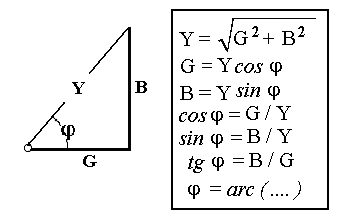, B — мнимая составляющая комплексной проводимости — реактивная проводимость, - угол сдвига фаз в рассматриваемом элементе.

В зависимости от того, каким характером обладает рассматриваемый элемент (индуктивным или ёмкостным) различают два вида реактивной проводимости: B _L — индуктивная проводимость, B _С — ёмкостная проводимость.

 Для вычисления активной и реактивных проводимостей обычно пользуются формулами, которые легко получить через известные (заданные) сопротивления элемента цепи R, X

_L или X _C и Z , выразив коэффициент мощности cos фи из треугольника сопротивлений ( cos  = R / Z ): G = Y cos  = (1/ Z ) cos  = R / Z ² [Ом], B _L = Y sin  = (1/ Z ) sin  = X _L / Z ² [Ом], B _C= Y sin  = (1/ Z ) sin  = X _C / Z ² [Ом]. Указанные соотношения могут быть представлены на плоскости в виде прямоугольного треугольника проводимостей :

(*) Если какая либо k- ветвь содержит несколько активных и реактивных элементов, то она должна быть приведена к эквивалентной схеме по формулам последовательной цепи: R_k = ∑ R _{k i} , X _{k (L,C)} = ∑ X _{k i (L)} — ∑ X _{k i (C)}

.

 

 МЕТОДИКА РАСЧЕТА ПАРАЛЛЕЛЬНОЙ ЦЕПИ

Резонанс напряжений — это… Что такое Резонанс напряжений?

Резонанс напряжений — резонанс, происходящий в последовательном колебательном контуре при его подключении к источнику напряжения, частота которого совпадает с собственной частотой контура.

Описание явления

Пусть имеется колебательный контур с частотой собственных колебаний f, и пусть внутри него работает генератор переменного тока такой же частоты f.

В начальный момент конденсатор контура разряжен, генератор не работает. После включения напряжение на генераторе начинает возрастать, заряжая конденсатор. Катушка в первое мгновение не пропускает ток из-за ЭДС самоиндукции. Напряжение на генераторе достигает максимума, заряжая до такого же напряжения конденсатор.

Далее: конденсатор начинает разряжаться на катушку. Напряжение на нем падает с такой же скоростью, с какой уменьшается напряжение на генераторе.

Далее: конденсатор разряжен до нуля, вся энергия электрического поля, имевшаяся в конденсаторе, перешла в энергию магнитного поля катушки. На клеммах генератора в этот момент напряжение нулевое.

Далее: так как магнитное поле не может существовать стационарно, оно начинает уменьшаться, пересекая витки катушки в обратном направлении. На выводах катушки появляется ЭДС индукции, которое начинает перезаряжать конденсатор. В цепи колебательного контура течет ток, только уже противоположно току заряда, так как витки пересекаются полем в обратном направлении. Обкладки конденсатора перезаряжаются зарядами, противоположными первоначальным. Одновременно растет напряжение на генераторе противоположного знака, причем с той же скоростью, с какой катушка заряжает конденсатор.)

Далее: катушка перезарядила конденсатор до максимального напряжения. Напряжение на генераторе к этому моменту тоже достигло максимального.

Возникла следующая ситуация. Конденсатор и генератор соединены последовательно и на обоих напряжение, равное напряжению генератора. При последовательном соединении источников питания их напряжения складываются.

Следовательно, в следующем полупериоде на катушку пойдет удвоенное напряжение (и от генератора, и от конденсатора), и колебания в контуре будут происходить при удвоенном напряжении на катушке.

В контурах с низкой добротностью напряжение на катушке будет ниже удвоенного, так как часть энергии будет рассеиваться (на излучение, на нагрев) и энергия конденсатора не перейдет полностью в энергию катушки). Соединены как бы последовательно генератор и часть конденсатора.

Замечания

Колебательный контур, работающий в режиме резонанса напряжений, не является усилителем мощности. Повышенные напряжения, возникающие на его элементах, возникают за счет заряда конденсатора в первую четверть периода после включения и исчезают при отборе от контура большой мощности.

Явление резонанса напряжений необходимо учитывать при разработке аппаратуры. Повышенное напряжение может повредить не рассчитаные на него элементы.

Применение

При совпадении частоты генератора и собственных колебаний контура на катушке появляется напряжение, более высокое, чем на клеммах генератора. Это можно использовать в удвоителях напряжений, работающих на высокоомную нагрузку, или полосовых фильтрах, реагирующих на определенную частоту.

См. также

Резонанс токов

Колебательный контур

Литература

• Власов В. Ф. Курс радиотехники. М.: Госэнергоиздат, 1962. С. 52.
• Изюмов Н. М., Линде Д. П. Основы радиотехники. М.: Госэнергоиздат, 1959. С. 512.

Ссылки

§56. Резонанс напряжений и резонанс токов

Явление резонанса. Электрическая цепь, содержащая индуктивность и емкость, может служить колебательным контуром, где возникает процесс колебаний электрической энергии, переходящей из индуктивности в емкость и обратно. В идеальном колебательном контуре эти колебания будут незатухающими. При подсоединении колебательного контура к источнику переменного тока угловая частота источника ? может оказаться равной угловой частоте ?₀, с которой происходят колебания электрической энергии в контуре. В этом случае имеет место явление резонанса, т. е. совпадения частоты свободных колебаний ?₀, возникающих в какой-либо физической системе, с частотой вынужденных колебаний ?, сообщаемых этой системе внешними силами.

Резонанс в электрической цепи можно получить тремя способами: изменяя угловую частоту ? источника переменного тока, индуктивность L или емкость С. Различают резонанс при последовательном соединении L и С — резонанс напряжений и при параллельном их соединении — резонанс токов. Угловая частота ?₀, при которой наступает резонанс, называется резонансной, или собственной частотой колебаний резонансного контура.

Резонанс напряжений. При резонансе напряжений (рис. 196, а) индуктивное сопротивление X_L равно емкостному Х_си полное сопротивление Z становится равным активному сопротивлению R:

Z = ?( R² + [?₀L — 1/(?₀C)]² ) = R

В этом случае напряжения на индуктивности U_L и емкости U_c равны и находятся в противофазе (рис. 196,б), поэтому при сложении они компенсируют друг друга. Если активное сопротивление цепи R невелико, ток в цепи резко возрастает, так как реактивное сопротивление цепи X = X_L—X_с становится равным нулю. При этом ток I совпадает по фазе с напряжением U и I=U/R. Резкое возрастание тока в цепи при резонансе напряжений вызывает такое же возрастание напряжений U_L и U_c, причем их значения могут во много раз превышать напряжение U источника, питающего цепь.

Угловая частота ?0, при которой имеют место условия резонанса, определяется из равенства ?_oL = 1/(?₀С).

Рис. 196. Схема (а) и векторная диаграмма (б) электрической цепи, содержащей R, L и С, при резонансе напряжений

Отсюда имеем

?_o = 1/?(LC) (74)

Если плавно изменять угловую частоту ? источника, то полное сопротивление Z сначала начинает уменьшаться, достигает наименьшего значения при резонансе напряжений (при ?_o), а затем увеличивается (рис. 197, а). В соответствии с этим ток I в цепи сначала возрастает, достигает наибольшего значения при резонансе, а затем уменьшается.

Резонанс токов. Резонанс токов может возникнуть при параллельном соединении индуктивности и емкости (рис. 198, а). В идеальном случае, когда в параллельных ветвях отсутствует активное сопротивление (R₁=R₂ = 0), условием резонанса токов является равенство реактивных сопротивлений ветвей, содержащих индуктивность и емкость, т. е. ?_oL = 1/(?_oC). Так как в рассматриваемом случае активная проводимость G = 0, ток в неразветвленной части
цепи при резонансе I=U?(G²+(B_L-B_C)²)= 0. Значения токов в ветвях I₁ и I₂ будут равны (рис. 198,б), но токи будут сдвинуты по фазе на 180° (ток IL в индуктивности отстает по фазе от напряжения U на 90°, а ток в емкости I с опережает напряжение U на 90°). Следовательно, такой резонансный контур представляет собой для тока I бесконечно большое сопротивление и электрическая энергия в контур от источника не поступает. В то же время внутри контура протекают токи I_L и I_с, т. е. имеет место процесс непрерывного обмена энергией внутри контура. Эта энергия переходит из индуктивности в емкость и обратно.

Как следует из формулы (74), изменяя значения емкости С или индуктивности L, можно изменять частоту колебаний ?₀ электрической энергии и тока в контуре, т. е. осуществлять настройку контура на требуемую частоту. Если бы в ветвях, в которых включены индуктивность и емкость, не было активного сопротивления, этот процесс колебания энергии продолжался бы бесконечно долго, т. е. в контуре возникли бы незатухающие колебания энергии и токов I_L и I_с. Однако реальные катушки индуктивности и конденсаторы всегда поглощают электрическую энергию (из-за наличия в катушках активного сопротивления проводов и возникновения

Рис. 197. Зависимость тока I и полного сопротивления Z от ? для последовательной (а) и параллельной (б) цепей переменного тока

Рис. 198. Электрическая схема (а) и векторные диаграммы (б и в) при резонансе токов

в конденсаторах токов смещения, нагревающих диэлектрик), поэтому в реальный контур при резонансе токов поступает от источника некоторая электрическая энергия и по неразветвленной части цепи протекает некоторый ток I.

Условием резонанса в реальном резонансном контуре, содержащем активные сопротивления R₁ и R₂, будет равенство реактивных проводимостей B_L = B_C ветвей, в которые включены индуктивность и емкость.

Из рис. 198, в следует, что ток I в неразветвленной части цепи совпадает по фазе с напряжением U, так как реактивные токи 1_L и I_с равны, но противоположны по фазе, вследствие чего их векторная сумма равна нулю.

Если в рассматриваемой параллельной цепи изменять частоту ?_о источника переменного тока, то полное сопротивление цепи начинает увеличиваться, достигает наибольшего значения при резонансе, а затем уменьшается (см. рис. 197,б). В соответствии с этим ток I начинает уменьшаться, достигает наименьшего значения I_min = I_a при резонансе, а затем увеличивается.

В реальных колебательных контурах, содержащих активное сопротивление, каждое колебание тока сопровождается потерями энергии. В результате сообщенная контуру энергия довольно быстро расходуется и колебания тока постепенно затухают. Для получения незатухающих колебаний необходимо все время пополнять потери энергии в активном сопротивлении, т. е. такой контур должен быть подключен к источнику переменного тока соответствующей частоты ?₀.

Явления резонанса напряжения и тока и колебательный контур получили весьма широкое применение в радиотехнике и высокочастотных установках. При помощи колебательных контуров мы получаем токи высокой частоты в различных радиоустройствах и высокочастотных генераторах. Колебательный контур — важнейший элемент любого радиоприемника. Он обеспечивает его избирательность, т. е. способность выделять из радиосигналов с различной длиной волны (т. е. с различной частотой), посланных различными радиостанциями, сигналы определенной радиостанции.

Резонанс напряжений. Что такое резонанс в электрической цепи

Резонанс является одним из самых распространенных в природе физических явлений. Явление резонанса можно наблюдать в механических, электрических и даже тепловых системах. Без резонанса у нас не было бы радио, телевидения, музыки и даже качелей на детских площадках, не говоря уже об эффективнейших диагностических системах, применяемых в современной медицине. Одним из самых интересных и полезных видов резонанса в электрической цепи является резонанс напряжений.

Элементы резонансной цепи

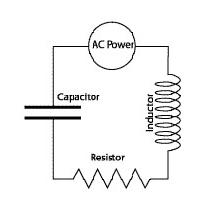
Явление резонанса может возникнуть в так называемой RLC-цепи, содержащей следующие компоненты:

• R — резисторы. Эти устройства, относящиеся к так называемым активным элементам электрической цепи, преобразуют электрическую энергию в тепловую. Другими словами, они удаляют энергию из контура и преобразуют ее в тепло.
• L — индуктивность. Индуктивность в электрических цепях — аналог массы или инерции в механических системах. Этот компонент не очень заметен в электрической цепи, пока не попробуешь сделать в ней какие-либо изменения. В механике, например, таким изменением является изменение скорости. В электрической цепи — изменение тока. Если оно по какой-либо причине происходит, индуктивность противодействует такому изменению режима цепи.
• С – обозначение для конденсаторов, которые представляют собой устройства, хранящие электрическую энергию подобно тому, как пружины сохраняют механическую энергию. Индуктивность концентрирует и сохраняет магнитную энергию, в то время как конденсатор концентрирует заряд и тем самым хранит электрическую энергию.

Понятие резонансного контура

Ключевыми элементами резонансного контура являются индуктивность (L) и емкость (C). Резистор имеет тенденцию к гашению колебаний, поэтому он удаляет энергию из контура. При рассмотрении процессов, происходящих в колебательном контуре, мы его временно игнорируем, но необходимо помнить, что подобно силе трения в механических системах электрическое сопротивление в цепях невозможно устранить.

Резонанс напряжений и резонанс токов

В зависимости от способа соединения ключевых элементов резонансный контур может быть последовательным и параллельным. При подключении последовательного колебательного контура к источнику напряжения с частотой сигнала, совпадающей с собственной частотой, при определенных условиях в нем возникает резонанс напряжений. Резонанс в электрической цепи с параллельно соединенными реактивными элементами называется резонансом токов.

Собственная частота резонансного контура

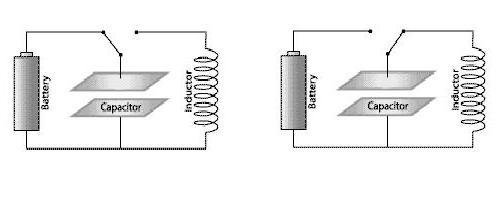
Мы можем заставить систему колебаться с собственной частотой. Для этого сначала необходимо зарядить конденсатор, как показано на верхнем рисунке слева. Когда это будет выполнено, ключ переводится в положение, показанное на том же рисунке справа.

В момент времени «0» вся электрическая энергия сохраняется в конденсаторе, и ток в контуре равен нулю (рисунок внизу). Обратите внимание, что верхняя пластина конденсатора заряжена положительно, а нижняя — отрицательно. Мы не можем видеть колебания электронов в цепи, но мы можем измерить ток амперметром, а при помощи осциллоскопа отследить характер зависимости тока от времени. Отметим, что T на нашем графике — это время, необходимое для завершения одного колебания, носящего в электротехнике название «период колебания».

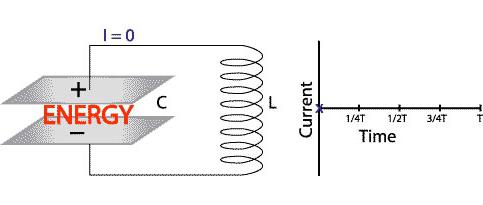
Ток течет по часовой стрелке (рисунок внизу). Энергия передается из конденсатора в катушку индуктивности. На первый взгляд может показаться странным, что индуктивность содержит энергию, однако это похоже на кинетическую энергию, содержащуюся в движущейся массе.

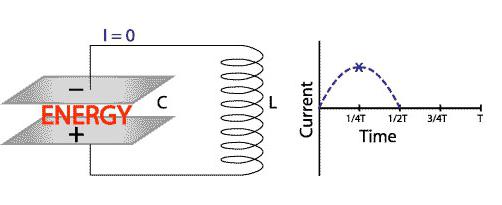
Поток энергии возвращается обратно в конденсатор, но обратите внимание, что полярность конденсатора теперь изменилась. Другими словами, нижняя пластина теперь имеет положительный заряд, а верхняя пластина — отрицательный заряд (рисунок внизу).

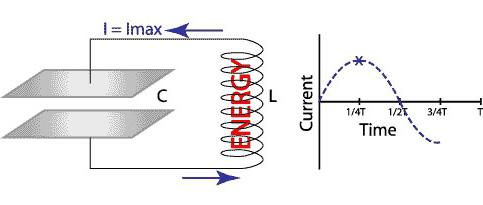
Теперь система полностью обратилась, и энергия начинает поступать из конденсатора опять в индуктивность (рисунок внизу). В итоге энергия полностью возвращается к своей отправной точке и готова начать цикл заново.

Частота колебаний может быть аппроксимирована следующим образом:

где: F — частота, L — индуктивность, C — емкость.

Рассмотренный на этом примере процесс отражает физическую суть резонанса напряжений.

Исследование резонанса напряжений

В реальных схемах LC всегда присутствует небольшое сопротивление, которое с каждым циклом уменьшает прирост амплитуды тока. После нескольких циклов ток уменьшается до нуля. Этот эффект называется «затухание синусоидального сигнала». Скорость затухания тока до нулевого значения зависит от величины сопротивления в цепи. Тем не менее, сопротивление не изменяет частоту колебаний резонансного контура. Если сопротивление достаточно велико, синусоидальные колебания в контуре не возникнут вообще.

Очевидно, там, где существует собственная частота колебаний, есть возможность возбуждения резонансного процесса. Мы делаем это, включая в последовательную цепь источник питания переменного ток (АС), как показано на рисунке слева. Термин «переменный» означает, что выходное напряжение источника колеблется с определенной частотой. Если частота источника питания совпадает с собственной частотой контура, возникает резонанс напряжений.

Условия возникновения

Сейчас мы рассмотрим условия возникновения резонанса напряжений. Как показано на последнем рисунке, мы вернули резистор в контур. При отсутствии резистора в контуре ток в резонансной цепи будет нарастать до некоторого максимального значения, определяемого параметрами элементов контура и мощностью источника питания. Увеличение сопротивления резистора в резонансной цепи повышает тенденцию к затуханию тока в контуре, но не влияет на частоту резонансных колебаний. Как правило, режим резонанса напряжений не наступает, если сопротивление цепи резонанса удовлетворяет условию R = 2(L/C)^0,5.

Использование резонанса напряжений для передачи радиосигнала

Явление резонанса напряжений является не только любопытнейшим физическим феноменом. Оно играет исключительную роль в технологии беспроводных коммуникаций – радио, телевидении, сотовой телефонии. Передатчики, используемые для беспроводной передачи информации, в обязательном порядке содержат схемы, предназначенные для резонирования на определенной для каждого устройства частоте, называемой несущей частотой. При помощи передающей антенны, подключенной к передатчику, он излучает электромагнитные волны на несущей частоте.

Антенна на другом конце приемо-передающего тракта получает этот сигнал и подает его на приемный контур, предназначенный для резонирования на частоте несущей. Очевидно, что антенна принимает множество сигналов на различных частотах, не говоря уже о фоновом шуме. Благодаря наличию на входе приемного устройства, настроенного на несущую частоту резонансного контура, приемник выбирает единственно правильную частоту, отсеивая все ненужные.

После детектирования амплитудно-модулированного (AM) радиосигнала, выделенный из него низкочастотный сигнал (НЧ) усиливается и подается на звуковоспроизводящее устройство. Это простейшая форма радиопередачи очень чувствительна к шумам и помехам.

Для повышения качества принимаемой информации разработаны и успешно используются другие, более совершенные способы передачи радиосигнала, которые также базируются на использовании настроенных резонансных систем.

Частотная модуляция или FM-радио решает многие из проблем радиопередачи с амплитудно-модулированным передающим сигналом, однако это достигается ценой существенного усложнения системы передачи. В FM-радио системные звуки в электронном тракте превращаются в небольшие изменения несущей частоты. Часть оборудования, которое выполняет это преобразование, называется «модулятор» и используется с передатчиком.

Соответственно, к приемнику должен быть добавлен демодулятор для преобразования сигнала обратно в форму, которая может быть воспроизведена через громкоговоритель.

Другие примеры использования резонанса напряжения

Резонанс напряжений как основополагающий принцип заложен также в схемотехнике многочисленных фильтров, широко применяемых в электротехнике для устранения вредных и ненужных сигналов, сглаживания пульсаций и генерирования синусоидальных сигналов.

Резонанс напряжений

Рассмотрим последовательный колебательный контур. Полное сопротивление последовательной цепи: .

Условие резонанса: , при этом ток совпадает по фазе с напряжением, угол сдвига фаз.

В этом случае значения противоположных по фазе напряжений на индуктивности и емкости будут равны, а вектор приложенного к цепи напряжения будет совпадать с вектором падения напряжения на активном сопротивлении.

При резонансе в последовательной цепи напряжения на индуктивности и емкости могут значительно превышать приложенное напряжение. Это имеет место, когда R→ 0, а следовательно и полное сопротивлениеZ→ 0. В этом случае, при любом конечном значении приложенного напряжения, токI → ∞. Поэтому бесконечно велики могут быть напряжения на индуктивности и емкости.

Превышение напряжения на реактивных элементах цепи над напряжением на зажимах цепи имеет место, если .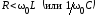

Так как , то оба этих условия сводятся к одному:. Эта величина имеет размерность сопротивления и называетсяхарактеристическимиливолновым сопротивлениемконтура.

Кратность перенапряжения на реактивном элементе, находят из отношений: .

Эта величина называется добротностьюрезонансного контура.

Величину, обратную добротности 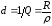, называютзатуханием контура.

Рассмотрим энергетические процессы в последовательном контуре при резонансе. Пусть имеем ток в контуре .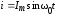

Напряжение на емкости .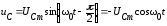

Но , тогда.

Суммарная электромагнитная энергия может быть записана в виде:

.

Таким образом, при резонансе сумма энергий магнитного и электрического полей с течением времени не изменяется.

Частотные характеристики последовательногоR-l-Cконтура.

Зависимости параметров цепи (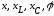и т.д.) от частоты () называютсячастотными характеристиками. Примеры частотных характеристик приведены на рисунках.

Резонансные характеристики

Действующее значение тока в последовательном резонансном контуре:

.

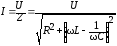Построим зависимости напряжений на элементах контура от частоты при поддержании на зажимах цепи постоянного напряжения.

Падение напряжения на индуктивности: ;

на емкости: .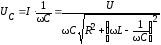

Имеет место симметрия максимумов кривых напряжения на реактивных элементах: .

Представив =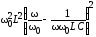, после подстановки в действующее значение для тока, получим:

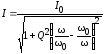, где— действующий ток при резонансе.

Из последнего выражения следует, что влияние параметров на вид резонансной кривой учитывается добротностью Q контура, причем, чем выше добротность резонансного контура, тем уже относительная ширина полосы пропускания контура. Это свойство резонансных колебательных контуров используется в практических целях, для выделения сигнала данной частоты из совокупности различных частот.

Параллельный колебательный контур. Резонанс токов.

Рассмотрим цепь, состоящую из параллельно включенных активного, индуктивного и емкостного сопротивлений.

Для этой цепи комплексная проводимость: ,. Угол сдвига фаз: . Модуль проводимости: .

Из этого выражения видно, что взаимная компенсация реактивных проводимостей (угол 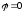) достигается при условии когда:, притом, что.

При резонансе реактивная проводимость цепи b= 0. Поэтому полная проводимостьy достигает минимального значения. Поэтому ток в общей ветви при неизменном напряжении так же минимален.

Векторная диаграмма при резонансе имеет вид:

Общий вектор тока является геометрической суммой векторов трех токов, два из которых ILиICнаходятся в противофазе. Следовательно, возможны случаи, когда токи в индуктивной катушке и конденсаторе могут значительно превосходить суммарный ток в цепи. Поэтому резонанс при параллельном соединении называютрезонансом токов.

Энергетические процессыв параллельной цепи аналогичны соответствующим процессам в последовательной цепи, т.е. и в этом случае происходят колебания энергии в цепи. Энергия полей переходит из конденсатора в катушку и обратно. Источник энергии покрывает потери энергии в ветви с активной проводимостью.

Резонанс напряжений

Допустим, что в цепи рис.1 действует переменная ЭДС. Она изменяется по закону:

Рисунок 1.

В цепи течет ток вида:

Амплитуда силы тока${\ (I}_m)$ связана с амплитудой ${{\mathcal E}}_m$ «законом Ома» для переменного тока:

Выражение:

полное электросопротивление. Угол ($\varphi $) на который колебания тока отстают от колебаний напряжения определен выражением:

Если изменить частоту колебаний ($\omega $). Как следует из формул (3) , (5) произойдёт изменение амплитуды силы тока ($I_m$) и сдвига фаз ($\varphi $).

Если $\omega =0$, то выражение $\frac{1}{\omega C}\to \infty $. Импеданс ($Z$) становится бесконечным, следовательно, $I_m=0.$ При $\omega =0$ мы имеем дело с постоянным током, который не проходит через конденсатор. Если начать увеличивать частоту, то величина реактивного сопротивления (${\left(\omega L-\frac{1}{\omega C}\right)}^2$) сначала уменьшается, следовательно, уменьшается импеданс, увеличивается $I_m.$ Когда частота ($\omega $) становится равной резонансной частоте контура (${\omega }_0$):

полное сопротивление цепи ($Z$) становится минимальным и равным активному сопротивлению цепи ($R$). Сила тока при этом достигает максимума. При $\omega >{\omega }_0$ выражение ${\left(\omega L-\frac{1}{\omega C}\right)}^2\ne 0$ и растет при росте частоты. Импеданс вновь увеличивается, амплитуда силы тока уменьшается, приближаясь к нулю асимптотически.

Графически вышеописанный процесс изображен на рис.2.

Рисунок 2.

Амплитуда силы тока при резонансной частоте ($\omega ={\omega }_0$) равна:

при этом разность фаз равна нулю ($\varphi =0$). В цепи как бы нет емкости и индуктивности. При этой частоте напряжения на емкости и индуктивности полностью взаимно компенсируются, становясь равными по модулю, так как они по фазе противоположны всегда. Такой резонанс называют резонансом напряжений. Векторная схема резонанса напряжений изображена на рис.3. При резонансе контур ведет себя как активное сопротивление.

Рисунок 3.

Замечание

Итак, случай вынужденных колебаний, когда частота генератора ЭДС (или приложенного внешнего напряжения) равна резонансной частоте, представляет особый интерес. При этом амплитуда тока достигает максимума, а сдвиг фаз между током и напряжением равен нулю. Контур действует как активное сопротивление.

Применение резонанса напряжений

Явление резонанса напряжений используют в радиотехнике, если необходимо усилить колебания напряжения какой либо частоты, например в устройствах входной части радиоприемника. В этой части есть колебательный контур ($LC$). Добротность этого контура высока, напряжение с конденсатора контура подается на вход усилителя. Входные сигналы вызывают в антенне переменный ток довольно высокой частоты, который вызывает в катушке $L$ ЭДС взаимной индукции, амплитуда которой ${{\mathcal E}}_m\ \ $. Из-за резонанса на конденсаторе (значит и на входе) появляется напряжение с амплитудой ${{\mathcal E}}_mO>{{\mathcal E}}_m.$ Это усиление работает только в узком интервале частот, около резонансной частоты, что позволит выделить из большого количества сигналов разных радиостанций только колебания нужной частоты.

Пример 1

Задание: Чему равна амплитуда напряжения на конденсаторе ($U_{mC}$) при резонансе напряжений, если колебания затухают слабо? Добротность контура равна$\ O$. Внешняя ЭДС изменяется в соответствии с законом: ${\mathcal E}={{\mathcal E}}_m{sin \left(\omega t\right)\ }.$

Решение:

Амплитуда тока при резонансе достигает максимума, она равна:

\[I_{m\ }\left({\omega }_0\right)=\frac{{{\mathcal E}}_m}{R}\left(1.1\right),\]

где ${\omega }_0$ — резонансная частота.

Следовательно, амплитуда напряжения на конденсаторе будет равна:

\[U_{mC}=X_CI_{m\ }\left(1.2\right),\]

где емкостное сопротивление равно:

\[X_C=\frac{1}{\omega_0С}\left(1.3\right).\]

Подставим в формулу (1.2) $X_C$ из (1.3) и $I_{m\ }$ из (1.1) получим амплитуду напряжения на конденсаторе при резонансе:

\[U_{mC}=\frac{{{\mathcal E}}_m}{{\omega }_0RС}(1.4).\]

Учтем, что:

\[{\omega }_0=\frac{1}{\sqrt{LC}}(1.5)\]

подставим выражение для резонансной частоты в формулу (1.4), получим:

\[U_{mC}=\frac{{{\mathcal E}}_m\sqrt{LC}}{RС}={{\mathcal E}}_m\frac{1}{R}\sqrt{\frac{L}{C}}={{\mathcal E}}_mO\ \left(1.6\right),\]

где $O=\frac{1}{R}\sqrt{\frac{L}{C}}$ — добротность контура.

Ответ: $U_{mC}={{\mathcal E}}_mO.$

Пример 2

Задание: Чему равна амплитуда напряжения на индуктивности ($U_{mL}$) при резонансе напряжений, если колебания затухают слабо? Добротность контура равна$\ O$. Внешняя ЭДС изменяется в соответствии с законом: ${\mathcal E}={{\mathcal E}}_m{sin \left(\omega t\right)\ }.$

Решение:

Выражение для напряжения на индуктивности можно записать как:

\[U_{mL}=I_m{\omega }_0L\ \left(2.1\right),\]

где выражение для амплитуды тока ($I_m(\omega_0)$) при резонансе напряжений:

\[I_{m\ }\left({\omega }_0\right)=\frac{{{\mathcal E}}_m}{R}\left(2.2\right).\]

Получим:

\[U_{mL}=\frac{{{\mathcal E}}_m}{R}{\omega }_0L\ \left(2.3\right).\]

Проведем замену:

\[{\omega }_0=\frac{1}{\sqrt{LC}}\left(2.4\right).\]

Получим, что амплитуда напряжения на индуктивности равна:

\[U_{mL}=\frac{{{\mathcal E}}_m}{R}\frac{1}{\sqrt{LC}}L=\frac{{{\mathcal E}}_m}{R}\frac{\sqrt{L}}{\sqrt{C}}{={\mathcal E}}_mO.\]

Ответ: $U_{mL}{={\mathcal E}}_mO.$

Колебания напряжения на конденсаторе и индуктивности имеют равные амплитуды, но их разность фаз равна $\pi $.

Резонансные режимы работы электрических цепей

В электротехнике при анализе режимов работы электрических цепей широко используется понятие двухполюсника. Двухполюсникомпринято называть часть электрической цепи произвольной конфигурации, рассматриваемую относительно двух выделенных выводов (полюсов). Двухполюсники, не содержащие источников энергии, называются пассивными. Всякий пассивный двухполюсник характеризуется одной величиной – входным сопротивлением, т.е. сопротивлением, измеряемым (или вычисляемым) относительно двух выводов двухполюсника. Входное сопротивление и входная проводимость являются взаимно обратными величинами.

Пусть пассивный двухполюсник содержит одну или несколько индуктивностей и один или несколько конденсаторов. Под резонансным режимом работы такого двухполюсника понимают режим (режимы) двухполюсника при котором входное сопротивление является чисто активным. По отношению к внешней цепи двухполюсник ведет себя как активное сопротивление, вследствие чего входные напряжение и ток совпадают по фазе. Различают две разновидности резонансных режимов: резонанс напряжения и резонанс тока.

Резонанс напряжений

В простейшем случае резонанс напряжений может быть получен в электрической цепи переменного тока при последовательном включении катушки индуктивности и конденсаторов. При этом, изменяя емкость конденсаторов при постоянных параметрах катушки, получают резонанс напряжений при неизменных значениях напряжения и индуктивности, частоты и активного сопротивления цепи. При изменении емкости конденсаторов Спроисходит изменение реактивного емкостного сопротивления. При этом полное сопротивление цепи также изменяется, следовательно, изменяются ток, коэффициент мощности, напряжения на катушке индуктивности, конденсаторах, а также активная, реактивная и полная мощности электрической цепи. Зависимости токаI, коэффициента мощности cosи полного сопротивленияZцепи переменного тока в функции емкостного сопротивления (резонансные кривые) для рассматриваемой цепи приведены на рис. 9,а. Векторная диаграмма тока и напряжений этой цепи при резонансе представлена на рис. 9,б.

Как видно из этой диаграммы, реактивная составляющая напряжения U_Lна катушке при резонансе равна напряжениюU_Сна конденсаторе. При этом напряжение на катушке индуктивностиU_кпри резонансе вследствие того, что катушка кроме реактивного сопротивленияX_Lобладает еще и активным сопротивлениемR, несколько больше, чем напряжение на конденсаторе.

Анализ представленных выражений (2), а также рис. 9,аибпоказывают, что резонанс напряжений имеет ряд отличительных особенностей.

1. При резонансе напряжений полное сопротивление электрической цепи переменного тока принимает минимальное значение и оказывается равным ее активному сопротивлению, т.е.

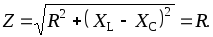
2. Из этого следует, что при неизменном напряжении питающей сети (U= const) при резонансе напряжений ток в цепи достигает наибольшего значенияI =U/Z =U/R. Теоретически ток может достигать больших значений, определяемых напряжением сети и активным сопротивлением катушки.

а)б)

Рис. 9

3. Коэффициент мощности при резонансе cos=R/Z =R/R = 1, т.е. принимает наибольшее значение, которому соответствует угол= 0. Это означает, что вектор тока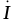и вектор напряжения сети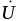при этом совпадают по направлению, так как они имеют равные начальные фазы_i=_u.

4. Активная мощность при резонансе P=RI ²имеет наибольшее значение, равное полной мощностиS, в то же время реактивная мощность цепиQ=XI ²= (X_LX_C)I ²оказывается равной нулю:Q =Q_LQ_C= 0.

5. При резонансе напряжений напряжения на емкости и индуктивности оказываются равными U_С=U_L=X_CI =X_LIи в зависимости от тока и реактивных сопротивлений могут принимать большие значения, во много раз превышающие напряжение питающей сети. При этом напряжение на активном сопротивлении оказывается равным напряжению питающей сети, т.е.U_R=U.

Резонанс напряжений в промышленных электротехнических установках нежелательное и опасное явление, так как оно может привести к аварии вследствие недопустимого перегрева отдельных элементов электрической цепи или пробою изоляции обмоток электрических машин и аппаратов, изоляции кабелей и конденсаторов при возможном перенапряжении на отдельных участках цепи. В то же время резонанс напряжений широко используется в различного рода приборах и устройствах электроники.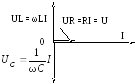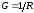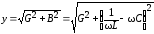