Физическая работа — урок. Физика, 8 класс.

Совершённая работа равна изменению энергии, потраченной на совершение работы.

Величину работы можно определить, вычитая из конечного значения энергии начальное значение энергии.

 

A=Eконеч.−Eнач.,или A=ΔE, где A — работа (Дж); E — энергия (Дж).

 

Работу, как и энергию, измеряют в джоулях (Дж).

 

Если энергия тела увеличивается, тогда общая совершённая работа является положительной.

Пример:

Когда автомобиль начинает двигаться, его кинетическая энергия увеличивается. Значит, двигатель автомобиля совершает положительную работу.

Если энергия тела уменьшается, тогда общая совершённая работа является отрицательной.

Пример:

Когда автомобиль свободно катится по горизонтальной поверхности, его скорость и кинетическая энергия уменьшаются. Значит, сила сопротивления совершает отрицательную работу.

 

В физике рассматривают физическую работу, которая связана с перемещением тел.

Если при прямолинейном движении на тело действует неизменная сила, направленная в сторону движения тела, тогда работа, произведённая приложенной силой, равна произведению величины силы на величину проделанного перемещения.

Если к телу приложена сила под вертикальным углом к направлению движения тела, как это показано на рисунке, тогда величина совершённой работы зависит от:

1) величины приложенной силы (F), которая совершает работу;

2) расстояния (l), на которое перемещается тело;

3) угла \(α\) между направлением действия силы и направлением движения тела.

Работа определяется по формуле: A=F⋅l⋅cosα.

  

 

Рис. \(1\). Под углом

  

Обрати внимание!

Если сила направлена параллельно направлению перемещения, тогда угол \(α = 0\), а \(косинус\) угла \(α\) равен \(1\). В этом случае формула упрощается: A=F⋅l.

Если проделанный путь является прямолинейным, тогда вместо пути \(l\) можно использовать перемещение (s).  

В этом случае формула для расчёта работы приобретает такой вид: A=F⋅s.

На трёх рисунках изображены случаи, когда направление силы и направление движения тела совпадают.

1) Действие силы и направление движения тела направлены горизонтально. Например, автомобиль едет по прямому пути, и сила тяги автомобиля приложена в том же направлении.

 

 

Рис. \(2\). Параллельно

 

2) Действие силы и направление движения тела направлены под одинаковым углом наклона по отношению к горизонту. Например, автомобиль едет в гору.

  

 

Рис.\(3\). Движение «в гору»

  

3) Действие силы и направление движения тела направлены вертикально. Например, груз поднимается вверх, и сила упругости троса тоже направлена вверх. В этом случае величину совершённой работы можно рассчитать также по формуле A=m⋅g⋅h, где

(m) — масса тела, (g) — ускорение свободного падения,

(h) — высота подъёма тела над поверхностью земли.

 

 

Рис. \(4\). Движение вверх

 

Обрати внимание!

Если направление действия силы противоположно направлению движения, тогда совершаемая этой силой работа отрицательна.

Работа отрицательна, так как функция \(косинус\) в интервале значений угла \(90° — 180°\) является отрицательной.

Таким образом, любая работа, совершённая силой трения или сопротивления, является отрицательной.

Пример:

Когда автомобиль едет с равномерной скоростью по прямой дороге, как это показано на рисунке, работа силы тяги автомобиля является положительной, а работа силы сопротивления равна по величине, но является отрицательной. В результате этого кинетическая и потенциальная энергия автомобиля остаются неизменными. 

Если сила направлена прямо противоположно направлению движения, тогда работу вычисляют по формуле: A=−F⋅l.

 

Рис. \(5\). Автомобиль

Источники:

Рис. 1. Под углом. © ЯКласс.

Рис. 2. Параллельно. © ЯКласс.

Рис. 3. Движение «в гору». © ЯКласс.

Рис. 4. Движение вверх. © ЯКласс.

Рис. 5. Автомобиль. © ЯКласс.

Механическая работа: определение и формула

 

Вы знаете, что такое работа? Вне всякого сомнения. Что такое работа, знает каждый человек, при условии, что он рожден и живет на планете Земля. А что такое механическая работа?

Это понятие тоже известно большинству людей на планете, хотя некоторые отдельные личности и имеют довольно смутное представление об этом процессе. Но речь сейчас не о них. Еще меньшее число людей имеют представление, что такое механическая работа с точки зрения физики. В физике механическая работа – это не труд человека ради пропитания, это физическая величина, которая может быть совершенно никак не связана ни с человеком, ни с другим каким-нибудь живым существом. Как так? Сейчас разберемся.

Механическая работа в физике

Приведем два примера. В первом примере воды реки, столкнувшись с пропастью, шумно падают вниз в виде водопада. Второй пример – это человек, который держит на вытянутых руках тяжелый предмет, например, удерживает надломившуюся крышу над крыльцом дачного домика от падения, пока его жена и дети судорожно ищут, чем ее подпереть.

В каком случае совершается механическая работа?

Определение механической работы

Практически все, не задумываясь, ответят: во втором. И будут неправы. Дело обстоит как раз наоборот. В физике механическая работа описывается следующими определениями: механическая работа совершается тогда, когда на тело действует сила, и оно движется. Механическая работа прямо пропорциональна приложенной силе и пройденному пути.

Формула механической работы

Определяется механическая работа формулой:

A=Fs,

где A – работа,
F – сила,
s – пройденный путь.

Так что, несмотря на весь героизм уставшего держателя крыши, проделанная им работа равна нулю, а вот вода, падая под действием силы тяжести с высокого утеса, совершает самую, что ни на есть, механическую работу. То есть, если мы будем толкать тяжелый шкаф безуспешно, то проделанная нами работа с точки зрения физики будет равна нулю, несмотря на то, что мы прикладываем много сил. А вот если мы сдвинем шкаф на некоторое расстояние, то тогда мы проделаем работу, равную произведению приложенной силы на расстояние,  на которое мы передвинули тело.

Единица работы – 1 Дж. Это работа, совершенная силой в 1 ньютон, по передвижению тела на расстояние в 1 м. Если направление приложенной силы совпадает с направлением движения тела, то данная сила совершает положительную работу. Пример – это когда мы толкаем какое-либо тело, и оно двигается. А в случае, когда сила приложена в противоположную движению тела сторону, например, сила трения, то данная сила совершает отрицательную работу. Если же приложенная сила никак не влияет на движение тела, то сила, совершаемая этой работой, равна нулю.

Нужна помощь в учебе?

Предыдущая тема: Воздухоплавание в физике
Следующая тема:&nbsp&nbsp&nbspМощность: формула и применение в физике

Механическая работа — определение, формула, виды, свойства

Для нас привычно понятие «работа» в бытовом смысле.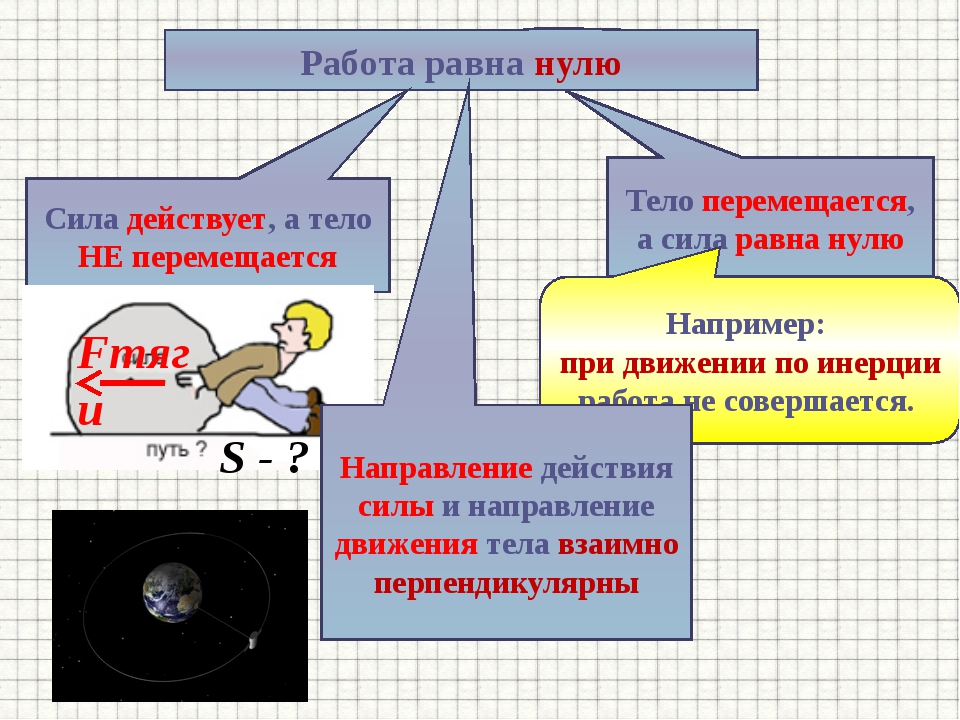

Работая, мы совершаем какое-либо действие, чаще всего полезное. В физике (если точнее, то в механике) термин «работа» показывает, какую силу в результате действия приложили, и на какое расстояние тело в результате действия этой силы переместилось.

Например, нам нужно поднять велосипед по лестнице в квартиру. Тогда работа будет определяться тем, сколько весит велосипед и на каком этаже (на какой высоте) находится квартира.

Механическая работа — это физическая величина, прямо пропорциональная приложенной к телу силе и пройденному телом пути.

Чтобы рассчитать работу, нам необходимо умножить численное значение приложенной к телу силы F на путь, пройденный телом в направлении действия силы S. Работа обозначается латинской буквой А.

Механическая работа А = FS A — механическая работа [Дж] F — приложенная сила [Н] S — путь [м]

Если под действием силы в 1 ньютон тело переместилось на 1 метр, то данной силой совершена работа в 1 джоуль.

Поскольку сила и путь — векторные величины, в случае наличия между ними угла формула принимает вид.

Механическая работа А = FScosα A — механическая работа [Дж] F — приложенная сила [Н] S — путь [м] α — угол между векторами силы и перемещения []

Числовое значение работы может становиться отрицательным, если вектор силы противоположен вектору скорости. Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае сила называется противодействующей.

Для совершения работы необходимы два условия:

• чтобы на тело действовала сила,
• чтобы происходило перемещение тела.

Сила, действующая на тело, может и не совершать работу. Например, если кто-то безуспешно пытается сдвинуть с места тяжелый шкаф. Сила, с которой человек действует на шкаф, не совершает работу, поскольку перемещение шкафа равно нулю.

Запомнить!

Работа равна нулю, если при приложенной силе перемещение отсутствует.

Полезная и затраченная работа

Был такой мифологический персонаж у древних греков — Сизиф. За то, что он обманул богов, те приговорили его после смерти вечно таскать огромный булыжник вверх по горе, откуда этот булыжник скатывался — и так без конца. В общем, Сизиф делал совершенно бесполезное дело с нулевым КПД. Поэтому бесполезную работу и называют «сизифов труд».

Чтобы разобраться в понятиях полезной и затраченной работы, давайте пофантазируем и представим, что Сизифа помиловали и камень больше не скатывается с горы, а КПД перестал быть нулевым.

Полезная работа в этом случае равна потенциальной энергии, приобретенной булыжником.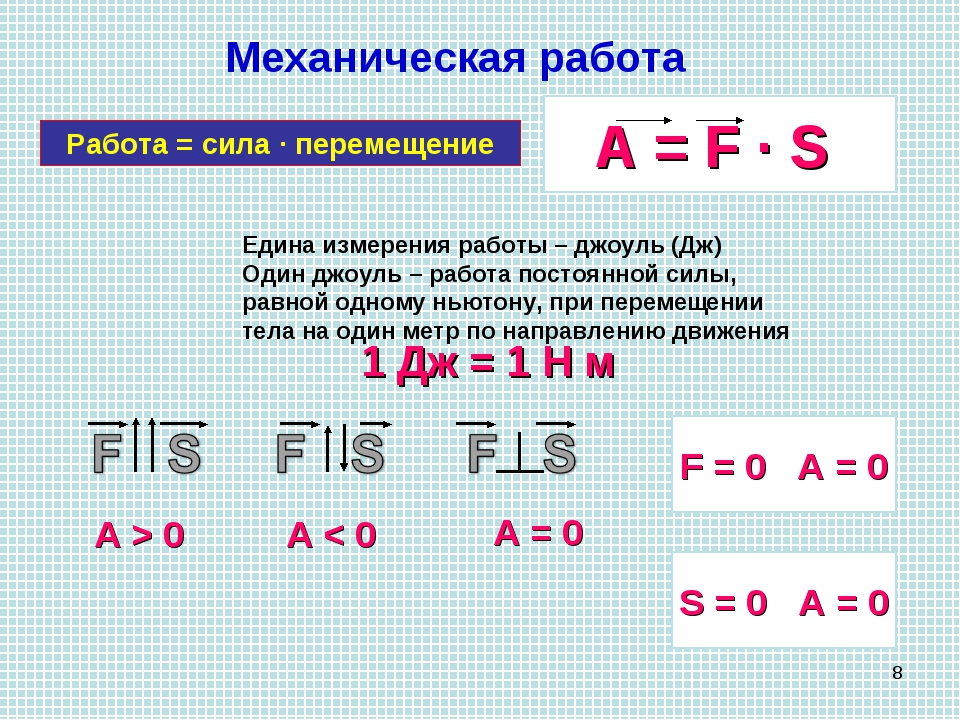 Потенциальная энергия, в свою очередь, прямо пропорциональна высоте: чем выше расположено тело, тем больше его потенциальная энергия. Выходит, чем выше Сизиф прикатил камень, тем больше полезная работа.

Потенциальная энергия Еп = mgh m — масса тела [кг] g — ускорение свободного падения [м/с2] h — высота [м] На планете Земля g ≈ 9,8 м/с2

Затраченная работа в нашем примере — это механическая работа Сизифа. Механическая работа зависит от приложенной силы и пути, на протяжении которого эта сила была приложена.

Механическая работа А = FS A — механическая работа [Дж] F — приложенная сила [Н] S — путь [м]

И как же достоверно определить, какая работа полезная, а какая затраченная?

Все очень просто! Задаем два вопроса:

1. За счет чего происходит процесс?


2. Ради какого результата?

В примере выше процесс происходит ради того, чтобы тело поднялось на какую-то высоту, а значит — приобрело потенциальную энергию (для физики это синонимы).

Происходит процесс за счет энергии, затраченной Сизифом — вот и затраченная работа.

Мощность

На заводах по всему миру большинство задач выполняют машины. Например, если нам нужно закрыть крышечками тысячу банок колы, аппарат сделает это в считанные минуты. У человека эта задача заняла бы намного больше времени. Получается, что машина и человек выполняют одинаковую работу за разные промежутки времени. Для того, чтобы описать скорость выполнения работы, нам потребуется понятие мощности.

Мощностью называется физическая величина, равная отношению работы ко времени ее выполнения.

Мощность N = A/t N — мощность [Вт] A — механическая работа [Дж] t — время [с]

Один ватт — это мощность, при которой работа в один джоуль совершается за одну секунду.

Также для мощности справедлива другая формула:

Мощность N = Fv N — мощность [Вт] F — приложенная сила [Н] v — скорость [м/с]

Как и для работы, для мощности справедливо правило знаков: если векторы направлены противоположно, значение мощности будет отрицательным.

Поскольку сила и скорость — векторные величины, в случае наличия между ними угла формула принимает следующий вид:

Мощность N = Fvcosα N — мощность [Вт] F — приложенная сила [Н] v — скорость [м/с] α — угол между векторами силы и скорости []

Примеры решения задач

Задача 1

Ложка медленно тонет в большой банке меда. На нее действуют сила тяжести, сила вязкого трения и выталкивающая сила. Какая из этих сил при движении тела совершает положительную работу? Выберите правильный ответ:

1. Выталкивающая сила.


2. Сила вязкого трения.


3. Сила тяжести.


4. Ни одна из перечисленных сил.

Решение

Поскольку ложка падает вниз, перемещение направлено вниз. В ту же сторону, что и перемещение, направлена только сила тяжести. Это значит, что она совершает положительную работу.

Ответ: 3.

Задача 2

Ящик тянут по земле за веревку по горизонтальной окружности длиной L = 40 м с постоянной по модулю скоростью. Модуль силы трения, действующей на ящик со стороны земли, равен 80 H. Чему равна работа силы тяги за один оборот?

Решение

Поскольку ящик тянут с постоянной по модулю скоростью, его кинетическая энергия не меняется. Вся энергия, которая расходуется на работу силы трения, должна поступать в систему за счет работы силы тяги. Отсюда находим работу силы тяги за один оборот:

Ответ: 3200 Дж.

Задача 3

Тело массой 2 кг под действием силы F перемещается вверх по наклонной плоскости на расстояние l = 5 м. Расстояние тела от поверхности Земли при этом увеличивается на 3 метра. Вектор силы F направлен параллельно наклонной плоскости, модуль силы F равен 30 Н. Какую работу при этом перемещении в системе отсчета, связанной с наклонной плоскостью, совершила сила F?

Решение

В данном случае нас просят найти работу силы F, совершенную при перемещении тела по наклонной плоскости. Это значит, что нас интересуют сила F и пройденный путь. Если бы нас спрашивали про работу силы тяжести, мы бы считали через силу тяжести и высоту.

Работа силы определяется как скалярное произведение вектора силы и вектора перемещения тела. Следовательно:

A = Fl = 30 * 5 = 150 Дж

Ответ: 150 Дж.

Задача 4

Тело движется вдоль оси ОХ под действием силы F = 2 Н, направленной вдоль этой оси. На рисунке приведен график зависимости проекции скорости v^x тела на эту ось от времени t. Какую мощность развивает эта сила в момент времени t = 3 с?

Решение

На графике видно, что проекция скорости тела в момент времени 3 секунды равна 5 м/с.

Мощность можно найти по формуле N = Fv.

N = FV = 2×5 = 10 Вт

Ответ: 10 Вт.

07. Работа и Энергия — Физика это просто!!! 2016

Взглянем с «точки зрения Джоуля» на работу и энергию. Попробуем понять, почему они одной размерности.

Термином «работа» в механике определяется физическая величина, равная произведению силы, перемещения и косинуса угла между направлением действия силы и перемещением:

Рисунок 5

Работа равна нулю, если тело движется по инерции (F = 0), если нет перемещения (s = 0) или, если угол между перемещением и силой равен 90° (cos α = 0). Единицей работы в СИ служит Джоуль (Дж).

1 джоуль — это такая работа, которая совершается силой 1 Н при перемещении тела на 1 м по линии действия силы.

Для определения количества совершения работы в единицу времени вводят величину «мощность».

Мощность равняется отношению совершенной работы ко времени, за которое она выполнена:

Единицей мощности в СИ служит 1 ватт (Вт). 1 Вт — мощность, при которой совершается работа в 1 Дж за 1 секунду.

Рассмотрим действие на тело некоторой постоянной силы F. И пусть она действует вдоль перемещения. Одномерный случай. На участке пути s будет произведена работа А. В результате у тела изменится скорость:

 Я надеюсь, все поняли, почему ?

И почему это справедливо только для прямолинейного равноускоренного движения? Движения под действием постоянной силы.

Величину  (m _* v²)/2  для материальной точки называют кинетической энергией тела. Ее размерность, как видно из формулы, совпадает с размерностью работы.

!!!        Вообще говоря, энергия – это такая величина, которая своим изменением характеризует величину работы. И еще она (энергия) сохраняется в замкнутой системе. Это все, что мы знаем про энергию. (Подробности у Фейнмана в первом томе его «Лекций по физике»!)

Кинетическая энергия — энергия движения, ею обладают все движущиеся тела. Эта величина является относительной, то есть она изменяется в зависимости от выбранной системы отсчета.

Кроме этого, существует и другой вид механической энергии — потенциальная энергия. Рассмотрим систему двух взаимодействующих тел.  Например, тела, приподнятого над Землей, и саму Землю. Так как Земля очень-очень большая и тяжелая, а тело маленькое и относительно легкое и, к тому же, оно не сильно меняет свою высоту над уровнем поверхности Земли, то можно считать, что тело находится в поле постоянной силы. Силы тяжести.

Работа силы тяжести при перемещении тела на отрезке |h₁ — h₂| будет равна:

Величину m*g*h в соответствующей точке, которая расположена на высоте h, называют потенциальной энергией тела, находящегося в поле тяжести.

Из формулы (21) вытекает, что работа не зависит от траектории движения в поле силы тяжести, а определяется лишь изменением высоты.

Потенциальная энергия характеризует и другие взаимодействующие тела. Потенциальной энергией обладает сжатая пружина:

где k — модуль упругости, х — смещение от положения равновесия.

Потенциальная энергия, как и кинетическая, является величиной относительной. И высота, и скорость зависят от выбора системы координат.

           

Работа в физике | Физика

– Что вам задано на завтра по физике, Игорь? — спросил Иван Иванович, подходя к столу, за которым сидел его сын, перелистывая учебник физики.

– Повторить о работе. Очень мало, всего три параграфа и две задачи. Это очень просто. Я уже приготовил уроки.

– Мало — это верно, но просто ли? Вот скажи, пожалуйста, что называется работой?

– Что называется работой? М-м-м, пожалуй, прямого ответа на этот вопрос в книге нет. Приводятся примеры работы, говорится, что понятие о работе в механике не совпадает с представлением о работе в обыденной жизни. В механике понятие работы относится только к тем случаям, когда какое-либо тело перемещается под действием приложенной к нему силы… Но что называется работой?! Постой, учитель задал, например, такой вопрос: «По гладкому горизонтальному льду катится стальной шарик. Допустим, что сопротивление движению (трение) отсутствует.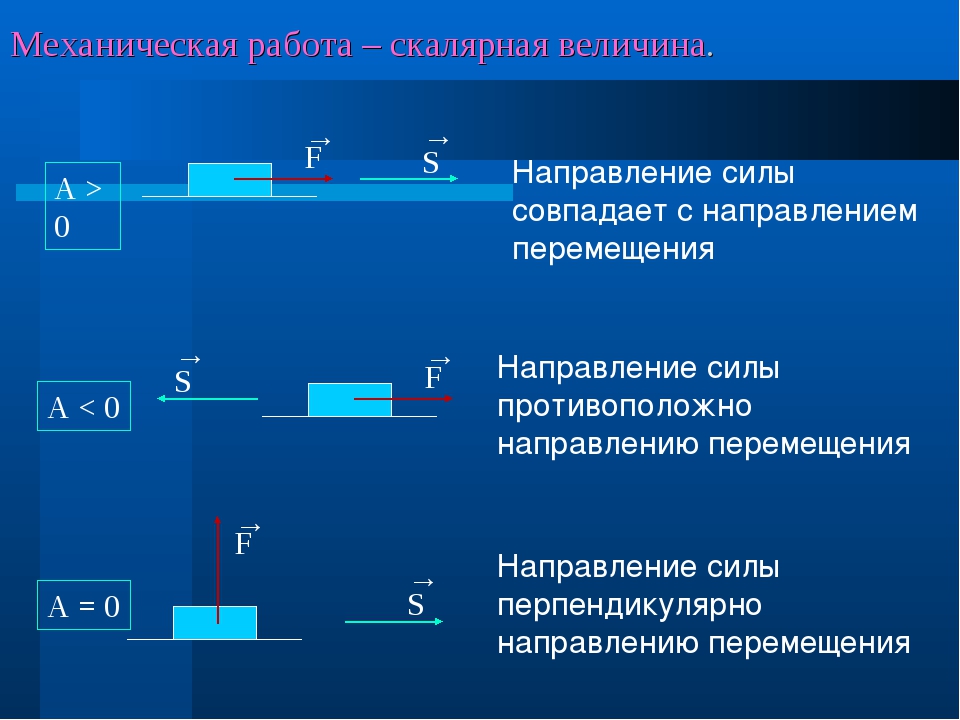 Совершается ли при этом механическая работа?» Может быть, механическая работа представляет собой преодоление сопротивления на пути движения тела. Работой называют произведение силы на путь, пройденный по направлению силы:

A = Fs.

– Так, преодоление сопротивления, говоришь? Скажи, если тело массой m, падая в пустоте, например в трубке Ньютона, проходит путь h, то совершает ли работу сила тяжести?

– Конечно, A = mgh.

– Ну, а что же здесь преодолевается?

Лицо Игоря выражает крайнее изумление. Как же так? Есть и перемещение, и сила, приложенная к телу, т. е. соблюдены оба условия, необходимые для того, чтобы можно было говорить о работе, а в чем же тут состоит работа? Что преодолевается? Нельзя же сказать, что преодолевается инерция тела. Учитель не один раз разъяснял, что сохранение состояния покоя или равномерного и прямолинейного движения по инерции никак нельзя понимать как сопротивление тала изменению его состояния. В чем же тут дело?

– Что же произошло с телом? Как изменилось его состояние? Как движется свободно падающее тело?

– Равноускоренно.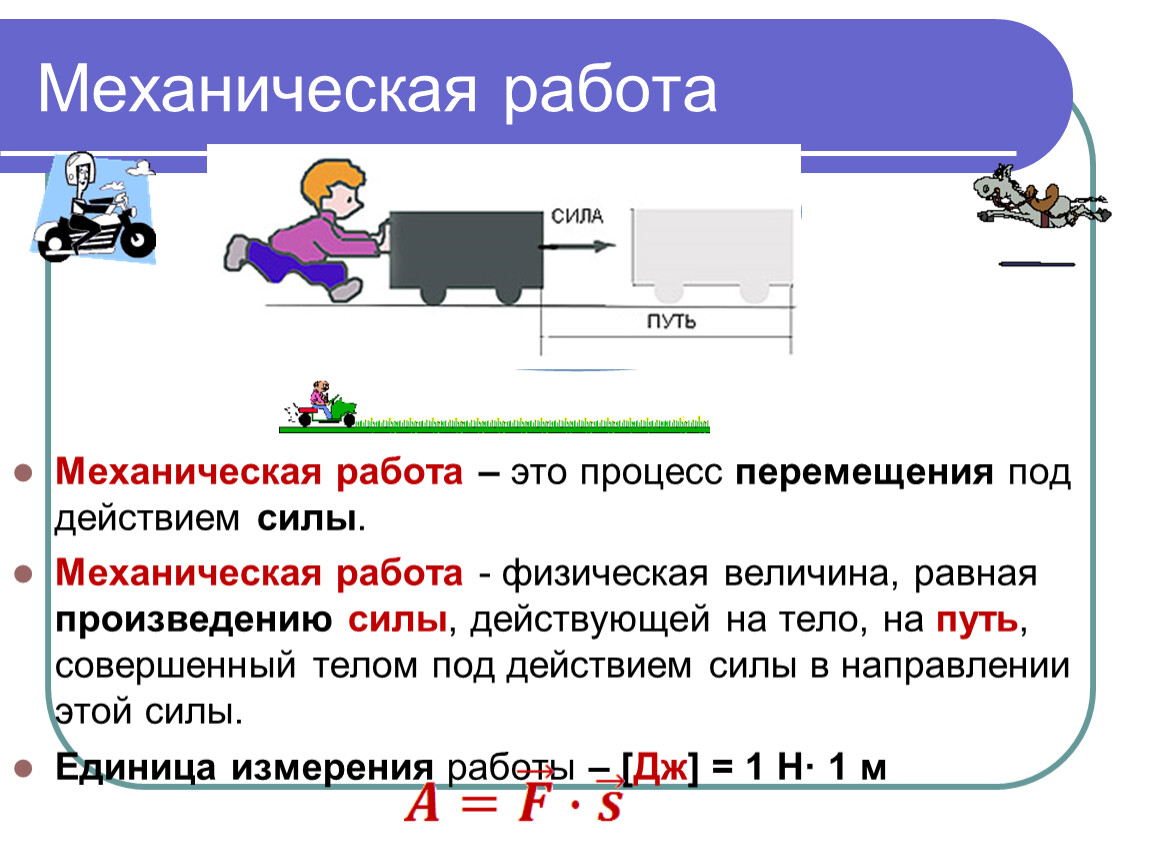 Тело под действием силы тяжести стало двигаться, и притом ускоренно. Теперь оно обладает кинетической энергией! Результат работы: тело получило энергию.

– Неужели ты думаешь, что тело не имело энергии в верхней точке?

– Имело, потенциальную. Теперь ее стало меньше, но появилась кинетическая энергия.

– А вот другой пример. Когда я поднимаю вот эту книгу и ставлю ее на верхнюю полку, я совершаю работу против силы тяжести. Книга поднята. У нее добавилась потенциальная энергия по сравнению с прежним ее положением. Откуда она взялась?

Игорь (радостно). Знаю, это твоя энергия! Ты отдал часть энергии книге. Работа, стало быть, есть передача энергии от одного тела к другому. Поднимая книгу, ты совершал работу, т. е. передавал энергию.

– Хорошо, думай дальше. Я снимаю книгу с полки и опять кладу ее на стол. Вернулась ли ком не прежняя энергия?

Лицо Игоря снова вытягивается, он морщит лоб, силясь разрешить задачу.

– Потенциальная энергия книги, снятой с полки, стала меньше.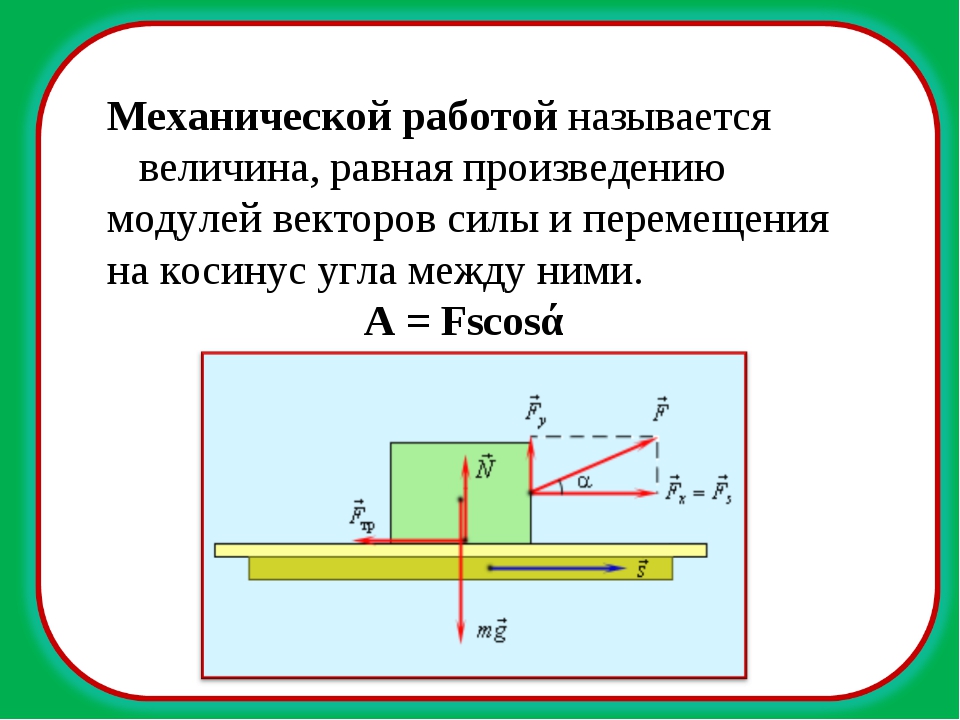 Куда же делась кинетическая энергия, какую она приобрела бы, падая с той же высоты? Эта энергия, конечно, досталась мне, но не вернула меня в прежнее состояние. Удерживая книгу от падения, я должен был напрягать мускулы, произошли физиологические изменения, которые нельзя учесть по законам механики.

– Работа по преодолению силы трения, силы сопротивления среды…

– Опять преодоление? Нет, мне решительно не нравится такое определение работы. Гораздо лучше, если ты всегда будешь рассматривать работу как передачу энергии от одного тела к другому, причем почти всегда будет происходить превращение энергии из одного вида в другой.

На что расходуется энергия лошади при перевозке дров на санях? Учти, что ответ: «Энергия пошла на преодоление трения» — я не зачту.

Игорь пытается ответить, но ему не хватает нужных слов.

Отец. Принеси мне, пожалуйста, из соседней комнаты со стола книгу «Избранные сочинения» Горького. Я прочту тебе замечательное описание работы грузчиков на пристани.

Игорь нашел требуемую книгу и передал ее отцу.

– Спасибо. Пока я найду нужную страницу, скажи, в чем заключалась сейчас твоя работа, когда ты нес книгу. Не о работе по преодолению силы трения тут речь, ты же не шаркал ногами по полу, да и не так велико сопротивление среды. Может быть, ты поднимал груз?

Нет, положительно не везло в этот вечер Игорю. Что ни вопрос, то загадка. И на этот вопрос он не может самостоятельно ответить.

– Ну, так и быть, я тебе помогу ответить на эти вопросы. Когда ты идешь с книгой или без книги, то при каждом шаге центр тяжести твоего тела поднимается и опускается. По существу при ходьбе ты совершаешь работу, связанную с многократным подниманием центра тяжести. А теперь слушай, как написал Горький в повести «Мои университеты»: «Мне хорошо памятен день, когда я впервые почувствовал героическую поэзию труда.

Под Казанью села на камень, проломив днище, большая баржа с персидским товаром; был сентябрь, дул верховой ветер, по серой реке сердито прыгали волны, ветер бешено срывал их гребни, кропил реку холодным дождем.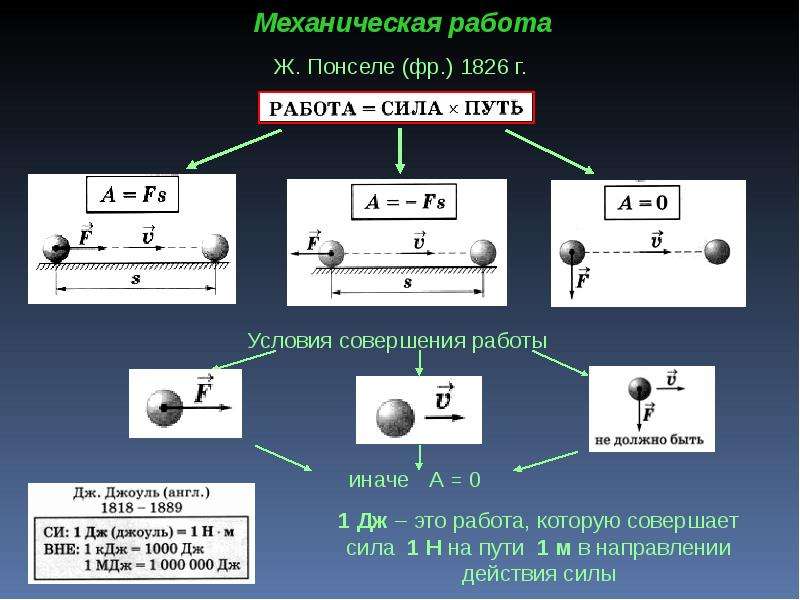 Артель, человек полсотни, угрюмо расположилась на палубе пустой баржи, кутаясь рогожами и брезентом…

К полуночи доплыли до переката, причалили пустую баржу борт о борт к сидевшей на камнях; артельный староста, ядовитый старичишка, рябой хитрец и сквернослов, с глазами и носом коршуна, сорвав с лысого черепа мокрый картуз, крикнул высоким, бабьим голосом:

– Молись, ребята!

В темноте, на палубе баржи, грузчики сбились в черную кучу и заворчали, как медведи, а староста, кончив молиться раньше всех, завизжал:

– Фонарей! Ну, молодчики, покажи работу! Честно, детки! С богом – начинай!

И тяжелые, мокрые люди начали «показывать работу». Они, точно в бой, бросились на палубу и в трюмы затонувшей баржи — с гиком, ревом, с прибаутками. Вокруг меня с легкостью пуховых подушек летали мешки риса, тюки изюма, кож, каракуля, бегали коренастые фигуры, ободряя друг друга воем, свистом, крепкой руганью. Трудно было поверить, что так весело, легко и споро работали те самые люди, которые только что жаловались на жизнь, на дождь. Дождь стал гуще, холоднее, ветер усилился, рвал рубахи, закидывал подолы на головы, обнажая животы. В мокрой тьме при слабом свете шести фонарей метались черные люди, глухо топая ногами о палубы барж. Работали так, как будто ожидали удовольствия швырять с рук на руки четырехпудовые мешки, бегом носиться с тюками на спине…

Я тоже хватал мешки, бросал, снова бежал и хватал, и казалось мне, что и я сам, и все вокруг завертелось в бурной пляске, что эти люди могут так страшно и весело работать без устали, не щадя себя — месяца, года, что они могут, ухватясь за колокольни и минареты города, стащить его с места, куда захотят.

Я жил эту ночь в радости, не испытанной мною, душу озаряло желание прожить всю жизнь в этом полубезумном восторге делания.

И до двух часов дня, пока не перегрузили весь товар, полуголые люди работали без отдыха под проливных дождем и резким ветром, заставив меня благоговейно понять, какими могучими силами богата человеческая земля».

Иван Иванович захлопнул книгу.

– Так-то, брат! Поэзия ручного труда! Горький, конечно, великий писатель, перец человека и его творческих сил. Но давай посмотрим на всю эту историю глазами физика. Давай подсчитаем работу, проделанную 50 грузчиками за 14 ч. Мощность человека в среднем равна одной десятой лошадиной силы (1 л. с. = 736 Вт), хотя в минуту душевного подъема, в экстазе, она может быть и больше одной лошадиной силы, но ненадолго. В данном случае, при длительной работе, я думаю, мы все же не сможем оценить ее свыше 0,15 л. с.
Зная мощность и время работы, мы можем вычислить проделанную работу:

A = Nt = 0,15 л. с. · 50 · 14 · ч · 736 · 10^-3 кВт/л.с. = 76,3 кВт · ч.

Описанный Горьким случай относится к 1886 году.

Разгрузка такой баржи современными механизмами заняла бы не больше 3 ч, а главное, избавила бы людей от изнурительно тяжелой работы. Портальные краны, транспортеры, нории (вертикальные транспортеры), плавучие краны, судовые стрелы, пневматические перегрузчики совершенно преобразили работу крупных морских портов и речных пристаней.

А рекорды строительной техники! Я читал, что на постройке пирамиды Хеопса трудились 10000 рабов в течение 20 лет. В наши дни такую пирамиду можно было бы соорудить за 9 месяцев при участии всего 500 рабочих.

Вам, конечно, рассказывали в школе, что землеройные машины с вместимостью ковша 20 м3 заменяют 10 тысяч рабочих.

Разумеется, в основе успехов техники лежит наука, и в первую очередь физика. Вот почему ты должен особенно ценить уроки физики, читать дополнительную литературу.

Пока же предлагаю тебе несколько вопросов по теме, заданной на дом. Эти вопросы ты можешь предложить завтра товарищам.

1. Человек, держащий в руках груз (корзину с продуктами), не совершает механической работы. Совершает ли работу этот человек, если он поднимается в лифте?
2. Тело покоится на тележке, движущейся по инерции. Совершается ли при этом работа?
3. При занятии гимнастикой человек поднимает и опускает гантели. Совершает ли он работу?
4. Если человек стоит с грузом на плечах, он не совершает никакой работы, так как ничего не движет. Почему же устает стоящий человек, если у него на плечах какой-нибудь груз?
5. Первый раз футбольный мяч ударился о штангу ворот и остановился. Второй раз мяч был схвачен вратарем, двигавшимся навстречу мячу с такой же по модулю скоростью, что и мяч. Будет ли разница в работах, произведенных мячом в первый и во второй раз? (Ответ: во втором случае работа будет в 4 раза больше.)

Что такое работа в физике формула. Механическая работа

Вы знаете, что такое работа? Вне всякого сомнения. Что такое работа, знает каждый человек, при условии, что он рожден и живет на планете Земля. А что такое механическая работа?

Это понятие тоже известно большинству людей на планете, хотя некоторые отдельные личности и имеют довольно смутное представление об этом процессе. Но речь сейчас не о них. Еще меньшее число людей имеют представление, что такое механическая работа с точки зрения физики. В физике механическая работа — это не труд человека ради пропитания, это физическая величина, которая может быть совершенно никак не связана ни с человеком, ни с другим каким-нибудь живым существом. Как так? Сейчас разберемся.

Механическая работа в физике

Приведем два примера. В первом примере воды реки, столкнувшись с пропастью, шумно падают вниз в виде водопада. Второй пример — это человек, который держит на вытянутых руках тяжелый предмет, например, удерживает надломившуюся крышу над крыльцом дачного домика от падения, пока его жена и дети судорожно ищут, чем ее подпереть. В каком случае совершается механическая работа?

Определение механической работы

Практически все, не задумываясь, ответят: во втором. И будут неправы. Дело обстоит как раз наоборот. В физике механическая работа описывается следующими определениями: механическая работа совершается тогда, когда на тело действует сила, и оно движется. Механическая работа прямо пропорциональна приложенной силе и пройденному пути.

Формула механической работы

Определяется механическая работа формулой:

где A — работа,
F — сила,
s — пройденный путь.

Так что, несмотря на весь героизм уставшего держателя крыши, проделанная им работа равна нулю, а вот вода, падая под действием силы тяжести с высокого утеса, совершает самую, что ни на есть, механическую работу. То есть, если мы будем толкать тяжелый шкаф безуспешно, то проделанная нами работа с точки зрения физики будет равна нулю, несмотря на то, что мы прикладываем много сил. А вот если мы сдвинем шкаф на некоторое расстояние, то тогда мы проделаем работу, равную произведению приложенной силы на расстояние, на которое мы передвинули тело.

Единица работы — 1 Дж. Это работа, совершенная силой в 1 ньютон, по передвижению тела на расстояние в 1 м. Если направление приложенной силы совпадает с направлением движения тела, то данная сила совершает положительную работу. Пример — это когда мы толкаем какое-либо тело, и оно двигается. А в случае, когда сила приложена в противоположную движению тела сторону, например, сила трения , то данная сила совершает отрицательную работу. Если же приложенная сила никак не влияет на движение тела, то сила, совершаемая этой работой, равна нулю.

В повседневной жизни часто приходится встречаться с таким понятием как работа. Что это слово означает в физике и как определить работу силы упругости? Ответы на эти вопросы вы узнаете в статье.

Механическая работа

Работа — это скалярная алгебраическая величина, которая характеризует связь между силой и перемещением. При совпадении направления этих двух переменных она вычисляется по следующей формуле:

• F — модуль вектора силы, которая совершает работу;
• S — модуль вектора перемещения.

Не всегда сила, которая действует на тело, совершает работу. Например, работа силы тяжести равна нулю, если ее направление перпендикулярно перемещению тела.

Если вектор силы образует отличный от нуля угол с вектором перемещения, то для определения работы следует воспользоваться другой формулой:

A=FScosα

α — угол между векторами силы и перемещения.

Значит, механическая работа — это произведение проекции силы на направление перемещения и модуля перемещения, или произведение проекции перемещения на направление силы и модуля этой силы.

Знак механической работы

В зависимости от направления силы относительно перемещения тела работа A может быть:

• положительной (0°≤ α
• отрицательной (90°
• равной нулю (α=90°).

Если A>0, то скорость тела увеличивается. Пример — падение яблока с дерева на землю. При A

Единица измерения работы в СИ (Международной системе единиц) — Джоуль (1Н*1м=Дж). Джоуль — это работа силы, значение которой равно 1 Ньютону, при перемещении тела на 1 метр в направлении действия силы.

Работа силы упругости

Работу силы можно определить и графическим способом. Для этого вычисляется площадь криволинейной фигуры под графиком F s (x).

Так, по графику зависимости силы упругости от удлинения пружины, можно вывести формулу работы силы упругости.

Она равна:

A=kx 2 /2

• k — жесткость;
• x — абсолютное удлинение.

Что мы узнали?

Механическая работа совершается при действии на тело силы, которая приводит к перемещению тела. В зависимости от угла, который возникает между силой и перемещением, работа может быть равна нулю или иметь отрицательный или положительный знак. На примере силы упругости вы узнали о графическом способе определения работы.

Каждое тело, совершающее движение, можно охарактеризовать работой. Иными словами, она характеризует действие сил.

Работа определяется как:
Произведение модуля силы и пути пройденного телом, умноженное на косинус угла между направлением силы и движения.

Работа измеряется в Джоулях:
1 [Дж] = = [кг* м2/c2]

К примеру, тело A под действием силы в 5 Н, прошло 10 м. Определить работу совершенную телом.

Так как направление движения и действия силы совпадают, то угол между вектором силы и вектором перемещения будет равен 0°. Формула упроститься, потому что косинус угла в 0° равен 1.

Подставляя исходные параметры в формулу, находим:
A= 15 Дж.

Рассмотрим другой пример, тело массой 2 кг, двигаясь с ускорением 6 м/ с2, прошло 10 м. Определить работу проделанную телом, если оно двигалось по наклоненной плоскости вверх под углом 60°.

Для начала, вычислим какую силу нужно приложить, что бы сообщить телу ускорение 6 м/ с2.

F = 2 кг * 6 м/ с2 = 12 H.
Под действием силы 12H, тело прошло 10 м. Работу можно вычислить по уже известной формуле:

Где, а равно 30°. Подставляя исходные данные в формулу получаем:
A= 103, 2 Дж.

Мощность

Множество машин механизмов выполняют одну и ту же работу за различный промежуток времени. Для их сравнения вводится понятие мощности.
Мощность – это величина, показывающая объем работы выполненный за единицу времени.

Мощность измеряется в Ватт, в честь Шотландского инженера Джеймса Ватта.
1 [Ватт] = 1 [Дж/c].

К примеру, большой кран поднял груз весом 10 т на высоту 30 м за 1 мин. Маленький кран на эту же высоту за 1 мин поднял 2 т кирпича. Сравнить мощности кранов.
Определим работу выполняемую кранами. Груз поднимается на 30м, при этом преодолевая силу тяжести, поэтому сила, затрачиваемая на поднятие груза, будет равна силе взаимодействия Земли и груза(F = m * g). А работа – произведению сил на расстояние пройденное грузами, то есть на высоту.

Для большого крана A1 = 10 000 кг * 30 м * 10 м / с2 = 3 000 000 Дж, а для маленького A2 = 2 000 кг * 30 м * 10 м / с2 = 600 000 Дж.
Мощность можно вычислить, разделив работу на время. Оба крана подняли груз за 1 мин (60 сек).

Отсюда:
N1 = 3 000 000 Дж/60 c = 50 000 Вт = 50 кВт.
N2 = 600 000 Дж/ 60 c = 10 000 Вт = 10 к Вт.
Из выше приведенных данных наглядно видно, что первый кран в 5 раз мощнее второго.

Если на тело действует сила, то эта сила совершает работу по перемещению этого тела. Прежде чем дать определение работе при криволинейном движении мате­риальной точки, рассмотрим частные случаи:

В этом случае механиче­ская работа A равна:

A = F s cos =
,

или A = Fcos × s = F S × s ,

где F S – проекция силы на перемеще­ние. В данном случае F s = const , и геометрический смысл работы A – это площадь прямо­угольника, построенного в координатах F S , , s .

Построим график проекции силы на направление перемещения F S как функции перемещения s. Полное перемещение представим как сумму n малых перемещений
. Для ма­лого i -ого перемещения
работа равна

или площади заштрихованной трапеции на рисунке.

Полная механическая работа по перемещению из точки 1 в точку 2 будет равна:

.

Величина, стоящая под интегралом будет представлять элементарную работу по бесконечно малому перемещению
:

­– элементарная работа.

Разбиваем траекторию движения материальной точки на бесконечно малые перемещения и работу силы по перемещению материальной точки из точки 1 в точку 2 определяем как криволинейный интеграл:

–работа при криволинейном движении.

Пример 1: Работа силы тяжести
при криволинейном движении материальной точки.

.

Далее как постоянную величину можно вынести за знак интеграла, а интеграл согласно рисунку будет представлять полное перемещение . .

Если обозначить высоту точки 1 от поверхности Земли через , а высоту точки 2 через , то

Мы видим, что в данном случае работа определяется положением материальной точки в начальный и конечный момент времени и не зависит от формы траектории или пути. Работа силы тяжести по замкнутому пути равна нулю:
.

Силы, работа которых на замкнутом пути равна нулю, называется консервативными .

Пример 2 : Работа силы трения.

Это пример неконсервативной силы. Чтобы показать это достаточно рассмотреть элементарную работу силы трения:

,

т.е. работа силы трения всегда отрицательная величина и на замкнутом пути не может быть равной нулю. Работа, совершаемая в единицу времени, называется мощностью . Если за время
совершается работа
, то мощность равна

–механическая мощность .

Взяв
в виде

,

получим для мощности выражение:

.

В СИ единицей работы является джоуль:
= 1 Дж = 1 Н1 м, а единицей мощности является ватт: 1 Вт = 1 Дж/с.

Механическая энергия.

Энергия является общей количественной мерой движения взаимодействия всех видов материи. Энергия не исчезает и не возникает из нечего: она лишь может переходить из одной формы в другую. Понятие энергии связывает воедино все явления в природе. В соответствии с различными формами движения материи рассматривают разные виды энергии – механическую, внутреннюю, электромагнитную, ядерную и др.

Понятия энергии и работы тесно связаны друг с другом. Известно, что работа совершается за счет запаса энергии и, наоборот, совершая работу, можно увеличить запас энергии в каком-либо устройстве. Другими словами работа – это количественная мера изменения энергии:

.

Энергия также как и работа в СИ измеряется в джоулях: [E ]=1 Дж.

Механическая энергия бывает двух видов – кинетическая и потенциальная.

Кинетическая энергия (или энергия движения) определяется массами и скоростями рассматриваемых тел. Рассмотрим материальную точку, движущуюся под действием силы . Работа этой силы увеличивает кинетическую энергию материальной точки
. Вычислим в этом случае малое приращение (дифференциал) кинетической энергии:

При вычислении
использован второй закон Ньютона
, а также
— модуль скорости материальной точки. Тогда
можно представить в виде:

—

— кинетическая энергия движущейся материальной точки .

Умножив и разделив это выражение на
, и учитывая, что
, получим

—

— связь между импульсом и кинетической энергией движущейся материальной точки .

Потенциальная энергия (или энергия положения тел) определяется действием на тело консервативных сил и зависит только от положения тела.

Мы видели, что работу силы тяжести
при криволинейном движении материальной точки
можно представить в виде разности значений функции
, взятых в точке 1 и в точке 2 :

.

Оказывается, что всегда, когда силы консервативны, работу этих сил на пути 1
2 можно представить в виде:

.

Функция , которая зависит только от положения тела – называется потенциальной энергией .

Тогда для элементарной работы получим

–работа равна убыли потенциальной энергии .

Иначе можно сказать, что работа совершается за счёт запаса потенциальной энергии.

Величину , равную сумме кинетической и потенциальной энергий частицы, называют полной механической энергией тела:

–полная механическая энергия тела .

В заключении заметим, что используя второй закон Ньютона
, дифференциал кинетической энергии
можно представить в виде:

.

Дифференциал потенциальной энергии
, как указывали выше, равен:

.

Таким образом, если сила – консервативная сила и отсутствуют другие внешние силы, то , т.е. в этом случае полная механическая энергия тела сохраняется.

Механическая работа. Единицы работы.

В обыденной жизни под понятием «работа» мы понимаем всё.

В физике понятие работа несколько иное. Это определенная физическая величина, а значит, ее можно измерить. В физике изучается прежде всего механическая работа .

Рассмотрим примеры механической работы.

Поезд движется под действием силы тяги электровоза, при этом совершается механическая работа. При выстреле из ружья сила давления пороховых газов совершает работу — перемещает пулю вдоль ствола, скорость пули при этом увеличивается.

Из этих примеров видно, что механическая работа совершается, когда тело движется под действием силы. Механическая работа совершается и в том случае, когда сила, действуя на тело (например, сила трения), уменьшает скорость его движения.

Желая передвинуть шкаф, мы с силой на него надавливаем, но если он при этом в движение не приходит, то механической работы мы не совершаем. Можно представить себе случай, когда тело движется без участия сил (по инерции), в этом случае механическая работа также не совершается.

Итак, механическая работа совершается, только когда на тело действует сила, и оно движется .

Нетрудно понять, что чем большая сила действует на тело и чем длиннее путь, который проходит тело под действием этой силы, тем большая совершается работа.

Механическая работа прямо пропорциональна приложенной силе и прямо пропорциональна пройденному пути .

Поэтому, условились измерять механическую работу произведением силы на путь, пройденный по этому направлению этой силы:

работа = сила × путь

где А — работа, F — сила и s — пройденный путь.

За единицу работы принимается работа, совершаемая силой в 1Н, на пути, равном 1 м.

Единица работы — джоуль (Дж ) названа в честь английского ученого Джоуля. Таким образом,

1 Дж = 1Н · м.

Используется также килоджоули (кДж ) .

1 кДж = 1000 Дж.

Формула А = Fs применима в том случае, когда сила F постоянна и совпадает с направлением движения тела.

Если направление силы совпадает с направлением движения тела, то данная сила совершает положительную работу.

Если же движение тела происходит в направлении, противоположном направлению приложенной силы, например, силы трения скольжения, то данная сила совершает отрицательную работу.

Если направление силы, действующей на тело, перпендикулярно направлению движения, то эта сила работы не совершает, работа равна нулю:

В дальнейшем, говоря о механической работе, мы будем кратко называть ее одним словом — работа.

Пример . Вычислите работу, совершаемую при подъеме гранитной плиты объемом 0,5 м3 на высоту 20 м. Плотность гранита 2500 кг/м 3 .

Дано :

ρ = 2500 кг/м 3

Решение :

где F -сила, которую нужно приложить, чтобы равномерно поднимать плиту вверх. Эта сила по модулю равна силе тяж Fтяж, действующей на плиту, т. е. F = Fтяж. А силу тяжести можно определить по массе плиты: Fтяж = gm. Массу плиты вычислим, зная ее объем и плотность гранита: m = ρV; s = h, т. е. путь равен высоте подъема.

Итак, m = 2500 кг/м3 · 0,5 м3 = 1250 кг.

F = 9,8 Н/кг · 1250 кг ≈ 12 250 Н.

A = 12 250 Н · 20 м = 245 000 Дж = 245 кДж.

Ответ : А =245 кДж.

Рычаги.Мощность.Энергия

На совершение одной и той же работы различным двигателям требуется разное время. Например, подъемный кран на стройке за несколько минут поднимает на верхний этаж здания сотни кирпичей. Если бы эти кирпичи перетаскивал рабочий, то ему для этого потребовалось бы несколько часов. Другой пример. Гектар земли лошадь может вспахать за 10-12 ч, трактор же с многолемешным плугом (лемех — часть плуга, подрезающая пласт земли снизу и передающая его на отвал; многолемешный — много лемехов), эту работу выполнит на 40-50 мин.

Ясно, что подъемный кран ту же работу совершает быстрее, чем рабочий, а трактор — быстрее чем лошадь. Быстроту выполнения работы характеризуют особой величиной, называемой мощностью.

Мощность равна отношению работы ко времени, за которое она была совершена.

Чтобы вычислить мощность, надо работу разделить на время, в течение которого совершена эта работа. мощность = работа/время.

где N — мощность, A — работа, t — время выполненной работы.

Мощность — величина постоянная, когда за каждую секунду совершается одинаковая работа, в других случаях отношение A/t определяет среднюю мощность:

N ср = A/t . За единицу мощности приняли такую мощность, при которой в 1 с совершается работа в Дж.

Эта единица называется ваттом (Вт ) в честь еще одного английского ученого Уатта.

1 ватт = 1 джоуль/ 1 секунда , или 1 Вт = 1 Дж/с.

Ватт (джоуль в секунду) — Вт (1 Дж/с).

В технике широко используется более крупные единицы мощности — киловатт (кВт ), мегаватт (МВт ) .

1 МВт = 1 000 000 Вт

1 кВт = 1000 Вт

1 мВт = 0,001 Вт

1 Вт = 0,000001 МВт

1 Вт = 0,001 кВт

1 Вт = 1000 мВт

Пример . Найти мощность потока воды, протекающей через плотину, если высота падения воды 25 м, а расход ее — 120 м3 в минуту.

Дано :

ρ = 1000 кг/м3

Решение :

Масса падающей воды: m = ρV ,

m = 1000 кг/м3 · 120 м3 = 120 000 кг (12 · 104 кг).

Сила тяжести, действующая на воду:

F = 9.8 м/с2 · 120 000 кг ≈ 1 200 000 Н (12 · 105 Н)

Работа, совершаемая потоком в минуту:

А — 1 200 000 Н · 25 м = 30 000 000 Дж (3 · 107 Дж).

Мощность потока: N = A/t,

N = 30 000 000 Дж / 60 с = 500 000 Вт = 0,5 МВт.

Ответ : N = 0.5 МВт.

Различные двигатели имеют мощности от сотых и десятых долей киловатта (двигатель электрической бритвы, швейной машины) до сотен тысяч киловатт (водяные и паровые турбины).

Таблица 5.

Мощность некоторых двигателей, кВт.

На каждом двигателе имеется табличка (паспорт двигателя), на которой указаны некоторые данные о двигателе, в том числе и его мощность.

Мощность человека при нормальный условиях работы в среднем равна 70-80 Вт. Совершая прыжки, взбегая по лестнице, человек может развивать мощность до 730 Вт, а в отдельных случаях и еще бóльшую.

Из формулы N = A/t следует, что

Чтобы вычислить работу, необходимо мощность умножить на время, в течение которого совершалась эта работа.

Пример. Двигатель комнатного вентилятора имеет мощность 35 Вт. Какую работу он совершает за 10 мин?

Запишем условие задачи и решим ее.

Дано :

Решение :

A = 35 Вт * 600с = 21 000 Вт* с = 21 000 Дж = 21 кДж.

Ответ A = 21 кДж.

Простые механизмы.

С незапамятных времен человек использует для совершения механической работы различные приспособления.

Каждому известно, что тяжелый предмет (камень, шкаф, станок), который невозможно сдвинуть руками, можно сдвинуть с помощью достаточно длинной палки — рычага.

На данный момент считается, что с помощью рычагов три тысячи лет назад при строительстве пирамид в Древнем Египте передвигали и поднимали на большую высоту тяжелые каменные плиты.

Во многих случаях, вместо того, чтобы поднимать тяжелый груз на некоторую высоту, его можно вкатывать или втаскивать на ту же высоту по наклонной плоскости или поднимать с помощью блоков.

Приспособления, служащие для преобразования силы, называются механизмами .

К простым механизмам относятся: рычаги и его разновидности — блок, ворот; наклонная плоскость и ее разновидности — клин, винт . В большинстве случаев простые механизмы применяют для того, чтобы получить выигрыш в силе, т. е. увеличить силу, действующую на тело, в несколько раз.

Простые механизмы имеются и в бытовых, и во всех сложных заводских и фабричных машинах, которые режут, скручивают и штампуют большие листы стали или вытягивают тончайшие нити, из которых делаются потом ткани. Эти же механизмы можно обнаружить и в современных сложных автоматах, печатных и счетных машинах.

Рычаг. Равновесие сил на рычаге.

Рассмотрим самый простой и распространенный механизм — рычаг.

Рычаг представляет собой твердое тело, которое может вращаться вокруг неподвижной опоры.

На рисунках показано, как рабочий для поднятия груза в качестве рычага, использует лом. В первом случае рабочий с силой F нажимает на конец лома B , во втором — приподнимает конец B .

Рабочему нужно преодолеть вес груза P — силу, направленную вертикально вниз. Он поворачивает для этого лом вокруг оси, проходящей через единственную неподвижную точку лома — точку его опоры О . Сила F , с которой рабочий действует на рычаг, меньше силы P , таким образом, рабочий получает выигрыш в силе . При помощи рычага можно поднять такой тяжелый груз, который своими силами поднять нельзя.

На рисунке изображен рычаг, ось вращения которого О (точка опоры) расположена между точками приложения сил А и В . На другом рисунке показана схема этого рычага. Обе силы F 1 и F 2, действующие на рычаг, направлены в одну сторону.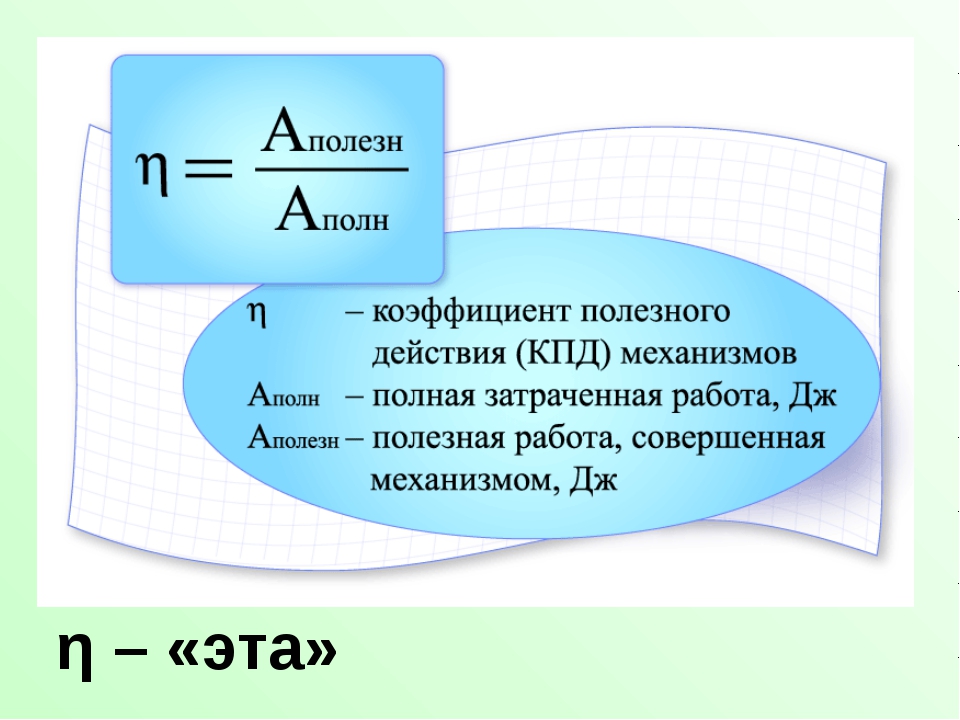

Кратчайшее расстояние между точкой опоры и прямой, вдоль которой действует на рычаг сила, называется плечом силы.

Чтобы найти плечо силы, надо из точки опоры опустить перпендикуляр на линию действия силы.

Длина этого перпендикуляра и будет плечом данной силы. На рисунке показано, что ОА — плечо силы F 1; ОВ — плечо силы F 2 . Силы, действующие на рычаг могут повернуть его вокруг оси в двух направлениях: по ходу или против хода часовой стрелки. Так, сила F 1 вращает рычаг по ходу часовой стрелки, а сила F 2 вращает его против часовой стрелки.

Условие, при котором рычаг находится в равновесии под действием приложенных к нему сил, можно установить на опыте. При этом надо помнить, что результат действия силы, зависит не только от ее числового значения (модуля), но и от того, в какой точке она приложена к телу, или как направлена.

К рычагу (см рис.) по обе стороны от точки опоры подвешиваются различные грузы так, что каждый раз рычаг оставался в равновесии. Действующие на рычаг силы, равны весам этих грузов. Для каждого случая измеряются модули сил и их плечи. Из опыта изображенного на рисунке 154, видно, что сила 2 Н уравновешивает силу 4 Н . При этом, как видно из рисунка, плечо меньшей силы в 2 раза больше плеча большей силой.

На основании таких опытов было установлено условие (правило) равновесия рычага.

Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил.

Это правило можно записать в виде формулы:

F 1/F 2 = l2/ l1 ,

где F 1 и F2 — силы, действующие на рычаг, l 1 и l2 , — плечи этих сил (см. рис.).

Правило равновесия рычага было установлено Архимедом около 287 — 212 гг. до н. э. (но ведь в прошлом параграфе говорилось, что рычаги использовались египтянами? Или тут важную роль играет слово «установлено»?)

Из этого правила следует, что меньшей силой можно уравновесить при помощи рычага бóльшую силу. Пусть одно плечо рычага в 3 раза больше другого (см рис.). Тогда, прикладывая в точке В силу, например, в 400 Н, можно поднять камень весом 1200 Н. Что0бы поднять еще более тяжелый груз, нужно увеличить длину плеча рычага, на которое действует рабочий.

Пример . С помощью рычага рабочий поднимает плиту массой 240 кг (см рис. 149). Какую силу прикладывает он к большему плечу рычага, равному 2,4 м, если меньшее плечо равно 0,6 м?

Запишем условие задачи, и решим ее.

Дано :

Решение :

По правилу равновесия рычага F1/F2 = l2/l1, откуда F1 = F2 l2/l1, где F2 = Р — вес камня. Вес камня asd = gm, F = 9,8 Н · 240 кг ≈ 2400 Н

Тогда, F1 = 2400 Н · 0,6/2,4 = 600 Н.

Ответ : F1 = 600 Н.

В нашем примере рабочий преодолевает силу 2400 Н, прикладывая к рычагу силу 600 Н. Но при этом плечо, на которое действует рабочий, в 4 раза длиннее того, на которое действует вес камня (l 1 : l2 = 2,4 м: 0,6 м = 4).

Применяя правило рычага, можно меньшей силой уравновесить бóльшую силу.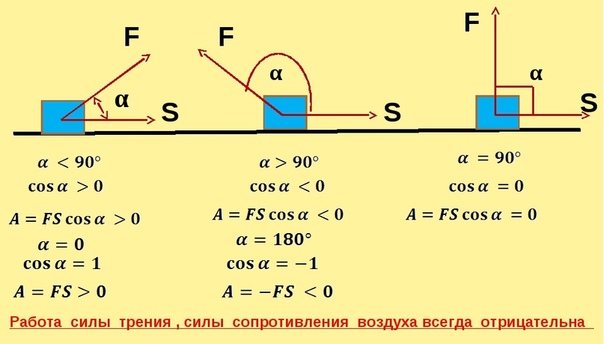 При этом плечо меньшей силы должно быть длиннее плеча большей силы.

Момент силы.

Вам уже известно правило равновесия рычага:

F 1 / F2 = l 2 / l1 ,

Пользуясь свойством пропорции (произведение ее крайних членов, равно произведению ее средних членов), запишем его в таком виде:

F 1l 1 = F2 l2 .

В левой части равенства стоит произведение силы F 1 на ее плечо l 1, а в правой — произведение силы F 2 на ее плечо l 2 .

Произведение модуля силы, вращающей тело, на ее плечо называется моментом силы ; он обозначается буквой М. Значит,

Рычаг находится в равновесии под действием двух сил, если момент силы, вращающий его по часовой стрелке, равен моменту силы, вращающей его против часовой стрелки.

Это правило, называемое правилом моментов , можно записать в виде формулы:

М1 = М2

Действительно, в рассмотренном нами опыте, (§ 56) действующие силы были равны 2 Н и 4 Н, их плечи соответственно составляли 4 и 2 давления рычага, т. е. моменты этих сил одинаковы при равновесии рычага.

Момент силы, как и всякая физическая величина, может быть измерена. За единицу момента силы принимается момент силы в 1 Н, плечо которой ровно 1 м.

Эта единица называется ньютон-метр (Н · м ).

Момент силы характеризует действие силы, и показывает, что оно зависит одновременно и от модуля силы, и от ее плеча. Действительно, мы уже знаем, например, что действие силы на дверь зависит и от модуля силы, и от того, где приложена сила. Дверь тем легче повернуть, чем дальше от оси вращения приложена действующая на нее сила. Гайку, лучше отвернуть длинным гаечным ключом, чем коротким. Ведро тем легче поднять из колодца, чем длиннее ручка вóрота, и т. д.

Рычаги в технике, быту и природе.

Правило рычага (или правило моментов) лежит в основе действия различного рода инструментов и устройств, применяемых в технике и быту там, где требуется выигрыш в силе или в пути.

Выигрыш в силе мы имеем при работе с ножницами. Ножницы — это рычаг (рис), ось вращения которого, происходит через винт, соединяющий обе половины ножниц. Действующей силой F 1 является мускульная сила руки человека, сжимающего ножницы. Противодействующей силой F 2 — сила сопротивления такого материала, который режут ножницами. В зависимости от назначения ножниц их устройство бывает различным. Конторские ножницы, предназначенные для резки бумаги, имеют длинные лезвия и почти такой же длины ручки. Для резки бумаги не требуется большой силы, а длинным лезвием удобнее резать по прямой линии. Ножницы для резки листового металла (рис.) имеют ручки гораздо длиннее лезвий, так как сила сопротивления металла велика и для ее уравновешивания плечо действующей силы приходится значительно увеличивать. Еще больше разница между длиной ручек и расстоянии режущей части и оси вращения в кусачках (рис.), предназначенных для перекусывания проволоки.

Рычаги различного вида имеются у многих машин. Ручка швейной машины, педали или ручной тормоз велосипеда, педали автомобиля и трактора, клавиши пианино — все это примеры рычагов, используемых в данных машинах и инструментах.

Примеры применения рычагов — это рукоятки тисков и верстаков, рычаг сверлильного станка и т. д.

На принципе рычага основано действие и рычажных весов (рис.). Учебные весы, изображенные на рисунке 48 (с. 42), действуют как равноплечий рычаг . В десятичных весах плечо, к которому подвешена чашка с гирями, в 10 раз длиннее плеча, несущего груз. Это значительно упрощает взвешивание больших грузов. Взвешивая груз на десятичных весах, следует умножить массу гирь на 10.

Устройство весов для взвешивания грузовых вагонов автомобилей также основано на правиле рычага.

Рычаги встречаются также в разных частях тела животных и человека. Это, например, руки, ноги, челюсти. Много рычагов можно найти в теле насекомых (прочитав книгу про насекомых и строение их тела), птиц, в строении растений.

Применение закона равновесия рычага к блоку.

Блок представляет собой колесо с желобом, укрепленное в обойме. По желобу блока пропускается веревка, трос или цепь.

Неподвижным блоком называется такой блок, ось которого закреплена, и при подъеме грузов не поднимается и не опускается (рис).

Неподвижный блок можно рассматривать как равноплечий рычаг, у которого плечи сил равны радиусу колеса (рис): ОА = ОВ = r . Такой блок не дает выигрыша в силе. (F 1 = F 2), но позволяет менять направление действие силы. Подвижный блок — это блок. ось которого поднимается и опускается вместе с грузом (рис.). На рисунке показан соответствующий ему рычаг: О — точка опоры рычага, ОА — плечо силы Р и ОВ — плечо силы F . Так как плечо ОВ в 2 раза больше плеча ОА , то сила F в 2 раза меньше силы Р :

F = P/2 .

Таким образом, подвижный блок дает выигрыш в силе в 2 раза .

Это можно доказать и пользуясь понятием момента силы. При равновесии блока моменты сил F и Р равны друг другу. Но плечо силы F в 2 раза больше плеча силы Р , а, значит, сама сила F в 2 раза меньше силы Р .

Обычно на практике применяют комбинацию неподвижного блока с подвижным (рис.). Неподвижный блок применяется только для удобства. Он не дает выигрыша в силе, но изменяет направление действия силы. Например, позволяет поднимать груз, стоя на земле. Это пригождается многим людям или рабочим. Тем не менее, он даёт выигрыш в силе в 2 раза больше обычного!

Равенство работ при использовании простых механизмов. «Золотое правило» механики.

Рассмотренные нами простые механизмы применяются при совершении работы в тех случаях, когда надо действием одной силы уравновесить другую силу.

Естественно, возникает вопрос: давая выигрыш в силе или пути, не дают ли простые механизмы выигрыша в работе? Ответ на поставленный вопрос можно получить из опыта.

Уравновесив на рычаге две какие-нибудь разные по модулю силы F 1 и F 2 (рис.), приводим рычаг в движение. При этом оказывается, что за одно и то же время точка приложения меньшей силы F 2 проходит больший путь s 2 , а точка приложения большей силы F 1 — меньший путь s 1. Измерив эти пути и модули сил, находим, что пути, пройденные точками приложения сил на рычаге, обратно пропорциональны силам:

s 1 / s 2 = F 2 / F 1.

Таким образом, действуя на длинное плечо рычага, мы выигрываем в силе, но при этом во столько же раз проигрываем в пути.

Произведение силы F на путь s есть работа. Наши опыты показывают, что работы, совершаемые силами, приложенными к рычагу, равны друг другу:

F 1 s 1 = F 2 s 2, т. е. А 1 = А 2.

Итак, при использовании рычага выигрыша в работе не получится.

Пользуясь рычагом, мы можем выиграть или в силе, или в расстоянии. Действуя же силой на короткое плечо рычага, мы выигрываем в расстоянии, но во столько же раз проигрываем в силе.

Существует легенда, что Архимед, восхищенный открытием правила рычага, воскликнул: «Дайте мне точку опоры, и я переверну Землю!».

Конечно, Архимед не мог бы справиться с такой задачей, если бы даже ему и дали бы точку опоры (которая должна была бы быть вне Земли) и рычаг нужной длины.

Для подъема земли всего на 1 см длинное плечо рычага должно было бы описать дугу огромной длины. Для перемещения длинного конца рычага по этому пути, например, со скоростью 1 м/с, потребовались бы миллионы лет!

Не дает выигрыша в работе и неподвижный блок, в чем легко убедиться на опыте (см. рис.). Пути, проходимые точками приложения сил F и F , одинаковы, одинаковы и силы, а значит, одинаковы и работы.

Можно измерить и сравнить между собой работы, совершаемые с помощью подвижного блока. Чтобы при помощи подвижного блока поднять груз на высоту h, необходимо конец веревки, к которому прикреплен динамометр, как показывает опыт (рис.), переместить на высоту 2h.

Таким образом, получая выигрыш в силе в 2 раза, проигрывают в 2 раза в пути, следовательно, и подвижный блок, на дает выигрыша в работе.

Многовековая практика показала, что ни один из механизмов не дает выигрыш в работе. Применяют же различные механизмы для того, чтобы в зависимости от условий работы выиграть в силе или в пути.

Уже древним ученым было известно правило, применимое ко всем механизмом: во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии. Это правило назвали «золотым правилом» механики.

Коэффициент полезного действия механизма.

Рассматривая устройство и действие рычага, мы не учитывали трение, а также вес рычага. в этих идеальных условиях работа, совершенная приложенной силой (эту работу мы будем называть полной ), равна полезной работе по подъему грузов или преодоления какого — либо сопротивления.

На практике совершенная с помощью механизма полная работа всегда несколько больше полезной работы.

Часть работы совершается против силы трения в механизме и по перемещению его отдельных частей. Так, применяя подвижный блок, приходится дополнительно совершать работу по подъему самого блока, веревки и по определению силы трения в оси блока.

Какой мы механизм мы не взяли, полезная работа, совершенная с его помощью, всегда составляет лишь часть полной работы. Значит, обозначив полезную работу буквой Ап, полную(затраченную) работу буквой Аз, можно записать:

Ап

Отношение полезной работы к полной работе называется коэффициентом полезного действия механизма.

Сокращенно коэффициент полезного действия обозначается КПД.

КПД = Ап / Аз.

КПД обычно выражается в процентах и обозначается греческой буквой η, читается он как «эта»:

η = Ап / Аз · 100%.

Пример : На коротком плече рычага подвешен груз массой 100 кг. Для его подъема к длинному плечу приложена сила 250 Н. Груз подняли на высоту h2 = 0,08 м, при этом точка приложения движущей силы опустилась на высоту h3 = 0,4 м. Найти КПД рычага.

Запишем условие задачи и решим ее.

Дано :

Решение :

η = Ап / Аз · 100%.

Полная (затраченная) работа Аз = Fh3.

Полезная работа Ап = Рh2

Р = 9,8 · 100 кг ≈ 1000 Н.

Ап = 1000 Н · 0,08 = 80 Дж.

Аз = 250 Н · 0,4 м = 100 Дж.

η = 80 Дж/100 Дж · 100% = 80%.

Ответ : η = 80%.

Но «золотое правило» выполняется и в этом случае. Часть полезной работы — 20% ее-расходуется на преодоление трения в оси рычага и сопротивления воздуха, а также на движение самого рычага.

КПД любого механизма всегда меньше 100%. Конструируя механизмы, люди стремятся увеличить их КПД. Для этого уменьшаются трение в осях механизмов и их вес.

Энергия.

На заводах и фабриках, станки и машины приводятся в движения с помощью электродвигателей, которые расходуют при этом электрическую энергию (отсюда и название).

Сжатая пружина (рис), распрямляясь, совершить работу, поднять на высоту груз, или заставить двигаться тележку. Поднятый над землей неподвижный груз не совершает работы, но если этот груз упадет, он может совершить работу (например, может забить в землю сваю). Способностью совершить работу обладает и всякое движущееся тело. Так, скатившийся с наклонной плоскости стальной шарик А (рис), ударившись о деревянный брусок В, передвигает его на некоторое расстояние. При этом совершается работа. Если тело или несколько взаимодействующих между собой тел (система тел) могут совершить работу, говорится, что они обладают энергией. Энергия — физическая величина, показывающая, какую работу может совершить тело (или несколько тел). Энергия выражается в системе СИ в тех же единицах, что и работу, т. е. в джоулях . Чем большую работу может совершить тело, тем большей энергией оно обладает. При совершении работы энергия тел изменяется. Совершенная работа равна изменению энергии. Потенциальная и кинетическая энергия. Потенциальной (от лат. потенция — возможность) энергией называется энергия, которая определяется взаимным положением взаимодействующих тел и частей одного и того же тела. Потенциальной энергией, например, обладает тело, поднятое относительно поверхности Земли, потому что энергия зависит от взаимного положения его и Земли. и их взаимного притяжения. Если считать потенциальную энергию тела, лежащего на Земле, равной нулю, то потенциальная энергия тела, поднятого на некоторую высоту, определится работой, которую совершит сила тяжести при падении тела на Землю. Обозначим потенциальную энергию тела Е п, поскольку Е = А , а работа, как мы знаем, равна произведению силы на путь, то А = Fh , где F — сила тяжести. Значит, и потенциальная энергия Еп равна: Е = Fh, или Е = gmh, где g — ускорение свободного падения, m — масса тела, h — высота, на которую поднято тело. Огромной потенциальной энергией обладает вода в реках, удерживаемая плотинами. Падая вниз, вода совершает работу, приводя в движение мощные турбины электростанций. Потенциальную энергию молота копра (рис.) используют в строительстве для совершению работы по забиванию свай. Открывая дверь с пружиной, совершается работа по растяжению (или сжатию) пружины. За счет приобретенной энергии пружина, сокращаясь (или распрямляясь), совершает работу, закрывая дверь. Энергию сжатых и раскрученных пружин используют, например, в ручных часах, разнообразных заводных игрушках и пр. Потенциальной энергией обладает всякое упругое деформированное тело. Потенциальную энергию сжатого газа используют в работе тепловых двигателей, в отбойных молотках, которые широко применяют в горной промышленности, при строительстве дорог, выемке твердого грунта и т. д. Энергия, которой обладает тело вследствие своего движения, называется кинетической (от греч. кинема — движение) энергией. Кинетическая энергия тела обозначается буквой Е к. Движущаяся вода, приводя во вращение турбины гидроэлектростанций, расходует свою кинетическую энергию и совершает работу. Кинетической энергией обладает и движущийся воздух — ветер. От чего зависит кинетическая энергия? Обратимся к опыту (см. рис.). Если скатывать шарик А с разных высот, то можно заметить, что чем с большей высоты скатывается шарик, тем больше его скорость и тем дальше он продвигает брусок, т. е. совершает большую работу. Значит, кинетическая энергия тела зависит от его скорости. За счет скорости большой кинетической энергией обладает летящая пуля. Кинетическая энергия тела зависит и от его массы. Еще раз проделаем наш опыт, но будем скатывать с наклонной плоскости другой шарик — большей массы. Брусок В передвинется дальше, т. е. будет совершена бóльшая работа. Значит, и кинетическая энергия второго шарика, больше, чем первого. Чем больше масса тела и скорость, с которой он движется, тем больше его кинетическая энергия. Для того чтобы определить кинетическую энергию тела, применяется формула: Ек = mv^2 /2, где m — масса тела, v — скорость движения тела. Кинетическую энергию тел используют в технике. Удерживаемая плотиной вода обладает, как было уже сказано, большой потенциальной энергией. При падении с плотины вода движется и имеет такую же большую кинетическую энергию. Она приводит в движение турбину, соединенную с генератором электрического тока. За счет кинетической энергии воды вырабатывается электрическая энергия. Энергия движущейся воды имеет большое значение в народном хозяйстве. Эту энергию используют с помощью мощных гидроэлектростанций. Энергия падающей воды является экологически чистым источником энергии в отличие от энергии топлива. Все тела в природе относительно условного нулевого значения обладают либо потенциальной, либо кинетической энергией, а иногда той и другой вместе. Например, летящий самолет обладает относительно Земли и кинетической и потенциальной энергией. Мы познакомились с двумя видами механической энергии. Иные виды энергии (электрическая, внутренняя и др.) будут рассмотрены в других разделах курса физики. Превращение одного вида механической энергии в другой. Явление превращения одного вида механической энергии в другой очень удобно наблюдать на приборе, изображенном на рисунке. Накручивая на ось нить, поднимают диск прибора. Диск, поднятый вверх, обладает некоторой потенциальной энергией. Если его отпустить, то он, вращаясь, начнет падать. По мере падения потенциальная энергия диска уменьшается, но вместе с тем возрастает его кинетическая энергия. В конце падения диск обладает таким запасом кинетической энергии, что может опять подняться почти до прежней высоты. (Часть энергии расходуется на работу против силы трения, поэтому диск не достигает первоначальной высоты.) Поднявшись вверх, диск снова падает, а затем снова поднимается. В этом опыте при движении диска вниз его потенциальная энергия превращается в кинетическую, а при движении вверх кинетическая превращается в потенциальную. Превращение энергии из одного вида в другой происходит также при ударе двух каких-нибудь упругих тел, например резинового мяча о пол или стального шарика о стальную плиту. Если поднять над стальной плитой стальной шарик (рис) и выпустить его из рук, он будет падать. По мере падения шарика его потенциальная энергия убывает, а кинетическая растет, так как увеличивается скорость движения шарика. При ударе шарика о плиту произойдет сжатие как шарика, так и плиты. Кинетическая энергия, которой шарик обладал, превратится в потенциальную энергию сжатой плиты и сжатого шарика. Затем благодаря действию упругих сил плита и шарик, примут свою первоначальную форму. Шарик отскочит от плиты, а их потенциальная энергия вновь превратится в кинетическую энергию шарика: шарик отскочит вверх со скоростью, почти равной скорости, которой обладал в момент удара о плиту. При подъеме вверх скорость шарика, а значит, и его кинетическая энергия уменьшаются, потенциальная энергия увеличивается. отскочив от плиты, шарик поднимается почти до той же высоты, с которой начал падать. В верхней точке подъема вся его кинетическая энергия вновь превратится в потенциальную. Явления природы обычно сопровождается превращением одного вида энергии в другой. Энергия может и передаваться от одного тела к другому. Так, например, при стрельбе из лука потенциальная энергия натянутой тетивы переходит в кинетическую энергию летящей стрелы.

Главная » Наружная канализация » Что такое работа в физике формула. Механическая работа

Работа в термодинамике | ЕГЭ по физике

Работа в термодинамике

В термодинамике, в отличие от механики, рассматривается не движение тела как целого, а лишь относительное изменение частей термодинамической системы, в результате которого меняется ее объем.

Рассмотрим работу газа при изобарическом расширении.

Вычислим работу, совершаемую газом при его действии на поршень с силой ${F’}↖{→}$, равной по величине и противоположной по направлению силе ${F’}↖{→}$, действующей на газ со стороны поршня: ${F’}↖{→}=-{F’}↖{→}$ (согласно третьему закону Ньютона), $F’=pS$, где $p$ — давление газа, а $S$ — площадь поверхности поршня. Если перемещение поршня $∆h$ в результате расширения мало, то давление газа можно считать постоянным и работа газа равна:

$A’=F’∆h=pS∆h=p∆V$

Если газ расширяется, он совершает положительную работу, та к как перемещение поршня совпадает по направлению с силой ${F’}↖{→}$. Если газ сжимается, то работа газа отрицательна, поскольку перемещение поршня противоположно силе ${F’}↖{→}$. В формуле $A’=F’∆h=pS∆h=p∆V$ появится знак «минус»: $∆V

Работа внешних сил $А$, наоборот, положительна при сжатии газа и отрицательна при расширении:

$A=-A’=-p∆V$

Совершая над газом положительную работу, внешние тела передают ему часть своей энергии. При расширении газа внешние тела отбирают у газа часть его энергии — работа внешних сил отрицательна.

На графике зависимости давления от объема $р(V)$ работа определяется как площадь, ограниченная кривой $р(V)$, осью $V$ и отрезками $ab$ и $cd$, равными давлениям $р_1$ в начальном ($V_1$) и $р_2$ в конечном ($V_2$) состояниях, как для изобарного, так и для изотермического процессов.

Первый закон термодинамики

Первое начало (первый закон) термодинамики — это закон сохранения и превращения энергии для термодинамической системы.

Согласно первому началу термодинамики, работа может совершаться только за счет теплоты или какой-либо другой формы энергии. Следовательно, работу и количество теплоты измеряют в одних единицах — джоулях (как и энергию).

Первое начало термодинамики было сформулировано немецким ученым Ю. Л. Майером в 1842 г. и подтверждено экспериментально английским ученым Дж. Джоулем в 1843 г.

Первый закон термодинамики формулируется так:

Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе:

$∆U=A+Q$

где $∆U$ — изменение внутренней энергии, $А$ — работа внешних сил, $Q$ — количество теплоты, переданной системе.

Из $∆U=A+Q$ следует закон сохранения внутренней энергии. Если систему изолировать от внешних воздействий, $A=0$ и $Q=0$,а следовательно, $∆U=0$.

При любых процессах, происходящих в изолированной системе, ее внутренняя энергия остается постоянной.

Если работу совершает система, а не внешние силы, то уравнение ($∆U=A+Q$) записывается в виде:

$Q=∆U+A’$

где $А’$ — работа, совершаемая системой ($А’=-А$).

Количество теплоты, переданное системе, идет на изменение ее внутренней энергии и на совершение системой работы над внешними телами.

Первое начало термодинамики может быть сформулировано как невозможность существования вечного двигателя первого рода, который совершал бы работу, не черпая энергию из какого-либо источника, т. е. только за счет внутренней энергии.

Действительно, если к телу не поступает теплота ($Q=0$), то работа $А’$, согласно уравнению $Q=∆U+A’$, совершается только за счет убыли внутренней энергии $A’=-∆U$. После того, как запас энергии окажется исчерпанным, двигатель перестает работать.

Следует помнить, что как работа, так и количество теплоты являются характеристиками процесса изменения внутренней энергии, поэтому нельзя говорить, что в системе содержится определенное количество теплоты или работы. Система в любом состоянии обладает лишь определенной внутренней энергией.

Применение первого закона термодинамики к различным процессам

Рассмотрим применение первого закона термодинамики к различным термодинамическим процессам.

Изохорный процесс. Зависимость $р(Т)$ на термодинамической диаграмме изображается изохорой.

Изохорный (изохорический) процесс — термодинмический процесс, происходящий в системе при постоянном объеме.

Изохорный процесс можно осуществить в газах и жидкостях, заключенных в сосуд с постоянным объемом.

При изохорном процессе объем газа не меняется ($∆V=0$), и, согласно первому началу термодинамики $Q=∆U+A’$,

$∆U=Q$

т. е. изменение внутренней энергии равно количеству переданного тепла, т. к. работа ($A=p∆V=0$) газом не совершается.

Если газ нагревается, то $Q > 0$ и $∆U > 0$, его внутренняя энергия увеличивается. При охлаждении газа $Q

Изотермический процесс графически изображается изотермой.

Изотермический процесс — это термодинамический процесс, происходящий в системе при постоянной температуре.

Поскольку при изотермическом процессе внутренняя энергия газа не меняется ($T=const$), то все переданное газу количество теплоты идет на совершение работы:

$Q=A’$

При получении газом теплоты ($Q > 0$) он совершает положительную работу ($А’ > 0$). Если газ отдает тепло окружающей среде, $Q

Изобарный процесс на термодинамической диаграмме изображается изобарой.

Изобарный (изобарический) процесс — термодинамический процесс, происходящий в системе с постоянным давлением $p$.

Примером изобарного процесса является расширение газа в цилиндре со свободно ходящим нагруженным поршнем.

При изобарном процессе согласно формуле $Q=∆U+A’$ передаваемое газу количество теплоты идет на изменение его внутренней энергии $∆U$ и на совершение им работы $A’$ при постоянном давлении:

$Q=∆U+A’$

Работа идеального газа определяется по графику зависимости $p(V)$ для изобарного процесса ($A’=p∆V$).

Для идеального газа при изобарном процессе объем пропорционален температуре, в реальных газах часть теплоты расходуется на изменение средней энергии взаимодействия частиц.

Адиабатический процесс

Адиабатический процесс (адиабатный процесс) — это термодинамический процесс, происходящий в системе без теплообмена с окружающей средой ($Q=0$).

Адиабатическая изоляция системы приближенно достигается в сосудах Дьюара, в так называемых адиабатных оболочках. На адиабатически изолированную систему не оказывает влияния изменение температуры окружающих тел. Ее внутренняя энергия и может меняться только за счет работы, совершаемой внешними телами над системой, или самой системой.

Согласно первому началу термодинамики ($∆U=A+Q$), в адиабатной системе

$∆U=A$

где $А$ — работа внешних сил.

При адиабатном расширении газа $А

Следовательно,

$∆U={i}/{2}·{m}/{M}R∆T

что означает уменьшение температуры при адиабатном расширении. Оно приводит к тому, что давление газа уменьшается более резко, чем при изотермическом процессе.

На рисунке адиабата $1—2$, проходящая между двумя изотермами, наглядно иллюстрирует сказанное. Площадь под адиабатой численно равна работе, совершаемой газом при его адиабатическом расширении от объема $V_1$ до $V_2$.

Адиабатное сжатие приводит к повышению температуры газа, т. к. в результате упругих соударений молекул газа с поршнем их средняя кинетическая энергия возрастает, в отличие от расширения, когда она уменьшается (в первом случае скорости молекул газа увеличиваются, во втором — уменьшаются).

Резкое нагревание воздуха при адиабатическом сжатии используется в двигателях Дизеля.

Принцип действия тепловых двигателей

Тепловой двигатель — это устройство, преобразующее внутреннюю энергию топлива в механическую энергию.

Согласно второму началу термодинамики, тепловой двигатель может непрерывно совершать периодически повторяющуюся механическую работу за счет охлаждения окружающих тел, если он не только получает теплоту от более горячего тела (нагревателя), но при этом отдает теплоту менее нагретому телу (холодильнику). Следовательно, на совершение работы идет не все количество теплоты, полученное от нагревателя, а только часть ее.

Таким образом, основными элементами любого теплового двигателя являются:

1. рабочее тело (газ или пар), совершающее работу;
2. нагреватель, сообщающий энергию рабочему телу;
3. холодильник, поглощающий часть энергии от рабочего тела.

Коэффициент полезного действия теплового двигателя

Согласно закону сохранения энергии, работа, совершаемая двигателем, равна:

$A’=|Q_1|-|Q_2|$

где $Q_1$ — количество теплоты, полученное от нагревателя, $Q_2$ — количество теплоты, отданное холодильнику.

Коэффициентом полезного действия (КПД) теплового двигателя называется отношение работы $А’$, совершаемой двигателем, к количеству теплоты, полученному от нагревателя:

$η={A’}/{|Q_1|}={|Q_1|-|Q_2|}/{|Q_1|}=1-{|Q_2|}/{|Q_1|}$

Так как у всех двигателей некоторое количество теплоты передается холодильнику, то $η

КПД теплового двигателя пропорционален разности температур нагревателя и холодильника. При $T_1 — T_2=0$ двигатель не может работать.

Цикл Карно

Цикл Карно — это круговой обратимый процесс, состоящий из двух изотермических и двух адиабатических процессов.

Впервые этот процесс был рассмотрен французским инженером и ученым Н. Л. С. Карно в 1824 г. в книге «Размышления о движущей силе огня и о машинах, способных развивать эту силу».

Целью исследований Карно было выяснение причин несовершенства тепловых машин того времени (они имели КПД $< 5%$)и поиски путей их усовершенствования.

Выбор двух изотермических и двух адиабатических процессов был обусловлен тем, что работа газа при изотермическом расширении совершается за счет внутренней энергии нагревателя, а при адиабатном процессе — за счет внутренней энергии расширяющегося газа. В этом цикле исключен контакт тел с разной температурой, следовательно, исключена теплопередача без совершения работы.

Цикл Карно — самый эффективный из всех возможных. Его КПД максимален.

На рисунке изображены термодинамические процессы цикла. В процессе изотермического расширения ($1-2$) при температуре $Т_1$ работа совершается за счет изменения внутренней энергии нагревателя, т. е. за счет подведения к газу количества теплоты $Q_1$:

$A_{12}=Q_1.$ Охлаждение газа перед сжатием ($3-4$) происходит при адиабатном расширении ($2-3$). Изменение внутренней энергии $∆U_{23}$ при адиабатном процессе ($Q=0$) полностью преобразуется в механическую работу:

$A_{23}=-∆U_{23}$

Температура газа в результате адиабатического расширения ($2-3$) понижается до температуры холодильника $Т_2

$A_{34}=Q_2,$

Цикл завершается процессом адиабатического сжатия ($4—1$), при котором газ нагревается до температуры $Т_1$.

Максимальное значение КПД тепловых двигателей, работающих на идеальном газе, по циклу Карно:

$η={T_1-T_2}/{T_1}=1-{T_2}/{T_1}$

Суть формулы $η={T_1-T_2}/{T_1}=1-{T_2}/{T_1}$ выражена в доказанной С. Карно теореме о том, что КПД любого теплового двигателя не может превышать КПД цикла Карно, осуществляемого при той же температуре нагревателя и холодильника.

Work — The Physics Hypertextbook

Обсуждение

что такое работа?

Целевая аудитория этой книги — люди с некоторым образованием. Это не детская книга; и под детьми я не имею в виду противоположность взрослым. Я считаю подростков (или подростков, если хотите) прото-взрослыми. Если это относится к вам, значит, у вас было формальное научное образование (хорошее, плохое или уродливое). Где-то по ходу дела вы должны были познакомиться с концепцией энергии.Если нет, то перестаньте читать это и найдите себе образование (или хотя бы какой-то жизненный опыт).

Те из вас, у кого было небольшое формальное образование, вероятно, в какой-то момент своей жизни получили урок энергии. Если так, то велики шансы, что вам дали определение энергии как «способность выполнять работу». Если вы были хорошим учеником или просто хотели доставить удовольствие своему учителю, вы, вероятно, слышали это и сказали себе: «Хорошо, энергия — это способность выполнять работу.«Если бы вы были действительно хорошим учеником с желанием учиться или очень плохим учеником с желанием указать на интеллектуальные недостатки вашего учителя, тогда вам следовало бы задать следующий логичный вопрос. Что такое работа?

Надеюсь, вам дали правильный ответ, но шансы пятьдесят на пятьдесят, что вы проигнорировали. Не потому, что правильный ответ так сложно узнать, а потому, что правильный ответ так трудно объяснить или, по крайней мере, трудно объяснить так, чтобы его можно было быстро уловить.Я думаю, это в основном связано с тем, что слово «работа» имеет два значения: обычное для повседневной жизни и техническое — для физики.

Технически, работа представляет собой произведение силы-смещения (для тех из вас, кто предпочитает алгебру)

Вт = F ∆ с cos θ

или интеграл по траектории сила-смещение (для тех из вас, кто предпочитает исчисление).

Я понимаю, что для многих из вас это бессмысленное определение.Так много слов и так мало сказано, не так ли? На самом деле, как раз наоборот. Это определение настолько компактно, что похоже на поэзию. Он говорит как можно больше, используя как можно меньше слов. Оно настолько компактно, что объяснение его на обычном языке приводит к тому, что полдюжины слов технического определения расширяются до почти сотни слов так называемого «естественного языка». Позвольте мне объяснить, что такое работа, с помощью серии мысленных образов. Каждый раз, когда приводится пример, помните, что работа выполняется всякий раз, когда сила вызывает смещение.

Представьте, что учитель физики неподвижно стоит перед классом учеников. Поскольку он не прилагает никаких сил, которые могли бы сместить что-либо за пределами его тела, он не выполняет никакой работы. Очевидно. Но выполнение этого в течение любого промежутка времени, безусловно, истощит его энергию, как если бы он весь день толкал бумаги по своему столу (пример, когда сила приводит к тому, что сила приводит к смещению). Конечно, теперь вы могли бы убедить его, что его определение работы должно быть неправильным. Может быть, под давлением уступит меньший учитель, но не учитель физики.

Безусловно, учитель физики или любой другой человек, стоящий под номером , — это , выполняющий работу, но выполняемую работу не так-то легко увидеть. Внутри тела сердце перекачивает кровь, пищеварительная система переваривает завтрак, рецепторы перемещают молекулы через клеточные мембраны. Мы работаем, даже когда спим. Силы, вызывающие смещения, происходят повсюду у нас под кожей. Человеческое тело — это занятое место.

Если система в целом оказывает силу на свое окружение и происходит смещение, выполненная работа называется внешней работой .Учитель физики, толкая бумаги через стол, выполняет внешнюю работу. Стоящий неподвижно учитель физики не выполняет значительной внешней работы.

Если часть системы воздействует на другую часть той же системы и происходит смещение, выполненная работа называется внутренней работой . Учитель физики глубоко мыслящий или лежащий в коме выполняет внутреннюю работу. (Дополнительный балл, если вы можете отличить их.) Учитель физики, который что-то делает — или ничего не делает — выполняет внутреннюю работу.Умерший учитель физики не выполняет никакой работы, внутренней или внешней. В механике, когда мы говорим, что работа сделана, мы часто имеем в виду внешнюю работу.

Теперь, когда мы решили, что учитель, стоящий на месте, не выполняет никакой работы, давайте представим, что учитель двигается и спрашивает, была ли работа выполнена. Хм, хорошо, когда руки и ноги начинают двигаться, ситуация умеренно сложная. Это затрудняет определение того, что в движении требует работы, а что нет. Нам нужно еще немного упростить.Дайте учителю книгу (например, учебник физики) и попросите его переместить книгу несколькими простыми способами. Теперь возникает вопрос: «Выполнил ли учитель какую-нибудь работу над книгой ?» Это гораздо уже, чем спрашивать, выполнял ли учитель какую-либо работу, а это значит, что на него легче ответить и он лучше подходит для ознакомления с концепцией.

Для учителя, держащего книгу или любую другую систему в этом отношении, работа выполняется всякий раз, когда сила приводит к смещению. Рассмотрим следующие шесть примеров, представленных по три за раз.

Никакая работа не выполняется с учебником, когда он находится в состоянии покоя. Положительная работа выполняется с учебником, когда он поднимается вертикально с постоянной скоростью. Положительная работа также выполняется с учебником, когда он поднимается по диагонали с постоянной скоростью.

Первый пример имеет очевидный смысл. Если держать книгу, не перемещая ее, работа с книгой не выполняется. Замени учителя на стол или пол. На полу лежит книга. Какую работу выполняет пол? Ничего никуда не денется.Ничего не происходит. Ничего не делается — даже не работает.

Второй и третий примеры тоже имеют смысл. Учитель толкает книгу, и она движется. Сила привела к смещению. Работа была сделана. Это согласуется с нашим повседневным представлением о работе. Все в порядке с миром.

Рассмотрим еще три примера.

Работа с учебником не выполняется, если его переносят горизонтально с постоянной скоростью. Отрицательная работа выполняется с учебником, когда его опускают по диагонали с постоянной скоростью.Отрицательная работа также выполняется над учебником, когда он опускается вертикально с постоянной скоростью.

Первый в этом наборе надоедливый. Это нелогично. По сути, это говорит о том, что не нужно переносить книгу по ровной поверхности. Это настолько очевидно глупо, что должно быть неправильно, верно? Неправильный! Это верно. (Вы должны прочитать этот последний бит как внутренний диалог, чтобы он имел смысл.) Работа над объектом выполняется всякий раз, когда сила вызывает смещение. В этом примере приложенная сила вертикальна, но смещение горизонтально.Как вертикальная сила влияет на горизонтальное движение? Короткий ответ: «Это не так».

Вертикальные силы влияют на вертикальное движение. Горизонтальные силы влияют на горизонтальное движение. Когда движение и сила параллельны, жизнь проста. Когда движение и сила , а не параллельны, жизнь , а не просто. Ангелы уходят, и демоны вступают во владение. Под демонами я подразумеваю векторы — в частности, векторные компоненты. Работа выполняется всякий раз, когда сила или составляющая силы приводит к смещению.Никакая составляющая силы не действует в направлении движения, когда книга перемещается горизонтально с постоянной скоростью. Сила и смещение независимы. Ручная работа над книгой не выполняется.

Взгляните на последние два примера в этом наборе из шести. Здесь мы видим, что ведется негативная работа. Учитывая то, что я сказал о компонентах, это может иметь или не иметь для вас смысла. И снова, когда сила и смещение параллельны, жизнь проста.

Применить силу → Переместить объект → Выполнить работу

Когда сила не совсем параллельна смещению, это похоже на то, что для выполнения работы используется меньшая сила.

Приложите меньшее усилие → Сделайте меньше работы

Это тоже довольно просто. Когда угол между силой и смещением достигает 90 °, составляющая силы, параллельная смещению, уменьшается до нуля.

Не прилагать усилия → Не работать

Хорошо, сначала это было нелогично, но теперь в этом есть смысл.

Чем дальше два вектора удаляются от параллели, тем меньше работы выполняется. Увеличьте угол до 90 °. Сила и смещение начинают двигаться в противоположных направлениях.При 90 ° никаких работ не производилось. Если угол превышает 90 °, работа не должна выполняться. Это отрицательная работа.

Не прилагать усилия → Не работать

Есть еще одна причина принять негативную работу. Знак работы указывает направление изменения. Отрицательный знак указывает на потерю чего-либо. В случае опускания книги это означает снижение ее способности выполнять работу — снижение ее энергии.

Следуйте этой цепочке рассуждений. Чтобы поднять книгу, нужно потрудиться.Поднятие книги повышает ее энергию. Теперь я могу использовать энергию, хранящуюся в книге, для работы — и под «работой» я имею в виду физический труд, а не обучение американской молодежи. Я могу толкать им разные вещи — грецкие орехи, насекомых, квадратные колышки в круглые отверстия. Я делаю эту работу, опуская книгу. Это также снижает его энергию. Он больше не может работать, когда снова лежит на столе. Поднятие книги действительно работает. Его опускание отменяет работу над ним. С точки зрения работы или энергии книга вернулась в исходное состояние.В числовом выражении положительная работа, проделанная при ее повышении, была отменена отрицательной работой, сделанной при ее понижении, что привело к нулю выполненной работы в целом по книге . (Ситуация иная с разбитым орехом, насекомым или квадратным колышком.)

алгебра

Работа выполняется всякий раз, когда сила вызывает смещение. При прочих равных условиях применение большей силы должно приводить к выполнению большего объема работы. Точно так же приложение заданной силы на большем расстоянии должно привести к выполнению большего количества работы.И, как мы обсуждали в дюжине параграфов, предшествующих этому, важна составляющая силы, параллельная смещению. Работа прямо пропорциональна первым двум факторам: силе и перемещению. Направление обрабатывается функцией косинуса. Косинус наибольший, когда угол равен нулю (угол между двумя векторами, указывающими в одном направлении, равен нулю), ноль при девяноста градусах (силы, перпендикулярные смещению, не действуют), и отрицательный для тупых углов (силы, действующие в противоположном направлении смещения, отменяют работу). .

Работа лучше всего определяется уравнением. Вот одна распространенная версия…

Вт = F ∆ с cos θ

где…

Вт =	работ выполнено
F =	среднее приложенное усилие
∆ с =	смещение, вызванное силой
θ =	угол усилие-смещение

Это уравнение предполагает, что сила постоянна как по величине, так и по направлению относительно смещения в любое время.Для многих задач это предположение разумно, поэтому оно написано здесь.

исчисление

Для тех случаев, когда изменения в величине или направлении значительны, мы представляем наше знакомое исчисление. При некотором конечном смещении сила может изменяться по величине и направлению. При меньшем смещении он наверняка изменится меньше. Разрежьте смещение на серию небольших смещений, вычислите работу, проделанную на каждом шаге, и сложите результаты вместе. Для достижения наилучших результатов позвольте ступенькам приблизиться к бесконечно малому размеру.

Пока мы занимаемся этим, давайте также заменим функцию косинуса более компактной нотацией скалярного произведения. Есть два способа умножения векторов — скалярное произведение , · и перекрестное произведение , ×. Скалярное произведение — это скалярный продукт, который увеличивается с увеличением сходства направления. Триггерная функция, которая делает это, — косинус. Перекрестное произведение — это векторное произведение, которое увеличивается с увеличением перпендикулярности и выходит за пределы плоскости, содержащей два вектора.Триггерная функция, которая это делает, — синус. Поскольку мы ранее определили косинус как правильную функцию, мы будем использовать скалярное произведение.

В пределе конечное ∆ s становится бесконечно малым d s , а конечное ∑ становится бесконечным. Конечная сумма конечных величин всегда конечна. Бесконечный интеграл бесконечно малых дифференциалов также может быть конечным. Магия исчисления в том, что последнее вообще может быть правдой.

Работа лучше всего определяется уравнением.Вот еще одна распространенная версия…

Это уравнение является примером интеграла по пути (или линейного интеграла ). Когда большинство студентов знакомятся с интеграцией, им говорят, что интеграция — это способ найти площадь под кривой. Это делается путем математического разбиения кривой на бесконечно малые сегменты одинаковой ширины, измерения площади прямоугольной полосы, которая помещается между каждым сегментом кривой и горизонтальной осью, а затем сложения площадей сегментов вместе.Нет ничего плохого в том, что это введение в интеграцию, но иногда студенты зацикливаются на понятии, что интеграция — это просто «поиск области». Интеграция — это действительно соединение частей в единое целое. Это основное значение слова на английском языке и — основное значение слова в исчислении. Интегрирование можно использовать для нахождения площади под кривой (я назову это традиционным интегралом ), но его также можно использовать для нахождения количества некоторой величины, накопленной на пути (интеграл по пути ), чтобы найти количество некоторого количества, захваченного поверхностью (интеграл поверхности ), или количество некоторого количества, содержащегося в объеме (интеграл объема ).

шт.

Единица измерения в системе СИ — джоуль .

[J = Н · м = кг · м ² / с ² ]

Работа и энергия могут быть выражены в одних и тех же единицах. К сожалению, помимо джоуля есть много единиц энергии. (Это обсуждается в другом разделе этой книги.) Наиболее часто встречающиеся в США в начале 21 века, вероятно, калории (диета и питание), британские тепловые единицы (отопление и охлаждение), киловатт-час (счета за электричество), тепловые ( счета за природный газ), квадроцикл (макроэкономика), тонна тротила (ядерное оружие), эрг (ученые старшего возраста) и фут-фунт (инженеры старшего возраста).Первые два в этом списке, калорийность и британская тепловая единица, были впервые введены учеными XIX века, изучающими калориметрию. (Французы дали нам калорию, а англичане дали британские тепловые единицы или британские тепловые единицы.) Последний в списке фунт-фут был введен учеными 19 века, изучающими механику. В XIX веке калориметрия и механика были отдельными дисциплинами. Калориметрия — это исследование тепла. Механика — это изучение движения и сил. Образованный джентльмен (а в то время они обычно были мужчинами) мог изучать и то, и другое, но он, вероятно, не связывал их сколько-нибудь значительным образом.То есть, если только его не звали Джоуль.

Джеймс Джоуль (1818–1889) был богатым английским пивоваром, занимавшимся различными аспектами науки и экономики. Иногда эти усилия совпадали. Он изобрел фут-фунт как единицу работы: фут является единицей перемещения, а фунт — единицей силы. Это позволило ему количественно сравнить «экономичность» различных механических систем. В то время паровые двигатели, работающие на угле, были основным источником промышленной мощи, но тогда на горизонте высоких технологий появилась электроэнергия.Джоуль понял, что механическая работа, тепло и электрическая энергия каким-то образом взаимозаменяемы. Тепло может работать. Работа может вызвать тепло. Работа может производить электричество, Электричество может производить работу, Электричество может производить тепло. Тепло может производить электричество. Энергия — актер разносторонний.

Самый известный эксперимент

Джоуля — это, вероятно, определение механического эквивалента тепла (я надеюсь, что он будет обсуждаться более подробно в другом месте в этой книге). Теплота измерялась в британских тепловых единицах (по крайней мере, британцами), а работа — в фут-фунтах (что изобрел Джоуль).Джоуль установил, что одна британская тепловая единица тепла эквивалентна приблизительно 770 фут-фунтам механической работы — очень близко к сегодняшнему значению 778 фут-фунт / британских тепловых единиц. Этот результат был важен для осознания того, что, несмотря на наличие множества форм, энергия — это одно.

Международная система единиц, которая начала доминировать в научном мире в середине 20 века, имела французское происхождение. Футам-фунтам и британским тепловым единицам не место в этой гораздо более логичной системе.12 дюймов в футе. 16 унций в фунте. 128 унций в галлоне в США и неизвестно сколько в Великобритании. Математика была слишком сложной. Parlez-vous les unités métriques ? СИ был французским по происхождению, но международным по своему характеру. Когда прозвучал призыв назвать единицу энергии, ответ был громким: Джоуль! Отпущение грехов!

Некоторые примечания к агрегатам.

• Джоуль эквивалентен ньютон-метру , но его нельзя называть таковым.Эта единица зарезервирована для крутящего момента. Крутящий момент также является произведением силы-смещения, но другого вида. Крутящий момент максимизируется, когда сила и смещение перпендикулярны, что означает, что он использует синус вместо косинуса для согласования направления (или для более продвинутых читателей он использует перекрестное произведение вместо скалярного произведения). Крутящий момент не измеряется в джоулях, и работу никогда не следует измерять в ньютон-метрах.
• Гауссовская единица работы — эрг [эрг = дин см = г см ² / с ² ].10 000 000 эрг = 1 джоуль. Слово эрг происходит от классического греческого слова, обозначающего работу: εργον ( ergon ). ERG также было названием спортивного напитка, появившегося в США в конце 1960-х или начале 1970-х годов. ERG расшифровывалось как «замена электролита глюкозой».
• Англо-американская единица работы — фут-фунт (когда фунт является единицей силы) или фут-фунтал (когда фунт является единицей массы). Первое встречается чаще, чем второе. Путаницы с единицами крутящего момента можно избежать, изменив порядок.Англо-американская единица крутящего момента — фунт-фут или фунт-фут в зависимости от вашего определения фунта. Опять же, первое встречается чаще, чем второе. Джеймс Джоуль изобрел фут-фунт.

консервативные и неконсервативные силы

текст

Положительная работа выполняется, когда учебник перемещается вправо по поверхности стола уровня с постоянной скоростью. Положительная работа также выполняется, когда учебник перемещается влево по поверхности стола уровня с постоянной скоростью.

текст

Положительная работа выполняется над учебником, когда он поднимается вертикально с постоянной скоростью. Отрицательная работа выполняется над учебником, когда он опускается вертикально с постоянной скоростью.

текст

теорема об энергии работы

текст

Вт = ∆ E

• работа вызывает изменение энергии
• работа переносит энергию из одной системы в другую

Условные обозначения:

• Когда система работает в своей среде, W <0; то есть полная энергия системы уменьшается.Работа выполняется по системе.
• Когда среда работает в системе, Вт > 0; то есть полная энергия системы увеличивается. Работа ведется по системе .

Томас Янг (1773–1829) был первым, кто использовал эту формулу. ← Это правда?

Определение работы по физике

В физике работа определяется как сила, вызывающая движение или смещение объекта. В случае постоянной силы работа — это скалярное произведение силы, действующей на объект, и смещения, вызванного этой силой.Хотя и сила, и смещение являются векторными величинами, работа не имеет направления из-за природы скалярного произведения (или скалярного произведения) в векторной математике. Это определение согласуется с правильным определением, потому что постоянная сила интегрируется просто как произведение силы и расстояния.

Читайте дальше, чтобы узнать о некоторых реальных примерах работы, а также о том, как рассчитать объем выполняемой работы.

Примеры работ

Примеров работы в повседневной жизни много.В классе физики есть несколько заметок: лошадь, тащащая плуг по полю; отец толкает тележку с продуктами по проходу продуктового магазина; студентка поднимает на плечо рюкзак, полный книг; штангист поднимает над головой штангу; и олимпиец запускает толкание ядра.

В общем, для того, чтобы работа произошла, к объекту должна быть приложена сила, заставляющая его двигаться. Итак, разочарованный человек, толкающийся о стену только для того, чтобы истощить себя, не выполняет никакой работы, потому что стена не двигается.Но если книга упадет со стола и ударится о землю, это будет считаться работой, по крайней мере, с точки зрения физики, потому что сила (гравитация) действует на книгу, заставляя ее смещаться вниз.

Что не работает

Интересно, что официант, несущий поднос высоко над его головой и поддерживаемый одной рукой, когда он идет равномерным шагом через комнату, может подумать, что он много работает. (Он может даже вспотеть.) Но, по определению, он не выполняет никакой работы .Правда, официант силой толкает поднос над головой, и правда, поднос движется по комнате, пока официант идет. Но сила — поднятие подноса официантом — не заставляет поднос двигаться. «Чтобы вызвать смещение, должен быть компонент силы в направлении смещения», — отмечает The Physics Classroom.

Расчетная работа

Базовый расчет работы на самом деле довольно прост:

W = Fd

Здесь «W» обозначает работу, «F» — силу, а «d» — смещение (или расстояние, на которое перемещается объект).Physics for Kids дает следующий пример задачи:

Бейсболист бросает мяч с силой 10 ньютонов. Мяч летит на 20 метров. Какая общая работа?

Чтобы решить эту проблему, вам сначала нужно знать, что Ньютон определяется как сила, необходимая для обеспечения массы в 1 килограмм (2,2 фунта) с ускорением 1 метр (1,1 ярда) в секунду. Ньютон обычно обозначается сокращенно как «Н.» Итак, воспользуйтесь формулой:

Вт = Fd

Таким образом:

Вт = 10 Н * 20 метров (где символ «*» обозначает время)

Так:

Работа = 200 джоулей

Джоуль, термин, используемый в физике, равен кинетической энергии 1 килограмма, движущегося со скоростью 1 метр в секунду.

Работа: Научное определение | Физика

Цели обучения

К концу этого раздела вы сможете:

• Объясните, как объект должен перемещаться, чтобы сила, действующая на него, выполняла работу.
• Объясните, как относительные направления силы и смещения определяют, является ли выполненная работа положительной, отрицательной или нулевой.

Что значит делать работу

Научное определение труда несколько отличается от его повседневного значения.Некоторые вещи, которые мы считаем тяжелой работой, например написание экзамена или ношение тяжелой ноши на ровной поверхности, не являются работой, как это определено ученым. Научное определение работы показывает ее связь с энергией — когда работа выполняется, энергия передается.

Для выполнения работы в научном смысле необходимо приложить силу и должно быть движение или смещение в направлении силы.

Формально, работа , совершаемая в системе постоянной силой, определяется как произведение составляющей силы в направлении движения на расстояние, на которое действует сила .Для одностороннего движения в одном измерении это выражается в форме уравнения как W = | F | (cos θ ) | d |, где W — работа, d — смещение системы, а θ — угол между вектором силы F и вектором смещения d , как на рисунке 1. Мы также можно записать это как W = Fd cos θ .

Чтобы найти работу, выполненную в системе, которая претерпевает движение, которое не является односторонним или которое находится в двух или трех измерениях, мы делим движение на односторонние одномерные сегменты и складываем работу, выполненную по каждому сегменту.

Что такое работа?

Работа, совершаемая в системе постоянной силой, равна произведению составляющей силы в направлении движения на расстояние, на которое действует сила . Для одностороннего движения в одном измерении это выражается в форме уравнения как W = Fd cos θ , где W — работа, F — величина силы, действующей на систему, d. — величина смещения системы, а θ — угол между вектором силы F и вектором смещения d .

Рисунок 1. Примеры работы. (a) Работа, выполняемая силой F на этой газонокосилке, составляет Fd cos θ . Обратите внимание, что F cos θ — это составляющая силы в направлении движения. (б) Человек, держащий портфель, не работает с ним, потому что нет движения. Энергия не передается ни в чемодан, ни из него. (c) Человек, перемещающий портфель в горизонтальном направлении с постоянной скоростью, не работает с ним и не передает ему энергию.(d) Работа с портфелем выполняется путем его подъема по лестнице с постоянной скоростью, поскольку обязательно присутствует составляющая силы F в направлении движения. Энергия передается в портфель и, в свою очередь, может использоваться для работы. e) когда портфель опускается, энергия передается из портфеля в электрический генератор. Здесь работа, выполняемая генератором с портфелем, является отрицательной, что приводит к снятию энергии с портфеля, поскольку F и d находятся в противоположных направлениях.

Чтобы изучить, что означает определение работы, давайте рассмотрим другие ситуации, показанные на рисунке 1. Например, человек, держащий портфель на рисунке 1b, не работает. Здесь d = 0, значит W = 0. Почему вы устаете просто держать груз? Ответ заключается в том, что ваши мышцы работают друг против друга, , но они не работают в интересующей системе («система портфель-Земля» — см. Подробнее «Энергия гравитационного потенциала»).Для выполнения работы должно быть движение, и должна быть составляющая силы в направлении движения. Например, человек, несущий портфель на ровной поверхности на рисунке 1c, не работает с ним, потому что сила перпендикулярна движению. То есть cos 90º = 0, и поэтому W = 0.

Напротив, когда сила, действующая на систему, имеет компонент в направлении движения, как на рисунке 1d, работа выполняется на — энергия передается портфелю.Наконец, на рисунке 1e энергия передается от портфеля к генератору. Есть два хороших способа интерпретировать эту передачу энергии. Одно из объяснений состоит в том, что вес портфеля действительно воздействует на генератор, давая ему энергию. Другая интерпретация заключается в том, что генератор отрицательно воздействует на портфель, тем самым забирая из него энергию. На чертеже показано последнее, где сила от генератора направлена ​​вверх на портфель, а смещение — вниз. Это составляет θ = 180º, а cos 180º = -1; следовательно, W отрицательно.

Расчетная работа

Работа и энергия имеют одинаковые единицы. Из определения работы мы видим, что эти единицы — это сила, умноженная на расстояние. Таким образом, в единицах СИ работа и энергия измеряются в ньютон-метров . Ньютон-метр получает специальное название джоуль (Дж), а 1Дж = 1Н · м = 1 кг · м ² / с ² . Один джоуль — это не большое количество энергии; он поднимет небольшое 100-граммовое яблоко на расстояние около 1 метра.

Пример 1.Расчет работы, которую вы выполняете, чтобы толкать газонокосилку по большой лужайке

Сколько работы проделал с газонокосилкой человек, изображенный на Рисунке 1а, если он прикладывает постоянную силу 75,0 Н под углом 35º ниже горизонтали и толкает газонокосилку на 25,0 м по ровной поверхности? Преобразуйте объем работы из джоулей в килокалории и сравните его со средним дневным потреблением этого человека 10 000 кДж (около 2400 ккал) пищевой энергии. Одна калорий (1 кал) тепла — это количество, необходимое для нагрева 1 г воды на 1ºC, и эквивалентно 4.184 Дж, а на одну пищевую калорию (1 ккал) эквивалентно 4184 Дж.

Стратегия

Мы можем решить эту проблему, подставив указанные значения в определение работы, выполняемой в системе, указанное в уравнении Вт = Fd cos θ . Приведены сила, угол и перемещение, так что неизвестна только работа W .

Решение

Уравнение для работы: Вт = Fd cos θ .{-4} \\ [/ латекс]

Обсуждение

Это соотношение — крошечная доля того, что человек потребляет, но это типичное значение. Очень мало энергии, выделяемой при потреблении пищи, используется для работы. Даже когда мы «работаем» весь день, менее 10% потребляемой нами энергии уходит на работу, а более 90% преобразуется в тепловую энергию или сохраняется в виде химической энергии в жире.

Сводка раздела

Работа — это передача энергии силой, действующей на объект при его перемещении.

Работа W , которую сила F производит на объект, является произведением величины F силы, умноженной на величину d смещения, умноженную на косинус угла θ между ними. . В символах Вт = Fd cos θ .

Единицей измерения работы и энергии в системе СИ является джоуль (Дж), где 1 Дж = 1 Н · м = 1 кг · м ² / с ² .

Работа, совершаемая силой, равна нулю, если смещение равно нулю или перпендикулярно силе.

Выполненная работа является положительной, если сила и смещение имеют одинаковое направление, и отрицательной, если они имеют противоположное направление.

Концептуальные вопросы

1. Приведите пример того, что мы считаем работой в повседневных обстоятельствах, что не является работой в научном смысле. В вашем примере энергия передается или изменяется по форме? Если да, объясните, как это достигается без выполнения работы.
2. Приведите пример ситуации, в которой есть сила и смещение, но сила не работает.Объясните, почему это не работает.
3. Опишите ситуацию, в которой сила действует в течение длительного времени, но не работает. Объяснять.

Задачи и упражнения

1. Сколько работы кассир в супермаркете проделывает с банкой с супом, которую он толкает на 0,600 м по горизонтали с силой 5,00 Н? Выразите свой ответ в джоулях и килокалориях.
2. Человек весом 75,0 кг поднимается по лестнице, набирая высоту 2,50 метра. Найдите работу, проделанную для выполнения этой задачи.
3. (a) Рассчитайте работу, проделанную с кабиной лифта весом 1500 кг, чтобы поднять ее 40.0 м при постоянной скорости, предполагая, что трение в среднем составляет 100 Н. (b) Какую работу совершает в этом процессе сила тяжести на подъемнике? (c) Какова общая работа подъемника?
4. Предположим, автомобиль проезжает 108 км со скоростью 30,0 м / с и использует 2,0 галлона бензина. Только 30% бензина расходуется на полезную работу за счет силы, которая позволяет автомобилю двигаться с постоянной скоростью, несмотря на трение. (В галлоне бензина 1,2 × 10 ⁸ Дж.) (A) Какова величина силы, прилагаемой, чтобы автомобиль двигался с постоянной скоростью? (b) Если требуемая сила прямо пропорциональна скорости, сколько галлонов будет использовано для проезда 108 км со скоростью 28.0 м / с?
5. Рассчитайте работу, проделанную мужчиной весом 85,0 кг, который толкает ящик на 4,00 м по пандусу, составляющему угол 20,0 ° с горизонтом. (См. Рис. 2.) Он прилагает силу 500 Н к ящику параллельно рампе и перемещается с постоянной скоростью. Обязательно укажите работу, которую он проделывает с ящиком и телом, чтобы подняться по пандусу.

   Рис. 2. Мужчина толкает ящик по пандусу.

6. Сколько работы выполняет мальчик, тащащий свою сестру 30,0 м в фургоне, как показано на рисунке 3? Предположим, что на вагон не действует трение.

   Рис. 3. Мальчик работает с системой телеги и ребенка, когда тянет их, как показано.

7. Покупатель толкает тележку для продуктов на 20,0 м с постоянной скоростью по ровной поверхности, преодолевая силу трения 35,0 Н. Он толкает в направлении на 25,0 ° ниже горизонтали. а) Какая работа происходит в тележке за счет трения? б) Какую работу совершает гравитационная сила на тележке? (c) Какую работу выполняет покупатель с тележкой? (d) Найдите силу, которую оказывает покупатель, используя соображения энергии.(e) Какова общая работа, проделанная с тележкой?
8. Предположим, что лыжный патруль спускает спасательные сани и пострадавшего, общая масса которого составляет 90,0 кг, вниз по склону 60,0 ° с постоянной скоростью, как показано на рисунке 4. Коэффициент трения между санями и снегом составляет 0,100. а) Сколько работы совершает трение, когда сани движутся по холму на 30,0 м? б) Сколько работы на этом расстоянии совершает веревка на санях? (c) Какую работу совершает сила тяжести на салазках? (г) Какова общая проделанная работа?

   Рисунок 4.Спасательные сани и пострадавший спускаются по крутому склону.

Глоссарий

энергия: работоспособность

работа: передача энергии силой, которая заставляет объект перемещаться; произведение составляющей силы в направлении смещения на величину смещения

джоуль: единица работы и энергии в СИ, равная одному ньютон-метру

Избранные решения проблем и упражнения

1.3,00 Дж = 7,17 × 10 ⁻⁴ ккал

3. (а) 5.92 × 10 ⁵ Дж; (б) −5,88 × 10 ⁵ Дж; (c) Чистая сила равна нулю.

5. 3,14 × 10 ³ Дж

7. (а) -700 Дж; (б) 0; (c) 700 Дж; (d) 38,6 N; (д) 0

Работа — результат силы Рон Куртус

SfC Home> Физика>

Рон Куртус

Когда вы прикладываете достаточно силы к объекту, чтобы преодолеть некоторое сопротивление , так что вы перемещаете этот объект, вы выполняете работу с этим объектом.Другими словами, работа равна приложенной силе, умноженной на пройденное расстояние.

Если вы перемещаете объект, который изначально неподвижен, вы ускоряете объект, а сопротивление движению — это инерция объекта. Таким образом, вы делаете работу против инерции. Поскольку объекты имеют тенденцию продолжать движение после приложения силы, расстояние измеряется только во время приложения силы.

Обычно вы рассматриваете возможность работы против силы сопротивления, такой как трение или гравитация.Приложенная сила должна быть больше, чем сила сопротивления.

Вопросы, которые могут у вас возникнуть:

• Какая связь между работой и силой?
• Что такое работа против инерции?
• Что такое работа против силы сопротивления?

Этот урок ответит на эти вопросы. Полезный инструмент: Конвертация единиц

---

---

Работа — это сила, умноженная на расстояние

Определение работы состоит в том, что она равна силе преодоления сопротивления, умноженной на расстояние, пройденное при приложении этой силы.Уравнение:

Вт = Fd

где:

• W — работа в джоулях (Дж или кг-м² / с²) или фут-фунтах
• F — сила, необходимая для перемещения объекта, в ньютонах (Н или кг-м / с²) или фунтах (фунтах)
• d — расстояние, на которое перемещается объект, в метрах (м) или футах (футах)
• Fd равно F раз d

Примечание : W указывает на работу.Иногда W также указывается как вес. Вы всегда должны обязательно читать определение под уравнением, чтобы убедиться, что вы понимаете, что обозначают буквы.

Когда сопротивление слишком велико

Если к объекту приложена сила и нет движения из-за слишком большого сопротивления, то работы нет. Если вы толкаете тяжелый предмет, но не можете его сдвинуть, вы делаете усилие, но не выполняете никакой работы, согласно научному определению работы.

Работа по инерции

Когда вы прикладываете силу к неподвижному, но свободно движущемуся объекту, вы работаете против его инерции или тенденции оставаться неподвижным. Это также относится к изменению скорости или направления объекта.

Первый закон движения Ньютона часто называют законом инерции . В нем говорится, что:

Материя остается в своем состоянии движения и направления, если на нее не действует сила.

(См. Движение и Закон инерции для получения дополнительной информации.)

Требуемая сила

Сила, необходимая для перемещения объекта против инерции:

F = ma

где

• м — масса объекта
• a — результирующее ускорение

Таким образом, работа по инерции:

F = mad

(Не сердитесь на это!)

Работа, выполняемая над свободно движущимся объектом, происходит только на расстоянии , когда вы прикладываете силу .Как только вы перестанете прилагать силу, объект будет двигаться свободно, и работа больше не будет выполняться.

Бросок мяча

Например, если вы бросаете мяч, проделанная работа состоит из расстояния, на которое вы ускоряли мяч, пока не отпустили его. После того, как вы бросили мяч, он продолжит движение с постоянной скоростью (за вычетом эффекта сопротивления воздуха), и дальнейшая работа не будет выполняться.

Переноска тяжелого ящика

Если вы держите тяжелую коробку и переносите ее через комнату, то работа, которую вы выполняете против инерции, — это сила, которую вы прикладываете для перемещения коробки ( F = ma ), умноженная на расстояние, на которое вы ее несете.

Обратите внимание на , в некоторых учебниках говорится, что это , а не работа, потому что сила тяжести перпендикулярна вашему движению. К сожалению, им неясно, о какой работе они говорят.

Перемещение коробки через комнату — это работа против инерции коробки, а подъем коробки вверх — работа против силы сопротивления тяжести .

Работа против силы сопротивления

Сила сопротивления — это сила, которая заставляет движущийся объект замедляться или препятствует движению неподвижного объекта.Сила сопротивления действует в направлении, противоположном тому, по которому вы хотите переместить объект.

Как и при движении против инерции, расстояние измеряется только при приложении силы, поскольку объект может продолжить движение на короткое расстояние после того, как сила высвободилась, даже если он движется против силы сопротивления.

Работа против силы тяжести

Когда вы поднимаете тяжелый предмет, вы выполняете работу против силы тяжести. Сила, необходимая для жизни объекта, равна его весу

кг.

F = мг

где

• F — сила, необходимая для подъема объекта, а также его вес
• м — масса объекта
• g — ускорение, вызванное силой тяжести (9.8 м / с² или 32 фут / с²)

Объем работы, который вы должны выполнить, равен весу объекта, умноженному на высоту, которую вы его поднимаете. Таким образом, W = mgh , где h — высота, на которую вы его поднимаете. Объем работы, который вы выполняете, чтобы поднять объект массой м на высоту х , является таким же объемом работы, выполняемой под действием силы тяжести, если вы уроните объект с этой высоты.

Другой пример работы против инерции — это работа, совершаемая силой тяжести, когда вы роняете объект с некоторой высоты.Поскольку сила тяжести равна F = mg , где м, — масса объекта, а g, — ускорение свободного падения, работа, выполненная при падении объекта с высоты h , составляет W = Fd. = mgh .

Обратите внимание на , что уравнение W = mgh то же, что и для потенциальной энергии объекта на некоторой заданной высоте: PE = mgh . ( См. Дополнительную информацию в разделе «Потенциальная энергия». )

Работа против трения

Трение — это сила сопротивления всему, что движется или скользит по поверхности или материалу.Например, если вы толкаете предмет по полу, сила трения оказывает сопротивление движению. Если сдвинуть объект на определенное расстояние по полу, работа будет выполнена

.

W = F _r d

где:

• W это проделанная работа
• F _r — сила сопротивления трения
• d — расстояние, на которое вы сдвинули объект

( См. Дополнительную информацию в разделе «Сила сопротивления трения».)

Если вы толкнули предмет по скользкому полу, он может продолжить скольжение на короткое расстояние после того, как вы перестанете толкать. Ваша работа будет измеряться только на расстоянии, на которое вы толкнули объект.

Сводка

Работа — это результат силы, перемещающей объект на расстояние, измеряемый при приложении этой силы. Уравнение для работы: W = Fd . Работа может быть направлена ​​на преодоление инерции, а также на работу против силы сопротивления. Гравитация может работать против инерции, а вы можете работать против силы тяжести.

---

Упорно работать для достижения своих целей

---

Ресурсы и ссылки

Полномочия Рона Куртуса

Сайтов

Физические ресурсы

Книги

(Примечание: Школа чемпионов может получать комиссионные от покупки книг)

Книги по физике труда с самым высоким рейтингом

---

Вопросы и комментарии

У вас есть вопросы, комментарии или мнения по этой теме? Если да, отправьте свой отзыв по электронной почте.Я постараюсь вернуться к вам как можно скорее.

---

Поделиться страницей

Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:

---

Студенты и исследователи

Веб-адрес этой страницы:
www.school-for-champions.com/science/work.htm

Пожалуйста, включите его в качестве ссылки на свой веб-сайт или в качестве ссылки в своем отчете, документе или диссертации.

Авторские права © Ограничения

---

Где ты сейчас?

Школа чемпионов

По физике

Работа — результат силы

---

Работа — Энергетическое образование

Работа — это передача механической энергии от одного объекта к другому.Поскольку работа — это движение энергии, она измеряется в тех же единицах, что и энергия: джоулях (Дж). Определение работы в контексте физики сильно отличается от того, как оно используется в повседневной жизни человека, и выглядит следующим образом: ^[1]

Работа выполняется, когда к объекту на расстоянии прикладывается сила.

Это означает, что когда к объекту на расстоянии применяется сила, это влияет на общую энергию объекта. Объект будет либо ускоряться, либо замедляться, что приведет к изменению его кинетической энергии (см. Рисунок 1), либо у него будет измененная потенциальная энергия, если, например, он был поднят на определенную высоту под действием силы тяжести. ^[1]

Рис. 1. Питчер работает с бейсбольным мячом, чтобы увеличить его кинетическую энергию. Его рука отводится как можно дальше назад, а затем как можно дальше вперед, чтобы максимально увеличить расстояние, на которое была приложена сила. ^[2]

Работа также выходит за рамки того, что человек может физически видеть; он также может влиять на микроскопические свойства системы, такие как температура. В 1843 году эту идею начали исследовать ученые, ^[3] , и ее результаты привели к формулировке того, что сейчас известно как термодинамика.Работа с системой может повлиять на ее внутреннюю энергию, как и добавление тепла; однако они принципиально разные, и их можно изучить на странице «Теплота против работы».

Все описанные до сих пор случаи того, как работа может влиять на систему, можно суммировать в одном уравнении: ^[1]

[математика] W = \ Delta K + \ Delta U + \ Delta E_ {th} [/ math]

Это уравнение говорит о том, что работа ([math] W [/ math]) может изменять ([math] \ Delta [/ math]): кинетическую энергию ([math] K [/ math]), потенциальную энергию ( [math] U [/ math]), тепловая энергия ([math] E_ {th} [/ math]) или любая их комбинация.

Фактически выполненную работу можно рассчитать по следующей формуле: ^[4]

[математика] W = \ vec {F} \ cdot \ vec {d} [/ math]

Где:

• [математика] W [/ математика] — работа или изменение механической энергии, измеряемое в джоулях (Дж)
• [math] F [/ math] — сила, измеряемая в ньютонах (Н)
• [math] d [/ math] — смещение объекта

Стрелки над силой и смещением указывают, что они являются векторами. Это означает, что у них есть связанное с ними направление, которое имеет важное значение для того, сколько работы выполняется с объектом.Если оба направления совпадают, как показано на рисунке 1, энергия системы увеличится, что означает, что положительная работа была выполнена. Если направления противоположны, например сила трения и сопротивления воздуха движущемуся автомобилю, энергия системы будет уменьшаться, что приведет к выполнению отрицательной работы.

С точки зрения физики работа никогда не бывает чем-то, что есть у объекта. Это всего лишь то, что один объект делает с другим. Работа изменяет количество механической и внутренней энергии, которой обладают объекты.Когда работа выполняется на системе или объекте , к этому добавляется энергия. Когда работа выполняется на над системой или объектом, она отдает часть своей энергии чему-то другому.

Бросок мяча означает, что рука прикладывает силу, когда рука движется вперед. Приложив силу к мячу на этом расстоянии, рука выполняет работу с мячом, и мяч получает кинетическую энергию. Это то, что придает ему скорость.

Математические отношения между полной работой и полной энергией описываются теоремой работы-энергии и сохранения энергии.Простые машины могут изменять количество силы, необходимой для перемещения объекта, но сила должна применяться на большем расстоянии: они не меняют объем проделанной работы.

Список литературы

1. ↑ ^{1.0 1.1 1.2} Р. Д. Найт, «Работа и кинетическая энергия» в книге Физика для ученых и инженеров: стратегический подход, 3-е изд. Сан-Франциско, США: Pearson Addison-Wesley, 2008, глава 11, разделы 2 и 3, стр. 278-301.
2. ↑ Wikimedia Commons [Online], доступно: https: // upload.wikimedia.org/wikipedia/commons/2/25/Baseball_pitching_motion_2004.jpg
3. ↑ Hyperphysics, Механический эквивалент тепла [Online], Доступно: http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/heat.html#c3
4. ↑ R. Nave. (2015, 21 июня) Работа Онлайн. Доступно: http://hyperphysics.phy-astr.gsu.edu/hbase/wcon.html

Работа и энергия

Концепции работы и энергии тесно связаны с концепцией силы, потому что приложенная сила может работать с объектом и вызывать изменение энергии. Энергия определяется как способность выполнять работу.

Работа

Понятие работы в физике имеет гораздо более узкое определение, чем обычное употребление этого слова. Работа выполняется с объектом, когда приложенная сила перемещает его на расстояние. На нашем повседневном языке работа связана с затратами мышечных усилий, но это , а не на языке физики. Человек, держащий тяжелый предмет, не выполняет никакой физической работы, потому что сила не перемещает предмет на расстояние.Согласно физическому определению работа выполняется, пока тяжелый объект поднимается, но не когда объект неподвижен. Другой пример отсутствия работы — это масса на конце струны, вращающаяся по горизонтальному кругу на поверхности без трения. Центростремительная сила направлена ​​к центру круга и, следовательно, не перемещает объект на расстояние; то есть сила направлена ​​не в направлении движения объекта. (Однако была проделана работа, чтобы привести массу в движение.) Математически работа равна Вт, = F · x, где F, — приложенная сила, а x — это пройденное расстояние, то есть смещение. Работа — это скаляр. Единицей измерения работы в системе СИ является джоуль (Дж), который представляет собой ньютон-метр или кг м / с ² .

Если работа выполняется с помощью переменной силы, приведенное выше уравнение использовать нельзя. На рисунке показан график зависимости силы от смещения для объекта, на который действуют три различных последовательных силы. Сила увеличивается в сегменте I, постоянна в сегменте II и уменьшается в сегменте III.Работа, выполняемая над объектом каждой силой, представляет собой область между кривой и осью x . Общая проделанная работа — это общая площадь между кривой и осью x . Например, в этом случае работа, выполняемая тремя последовательными силами, показана на рисунке 1.

Рисунок 1

Действующая сила изменяется в зависимости от положения.

В этом примере общая выполненная работа равна (1/2) (15) (3) + (15) (2) + (1/2) (15) (2) = 22,5 + 30 + 15; работа = 67.5 Дж. Для постепенно изменяющейся силы работа выражается в интегральной форме: Вт = ∫ F · d x.

Кинетическая энергия

Кинетическая энергия — это энергия движущегося объекта. Выражение для кинетической энергии может быть получено из определения работы и кинематических отношений. Рассмотрим силу, приложенную параллельно поверхности, которая перемещает объект с постоянным ускорением.

Исходя из определения работы, второго закона движения Ньютона и кинематики, W = Fx = max и v _f ² = v _o ² + 2 ax , или a = ( v _f ² — v _o ² ) / 2 x .Подставьте последнее выражение для ускорения в выражение для работы, чтобы получить W = m ( v _f ² — v _o ² ) или W = (1/2) мв _f ² — (1/2) мв _o ² . Правая часть последнего уравнения дает определение кинетической энергии: K . E . = (1/2) mv ² Кинетическая энергия — это скалярная величина с теми же единицами, что и работа, джоули (Дж). Например, масса 2 кг, движущаяся со скоростью 3 м / с, имеет кинетическую энергию 9 Дж.

Приведенный выше вывод показывает, что чистая работа равна изменению кинетической энергии. Это соотношение называется теоремой работы-энергии: Вт _нетто = К . E . _f — K . E . _o , где K . E . _f — конечная кинетическая энергия и K . E . _o — исходная кинетическая энергия.

Потенциальная энергия

Потенциальная энергия, , также называемая накопленной энергией, — это способность системы выполнять работу, обусловленную ее положением или внутренней структурой. Примерами могут служить энергия, запасенная в сваях в верхней части его пути, или энергия, запасенная в спиральной пружине.Потенциальная энергия измеряется в джоулях.

Гравитационная потенциальная энергия — энергия положения. Во-первых, рассмотрим потенциальную гравитационную энергию вблизи поверхности земли, где ускорение свободного падения (g) приблизительно постоянно. В этом случае гравитационная потенциальная энергия объекта относительно некоторого опорного уровня составляет P.E . = mgh , где h — вертикальное расстояние над контрольным уровнем.Чтобы поднять объект медленно, сила, равная его весу (мг) , прилагается через высоту (h) . Совершенная работа равна изменению потенциальной энергии: Вт = P . E . _f — P . E . _o = mgh _f — mgh _o , где нижние индексы (f и o) относятся к окончательной и исходной высоте корпуса.

Запуск ракеты в космос требует работы, чтобы разделить массу Земли и ракеты для преодоления силы тяжести. Для больших расстояний от центра Земли вышеприведенное уравнение неадекватно, потому что g непостоянно. Общая форма гравитационной потенциальной энергии — это P.E . = — GMm / r , где M и m относятся к массам двух разделенных тел, а r — это расстояние между центрами масс.Отрицательный знак является результатом выбора нулевого задания при r , равном бесконечности, то есть при очень большом разносе .

Упругая потенциальная энергия — это энергия, запасенная в пружине. Величина силы, необходимой для растяжения пружины, определяется выражением F = — kx , где x — это расстояние растяжения (или сжатия) пружины из ненагруженного положения, а k — это пружинная постоянная. Жесткость пружины — это мера жесткости пружины, при этом более жесткие пружины имеют большие значения k .Потенциальная энергия, запасенная в пружине, определяется как P . E . = (1/2) kx ² .

Изменение потенциальной энергии равно работе. Сила тяжести и сила растяжения пружины — это разные силы; следовательно, приведенные выше уравнения потенциальной энергии для этих двух случаев также могут быть выведены из интегральной формы работы Δ P . E . = Вт = ∫ F · d x.

Мощность

Мощность — это скорость выполнения работы, средняя P = Вт / т , где t — временной интервал, в течение которого выполняется работа (Вт) .Другая форма мощности находится из Вт = F Δ x и замены средней скорости объекта за время т на Δ x / т : среднее P = F Δ x / Δ t = F (в среднем v ).

Сохранение энергии

Принцип сохранения энергии — один из самых далеко идущих общих законов физики.В нем говорится, что энергия не создается и не уничтожается, а может быть преобразована из одной формы в другую только в изолированной системе.

Поскольку полная энергия системы всегда остается постоянной, закон сохранения энергии является полезным инструментом для анализа физической ситуации, когда энергия меняет форму. Представьте себе качающийся маятник с незначительными силами трения. На вершине его подъема вся энергия является гравитационной потенциальной энергией из-за высоты над неподвижным положением.Внизу качелей вся энергия преобразована в кинетическую энергию движения. Полная энергия — это сумма кинетической и потенциальной энергий. Он поддерживает одно и то же значение во время движения качелей вперед и назад (см. Рисунок 2).

Рисунок 2

Маятник подчиняется закону сохранения энергии.

В точке C потенциальная энергия зависит от высоты, а остальная часть полной энергии — кинетическая энергия.

Хотя общая энергия сохраняется, кинетическая энергия не требуется. Столкновение двух объектов с сохранением кинетической энергии называется упругим столкновением . сталкивающиеся объекты, взаимодействующие с потерями кинетической энергии из-за потерь на трение или деформации объекта, называются неупругими столкновениями. В макроскопическом мире большинство столкновений неупругие; однако потери кинетической энергии незначительны в почти упругих столкновениях между атомными частицами и субатомными частицами.Для этих случаев закон сохранения количества движения и кинетической энергии дает полезные уравнения.

Рассмотрим простое лобовое упругое столкновение, когда одна масса ( м ₁ ) с заданной скоростью ( v ₁ ) сталкивается со второй массой ( м ₂ ), которая изначально находится в состоянии покоя. Примените законы сохранения количества движения и кинетической энергии, чтобы получить м ₁ v ₁ = м ₁ ′ v ₁ + m ₂ v ₂ ′ и (1/2) м ₁ v ₁ ² = (1/2) м ₁ v ₁ ′ ² + (1 / 2) м ₂ v ′ ₂ ² , где штрихи относятся к скоростям после столкновения.Решение уравнений дает скорости двух масс после взаимодействия:

Поучительны три особых случая:

Для равных масс, где м ₁ = м ₂ , обратите внимание, что v ₁ ′ становится равным нулю, а v ₂ ′ равно v ₁ ; таким образом, при равных массах объекты просто обмениваются скоростями, как это иногда наблюдается с шарами для пула. (Шары для пула имеют энергию вращения и несколько неупругие столкновения, поэтому их поведение только приближается к примеру.)

Если м ₂ является массивным, числитель и знаменатель почти совпадают в уравнении для v ₁ ′. Тогда v ₁ ′ примерно равно v ₁ , но в противоположном направлении. Знаменатель выражения для v ₂ ′ будет настолько большим, что скорость второй массы после столкновения будет небольшой. Другими словами, входящая масса ( м, , _{, 1} ) отскочит от второй массы почти с начальной скоростью, а ударная масса ( м, , _{, 2,} ) будет медленно перемещаться после столкновения.

Если m ₁ является массивным, то v ₁ ′ примерно равно v ₁ , а v ₂ ′ почти вдвое больше v ₁ ; или падающая массивная частица продолжает двигаться почти с той же скоростью, а ударная масса движется вперед со скоростью, почти в два раза превышающей начальную скорость первой массы после столкновения.

Центр масс

Концепция центра масс (CM) полезна для анализа движения системы частиц.Система частиц действует так, как будто вся ее масса сосредоточена в КМ. В отсутствие внешней силы, если ЦМ системы находится в состоянии покоя, тогда он будет оставаться в покое, а если он изначально находится в движении, он будет поддерживать это движение. Другими словами, КМ движется в соответствии со вторым законом Ньютона. Координаты центра масс x и y равны

.

Рассмотрим предыдущий пример лобового столкновения двух равных масс, которые слиплись после столкновения.КМ изначально движется с постоянной скоростью и сохраняет ту же скорость после столкновения. Когда первая масса катится ко второй массе, CM всегда находится посередине между двумя массами. Перед столкновением КМ преодолевает половину расстояния приближающегося объекта за одно и то же время, и, следовательно, скорость КМ составляет половину начальной скорости приходящей массы. В тот момент, когда две массы взаимодействуют, CM находится прямо между двумя объектами. После столкновения массы слипаются и имеют половину начальной скорости, потому что эффективная масса удвоилась.CM продолжает оставаться на полпути между массами. Он сохраняет ту же скорость (1/2) v _o после столкновения. На рисунке движущийся белый шар ударяется о неподвижный черный шар. Пронумерованные и обведенные кружком позиции CM соответствуют пронумерованным позициям шаров.

Рисунок 3

Неупругое столкновение двух шаров.

Doing Work — Физика тела: движение к метаболизму

Мы начали предыдущий блок с обсуждения движений Джолин во время смены на медицинском этаже больницы, включая все ее запуски и остановки.Когда Джолин стоит на месте, у нее нулевая кинетическая энергия. Когда она делает шаг, чтобы начать ходить, у нее появляется кинетическая энергия. Джолин должна была обеспечивать эту энергию изнутри. Когда Джолин останавливается, ее кинетическая энергия передается тепловой энергии за счет трения. Когда она снова начнет ходить, ей нужно будет снова подавать новую кинетическую энергию. Даже если Джолин идет непрерывно, каждый шаг, который она делает, включает в себя два неупругих столкновения (отталкивание и приземление), поэтому кинетическая энергия постоянно преобразуется в тепловую.Чтобы оставаться в движении, Джолин необходимо восполнить эту кинетическую энергию. Хождение в течение всей смены расходует запасенную энергию Джолин, поэтому она устает.

Количество энергии, переданное от одной формы к другой и / или от одного объекта к другому, называется работой. Выполнение работы — это акт передачи этой энергии. Выполнение работы требует приложения силы на некотором расстоянии. Знак выполненной работы на объекте определяет, передается ли энергия в или из объекта.Например, спортсмен справа выполняет положительную работу над шестом, потому что он прилагает силу в том же направлении, что и движение шеста. Это приведет к ускорению полюса и увеличению кинетической энергии полюса. Атлет слева выполняет отрицательную работу над шестом, потому что прилагаемая им сила имеет тенденцию уменьшать энергию шеста.

Инсунаур, или спорт с толканием стержней, — это игра коренных народов Мизорама, одного из северо-восточных штатов Индии. Сила, приложенная в том же направлении, что и движение объекта, совершает положительную работу.Сила, приложенная в направлении, противоположном движению, совершает отрицательную работу. Изображение адаптировано из книги Х. Тхангчунгнунги «Инсунаур» («Спорт с толканием штанги») через Wikimedia Commons.

Положительный или отрицательный знак работы относится к передаче энергии внутрь или из объекта, а не к противоположным направлениям в пространстве, поэтому работа не является вектором, и мы не будем выделять ее жирным шрифтом в уравнениях.

Фактический объем выполненной работы рассчитывается исходя из комбинации средней силы и расстояния, на котором она применяется, и угла между ними:

(1)

Повседневный пример: подъем пациента

Джолин вместе с двумя другими медсестрами поднимает пациента весом 867 N (190 фунтов ) на расстояние 0.5 м по прямой . Сколько работы она сделала? Если предположить, что Джолин подняла 1/3 веса пациента, ей нужно было приложить восходящую силу 289 Н . Пациент также двигался вверх, поэтому угол между силой и движением составлял 0 °. Ввод этих значений в уравнение работы:

Мы видим, что работа имеет единицы Нм, , которые называются Джоулями ( Дж, ). Работа и все другие формы энергии имеют одинаковые единицы, потому что работа — это количество энергии, но работа — это не вид энергии.При расчете работы учитывается направление силы, поэтому мы используем только величину силы ( F ) в уравнении, поэтому мы не выделили силу жирным шрифтом в уравнении работы.

Уравнение работы автоматически сообщает нам, передает ли работа энергию в конкретный объект или из него:

1. Сила, приложенная к объекту в направлении, противоположном его движению, будет иметь тенденцию замедлять его и, таким образом, передавать кинетическую энергию от объекта.Когда энергия покидает объект, работа, выполняемая с объектом, должна быть отрицательной. Угол между движением объекта и силой в этом случае составляет 180 °, и это подтверждается.
2. Сила, приложенная к объекту в том же направлении, что и его движение, будет иметь тенденцию вызывать его ускорение и, таким образом, будет передавать кинетическую энергию объекту. Когда энергия поступает в объект, работа, выполняемая с объектом, должна быть положительной. Угол между движением объекта и силой в этом случае равен 0 °, и это тоже подтверждается.
3. Наконец, если сила действует перпендикулярно движению объекта, она может только изменить его направление движения, но не заставит его ускоряться или замедляться, поэтому кинетическая энергия не изменяется. Такой тип силы не должен работать. Угол между движением объекта и силой в этом случае составляет 90 °, и, опять же, уравнение работы дает требуемый результат. Подробнее об этом конкретном типе ситуаций читайте в главе о невесомости в конце этого раздела.

Уравнение работы дает правильную работу, выполняемую силой, независимо от угла между направлением силы и направлением движения, даже если сила направлена ​​под некоторым углом, отличным от 0 °, 90 ° или 180 °.В таком случае некоторая часть силы будет выполнять работу, а некоторая часть — нет, но это говорит нам, какая часть вектора силы вносит свой вклад в работу.

.