Электрическая проводимость. Определение, единицы измерения.
 Электрическая проводимость характеризует способность тела проводить электрический ток. Проводимость — величина обтаная сопротивлению. В формуле она обратно пропорциональна электрическому сопротивлению, и используются они фактически для обозначения одних и тех же свойств материала. Измеряется проводимость в Сименсах: [См]=[1/Ом].
Электрическая проводимость характеризует способность тела проводить электрический ток. Проводимость — величина обтаная сопротивлению. В формуле она обратно пропорциональна электрическому сопротивлению, и используются они фактически для обозначения одних и тех же свойств материала. Измеряется проводимость в Сименсах: [См]=[1/Ом].
Виды электропроводимости:
— Электронная проводимость, где переносчиками зарядов являются электроны. Такая проводимость характерна в первую очередь для металлов, но присутствует в той или иной степени практически в любых материалах. С увеличением температуры электронная проводимость снижается.
— Ионная проводимость. Существует в газообразных и жидких средах, где имеются свободные ионы, которые также переносят заряды, перемещаясь по объёму среды под действием электромагнитного поля или другого внешнего воздействия. Используется в электролитах. С ростом температуры ионная проводимость увеличивается, поскольку образуется большее количество ионов с высокой энергией, а также снижается вязкость среды.
— Дырочная проводимость. Эта проводимость обуславливается недостатком электронов в кристаллической решётке материала. Фактически, переносят заряд здесь опять же электроны, но они как бы движутся по решётке, занимая последовательно свободные места в ней, в отличии от физического перемещения электронов в металлах. Такой принцип используется в полупроводниках, наряду с электронной проводимостью.

Самыми первыми материалами, которые стали использоваться в электротехнике исторически были металлы и диэлектрики (изоляторы, которым присуща маленькая электрическая проводимость). Сейчас получили широкое применение в электронике полупроводники. Они занимают промежуточное положение между проводниками и диэлектриками и характеризуются тем, что величину электрической проводимости в полупроводниках можно регулировать различным воздействием. Для производства большинства современных проводников используются кремний, германий и углерод. Кроме того, для изготовления ПП могут использоваться другие вещества, но они применяются гораздо реже.
В электротехнике важное значение имеет передача тока с минимальными потерями. В этом отношении важную роль играют металлы с большой электропроводностью и, соответственно, маленьким электросопротивлением. Самым лучшим в этом отношении является серебро (62500000 См/м), далее следуют медь (58100000 См/м), золото (45500000 См/м), алюминий (37000000 См/м). В соответствии с экономической целесообразностью чаще всего используются алюминий и медь, при этом медь по проводимости совсем немного уступает серебру. Все остальные металлы не имеют промышленного значения для производства проводников.
Проводник (физика) — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 2 марта 2015; проверки требуют 32 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 2 марта 2015; проверки требуют 32 правки. У этого термина существуют и другие значения, см. Проводник. Электрический провод с проводником из меди
Электрический провод с проводником из медиПроводни́к — вещество, среда, материал, хорошо проводящие электрический ток[1][2].
В проводнике имеется большое число свободных носителей заряда, то есть заряженных частиц, которые могут свободно перемещаться внутри объёма проводника и под действием приложенного к проводнику электрического напряжения создают ток проводимости[3]
С точки зрения электродинамики проводник — среда с большим на рассматриваемой частоте значением тангенса угла диэлектрических потерь (tgδ >> 1)[4], в такой среде сила тока проводимости много больше силы тока смещения. При этом под идеальным проводником (сверхпроводником) понимают среду с бесконечно большим значением tgδ, прочие проводники называют реальными или проводниками с потерями.
Проводниками называют также части электрических цепей — соединительные провода[5], металлические шины и др.
Среди наиболее распространённых твёрдых проводников известны металлы, полуметаллы, углерод (в виде угля и графита). Пример проводящих жидкостей при нормальных условиях — ртуть, электролиты, при высоких температурах — расплавы металлов. Пример проводящих газов — ионизированный газ (плазма). Некоторые вещества, при нормальных условиях являющиеся изоляторами, при внешних воздействиях могут переходить в проводящее состояние, а именно проводимость полупроводников может сильно варьироваться при изменении температуры, освещённости, легировании и т. п.
Микроскопическое описание проводников связано с электронной теорией металлов. Наиболее простая модель описания проводимости известна с начала прошлого века и была развита Друде.
Проводники, в которых преобладает электронная проводимость, обусловленная движением электронов, относят к проводникам первого рода. К проводникам второго рода относят проводники с ионной проводимостью (электролиты).
- Жан М. Рабаи, Ананта Чандракасан, Боривож Николич. 4. Проводник // Цифровые интегральные схемы. Методология проектирования = Digital Integrated Circuits. — 2-ое изд. — М.: Вильямс, 2007. — С. 912. — ISBN 0-13-090996-3.
Электрическое сопротивление и проводимость
Дата публикации: .
Категория: Электротехника.
При замыкании электрической цепи, на зажимах которой имеется разность потенциалов, возникает электрический ток. Свободные электроны под влиянием электрических сил поля перемещаются вдоль проводника. В своем движении электроны наталкиваются на атомы проводника и отдают им запас своей кинетической энергии. Скорость движения электронов непрерывно изменяется: при столкновении электронов с атомами, молекулами и другими электронами она уменьшается, потом под действием электрического поля увеличивается и снова уменьшается при новом столкновении. В результате этого в проводнике устанавливается равномерное движение потока электронов со скоростью нескольких долей сантиметра в секунду. Следовательно, электроны, проходя по проводнику, всегда встречают с его стороны сопротивление своему движению. При прохождении электрического тока через проводник последний нагревается.
Электрическое сопротивление
Электрическим сопротивлением проводника, которое обозначается латинской буквой r, называется свойство тела или среды превращать электрическую энергию в тепловую при прохождении по нему электрического тока.
На схемах электрическое сопротивление обозначается так, как показано на рисунке 1, а.
 |
| Рисунок 1. Условное обозначение электрического сопротивления |
Переменное электрическое сопротивление, служащее для изменения тока в цепи, называется реостатом. На схемах реостаты обозначаются как показано на рисунке 1, б. В общем виде реостат изготовляется из проволоки того или иного сопротивления, намотанной на изолирующем основании. Ползунок или рычаг реостата ставится в определенное положение, в результате чего в цепь вводится нужное сопротивление.
Длинный проводник малого поперечного сечения создает току большое сопротивление. Короткие проводники большого поперечного сечения оказывают току малое сопротивление.
Если взять два проводника из разного материала, но одинаковой длины и сечения, то проводники будут проводить ток по-разному. Это показывает, что сопротивление проводника зависит от материала самого проводника.
Температура проводника также оказывает влияние на его сопротивление. С повышением температуры сопротивление металлов увеличивается, а сопротивление жидкостей и угля уменьшается. Только некоторые специальные металлические сплавы (манганин, констаитан, никелин и другие) с увеличением температуры своего сопротивления почти не меняют.
Итак, мы видим, что электрическое сопротивление проводника зависит от: 1) длины проводника, 2) поперечного сечения проводника, 3) материала проводника, 4) температуры проводника.
За единицу сопротивления принят один Ом. Ом часто обозначается греческой прописной буквой Ω (омега). Поэтому вместо того чтобы писать «Сопротивление проводника равно 15 Ом», можно написать просто: r = 15 Ω.
1 000 Ом называется 1 килоом (1кОм, или 1кΩ),
1 000 000 Ом называется 1 мегаом (1мгОм, или 1МΩ).
При сравнении сопротивления проводников из различных материалов необходимо брать для каждого образца определенную длину и сечение. Тогда мы сможем судить о том, какой материал лучше или хуже проводит электрический ток.
Видео 1. Сопротивление проводников
Удельное электрическое сопротивление
Сопротивление в омах проводника длиной 1 м, сечением 1 мм² называется удельным сопротивлением и обозначается греческой буквой ρ (ро).
В таблице 1 даны удельные сопротивления некоторых проводников.
Таблица 1
Удельные сопротивления различных проводников
| Материал проводника | Удельное сопротивление ρ в  |
| Серебро Медь Алюминий Вольфрам Железо Свинец Никелин (сплав меди, никеля и цинка) Манганин (сплав меди, никеля и марганца) Константан (сплав меди, никеля и алюминия) Ртуть Нихром (сплав никеля, хрома, железа и марганца) | 0,016 0,0175 0,03 0,05 0,13 0,2 0,42 0,43 0,5 0,94 1,1 |
Из таблицы видно, что железная проволока длиной 1 м и сечением 1 мм² обладает сопротивлением 0,13 Ом. Чтобы получить 1 Ом сопротивления нужно взять 7,7 м такой проволоки. Наименьшим удельным сопротивлением обладает серебро. 1 Ом сопротивления можно получить, если взять 62,5 м серебряной проволоки сечением 1 мм². Серебро – лучший проводник, но стоимость серебра исключает возможность его массового применения. После серебра в таблице идет медь: 1 м медной проволоки сечением 1 мм² обладает сопротивлением 0,0175 Ом. Чтобы получить сопротивление в 1 Ом, нужно взять 57 м такой проволоки.
Химически чистая, полученная путем рафинирования, медь нашла себе повсеместное применение в электротехнике для изготовления проводов, кабелей, обмоток электрических машин и аппаратов. Широко применяют также в качестве проводников алюминий и железо.
Сопротивление проводника можно определить по формуле:

где r – сопротивление проводника в омах; ρ – удельное сопротивление проводника; l – длина проводника в м; S – сечение проводника в мм².
Пример 1. Определить сопротивление 200 м железной проволоки сечением 5 мм².

Пример 2. Вычислить сопротивление 2 км алюминиевой проволоки сечением 2,5 мм².

Из формулы сопротивления легко можно определить длину, удельное сопротивление и сечение проводника.
Пример 3. Для радиоприемника необходимо намотать сопротивление в 30 Ом из никелиновой проволоки сечением 0,21 мм². Определить необходимую длину проволоки.

Пример 4. Определить сечение 20 м нихромовой проволоки, если сопротивление ее равно 25 Ом.

Пример 5. Проволока сечением 0,5 мм² и длиной 40 м имеет сопротивление 16 Ом. Определить материал проволоки.
Материал проводника характеризует его удельное сопротивление.

По таблице удельных сопротивлений находим, что таким сопротивлением обладает свинец.
Выше было указано, что сопротивление проводников зависит от температуры. Проделаем следующий опыт. Намотаем в виде спирали несколько метров тонкой металлической проволоки и включим эту спираль в цепь аккумулятора. Для измерения тока в цепь включаем амперметр. При нагревании спирали в пламени горелки можно заметить, что показания амперметра будут уменьшаться. Это показывает, что с нагревом сопротивление металлической проволоки увеличивается.
У некоторых металлов при нагревании на 100° сопротивление увеличивается на 40 – 50 %. Имеются сплавы, которые незначительно меняют свое сопротивление с нагревом. Некоторые специальные сплавы практически не меняют сопротивления при изменении температуры. Сопротивление металлических проводников при повышении температуры увеличивается, сопротивление электролитов (жидких проводников), угля и некоторых твердых веществ, наоборот, уменьшается.
Способность металлов менять свое сопротивление с изменением температуры используется для устройства термометров сопротивления. Такой термометр представляет собой платиновую проволоку, намотанную на слюдяной каркас. Помещая термометр, например, в печь и измеряя сопротивление платиновой проволоки до и после нагрева, можно определить температуру в печи.
Изменение сопротивления проводника при его нагревании, приходящееся на 1 Ом первоначального сопротивления и на 1° температуры, называется температурным коэффициентом сопротивления и обозначается буквой α.
Если при температуре t0 сопротивление проводника равно r0, а при температуре t равно rt, то температурный коэффициент сопротивления

Примечание. Расчет по этой формуле можно производить лишь в определенном интервале температур (примерно до 200°C).
Приводим значения температурного коэффициента сопротивления α для некоторых металлов (таблица 2).
Таблица 2
Значения температурного коэффициента для некоторых металлов
| Металл | α |
| Металл | α |
| Серебро Медь Железо Вольфрам Платина | 0,0035 0,0040 0,0066 0,0045 0,0032 | Ртуть Никелин Константан Нихром Манганин | 0,0090 0,0003 0,000005 0,00016 0,00005 |
Из формулы температурного коэффициента сопротивления определим rt:
rt = r0 [1 ± α (t – t0)].
Пример 6. Определить сопротивление железной проволоки, нагретой до 200°C, если сопротивление ее при 0°C было 100 Ом.
rt = r0 [1 ± α (t – t0)] = 100 (1 + 0,0066 × 200) = 232 Ом.
Пример 7. Термометр сопротивления, изготовленный из платиновой проволоки, в помещении с температурой 15°C имел сопротивление 20 Ом. Термометр поместили в печь и через некоторое время было измерено его сопротивление. Оно оказалось равным 29,6 Ом. Определить температуру в печи.

Электрическая проводимость
До сих пор мы рассматривали сопротивление проводника как препятствие, которое оказывает проводник электрическому току. Но все же ток по проводнику проходит. Следовательно, кроме сопротивления (препятствия), проводник обладает также способностью проводить электрический ток, то есть проводимостью.
Чем большим сопротивлением обладает проводник, тем меньшую он имеет проводимость, тем хуже он проводит электрический ток, и, наоборот, чем меньше сопротивление проводника, тем большей проводимостью он обладает, тем легче току пройти по проводнику. Поэтому сопротивление и проводимость проводника есть величины обратные.
Из математики известно, что число, обратное 5, есть 1/5 и, наоборот, число, обратное 1/7, есть 7. Следовательно, если сопротивление проводника обозначается буквой r, то проводимость определяется как 1/r. Обычно проводимость обозначается буквой g.
Электрическая проводимость измеряется в (1/Ом) или в сименсах.
Пример 8. Сопротивление проводника равно 20 Ом. Определить его проводимость.
Если r = 20 Ом, то

Пример 9. Проводимость проводника равна 0,1 (1/Ом). Определить его сопротивление,
Если g = 0,1 (1/Ом), то r = 1 / 0,1 = 10 (Ом)
Источник: Кузнецов М. И., «Основы электротехники» – 9-е издание, исправленное – Москва: Высшая школа, 1964 – 560с.
Полупроводник — Википедия
Монокристаллический кремний — полупроводниковый материал, наиболее широко используемый в промышленности сегодня.Полупроводни́к — материал, по удельной проводимости занимающий промежуточное место между проводниками и диэлектриками, и отличающийся от проводников сильной зависимостью удельной проводимости от концентрации примесей, температуры и воздействия различных видов излучения. Основным свойством полупроводников является увеличение электрической проводимости с ростом температуры
Полупроводниками являются кристаллические вещества, ширина запрещённой зоны которых составляет порядка электрон-вольта (эВ). Например, алмаз можно отнести к широкозонным полупроводникам (около 7 эВ), а арсенид индия — к узкозонным (0,35 эВ). К числу полупроводников относятся многие химические элементы (германий, кремний, селен, теллур, мышьяк и другие), огромное количество сплавов и химических соединений (арсенид галлия и др.).
Атом другого химического элемента в чистой кристаллической решётке (например, атом фосфора, бора и т. д. в кристалле кремния) называется примесью. В зависимости от того, отдаёт ли примесной атом электрон в кристалл (в вышеприведённом примере – фосфор) или захватывает его (бор), примесные атомы называют донорными или акцепторными. Характер примеси может меняться в зависимости от того, какой атом кристаллической решётки она замещает, в какую кристаллографическую плоскость встраивается.
Проводимость полупроводников сильно зависит от температуры. Вблизи температуры абсолютного нуля полупроводники имеют свойства диэлектриков.
Механизм электрической проводимости[править | править код]
Дырка[править | править код]
Во время разрыва связи между электроном и ядром появляется свободное место в электронной оболочке атома. Это обуславливает переход электрона с другого атома на атом со свободным местом. На атом, откуда перешёл электрон, входит другой электрон из другого атома и т. д. Этот процесс обуславливается ковалентными связями атомов. Таким образом, происходит перемещение положительного заряда без перемещения самого атома. Этот условный положительный заряд называют дыркой.
Обычно подвижность дырок в полупроводнике ниже подвижности электронов.
Энергетические зоны[править | править код]
Между зоной проводимости Еп и валентной зоной Ев расположена зона запрещённых значений энергии электронов Ез. Разность Еп−Ев равна ширине запрещенной зоны Ез. С ростом ширины Ез число электронно-дырочных пар и проводимость собственного полупроводника уменьшается, а удельное сопротивление возрастает.
Подвижность[править | править код]

Подвижностью μ{\displaystyle \mu } называют коэффициент пропорциональности между дрейфовой скоростью v→{\displaystyle {\vec {v}}} носителей тока и величиной приложенного электрического поля E→{\displaystyle {\vec {E}}}:
- v→=μE→.{\displaystyle {\vec {v}}=\mu {\vec {E}}.}
При этом, вообще говоря, подвижность является тензором:
- vα=μαβEβ.{\displaystyle \ v_{\alpha }=\mu _{\alpha \beta }E_{\beta }.}
Подвижность электронов и дырок зависит от их концентрации в полупроводнике (см. рисунок). При большой концентрации носителей заряда вероятность столкновения между ними вырастает, что приводит к уменьшению подвижности и проводимости.
Размерность подвижности — м²/(В·с) в СИ или см/(В·с)в системе СГС.
При термодинамическом равновесии, концентрация электронов полупроводника связана с температурой следующим соотношением:
- n¯=2h4(2πmkT)3/2e−EC−EFkT{\displaystyle {\bar {n}}={\frac {2}{h^{3}}}(2\pi mkT)^{3/2}e^{-{\frac {E_{C}-E_{F}}{kT}}}}
где:
- h{\displaystyle h} — Постоянная Планка;
- m{\displaystyle m} — масса электрона;
- T{\displaystyle T} — абсолютная температура;
- EC{\displaystyle E_{C}} — уровень зоны проводимости;
- EF{\displaystyle E_{F}} — уровень Ферми.
Также, концентрация дырок полупроводника связана с температурой следующим соотношением:
- p¯=2h4(2πmkT)3/2e−EF−EVkT{\displaystyle {\bar {p}}={\frac {2}{h^{3}}}(2\pi mkT)^{3/2}e^{-{\frac {E_{F}-E_{V}}{kT}}}}
где:
- h{\displaystyle h} — Постоянная Планка.
- m{\displaystyle m} — эффективная масса дырки;
- T{\displaystyle T} — абсолютная температура;
- EF{\displaystyle E_{F}} — уровень Ферми;
- EV{\displaystyle E_{V}} — уровень валентной зоны.
Собственная концентрация ni{\displaystyle n_{i}} связана с n¯{\displaystyle {\bar {n}}} и p¯{\displaystyle {\bar {p}}} следующим соотношением:
- n¯p¯=ni2{\displaystyle {\bar {n}}{\bar {p}}=n_{i}^{2}}
По характеру проводимости[править | править код]
Собственная проводимость[править | править код]
Полупроводники, в которых свободные электроны и «дырки» появляются в процессе ионизации атомов, из которых построен весь кристалл, называют полупроводниками с собственной проводимостью. В полупроводниках с собственной проводимостью концентрация свободных электронов равняется концентрации «дырок».
Проводимость связана с подвижностью частиц следующим соотношением:
- σ=1ρ=q(Nnμn+Npμp){\displaystyle \sigma ={\frac {1}{\rho }}=q(N_{\rm {n}}\mu _{\rm {n}}+N_{\rm {p}}\mu _{\rm {p}})}
где ρ{\displaystyle \rho } — удельное сопротивление, μn{\displaystyle \mu _{\rm {n}}} — подвижность электронов, μp{\displaystyle \mu _{\rm {p}}} — подвижность дырок, Nn,p{\displaystyle N_{n,p}} — их концентрация, q — элементарный электрический заряд (1,602⋅10−19 Кл).
Для собственного полупроводника концентрации носителей совпадают и формула принимает вид:
- σ=1ρ=qN(μn+μp){\displaystyle \sigma ={\frac {1}{\rho }}=qN(\mu _{\rm {n}}+\mu _{\rm {p}})}
Примесная проводимость[править | править код]
Для создания полупроводниковых приборов часто используют кристаллы с примесной проводимостью. Такие кристаллы изготавливаются с помощью внесения примесей с атомами трехвалентного или пятивалентного химического элемента.
По виду проводимости[править | править код]
Электронные полупроводники (n-типа)[править | править код]
Термин «n-тип» происходит от слова «negative», обозначающего отрицательный заряд основных носителей. Этот вид полупроводников имеет примесную природу. В четырёхвалентный полупроводник (например, кремний) добавляют примесь пятивалентного полупроводника (например, мышьяка). В процессе взаимодействия каждый атом примеси вступает в ковалентную связь с атомами кремния. Однако для пятого электрона атома мышьяка нет места в насыщенных валентных связях, и он переходит на дальнюю электронную оболочку. Там для отрыва электрона от атома нужно меньшее количество энергии. Электрон отрывается и превращается в свободный. В данном случае перенос заряда осуществляется электроном, а не дыркой, то есть данный вид полупроводников проводит электрический ток подобно металлам. Примеси, которые добавляют в полупроводники, вследствие чего они превращаются в полупроводники n-типа, называются донорными.
Проводимость N-полупроводников приблизительно равна:
- σ≈qNnμn{\displaystyle \sigma \approx qN_{\rm {n}}\mu _{\rm {n}}}
Дырочные полупроводники (р-типа)[править | править код]
Термин «p-тип» происходит от слова «positive», обозначающего положительный заряд основных носителей. Этот вид полупроводников, кроме примесной основы, характеризуется дырочной природой проводимости. В четырёхвалентный полупроводник (например, в кремний) добавляют небольшое количество атомов трехвалентного элемента (например, индия). Каждый атом примеси устанавливает ковалентную связь с тремя соседними атомами кремния. Для установки связи с четвёртым атомом кремния у атома индия нет валентного электрона, поэтому он захватывает валентный электрон из ковалентной связи между соседними атомами кремния и становится отрицательно заряженным ионом, вследствие чего образуется дырка. Примеси, которые добавляют в этом случае, называются акцепторными.
Проводимость p-полупроводников приблизительно равна:
- σ≈qNpμp{\displaystyle \sigma \approx qN_{\rm {p}}\mu _{\rm {p}}}
Полупроводниковый диод[править | править код]
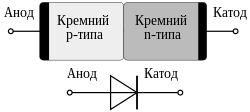 Схема полупроводникового кремниевого диода. Ниже приведено его символическое изображение на электрических принципиальных схемах.
Схема полупроводникового кремниевого диода. Ниже приведено его символическое изображение на электрических принципиальных схемах.Полупроводниковый диод состоит из двух типов полупроводников — дырочного и электронного. В процессе контакта между этими областями из области с полупроводником n-типа в область с полупроводником p-типа проходят электроны, которые затем рекомбинируют с дырками. Вследствие этого возникает электрическое поле между двумя областями, что устанавливает предел деления полупроводников — так называемый p-n переход. В результате в области с полупроводником p-типа возникает некомпенсированный заряд из отрицательных ионов, а в области с полупроводником n-типа возникает некомпенсированный заряд из положительных ионов. Разница между потенциалами достигает 0,3-0,6 В.
Связь между разницей потенциалов и концентрацией примесей выражается следующей формулой:
- φ=VTln(NnNpni2){\displaystyle \varphi =V_{\rm {T}}\ln \left({\frac {N_{\rm {n}}N_{\rm {p}}}{n_{\rm {i}}^{2}}}\right)}
где VT{\displaystyle V_{\rm {T}}} — термодинамическое напряжение, Nn{\displaystyle N_{\rm {n}}} — концентрация электронов, Np{\displaystyle N_{\rm {p}}} — концентрация дырок, ni{\displaystyle n_{\rm {i}}} — собственная концентрация[2].
В процессе подачи напряжения плюсом на p-полупроводник и минусом на n-полупроводник внешнее электрическое поле будет направлено против внутреннего электрического поля p-n перехода и при достаточном напряжении электроны преодолеют p-n переход, и в цепи диода появится электрический ток (прямая проводимость, диод пропускает максимальный электрический ток).При подаче напряжения минусом на область с полупроводником p-типа и плюсом на область с полупроводником n-типа между двумя областями возникает область, которая не имеет свободных носителей электрического тока (обратная проводимость, диод сопротивляется пропусканию электрического тока). Обратный ток полупроводникового диода близок к нулю, но не равен нулю, так как в обеих областях всегда есть неосновные носители заряда. Для этих носителей p-n переход будет открыт.
Таким образом, p-n переход проявляет свойства односторонней проводимости, что обуславливается подачей напряжения с различной полярностью. Это свойство используют для выпрямления переменного тока.
Транзистор[править | править код]
Структура биполярного n-p-n транзистора.Транзистор — полупроводниковое устройство, которое состоит из двух областей с полупроводниками p- или n-типа, между которыми находится область с полупроводником n- или p-типа. Таким образом, в транзисторе есть две области p-n перехода.
Типы полупроводников в периодической системе элементов[править | править код]
В нижеследующей таблице представлена информация о большом количестве полупроводниковых элементов и их соединений, разделённых на несколько типов:
- одноэлементные полупроводники IV группы периодической системы элементов,
- сложные: двухэлементные AIIIBV и AIIBVI из третьей и пятой группы и из второй и шестой группы элементов соответственно.
Все типы полупроводников обладают интересной зависимостью ширины запрещённой зоны от периода, а именно — с увеличением периода ширина запрещённой зоны уменьшается.
| Группа | IIB | IIIA | IVA | VA | VIA |
| Период | |||||
| 2 | 5 B | 6 C | 7 N | ||
| 3 | 13 Al | 14 Si | 15 P | 16 S | |
| 4 | 30 Zn | 31 Ga | 32 Ge | 33 As | 34 Se |
| 5 | 48 Cd | 49 In | 50 Sn | 51 Sb | 52 Te |
| 6 | 80 Hg |
Физические явления в полупроводниках[править | править код]
 Диаграмма заполнения электронных уровней энергии в различных типах материалов в равновесном состоянии. На рисунке по высоте условно показана энергия, а ширина фигур — плотность состояний для данной энергии в указанном материале.
Диаграмма заполнения электронных уровней энергии в различных типах материалов в равновесном состоянии. На рисунке по высоте условно показана энергия, а ширина фигур — плотность состояний для данной энергии в указанном материале.Полутона соответствует распределению Ферми — Дирака (черный — все состояния заполнены, белый — состояние пустое).
В металлах и полуметаллах уровень Ферми EF{\displaystyle E_{F}} находится внутри, по меньшей мере, одной разрешённой зоны. В диэлектриках и полупроводниках уровень Ферми находится внутри запрещённой зоны, но в полупроводниках зоны находятся достаточно близко к уровню Ферми для заполнения их электронами или дырками в результате теплового движения частиц.
Физические свойства полупроводников наиболее изучены по сравнению с металлами и диэлектриками. В немалой степени этому способствует огромное количество физических эффектов, которые не наблюдаемы ни в тех, ни в других веществах и связаны с устройством зонной структуры полупроводников и с достаточно узкой запрещённой зоной.
Основным стимулом для изучения полупроводниковых материалов является производство полупроводниковых приборов и интегральных микросхем — это в первую очередь относится к кремнию, но затрагивает и другие полупроводниковые материалы (Ge, GaAs, InP, InSb).
Кремний — непрямозонный полупроводник, оптэлектрические свойства которого широко используются для создания фотодиодов и солнечных батарей, однако на основе кремния трудно создать источник излучения и здесь используются прямозонные полупроводники — соединения типа AIIIBV, среди которых можно выделить GaAs, GaN, которые используются для создания светодиодов и полупроводниковых лазеров.
Собственный полупроводник при температуре абсолютного нуля не имеет свободных носителей в зоне проводимости в отличие от проводников и ведёт себя как диэлектрик. При сильном легировании ситуация может поменяться (см. вырожденные полупроводники).
Легирование[править | править код]
Электрические свойства полупроводника могут сильно зависеть от дефектов в кристаллической структуре. Поэтому стремятся использовать очень чистые вещества, в основном, для электронной промышленности.
Легирующие примеси вводят для управления величиной и типом проводимости полупроводника. Например, широко применяемый кремний можно легировать элементами V подгруппы периодической системы элементов — фосфором, мышьяком которые являются донорами и получить кремний с электронным типом проводимости (n-Si). Для получения кремния с дырочным типом проводимости (p-Si) используют элементы III подгруппы бор или алюминий (акцептор). Также получают компенсированные полупроводники для расположения уровня Ферми в середине запрещённой зоны.
Свойства полупроводников зависят от способа получения, так как различные примеси в процессе роста могут изменить их. Наиболее дешёвый способ промышленного получения монокристаллического технологического кремния — метод Чохральского. Для очистки технологического кремния используют также метод зонной плавки.
Для получения монокристаллов полупроводников используют различные методы физического и химического осаждения. Наиболее прецизионный и дорогой инструмент в руках технологов для роста монокристаллических плёнок — установки молекулярно-лучевой эпитаксии, позволяющей выращивать кристалл с точностью до монослоя.
Поглощение света полупроводниками обусловлено переходами между энергетическими состояниями зонной структуры. Учитывая принцип запрета Паули, электроны могут переходить только из заполненного энергетического уровня на незаполненный. В собственном полупроводнике все состояния валентной зоны заполнены, а все состояния зоны проводимости незаполненные, поэтому переходы возможны лишь из валентной зоны в зону проводимости. Для осуществления такого перехода электрон должен получить от света энергию, превышающую ширину запрещённой зоны. Фотоны с меньшей энергией не вызывают переходов между электронными состояниями полупроводника, поэтому такие полупроводники прозрачны в области частот ω<Eg/ℏ{\displaystyle \omega <E_{g}/\hbar } , где Eg{\displaystyle E_{g}} — ширина запрещённой зоны, ℏ{\displaystyle \hbar } — постоянная Планка. Эта частота определяет фундаментальный край поглощения для полупроводника. Для полупроводников, которые зачастую применяются в электронике (кремний, германий, арсенид галлия) она лежит в инфракрасной области спектра.
Дополнительные ограничения на поглощение света полупроводников накладывают правила отбора, в частности закон сохранения импульса. Закон сохранения импульса требует, чтобы квазиимпульс конечного состояния отличался от квазиимпульса начального состояния на величину импульса поглощённого фотона. Волновое число фотона 2π/λ{\displaystyle 2\pi /\lambda }, где λ{\displaystyle \lambda } — длина волны, очень мало по сравнению с волновым вектором обратной решётки полупроводника, или, что то же самое, длина волны фотона в видимой области намного больше характерного межатомного расстояния в полупроводнике, что приводит к требованию того, чтобы квазиимпульс конечного состояния при электронном переходе практически равнялся квазиимпульсу начального состояния. При частотах, близких к фундаментальному краю поглощения, это возможно только для прямозонных полупроводников. Оптические переходы в полупроводниках, при которых импульс электрона почти не меняется называются прямыми или вертикальными. Импульс конечного состояния может значительно отличаться от импульса начального состояния, если в процессе поглощения фотона участвует ещё одна, третья частица, например, фонон. Такие переходы тоже возможны, хотя и менее вероятны. Они называются непрямыми переходами.
Таким образом, прямозонные полупроводники, такие как арсенид галлия, начинают сильно поглощать свет, когда энергия кванта превышает ширину запрещённой зоны. Такие полупроводники очень удобны для использования в оптоэлектронике.
Непрямозонные полупроводники, например, кремний, поглощают в области частот света с энергией кванта чуть больше ширины запрещённой зоны значительно слабее, только благодаря непрямым переходам, интенсивность которых зависит от присутствия фононов, и следовательно, от температуры. Граничная частота прямых переходов кремния больше 3 эВ, то есть лежит в ультрафиолетовой области спектра.
При переходе электрона из валентной зоны в зону проводимости в полупроводнике возникают свободные носители заряда, а следовательно фотопроводимость.
При частотах ниже края фундаментального поглощения также возможно поглощение света, которое связано с возбуждением экситонов, электронными переходами между уровнями примесей и разрешенными зонами, а также с поглощением света на колебаниях решётки и свободных носителях. Экситонные зоны расположены в полупроводнике несколько ниже дна зоны проводимости благодаря энергии связи экситона. Экситонные спектры поглощения имеют водородоподобную структуру энергетических уровней. Аналогичным образом примеси, акцепторы или доноры, создают акцепторные или донорные уровни, лежащие в запрещённой зоне. Они значительно модифицируют спектр поглощения легированного полупроводника. Если при непрямозонном переходе одновременно с квантом света поглощается фонон, то энергия поглощенного светового кванта может быть меньше на величину энергии фонона, что приводит к поглощению на частотах несколько ниже по энергии от фундаментального края поглощения.
Полупроводниковые соединения делят на несколько типов:
- простые полупроводниковые материалы — собственно химические элементы: бор B, углерод C, германий Ge, кремний Si, селен Se, сера S, сурьма Sb, теллур Te и йод I. Самостоятельное применение широко нашли германий, кремний и селен. Остальные чаще всего применяются в качестве легирующих добавок или в качестве компонентов сложных полупроводниковых материалов;
- в группу сложных полупроводниковых материалов входят химические соединения из двух, трёх и более химических элементов. Полупроводниковые материалы из двух элементов называют бинарными, и так же, как это принято в химии, имеют наименование того компонента, металлические свойства которого выражены слабее. Так, бинарные соединения, содержащие мышьяк, называют арсенидами, серу — сульфидами, теллур — теллуридами, углерод —
Широкое применение получили следующие соединения:
- AIIIBV
- InSb, InAs, InP, GaSb, GaP, AlSb, GaN, InN
- AIIBV
- AIIBVI
- ZnS, ZnSe, ZnTe, CdS, CdTe, HgSe, HgTe, HgS
- AIVBVI
- PbS, PbSe, PbTe, SnTe, SnS, SnSe, GeS, GeSe
а также некоторые окислы свинца, олова, германия, кремния а также феррит, аморфные стёкла и многие другие соединения (AIBIIIC2VI, AIBVC2VI, AIIBIVC2V, AIIB2IIC4VI, AIIBIVC3VI).
На основе большинства из приведённых бинарных соединений возможно получение их твёрдых растворов: (CdTe)x(HgTe)1-x, (HgTe)x(HgSe)1-x, (PbTe)x(SnTe)1-x, (PbSe)x(SnSe)1-x и других.
Соединения AIIIBV, в основном, применяются для изделий электронной техники, работающих на сверхвысоких частотах
Соединения AIIBV используют в качестве люминофоров видимой области, светодиодов, датчиков Холла, модуляторов.
Соединения AIIIBV, AIIBVI и AIVBVI применяют при изготовлении источников и приёмников света, индикаторов и модуляторов излучений.
Окисные полупроводниковые соединения применяют для изготовления фотоэлементов, выпрямителей и сердечников высокочастотных индуктивностей.
| Параметры | AlSb | GaSb | InSb | AlAs | GaAs | InAs |
|---|---|---|---|---|---|---|
| Температура плавления, К | 1333 | 998 | 798 | 1873 | 1553 | 1218 |
| Постоянная решётки, Å | 6,14 | 6,09 | 6,47 | 5,66 | 5,69 | 6,06 |
| Ширина запрещённой зоны ΔE, эВ | 0,52 | 0,7 | 0,18 | 2,2 | 1,41 | 0,35 |
| Диэлектрическая проницаемость ε | 8,4 | 14,0 | 15,9 | — | — | — |
| Подвижность, см²/(В·с): | ||||||
| электронов | 50 | 5000 | 60 000 | — | 4000 | 34000[3] |
| дырок | 150 | 1000 | 4000 | — | 400 | 460[3] |
| Показатель преломления света, n | 3,0 | 3,7 | 4,1 | — | 3,2 | 3,2 |
| Линейный коэффициент теплового расширения, K-1 | — | 6,9·10-6 | 5,5·10-6 | 5,7·10-6 | 5,3·10-6 | — |
Группа IV[править | править код]
- собственные полупроводники
- составной полупроводник
Удельное электрическое сопротивление — Википедия
Уде́льное электри́ческое сопротивле́ние (удельное сопротивление) — физическая величина, характеризующая способность материала препятствовать прохождению электрического тока, выражается в Ом·метр. Удельное электрическое сопротивление принято обозначать греческой буквой ρ. Значение удельного сопротивления зависит от температуры в различных материалах по-разному: в проводниках, удельное электрическое сопротивление с повышением температуры возрастает, а в полупроводниках и диэлектриках — наоборот, уменьшается. Величина, учитывающая изменение электрического сопротивления от температуры называется температурный коэффициент удельного сопротивления. Величина, обратная удельному сопротивлению, называется удельной проводимостью (удельной электропроводностью). В отличие от электрического сопротивления, являющегося свойством проводника и зависящего от его материала, формы и размеров, удельное электрическое сопротивление является свойством только вещества.
Электрическое сопротивление однородного проводника с удельным сопротивлением ρ, длиной l и площадью поперечного сечения S может быть рассчитано по формуле R=ρ⋅lS{\displaystyle R={\frac {\rho \cdot l}{S}}} (при этом предполагается, что ни площадь, ни форма поперечного сечения не меняются вдоль проводника). Соответственно, для ρ выполняется ρ=R⋅Sl.{\displaystyle \rho ={\frac {R\cdot S}{l}}.}
Из последней формулы следует: физический смысл удельного сопротивления вещества заключается в том, что оно представляет собой сопротивление изготовленного из этого вещества однородного проводника единичной длины и с единичной площадью поперечного сечения.
Единица измерения удельного сопротивления в Международной системе единиц (СИ) — Ом·м[1]. Из соотношения ρ=R⋅Sl{\displaystyle \rho ={\frac {R\cdot S}{l}}} следует, что единица измерения удельного сопротивления в системе СИ равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 м², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом[2]. Соответственно, удельное сопротивление произвольного вещества, выраженное в единицах СИ, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 м².
В технике также применяется устаревшая внесистемная единица Ом·мм²/м, равная 10−6 от 1 Ом·м[1]. Данная единица равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 мм², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом[2]. Соответственно, удельное сопротивление какого-либо вещества, выраженное в этих единицах, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 мм².
В проводниках удельное электрическое сопротивление увеличивается с увеличением температуры. Это объясняется тем, что с ростом температуры увеличивается интенсивность колебания атомов в узлах кристаллической решетки проводника, что препятствует движению свободных электронов[3].
В полупроводниках и диэлектриках удельное электрическое сопротивление уменьшается. Это объясняется тем, что с увеличением температуры увеличивается концентрация основных носителей заряда.
Величина, учитывающая изменение удельного электрического сопротивление от температуры называют температурным коэффициентом удельного сопротивления.
Обобщение понятия удельного сопротивления[править | править код]
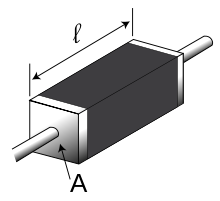 Кусок резистивного материала с электрическими контактами на обоих концах
Кусок резистивного материала с электрическими контактами на обоих концахУдельное сопротивление можно определить также для неоднородного материала, свойства которого меняются от точки к точке. В этом случае оно является не константой, а скалярной функцией координат — коэффициентом, связывающим напряжённость электрического поля E→(r→){\displaystyle {\vec {E}}({\vec {r}})} и плотность тока J→(r→){\displaystyle {\vec {J}}({\vec {r}})} в данной точке r→{\displaystyle {\vec {r}}}. Указанная связь выражается законом Ома в дифференциальной форме:
- E→(r→)=ρ(r→)J→(r→).{\displaystyle {\vec {E}}({\vec {r}})=\rho ({\vec {r}}){\vec {J}}({\vec {r}}).}
Эта формула справедлива для неоднородного, но изотропного вещества. Вещество может быть и анизотропно (большинство кристаллов, намагниченная плазма и т. д.), то есть его свойства могут зависеть от направления. В этом случае удельное сопротивление является зависящим от координат тензором второго ранга, содержащим девять компонент ρij{\displaystyle \rho _{ij}}. В анизотропном веществе векторы плотности тока и напряжённости электрического поля в каждой данной точке вещества не сонаправлены; связь между ними выражается соотношением
- Ei(r→)=∑j=13ρij(r→)Jj(r→).{\displaystyle E_{i}({\vec {r}})=\sum _{j=1}^{3}\rho _{ij}({\vec {r}})J_{j}({\vec {r}}).}
В анизотропном, но однородном веществе тензор ρij{\displaystyle \rho _{ij}} от координат не зависит.
Тензор ρij{\displaystyle \rho _{ij}} симметричен, то есть для любых i{\displaystyle i} и j{\displaystyle j} выполняется ρij=ρji{\displaystyle \rho _{ij}=\rho _{ji}}.
Как и для всякого симметричного тензора, для ρij{\displaystyle \rho _{ij}} можно выбрать ортогональную систему декартовых координат, в которых матрица ρij{\displaystyle \rho _{ij}} становится диагональной, то есть приобретает вид, при котором из девяти компонент ρij{\displaystyle \rho _{ij}} отличными от нуля являются лишь три: ρ11{\displaystyle \rho _{11}}, ρ22{\displaystyle \rho _{22}} и ρ33{\displaystyle \rho _{33}}. В этом случае, обозначив ρii{\displaystyle \rho _{ii}} как ρi{\displaystyle \rho _{i}}, вместо предыдущей формулы получаем более простую
- Ei=ρiJi.{\displaystyle E_{i}=\rho _{i}J_{i}.}
Величины ρi{\displaystyle \rho _{i}} называют главными значениями тензора удельного сопротивления.
В изотропных материалах связь между удельным сопротивлением ρ{\displaystyle \rho } и удельной проводимостью σ{\displaystyle \sigma } выражается равенством
- ρ=1σ.{\displaystyle \rho ={\frac {1}{\sigma }}.}
В случае анизотропных материалов связь между компонентами тензора удельного сопротивления ρij{\displaystyle \rho _{ij}} и тензора удельной проводимости σij{\displaystyle \sigma _{ij}} имеет более сложный характер. Действительно, закон Ома в дифференциальной форме для анизотропных материалов имеет вид:
- Ji(r→)=∑j=13σij(r→)Ej(r→).{\displaystyle J_{i}({\vec {r}})=\sum _{j=1}^{3}\sigma _{ij}({\vec {r}})E_{j}({\vec {r}}).}
Из этого равенства и приведённого ранее соотношения для Ei(r→){\displaystyle E_{i}({\vec {r}})} следует, что тензор удельного сопротивления является обратным тензору удельной проводимости. С учётом этого для компонент тензора удельного сопротивления выполняется:
- ρ11=1det(σ)[σ22σ33−σ23σ32],{\displaystyle \rho _{11}={\frac {1}{\det(\sigma )}}[\sigma _{22}\sigma _{33}-\sigma _{23}\sigma _{32}],}
- ρ12=1det(σ)[σ33σ12−σ13σ32],{\displaystyle \rho _{12}={\frac {1}{\det(\sigma )}}[\sigma _{33}\sigma _{12}-\sigma _{13}\sigma _{32}],}
где det(σ){\displaystyle \det(\sigma )} — определитель матрицы, составленной из компонент тензора σij{\displaystyle \sigma _{ij}}. Остальные компоненты тензора удельного сопротивления получаются из приведённых уравнений в результате циклической перестановки индексов 1, 2 и 3[4].
Удельное электрическое сопротивление некоторых веществ[править | править код]
Металлические монокристаллы[править | править код]
В таблице приведены главные значения тензора удельного сопротивления монокристаллов при температуре 20 °C[5].
| Кристалл | ρ1=ρ2, 10−8 Ом·м | ρ3, 10−8 Ом·м |
|---|---|---|
| Олово | 9,9 | 14,3 |
| Висмут | 109 | 138 |
| Кадмий | 6,8 | 8,3 |
| Цинк | 5,91 | 6,13 |
| Теллур | 2,90·109 | 5,9·109 |
Металлы и сплавы, применяемые в электротехнике[править | править код]
Разброс значений обусловлен разной химической чистотой металлов, способов изготовления образцов, изученных разными учеными и непостоянством состава сплавов.
|
|
Значения даны при температуре t = 20 °C. Сопротивления сплавов зависят от их химического состава и могут варьироваться. Для чистых веществ колебания численных значений удельного сопротивления обусловлены различными методами механической и термической обработки, например, отжигом проволоки после волочения.
Другие вещества[править | править код]
Сопротивление тонких плоских плёнок (когда её толщина много меньше расстояния между контактами) принято называть «удельным сопротивлением на квадрат», RSq.{\displaystyle R_{\mathrm {Sq} }.} Этот параметр удобен тем, что сопротивление квадратного куска проводящей плёнки не зависит от размеров этого квадрата, при приложении напряжения по противоположным сторонам квадрата. При этом сопротивление куска плёнки, если он имеет форму прямоугольника, не зависит от его линейных размеров, а только от отношения длины (измеренной вдоль линий тока) к его ширине L/W: RSq=RW/L,{\displaystyle R_{\mathrm {Sq} }=RW/L,} где R — измеренное сопротивление. В общем случае, если форма образца отличается от прямоугольной, и поле в плёнке неоднородное, используют метод ван дер Пау.
- ↑ 1 2 Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 93. — 240 с. — ISBN 5-7050-0118-5.
- ↑ 1 2 Чертов А. Г. Единицы физических величин. — М.: «Высшая школа», 1977. — 287 с.
- ↑ Никулин Н. В., Назаров А. С. Радиоматериалы и радиокомпоненты. — 3-е изд. — М.: Высшая школа, 1986. — 208 с.
- ↑ Давыдов А. С. Теория твёрдого тела. — М.: «Наука», 1976. — С. 191—192. — 646 с.
- ↑ Шувалов Л. А. и др. Физические свойства кристаллов // Современная кристаллография / Гл. ред. Б. К. Вайнштейн. — М.: «Наука», 1981. — Т. 4. — С. 317.
- Никулин Н. В., Назаров А. С. Радиоматериалы и радиокомпоненты. — 3-е изд., переработанное и дополненное. — М.: Высшая школа, 1986. — С. 6—7. — 208 с.
Удельное сопротивление и электропроводимость: формулы и объяснение
В данной статье мы подробно разберем что такое удельное сопротивление и электропроводность, ясно опишем все формулы с помощью примеров задач, а так же дадим вам таблицу удельных сопротивлений некоторых проводников.
Описание
Закон Ома гласит, что, когда источник напряжения (V) подается между двумя точками в цепи, между ними будет протекать электрический ток (I), вызванный наличием разности потенциалов между этими двумя точками. Количество протекающего электрического тока ограничено величиной присутствующего сопротивления (R). Другими словами, напряжение стимулирует протекание тока (движение заряда), но это сопротивление препятствует этому.
Мы всегда измеряем электрическое сопротивление в Омах, где Ом обозначается греческой буквой Омега, Ω. Так, например: 50 Ом, 10 кОм или 4,7 МОм и т.д. Проводники (например, провода и кабели) обычно имеют очень низкие значения сопротивления (менее 0,1 Ом), и, таким образом, мы можем пренебречь ими, как мы предполагаем в расчетах анализа цепи, что провода имеют ноль сопротивление. С другой стороны, изоляторы (например, пластиковые или воздушные), как правило, имеют очень высокие значения сопротивления (более 50 МОм), поэтому мы можем их игнорировать и для анализа цепи, поскольку их значение слишком велико.
Но электрическое сопротивление между двумя точками может зависеть от многих факторов, таких как длина проводников, площадь их поперечного сечения, температура, а также фактический материал, из которого он изготовлен. Например, давайте предположим, что у нас есть кусок провода (проводник), который имеет длину L, площадь поперечного сечения A и сопротивление R, как показано ниже.

Электрическое сопротивление R этого простого проводника является функцией его длины, L и площади поперечного сечения A. Закон Ома говорит нам, что для данного сопротивления R ток, протекающий через проводник, пропорционален приложенному напряжению, поскольку I = V / R. Теперь предположим, что мы соединяем два одинаковых проводника вместе в последовательной комбинации, как показано на рисунке.

Здесь, соединив два проводника вместе в последовательной комбинации, то есть, к концу, мы фактически удвоили общую длину проводника (2L), в то время как площадь поперечного сечения A остается точно такой же, как и раньше. Но помимо удвоения длины, мы также удвоили общее сопротивление проводника, дав 2R как: 1R + 1R = 2R.
Таким образом , мы можем видеть , что сопротивление проводника пропорционально его длину, то есть: R ∝ L. Другими словами, мы ожидаем, что электрическое сопротивление проводника (или провода) будет пропорционально больше, чем оно длиннее.
Отметим также, что, удваивая длину и, следовательно, сопротивление проводника (2R), чтобы заставить тот же ток I, чтобы течь через проводник, как и раньше, нам нужно удвоить (увеличить) приложенное напряжение I = (2 В) / (2R). Далее предположим, что мы соединяем два идентичных проводника вместе в параллельной комбинации, как показано.

Здесь, соединяя два проводника в параллельную комбинацию, мы фактически удвоили общую площадь, дающую 2А, в то время как длина проводников L остается такой же, как у исходного одиночного проводника. Но помимо удвоения площади, путем параллельного соединения двух проводников мы фактически вдвое сократили общее сопротивление проводника, получив 1 / 2R, поскольку теперь каждая половина тока протекает через каждую ветвь проводника.
Таким образом, сопротивление проводника обратно пропорционально его площади, то есть: R 1 / ∝ A или R ∝ 1 / A. Другими словами, мы ожидаем, что электрическое сопротивление проводника (или провода) будет пропорционально меньше, чем больше его площадь поперечного сечения.
Кроме того, удваивая площадь и, следовательно, вдвое увеличивая суммарное сопротивление ветви проводника (1 / 2R), для того же тока, чтобы I протекал через параллельную ветвь провода, как раньше, нам нужно только наполовину уменьшить приложенное напряжение I = (1 / 2V) / (1 / 2R).
Надеемся, мы увидим, что сопротивление проводника прямо пропорционально длине (L) проводника, то есть: R ∝ L, и обратно пропорционально его площади (A), R ∝ 1 / A. Таким образом, мы можем правильно сказать, что сопротивление это:
Пропорциональность сопротивления

Но помимо длины и площади проводника, мы также ожидаем, что электрическое сопротивление проводника будет зависеть от фактического материала, из которого он изготовлен, потому что разные проводящие материалы, медь, серебро, алюминий и т.д., имеют разные физические и электрические свойства. Таким образом, мы можем преобразовать знак пропорциональности (∝) вышеприведенного уравнения в знак равенства, просто добавив «пропорциональную константу» в вышеприведенное уравнение, давая:
Уравнение удельного электрического сопротивления

Где: R — сопротивление в омах (Ω), L — длина в метрах (м), A — площадь в квадратных метрах (м 2 ), и где известна пропорциональная постоянная ρ (греческая буква «rho») — удельное сопротивление .
Удельное электрическое сопротивление
Удельное электрическое сопротивление конкретного материала проводника является мерой того, насколько сильно материал противостоит потоку электрического тока через него. Этот коэффициент удельного сопротивления, иногда называемый его «удельным электрическим сопротивлением», позволяет сравнивать сопротивление различных типов проводников друг с другом при определенной температуре в соответствии с их физическими свойствами без учета их длины или площади поперечного сечения. Таким образом, чем выше значение удельного сопротивления ρ, тем больше сопротивление, и наоборот.
Например, удельное сопротивление хорошего проводника, такого как медь, составляет порядка 1,72 х 10 -8 Ом (или 17,2 нОм), тогда как удельное сопротивление плохого проводника (изолятора), такого как воздух, может быть значительно выше 1,5 х 10 14 или 150 трлн.
Такие материалы, как медь и алюминий, известны низким уровнем удельного сопротивления, благодаря чему электрический ток легко проходит через них, что делает эти материалы идеальными для изготовления электрических проводов и кабелей. Серебро и золото имеют очень низкие значения удельного сопротивления, но по понятным причинам дороже делать из них электрические провода.
Тогда факторы, которые влияют на сопротивление (R) проводника в омах, могут быть перечислены как:
- Удельное сопротивление (ρ) материала, из которого сделан проводник.
- Общая длина (L) проводника.
- Площадь поперечного сечения (А) проводника.
- Температура проводника.
Пример удельного сопротивления № 1
Рассчитайте общее сопротивление постоянному току 100-метрового рулона медного провода 2,5 мм 2, если удельное сопротивление меди при 20 o C составляет 1,72 x 10 -8 Ом метр.
Приведенные данные: удельное сопротивление меди при 20 o C составляет 1,72 x 10 -8 , длина катушки L = 100 м, площадь поперечного сечения проводника составляет 2,5 мм 2, что дает площадь: A = 2,5 x 10 -6 м 2 .

Ответ: 688 МОм или 0,688 Ом.
Удельное электрическое сопротивление материала
Ранее мы говорили, что удельное сопротивление — это электрическое сопротивление на единицу длины и на единицу площади поперечного сечения проводника, таким образом, показывая, что удельное сопротивление ρ имеет размеры в Ом-метрах или Ом · м, как это обычно пишется. Таким образом, для конкретного материала при определенной температуре его удельное электрическое сопротивление определяется как.

Электрическая проводимость
Хотя как электрическое сопротивление (R), так и удельное сопротивление ρ, являются функцией физической природы используемого материала, а также его физической формы и размера, выраженных его длиной (L) и площадью его сечения ( А), Проводимость или удельная проводимость относится к легкости, с которой электрический ток проходит через материал.
Проводимость (G) является обратной величиной сопротивления (1 / R) с единицей проводимости, являющейся сименсом (S), и ей дается перевернутый символ омов mho, ℧. Таким образом, когда проводник имеет проводимость 1 сименс (1S), он имеет сопротивление 1 Ом (1 Ом). Таким образом, если его сопротивление удваивается, проводимость уменьшается вдвое, и наоборот, как: Сименс = 1 / Ом, или Ом = 1 / Ом.
В то время как сопротивление проводников дает степень сопротивления потоку электрического тока, проводимость проводника указывает на легкость, с которой он пропускает электрический ток. Таким образом, металлы, такие как медь, алюминий или серебро, имеют очень большие значения проводимости, что означает, что они являются хорошими проводниками.
Проводимость, σ (греческая буква сигма), является обратной величиной удельного сопротивления. Это 1 / ρ и измеряется в сименах на метр (S / m). Поскольку электропроводность σ = 1 / ρ, предыдущее выражение для электрического сопротивления R можно переписать в виде:
Электрическое сопротивление как функция проводимости

Тогда мы можем сказать, что проводимость — это эффективность, посредством которой проводник пропускает электрический ток или сигнал без потери сопротивления. Поэтому материал или проводник, который имеет высокую проводимость, будет иметь низкое удельное сопротивление, и наоборот, поскольку 1 сименс (S) равен 1 Ом -1 . Таким образом, медь, которая является хорошим проводником электрического тока, имеет проводимость 58,14 x 10 6 Симен на метр.
Пример удельного сопротивления №2
Кабель длиной 20 метров имеет площадь поперечного сечения 1 мм 2 и сопротивление 5 Ом. Рассчитать проводимость кабеля.
Приведенные данные: сопротивление постоянному току, R = 5 Ом, длина кабеля, L = 20 м, а площадь поперечного сечения проводника составляет 1 мм 2, что дает площадь: A = 1 x 10 -6 м 2 .

Ответ: 4 мега-симена на метр длины.
Таблица удельных сопротивлений проводников
| Проводник | Удельное сопротивление ρ | Температурный коэффициент α |
| Алюминий | 0,028 | 4,2 |
| Бронза | 0,095 — 0,1 | — |
| Висмут | 1,2 | — |
| Вольфрам | 0,05 | 5 |
| Железо | 0,1 | 6 |
| Золото | 0,023 | 4 |
| Иридий | 0,0474 | — |
| Константан | 0,5 | 0,05 |
| Латунь | 0,025 — 0,108 | 0,1-0,4 |
| Магний | 0,045 | 3,9 |
| Манганин | 0,43 — 0,51 | 0,01 |
| Медь | 0,0175 | 4,3 |
| Молибден | 0,059 | — |
| Нейзильбер | 0,2 | 0,25 |
| Натрий | 0,047 | — |
| Никелин | 0,42 | 0,1 |
| Никель | 0,087 | 6,5 |
| Нихром | 1,05 — 1,4 | 0,1 |
| Олово | 0,12 | 4,4 |
| Платина | 0.107 | 3,9 |
| Ртуть | 0,94 | 1,0 |
| Свинец | 0,22 | 3,7 |
| Серебро | 0,015 | 4,1 |
| Сталь | 0,103 — 0,137 | 1-4 |
| Титан | 0,6 | — |
| Фехраль | 1,15 — 1,35 | 0,1 |
| Хромаль | 1,3 — 1,5 | — |
| Цинк | 0,054 | 4,2 |
| Чугун | 0,5-1,0 | 1,0 |
Где: удельное сопротивление ρ измеряется в Ом*мм2/м и температурный коэффициент электрического сопротивления металлов α измеряется в 10 -3*C-1(или K -1) .
Краткое описание удельного сопротивления
Мы поговорили в этой статье об удельном сопротивлении, что удельное сопротивление — это свойство материала или проводника, которое указывает, насколько хорошо материал проводит электрический ток. Мы также видели, что электрическое сопротивление (R) проводника зависит не только от материала, из которого сделан проводник, меди, серебра, алюминия и т.д., но также от его физических размеров.
Сопротивление проводника прямо пропорционально его длине (L) как R ∝ L. Таким образом, удвоение его длины удвоит его сопротивление, в то время как последовательное удвоение проводника уменьшит вдвое его сопротивление. Также сопротивление проводника обратно пропорционально его площади поперечного сечения (A) как R ∝ 1 / A. Таким образом, удвоение его площади поперечного сечения уменьшило бы его сопротивление вдвое, тогда как удвоение его площади поперечного сечения удвоило бы его сопротивление.
Мы также узнали, что удельное сопротивление (символ: ρ) проводника (или материала) связано с физическим свойством, из которого он изготовлен, и варьируется от материала к материалу. Например, удельное сопротивление меди обычно дается как: 1,72 х 10 -8 Ом · м. Удельное сопротивление конкретного материала измеряется в единицах Ом-метров (Ом), которое также зависит от температуры.
В зависимости от значения удельного электрического сопротивления конкретного материала его можно классифицировать как «проводник», «изолятор» или «полупроводник». Обратите внимание, что полупроводники — это материалы, в которых их проводимость зависит от примесей, добавляемых в материал.
Удельное сопротивление также важно в системах распределения электроэнергии, так как эффективность системы заземления для системы электропитания и распределения сильно зависит от удельного сопротивления земли и материала почвы в месте расположения системы.
Проводимость — это имя, данное движению свободных электронов в форме электрического тока. Проводимость, σ является обратной величиной удельного сопротивления. Это 1 / ρ и имеет единицу измерения сименс на метр, S / m. Проводимость варьируется от нуля (для идеального изолятора) до бесконечности (для идеального проводника). Таким образом, сверхпроводник имеет бесконечную проводимость и практически нулевое омическое сопротивление.
18. Электрическое сопротивление проводников. Электрическая проводимость. Последовательное и параллельное соединение проводников.
Последовательное и параллельное соединения в электротехнике — два основных способа соединения элементовэлектрической цепи. При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла. При параллельном соединении все входящие в цепь элементы объединены двумяузлами и не имеют связей с другими узлами, если это не противоречит условию.
При последовательном соединении проводников сила тока во всех проводниках одинакова.
При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов. При этом величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
При
последовательном соединении проводников
сила тока в любых частях цепи одна и та
же: 
Полное
напряжение в цепи при последовательном
соединении, или напряжение на полюсах
источника тока, равно сумме напряжений
на отдельных участках цепи: 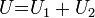

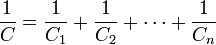 .
.
Параллельное соединение
Сила
тока в неразветвленной части цепи равна
сумме сил токов в отдельных параллельно
соединённых проводниках: 
Напряжение
на участках цепи АВ и на концах всех
параллельно соединённых проводников
одно и то же: 
Резистор
При
параллельном соединении резисторов
складываются величины, обратно
пропорциональные сопротивлению (то
есть общая проводимость 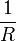 складывается
из проводимостей каждого резистора
складывается
из проводимостей каждого резистора  )
)


Электри́ческое сопротивле́ние — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношению напряжения на концах проводника к силе тока, протекающего по нему[1]. Сопротивление для цепей переменного тока и для переменных электромагнитных полей описывается понятиямиимпеданса и волнового сопротивления. Сопротивлением (резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопротивления.
Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как
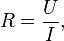
где
R — сопротивление;
U — разность электрических потенциалов на концах проводника;
I — сила тока, протекающего между концами проводника под действием разности потенциалов.
Электри́ческая проводи́мость (электропроводность, проводимость) — способность тела проводить электрический ток, а такжефизическая величина, характеризующая эту способность и обратная электрическому сопротивлению. В СИ единицей измеренияэлектрической проводимости является сименс (называемая также в некоторых странах Мо)[1].
Удельной проводимостью (удельной электропроводностью) называют меру способности вещества проводить электрический ток. Согласно закону Ома в линейном изотропном веществе удельная проводимость является коэффициентом пропорциональности между плотностью возникающего токаи величиной электрического поля в среде:

где
 —удельная
проводимость,
—удельная
проводимость, —вектор плотности
тока,
—вектор плотности
тока, —вектор напряжённости
электрического поля.
—вектор напряжённости
электрического поля.




 —удельная
проводимость,
—удельная
проводимость,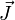 —вектор плотности
тока,
—вектор плотности
тока,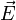 —вектор напряжённости
электрического поля.
—вектор напряжённости
электрического поля.