ПЕРЕМЕННАЯ — это… Что такое ПЕРЕМЕННАЯ?

Переменная — в языках программирования именованная часть памяти, в которую могут помещаться разные значения переменной. Причем в каждый момент времени переменная имеет единственное значение. В процессе выполнения программы значение переменной может изменяться …   Финансовый словарь

переменная — аргумент Словарь русских синонимов. переменная сущ., кол во синонимов: 1 • аргумент (12) Словарь синонимов ASIS. В.Н. Тришин …   Словарь синонимов

переменная — одно из основных понятий для описания эксперимента, хотя оно может относиться и к наблюдению. Под переменной понимается любая реальность, коя может изменяться в экспериментальной ситуации. Переменные все измеряемые факторы, кои предположительно… …   Большая психологическая энциклопедия

ПЕРЕМЕННАЯ — в логике неопределенное имя предмета из некоторой выделенной предметной области области значений этой переменной …   Большой Энциклопедический словарь

ПЕРЕМЕННАЯ — англ. variable,;нем. Variable. 1. Знак в идеографических языках науки, к рый может принимать различные значения. 2. В математике величина, принимающая различные значения. Antinazi. Энциклопедия социологии, 2009 …   Энциклопедия социологии

ПЕРЕМЕННАЯ — (variable) Величина, способная изменяться. Переменные могут отражать цены, процентные ставки, уровни дохода, количества товаров и т.д. Экзогенные переменные – это такие переменные, причины изменения которых лежат за пределами рассматриваемой… …   Экономический словарь

переменная — Терм, который обозначает неконкретизированную сущность в проблемной области. [ГОСТ 34.320 96] Тематики базы данных EN variable …   Справочник технического переводчика

Переменная — * пераменная * argument .>> …   Генетика. Энциклопедический словарь

переменная — 3.3.15 переменная (variable): Представление значения, которое должно принадлежать к определенному типу данных. Источник …   Словарь-справочник терминов нормативно-технической документации

Переменная — Термин переменная может означать: Переменная (программирование) поименованная, либо адресуемая иным способом область памяти, адрес которой можно использовать для осуществления доступа к данным. Переменная величина в математике символ,… …   Википедия

Переменная величина — Википедия

Переме́нная — атрибут физической или абстрактной системы, который может изменять своё, как правило численное, значение. Понятие переменной широко используется в таких областях как математика, естественные науки, техника и программирование. Примерами переменных могут служить: температура воздуха, параметр функции и многое другое.

Переменная характеризуется только множеством значений, которые она может принимать^[1]. Переменную обозначают символом, общим для каждого из её значений.

Русский термин «переменная величина» происходит от латинской формулировки quantitas variabilis, так же, как в русском языке, сокращаемой до единственного слова variabilis.

В математике переменной может быть как реальная измеримая физическая величина, так и некая абстрактная величина, прямо не связанная с процессами реального мира.

В математическом анализе и большинстве смежных разделов математики под переменной x{\displaystyle x} понимают каждый элемент некоторого множества, состоящего, например, из вещественных чисел. Фиксированный элемент этого множества называется значением переменной. Само множество называется областью изменения переменной.

Задание области изменения переменной эквивалентно заданию самой переменной.

• Переменные обозначаются малыми буквами латинского или греческого алфавита (возможно, с индексами): x, y, ε.{\displaystyle x,~y,~\varepsilon .}
• Области изменения соответствующих переменных обозначаются обычно теми же символами, взятыми в фигурные скобки: {x}, {y}, {ε}{\displaystyle \left\{x\right\},~\left\{y\right\},~\left\{\varepsilon \right\}}.

При моделировании процессов переменные необходимо отличать от параметров, несмотря на то, что переменная в одном контексте может быть параметром в другом.

В прикладной статистике переменная — оценочный фактор или характеристика, индивидуальный или системный атрибут, изменение которых ожидается с течением времени или между отдельными лицами, например переменная возраст

.

Переменная и неизвестное[править | править код]

Нужно отметить, что аналогично переменным обозначаются неизвестные в уравнениях, неравенствах и других подобных задачах, например в уравнении 2x=6{\displaystyle 2x=6}, где буквой x{\displaystyle x} обозначено неизвестное, а не переменная, хотя эти понятия весьма схожи и зависят от контекста.

Суть различия между этими понятиями можно пояснить так.

Запись 2x=6{\displaystyle 2x=6} можно, с одной стороны, трактовать как утверждение о возможности найти значение неизвестного x{\displaystyle x}. В этом случае x{\displaystyle x} — обозначение неизвестного числа.

С другой стороны запись 2x=6{\displaystyle 2x=6} можно трактовать как предикат, принимающий значение «истина» при одних значениях x{\displaystyle x}, и значение «ложь» при других. В этом случае x{\displaystyle x} —

переменная. На её место в выражении могут подставляться различные значения с целью определения логического (булева) значения записанного предиката.

История[править | править код]

В середине XVII века Рене Декарт в своей «Геометрии» предложил использовать для известных параметров начальные буквы алфавита: a,b,c…,{\displaystyle a,b,c\dots ,} а для неизвестных — последние буквы: x,y,z.{\displaystyle x,y,z.} Декарт не объяснял свой выбор. Некоторые историки пытались объяснить выбор буквы x{\displaystyle x} в качестве неизвестной. Так, например, словарь Уэбстера (1909—1916) утверждал, что переменная x{\displaystyle x} появилась как транскрипция арабской буквы

ش — первой буквой в слове شيء‎, которое переводится на русский языка как «что-то», «нечто». Тем не менее эта и другие подобные версии не находят подтверждений и игнорируют тот факт, что Декарт использовал наряду с x{\displaystyle x} еще y{\displaystyle y} и z{\displaystyle z}^[2][3].

Декарт считал значения переменных всегда неотрицательными, а отрицательные величины отражал знаком «минус» перед переменной. Если знак коэффициента был неизвестен, Декарт ставил многоточие^[4]. Нидерландский математик Иоганн Худде уже в 1657 году позволил буквенным переменным принимать значения любого знака

[5].

Ф. Кэджори характеризует декартовскую запись степеней как самую удачную и гибкую символику во всей алгебре — она не только облегчает преобразования, но стимулировала расширение понятия возведения в степень на отрицательные, дробные и даже комплексные показатели, а также появление в математике степенной и показательной функции; все эти достижения трудно было бы осуществить при использовании обозначений XVI века^[6]

В языках программирования переменная реализуется как некоторая область машинной памяти, на которую указывает идентификатор переменной.

Машинная переменная принадлежит одному из типов данных и имеет некоторый допустимый диапазон значений, которые она может принимать. Например, логическая (булевская) переменная может принимать только два значения, — «истина» и «ложь», допустимые диапазоны изменения целых и вещественных переменных зависят от конкретного компилятора и платформы исполнения.

В высокоуровневых языках программировании, переменные, как правило, обозначаются произвольной последовательностью символов из букв и цифр — словом, обязательно начинающегося с буквы, например, «time», «x12», «foo».

Такое понятие переменной в некотором смысле схоже с математическим. Математики в XVII веке уже использовали переменную, чтобы «забронировать» в формуле место, на которое можно подставлять конкретные значения. Буквенные обозначения резервируют и именуют области этой памяти. Если формула в математике является алгоритмом вычисления, то понятие переменной совпадает с понятием переменной в программировании.

Если формула используется только для выражения отношения между элементами множеств, то нет необходимости в понятии переменных как ячеек памяти.

В физике переменная — это некоторый атрибут модели реального физического процесса, принимающий количественные значения, физическая величина. Множество значений, которые может принимать конкретная переменная, определяется из физических соображений. Физические переменные связаны друг с другом физическими законами, на основе которых строятся математические модели различной степени сложности. Переменные в физике, как правило, характеризуются размерными значениями.

1. ↑ В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Глава 3. Теория пределов // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. 1. — С. 105—121. — 672 с. — ISBN 5-482-00445-7.
2. ↑ History of Mathematical Notations, vol. 1, 2007, §340.
3. ↑ Jeff Miller. Earliest Uses of Symbols for Variables (англ.). Дата обращения 22 августа 2015.
4. ↑ История математики, том II, 1970, с. 40—46.
5. ↑ History of Mathematical Notations, vol. 2, 2007, §392.
6. ↑ History of Mathematical Notations, vol. 1, 2007, §315.

переменный — Викисловарь

Морфологические и синтаксические свойства[править]

падеж		ед. ч.			мн. ч.
		муж. р.	ср. р.	жен. р.
Им.		переме́нный	переме́нное	переме́нная	переме́нные
Рд.		переме́нного	переме́нного	переме́нной	переме́нных
Дт.		переме́нному	переме́нному	переме́нной	переме́нным
Вн.	одуш.	переме́нного	переме́нное	переме́нную	переме́нных
	неод.	переме́нный			переме́нные
Тв.		переме́нным	переме́нным	переме́нной переме́нною	переме́нными
Пр.		переме́нном	переме́нном	переме́нной	переме́нных
Кратк. форма		переме́нен	переме́нно	переме́нна	переме́нны

пе-ре-ме́н-ный

Прилагательное, тип склонения по классификации А. Зализняка — 1*a.

Приставка: пере-; корень: -мен-; суффикс: -н; окончание: -ый ^{[Тихонов, 1996]}.

Произношение[править]

• МФА: ед. ч. [pʲɪrʲɪˈmʲenːɨɪ̯]  мн. ч. [pʲɪrʲɪˈmʲenːɨɪ]

Семантические свойства[править]

Значение[править]

1. изменяющийся время от времени. ◆ Отсутствует пример употребления (см. рекомендации).
2. сменяемый, заменяемый кем-либо, чем-либо ◆ Это ночное мытьё производилось самою Катериной Ивановной, собственноручно, по крайней мере два раза в неделю, а иногда и чаще, ибо дошли до того, что переменного белья уже совсем почти не было, и было у каждого члена семейства по одному только экземпляру, а Катерина Ивановна не могла выносить нечистоты и лучше соглашалась мучить себя по ночам и не по силам, когда все спят, чтоб успеть к утру просушить мокрое бельё на протянутой верёвке и подать чистое, чем видеть грязь в доме. Ф. М. Достоевский, «Преступление и наказание» (цитата из Викитеки)

Синонимы[править]

1. непостоянный, изменчивый

Антонимы[править]

1. постоянный

Гиперонимы[править]

1. —

Гипонимы[править]

1. равнопеременный

Родственные слова[править]

Ближайшее родство
существительные: перемена, замена, смена, мена, обмен, измена, изменение прилагательные: сменный, переменчивый, изменчивый; беспеременный глаголы: переменить, заменить, сменить, изменить, менять, заменять, сменять, изменять, выменять, обменять, выменивать, обменивать

Этимология[править]

Происходит от существительного перемена, далее от существительного мена, далее от праслав. *měna, от кот. в числе прочего произошли: др.-русск., ст.-слав. мѣна (греч. συνάλλαγμα), русск. мена, укр. мiна «мена», болг. мя́на, сербохорв. миjѐна, словенск. mẹ́na, чешск. měna, словацк. mena, др.-польск. miana, польск. zmiana «изменение»

Фразеологизмы и устойчивые сочетания[править]

Перевод[править]

Список переводов

Метаграммы[править]

Библиография[править]

Для улучшения этой статьи желательно: Добавить примеры словоупотребления для всех значений с помощью {{пример}} Добавить все семантические связи (отсутствие можно указать прочерком, а неизвестность — символом вопроса) Добавить хотя бы один перевод в секцию «Перевод»

ПЕРЕМЕННЫЙ — это… Что такое ПЕРЕМЕННЫЙ?

переменный — неустойчивый, непостоянный, изменчивый, переменчивый, переходный, неустановившийся, изменяемый; капризный, резкопеременный, альтернирующий, вариационный. Ant. постоянный, устойчивый, установившийся, неизменяемый Словарь русских синонимов.… …   Словарь синонимов

ПЕРЕМЕННЫЙ — ПЕРЕМЕННЫЙ, ая, ое. Меняющийся, с переменами. Переменная облачность. П. ток (электрический ток, изменяющийся во времени). Переменная величина и (сущ.) переменная (величина, к рая может по условиям задачи принимать различные значения). П. капитал… …   Толковый словарь Ожегова

переменный — Пробегающий ряд значений. [http://www.rfcmd.ru/glossword/1.8/index.php?a=index&d=4155] Тематики защита информации EN running …   Справочник технического переводчика

переменный — ▲ изменяющийся ↑ когда л. переменный изменяющийся когда л; имеющий возможность изменения. плавающий. знакопеременный …   Идеографический словарь русского языка

переменный — ая, ое. Меняющийся, непостоянный, чередующийся с чем л. Переме/нный ветер. П ая погода. Переме/нный ток. Переме/нный успех. переменная величина …   Словарь многих выражений

Переменный — прил. 1. Не все время одинаковый, не один и тот же; меняющийся. отт. Иногда исчезающий. 2. Сменяемый, заменяемый кем либо, чем либо. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 …   Современный толковый словарь русского языка Ефремовой

переменный — переменный, переменная, переменное, переменные, переменного, переменной, переменного, переменных, переменному, переменной, переменному, переменным, переменный, переменную, переменное, переменные, переменного, переменную, переменное, переменных,… …   Формы слов

переменный — прил., употр. сравн. часто 1. Переменным ветром называют ветер, который в течение дня (или другого времени) часто меняет направление. 2. Переменным током называют электрический ток, который периодически меняет направление движения заряженных… …   Толковый словарь Дмитриева

переменный — перем енный …   Русский орфографический словарь

переменный — …   Орфографический словарь русского языка

переменный — это… Что такое переменный?

ПЕРЕМЕННЫЙ — ПЕРЕМЕННЫЙ, переменная, переменное. Меняющийся, изменчивый, непостоянный; бывающий не всегда, чередующийся с чем нибудь. Переменная погода. Переменный ветер. Переменная величина (могущая принимать различные значения; мат.). Переменные звезды… …   Толковый словарь Ушакова

переменный — неустойчивый, непостоянный, изменчивый, переменчивый, переходный, неустановившийся, изменяемый; капризный, резкопеременный, альтернирующий, вариационный. Ant. постоянный, устойчивый, установившийся, неизменяемый Словарь русских синонимов.… …   Словарь синонимов

ПЕРЕМЕННЫЙ — ПЕРЕМЕННЫЙ, ая, ое. Меняющийся, с переменами. Переменная облачность. П. ток (электрический ток, изменяющийся во времени). Переменная величина и (сущ.) переменная (величина, к рая может по условиям задачи принимать различные значения). П. капитал… …   Толковый словарь Ожегова

переменный — Пробегающий ряд значений. [http://www.rfcmd.ru/glossword/1.8/index.php?a=index&d=4155] Тематики защита информации EN running …   Справочник технического переводчика

переменный — ▲ изменяющийся ↑ когда л. переменный изменяющийся когда л; имеющий возможность изменения. плавающий. знакопеременный …   Идеографический словарь русского языка

переменный — ая, ое. Меняющийся, непостоянный, чередующийся с чем л. Переме/нный ветер. П ая погода. Переме/нный ток. Переме/нный успех. переменная величина …   Словарь многих выражений

Переменный — прил. 1. Не все время одинаковый, не один и тот же; меняющийся. отт. Иногда исчезающий. 2. Сменяемый, заменяемый кем либо, чем либо. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 …   Современный толковый словарь русского языка Ефремовой

переменный — переменный, переменная, переменное, переменные, переменного, переменной, переменного, переменных, переменному, переменной, переменному, переменным, переменный, переменную, переменное, переменные, переменного, переменную, переменное, переменных,… …   Формы слов

переменный — перем енный …   Русский орфографический словарь

переменный — …   Орфографический словарь русского языка

Переменная величина — это… Что такое Переменная величина?

Переме́нная — атрибут физической или абстрактной системы, который может изменять своё значение. Значение может меняться в зависимости от контекста, в котором рассматривается система, или в случае уточнения, о какой конкретно системе идёт речь. Концепция переменной широко используется в таких областях как математика, естественные науки, техника и программирование. Примерами переменных могут служить температура воздуха, параметр функции и многое другое. В широком смысле, переменная характеризуется лишь множеством значений, которые она может принимать.

В математике переменная — это величина, характеризующаяся множеством значений, которое она может принимать.^[1] При этом может иметься в виду как реальная физическая величина, временно рассматриваемая в отрыве от своего физического контекста, так и некая абстрактная величина, не имеющая никаких аналогов в реальном мире. В математическом анализе и большинстве смежных разделов математики под «переменной» обычно понимают численную величину, множество принимаемых значений которой включено в множество вещественных чисел.

Множество всех значений, которые может принимать данная переменная, называется областью изменения этой переменной. Это множество и задаёт переменную, то есть формально и является ей.

При моделировании переменные необходимо отличать от параметров, несмотря на то что переменная в одном контексте может быть параметром в другом.

В прикладной статистике переменная — оценочный фактор, или характеристика, или индивидуальный или системный атрибут. Иными словами, нечто, изменение чего ожидается с течением времени или между отдельными лицами.

Обозначения

• Переменные обозначаются малыми буквами латинского или греческого алфавита (возможно, с индексами): .
• Области изменения соответствующих переменных обозначаются обычно теми же символами, взятыми в фигурные скобки: .

Нужно отметить, что аналогичным образом обозначаются неизвестные в уравнениях, неравенствах и других подобных задачах. Например, . В этом случае имеются ввиду не переменные, хотя понятия весьма схожи и зависят от контекста.

Суть этого различия между неизвестной и переменной можно пояснить так. Запись можно, с одной стороны, трактовать как утверждение о свойстве неизвестной (в момент высказывания утверждения) величины , значение которой можно найти (или уточнить), отталкиваясь от приведенного утверждения как от исходной посылки. В этом случае будет обозначением конкретной, но до проведения выкладок (например, решения уравнения) неизвестной величины. С другой стороны запись можно трактовать как предикат, принимающий значение «истина» при одних значениях, подставляемых на место , и значение «ложь» при других. В этом случае является обозначением места в выражении, на которое могут подставляться различные (переменные) значения с целью определения логического (булева) значения записанного предиката. В этом случае правильнее рассматривать как переменную.

В программировании переменная — это идентификатор, определяющий данные. Обычно это бывает имя, скрывающее за собой область памяти с хранящимися там данными. Переменная может иметь тип, характеризующий множество значений, которые она может принимать. В программировании, переменные, как правило, обозначаются одним или несколькими словами или символами, такими, как «time», «x», «foo» и тому подобное.

Следует отметить, что это значение в некотором смысле схоже с математическим. Математики в XVII веке придумали переменную именно для того, чтобы «забронировать» в формуле место, на которое в нужный момент можно подставить конкретное значение. Бумага в этом процессе является памятью, а обозначения (чаще, буквы) резервируют и именуют области этой памяти. Ощущение неоднозначности возникает из-за того, что формула в математике играет двоякую роль: если это алгоритм вычисления, смысл совпадает с программистским определением; если же формула визуализирует отношения своих элементов, мы абстрагируемся от роли переменной, как ячейки памяти, такое понимание теряет смысл.

В физике переменная — это некоторый атрибут модели реального физического процесса, принимающий количественные значения, физическая величина. Множество значений, которые может принимать конкретная переменная, определяется из физических соображений. Физические переменные связываются друг с другом физическими законами, в результате чего получаются математические модели различной степени сложности. Переменные в физике, как правило, кроме количественного значения характеризуются также размерностью.

Примечания

Переменная — это… Что такое Переменная?

        переменное, одно из основных понятий математики и логики. Начиная с работ П. Ферма, Р. Декарта, И. Ньютона, Г. В. Лейбница и др. основоположников «высшей» математики под П. понимали некоторую «величину», которая может «изменяться», принимая в процессе этого изменения различные «значения». Тем самым П. противопоставлялись «постоянным» (или константам) — числам или каким-либо др. «величинам», каждая из которых имеет единственное, вполне определённое значение (см. Переменные и постоянные величины). По мере развития математики и в ходе её обоснования представления о «процессах», «изменении величин» и т. п. тщательно изгонялись из математического арсенала как «внематематические», в результате чего П. стала пониматься как обозначение для произвольного элемента рассматриваемой предметной области (например, области натуральных чисел или действительных чисел), то есть как родовое имя всей этой области (в отличие от констант — «собственных имён» для чисел или др. конкретных предметов рассматриваемой области). Этот пересмотр взглядов на понятие П. был тесно связан с перестройкой математики на базе множеств теории (См. Множеств теория), завершившейся в конце 19 в. При всей простоте и «естественности» такой перестройки она существенным образом опирается на так называемую абстракцию актуальной бесконечности, позволяющую рассматривать произвольные бесконечные множества в качестве «данных» («завершенных», «готовых», «актуальных») объектов и применять по отношению к ним любые средства классической логики, отвлекаясь от незавершённости и принципиальной незавершимости процесса образования такого множества. Трудности решения логических проблем, связанных с принятием этой абстракции, делают понятной частичную «реабилитацию» старинных представлений о «переменных величинах»; при построении математических теорий представители некоторых школ (см. Математический интуиционизм, Конструктивное направление) предпочитают обходиться боле (слабой, но зато менее уязвимой в логическом отношении абстракцией потенциальной осуществимости, с точки зрения которой с бесконечными множествами как раз связываются представления о процессах их «порождения»,— сколь угодно далеко заходящих, но никогда не завершающихся (см. Бесконечность в математике). При исследовании вопроса непротиворечивости (См. Непротиворечивость) различных областей математики на такую позицию фактически встаёт значительное большинство математиков и логиков (см. Метаматематика).          В формализованных языках (исчислениях (См. Исчисление), формальных системах) математической логики П. называются символы строго фиксированного вида, могущие при определённых условиях заменяться выражениям данного исчисления. Это относится к так называемым свободным (или значащим) П. примером которых может служить П. в неравенстве х > 5, обращающемся при подстановке вместо х, скажем, цифры 7 (то есть обозначения для числа) 7 в истинное высказывание, а при подстановке цифры 2 — в ложное высказывание. Что касается так называемых связанных (или фиктивных) П., то они сами по себе вообще ничего не означают, несут чисто синтаксические функции и могут (при соблюдении некоторых элементарных предосторожностей) «переименовываться», то есть заменяться др. П. Такова, например, П. у в записях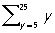 yP (y), в интерпретации (прочтения) которых она вообще не входит и может быть заменена любой др. П. так, первая из них (читаемая как «сумма целых чисел от 5 до 25») может быть заменена на 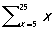tP (t). Различают индивидные, пропозициональные, предикатные, функциональные, числовые и др. виды П., вместо которых можно (согласно специальным правилам подстановки) подставлять соответственно обозначения предметов из рассматриваемой области («термы»), обозначения для конкретных высказываний, предикатов, функций, чисел и др. Т. о., П. можно содержательно понимать как «пустое место» в формуле, снабженное указанием, чем это «место» может быть «заполнено» (своего рода «тара под строго определенный товар»).          Свободные вхождения П. в выражения содержательных научных теорий и формулы логико-математических исчислений (соответствующие употреблению неопределенных местоимений в обычной речи) допускают различные интерпретации. Первая (соответствующая применению всякого рода процедур подстановок) — так называемая предикатная интерпретация: формула A (x₁,…, x_n) какого-либо исчисления понимается как некоторый местный Предикат. Та же формула может интерпретироваться и как предложение (Высказывание), а именно как предложение ∀x₁ … ∀x_n A (x₁ … x_n), являющееся ее «замыканием»,— это так называемая интерпретация всеобщности (употребительная, например, при формулировке аксиом (См. Аксиома) различных научных теорий). Свободным П. могут, наконец, приписываться значения, постоянные в пределах некоторого контекста (например, вывода из данной совокупности формул), их тогда называют параметрами этого контекста и говорят об их условной интерпретации. Например, П. х в выражении cos х, взятом изолированно, имеет предикатную интерпретацию, в тождестве sin²x + cos²x = 1 — интерпретацию всеобщности, в уравнении cos х = 1 (в процессе его решения, когда эта П. именуется «неизвестным») — условную интерпретацию.

         Таким образом, на различных уровнях формализации понятие П. выступает как уточнение средств, общеупотребительных в обычных разговорных языках (неопределенные местоимения, неопределенные артикли), и различных способов использования этих средств.

        

         Лит.: Клини С. К, Введение в метаматематику, пер с англ, М., 1957, §§ 31, 32, 45, Чёрч А, Введение в математическую логику, пер с англ, т. 1, М., 1960, §§ 02, 04, 06.