начальная фаза — это… Что такое начальная фаза?



начальная фаза

начальная фаза гармонических колебаний; начальная фаза

Значение фазы гармонических колебаний в начальный момент времени.

Политехнический терминологический толковый словарь. Составление: В. Бутаков, И. Фаградянц. 2014.

• начальная фаза гармонических колебаний
• начальная фаза синусоидального электрического тока

Смотреть что такое «начальная фаза» в других словарях:

• начальная фаза — Значение фазы синусоидального тока в начальный момент времени. Примечание — Аналогично определяют начальные фазы синусоидальных электрического напряжения, электродвижущей силы, магнитного потока и т. д. [ГОСТ Р 52002 2003] Тематики… …   Справочник технического переводчика

• начальная фаза

  — pradinė fazė statusas T sritis automatika atitikmenys: angl. initial phase vok. Anfangsphase, f rus. начальная фаза, f pranc. phase initiale, f …   Automatikos terminų žodynas

• начальная фаза — pradinė fazė statusas T sritis fizika atitikmenys: angl. initial phase vok. Anfangsphase, f rus. начальная фаза, f pranc. phase initiale, f …   Fizikos terminų žodynas

• начальная фаза гармонических колебаний — начальная фаза Значение фазы гармонических колебаний в начальный момент времени. [Сборник рекомендуемых терминов. Выпуск 106. Механические колебания. Академия наук СССР. Комитет научно технической терминологии. 1987 г.] начальная фаза… …   Справочник технического переводчика

• начальная фаза гармонических колебаний — начальная фаза гармонических колебаний; начальная фаза Значение фазы гармонических колебаний в начальный момент времени …   Политехнический терминологический толковый словарь

• начальная фаза развития трещины — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN pop in …   Справочник технического переводчика

• Начальная фаза гармонических колебаний (вибрации) — 32. Начальная фаза гармонических колебаний (вибрации) Начальная фаза Фаза гармонических колебаний (вибрации) в начальный момент времени (см. термин 29) Источник: ГОСТ 24346 80: Вибрация. Термины и определения оригинал документа …   Словарь-справочник терминов нормативно-технической документации

• начальная фаза колебаний — pradinė virpesių fazė statusas T sritis automatika atitikmenys: angl. initial phase of oscillation vok. Anfangsschwingungsphase, f rus. начальная фаза колебаний, f pranc. phase initiale d oscillations, f …   Automatikos terminų žodynas

• начальная фаза (синусоидального электрического тока) — 243 начальная фаза (синусоидального электрического тока) Значение фазы синусоидального тока в начальный момент времени. Примечание Аналогично определяют начальные фазы синусоидальных электрического напряжения, электродвижущей силы, магнитного… …   Словарь-справочник терминов нормативно-технической документации

• Начальная фаза (синусоидального электрического тока) — 1. Значение фазы синусоидального тока в начальный момент времени Употребляется в документе: ГОСТ Р 52002 2003 Электротехника. Термины и определения основных понятий …   Телекоммуникационный словарь

Фаза колебаний — Класс!ная физика

Фаза колебаний

Фаза колебаний (φ) характеризует гармонические колебания.
Выражается фаза в угловых единицах — радианах.

При заданной амплитуде колебаний координата колеблющегося тела в любой момент времени однозначно определяется аргументом косинуса или синуса:

φ = ω₀t.

Фаза колебаний определяет при заданной амплитуде состояние колебательной системы (значение координаты, скорости и ускоренияв) любой момент времени.

Колебания с одинаковыми амплитудами и частотами могут различаться фазами.

Отношение указывает, сколько периодов прошло от момента начала колебаний.

График зависимости координаты колеблющейся точки от фазы.

Гармонические колебания можно представить как с помощью функции синуса, так и косинуса, т.к.
синус отличается от косинуса сдвигом аргумента на .

Поэтому вместо формулы

х = х_m cos ω₀t

можно для описания гармонических колебаний использовать формулу

Но при этом начальная фаза, т. е. значение фазы в момент времени t = 0, равна не нулю, а .
В разных ситуациях удобно использовать синус или косинус.

Какой формулой пользоваться при расчетах?

1. Если в начале колебаний выводят маятник из положения равновесия, то удобнее пользоваться формулой с применением косинуса.
2. Если координата тела в начальный момент была бы равна нулю, то удобнее пользоваться формулой с применением синуса х = х_m sin ω₀t, т.к. при этом начальная фаза равна нулю.

3. Если в начальный момент времени (при t — 0) фаза колебаний равна φ, то уравнение колебаний можно записать в виде х = х_m sin (ω₀t + φ).

Сдвиг фаз

Колебания, описываемые формулами через синус и косинус, отличаются друг от друга только фазами.
Разность фаз (или сдвиг фаз) этих колебаний составляет .
Графики зависимости координат от времени для двух гармонических колебаний, сдвинутых по фазе на :
где
график 1 — колебания, совершающиеся по синусоидальному закону,
график 2 — колебания, совершающиеся по закону косинуса.

Для определения разности фаз двух колебаний надо колеблющиеся величины выразить через одну и ту же тригонометрическую функцию — косинус или синус.

Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин

Механические колебания. Физика, учебник для 11 класса — Класс!ная физика

Свободные, затухающие и вынужденные колебания — Условия возникновения свободных колебаний. Математический маятник — Динамика колебательного движения. Уравнение движения маятника — Гармонические колебания — Фаза колебаний — Превращение энергии при гармонических колебаниях — Вынужденные колебания. Резонанс — Примеры решения задач — Краткие итоги главы

Фаза колебаний — это… Что такое Фаза колебаний?

У этого термина существуют и другие значения, см. Фаза.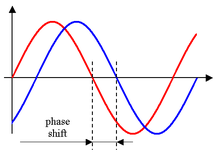 Иллюстрация разности фаз двух колебаний одинаковой частоты

Фа́за колеба́ний — физическая величина, используемая по преимуществу для описания гармонических или близких к гармоническим^[1][2] колебаний, меняющаяся со временем (чаще всего равномерно растущая со временем), при заданной амплитуде (для затухающих колебаний — при заданной начальной амплитуде и коэффициенте затухания) определяющая состояние колебательной системы в (любой) данный момент времени.

[3] Равно применяется для описания волн, главным образом — монохроматических или близких к монохроматичности.

Фаза колебания (в электросвязи для периодического сигнала f(t) с периодом T) — это дробная часть t/T периода T, на которую t сдвинуто относительно произвольного начала координат. Началом координат обычно считается момент предыдущего перехода функции через нуль в направлении от отрицательных значений к положительным.

В большинстве случаев о фазе говорят применительно к гармоническим (синусоидальным или описывающимся мнимой экспонентой) колебаниям (или монохроматическим волнам, также синусоидальным или описывающимся мнимой экспонентой).

Для таких колебаний:

,

,

,

или волн,

например волн, распространяющихся в одномерном пространстве:

,

,

,

или волн, распространяющихся в трехмерном пространстве (или пространстве любой размерности):

,

,

,

фаза колебаний определяется как аргумент этой функции (одной из перечисленных, в каждом случае из контекста ясно, какой именно), описывающей гармонический колебательный процесс или монохроматическую волну.

• Поскольку синус и косинус совпадают друг с другом при сдвиге аргумента (то есть фазы) на во избежание путаницы лучше пользоваться для определения фазы только одной из этих двух функций, а не той и другой одновременно. По обычному соглашению фазой считают
  аргумент косинуса, а не синуса.^[4][5]

То есть, для колебания фаза

,

для волны в одномерном пространстве

,

для волны в трехмерном пространстве или пространстве любой другой размерности:

,

где — угловая частота (чем величина выше, тем быстрее растет фаза с течением времени), t— время, — фаза при t=0 — начальная фаза; k — волновое число, x — координата, k — волновой вектор, x — набор (декартовых) координат, характеризующих точку пространства (радиус-вектор).

Фаза выражается в угловых единицах (радианах, градусах) или в циклах (долях периода):

1 цикл = 2 радиан = 360 градусов.

• В физике, особенно при написании формул, преимущественно (и по умолчанию) используется радианное представление фазы, измерение ее в циклах или периодах (за исключением словесных формулировок) в целом довольно редко, однако измерение в градусах встречается достаточно часто (по-видимому, как предельно явное и не приводящее к путанице, поскольку знак градуса принято никогда не опускать ни в устной речи, ни на письме), особенно часто в инженерных приложениях (как, например, электротехника).

Иногда (в квазиклассическом приближении, где используются волны, близкие к монохроматическим, но не строго монохроматические, а также в формализме интеграла по траекториям, где волны могут быть и далекими от монохроматизма, хотя всё же подобны монохроматическим) фаза рассматривается как зависящая от времени и пространственных координат не как линейная функция, а как в принципе произвольная^[6] функция координат и времени:

Связанные термины

Если две волны (два колебания) полностью совпадают друг с другом, говорят, что волны находятся в фазе. В случае, если моменты максимума одного колебания совпадают с моментами минимума другого колебания (или максимумы одной волны совпадают с минимумами другой), говорят, что колебания (волны) находятся в противофазе. При этом, если волны одинаковы (по амплитуде), в результате сложения происходит их взаимное уничтожение (точно, полностью — лишь при условии монохроматичности или хотя бы симметричности волн, в предположении линейности среды распространения итд).

Действие

Одна из наиболее фундаментальных физических величин, на которой построено современное описание практически любой достаточно фундаментальной физической системы^[7] — действие — по своему смыслу является фазой.

Примечания

1. ↑ В специальном случае формализма интеграла по траекториям близость колебания к гармоническому (или волны к монохроматической) имеет довольно необычный смысл.
2. ↑ Иногда понятие фазы может оказаться небесполезным и для описания достаточно произвольных (далеких от гармонических) колебаний или волн, или даже непериодических процессов, однако это применение достаточно редко, и польза его в этом случае обычно достаточно ограниченна.
3. ↑ Фаза колебаний в словаре по естественным наукам.(недоступная ссылка — история) Проверено 29 апреля 2010.
4. ↑ Хотя нет принципиальной причины не сделать противоположный выбор, что иногда и делается некоторыми авторами.
5. ↑ Таким образом, обычно, в соответствии с этим соглашением начальная фаза колебания вида считается равной (синус отстает от косинуса по фазе).
6. ↑ Хотя в части случаев с наложением условий на скорость изменения итп, несколько ограничивающих произвольность функции.
7. ↑ Существуют системы, формализм действия к которым применять неудобно и даже такие, к которым он по сути неприменим, однако в современном понимании такие системы делятся на два класса: 1) не фундаментальные (т.е. описываемые неточно, и мыслится, что будучи описана более точно такая система может быть — в принципе — описана через действие), 2) относящиеся к далеко не общепризнанным теоретическим построениям.

Фаза колебаний, сдвиг фаз

 

Еще одной характеристикой гармонических колебаний является фаза колебаний.

Как нам уже известно, при заданной амплитуде колебаний, в любой момент времени мы можем определить координату тела. Она будет однозначно задаваться аргументом тригонометрической функции φ = ω0*t. Величина φ, которая стоит под знаком тригонометрической функции, называется фазой колебаний.

Для фазы единицами измерения являются радианы. Фаза однозначно определяет не только координату теда в любой момент времени, но так же скорость или ускорение. Поэтому считается, что фаза колебаний определяет состояние колебательной системы в любой момент времени.

Конечно же при условии что задана амплитуда колебаний. Два колебания, у которых одинаковые частота и период колебаний могут отличаться друг от друга фазами.

Если выразить время t в количестве периодов, которые пройдены от начала колебаний, то любому значению времени t, соответствует значение фазы, выраженной в радианах. Например, если взять время t = Т/4, то этому значению будет соответствовать значение фазы pi/2.

Таким образом, мы можем изобразить график зависимости координаты не от времени, а от фазы, и получим точно такую же зависимость. На следующем рисунке представлен такой график.

Начальная фаза колебаний

При описании координаты колебательного движения мы использовали функции синуса и косинуса. Для косинуса мы записывали следующую формулу:

Но мы можем описать эту же траекторию движения и с помощью синуса. При этом нам необходимо сдвинуть аргумент на pi/2, то есть отличие синуса от косинуса — pi/2 или четверть периода.

Значение pi/2 называется начальной фазой колебания. Начальная фаза колебания — положение тела в начальный момент времени t = 0. Для того, чтобы заставить маятник колебаться, мы должны вывести его из положения равновесия. Мы можем это сделать двумя путями:

• Отвести его в сторону и отпустить.
• Ударить по нему.

В первом случае, мы сразу же изменяем координату тела, то есть, в начальный момент времени координата будет равна значению амплитуды. Для описания такого колебания удобнее использовать функцию косинуса и форму

либо же формулу

где φ- начальная фаза колебания.

Если мы ударим по телу, то в начальный момент времени его координата равняется нулю, и в таком случае удобнее использовать форму:

Два колебания, которые различаются только начальной фазой, называются сдвинутыми по фазе.

Например, для колебаний описанных следующими формулами:

• x = Xm*sin(ω0*t),
• x = Xm*sin(ω0*t+pi/2),

сдвиг фаз равен pi/2.

Сдвиг фаз еще иногда называют разностью фаз.

На следующем рисунке представлены два колебания сдвинутые друг относительно друга на разность фаз pi/2.

Нужна помощь в учебе?

Предыдущая тема: Гармонические колебания: амплитуда и период колебаний
Следующая тема:&nbsp&nbsp&nbspПревращение энергии при гармонических колебаниях: формулы и рисунки

Все неприличные комментарии будут удаляться.

Как найти начальную фазу колебаний

При расчетах, связанных с циклическими явлениями (например, при описании колебаний математического маятника) важно уметь находить состояние системы, с которого начался отсчет процесса — начальную фазу.

Фаза представляет собой угловую координату, описываемую формулой

$\varphi = ω_0 \cdot t$,

где $ω_0$ — угловая скорость, $t$ — прошедшее время.

Выбрав в качестве единицы измерения углов радианы, формулу можно переписать как

$\varphi = 2 \cdot \pi \cdot \frac{t}{T}$,

где $2 \cdot \pi$ — количество радиан в полном цикле, $T$ — период одного колебания. Отношение $\frac{t}{T}$ показывает, сколько колебаний (полных и неполных) выполнила система.

Фазы циклических процессов с одинаковыми угловыми скоростями и длящиеся одинаковое время, могут отличаться в связи с тем, что они в момент начала наблюдений находились в разных состояниях. Такая разница называется сдвигом фаз. Например, углы отклонения от вертикали двух идентичных маятников, колеблющиеся с одинаковой частотой, могут различаться. Это зависит от того, на какой начальный угол каждый из них был отклонен в момент начала отсчета времени. Сдвиг фаз может быть обусловлен тем, что маятники были запущены в разное время (до начала отсчета), или одному из них при меньшем начальном отклонении от вертикали было придано дополнительное угловое ускорение за счет удара и т.п.

Циклический процесс, в отличие от движения по незамкнутой траектории, характеризуется повторяемостью некоторой характеристики (например, напряжения в сети переменного тока), что можно описать с помощью функций синуса или косинуса:

$x = A \cdot \cos(ω_0 \cdot t + \varphi)$,

$x = A \cdot \sin(ω_0 \cdot t + \varphi)$.

где $A$ — амплитуда (максимальный размах) колебаний, $\varphi$ — начальная фаза.

Функцией синуса удобнее пользоваться, когда угловая координата тела в момент начала наблюдений равна нулю, функцией косинуса — когда имеет место сдвиг фаз. Так, «косинус фи» — устойчивое понятие, применяемое в электротехнике при описании переменного тока.

Пример 1

Найти начальную фазу колебаний с амплитудой $A = 0,2 м$, если в момент начала измерений $t_0$ смещение циклического параметра $x$ составляло $-0,2 м$.

Подставим в уравнение числовые значения:

$x = A \cdot \sin(\omega_0 \cdot t + \varphi)$

$-0,2 = 0,2 \cdot \sin(\omega_0 \cdot 0 + \varphi) \implies -0,2 = 0,2 \cdot \sin(\varphi)$

$\sin(\varphi) = \frac{-0,2}{0,2}$

$\varphi = \arcsin(\frac{-0,2}{0,2}) = \frac{3 \pi}{2}$

Ответ: колебания начались с фазы $1\frac{1}{2} \pi$

начальная фаза — это… Что такое начальная фаза?



начальная фаза

 

начальная фаза
Значение фазы синусоидального тока в начальный момент времени.
Примечание — Аналогично определяют начальные фазы синусоидальных электрического напряжения, электродвижущей силы, магнитного потока и т. д.
[ГОСТ Р 52002-2003]

 

Тематики

• электротехника, основные понятия

Синонимы

• начальная фаза синусоидального электрического тока

Справочник технического переводчика. – Интент. 2009-2013.

• начальная угловая скорость вращения катапультируемой системы
• подводный фотоаппарат

Смотреть что такое «начальная фаза» в других словарях:

• начальная фаза — гармонических колебаний; начальная фаза Значение фазы гармонических колебаний в начальный момент времени …   Политехнический терминологический толковый словарь

• начальная фаза — pradinė fazė statusas T sritis automatika atitikmenys: angl. initial phase vok. Anfangsphase, f rus. начальная фаза, f pranc. phase initiale, f …   Automatikos terminų žodynas

• начальная фаза — pradinė fazė statusas T sritis fizika atitikmenys: angl. initial phase vok. Anfangsphase, f rus. начальная фаза, f pranc. phase initiale, f …   Fizikos terminų žodynas

• начальная фаза гармонических колебаний — начальная фаза Значение фазы гармонических колебаний в начальный момент времени. [Сборник рекомендуемых терминов. Выпуск 106. Механические колебания. Академия наук СССР. Комитет научно технической терминологии. 1987 г.] начальная фаза… …   Справочник технического переводчика

• начальная фаза гармонических колебаний — начальная фаза гармонических колебаний; начальная фаза Значение фазы гармонических колебаний в начальный момент времени …   Политехнический терминологический толковый словарь

• начальная фаза развития трещины — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN pop in …   Справочник технического переводчика

• Начальная фаза гармонических колебаний (вибрации) — 32. Начальная фаза гармонических колебаний (вибрации) Начальная фаза Фаза гармонических колебаний (вибрации) в начальный момент времени (см. термин 29) Источник: ГОСТ 24346 80: Вибрация. Термины и определения оригинал документа …   Словарь-справочник терминов нормативно-технической документации

• начальная фаза колебаний — pradinė virpesių fazė statusas T sritis automatika atitikmenys: angl. initial phase of oscillation vok. Anfangsschwingungsphase, f rus. начальная фаза колебаний, f pranc. phase initiale d oscillations, f …   Automatikos terminų žodynas

• начальная фаза (синусоидального электрического тока) — 243 начальная фаза (синусоидального электрического тока) Значение фазы синусоидального тока в начальный момент времени. Примечание Аналогично определяют начальные фазы синусоидальных электрического напряжения, электродвижущей силы, магнитного… …   Словарь-справочник терминов нормативно-технической документации

• Начальная фаза (синусоидального электрического тока) — 1. Значение фазы синусоидального тока в начальный момент времени Употребляется в документе: ГОСТ Р 52002 2003 Электротехника. Термины и определения основных понятий …   Телекоммуникационный словарь

начальная фаза гармонических колебаний — это… Что такое начальная фаза гармонических колебаний?



начальная фаза гармонических колебаний

начальная фаза гармонических колебаний; начальная фаза

Значение фазы гармонических колебаний в начальный момент времени.

Политехнический терминологический толковый словарь. Составление: В. Бутаков, И. Фаградянц. 2014.

• начальная потеря напора в фильтре
• начальная фаза

Смотреть что такое «начальная фаза гармонических колебаний» в других словарях:

• начальная фаза гармонических колебаний — начальная фаза Значение фазы гармонических колебаний в начальный момент времени. [Сборник рекомендуемых терминов. Выпуск 106. Механические колебания. Академия наук СССР. Комитет научно технической терминологии. 1987 г.] начальная фаза… …   Справочник технического переводчика

• Начальная фаза гармонических колебаний (вибрации) — 32. Начальная фаза гармонических колебаний (вибрации) Начальная фаза Фаза гармонических колебаний (вибрации) в начальный момент времени (см. термин 29) Источник: ГОСТ 24346 80: Вибрация. Термины и определения оригинал документа …   Словарь-справочник терминов нормативно-технической документации

• начальная фаза — гармонических колебаний; начальная фаза Значение фазы гармонических колебаний в начальный момент времени …   Политехнический терминологический толковый словарь

• начальная — 3.1 начальная общеобразовательная школа: Школа, организуемая как самостоятельное учреждение, а также в составе основной или средней общеобразовательной школы (срок обучения в начальной школе 4 года). Источник: ТСН 31 328 2004: Общеобразовательные …   Словарь-справочник терминов нормативно-технической документации

• фаза — 15 фаза Проводник, пучок проводников, ввод, обмотка или иной элемент многофазной системы переменного тока, являющийся токоведущим при нормальном режиме работы 601 03 09 de Aussenleiter en phase fr phase Источник: ГОСТ 24291 90: Электрическая… …   Словарь-справочник терминов нормативно-технической документации

• Фаза колебаний — Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей. У этого термина существуют и другие значения, см. Фаза …   Википедия

• Фаза колебаний —         Аргумент функции cos (ωt + φ), описывающей гармонический колебательный процесс (ω– круговая частота, t – время, φ– начальная Ф. к., т. е. Ф. к. в начальный момент времени t = 0). Ф. к. определяется с точностью до произвольного слагаемого …   Большая советская энциклопедия

• ГОСТ 24346-80: Вибрация. Термины и определения — Терминология ГОСТ 24346 80: Вибрация. Термины и определения оригинал документа: 112. Автоколебания Колебания системы, возникающие в результате самовозбуждения Определения термина из разных документов: Автоколебания 137. Активная виброзащита… …   Словарь-справочник терминов нормативно-технической документации

• Гармонический осциллятор — У этого термина существуют и другие значения, см. Осциллятор. Гармонический осциллятор (в классической механике)  система, которая при смещении из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению x… …   Википедия

• Гармонические колебания — Графики функций f(x) = sin(x) и g(x) = cos(x) на декартовой плоскости. Гармоническое колебание  колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидально …   Википедия