определения, формулы, примеры, угол поворота
Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функцийСинус угла (sin α) — отношение противолежащего этому углу катета к гипотенузе.
Косинус угла (cosα) — отношение прилежащего катета к гипотенузе.
Тангенс угла (tg α) — отношение противолежащего катета к прилежащему.
Котангенс угла (ctg α) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
Приведем иллюстрацию.
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Важно помнить!Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.
Угол поворота
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.
Угол поворота в градусах или радианах выражается любым действительным числом от -∞ до +∞.
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами (1, 0) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A1. Определение дается через координаты точки A1(x , y).
Синус (sin) угла поворотаСинус угла поворота α — это ордината точки A1(x , y). sin α=y
Косинус (cos) угла поворотаКосинус угла поворота α — это абсцисса точки A1(x , y). cos α=х
Тангенс (tg) угла поворотаТангенс угла поворота α — это отношение ординаты точки A1(x , y) к ее абсциссе. tg α=yx
Котангенс (ctg) угла поворотаКотангенс угла поворота α — это отношение абсциссы точки A1(x , y) к ее ординате. ctg α=xy
Синус и косинус определены для любого угла поворота.
Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (0, 1) и (0, -1). В таких случаях выражение для тангенса tg α=yx просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Синус и косинус определены для любых углов α.
Тангенс определен для всех углов, кроме α=90°+180°·k, k∈Z (α=π2+π·k, k∈Z)
Котангенс определен для всех углов, кроме α=180°·k, k∈Z (α=π·k, k∈Z)
При решении практических примеров не говорят «синус угла поворота α». Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеЧисла
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числаСинусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в 
Например, синус числа 10π равен синусу угла поворота величиной 10π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности — точка A c координатами (1, 0).
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус числа t — ордината точки единичной окружности, соответствующей числу t. sin t=y
Косинус числа t — абсцисса точки единичной окружности, соответствующей числу t. cos t=x
Тангенс (tg) числа tТангенс числа t — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. tg t=yx=sin tcos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α, отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса.
Можно сказать, что sin α, cos α, tg α, ctg α — это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа
Синус, косинус, тангенс и котангенс — основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов.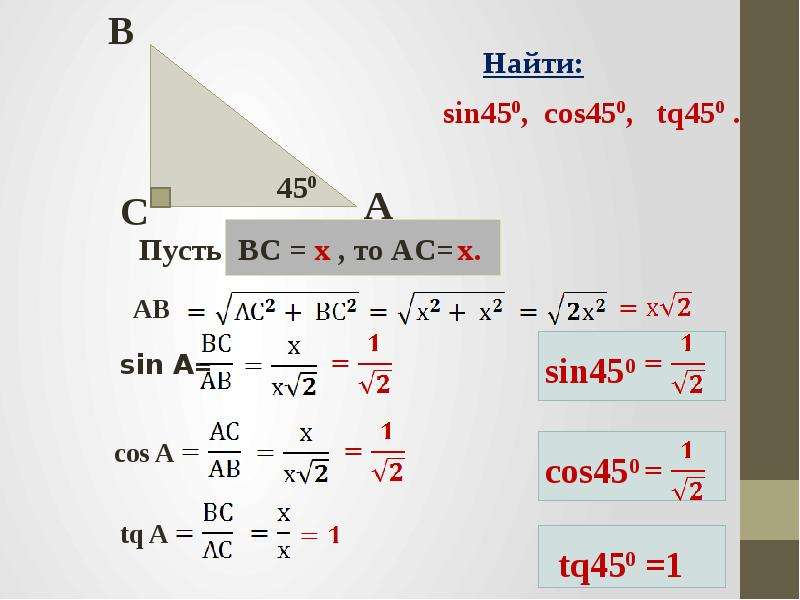
Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A(1,0) на угол величиной до 90 градусов и проведем из полученной точки A1(x,y) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A1OH равен углу поворота α, длина катета OH равна абсциссе точки A1(x,y). Длина катета, противолежащего углу, равна ординате точки A1(x,y), а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α=A1HOA1=y1=y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α, при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Синус, косинус, тангенс и котангенс: основные формулы
определения, формулы, примеры, угол поворота
Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Синус угла (sin α) — отношение противолежащего этому углу катета к гипотенузе.
Косинус угла (cosα) — отношение прилежащего катета к гипотенузе.
Тангенс угла (tg α) — отношение противолежащего катета к прилежащему.
Котангенс угла (ctg α) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
Приведем иллюстрацию.
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Важно помнить!Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.
Угол поворота
Определения, данные выше, относятся к острым углам.
В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от -∞ до +∞.
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами (1, 0) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A1. Определение дается через координаты точки A1(x , y).
Синус (sin) угла поворотаСинус угла поворота α — это ордината точки A1(x , y). sin α=y
Косинус (cos) угла поворотаКосинус угла поворота α — это абсцисса точки A1(x , y). cos α=х
Тангенс (tg) угла поворотаТангенс угла поворота α — это отношение ординаты точки A1(x , y) к ее абсциссе.
tg α=yx
Котангенс угла поворота α — это отношение абсциссы точки A1(x , y) к ее ординате. ctg α=xy
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (0, 1) и (0, -1). В таких случаях выражение для тангенса tg α=yx просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Важно помнить!Синус и косинус определены для любых углов α.
Тангенс определен для всех углов, кроме α=90°+180°·k, k∈Z (α=π2+π·k, k∈Z)
Котангенс определен для всех углов, кроме α=180°·k, k∈Z (α=π·k, k∈Z)
При решении практических примеров не говорят «синус угла поворота α».
Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеЧисла
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числаСинусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10π равен синусу угла поворота величиной 10π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности — точка A c координатами (1, 0).
Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус (sin) числа tСинус числа t — ордината точки единичной окружности, соответствующей числу t. sin t=y
Косинус (cos) числа tКосинус числа t — абсцисса точки единичной окружности, соответствующей числу t. cos t=x
Тангенс (tg) числа tТангенс числа t — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t.
tg t=yx=sin tcos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α, отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).
Можно сказать, что sin α, cos α, tg α, ctg α — это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t._10.1.jpg)
Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Синус, косинус, тангенс и котангенс — основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A(1,0) на угол величиной до 90 градусов и проведем из полученной точки A1(x,y) перпендикуляр к оси абсцисс.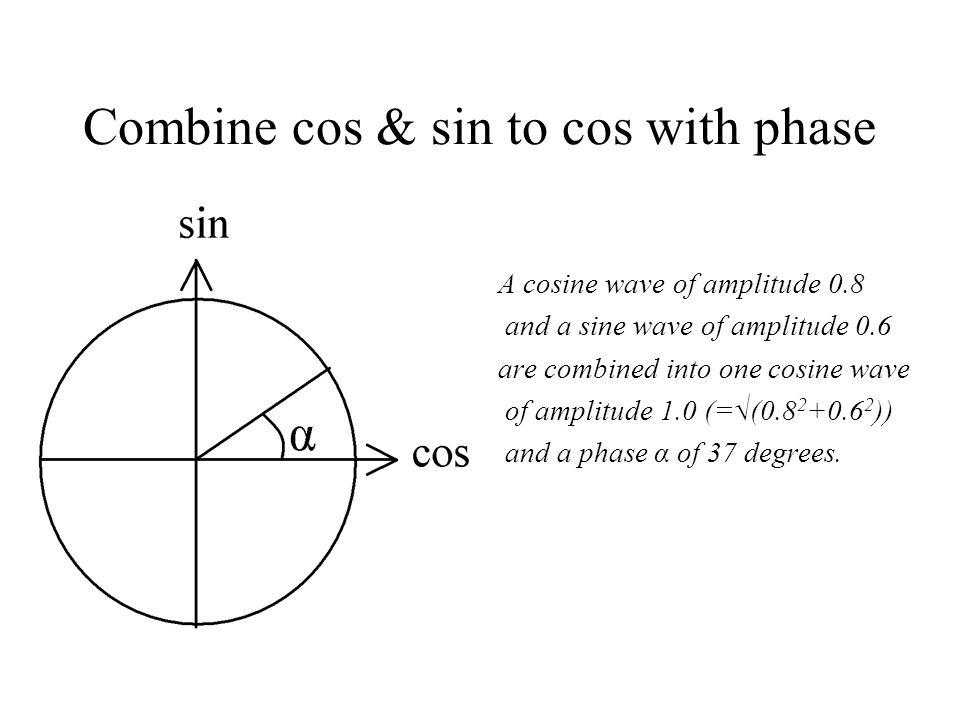
В полученном прямоугольном треугольнике угол A1OH равен углу поворота α, длина катета OH равна абсциссе точки A1(x,y). Длина катета, противолежащего углу, равна ординате точки A1(x,y), а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α=A1HOA1=y1=y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α, при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Синус, косинус, тангенс и котангенс: основные формулы
определения, формулы, примеры, угол поворота
Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии.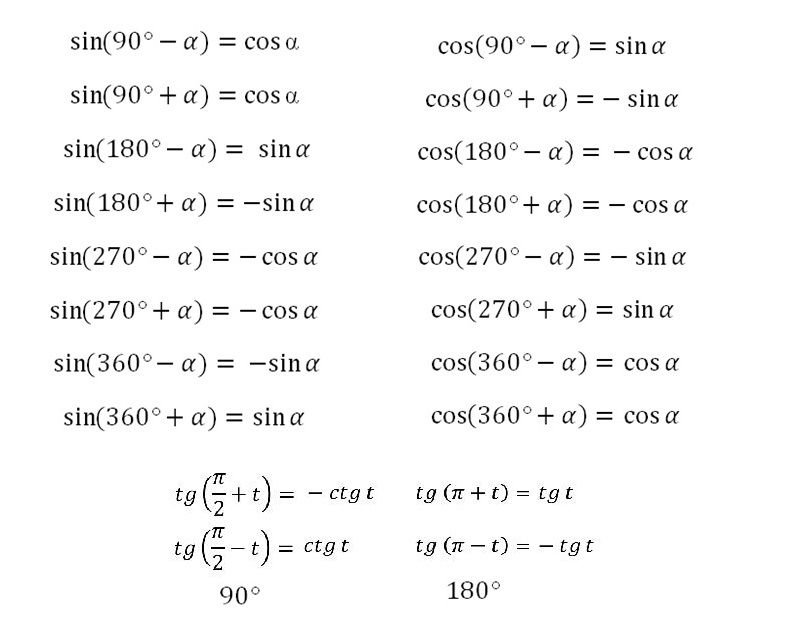
Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функцийСинус угла (sin α) — отношение противолежащего этому углу катета к гипотенузе.
Косинус угла (cosα) — отношение прилежащего катета к гипотенузе.
Тангенс угла (tg α) — отношение противолежащего катета к прилежащему.
Котангенс угла (ctg α) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
Приведем иллюстрацию.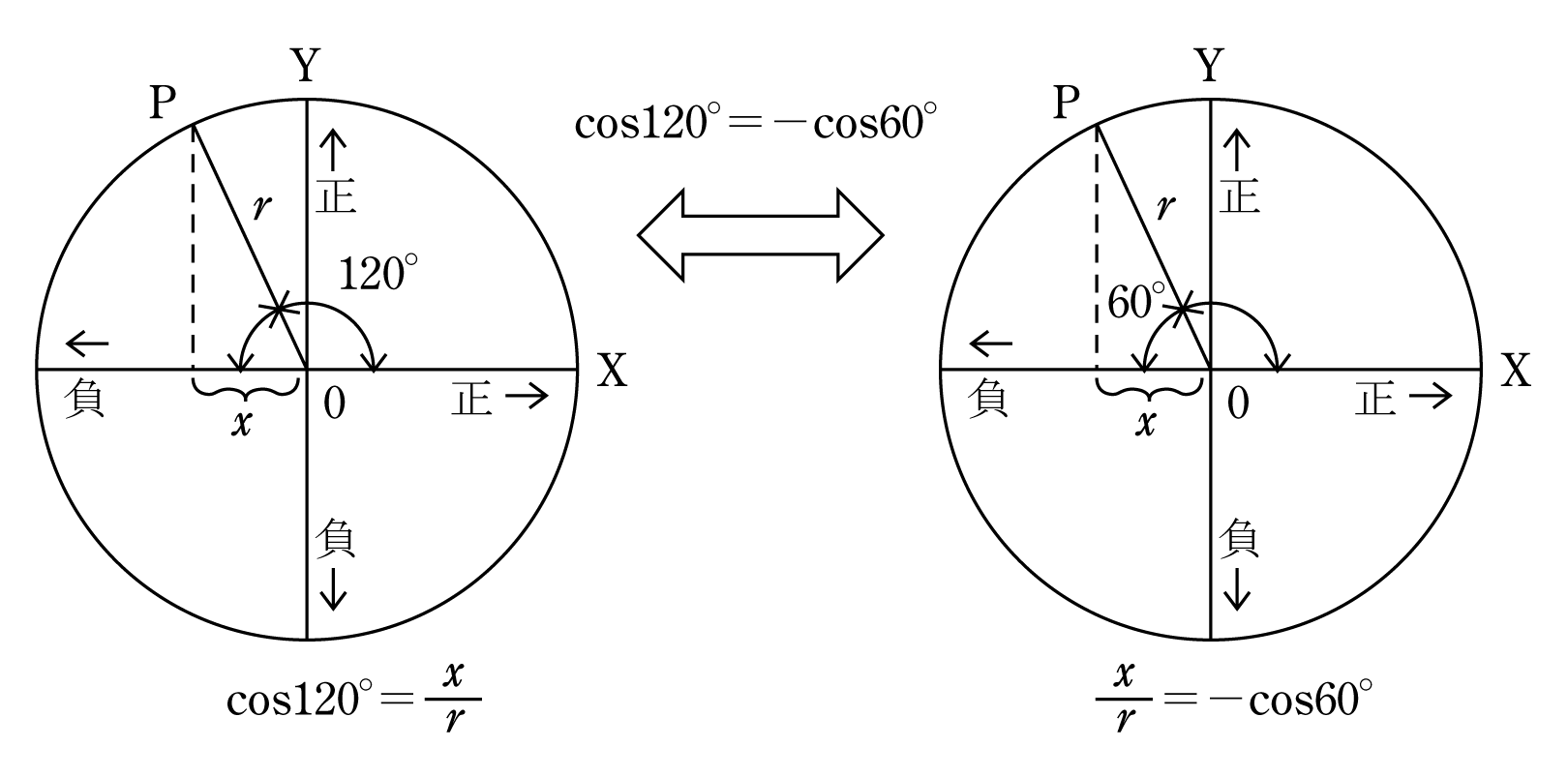
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Важно помнить!Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.
Угол поворота
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от -∞ до +∞.
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами (1, 0) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A1. Определение дается через координаты точки A1(x , y).
Синус (sin) угла поворотаСинус угла поворота α — это ордината точки A1(x , y). sin α=y
Косинус (cos) угла поворотаКосинус угла поворота α — это абсцисса точки A1(x , y). cos α=х
Тангенс (tg) угла поворотаТангенс угла поворота α — это отношение ординаты точки A1(x , y) к ее абсциссе. tg α=yx
Котангенс (ctg) угла поворотаКотангенс угла поворота α — это отношение абсциссы точки A1(x , y) к ее ординате. ctg α=xy
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (0, 1) и (0, -1).
В таких случаях выражение для тангенса tg α=yx просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Синус и косинус определены для любых углов α.
Тангенс определен для всех углов, кроме α=90°+180°·k, k∈Z (α=π2+π·k, k∈Z)
Котангенс определен для всех углов, кроме α=180°·k, k∈Z (α=π·k, k∈Z)
При решении практических примеров не говорят «синус угла поворота α». Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеЧисла
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числаСинусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10π равен синусу угла поворота величиной 10π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности — точка A c координатами (1, 0).
Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус числа t — ордината точки единичной окружности, соответствующей числу t. sin t=y
Косинус (cos) числа tКосинус числа t — абсцисса точки единичной окружности, соответствующей числу t. cos t=x
Тангенс (tg) числа tТангенс числа t — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. tg t=yx=sin tcos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α, отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса.
Котангенс, как сказано выше, определен для всех α, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).
Можно сказать, что sin α, cos α, tg α, ctg α — это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Основные функции тригонометрииСинус, косинус, тангенс и котангенс — основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов.
Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A(1,0) на угол величиной до 90 градусов и проведем из полученной точки A1(x,y) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A1OH равен углу поворота α, длина катета OH равна абсциссе точки A1(x,y). Длина катета, противолежащего углу, равна ординате точки A1(x,y), а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α=A1HOA1=y1=y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α, при альфа лежащем в пределах от 0 до 90 градусов.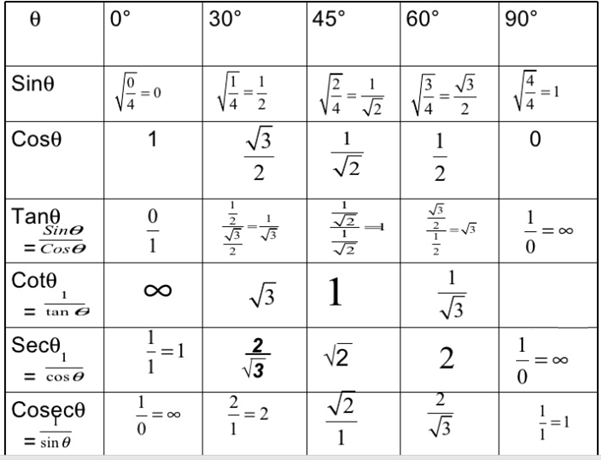
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Синус, косинус, тангенс и котангенс: основные формулы
Функция COS
В этой статье описаны синтаксис формулы и использование функции COS в Microsoft Excel.
Описание
Возвращает косинус заданного угла.
Синтаксис
COS(число)
Аргументы функции COS описаны ниже.
Замечания
Если угол задан в градусах, умножьте его на ПИ()/180 или воспользуйтесь функцией РАДИАНЫ, чтобы преобразовать его в радианы.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel.
Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Формула |
Описание |
Результат |
|
=COS(1,047) |
Косинус 1,047 радиан |
0,5001711 |
|
=COS(60*ПИ()/180) |
Косинус 60 градусов |
0,5 |
|
=COS(РАДИАНЫ(60)) |
Косинус 60 градусов |
0,5 |
Тригонометрия за 5 минут! Тригонометрические функции и тригонометрический круг простыми словами | Клуб любителей математики
Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии «на пальцах».
Тригонометрические функции связаны с соотношениями сторон в прямоугольном треугольнике:
- Синус угла – отношение противолежащего катета к гипотенузе;
- Косинус угла – отношение прилежащего катета к гипотенузе;
- Тангенс угла – отношение противолежащего катета к прилежащему;
- Котангенс угла – отношение прилежащего катета к противолежащему.
Или в виде формул:
Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).
Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.
Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.
Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.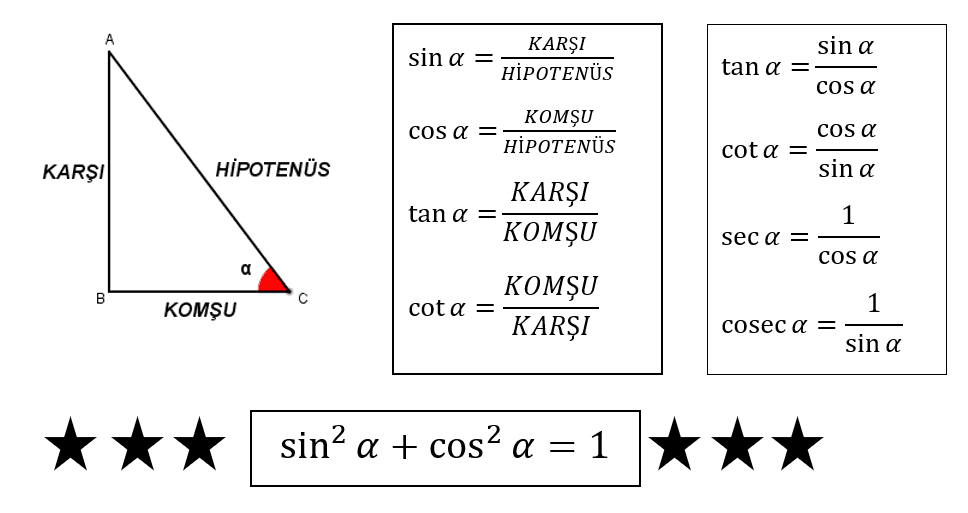
Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.
Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.
Значения тригонометрических функций
для первой четверти круга (0° – 90°)
| 0° | 30° | 45° | 60° | 90° | sin | 0 | 1 | cos | 1 | 0 | tg | 0 | 1 | √3 | – | ctg | – | √3 | 1 | 0 |
|---|
Принцип повтора знаков тригонометрических функций
Угол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону.
В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ.
Например, значения тригонометрических функций для углов 270° и -90° равны.
Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно.
Тригонометрический круг
Углы в радианах
Для математических вычислений тригонометрических функций используются углы не в градусах, а в радианах. Что такое радиан? Угол в радианах равен отношению длины дуги окружности к радиусу. Полный круг в 360° соответствует длине окружности 2πr. Следовательно 360° в радианах равно 2π, а 180° равно π радиан.
Как преобразовывать градусы в радианы? Нужно значение в градусах разделить на 180° и умножить на π.
Например, для угла 90° будет · π = πЧтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций.
Онлайн тренажердля запоминания значений тригонометрических функций для разных углов |
Простые тригонометрические тождества
Используя вышеописанные формулы:
тангенс угла выражается через отношение синуса к косинусу:
Соответственно котангенс выражается аналогично:
Также можно заметить, что произведение тангенса на котангес равно единице:
tg(a) · ctg(a) = · =- sin(a) · cos(a)
- cos(a) · sin(a)
Иными словами, тангенс угла обратно пропорционален котангенсу угла и наоборот:
tg(a) · ctg(a) = 1 ; tg(a) = ; сtg(a) =Используя теорему Пифагора в треугольнике, что сумма квадратов катетов равно квадрату гипотенузы
r2 = s2 + c2 = (sin(a) · r)2 + (cos(a) · r)2;
r2 · (sin(a)2 + cos(a)2) = r2
Сократим обе части на r2, получим:
sin2a + cos2a = 1
Разделив обе части на квадрат синуса или квадрат косинуса, получим еще два основных тригонометрических тождества:
Косинус
Примеры:
\(\cos{30^°}=\)\(\frac{\sqrt{3}}{2}\)
\(\cos\)\(\frac{π}{3}\)\(=\)\(\frac{1}{2}\)
\(\cos2=-0,416…\)
Содержание:
Аргумент и значение
Косинус острого угла
Косинус острого угла можно определить с помощью прямоугольного треугольника — он равен отношению прилежащего катета к гипотенузе.
Пример:
1) Пусть дан угол и нужно определить косинус этого угла.
2) Достроим на этом угле любой прямоугольный треугольник.
3) Измерив, нужные стороны, можем вычислить косинус.
Косинус острого угла больше \(0\) и меньше \(1\)
Если при решении задачи косинус острого угла получился больше 1 или отрицательным, то значит где-то в решении есть ошибка.
Косинус числа
Числовая окружность позволяет определить косинус любого числа, но обычно находят косинус чисел как-то связанных с Пи: \(\frac{π}{2}\), \(\frac{3π}{4}\), \(-2π\).
Например, для числа \(\frac{π}{6}\) — косинус будет равен \(\frac{\sqrt{3}}{2}\). А для числа \(-\)\(\frac{3π}{4}\) он будет равен \(-\)\(\frac{\sqrt{2}}{2}\) (приблизительно \(-0,71\)).
Косинус для других часто встречающихся в практике чисел смотри в тригонометрической таблице.
Значение косинуса всегда лежит в пределах от \(-1\) до \(1\). При этом вычислен косинус может быть для абсолютно любого угла и числа.
Косинус любого угла
Благодаря числовой окружности можно определять косинус не только острого угла, но и тупого, отрицательного, и даже большего, чем \(360°\) (полный оборот). Как это делать — проще один раз увидеть, чем \(100\) раз услышать, поэтому смотрите картинку.
Теперь пояснение: пусть нужно определить косинус угла КОА с градусной мерой в \(150°\). Совмещаем точку О с центром окружности, а сторону ОК – с осью \(x\). После этого откладываем \(150°\) против часовой стрелки. Тогда ордината точки А покажет нам косинус этого угла.
Если же нас интересует угол с градусной мерой, например, в \(-60°\) (угол КОВ), делаем также, но \(60°\) откладываем по часовой стрелке.
И, наконец, угол больше \(360°\) (угол КОС) — всё аналогично тупому, только пройдя по часовой стрелке полный оборот, отправляемся на второй круг и «добираем нехватку градусов». Конкретно в нашем случае угол \(405°\) отложен как \(360° + 45°\).
Несложно догадаться, что для откладывания угла, например, в \(960°\), надо сделать уже два оборота (\(360°+360°+240°\)), а для угла в \(2640°\) — целых семь.
Стоит запомнить, что:
Косинус прямого угла равен нулю. Косинус тупого угла — отрицателен.
Знаки косинуса по четвертям
С помощью оси косинусов (то есть, оси абсцисс, выделенной на рисунке красным цветом) легко определить знаки косинусов по четвертям числовой (тригонометрической) окружности:
— там, где значения на оси от \(0\) до \(1\), косинус будет иметь знак плюс (I и IV четверти – зеленая область),
— там, где значения на оси от \(0\) до \(-1\), косинус будет иметь знак минус (II и III четверти – фиолетовая область).
Пример. Определите знак \(\cos 1\).2x}\)
— котангенсом и синусом того же угла (или числа): формулой \(ctgx=\)\(\frac{\cos{x}}{\sinx}\)
Другие наиболее часто применяемые формулы смотри здесь.
Функция \(y=\cos{x}\)
Если отложить по оси \(x\) углы в радианах, а по оси \(y\) — соответствующие этим углам значения косинуса, мы получим следующий график:
График данной функции называется косинусоида и обладает следующими свойствами:
— область определения – любое значение икса: \(D(\cos{x} )=R\)
— область значений – от \(-1\) до \(1\) включительно: \(E(\cos{x} )=[-1;1]\)
— четная: \(\cos(-x)=\cos{x}\)
— периодическая с периодом \(2π\): \(\cos(x+2π)=\cos{x}\)
— точки пересечения с осями координат:
ось абсцисс: \((\)\(\frac{π}{2}\)\(+πn\),\(;0)\), где \(n ϵ Z\)
ось ординат: \((0;1)\)
— промежутки знакопостоянства:
функция положительна на интервалах: \((-\)\(\frac{π}{2}\)\(+2πn;\) \(\frac{π}{2}\)\(+2πn)\), где \(n ϵ Z\)
функция отрицательна на интервалах: \((\)\(\frac{π}{2}\)\(+2πn;\)\(\frac{3π}{2}\)\(+2πn)\), где \(n ϵ Z\)
— промежутки возрастания и убывания:
функция возрастает на интервалах: \((π+2πn;2π+2πn)\), где \(n ϵ Z\)
функция убывает на интервалах: \((2πn;π+2πn)\), где \(n ϵ Z\)
— максимумы и минимумы функции:
функция имеет максимальное значение \(y=1\) в точках \(x=2πn\), где \(n ϵ Z\)
функция имеет минимальное значение \(y=-1\) в точках \(x=π+2πn\), где \(n ϵ Z\).
Смотрите также:
Синус
Тангенс
Котангенс
Решение уравнения \(\cosx=a\)
Что означает COS? -определения COS
Вы ищете значения COS? На следующем изображении вы можете увидеть основные определения COS. При желании вы также можете загрузить файл изображения для печати или поделиться им со своим другом через Facebook, Twitter, Pinterest, Google и т. Д. Чтобы увидеть все значения COS, пожалуйста, прокрутите вниз. Полный список определений приведен в таблице ниже в алфавитном порядке.
Основные значения COS
На следующем изображении представлены наиболее часто используемые значения COS. Вы можете записать файл изображения в формате PNG для автономного использования или отправить его своим друзьям по электронной почте.Если вы являетесь веб-мастером некоммерческого веб-сайта, пожалуйста, не стесняйтесь публиковать изображение определений COS на вашем веб-сайте.Все определения COS
Как упомянуто выше, вы увидите все значения COS в следующей таблице. Пожалуйста, знайте, что все определения перечислены в алфавитном порядке.Вы можете щелкнуть ссылки справа, чтобы увидеть подробную информацию о каждом определении, включая определения на английском и вашем местном языке.Что означает COS в тексте
В общем, COS является аббревиатурой или аббревиатурой, которая определяется простым языком. Эта страница иллюстрирует, как COS используется в обмена сообщениями и чат-форумах, в дополнение к социальным сетям, таким как VK, Instagram, Whatsapp и Snapchat. Из приведенной выше таблицы, вы можете просмотреть все значения COS: некоторые из них образовательные термины, другие медицинские термины, и даже компьютерные термины. Если вы знаете другое определение COS, пожалуйста, свяжитесь с нами. Мы включим его во время следующего обновления нашей базы данных. Пожалуйста, имейте в информации, что некоторые из наших сокращений и их определения создаются нашими посетителями. Поэтому ваше предложение о новых аббревиатур приветствуется! В качестве возврата мы перевели аббревиатуру COS на испанский, французский, китайский, португальский, русский и т.д. Далее можно прокрутить вниз и щелкнуть в меню языка, чтобы найти значения COS на других 42 языках.Синус, косинус, тангенс
Три функции, но та же идея.
Прямой треугольник
Синус, косинус и тангенс — основные функции, используемые в тригонометрии, они основаны на прямоугольном треугольнике.
Прежде чем углубляться в функции, полезно присвоить имя каждой стороне прямоугольного треугольника:
- «Противоположно» противоположно углу θ
- «Соседний» примыкает (рядом) к углу θ
- «Гипотенуза» — длинная
Соседний всегда находится рядом с углом
И Напротив находится напротив угла
Синус, косинус и тангенс
Синус , Косинус и Касательная (часто сокращается до sin , cos и tan ), каждый является отношением сторон прямоугольного треугольника :
Для заданного угла θ каждое отношение остается неизменным
независимо от того, насколько велик или мал треугольник
Для их расчета:
Разделите длину одной стороны на другую
Пример: Что такое синус 35 °?
Используя этот треугольник (длины до одного десятичного знака):
| sin (35 °) | = Напротив Гипотенуза |
| = 2.8 4,9 | |
| = 0,57 … | |
| cos (35 °) | = Соседний Гипотенуза |
| = 4,0 4,9 | |
| = 0,82 … | |
| загар (35 °) | = Напротив Соседний |
| = 2.8 4,0 | |
| = 0,70 … |
Размер не имеет значения
Треугольник может быть большим или маленьким, и соотношение сторон остается неизменным .
Только угол меняет соотношение.
Попробуйте перетащить точку «A», чтобы изменить угол, и точку «B», чтобы изменить размер:
На хороших калькуляторах есть sin, cos и tan, чтобы облегчить вам задачу.Просто вставьте угол и нажмите кнопку.
Но все же нужно помнить , что они означают !
В форме изображения:
Практика здесь:
Sohcahtoa
Как запомнить? Подумайте о «Sohcahtoa» !
Работает так:
Soh … | S ine = O pposite / H ypotenuse |
…ка … | C osine = A djacent / H ypotenuse |
… toa | T angent = O pposite / A djacent |
Вы можете узнать больше о sohcahtoa … пожалуйста, запомните это, это может помочь на экзамене!
Углы от 0 ° до 360 °
Перемещайте мышь, чтобы увидеть, как разные углы (в радианах или градусах) влияют на синус, косинус и тангенс.
алгебра / изображения / круг-треугольник.js
На этой анимации гипотенуза равна 1, образуя единичную окружность.
Обратите внимание, что соседняя сторона и противоположная сторона могут быть положительными или отрицательными, что также приводит к изменению синуса, косинуса и тангенса между положительными и отрицательными значениями.
| «Почему sin и tan не пошли на вечеринку?» «… всего cos !» |
Примеры
Пример: каковы синус, косинус и тангенс 30 °?
Классический треугольник 30 ° имеет гипотенузу длины 2, противоположную сторону длины 1 и смежную сторону √3:
Теперь мы знаем длины, можем вычислить функции:
Синус | sin (30 °) = 1/2 = 0.5 | |
Косинус | cos (30 °) = 1,732 / 2 = 0,866 … | |
Касательная | тангенс угла (30 °) = 1 / 1,732 = 0,577 … |
(возьмите калькулятор и проверьте его!)
Пример: каковы синус, косинус и тангенс угла 45 °?
Классический треугольник 45 ° имеет две стороны 1 и гипотенузу √2:
Синус | sin (45 °) = 1/1.414 = 0,707 … | |
Косинус | cos (45 °) = 1 / 1,414 = 0,707 … | |
Касательная | тангенс угла (45 °) = 1/1 = 1 |
Почему?
Почему эти функции важны?
- Потому что они позволяют нам вычислять углы, когда мы знаем стороны
- И они позволяют нам определять стороны, когда мы знаем углы
Пример: используйте синусоидальную функцию
, чтобы найти «d»Мы знаем:
- Кабель образует угол 39 ° с дном
- Кабель длиной 30 метров .
И мы хотим знать «d» (расстояние вниз).
Начать с: sin 39 ° = противоположно / гипотенуза
sin 39 ° = d / 30
Поменять местами стороны: d / 30 = sin 39 °
С помощью калькулятора найдите sin 39 °: d / 30 = 0,6293 …
Умножаем обе стороны на 30: d = 0,6293… x 30
d = 18,88 с точностью до 2 знаков после запятой.
Глубина «d» составляет 18,88 м
Упражнение
Попробуйте это бумажное упражнение, в котором вы можете вычислить синусоидальную функцию. для всех углов от 0 ° до 360 °, а затем нарисуйте результат.Это поможет вам понять эти относительно простые функции.
Вы также можете увидеть графики синуса, косинуса и тангенса.
И поиграйте с пружиной, создающей синусоидальную волну.
Менее распространенные функции
Чтобы завершить картину, есть еще 3 функции, в которых мы разделяем одну сторону на другую, но они не так часто используются.
Они равны 1, деленному на cos , 1, деленному на sin , и 1, деленному на tan :
Секущая функция: | сек ( θ ) = Гипотенуза Соседний | (= 1 / cos) | ||
Функция косеканса: | csc ( θ ) = Гипотенуза Напротив | (= 1 / sin) | ||
Функция котангенса: | детская кроватка ( θ ) = Соседний Напротив | (= 1 / tan) |
1494, 1495, 724, 725, 1492, 1493, 726, 727, 2362, 2363
Решающих треугольников
«Решение» означает поиск недостающих сторон и углов.
Когда мы знаем любые 3 стороны или углы … … мы можем найти остальные 3 | |
| (За исключением трех углов, потому что нам нужна как минимум одна сторона, чтобы определить размер треугольника.) |
Шесть различных типов
Если вам нужно собрать треугольник прямо сейчас , выберите один из шести вариантов ниже:
Какие стороны или углы вы уже знаете? (Нажмите на изображение или ссылку)
AAA
Три угла
AAS
Два угла и сторона , а не между
ASA
Два угла и сторона между
SAS
Две стороны и Угол между
SSA
Две стороны и Угол , а не между
SSS
Три стороны
… или читайте дальше, чтобы узнать, как стать экспертом по решению треугольников :
Ваш набор инструментов для решения проблем
Хотите научиться решать треугольники?
Представьте, что вы « The Solver » …
… тот, кого они просят, когда нужно решить треугольник!
В вашем наборе инструментов для решения (вместе с ручкой, бумагой и калькулятором) у вас есть эти 3 уравнения:
1. Углы всегда складываются до 180 °:
А + В + С = 180 °
Зная два угла, можно найти третий.
2. Закон синуса (правило синуса):
a sin (A) = b sin (B) = c sin (C)
Когда есть угол напротив стороны, это уравнение приходит на помощь.
Примечание: угол A противоположен стороне a, B противоположен b, а C противоположен c.
3. Закон косинусов (правило косинусов):
c 2 = a 2 + b 2 — 2ab cos (C)
Это сложнее всего использовать (и запомнить), но иногда требуется
, чтобы вывести вас из сложных ситуаций.
Это расширенная версия теоремы Пифагора, которая работает с
на любом треугольнике.
Шесть различных типов (подробнее)
Есть ШЕСТЬ различных типов головоломок, которые вам, возможно, придется решить. Познакомьтесь с ними:
1. AAA
Это означает, что нам даны все три угла треугольника, но нет сторон.
треугольников AAA невозможно решить дальше, так как нам нечего показать размер …. мы знаем форму, но не знаем, насколько она велика.
Нам нужно знать хотя бы одну сторону, чтобы идти дальше. См. Раздел «Решение треугольников AAA».
2. AAS
Это означает, что нам даны два угла треугольника и одна сторона, причем не является стороной, смежной с двумя данными углами.
Такой треугольник можно решить, используя Углы треугольника, чтобы найти другой угол, и Закон синусов, чтобы найти каждую из двух других сторон.См. Раздел «Решение треугольников AAS».
3. ASA
Это означает, что нам даны два угла треугольника и одна сторона, из которых соответствует стороне, смежной с двумя данными углами.
В этом случае мы находим третий угол, используя Углы треугольника, затем используем Закон синусов, чтобы найти каждую из двух других сторон. См. Раздел «Решение треугольников ASA».
4. SAS
Это означает, что нам даны две стороны и включенный угол.
Для этого типа треугольника мы должны сначала использовать Закон косинусов, чтобы вычислить третью сторону треугольника; затем мы можем использовать Закон синусов, чтобы найти один из двух других углов, и, наконец, использовать Углы треугольника, чтобы найти последний угол. См. Раздел «Решение треугольников SAS».
5. SSA
Это означает, что нам даны две стороны и один угол, который не входит в состав.
В этом случае сначала используйте Закон синусов, чтобы найти один из двух других углов, затем используйте Углы треугольника, чтобы найти третий угол, затем снова Закон синусов, чтобы найти последнюю сторону.См. Раздел «Решение треугольников SSA».
6. SSS
Это означает, что нам даны все три стороны треугольника, но нет углов.
В этом случае у нас нет выбора. Мы, , должны сначала использовать Закон косинусов, чтобы найти любой из трех углов, затем мы можем использовать Закон синусов (или снова использовать Закон косинусов), чтобы найти второй угол, и, наконец, Углы треугольника, чтобы найти третий угол. См. Раздел «Решение треугольников SSS».
Советы по решению
Вот простой совет:
Когда треугольник имеет прямой угол, использовать его, как правило, намного проще.
Когда известны два угла, рассчитайте третий, используя Углы треугольника, сложенные до 180 °.
Попробуйте закон синусов перед законом косинусов, так как его проще использовать.
косинусов
Затем рассмотрим углы 30 ° и 60 °.В прямоугольном треугольнике 30 ° -60 ° -90 ° отношения сторон равны 1: √3: 2. Отсюда следует, что sin 30 ° = cos 60 ° = 1/2, и sin 60 ° = cos 30 ° = √3 / 2.
Эти результаты занесены в эту таблицу.
| Угол | Градусы | Радианы | Косинус | синус |
|---|---|---|---|---|
| 90 ° | π /2 | 0 | ||
| 900π /3 | 1/2 | √3 / 2 | ||
| 45 ° | π /4 | √2 / 2 | √2 / 2 | |
| 30 ° | π /6 | √3 / 2 | 1/2 | |
| 0 ° | 0 | 1 | 0 |
Упражнения
Все эти упражнения относятся к прямоугольным треугольникам со стандартной маркировкой.30. b = 2,25 метра и cos A = 0,15. Найдите a и c.
33. b = 12 футов и cos B = 1/3. Найдите c и a.
35. b = 6,4, c = 7,8. Найдите A и a.
36. A = 23 ° 15 ‘, c = 12.15. Найдите a и b.
Подсказки
30. Косинус A связывает b с гипотенузой c, , поэтому вы можете сначала вычислить c. Если вы знаете b и c, , вы можете найти a по теореме Пифагора.
33. Вы знаете b и cos B. К сожалению, cos B — это отношение двух сторон, которых вы не знаете, а именно a / c. Тем не менее, это дает вам уравнение, с которым можно работать: 1/3 = a / c. Тогда c = 3 a. Тогда из теоремы Пифагора следует, что a 2 + 144 = 9 a 2 . Вы можете решить это последнее уравнение для a , а затем найти c.
35. b и c дают A по косинусам и a по теореме Пифагора.
36. A и c дают a по синусам и b по косинусам.
ответы
30. c = b / cos A = 2,25 / 0,15 = 15 метров; a = 14,83 метра.
33. 8 a 2 = 144, поэтому a 2 = 18. Следовательно, a равно 4,24 ‘или 4’3 «.
c = 3 a , что равно 12.73 ‘или 12’9 «.
35. cos A = b / c = 6,4 / 7,8 = 0,82. Следовательно, A = 34,86 ° = 34 ° 52 ‘, или около 35 °.
a 2 = 7,8 2 — 6,4 2 = 19,9, поэтому a составляет около 4,5.
36. a = c sin A = 12,15 sin 23 ° 15 ‘= 4,796.
b = c cos A = 12,15 cos 23 ° 15 ‘= 11.17.
Косинус
Косинус, записываемый как cos (θ), является одной из шести основных тригонометрических функций.
Определения косинусов
Существует два основных способа обсуждения тригонометрических функций: в терминах прямоугольных треугольников и в терминах единичной окружности. Чаще всего вводят определение тригонометрических функций в виде прямоугольного треугольника, за которым следуют их определения в терминах единичной окружности.
Определение прямоугольного треугольника
Для прямоугольного треугольника с острым углом θ значение синуса этого угла определяется как отношение длины соседней стороны к длине гипотенузы.
Стороны прямоугольного треугольника обозначаются следующим образом:
- Соседний: сторона рядом с θ, которая не является гипотенузой
- Справа: сторона, противоположная θ.
- Гипотенуза: самая длинная сторона треугольника напротив прямого угла.
Пример:
Найдите cos (θ) для прямоугольного треугольника ниже.
Мы также можем использовать функцию косинуса при решении реальных задач, связанных с прямоугольными треугольниками.
Пример:
Самолет пролетает над человеком. Человек регистрирует угол возвышения 25 °, когда расстояние по прямой (гипотенуза треугольника) между человеком и самолетом составляет 14 миль. Какое расстояние по горизонтали между самолетом и человеком?
Учитывая информацию выше, мы можем сформировать прямоугольный треугольник, в котором x — это расстояние по горизонтали между человеком и плоскостью, расстояние по прямой между человеком и плоскостью — это гипотенуза, а расстояние по вертикали между конечными концами x, а гипотенуза образует прямой угол треугольника.Затем мы можем найти горизонтальное расстояние x, используя функцию косинуса:
x = 14 × cos (25 °) ≈ 12,69
Горизонтальное расстояние между человеком и самолетом составляет около 12,69 миль.
Определение единичной окружности
Тригонометрические функции также могут быть определены как значения координат на единичной окружности. Единичный круг — это круг радиуса 1 с центром в начале координат. Определение тригонометрических функций в прямоугольном треугольнике допускает углы от 0 ° до 90 ° (0 и в радианах).Использование определений единичного круга позволяет нам расширить область определения тригонометрических функций на все действительные числа. См. Рисунок ниже.
Учитывая точку (x, y) на окружности единичной окружности, мы можем сформировать прямоугольный треугольник, как показано на рисунке. В таком треугольнике гипотенуза — это радиус единичного круга, или 1. θ — это угол, образованный между начальной стороной угла вдоль оси x и конечной стороной угла, образованной вращением луча по часовой стрелке или против часовой стрелки.Конечная сторона угла — это гипотенуза прямоугольного треугольника и радиус единичной окружности. Следовательно, он всегда имеет длину 1. Таким образом, мы можем использовать определение косинуса из прямоугольного треугольника, чтобы определить, что
означает, что значение x любой точки на окружности единичной окружности равно cos (θ).
В отличие от определений тригонометрических функций, основанных на прямоугольных треугольниках, это определение работает для любого угла, а не только для острых углов прямоугольных треугольников, если он находится в пределах области cos (θ).Область определения функции косинуса — (-∞, ∞), а диапазон функции косинуса — [-1, 1].
Значения функции косинуса
Существует множество методов, которые можно использовать для определения значения косинуса, например, обращение к таблице косинусов, использование калькулятора и аппроксимация с использованием ряда косинусов Тейлора. В большинстве практических случаев нет необходимости вычислять значение косинуса вручную, и вам будет предоставлена таблица, калькулятор или другие справочные материалы.
Калькулятор косинусов
Ниже приведен калькулятор, позволяющий определить значение косинуса угла или угол по значению косинуса.
Часто используемые уголки
Хотя мы можем найти cos (θ) для любого угла, есть некоторые углы, которые чаще используются в тригонометрии. Ниже приведены 16 часто используемых углов как в радианах, так и в градусах, а также координаты их соответствующих точек на единичной окружности.
Приведенный выше рисунок служит справочным материалом для быстрого определения косинусов (значение x) и синусов (значение y) углов, которые обычно используются в тригонометрии. Как видно из рисунка, косинус имеет значение 0 при 90 ° и значение 1 при 0 °.Синус следует противоположному шаблону; это потому, что синус и косинус являются совместными функциями (описанными позже). Другие часто используемые углы — 30 ° (), 45 ° (), 60 ° () и их соответствующие кратные. Значения косинуса и синуса этих углов стоит запомнить в контексте тригонометрии, поскольку они очень часто используются.
Один из методов, который может помочь запомнить эти значения, — это выразить все значения cos (θ) в виде дробей, содержащих квадратный корень. Начиная с 0 ° и до 90 °, cos (0 °) = 1 =.Последующие значения cos (30 °), cos (45 °), cos (60 °) и cos (90 °) следуют шаблону, так что, используя значение cos (0 °) в качестве эталона, найти значений косинуса для последующих углов, мы просто уменьшаем число под знаком корня в числителе на 1, как показано ниже:
С 90 ° до 180 ° вместо этого мы увеличиваем число под корнем на 1, но также должны учитывать квадрант, в котором находится угол. Косинус отрицателен в квадрантах II и III, поэтому значения будут равными, но отрицательными. .В квадрантах I и IV значения будут положительными. Этот шаблон периодически повторяется для соответствующих угловых измерений. Аналогичный метод запоминания можно использовать и для синуса. При необходимости обратитесь к странице синуса.
Знание значений косинуса и синуса для углов в первом квадранте позволяет нам определить их значения для соответствующих углов в остальных квадрантах в координатной плоскости с помощью опорных углов.
Базовые углы
Базовый угол — это острый угол (<90 °), который можно использовать для обозначения угла любой меры.Любой угол в координатной плоскости имеет опорный угол от 0 ° до 90 °. Это всегда наименьший угол (относительно оси x), который может быть получен с конечной стороны угла. На рисунке ниже показан угол θ и его опорный угол θ '.
Поскольку θ ‘является опорным углом θ, cos (θ) и cos (θ’) имеют одинаковое значение. Например, 30 ° — это опорный угол 150 °, и если мы обратимся к единичному кругу, мы увидим, что косинусы обоих имеют величину, хотя и имеют разные знаки.Поскольку все углы имеют опорный угол, нам действительно нужно знать только значения cos (θ) (а также значения других тригонометрических функций) в квадранте I. Все другие соответствующие углы будут иметь значения той же величины, и мы просто нужно обратить внимание на их знаки, основанные на квадранте, в котором находится конечная сторона угла. Ниже приведена таблица, показывающая знаки косинуса, синуса и тангенса в каждом квадранте.
| Косинус | Синус | Касательная | ||
| Квадрант I | + | + | + | |
| Квадрант II | — | + | — | |
| Квадрант III | — | — | + | |
| Квадрант IV | + | — | — |
После определения опорного угла мы можем определить значение тригонометрических функций в любом из других квадрантов, применив соответствующий знак их значения для опорного угла.Следующие шаги можно использовать, чтобы найти опорный угол заданного угла, θ:
- Вычтите 360 ° или 2π из угла столько раз, сколько необходимо (угол должен быть от 0 ° до 360 ° или от 0 до 2π). Если полученный угол составляет от 0 ° до 90 °, это опорный угол.
- Определите, в каком квадранте лежит конечная сторона угла (начальная сторона угла расположена вдоль положительной оси x)
- В зависимости от того, в каком квадранте находится конечная сторона угла, используйте уравнения в таблице ниже, чтобы найти опорный угол.В квадранте I θ ‘= θ.
| Квадрант II | Квадрант III | Квадрант IV |
|---|---|---|
| θ ‘= 180 ° — θ | θ ‘= θ — 180 ° | θ ‘= 360 ° — θ |
Пример:
Найдите cos (120 °).
- θ уже находится между 0 ° и 360 °
- 120 ° лежит во II квадранте
- 180 ° — 120 ° = 60 °, поэтому исходный угол составляет 60 °
.120 ° находится в квадранте II, а косинус отрицателен во втором квадранте, поэтому:
Пример:
Найдите cos (1050 °).
- 1050 ° — 360 ° = 690 ° — 360 ° = 330 °
- 330 ° лежит в квадранте IV
- 360 ° — 330 ° = 30 °, поэтому исходный угол равен 30 °
. 330 ° находится в квадранте IV, а косинус положительный в квадранте IV, поэтому:
Свойства функции косинуса
Ниже приводится ряд свойств функции косинуса, которые может быть полезно знать при работе с тригонометрическими функциями.
Косинус является совместной функцией синуса
Кофункция — это функция, в которой f (A) = g (B) при условии, что A и B являются дополнительными углами. В контексте косинуса и синуса
cos (θ) = sin (90 ° — θ)
sin (θ) = cos (90 ° — θ)
Пример:
cos (30 °) = sin (90 ° — 30 °) = sin (60 °)
Ссылаясь на единичный круг, показанный выше, мы можем подставить значения для cos (30 °) и sin (60 °) и увидеть, что:
Косинус — четная функция
Четная функция — это функция, в которой f (x) = f (-x), что означает, что отражение графика по оси Y даст тот же график.Таким образом,
cos (θ) = cos (-θ)
Пример:
cos (60 °) = cos (-60 °)
cos (60 °) = cos (300 °)
Обращаясь к единичной окружности, мы видим, что cos (60 °) = и cos (-60 °) эквивалентен cos (300 °), который также равен. Это только один пример, но это свойство верно для всех θ.
Косинус — периодическая функция
Периодическая функция — это функция f, в которой существует некоторое положительное значение p, такое что
е (х + р) = е (х)
для всех x в области f, p — наименьшее положительное число, для которого f является периодическим, и называется периодом f.
Тригонометрические функции обычно используются для моделирования периодических явлений из-за их периодичности; независимо от того, с какой точки мы начинаем на единичной окружности, если мы пройдем расстояние 2π (360 °) по единичной окружности от этой точки, мы вернемся к нашей начальной точке. Если мы посмотрим на функцию косинуса, мы обнаружим, что она повторяется каждые 2π, поэтому 2π — это период функции косинуса. Мы можем записать это как:
cos (θ + 2π) = cos (θ)
Для учета нескольких полных оборотов это также можно записать как
cos (θ + 2πn) = cos (θ)
, где n — целое число.
На рисунке ниже показан пример этой периодичности.
Синим цветом мы это видим. . Если мы прибавим 2π к, мы получим угол, показанный красным,. Как видно из рисунка, несмотря на разную степень поворота в обоих углах, их конечные стороны совершенно одинаковы, что означает, что. Мы могли бы добавить еще 2π и все равно увидеть, что оно имеет то же значение косинуса, что и. Такова природа периодических функций. называются концевыми углами; это углы с одинаковой начальной и конечной сторонами, но с разными поворотами.
Примеры:
1.
2.
График функции косинуса
График косинуса является периодическим, что означает, что он повторяется бесконечно и имеет область значений -∞ Если бесконечно повторять эту часть y = cos (x) слева и справа, то получится полный график косинуса.Ниже приведен график, показывающий четыре периода функции косинуса в интервале [-4π, 4π]. На этом графике мы видим, что y = cos (x) демонстрирует симметрию оси y; отражение графика косинуса по оси y дает тот же график. Это подтверждает, что косинус является четной функцией, поскольку cos (x) = cos (-x). Общий вид функции косинуса y = A · cos (B (x — C)) + D где A, B, C и D — константы.Чтобы иметь возможность изобразить уравнение косинуса в общем виде, нам нужно сначала понять, как каждая из констант влияет на исходный график y = cos (x), как показано выше. Чтобы применить все, что написано ниже, уравнение должно иметь форму, указанную выше; будьте осторожны со знаками. A — амплитуда функции; высота от центра графика до максимума или минимума. В y = cos (x) центром является ось x, а амплитуда равна 1, или A = 1, поэтому самая высокая и самая низкая точки, которых достигает график, равны 1 и -1, диапазон cos (x) . По сравнению с y = cos (x), показанным ниже фиолетовым цветом, функция y = 2 cos (x) (красный) имеет амплитуду, которая в два раза больше, чем у исходного графика косинуса. B — используется для определения периода функции; период функции — это расстояние от пика до пика (или любой точки на графике до следующей совпадающей точки) и может быть найден как. В y = cos (x) период равен 2π. Мы можем подтвердить это, посмотрев на пики на графике косинусов. При x = 0 y = cos (x) имеет пик.Первый раз на функции появляется еще один пик при x = & plusmn2π, подтверждая, что период косинуса равен 2π. По сравнению с y = cos (x), показанным ниже фиолетовым цветом, который имеет период 2π, y = cos (2x) (красный) имеет период
. Это означает, что график повторяется каждое π, а не каждые 2π. C — фазовый сдвиг функции; фазовый сдвиг определяет, как функция сдвигается по горизонтали. Если C отрицательно, функция сдвигается влево. Если C положительно, функция сдвигается вправо.Остерегайтесь знака; если у нас есть уравнение, то C нет, потому что это уравнение в стандартной форме есть. Таким образом, мы бы сместили единицы графика влево. На рисунке ниже показаны y = cos (x) (фиолетовый) и (красный). Используя один из пиков графика косинуса в качестве ориентира, мы можем увидеть, что пик в точке (0,1) был смещен влево от своего исходного положения и теперь находится в точке (, 1). D — сдвиг функции по вертикали; если D положительно, график сдвигается вверх на D единиц, а если он отрицателен, график сдвигается вниз. По сравнению с y = cos (x), показанным ниже фиолетовым цветом, с центром на оси x (y = 0), y = cos (x) +5 (красный) с центром на линии y = 5 (синий). Объединив все приведенные выше примеры, на рисунке ниже показан график (красный) по сравнению с графиком y = cos (x) (фиолетовый). См. Также синус, тангенс, единичную окружность, тригонометрические функции, тригонометрию. В математике функция косинуса (cos) — это функция, которая связывает внутренний угол треугольника с длиной его сторон.Функция косинуса, а также функция синуса и тангенса являются тремя основными тригонометрическими функциями. В прямоугольном треугольнике косинус угла равен отношению стороны, прилегающей к углу, к длине гипотенузы прямоугольного треугольника. Математически это: cos (A) = смежный / гипотенуза Функция косинуса принимает угловые измерения в качестве входных данных и возвращает отношение в качестве выходных данных. Когда угол A = 0 °, функция косинуса принимает значение: cos (0) = 1 Косинус угла нулевого градуса равен 1.Чтобы понять, почему, рассмотрим, что происходит с прямоугольным треугольником, когда один из его углов стремится к 0. По мере приближения угла к 0 противоположная сторона становится все меньше и меньше. По мере уменьшения этого угла длины гипотенузы и стороны, прилегающей к углу, становятся все ближе и ближе. Как только значение угла достигнет 0, гипотенуза и прилегающая сторона будут идеально лежать друг на друге, попадая в соотношение 1: 1. Таким образом, косинус 0 равен 1. Три триггерные функции представляют собой общее соответствие между внутренними углами треугольника и длинами его сторон.Тот факт, что существует повторяющееся соотношение между сторонами и углами прямоугольного треугольника, является следствием того факта, что подобные треугольники поддерживают соотношение между своими сторонами. Прямоугольный треугольник 3-4-5 имеет те же пропорции, что и треугольник 6-8-10; последнее является целым кратным первому. Таким образом, любые соотношения между длинами сторон двух треугольников будут точно такими же. Рассмотрим простой прямоугольный треугольник: Начиная с некоторого угла A, стороны треугольника обозначаются следующим образом: Гипотенуза — это сторона, противоположная прямому углу.Гипотенуза всегда является самой длинной стороной треугольника. Противоположная сторона — сторона, находящаяся прямо напротив исследуемого угла. Соседняя сторона — это та сторона, которая находится непосредственно рядом с углом, который не является гипотенузой. Следуя этим обозначениям, мы можем определить три основные триггерные функции следующим образом: sin (A) = противоположный / гипотенуза cos (A) = смежный / гипотенуза tan (A) = противоположный / смежный Поскольку одинаковые треугольники имеют одинаковые пропорции, значения этих функций не зависят от размера прямоугольного треугольника, а зависит только от угла оценки (A).Хорошей мнемоникой для запоминания определений триггерных функций является аббревиатура SOH-CAH-TOA (произносится «со-ка-тоа») Давайте добавим несколько цифр к этим абстрактным формулам. Скажем, у нас есть прямоугольный треугольник со сторонами 3 и 4 и гипотенуза длиной 5: Мы можем вычислить значения триггерных функций относительно угла A следующим образом: sin (A) = противоположное. / гипотенуза = 4/5 = 0,8 cos (A) = смежный / гипотенуза = 3/5 = 0,6 tan (A) = противоположный / смежный = 4/3 = 1.3 Обратите внимание, что функции синуса и косинуса эквивалентны с учетом разных углов. Установив угол B в качестве интересующего нас угла, мы можем вычислить триггерные функции следующим образом: sin (B) = 3/5 = cos (A) = 0,6 cos (B) = 4/5 = sin (A) = 0,8 Это приводит нас к общему правилу, что для любого прямоугольного треугольника, где углы A и B не являются прямым углом: sin (A) = cos (B) и sin (B) = cos (A) В дополнение к 3 основным функциям триггера есть 3 взаимные триггерные функции.Обратные функции являются обратными базисным функциям и называются секансом, косекансом и котангенсом. Их можно определить как: сек (A) = 1 / sin (A) = гипотенуза / противоположная сек (A) = 1 / cos (A) = гипотенуза / смежная котановая (A) = 1 / tan (A) = смежный / противоположный Допустим, вам дано только измерение угла, и вас просят вычислить синус этого угла только по этому значению. К сожалению, для этого не существует простого алгоритма.Вычисление значений sin вручную под заданным углом требует много времени и сложных вычислений. Вместо этого большинство калькуляторов используют справочные таблицы, таблицы со списком измерений углов и соответствующих значений sin. Эти таблицы были рассчитаны с высочайшей точностью. Однако есть интересный способ концептуализации угловых измерений, который делает вычисление некоторых значений триггерных функций интуитивно понятным и простым. Внутреннюю работу триггерных функций можно понять по структуре единичной окружности на координатной плоскости.Единичный круг — это круг радиуса один, центр которого находится в начале координатной плоскости (0,0). Перетаскивание радиуса вокруг исходной точки приведет к появлению круга, длина окружности которого составляет ровно 2π единицы. По теореме Пифагора этот круг представляет собой набор всех точек (x, y), таких что x 2 + y 2 = 1 Углы могут быть измерены в терминах длины дуги на окружности, которую угол выводит наружу. Эти единицы называются радианами. Поскольку окружность единичной окружности равна точно 2π, угловая мера 2π в радианах соответствует 360 °.Аналогично, π / 2 радиан соответствует 90 °, π радиан — 180 °, π / 3 радиан — 60 ° и так далее. Любая точка на единичной окружности может быть представлена как конечная точка линии, идущей от центральной точки под углом θ с центром в начале координат. Значения x и y этой точки соответствуют сторонам прямоугольного треугольника. Это понимание приводит к некоторым интересным свойствам триггерных функций.Поскольку по определению единичный круг имеет радиус 1, sin (θ) = y и cos (θ) = x. Согласно теореме Пифагора и определению единичной окружности, верно, что cos 2 (θ) + sin 2 (θ) = 1. Что произойдет с прямоугольным треугольником, если мы изменим угол луча от происхождения? Изменение угла, на который линия простирается от начала координат, приводит к соответствующему изменению других сторон треугольника. Чем меньше угол, тем меньше и сторона, противоположная углу.а соседняя сторона становится больше. По мере увеличения угла противоположная сторона становится больше, а соседняя — меньше. Таким образом, когда мы меняем угол, мы можем визуализировать, как изменяется соотношение сторон треугольника. Сразу обратите внимание на несколько вещей. Что происходит, когда угол равен 0? Какое соотношение сторон друг к другу? По мере приближения угла к 0 синус угла (противоположный / гипотенуза) становится все меньше и меньше.Когда угол достигает 0, длина противоположной стороны достигает 0, поэтому полное отношение между противоположной стороной и гипотенузой равно 0. Итак, мы знаем, что sin (0) = 0. А что насчет того, когда мы сделаем угол больше? По мере увеличения угла противоположная сторона увеличивается в длине, пока мы не дойдем до π / 2 рад (90 °), после чего противоположная сторона и гипотенуза станут равной длины. Если стороны равны по длине, то их отношение равно 1, поэтому мы знаем, что sin (π / 2) = 1. Рассмотрим функцию косинуса.Что происходит со значением косинуса при уменьшении угла? По мере приближения к 0 отношение между соседней стороной и гипотенузой увеличивается, пока смежная сторона и гипотенуза не станут равными, когда угол равен 0. Итак, мы знаем, что cos (0) = 1. Аналогичным образом, когда угол приближается π / 2, соседняя сторона становится все меньше и меньше относительно гипотенузы, пока не станет равной 0; таким образом, cos (π / 2) = 0 А как насчет касательной функции? Когда угол равен 0, отношение противоположной стороны к соседней стороне также равно 0, поэтому мы можем определить, что tan (0) = 0. По мере увеличения угла противоположная сторона становится больше, а соседняя — меньше, пока не достигнет точки, в которой две стороны имеют одинаковую длину. Прямоугольный треугольник может иметь только две стороны равной длины, если оба непрямых угла составляют углы 45 °. Это означает, что под углом 45 ° длины двух сторон равны, и поэтому их отношение равно 1. 45 ° равно π / 4 рад, поэтому мы знаем, что tan (π / 4) = 1 А как насчет значения tan (π / 2)? Обратите внимание, что по мере того, как угол увеличивается и приближается к π / 2 рад, противоположная сторона становится больше, а соседняя сторона сжимается до 0.Это означает, что tan (π / 2) равен выражению 1/0. Деление на 0 не определено, поэтому функция tan (π / 2) не определена и не имеет допустимого значения. Осмысление угловых измерений в радианах единичной окружности также объясняет еще одно интересное свойство триггерной функции; их периодичность. Значения триггерных функций колеблются между фиксированными выходами от входов от 0 до 2π, потому что угловые измерения, превышающие 2π, могут быть представлены как кратные 2π. Графический вывод функций sin и косинуса дает красивый волнообразный узор: Пики и впадины приведенных выше графиков представляют выходные значения 1 и -1 соответственно. Интересно отметить, что функции синуса и косинуса идентичны по форме, но функция косинуса смещена от функции синуса на половину длины волны. Периодичность триггерной функции (в частности, синуса и косинуса) делает их полезными в науке для моделирования периодических явлений, таких как механические или электромагнитные волны. Была ли эта статья полезной? Чтобы лучше понять некоторые проблемы, связанные с самолетами
и двигательная установка
необходимо использовать некоторые математические идеи из
тригонометрия,
изучение треугольников.
Начнем с некоторых определений и терминологии.
который мы будем использовать на этом слайде.
Прямоугольный треугольник — это
трехсторонняя фигура с одним углом, равным 90 градусам. Угол 90 градусов
называется прямым углом , что дало название прямоугольному треугольнику.Выбираем один из двух оставшихся углов и маркируем его c а третий угол обозначим d .
Сумма углов любого треугольника равна 180 градусам.
Если мы знаем значение c ,
тогда мы знаем, что значение d : 90 + с + г = 180 г = 180 — 90 — в d = 90 — c Определим сторону треугольника противоположную от прямого угла к
гипотенуза .Это самая длинная из трех сторон.
прямоугольного треугольника. Слово «гипотенуза» происходит от двух греческих слов.
означает «растягивать», так как это самая длинная сторона. Обозначим гипотенузу символом h .
Есть сторона, противоположная углу c , которую мы обозначаем как o .
для «противоположного». Оставшуюся сторону мы маркируем как для «смежных».
Угол c образован пересечением гипотенузы h и соседняя сторона а . Нас интересует соотношение сторон и углов
прямоугольный треугольник.
Начнем с некоторых определений.
Мы будем называть
соотношение
стороны прямоугольного треугольника, противоположной гипотенузе
синус и присвоить ему символ sin . грех = о / ч Отношение смежной стороны прямоугольного треугольника к гипотенузе называется
косинус и обозначен символом cos . cos = а / ч Наконец, отношение противоположной стороны к соседней стороне называется
касательная и обозначена символом tan . загар = о / а Мы утверждаем, что значение каждого коэффициента зависит только от значения
угол c , образованный смежной и гипотенузой.
Чтобы продемонстрировать этот факт,
давайте изучим три фигуры в середине страницы.В этом примере у нас есть
8-футовая лестница, которую мы собираемся прислонить к стене. Стена
8 футов высотой, и мы нарисовали белые линии на стене
и синие линии на земле с интервалом в один фут.
Длина лестницы фиксированная.
Если наклонить лестницу так, чтобы ее основание находилось на расстоянии 2 фута от стены,
лестница образует угол около 75,5 градусов с землей.
Лестница, земля и стена образуют прямоугольный треугольник. Соотношение расстояния от
стены (а — прилегающая) к длине лестницы (h — гипотенуза) составляет 2/8 =.25.
Это определено как косинус c = 75,5 градусов. (На
другая страница
покажем, что если бы лестница была вдвое длиннее (16 футов),
и наклонена под тем же углом (75,5 градусов), чтобы он сидел вдвое
далеко (4 фута) от стены. Соотношение остается неизменным для любого прямоугольного треугольника.
под углом 75,5 градусов.)
Если мы измеряем точку на стене, где лестница касается (о — напротив), расстояние будет
7,745 футов. Вы можете проверить это расстояние, используя
Теорема Пифагора
который связывает стороны прямоугольного треугольника: ч ^ 2 = а ^ 2 + о ^ 2 о ^ 2 = ч ^ 2 — а ^ 2 о ^ 2 = 8 ^ 2 — 2 ^ 2 о ^ 2 = 64 — 4 = 60 о = 7.745 Отношение противоположности к гипотенузе равно 0,967 и определяется как
синус угла c = 75,5 градусов. Теперь предположим, что мы наклоняем 8-футовую лестницу так, чтобы ее основание находилось на 4 футах от стены.
Как показано на рисунке, теперь лестница наклонена под меньшим углом, чем в
первый пример. Угол составляет 60 градусов, а соотношение прилегающих к
гипотенуза теперь 4/8 = 0,5. Уменьшение угла c увеличивает косинус угла, потому что гипотенуза фиксирована
а соседний увеличивается с уменьшением угла.Если мы наклоним 8 футов
лестнице так, чтобы ее основание находилось на расстоянии 6 футов от стены, угол уменьшается до
около 41,4 градуса, и соотношение увеличивается до 6/8, что составляет 0,75.
Как видите, для каждого угла
на земле есть уникальная точка, которой соприкасается 8-футовая лестница,
И это одна и та же точка каждый раз, когда мы устанавливаем лестницу под этим углом.
Математики называют эту ситуацию
функция.
Соотношение соседних
сторона гипотенузы является функцией угла c , поэтому мы можем записать
символ как cos (c) = значение . Также обратите внимание, что по мере увеличения cos (c) уменьшается sin (c) .
Если мы наклоним лестницу так, чтобы основание находилось на расстоянии 6,938 фута от стены,
угол c становится 30 градусов, а отношение соседних к
гипотенуза 0,866.
Сравнивая этот результат со вторым примером, мы обнаруживаем, что: cos (c = 60 градусов) = sin (c = 30 градусов) sin (c = 60 градусов) = cos (c = 30 градусов) Мы можем обобщить это соотношение: sin (c) = cos (90 — c) 90 — c — величина угла d .Вот почему мы
назовем соотношение смежного и гипотенузы «косинусом» угла. sin (c) = cos (d) Поскольку синус, косинус и тангенс являются функциями угла c , мы можем
определить (измерить) коэффициенты один раз и составить таблицы значений
синус, косинус и тангенс для различных значений c . Позже, если мы узнаем
значение угла в прямоугольном треугольнике, таблицы покажут нам соотношение
сторон треугольника.Если нам известна длина одной стороны, мы можем найти длину другой.
стороны.
Или, если мы знаем соотношение любых двух сторон прямоугольного треугольника, мы можем
найти значение угла между сторонами. Мы можем использовать таблицы для решения проблем. Некоторые примеры проблем, связанных с треугольниками и углами, включают
силы
на самолете в полете,
применение
крутящие моменты,
и разрешение
компоненты
вектора. Вот таблицы синуса, косинуса и тангенса, которые вы можете использовать для решения
проблемы. Навигация .. Фильтр категорий: Показать все (165) Наиболее распространенные (1) Технологии (33) Правительство и военные (39) Наука и медицина (31) Бизнес (29) Организации (45) Сленг / жаргон (18) Уравнение общего косинуса
Чему равен cos (0)?
Кредит: WikiCommons CC0 1.0 Основы триггерных функций
Числовые значения триггерных функций
Триггерные функции и единичная окружность
Синус-косинус-касательная
Действия:
Экскурсии с гидом
. Что означает COS? Бесплатный словарь
Акроним Определение COS Стоимость продаж COS Класс обслуживания COS Коллекция стиля (линия моды) COS Colorado Springs (код станции Amtrak; Колорадо-Спрингс, Колорадо) COS Начальник штаба COS Тайная комната (книга Дж.К. Роулинг) COS Коммерческая готовая продукция COS Косинус (математика) COS Условия успеха COS Условия удовлетворения COS Церковь Саентологии COS Совет студентов (различные организации) COS Консул (в Древнем Риме) COS Колледж безопасности (Star Trek gaming) COS Children of Sin (песня) COS Конвенция государств (Хьюстон, Техас) COS Общество благотворительных организаций COS Cosinus COS Cosme tology COS Изменение статуса COS Comite des Oeuvres Sociales (французский: Комитет социальных работ) COS Chance of Success (Oil and Gas) COS College of the Siskiyous (Калифорния) COS Chicks on Speed (band) COS Смена штата COS Свидетельство о спонсорстве (Великобритания) COS Комитет по устойчивому развитию (различные местоположения) COS Контроллер магазинов (индийские железные дороги) COS Сертификат статуса (различные местоположений) COS Город Саскатун (Канада) COS Circle of Swords (игровая гильдия) COS Collège Ostéopathique Sutherland (Французский остеопатический колледж) COS COSENING Изменение предмета Операционная площадка (Ирак) COS Carnival of Space (ведение блога) COS Coefficient d’Occupation des Sols (французский: коэффициент землепользования) COS Условия обслуживания COS Постоянная безопасность эксплуатации (авиация) COS Церковь Сатаны COS Служба кредитного омбудсмена (разрешение споров; Австралия) COS Набор объектов конфигурации COS Криптографическая операционная система COS Система связи COS Службы общих операций COS Клип на Socket COS Коммерческая операционная система COS Операционная система кассеты COS Система управления COS Cosine COS Corporation of Open Systems COS Пользовательская операционная система COS Corba Object Services COS Common Object Services COS Центральные офисы COS Церковь Шотландии 9 0077 COS Служба охраны (Канада) COS Спектрограф Cosmic Origins COS Стоимость обслуживания COS Сотрудничество для открытых систем (Интернет) COS Centre d’Orientation Scolaire (французский: Консультационный центр школы) COS Commandement des Opérations Spéciales (французский: Командование специальных операций) COS of Silence (игровой клан) COS Сертификат обслуживания COS Carbonyl Sulphide COS Cone of Silence (Get Smart; Сериал 1960-х) COS Код молчания COS Канадское офтальмологическое общество COS Центр поддержки операций COS Корпорация открытых систем COS Сертификат соответствия (Европейский директорат по качеству лекарственных средств; Совет Европы; Франция) COS Непрерывность обслуживания COS Смена станции COS Операционная система карты COS Служба поддержки корпуса COS Начальник участка (CIA) COS Обязательное открытое пространство (строительные нормы; различные места) COS Чип Операционная система tem COS Совместимая операционная система COS Операционная система консоли (НАСА) COS Chimie Organique de Synthèse (французский: Synthetic Organic Chemistry) COS Закрытие службы (Корпус мира) COS Начальник Генерального штаба (Израиль) COS Общая операционная система COS Центр окинавских исследований (Гавайский университет в Маноа) COS Сертифицированный специалист по занятости (жилищное строительство) COS Служба по работе с населением (в разных местах) COS Критическая специальность (Министерство обороны США) COS 9 0077 Чикагское орнитологическое общество (Чикаго, Иллинойс) COS Плащ теней (World of Warcraft, игры) COS Центр исследований Оксфордшира (Великобритания) COS Операционная система Cray COS Club Olympique de Sartrouville (клуб французских боевых искусств) COS Сервер комбинаторных объектов COS Colectivo de Organizaciones (испанский) , Гватемала) COS Операционная система клиента COS Система возможностей карьерного роста COS Услуга, ориентированная на подключение COS Категории услуг (Medicaid) COS Непрерывность питания слой COS Culling of Stratholme (World of Warcraft; игры) COS Caress of Steel (альбом Rush) COS Церковь Спасителя COS Сегмент связи COS Contrat d’Objectifs Scolaires (французский: контракт на образовательные цели) COS Columbia Online Style COS Chip on Submount COS China Oilfield Services Ltd. На ремне (производство батарей) COS Шумоподавитель с оператором связи (двусторонняя радиосвязь) COS Центральная операционная система (X-Files) COS Служба общих объектов COS Служба CORBA 9007 6 COS Переключатель переключения COS Эскадрилья боевых действий COS City of Sails (Парикмахерская, Окленд, Новая Зеландия) COS Начальник службы безопасности COS Общество консервативных возможностей COS Начальник отдела снабжения COS Онлайн-сервисы для клиентов (различные предприятия) COS Cadet Officer School Cadet Officer School Когезивный конечный участок (бактериофаги) COS Наличными при отгрузке COS Канадское онкологическое общество COS Комитет по техническим условиям (AISI)7 COS 900 Коронарный обструктивный синдром COS Полная ортонормальная система COS Клиент размера (пассажир с избыточным весом, требующий два места в авиалинии экономического класса) COS Колорадо-Спрингс, Колорадо, США — муниципальный район Колорадо-Спрингс (аэропорт Код) COS Переключатель с кодовым управлением COS Поддержка капитальных затрат COS Давай, весна COS Сержант по порядку компании COS Cult of Slaanesh (игры, Warhammer) COS Corona Oxide Semiconductor COS Проверить на месте COS Начальники службы (больницы) 74 Служба поддержки кампуса (г.Дэвидс, Пенсильвания) COS Камерный оркестр Спрингс (Колорадо-Спрингс, Колорадо) COS Состояние поставки (аэрокосмическая промышленность) COS Переключатель выхода ячейки COS Канадский стандарт органического происхождения COS Переносная кислородная система (НАСА) COS Отдел текущих операций COS Коалиция по видам орхидей COS Caked on Stripes (подкаст) COS Гражданская профессиональная специальность COS Система заказа клиентов COS Casualty of Sound (Музыкальный компакт-диск Maniacal Plan) COS Статус вызова COS Компьютер на кремнии COS Спутник на совместной орбите (НАСА) COS Конвергентная операционная система (Mariposa Technology) COS Специалист по химическим операциям COS Chosen of Solclaim (игровой клан) COS Критические операционные особенности COS Citizens for Open Space (различные локации) 900OS Специалист по оказанию помощи (социальная работа) COS Смена абонента COS Конференц-услуги и офисные услуги COS Центр хирургии ожирения COS Надзор за компонентами COS Служба удаления CO2 COS Клиентский операционный сервер COS Собственные запасы клиента (FedEx Kinko’s) COS Общественные и организационные услуги